Introduction

In eHealth services, web-delivered trials or interventions are in increasing demand due to their cost-effective potential in accessing a large population [1]. These trials commonly generate big, complex, heterogenous and high-dimensional longitudinal data with missing values. These data have the typical five “V” properties of big data [2]. Specifically, the Volume of such data is substantially large in terms of the number of participants and attributes, with which traditional clinical trials are incomparable; its Variety refers to different web-delivered components; its Velocity is undoubtly superior to traditional offline trials, because the data are recorded real-time; its Veracity is obvious because of its unstructured nature and messiness; and its Value would be substantial as long as its efficacy is clarified.

Our line of research focuses on multiple imputation based fuzzy clustering (MIfuzzy), as it fits better to longitudinal behavioral trial data than other methods based on our previous studies [3–5]. There is a paucity of literature in validating the clustering results from big longitudinal eHealth trial data with missing values and our line of research [3–6] attempts to fill this gap. Probabilistic clustering (e.g., Gaussian Mixture models [7]) and Hidden Markov Model-based Bayesian clustering [8], Neural networks models [9, 10] (e.g, Kohonen’s Self Organizing Map, SOM), Hierarchical clustering [11], Partition- based clustering (e.g, K-means or Fuzzy C Means) are commonly used for clustering and demonstrated efficiently for specific data structure in other fields. However, these methods have at least one of these following disadvantages and are less appealing to big behavioral trial data which are typically high dimensional, heterogeneous, non-normal, longitudinal with missing values: Assumption of underlying statistical distributions (Gaussian) or prior distributions (Bayesian approach); (slow) convergence to a local maximum or no convergence at all especially for multi-modal distributions and large proportions of missing values with high-dimensional data and many clusters; unclear validation indices or procedures; inability to handle missing values or incorporate information about the shape and size of clusters; computational inefficiency; and their unknown utility in behavioral trial studies. With a pre-specified number of clusters, MI-Fuzzy was demonstrated to perform better than these methods in terms of its clustering accuracy and inconsistency rates using real trial data [3–5].

As aforementioned, missing data are common in longitudinal trial studies [3, 12, 13]. The performance of MI-Fuzzy was evaluated under these three mechanisms: Missing Completely at Random, Missing at Random (MAR) and Missing not at Random (NMAR). The preliminary results indicate that MIfuzzy is invariant to the three mechanisms and accounts for the clustering uncertainty in comparison to non- or single-imputed fuzzy clustering [14].

Built upon our multiple imputation (MI) based fuzzy clustering, MIfuzzy [4, 6, 15], we proposed MI-based validation framework (MIV) and corresponding MIV algorithms for clustering such big longitudinal web-delivered trial data with missing values. Briefly, MIfuzzy is a new trajectory pattern recognition method with a full integration and enhancement of multiple imputation theory for missing data [3, 16–23] and fuzzy logic theories [24–26]. Here, we focus on cluster validation and extend traditional validation of complete data to MI-based validation of incomplete big longitudinal data, especially for fuzzy-logic based clustering [27–29]. Unlike simple imputation such as mean, regression, and hot deck that cause bias and lose statistical precision, multiple-imputation accounts for imputation uncertainty [30–32].

To build the MIV, we will consider two clustering stability testing methods, cross-validation and bootstrapping; to adapt to fuzzy clustering, we will use Xie and Beni (XB), a widely-accepted fuzzy clustering validation index [33–35], and another newly emerging index, modularity [36, 37]. All four validation methods will be integrated with MI to demonstrate our proposed MIV framework.

Clustering stability has been used in recent years to help select the number of clusters [38–40]. It measures the robustness against the randomness of clustering results. The core idea is based on the intuition that a good clustering will produce a stable result that does not vary from one sample to another. The clustering stability method can be used in both distance based and non-distance based clustering methods, such as model based clustering [41–43] and spectrum clustering [44–46]. Bootstrap and cross-validation are two common clustering stability testing methods. Bootstrap is a statistical technique to assign measures of accuracy, such as bias, variance and confidence intervals, to sample estimates [47–49]. Bootstrap is used when the sampling size is small or impossible to draw repeated samples from the population of interest. In such cases, bootstrap can be used to approximate the sampling distribution of a statistic [50–52]. Cross-validation can be used in clustering algorithms to estimate its predictive strength [53–56]. In cross-validation, the data is split to two or more partitions. Some partitions are used for training the model parameters, and the others, namely the validation (testing) set, are used to measure the performance of the model.

Two types of cross-validation can be distinguished, exhaustive and non-exhaustive: The first one includes leave-p-out and leave-one-out cross-valuation; the latter does not compute all ways of splitting the original data. The non-exhaustive cross-validation contains k-fold cross-validation, holdout and repeated random sub-sampling validation [57, 58]. The holdout method is the simplest among cross-validation methods, with which the data set is only separated into one training and one testing set. Although computationally efficient, the evaluation may be significantly different depending on how the division of the dataset is made between the training and testing sets. The k-fold cross validation improves and generalizes the holdout method by dividing a dataset into k subsets, where the variance of the resulting estimate is reduced as k is increased. A variant of this method is called repeated random sub-sampling validation, also known as Monte Carlo cross-validation to randomly divide the data into a test and training set k different times. Due to randomness, some data may never be selected while others may be selected more than once, resulting in potential overlapped validation subsets. The k-fold cross validation was used in this work to ensure that all data points are used for both training and validation, and each data point is used for validation exactly once. Modularity can measure the structure of networks or graphs [36, 37, 59], and can be used to cluster data by transforming the data points into a graph with their similarities [60]. Thus, modularity can be used to determine the number of clusters in data analyses. Most importantly, for fuzzy clustering, Xie and Beni [33], this widely accepted validation fuzzy clustering index was incorporated into this MI validation framework.

Here, we propose MIV algorithms to auto-search, compare, synthesize and detect the optimal number of clusters for incomplete big longitudinal data based on MI-based clustering stability tests (MI-cross-validation and MI-bootstrapping), MI-XB, and MI-modularity. The rest of the paper is organized as follows: Section “Multiple-im putation-based validation framework (MIV) for incomplete big web trial data in eHealth” presents MIV theoretical framework and algorithms; Section “Numerical analyses and simulation” performs numerical analyses using real and simulated incomplete big longitudinal data and simulation; and Section “Conclusion” concludes the paper. Table 1 lists notations used in this paper.

Table 1 Notations
Full size table

Multiple-imputation-based validation framework (MIV) for incomplete big web trial data in eHealth

Our MI-based validation framework (MIV) is designed to detect the optimal number of clusters from incomplete big longitudinal data in eHealth, using a suite of MI-based methods and indices, such as MI-based clustering stability (MI-S), MI-based XB index (MI-XB) and MI-based Modularity (MI-Q). The procedure of the proposed MIV platform is described in Fig. 1. Briefly, the MIV is an auto- iterative validation procedure where the MI-based index is calculated for a set of cluster numbers on each imputed dataset, incorporating the idea of the multiple imputation theory to minimize the “uncertainty” in selecting the optimal number of clusters for incomplete data sets.

Fig. 1
figure 1

The proposed MIV platform for big web trial data in eHealth

Full size image

MI-based clustering stability for incomplete big web trial data in eHealth

For incomplete big longitudinal web trial data, rather than single imputation, we incorporate Multiple Imputations (MI) to impute missing values to reduce imputation uncertainty [30–32]. In the imputation step, Markov chain Monte Carlo (MCMC) was used to estimate the missing values. The expectation-maximization (EM) algorithm was first applied to find the maximum likelihood estimates of the parameters for the distribution of incomplete big web trial data, then Markov chains were constructed such that the pseudo random samples were drawn from the limiting, or stationary distribution of the data to stabilize to a stationary distribution [17]. Specifically, denote g as different missing patterns, the maximized observed data log likelihood is expressed as,

$$ \log L(\theta |{Y_{obs}}) = {\sum}_{g = 1}^{G} {\log {L_{g}}(\theta |{Y_{obs}})}, $$
(1)

in which

$$\begin{array}{@{}rcl@{}} \log {L_{g}}(\theta |{Y_{obs}}) &=& - \frac{{{n_{g}}}}{2}\log \left| {{\Sigma_{g}}} \right| \\ &&- \frac{1}{2}\sum\limits_{ig} {({y_{ig}} - {\mu_{g}})'{\Sigma_{g}}^{ - 1}({y_{ig}} - {\mu_{g}})},\\ \end{array} $$
(2)

where n g is the number of observations in the g-th group, y i g is a vector of observed values corresponding to observed variables, μ g is the corresponding mean vector, and Σ g is the associated covariance matrix. The EM algorithm was also used to find the posterior mode where the observed data posterior density is used instead of the observed data likelihood as it is guaranteed to be non-decreasing at each iteration. The logarithm of the observed data posterior density is calculated by

$$ \log P(\theta |{Y_{obs}}) = L(\theta |{Y_{obs}}) + \log \pi (\theta ), $$
(3)

in which

$$\begin{array}{@{}rcl@{}} \log \pi (\theta ) &=& - \frac{{m + p + 2}}{2}\log \left| \Sigma \right| - \frac{1}{2}\text{{tr}}{\Sigma^{ - 1}}{M_{0}},\\ {M_{0}} &=& {\Lambda^{ - 1}} + \tau (\mu - {\mu_{0}}){(\mu - {\mu_{0}})^{T}}, \end{array} $$
(4)

where (τ,m,μ 0,Λ) are the parameters for the normal inverted -Wishart prior. When the prior information about the is unknown, we apply the Bayes’ theorem with the prior,

$$ \pi (\theta ) \propto {\left| \Sigma \right|^{ - \left( {\frac{{p + 1}}{2}} \right)}}, $$
(5)

which is the limiting form of the normal inverted-Wishart density as τ→0, m→−1 and Λ−1→0. The prior distribution of μ 0 is assumed to be uniform and μ 0→0. This noninformative prior is also called jeffreys prior in [17].

Next, MCMC was used to impute the missing values by making pseudorandom draws from the probability distributions with parameters obtained by the EM algorithm. Information about known parameters can be expressed in the form of a posterior probability distribution by Bayesian inference,

$$ p(\theta |y) = \frac{{p(y|\theta )p(\theta )}}{{\int {p(y|\theta )p(\theta )d\theta } }}. $$
(6)

The entire joint posterior distribution of the known variables can be simulated and the posterior parameters of interest can be estimated.

Similar to the EM algorithm, the imputation algorithm has two steps, 1) I-step: make pseudorandom draws from the probability distribution for the missing values,

$$ Y_{mis}^{(t + 1)}\sim P({Y_{mis}}|{Y_{obs}},{\theta^{(t)}}), $$
(7)

and 2) P-step: update the parameters,

$$ {\theta^{(t + 1)}}\sim P(\theta |{Y_{obs}},Y_{mis}^{(t + 1)}). $$
(8)

If the parameter is multivariate normal, the I-step involves the independent simulation of random normal vectors for each row in the incomplete big dataset.

Assuming a normal distribution of the incomplete big data and Jeffreys prior, the parameter 𝜃 is updated at the P-step by

$$\begin{array}{@{}rcl@{}} {\Sigma^{(t + 1)}}|\mathbf{{Y}} &\sim&{W^{ - 1}}(N - 1,(N - 1)\mathbf{{S}}),\\ {\mu^{(t + 1)}}|({\Sigma^{(t + 1)}},\mathbf{{Y}})&\sim& N\left( {\overline y ,\frac{1}{n}{\Sigma^{(t + 1)}}} \right), \end{array} $$
(9)

where n is the number of observations, Y is completed data generated by previous I-step, \(\overline y\) is the mean vector, and \((N - 1)\mathbf {{S}} = \mathbf {{Y}}^{\prime }\mathbf {{Y}} = \sum \limits _{i} {{y_{i}}{y_{i}^{T}}} \).

To obtain multiply imputed datasets, Multiple Markov Chains were constructed, where the I- and P-steps were performed iteratively until the stationary distributions were reached. The initial portion of these Markov chain samples, called burn-in, were discarded, where the default was set as 200 according to literature [17, 61]. After the burn-in periods, the Markov Chains continue, as shown in Fig. 2, until additional I-steps were performed to obtain a complete dataset from the stationary distribution for each Markov chain, marked as X i , i.e., the i-th imputation data.

Fig. 2
figure 2

Illustrative procedure of MI-based stability algorithm

Full size image

A fuzzy clustering method ψ is applied to each imputed dataset X i ,i=1,2,...,M, where M is the number of imputations, Ψ i,k = ψ(X i ,k),i=1,2,...,M,k=1,2,...,K, where ψ is a fuzzy clustering method that clusters the data X into k latent groups. K is the maximum number of clusters. For each k, M clustering outputs were obtained, and each case has M cluster memberships. We count how many times a case belongs to a cluster and the maximum count determines his final cluster membership. For the j-th case x j ,1≤j≤N, c u ,(u=1,2,...,k) is the frequency the case belongs to the u-th cluster, thus \(\sum \nolimits _{u = 1}^{k} {{c_{u}}} = M\). The final cluster membership of x j , denoted by v j is decided by \({v_{j}} = \underset {u}{\arg \max } {c_{u}}\).

If we have N Cases O n={x 1,x 2,...,x n }, and each case has p features, Ψ(X,k),k=1,2,... is the clustering method that can cluster the data X into k clusters, as defined above. Note that when k=1, Ψ(X n,1)≡1 for any data X.

Definition 1

The clustering distance between any two clustering method ψ 1(x) and ψ 2(x) is defined as [62],

$$\begin{array}{@{}rcl@{}} D({{\psi_{1}},{\psi_{2}}}) &=&~\\ \Pr (I({\psi_{1}}(X) &=& {\psi_{1}}(Y))+ I({\psi_{2}}(X) = {\psi_{2}}(Y))=1), \end{array} $$
(10)

where I(⋅) is an indicator function and X,Y are independently sampled from O.

Based on this definition, the clustering distance measures the disagreement between two clusters. It equals to the sum of Pr(ψ 1(x 0) = ψ 1(y 0),ψ 2(x 0)≠ψ 2(y 0)) and Pr(ψ 1(x 0)≠ψ 1(y 0),ψ 2(x 0) = ψ 2(y 0)).

Definition 2

The clustering stability of Ψ(⋅,k) is defined as,

$$ {s_{k}} = 1 - E({D({{\psi_{1}}(X,k),{\psi_{2}}(Y,k)} )} ), $$
(11)

where E(⋅) is the expectation function, k, X and Y are the same as in Definition 1.

We proposed two MI-based bootstrap and cross-validation methods to assess the clustering stability. The procedure of MI-based stability validation is shown in Fig. 2. Briefly, multiple samples are generated by bootstrapping or permutation, then the stabilities are calculated for a range of number of clusters. Finally, the optimal number of clusters is identified at the largest stability value.

MI-based bootstrapping for incomplete big web trial data in eHealth

The MI-based clustering stability using bootstrap method for k clusters is expressed as

$$ \text{MI-S}_{BS}(k) = \frac{1}{{MB}}\sum\limits_{m = 1}^{M} {\sum\limits_{b = 1}^{B} {D(\Psi ({X_{mb1}},k),\Psi ({X_{mb2}},k))} }, $$
(12)

where D(Ψ(X m b1,k),Ψ(X m b2,k)) is the clustering distance for clustering methods Ψ(X m b1,k),Ψ(X m b2,k),k=1,2,...,K, which are based on the B independent bootstrap sampling pairs (X m b1,X m b2),b=1,2,...,B where each sample has N cases.

The maximum number of clusters K is set to be \(K = \sqrt {N/2} \) in our numerical examples [4, 15]. However, this value may not fit all kinds of datasets. If \(\widehat k = K\) , we need to increase the maximum number of clusters K and auto-search the location of the maximum stability value.

MI-based cross-validation for incomplete big web trial data in eHealth

The MI-based clustering stability using cross-validation for k clusters is expressed by,

$$ \text{MI-S}_{CV}(k) = \frac{1}{{MU}} \sum\limits_{m = 1}^{M} { \sum\limits_{u = 1}^{U} {\sum\limits_{i < j} {V_{ij}^{*}\left( {X_{1}^{*},X_{2}^{*},k} \right)} }}, $$
(13)

where \(V_{ij}^{*}(\cdot )\) is clustering similarity, which is equal to \(I\left ({I\left ({\psi _{1}^{*}(x_{i}^{*}) = \psi _{1}^{*}(x_{j}^{*})} \right ) + I\left ({\psi _{2}^{*}(x_{i}^{*}) = \psi _{2}^{*}(x_{j}^{*})} \right ) = 1} \right )\), U is the number of permutations, \(\psi _{1}^{*}(x_{i}^{*}) = \Psi \left ({X_{1}^{*},k} \right )\) and \(\psi _{2}^{*}(x_{i}^{*}) = \Psi \left ({X_{2}^{*},k} \right )\) are two clustering methods, \({X^{*}} = \left \{ {x_{1}^{*},x_{2}^{*},...,x_{n}^{*}} \right \}\) is a permutation on the m-th imputed dataset, \(X_{1}^{*} = \left \{ {x_{1}^{*},x_{2}^{*},...,x_{c}^{*}} \right \}\), \(X_{2}^{*} = \left \{ {x_{c + 1}^{*},x_{c + 2}^{*},...,x_{2c}^{*}} \right \}\) and \(X_{3}^{*} = \left \{ {x_{2c + 1}^{*},x_{2c + 2}^{*},...,x_{n - c}^{*}} \right \}\) are the splits of X ∗. Overall, the higher MI-S B S and MI-S C V , the better the clustering stability.

MI-based Xie and Beni (MI-XB) index for incomplete big web trial data in eHealth

The XB index has been used in fuzzy clustering validation since it was proposed in 1991 [33]. It is defined as the quotient between the means of the quadratic error and the minimum of the minimal squared distance between the points and cluster centroids. The XB index can be calculated by,

$$ {\text{XB}} = \frac{{{\sum}_{i = 1}^{N} {{\sum}_{j = 1}^{c} {{f_{0}}^{m}{{\left\| {{x_{i}} - {v_{j}}} \right\|}^{2}}} } }}{{N \cdot {{\min }_{i,k}}{{\left\| {{x_{i}} - {v_{k}}} \right\|}^{2}}}}, $$
(14)

in which x i ,i=1,2,...,N are the cases, N is the number of cases, c is the number of clusters, v k ,k=1,2,...,c are the cluster centroids and m is fuzziness. A smaller XB index value indicates a partition that all clusters are compact and separate to each other, which means a “better clustering. Thus, we find the optimal number of clusters by minimizing the XB indices over a set of number of cluster. The MI-based XB index is represented as,

$$ \text{MI-XB}(k) = \frac{1}{M}\sum\limits_{m = 1}^{M} {XB_{q,k}}, $$
(15)

in which X B q,k is the XB index for clustering q-th imputed dataset for k clusters, and M is the number of imputations. The smaller the MI-XB, the better the clustering. The XB indices are calculated for a set of number of clusters and the optimal number of clusters is identified with the minimal XB value.

MI-based modularity for incomplete big web trial data in eHealth

In recent years, network-based validation approach has been used for clustering data, where the data vectors are treated as “nodes” in the graph and the similarities between two data vectors are defined as the “edges” between them. Suppose N vector nodes n i ,i=1,2,...,N represent the N cases, the Gaussian radial basis function kernel (RBF) is used to calculate the similarities between these nodes. The similarity between nodes n i and n j , 1≤i,j≤N is defined as,

$$ W({\mathbf{{n}}_{i}},{\mathbf{{n}}_{j}}) = \exp \left( {\gamma {{\left\| {{\mathbf{{n}}_{i}} - {\mathbf{{n}}_{j}}} \right\|}^{2}}} \right). $$
(16)
figure a

Note if i = j the similarity between n i and n j is 1, which means that there is a self-loop in the graph. Here, the similarity means how a vector is similar to its neighbors not to itself, thus

$$ W({\mathbf{{n}}_{i}},{\mathbf{{n}}_{j}})=\left\{\begin{array}{cc} {\exp \left( {\gamma {{\left\| {{\mathbf{{n}}_{i}} - {\mathbf{{n}}_{j}}} \right\|}^{2}}} \right)}, & {\text{{if }} i \ne j}\\ 0,& {\text{{otherwise}}} \end{array}\right. $$
(17)

Modularity has been widely used in finding communities in network mining. The modularity Q for a weighted network is calculated by,

$$ Q = \frac{1}{{2e}}\sum\limits_{i,j} {\left[ {{W_{ij}} - \frac{{{d_{i}}{d_{j}}}}{{2e}}} \right]} \delta \left( {{v_{i}},{v_{j}}} \right), $$
(18)

in which d i and d j are nodes strength, \({d_{i}} = \sum \limits _{j} {{W_{ij}}} \) and \({d_{j}} = \sum \limits _{i} {{W_{ij}}} \), e is the total strength of the network, \(e = \frac {1}{2}\sum \limits _{i} {{d_{i}}} \). v i and v j are the cluster membership of the i-th and j-th nodes; δ(v i ,v j )=1 only when v i = v j and δ(v i ,v j )=0, otherwise.

The MI-based Modularity (MI-Q) is calculated by,

$$ {\text{MI-Q}}(k) = \frac{1}{M}\sum\limits_{q} {{Q_{q,k}}}. $$
(19)

Note that if \(\widehat k = K\), we need to increase K and compare MI-Q to find the optimal number of clusters. The higher MI-Q, the better the clustering. The entirely procedure of the proposed MIV framework is shown in Algorithm 1.

In the proposed MIV algorithm, each imputed dataset is analyzed and the results of all imputed data are combined to obtain the validation for the incomplete data. The computation complexity of the MIV algorithm is \(\mathcal {O}(rNdMK)\), in which r is missing rate, N is the number of cases, d is the dimensions, M is the number of imputation, and K is the maximal number of clusters.

Numerical analyses and simulation

Our MI based Validation (MIV) algorithms were first evaluated using the big data from a longitudinal web-delivered trial for smoking cessation (called QuitPrimo, see details in [63, 64]). Briefly, QuitPrimo study aims to evaluate an integrated informatics solution to increase access to web-delivered smoking cessation support. The trail includes 1320 cases with missing rate less than 8.4 %. The three intervention web trail components are 1) My Mail, 2) Online Community, and 3) Our Advice. As aforementioned, this big web trial data set is unstructured and formatted simply as time, e.g., each smoker has data like “27APR10:15:43:00”. However, the primary values of big data come not from its raw form, but from its processing and analysis. Four clusters were identified using six monthly measures for each intervention component and web duration (total 19 attributes) in [63, 64].

Ten imputations (M=10) are used according to [23]. Applying our MIV algorithm introduced in Section “Multiple-imputation-based validation framework (MIV) for incomplete big web trial data in eHealth,” we auto-com- pute, search, and synthesize, the results for MI-based clustering stability, i.e., MI-Bootstrap and MI-Cross Validation, (MI-S B S and MI-S C V ), as well as MI-XB and MI-Q.

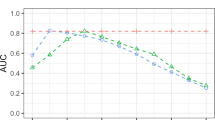
Figure 3a displays the MI clustering stability indices, MI-S B S and MI-S C V , obtained by bootstrapping and cross- validation, respectively. The MI-S B S shows the stability achieves the highest at 3 clusters, while the MI-S C V indicates the 5 clusters. The minimal value of MI-XB in Fig. 3b clearly points to 4 clusters which is the correct optimal number of clusters. Figure 3c also indicates 2 clusters based on MI-based modularity (MI-Q). These results demonstrate that the stabilities and network-based validation methods may not be suitable for big longitudinal web trial data analyses.

Fig. 3
figure 3

MI-based validation indices for a big web-delivered trial dataset (QuitPrimo)

Full size image

Figure 4 shows the four identified behavioral trajectory patterns of this big web-delivered trial. The x-axis shows the time slots for the three web intervention components, My Advice, Our Advice, and Our Community; the y-axis displays individual IDs, and z-axis are the counts of each component. The colored trajectory layers represent the average engagement level for each cluster. In QuitPrimo data, r=0.084, N=1320, d=18, M=10, and K=10, the running time of the proposed MIV algorithm is about 1 minute on our lab PC (i7-4770 double 3.4GHz CPU with 16G RAM).

Fig. 4
figure 4

The identified big longitudinal trajectory clusters of QuitPrimo data

Full size image

Our simulation uses the joint zero-inflated Poisson (ZIP) and autoregressive (AR) model to simulate the QuitPrimo data [65]. We first train the joint model using the QuitPrimo data, to obtain the parameters which were used to simulate a bigger longitudinal web trial data with 10,000 cases and 54 dimensions (9 variables with 6 repeated meatures each). Then we evaluated our proposed MIV algorithms on the simulated data. Figure 5 again demonstrates that MI-XB (Fig. 5b) correctly identifies the 4 trajectory patterns while MI-S B S and MI-S C V (Fig. 5a) and MI-Q (Fig. 5c) did not. Our preliminary evaluation results [14] indicate that MIfuzzy is most robust to missing rates less than 20 %, although one empirical observational study showed that it could be robust to the missing rate up to 40 % where other included variables with missing values may be more or as informative as the variables without missingness for the subjects [14].

Fig. 5
figure 5

MI-based validation indices for simulated big web-delivered trial dataset

Full size image

Conclusion

In eHealth services, big data from web-delivered longitudinal trials are complex. Determining the optimal number of clusters in such data is especially challenging. This paper, built upon our MIfuzzy clustering designed a MI-based validation (MIV) framework and algorithms for big data processing, particularly for fuzzy clustering of big incomplete longitudinal web-delieved trial data. Although we included two conventional methods for testing clustering stability, bootstrap and cross-validation, they did not seem to add incremental value for detecting the optimal number of clusters. Although they seem to be useful for complete datasets. One major reason could be that the multiple imputation component in MIfuzzy already accounts for the imputation uncertainty to ensure the clustering stability using several complete imputed datasets. This concept is similar to the bootstrap and cross validation for stability tests, therefore this overlap decreases the incremental value of these conventional methods which are typically used for complete data sets. Another reason might be that the two methods were not specifically designed for or directly related to the fuzzy clustering which is widely accepted for biomedical data where clusters overlap or touch. Also the modularity validation index is widely accepted for network-based data, but appears not feasible for the structure of these big incomplete longitudinal web-delivered trial data in eHealth services. Consistently, we found multiple-imputation based XB index, specifically designed for fuzzy clustering, could facilitate detecting the optimal number of clusters for big incomplete longitudinal trial data, either from web-delivered or traditional clinical trials [4, 6, 15]. Different from the MI approach used for statistical analyses, MI based clustering only uses the imputation step, thus has no connection with the possible inconsistent analytical models for statistical inference. As our research indicates, it will especially contribute more to non-model-based clustering approaches, and could potentially improve clustering accuracy and computational efficiency for model-based clustering approaches. In future, embedding MIV algorithms into eHealth system could warrant the validity of identifying at-risk or abnormal patterns of patients, events, diagnoses or services using various unsupervised learning methods, and reduce the uncertainty in implementing pattern-derived adaptive trials or services.