A Strongly Conservative Hybrid DG/Mixed FEM for the Coupling of Stokes and Darcy Flow

Abstract

We consider the coupling of free and porous media flow governed by Stokes and Darcy equations with the Beavers–Joseph–Saffman interface condition. This model is discretized using a divergence-conforming finite element for the velocities in the whole domain. Hybrid discontinuous Galerkin techniques and mixed methods are used in the Stokes and Darcy subdomains, respectively. The discretization achieves mass conservation in the sense of $H(\mathrm {div},\Omega )$, and we obtain optimal velocity convergence. Numerical results are presented to validate the theoretical findings.

1 Introduction

The construction of new finite element methods for the Stokes–Darcy coupled problem, in which the respective interface conditions are given by mass conservation, balance of normal forces, and the Beavers–Joseph–Saffman law, is a very active research area; see [1, 3, 4, 7, 8, 12,13,14, 16,17,18, 20,21,22, 31,32,33, 37, 39] and the references therein. These problems have many important applications such as the modeling of groundwater contamination through streams and filtration problems [27, 28].

Among the methods cited above, Kanschat and Riviére [21] proposed a strongly conservative finite element method, where the Darcy flow is discretized by a mixed finite element method and Stokes flow by a mixed (velocity–pressure) discontinuous Galerkin (DG) method using a globally divergence-conforming velocity space on the whole domain. Such a method has the advantage that mass conservation is achieved in the sense of $H(\mathrm {div};\Omega )$, hence the name strongly conservative. Optimal error estimates of the method were proven in [20].

The divergence-conforming hybrid DG (HDG) method [9, 15, 24, 25] for the Stokes flow is an efficient variant of the divergence-conforming DG method [11]. Due to hybridization, the HDG method has significant less globally coupled degrees of freedom, and has a better sparsity pattern than the DG method to achieve the same accuracy; see [25, Table 2] for a comparison.

In this paper, we present a strongly conservative HDG/mixed method for the Stokes-Darcy coupled problem by replacing the divergence-conforming DG method in the Stokes region with a divergence-conforming HDG method. Optimal error estimates of the method are proven. We maintain the advantage of mass conservation in terms of $H(\mathrm {div};\Omega )$, and have a reduced globally coupled degrees of freedom than the degrees of freedom for the method [21].

The rest of the paper is organized as follows. In Sect. 2, we first introduce the model problem then present our numerical method and show its wellposedness. In Sect. 3, we prove our main results on the optimal velocity error estimates. In Sect. 4, numerical results are presented to validate the theoretical findings. Finally, we conclude in Sect. 5.

Fig. 1

Sketch of Darcy and Stokes domains and boundaries

2 Model Problem and Discretization

2.1 Model Problem

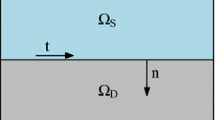
Let $\Omega$ be a bounded polygonal/polyhedral domain in $\mathbb {R}^d$, $d = 2, 3$, split into two polygonal/polyhedral subdomains $\Omega _S$ and $\Omega _D$ of free and porous media flow, respectively. Denote by $\Gamma _{SD}$ the polygonal interface between $\Omega _S$ and $\Omega _D$, cf. Fig. 1. The external boundaries are defined by

$$\begin{aligned} \Gamma _{S} = \partial \Omega \cap \partial \Omega _S,\quad \Gamma _{D} = \partial \Omega \cap \partial \Omega _D. \end{aligned}$$

The coupled Darcy/Stokes problem in conservative form reads

$$\begin{aligned} -{\nabla \cdot }(2\nu \,\varepsilon (\varvec{u}))+{\nabla }p =&\; \varvec{f}_S,&\text { in }\Omega _S, \end{aligned}$$

(1a)

$$\begin{aligned} K^{-1}\varvec{u}+{\nabla }p =&\; \varvec{0},&\text { in }\Omega _D, \end{aligned}$$

(1b)

$$\begin{aligned} {\nabla \cdot }\varvec{u} =&\; f_D\,\chi _{\Omega _D},&\text { in }\Omega . \end{aligned}$$

(1c)

Here $\varvec{u}$ is the velocity and p is the pressure. The deformation tensor is $\varepsilon (\varvec{u}) = \frac{1}{2}({\nabla }u+({\nabla }u)^T)$, the coefficient $\nu >0$ is the fluid kinematic viscosity, the variable $K >0$ is ratio of the intrinsic permeability tensor to the fluid viscosity, which is symmetric and positive definite, and the function $\varvec{f}_S$ is a body force in Stokes region, and $f_D$ models source or sink in the porous medium. Whenever we want to distinguish between the solution of the Stokes and the Darcy subproblem, we refer to and and analogously for the pressures $p_S$ and $p_D$. On the interface $\Gamma _{SD}$, this notation refers to the traces taken from the respective subdomains.

On the interface, we impose the Beavers–Joseph–Saffman conditions (see Beavers and Joseph [2] and Saffman [34]), and on the boundary, we assume no-slip and Neumann for simplicity:

$$\begin{aligned} \varvec{u}_S\cdot \varvec{n} =&\; \varvec{u}_D\cdot \varvec{n},&\text { on }\Gamma _{SD}, \end{aligned}$$

(2a)

$$\begin{aligned} p_S- 2\nu \varepsilon (\varvec{u}_S)\varvec{n}\cdot \varvec{n} =&\; p_D,&\text { on }\Gamma _{SD},\end{aligned}$$

(2b)

$$\begin{aligned} \gamma \, K^{-1/2}(\varvec{u}_S)^t + 2\nu (\varepsilon (\varvec{u}_S)\varvec{n})^t =&\; 0,&\text { on }\Gamma _{SD}, \end{aligned}$$

(2c)

$$\begin{aligned} \varvec{u}_S =&\; \varvec{0},&\text { on }\Gamma _{S}, \end{aligned}$$

(2d)

$$\begin{aligned} \varvec{u}_D\cdot \varvec{n} =&\; 0,&\text { on }\Gamma _{D}. \end{aligned}$$

(2e)

Here, $\gamma >0$ is the phenomenological friction coefficient. On the interface $\Gamma _{SD}$, $\varvec{n}$ is the unit normal vector pointing outward of $\Omega _S$, and, on $\Gamma _D$, $\varvec{n}$ is the unit normal vector pointing outward of $\Omega _D$. The tangential component $(\cdot )^t$ of a vector $\varvec{v}$ is denoted by $(\varvec{v})^t = \varvec{v} - (\varvec{v}\cdot \varvec{n})\varvec{n}.$

2.2 Discretization

2.2.1 Preliminaries

Let $\mathcal {T}_h$ be a conforming simplicial triangulation of $\Omega$ such that the interface $\Gamma _{SD}$ is the union of element facets. For any element $T \in \mathcal {T}_h$, we denote by $h_T$ its diameter and we denote by h the maximum diameter over all mesh elements. Denote by $\mathcal {T}_{h,S}$ the set of mesh elements that belong to ${\Omega _S}$ and by $\mathcal {T}_{h,D}$ those belong to ${\Omega _D}$. Denote by $\mathcal {F}_h$ the set of facets of $\mathcal {T}_h$, by $\mathcal {F}_{h,S}$ the set of facets that are interior to $\overline{\Omega _S}$, and by $\mathcal {F}_{h,SD}$ the set of facets that lie on the interface $\Gamma _{SD}$. We also denote by $\Gamma _{h,S}$ the set of facets that lie on the boundary $\Gamma _S$.

In the sequel, for the approximation of viscous forces in the Stokes region, we distinguish functions with support only on facets indicated by a subscript F and those with support also on the volume elements which is indicated by a subscript T. Compositions of both types are used for the HDG discretization of the velocity and indicated by underlining, ${{\underline{\varvec{{u}}}}}= (\varvec{u}_T, \varvec{u}_F)$.

2.2.2 Finite Elements

We use the following stable pair of divergence-conforming velocity space and the matching pressure space $Q_h\subset L_0^2(\Omega )=\{q\in L^2(\Omega ):\; \int _{\Omega } q \,\mathrm {dx} = 0\}$:

$$\begin{aligned} \varvec{\Sigma }_h: =&\; \left\{ \varvec{v}_T\in \prod _{T\in \mathcal {T}_h}[\mathbb {P}^k(T)]^d, \;\; [\![\varvec{v}_T\cdot \varvec{n} ]\!]_F = 0 \,\forall F\in \mathcal {F}_h.\right\} \subset H_0(\mathrm {div},\Omega ), \end{aligned}$$

(3a)

$$\begin{aligned} Q_h : =&\; \left( \prod _{T\in \mathcal {T}_h} \mathbb {P}^{k-1}(T)\right) \cap L_0^2(\Omega ), \end{aligned}$$

(3b)

where $[\![\cdot ]\!]$ is the usual jump operator and $\mathbb {P}^k$ the space of polynomials up to degree k for $k\ge 1$. The Stokes operator is discretized by a divergence-conforming HDG method [25]. The benefits of divergence-conforming finite element discretizations for Stokes (or Navier–Stokes) problems is manifold. On the one hand divergence-conforming discretizations lead to solenoidal discrete solutions which can be crucial to obtain energy-stable discretizations for Navier–Stokes simulations, cf. [10]. On the other hand, already for Stokes problems the compatible treatment of the divergence-constraint is important to obtain pressure-robustness, i.e. a numerical scheme where the velocity error does not depend on the regularity of the pressure, cf. [26] and Theorems 1, 2 and 3 below. For a more detailed discussion of the benefit of divergence-conforming methods, we also refer to [36].

Divergence-conforming DG discretizations for Stokes (or Navier–Stokes) problems come with an increase of computational costs due to an increase of global couplings. To compensate for that we consider a corresponding HDG method. For that, we need to introduce additional unknowns on the skeleton $\mathcal {F}_{h,S}$, the facet unknowns, which represent an approximation of the tangential trace of the solution in the Stokes region:

$$\begin{aligned} M_h := \left\{ \varvec{v}_F\in \prod _{F\in \mathcal {F}_{h,S}}[\mathbb {P}^{k_{\!f}}(T)]^d, \quad \varvec{v}_F\cdot \varvec{n} = 0 \,\forall F\in \mathcal {F}_{h,S}, \quad \varvec{v}_F = 0 \,\forall F\in \Gamma _{h,S},\right\} \end{aligned}$$

(3c)

where

. Functions in $M_h$ are defined only on the mesh skeleton in the Stokes region $\mathcal {F}_{h,S}$ and have normal component zero, and vanish on the Stokes boundary $\Gamma _S$. Here, due to a technical difficulty in proving a norm equivalence result, see Lemma 1 below, we can not decrease the polynomial degree $k_{\!f}$ to one order less for the lowest order case $k=1$. Note however that in the numerical example below, we obtain optimal order results also for the choice $k_f=0$ for $k=1$. The reduction of $k_f$ from k to $k-1$ results in an additional significant reduction of global couplings in arising linear systems for the Stokes part of the problem, cf. [24, 25, 29].

For the discretization of the velocity field we use the composite space

$$\begin{aligned} {{\underline{\varvec{{U}\!}}}}_h: = \varvec{\Sigma }_h\times {M}_h. \end{aligned}$$

2.2.3 The Numerical Scheme

First, we introduce the $L^2$ projection $\Pi$ for a fixed facet $F\in \mathcal {F}_{h,S}$:

$$\begin{aligned} \Pi : [\mathbb {P}^k(F)]^d\rightarrow [\mathbb {P}^{k_{\!f}}(F)]^d, \quad \int _F (\Pi f) v \, \mathrm {ds} = \int _{F}f\,v\, \mathrm {ds} \quad \forall v\in [\mathbb {P}^{k_{\!f}}(F)]^d. \end{aligned}$$

Then, for all ${{\underline{\varvec{{u}}}}}, {{\underline{\varvec{{v}}}}}\in {{\underline{\varvec{{U}\!}}}}_h$ and $q\in Q_h$, we introduce the bilinear and linear forms

$$\begin{aligned} a_{S,h}({{\underline{\varvec{{u}}}}}, {{\underline{\varvec{{v}}}}}) :=&\; \sum _{T\in \mathcal {T}_{h,S}}\int _T2\nu \,\varepsilon (\varvec{u}_T):\varepsilon (\varvec{v}_T)\,\mathrm {dx} -\int _{\partial T}2\nu \,\varepsilon (\varvec{u}_T)\varvec{n}\cdot [\![{{\underline{\varvec{{v}}}}}^t ]\!]\,\mathrm {ds} \nonumber \\&\; -\int _{\partial T}2\nu \,\varepsilon (\varvec{v}_T)\varvec{n}\cdot [\![{{\underline{\varvec{{u}}}}}^t ]\!]\,\mathrm {ds} + \int _{\partial T}\nu \frac{\alpha }{h}\Pi [\![{{\underline{\varvec{{u}}}}}^t ]\!]\cdot \Pi [\![{{\underline{\varvec{{v}}}}}^t ]\!]\,\mathrm {ds}, \end{aligned}$$

(4a)

$$\begin{aligned} a_{D}({{\underline{\varvec{{u}}}}}, {{\underline{\varvec{{v}}}}}) :=&\; \sum _{T\in \mathcal {T}_{h,S}}\int _T K^{-1}\varvec{u}_T\cdot \varvec{v}_T\,\mathrm {dx},\end{aligned}$$

(4b)

$$\begin{aligned} a_{I}({{\underline{\varvec{{u}}}}}, {{\underline{\varvec{{v}}}}}) :=&\; \sum _{F\in \mathcal {F}_{h,SD}}\int _F \gamma K^{-1/2}\varvec{u}_F\cdot \varvec{v}_F\,\mathrm {ds},\end{aligned}$$

(4c)

$$\begin{aligned} a_h({{\underline{\varvec{{u}}}}}, {{\underline{\varvec{{v}}}}}) : =&\; a_{S,h}({{\underline{\varvec{{u}}}}}, {{\underline{\varvec{{v}}}}}) + a_{D}({{\underline{\varvec{{u}}}}}, {{\underline{\varvec{{v}}}}}) +a_{I}({{\underline{\varvec{{u}}}}}, {{\underline{\varvec{{v}}}}}),\nonumber \\ b({{\underline{\varvec{{u}}}}}, q) =&\;-\sum _{T\in \mathcal {T}_h}\int _T {\nabla \cdot }\varvec{u}_T q\,\mathrm {dx}, \end{aligned}$$

(4d)

$$\begin{aligned} f_1({{\underline{\varvec{{v}}}}}) =&\;\sum _{T\in \mathcal {T}_{h,S}}\int _T \varvec{f}_S\cdot \varvec{v}_T \,\mathrm {dx}, \end{aligned}$$

(4e)

$$\begin{aligned} f_2(q) =&\;\sum _{T\in \mathcal {T}_{h,D}}\int _T f_D\,q\,\mathrm {dx}, \end{aligned}$$

(4f)

where $[\![{{\underline{\varvec{{u}}}}}^t ]\!]= \varvec{u}_T^t-\varvec{u}_F$ is the (tangential) jump between interior and facet unknowns, and $\alpha = \alpha _0 k^2$ with $\alpha _0$ a sufficiently large positive constant. We note that (only) as long as ${{\underline{\varvec{{u}}}}},~{{\underline{\varvec{{v}}}}}$ are finite element functions in ${{\underline{\varvec{{U}\!}}}}_h$ we have

$$\begin{aligned} \int _{\partial T} 2 \nu \varepsilon (\varvec{u}_T) \varvec{n} \cdot [\![{{\underline{\varvec{{v}}}}}^t ]\!] ds = \int _{\partial T} 2 \nu \varepsilon (\varvec{u}_T) \varvec{n} \cdot \Pi [\![{{\underline{\varvec{{v}}}}}^t ]\!] ds \end{aligned}$$

for (4a) as $2 \nu \varepsilon (\varvec{u}_T) \varvec{n}$ is a polynomial of degree $k-1$ on each facet.

The numerical scheme then reads: Find $({{\underline{\varvec{{u}}}}}_h, p_h)\in {{\underline{\varvec{{U}\!}}}}_h\times Q_h$ such that

$$\begin{aligned} a_h({{\underline{\varvec{{u}}}}}_h, {{\underline{\varvec{{v}}}}}_h) + b({{\underline{\varvec{{v}}}}}_h, p_h)&= f_1({{\underline{\varvec{{v}}}}}_h), \quad \forall {{\underline{\varvec{{v}}}}}_h\in {{\underline{\varvec{{U}\!}}}}_h, \end{aligned}$$

(5a)

$$\begin{aligned} b({{\underline{\varvec{{u}}}}}_h, q_h)&= -f_2(q_h), \quad \forall q_h\in Q_h. \end{aligned}$$

(5b)

Remark 1

(Strong mass conservation) By the divergence conformity of the space $\varvec{\Sigma }_h$, Eq. (5b) can be written as

$$\begin{aligned} -\int _{\Omega } {\nabla \cdot }\varvec{u}_{h,T}\,q_h \,\mathrm {dx} = -\int _{\Omega } \chi _D f_D\,q_h \,\mathrm {dx} \quad \forall q_h\in Q_h. \end{aligned}$$

Hence, ${\nabla \cdot }\varvec{u}_{h,T}-\chi _DP_Q f_D \equiv 0$ where $P_Q$ is the $L^2$-projection onto $Q_h$. This is a strong mass conservation in terms of $H(\mathrm {div};\Omega )$.

We define the following seminorms:

$$\begin{aligned} |{{{\underline{\varvec{{u}}}}}}|^2_{e,S} :=&\;\sum _{T\in \mathcal {T}_{h,S}}\nu \left( \Vert \varepsilon (\varvec{u}_T)\Vert _T^2+\frac{1}{h}\Vert \Pi [\![{{\underline{\varvec{{u}}}}}^t ]\!]\Vert ^2_{\partial T}\right) , \end{aligned}$$

(6a)

$$\begin{aligned} |{{{\underline{\varvec{{u}}}}}}|^2_{1,S} :=&\;\sum _{T\in \mathcal {T}_{h,S}}\nu \left( \Vert {\nabla }\varvec{u}_T\Vert _T^2+\frac{1}{h}\Vert [\![{{\underline{\varvec{{u}}}}}^t ]\!]\Vert ^2_{\partial T}\right) , \end{aligned}$$

(6b)

$$\begin{aligned} |{{{\underline{\varvec{{u}}}}}}|^2_{1*,S} :=&\;\sum _{T\in \mathcal {T}_{h,S}}\nu \left( \Vert {\nabla }\varvec{u}_T\Vert _T^2+ h^2 \Vert {\nabla }^2(\varvec{u}_T)\Vert _T^2+ \frac{1}{h}\Vert \Pi [\![{{\underline{\varvec{{u}}}}}^t ]\!]\Vert ^2_{\partial T}\right) , \end{aligned}$$

(6c)

$$\begin{aligned} |{{{\underline{\varvec{{u}}}}}}|^2_{D} :=&\;\sum _{T\in \mathcal {T}_{h,D}}\Vert K^{-1/2} \varvec{u}_T\Vert _T^2, \end{aligned}$$

(6d)

$$\begin{aligned} |{{{\underline{\varvec{{u}}}}}}|^2_{I} :=&\;\sum _{F\in \mathcal {F}_{h,SD}}\Vert \gamma ^{1/2}K^{-1/4} \varvec{u}_F\Vert _F^2, \end{aligned}$$

(6e)

where $\Vert \cdot \Vert _D$ denotes the standard $L^2$-norm on the domain D. We note that the semi-norms in (6a)–(6c) are slight variations of each other with different handling of the volume control ($\varepsilon (\varvec{u}_T)$ vs. $\nabla (\varvec{u}_T)$), the jump terms ($\Pi [\![{{\underline{\varvec{{u}}}}}^t ]\!]$ vs. $[\![{{\underline{\varvec{{u}}}}}^t ]\!]$) and control in higher order derivatives ($\nabla ^2 (\varvec{u}_T)$ vs. no control). All three norms (and their equivalence on discrete spaces) will be used in the analysis below.

Throughout this work, we write

$$\begin{aligned} A\preceq B \end{aligned}$$

to indicate that there exists a constant C, independent of the mesh size h and the numerical solution, such that $A\le CB.$

2.2.4 Wellposedness

Lemma 1

For ${{\underline{\varvec{{v}}}}}_h\in {{\underline{\varvec{{U}\!}}}}_h$, there holds

$$\begin{aligned} |{{{\underline{\varvec{{v}}}}}_h}|_{1*,S} \preceq |{{{\underline{\varvec{{v}}}}}_h}|_{1,S},\quad \text { and }\; |{{{\underline{\varvec{{v}}}}}_h}|_{1,S} \preceq |{{{\underline{\varvec{{v}}}}}_h}|_{e,S}. \end{aligned}$$

Proof

Take ${{\underline{\varvec{{v}}}}}_h= (\varvec{v}_T,\varvec{v}_F)\in {{\underline{\varvec{{U}\!}}}}_h$. The first inequality comes from the inverse inequality for finite dimensional spaces and stability of the $L^2$ projection. To prove the second inequality, we shall use the following discrete Korn’s inequality [6]:

$$\begin{aligned} |{{{\underline{\varvec{{v}}}}}_h}|^2_{1,S} \preceq \sum _{T\in \mathcal {T}_{h,S}}\nu \left( \Vert \varepsilon (\varvec{v}_T)\Vert _T^2+\frac{1}{h}\Vert [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\Vert ^2_{\partial T}\right) . \end{aligned}$$

Since the space of rigid motions RM(T) lies in $[\mathbb {P}_{1}(T)]^d\subset [\mathbb {P}_{k_{\!f}}(T)]^d$,

$$\begin{aligned} h^{-1/2} \Vert [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\Vert _{\partial T}=&\; h^{-1/2} \Vert \Pi [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\Vert _{\partial T} +h^{-1/2}\Vert \varvec{v}_T- \Pi \,\varvec{v}_T \Vert _{\partial T}\\ =&\; h^{-1/2} \Vert \Pi [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\Vert _{\partial T} +h^{-1/2}\inf _{\Lambda \in RM(T)}\Vert (\varvec{v}_T-\Lambda )- \Pi \,(\varvec{v}_T-\Lambda ) \Vert _{\partial T}\\ \le&\; h^{-1/2} \Vert \Pi [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\Vert _{\partial T} +h^{-1/2}\inf _{\Lambda \in RM(T)}\Vert (\varvec{v}_T-\Lambda )- \overline{(\varvec{v}_T-\Lambda )} \Vert _{\partial T}\\ \le&\; h^{-1/2}\Vert \Pi [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\Vert _{\partial T} +C \inf _{\Lambda \in RM(T)}\Vert {\nabla }(\varvec{v}_T-\Lambda )\Vert _{T}\\ \le&\; h^{-1/2}\Vert \Pi [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\Vert _{\partial T} +C \Vert \varepsilon (\varvec{v}_T)\Vert _{T}, \end{aligned}$$

where $\overline{\star }$ is the average of $\star$ in T, and the last step follows from the local Korn’s inequality [30, Lemma 4.1]. The proof is completed by combing the above two inequalities. $\square$

Lemma 2

The bilinear form $a_{S,h}(\cdot ,\cdot )$ chosen in the Stokes subdomain $\Omega _S$ has the following properties:

• (a) Coercivity: For $\alpha _0$ sufficiently large, there holds

  $$\begin{aligned} |{{\underline{\varvec{{v}}}}}_h|_{1,S}^2\preceq a_{S,h}({{\underline{\varvec{{v}}}}}_h, {{\underline{\varvec{{v}}}}}_h)\quad \forall {{\underline{\varvec{{v}}}}}_h\in {{\underline{\varvec{{U}\!}}}}_h. \end{aligned}$$

  (7a)

• (b) Boundedness: There holds

  $$\begin{aligned} a_{S,h}({{\underline{\varvec{{v}}}}}, {{\underline{\varvec{{w}}}}})\preceq |{{\underline{\varvec{{v}}}}}|_{1*,S} |{{\underline{\varvec{{w}}}}}|_{1*,S}, \quad \forall {{\underline{\varvec{{v}}}}}, {{\underline{\varvec{{w}}}}}\in {{\underline{\varvec{{V}\!}}}}\,+{{\underline{\varvec{{U}\!}}}}_h, \end{aligned}$$

  (7b)

  where

  $$\begin{aligned} {{\underline{\varvec{{V}\!}}}}\,=&\;\Big \{\left( \varvec{v}_T,(\varvec{v}_T)^t|_{\mathcal {F}_{h,S}}\right) : \varvec{v}_T|_{\Omega _S}\in \varvec{H}^2(\Omega _S), \;\;\varvec{v}_T|_{\Gamma _S}=0,\nonumber \\&\quad \quad \quad \quad \quad \quad \qquad \qquad \;\;\; \varvec{v}_T|_{\Omega _D}\in \varvec{H}^1(\Omega _D),\;\; \varvec{v}_T\cdot \varvec{n}|_{\Gamma _D}=0 \Big \}. \end{aligned}$$

  (7c)

• (c) Consistency: Let $(\varvec{u}_S, p_S)\in \varvec{H}^2(\Omega _S)\times H^1(\Omega _S)$ be part of the solution to Eqs. (1) and (2), and set ${{\underline{\varvec{{u}}}}}= (\varvec{u}_S, \varvec{u}_S^t|_{\mathcal {F}_{h,S}})$. Then, for all $\varvec{v}= (\varvec{v}_T,\varvec{v}_F)\in {{\underline{\varvec{{V}\!}}}}\,+{{\underline{\varvec{{U}\!}}}}_h$, there holds

  $$\begin{aligned} a_{S,h}({{\underline{\varvec{{u}}}}}, \varvec{v}) =&\; \int _{\Omega _S}(\varvec{f}_S-{\nabla }p_S)\cdot \varvec{v}_T\,\mathrm {dx} +\int _{\Gamma _{SD}}(2\nu \varepsilon (\varvec{u}_S)\varvec{n}\cdot \varvec{n})\varvec{v}_T\cdot \varvec{n}\,\mathrm {ds}\nonumber \\&\; - \int _{\Gamma _{SD}}\gamma K^{-1/2} \varvec{u}_S^t\cdot \varvec{v}_F\,\mathrm {ds}. \end{aligned}$$

  (7d)

Proof

Take ${{\underline{\varvec{{v}}}}}_h= (\varvec{v}_{T}, \varvec{v}_{F})\in {{\underline{\varvec{{U}\!}}}}_h$. By Lemma 1, we only need to prove coercivity on the weaker seminorm $|\cdot |_{e,S}$. Since $\varepsilon (\varvec{v}_T)\varvec{n}|_F\in [\mathbb {P}^{k-1}(F)]^d$, we have

$$\begin{aligned}&\int _{\partial T}\nu \,\varepsilon (\varvec{v}_T)\varvec{n}\cdot [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\,\mathrm {ds} = \;\int _{\partial T}\nu \,\varepsilon (\varvec{v}_T)\varvec{n}\cdot \Pi [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\,\mathrm {ds} \\&\quad \le \; \nu \Vert \varepsilon (\varvec{v}_T)\varvec{n}\Vert _{\partial T}\Vert \Pi [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\Vert _{\partial T} \le C\, \nu h_T^{-1/2} \Vert \varepsilon (\varvec{v}_T)\Vert _{T}\Vert \Pi [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\Vert _{\partial T} \\&\quad \le \; \frac{1}{4} \nu \Vert \varepsilon (\varvec{v}_{T})\Vert _{T}^2+ {C^2}\, \nu h_T^{-1}\Vert \Pi [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\Vert _{\partial T}^2, \end{aligned}$$

where C is the constant arising in the trace-inverse inequality [38]. Now,

$$\begin{aligned} a_{S,h}({{\underline{\varvec{{v}}}}}_h,{{\underline{\varvec{{v}}}}}_h)&= \sum _{T\in \mathcal {T}_{h,S}}\int _T2\nu \,\varepsilon (\varvec{v}_T):\varepsilon (\varvec{v}_T)\,\mathrm {dx} -4\int _{\partial T}\nu \,\varepsilon (\varvec{v}_T)\varvec{n}\cdot [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\,\mathrm {ds}\\&\;\quad + \int _{\partial T}\nu \frac{\alpha }{h}\Pi [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\cdot \Pi [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\,\mathrm {ds}\\&\ge \sum _{T\in \mathcal {T}_{h,S}}\nu \left( \Vert \varepsilon (\varvec{v}_T) \Vert _T^2 +\left( \frac{\alpha }{h}-4{C^2} h_T^{-1}\right) \Vert \Pi [\![{{\underline{\varvec{{v}}}}}_h^t ]\!]\Vert _{\partial T}^2 \right) . \end{aligned}$$

The right hand side of the above expression is an upper bound for $|{{\underline{\varvec{{v}}}}}_h|_{1,S}^2$ for sufficiently large $\alpha _0$. This completes the proof of coercivity (7a).

Boundedness (7b) is a direct consequence of the Cauchy–Schwarz inequality and the trace inequality.

Finally, let us prove the consistency result (7d). By definition, we have

$$\begin{aligned} a_{S,h}({{{\underline{\varvec{{u}}}}}}, \varvec{v}) =&\; \sum _{T\in \mathcal {T}_{h,S}}\int _T2\nu \,\varepsilon (\varvec{u}_S):\varepsilon (\varvec{v}_T)\,\mathrm {dx} -\int _{\partial T}2\nu \,\varepsilon (\varvec{u}_S)\varvec{n}\cdot [\![{{\underline{\varvec{{v}}}}}^t ]\!]\,\mathrm {ds}\nonumber \\ =&\; \sum _{T\in \mathcal {T}_{h,S}}\int _T2\nu \,\varepsilon (\varvec{u}_S):\varepsilon (\varvec{v}_T)\,\mathrm {dx} -\int _{\partial T}2\nu \,\varepsilon (\varvec{u}_S)\varvec{n}\cdot \left( \varvec{v}_T^t-\varvec{v}_F\right) \,\mathrm {ds}\nonumber \\ =&\; \sum _{T\in \mathcal {T}_{h,S}}\int _T-({\nabla \cdot }2\nu \,\varepsilon (\varvec{u}_S))\cdot \varvec{v}_T\,\mathrm {dx} +\int _{\partial T}2\nu \,\varepsilon (\varvec{u}_S)\varvec{n}\cdot \left( \varvec{v}_T-\varvec{v}_T^t\right) \,\mathrm {ds}\nonumber \\&\;\;\; +\int _{\partial T}2\nu \,\varepsilon (\varvec{u}_S)\varvec{n}\cdot \varvec{v}_F\,\mathrm {ds}. \end{aligned}$$

(8)

By Eq. (1a), we have

$$\begin{aligned} \sum _{T\in \mathcal {T}_{h,S}}\int _T-({\nabla \cdot }2\nu \,\varepsilon (\varvec{u}_S))\cdot \varvec{v}_T\,\mathrm {dx} = \int _{\Omega _S}(\varvec{f}_S-{\nabla }p_S)\cdot \varvec{v}_T\,\mathrm {dx}. \end{aligned}$$

By smoothness of $\varvec{u}$, $H(\mathrm {div})$-conformity of $\varvec{v}_T$, and the boundary conditions (2c)–(2d), the first boundary term on the right hand side of (8) can be simplified as

$$\begin{aligned} \sum _{T\in \mathcal {T}_{h,S}}\int _{\partial T}2\nu \,\varepsilon (\varvec{u}_S)\varvec{n}\cdot \left( \varvec{v}_T-\varvec{v}_T^t\right) \,\mathrm {ds} = \int _{\Gamma _{SD}}2\nu \,\varepsilon (\varvec{u}_S)\varvec{n}\cdot \varvec{n} (\varvec{v}_T\cdot \varvec{n})\,\mathrm {ds}, \end{aligned}$$

and the second boundary term can be simplified as

$$\begin{aligned} \sum _{T\in \mathcal {T}_{h,S}}\int _{\partial T}2\nu \,\varepsilon (\varvec{u}_S)\varvec{n}\cdot \varvec{v}_F\,\mathrm {ds}&= \; \int _{\Gamma _{SD}}2\nu \,(\varepsilon (\varvec{u}_S)\varvec{n})^t\cdot \varvec{v}_F\,\mathrm {ds}\\&= \; -\int _{\Gamma _{SD}}\gamma K^{-1/2}\varvec{u}_S^t \cdot \varvec{v}_F\,\mathrm {ds}. \end{aligned}$$

The equality (7d) is obtained by combining the above identities. $\square$

Proposition 1

For $\alpha _0$ sufficiently large, there exists a unique solution $({{\underline{\varvec{{u}}}}}_h, p_h)\in {{\underline{\varvec{{U}\!}}}}_h\times Q_h$ for the scheme (5).

Proof

Since the equations in (5) form a quadratic system, we only need to proof uniqueness of the solution, that is, the only solution to the scheme (5) with vanishing right hand sides is zero.

Assuming $f_1=f_2 = 0$, taking ${{\underline{\varvec{{v}}}}}_h= {{\underline{\varvec{{u}}}}}_h$ and $q_h = -p_h$ in (5), and adding up the resulting equations, we obtain

$$\begin{aligned} a_h({{\underline{\varvec{{u}}}}}_h, {{\underline{\varvec{{u}}}}}_h) = a_{S,h}({{\underline{\varvec{{u}}}}}_h, {{\underline{\varvec{{u}}}}}_h) +|{{\underline{\varvec{{u}}}}}_h|_D^2+|{{\underline{\varvec{{u}}}}}_h|_I^2= 0. \end{aligned}$$

Hence, for sufficiently large $\alpha _0$, ${{\underline{\varvec{{u}}}}}_h= 0$ by (7a) in Lemma 2. Then, Eq. (5a) implies that $b({{\underline{\varvec{{v}}}}}_h, p_h)= -\int _{\Omega } {\nabla \cdot }\varvec{v}_T p_h\,\mathrm {dx}=0$. Due to the special compatibility of pressure and velocity spaces we can take $\varvec{v}_T$ be such that ${\nabla \cdot }\varvec{v}_T=p_h$ which yields $p_h=0$ and completes the proof. $\square$

3 Error Analysis

In this section, we present our main result on the velocity error estimates. The analysis is based on the results in [20, 25].

Denote $P_M$, $P_Q$ as the standard $L^2$ projections onto the spaces $M_h$ and $Q_h$, and $\Pi _V$ as the following $H(\mathrm {div})$-conforming BDM projection [5]: for all $T\in \mathcal {T}_h$,

$$\begin{aligned} \int _T \Pi _V \varvec{u} \cdot \varvec{v}\,\mathrm {dx} =&\; \int _T \varvec{u} \cdot \varvec{v}\,\mathrm {dx},&\quad \forall \varvec{v}\in {\nabla }\mathbb {P}^{k-1}(T)\oplus B^k(T),\\ \int _F \Pi _V \varvec{u}\cdot \varvec{n} \mu \,\mathrm {ds} =&\; \int _F \varvec{u} \cdot \varvec{n} \mu \,\mathrm {ds},&\quad \forall \varvec{v}\in \mathbb {P}^{k}(F),\forall F\in \mathcal {F}(T), \end{aligned}$$

where $B^k(T):=\{\varvec{v}\in [\mathbb {P}^k(T)]^d: {\nabla \cdot }\varvec{v}|_T=0, \;\;\varvec{v}\cdot \varvec{n}|_{\partial T} = 0\}$ is the divergence-free bubble space.

The following commuting diagram property of the projection pair $(\Pi _V, P_Q)$ is well-known:

$$\begin{aligned} {\nabla \cdot }\Pi _V \varvec{\phi }= P_Q{\nabla \cdot }\varvec{\phi },\quad \forall \varvec{\phi }\in \varvec{H}^1(\Omega ). \end{aligned}$$

We define discrete error $({{\underline{\varvec{e}}}}_{u},{e}_{p})$ and an approximation error $(\underline{\varvec{\delta }}_{u},\delta _{p})$ to simplify notation:

$$\begin{aligned} \varvec{e}_{u,T}=\,&\Pi _V\varvec{u} - \varvec{u}_{h,T},\;\; \varvec{e}_{u,F}= P_M\varvec{u}^t - \varvec{u}_{h,F},&\;\; {{\underline{\varvec{e}}}}_{u}= (\varvec{e}_{u,T}, \varvec{e}_{u,F}), \end{aligned}$$

(9a)

$$\begin{aligned} \varvec{\delta }_{u,T}=\,&\Pi _V\varvec{u}-\varvec{u}, \;\; \varvec{\delta }_{u,F}= P_M\varvec{u}^t|_{\mathcal {F}_{h,S}}-\varvec{u}^t|_{\mathcal {F}_{h,S}},&\;\; \underline{\varvec{\delta }}_{u}= (\varvec{\delta }_{u,T}, \varvec{\delta }_{u,F}),\end{aligned}$$

(9b)

$$\begin{aligned} {e}_{p}=\,&P_Qp - p_h,\;\; \delta _{p}= P_Qp-p. \end{aligned}$$

(9c)

Here $\varvec{u}^t|_{\mathcal {F}_{h,S}}$ is the restriction of the tangential component of $\varvec{u}$ on the facets $\mathcal {F}_{h,S}$.

3.1 Energy Norm Estimate

Theorem 1

Assume that the solution $(\varvec{u}, p)$ of the Eqs. (1), (2) is in $\varvec{X}_s\times Y_{s}$ where

$$\begin{aligned} \varvec{X}_s =&\;\{\varvec{v}\in H_0(\mathrm {div};\Omega ):&\;\; \varvec{v}|_{\Omega _S}\in \varvec{H}^s(\Omega _S), \; \varvec{v}|_{\Omega _D}\in \varvec{H}^{s-1}(\Omega _D), \varvec{v}|_{\Gamma _S}=0 \},\\ Y_s =&\;\{q\in L^2_0(\Omega ):&\;\; q|_{\Omega _S}\in H^{s-1}(\Omega _S), \; q|_{\Omega _D}\in H^{s}(\Omega _D) \}. \end{aligned}$$

for some $s\in [2,k+1]$. Then, for stabilization parameter $\alpha _0$ sufficiently large, the solution ${{\underline{\varvec{{u}}}}}_h$ to the system (5) has the energy error estimate

$$\begin{aligned} {|{{\underline{\varvec{e}}}}_{u}|}_{1,S} + |{{\underline{\varvec{e}}}}_{u}|_{I} + |{{\underline{\varvec{e}}}}_{u}|_{D}&\preceq {|\underline{\varvec{\delta }}_{u}|}_{1*,S} + |\underline{\varvec{\delta }}_{u}|_{D} \end{aligned}$$

(10a)

$$\begin{aligned}&\preceq h^{s-1}\left( \nu \Vert \varvec{u}\Vert _{\varvec{H}^s(\Omega _S)} + \lambda _{\min }^{-1/2}\Vert \varvec{u}\Vert _{\varvec{H}^{s-1}(\Omega _D)}\right) , \end{aligned}$$

(10b)

where $\lambda _{\min }$ is the minimal eigenvalue of the permeability tensor K.

The following Lemmas will be used to prove Theorem 1.

Lemma 3

(Approximation) For $\varvec{u}\in \varvec{H}^s(\Omega _S)$ with some $s\in [2,k+1]$, there holds

$$\begin{aligned} |\underline{\varvec{\delta }}_{u}|_{1*,S} \preceq \nu ^{1/2} h^{s-1}\Vert \varvec{u}\Vert _{\varvec{H}^s(\Omega _S)}. \end{aligned}$$

Proof

We have

$$\begin{aligned} |\underline{\varvec{\delta }}_{u}|^2_{1*,S} = \;\sum _{T\in \mathcal {T}_{h,S}}\nu \left( \Vert {\nabla }\varvec{\delta }_{u,T}\Vert _T^2+ h^2 \Vert {\nabla }^2(\varvec{\delta }_{u,T})\Vert _T^2+ \frac{1}{h}\Vert \Pi [\![\underline{\varvec{\delta }}_{u}^t ]\!]\Vert ^2_{\partial T}\right) , \end{aligned}$$

where we obtain the desired bounds for the first two terms by standard estimates for the BDM projection. For the latter boundary term, we have

$$\begin{aligned} \Vert \Pi [\![\underline{\varvec{\delta }}_{u}^t ]\!]\Vert ^2_{\partial T} =\,&\Vert P_M[\![\underline{\varvec{\delta }}_{u}^t ]\!]\Vert ^2_{\partial T}= \Vert P_M\left( (\Pi _V \varvec{u})^t - P_M \varvec{u}^t\right) \Vert ^2_{\partial T} \\ =&\,\Vert P_M\left( (\Pi _V \varvec{u})^t - \varvec{u}^t\right) \Vert ^2_{\partial T} \le \Vert \Pi _V \varvec{u} - \varvec{u} \Vert ^2_{\partial T}, \end{aligned}$$

The above right hand side is further handled by a trace inequality:

$$\begin{aligned} \Vert \Pi _V \varvec{u} - \varvec{u} \Vert _{\partial T} \preceq h^{-\frac{1}{2}} \Vert \Pi _V \varvec{u} - \varvec{u} \Vert _{T} + h^{\frac{1}{2}} \Vert \nabla ( \Pi _V \varvec{u} - \varvec{u} ) \Vert _{T} \preceq h^{s-\frac{1}{2}} \Vert \varvec{u}\Vert _{\varvec{H}^{s}(T)}. \end{aligned}$$

$\square$

Lemma 4

(Galerkin orthogonality) Let the assumptions of Theorem 1 hold. Denoting , then

$$\begin{aligned} a_h({{{\underline{\varvec{{u}}}}}}- {{\underline{\varvec{{u}}}}}_h, {{\underline{\varvec{{v}}}}}_h) + b({{\underline{\varvec{{v}}}}}_h, p - p_h) =&\;0, \quad \forall {{\underline{\varvec{{v}}}}}_h\in {{\underline{\varvec{{U}\!}}}}_h, \end{aligned}$$

(11a)

$$\begin{aligned} b({{{\underline{\varvec{{u}}}}}}-{{\underline{\varvec{{u}}}}}_h, q_h) =&\; 0, \quad \forall q_h\in Q_h. \end{aligned}$$

(11b)

Proof

Let $\varvec{v} = (\varvec{v}_T,\varvec{v}_F)\in {{\underline{\varvec{{V}\!}}}}\,+{{\underline{\varvec{{U}\!}}}}_h$, where the space ${{\underline{\varvec{{V}\!}}}}\,$ is given by (7c). By smoothness of p and boundary conditions (2d), (2e), we have

$$\begin{aligned} b(\varvec{v}, p) =&\; -\int _{\Omega } {\nabla \cdot }\varvec{v}_T p\,\mathrm {dx}\\ =&\;\int _{\Omega _D}\varvec{v}_T\cdot {\nabla }p_D\,\mathrm {dx} + \int _{\Omega _S}\varvec{v}_T\cdot {\nabla }p_S\,\mathrm {dx} - \int _{\Gamma _{SD}}\varvec{v}_T\cdot \varvec{n} (p_S-p_D)\,\mathrm {ds}, \end{aligned}$$

where the normal direction on $\Gamma _{SD}$ points outward of $\Omega _S$. Hence, by (7d) and boundary condition (2b), we get

$$\begin{aligned} a_h({{{\underline{\varvec{{u}}}}}}, \varvec{v}) + b(\varvec{v}, p) =&\; \int _{\Omega _S}\varvec{f}_S\cdot \varvec{v}_T\,\mathrm {dx} + \int _{\Omega _D}(K^{-1} \varvec{u}_D+{\nabla }p_D) \cdot \varvec{v}_T\,\mathrm {dx}\nonumber \\&\; - \int _{\Gamma _{SD}} (p_S-p_D-2\nu \varepsilon (\varvec{u}_S)\varvec{n}\cdot \varvec{n})\varvec{v}_T\cdot \varvec{n} \,\mathrm {ds}\nonumber \\ =&\; \int _{\Omega _S} \varvec{f}_S\varvec{v}_T\,\mathrm {dx}. \end{aligned}$$

(12)

Moreover, for any $q_h\in Q_h$, we have

$$\begin{aligned} b({{\underline{\varvec{{u}}}}}, q_h) = -\int _{\Omega }{\nabla \cdot }\varvec{u}\, q_h\,\mathrm {dx} =- \int _{\Omega _D}f_D\,q_h\,\mathrm {dx}. \end{aligned}$$

We complete the proof by comparing the above equations with the scheme (5). $\square$

Now, we are ready to prove Theorem 1.

3.1.1 Proof of Theorem 1

By definition of the projections $P_Q$ and $\Pi _V$, we have

$$\begin{aligned} b({{\underline{\varvec{{v}}}}}_h, \delta _{p}) = 0\quad \forall {{\underline{\varvec{{v}}}}}_h\in {{\underline{\varvec{{U}\!}}}}_h, \text { and }\; b(\underline{\varvec{\delta }}_{u}, q_h)= 0\quad \forall q_h\in Q_h. \end{aligned}$$

Hence, by Lemma 4, the following error equation holds

$$\begin{aligned} a_h({{\underline{\varvec{e}}}}_{u}, {{\underline{\varvec{{v}}}}}_h) + b({{\underline{\varvec{{v}}}}}_h, {e}_{p}) =&\;-a_h(\underline{\varvec{\delta }}_{u}, {{\underline{\varvec{{v}}}}}_h), \quad \forall {{\underline{\varvec{{v}}}}}_h\in {{\underline{\varvec{{U}\!}}}}_h,\\ b({{\underline{\varvec{e}}}}_{u}, q_h) =&\; 0, \quad \forall q_h\in Q_h. \end{aligned}$$

Taking ${{\underline{\varvec{{v}}}}}_h= {{\underline{\varvec{e}}}}_{u}$ in the first equation and $q_h = -{e}_{p}$ in the second equation, and adding, we obtain

$$\begin{aligned} a_h({{\underline{\varvec{e}}}}_{u}, {{\underline{\varvec{e}}}}_{u}) = -a_h(\underline{\varvec{\delta }}_{u}, {{\underline{\varvec{e}}}}_{u}) =-a_{S,h}(\underline{\varvec{\delta }}_{u}, {{\underline{\varvec{e}}}}_{u})-a_D(\underline{\varvec{\delta }}_{u}, {{\underline{\varvec{e}}}}_{u})-\underbrace{a_I(\underline{\varvec{\delta }}_{u}, {{\underline{\varvec{e}}}}_{u})}_{=0}. \end{aligned}$$

(13)

where the last part vanishes due to the definition of the $L^2$ projection $P_M$,

$$\begin{aligned} a_{I}(\underline{\varvec{\delta }}_{u}, {{\underline{\varvec{e}}}}_{u}) = \; 0. \end{aligned}$$

Now, with continuity, cf. Lemma 2 and the norm equivalence on ${{\underline{\varvec{{U}\!}}}}_h$ of Lemma 1 we have

$$\begin{aligned} a_{S,h}(\underline{\varvec{\delta }}_{u}, {{\underline{\varvec{e}}}}_{u}) \preceq |\underline{\varvec{\delta }}_{u}|_{1*,S} |{{\underline{\varvec{e}}}}_{u}|_{1*,S} \preceq |\underline{\varvec{\delta }}_{u}|_{1*,S} |{{\underline{\varvec{e}}}}_{u}|_{1,S} \end{aligned}$$

which combined with coercivity from Lemma 2 yields

$$\begin{aligned} {|{{\underline{\varvec{e}}}}_{u}|}_{1,S}^2&+ |{{\underline{\varvec{e}}}}_{u}|_{I}^2 + |{{\underline{\varvec{e}}}}_{u}|_{D}^2 \preceq a_h({{\underline{\varvec{e}}}}_{u}, {{\underline{\varvec{e}}}}_{u}) = -a_{S,h}(\underline{\varvec{\delta }}_{u}, {{\underline{\varvec{e}}}}_{u}) - a_D(\underline{\varvec{\delta }}_{u},{{\underline{\varvec{e}}}}_{u}) \\&\preceq \left( {|\underline{\varvec{\delta }}_{u}|}_{1*,S}^2 + |\underline{\varvec{\delta }}_{u}|_{D}^2 \right) ^{\frac{1}{2}} \left( {|{{\underline{\varvec{e}}}}_{u}|}_{1,S}^2 + |{{\underline{\varvec{e}}}}_{u}|_{D}^2 \right) ^{\frac{1}{2}} \end{aligned}$$

which implies (10a). We bound both terms on the right hand side of (10a) to obtain (10b). There holds

$$\begin{aligned} |\underline{\varvec{\delta }}_{u}|_D = \Vert K^{-1/2}\varvec{\delta }_{u,T}\Vert _{\Omega _D}\Vert \preceq \lambda _{\min }^{-1/2}h^{s-1}\Vert \varvec{u}\Vert _{\varvec{H}^{s-1}(\Omega _D)}. \end{aligned}$$

and by Lemma 3, we further have

$$\begin{aligned} |\underline{\varvec{\delta }}_{u}|_{1*,S} \preceq (\nu ^{1/2} h^{s-1}\Vert \varvec{u}\Vert _{\varvec{H}^s(\Omega _S)}). \end{aligned}$$

This completes the proof. $\square$

3.2 $L^2$-Estimate in the Stokes Subdomain

We will use the following dual problem: Assume $(\varvec{u}^*, p^*)$ solve Eqs. (1), (2) with source terms $\varvec{f}_S = \varvec{\psi }$ and $f_D=0$, and further assume the following regularity estimates:

$$\begin{aligned}&\Vert \varvec{u}^*\Vert _{\varvec{H}^{1+r}(\Omega _S)}&\le C\Vert \varvec{\psi }\Vert _{\Omega _S}, \qquad&\Vert \varvec{u}^*\Vert _{\varvec{H}^{r}(\Omega _D)}&\le C\Vert \varvec{\psi }\Vert _{\Omega _S}, \end{aligned}$$

(14a)

$$\begin{aligned}&\Vert p^*\Vert _{\varvec{H}^{r}(\Omega _S)}&\le C\Vert \varvec{\psi }\Vert _{\Omega _S}, \qquad&\Vert p^*\Vert _{\varvec{H}^{1+r}(\Omega _D)}&\le C\Vert \varvec{\psi }\Vert _{\Omega _S}, \end{aligned}$$

(14b)

for some real number $1/2<r\le 1$. This assumption is justified, for instance if $\Omega _S$ and $\Omega _D$ are convex.

Theorem 2

Let the assumptions of Theorem 1 hold. Assume further the regularity estimates (14) hold. Then, the following error estimate holds

$$\begin{aligned} \Vert {{\varvec{u}}-\varvec{u}_{h,T}}\Vert _{\Omega _S}\preceq h^{s-1+r} (\Vert \varvec{u}\Vert _{\varvec{H}^s(\Omega _S)}+\Vert \varvec{u}\Vert _{\varvec{H}^{s-1}(\Omega _D)}+\Vert f_D\Vert _{H^{s-1}(\Omega _D)}). \end{aligned}$$

(15)

Proof

Let $(\varvec{u}^*, p^*)$ be solutions to (1), (2) with $\varvec{f}_S = \varvec{u} - \varvec{u}_{h,T}$, and $f_D=0$. Denote ${{\underline{\varvec{{u}}}}}^*= (\varvec{u}^*, (\varvec{u}^*)^t|_{\mathcal {F}_{h,S}})$. By (12), we get

$$\begin{aligned} a_h({{\underline{\varvec{{u}}}}}^*, {{\underline{\varvec{{v}}}}}) +b({{\underline{\varvec{{v}}}}}, p^*) = (\varvec{u} - \varvec{u}_{h,T}, \varvec{v}_T)_{\Omega _S}, \quad \forall \varvec{v}\in {{\underline{\varvec{{V}\!}}}}\,+{{\underline{\varvec{{U}\!}}}}_h. \end{aligned}$$

Taking ${{\underline{\varvec{{v}}}}}= {{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h$, we get

$$\begin{aligned} \Vert \varvec{u} - \varvec{u}_{h,T}\Vert _{\Omega _S}^2 =&\; a_h({{\underline{\varvec{{u}}}}}^*, {{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h) +b({{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h, p^*)\\ =&\; a_h({{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h, {{\underline{\varvec{{u}}}}}^*) +b({{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h, p^*) \end{aligned}$$

Let us bound each of the above terms on the right hand side. We denote ${{\underline{\varvec{{u}}}}}_h^*= (\Pi _V\varvec{u}^*, P_M(\varvec{u}^*)^t)$. We have ${\nabla \cdot }\Pi _V\varvec{u}^*={\nabla \cdot }\varvec{u}^*=0$. Taking ${{\underline{\varvec{{v}}}}}_h= {{\underline{\varvec{{u}}}}}_h^*$ in (11a), we get $a_h({{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h, {{\underline{\varvec{{u}}}}}_h^*)=0.$ Hence,

$$\begin{aligned} a_h({{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h, {{\underline{\varvec{{u}}}}}^*)= a_h({{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h, {{\underline{\varvec{{u}}}}}^*-{{\underline{\varvec{{u}}}}}_h^*). \end{aligned}$$

We have

$$\begin{aligned} a_{S,h}({{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h, {{\underline{\varvec{{u}}}}}^*-{{\underline{\varvec{{u}}}}}_h^*)&\;\preceq |{{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h|_{1*,S} | {{\underline{\varvec{{u}}}}}^*-{{\underline{\varvec{{u}}}}}_h^*|_{1*,S}\\&\; \preceq \nu ^{1/2}h^{r} | \varvec{u}^*|_{\varvec{H}^{1+r}(\Omega _S)} |{{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h|_{1*,S},\\ a_{I}({{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h, {{\underline{\varvec{{u}}}}}^*-{{\underline{\varvec{{u}}}}}_h^*)&\; \le |{{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h|_I |{{\underline{\varvec{{u}}}}}^*-{{\underline{\varvec{{u}}}}}_h^*|_{I}\\&\; \preceq \gamma ^{1/2}\lambda _{\min }^{-1/4}h^{1/2+r} | \varvec{u}^*|_{\varvec{H}^{1+r}(\Omega _S)} |{{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h|_I, \\ a_{D}({{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h, {{\underline{\varvec{{u}}}}}^*-{{\underline{\varvec{{u}}}}}_h^*)&\;\le |{{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h|_D |{{\underline{\varvec{{u}}}}}^*-{{\underline{\varvec{{u}}}}}_h^*|_{D}\\&\; \preceq \lambda _{\min }^{-1/2}h^{r} | \varvec{u}^*|_{\varvec{H}^{r}(\Omega _D)} |{{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h|_D. \end{aligned}$$

Combing the above estimates with the regularity assumption (14), we get

$$\begin{aligned} a_h({{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h, {{\underline{\varvec{{u}}}}}^*) \preceq h^r\left( |{{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h|_{1*,S} +h^{1/2}|{{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h|_{I} + |{{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h|_{D} \right) \Vert \varvec{u} - \varvec{u}_{h,T}\Vert _{\Omega _S}. \end{aligned}$$

The norm in the parentheses of the above right hand side is bounded by $C h^{s-1}(\Vert \varvec{u}\Vert _{\varvec{H}^s(\Omega _S)}+\Vert \varvec{u}\Vert _{\varvec{H}^{s-1}(\Omega _D)})$ by Theorem 1.

On the other hand, we have

$$\begin{aligned} b({{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h, p^*) =&\; -\int _{\Omega }{\nabla \cdot }(\varvec{u}-{{\underline{\varvec{{u}}}}}_h)p^* \,\mathrm {dx} \\ =&\; -\int _{\Omega _D}(f_D-P_Q f_D)p^*\,\mathrm {dx} \qquad \text { since } {\nabla \cdot }\varvec{u}_{h,T} = P_Q f_D\\ =&\; -\int _{\Omega _D}(f_D-P_Q f_D)(p^*-P_Q p^*)\,\mathrm {dx}\\ \le \,&\Vert f_D-P_Qf_D\Vert _{\Omega _D} \Vert p^*-P_Q p^*\Vert _{\Omega _D} \;\;\preceq h^{s-1+r}\Vert f_D\Vert _{H^{s-1}(\Omega _D)} \Vert p^*\Vert _{H^r(\Omega _D)}\\ \preceq \,&h^{s-1+r}\Vert f_D\Vert _{H^{s-1}(\Omega _D)} \Vert \varvec{u} - \varvec{u}_{h,T}\Vert _{\Omega _S}. \end{aligned}$$

The proof is concluded by combing the above estimates. $\square$

3.3 $L^2$-Estimate in the Darcy Subdomain

Theorem 3

Let the assumptions of Theorem 2 hold. Assume further that $\varvec{u}_D\in \varvec{H}^{s}(\Omega _D)$ for $s\in [2,k+1]$. Then, the following error estimate holds

$$\begin{aligned} \Vert {{\varvec{u}}-\varvec{u}_{h,T}}\Vert _{\Omega _D} \preceq h^{s-1+r}(\Vert \varvec{u}\Vert _{H^s(\Omega _S)}+\Vert \varvec{u}\Vert _{H^{s}(\Omega _D)}+\Vert f_D\Vert _{H^{s-1}(\Omega _D)}). \end{aligned}$$

(16)

We need the following Lemma to prove Theorem 3.

Lemma 5

We have

$$\begin{aligned} \Vert (\varvec{u}-\varvec{u}_{h,T})\cdot \varvec{n}\Vert _{H^{-1/2}(\Gamma _{SD})} \preceq h^{s-1+r}(\Vert \varvec{u}\Vert _{H^s(\Omega _S)}+\Vert \varvec{u}\Vert _{H^{s-1}(\Omega _D)}+\Vert f_D\Vert _{H^{s-1}(\Omega _D)}). \end{aligned}$$

Moreover, there is a function $\varvec{w}\in \varvec{H}(\mathrm {div};\Omega _D)\cap \varvec{H}^{1/2}(\Omega _D)$ satisfying ${\nabla \cdot }\varvec{w} =0$ on $\Omega$, $\varvec{w}\cdot \varvec{n}=0$ on $\Gamma _D$, and $\varvec{w}\cdot \varvec{n}=(\varvec{u}-\varvec{u}_{h,T})\cdot \varvec{n}$ on $\Gamma _{SD}$, such that

$$\begin{aligned} \Vert \varvec{w}\Vert _{\Omega _D}\preceq&\; \Vert (\varvec{u}-\varvec{u}_{h,T})\cdot \varvec{n}\Vert _{H^{-1/2}(\Gamma _{SD})},\\ \Vert \varvec{w}\Vert _{\varvec{H}^{1/2}(\Omega _D)}\preceq&\; \Vert (\varvec{u}-\varvec{u}_{h,T})\cdot \varvec{n}\Vert _{\Gamma _{SD}}. \end{aligned}$$

Proof

Since $\varvec{u}-\varvec{u}_{h,T}\in H(\mathrm {div};\Omega _S)$, its normal trace satisfies, c.f. [19],

$$\begin{aligned} \Vert (\varvec{u}-\varvec{u}_{h,T})\cdot \varvec{n}\Vert _{H^{-1/2}(\partial \Omega _{S})}\preceq \Vert \varvec{u}-\varvec{u}_{h,T}\Vert _{\varvec{H}(\mathrm {div};\Omega _S)}. \end{aligned}$$

Since $(\varvec{u}-\varvec{u}_{h,T})\cdot \varvec{n} = 0$ on $\Gamma _S$, following the approach [16], we have

$$\begin{aligned} \Vert (\varvec{u}-\varvec{u}_{h,T})\cdot \varvec{n}\Vert _{H^{-1/2}(\Gamma _{SD})}\preceq \Vert \varvec{u}-\varvec{u}_{h,T}\Vert _{\varvec{H}(\mathrm {div};\Omega _S)}. \end{aligned}$$

Since ${\nabla \cdot }(\varvec{u}-\varvec{u}_{h,T}) = 0$ on $\Omega _S$, we have with Theorem 2

$$\begin{aligned} \Vert \varvec{u}-\varvec{u}_{h,T}\Vert _{\varvec{H}(\mathrm {div};\Omega _S)}&= \Vert \varvec{u}-\varvec{u}_{h,T}\Vert _{\Omega _S} \\&\preceq h^{s-1+r} (\Vert \varvec{u}\Vert _{\varvec{H}^s(\Omega _S)}+\Vert \varvec{u}\Vert _{\varvec{H}^{s-1}(\Omega _D)}+\Vert f_D\Vert _{H^{s-1}(\Omega _D)}). \end{aligned}$$

The other two inequalities are given in [20, Lemma 11]. $\square$

Now, we are ready to prove Theorem 3.

3.3.1 Proof of Theorem 3

Let $\varvec{w}$ be given by Lemma 5. Let $\varvec{v}$ be such that $\varvec{v} = 0$ on $\Omega _S$, and $\varvec{v} = \Pi _V\varvec{u}-\varvec{u}_{h,T}-\Pi _V\varvec{w}$ on $\Omega _D$. We have $\varvec{v}\cdot \varvec{n} = (\Pi _V\varvec{u}-\varvec{u}_{h,T}-\Pi _V\varvec{w})\cdot \varvec{n} = 0$ on $\Gamma _{SD}$, hence $\varvec{v}\in \varvec{\Sigma }_h$ and ${\nabla \cdot }\varvec{v} = 0$. Taking ${{\underline{\varvec{{v}}}}}_h=(\varvec{v},0)$ in Eq. (11a), we get

$$\begin{aligned} a_h({{\underline{\varvec{{u}}}}}-{{\underline{\varvec{{u}}}}}_h,{{\underline{\varvec{{v}}}}}_h)= \int _{\Omega _D}K^{-1}(\varvec{u}-\varvec{u}_{h,T})(\Pi _V\varvec{u}-\varvec{u}_{h,T}-\Pi _V\varvec{w})\,\mathrm {dx}= 0. \end{aligned}$$

This implies that

$$\begin{aligned} \Vert \varvec{u}-&\,\varvec{u}_{h,T}\Vert _{\Omega _D} \le \Vert \varvec{u}-\Pi _V\varvec{u} -\Pi _V\varvec{w}\Vert _{\Omega _D} \\ \preceq&\,\Vert \varvec{u}-\Pi _V\varvec{u}\Vert _{\Omega _D} + \Vert \Pi _V \varvec{w}\Vert _{\Omega _D}\\ \preceq&\,h^{s}\Vert \varvec{u}\Vert _{\varvec{H}^s(\Omega _D)}+ \Vert (\varvec{u}-\varvec{u}_{h,T})\cdot \varvec{n}\Vert _{H^{-1/2}(\Gamma _{SD})}\\ \preceq&\, h^{s}\Vert \varvec{u}\Vert _{\varvec{H}^s(\Omega _D)}+ h^{s-1+r} \left( \Vert \varvec{u}\Vert _{\varvec{H}^s(\Omega _S)}+\Vert \varvec{u}\Vert _{\varvec{H}^{s-1}(\Omega _D)}+\Vert f_D\Vert _{H^{s-1}(\Omega _D)}\right) . \end{aligned}$$

$\square$

4 Numerical Results

In this section, we present numerical results in two dimensions to verify the theoretical findings in Sect. 3. The numerical results are performed using the NGSolve software [35].

We consider an example with a smooth manufactured exact solution constructed in [12]. The domain is a unit square $\Omega =[0,1]\times [0,1]$ with the Darcy subdomain $\Omega _D = [0,1]\times [0,0.5]$, and Stokes subdomain $\Omega _S=[0,1]\times [0.5,1]$. We take $\nu =K = 1$, and $\gamma = (1+4\pi ^2)/2$. The source terms are chosen such that the problem has the exact solution:

We apply the numerical scheme (5) using polynomial degree k for the velocity space $\varvec{\Sigma }_h$, $k-1$ for the pressure space $Q_h$, and $k-1$ for the facet tangential velocity space $M_h$ with k varying from 1 to 4. For all the tests, we take the stabilization parameter $\alpha = 10\,k^2$. The history of convergence for the $L^2$-error of the velocity in each subdomain and the $L^2$ norm of the quantity ${\nabla \cdot }\varvec{u}_{h,T}-\chi _D P_Q f_D$ are recorded in Table 1. We observe optimal order of convergence $k+1$ for each error. This result is in full agreement with our main results in Theorems 2 and 3 for $k\ge 2$. However, our analysis could not explain the optimal convergence for the lowest-order case ($k=1$), since the analysis requires the facet tangential velocity space to include polynomials of degree 1, see Lemma 1. The optimal convergence of this lowest order case requires further investigation. We also observe the strong mass conservation result, c.f. Remark 1, that the quantity ${\nabla \cdot }\varvec{u}_{h,T}-\chi _D P_Q f_D$ is machine zero for all the tests.

Finally, we remark that, if we increase the polynomial degree of the facet tangential velocity space to be k, similar error and convergence rates were obtained in our numerical results not recorded here.

Hence, this modification is less attractive to the method tested here as it gives similar accuracy but has a lot more globally coupled degrees of freedom, see also the performance comparisons for vector-Laplace and Stokes problems with similar discretizations in [25, Section 4.3] and [23, Section 5.2].

Table 1 History of convergence of the $L^2$-velocity errors

5 Conclusion

We presented a new finite element method for the coupling of Stokes and Darcy flow, where the Stokes flow is discretized by a divergence-conforming HDG method, and the Darcy flow by a mixed finite element method. Exact mass conservation is guaranteed. We presented optimal error estimates of the proposed method with numerical results supporting the theoretical findings.