The Linear Barycentric Rational Method for a Class of Delay Volterra Integro-Differential Equations

Abstract

A method for solving delay Volterra integro-differential equations is introduced. It is based on two applications of linear barycentric rational interpolation, barycentric rational quadrature and barycentric rational finite differences. Its zero–stability and convergence are studied. Numerical tests demonstrate the excellent agreement of our implementation with the predicted convergence orders.

1 Introduction

Natural phenomena in which a quantity varies in time and simultaneously depends on its past values are often modeled with Volterra integral equations. When these past values arise at a shifted abscissa as well as at present time, one speaks of an equation with delay or a delay equation. A classical system of delay Volterra integral equations (DVIEs) of the second kind is therefore often assumed to be

$$\begin{aligned} \left\{ \begin{array}{ll} y(t)=f\Big (t, y(t), y(t-\tau ),\displaystyle \int _{t-\tau }^t K(t,s,y(s))\,\mathrm {d}s\Big ), &{} t\in [t_0,T],\\ y(t)=\upvarphi (t), &{} t\in [t_0-\tau ,t_0], \end{array} \right. \end{aligned}$$

in which $y:\mathbb {R}\rightarrow \mathbb {R}^{D_1}$ is the unknown function and $K:\mathbb {R}^2\times \mathbb {R}^{D_1}\rightarrow \mathbb {R}^{D_2}$, $D_1, D_2\in \mathbb {N}$, the given so-called kernel of the integral operator characterizing the equation together with the given functions $f:\mathbb {R}\times \mathbb {R}^{D_1}\times \mathbb {R}^{D_1}\times \mathbb {R}^{D_2}\rightarrow \mathbb {R}^{D_1}$ and $\upvarphi :\mathbb {R}\rightarrow \mathbb {R}^{D_1}$; $\upvarphi$ is the initial function and $\tau >0$ is the (constant) delay. (An equation of the first kind is one in which the lone y on the left-hand side is absent, i.e., zero.)

In some models, f rather describes the behavior of the derivative of the unknown: one then obtains a system of so-called delay Volterra integro-differential equations (DVIDEs)

$$\begin{aligned} \left\{ \begin{array}{ll} y'(t)=f\Big (t,y(t),y(t-\tau ),\displaystyle \int _{t-\tau }^t K(t,s,y(s))\,\mathrm {d}s\Big ),&{} t\in [t_0,T],\\ y(t)=\upvarphi (t), &{} t\in [t_0-\tau ,t_0] \end{array} \right. \end{aligned}$$

(1)

for the same classes of functions as above. Practical examples of (1) are the modelling of the cohabitation of different biological species [19] or of the human immune response [25]. In the present paper, we shall introduce a numerical procedure for the solution of systems of equations such as (1). We thereby assume that the given functions f, K and $\upvarphi$ are smooth enough for the system to have a unique solution y (for conditions guaranteeing this, see [34]). We further assume that the initial function $\upvarphi$ is compatible with the solution y in the sense that $\upvarphi \in C^{d+2}[t_0-\tau ,t_0]$ and for the derivatives at $t_0$,

$$\begin{aligned} \upvarphi {}^{(j)}(t_0-) = y^{(j)}(t_0+),\qquad j=0,\ldots ,d+2, \end{aligned}$$

(2)

where d is the parameter in the barycentric approximation which lies at the basis of our method, see the convergence theorem (Theorem 1). This eliminates the risk of primary singularities in the solution at multiples of $\tau$ [11, 24, 26], singularities which do not occur in most applications of DVIDEs in the natural sciences. (In fact, it would perhaps be preferable to call this property “consistency”, but this term is already taken in the context of functional equations.)

In view of the advance in time, it is very natural, at least if nothing particular is known about the behavior of the solution, to approximate it at equispaced values of the t-variable, i.e., to calculate values $y_m\approx y(t_m)$, $t_m=t_0+mh$. Several methods are already available [12, 17, 27, 33,34,35,36]. Most of them, in particular the very popular Runge–Kutta and collocation ones, consider and/or compute values of y and/or f at intermediate points as well, e.g., Legendre points stretched to fit into the interval $[t_m, t_{m+1}]$; the resulting piecewise Legendre point set obviously breaks the regularity of the time variable. (We leave off here global methods which treat Volterra equations as the Fredholm ones: although their convergence may be spectral [30], they require the determination of T in advance and a restart from scratch for any increase of T; moreover, they require solving a dense system of equations, which becomes very costly for large $D_1$ and/or $D_2$.)

In contrast, quadrature methods merely consider values at the equispaced $t_m$. The method we shall present is an extension to DVIDEs of the quadrature method introduced in [6]. The treatment of the right-hand side will thereby be an application of the composite barycentric rational quadrature (CBRQ) rule presented in that same article. Thus the approximation at $t_m$ of $y'$, the left-hand side of (1), remains to be chosen. To stay with the mere values at equispaced $t_m$, divided differences are the natural way to go. Since only values at $t_k$, $k\le m$, are known at time $t_m$, left one-sided differences should be used. For relatively large time steps h, customary polynomial differences work well only for small numbers of points, for as this number increases, the approximation becomes ill-conditioned in view of the Runge phenomenon affecting the underlying polynomial interpolant [22]; this limits the order of convergence of the polynomial method. We therefore use instead the barycentric rational finite differences (RFD) formula introduced in [22]; they have the advantage of leading to a fully (linear) rational method. We recall that both the quadrature and the differentiation methods introduced in [21], resp. [22], are based on the exact integration, resp. differentiation, of the linear barycentric rational interpolant presented in [14] and further discussed in [7] and [16].

After the present introduction, Sect. 2 briefly reviews the two applications of linear barycentric rational interpolation which lie at the basis of this work, namely the composite barycentric rational quadrature and the barycentric rational finite differences. Section 3 introduces the method for solving DVIDEs based on barycentric rational interpolation and discuss its zero–stability and convergence. Section 4 illustrates the results with numerical experiments. General remarks about the method conclude the paper.

2 A Short Review of the CBRQ Rule and the RFD Formulas

In this section, we recall the construction of the CBRQ rule for the approximation of definite integrals and of the RFD formulas for the approximation of the first derivative of a function at a grid point. Both are based on an exact application of the corresponding operator to a linear barycentric rational interpolant instead of the interpolating polynomial. Linear barycentric rational interpolants have been introduced by the second author in [4]. They consist in replacing the weights $\lambda _j$ in the barycentric formula

$$\begin{aligned} p_n(t) =\sum \limits _{j=0}^{n} {\lambda _j \over t - t_j}f(t_j)\bigg / \sum _{j=0}^n {\lambda _j\over t - t_j} , \qquad \lambda _i = 1\bigg / \prod _{{j=0}, {j\ne i}}^n(t_i-t_j) \end{aligned}$$

for the interpolating polynomial $p_n$ with more appropriate weights $\beta _j$, which are still independent of the interpolated function, but are chosen in such a way that bad properties of the polynomial such as ill–conditioning and Runge’s phenomenon are avoided, and convergence and well–conditioning are guaranteed.

The two sets of weights presented in [4] are $\beta _j = (-1)^j$ and the same with the first and last ones halved; this requires that the nodes are ordered according to $t_0<t_1<\ldots <t_n$. The corresponding two interpolants are excellently conditioned, but the first converges as O(h) and the second as $O(h^2)$, where h is the usual steplength $h:= \max \left\{ t_{i+1}-t_i\right\}$. Another linear rational interpolant, which depends on a parameter d and converges at the rate $O(h^{d+1})$, has been introduced in [14]. Its barycentric weights for equispaced nodes—only the latter are used in the present work—are

$$\begin{aligned} \beta _j = {(-1)^{j-d}\over 2^d}\sum _{i\in J_j}{d\atopwithdelims ()j-i},\qquad J_j := \left\{ i\in \{0,\ldots ,n-d\}:j-d\le i\le j\right\} . \end{aligned}$$

(3)

As it is based on a blend of all interpolating polynomials of $d+1$ consecutive nodes, it may be ill-conditioned and/or unstable for large d and/or arbitrary sets of points [5], but is excellent for equispaced nodes and not too large d. This makes it an interesting choice for solving smooth problems on the basis of equispaced samples [7]. This is the case of the quadrature method for Volterra integral equations introduced in [6].

2.1 The CBRQ Rule

The basic idea here is to replace the function to be approximated, say g, by the linear barycentric rational interpolant and apply the operator to the latter. In the global barycentric rational quadratic rule [21], the integrand is approximated by a single interpolant on the whole interval of integration,

$$\begin{aligned} r_n(t) = \sum _{j=0}^n g(t_j)\ell _j(t),\quad \ell _j(t) := {\beta _j\over t - t_j}\bigg / \sum _{i=0}^n {\beta _i\over t - t_i}, \end{aligned}$$

which for equispaced nodes leads to the rule $\int _{t_0}^{t_n} g(s) \mathrm {d}s \approx h \sum _{k=0}^n w_kg(t_k)$, with the quadrature weights $w_k = h^{-1}\cdot$ $\int _{t_0}^{t_n}\ell _k(t)\mathrm {d}t$; the latter are evaluated in machine precision by means of an accurate quadrature rule such as Gauss or Clenshaw–Curtis, both provided in the Chebfun system [31]. In the corresponding quadrature method for the solution of classical VIEs, the number of terms in the rule becomes larger and larger with increasing n. The last two authors have therefore suggested with Klein in [6] to construct instead a composite barycentric rational quadrature rule, in which the interval of interpolation is divided into subintervals of length nh and a last interval of smaller length, and to use only the weights corresponding to the said subintervals; we shall use the same rules here.

For integrals such as that in (1.1) over intervals of length $\tau >0$, we assume that there exists a positive integer q, such that

$$\begin{aligned} h=\frac{\tau }{q}, \end{aligned}$$

and consider a uniform grid

$$\begin{aligned} 0=x_0<x_1<\cdots <x_q=\tau , \end{aligned}$$

with $x_{j+1}-x_j=h$, $j=0,1,\ldots ,q-1$. We choose a value of the parameter d, a fixed number n of nodes with $d\le n\le q/2$ and we set $p:=\lfloor q/n\rfloor -1$. After an obvious change of variable, we approximate the integral with the composite rule

$$\begin{aligned} \int _0^\tau g(s) \mathrm {d}s \approx h \sum _{j=0}^{p-1} \sum _{k=0}^{n} w_{k}^{(n)} g(x_{jn+k}) + h \sum _{k=0}^{q-pn} w_{k}^{(q-pn)} g(x_{pn+k}), \end{aligned}$$

(4)

where

$$\begin{aligned} w_{k}^{(r)} = r\int _0^1 \frac{\frac{\beta _k}{rs-k}}{\sum _{j=0}^r \frac{\beta _j}{rs-j}} \mathrm {d}s, \quad r=n,n+1,\ldots ,2n-1. \end{aligned}$$

The convergence order of the rule (4) is given in the following proposition.

Proposition 1

[6] Suppose n, d and q, $d\le n \le q/2$, are positive integers, $g\in C^{d+2}[0,\tau ]$. Then the absolute error in the approximation of the integral of g with (4) is bounded by $Ch^{d+1}$, where the constant C depends only on d, on derivatives of g and on the interval length $\tau$.

When $n-d$ is odd, the bound on the interpolation error given in [14], Thm. 2, involves an additional factor nh, so that the order of the related quadrature rule increases to $d+2$. Notice that in some of our computations we used n close to q, which implies $p=0$; then the method is global, not composite [6].

2.2 The RFD Formulas

In the same fashion, linear rational finite differences are obtained by exactly differencing the linear barycentric rational interpolant [22]. In practice, central differences do not perform better than polynomial differences, when the nodes are equispaced. In the case we are concerned with here, however, the derivatives are needed at $t_m$, the right extremity of the interval of interpolation, so that left–sided differences are necessary. In that case and with a large number of nodes, rational differences are much more accurate than polynomial ones [22].

Let m be a positive integer. For the approximation of the first derivative of a sufficiently smooth function g at the node $t_m$ via $t_{m-n}$, $\ldots$, $t_{m}$, we compute [2, 20, 22]

$$\begin{aligned} g'(t_m)\approx \frac{1}{h}\sum _{j=0}^n v_j g(t_{m-j}), \end{aligned}$$

(5)

where

$$\begin{aligned} v_j=\left\{ \begin{array}{ll} \dfrac{\beta _{n-j}}{j\beta _n}\,, &{} j\ne 0,\\ -\displaystyle \sum _{l=1}^n v_l\,, &{} j=0. \\ \end{array}\right. \end{aligned}$$

Proposition 2

[20, 22] Suppose m, n and d, $d\le n$, are positive integers, $t_{m-n}$, $\ldots$, $t_m$ are equispaced nodes in the interval [a, b] and $g\in C^{d+2}[a,b]$. Then the absolute error of the approximation formula (5) is bounded by $Ch^d$.

One can prove that

$$\begin{aligned} \sum _{j=0}^n v_j e^{-jz} = z + O(z^{d+1}). \end{aligned}$$

Some values of $v_j$ are given in Sect. 3.1 below.

In fact, when $n-d$ is odd, and in view of the increase of the guaranteed order of the interpolation error by one unit mentioned after Proposition 1, the order of the related divided difference increases to $d+1$.

Further results on the convergence of the derivatives of the Floater–Hormann family of interpolants have just been published [13].

3 Description of the Method for DVIDEs

Consider a uniform grid

$$\begin{aligned} t_0-\tau =t_{-q}<t_{-q+1}<\cdots<t_0<t_1<\cdots <t_N, \quad t_N\ge T, \end{aligned}$$

and let $t_{i+1}-t_i=h$, $i=-\,q,-\,q+1,\ldots ,N-1$, with $h=\tau /q$ as in Sect. 2. Let d, n, and p be as in Sect. 2.1. Applying the RFD formula (5) and the CBRQ rule (4) to the derivative and integral parts of (1) at the point $t_m$, respectively, yields

$$\begin{aligned} \sum _{j=0}^n v_j y_{m-j} = hf\bigl (t_m,y_m,y_{m-q},\widetilde{Q}_m(h)\bigr ), \quad m=1,2,\ldots ,N, \end{aligned}$$

(6)

for the unknown $y_m$, where

$$\begin{aligned} \widetilde{Q}_m(h)&= h\sum _{j=0}^{p-1} \sum _{k=0}^{n} w_{k}^{(n)} K(t_m,t_{jn+k+m-q},y_{jn+k+m-q})\\&\qquad \quad + h \sum _{k=0}^{q-pn} w_{k}^{(q-pn)} K(t_m,t_{pn+k+m-q},y_{pn+k+m-q}). \end{aligned}$$

Here $y_m$, $m=1,2,\ldots ,N$, is an approximation to the exact solution y of (1) at the mesh point $t_m$. According to the initial condition in (1), we may take

$$\begin{aligned} y_m=\upvarphi (t_m),\quad m=-q,-q+1,\ldots ,0. \end{aligned}$$

If the functions f and/or K are nonlinear in y, the fact that $y_m$ appears on both sides of (6) implies that nonlinear algebraic equations must be solved at each step; our implementation uses Newton’s method for this purpose.

In the next two subsections, we shall discuss the zero–stability and the convergence of the method (6).

3.1 Zero–Stability

It is well-known that the zero–stability of a method is a necessary condition for the convergence of that method [23]. The zero–stability of a method is warranted, if the numerical solution $y_m$ of problem (1) with $f(\cdot ,\cdot ,\cdot ,\cdot )\equiv 0$ is bounded. The method (6) applied to such problems gives the difference equation $\sum _{j=0}^n v_j y_{m-j}=0$. We may then define its zero–stability as follows.

Definition 1

The method (6) is said to be zero–stable, if the roots of the polynomial

$$\begin{aligned} \rho (x) := v_0x^n+v_1x^{n-1}+\cdots +v_n \end{aligned}$$

lie inside or on the unit circle, those on the circle being simple.

To assist the reader in the use of the method (6) and the study of its zero–stability, the vector $v= [v_0\quad v_1\quad \cdots \quad v_n]^T$ is given for some special cases in Table 1. Note that for $d=n-1$ the Floater–Hormann interpolant coincides with the interpolating polynomial. As a consequence, the coefficients $v_i$’s, $i=0,1,\ldots ,n$, are those of the cooresponding backward differentiation formula (BDF) [10, 23]. For example, in the case of $(n,d)=(4,3)$ and $(n,d)=(6,5)$, the $v_i$’s are the coefficients of the BDFs of orders 4 and 6, respectively.

Table 1 Weights for left-sided RFD formula (5) for various pairs (n, d)

To investigate the zero–stability of the method (6), we use Bistritz’ stability criterion [8], which determines how many zeros of $\rho (x)/(1-x)$ lie strictly inside the unit disk. For example, the Bistritz stability sequences of the polynomial $\rho (x)/(1-x)$ corresponding to the pairs (n, d) of Table 1 are given in Table 2. The number of sign changes, nsc, in these sequences gives the number of zeros of $\rho (x)/(1-x)$ that lie outside of the closed unit disk. From this table, we find that the method with the values of (n, d) given in Table 1 is zero–stable except for $(n,d)=(7,6)$ and (11, 6). Continuing in this way, one can show that the method (6) is zero–stable for every choice of $n\ge d$ with $n\le 20$ and $d\le 6$, except for $(n,d)=(7,6)$, (8, 6), (11, 6), and (12, 6).

Table 2 Bistritz stability sequences of the polynomial $\rho (x)/(1-x)$ for various pairs (n, d)

3.2 Convergence Analysis

Let $y\in C^{d+2}[t_0-\tau ,T]$, $K\in C^{d+2}(\varOmega )$ where $\varOmega :=S\times \mathbb {R}^{D_1}$ with $S=\{(t,s):t_0\le t\le T,~ t-\tau \le s\le t\}$, f be continuous on $\mathscr {R}:=[t_0,T]\times \mathbb {R}^{D_1}\times \mathbb {R}^{D_1}\times \mathbb {R}^{D_2}$, and

$$\begin{aligned} \forall \; (t,y_1,u,z),(t,y_2,u,z)\in \mathscr {R}:&\quad \bigl \Vert f(t,y_1,u,z)-f(t,y_2,u,z)\bigr \Vert \le L_1\bigl \Vert y_1-y_2\bigr \Vert ,\nonumber \\\end{aligned}$$

(7a)

$$\begin{aligned} \forall \; (t,y,u_1,z),(t,y,u_2,z)\in \mathscr {R}:&\quad \bigl \Vert f(t,y,u_1,z)-f(t,y,u_2,z)\bigr \Vert \le L_2\bigl \Vert u_1-u_2\bigr \Vert ,\nonumber \\\end{aligned}$$

(7b)

$$\begin{aligned} \forall \; (t,y,u,z_1),(t,y,u,z_2)\in \mathscr {R}:&\quad \bigl \Vert f(t,y,u,z_1)-f(t,y,u,z_2)\bigr \Vert \le L_3\bigl \Vert z_1-z_2\bigr \Vert ,\nonumber \\\end{aligned}$$

(7c)

$$\begin{aligned} \forall \; (t,s,y_1),(t,s,y_2)\in \varOmega :&\quad \bigl \Vert K(t,s,y_1)-K(t,s,y_2)\bigr \Vert \le L_4\bigl \Vert y_1-y_2\bigr \Vert ,\quad \quad \end{aligned}$$

(7d)

where $\Vert \cdot \Vert$ is any norm in the corresponding spaces.

Definition 2

The local truncation error of the method (6) at the point $t_m$ is defined by

$$\begin{aligned} \mathscr {L}[y(t_m);h]:=\sum _{j=0}^n v_j y(t_{m-j})- hf\bigl (t_m,y(t_m),y(t_{m-q}),Q_m(h)\bigr ), \quad m=1,2,\ldots ,N, \end{aligned}$$

(8)

where

$$\begin{aligned} Q_m(h)&= h\sum _{j=0}^{p-1} \sum _{k=0}^{n} w_{k}^{(n)} K(t_m,t_{jn+k+m-q},y(t_{jn+k+m-q}))\\&\qquad \quad + h \sum _{k=0}^{q-pn} w_{k}^{(q-pn)} K(t_m,t_{pn+k+m-q},y(t_{pn+k+m-q})). \end{aligned}$$

In view of proving the convergence of the proposed method, we state some lemmas.

Lemma 1

Let $y\in C^{d+2}[t_0-\tau ,T]$, $K\in C^{d+2}(\varOmega )$, f be continuous on $\mathscr {R}$ and let the condition (7c) be satisfied. Then

$$\begin{aligned} \mathscr {L}[y(t_m);h]=O(h^{d+1}), \quad m=1,2,\ldots ,N. \end{aligned}$$

Proof

Equation (1) at the mesh point $t_m$ is

$$\begin{aligned} y'(t_m)-f\Big (t_m,y(t_m),y(t_{m-q}),\displaystyle \int _{t_m-\tau }^{t_m} K(t_m,s,y(s))\,\mathrm {d}s\Big )=0, \quad m=1,2,\ldots ,N. \end{aligned}$$

(9)

Subtracting (9) from (8) yields

$$\begin{aligned} \frac{1}{h} \mathscr {L}[y(t_m);h]&=\frac{1}{h} \sum _{j=0}^n v_j y(t_{m-j})-y'(t_m)\\&\quad +f\bigg (t_m,y(t_m),y(t_{m-q}),\int _{t_m-\tau }^{t_m} K(t_m,s,y(s))\,\mathrm {d}s\bigg )\\&\quad -f\bigl (t_m,y(t_m),y(t_{m-q}),Q_m(h)\bigr ). \end{aligned}$$

Using Proposition 2 and (7c), we have

$$\begin{aligned} \frac{1}{h} \mathscr {L}[y(t_m);h]\le C_1h^d+L_3\left\| \int _{t_m-\tau }^{t_m} K(t_m,s,y(s))\,\mathrm {d}s-Q_m(h)\right\| , \end{aligned}$$

and with Proposition 1,

$$\begin{aligned} \frac{1}{h} \mathscr {L}[y(t_m);h]\le C_1h^d+L_3C_2h^{d+1}, \end{aligned}$$

where $C_1$ and $C_2$ are constants. So,

$$\begin{aligned} \mathscr {L}[y(t_m);h]=O(h^{d+1}). \square \end{aligned}$$

Lemma 2

Let n and d be such that (6) is zero–stable. If the sequences $\{e_k\}$, $\{\tilde{e}_k\}$ and $\{\ell _k\}$ satisfy the difference equation

$$\begin{aligned} \sum _{j=0}^n v_je_{m-j} = h\tilde{e}_m+\ell _m, \quad m=0,1,\ldots , \end{aligned}$$

where $e_{-n}=\cdots =e_{-1}=0$, then

$$\begin{aligned} e_m = h\sum _{j=0}^m a_{m-j}\tilde{e}_j+\sum _{j=0}^m a_{m-j}\ell _j, \end{aligned}$$

where $\displaystyle \sum _{j=0}^\infty a_j x^j$ is the power series for $(v_n+v_{n-1}x+\ldots +v_0x^n)^{-1}$ and $|a_j|\le C<\infty$ for all j.

Proof

The proof is similar to that of Lemma 2.4 in [1]. $\square$

Lemma 3

(Discrete Gronwall inequality) Suppose the nonnegative sequences $\{r_m\}$ and $\{\delta _m\}$ satisfy the difference inequality

$$\begin{aligned} r_m \le h\varLambda \sum _{j=0}^{m-1}r_j+\delta _m, \quad m=1,2,\ldots \end{aligned}$$

where $\delta _m \le \Delta$. Then,

$$\begin{aligned} r_m \le \Delta e^{\varLambda Nh}, \quad m=1,2,\ldots ,N. \end{aligned}$$

We are now in position to state our main theorem about the convergence of the method (6).

Theorem 1

Let $y\in C^{d+2}[t_0-\tau ,T]$, $K\in C^{d+2}(\varOmega )$, f be continuous on $\mathscr {R}$ and the conditions (7) hold. Also, let n and d be such that (6) is zero–stable. Then, the method (6) is convergent of order d:

$$\begin{aligned} \Vert y_m - y(t_m)\Vert \le Ch^d. \end{aligned}$$

Proof

Define $e_m=y(t_m)-y_m$. From (6) and (8), we have

$$\begin{aligned} \sum _{j=0}^n v_je_{m-j} = h\tilde{e}_m+\mathscr {L}[y(t_m);h], \quad m=1,2,\ldots \end{aligned}$$

(10)

where

$$\begin{aligned} \tilde{e}_m = f\bigl (t_m,y(t_m),y(t_{m-q}),Q_m(h)\bigr )-f\bigl (t_m,y_m,y_{m-q},\widetilde{Q}_m(h)\bigr ), \quad m=1,2,\ldots \end{aligned}$$

and $e_{-q}=\cdots =e_0=0$. Applying Lemma 2 to (10) yields

$$\begin{aligned} e_m=h\sum _{j=0}^ma_{m-j}\tilde{e}_j+S_m, \end{aligned}$$

(11)

where

$$\begin{aligned} S_m = \sum _{j=0}^m a_{m-j} \mathscr {L}[y(t_j);h] = \sum _{j=1}^m a_{m-j} \mathscr {L}[y(t_j);h]. \end{aligned}$$

By Lemma 1, we have $\Vert S_m\Vert =mC\cdot O(h^{d+1})=mhC\cdot O(h^d)$, where C is the constant appearing in Lemma 2. So,

$$\begin{aligned} \sup _{1\le m\le N}\Vert S_m\Vert = O(h^d),\quad \text{ as }\quad h\rightarrow 0, \end{aligned}$$

(12)

with $Nh=T-t_0$ remaining fixed.

Now, using (7), we have

$$\begin{aligned} \Vert \tilde{e}_j\Vert&\le \bigl \Vert f\bigl (t_j,y(t_j),y(t_{j-q}),Q_j(h)\bigr )-f\bigl (t_j,y_j,y(t_{j-q}),Q_j(h)\bigr )\bigr \Vert \nonumber \\&\quad +\bigl \Vert f\bigl (t_j,y_j,y(t_{j-q}),Q_j(h)\bigr )-f\bigl (t_j,y_j,y_{j-q},Q_j(h)\bigr )\bigr \Vert \nonumber \\&\quad +\bigl \Vert f\bigl (t_j,y_j,y_{j-q},Q_j(h)\bigr )-f\bigl (t_j,y_j,y_{j-q},\widetilde{Q}_j(h)\bigr )\bigr \Vert \nonumber \\&\le L_1\Vert e_j\Vert +L_2\Vert e_{j-q}\Vert +hL_5\sum _{i=0}^q \Vert e_{j-q+i}\Vert , \end{aligned}$$

(13)

with $L_5=2L_3L_4\max \left\{ |w_{k}^{(n)}|,|w_{k}^{(q-pn)}|\right\}$. Substituting (13) in (11) yields

$$\begin{aligned} \Vert e_m\Vert \le hC\sum _{j=0}^m \Big \{L_1\Vert e_j\Vert +L_2\Vert e_{j-q}\Vert +hL_5\sum _{i=0}^q\Vert e_{j-q+i}\Vert \Big \}+\Vert S_m\Vert . \end{aligned}$$

Define $E_j=\max \{\Vert e_l\Vert ,~l=j-q,\ldots ,j\}$. So,

$$\begin{aligned} \Vert e_m\Vert \le hC\sum _{j=0}^m(L_1+L_2+(q+1)hL_5)E_j+\Vert S_m\Vert . \end{aligned}$$

This implies

$$\begin{aligned} E_m \le hL\sum _{j=0}^m E_j+\Vert S_m\Vert , \end{aligned}$$

where

$$\begin{aligned} L = C(L_1+L_2+2\tau L_5) \ge C(L_1+L_2+(q+1)hL_5). \end{aligned}$$

Thus, for $hL<1$,

$$\begin{aligned} E_m \le \frac{hL}{1-hL}\sum _{j=0}^{m-1} E_j+\frac{\Vert S_m\Vert }{1-hL}. \end{aligned}$$

Using Lemma 3 yields

$$\begin{aligned} E_m \le \Big (\frac{1}{1-hL}\sup _{m}\Vert S_m\Vert \Big )e^{\frac{L}{1-hL}Nh}. \end{aligned}$$

From this and (12), we conclude that $E_m=O(h^d)$, and so $\Vert e_m\Vert =O(h^d)$. $\square$

According to the remarks following Propositions 1 and 2, the error may be expected to be of order $d+1$, when $n-d$ is odd.

To construct an infinitely smooth approximate solution on the whole interval $[t_0,T]$, it is natural and elegant to make use of the same barycentric rational interpolant as the one which lies at the basis of our scheme for determining the discrete approximations $y_0,\ldots ,y_N$, i.e.,

$$\begin{aligned} r_N(t) = \sum _{j=0}^N \frac{\beta _j}{t-t_j} y_j \Bigg / \sum _{j=0}^N \frac{\beta _j}{t-t_j}, \end{aligned}$$

(14)

with the weights $\beta _j$ from (3). Under the hypotheses of Theorem 1 and with the choice d of the parameter, by Theorem 2 in [14] and Theorem 1 the maximum absolute error in $r_N$ may be bounded as

$$\begin{aligned} \max _{t_0\le t\le T}\Vert r_N - y\Vert _{\infty }&\le \max _{t_0\le t\le T} \left\| \frac{\sum _{j=0}^N\frac{\beta _j}{t-t_j}y(t_j)}{\sum _{j=0}^N\frac{\beta _j}{t-t_j}} - y(t) \right\| _\infty \\&\qquad + \max _{t_0\le t\le T} \left\| \frac{\sum _{j=0}^N\frac{\beta _j}{t-t_j}\big (y_j-y(t_j)\big )}{\sum _{j=0}^N\frac{\beta _j}{t-t_j}} \right\| _\infty \\&\le C h^{d+1} + \varLambda _N \max _{0 \le j \le N} \left\| y(t_j) - y_j\right\| _\infty , \end{aligned}$$

where C is a generic constant that does not depend on N, and $\varLambda _N$ is the Lebesgue constant associated with the linear barycentric rational interpolant $r_N$:

$$\begin{aligned} \varLambda _N = \max _{t_0 \le t \le T} \sum _{j=0}^{N}\Big |{\frac{\beta _j}{t-t_j}} \Big | \Bigg / \bigg | \sum _{j=0}^{N}\frac{\beta _j}{t-t_j} \bigg |. \end{aligned}$$

Since $\varLambda _N$ is known to be bounded by $C\log (N)$ for equispaced nodes [9], one has

$$\begin{aligned} \max _{t_0\le t\le T}\Vert r_N - y\Vert _{\infty } \le C\log (N)h^{d}. \end{aligned}$$

The derivatives of any order of y may be approximated with the corresponding derivatives of (14) by means of the simple formula by Schneider and Werner [28].

4 Numerical Verifications

In this section, we apply the method (6) with various choices of n, d, and q to a number of linear and nonlinear DVIDEs to demonstrate the efficiency and accuracy of the scheme. The numerical results below confirm the theoretical convergence estimates derived in Sect. 3.2.

Following a suggestion by a referee, we also present results of numerical experiments with the Runge–Kutta–Gauss method and Pouzet quadrature formula (RKGP) [35], in the form

$$\begin{aligned} \begin{aligned} Y_i^{[m]}&=y_m+h\sum _{j=1}^s a_{ij}f\left( t_j^{[m]},Y_j^{[m]},Y_j^{[m-q]},z_j^{[m]}\right) ,\qquad i=1,2,\ldots ,s\\ y_{m+1}&=y_m+h\sum _{j=1}^s b_{j}f\left( t_j^{[m]},Y_j^{[m]},Y_j^{[m-q]},z_j^{[m]}\right) ,\qquad m\ge 0. \end{aligned} \end{aligned}$$

(15)

Here $h=\tau /q$ is the stepsize with q as a given positive integer, $t_j^{[m]}:=t_m+c_jh$ with $t_m=t_0+mh$ are the stage points, and $Y_j^{[m]}$,

$$\begin{aligned} z_j^{[m]}&:=h\sum _{r=1}^s a_{jr}K\left( t_j^{[m]},t_r^{[m]},Y_r^{[m]} \right) +h\sum _{k=1}^q\sum _{r=1}^s b_{r}K\left( t_j^{[m]},t_r^{[m-k]},Y_r^{[m-k]}\right) \\&\quad \quad -h\sum _{r=1}^s a_{jr}K\left( t_j^{[m]},t_r^{[m-q]},Y_r^{[m-q]}\right) \end{aligned}$$

and $y_m$ are approximations to

$$\begin{aligned} y\left( t_j^{[m]} \right) ,\;\; z\left( t_j^{[m]} \right) :=\int _{t_j^{[m-q]}}^{t_j^{[m]}}K\left( t_j^{[m]},s,y(s)\right) \mathrm {d}s,\;\; \text{ and }\;\;y(t_m), \end{aligned}$$

respectively. The method (15) is characterized by the abscissae $c_j$, the coefficients $a_{ij}$ and the weights $b_j$, which are given for Gauss methods of various orders in [10, p. 232]. The stability of such methods has been studied in [18].

Let us denote by $e_m$ the absolute error of the approximation $y_m$, $m=0,1,\ldots ,N$, and by $e_{\max }$ the maximum of these errors, i.e.,

$$\begin{aligned}&e_m:=\Vert y(t_m)-y_m\Vert _{\infty },\;\; m=0,1,\ldots ,N,\\&e_{\max }:=\max _{1\le m\le N}e_m. \end{aligned}$$

Also, we denote by $e_I$ the maximal absolute error of the interpolation (14) of the approximations $y_m$, $m=0,1,\ldots ,N$, i.e.,

$$\begin{aligned} e_I:=\max _{t_0\le t\le T}\Vert r_N(t)-y(t)\Vert _{\infty }. \end{aligned}$$

To estimate $e_I$, the maximum was taken over the values $|r_N(t)-y(t)|$ at about 3000 equispaced t in the interval $[t_0,T]$, with $r_N(t)$ evaluated by formula (14). Finally, we denote the experimental orders in the approximation of $y(t_N)$ by $O_N$ and in the interpolation by $O_I$.

As a first example, we considered the DVIDE with partially variable coefficients [34]

$$\begin{aligned} y'(t) = -(6+\sin t)y(t) + y\left( t-\frac{\pi }{4}\right) - \int _{t-\frac{\pi }{4}}^t \sin (s) y(s) \mathrm {d}s + 5\exp (\cos t),\quad t\ge 0, \end{aligned}$$

(16)

with an initial condition on the interval $\bigl [-\frac{\pi }{4},0\bigr ]$ such that the exact solution is given by $y(t) = \exp (\cos t)$. Here we chose $T=9\pi$.

Table 3 shows the numerical results for (n, d) equal to (4, 3) and (6, 4). In both cases, as to be expected from the comments following Propositions 1 and 2, the observed order was four. The interpolation errors decreased with order four as well. The accuracy of the obtained numerical solutions over the whole interval $[t_0,T]$ is displayed in Fig. 1. Also, the number of kernel evaluations versus the error with both the method (6) and RKGP are plotted in Fig. 2, which illustrates that the method (6) is competitive with RKGP of the same order. Let us recall that the barycentric rational method computes the solution only at equispaced abscissae and yields, through formula (14), a global infinitely smooth approximation to y (see the $e_I$–column of our tables), this in contrast to Runge–Kutta methods, which require quite some thoughts and computation for a dense output [32].

Table 3 Numerical results for example (16) with (n, d) equal to (4, 3) and (6, 4)

Fig. 1

Error for example (16) with $(n,d)=(7,5)$ and $q=16,64$ over the interval $[0,9\pi ]$

Fig. 2

Comparison of the number of kernel evaluations with the methods of order 4 and order 6 applied to example (16)

Table 4 Numerical results for example (17) with (n, d) equal to (8, 5) and (13, 6)

Next we studied the equation

$$\begin{aligned} y'(t) = y^3(t)+y(t-1)-\int _{t-1}^t \bigl (10+2(t-s)^2\bigr ) y^2(s) \mathrm {d}s +f(t),\quad t\in [-\,1,1], \end{aligned}$$

(17)

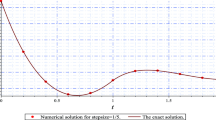
whose exact solution is Runge’s function $y(t) = 1/(1+25t^2)$. The initial condition on $[-\,2,-\,1]$ was the value of that exact solution.

Table 4 shows the numerical results for (n, d) equal to (8, 5) and (13, 6). There is no Runge phenomenon, as the latter does not occur with this kind of rational interpolants and fixed d [14]. As to be expected from the comment following Propositions 1 and 2, the observed order was six and seven, respectively. The corresponding interpolation errors decreased with the same orders. The accuracy of the obtained numerical solutions over the whole interval $[-1,1]$ is displayed in Fig. 3.

Fig. 3

Error for example (17) with $(n,d)=(10,6)$ and $q=256, 512$ over the interval $[-1,1]$

We also studied the nonlinear two-dimensional system [34]

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}\left( \begin{array}{l} y_1(t)\\ y_2(t) \end{array} \right)&= -4\left( \begin{array}{l} y_1(t)\\ y_2(t) \end{array} \right) +\left( \begin{array}{ll} 0 &{} \sin t \\ \cos t &{} 0 \\ \end{array} \right) \cdot \left( \begin{array}{l} y_1(t-\frac{\pi }{5})\\ y_2(t-\frac{\pi }{5}) \end{array}\right) \nonumber \\&\quad + \frac{1}{\sqrt{2}}\int _{t-\frac{\pi }{5}}^t \left( \begin{array}{l} \frac{(1+\sin ^2 s)y_1^2(s)}{1+y_1^2(s)}\\ \frac{(1+\cos ^2 s)y_2^2(s)}{1+y_2^2(s)} \end{array}\right) \mathrm {d}s +\left( \begin{array}{l} f_1(t)\\ f_2(t) \end{array} \right) ,\quad t\ge 0, \end{aligned}$$

(18)

where $f(t)=(f_1(t),f_2(t))^T$ and where the initial condition on $[-\frac{\pi }{5},0]$ is chosen in such a way that the solution equals $y(t) = (\sin t,\cos t)^T$. We considered $T=9\pi$ again.

Table 5 Numerical results for example (18) with (n, d) equal to (8, 5) and (10, 6)

Table 5 shows the numerical results for (n, d) equal to (8, 5) and (10, 6). The errors decreased with N until about machine precision. As to be expected from the comment following Propositions 1 and 2, the observed order is six in both cases. The interpolation errors also decreased with order six. They reached machine precision with $N=80$, which explains some smaller experimental orders in the last row of the table. Moreover, in Fig. 4, we have plotted $\log (e_N)$ versus $\log (h)$, together with a line of slope d, if $n-d$ is even, and $d+1$, if $n-d$ is odd, for two other choices of (n, d). The accuracy of the obtained numerical solutions over the whole interval $[t_0,T]$ is displayed in Fig. 5. Also, the number of kernel evaluations versus the error with the method (6) and RKGP are plotted in Fig. 6, which illustrates that the method (6) is competitive with RKGP of the same order.

Fig. 4

Numerical results for example (18) with (n, d) equal to (4, 2) and (7, 4)

Fig. 5

Error for example (18) with $(n,d)=(9,4)$ and $q=16,64$ over the interval $[0,9\pi ]$

Fig. 6

Comparison of the number of kernel evaluations with the methods of order 4 and order 6 applied to example (18)

To demonstrate the capability and efficiency of the proposed method in solving stiff problems, we studied the singularly perturbed nonlinear system of DVIDEs [33]

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}\left( \begin{array}{l} y_1(t)\\ \varepsilon y_2(t) \end{array} \right)= & {} \left( \begin{array}{l} \alpha y_1(t) + 2y_2^2(t)\\ -(1+y_1(t))y_2(t) \end{array}\right) \nonumber \\&\quad + \int _{t-1}^t \left( \begin{array}{l} y_1(s)y_2(s)\\ y_1(s)-y_2(s) \end{array} \right) \mathrm {d}s + \left( \begin{array}{l} f_1(t)\\ f_2(t) \end{array} \right) ,\quad t>0, \end{aligned}$$

(19)

where $\alpha$ and $\varepsilon$ are fixed parameters. For this problem, $f_1(t)$ and $f_2(t)$ and the initial condition on $[-1,0]$ are chosen in such a way that the exact solution equals $y(t)=\bigl (\exp (-0.5t)+\exp (-0.2t), -\exp (-0.5t)+\exp (-0.2t)\bigr )^T$.

The authors of [33] have chosen $\alpha =-1000$ and $\varepsilon =10^{-6}$. However, with these values of $\alpha$ and $\varepsilon$, the problem does not seem very stiff: we achieved machine precision already with small values of q and d. For that reason we have taken $\alpha =-10^{-5}$ and $\varepsilon =10^{-10}$. Here we considered $T=6$.

In Fig. 7, we have again plotted $\log (e_N)$ versus $\log (h)$ together with a line of slope d, if $n-d$ is even, or $d+1$, if $n-d$ is odd, for (n, d) equal to (9, 3) and (6, 5). The accuracy of the solutions over the whole interval $[t_0,T]$ is displayed in Fig. 8. Moreover, in Table 6, we present the numerical results of our method with $(n,d)=(4,3)$ and RKGP of order four and stage order two. They show that the accuracy of our method with the stiff problem (19) is higher than that of RKGP and the same order. Also, this table indicates that RKGP suffers from order reduction [15, p. 225-227], which is not the case of method (6).

Fig. 7

Numerical results for example (19) with (n, d) equal to (9, 3) and (6, 5)

Fig. 8

Error for example (19) with $(n,d)=(9,6)$ and $q=16,32$ over the interval [0, 6]

Table 6 Numerical results for example (19) with $(n,d) \,=\, (4,3)$ and RKGP of order four and stage order two

Finally, following a suggestion by the other referee, we considered a realistic example in the form of a mathematical model of the human immune response with delay [3, 25]

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{\mathrm {d}}{\mathrm {d}t}X_U(t)=s_U-\alpha _1X_U(t)B(t)-\mu _{X_U} X_U(t), \\ \displaystyle \frac{\mathrm {d}}{\mathrm {d}t}X_I(t)=\alpha _1X_U(t)B(t)-\alpha _2X_I(t)A_R(t)-\mu _{X_I} X_I(t), \\ \displaystyle \frac{\mathrm {d}}{\mathrm {d}t}B(t)=\alpha _{20}B(t)\Bigl (1-\frac{B(t)}{\sigma }\Bigr )-\alpha _3B(t)I_R(t)-\alpha _4 B(t)A_R(t), \\ \displaystyle \frac{\mathrm {d}}{\mathrm {d}t}I_R(t)=s_{I_R}+\int _{t-\tau }^t w(s-t)B(s)\mathrm {d}s-\mu _{I_R} I_R(t), \\ \displaystyle \frac{\mathrm {d}}{\mathrm {d}t}A_R(t)=s_{A_R}+\int _{t-\tau }^t w(s-t)B(s)\mathrm {d}s-\mu _{A_R} A_R(t), \\ \end{array}\right. \end{aligned}$$

(20)

in which the components $X_U$, $X_I$, and B stand for uninfected target cells, infected cells, and bacteria, and the variables $I_R$ and $A_R$ denote innate and adaptive responses, respectively. Here we considered $t\in [0,50]$ with $\tau =6$ and $w(t)=\frac{\ln 2}{6}\exp (\frac{\ln 2}{6}t)$. For a detailed description of the model and the selection of parameter values, as well as initial conditions, see [3, 25].

We compared our results with the reference solution obtained by solving the equivalent system of DDEs using the dde23 command from the Matlab DDE suite [29] with the tolerance $10^{-12}$. Table 7 shows the numerical results for (n, d) equal to (3, 2) and (6, 4). We see from this table that the order of convergence does appear to be three and four, in line with the orders expected from the theory.

Table 7 Numerical results for example (20) with (n, d) equal to (3, 2) and (6, 4)

5 Conclusion

Linear barycentric rational interpolation provides a simple yet very efficient way of approximating a function by an infinitely smooth one from a sample at equispaced nodes. In this paper, we have presented an exemplary application, namely the numerical solution of a class of DVIDEs with constant delay. We have analyzed the convergence behavior of the corresponding method and discussed some numerical experiments, which demonstrate its efficiency and beautifully agree with the theoretical results. In fact, the accuracy was even better than that attained in [6] with the original method for classical Volterra integral equations. This likely is a consequence of the fact that the right–hand side approximates $y'$, the derivative of the solution, so that the mathematical problem involves yet another integration.

The method is very elegant in the sense that it is fully based on linear barycentric rational interpolation with Floater–Hormann weights. The later are the best known today for equispaced nodes [5]. One may program the method with arbitrary weights as variable input: should in the future weights for equispaced nodes be discovered which are even better than (3), the user would then just have to introduce them into the existing program.