1 Introduction

IMAGE segmentation is a fundamental and challenging task in image processing and computer vision. It can serve as a preliminary step for object recognition and interpretation. The goal of image segmentation is to group parts of the given image with similar characteristics together. These characteristics include, for example, edges, intensities, colors and textures. For a human observer, image segmentation seems obvious, but consensus among different observers is seldom found. The problem is much more difficult to solve by a computer. A nice overview of region-based and edge-based segmentation methods is given in [16]. In our work we investigate the image segmentation problem for color images corrupted by different types of degradations: noise, information loss and blur.

Let \({\varOmega }\subset {\mathbb {R}}^2\) be a bounded open connected set, and \(f: {\varOmega }\rightarrow {\mathbb {R}}^d\) with \(d\ge 1\) be a given vector-valued image. For example, \(d = 1\) for gray-scale images and \(d=3\) for the usual RGB (red-green-blue) color images. One has \(d>3\) in many cases such as in hyperspectral imaging [35] or in medical imaging [44]. In this paper, we are mainly concerned with color images (i.e. \(d=3\)) though our approach can be extended to higher-dimensional vector-valued images. Without loss of generality, we restrict the range of f to \([0,1]^3\) and hence \(f\in L^{\infty }({\varOmega })^3\).

In the literature, various studies have been carried out and many techniques have been considered for image segmentation [14, 21, 26, 28, 40, 41, 43]. For gray-scale images, i.e. \(d=1\), Mumford and Shah proposed in [32, 33] an energy minimization problem for image segmentation which finds optimal piecewise smooth approximations. More precisely, this problem was formulated in [33] as

$$\begin{aligned} E_{\mathrm{MS}}(g, {\varGamma }):=\frac{\lambda }{2}\int _{{\varOmega }}(f-g)^2 dx+ \frac{\mu }{2} \int _{{\varOmega }\setminus {\varGamma }}|\nabla g|^2 dx + \mathrm{Length}({\varGamma }), \end{aligned}$$
(1)

where \(\lambda \) and \(\mu \) are positive parameters, and \(g:{\varOmega }\rightarrow {\mathbb {R}}\) is continuous in \({\varOmega }\setminus {\varGamma }\) but may be discontinuous across the sought-after boundary \({\varGamma }\). Here, the length of \({\varGamma }\) can be written as \({\mathcal {H}}^{1}({\varGamma })\), the one-dimensional Hausdorff measure in \({\mathbb {R}}^2\). Model (1) has attractive properties even though finding a globally optimal solution remains an open problem and it is an active area of research. A recent overview can be found in [1]. For image segmentation, the Chan–Vese model [14] pioneered a simplification of functional (1) where \({\varGamma }\) partitions the image domain into two constant segments and thus \(\nabla g = 0\) on \({\varOmega }\setminus {\varGamma }\). More generally, for K constant regions \({\varOmega }_i\), \(i\in \{1,\ldots ,K\}\), the multiphase piecewise constant Mumford–Shah model [46] reads as

$$\begin{aligned} E_{\mathrm{PCMS}}\left( \left\{ {\varOmega }_i, c_i\right\} _{i=1}^K\right) =\frac{\lambda }{2}\sum _{i=1}^K\int _{{\varOmega }_i}(f-c_i)^2 dx + \frac{1}{2}\sum _{i=1}^K \mathrm {Per}( {\varOmega }_i), \end{aligned}$$
(2)

where \(\mathrm {Per}( {\varOmega }_i)\) is the perimeter of \({\varOmega }_i\) in \({\varOmega }\), all \({\varOmega }_i\)’s are pairwise disjoint and \({\varOmega }= \bigcup _{i=1}^K{\varOmega }_i\). The Chan–Vese model where \(K=2\) in (2) has many applications for two-phase image segmentation. Model (2) is a nonconvex problem, so the obtained solutions are in general local minimizers. To overcome the problem, convex relaxation approaches [4, 9, 12, 36], graph cut method [22] and fuzzy membership functions [28] were proposed.

After [14], many approaches have decomposed the segmentation process into several steps and here we give a brief overview of recent work in this direction. The paper [25] performs a simultaneous segmentation of the input image into arbitrarily many pieces using a modified version of model (1) and the final segmented image results from a stopping rule using a multigrid approach. In [27], after involving a bias field estimation, a level set segmentation method dealing with images with intensity inhomogeneity was proposed and applied to MRI images. In [8], an initial hierarchy of regions was obtained by greedy iterative region merging using model (2); the final segmentation is obtained by thresholding this hierarchy using hypothesis testing. The paper [2] first determined homogeneous regions in the noisy image with a special emphasis on topological changes; then each region was restored using model (2). Further multistage methods extending model (2) can be found in [42] where wavelet frames were used, and in [7] which was based on iterative thresholding of the minimizer of the ROF functional [39], just to cite a few. In the discrete setting, the piecewise constant Mumford–Shah model (2) amounts to the classical Potts model [37]. The use of this kind of functionals for image segmentation was pioneered by Geman and Geman [19]. In [41], a coupled Potts model was used for direct partitioning of images using a convergent minimization scheme. In [6], a conceptually different two-stage method for the segmentation of gray-scale images was proposed. In the first stage, a smoothed solution g is extracted from the given image f by minimizing a non-tight convexification of the Mumford–Shah model (1). The segmented image was obtained in the second stage by applying a thresholding technique to g. This approach was extended in [11] to images corrupted by Poisson and Gamma noises. Since the basic concept of our method in this paper is similar, we will give more details on [6, 11] in Sect. 2.

Extending or conceiving segmentation methods for color images is not a simple task since one needs to discriminate segments with respect to both luminance and chrominance information. The two-phase Chan–Vese model [14] was generalized to deal with vector-valued images in [13] by combining the information in the different channels using the data fidelity term. Many methods are applied in the usual RGB color space [5, 13, 16, 23, 25, 31, 36, 41], among others. It is often mentioned that the RGB color space is not well adapted to segmentation because for real-world images the R, G and B channels can be highly correlated. In [38], RGB images are transformed into HSI (hue, saturation, and intensity) color space in order to perform segmentation. In [2] a general segmentation approach was developed for gray-value images and further extended to color images in the RGB, the HSV (hue, saturation, and value) and the chromaticity–brightness (CB) color spaces. However, a study on this point in [34] has shown that the Lab (perceived lightness, red-green and yellow-blue) color space defined by the Commission Internationale de l’Eclairage (CIE) is better adapted for color image segmentation than the RGB and the HSI color spaces. In [8] RGB input images were first converted to Lab space. In [47] color features were described using the Lab color space and texture using histograms in RGB space.

A careful examination of the methods that transform a given RGB image to another color space (HSI, CB, Lab, ...) before performing the segmentation task has shown that these algorithms are always applied only to noise-free RGB images (though these images unavoidably contain quantization and compression noise). For instance, this is the case of [2, 8, 38, 47], among others. One of the main reasons is that if the input RGB image is degraded, the degradation would be hard to control after a transformation to another color space [34]. Our goal is to develop an image segmentation method that has the following properties:

  1. (i)

    work on vector-valued (color) images possibly corrupted with noise, blur and missing data;

  2. (ii)

    initialization independent and non-supervised (the number of segments is not fixed in advance);

  3. (iii)

    take into account perceptual edges between colors and between intensities so as to detect vector-valued objects with edges and also objects without edges;

  4. (iv)

    obtain an image adapted for segmentation using convex methods;

  5. (v)

    the segmentation is done at the last stage: no need to solve the previous stage when the number of segments required is changed.

Contributions The main contribution of this paper is to propose a segmentation method having all these properties. Goals (a)–(d) lead us to explore possible extensions of the methods [6, 11] to vector-valued (color) images. Goal (e) requires finding a way to use information from perceptual color spaces even though our input images are corrupted; see goal (a). Let \({{{\mathcal {V}}}}_1\) and \({{\mathcal {V}}}_2\) be two color spaces. Our method has the following 3 steps:

  1. 1.

    Let the given degraded image be in \({{\mathcal {V}}}_1\). The convex variational model [6, 11] is applied in parallel to each channel of \({{\mathcal {V}}}_1\). This yields a restored smooth image. We show that the model has unique solution.

  2. 2.

    The second stage consists of color dimension lifting: we transform the smooth color image obtained at Stage 1 to a secondary color space \({{\mathcal {V}}}_2\) that provides us with complementary information. Then we combine these images as a new vector-valued image composed of all the channels from color spaces \({{\mathcal {V}}}_1\) and \({{\mathcal {V}}}_2\).

  3. 3.

    According to the desired number of phases K, we apply a multichannel thresholding to the combined \({{\mathcal {V}}}_1\)–\({{\mathcal {V}}}_2\) image to obtain a segmented image.

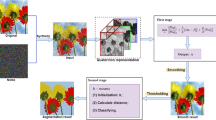
We call our method “SLaT” for Smoothing, Lifting and Thresholding. Unlike the methods that perform segmentation in a different color space like [2, 8, 38, 45, 47], we can deal with degraded images thanks to Stage 1 which yields a smooth image that we can transform to another color space. We will fix \({{\mathcal {V}}}_1\) to be the RGB color space since one usually has RGB color images. We use the Lab color space [30] as the secondary color space \({{\mathcal {V}}}_2\) since it is often recommended for color segmentation [8, 16, 34]. The crucial importance of the dimension lifting Stage 2 is illustrated in Fig. 1 which shows the results without Stage 2, i.e. \({{\mathcal {V}}}_2=\emptyset \) (middle) or with Stage 2 (right). To the best of our knowledge, it is the first time that two color spaces are used jointly in variational methods for segmentation.

Fig. 1
figure 1

Segmentation results for a noisy image (a) without the dimension lifting in Stage 2 (b) and with Stage 2 (c)

Full size image

This provides us with additional information on the color image so that in all cases we can obtain very good segmentation results. The number of phases K is needed only in Stage 3. Its value can reasonably be selected based on the RGB image obtained at Stage 1.

Extensive numerical tests on synthetic and real-world images have shown that our method outperforms state-of-the-art variational segmentation methods like [28, 36, 41] in terms of segmentation quality, speed and parallelism of the algorithm, and the ability to segment images corrupted by different kind of degradations.

Outline In Sect. 2, we briefly review the models in [6, 11]. Our SLaT segmentation method is presented in Sect. 3. In Sect. 4, we provide experimental results on synthetic and real-world images. Conclusion remarks are given in Sect. 5.

2 Review of the Two-Stage Segmentation Methods in [6, 11]

The methods in [6, 11] for the segmentation of gray-scale images are motivated by the observation that one can obtain a good segmentation by properly thresholding a smooth approximation of the given image. Thus in their first stage, these methods solve a minimization problem of the form

$$\begin{aligned} \inf _{g\in W^{1,2}({\varOmega })} \left\{ \frac{\lambda }{2}\int _{\varOmega }{\varPhi }(f, g) dx +\frac{\mu }{2}\int _{\varOmega }|\nabla g|^2 dx + \int _{\varOmega }|\nabla g|dx \right\} , \end{aligned}$$
(3)

where \({\varPhi }(f, g)\) is the data fidelity term, \(\mu \) and \(\lambda \) are positive parameters. We note that the model (3) is a convex non-tight relaxation of the Mumford–Shah model in (1). Paper [6] considers \({\varPhi }(f, g) = (f-{{\mathcal {A}}} g)^2\) where \(\mathcal {A}\) is a given blurring operator; when f is degraded by Poisson or Gamma noise, the statistically justified choice \({\varPhi }(f, g) = {{\mathcal {A}}}g - f \log ( {{\mathcal {A}}}g)\) is used in [11]. Under a weak assumption, the functional in (3) has a unique minimizer, say \({\bar{g}}\), which is a smooth approximation of f. The second stage is to use the K-means algorithm [24] to determine the thresholds for segmentation. These methods have important advantages: they can segment degraded images and the minimizer \({{\bar{g}}}\) is unique. Further, the segmentation stage being independent from the optimization problem (3), one can change the number of phases K without solving (3) again.

3 SLaT: Our Segmentation Method for Color Images

Let \(f = (f_1, \ldots , f_d )\) be a given color image with channels \(f_i: {\varOmega }\rightarrow {\mathbb {R}}, i=1, \cdots , d\). For f an RGB image, \(d=3\). This given image f is typically a blurred and noisy version of an original unknown image. It can also be incomplete: we denote by \({\varOmega }_0^i\) the open nonempty subset of \({\varOmega }\) where the given \(f_i\) is known for channel i. Our SLaT segmentation method consists of three stages described next.

3.1 First Stage: Recovery of a Smooth Image

First, we restore each channel \(f_i\) of f separately by minimizing the functional E below

$$\begin{aligned} E(g_i)=\frac{\lambda }{2} \int _{{\varOmega }}\omega _i\cdot {\varPhi }(f_i, g_i) dx + \frac{\mu }{2} \int _{{\varOmega }}|\nabla g_i|^2 dx + \int _{{\varOmega }} |\nabla g_i| dx, \quad i=1, \ldots , d, \end{aligned}$$
(4)

where \(|\cdot | \) stands for Euclidian norm and \(\omega _i(\cdot )\) is the characteristic function of \({\varOmega }_0^i\), i.e.

$$\begin{aligned} \omega _i(x) = {\left\{ \begin{array}{ll} 1, &{} \quad x \in {\varOmega }_0^i, \\ 0, &{}\quad x \in {\varOmega }\setminus {\varOmega }_0^i. \end{array}\right. } \end{aligned}$$
(5)

For \({\varPhi }\) in (4) we consider the following options:

  1. (i)

    \({\varPhi }(f, g) = (f-{{\mathcal {A}}} g)^2\), the usual choice;

  2. (ii)

    \({\varPhi }(f, g) = {{\mathcal {A}}}g - f \log ({{\mathcal {A}}}g)\) if data are corrupted by Poisson noise.

Theorem 1 below proves the existence and the uniqueness of the minimizer of (4). In view of (4) and (5), we define the linear operator \((\omega _i{{\mathcal {A}}})\) by

$$\begin{aligned} (\omega _i {{\mathcal {A}}}) : u(x) \in L^2({\varOmega }) \mapsto \omega _i(x) ({{\mathcal {A}}}u)(x) \in L^2({\varOmega }). \end{aligned}$$
(6)

Theorem 1

Let \({\varOmega }\) be a bounded connected open subset of \({\mathbb {R}}^2\) with a Lipschitz boundary. Let \({{\mathcal {A}}}:L^2({\varOmega })\rightarrow L^2({\varOmega })\) be bounded and linear. For \(i\in \{1,\ldots ,d\}\), assume that \(f_i \in L^2({\varOmega })\) and that \(\mathrm{Ker} (\omega _i {{\mathcal {A}}} )\bigcap \mathrm{Ker} (\nabla ) = \{0 \}\) where \(\mathrm{Ker} \) stands for null-space. Then (4) with either \({\varPhi }(f_i, g_i) = (f_i-{{\mathcal {A}}} g_i)^2\) or \({\varPhi }(f_i, g_i) = {{\mathcal {A}}}g_i - f_i \log ({{\mathcal {A}}}g_i)\) has a unique minimizer \({{\bar{g}}}_i \in W^{1,2}({\varOmega })\).

Proof

First consider \({\varPhi }(f_i, g_i) = (f_i-{{\mathcal {A}}} g_i)^2\). Using (6), \(E(g_i)\) defined in (4) can be rewritten as

$$\begin{aligned} E(g_i)=\frac{\lambda }{2} \int _{{\varOmega }}(\omega _i\cdot f_i -(\omega _i{{\mathcal {A}}} )g_i)^2 dx + \frac{\mu }{2} \int _{{\varOmega }}|\nabla g_i|^2 dx + \int _{{\varOmega }} |\nabla g_i| dx. \end{aligned}$$
(7)

Noticing that \(\omega _i\cdot f_i\in L^2({\varOmega })\) and that \((\omega _i{{\mathcal {A}}}) :L^2({\varOmega })\rightarrow L^2({\varOmega })\) is linear and bounded, the statement follows from [6, Theorem 2.4.].

Next consider that \({\varPhi }(f_i, g_i) = {{\mathcal {A}}}g_i - f_i \log ({{\mathcal {A}}}g_i)\). Then

$$\begin{aligned}&E(g_i)=\frac{\lambda }{2} \int _{{\varOmega }} \omega _i\cdot ({{\mathcal {A}}}g_i) - (\omega _i\cdot f_i) \log ({{\mathcal {A}}}g_i) dx \nonumber \\&\qquad \quad \qquad + \frac{\mu }{2} \Vert \nabla g_i\Vert ^2_{L^2({\varOmega })} + \Vert \nabla g_i\Vert _{L^2({\varOmega })}. \end{aligned}$$
(8)
  1. 1.

    Existence Since \(W^{1,2}({\varOmega })\) is a reflective Banach space and \(E(g_i)\) is convex lower semi-continuous, by Ekeland and Temam [17, Proposition 1.2] we need to prove that \(E(g_i)\) is coercive on \(W^{1,2}({\varOmega })\), i.e. that \(E(g_i)\rightarrow +\infty \) as \(\Vert g_i\Vert _{ W^{1,2}({\varOmega }) }:=\Vert g_i\Vert _{L^2({\varOmega })} + \Vert \nabla g_i\Vert _{L^2({\varOmega })}\rightarrow +\infty \).

    The function \({{\mathcal {A}}} g_i\mapsto ({{\mathcal {A}}} g_i - f \log {{\mathcal {A}}} g_i)\) is strictly convex with a minimizer pointwisely satisfying \({{\mathcal {A}}} g_i = f \in [0,1]\), hence \({\varPhi }(f_i, g_i) \ge 0\). Thus \(\Vert \nabla g_i\Vert _{L^2({\varOmega })} \) is upper bounded by \(E(g_i)>0\) for any \(g_i\in W^{1,2}({\varOmega })\) and \(f\ne 0\). Using the Poincaré inequality, see [18], we have:

    $$\begin{aligned} \Vert g_i-g_{i_{{\varOmega }}}\Vert _{L^2({\varOmega })} \le C_1\Vert \nabla g_i\Vert _{L^2({\varOmega })} \le C_1 E(g_i), \end{aligned}$$
    (9)

    where \(C_1>0\) is a constant and \(g_{i_{{\varOmega }}}=\frac{1}{|{\varOmega }|}\int _{{\varOmega }} g_idx\). Let us set \(C_2:= \left( 1-\frac{1}{e} \Vert f_i\Vert _\infty \right) \). We have \(C_2>0\) because \( \Vert f_i\Vert _\infty \le 1\). Recall the fact that \(\frac{t}{e}\ge \log t\) for any \(t>0\) which can be easily verified by showing that \(t/e-\log t\) is convex for \(t>0\) with minimum at e. Hence we have

    $$\begin{aligned} \omega _i\cdot {\varPhi }(f_i, g_i)\ge & {} (\omega _i {{\mathcal {A}}}) \;g_i- \frac{1}{e} (\omega _i\cdot f_i) {{\mathcal {A}}}g_i \\= & {} \omega _i\cdot (1-\frac{1}{e} f_i) {{\mathcal {A}}}g_i \ge C_2 \; (\omega _i {{\mathcal {A}}}) \;g_i \end{aligned}$$

    which should be understood pointwisely. Hence,

    $$\begin{aligned} \Vert (\omega _i {{\mathcal {A}}}) \;g_i\Vert _{L^1({\varOmega })} \le \frac{2}{C_2\lambda }E(g_i). \end{aligned}$$
    (10)

    Let \(C_3:=\Vert (\omega _i{{\mathcal {A}}}){\mathbf {1}}\Vert _{L^1({\varOmega })} \) where \({\mathbf {1}}(x)=1\) for any \(x\in {\varOmega }\). Using \(\mathrm {Ker} (\nabla ) =\{u\in L^2({\varOmega }) : u=c\;1~ \mathrm {a.e.} \ \mathrm{for} \ x\in {\varOmega }, c\in {\mathbb {R}}\} \) together with the assumption \(\mathrm{Ker} (\omega _i {{\mathcal {A}}} )\bigcap \mathrm{Ker} (\nabla ) = \{0 \}\) one has \(C_3>0\). Using (10) together with the fact that \(g_{i_{{\varOmega }}} >0\) yields

    $$\begin{aligned} |g_{i_{{\varOmega }}} | \; \Vert (\omega _i {{\mathcal {A}}}){\mathbf {1}}\Vert _{L^1({\varOmega })}= & {} |g_{i_{{\varOmega }}} | \; C_3 \nonumber \\= & {} \Vert \omega _i\cdot ({{\mathcal {A}}}{\mathbf {1}} g_{i_{{\varOmega }}} ) \Vert _{L^1({\varOmega })} \nonumber \\\le & {} \frac{2}{C_2\lambda } E(g_i), \end{aligned}$$

    and thus

    $$\begin{aligned} |g_{i_{{\varOmega }}} | \le \frac{2}{C_2C_3\lambda } E(g_i). \end{aligned}$$

    Applying the triangular inequality in (9) gives \(\Vert g_i\Vert _{L^2({\varOmega })}-|g_{i_{{\varOmega }}}| \le C_1\Vert \nabla g_i\Vert _{L^2({\varOmega })}\). Hence

    $$\begin{aligned} \Vert g_i\Vert _{L^2({\varOmega })}\le |g_{i_{{\varOmega }}}| + C_1\Vert \nabla g_i\Vert _{L^2({\varOmega })} \le \left( \frac{2}{C_2C_3\lambda } + 1 \right) E(g_i). \end{aligned}$$

    Comparing with (9) yet again shows that we have obtained

    $$\begin{aligned} \Vert g_i\Vert _{ W^{1,2}({\varOmega }) }= & {} \Vert g_i\Vert _{L^2({\varOmega })} + \Vert \nabla g_i\Vert _{L^2({\varOmega })} \nonumber \\\le & {} \left( \frac{2}{C_2C_3\lambda } + 1 +C_1\right) E(g_i). \end{aligned}$$

    Therefore, E is coercive.

  2. 2.

    Uniqueness Suppose \({{\bar{g}}}_{i_1}\) and \({{\bar{g}}}_{i_2}\) are both minimizers of \(E(g_i)\). The convexity of E and the strict convexity of \({{\mathcal {A}}} g_i\mapsto ({{\mathcal {A}}} g_i - f \log {{\mathcal {A}}} g_i)\) entail \({{\mathcal {A}}} {{\bar{g}}}_{i_1} = {{\mathcal {A}}} {{\bar{g}}}_{i_2}\) on \({\varOmega }_0^i\) and \(\nabla {{\bar{g}}}_{i_1} = \nabla {{\bar{g}}}_{i_2}\). Further, the assumption on \(\mathrm{Ker} (\omega _i {{\mathcal {A}}} )\bigcap \mathrm{Ker} (\nabla ) \) shows that \({{\bar{g}}}_{i_1}={{\bar{g}}}_{i_2}\). \(\square \)

The condition \(\mathrm{Ker} (\omega _i {{\mathcal {A}}} )\bigcap \mathrm{Ker} (\nabla ) = \{0 \}\) is mild which means that \(\mathrm{Ker} (\omega _i {{\mathcal {A}}} )\) does not contain constant images.

The discrete model In the discrete setting, \({\varOmega }\) is an array of pixels, say of size \(M\times N\), and our model (4) reads as

$$\begin{aligned} E(g_i)=\frac{\lambda }{2} {\varPsi }(f_i, g_i) +\frac{\mu }{2}\Vert \nabla g_i\Vert _F^2+\Vert \nabla g_i\Vert _{2,1}, \quad i=1, \ldots , d. \end{aligned}$$
(11)

Here

$$\begin{aligned} {\varPsi }(f_i,g_i):=\sum _{j\in {\varOmega }} \left( \omega _i \cdot (f_i-{{\mathcal {A}}} g_i)^2\right) _j, \end{aligned}$$

or

$$\begin{aligned} {\varPsi }(f_i,g_i):=\sum _{j\in {\varOmega }} \left( \omega _i \cdot \big ( {{\mathcal {A}}}g_i - f_i \log ({{\mathcal {A}}}g_i)\big )\right) _j. \end{aligned}$$

The operator \(\nabla =(\nabla _x,\nabla _y )\) is discretized using backward differences with Neumann boundary conditions. Further, \(\Vert \cdot \Vert _F^2\) is the Frobenius norm, so

$$\begin{aligned} \Vert \nabla g_i\Vert _F^2 = \sum _{j\in {\varOmega }}\big ((\nabla _x g_i)_j^2+(\nabla _y g_i)_j^2\big ), \end{aligned}$$

and \(\Vert \nabla g_i\Vert _{2,1}\) is the usual discretization of the TV semi-norm given by

$$\begin{aligned} \Vert \nabla g_i\Vert _{2,1} =\sum _{j\in {\varOmega }}\sqrt{(\nabla _x g_i)_j^2+(\nabla _y g_i)_j^2}. \end{aligned}$$

For each i, the minimizer \({\bar{g}}_i\) can be computed easily using different methods, for example the primal-dual algorithm [10, 15], alternating direction method with multipliers (ADMM) [3], or the split-Bregman algorithm [20]. Then we rescale each \({{\bar{g}}}_i\) onto [0, 1] to obtain \(\{{{\bar{g}}}_i\}_{i=1}^d\in [0,1]^d\).

3.2 Second Stage: Dimension Lifting with Secondary Color Space

For the ease of presentation, in the following, we assume \({{\mathcal {V}}}_1\) is the RGB color space. The goal in color segmentation is to recover segments both in the luminance and in the chromaticity of the image. It is well known that the R, G and B channels can be highly correlated. For instance, the R, G and B channels of the output of Stage 1 for the noisy pyramid image in Fig. 1 are depicted in Fig. 2a–c. One can hardly expect to make a meaningful segmentation based on these channels—see the result in Fig. 1b, as well as Fig. 8 where other contemporary methods are compared.

Fig. 2
figure 2

Channels comparison for the restored (smoothed) \({{\bar{g}}}\) in Stage 1 used in Fig. 1. a–c The R, G and B channels of \({{\bar{g}}}\); d–f the L, a and b channels of \({{\bar{g}}}^t\)—the Lab transform of \({{\bar{g}}}\). Both \({{\bar{g}}}\) and \({{\bar{g}}}^t\) were used to obtain the result in Fig. 1c

Full size image

Stage 1 provides us with a restored smooth image \({\bar{g}}\). In Stage 2, we perform dimension lifting in order to acquire additional information on \({{\bar{g}}}\) from a different color space that will help the segmentation in Stage 3. The choice is delicate. Popular choices of less-correlated color spaces include HSV, HSI, CB and Lab, as described in the Introduction. The Lab color space was created by the CIE with the aim to be perceptually uniform [30] in the sense that the numerical difference between two colors is proportional to perceived color difference. This is an important property for color image segmentation, see e.g. [8, 16, 34]. For this reason in the following we use the Lab as the additional color space. Here the L channel correlates to perceived lightness, while the a and b channels correlate approximately with red-green and yellow-blue, respectively. As an example we show in Fig. 2d–f the L, a and b channels of the smooth \({\bar{g}}\) in Stage 1 for the noisy pyramid in Fig. 1a. From Fig. 2 one can see that the collection of 6 channels gives different information with respect to a further segmentation. The result in Fig. 1c have shown that this additional color space helps the segmentation significantly.

Let \({{\bar{g}}}'\) denote Lab transform of \({{\bar{g}}}\). In order to compare \({{\bar{g}}}'\) with \({{\bar{g}}}\in [0,1]^3\), we rescale on [0,1] the channels of \({{\bar{g}}}'\) which yields an image denoted by \({{\bar{g}}}^t\in [0,1]^3\). By stacking together \({{\bar{g}}}\) and \({{\bar{g}}}^t\) we obtain a new vector-valued image \({{\bar{g}}}^*\) with \(2d=6\) channels:

$$\begin{aligned} {\bar{g}}^*: = \left( {\bar{g}}_1, {\bar{g}}_2, {\bar{g}}_3, {\bar{g}}^t_1, {\bar{g}}^t_2, {\bar{g}}^t_3\right) . \end{aligned}$$

Our segmentation in Stage 3 is done on this \({\bar{g}}^*\).

Remark 1

The transformation from RGB to Lab color space is based on the intermediate CIE XYZ tristimulus values. The transformation of \({{\bar{g}}}\) (in RGB color space) to \({\tilde{g}}\) in XYZ is given by a linear transform \({\tilde{g}} = H {{\bar{g}}}\). Then the Lab transform \({{\bar{g}}}'\) of \({{\bar{g}}}\), see e.g., [29, chapter 1], is defined in terms of \({\tilde{g}} \) as

$$\begin{aligned} \begin{aligned}&{\bar{g}}'_1 = {\left\{ \begin{array}{ll} 116 \root 3 \of {{\tilde{g}}_2/Y_r}, &{}\quad \mathrm{if} \ {\tilde{g}}_2/Y_r > 0.008856, \\ 903.3 {\tilde{g}}_2/Y_r, &{}\quad \mathrm{otherwise}, \end{array}\right. }\\&{\bar{g}}'_2 = 500 \left( \rho ({\tilde{g}}_1/X_r) - \rho ({\tilde{g}}_2/Y_r) \right) , \ \ {\bar{g}}'_3 = 200\left( \rho ({\tilde{g}}_2/Y_r) - \rho ({\tilde{g}}_3/Z_r) \right) , \end{aligned} \end{aligned}$$

where \(\rho (x) = \root 3 \of {x}\), if \(x > 0.008856\), otherwise \(\rho (x) = (7.787 x +16)/116\), and \(X_r, Y_r\) and \(Z_r\) are the XYZ tristimulus values of the reference white point. The cube root function compresses some values more than others and the transform corresponds to the CIE chromaticity diagram. The transform takes into account the observation that the human eye is more sensitive to changes in chroma than to changes in lightness. As mentioned before, the Lab space is perceptually uniform [34]. So the Lab channels provide important complementary information to the restored RGB image \({{\bar{g}}}\). Following an aggregation approach, we use all channels of the two color spaces.

3.3 Third Stage: Thresholding

Given the vector-valued image \({\bar{g}}^*\in [0,1]^{2d} \) for \(d=3\) from Stage 2 we want now to segment it into K segments. Here we design a properly adapted strategy to partition vector-valued images into K segments. It is based on the K-means algorithm [24] because of its simplicity and good asymptotic properties. According to the value of K, the algorithm clusters all points of \(\{{{\bar{g}}}^*(x)~:~x\in {\varOmega }\}\) into K Voronoi-shaped cells, say \( {{\varSigma }}_1 \cup {{\varSigma }}_2 \cdots \cup {{\varSigma }}_K={\varOmega }\). Then we compute the mean vector \(c_k\in {\mathbb {R}}^{6}\) on each cell \({{\varSigma }}_k\) by

$$\begin{aligned} {c}_k = \frac{\int _{{{\varSigma }}_k} {{\bar{g}}}^* dx}{\int _{{{\varSigma }}_k} dx}, \quad k=1, \ldots , K. \end{aligned}$$
(12)

We recall that each entry \(c_k[i]\) for \(i=1,\cdots ,6\) is a value belonging to \(\{\mathrm {R,G,B,L,a,b}\}\), respectively. Using \(\{{c}_k\}_{k=1}^K\), we separate \({{\bar{g}}}^*\) into K phases by

$$\begin{aligned} {\varOmega }_k :=&\Big \{x\in {\varOmega }~:~ \Vert {{\bar{g}}}^*(x) - {c}_k \Vert _2 = \min _{1\le j\le K} \Vert {{\bar{g}}}^*(x) - {c}_j\Vert _2 \Big \}, \nonumber \\&\quad k=1, \ldots , K. \end{aligned}$$
(13)

It is easy to verify that \(\{{\varOmega }_k\}_{k=1}^K\) are disjoint and that \(\bigcup _{k=1}^K {\varOmega }_k = {\varOmega }\). The use of the \(\ell _2\) distance here follows from our model (4) as well as from the properties of the Lab color space [8, 30].

3.4 The SLaT Algorithm

We summarize our three-stage segmentation method for color images in Algorithm 1. Like the Mumford–Shah model, our model (4) has two parameters \(\lambda \) and \(\mu \). Extensive numerical tests have shown that we can fix \(\mu =1\). We choose \(\lambda \) empirically; the method is quite stable with respect to this choice. We emphasize that our method is quite suitable for parallelism since \(\{{{\bar{g}}}_i\}_{i=1}^3\) in Stage 1 can be computed in parallel.

figure a
Fig. 3
figure 4

Images used in our tests

Full size image
Fig. 4
figure 5

Six-phase synthetic image segmentation (size: \(100 \times 100\)). a Given Gaussian noisy image with mean 0 and variance 0.1; b given Gaussian noisy image with \(60\%\) information loss; c given blurry image with Gaussian noise; (a1–a4), (b1–b4) and (c1-c4): Results of methods [28, 36, 41], and our SLaT on (a, b, c), respectively

Full size image

4 Experimental Results

In this section, we compare our SLaT method with three state-of-the-art variational color segmentation methods [28, 36, 41]. Method [28] uses fuzzy membership functions to approximate the piecewise constant Mumford–Shah model (2). Method [36] uses a primal-dual algorithm to solve a convex relaxation of model (2) with a fixed code book. Method [41] uses an ADMM algorithm to solve the model (2) (without phase number K) with structured Potts priors. These methods were originally designed to work on color images with degradation such as noise, blur and information loss. The codes we used were provided by the authors, and the parameters in the codes were chosen by trial and error to give the best results of each method. For our model (4), we fix \(\mu =1\) and only vary \(\lambda \). In the segmented figures below, each phase is represented by the average intensity of that phase in the image. All the results were tested on a MacBook with 2.4 GHz processor and 4GB RAM, and Matlab R2014a. We present the tests on two synthesis and seven real-world images given in Fig. 3 [images (v)–(ix) are chosen from the Berkeley Segmentation Dataset and BenchmarkFootnote 1]. The images are all in RGB color space. We considered combinations of three different forms of image degradation: noise, information loss, and blur. The Gaussian and Poisson noisy images are all generated using Matlab function imnoise. For Gaussian noisy images, the Gaussian noise we added are all of mean 0 and variance 0.001 or 0.1. To apply the Poisson noise, we linearly stretch the given image f to [1, 255] first, then linearly stretch the noisy image back to [0, 1] for testing. The mean of the Poisson distribution is 10. For information loss case, we deleted 60% pixels values randomly. The blur in the test images were all obtained by a vertical motion-blur with 10 pixels length. In Stage 1 of our method, the primal-dual algorithm [10, 15] and the split-Bregman algorithm [20] are adopted to solve (4) for \({\varPhi }(f, g) = {{\mathcal {A}}}g - f \log ({{\mathcal {A}}}g)\) and \({\varPhi }(f, g) = (f-{{\mathcal {A}}} g)^2\), respectively. We terminate the iterations when \(\frac{||g_i^{(k)}-g_i^{(k+1)}||_2}{||g_i^{(k+1)}||_2} < 10^{-4}\) for \(i = 1, 2, 3\) or when the maximum iteration number 200 is reached. In Stage 2, the transformation from RGB to Lab color spaces is implemented by Matlab build-in function makecform(’srgb2lab’). In Stage 3, given the user defined number of phases K, the thresholds are determined automatically by Matlab K-means function kmeans. Since \({\bar{g}}^*\) is calculated prior to the choice of K, users can try different K and segment the image all without re-computing \({\bar{g}}^*\).

Table 1 Comparison of percentage of correct pixels for the 6-phase synthetic image
Full size table
Table 2 Iteration numbers and CPU time in seconds
Full size table
Fig. 5
figure 6

Four-phase synthetic image segmentation (size: \(256\times 256\)). a Given Gaussian noisy image with mean 0 and variance 0.001; b given Gaussian noisy image with \(60\%\) information loss; c given blurry image with Gaussian noise; (a1–a4), (b1–b4) and (c1–c4): Results of methods [28, 36, 41], and our SLaT on (a, b, c), respectively

Full size image

4.1 Segmentation of Synthetic Images

Example 1. Six-phase segmentation Figure 4 gives the result on a six-phase synthetic image containing five overlapping circles with different colors. The image is corrupted by Gaussian noise, information loss, and blur, see Fig. 4a–c respectively. From the figures, we see that method Li et al. [28] and method Storath and Weinmann [41] both fail for the three experiments while method Pock et al. [36] fails for the case of information lost. Table 1 shows the segmentation accuracy by giving the ratio of the number of correctly segmented pixels to the total number of pixels. The best ratios are printed in bold face. From the table, we see that our method gives the highest accuracy for the case of information loss and blur. For denoising, method [36] is 0.02% better. Table 2 gives the iteration numbers of each method and the CPU time cost. We see that our method outperforms the others compared. Moreover, if using parallel technique, the time can be reduced roughly by a factor of 3.

Fig. 6
figure 7

Two-phase rose segmentation (size: \(303\times 250\)). a Given Poisson noisy image; b given Poisson noisy image with \(60\%\) information loss; c given blurry image with Poisson noise; (a1–a4), (b1–b4) and (c1–c4): Results of methods [28, 36, 41], and our SLaT on (a, b, c), respectively

Full size image
Fig. 7
figure 8

Four-phase sunflower segmentation (size: \(375\times 500\)). a Given Gaussian noisy image with mean 0 and variance 0.1; b given Gaussian noisy image with \(60\%\) information loss; c given blurry image with Gaussian noise; (a1–a4), (b1–b4) and (c1–c4): Results of methods [28, 36, 41], and our SLaT on (a, b, c), respectively

Full size image
Fig. 8
figure 9

Two-phase pyramid segmentation (size: \(321\times 481\)). a Given Gaussian noisy image with mean 0 and variance 0.001; b given Gaussian noisy image with \(60\%\) information loss; c given blurry image with Gaussian noise; (a1–a4), (b1–b4) and (c1–c4): Results of methods [28, 36, 41], and our SLaT on (a, b, c), respectively

Full size image
Fig. 9
figure 10

Two-phase kangaroo segmentation (size: \(321\times 481\)). a Given Poisson noisy image; b given Poisson noisy image with \(60\%\) information loss; c given blurry image with Poisson noise; (a1–a4), (b1–b4) and (c1–c4): Results of methods [28, 36, 41], and our SLaT on (a, b, c), respectively

Full size image
Fig. 10
figure 11

Three-phase vase segmentation (size: \(481\times 321\)). a Given Gaussian noisy image with mean 0 and noise 0.001; b given Gaussian noisy image with \(60\%\) information loss; c given blurry image with Gaussian noise; (a1–a4), (b1–b4) and (c1–c4): Results of methods [28, 36, 41], and our SLaT on (a, b, c), respectively

Full size image
Fig. 11
figure 12

Three-phase elephant segmentation (size: \(321\times 481\)). a Given Poisson noisy image; b given Poisson noisy image with \(60\%\) information loss; c given blurry image with Poisson noise; (a1–a4), (b1–b4) and (c1–c4): Results of methods [28, 36, 41], and our SLaT on (a, b, c), respectively

Full size image
Fig. 12
figure 13

Four-phase man segmentation (size: \(321\times 481\)). a Given Poisson noisy image; b given Poisson noisy image with \(60\%\) information loss; c given blurry image with Poisson noise; (a1–a4), (b1–b4) and (c1–c4) results of methods [28, 36, 41], and our SLaT on (a, b, c), respectively

Full size image
Fig. 13
figure 14

Segmentation results by humans on test images used in Figs. 8, 9, 10, 11, and 12. First to third rows: original images, segmentation results by human with low segments and with high segments, respectively

Full size image

Example 2. Four-phase segmentation Our next test is on a four-phase synthetic image containing four rectangles with different colors, see Fig. 5. The variable illumination in the figure make the segmentation very challenging. The results shows that in all cases (noise, information loss and blur) all three competing methods [28, 36, 41] fail while our method gives extremely good results. Table 2 shows further that the time cost of our method is the least.

4.2 Segmentation of Real-World Color Images

In this section, we compare our method with the three competing methods for seven real-world color images in two-phase and multiphase segmentations, see Figs. 6, 7, 8, 9, 10, 11, and 12. Moreover, for the images from the Berkeley Segmentation Dataset and Benchmark used in Figs. 8, 9, 10, 11, and 12, the segmentation results by humans are shown in Fig. 13 as ground truth for visual comparison purpose. We see from the figures that our method is far superior than those by the competing methods, and our results are consistent with the segmentations provided by humans. The timing of the methods given in Table 2 shows that our method in most of the cases gives the least timing. Again, we emphasize that our method is easily parallelizable. All presented experiments clearly show that all goals listed in Introduction are fulfilled.

5 Conclusions

In this paper we proposed a three-stage image segmentation method for color images. At the first stage of our method, a convex variational model is used in parallel on each channel of the color image to obtain a smooth color image. Then in the second stage we transform this smooth image to a secondary color space so as to obtain additional information of the image in the less-correlated color space. In the last stage, multichannel thresholding is used to threshold the combined image from the two color spaces. The new three-stage method, named SLaT for Smoothing, Lifting and Thresholding, has the ability to segment images corrupted by noise, blur, or when some pixel information is lost. Experimental results on RGB images coupled with Lab secondary color space demonstrate that our method gives much better segmentation results for images with degradation than some state-of-the-art segmentation models both in terms of quality and CPU time cost. Our future work includes finding an automatical way to determine \(\lambda \) and possibly an improved model (4) that can better promote geometry. It is also interesting to optimize channels from the selected color spaces, and analyze the effect in color image segmentation.