Unconditional Superconvergence Analysis of a Crank–Nicolson Galerkin FEM for Nonlinear Schrödinger Equation

Abstract

A linearized Crank–Nicolson Galerkin finite element method with bilinear element for nonlinear Schrödinger equation is studied. By splitting the error into two parts which are called the temporal error and the spatial error, the unconditional superconvergence result is deduced. On one hand, the regularity for a time-discrete system is presented based on the proof of the temporal error. On the other hand, the classical Ritz projection is applied to get the spatial error with order $O(h^2)$ in $L^2$-norm, which plays an important role in getting rid of the restriction of $\tau$. Then the superclose estimates of order $O(h^2+\tau ^2)$ in $H^1$-norm is arrived at based on the relationship between the Ritz projection and the interpolated operator. At the same time, global superconvergence property is arrived at by the interpolated postprocessing technique. At last, three numerical examples are provided to confirm the theoretical analysis. Here, h is the subdivision parameter and $\tau$ is the time step.

1 Introduction

Consider the following nonlinear Schrödinger equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} iu_t+\Delta u+ f(|u|^2)u=0, &{} (X, t)\in \Omega \times (0, T], \\ u=0,&{} (X, t)\in \ \partial \Omega \times (0, T], \\ u(X, 0)=u_{0}(X), &{} X\in \Omega , \end{array}\right. } \end{aligned}$$

(1.1)

where $X=(x, y)$, $0<T<\infty$, and $\Omega \subset \mathbb {R}^{2}$ is a rectangle with the boundary $\partial \Omega$. i is the imaginary unit, $u_0(X)$ is a known complex-valued function. Moreover, f(s) is a real-valued nonlinear function which is twicely continuously differentiable with respective to s.

The NLSE plays an important role in describing physical phenomena, such as optical pulses, plasma physics and water waves and so on. Different numerical methods for the NLSE have been investigated extensively. For example,  [1] discussed an iterative modification of the linearized scheme and proved second-order error estimates by use of Newtons method to linearize the equations at each time level. Continuous Galerkin methods were employed in  [2] and optimal order error estimates in $L^{\infty }(L^2)$ and $L^{\infty }(H^1)$, and the corresponding superconvergence results at the temporal nodes $t^n$ were obtained.  [3] and  [4] studied the normal Galerkin method and introduced the semi-discrete scheme and fully-discrete schemes for NLSE, respectively and both derived the superclose and superconvergence results in $H^1$-norm. A meshless local boundary integral equation method and two-grid mixed finite element method were proposed to solve the unsteady Schrödinger equation in  [5] and  [6], respectively.  [7] and  [8] researched the discontinuous Galerkin method and get optimal order error estimates. Finite difference method were also considered extensively in  [9,10,11,12].

In fact, studying a nonlinear physical system often involves the boundedness of $U_h^n$ in $L^\infty$-norm or a stronger norm, where $U_h^n$ is the numerical solution. The usual technique is employing the inverse inequality to deal with such issue, which will result in some time-step restrictions, such as $\tau =o(h^{\frac{1}{4}})$ and $\tau =O(h^2)/\tau =O(h)$ in  [1] and  [3], respectively. Moreover, such restrictions also arise in the studies on other nonlinear evolution equations, such as nonlinear hyperbolic equations [13, 14], nonlinear parabolic equation [15,16,17,18], nonlinear Sobolev problems [19, 20], Navier–Stokes equations [21, 22], and so on. Therefore, how to get rid of such restriction becomes a hot topic and for this issue, a lot of efforts have been devoted. For instance, a corresponding time-discrete system was introduced in  [23] to split the error into two parts, the temporal error and the spatial error, and the spatial error was reduced to the unconditional boundedness of numerical solution in $L^\infty$-norm. Then the optimal $L^2$ error estimate without any time-step restrictions for the NLSE was obtained. Subsequently, this so-called splitting technique was also applied to other equations [24,25,26,27,28,29,30]. Especially,  [31] used different technique from the above studies to get the unconditional superclose for Sobolev equation with conforming mixed FEM.

Different from  [3] and  [23], we discuss the unconditional superconvergence estimate for (1.1) with bilinear element[32]. A time-discrete system with solution $U^n$ is developed to split the error $u^n-U_h^n$ into the temporal error $u^n-U^n$ and the spatial error $U^n-U_h^n$. On one hand, we obtain the temporal error $\Vert u^n-U^n\Vert _2=O(\tau ^2)$, which is one order higher than that of  [23]. Then the boundedness of $\tilde{\partial }_{tt}U^n$, which plays an important role in the analysis of the spatial error, is arrived at. As it is shown in our paper, $H^2$ error estimate of the temporal error is important for getting rid of the restriction of $\tau$. In the existing literature, there have also been other related works of $H^2$ error estimate for certain nonlinear PDEs, such as  [32, 33]. On the other hand, we introduce the classical Ritz prjection operator $R_h$ to get the unconditional result of $\Vert R_hU^n-U_h^n\Vert _0$ with order $O(h^2)$, which implies the unconditional boundedness of $\Vert U_h^n\Vert _{0,\infty }$. Consequently, the superclose property of $\Vert R_hU^n-U_h^n\Vert _1$ with order $O(h^2+\tau ^2)$ is deduced on the basis of the above achievements. Furthermore, through the relationship between $R_h$ and the corresponding interpolation operator $I_h$, we get $\Vert I_hu^n-U_h^n\Vert _1$ with order $O(h^2+\tau ^2)$ unconditionally. At the same time, we derive the global superconvergence by using the postprocessing operator in  [31]. At last, some numerical results also show the validity of the theoretical analysis.

Throughout this paper, we denote the natural inner product in $L^{2}(\Omega )$ by $(\cdot ,\cdot )$ and the norm by $\Vert \cdot \Vert _{0}$, and let $H_{0}^{1}(\Omega )=\{v\in H^{1}(\Omega ):v|_{\partial \Omega }=0\}$. Further, we use the classical Sobolev spaces $W^{m,p}(\Omega ), 1\le p\le \infty$, denoted by $W^{m,p}$, with norm $\Vert \cdot \Vert _{m,p}$. When $p=2$, we simply write $\Vert \cdot \Vert _{m,p}$ as $\Vert \cdot \Vert _{m}$. Besides, we define the space $L^p(a,b;Y)$ with the norm $\Vert f\Vert _{L^p(a,b; Y)}=(\int _a^b\Vert f(\cdot ,t)\Vert _Y^pdt)^{\frac{1}{p}}$, and if $p=\infty$, the integral is replaced by the essential supremum.

2 A Linearized Galerkin Approximation Scheme

Let $\Omega$ be a rectangle in (x, y) plane with edges parallel to the coordinate axes, $\Gamma _{h}$ be a quasiuniform partition of $\Omega$ into rectangular $\pi _h$. Denote $h=\max \limits _{\pi _h\in \Gamma _h}{\mathrm {diam} \pi _h}$ the mesh size, $V_{h}$ be the usual bilinear FE space, $V_{h0}=\{v_h\in V_h, v_h|_{\partial \Omega }=0\}$. Let $R_h: H_0^1\rightarrow V_{h0}$ be the associated Ritz projection operator on $V_{h0}$ defined by

$$\begin{aligned} (\nabla (u-R_hu),\nabla v_h)=0, \forall v_h\in V_{h0}. \end{aligned}$$

(2.1)

It follows from  [17] that

$$\begin{aligned} \Vert \nabla R_hu\Vert _0\le C\Vert \nabla u\Vert _{0}, \end{aligned}$$

(2.2)

and

$$\begin{aligned} \Vert u-R_hu\Vert _0\le Ch^s\Vert u\Vert _{s},s=1,2, \forall u\in H^1_0(\Omega )\cap H^2(\Omega ). \end{aligned}$$

(2.3)

Moreover, for $u\in H^{3}(\Omega )$, we can found in  [34] that

$$\begin{aligned} \Vert I_hu-R_hu\Vert _1=O(h^2)\Vert u\Vert _3, \end{aligned}$$

(2.4)

where $I_h$ be the associated interpolated operator over $V_{h0}$.

Let $\{t_n:t_n=n\tau ;0\le n\le N\}$ be a uniform partition of [0, T] with the time step $\tau =T/N$, $t_{n-\frac{1}{2}}=\frac{1}{2}(t_n+t_{n-1})$ and $\sigma ^n=\sigma (X,t_n)$. For a sequence of functions $\{\sigma ^n\}_{n=0}^{N}$, we remark

$$\begin{aligned} \tilde{\partial }_t\sigma ^n= & {} \frac{\sigma ^n-\sigma ^{n-1}}{\tau }, \tilde{\partial }_{tt}\sigma ^n=\frac{\tilde{\partial }_t\sigma ^n-\tilde{\partial }_t\sigma ^{n-1}}{\tau }, \tilde{\sigma }^n=\frac{\sigma ^n+\sigma ^{n-1}}{2}, \quad n=1,2,\ldots ,N,\\ \hat{\sigma }^n= & {} \frac{3}{2}\sigma ^{n-1}-\frac{1}{2}\sigma ^{n-2}, \quad n=2,\ldots ,N. \end{aligned}$$

With these notations, we develop the linearized Galerkin FEM to problem (1.1): seek $U_h^n\in V_{h0}$, such that for $n\ge 2$,

$$\begin{aligned} i(\tilde{\partial }_tU_h^n,v_h)-(\nabla \tilde{U}_h^n, \nabla v_h)+(f(|\hat{U}_h^{n}|^2)\tilde{U}_h^n,v_h)=0, \quad \forall v_h\in V_{h0}, \end{aligned}$$

(2.5)

and we will analyze a predictor corrector method to determine $U_h^1$:

$$\begin{aligned} i\left( \frac{U^{1,0}_h-U^0_h}{\tau },v_h\right) - \left( \frac{\nabla U^{1,0}_h+\nabla U^0_h}{2},\nabla v_h\right) = \left( f(|U^0_h|^2)\frac{ U^{1,0}_h+ U^0_h}{2},v_h\right) , \end{aligned}$$

(2.6)

followed by

$$\begin{aligned} i\left( \frac{U^{1}_h-U^0_h}{\tau },v_h\right) - \left( \frac{\nabla U^{1}_h+\nabla U^0_h}{2},\nabla v_h\right) = \left( f\left( \left| \frac{ U^{1,0}_h+ U^0_h}{2}\right| ^2\right) \frac{ U^{1}_h+ U^0_h}{2}, v_h\right) , \end{aligned}$$

(2.7)

where $U_h^0=R_hu_0$. Obviously, only a linear system with certain constant coefficients need to be solved now.

3 Error Estimates for Time-Discrete System

In this section, we introduce the following time-discrete system:

$$\begin{aligned} {\left\{ \begin{array}{ll} i\tilde{\partial }_tU^n+\Delta \tilde{U}^n+f(|\hat{U}^{n}|^2)\tilde{U}^n=0, &{} (X, t)\in \Omega \times (0, T], n\ge 2\\ U^n=0,&{} (X, t)\in \ \partial \Omega \times (0, T], n\ge 1\\ U(X, 0)=u_{0}(X), &{} X\in \Omega , \end{array}\right. } \end{aligned}$$

(3.1)

When $n=1$, we determine $U^1$ by

$$\begin{aligned} i\frac{U^{1,0}-U^0}{\tau }+ \frac{\Delta U^{1,0}+\Delta U^0}{2}+f(|U^0|^2)\frac{U^{1,0}+U^0}{2}=0 \end{aligned}$$

(3.2)

and

$$\begin{aligned} i\frac{U^{1}-U^0}{\tau }+ \frac{\Delta U^{1}+\Delta U^0}{2}+f\left( \left| \frac{U^{1,0}+U^0}{2}\right| ^2\right) \frac{U^{1}+U^0}{2}=0, \end{aligned}$$

(3.3)

where $U^{1,0}|_{\partial \Omega }=0$. The above system can be viewed as a system of linear elliptic equations, and the existence and uniqueness of solution can be proved immediately. In what follows, we will set $e^n=u^n-U^n (n=0,1,2,\ldots N)$, analyze $\Vert u^n-U^n\Vert _i (i=0,1,2)$ and give the regularity result of $U^n$.

Theorem 1

Let u and $U^m (m=0,1,2,\ldots N)$ be the solutions of (1.1) and (3.1)–(3.3), respectively, $u\in L^{2}(0,T;H^{3}(\Omega )), u_t\in L^{\infty }(0,T;H^{2}(\Omega )), u_{tt}\in L^{\infty }(0,T;H^{2}(\Omega ))$, then for $m=1,\ldots , N,$ there exists $\tau _0$ such that when $\tau \le \tau _0$, we have

$$\begin{aligned} \Vert \tilde{\partial }_te^m\Vert _0+\Vert e^m\Vert _2\le C_0\tau ^2 \end{aligned}$$

(3.4)

and

$$\begin{aligned} \left\| \frac{U^{1,0}-U^{0}}{\tau }\right\| _2+\Vert \tilde{\partial }_{tt}U^m\Vert _2\le C_0. \end{aligned}$$

(3.5)

Proof

Setting $K_0\triangleq 1+\max \limits _{1\le m\le N}(\Vert u^m\Vert _{0,\infty }+\Vert \tilde{\partial }_tu^m\Vert _{0,\infty })$. Then we begin to prove (3.4) and (3.5) by mathematical induction. When $m=1$, we have the error equations by (1.1) and (3.2)–(3.3) as follows:

$$\begin{aligned} i\frac{e^{1,0}}{\tau }+ \frac{\Delta e^{1,0}}{2}+f\left( \left| u^0\right| ^2\right) \frac{e^{1,0}}{2}=S_1+S_2+S_3 \end{aligned}$$

(3.6)

and

$$\begin{aligned} i\frac{e^{1}}{\tau }+ \frac{\Delta e^{1}}{2}+P_1^1=S_1+S_2+S_4, \end{aligned}$$

(3.7)

where $S_1=\frac{u^{1}-u^{0}}{\tau }-u_t^{\frac{1}{2}}, S_2=\frac{\Delta u^{1}+\Delta u^{0}}{2}-\Delta u^{\frac{1}{2}}, S_3=f(|u^0|^2)\frac{u^{1}+u^{0}}{2}-f(|u^{\frac{1}{2}}|^2)u^{\frac{1}{2}}, S_4=f(|\frac{u^{1}+u^0}{2}|^2)\frac{u^{1}+u^{0}}{2}-f(|u^{\frac{1}{2}}|^2)u^{\frac{1}{2}}$ and $P_1^1=f(|\frac{u^{1}+u^0}{2}|^2)\frac{u^{1}+u^0}{2}-f(|\frac{U^{1,0}+U^0}{2}|^2)\frac{U^{1}+U^0}{2}$. It is easy to see that $\Vert S_1\Vert _0+\Vert S_2\Vert _0+\Vert S_4\Vert _0\le C\tau ^2,\Vert S_3\Vert _0\le C\tau$.

On one hand, multiplying (3.6) by $\frac{e^{1,0}}{\tau }$, integrating it over $\Omega$ and then we get

$$\begin{aligned} i\left\| \frac{e^{1,0}}{\tau }\right\| _0^2-\frac{1}{2\tau }\left\| \nabla e^{1,0}\right\| _0^2=-\left( f\left( \left| u^0\right| ^2\right) \frac{e^{1,0}}{2},\frac{e^{1,0}}{\tau }\right) +\left( S_1+S_2+S_3,\frac{e^{1,0}}{\tau }\right) . \end{aligned}$$

(3.8)

Taking the imaginary part of (3.8), it is easy to get

$$\begin{aligned} \left\| \frac{e^{1,0}}{\tau }\right\| _0^2\le C\tau ^2+\frac{1}{2}\left\| \frac{e^{1,0}}{\tau }\right\| _0^2+C\left\| e^{1,0}\right\| _0^2. \end{aligned}$$

(3.9)

Then there exist $\tau _1, C_1$, such that when $\tau \le \tau _1$, we have

$$\begin{aligned} \Vert e^{1,0}\Vert _0\le C_1\tau ^2. \end{aligned}$$

(3.10)

Again, multiplying (3.6) by $\frac{\Delta e^{1,0}}{\tau }$ and integrating it over $\Omega$ to yield

$$\begin{aligned} -i\left\| \frac{\nabla e^{1,0}}{\tau }\right\| _0^2+\frac{1}{2\tau }\left\| \Delta e^{1,0}\right\| _0^2=-\left( f\left( \left| u^0\right| ^2\right) \frac{e^{1,0}}{2},\frac{\Delta e^{1,0}}{\tau }\right) +\left( S_1+S_2+S_3,\frac{\Delta e^{1,0}}{\tau }\right) . \end{aligned}$$

(3.11)

Noting

$$\begin{aligned} \left| \left( f\left( \left| u^0\right| ^2\right) \frac{e^{1,0}}{2},\frac{\Delta e^{1,0}}{\tau }\right) \right| \le \frac{1}{8}\left\| \frac{\nabla e^{1,0}}{\tau }\right\| _0^2+ C\left\| \Delta e^{1,0}\right\| _0^2 \end{aligned}$$

and

$$\begin{aligned} \left| \left( S_1+S_2+S_3,\frac{\Delta e^{1,0}}{\tau }\right) \right| \le C\tau +\frac{1}{8\tau }\left\| \Delta e^{1,0}\right\| _0^2. \end{aligned}$$

Then by taking the imaginary part and the real part of (3.11), and summing them together, we have

$$\begin{aligned} \left\| \frac{\nabla e^{1,0}}{\tau }\right\| _0^2+\frac{1}{2\tau }\left\| \Delta e^{1,0}\right\| _0^2 \le C\tau +\frac{1}{4\tau }\left\| \Delta e^{1,0}\right\| _0^2+\frac{1}{4}\left\| \frac{\nabla e^{1,0}}{\tau }\right\| _0^2+ C\Vert \Delta e^{1,0}\Vert _0^2. \end{aligned}$$

(3.12)

Since $e^{1,0}\in H^2(\Omega )\cap H_0^1(\Omega )$, there exist $\tau _2, C_2, C_3$, such that when $\tau \le \tau _2$, we have

$$\begin{aligned} \sqrt{\tau }\left\| \frac{e^{1,0}}{\tau }\right\| _1+\left\| e^{1,0}\right\| _2 \le C_2\tau , \end{aligned}$$

(3.13)

which implies

$$\begin{aligned} \left\| \frac{U^{1,0}-U^{0}}{\tau }\right\| _2\le C_3 \end{aligned}$$

(3.14)

and

$$\begin{aligned} \Vert U^{1,0}\Vert _{0,\infty }\le \Vert e^{1,0}\Vert _{0,\infty }+\Vert u^{1}\Vert _{0,\infty } \le C\Vert e^{1,0}\Vert _{2}+\Vert u^{1}\Vert _{0,\infty }\le CC_2\tau +\Vert u^{1}\Vert _{0,\infty } \le K_0, \end{aligned}$$

(3.15)

where $\tau \le \tau _3\le 1/CC_2.$

On the other hand, multiplying (3.7) by $\frac{e^{1}}{\tau }$, integrating it over $\Omega$ and then we get

$$\begin{aligned} i\left\| \frac{e^{1}}{\tau }\right\| _0^2-\frac{1}{2\tau }\Vert \nabla e^{1}\Vert _0^2=-\left( P_1^1,\frac{e^{1}}{\tau }\right) +\left( S_1+S_2+S_4,\frac{e^{1}}{\tau }\right) . \end{aligned}$$

(3.16)

By the help of (3.10) and (3.15), we get

$$\begin{aligned} \Vert P_1^1\Vert _0&=\left\| f\left( \left| \frac{U^{1,0}+U^0}{2}\right| ^2\right) \frac{e^{1}}{2}+\frac{u^{1} +u^0}{2}\left( f\left( \left| \frac{u^{1}+u^0}{2}\right| ^2\right) -f\left( \left| \frac{U^{1,0}+U^0}{2}\right| ^2\right) \right) \right\| _0\nonumber \\&\le C\Vert e^{1}\Vert _0+C\Vert e^{1,0}\Vert _0\le C\tau ^2+C\Vert e^{1}\Vert _0. \end{aligned}$$

(3.17)

Taking the imaginary part of (3.16), it is obvious to see that there exist $\tau _4, C_4$, such that $\tau \le \tau _4$, it follows that

$$\begin{aligned} \left\| \frac{e^{1}}{\tau }\right\| _0\le C_4\tau ^2. \end{aligned}$$

(3.18)

Once more, multiplying (3.7) by $\frac{\Delta e^{1}}{\tau }$, integrating it over $\Omega$ and then we get

$$\begin{aligned} -i\left\| \frac{\nabla e^{1}}{\tau }\right\| _0^2+\frac{1}{2\tau }\Vert \Delta e^{1}\Vert _0^2=-\left( P_1^1,\frac{\Delta e^{1}}{\tau }\right) +\left( S_1+S_2+S_4,\frac{\Delta e^{1}}{\tau }\right) . \end{aligned}$$

(3.19)

Similarly to the estimates of $e^{1,0}$, we get

$$\begin{aligned} \left| \left( P_1^1,\frac{\Delta e^{1}}{\tau }\right) \right|&=\left| \left( f\left( \left| \frac{U^{1,0}+U^0}{2}\right| ^2\right) \frac{e^{1}}{2},\frac{\Delta e^{1}}{\tau }\right) + \left( \frac{u^{1}+u^0}{2} \left( f\left( \left| \frac{u^{1}+u^0}{2}\right| ^2\right) \right. \right. \right. \\&\left. \left. \left. \quad -\,f\left( \left| \frac{U^{1,0}+U^0}{2}\right| ^2\right) \right) ,\frac{\Delta e^{1}}{\tau }\right) \right| \\&\le C\tau ^3+\frac{1}{8}\left\| \frac{\nabla e^{1}}{\tau }\right\| _0^2+\frac{1}{16\tau }\Vert \Delta e^{1}\Vert _0^2+C\Vert \Delta e^{1}\Vert _0^2 \end{aligned}$$

and

$$\begin{aligned} \left| \left( S_1+S_2+S_4,\frac{\Delta e^{1}}{\tau }\right) \right| \le C\tau ^3+\frac{1}{16\tau }\Vert \Delta e^{1}\Vert _0^2, \end{aligned}$$

which implies

$$\begin{aligned} \left\| \frac{\nabla e^{1}}{\tau }\right\| _0^2+\frac{1}{2\tau }\Vert \Delta e^{1}\Vert _0^2\le C\tau ^3+\frac{1}{4}\left\| \frac{\nabla e^{1}}{\tau }\right\| _0^2+\frac{1}{4\tau }\Vert \Delta e^{1}\Vert _0^2+C\Vert \Delta e^{1}\Vert _0^2. \end{aligned}$$

(3.20)

It is apparent to see that there exist $\tau _5, C_5, C_6$, such that when $\tau \le \tau _5$, we have

$$\begin{aligned} \Vert e^{1}\Vert _2\le C_5\tau ^2, \end{aligned}$$

(3.21)

which leads to

$$\begin{aligned} \Vert \tilde{\partial }_{tt}U^{1}\Vert _{2}\le C_6, \end{aligned}$$

(3.22)

and

$$\begin{aligned} \Vert \tilde{\partial }_tU^{1}\Vert _{0,\infty }+\Vert U^{1}\Vert _{0,\infty }&\le \Vert \tilde{\partial }_te^{1}\Vert _{0,\infty }+\Vert \tilde{\partial }_tu^{1}\Vert _{0,\infty }+\Vert e^{1}\Vert _{0,\infty }+\Vert u^{1}\Vert _{0,\infty }\nonumber \\&\le CC_5\tau +\Vert \tilde{\partial }_tu^{1}\Vert _{0,\infty }+\Vert u^{1}\Vert _{0,\infty } \le K_0, \end{aligned}$$

(3.23)

where $\tau \le \tau _6=1/CC_5$.

By mathematical induction, we assume that (3.4) and (3.5) hold for $m\le n-1$. Then

$$\begin{aligned} \Vert \tilde{\partial }_tU^{m}\Vert _{0,\infty }+\Vert U^{m}\Vert _{0,\infty }&\le \Vert \tilde{\partial }_te^{m}\Vert _{0,\infty }+\Vert \tilde{\partial }_tu^{m}\Vert _{0,\infty }+\Vert e^{m}\Vert _{0,\infty }+\Vert u^{m}\Vert _{0,\infty }\\&\le CC_0\tau +\Vert \tilde{\partial }_tu^{m}\Vert _{0,\infty } +\Vert u^{m}\Vert _{0,\infty } \le K_0, \end{aligned}$$

where $\tau \le \tau _7=1/CC_0$.

Now we prove (3.4) and (3.5) also hold for $m=n$. To estimate $e^n$, we subtract (3.1) from (1.1) to obtain

$$\begin{aligned} i\tilde{\partial }_te^n+\Delta \tilde{e}^n+P_1^n=R_1^n+R_2^n+R_3^n, \end{aligned}$$

(3.24)

where $R_1^n=i(\tilde{\partial }_tu^{n}-u_t^{n-\frac{1}{2}}), R_2^n=\Delta \tilde{u}^n-\Delta u^{n-\frac{1}{2}}, R_3^n=f(|\hat{u}^{n}|^2)\tilde{u}^n-f(|u^{n-\frac{1}{2}}|^2)u^{n-\frac{1}{2}}$ and $P_1^n=f(|\hat{u}^{n}|^2)\tilde{u}^n- f(|\hat{U}^{n}|^2)\tilde{U}^n$. By Taylor’s expansion, we have

$$\begin{aligned} \Vert R_1^n\Vert _0+\Vert R_2^n\Vert _0+\Vert R_3^n\Vert _0=O(\tau ^2). \end{aligned}$$

(3.25)

We multiply (3.24) by $\tilde{\partial }_t\Delta e^n$ and integrate it over $\Omega$ to get

$$\begin{aligned} -i\Vert \tilde{\partial }_t\nabla e^n\Vert _0^2+(\Delta \tilde{e}^n,\tilde{\partial }_t\Delta e^n)=-(P_1^n,\tilde{\partial }_t\Delta e^n) +(R_1^n+R_2^n+R_3^n,\tilde{\partial }_t\Delta e^n). \end{aligned}$$

(3.26)

Taking the real part, the left hand can be rewritten as

$$\begin{aligned} Re(\Delta \tilde{e}^n,\tilde{\partial }_t\Delta e^n)=\frac{1}{2\tau }(\Vert \Delta e^n\Vert _0^2-\Vert \Delta e^{n-1}\Vert _0^2). \end{aligned}$$

(3.27)

As to the right hand of (3.26), we need to transfer $\tau$ from one part of the inner product to the other, for there is no term concerning with $\tilde{\partial }_t\Delta e^n$ on the left hand. Define $\hat{u}^{1}=\tilde{u}^1, \hat{U}^{1}=\tilde{U}^1$ and $\hat{e}^{1}=\tilde{e}^1$, rewrite $(P_1^n,\tilde{\partial }_t\Delta e^n)$ by

$$\begin{aligned} (P_1^n,\tilde{\partial }_t\Delta e^n)=-(\tilde{\partial }_t P_1^n,\Delta e^{n-1}) +\tilde{\partial }_t(P_1^n,\Delta e^n). \end{aligned}$$

(3.28)

Indeed, by the assumption of the mathematical induction, we have

$$\begin{aligned} \Vert \tilde{\partial }_t P_1^n\Vert _0=&\left\| \frac{(f(|\hat{u}^{n}|^2)\tilde{u}^n- f(|\hat{U}^{n}|^2)\tilde{U}^n)-(f(|\hat{u}^{n-1}|^2)\tilde{u}^{n-1}- f(|\hat{U}^{n-1}|^2)\tilde{U}^{n-1})}{\tau }\right\| _0\\ =&\left\| f(|\hat{U}^{n-1}|^2)\tilde{\partial }_t\tilde{e}^n +\tilde{\partial }_t\tilde{u}^n (f(|\hat{u}^{n-1}|^2)-f(|\hat{U}^{n-1}|^2))\right. \\&\left. \quad +\,\frac{(f(|\hat{U}^{n}|^2)- f(|\hat{U}^{n-1}|^2))\tilde{e}^n}{\tau }\right. \\&\left. \quad +\,\frac{\tilde{u}^n((f(|\hat{u}^{n}|^2)-f(|\hat{u}^{n-1}|^2))-(f(|\hat{U}^{n}|^2)- f(|\hat{U}^{n-1}|^2)))}{\tau }\right\| _0\\ \le&\,C\Vert \tilde{\partial }_t\tilde{e}^n\Vert _0 +C\Vert \hat{e}^{n-1}\Vert _0+C\Vert \tilde{e}^{n}\Vert _0\\&\quad +\,C\left\| \frac{(f(|\hat{u}^{n}|^2)-f(|\hat{u}^{n-1}|^2))-(f(|\hat{U}^{n}|^2)- f(|\hat{U}^{n-1}|^2))}{\tau }\right\| _0. \end{aligned}$$

Note that

$$\begin{aligned}&\frac{(f(|\hat{u}^{n}|^2)-f(|\hat{u}^{n-1}|^2))-(f(|\hat{U}^{n}|^2)- f(|\hat{U}^{n-1}|^2))}{\tau }\\&\quad =\frac{(f^{'}(|\hat{u}^{n-1}|^2)(|\hat{u}^{n}|^2-|\hat{u}^{n-1}|^2)+\frac{1}{2}f^{''}(\mu _1^n) (|\hat{u}^{n}|^2-|\hat{u}^{n-1}|^2)^2)}{\tau }\\&\qquad -\,\frac{(f^{'}(|\hat{U}^{n-1}|^2)(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2) +\frac{1}{2}f^{''}(\mu _2^n)(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)^2)}{\tau }\\&\quad =\frac{f^{'}(|\hat{U}^{n-1}|^2)((|\hat{u}^{n}|^2-|\hat{u}^{n-1}|^2)-(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2))}{\tau }\\&\qquad +\,\frac{(|\hat{u}^{n}|^2-|\hat{u}^{n-1}|^2)(f^{'}(|\hat{u}^{n-1}|^2)-f^{'}(|\hat{U}^{n-1}|^2))}{\tau }\\&\qquad +\,\frac{1}{2}\frac{f^{''}(\mu _2^n)((|\hat{u}^{n}|^2-|\hat{u}^{n-1}|^2)^2-(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)^2)}{\tau }\\&\qquad +\,\frac{1}{2}\frac{(|\hat{u}^{n}|^2-|\hat{u}^{n-1}|^2)^2(f^{''}(\mu _1^n)-f^{''}(\mu _2^n))}{\tau }, \end{aligned}$$

where

$$\begin{aligned} \mu _1^n=|\hat{u}^{n-1}|^2+\lambda _1^n(|\hat{u}^{n}|^2-|\hat{u}^{n-1}|^2), \mu _2^n=|\hat{U}^{n-1}|^2+\lambda _2^n(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2). \end{aligned}$$

We find that

$$\begin{aligned}&\left\| \frac{(|\hat{u}^{n}|^2-|\hat{u}^{n-1}|^2)-(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)}{\tau }\right\| _0\nonumber \\&\quad =\left\| \frac{(\hat{u}^{n}\bar{\hat{u}}^{n}-\hat{u}^{n-1}\bar{\hat{u}}^{n-1}) -(\hat{U}^{n}\bar{\hat{U}}^{n}-\hat{U}^{n-1}\bar{\hat{U}}^{n-1})}{\tau }\right\| _0\nonumber \\&\quad =\Vert (\hat{u}^{n-1}\tilde{\partial }_t\bar{\hat{u}}^{n}+\bar{\hat{u}}^{n}\tilde{\partial }_t\hat{u}^{n}) -(\hat{U}^{n-1}\tilde{\partial }_t\bar{\hat{U}}^{n}+\bar{\hat{U}}^{n}\tilde{\partial }_t\hat{U}^{n})\Vert _0\nonumber \\&\quad =\Vert \hat{U}^{n-1}\tilde{\partial }_t\bar{\hat{e}}^{n}+\tilde{\partial }_t\bar{\hat{u}}^{n}\hat{e}^{n-1} +\bar{\hat{U}}^{n}\tilde{\partial }_t\hat{e}^{n}+\tilde{\partial }_t\hat{u}^{n}\bar{\hat{e}}^{n}\Vert _0\nonumber \\&\quad \le C\Vert \tilde{\partial }_t\hat{e}^{n}\Vert _0+C\Vert \hat{e}^{n-1}\Vert _0+C\Vert \hat{e}^{n}\Vert _0, \end{aligned}$$

(3.29)

which implies

$$\begin{aligned}&\left\| \frac{(|\hat{u}^{n}|^2-|\hat{u}^{n-1}|^2)^2-(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)^2}{\tau }\right\| _0\nonumber \\&=\left\| \frac{((|\hat{u}^{n}|^2-|\hat{u}^{n-1}|^2)-(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)) ((|\hat{u}^{n}|^2-|\hat{u}^{n-1}|^2)+(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2))}{\tau }\right\| _0 \nonumber \\&\le C\Vert \tilde{\partial }_t\hat{e}^{n}\Vert _0+C\Vert \hat{e}^{n-1}\Vert _0+C\Vert \hat{e}^{n}\Vert _0. \end{aligned}$$

(3.30)

Moreover

$$\begin{aligned}&\left\| \frac{\mu _1^n-\mu _2^n}{\tau }\right\| _{0,\infty } =\left\| \frac{|\hat{u}^{n-1}|^2-|\hat{U}^{n-1}|^2 +\lambda _1^n(|\hat{u}^{n}|^2-|\hat{u}^{n-1}|^2) -\lambda _2^n(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)}{\tau }\right\| _{0,\infty } \le C. \end{aligned}$$

(3.31)

Allocating (3.29)–(3.31), we have

$$\begin{aligned}&\left\| \frac{(f(|\hat{u}^{n-1}|^2)-f(|\hat{u}^{n-2}|^2))-(f(|\hat{U}^{n-1}|^2)- f(|\hat{U}^{n-2}|^2))}{\tau }\right\| _0\\&\quad \le C\tau ^2+C\Vert \tilde{\partial }_t\hat{e}^{n}\Vert _0 +C\Vert \hat{e}^{n-1}\Vert _0+C\Vert \hat{e}^{n}\Vert _0, \end{aligned}$$

which leads to

$$\begin{aligned} \Vert \tilde{\partial }_t P_1^n\Vert _0&\le C\tau ^2+C\Vert \tilde{\partial }_t\hat{e}^{n}\Vert _0 +C\Vert \hat{e}^{n-1}\Vert _0+C\Vert \hat{e}^{n}\Vert _0+C\Vert \tilde{\partial }_t\tilde{e}^{n}\Vert _0 +C\Vert \tilde{e}^{n}\Vert _0. \end{aligned}$$

(3.32)

Thus

$$\begin{aligned} (P_1^n,\tilde{\partial }_t\Delta e^n)&\le C\tau ^2+C\Vert \tilde{\partial }_t\hat{e}^{n}\Vert _0 +C\Vert \hat{e}^{n-1}\Vert _0+C\Vert \hat{e}^{n}\Vert _0+C\Vert \tilde{\partial }_t\tilde{e}^{n}\Vert _0 +C\Vert \tilde{e}^{n}\Vert _0\nonumber \\&\quad +\,C\Vert \Delta e^{n-1}\Vert _0^2+\tilde{\partial }_t(P_1^n,\Delta e^n). \end{aligned}$$

(3.33)

Similar to (3.28), we rewrite $(R_1^n+R_2^n+R_3^n,\tilde{\partial }_t\Delta e^n)$ as

$$\begin{aligned} (R_1^n+R_2^n+R_3^n,\tilde{\partial }_t\Delta e^n)= -(\tilde{\partial }_tR_1^n+\tilde{\partial }_tR_2^n+\tilde{\partial }_tR_3^n,\Delta e^{n-1})+\tilde{\partial }_t(R_1^n+R_2^n+R_3^n,\Delta e^{n}). \end{aligned}$$

(3.34)

It is not difficult to check that

$$\begin{aligned}&\Vert \tilde{\partial }_tR_1^n\Vert _0 =\left\| \frac{(\tilde{\partial }_tu^n-u_t^{n})-(\tilde{\partial }_tu^{n-1}-u_t^{n-1})}{\tau }\right\| _0\le C\tau ^2, \end{aligned}$$

(3.35)

and

$$\begin{aligned}&\Vert \tilde{\partial }_tR_2^n\Vert _0=\left\| \frac{(\Delta \tilde{u}^n-\Delta u^{n-\frac{1}{2}})-(\Delta \tilde{u}^{n-1}-\Delta u^{n-1-\frac{1}{2}})}{\tau }\right\| _0\le C\tau ^2. \end{aligned}$$

(3.36)

Note that

$$\begin{aligned}&\left\| \tilde{\partial }_tR_3^n\Vert _0=\Vert \frac{(f(|\hat{u}^{n}|^2)\tilde{u}^n-f(|u^{n-\frac{1}{2}}|^2)u^{n-\frac{1}{2}}) -(f(|\hat{u}^{n-1}|^2)\tilde{u}^{n-1}-f(|u^{n-1-\frac{1}{2}}|^2)u^{n-1-\frac{1}{2}})}{\tau }\right\| _0\nonumber \\&=\left\| \frac{f(|u^{n-1-\frac{1}{2}}|^2)((\tilde{u}^n-\tilde{u}^{n-1})-(u^{n-\frac{1}{2}}-u^{n-1-\frac{1}{2}}))}{\tau } +\frac{(\tilde{u}^n-\tilde{u}^{n-1})(f(|\hat{u}^{n-1}|^2)-f(|u^{n-1-\frac{1}{2}}|^2))}{\tau }\right. \nonumber \\&\quad \quad +\,\frac{u^{n-\frac{1}{2}}((f(|\hat{u}^{n}|^2)-f(|\hat{u}^{n-1}|^2)) -(f(|u^{n-\frac{1}{2}}|^2)-f(|u^{n-1-\frac{1}{2}}|^2)))}{\tau }\nonumber \\&\qquad \left. +\,\frac{(f(|\hat{u}^{n}|^2)-f(|\hat{u}^{n-1}|^2)) (\tilde{u}^n-u^{n-\frac{1}{2}})}{\tau }\right\| _0\nonumber \\&\le C\tau ^2. \end{aligned}$$

(3.37)

Therefore,

$$\begin{aligned} (R_1^n+R_2^n+R_3^n,\bar{\partial }_t\Delta e^n) \le C\tau ^4+C\Vert \Delta e^{n-1}\Vert _0^2+\bar{\partial }_t(R_1^n+R_2^n+R_3^n,\Delta e^{n}). \end{aligned}$$

(3.38)

Allocating all the estimates above to get

$$\begin{aligned} \frac{1}{2\tau }(\Vert \Delta e^n\Vert _0^2-\Vert \Delta e^{n-1}\Vert _0^2)&\le C\tau ^4+C\Vert \tilde{\partial }_te^n\Vert _0^2 +C\Vert \tilde{\partial }_te^{n-1}\Vert _0^2+C\Vert \tilde{\partial }_t\hat{e}^{n}\Vert _0^2\nonumber \\&\quad +\,C\Vert \Delta \hat{e}^{n}\Vert _0^2 +C\Vert \Delta \hat{e}^{n-1}\Vert _0^2+C\Vert \Delta e^{n}\Vert _0^2+C\Vert \Delta e^{n-1}\Vert _0^2\nonumber \\&\quad +\,\tilde{\partial }_t(P_1^n,\Delta e^n)+\tilde{\partial }_t(R_1^n+R_2^n+R_3^n,\Delta e^{n}). \end{aligned}$$

(3.39)

Replacing n by i in (3.39), then summing it from 2 to n, it follows that

$$\begin{aligned} \Vert \Delta e^n\Vert _0^2&\le \Vert \Delta e^{1}\Vert _0^2+C\tau ^4+C\tau \sum _{i=1}^{n}(\Vert \tilde{\partial }_te^i\Vert _0^2+\Vert \Delta e^{i}\Vert _0^2)+C\Vert \tilde{\partial }_t\hat{e}^{2}\Vert _0^2+C\Vert \Delta \hat{e}^{1}\Vert _0^2\nonumber \\&\quad +\,(P_1^n,\Delta e^n)-(P_1^1,\Delta e^1) +(R_1^n+R_2^n+R_3^n,\Delta e^{n})-(R_1^1+R_2^1+R_3^1,\Delta e^{1}). \end{aligned}$$

(3.40)

Since

$$\begin{aligned} \Vert P_1^n\Vert _0^2&=\Vert f(|\hat{U}^{n-1}|^2)\tilde{e}^n+\tilde{u}^n (f(|\hat{u}^{n-1}|^2)-f(|\hat{U}^{n-1}|^2))\Vert _0^2\nonumber \\&\le C\Vert \tilde{e}^{n}\Vert _0^2+C\Vert \hat{e}^{n-1}\Vert _0^2=C\tau ^2 \left\| \sum _{i=1}^{n}\bar{\partial }_te^{i}\right\| _0^2 \le C\tau \sum _{i=1}^{n}\Vert \bar{\partial }_te^{i}\Vert _0^2, \end{aligned}$$

(3.41)

together with (3.18) and (3.21), we have

$$\begin{aligned} \Vert \Delta e^n\Vert _0^2&\le C\tau ^4+C\tau \sum _{i=1}^{n}(\Vert \tilde{\partial }_te^i\Vert _0^2+\Vert \Delta e^{i}\Vert _0^2). \end{aligned}$$

(3.42)

In order to estimate $\Vert \bar{\partial }_te^n\Vert _0$, we take difference between two time levels n and $n-1$ of (3.24), and multiply it by $\frac{1}{\tau }$ on both sides, then there holds

$$\begin{aligned} i\tilde{\partial }_{tt}e^n+\tilde{\partial }_{t}\Delta \bar{e}^n+\tilde{\partial }_{t}P_1^n=\tilde{\partial }_{t}R_1^n+\tilde{\partial }_{t}R_2^n+\tilde{\partial }_{t}R_3^n. \end{aligned}$$

(3.43)

On the other hand, multiplying (3.43) by $\tilde{\partial }_t\tilde{e}^n$, integrating it over $\Omega$ and then it follows that

$$\begin{aligned} i(\tilde{\partial }_{tt}e^n,\tilde{\partial }_t\tilde{e}^n)-\Vert \tilde{\partial }_{t}\nabla \tilde{e}^n\Vert _0^2+(\tilde{\partial }_{t}P_1^n,\tilde{\partial }_t\tilde{e}^n)=(\tilde{\partial }_{t}R_1^n,\tilde{\partial }_t\tilde{e}^n) +(\tilde{\partial }_{t}R_2^n,\tilde{\partial }_t\tilde{e}^n)+(\tilde{\partial }_{t}R_3^n,\tilde{\partial }_t\tilde{e}^n). \end{aligned}$$

(3.44)

Then taking the impartial part of (3.44) and using (3.32), (3.35)–(3.37), it follows that

$$\begin{aligned} \frac{1}{2\tau }(\Vert \tilde{\partial }_{t}e^n\Vert _0^2-\Vert \tilde{\partial }_{t}e^{n-1}\Vert _0^2)&= -Im(\tilde{\partial }_{t}P_1^n,\tilde{\partial }_t\tilde{e}^n)+Im(\tilde{\partial }_{t}R_1^n,\tilde{\partial }_t\tilde{e}^n)\nonumber \\&\quad +\,Im(\tilde{\partial }_{t}R_2^n,\tilde{\partial }_t\tilde{e}^n)+Im(\tilde{\partial }_{t}R_3^n,\tilde{\partial }_t\tilde{e}^n)\nonumber \\&\le C\tau ^4+C\Vert \tilde{\partial }_te^n\Vert _0^2+C\Vert \tilde{\partial }_t e^{n-1}\Vert _0^2+C\Vert \Delta e^{n}\Vert _0^2\nonumber \\&\quad +\,C\Vert \Delta e^{n-1}\Vert _0^2+C\Vert \Delta e^{n-2}\Vert _0^2. \end{aligned}$$

(3.45)

Replacing n by i in (3.45), then summing it from 2 to n, with the result of $e^1$, we get

$$\begin{aligned} \Vert \tilde{\partial }_{t}e^n\Vert _0^2&\le C\tau ^4+C\tau \sum _{i=1}^{n}(\Vert \tilde{\partial }_te^i\Vert _0^2+\Vert \Delta e^{i}\Vert _0^2). \end{aligned}$$

(3.46)

Combining (3.42) and (3.46), we have

$$\begin{aligned} \Vert \tilde{\partial }_te^n\Vert _0^2+\Vert \Delta e^n\Vert _0^2&\le C\tau ^4+C\tau \sum _{i=1}^{n}(\Vert \tilde{\partial }_te^i\Vert _0^2+\Vert \Delta e^{i}\Vert _0^2). \end{aligned}$$

(3.47)

Applying the Gronwall’s inequality to (3.47), there exist $\tau _8, C_7, C_8$, such that when $\tau \le \tau _8$, there holds

$$\begin{aligned} \Vert \tilde{\partial }_te^n\Vert _0+\Vert e^n\Vert _2&\le C_7\tau ^2, \end{aligned}$$

(3.48)

which implies

$$\begin{aligned} \Vert \tilde{\partial }_{tt}U^n\Vert _2&\le C_8, \end{aligned}$$

(3.49)

and

$$\begin{aligned} \Vert U^n\Vert _{0,\infty }+\Vert \tilde{\partial }_tU^n\Vert _{0,\infty }&\le \Vert e^n\Vert _{0,\infty }+\Vert \tilde{\partial }_te^n\Vert _{0,\infty }+C\Vert u^n\Vert _{0,\infty }+\Vert \tilde{\partial }_tu^n\Vert _{0,\infty }\nonumber \\&\le CC_7\tau +C\Vert u^n\Vert _{0,\infty }+\Vert \tilde{\partial }_tu^n\Vert _{0,\infty }\le K_0, \end{aligned}$$

(3.50)

where $\tau \le \tau _9\le 1/CC_7$. It can be seen that $C_7$ and $C_8$ have nothing to do with $C_0$. Then (3.2) and (3.3) hold for $m=n$ if we take $C_0\ge \sum \limits _{i=1}^{8}C_i$ and $\tau _0\le \min \limits _{1\le i\le 9}\tau _i$. $\square$

Remark 1

It can be seen that the result of $\Vert e^n\Vert _2=O(\tau ^2)$ is one order higher that in  [23], which leads to $\Vert \tilde{\partial }_{tt}U^m\Vert _2\le C_0$. This will play an important role in the foregoing superconvergence analysis.

Remark 2

If we use a fully explicit method for the nonlinear term in (3.1)–(3.3), the unconditional convergence analysis is still valid by an $H^2$ error estimate for the time semi-discrete. The idea is very similar and the process of proof is much easier.

4 Superconvergence Results for the Fully Discrete System

In this section, we will establish an estimate for $\Vert R_hU^n-U_h^n\Vert _0=O(h^2)$, which results in the unconditional boundedness of $\Vert U_h^n\Vert _{0,\infty }$. Then $\Vert \nabla (R_hU^n-U_h^n)\Vert _0$ with order $O(h^2+\tau ^2)$ is deduced which will result in the superclose results $\Vert \nabla (I_hu^n-U_h^n)\Vert _0$ with order $O(h^2+\tau ^2)$ unconditionally on the basis of the relationship between $I_h$ and $R_h$. At last, the global superconvergence is deduced through the interpolated postprocessing technique. A pervading strategy throughout the error analysis in the rest of this paper is splitting the error to a sum of two terms:

$$\begin{aligned} U^i-U^i_h=U^i-R_hU^i+R_hU^i-U^i_h\triangleq r^i+\theta ^i, i=0,1,2,\ldots , N. \end{aligned}$$

(4.1)

Theorem 2

Let u and $U_h^m$ be the solutions of (1.1) and (2.5)–(2.7) respectively, for $m=1,2,\ldots , N$, under the conditions in Theorem  1, we have

$$\begin{aligned} \Vert \nabla (I_h u^m- U_h^m)\Vert _0=O(h^2+\tau ^2). \end{aligned}$$

(4.2)

Proof

Since $\Vert R_hU^{1,0}\Vert _{0}+\Vert R_hU^{1,0}\Vert _{0,\infty }+\Vert R_hU^m\Vert _{0,\infty }\le C\Vert U^{0}\Vert _{2}+C\Vert U^{1,0}\Vert _{2}+C\Vert U^m\Vert _{2}\le C$, let $K_0^{'}\triangleq 1+\Vert R_hU^{1,0}\Vert _{0,\infty }+\max \limits _{0\le i\le N}\Vert R_hU^i\Vert _{0,\infty }$. First of all, we obtain the result that there exist $\tau _0^{'}$ and $h_0^{'}$, when $\tau \le \tau _0^{'}$ and $h\le h_0^{'}$, it follows

$$\begin{aligned} \Vert \theta ^m\Vert _0\le C_0^{'}h^2, \end{aligned}$$

(4.3)

which bounds $\Vert U_h^m\Vert _{0,\infty }$ unconditionally. For $m=1$, we have $\Vert U_h^0\Vert _{0,\infty }=\Vert R_hU^0\Vert _{0,\infty }\le K_0^{'}$. Using (2.6) and (3.2), the error equation is deduced by

$$\begin{aligned} i\left( \frac{\theta ^{1,0}}{\tau },v_h\right) - \left( \frac{\nabla \theta ^{1,0}}{2},\nabla v_h\right) =&-i(\frac{r^{1,0}-r^0}{\tau },v_h)+ \left( \frac{\nabla r^{1,0}+\nabla r^0}{2},\nabla v_h\right) \nonumber \\&\quad +\left( f(|U^0|^2)\frac{ U^{1,0}+ U^0}{2}-f(|U^0_h|^2)\frac{ U^{1,0}_h+ U^0_h}{2},v_h\right) . \end{aligned}$$

(4.4)

Substituting $v_h=\frac{\theta ^{1,0}}{\tau }$ in (4.4), we get

$$\begin{aligned} i\left\| \frac{\theta ^{1,0}}{\tau }\right\| _0^2-\frac{1}{2\tau }\left\| \nabla \theta ^{1,0}\right\| _0^2=&-i\left( \frac{r^{1,0}-r^0}{\tau },\frac{\theta ^{1,0}}{\tau }\right) +\left( \frac{\nabla r^{1,0}+\nabla r^0}{2}, \frac{\nabla \theta ^{1,0}}{\tau }\right) \nonumber \\&\quad +\,\left( f(|U^0|^2)\frac{ U^{1,0}+ U^0}{2}-f(|U^0_h|^2)\frac{ U^{1,0}_h+ U^0_h}{2},\frac{\theta ^{1,0}}{\tau }\right) . \end{aligned}$$

(4.5)

By (2.1) and (2.3), it follows that

$$\begin{aligned}&\left| \left( \frac{r^{1,0}-r^0}{\tau },\frac{\theta ^{1,0}}{\tau }\right) \right| \le Ch^2\left\| \frac{U^{1,0}-U^0}{\tau }\right\| _2\left\| \frac{\theta ^{1,0}}{\tau }\right\| _0 \le Ch^4+\frac{1}{8}\left\| \frac{\theta ^{1,0}}{\tau }\right\| _0^2\\&\left( \frac{\nabla r^{1,0}+\nabla r^0}{2}, \frac{\nabla \theta ^{1,0}}{\tau }\right) =0\\&\left| \left( f(|U^0|^2)\frac{ U^{1,0}+ U^0}{2}-f(|U^0_h|^2) \frac{ U^{1,0}_h+ U^0_h}{2},\frac{\theta ^{1,0}}{\tau }\right) \right| \\&\quad =\left| \left( f(|U^0_h|^2)\left( \frac{ \theta ^{1,0}}{2}+\frac{ r^{1,0}+ r^0}{2}\right) ,\frac{\theta ^{1,0}}{\tau }\right) +\left( \frac{ U^{1,0}+ U^0}{2}(f(|U^0|^2)-f(|U^0_h|^2)),\frac{\theta ^{1,0}}{\tau }\right) \right| \\&\quad \le Ch^4+C\Vert \theta ^{1,0}\Vert _0^2+\frac{1}{8}\left\| \frac{\theta ^{1,0}}{\tau }\right\| _0^2. \end{aligned}$$

Taking the imaginary part and the real part, respectively, summing them together, then we get

$$\begin{aligned} \left\| \frac{\theta ^{1,0}}{\tau }\right\| _0^2+\frac{1}{2\tau }\Vert \nabla \theta ^{1,0}\Vert _0^2\le Ch^4+C\Vert \theta ^{1,0}\Vert _0^2+\frac{1}{2}\left\| \frac{\theta ^{1,0}}{\tau }\right\| _0^2. \end{aligned}$$

(4.6)

Thus there exist $\tau _1^{'}, C_1^{'}$, such that when $\tau \le \tau _1^{'}$, we have

$$\begin{aligned} \frac{1}{\tau }\Vert \theta ^{1,0}\Vert _0+\Vert \nabla \theta ^{1,0}\Vert _0\le C_1^{'}h^2, \end{aligned}$$

(4.7)

which implies

$$\begin{aligned} \Vert U_h^{1,0}\Vert _{0,\infty }\le Ch^{-1}\Vert \theta ^{1,0}\Vert _{0}+\Vert R_hU^{1,0}\Vert _{0,\infty } \le CC_1^{'}h+\Vert R_hU^{1,0}\Vert _{0,\infty }\le K_0^{'}, \end{aligned}$$

(4.8)

where $h\le h_1^{'}\le 1/CC_1^{'}$. Making use of (2.7) and (3.3) to deduce the error equation and setting $v_h=\frac{\theta ^{1}}{\tau }$, then we have

$$\begin{aligned} i\left\| \frac{\theta ^{1}}{\tau }\right\| _0^2-\frac{1}{2\tau }\Vert \nabla \theta ^{1}\Vert _0^2=&-i\left( \frac{r^{1}-r^0}{\tau },\frac{\theta ^{1}}{\tau }\right) +\left( \frac{\nabla r^{1}+\nabla r^0}{2}, \frac{\nabla \theta ^{1}}{\tau }\right) \nonumber \\&\quad +\,\left( f\left( \left| \frac{ U^{1,0}+ U^0}{2}\right| ^2\right) \frac{ U^{1}+ U^0}{2}-f\left( \left| \frac{ U^{1,0}_h+ U^0_h}{2}\right| ^2\right) \frac{ U^{1}_h+ U^0_h}{2}, \frac{\theta ^{1}}{\tau }\right) . \end{aligned}$$

(4.9)

Similar to the proof of $\theta ^{1,0}$, we get

$$\begin{aligned}&\left| \left( \frac{r^{1}-r^0}{\tau },\frac{\theta ^{1}}{\tau }\right) \right| \le Ch^2\left\| \frac{U^{1}-U^0}{\tau }\right\| _2\left\| \frac{\theta ^{1}}{\tau }\right\| _0 \le Ch^4+\frac{1}{8}\left\| \frac{\theta ^{1}}{\tau }\right\| _0^2,\\&\left( \frac{\nabla r^{1}+\nabla r^0}{2}, \frac{\nabla \theta ^{1}}{\tau }\right) =0,\\&\left| \left( f\left( \left| \frac{ U^{1,0}+ U^0}{2}\right| ^2\right) \frac{ U^{1} + U^0}{2}-f\left( \left| \frac{ U^{1,0}_h+ U^0_h}{2}\right| ^2\right) \frac{ U^{1}_h + U^0_h}{2}, \frac{\theta ^{1}}{\tau }\right) \right| \\&\quad =\left| \left( f\left( \left| \frac{ U^{1,0}_h+ U^0_h}{2}\right| ^2\right) \left( \frac{ \theta ^{1}}{2}+\frac{ r^{1}+ r^0}{2}\right) ,\frac{\theta ^{1}}{\tau }\right) \right. \\&\qquad \left. +\,\frac{ U^{1}+ U^0}{2}\left( f\left( \left| \frac{ U^{1,0}+ U^0}{2}\right| ^2\right) -f\left( \left| \frac{ U^{1,0}_h+ U^0_h}{2}\right| ^2\right) ,\frac{\theta ^{1}}{\tau }\right) \right| \\&\quad \le Ch^4+C\Vert \theta ^{1}\Vert _0^2+C\Vert \theta ^{1,0}\Vert _0^2+\frac{1}{8}\left\| \frac{\theta ^{1}}{\tau }\right\| _0^2 \le Ch^4+C\Vert \theta ^{1}\Vert _0^2+\frac{1}{8}\left\| \frac{\theta ^{1}}{\tau }\right\| _0^2, \end{aligned}$$

where the last step is deduced by the help of (4.7). Also, taking the imaginary part and the real part, respectively, summing them together, then we get

$$\begin{aligned} \left\| \frac{\theta ^{1}}{\tau }\right\| _0^2+\frac{1}{2\tau }\Vert \nabla \theta ^{1}\Vert _0^2\le Ch^4+C\Vert \theta ^{1}\Vert _0^2+\frac{1}{2}\left\| \frac{\theta ^{1}}{\tau }\right\| _0^2. \end{aligned}$$

(4.10)

Thus there exist $\tau _2^{'}, C_2^{'}$, such that when $\tau \le \tau _2^{'}$, we have

$$\begin{aligned} \left\| \frac{\theta ^{1}}{\tau }\right\| _0+\Vert \nabla \theta ^{1}\Vert _0\le C_2^{'}h^2, \end{aligned}$$

(4.11)

which implies

$$\begin{aligned} \Vert U_h^{1}\Vert _{0,\infty }\le Ch^{-1}\Vert \theta ^{1}\Vert _{0}+\Vert R_hU^{1}\Vert _{0,\infty } \le CC_2^{'}h+\Vert R_hU^{1}\Vert _{0,\infty }\le K_0^{'}, \end{aligned}$$

(4.12)

where $h\le h_2^{'}\le 1/CC_2^{'}$. By mathematical induction, we assume that (4.3) holds for $m\le n-1$, then we have

$$\begin{aligned} \Vert U_h^m\Vert _{0,\infty }\le Ch^{-1}\Vert \theta ^m\Vert _{0}+\Vert R_hU^m\Vert _{0,\infty } \le CC_0^{'}h+\Vert R_hU^m\Vert _{0,\infty }\le K_0^{'}, \end{aligned}$$

(4.13)

where $h\le h_3^{'}\le 1/CC_0^{'}$.

Then when $m=n$, setting $P_2^n=f(|\hat{U}^{n}|^2)\tilde{U}^n-f(|\hat{U}_h^{n}|^2)\tilde{U}_h^n$, we get the error equation from (2.5) and (3.1) as follows:

$$\begin{aligned} i(\tilde{\partial }_t\theta ^n,v_h)-(\nabla \tilde{\theta }^n, \nabla v_h)=-i(\tilde{\partial }_tr^n,v_h) +(\nabla \tilde{r}^n, \nabla v_h)-(P_2^n,v_h). \end{aligned}$$

(4.14)

Choosing $v_h=\tilde{\theta }^n$ in (4.14), the impartial part results in

$$\begin{aligned} \frac{1}{2\tau }(\Vert \theta ^n\Vert _0^2-\Vert \theta ^{n-1}\Vert _0^2)= -Re(\bar{\partial }_tr^n,\tilde{\theta }^n) +Im(\nabla r^n, \nabla \tilde{\theta }^n)-Im(P_2^n,\tilde{\theta }^n). \end{aligned}$$

(4.15)

We bound $P_2^n$ as

$$\begin{aligned} \Vert P_2^n\Vert _0&=\Vert f(|\hat{U}_h^{n}|^2)(\tilde{\theta }^n+\tilde{r}^n)+\tilde{U}^n f^{'}(\mu _6^n)(|\hat{U}^{n}|^2-|\hat{U}_h^{n}|^2)\Vert _0\\&\le C\Vert \tilde{\theta }^n\Vert _0+C\Vert \tilde{r}^n\Vert _0+C\Vert \hat{\theta }^n\Vert _0+C\Vert \hat{r}^n\Vert _0\le C\Vert \tilde{\theta }^n\Vert _0+C\Vert \hat{\theta }^n\Vert _0+Ch^2, \end{aligned}$$

where $\mu _6^n=|\hat{U}^{n-1}|^2+\lambda _6^n(|\hat{U}_h^{n-1}|^2-|\hat{U}^{n-1}|^2)$.

Thus,

$$\begin{aligned} \frac{1}{2\tau }(\Vert \theta ^n\Vert _0^2-\Vert \theta ^{n-1}\Vert _0^2)\le C\Vert \theta ^{n}\Vert _0^2+C\Vert \theta ^{n-1}\Vert _0^2+C\Vert \theta ^{n-2}\Vert _0^2+Ch^4. \end{aligned}$$

(4.16)

Summing (4.16) up gives

$$\begin{aligned} \Vert \theta ^n\Vert _0^2\le \Vert \theta ^1\Vert _0^2+ C\tau \sum _{i=1}^{n}\Vert \theta ^i\Vert _0^2+Ch^4. \end{aligned}$$

(4.17)

Applying the Gronwall’s inequality to (4.17), together with (4.11), there exist $\tau _3^{'}, C_3^{'}$, when $\tau \le \tau _3^{'}$, we have

$$\begin{aligned} \Vert \theta ^n\Vert _0\le C_3^{'}h^2, \end{aligned}$$

(4.18)

which leads to

$$\begin{aligned} \Vert U_h^n\Vert _{0,\infty }\le Ch^{-1}\Vert \theta ^n\Vert _{0}+\Vert R_hU^n\Vert _{0,\infty } \le CC_3^{'}h+\Vert R_hU^n\Vert _{0,\infty }\le K_0^{'}, \end{aligned}$$

(4.19)

where $h\le h_4^{'}\le 1/CC_3^{'}$. Clearly, $C_3^{'}$ has nothing to do with $C_0^{'}$. Thus (4.3) holds for $m=n$, if we take $C_0^{'}\ge \sum \limits _{i=1}^{3}C_i^{'}$, $\tau _0^{'}\le \min \limits _{1\le \tau \le 3}\tau _i^{'}$ and $h_0^{'}\le \min \limits _{1\le \tau \le 4}h_i^{'}$.

Secondly, we will give the result

$$\begin{aligned} \Vert \nabla \theta ^m\Vert _0\le C(h^2+\tau ^2) \end{aligned}$$

(4.20)

unconditionally. Because of (4.11), it is apparent to see that (4.20) holds for $m=1$. When $m=n, (n\ge 2)$, choosing $v_h=\tilde{\partial }_t\theta ^n$ in (4.14) and taking the real part result in

$$\begin{aligned} \frac{1}{2\tau }(\Vert \nabla \theta ^n\Vert _0^2-\Vert \nabla \theta ^{n-1}\Vert _0^2)= Im(\tilde{\partial }_tr^n,\tilde{\partial }_t\theta ^n) +Re(\nabla r^n, \nabla \tilde{\partial }_t\theta ^n)-Re(P_2^n,\tilde{\partial }_t\theta ^n). \end{aligned}$$

(4.21)

Then (4.21) leads to

$$\begin{aligned} \frac{1}{2\tau }(\Vert \nabla \theta ^n\Vert _0^2-\Vert \nabla \theta ^{n-1}\Vert _0^2)&\le Ch^4+C\Vert \tilde{\partial }_t\theta ^n\Vert _0^2. \end{aligned}$$

(4.22)

Summing (4.22) from 2 to n, we obtain

$$\begin{aligned} \Vert \nabla \theta ^n\Vert _0^2&\le Ch^4+C\tau \sum _{i=1}^{n}\Vert \tilde{\partial }_t\theta ^i\Vert _0^2. \end{aligned}$$

(4.23)

Obviously, to obtain the estimate of $\Vert \nabla \theta ^n\Vert _0$, we need the boundedness of $\Vert \tilde{\partial }_t\theta ^i\Vert _0$. Taking difference between two time levels n and $n-1$ of (4.14), with $\hat{U}_h^1=\tilde{U}_h^1,\hat{r}^1=\tilde{r}^1,\hat{\theta }^1=\tilde{\theta }^1$ we have

$$\begin{aligned} i(\tilde{\partial }_{tt}\theta ^n,v_h)-(\nabla \tilde{\partial }_t\tilde{\theta }^n, \nabla v_h)=-i(\tilde{\partial }_{tt}r^n,v_h) +(\nabla \tilde{\partial }_t\tilde{r}^n, \nabla v_h)-(\tilde{\partial }_tP_2^n,v_h). \end{aligned}$$

(4.24)

Setting $v_h=\tilde{\partial }_t\tilde{\theta }^n$ in (4.24), the imaginary part gives

$$\begin{aligned} \frac{1}{2\tau }(\Vert \tilde{\partial }_t\theta ^n\Vert _0^2-\Vert \tilde{\partial }_t\theta ^{n-1}\Vert _0^2)&= -Re(\tilde{\partial }_{tt}r^n,\tilde{\partial }_t\tilde{\theta }^n) +Im(\nabla \tilde{\partial }_t\tilde{r}^n, \nabla \tilde{\partial }_t\tilde{\theta }^n)-Im(\tilde{\partial }_tP_2^n,\tilde{\partial }_t\tilde{\theta }^n). \end{aligned}$$

(4.25)

Similar to the estimate of $\theta ^n$, it is not difficult to check that

$$\begin{aligned} |(\tilde{\partial }_{tt}r^n,\tilde{\partial }_t\tilde{\theta }^n)|&\le Ch^2\Vert \tilde{\partial }_{tt}U^n\Vert _2\Vert \tilde{\partial }_t\tilde{\theta }^n\Vert _0\le Ch^4+C\Vert \tilde{\partial }_t\tilde{\theta }^n\Vert _0^2, \end{aligned}$$

(4.26)

$$\begin{aligned} (\nabla \tilde{\partial }_t\tilde{r}^n, \nabla \tilde{\partial }_t\tilde{\theta }^n)&=0. \end{aligned}$$

(4.27)

Based on the achievements above, it follows that

$$\begin{aligned} \Vert \tilde{\partial }_tP_2^n\Vert _0&=\left\| \frac{(f(|\hat{U}^{n}|^2)\tilde{U}^n-f(|\hat{U}^{n-1}|^2)\tilde{U}^{n-1}) -(f(|\hat{U}_h^{n}|^2)\tilde{U}_h^n)-f(|\hat{U}_h^{n-1}|^2)\tilde{U}_h^{n-1})}{\tau }\right\| _0\\&=\left\| f(|\hat{U}^{n-1}|^2)\tilde{\partial }_t\tilde{U}^n -f(|\hat{U}_h^{n-1}|^2)\tilde{\partial }_t\tilde{U}_h^n\right. \\&\quad \left. +\,\frac{ \tilde{U}^n (f(|\hat{U}^{n}|^2)-f(|\hat{U}^{n-1}|^2)) -\tilde{U}_h^n(f(|\hat{U}_h^{n}|^2)-f(|\hat{U}_h^{n-1}|^2))}{\tau }\right\| _0\\&\le \Vert f(|\hat{U}_h^{n-1}|^2)(\tilde{\partial }_t\tilde{\theta }^n+\tilde{\partial }_t\tilde{r}^n) +\tilde{\partial }_t\tilde{U}^n (f(|\hat{U}^{n-1}|^2)-f(|\hat{U}_h^{n-1}|^2))\Vert _0\\&\quad +C\left\| \frac{(f(|\hat{U}^{n}|^2)-f(|\hat{U}^{n-1}|^2)) -(f(|\hat{U}_h^{n}|^2)-f(|\hat{U}_h^{n-1}|^2)) }{\tau }\right\| _0\\&\quad +C\left\| \frac{ (f(|\hat{U}^{n}|^2)-f(|\hat{U}^{n-1}|^2))(\tilde{U}^n -\tilde{U}_h^n)}{\tau }\right\| _0. \end{aligned}$$

Note that

$$\begin{aligned}&\left\| \frac{(f(|\hat{U}^{n}|^2)-f(|\hat{U}^{n-1}|^2)) -(f(|\hat{U}_h^{n}|^2)-f(|\hat{U}_h^{n-1}|^2))}{\tau }\right\| _0\\&=\left\| f^{'}(|\hat{U}_h^{n-1}|^2)\frac{(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2) -(|\hat{U}_h^{n}|^2-|\hat{U}_h^{n-1}|^2)}{\tau }\right. \\&\quad \left. +\,\frac{(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)}{\tau }(f^{'}(|\hat{U}^{n-1}|^2)-f^{'}(|\hat{U}_h^{n-1}|^2))\right. \\&\quad \left. +\,\frac{1}{2}f^{''}(\mu _{9}^n)\frac{(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)^2-(|\hat{U}_h^{n}|^2-|\hat{U}_h^{n-1}|^2)^2)}{\tau }\right. \\&\quad \left. +\,\frac{(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)^2 }{2\tau }(f^{''}(\mu _{8}^n)-f^{''}(\mu _{9}^n))\right\| _0, \end{aligned}$$

where

$$\begin{aligned} \mu _8^n=|\hat{U}^{n-1}|^2+\lambda _8^n(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2), \mu _9^n=|\hat{U}_h^{n-1}|^2+\lambda _9^n(|\hat{U}_h^{n}|^2-|\hat{U}_h^{n-1}|^2). \end{aligned}$$

In fact,

$$\begin{aligned}&\left\| \frac{(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)-(|\hat{U}_h^{n}|^2-|\hat{U}_h^{n-1}|^2)}{\tau }\right\| _0\\&\quad =\left\| \frac{(\hat{U}^{n}\bar{\hat{U}}^{n}-\hat{U}^{n-1}\bar{\hat{U}}^{n-1}) -(\hat{U}_h^{n}\bar{\hat{U}}_h^{n}-\hat{U}_h^{n-1}\bar{\hat{U}}_h^{n-1})}{\tau }\right\| _0\\&\quad = \Vert \hat{U}^{n-1}\tilde{\partial }_t\bar{\hat{U}}^{n}- \hat{U}_h^{n-1}\tilde{\partial }_t\bar{\hat{U}}_h^{n}+\bar{\hat{U}}^{n}\tilde{\partial }_t\hat{U}^{n} -\bar{\hat{U}}_h^{n}\tilde{\partial }_t\hat{U}_h^{n}\Vert _0\\&\quad = \Vert \hat{U}_h^{n-1}(\tilde{\partial }_t\bar{\hat{U}}^{n}-\tilde{\partial }_t\bar{\hat{U}}_h^{n}) +\tilde{\partial }_t\bar{\hat{U}}^{n}(\hat{U}^{n-1}-\hat{U}_h^{n-1}) +\bar{\hat{U}}_h^{n}(\tilde{\partial }_t\hat{U}^{n}-\tilde{\partial }_t\hat{U}_h^{n}) +\tilde{\partial }_t\hat{U}^{n}(\bar{\hat{U}}^{n}-\bar{\hat{U}}_h^{n})\Vert _0\\&\quad \le C\Vert \tilde{\partial }_t\hat{\theta }^{n}\Vert _0^2+\Vert \tilde{\partial }_t\hat{r}^{n}\Vert _0^2 +C\Vert \hat{\theta }^{n}\Vert _0^2+\Vert \hat{r}^{n}\Vert _0^2+C\Vert \hat{\theta }^{n-1}\Vert _0^2+\Vert \hat{r}^{n-1}\Vert _0^2\\&\quad \le Ch^4+ C\Vert \tilde{\partial }_t\hat{\theta }^{n}\Vert _0^2 +C\Vert \hat{\theta }^{n}\Vert _0^2+C\Vert \hat{\theta }^{n-1}\Vert _0^2, \end{aligned}$$

and

$$\begin{aligned}&\left\| \frac{(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)^2- (|\hat{U}_h^{n}|^2-|\hat{U}_h^{n-1}|^2)^2)}{\tau }\right\| _0\\&\quad =\left\| (|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2) +(|\hat{U}_h^{n}|^2-|\hat{U}_h^{n-1}|^2))\frac{(|\hat{U}^{n}|^2 -|\hat{U}^{n-1}|^2)-(|\hat{U}_h^{n}|^2-|\hat{U}_h^{n-1}|^2))}{\tau }\right\| _0\\&\quad \le Ch^4+ C\Vert \tilde{\partial }_t\hat{\theta }^{n}\Vert _0^2 +C\Vert \hat{\theta }^{n}\Vert _0^2+C\Vert \hat{\theta }^{n-1}\Vert _0^2. \end{aligned}$$

Moreover,

$$\begin{aligned} \Vert f^{''}(\mu _{8}^n)-f^{''}(\mu _{9}^n)\Vert _0&= \Vert |\hat{U}^{n-1}|^2-|\hat{U}_h^{n-1}|^2 +\lambda _9^n((|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)\\&\quad -\,(|\hat{U}_h^{n}|^2-|\hat{U}_h^{n-1}|^2)) +(|\hat{U}^{n}|^2-|\hat{U}^{n-1}|^2)(\lambda _8^n-\lambda _9^n)\Vert _0\\&\le C\Vert \hat{\theta }^{n}\Vert _0 +C\Vert \hat{\theta }^{n-1}\Vert _0+Ch^2+C\tau . \end{aligned}$$

Therefore

$$\begin{aligned}&|(\tilde{\partial }_tP_2^n,\tilde{\partial }_t\theta ^n)| \le Ch^4+C\tau ^4+\Vert \tilde{\partial }_t\tilde{\theta }^n\Vert _0+ C\Vert \tilde{\partial }_t\hat{\theta }^{n}\Vert _0^2 +C\Vert \hat{\theta }^{n}\Vert _0^2+C\Vert \hat{\theta }^{n-1}\Vert _0^2. \end{aligned}$$

(4.28)

Recalling (4.26)–(4.28), it follows that

$$\begin{aligned} \frac{1}{2\tau }(\Vert \tilde{\partial }_t\theta ^n\Vert _0^2-\Vert \tilde{\partial }_t\theta ^{n-1}\Vert _0^2)&\le Ch^4+C\tau ^4+\Vert \tilde{\partial }_t\tilde{\theta }^n\Vert _0+ C\Vert \tilde{\partial }_t\hat{\theta }^{n}\Vert _0^2 +C\Vert \hat{\theta }^{n}\Vert _0^2+C\Vert \hat{\theta }^{n-1}\Vert _0^2. \end{aligned}$$

(4.29)

Summing (4.29), together with (4.23), it gives that

$$\begin{aligned} \Vert \tilde{\partial }_t\theta ^n\Vert _0^2&\le Ch^4+C\tau ^4+C\tau \sum _{i=1}^{n}\Vert \tilde{\partial }_t\theta ^{i}\Vert _0^2. \end{aligned}$$

(4.30)

Applying the Gronwall’s inequality to (4.30), we have

$$\begin{aligned} \Vert \tilde{\partial }_t\theta ^n\Vert _0^2&\le Ch^4+C\tau ^4, \end{aligned}$$

(4.31)

which results in

$$\begin{aligned} \Vert \nabla \theta ^{n}\Vert _0&\le Ch^2+C\tau ^2. \end{aligned}$$

(4.32)

At last, by the help of (2.2)–(2.4), it reduces to

$$\begin{aligned} \Vert \nabla (I_hu^n-U_h^n)\Vert _0&\le C\Vert \nabla (I_hu^n-R_hu^n)\Vert _0+C\Vert \nabla (R_hu^n-R_hU^n)\Vert _0\\&\quad +\,C\Vert \nabla (R_hU^n-U_h^n)\Vert _0\\&\le Ch^2\Vert u^n\Vert _3+C\Vert e^n\Vert _2+C\Vert \nabla \theta ^n\Vert _0\\&\le Ch^2+C\tau ^2. \end{aligned}$$

$\square$

Remark 3

It is worthy to note that Theorem 2 can not be obtained by $I_h$ alone. In order to keep the order of $\Vert I_hU^n-U_h^n\Vert _{0}$ and $\Vert \nabla (I_hU^n-U_h^n)\Vert _{0}$, we should employ $(\nabla (u^n-I_hu^n),\nabla v_h)=O(h^2)\Vert u^n\Vert _3\Vert v_h\Vert _1$ or $(\nabla (u^n-I_hu^n),\nabla v_h)=O(h^2)\Vert u^n\Vert _4\Vert v_h\Vert _0$ as that in  [3]. Thus the regularity of $U^n$ and $u^n$ should be much stricter. However, we can only bound $\Vert U^n\Vert _2$ under the assumption that $\Omega$ is a rectangle. On the other hand, we take different approach to bound $\Vert \tilde{\partial }_tP_2^n\Vert _0$, comparing with that in  [3], then we avoid the appearance of the boundedness about $\Vert \tilde{\partial }_tU_h^n\Vert _{0,\infty }$. Thus we get our final result unconditionally, which improves the conclusion of  [3].

Based on Theorem 2 and interpolated postprocessing operator $I_{2h}^2$ constructed in  [31], we can deduce the following global superconvergence easily.

Theorem 3

Let u and $U_h^m$ be the solutions of (1.1) and (2.2)–(2.4) respectively, for $m=1,\ldots , N$, under the conditions of Theorem  1, we have

$$\begin{aligned} \Vert u^m-I_{2h}^2U_h^m\Vert _1=O(h^2+\tau ^2). \end{aligned}$$

(4.33)

Table 1 Numerical results at $t=0.25$ with $\tau =h$

5 Numerical Results

In this section, we present three numerical examples to confirm our theoretical analysis.

Example 1

Considering the cubic Schrödinger equation [23] with $\Omega =[0, 1]\times [0, 1]$, we set $f(s)=s$, $u=5e^{it}(1+2t^2)(1-x)(1-y)\sin (x)\sin (y)$ and g(X, t) is chosen corresponding to the exact solution. A uniform rectangular partition with $M+1$ nodes in each direction is used in our computation.

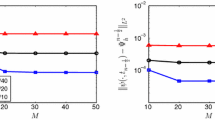
We solve the system by the linearized Galerkin method with bilinear element. To confirm our error estimates in $H^1$-norm, we choose $\tau =h$ and the numerical results with respect to time $t=0.25, 0.5, 0.75, 1.0$ are listed in the following Tables 1, 2, 3 and 4 respectively. We can see clearly from them that when $h\rightarrow 0$, $\Vert u^n-U_h^n\Vert _1$ is convergent at an optimal rate O(h), and $\Vert U_h^n-I_hu^n\Vert _1$, $\Vert u^n-I_{2h}^2U_h^n\Vert _1$ are superconvergent at $O(h^{2})$, which coincide with our theoretical analysis. To show the unconditional stability, we choose $h=1/128$ and the large time steps $\tau =h, 4h, 8h, 16h$, respectively. We present the numerical results in Table 5, which suggest that the scheme is stable for large time steps.We also describe the error reduction results at $t = 0.25, 0.5, 0.75, 1.0$ in Figs. 1, 2, 3 and 4 respectively, where $E_h^1=\Vert u^n-U^n_h\Vert _1, E_h^2=\Vert U^n_h-I_hu^n\Vert _1, E_h^3=\Vert u^n-I_{2h}^2U_h^n\Vert _1$.

Table 2 Numerical results at $t=0.5$ with $\tau =h$

Table 3 Numerical results at $t=0.75$ with $\tau =h$

Table 4 Numerical results at $t=1.0$ with $\tau =h$

Fig. 1

Error reduction results at $t=0.25$

Fig. 2

Error reduction results at $t=0.5$

Fig. 3

Error reduction results at $t=0.75$

Fig. 4

Error reduction results at $t=1.0$

Table 5 Convergence results of $\Vert u^n-U^n_h\Vert _1$ with $h=\frac{1}{160}$ and $\tau =kh$

Example 2

We consider the Schrödinger equation with $\Omega =[0, 1]\times [0, 1]$, $f(s)=-s^2+s$ and $u=e^{(i+1)t}x^3 y^3(1-x)(1-y)$. g(X, t) is chosen corresponding to the exact solution. A uniform rectangular partition with $M+1$ nodes in each direction is used in our computation.

Similar to Example 1, we can see from Tables 6, 7, 8, 9 and 10 and Figs. 5, 6, 7 and 8 that all these results are in good agreement with our theoretical analysis.

Table 6 Numerical results at $t=0.25$ with $\tau =h$

Table 7 Numerical results at $t=0.5$ with $\tau =h$

Table 8 Numerical results at $t=0.75$ with $\tau =h$

Table 9 Numerical results at $t=1.0$ with $\tau =h$

Table 10 Convergence results of $\Vert u^n-U^n_h\Vert _1$ with $h=\frac{1}{160}$ and $\tau =kh$

Fig. 5

Error reduction results at $t=0.25$

Fig. 6

Error reduction results at $t=0.5$

Fig. 7

Error reduction results at $t=0.75$

Fig. 8

Error reduction results at $t=1.0$

Table 11 Numerical results at $t=0.5$ with $\tau =h$

Table 12 Numerical results at $t=1.0$ with $\tau =h$

Table 13 Convergence results of $\Vert u^n-U^n_h\Vert _1$ with $h=\frac{\pi }{80}$ and $\tau =kh$

Fig. 9

Error reduction results at $t=0.5$

Example 3

We consider the example [35] describing the dynamics of Bose-Einstein Condensate at extremely low temperature, reads

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}i\frac{\partial u(x,y,t)}{\partial t}=-\frac{1}{2}\triangle u+V(x,y)u+|u|^2u, (x,y)\in [0,2\pi ]\times [0,2\pi ],\\ &{}u_0(x,y)=\sin x\sin y, \end{array}\right. } \end{aligned}$$

where $V(x,y)=1-\sin ^2x\sin ^2y$ and $\Omega =[0, 1]\times [0, 1]$. The exact solution for the problem is $u=e^{-2ti}\sin x\sin y$. A uniform rectangular partition with $M+1$ nodes in each direction is used in our computation.

Fig. 10

Error reduction results at $t=1.0$

Tables 11, 12 and 13 and Figs. 9 and 10 confirm our theoretical analysis.