1 Introduction

A well-known approach in the numerical solution of evolutionary problems in partial differential equations is the method of lines. In this approach a partial differential equation is first discretized in space by finite difference or finite element techniques and converted into a system of ordinary differential equations (ODEs). In some cases the right hand side can be written as the sum of two terms, a stiff one and a non stiff one:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{du}{dt}(t) = F(t,u(t)) \,+\, \frac{1}{\varepsilon }\,G(t,u(t)), &{}\quad \forall \,t \ge t_0, \\ \, \\ \displaystyle u(t_0)= u_0, &{}\, \end{array}\right. \qquad (\mathcal {A}) \end{aligned}$$

where \(\varepsilon \) is a small parameter, which generates some stiffness in the system. We call such stiff problem of additive type and hereafter denoted by \((\mathcal {A})\).

The development of numerical schemes for systems of stiff ODEs of the form \((\mathcal {A})\) attracted a lot of attention in the last decades. Systems of such form often arise from the discretization of partial differential equations, such as convection–diffusion equations and hyperbolic systems with relaxation. In previous works we considered the latter case which in recent years has been a very active field of research, due to its great impact on applied sciences. In fact, relaxation is important in many physical situations, for example it arises in discrete kinetic theory of rarefied gases, hydrodynamical models for semiconductors, linear and non-linear waves, viscoelasticity, traffic flows, shallow water [1–8].

Hopefully, when a problem with easily separable stiff and non-stiff components is considered, a combination of implicit and explicit Runge–Kutta methods can be used. The implicit method is used to treat the stiff component \( G(t,u(t))/\varepsilon \) in a stable fashion while the non-stiff component F(t, u(t)) of the system is treated using the explicit scheme. These combined implicit/explicit (IMEX) schemes are already used for several problems, including convection–diffusion–reaction systems, hyperbolic systems with relaxation, collisional kinetic equations, and so on.

However not all systems containing stiff terms appear in partitioned or additive form, and therefore the use of standard IMEX schemes is not straightforward. In such cases one usually relies on fully implicit schemes.

In the context of ODEs, several authors usually call semi-implicit RK methods (in contrast to implicit RK methods) numerical schemes that require the solution of linear systems of equations for the computation of the numerical solution with no Newton iteration. A typical case is given by Rosenbrock schemes, [9], which are linearly implicit schemes, that do not make use of the particular structure of the system. Similarly, in the context of PDEs, some authors denote by semi-implicit additive schemes in which the two tableau correspond respectively to an explicit and an implicit scheme (see [10, 11]).

In other cases, semi-implicit schemes denote methods for the numerical solution of a problem of the form

$$\begin{aligned} \frac{du}{dt} \,=\, f(t,u), \end{aligned}$$

obtained by adding and subtracting an approximation g(t, u) of f(t, u) which is more amenable for an implicit treatment:

$$\begin{aligned} \frac{du}{dt} \,=\, f(t,u)-g(t,u) \,+\, g(t,u). \end{aligned}$$

Then the term \(f(t,u)-g(t,u)\) is treated explicitly, while g(t, u) is treated implicitly.

Examples of this type are given in [12], where the authors consider nonlinear hyperbolic systems containing fully nonlinear and stiff relaxation terms in the limit of arbitrary late times. The dynamics is asymptotically governed by effective systems which are of parabolic type and may contain degenerate and/or fully nonlinear diffusion terms. Fully nonlinear relaxation terms can arise, for instance, in presence of strong friction, see for example in [13] and references therein. Furthermore, a general class of models of the same type were introduced by Kawashima and LeFloch (see for example [12]). For such problems in [12], the authors introduced a semi-implicit formulation based on implicit–explicit (IMEX) Runge–Kutta methods. Similarly in [14], the author introduced a semi-implicit method for computing the two models of motion by mean curvature and motion by surface diffusion which is stable for large time steps. In all such models a semi-implicit method is more effective than a fully implicit one. Other examples are given in [15], where the authors construct a very effective solver for the Boltzmann equation near the fluid dynamic regime. In this case f denotes the Boltzmann operator, while g denotes a suitable BGK approximation. A similar technique is adopted in [16, 17] in the context of Navier–Stokes equations.

In other cases the stiffness is associated to some variables. For example, if a system can be written in the partitioned form, hereafter denoted by \((\mathcal {P})\),

$$\begin{aligned} \left\{ \begin{array}{c} \displaystyle \frac{dy}{dt}(t) = \mathcal {F}_1(t,y(t),z(t)), \\ \, \\ \displaystyle \varepsilon \frac{dz}{dt} (t) = \mathcal {F}_2(t,y(t),z(t)), \end{array}\right. \qquad (\mathcal {P}) \end{aligned}$$

then the stiffness is associated to variable z, and the corresponding equation will be treated implicitly, while the equation for y is treated explicitly. In other cases it is more convenient to associate the stiffness to a part of the right hand side, for example if a system has the additive form \((\mathcal {A})\), in this case the term F(t, u(t)) is treated explicitly while \( G(t,u(t))/\varepsilon \) is treated implicitly. It can be shown that the same system can be written in either form, however sometimes one of the two forms is more convenient.

Directly motivated by the above cases, we consider a more general class of problems of the form

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{du}{dt}(t) = \mathcal {H}(t,u(t),u(t)/\varepsilon ), &{} \forall \,t \ge t_0, \\ \, \\ \displaystyle u(t_0)= u_0, &{} \, \end{array}\right. \qquad (\mathcal {G}) \end{aligned}$$

where the function \(\mathcal {H}\): \(\mathbb {R}\times \mathbb {R}^m \times \mathbb {R}^m \rightarrow \mathbb {R}^m\) is sufficiently differentiable and the right hand side has a stiff dependence only on the last argument, emphasized by the appearance on the small parameter \(\varepsilon \) in the denominator. We denote this class of problems as generalized partitioned form and hereafter denoted by \((\mathcal {G})\). All the cases mentioned before belong to this more general class. In our paper we denote by semi-implicit schemes numerical methods which solve problems of the form \((\mathcal {G})\) in which the variable u appearing as the second argument of \(\mathcal {H}\) is treated explicitly, while u appearing as third argument is treated implicitly.

Remark 1.1

Note that the parameter \(\varepsilon \) in \((\mathcal {G})\) does not necessarily appear explicitly, but it just indicates some stiffness in the term. Sometime the stiffness is hidden, and is not explicitly expressed in terms of a small parameter \(\varepsilon \). For example, in the case of diffusion terms \(\varepsilon = \mathcal {O}(\Delta x^2)\), see [12, 18–20].

The main goal of the paper is to focus on the treatment of systems of the form \((\mathcal {G})\), by using some IMEX schemes already presented in the literature. Furthermore, in order to simplify the expression of the formulas, we drop the dependence of the parameter \(\varepsilon \) in the second argument as mentioned before, keeping in mind that the dependence on the second argument is stiff. Then in this paper we consider the general class of non-autonomous problems of the form

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{du}{dt}(t) = \mathcal {H}(t,u(t),u(t)), &{} \forall \,t \ge t_0, \\ \, \\ \displaystyle u(t_0)= u_0, &{}\, \end{array}\right. \end{aligned}$$
(1)

The aim of this paper is to propose a new approach, based on IMEX Runge–Kutta methods, for the construction of semi-implicit schemes. The approach is somehow inspired by partitioned Runge–Kutta methods [21] and related to the additive Runge–Kutta methods of Zhong [11].

In particular, we show several examples of systems of the form \(\mathcal {G}\) that can be efficiently solved with the new approach. In order to apply this idea, one has to identify where the dependence of the unknown is stiff. We do not propose a general technique to automatically identify the stiff dependence in the function \(\mathcal {H}\) that defines the system, rather we try to give arguments that help identifying the stiff dependence in each of the examples that we present. The problem of identifying the stiff term in a complicated system of equations is not new, and in several practical cases it is not so straightforward. In the context of numerical methods for systems of ODE’s, the problem of automatic stiffness detection is treated, for example, in the classical book of Hairer and Wanner ([9], p. 21). In the case in which a decision has to be made about where a variable has to be treated explicitly and where implicitly is an even more delicate one, and the research on techniques that automatically identify, in a general system, which is the dependence that is responsible for the stiffness, and whether it can be effectively treated linearly is far beyond the scope of the present paper.

In the next section, we describe the general framework to construct semi-implicit Runge–Kutta schemes based on approach outlined before. Several schemes are proposed with different stability properties and order of accuracy. We next compare the numerical solutions with exact ones available in the literature for reaction–diffusion problem and nonlinear convection–diffusion equation. After this validation step, we perform several numerical computations to show the robustness of our approach (nonlinear Fokker–Planck equation, Hele–Shaw flow and surface diffusion flow).

2 Relation Between the Various Types of Systems

In this section we show the following hierarchical dependence.

Proposition 2.1

Consider a system in partitioned form \((\mathcal {A})\). Then it can be written either in the additive form \((\mathcal {A})\) or in the generalized partitioned form \((\mathcal {G})\).

This hierarchical dependence can be illustrated by the following Fig. 1.

Fig. 1
figure 1

Illustration of the hierarchical dependence of (\(\mathcal {P}\)), with respect to (\(\mathcal {A}\)) and (\(\mathcal {G}\)) approach

Full size image

The first part of the Proposition, \(\mathcal {P} \subset \mathcal {A}\), is self evident. To show that \(\mathcal {P} \subset \mathcal {G}\) we consider the system \((\mathcal {P})\) and set \(u=(u_1,u_2)\) with \(u_1=y\) and \(u_2=\varepsilon \,z\), then we have from \((\mathcal {P})\)

$$\begin{aligned} \left\{ \begin{array}{c} \displaystyle \frac{du_1}{dt} (t) = \mathcal {F}_1(t,u_1(t),u_2(t)/\varepsilon ), \\ \, \\ \displaystyle \frac{du_2}{dt} (t) = \mathcal {F}_2(t,u_1(t),u_2(t)/\varepsilon ), \end{array}\right. \end{aligned}$$

that is, system \((\mathcal {G})\) with \(u =(u_1,u_2)\) and

$$\begin{aligned} \left( \begin{array}{c} \mathcal {F}_1(t,u_1(t),u_2(t)/\varepsilon ) \\ \, \\ \mathcal {F}_2(t,u_1(t),u_2(t)/\varepsilon ) \end{array}\right) = \mathcal {H}(t, u(t),u(t)/\varepsilon ). \end{aligned}$$

We note that in this two cases no duplications of unknowns is needed. Unfortunately there is no such hierarchical dependence between \((\mathcal {A})\) and \((\mathcal {G})\) systems. Note however that if we allow to double the number of unknowns, then we have the following dependence.

Proposition 2.2

We have the following assertions

  1. (1)

    Consider a system in the additive form \((\mathcal {A})\). Then by doubling the number of unknowns, it can be written in the partitioned form \((\mathcal {P})\).

  2. (2)

    Consider a system in the generalized partitioned form \((\mathcal {G})\). Then by doubling the number of unknowns, it can be written in the partitioned form \((\mathcal {P})\).

This hierarchical dependence can be illustrated by the following Fig. 2.

Fig. 2
figure 2

Illustration of hierarchical dependence between partitioned approach (\(\mathcal {P}\)), additive approach (\(\mathcal {A}\)) and generalised partitioned form (\(\mathcal {G}\)) approach where the dashed lines represent the set of systems with doubled number of unknowns

Full size image

Part (1) of the Proposition is well known in the literature (see, for example, [22]). To prove (2), we consider a solution to \((\mathcal {G})\) and set \(v = u/\varepsilon \). Thus, we have

$$\begin{aligned} \left\{ \begin{array}{c} \displaystyle \frac{du}{dt} (t) = \mathcal {H}(t,u(t),v(t)), \\ \, \\ \displaystyle \varepsilon \frac{dv}{dt} (t) = \mathcal {H}(t,u(t),v(t)), \end{array}\right. \end{aligned}$$
(2)

it is a particular case of system \((\mathcal {P})\). Note that these two last cases require duplication of unknowns.

Such inclusions are very important, since the analysis of the numerical schemes applied to one family of schemes is automatically valid also for schemes applied to the other two families. As far as we know, it is not possible to write system \((\mathcal {A})\) in the form \((\mathcal {G})\) or viceversa, without doubling the number of unknowns.

Nevertheless, we will see later (“Appendix”) that the computational cost and the number of evaluations of \(\mathcal {H}\) does not increase.

Thus, the formal equivalence among the various systems allows us to adopt techniques well known for additive or partitioned systems to more general cases.

A remark is in order at this point. A vast literature exists on the formal analysis of systems \((\mathcal {P})\), which are denoted as singular perturbation systems, [2, 9, 23–26]. However, system (2) is only formally a particular case of \((\mathcal {P})\), and the analysis developed for the former cannot be directly applied to this case, since now the two functions \(\mathcal {F}_1\) and \(\mathcal {F}_2\) are the same. Furthermore, a detailed asymptotic analysis of the schemes presented here goes beyond the scope of the paper, and will be considered in a future work for specific applications where the asymptotic behavior \(\varepsilon \rightarrow 0\) is well understood at the continuous level [27, 28].

3 Numerical Methods for ODEs

In this section we review the concept of partitioned Runge–Kutta methods and derive a new class of semi-implicit R–K schemes, and we propose several schemes up to third order of accuracy, based on IMEX Runge–Kutta schemes already existing in the literature.

3.1 From Partitioned to Semi-implicit Runge–Kutta Methods

In the literature some interesting numerical methods do not belong to the classical class of implicit or explicit Runge–Kutta methods. They are called partitioned Runge–Kutta methods, [9, 21]. In order to present these methods we consider non-autonomous differential equations in the partitioned form,

$$\begin{aligned} \left\{ \begin{array}{c} \displaystyle \frac{dy}{dt}(t) \,=\, \mathcal {F}_1(t,y(t),z(t)), \\ \, \\ \displaystyle \frac{dz}{dt}(t) \,=\, \mathcal {F}_2(t,y(t),z(t)), \end{array} \right. \end{aligned}$$
(3)

where y(t) and z(t) may be vectors of different dimensions and \(y(t_0) = y_0\), \(z(t_0) = z_0\) are the initial conditions.

The idea of the partitioned Runge–Kutta methods is to apply two different Runge–Kutta methods, i.e.

$$\begin{aligned} \begin{array}{c|c} {\hat{c}} &{} {\hat{A}} \\ \hline \\ &{} {\hat{b}}^T \end{array} \qquad \begin{array}{c|c} c &{} A \\ \hline \\ &{} b^T \end{array} \end{aligned}$$
(4)

where we treat the first variable y with the first method, \({\hat{A}}\), \({\hat{b}}^T = ({\hat{b}}_{1},\ldots , {\hat{b}}_{s})\), \({\hat{c}} = ({\hat{c}}_1, \ldots , {\hat{c}}_s)\) and the second variable z with the second method, A, \(b^T=(b_{1},\ldots , b_{s})\), \(c = (c_1, \ldots ,c_s)\) under the usual assumption

$$\begin{aligned} \sum _{j} {\hat{a}}_{i,j} \,=\, {\hat{c}}_i,\quad \mathrm{and }\quad \sum _{j} a_{ij} \,=\, c_i, \quad \mathrm{for}\quad 1\le i \le s. \end{aligned}$$
(5)

In other words, if we consider a numerical approximation \((y^n,z^n)\) of (3) at time \(t^n\), a partitioned Runge–Kutta method for the solution of (3) is given by

$$\begin{aligned} \left\{ \begin{array}{c} \displaystyle k_i \,=\, \mathcal {F}_1\left( t^n+{\hat{c}}_i\,\Delta t, \ y^n + \Delta t\, \sum _{j = 1}^{s}{\hat{a}}_{ij}k_j, \ z^n + \Delta t \sum _{j = 1}^{s}a_{ij}\ell _j\right) , \quad 1\le i \le s, \\ \, \\ \displaystyle \ell _i \,=\, \mathcal {F}_2\left( t^n+c_i\,\Delta t, \ y^n + \Delta t \,\sum _{j = 1}^{s}{\hat{a}}_{ij}k_j, \ z^n + \Delta t \sum _{j = 1}^{s}a_{ij}\ell _j\right) , \quad 1\le i \le s \end{array} \right. \end{aligned}$$
(6)

and the numerical solution at the next time step is given by

$$\begin{aligned} \left\{ \begin{array}{c} \displaystyle y^{n+1} \,=\, y^n \,+\, \Delta t \,\sum _{i = 1}^{s}{\hat{b}}_{i}\,k_i, \\ \, \\ \displaystyle z^{n+1} = z^n + \Delta t \,\sum _{i = 1}^{s}b_{i}\,\ell _i. \end{array} \right. \end{aligned}$$
(7)

We observe that we can rewrite system (1) as a partition one

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{dy}{dt}(t) \,=\, \mathcal {H}(t,y(t),z(t)), \\ \, \\ \displaystyle \frac{dz}{dt}(t) \,=\, \mathcal {H}(t,y(t),z(t)), \end{array} \right. \end{aligned}$$
(8)

with initial conditions \(y(t_0) = y_0\), \(z(t_0) = y_0\). In such a case the solution of system (8) satisfies \(z(t)=y(t)\) for any \(t \ge t_0\) and is also a solution of Eq. (1). The system is a particular case of partitioned system in which \(\mathcal {F}_1=\mathcal {F}_2\) but with an additional computational cost since we double the number of variables. Applying the partitioned Runge–Kutta method (6)–(7) we have

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle k_i \,= \, \mathcal {H}\left( t^n+{\hat{c}}_i\Delta t,Y_i, Z_i\right) , \quad 1\le i \le s, \\ \, \\ \displaystyle \ell _i \,=\, \mathcal {H}\left( t^n+{c}_i\Delta t,Y_i, Z_i\right) , \quad 1\le i \le s, \end{array}\right. \end{aligned}$$
(9)

with

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle Y_i \,=\, y^n \,+\, \Delta t \,\sum _{j = 1}^{s}{\hat{a}}_{i,j}\,k_j, \quad 1\le i \le s, \\ \displaystyle Z_i \,=\, z^n \,+\, \Delta t \,\sum _{j = 1}^{s}a_{ij}\,\ell _j, \quad 1\le i \le s, \end{array}\right. \end{aligned}$$

and the numerical solutions at the next time step are

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle y^{n+1} \,=\, y^n \,+\, \Delta t \,\sum _{i = 1}^{s}{\hat{b}}_{i}\,k_i, \\ \displaystyle z^{n+1} \,=\, z^n \,+\, \Delta t \,\sum _{i = 1}^{s}b_{i}\,\ell _i. \end{array}\right. \end{aligned}$$

In general, \(k_i\) and \(\ell _i\) given by (9) for all \(1\le i\le s\) are different. However, there are two cases in which \(k_i = \ell _i, \> i=1,\ldots , s\). The first one is when the system is autonomous, i.e. \(\mathcal {H}\) does not explicitly depend on time, and the second one is when \({\hat{c}}_i=c_i\), \(i=1,\ldots ,s\). In these two cases only one evaluation of \(\mathcal {H}\) is needed in (9), and only one set of stage fluxes is computed:

$$\begin{aligned} k_i \,=\, \mathcal {H}\left( y^n \,+\, \Delta t \,\sum _{i = 1}^{s}{\hat{a}}_{i,j}\,k_j,\, z^n \,+\, \Delta t \,\sum _{i = 1}^{s}a_{ij}\,k_j\right) , \quad 1\le i \le s. \end{aligned}$$

From now on we assume that the system is autonomous. This restriction can be removed: even in the general case of a non-autonomous system, and \({\hat{\mathbf{c}}}\ne \mathbf{c}\), it is still possible to derive a scheme that does not require two sets of stage fluxes. The details are reported in the “Appendix”.

Now we are ready to propose semi-implicit Runge–Kutta methods in order to solve autonomous problem of the form (8), i.e.

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{dy}{dt} \,=\, \mathcal {H}(y,z), \\ \, \\ \displaystyle \frac{dz}{dt} \,=\, \mathcal {H}(y,z), \end{array} \right. \end{aligned}$$
(10)

with initial conditions \(y(t_0) = y_0\), \(z(t_0) = y_0\), where we treat the first variable y explicitly, and the second one z, implicitly.

From now on we shall adopt IMEX R–K schemes with \(\mathbf{b} = {\hat{\mathbf{b}}}\). It is usual to consider diagonally implicit R–K (DIRK) schemes for the implicit part, [9]. In addition to be simpler to implement, this ensures that the terms involving the first argument of \(\mathcal {H}\) are indeed explicitly computed. The coefficients of the method are usually represented in a double Butcher tableau as (4).

Then a semi-implicit Runge–Kutta method is implemented as follows. First we set \(z^n = y^n\) and compute the stage fluxes for \(i = 1, \ldots , s\), we set \(Y_1={\tilde{Z}}_1=y^n\) and

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle Y_i \,=\, y^{n} \,+\, \Delta t\sum _{j =1}^{i-1} {\hat{a}}_{ij}\, k_j, \quad 2\le i \le s, \\ \, \\ \displaystyle {\tilde{Z}}_i \,=\, y^{n} \,+\, \Delta t\, \sum _{j =1}^{i-1} a_{ij} \, k_j, \quad 2\le i \le s \\ \, \\ \displaystyle k_i \,=\, \mathcal {H}\left( Y_i, {\tilde{Z}}_i \;+\, \Delta t\, a_{ii}\,k_i\right) , \quad 1\le i \le s, \end{array}\right. \end{aligned}$$
(11)

and, finally update the numerical solution by

$$\begin{aligned} y^{n+1} \, = \, y^{n} \,+\, \Delta t \,\sum _{i =1}^{s} {\hat{b}}_i \,k_i, \end{aligned}$$
(12)

and

$$\begin{aligned} z^{n+1} \, = \, y^{n} \,+\, \Delta t \,\sum _{i =1}^{s} b_i \,k_i. \end{aligned}$$
(13)

We observe that because \({\hat{b}}_i=b_i\) for \(i=1,\ldots ,s\) then the numerical solutions are the same, i.e. if \(z^0=y^0\) then \(z^{n} = y^{n} \, \forall n\ge 0\), therefore the duplication of the system is only apparent, since there is indeed only one set of numerical solution.

Remark 3.1

(Embedded methods). We can select a different vector of weights for the z variable, say the \({\tilde{b}}\ne b = {\hat{b}}\). Such a vector will provide a lower order approximation of the solution for z. Consider now a scheme in which, at the beginning of the time step, we set \(z^n=y^n\). Such a scheme would produce the same sequence \(y^n\) as scheme (11, 12), and would allow an automatic time step control. This procedure is commonly used in the context of numerical methods for ODEs [21]. Note that using \({\tilde{b}}\) for the y variable, advancing with the z variable and setting \(y_n=z_n\) at the beginning of each time step would give exactly the same scheme. In practice one advances the numerical solution with the more accurate one and uses the other variable to estimate the error. We shall not implement any time step control in the present paper.

Remark 3.2

We note that this new approach includes Zhong’s method [11] for autonomous systems. The theory developed in [11] for additive semi-implicit Runge–Kutta methods can be extended in a straightforward manner to the semi-implicit Runge–Kutta methods, (11), (12) and (13). In fact, by setting \(\mathcal {H}(y,y) = f(y) + g(y)\) we obtain by (11):

$$\begin{aligned} k_i= & {} \mathcal {H}\left( y^{n} \,+\, \sum _{j =1}^{j-1} {\hat{a}}_{ij}\, k_j, y^{n} \,+\, \sum _{j =1}^{j-1} a_{ij} \,k_j \,+\, a_{ii}\,k_i\right) , \nonumber \\= & {} f\left( y^{n} + \sum _{j =1}^{j-1} {\hat{a}}_{ij} \,k_j\right) \,+\, g\left( y^{n} + \sum _{j =1}^{j-1} a_{ij} \,k_j \,+\, a_{ii}\,k_i\right) , \end{aligned}$$
(14)

for \(i=1,\ldots s\). In particular, for updating the numerical solution, Zhong’s methods use only one set of weights, i.e. \(b_i\) for all \(i = 1,\ldots s\), and, in our case, this means that we have only on set of unknowns, namely \(y^n=z^n\). From Eq. (12), we have for numerical solution

$$\begin{aligned} y^{n+1} \,=\, y^{n} \,+\, \sum _{i =1}^{s} b_i \,k_i, \end{aligned}$$
(15)

therefore (14) and (15) represent exactly the additive semi-implicit Runge–Kutta methods proposed by Zhong, [11], applied in a more general context, and therefore they have to satisfy more order conditions than in Zhong’s case (see next section).

In the following we propose different types of semi-implicit Runge–Kutta methods and verify that the order conditions are the same as the ones satisfied by the explicit and implicit Runge–Kutta schemes.

3.2 Classification of IMEX Runge–Kutta Schemes

Next we give a classification of such schemes and recall the order conditions to obtain second and third order accuracy in time. Finally we list several second and third order IMEX R–K schemes presented in the literature, [6, 7] that we will use for our semi-implicit framework (11)–(13).

IMEX Runge–Kutta schemes presented in the literature can be classified in three different types characterized by the structure of the matrix \(A = (a_{ij})_{i,j=1}^s\) of the implicit scheme. Following [23], we will rely on the following notions [2, 7, 22].

Definition 3.3

An IMEX Runge–Kutta method is said to be of type A [7] if the matrix \(A \in \mathbb {R}^{s \times s}\) is invertible. It is said to be of type CK [2] if the matrix \(A \in \mathbb {R}^{s \times s}\) can be written in the form

$$\begin{aligned} A = \left( \begin{array}{ll} 0 &{} 0 \\ a &{} {\mathcal {A}} \end{array} \right) , \end{aligned}$$

in which the matrix \(\mathcal {A} \in \mathbb {R}^{(s-1) \times (s-1)}\) invertible. Finally, it is said to be of type ARS [22] if it is a special case of the type CK with the vector \(a = 0\).

Schemes of type CK are very attractive since they allow some simplifying assumptions, that make order conditions easier to treat, therefore permitting the construction of higher order IMEX Runge–Kutta schemes. On the other hand, schemes of type A are more amenable to a theoretical analysis, since the matrix A of the implicit scheme is invertible.

3.3 Order Conditions and Numerical Schemes

Runge–Kutta methods (11)–(13) are obtained from the semi-implicit schemes (6)-(7). Thus, the order conditions for (11)–(13) are a direct consequence of the classical order conditions computed for partitioned Runge–Kutta methods, [21, 29]. Here we recall some known results for IMEX R–K schemes presented in [2, 6, 7]. In particular the order conditions up to order 3 can be simplified if we set \({\hat{b}}_i=b_i\) for \(i=1,\ldots ,s\). Then using the previous notation for the explicit and implicit part and assuming (4) and (5), we have for a method of order 2

$$\begin{aligned} \sum _{i} b_i \,=\, 1, \quad \sum _{i} b_i\,c_i \,=\, 1/2, \quad \sum _{i} b_i\,{\hat{c}}_i \,=\, 1/2. \end{aligned}$$
(16)

and for a method of order 3

$$\begin{aligned}&\sum _{i} b_i c_i^2 \,=\, 1/3, \quad \sum _{i,j} b_i \,a_{ij}\, c_j \,=\, 1/6, \end{aligned}$$
(17)
$$\begin{aligned}&\sum _{i} b_i\,\hat{c}_i^2 \,=\, 1/3, \quad \sum _{i,j} b_i \,\hat{a}_{ij}\,\hat{c}_j \,=\, 1/6, \end{aligned}$$
(18)
$$\begin{aligned}&\sum _{i} b_i\,\hat{c}_i\, c_i \,=\, 1/3, \quad \sum _{i,j} b_i \, a_{ij}\,\hat{c}_j \,=\, 1/6, \quad \sum _{i,j} b_i \, \hat{a}_{ij}\,c_j \,=\, 1/6. \end{aligned}$$
(19)

The general conditions in case \({\hat{b}}\ne b\) can be found in [7].

We recall some well know definitions that we shall adopt in the paper.

Definition 3.4

An implicit R–K method is called stiffly accurate if \(b^T = e^T_s A\) with \(e^T_s = (0,\ldots ,0, 1)\), i.e. methods for which the numerical solution is identical to the last internal stage (see [9], p. 45).

Remark 3.5

This property is important for the L-stability of the implicit part of the method, i.e. an A-stable implicit method stiffly accurate is also L-stable, (see [9], p. 44–45).

Note that the coefficients of the implicit part of some IMEX RK schemes presented later in this paper satisfy the property given in the Definition 3.4.

Now, we first consider second order schemes with two stages that satisfy the set of order conditions (16). For practical reasons, in order to simplify the computations of the coefficients, we consider singly diagonally implicit Runge–Kutta (SDIRK) schemes, [9], for the implicit part, i.e. \(a_{ii} = \gamma \), for \(i = 1,\ldots s\). The Butcher tableau takes then the following form

$$\begin{aligned} \begin{array}{c|cc} 0 &{} 0 &{} 0 \\ {\hat{c}} &{} \hat{c} &{} 0\\ \hline &{} b_1 &{} b_2 \end{array} \qquad \begin{array}{c|cc} \gamma &{} \gamma &{} 0\\ c &{} c- \gamma &{} \gamma \\ \hline &{} b_1 &{} b_2 \end{array} \end{aligned}$$
(20)

with the following coefficients:

$$\begin{aligned} b_1 \,=\, 1-b_2, \quad {\hat{c}} \,=\, 1/(2\,b_2), \quad c = (1/2 - \gamma (1-b_2))/b_2, \end{aligned}$$
(21)

where \(b_2 \ne 0\) and \(\gamma \in \mathbb {R}\) free parameters. If we require that the implicit part of the scheme is A-stable, then we consider \(\gamma \ge 1/4\), [9].

We list below the second order schemes that we shall use in the paper.

3.3.1 The Second Order Semi-implicit Runge–Kutta Scheme: H-SDIRK2(2,2,2)

A first example of scheme satisfying the second order conditions given in (16) is \(b_2 = \gamma = 1/2\), which yields the following table

$$\begin{aligned} \begin{array}{c|cc} 0 &{} 0 &{} 0 \\ 1 &{} 1 &{} 0\\ \hline &{} 1/2 &{} 1/2 \end{array} \qquad \begin{array}{c|cc} 1/2 &{} 1/2 &{} 0\\ 1/2 &{} 0 &{} 1/2 \\ \hline &{} 1/2 &{} 1/2 \end{array} \end{aligned}$$
(22)

This scheme is the combination of Heun method (explicit part) and an A-stable second order singly diagonal implicit Runge–Kutta SDIRK method (implicit part), hence we call it H-SDIRK2(2,2,2).

3.3.2 The Stiffly Accurate Semi-implicit Runge–Kutta Scheme: LSDIRK2(2,2,2)

Another choice for the coefficients (21) is \(b_2 = \gamma \), \(c = 1\), where \(\gamma \) is chosen as the smallest root of the polynomial \(\gamma ^2 - 2\gamma + 1/2 = 0\), i.e. \(\gamma = 1 - 1/\sqrt{2}\) and \(\hat{c} = 1/(2\gamma )\). This gives

$$\begin{aligned} \begin{array}{c|cc} 0 &{} 0 &{} 0 \\ {\hat{c}} &{} \hat{c} &{} 0\\ \hline &{}1-\gamma &{} \gamma \end{array} \qquad \begin{array}{c|cc} \gamma &{} \gamma &{} 0\\ 1 &{} 1-\gamma &{} \gamma \\ \hline &{} 1-\gamma &{} \gamma \end{array} \end{aligned}$$
(23)

This scheme is the combination of Runge–Kutta method (explicit part) and an L-stable second order SDIRK method in the implicit part. Thus, we call it LSDIRK2(2,2,2).

3.3.3 The IMEX-SSP2(2,2,2) L-stable Scheme: H-LDIRKp(2,2,2)

We choose \(b_2 =1/2\), \(\hat{c}=1\), i.e. the corresponding Butcher tableau is given by

$$\begin{aligned} \begin{array}{c|cc} 0 &{} 0 &{} 0 \\ 1 &{} 1 &{} 0\\ \hline &{} 1/2 &{} 1/2 \end{array} \qquad \begin{array}{c|cc} \gamma &{} \gamma &{} 0\\ 1-\gamma &{} 1-2\gamma &{} \gamma \\ \hline &{} 1/2 &{} 1/2 \end{array} \end{aligned}$$
(24)

This scheme, introduced in [6], is based on Heun method coupled with an L-stable SDIRK Runge–Kutta. We call it H-LDIRKp(2,2,2). The implicit part has order \(p = 2\) with \(\gamma =1-1/\sqrt{2}\) and order \(p = 3\) with \(\gamma = (3 + 3\sqrt{(}6))/3\). The version for \(p = 2\) also has the strongly stability preserving (SSP) property, see [6]. The choice of \(\gamma \) for \(p = 3\) guarantees that the implicit part is a third-order DIRK scheme with the best dampening properties [21].

To conclude this subsection devoted to two stages second order schemes, let us give a second order scheme, which is not in the class of singly diagonally implicit Runge–Kutta schemes.

3.3.4 The Second Order Semi-implicit Runge–Kutta Scheme of Type CK: H-CN(2,2,2)

A variant of the previous scheme satisfying the second order conditions (16) is given by the following table

$$\begin{aligned} \begin{array}{c|cc} 0 &{} 0 &{} 0 \\ 1 &{} 1 &{} 0\\ \hline &{} 1/2 &{} 1/2 \end{array} \qquad \begin{array}{c|cc} 0 &{} 0 &{} 0\\ 1 &{} 1/2 &{} 1/2 \\ \hline &{} 1/2 &{} 1/2 \end{array} \end{aligned}$$
(25)

This scheme is the combination of Heun method (explicit part) and a trapezoidal rule Crank Nicolson (implicit part) which is A-stable second order implicit, hence we call it H-CN(2,2,2). It may be a natural choice when dealing with convection–diffusion equation, since the Heun method is an SSP explicit RK [30], and the trapezoidal rule (also known as Crank–Nicolson) is an A-stable method, widely used for diffusion problems.

Finally, we also propose a three stage, second order IMEX scheme.

3.3.5 The Stiffly Accurate IMEX-SSP2(3,3,2) L-stable Scheme: SSP-LDIRK2(3,3,2)

The last second order scheme is obtained by combining a three-stage, second-order SSP scheme with an L-stable, second-order DIRK scheme, and is denoted by SSP-LDIRK2(3,3,2). This scheme is given by

$$\begin{aligned} \begin{array}{c|ccc} 0 &{} 0 &{} 0 &{} 0\\ 1/2 &{} 1/2 &{} 0&{}0\\ 1 &{} 1/2 &{} 1/2&{} 0\\ \hline &{} 1/3 &{} 1/3 &{} 1/3 \end{array} \qquad \begin{array}{c|ccc} 1/4 &{} 1/4 &{} 0 &{} 0\\ 1/4 &{} 0 &{} 1/4 &{} 0\\ 1 &{} 1/3 &{} 1/3 &{} 1/3\\ \hline &{} 1/3 &{} 1/3 &{} 1/3 \end{array} \end{aligned}$$
(26)

3.3.6 The IMEX-SSP3(4,3,3) L-stable Scheme: SSP-LDIRK3(4,3,3)

As third semi-implicit Runge–Kutta methods of the type (11)–(13), that satisfies the set of order conditions (17), (18) and (19), a possible choice is given by the IMEX-SSP3(4,3,3) L-stable scheme with \({\hat{b}}_i=b_i\) for \(i=1,\ldots ,s\), i.e.

$$\begin{aligned} \begin{array}{c|cccc} 0&{} 0 &{} 0 &{} 0 &{} 0\\ 0&{} 0 &{} 0&{}0 &{} 0\\ 1 &{} 0&{} 1 &{} 0&{} 0\\ 1/2 &{} 0 &{} 1/4 &{} 1/4 &{} 0\\ \hline &{} 0 &{} 1/6 &{} 1/6 &{} 2/3 \end{array} \qquad \begin{array}{c|cccc} \alpha &{} \alpha &{} 0 &{} 0&{} 0\\ 0 &{} -\alpha &{} \alpha &{} 0&{} 0\\ 1 &{} 0 &{} 1-\alpha &{} \alpha &{} 0 \\ 1/2 &{} \beta &{} \eta &{} 1/2 - \beta -\eta -\alpha &{} \alpha \\ \hline &{} 0&{} 1/6 &{} 1/6 &{} 2/3 \end{array} \end{aligned}$$
(27)

with \(\alpha = 0.24169426078821\), \(\beta = \alpha /4\) and \(\eta = 0.12915286960590\). We call this scheme SSP-LDIRK3(4,3,3). For this particular choice, let us observe that the number of evaluations of the right hand side \(\mathcal {H}\) is still reasonable since the coefficients \(c_i=\hat{c}_i\) for \(2\le i \le 4\) and only \(c_1\) differs from \(\hat{c}_1\).

We remark that schemes H-LDIRK2(2,2,2), SSP-LDIRK2(3,3,2), and SSP-LDIRK3(4,3,3) were introduced in the context of hyperbolic systems with stiff relaxation in [6].

Remark 3.6

Even though IMEX R–K methods can be considered as additive R–K methods ([2, 22, 31]), we note that the coefficients in the Zhong form (14), (15) are not the standard coefficients of an IMEX R–K method. It is possible to show, by inspection, that Eqs. (14), (15) can be written as an IMEX R–K method. Let

$$\begin{aligned} {\hat{A}}=\left( \begin{array}{cccc} 0 &{} 0\\ {\hat{a}}_{21}&{} 0 \\ \vdots &{} \vdots &{} \ddots \\ a_{s1} &{} \cdots &{} \cdots &{} a_{ss-1} \end{array} \right) , \quad A=\left( \begin{array}{cccc} a_{11} &{} 0\\ {a}_{21}&{} a_{22}\\ \vdots &{} \vdots &{} \ddots \\ a_{s1} &{} \cdots &{} \cdots &{} a_{ss} \end{array} \right) \quad b=\left( \begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_s \end{array} \right) \end{aligned}$$

be the coefficients of the scheme (14), (15), with s stages. Then we write explicitly

$$\begin{aligned} y^{n+1} = y^n + \sum _{i =1}^{s} b_i \left( f({\hat{Y}}_i) + g(Y_i)\right) \end{aligned}$$
(28)

with

$$\begin{aligned} \left\{ \begin{array}{lll} {\hat{Y}}_1 &{}=&{} y^{n}, \\ Y_1 &{}=&{} y^{n} \,+\, \Delta t \,a_{11}\left( f({\hat{Y}}_1) + g(Y_1)\right) ,\\ {\hat{Y}}_2 &{}=&{} y^{n} \,+\, \Delta t \,{\hat{a}}_{21} \left( f({\hat{Y}}_1) + g(Y_1)\right) , \\ Y_2 &{}=&{} y^{n} \,+\, \Delta t \,a_{21} \left( f({\hat{Y}}_1) + g(Y_1)\right) \,+\, \Delta t \, a_{22} \left( f({\hat{Y}}_2) \,+\, g(Y_2)\right) ,\\ ...\\ {\hat{Y}}_s &{}=&{} y^{n} \,+\, \Delta t \,{\hat{a}}_{s1} \left( f({\hat{Y}}_1) + g(Y_1)\right) +\cdots +\, \Delta t \,{\hat{a}}_{ss-1} \left( f({\hat{Y}}_{s-1}) \,+\, g(Y_{s-1})\right) ,\\ Y_s &{}=&{} y^{n} \,+\, \Delta t \, a_{s1} \left( f({\hat{Y}}_1) + g(Y_1)\right) +\cdots + \, \Delta t \, a_{ss} \left( f({\hat{Y}}_{ss}) \,+\, g(Y_{ss})\right) . \end{array}\right. \end{aligned}$$
(29)

and the Butcher tableau is

$$\begin{aligned} \begin{array}{|ccccccc} 0 &{} \\ a_{11}&{} 0 \\ {\hat{a}}_{21} &{} 0 &{} 0 \\ a_{21} &{} 0 &{} a_{22} &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots \\ a_{s1} &{} 0 &{} a_{s2} &{}0&{} \cdots &{} a_{ss} &{} 0\\ \hline b_1 &{}0&{}b_2&{} 0 &{}\cdots &{} b_s&{} 0 \end{array}\quad \quad \begin{array}{|ccccccc} 0 &{} \\ 0 &{} {a}_{11}&{} \\ 0 &{} {\hat{a}}_{21} &{} 0\\ 0 &{} a_{21} &{} 0 &{} a_{22} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots \\ 0 &{} a_{s1} &{} 0 &{} a_{s2} &{} \cdots &{}a_{ss}\\ \hline 0 &{} b_1 &{}0&{}b_2&{} \cdots &{} b_s \end{array} \end{aligned}$$

Using the Kronecker product, this can be written in a more compact form as

$$\begin{aligned} \begin{array}{c|c} {\mathfrak c}&{} {\hat{\mathcal {A}}} \\ \hline \\ &{} \mathfrak {{\hat{b}}}^T \end{array} \quad \begin{array}{c|c} \mathfrak c &{} \mathcal {A}\\ \hline \\ &{} \mathfrak {b}^T \end{array} \end{aligned}$$

with

$$\begin{aligned} \mathfrak {{\hat{b}}}^T&= b^T \otimes (1,0), \quad {\mathfrak {b}^T = b^T \otimes (0,1)}\\ {\hat{\mathcal {A}}}&=({\hat{A}}\otimes {\hat{B}}_1) + (A \otimes {\hat{B}}_2), \quad \mathcal {A} = ({\hat{A}}\otimes B_1) + (A \otimes B_2), \\ {\hat{B}}_1&= \left( \begin{array}{cc} 1 &{} 0\\ 0 &{} 0 \end{array}\right) ,\quad {\hat{B}}_2 = \left( \begin{array}{cc} 0 &{} 0\\ 1 &{} 0 \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} B_1 = \left( \begin{array}{cc} 0 &{} 1\\ 0 &{} 0 \end{array}\right) , \quad B_2 = \left( \begin{array}{cc} 0 &{} 0\\ 0 &{} 1 \end{array}\right) , \end{aligned}$$

i.e., a double Butcher tableau (4) of scheme (28-29) with \({{\hat{\mathfrak {c}}} = {\mathfrak {c}} = {\hat{\mathcal {A}}} \mathfrak e = {\mathcal {A}} {\mathfrak {e}} }\), and \(\mathfrak e = (1,...,1)^T\) the unit vector of length 2s. Note that this is an IMEX scheme with a double Butcher tableau as (4). From this, we can derive the set of order conditions for scheme of the form (14)–(15) in terms of matrix \({\hat{\mathcal {A}}}\), \(\mathcal {A}\) and vectors \({\hat{\mathfrak {b}}}\), \(\mathfrak {b}\), from the order condition of partitioned Runge–Kutta schemes with the same value of \(\mathfrak c\) and \({\hat{\mathfrak {b}}}\ne \mathfrak b\). A similar analysis, with a slightly different notation, was already performed in [32]. Below we list these equations up to order \(p = 3\),

$$\begin{aligned} \mathfrak {{\hat{b}}}^T \mathfrak e= & {} 1, \quad \mathfrak {b}^T \mathfrak e = 1, \quad \text {(first order)},\\ {\mathfrak {\hat{b}}^T \mathfrak c}= & {} 1/2, \quad {\mathfrak {b}^T \mathfrak c = 1/2, }\quad \text {(second order)},\\ {\mathfrak {\hat{b}}^T \mathfrak c}^2= & {} 1/3, \quad {\mathfrak {b}^T \mathfrak c^2 = 1/3}, \quad \text {(third order)} \\ { \mathfrak {b}^T \mathcal {A} \mathfrak {c}}= & {} 1/6, \quad {\mathfrak {b}^T {\hat{\mathcal {A}}} \mathfrak c = 1/6}, \quad {\mathfrak {\hat{b}}^T \mathcal {A} \mathfrak c = 1/6}, \quad {\mathfrak {\hat{b}}^T {\hat{\mathcal {A}}} \mathfrak c = 1/6}. \end{aligned}$$

Explicit computation of these conditions give

$$\begin{aligned} \sum _{i}^s b_i= & {} 1, \quad \sum _{i}b_i {\hat{c}}_i = 1/2, \quad \sum _{i}b_i c_{i} = 1/2, \quad \sum _{i}b_i c_i^2 = 1/3, \quad {\sum _{i}b_i {\hat{c}}_i^2 = 1/3}, \\ { \sum _{i}b_i{a}_{ij} c_j}= & {} 1/6, \quad {\sum _{i}b_i {\hat{a}}_{ij} {\hat{c}}_j = 1/6}, \quad {\sum _{i}b_i a_{ij} {\hat{c}}_j = 1/6}, \quad {\sum _{i}b_i {\hat{a}}_{ij} c_i = 1/6}. \end{aligned}$$

which are a subset of the classical seven third order conditions (16–19) for IMEX schemes of order three with \({\hat{b}} = b\) and \({\hat{c}} \ne c\). The missing condition is the one corresponding to the mixed derivative \(\partial ^2_{yz} \mathcal {H}(y,z)\), which of course is zero for \(\mathcal {H}(y,z) = f(y)+g(z)\). We observe that the third order conditions are only five in the case of Zhong [11]. This discrepancy is clearly explained in the paper [32].

4 Applications

Semi-implicit schemes present a particular interest for nonlinear problems where stiff terms can be treated efficiently by a linear solver rather than by a nonlinear one. For instance, our semi-implicit method is well suited to semi-linear PDEs: for \(p\in \mathbb {N}\), \(t\ge 0\) and in \(x\in \Omega \subset \mathbb {R}^n\), we consider the differential equation of order \(p+1\) by

$$\begin{aligned} \frac{\partial u}{\partial t} \,+\, F(u, \nabla u, \ldots , \nabla ^{p} u) + \sum _{|k|=p+1} A_{k_1,\ldots ,k_n}\, \frac{\partial ^{p+1}}{\partial x_1^{k_1}\ldots \partial x_n^{k_n}}u \,=\, 0. \end{aligned}$$

Of course for this problem classical IMEX schemes are also adapted. However for quasi-linear problems where the function A depends on \(u,\ldots ,\nabla ^p u\), semi-implicit methods are particularly promising since only the term of order \(p+1\) can be treated implicitly. Tests 4 and 5 below belong to this category.

Furthermore, when the highest order term of order \(p+1\) is negligible, the term of order p can be eventually treated with a semi-implicit solver (convection-dominated diffusion problems, see Tests 2 and 3 below).

Another kind of applications concerns relaxation problems with nonlinear relaxation systems [33]

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{\partial u}{\partial t} \,+\, \mathrm{div} \, v = 0 \\ \, \\ \displaystyle \frac{\partial v}{\partial t} \,+\, A\nabla u = \frac{G(u,v)}{\varepsilon } \left( F(u)-v\right) , \end{array}\right. \end{aligned}$$

with \(G(u,v)\le \alpha \), with \(\alpha \) a positive real constant. The nonlinear term G(u, v) can be treated explicitly while the term \(\left( F(u)-v\right) \) is treated implicitly without any iterative solvers.

In this section we present several numerical tests for nonlinear PDEs for reaction–diffusion systems and nonlinear convection–diffusion equation for which we verify the order of accuracy and stability issues with respect to the CFL condition. Then, we treat a nonlinear Fokker–Planck equation to investigate the long time behavior of the numerical solution obtained from (11)–(13). Finally we complete this section with numerical tests on Hele–Shaw flow and surface diffusion flow.

We monitor \(L_1\) and \(L_\infty \) norms of the error, defined as:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {\varepsilon _\infty = \max _{0\le n\le N_T} \max _{i,j} \Vert \omega _{i,j}^n - \omega (t^n,x_{i},y_j)\Vert }, \\ \, \\ \displaystyle {\varepsilon _1 = \max _{0\le n\le N_T} \sum _{i,j} \Delta x\,\Delta y\,\Vert \omega _{i,j}^n - \omega (t^n,x_{i},y_j)\Vert }. \end{array}\right. \end{aligned}$$

where \(\omega (t,x,y)\) denotes the exact solution, while \(\omega _{i,j}^n\) indicates its numerical approximation at \((t^n,x_i,y_j)\). For space discretization we will apply basic fourth order discretization with central finite difference for first derivative

$$\begin{aligned} \nabla _h \omega _i = \frac{-\omega _{i+2} \,+\, 8\,\omega _{i+1} \,-\, 8\,\omega _{i-1} \,+\,\omega _{i-2}}{12\,h} \end{aligned}$$

where h is the space step, and for the second derivative is discretized using a fourth order central finite difference scheme as well

$$\begin{aligned} \nabla _h^2 \omega _i = \frac{-\omega _{i+2} \,+\, 16\,\omega _{i+1} \,-\, 30\,\omega _{i}\,+\, 16\,\omega _{i-1} \,-\,\omega _{i-2}}{12\,h^2}. \end{aligned}$$

For all numerical tests below, linear systems have been solved by a simple iterative C++ solver, that is, a successive over-relaxation (SOR(\(\omega \))) method even if more efficient solvers may be applied. This approach allows a comparison between various semi-implicit schemes, but of course it is not suitable to compare the efficiency of implicit and fully explicit methods. The use of a more efficient solver, such as for example a multigrid, would be desirable, but this goes beyond the scope of the present paper. The runs are performed on 2.8 GHz Intel core i7 machine.

4.1 Test 1: Reaction–Diffusion Problem

We first consider a very simple reaction–diffusion system with nonlinear source for which there are explicit solutions.

To demonstrate the optimal accuracy of the semi-implicit method in various norms, we consider the reaction–diffusion system problem [34] together with periodic boundary conditions: \(\omega =(\omega _1,\omega _2):\mathbb {R}^+\times (0,2\pi )^2\mapsto \mathbb {R}^2\)

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{\partial \omega _1}{\partial t} \,\,=\,\, \Delta \omega _1 \,\,-\,\, \alpha _1(t)\,\omega _1^2 \,\,+\,\,\frac{9}{2}\,\omega _1\,\,+\,\, \omega _2\,\,+\,\, f(t) , \qquad t\ge 0, \quad (x,y)\in (0,2\pi )^2, \\ \, \\ \displaystyle \frac{\partial \omega _2}{\partial t} \,\,=\,\, \Delta \omega _2 \,\,+\,\, \frac{7}{2}\,\omega _2\,, \qquad t\ge 0, \quad (x,y)\in (0,2\pi )^2, \end{array}\right. \end{aligned}$$
(30)

with \(\alpha (t)=2\,e^{t/2}\) and \(f(t)=-2e^{-t/2}\). The initial conditions are extracted from the exact solutions

$$\begin{aligned} \left\{ \begin{array}{l} \omega _1(t,x,y)\,=\,e^{-t/2}\,(1\,+\,\cos (x)), \\ \, \\ \omega _2(t,x, y)\; =\, e^{-t/2}\,\cos (2\,x). \end{array}\right. \end{aligned}$$

To apply our semi-implicit scheme (11)–(13) we rewrite this PDE in the form \((\mathcal {G})\) with \(u=(u_1,u_2)\) the component treated explicitly, \(v=(v_1,v_2)\) the component treated implicitly and

$$\begin{aligned} \mathcal {H}(t,u,v) = \left( \begin{array}{l} \displaystyle \Delta v_1 \,\,-\,\, \alpha (t) \,u_1 \,v_1 \,\,+\,\, \,\frac{9 \,u_1}{2} \,\,+\,\, v_2 \,\,+\,\, f(t) \\ \; \\ \displaystyle \Delta v_2 \,\,+\,\, \frac{7\,v_2}{2} \end{array} \right) . \end{aligned}$$

Since the \(\Delta \) operator induces some stiffness it is treated implicitly whereas reaction terms are treated according to the sign of the reaction term and are linearized in order to avoid the numerical solution of a fully nonlinear problem. Concerning the spatial discretization, we simply apply a fourth order central finite differente method to the \(\Delta \) operator. A fourth order accurate scheme for spatial derivatives is applied in order to bring out the order of accuracy of the second and third order time discretization.

To estimate the order of accuracy of the schemes we compute a numerical approximation and refine the time step \(\Delta t\) according to the space step \(\Delta x=\Delta y\) in such a way the CFL condition associated to the diffusion operator is violated, that is, we apply an hyperbolic CFL condition where we refine the time step and the space step simultaneously

$$\begin{aligned} \lambda \,\,=\,\, \frac{2\Delta t}{\Delta x}, \end{aligned}$$

with \(\lambda =1\).

Obviously, for a fully explicit scheme like the Runge–Kutta method, this condition would lead to some instabilities of the numerical solution since a parabolic CFL is necessary.

The semi-implicit schemes are expected to be stable even for large time step when the parabolic CFL condition is not satisfied.

Furthermore, the PDE system (30) is non autonomous since the source term depends on time, hence the two solutions given by the explicit coefficient \((\hat{b}_i, \hat{c}_i)_{1\le i \le s}\) in (12) and by the implicit coefficient \((b_i,c_i)_{1\le i \le s}\) in (13) are different and we want to explore numerically the two choices.

Absolute error in \(L^\infty \) norms at time \(T = 2\) are shown in Fig. 3 for all the schemes presented in the previous section. As expected the order of accuracy is satisfied for all second and third order schemes. The results obtained with the third order SSP-DIRK3(4,3,3) scheme (27) are much more accurate than the others obtained from second order schemes. Moreover, let us also emphasize that comparing the amplitude of the \(L^\infty \) error norm obtained with the second order schemes, the SSP-LDIRK2(3,3,2) scheme (26) with three stages is much more accurate than the others. Among the second order schemes with two stages the H-CN scheme (25) is the most accurate for this test. However, when we take into account the CPU time (see Fig. 4), most of the second order schemes are equivalent, whereas the third order scheme is clearly advantageous for this test.

Finally, we only observe a slight difference between the two solutions \(y^{n+1}\) from (12) and \(z^{n+1}\) from (13), even if it seems that for this numerical test, the amplitude of the error is smaller when we use the solution given by the implicit stencil (13).

Fig. 3
figure 3

Test 1: reaction–diffusion problem: \(L^\infty \) error norm when the last step is performed using the coefficients obtained from the (a) explicit scheme (12) and (b) and the implicit scheme (13) for the IMEX schemes described in the previous section. a \(y^{n+1}\) in (12). b \(z^{n+1}\) in (13)

Full size image
Fig. 4
figure 4

Test 1: reaction–diffusion problem: \(L^\infty \) error norm with respect to the number of operations obtained from the IMEX schemes described in the previous section

Full size image

4.2 Test 2: Nonlinear Convection–Diffusion Equation

We consider the following nonlinear convection diffusion equation on the whole space \(\mathbb {R}^2\) and apply a fourth order central finite difference scheme for the first and second spatial derivatives

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{\partial \omega }{\partial t} \,+\, \left[ V \,+\,\mu \nabla \log (\omega ) \right] \cdot \nabla \omega \; - \,\mu \,\Delta \omega \,=\, 0\,, \quad (t,x)\in \mathbb {R}^+\times \mathbb {R}^2, \\ \, \\ \displaystyle \omega _0(t=0)\,=\, e^{-\Vert x\Vert ^2/2} , \end{array}\right. \end{aligned}$$

where \(V=\,^t(1,1)\), \(\mu =0.5\) . The exact solution is given by

$$\begin{aligned} \omega (t,x) \,=\, \frac{1}{\sqrt{4\,\mu \, t \,+\, 1}}\, e^{-\frac{\Vert x-V\,t\Vert ^2}{8\,\mu \,t\,+\, 2}}\,,\quad t\ge 0, \quad x\in \mathbb {R}^2. \end{aligned}$$

After the space discretization, we apply our semi-implicit scheme (11)–(13) by writing the system of ODEs in the form \((\mathcal {G})\) with u the component treated explicitly, v the component treated implicitly and

$$\begin{aligned} \mathcal {H}(t,u,v) \,= \,-\left( V \,+\,\mu \nabla \log (u) \right) \cdot \nabla v\; + \,\mu \Delta v. \end{aligned}$$

We treat both the convection and diffusion implicitly (so that we do not have to worry in case the convection term dominates) but we only deal with a linear system at each time step. The computational domain in space is \((-10,10)^2\) and the final time is \(T=0.5\). As in the previous case, the space step is chosen sufficiently small to neglect the influence of the space discretization and the time step \(\Delta t\) is taken proportional to \(\Delta x\) such that \( \Delta t = \lambda \Delta x\), with \(\lambda =1\). Therefore, the classical CFL condition for convection diffusion problem \(\Delta t=O(\Delta x^2)\) is not verified.

In Fig. 5 we present the numerical error for the \(L^\infty \) norm for the semi-implicit schemes described in the previous section and still verify the correct order of accuracy. We also present the error norm with respect to the CPU time. Once more, the third order SSP-DIRK3(4,3,3) scheme (27) with four stages gives much more accurate results than second order schemes with several order of magnitude.

Fig. 5
figure 5

Test 2: nonlinear convection–diffusion problem: (a) \(L^\infty \) error norm for the second order schemes (22), (23), (24), (25) and (26) and the third order SSP-DIRK3(4,3,3) L-stable scheme (27). a \(L^\infty \) error norm with respect to \(\Delta t\). b \(L^\infty \) error norm with respect to the number of operations

Full size image

4.3 Test 3: Nonlinear Fokker–Planck Equations for Fermions and Bosons

In [35, 36], a nonlinear Fokker–Planck type equation modelling the relaxation of fermion and boson gases is studied. This equation has a linear diffusion and a nonlinear convection term:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{\partial \omega }{\partial t}\,\,=\,\,\text {div}\left( x\,(1\,+\,k\,\omega )\,\omega \,\,+\,\,\nabla \omega \right) , \quad x \in \mathbb {R}^{d}, \quad t>0,\\ \\ \, \\ \displaystyle \omega (x,0) = \omega _0(x), \end{array}\right. \end{aligned}$$
(31)

with \(k=1\) in the boson case and \(k=-1\) in the fermion case. For this equation, the explicit solution is not known except steady states, but there are several works devoted to the long time behavior based on the knowledge of the qualitative behavior of the entropy functional. The long time behavior of this model has been rigorously investigated quite recently in [35] via an entropy-dissipation approach. More precisely, the stationary solution of (31) is given by the Fermi-Dirac (\(k=-1)\) and Bose–Einstein (\(k=1\)) distributions:

$$\begin{aligned} \omega ^{eq}(x)=\frac{1}{\beta e^{\frac{|x|^{2}}{2}}-k}, \end{aligned}$$
(32)

where \( \beta \ge 0\) is such that \(\omega ^{eq}\) has the same mass as the initial data \(\omega _{0}\). For this equation, there exists an entropy functional given by

$$\begin{aligned} \mathcal {E}(t):=\int _{\mathbb {R}^{d}}\left( \frac{|x|^{2}}{2}\omega \,+\,\omega \log (\omega )-k(1+k\omega )\log (1+k\omega )\right) \, dx, \end{aligned}$$
(33)

such that

$$\begin{aligned} \frac{d}{dt} \mathcal {E}_\omega (t) \,=\, - \mathcal {I}(t), \end{aligned}$$

where the entropy dissipation \(\mathcal {I}(t)\) is defined by

$$\begin{aligned} \mathcal {I}(t)\,:=\, \int _{\mathbb {R}^{d}}\omega \,(1+k\omega )\left| \nabla \left( \frac{|x|^{2}}{2}+\log \left( \frac{\omega }{1+k\omega }\right) \right) \right| ^{2}\, dx. \end{aligned}$$
(34)

Then decay rates towards equilibrium are given in [35, 36] for fermion case in any dimension and for 1D boson case by relating the entropy and its dissipation. Here we want to investigate the long time behavior of the numerical solution using different semi-implicit solvers with large time step and compare the numerical solution with the one obtained with an explicit method with a small time step [37].

To apply our semi-implicit scheme, we treat the linear diffusion term implicitly, and the non-linear convective term semi-implicitly. We rewrite this PDE in the form \((\mathcal {G})\) with u the component treated explicitly, v the component treated implicitly and

$$\begin{aligned} \mathcal {H}(t,u,v) \,\,=\,\, \text {div}\left( x\,(1\,+\,k\,u)\,v\,+\,\nabla v\right) = \,\, \text {div}\left( x\,(1\,+\,k\,u)\,v \right) \,+\,\Delta v \end{aligned}$$

and we apply a fourth order spatial discretization for the convective and diffusive components.

We consider the nonlinear Fokker–Planck Eq. (31) for fermions (\(k=-1\)) in 2D. The initial condition is chosen as

$$\begin{aligned} \omega _{0}(x)=\frac{1}{2\pi } |x|^2\exp \left( -\frac{|x|^{2}}{2}\right) , \quad x \in \mathbb {R}^2, \end{aligned}$$

and the computational domain is \((-10,10)^2\) with the space step \(\Delta x=0.1\).

Evolution of the discrete relative entropy \( \mathcal {E}(t^{n})=\mathcal {E}_\omega (t^n)-\mathcal {E}_{\omega ^{eq}}\) and its dissipation \( \mathcal {I}(t^{n})\), given in (34), is presented in Fig. 6. This is obtained at the top by second order schemes, i.e. classical second order explicit Runge–Kutta scheme and H-LDIRKp(2,2,2) (24), and at the bottom by third order schemes, i.e. classical third order explicit Runge–Kutta scheme and SSP-DIRK3(4,3,3) (27).

We observe exponential decay rate of these quantities, which is in agreement with the result proved by Carrillo et al. [35] and the numerical results proposed in [37]. Classical Runge–Kutta schemes are subject to a parabolic condition whereas semi-implicit schemes can be used with a large time step without affecting the accuracy even for large time asymptotics.

Fig. 6
figure 6

Test 3: Fokker–Planck equation, (a) evolution of the relative entropy \(\mathcal {E}_\Delta (t^{n})\) and (b) the dissipation \(\mathcal {I}_\Delta (t^{n})\) for the second order explicit Runge–Kutta scheme and for the H-LDIRKp(2,2,2) scheme (24) (top) and for the third order explicit third order Runge–Kutta scheme and SSP-DIRK3(4,3,3) scheme (27) (bottom). a relative entropy functional \(\mathcal {E}(t)\). b entropy dissipation \(\mathcal {I}(t)\)

Full size image

4.4 Test 4: Hele–Shaw Flow

In this section we consider a fourth order nonlinear degenerate diffusion equation in one space dimension called the Hele–Shaw cell [38, 39]

$$\begin{aligned} \frac{\partial \omega }{\partial t} + \frac{\partial }{\partial x} \left( \omega \frac{\partial ^3 \omega }{\partial x^3}\right) \,=\, 0, \quad x\in \mathbb {R},\quad t \ge 0, \end{aligned}$$
(35)

with \(\omega (x, t=0) = \omega _0(x) \ge 0\). This example belongs to the first category of semi-linear equations recalled at the beginning of this section, and only the unknown appearing in the highest derivative is treated implicitly.

One of the remarkable features of Eq. (35) is that its nonlinearity guarantees the nonnegativity preserving property of the solution [40] and the conservation of mass

$$\begin{aligned} \int _{\mathbb {R}} \omega (t,x) dx = \int _{\mathbb {R}} \omega _0(x) dx. \end{aligned}$$

Moreover there is dissipation of surface-tension energy, that is,

$$\begin{aligned} \frac{d}{dt} \int _{\mathbb {R}} \left| \frac{\partial \omega }{\partial x}\right| ^2 dx = -\int _{\mathbb {R}} \omega \,\left| \frac{\partial ^3 \omega }{\partial x^3}\right| ^2 \,dx , \end{aligned}$$

and dissipation of an entropy which highlights similarities with the Boltzmann equation

$$\begin{aligned} \frac{d}{dt} \int _{\mathbb {R}} \omega \,\log (\omega ) dx = -\int _{\mathbb {R}} \left| \frac{\partial ^2 \omega }{\partial x^2}\right| ^2 \,dx. \end{aligned}$$

On the one hand, we compare the numerical results obtained with our numerical approximation with the similarity property of monotonicity in time of solution

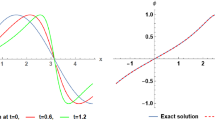
$$\begin{aligned} \omega (t,x) = \frac{1}{120(t+\tau )^{1/5}} \,\left[ r^2 - \frac{x^2}{(t+\tau )^{2/5}}\right] _ +^2, \end{aligned}$$

where \([\cdot ]_+\) denotes the positive part. We have chosen \(r= 2\), \(\tau = 4^{-5}\) and \(x \in (-2,2)\). This solution is only \(\omega \in C^1(\mathbb {R}\times \mathbb {R})\) but the second derivative in space is discontinuons, therefore we cannot expect high order accuracy. Exact and numerical solutions at various times are reported in Fig. 8.

On the other hand, we consider the same problem with a given source term

$$\begin{aligned} f(\tau ,x) =\frac{1}{8\tau ^4}\,\exp \left( -\frac{x^2}{4\tau }\right) \,\left( 2\,x^2\,\tau ^2 + \left( x^4 + 6 \tau ^2 - 9 x^2 \tau \right) \,\exp \left( -\frac{x^2}{4\tau }\right) \right) , \end{aligned}$$

with \(\tau =t+1\) such that the exact solution is smooth and given by \(\omega _{exact}(t,x) = \exp \left( -{x^2}/{4(t+1)}\right) \).

For the time discretization we apply the scheme (27) by writing the system of ODEs in the form \((\mathcal {G})\) with u the component treated explicitly and the v component treated implicitly:

$$\begin{aligned} \mathcal {H}(t,u,v) \,= \,-\frac{\partial }{\partial x}\left( u\frac{\partial ^3 v}{\partial x^3}\right) + f(t+1,x). \end{aligned}$$

Concerning the space discretization, we apply a second order centred finite difference scheme for the space discretization

$$\begin{aligned} \mathcal {H}_\Delta (t,u_i,v_i) \,=\, -\frac{\mathcal {F}_{i+1/2}-\mathcal {F}_{i-1/2}}{\Delta x} + f(t+1,x_i), \end{aligned}$$

with

$$\begin{aligned} \mathcal {F}_{i+1/2} = u_{i+1/2} \frac{v_{i+2} - 3 v_i + 3 v_{i-1} - v_{i-2}}{\Delta x^3}, \end{aligned}$$

with \(u_{i+1/2} = (u_i+u_{i+1})/2\). The time step is chosen as previously such that \(\Delta t\) is proportional to the space step \(\Delta x\). In this way the stability condition associated to an hypothetical fully explicit time discretization for this problem, i.e. \(\Delta t \le C \Delta x^4\), is strongly violated.

The numerical error in \(L^1\) and \(L^\infty \) for both test cases are reported in Fig. 7 at the final time \(t=0.35\). We observe a rate of convergence about 1.6 for both \(L^1\) and \(L^\infty \) norms for the non smooth solution and second order accuracy for the smooth solution.

Fig. 7
figure 7

Test 4: Hele–Shaw flow: a \(L^1\) error norm and b \(L^\infty \) error norm for the SSP-LDIRK2(3,3,2) L-stable scheme (24)

Full size image

Of course for these large time steps, the numerical scheme does not preserve positivity, but only some small spurious oscillations occur for short times and then they are damped after several time iteration thanks to the diffusion process (see Fig. 8).

Fig. 8
figure 8

Test 4: Hele–Shaw flow: time evolution of the numerical solution for the SSP-LDIRK3(4,3,3) L-stable scheme (27) for \(t=0\), 0.01, 0.15 and 0.35

Full size image

4.5 Test 5: Surface Diffusion Flow

In this section, we consider the surface diffusion of graphs [41]

$$\begin{aligned} \frac{\partial \omega }{\partial t} + \text {div}S(\omega ) \,=\, 0, \quad x\in \mathbb {R}^2,\quad t \ge 0, \end{aligned}$$

where the nonlinear differential operator S is given by

$$\begin{aligned} S(\omega ) \,{:=}\, \left( Q(\omega ) \left( I - \frac{\nabla \omega \otimes \nabla \omega }{Q^2(\omega )} \right) \,\nabla N(\omega ) \right) , \end{aligned}$$

where Q is the area element

$$\begin{aligned} Q(\omega ) = \sqrt{1+|\nabla \omega |^2} \end{aligned}$$

and N is the mean curvature of the domain boundary \(\Gamma \)

$$\begin{aligned} N(\omega ) {:=} \left( \frac{\nabla \omega }{Q(\omega )}\right) . \end{aligned}$$
(36)

The surface diffusion equation models the diffusion of mass within the bounding surface of a solid body, where \(V=\Delta _\Gamma N(\omega )\) is the normal velocity of the evolving surface \(\Gamma \),

$$\begin{aligned} V\,\,=\,\,- \frac{1}{Q(u)}\,\frac{\partial u}{\partial t}, \end{aligned}$$

and \(\Delta _\Gamma \) denotes the Laplace–Beltrami operator [41].

There are many applications of these models, such as body shape dynamics, surface construction, computer data processing or image processing. This equation is a highly nonlinear fourth-order PDE. The higher order differential operators and additional nonlinearities for these kind of problems are difficult to analyze and to simulate numerically due to the stiffness of order \(\Delta x^4\), where \(\Delta x\) is the space step [27, 42]. We will apply our stable high order accurate methods based on semi-implicit time discretizations. Moreover, we will compare our time discretization with the one proposed by Smereka [14] or in [15], where the operator S is split in two parts

$$\begin{aligned} S(\omega ) = \underbrace{S(\omega ) - \beta \,\Delta ^2 \omega }_{\text {less stiff part}} \,+\, \underbrace{\beta \,\Delta ^2 \omega ,}_{\text { stiff, dissipative part}} \end{aligned}$$

where \(\beta \) is a free parameter to be determined and in [14] it is chosen as \(\beta =2\). The first part is then treated explicitly whereas the stiff and dissipative part is treated implicitly. This splitting technique is very effective to stabilize numerical schemes but it may affect the numerical accuracy.

With our approach there is no need to add and subtract terms, because the system is automatically stabilized by the proper choice of the variable that will be implicitly treated, i.e. the numerator in the function \(N(\omega )\), Eq. (36).

The solution of the surface diffusion of graphs verifies

$$\begin{aligned} \frac{1}{2} \frac{d}{dt} \int _{\Omega } \omega ^2 dx + \int _{\omega } N^2(\omega ) dx = 0, \end{aligned}$$

giving \(L^2\) stability.

We consider numerical solutions of the two-dimensional surface diffusion of graphs equation with the initial condition

$$\begin{aligned} \omega _0(x) = \frac{1}{2\pi T} \exp \left( -\frac{|x|^2}{2T}\right) . \end{aligned}$$

The computational domain is \((-10, 10)^2\) and we use a second order central finite difference scheme together with the second order H-LDIRKp(2,2,2) scheme (24) with

$$\begin{aligned} \mathcal {H}(u,v) {:=}\left( Q(u) \left( I - \frac{\nabla u\otimes \nabla u}{Q^2(u)} \right) \,\nabla \mathcal {N}(u,v) \right) , \end{aligned}$$

and \(\mathcal {N}\)

$$\begin{aligned} \mathcal {N}(u,v) {:=} \left( \frac{\nabla v}{Q(u)}\right) . \end{aligned}$$

We present in Fig. 9 the time evolution of the \(L^2\) norm of the numerical solution and its dissipation:

$$\begin{aligned} \frac{d}{dt} \mathcal {E}(\omega ) \,=\, - \mathcal {I}(t), \end{aligned}$$

where the functional \(\mathcal {E}(\omega )\) and the dissipation \(\mathcal {I}(t)\) are defined by

$$\begin{aligned} \mathcal {E}(\omega ) = \int _{\Omega } \omega ^2(t,x) dx, \qquad \mathcal {I}(t) = \int _{\Omega } N^2(\omega (t,x)) dx. \end{aligned}$$

The results show that our second order numerical scheme (24) is stable and accurate for large time steps whereas the one based on the splitting technique given in [14] is stable but less accurate for large time step \(\Delta t = 0.1\). These numerical simulations illustrate the efficiency of our approach based on semi-implicit numerical schemes.

Fig. 9
figure 9

Test 5: surface diffusion flow, (a) evolution of the \(L^2\) norm and (b) the dissipation \(\mathcal {I}_\Delta (t^{n})\) for second order H-LDIRKp(2,2,2) L-stable scheme (24) and the one proposed in [14] based on a splitting technique in log scale. a functional \(\mathcal {E}(t)\). b dissipation \(\mathcal {I}(t)\)

Full size image

5 Conclusions

In this paper we show that classical IMEX schemes can be adopted in a much wider context that the one they were originally introduced for. Indeed, in several contexts, the stiffness of the problem is essentially linear, and therefore IMEX schemes can be successfully adopted by treating the linear stiff part implicitly. Note that this approach is not equivalent to a linearization of the problem, and in several cases it is much simpler to apply than linearization. The overall accuracy of the scheme is automatically guaranteed by the standard order conditions for IMEX schemes. Many practical examples showing how to apply IMEX schemes in this new context are presented. We believe that this new approach can be successfully applied in many other contexts well beyond the ones presented in the paper.