A Comparison Between the Interpolated Bounce-Back Scheme and the Immersed Boundary Method to Treat Solid Boundary Conditions for Laminar Flows in the Lattice Boltzmann Framework

Abstract

In this paper, the interpolated bounce-back scheme and the immersed boundary method are compared in order to handle solid boundary conditions in the lattice Boltzmann method. These two approaches are numerically investigated in two test cases: a rigid fixed cylinder invested by an incoming viscous fluid and an oscillating cylinder in a calm viscous fluid. Findings in terms of velocity profiles in several cross sections are shown. Differences and similarities between the two methods are discussed, by emphasizing pros and cons in terms of stability and computational effort of the numerical algorithm.

1 Introduction

In the last decades, the lattice Boltzmann (LB) method [1] arose as an effective tool to simulate fluid flows by recovering the incompressible Navier–Stokes equations with second-order accuracy [2]. The Boltzmann’s equation is solved on a Cartesian square grid which is kept fixed during the overall analysis and it is used to compute the evolution in space and time of a particle distribution function. Many applications have been developed, such as multiphase flow [3], the solution of reaction-diffusion [4] and Poisson equations [5], blood flow in deformable vessels [6] and even fluid-structure interaction [7–12]. Regarding the last application, an accurate description of the immersed solid body is required. Specifically, a proper boundary condition should be able to account for the position of an immersed solid body, to enforce the no-slip condition, to satisfy Newton’s law and to be mass-conservative. Two approaches are possible: the interpolated bounce-back (BB) scheme and the immersed boundary (IB) method.

In the interpolated bounce-back scheme, the basic idea is to compute the particle distribution function in an off-grid position by an interpolation/extrapolation of this function from the on-grid nodes [13]. Such idea is proven to be very effective and to preserve the second-order accuracy of the LB method [14, 15]. On the other hand, such approach is complex to be implemented, especially upon solid motion and whenever complex geometries are considered.

The IB method [16, 17] is a simpler approach for the solid boundary conditions treatment. The solid body is represented by a Lagrangian immersed mesh, generally unstructured, non-stationary and not aligned with the Eulerian fluid grid. The interaction between the two meshes is given by simple interpolation rules. Since the solid mesh is independent from the fluid one, the IB method is easier to be implemented in the lattice Boltzmann framework, regardless of the solid body geometry.

In this paper, the BB scheme and the IB method are compared in two scenarios. In the former, a rigid fixed cylinder is invested by an incoming flow. The velocity profiles in several cross sections computed by the two approaches are compared. In the latter, a rigid cylinder oscillates in a calm fluid. The drag coefficient computed by the two approaches are given, together with a convergence analysis. Considerations about stability and computational efficiency of the numerical algorithms are discussed in both the scenarios.

The paper is organized as follows. In Sect. 2, a brief summary of the LB method is given. In Sects. 3 and 4, the main features of the BB scheme and the IB method are discussed, together with some practical issues. In Sect. 5, the numerical comparisons are carried out. Some conclusions are drawn in Sect. 6. Finally, in Appendix the influence of the number of IB points idealizing the immersed solid body is discussed.

2 The Lattice Boltzmann Method

In this paper, the so called D2Q9 lattice Boltzmann model is considered. For more details the interested reader can refer to [1] and the references therein.

The single-phase two-dimensional lattice equation [18] is solved on a fixed square grid, where the evolution in space $\varvec{x}$ and time $t$ of the particle distribution function $f_i$ is described along prescribed directions with velocities $\mathbf {c}_i$. Such equation reads as follows:

$$\begin{aligned} f_i(\varvec{x} + \mathbf {c}_i\,\Delta t, t+\Delta t) = f_i(\varvec{x},t)+\frac{1}{\tau }[f_i^{eq}(\varvec{x},t)-f_i(\varvec{x},t)], \end{aligned}$$

(1)

being $\tau$ the relaxation parameter and $\Delta t$ the time step. The equilibrium particle distribution function $f_i^{eq}$ is derived in the form of a second-order expansion in the local Mach number, as described in [19]. Once Eq. (1) is solved, the fluid density $\rho$ and the flow velocity $\varvec{v}$ are computed as:

$$\begin{aligned} \rho = \sum _i f_i, \qquad \varvec{v} = \frac{\sum _i f_i \mathbf {c}_i}{\rho }, \end{aligned}$$

(2)

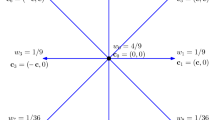
respectively. The pressure field $p$ can be immediately computed by means of the equation of state of an ideal gas, that is $p = \rho \, c_s^2$, where $c_s^2 = \sum _i w_i \mathbf {c}_i^2=1/3$ and $w_i$ is a set of 9 weights defined as $w_0=4/9$, $w_1=w_2=w_3=w_4=1/9$ and $w_5=w_6=w_7=w_8=1/36$ for the present LB model. As usual, for simplicity and computational efficiency, the grid size and the time step are both set equal to 1. This means that, in order to simulate a physical phenomenon, special attention should be paid to the unit conversion from the physical system to the LB one. It is worth to notice that the relaxation parameter $\tau$ is strictly related to the fluid viscosity $\nu$, that is

$$\begin{aligned} \nu = \left( \tau -\frac{1}{2}\right) c_s^2. \end{aligned}$$

(3)

Two schemes to account for the position of a solid body in the grid not aligned with the lattice nodes have been proposed in the literature. First, the so called interpolated bounce-back rule [14, 15] is discussed, which consists of computing the particle distribution function bouncing-back from each solid off-grid node to the surrounding fluid ones through an interpolation of the known on-grid $f_i$. Notice that this boundary condition is strictly related to the Eulerian nature of the LB method, as it will be discussed in the following. Secondly, the immersed boundary method is presented [16, 20]. It consists of the verification of the zero-velocity condition on a mesh, idealizing the immersed solid, by properly modifying the particle distribution functions based only on the boundary position. Differently from the previous one, the immersed boundary condition is characterized by a Lagrangian point of view.

3 Interpolated Bounce-Back

Here, the interpolated bounce-back condition proposed in [14, 17] is considered. Making reference to Fig. 1, the solid boundary is represented by the red curve, the solid and the fluid nodes involved by the bouncing-back scheme are black and blue, respectively, and denoted by $\varvec{x}_b$ and $\varvec{x}_f$. The intersection points of the grid lines (including the diagonals of each cell) with the solid boundary are indicated by red nodes and denoted by $\varvec{x}_w$. The off-grid particle distribution function $\tilde{f}_{\bar{i}}$ which bounces-back from a solid node $\varvec{x}_b$ to a fluid one $\varvec{x}_f$ is obtained by performing a quadratic interpolation of the populations located at the neighbour nodes, that is,

$$\begin{aligned} \tilde{f}_{\bar{i}}(\varvec{x}_f,t)&= \delta (1+2\delta )f_i(\varvec{x}_f+\mathbf {c}_i,t) + (1-4{\delta }^2) f_i(\varvec{x}_f,t)+\nonumber \\&-\delta (1-2\delta )f_i(\varvec{x}_f-\mathbf {c}_i,t) + 3w_i [\mathbf {c}_i \cdot \varvec{v}(\varvec{x}_w,t)] \quad \hbox {if} \quad \delta < 1/2, \end{aligned}$$

(4)

$$\begin{aligned} \tilde{f}_{\bar{i}}(\varvec{x}_f,t)&= \frac{1}{\delta (1+2\delta )}f_i(\varvec{x}_f+\mathbf {c}_i,t) + \frac{2\delta -1}{\delta }f_{\bar{i}}(\varvec{x}_f-\mathbf {c}_i,t)+\nonumber \\&-\frac{2\delta -1}{2\delta +1}f_{\bar{i}}(\varvec{x}_f-2\mathbf {c}_i,t)+ \frac{3 w_i}{\delta (1+2\delta )}[\mathbf {c}_i \cdot \varvec{v}(\varvec{x}_w,t)] \quad \hbox {if} \quad \delta \ge 1/2, \end{aligned}$$

(5)

where $\varvec{x}_w$ is the exact position of a wall node in the lattice background, $\delta$ is the fraction of intersected link $\delta = ||\varvec{x}_f-\varvec{x}_w||/||\varvec{x}_f - \varvec{x}_b||$ and $\varvec{v}(\varvec{x}_w,t)$ is the local velocity of the wall. Notice that the direction $\bar{i}$ is opposite to the direction $i$, i.e. $\mathbf {c}_{\bar{i}} = -\mathbf {c}_i$.

Fig. 1

Interpolated bounce-back scheme

The algorithm used to implement the above condition can be summarized as follows:

• 1. assign initial conditions;

• 2. solve Equation (1) (notice that populations are advected from fluid to solid nodes and vice versa);

• 3. assign the position of the solid body (it typically changes due to fluid-structure interaction);

• 4. detect all the quantities that should be used in the interpolated bounce-back scheme: $\varvec{x}_w, \varvec{x}_f, \varvec{x}_b$;

• 5. overwrite the particle distribution functions advected from solid to fluid nodes by using Eqs. (4) and (5);

• 6. compute the macroscopic variables, advance in time and restart in step 2.

Aiming at using the fluid solver for fluid-structure interaction, a proper procedure is needed to tackle moving boundaries due to structure deformation. In particular, because of the fixed nature of the grid employed for the fluid computation, new fluid nodes can be activated, as a consequence of structure deformation. Thus, the newly-activated nodes must be properly initialized, in terms of particle distribution function: to assign a proper initial value, a very simple refill procedure is often adopted [8, 21]. In particular, a linear interpolation at the surrounding nodes placed externally to the solid is applied. On the other hand, upon structure deformation some nodes may become inactive. In this case, the associated values are typically disregarded [7]. Notice that the outlined refill procedure does not exactly guarantee mass conservation, since it introduces mass in the system each time a new fluid node arises and removes mass from the system each time a node becomes inactive, but no balance is guaranteed between the two.

In addition, for fluid-structure interaction, computing fluid forces on the solid boundary is needed. Such force computation can be performed by a stress-integration procedure [15]. Specifically, first the stress tensor $\varvec{\sigma }$ must be computed at each lattice site, that is

$$\begin{aligned} \varvec{\sigma }= -\rho \,c_s^2 \mathbf {I}- \left( 1-\frac{1}{2\tau }\right) \varvec{\varPi }, \end{aligned}$$

(6)

where $\varvec{\varPi }= \sum _i f_i^{neq} \mathbf {c}_i \otimes \mathbf {c}_i$ is calculated with the non-equilibrium part of the particle distribution function $f_i^{neq} = f_i-f_i^{eq}$ and $\mathbf {I}$ is the unit tensor. Secondly, it must be interpolated/extrapolated at the off-grid positions $\varvec{x}_w$. Finally, it typically should be integrated to get local resultants. As discussed in [15], such stress-integration approach involves high computational effort, due to the large number of algebraic operations needed by the interpolation/extrapolation. Alternatively, the momentum-exchange method [22] could be adopted. However, even if this second procedure is simpler than the stress-integration one and involves a lower computational cost, the drawback to handling a complex geometry, especially upon solid deformation, still persists.

4 The Immersed Boundary Method

Here, the immersed boundary method proposed in [16, 23] is considered. As show in Fig. 2, the solid boundary is represented by a Lagrangian mesh (red line), generally non-stationary and unstructured.

Fig. 2

Immersed boundary method

Therefore, two different coordinate systems are used in this case: an Eulerian grid for the LB equation and a Lagrangian mesh for the immersed boundary, which communicate through interpolation rules satisfying the no-slip condition for velocity and the momentum conservation. The presence of the boundary influences the fluid domain computation indirectly, through a suitable correction of the particle distribution functions, that could be equivalently interpreted by an additional source term in the LB equation. Thus, there is no direct boundary condition for the fluid acting on the populations as in the interpolated bounce-back scheme [15]. This means that the populations could in principle travel through the boundary, but the modified populations should avoid it. Moreover, the fluid fills the entire domain, even inside the boundary region, thus no refill procedure is necessary. Let denote $\varvec{X}_w$ and $\varvec{V}_w$ the position and the velocity, respectively, of the generic Lagrangian boundary node. The fluid velocity $\varvec{v}$ can be interpolated at the boundary node, that is

$$\begin{aligned} \varvec{v}(\varvec{X}_k) = \sum _{\varvec{x}} \varvec{v}(\varvec{x}) W( \varvec{x}-\varvec{X}_w). \end{aligned}$$

(7)

Notice that capital letters indicate Lagrangian variables. The interpolation kernel $W$ is chosen to be short-ranged with a finite cut-off length in order to reduce the computational effort. Moreover, momentum and angular momentum have to be identical when evaluated in either the Eulerian or the Lagrangian frame. For convenience, the kernel is factorized as $W(x_{\varvec{x}}) = w(x_1)\cdot w(x_2)$, being ($x_1$,$x_2$) the Eulerian coordinates, and

$$\begin{aligned} w(x_j) = {\left\{ \begin{array}{ll} \displaystyle 1/8 \left( 3-2|x_j|+\sqrt{1+4|x_j|-4x_j^2}\right) \quad &{} \hbox {for} \quad 0 \le |x_j| \le 1, \\ \displaystyle 1/8 \left( 5-2|x_j|-\sqrt{-7+12|x_j|-4x_j^2}\right) \quad &{} \hbox {for} \quad 1 \le |x_j| \le 2,\\ 0 \quad &{} \hbox {otherwise,} \end{array}\right. } \end{aligned}$$

(8)

with $j=1,2$.

The IB method has been implemented with an implicit velocity-correction scheme [20] in order to satisfy the no-slip condition: $\varvec{v}(\varvec{X}_w) = \varvec{V}_w$. The corresponding term used iteratively to correct the populations is denoted by $\varvec{g}$.

The outlined IB method is implemented based on the following algorithm:

• 1. assign the initial conditions;

• 2. solve Equation (1);

• 3. compute the fluid macroscopic variables ($\rho$ and $\varvec{v}$) and compute the initial value of $\varvec{g}$ at the Lagrangian solid points $\varvec{g}^{(0)}(\varvec{X}_w) = \varvec{V}_w-\varvec{v}(\varvec{X}_w)$;

• 4. perform the following iterative procedure until the no-slip convergence criterion is satisfied:

  • (a) spread $\varvec{g}$ at iteration $l$ over the Eulerian lattice nodes:

    $$\begin{aligned} \displaystyle \varvec{g}^{(l)}(\varvec{x}) = \sum _{\varvec{X}_w} \varvec{g}^{(l)}(\varvec{X}_w) W( \varvec{x}-\varvec{X}_w) \Delta S, \end{aligned}$$

    (9)

    being $\Delta S$ the solid mesh spacing;

  • (b) compute the corrected fluid velocity: $\varvec{v}^{(l+1)}(\varvec{x}) = \varvec{v}^{(l)}(\varvec{x}) + \varvec{g}^{(l)}(\varvec{x})$;

  • (c) interpolate fluid velocity at the solid nodes:

    $$\begin{aligned} \displaystyle \varvec{v}^{(l+1)}(\varvec{X}_w) = \sum _{\varvec{x}} \varvec{v}^{(l+1)}(\varvec{x}) W( \varvec{x}-\varvec{X}_w); \end{aligned}$$

    (10)

  • (d) update the value of $\varvec{g}$: $\varvec{g}^{(l+1)}(\varvec{X}_w) = \varvec{g}^{(l)}(\varvec{X}_w) + \left[ \varvec{V}_w-\varvec{v}^{(l+1)}(\varvec{X}_w)\right]$;

  • (e) iterate until the no-slip convergence criterion is met:

    $$\begin{aligned} \displaystyle \frac{\varvec{V}_w-\varvec{v}^{(l+1)}(\varvec{X}_w)}{\varvec{V}_w} \le 10^{-4}; \end{aligned}$$

    (11)

• 5. update the populations $f_i$ based on the boundary correction term:

  $$\begin{aligned} f_i(\varvec{x} + \mathbf {c}_i\,\Delta t, t+\Delta t) = f_i(\varvec{x} + \Delta t\,\mathbf {c}_i, t+\Delta t) + 3w_i\,\mathbf {c}_i \cdot \varvec{g}(\varvec{x},t); \end{aligned}$$

  (12)

• 6. compute macroscopic variables and advance in time by going to step 2.

The fluid forces $\varvec{F}(\varvec{X}_w)$ acting on an immersed solid node are readly available, since they can be simply computed as

$$\begin{aligned} \varvec{F}(\varvec{X}_w) = -\sum _{\varvec{x}} \varvec{g}(\varvec{x})W( \varvec{x}-\varvec{X}_w). \end{aligned}$$

(13)

It should be remarked that, as already pointed by Peskin [16], the Lagrangian boundary points must be denser than the fluid grid in order to avoid momentum and pressure leaks. The practical restriction suggested in the technical literature is that the solid mesh size should be lesser than half the fluid grid ($\Delta S < 0.5$). A simple test confirming the effectiveness of such rule is reported in Appendix.

5 Results and Discussion

In this section, two tests are carried out. First, a rigid fixed cylinder is invested by a fluid. Secondly, a rigid cylinder harmonically oscillates in a calm fluid.

5.1 Rigid Fixed Cylinder Invested by a Fluid

A cylinder is immersed in a viscous fluid, and at the west section, a constant uniform velocity profile, $V=0.05$, is imposed. At the east section, outflow boundary conditions are used, that is fixed density and $\displaystyle \frac{\partial \varvec{v}}{\partial \mathbf {n}}=0$, being $\mathbf {n}$ the outer normal to the boundary. Free-slip boundary conditions are enforced at bottom and top walls. Referring to Fig. 3, the cylinder radius is $R=10$, the grid is composed of $35R$ and $22R$ lattice sites in the $x$ and $y$ directions, respectively. Moreover, the distance between the inlet section and the center of the cylinder is $11R$. Finally, the cylinder is placed symmetrically with respect to the longitudinal axis of the fluid domain.

Fig. 3

Sketch of the problem definition

The problem is characterized by a Mach number $\mathcal {M}a$ equal to $\mathcal {M}a= V/c_s=0.09$ and 128 immersed boundary points are used to idealize the surface of the cylinder. Simulations involving different values of the Reynolds number $\mathcal {R}e= 2RV / \nu$ are performed by varying the relaxation parameter $\tau$.

The attention is focused on three cross sections. The first one, called Rear, is horizontal, starting from the inlet section and ending to the leftmost point of the cylinder. The second one is called Front, still horizontal, ranging from the rightmost point of the cylinder to the outlet section. The last one, Up, is vertical and spans the region of the fluid domain from the topmost point of the cylinder to the upper bound. In Fig. 4, the horizontal component, $v$, of the fluid velocity is depicted at the three cross sections after 50,000 lattice time steps for different values of the Reynolds number: $\mathcal {R}e=10, 20, 50, 100$ and $200$.

Fig. 4

Velocity profiles in three sections for different values of $\mathcal {R}e$. IB and BB represent the immersed boundary method and the interpolated bounce-back scheme, respectively. (a) Rear at $\mathcal {R}e= 10$. (b) Front at $\mathcal {R}e= 10$. (c) Up at $\mathcal {R}e= 10$. (d) Rear at $\mathcal {R}e= 20$. (e) Front at $\mathcal {R}e= 20$. (f) Up at $\mathcal {R}e= 20$. (g) Rear at $\mathcal {R}e= 50$. (h) Front at $\mathcal {R}e= 50$. (i) Up at $\mathcal {R}e= 50$. (j) Rear at $\mathcal {R}e= 100$. (k) Front at $\mathcal {R}e= 100$. (l) Up at $\mathcal {R}e= 100$. (m) Rear at $\mathcal {R}e= 200$. (n) Front at $\mathcal {R}e= 200$. (o) Up at $\mathcal {R}e= 200$

Regarding the Rear section, a very close agreement between the immersed boundary method and the interpolated bounce-back scheme is experienced for all the values of $\mathcal {R}e$. Similar findings are shown for the Up cross section, even if for the largest value of the Reynolds number, $\mathcal {R}e=200$, a slightly higher peak of $v$ is computed by the interpolated bounce-back scheme. The major differences are experienced in the Front cross section, that is the one interested by vortex shedding phenomena, when $\mathcal {R}e$ grows. In particular, the velocity profile computed by the interpolated bounce-back scheme largely overestimates the negative peak close to the cylinder with respect to the IB method. Moreover, Fig. 5 shows the zoom of the peak zone of the Up section. As it can be immediately realized, the velocity profile predicted by the interpolated bounce-back scheme appears to be upset by higher frequency components, whereas the one given by the IB method is still smooth. This reveals an onset of instability of the computation in the bounce-back scheme.

Fig. 5

Velocity profile in section Up at $\mathcal {R}e=200$: zoom of Fig. 4o. IB and BB represent the immersed boundary method and the interpolated bounce-back scheme, respectively

In order to investigate this phenomenon, a simulation at $\mathcal {R}e=1000$ ($\tau =0.503$) is carried out. Using the interpolated bounce-back scheme, the simulation becomes rapidly unstable, so confirming the stability limitations of this approach as discussed in [24]. On the contrary, the IB method still leads to stable solutions. The velocity profiles after 50,000 lattice time steps and the velocity field at three different time instants are given in Figs. 6 and 7.

Fig. 6

Velocity profiles after 50,000 lattice time steps in three sections at $\mathcal {R}e=1000$ computed by the IB method. a Rear. b Front. c Up

Fig. 7

Velocity field at $\mathcal {R}e=1000$. a 4,000 lattice time steps. b 5,000 lattice time steps. c 8,500 lattice time steps

Thus, for a given grid resolution and Mach number, the IB method reveals a higher stability.

In order to compare the computational effort of the two approaches, Table 1 reports the CPU time needed to perform 50,000 lattice time steps is reported for both the BB and the IB method. As it can be noted, the cost involved by the BB method is about the 26 % lower than the one given by the IB computation. It is worth to remark that in the interpolated bounce-back computation, the larger part of the computation is due to the stress-integration procedure to compute forces along the solid boundary (as discussed in Sect. 3). If this procedure is skipped, the CPU time is even 10 times lower.

Table 1 Normalized CPU time needed to perform 50,000 iterations by using the BB and the IB method

5.2 Oscillating Rigid Cylinder

A circular cylinder oscillating in a calm viscous fluid [25] is considered. The diameter of the cylinder is $D=20$ lattice nodes and its surface is described by 100 immersed boundary points. The lattice dimension is set to $1100 \times 700$. The relaxation parameter is $\tau =0.524$. At the beginning of the simulation, the cylinder is placed in the center of the fluid domain. Everywhere, outflow boundary conditions are enforced, that is $\mathbf {n}\cdot \mathbf {\nabla } f_i=0$. The cylinder oscillates only in the horizontal direction with an imposed velocity $V(t)$

$$\begin{aligned} V(t) = -V_{max}\mathrm {cos}\left( \frac{2\pi t}{T} \right) , \end{aligned}$$

(14)

being $V_{max}=0.04$ and $T=2500$. Notice that these values correspond to a Reynolds number $\mathcal {R}e=V_{max}D/\nu =100$ and to a Keugelan–Carpenter number $\mathcal {K}c=V_{max}T/D=5$. In addition, in order to avoid compressibility effects, simulations are performed at a low Mach number, that is $\mathcal {M}a= V_{max}/c_s=0.007$.

The drag coefficient $C_d$ acting on the cylinder is computed by using the BB scheme and the IB method. It is plotted in Fig. 8, where a very close agreement between the two solutions is experienced. Moreover, it is worth to notice the agreement with the reference solution [25] too.

Fig. 8

Time history of the drag coefficient. IB and BB represent the immersed boundary method and the interpolated bounce-back scheme, respectively. Ref denotes the references values from [25]

A convergence analysis on the peak value of the drag coefficient is plotted in Fig. 9. The reference value is taken from [25].

Fig. 9

Convergence analysis on the peak value of the drag coefficient. IB and BB represent the immersed boundary method and the interpolated bounce-back scheme, respectively

The convergence behavior of the two approaches appears to be very similar. Both of them exhibit a convergence rate approximatively equal to 2. The slight mismatch between the two curves is due to the fact that, for a given grid resolution, the value of the relaxation parameter $\tau$ used in the present simulations is relatively low, thus negatively affecting the interpolated bounce-back procedure. Specifically, if a very coarse grid is used, i.e. $137 \times 87$ lattice nodes corresponding to $\tau =0.503$, the interpolated bounce-back scheme rapidly becomes unstable, as observed in the previous test case.

In order to quantify the computational cost, the CPU time involved by the two methods are compared in Table 2, where the grid dimensions are $1100 \times 700$. In this case, CPU times are very different if compared to the previous test case. In particular, the computation implementing the BB rule involves a CPU time that is about 17 times larger than the one needed by the IB computation. This difference is mainly due to the fact that for a fixed obstacle the identification of $\varvec{x}_w$, $\varvec{x}_b$ and $\varvec{x}_f$ can be performed just once at the beginning of the simulation. Upon solid motion, such quantities move with the cylinder, thus they should be identified at each time step before using Eqs. (4) and (5). Similarly, the stress-integration procedure is affected by a higher computational effort too, since Eq. (6) and the interpolation/extrapolation operation involve much more lattice nodes. In this case, even if the stress-integration procedure is avoided the cost of the BB procedure is still 70 % higher. However, notice that force computation can not be skipped in fluid-structure interaction problems.

Table 2 CPU time (s) needed to get a time $t/T=6$ by using the bounce-back rule (BB) and the IB method

6 Conclusions

In this paper, two strategies to handle the position of a solid body immersed in the lattice background have been compared. First, the interpolated bounce-back scheme has been discussed. It is characterized by an Eulerian nature, strictly related to the lattice framework. Even if this methodology is second-order accurate, it is affected by several drawbacks. In particular, handling a general geometry is an hard task. Moreover, upon solid motion/deformation, some nodes are activated/deactivated and, as a consequence, a refill procedure should be devised. Computing the fluid forces acting on the body involves a huge computational effort, especially if the stress-integration procedure is adopted. On the other hand, the immersed boundary method implemented in an implicit velocity-correction based version, with its characteristic Lagrangian point of view, offers a valid alternative to the previous scheme. The presence of a solid body with a complex shape is irrelevant, since the only required information is a set of coordinates describing the immersed solid. The numerical tests confirm that the IB method is more stable than the BB scheme, while exhibiting a comparable overall accuracy. Considerations about the computational effort have been carried out in terms of involved CPU time. In particular, if a fixed body is considered, the interpolated bounce-back rule is computationally cheaper than the immersed boundary method. The scenario is drastically different for moving boundaries and fluid-structure interaction problems. In these cases, the computational cost involved by the IB procedure is remarkably lower.

Appendix

In order to prevent momentum and pressure leakages, the immersed body should be represented by a sufficiently large [16, 26] number of Lagrangian IB points. Therefore, we performed and report here a preliminary analysis on the effect of the number of IB points for the test case of Sect. 5.1 (flow over a rigid cylinder). The drag coefficient $C_d$ experienced by the cylinder at $\mathcal {R}e=10$ is computed with $350 \times 220$ lattice points by progressively refining the number of Lagrangian IB points representing the cylinder surface, thus reducing the solid mesh spacing $\Delta S$. The drag coefficient is computed as

$$\begin{aligned} C_d = \frac{F_x}{\bar{\rho }V^2R}, \end{aligned}$$

(15)

where $F_x$ is the horizontal component of the total force acting upon the cylinder and $\bar{\rho }$ is the average density. The force is computed according to Eq. 13 over all the $\varvec{X}_w$ idealizing the cylinder. The relative error $\varepsilon$ is defined as

$$\begin{aligned} \varepsilon = \frac{C_d^{\mathrm {c}}-C_d^{\mathrm {r}}}{C_d^{\mathrm {r}}}, \end{aligned}$$

(16)

where $C_d^{\mathrm {c}}$ is the drag coefficient computed for a given number of IB points and the reference value $C_d^{\mathrm {r}}$ is computed for a very fine solid mesh consisting of 1024 IB points, which corresponds to a mesh size $\Delta S=0.06$. In Fig. 10, the relative error is plotted against the solid mesh spacing $\Delta S$. It is possible to observe that the error practically vanishes for $\Delta S \le 0.5$, which is therefore the value used in the numerical analyzes reported in the present paper. Specifically, a further refining over such value corresponds to a plateau of the curve. Finally, it is worth to notice that the relative error assumes negative values, since $C_d^{\mathrm {c}} < C_d^{\mathrm {r}}$. Such behavior has to be addressed to the fact that the lower the number of IB points, the more permeable the cylinder surface is, thus the resultant drag coefficient reduces as well.

Fig. 10

Relative error in the computation of $C_d$ at $\mathcal {R}e=10$ for different values of the solid mesh spacing $\Delta S$ (red curve). The blue line represents $\varepsilon =0$ (Color figure online)