A Family of Finite Volume Schemes of Arbitrary Order on Rectangular Meshes

Abstract

In this paper, we analyze vertex-centered finite volume method (FVM) of any order for elliptic equations on rectangular meshes. The novelty is a unified proof of the inf-sup condition, based on which, we show that the FVM approximation converges to the exact solution with the optimal rate in the energy norm. Furthermore, we discuss superconvergence property of the FVM solution. With the help of this superconvergence result, we find that the FVM solution also converges to the exact solution with the optimal rate in the $L^2$-norm. Finally, we validate our theory with numerical experiments.

1 Introduction

During the past several decades, the finite volume method (FVM) has attracted much attention. We refer to [2, 3, 5, 6, 11, 15, 17, 18, 25, 31, 35, 39] for an incomplete list of references. Due to its local conservation of numerical fluxes and other advantages, the FVM is very popular in scientific and engineering computations, especially in computational fluid dynamics, see, e.g., [18, 25, 26] and [31–35]

Comparing to its wide applications, the mathematical theory of FVM (cf., [4, 22, 27, 28]) has not been fully developed, at least, not as satisfactory as that for the finite element method (FEM). Most works concentrate on lower-order FV schemes. In fact, a linear FV scheme can be regarded as a small perturbation of its corresponding linear FE scheme, whose convergence properties have been well studied, see e.g., [3, 7, 19, 23]. On the other hand, higher-order FV schemes depends heavily on the underlying meshes, the error analysis in the literature was often done case-by-case. Since high-order FV schemes are substantially different from their corresponding FE schemes, therefore only a few special high-order schemes have been studied, see [8, 10, 11, 29, 34, 36, 39]. So far, we have not seen analysis for FV schemes of an arbitrary order.

In this paper, we provide a unified analysis for vertex-centered FV schemes of any order on rectangular meshes. We construct our FV schemes under the framework of the Petrov–Galerkin method by letting the trial space be the Lagrange finite element space with the interpolation points being the Lobatto points and by constructing control volumes with the Gauss points in a rectangular element. Note that this idea of control volumes construction was used on constructing quadratic FV schemes on rectangular meshes, see e.g., [30].

Stability analysis is a challenging task in error estimates for higher order FV schemes. To accomplish this task, most earlier works (see, e.g., [11, 28, 29, 39]) utilized element stiffness matrix analysis, which often requires to calculate all eigenvalues of an element stiffness matrix. This local result is stronger than a global one, but is difficult to be generalized to schemes of any order. Our new approach to prove stability is to establish a global inf-sup condition, which is weaker than element-wise stability, however is sufficient for optimal and superconvergent error estimates. Towards this end, a novel and non-traditional global mapping from the trial space to the test space is introduced. This special mapping avoids calculating eigenvalues of an element stiffness matrix and makes the establishment of the global inf-sup condition for any order possible. Once the inf-sup property has been established, the error analysis in the energy norm is then a routine work.

Another work of the paper is the superconvergence analysis. We prove that the FV solution $u_{\mathcal{P }}$ is super-close to the Lobatto interpolant $u_I$ of the exact solution, namely, $|u_{\mathcal{P }} - u_I|_1$ converges one order higher than the optimal rate. The result simulates the counterpart result in the FEM. A by-product of this superconvergence result is the optimal $L^2$ error estimate. Conventionally, the $L^2$ error estimate is accomplished by the duality argument or the so-called Aubin–Nitsche trick. Unfortunately, this technique is very difficult to be used in our case for higher-order FVM. The adoption of the superconvergence analysis avoids this difficulty.

We organize the rest of the paper as follows. In Sect. 2 we present FV schemes of any order for elliptic equations on rectangular meshes. In Sect. 3 we provide convergence analysis and establish the optimal convergence rate in both $H^1$ and $L^2$ norms. The superconvergence property of the FVM solution has also been studied in this section. Next, numerical examples are provided in Sect. 4 to confirm our theory. And lastly, some concluding remarks are given in Sect. 5.

In the rest of this paper, “$A\lesssim B$” means that $A$ can be bounded by $B$ multiplied by a constant which is independent of the parameters which $A$ and $B$ may depend on. “$A\sim B$” means “$A\lesssim B$” and “$B\lesssim A$”.

2 FVM Schemes of Any Order

In this section, we present finite volume schemes of any order to solve the following second-order elliptic boundary value problem

$$\begin{aligned} -{\bigtriangledown }\cdot (\alpha {\bigtriangledown }u)&= f \quad \mathrm{in}\;\Omega ,\end{aligned}$$

(2.1)

$$\begin{aligned} u&= 0 \quad \mathrm{on}\; \Gamma , \end{aligned}$$

(2.2)

where $\Omega =[a,b]\times [c,d]$ is a rectangle, $\Gamma =\partial \Omega ,\,\alpha \in L^\infty$ and it is bounded from below: There exists a constant $\alpha _0>0$ such that $\alpha (x)\ge \alpha _0$ for almost all $x\in \Omega$, and $f$ is a real-valued function defined on $\Omega$.

We present our finite volume schemes under the framework of Petrov–Galerkin method. We first construct the primal partition and the trial space. Let $\mathcal{P }$ be a partition of $\Omega$ which consists a finite number of rectangles. We denote by $\mathcal{N }$ and $\mathcal{E }$, respectively the set of all vertices and all edges of $\mathcal{P }$. Moreover, let $\mathcal{N }^\circ =\mathcal{N }\setminus \partial \Omega ,\,\mathcal{E }^\circ =\mathcal{E }\setminus \partial \Omega$ be the set of interior vertices and internal edges of $\mathcal{P }$, respectively.

We choose the trial space as the standard FEM space defined by

$$\begin{aligned} \mathcal{U }^r_\mathcal{P }=\{v\in C(\Omega ): v|_{\tau }\in \mathbb{Q }_r, \forall \tau \in \mathcal{P }, v|_{\partial \Omega }=0\}, \end{aligned}$$

where $\mathbb{Q }_r$ is the set of all bi-polynomials of degree no more than $r$.

We next describe the dual partition and the test space. We begin with a description of Gauss and Lobatto points in a rectangle $\tau \in \mathcal{P }$. Let ${\hat{\tau }}=[-1,1]^2$ be the reference element. For all $\tau =\square P_1P_2P_3P_4\in \mathcal{P }$ , where $P_i, i=1,\ldots , 4$ are four vertices of $\tau$, let $F_\tau :{\hat{\tau }}\rightarrow \tau$ be the affine mapping satisfying $F_\tau (-1,-1)=P_1, F_\tau (1,-1)=P_2, F_\tau (1,1)=P_3, F_\tau (-1,1)=P_4$. Note that if we denote by $(x_i,y_i), i=1,\ldots ,4$ the coordinates of $P_i,i=1,\ldots , 4$, then the $F_\tau$ maps a point $(\xi ,\eta )\in {\hat{\tau }}$ to a point $(x,y)\in \tau$ which satisfies

$$\begin{aligned} x = x_1 + \alpha _2^\tau (1+\xi ), y = y_1 + \beta _4^\tau (1+\eta ), \end{aligned}$$

where $\alpha _2^\tau =\frac{x_2-x_1}{2},\ \beta _4^\tau =\frac{y_4-y_1}{2}.$ For a positive integer $k$, let $\mathbb{Z }_k=\{1,\ldots ,k\}$ and $\mathbb{Z }_k^0=\{0,1,\ldots ,k\}$. Let $G_i, i\in \mathbb{Z }_r$ be $r$ Gauss points, i.e., zeros of the Legendre polynomial of $r$th degree, on the interval $[-1,1]$. Let

$$\begin{aligned} g^\tau _{i,j}=F_\tau (G_i,G_j), i,j\in \mathbb{Z }_r, \end{aligned}$$

be all Gauss points in $\tau$. We denote by $\mathcal{G }_\tau =\{g^\tau _{i,j}| i,j\in \mathbb{Z }_r \}$ and $\mathcal{G }=\cup _{\tau \in \mathcal{P }}\mathcal{G }_\tau$ the set of Gauss points in $\tau$ and that in the whole partition, respectively. Let $\{L_m|m\in \mathbb{Z }^0_r\}$ be $r+1$ Lobatto points of degree $r$ in the interval $[-1,1]$, that is, $L_0=-1, L_r=1$ and $\{L_m|m\in \mathbb{Z }_{r-1}\}$ are the $r-1$ zeros of the derivative of the Legendre polynomial of degree $r$ in $[-1,1]$. We denote the set of Lobatto points in $\tau$ as

$$\begin{aligned} \mathcal{N }_\tau =\{l^\tau _{i,j}\big |i,j\in \mathbb{Z }^0_r\}, \end{aligned}$$

where $l^\tau _{i,j}=F_\tau (L_i,L_j)$. Let $\mathcal{N }_L=\cup _{\tau \in \mathcal{P }}\mathcal{N }_\tau$ be the set of all Lobatto points. In Fig. 1, we plot all Gauss and Lobatto points in a rectangular element for a simple case where $r=2$. In this figure, Gauss points are depicted with ‘$\circ$’ while Lobatto points are depicted with ‘$*$’.

Fig. 1

Gauss (‘open circle’) and Lobatto (‘star’) points in a rectangular element ($r~=~2$)

We are ready to present control volumes in the dual partition. Each control volume is a rectangle surrounding a Lobatto point $P\in \mathcal{N }_L$ designed as follows. Let $\tau \in \mathcal{P }$ be a rectangle which contain the Lobatto point $P$. Then $P$ can be represented as $P=l^\tau _{i,j}$ for some $i,j\in \mathbb{Z }_r^0$. The contribution from $\tau$ to the control volume $V_P$ is the rectangle

$$\begin{aligned} V_{\tau ,P}= \Box g_{i,j}^\tau g_{i+1,j}^\tau g_{i+1,j+1}^\tau g_{i,j+1}^\tau , \end{aligned}$$

where the definition of Gauss point $g^\tau _{i,j}$ has been generalized to all indices $i,j\in \mathbb{Z }^0_{r+1}$ by letting $g^\tau _{i,j}=F_\tau (G_i,G_j)$ with $G_0=-1,G_{r+1}=1$, see Fig. 2 for a simple case where $r=2$. Note that in this simple case, the generalized Gauss points $g_{0,0}^\tau =l_{0,0}^\tau , g_{3,0}^\tau =l_{2,0}^\tau , g_{3,3}^\tau =l_{2,2}^\tau , g_{0,2}^\tau =l_{0,2}^\tau$.

Fig. 2

Contribution to control volumes from an element $\tau$ ($r~=~2$)

The whole control volume surrounding $P$ is then defined as

$$\begin{aligned} V_P=\bigcup _{\tau \ni P} V_{\tau ,P}. \end{aligned}$$

For the simple case $r=2$, whole control volumes surrounding Lobatto points in a rectangular element are plotted in Fig. 2. In this figure, each control volume is a rectangle surrounded by dash lines.

The dual mesh $\mathcal{P }^{\prime }$ consists of all control volumes $V_P,P\in \mathcal{N }_L$. That is,

$$\begin{aligned} \mathcal{P }^{\prime }=\{V_P\big |P\in \mathcal{N }_L\}. \end{aligned}$$

The test space $\mathcal{V }_{\mathcal{P }^{\prime }}$ consists of the piecewise constants with respect to the partition ${\mathcal{P }^{\prime }}$ which vanishes on the boundary control volumes. Precisely, the test space

$$\begin{aligned} \mathcal{V }_{\mathcal{P }^{\prime }}=\mathrm{Span } \{\psi _{V_P}\big |P\in \mathcal{N }_L^\circ \}, \end{aligned}$$

where $\mathcal{N }_L^\circ =\mathcal{N }_L\setminus \partial \Omega$ is the set of all interior Lobatto points and $\psi _{A}$ is the characteristic function of some set $A\subset \Omega$. From the above construction, we have

$$\begin{aligned} \dim \mathcal{U }_\mathcal{P }^r=\dim \mathcal{V }_{\mathcal{P }^{\prime }}=\#\mathcal{N }_L^\circ , \end{aligned}$$

where $\#S$ is the cardinality of some set $S$.

We are now ready to present our finite volume schemes. The finite volume solution of (2.1) and (2.2) is a function $u_\mathcal{P }\in \mathcal{U }^r_\mathcal{P }$ which satisfies the following conservation law

$$\begin{aligned} -\int \limits _{\partial V_P} \alpha \frac{\partial u_\mathcal{P }}{\partial \mathbf{n}}ds =\int \limits _{V_P}fdxdy \end{aligned}$$

(2.3)

on each control volume $V_P, P\in \mathcal{N }_L^\circ$, where $\mathbf{n}$ is the unit outward normal on the boundary $\partial V_P$. Let $w_{\mathcal{P }^{\prime }}\in \mathcal{V }_{\mathcal{P }^{\prime }},\,w_{\mathcal{P }^{\prime }}$ can be written as

$$\begin{aligned} w_{\mathcal{P }^{\prime }}=\sum _{P\in \mathcal{N }_L^\circ } w_{P}\psi _{V_P} \end{aligned}$$

where the coefficients $w_{P}, P\in \mathcal{N }_L^\circ$ are constants. Multiplying (2.3) with $w_{P}$ and then summing up for all $P\in \mathcal{N }_L^\circ$, we obtain

$$\begin{aligned} -\sum _{P\in \mathcal{N }_L^\circ } w_{P}\int \limits _{\partial V_P}\alpha \frac{\partial u_\mathcal{P }}{\partial \mathbf{n}}ds=\int \limits _{\Omega }f w_{\mathcal{P }^{\prime }}dxdy. \end{aligned}$$

Defining the FVM bilinear form for all $v\in H^1_0(\Omega ), w_{\mathcal{P }^{\prime }}\in V_{\mathcal{P }^{\prime }}$ as

$$\begin{aligned} a_\mathcal{P }(v,w_{\mathcal{P }^{\prime }})= -\sum _{P\in \mathcal{N }_L^\circ } w_{P}\int \limits _{\partial V_P}\alpha \frac{\partial v}{\partial \mathbf{n}}ds, \end{aligned}$$

(2.4)

the finite volume method for solving Eqs. (2.1) and (2.2) reads as: Find $u_\mathcal{P }\in \mathcal{U }^r_\mathcal{P }$ such that

$$\begin{aligned} a_\mathcal{P }(u_\mathcal{P },w_{\mathcal{P }^{\prime }}) =(f,w_{\mathcal{P }^{\prime }}), \forall w_{\mathcal{P }^{\prime }}\in \mathcal{V }_{\mathcal{P }^{\prime }}. \end{aligned}$$

(2.5)

3 Error Analysis

The error analysis of FVM can also be done under the framework of Petrov–Galerkin methods, see [3, 28], and [39]. Following this approach, our FVMs error analysis requires the study of the continuity (boundedness) and inf-sup property of the FVM bilinear form.

3.1 Continuity

Let $\mathcal{E }_{\mathcal{P }^{\prime }}$ be the set of interior edges of the dual partition ${\mathcal{P }^{\prime }}$. A simple calculation yields that for all $v\in \ H_0^1(\Omega ),\ w_{\mathcal{P }^{\prime }}\in \ V_{\mathcal{P }^{\prime }}$,

$$\begin{aligned} a_\mathcal{P }(v,w_{\mathcal{P }^{\prime }})= \sum _{E\in \mathcal{E }_{\mathcal{P }^{\prime }}}[w_{\mathcal{P }^{\prime }}]_E\int \limits _E \alpha \frac{\partial v}{\partial \mathbf{n}}ds, \end{aligned}$$

(3.1)

where $[w_{\mathcal{P }^{\prime }}]_E = w_{\mathcal{P }^{\prime }}|_{\tau _2} - w_{\mathcal{P }^{\prime }}|_{\tau _1}$ across the common edge $E=\tau _1\cap \tau _2$ of two rectangles $\tau _1, \tau _2 \in \mathcal{P }^{\prime }$ and $\mathbf{n}$ denotes the normal vector on $E$ pointing from $\tau _1$ to $\tau _2$.

To study the continuity of $a_\mathcal{P }(\cdot ,\cdot )$ , we define a semi-norm in the test space $V_{\mathcal{P }^{\prime }}$ for all $w_{\mathcal{P }^{\prime }}\in V_{\mathcal{P }^{\prime }}$ by

$$\begin{aligned} \big |w_{\mathcal{P }^{\prime }}\big |_{\mathcal{P }^{\prime }} =\left( \sum _{E\in \mathcal{E }_{{P}^{\prime }}} h_E^{-1}\int \limits _E \left[ w_{\mathcal{P }^{\prime }}\right] _E^2ds\right) ^{\frac{1}{2}}, \end{aligned}$$

where $h_E$ is the diameter of an edge $E$, and a semi-norm in the so-called broken $H^2$ space

$$\begin{aligned} H_\mathcal{P }^{2}(\Omega )=\{v\in C(\Omega ): v|_{\tau }\in H^2, \forall \tau \in \mathcal{P }\} \end{aligned}$$

for all $v\in H^2_\mathcal{P }(\Omega )$ by

$$\begin{aligned} \big |v\big |_\mathcal{P }=\left( \sum _{\tau \in {\mathcal{P }}}|v|_{1,\tau }^2+h_\tau ^2|v|_{2,\tau }^2\right) ^{\frac{1}{2}}, \end{aligned}$$

where $h_\tau$ is the diameter of $\tau$. Note that the mesh-dependent semi-norm $\big |\cdot \big |_\mathcal{P }$ has been used in the discontinuous Galerkin method (cf., [1]) and was introduced first into the FVM in [39].

Theorem 3.1

The finite volume bilinear form $a_\mathcal{P }(\cdot ,\cdot )$ is variationally exact: let $u\in H_0^1(\Omega )$ be the solution of (2.1) and (2.2), then

$$\begin{aligned} a_\mathcal{P }(u,w_{\mathcal{P }^{\prime }}) =(f,w_{\mathcal{P }^{\prime }}) \forall \ w_{\mathcal{P }^{\prime }}\in \ V_{\mathcal{P }^{\prime }}, \end{aligned}$$

(3.2)

and continuous: for all $v\in \ H_0^1(\Omega )\cap H_\mathcal{P }^{2}(\Omega ),\ w_{\mathcal{P }^{\prime }}\in \ V_{\mathcal{P }^{\prime }}$,

$$\begin{aligned} |a_\mathcal{P }(v,w_{\mathcal{P }^{\prime }})|\le M |v|_\mathcal{P } |w_{\mathcal{P }^{\prime }}|_{\mathcal{P }^{\prime }}, \end{aligned}$$

(3.3)

where the constant $M>0$ depends only on $\alpha$ and $r$.

Proof

First, (3.2) follows by multiplying (2.1) with an arbitrary function $w_{\mathcal{P }^{\prime }}\in V_{\mathcal{P }^{\prime }}$ and then using Green’s formula in each control volume $\tau \in \mathcal{P }^{\prime }$.

Secondly we prove (3.3). By the Cauchy–Schwartz inequality, for all $v\in \ H_0^1(\Omega )$ and all $w_{\mathcal{P }^{\prime }}\in \mathcal{V }_{\mathcal{P }^{\prime }}$, there holds

$$\begin{aligned} a_\mathcal{P }(v,w_{\mathcal{P }^{\prime }}) \le \Vert \alpha \Vert _\infty |w_{\mathcal{P }^{\prime }}|_{\mathcal{P }^{\prime }} \left( \sum _{E\in \mathcal{E }_{\mathcal{P }^{\prime }}} h_E\int \limits _E \left( \frac{\partial v}{\partial \mathbf{n}}\right) ^2ds\right) ^{\frac{1}{2}}. \end{aligned}$$

By the trace inequality and the shape regularity of $\mathcal{P },$

$$\begin{aligned} \left( h_E\int \limits _{E\cap \tau } \left( \frac{\partial v}{\partial \mathbf{n}}\right) ^2ds\right) ^{\frac{1}{2}}\lesssim |v|_{1,\tau }+ h_\tau |v|_{2,\tau } \end{aligned}$$

where $\tau \in \mathcal{P }$ and $\tau \cap E\not =\emptyset$. Since for any given $E\in \mathcal{E }_\mathcal{P ^{\prime }}$, there are at most two elements $\tau \in \mathcal{P }$ such that $\tau \cap E\not =\emptyset$, we have

$$\begin{aligned} a_\mathcal{P }(v,w_{\mathcal{P }^{\prime }})&\lesssim |w_{\mathcal{P }^{\prime }}|_{\mathcal{P }^{\prime }} \left( \sum _{E\in \mathcal{E }_{\mathcal{P }^{\prime }}}\sum _{\tau \in \mathcal{P },\tau \cap E\not =\emptyset } |v|^2_{1,\tau }+ h_\tau ^2|v|^2_{2,\tau }\right) ^{\frac{1}{2}}\\&\lesssim |w_{\mathcal{P }^{\prime }}|_{\mathcal{P }^{\prime }} \left( \sum _{\tau \in \mathcal{P }} |v|^2_{1,\tau }+ h_\tau ^2|v|^2_{2,\tau }\right) ^{\frac{1}{2}}. \end{aligned}$$

Then there exists a positive $M$ which depends only on $\alpha$ and $r$ such that (3.3) holds. $\square$

3.2 Inf-sup Condition

This subsection is the core of the paper. The analysis here is technical, and yet, it is new and no-traditional. A key step is the introduction of a global projection (3.6) based on the idea of the Gauss quadrature.

We begin with some definitions and notations. We denote by $A_j, j\in \mathbb{Z }_r$ the weights of the Gauss quadrature

$$\begin{aligned} Q_r(F)=\sum _{j=1}^r A_j F(G_j) \end{aligned}$$

for computing the integral

$$\begin{aligned} I(F)=\int \limits _{-1}^1 F(x) dx. \end{aligned}$$

It is well-known that $Q_r(F)=I(F)$ for all $F\in \mathbb{P }_{2r-1}(-1,1)$. For any given $\tau \in \mathcal{P }$, we denote by $h^x_\tau , h^y_\tau$ the length of $x$- and $y$-directional edges of the rectangle $\tau$. We define

$$\begin{aligned} A^\tau _{x,j}=\frac{1}{2}h^x_\tau A_j,\quad A^\tau _{y,j}=\frac{1}{2}h^y_\tau A_j,\ j\in \mathbb{Z }_r \end{aligned}$$

as the Gauss weights of $x$- and $y$-directions in $\tau$, respectively.

For a test function $w_{\mathcal{P }^{\prime }}=\sum \nolimits _{P\in \mathcal{N }_L^\circ } w_{P}\psi _{V_P}\in \mathcal{V }_{\mathcal{P }^{\prime }}$, we define its jump at each Gauss point $g^\tau _{i,j}$ as

$$\begin{aligned} \lfloor w \rfloor _{g^\tau _{i,j}}=w_{\mathcal{P }^{\prime }}(l^\tau _{i,j}) +w_{\mathcal{P }^{\prime }}(l^\tau _{i-1,j-1})-w_{\mathcal{P }^{\prime }} (l^\tau _{i-1,j})-w_{\mathcal{P }^{\prime }}(l^\tau _{i,j-1}), \quad \forall i,j\in \mathbb{Z }_r. \end{aligned}$$

The jump at Gauss points is related to the conventional jump across dual edges in $\mathcal{E }_{\mathcal{P }^{\prime }}$. In fact, since

$$\begin{aligned} \mathcal{E }_{\mathcal{P }^{\prime }}\cap \tau =\{E^{\tau ,y}_{i,j} \big |i\in \mathbb{Z }_r, j\in \mathbb{Z }^0_r\}\cup \{E^{\tau ,x}_{i,j}\big |i\in \mathbb{Z }^0_r, j\in \mathbb{Z }_r\}, \end{aligned}$$

where the segments $E^{\tau ,y}_{i,j}=\overline{g^\tau _{i,j}g^\tau _{i,j+1}}, E^{\tau ,x}_{i,j}=\overline{g^\tau _{i,j}g^\tau _{i+1,j}}$, see Fig. 2. Since

$$\begin{aligned} \left[ w_{\mathcal{P }^{\prime }}\right] _{E^{\tau ,y}_{i,j}}=w_{\mathcal{P }^{\prime }}(l^\tau _{i,j})-w_{\mathcal{P }^{\prime }}(l^\tau _{i-1,j}), \left[ w_{\mathcal{P }^{\prime }}\right] _{E^{\tau ,x}_{i,j}}=w_{\mathcal{P }^{\prime }}(l^\tau _{i,j})-w_{\mathcal{P }^{\prime }}(l^\tau _{i,j-1}), \end{aligned}$$

we have

$$\begin{aligned} \lfloor w \rfloor _{g^\tau _{i,j}}=[w_{\mathcal{P }^{\prime }}]_ {E^{\tau ,y}_{i,j}}-[w_{\mathcal{P }^{\prime }}]_{E^{\tau ,y}_{i,j-1}} =[w_{\mathcal{P }^{\prime }}]_{E^{\tau ,x}_{i,j}} -[w_{\mathcal{P }^{\prime }}]_{E^{\tau ,x}_{i-1,j}}, \quad \forall i,j\in \mathbb{Z }_r. \end{aligned}$$

(3.4)

We next define a subset of $\mathcal{G }$ whose cardinality equals to the dimension of the test space. Note that the boundary $\partial \Omega =E_a\cup E_b\cup E_c\cup E_d$ where

$$\begin{aligned} E_a=\{(a,y)|c\le y\le d\}, \quad E_b=\{(b,y)|c\le y\le d\}, \end{aligned}$$

and

$$\begin{aligned} E_c=\{(x,c)|a\le x\le b\}, \quad E_d=\{(x,d)|a\le x\le b\}. \end{aligned}$$

Moreover, for $i=a,b,c,d$, let

$$\begin{aligned} \mathcal{P }_i= \{\tau \in {\mathcal{P }}|\tau \cap E_i\not =\emptyset \} \end{aligned}$$

be the subset of boundary elements which are closed to the boundary $E_i$. We define

$$\begin{aligned} \mathcal{G }_a=\{g^\tau _{1,j}|\tau \in \mathcal{P }_a, j\in \mathbb{Z }_r\}, \quad \mathcal{G }_b=\{g^\tau _{r,j}|\tau \in \mathcal{P }_b, j\in \mathbb{Z }_r\} \end{aligned}$$

and

$$\begin{aligned} \mathcal{G }_c=\{g^\tau _{1,i}|\tau \in \mathcal{P }_c, i\in \mathbb{Z }_r\}, \quad \mathcal{G }_d=\{g^\tau _{i,r}|\tau \in \mathcal{P }_d, i\in \mathbb{Z }_r\} \end{aligned}$$

the four subsets of $G$ which consists of Gauss points closing to $E_a,E_b,E_c,E_d$, respectively. We define the subset

$$\begin{aligned} \mathcal{G }^{\circ \circ }=\mathcal{G }\setminus (\mathcal{G }_b\cup \mathcal{G }_d). \end{aligned}$$

We plot Gauss points in $\mathcal{G }^{\circ \circ }$ and $\mathcal{G }\setminus \mathcal{G }^{\circ \circ }$ in Fig. 3 ($r=2$). In this figure, Gauss points in $\mathcal{G }^{\circ \circ }$ are depicted by ‘$\circ$’ and Gauss points corresponding in $\mathcal{G }\setminus \mathcal{G }^{\circ \circ }$ are depicted by ’$\star$’.

Fig. 3

Gauss points in $\mathcal{G }^{\circ \circ }$ (depicted by ‘open circle’) and $\mathcal{G }\setminus \mathcal{G }^{\circ \circ }$ (depicted by ‘star’)

We have the following relationship

$$\begin{aligned} \#\mathcal{G }^{\circ \circ }=\#\mathcal{N }_L^\circ . \end{aligned}$$

(3.5)

In fact, let $m=\#\mathcal{P }_a(=\#\mathcal{P }_b)$ and $n=\#\mathcal{P }_c(=\#\mathcal{P }_d)$. A straightforward calculation yields that

$$\begin{aligned} \#\mathcal{N }_L^\circ =(mr-1)(nr-1). \end{aligned}$$

Moreover, $\#\mathcal{G }=mnr^2, \#\mathcal{G }_b=mr, \#\mathcal{G }_d=nr$ and $\#(\mathcal{G }_b\cap \mathcal{G }_d)=1$, then

$$\begin{aligned} \#\mathcal{G }^{\circ \circ }=mnr^2-mr-nr+1=(mr-1)(nr-1). \end{aligned}$$

The equality (3.5) is valid.

We are now in a perfect position to define our special mapping. Let $\Pi$ be a mapping from the the trial space $\mathcal{U }_\mathcal{P }^r$ to the test space $\mathcal{V }_{\mathcal{P }^{\prime }}$ defined by :

$$\begin{aligned} \Pi v_\mathcal{P }=\sum _{P\in \mathcal{N }_L^\circ } (\Pi v_\mathcal{P })_{P}\psi _{V_P}\in \mathcal{V }_{\mathcal{P }^{\prime }}, \quad v_\mathcal{P }\in \mathcal{U }_\mathcal{P }^r, \end{aligned}$$

(3.6)

where the coefficients $(\Pi v_\mathcal{P })_{P\in \mathcal{N }}$ are determined by the constraints

$$\begin{aligned} \lfloor \Pi v_\mathcal{P } \rfloor _{g^\tau _{i,j}}=A^\tau _{x,i}A^\tau _{y,j} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^\tau _{i,j}), \end{aligned}$$

(3.7)

for all $g^\tau _{i,j}\in \mathcal{G }^{\circ \circ }$.

Remark 3.2

We have defined a special projector from the trial to test space in [9] for one dimensional FV scheme. Apparently, $\Pi$ defined above is not a simple tensor-product of that in [9].

Remark 3.3

By (3.5), the degree of freedom of $\Pi v_\mathcal{P }$ equals to the number of equations given by (3.7). To explain that $\Pi$ is well defined, we next explain how to successively calculate all coefficients of $\Pi v_\mathcal{P }$ by (3.7) with the following “lexicographic” ordering. We observe that since $\Pi v_\mathcal{P }\in \mathcal{V }_{\mathcal{P }^{\prime }}$, for all $P\in \mathcal{N }_L\cap \partial \Omega$,

$$\begin{aligned} \Pi v_\mathcal{P }=0\ \mathrm{in} V_P. \end{aligned}$$

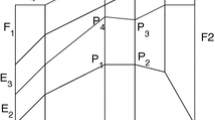
Let $\tau _1$ be the unique element in $\mathcal{P }_a\cap \mathcal{P }_c$, see Fig. 4. By (3.7), we have

$$\begin{aligned} \lfloor \Pi v_\mathcal{P } \rfloor _{g^{\tau _1}_{1,1}} =A^{\tau _1}_{x,1}A^{\tau _1}_{y,1} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^{\tau _1}_{1,1}). \end{aligned}$$

By the definition of the jump of the test function, we have

$$\begin{aligned} (\Pi v_\mathcal{P })(l^{\tau _1}_{1,1})+(\Pi v_\mathcal{P })(l^{\tau _1}_{0,0})-(\Pi v_\mathcal{P })(l^{\tau _1}_{0,1})-(\Pi v_\mathcal{P })(l^{\tau _1}_{1,0})=A^{\tau _1}_{x,1}A^{\tau _1}_{y,1} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^{\tau _1}_{1,1}). \end{aligned}$$

Since $l^{\tau _1}_{0,0}\in E_a\cap E_c ,l^{\tau _1}_{1,0}\in E_c, l^{\tau _1}_{0,1}\in E_a$ and $E_a,E_c\subset \partial \Omega$, we have

$$\begin{aligned} (\Pi v_\mathcal{P })(l^{\tau _1}_{0,0})=(\Pi v_\mathcal{P })(l^{\tau _1}_{0,1})=(\Pi v_\mathcal{P })(l^{\tau _1}_{1,0})=0. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} (\Pi v_\mathcal{P })_{l^{\tau _1}_{1,1}}=(\Pi v_\mathcal{P })(l^{\tau _1}_{1,1})=A^{\tau _1}_{x,1}A^{\tau _1}_{y,1} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^{\tau _1}_{1,1}). \end{aligned}$$

We next explain how to calculate all coefficients $(\Pi v_\mathcal{P })_{l^\tau _{i,j}}$ for all $l^{\tau }_{i,j}\in \mathcal{N }_L^\circ$. By (3.7) and the definition of jump at Gauss points, we have

$$\begin{aligned} (\Pi v_\mathcal{P })(l^{\tau }_{i,j})&= (\Pi v_\mathcal{P })(l^{\tau }_{i,j-1})+(\Pi v_\mathcal{P })(l^{\tau }_{i-1,j})+(\Pi v_\mathcal{P })(l^{\tau }_{i-1,j-1})\nonumber \\&\quad +A^{\tau }_{x,i}A^{\tau }_{y,j} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^{\tau }_{i,j}). \end{aligned}$$

(3.8)

This equation implies that when $(\Pi v_\mathcal{P })(l^{\tau }_{i,j-1}), (\Pi v_\mathcal{P })(l^{\tau }_{i-1,j}),$ and $(\Pi v_\mathcal{P })(l^{\tau }_{i-1,j-1})$, are known, $(\Pi v_\mathcal{P })(l^{\tau }_{i,j})$ can be straightforwardly calculated. Since $(\Pi v_\mathcal{P })_{l^{\tau _1}_{1,1}}$ and $(\Pi v_\mathcal{P })_{P}, P\in \mathcal{N }_L\cap \partial \Omega$ are known, all coefficients $(\Pi v_\mathcal{P })(l^{\tau }_{i,j})$ can be successively calculated following some given ordering such as that presented in Fig. 4.

Fig. 4

Order to calculate the coefficients of $\Pi v_\mathcal{P }$

Actually, the definition of $\Pi$ is independent of ordering, it depends only on the location of the Gauss points. There are many different “lexicographic” orders, the ordering we provide here is only one of them.

We next discuss properties of $\Pi$. First, we have

Lemma 3.4

Let $v_\mathcal{P }\in \mathcal{U }_\mathcal{P }^r$, the equality (3.7) holds for all Gauss points in $\mathcal{G }$.

Proof

Noticing $\mathcal{G }\setminus \mathcal{G }^{\circ \circ }=\mathcal{G }_b\cup \mathcal{G }_d$, we only need to prove (3.7) for all Gauss points in $\mathcal{G }_d$, since (3.7) for Gauss points $\mathcal{G }_b$ can be shown by the same arguments. We observe that $\mathcal{G }_d=\{g^{\tau }_{i,r}|\tau \in \mathcal{P }_d, i\in \mathbb{Z }_j\}$.

Since $v_\mathcal{P }=0$ on the boundary $\partial \Omega$,

$$\begin{aligned} \frac{\partial v_\mathcal{P }}{\partial x}(x, c)=\frac{\partial v_\mathcal{P }}{\partial x}(x, d)=0, \quad \forall x\in [a,b]. \end{aligned}$$

Then for any given $x_0\in [a,b]$,

$$\begin{aligned} \int \limits _c^d\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(x_0, y)dy=\frac{\partial v_\mathcal{P }}{\partial x}(x_0, d)-\frac{\partial v_\mathcal{P }}{\partial x}(x_0, c)=0. \end{aligned}$$

Let the segment $E_{x_0}=\{(x_0,y)|c\le y\le d\}$ and the subset of partition $\mathcal{P }_{x_0}=\{\tau \in \mathcal{P }|\tau \cap E_{x_0}\not =\emptyset \}$. We write the coordinates of the Gauss point $g^\tau _{i,j}=(g^{\tau }_{x,i},g^{\tau }_{y,j})$. We now choose $x_0=g^{\tau _0}_{x,i_0}$ for some fixed $\tau _0\in \mathcal{P }_d$ and $i_0\in \mathbb{Z }_r$. Then for all $\tau \in \mathcal{P }_{x_0}$, we have $g^\tau _{x,i_0}=x_0$. Therefore, noting that in each $\tau \in \mathcal{P }_{x_0},\,\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(x_0, y)$ is a polynomial of degree $r-1$ with respect to the second variable $y$, we have

$$\begin{aligned} 0&= \int \limits _c^d\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(x_0, y)dy=\sum _{\tau \in \mathcal{P }_{x_0}}\int \limits _{E_{x_0}\cap \tau }\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(x_0, y)dy\\&= \sum _{\tau \in \mathcal{P }_{x_0}}\sum _{j\in \mathbb{Z }_r} A^\tau _{y,j}\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^{\tau }_{x,i_0}, g^{\tau }_{y,j}). \end{aligned}$$

Since $A^{\tau }_{x,i_0}=A^{\tau _0}_{x,i_0}$ for all $\tau \in \mathcal{P }_{x_0}$, we have

$$\begin{aligned} A^{\tau _0}_{x,i_0} A^{\tau _0}_{y,r}\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^{\tau _0}_{i_0,r})=-\sum _{\tau \in \mathcal{P }_{x_0}}\sum _{j\in \mathbb{Z }_r, g^{\tau }_{i_0,j}\notin \mathcal{G }_d} A^{\tau }_{x,i_0}A^\tau _{y,j}\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^{\tau }_{i_0,j}). \end{aligned}$$

By the fact that (3.7) holds for all Gauss points in $\mathcal{G }^{\circ \circ }$, we obtain

$$\begin{aligned} A^{\tau _0}_{x,i_0} A^{\tau _0}_{y,r}\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^{\tau _0}_{i_0,r})=-\sum _{\tau \in \mathcal{P }_{x_0}}\sum _{j\in \mathbb{Z }_r, g^{\tau }_{i_0,j}\notin \mathcal{G }_d} \lfloor \Pi v_\mathcal{P }\rfloor _{g^\tau _{i_0,j}} \end{aligned}$$

On the other hand, by (3.4) and the fact that $\Pi v_\mathcal{P }=0$ in $\tau \in \mathcal{P }_c\cup \mathcal{P }_d$,

$$\begin{aligned} \sum _{\tau \in \mathcal{P }_{x_0}}\sum _{j\in \mathbb{Z }_r} \lfloor \Pi v_\mathcal{P }\rfloor _{g^\tau _{i_0,j}}=0. \end{aligned}$$

Then,

$$\begin{aligned} \lfloor \Pi v_\mathcal{P }\rfloor _{g^{\tau _0}_{i_0,r}}=-\sum _{\tau \in \mathcal{P }_{x_0}}\sum _{j\in \mathbb{Z }_r, g^{\tau }_{i_0,j}\notin \mathcal{G }_d} \lfloor \Pi v_\mathcal{P }\rfloor _{g^\tau _{i_0,j}}=A^{\tau _0}_{x,i_0} A^{\tau _0}_{y,r}\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^{\tau _0}_{i_0,r}). \end{aligned}$$

In other words, (3.7) holds for the Gauss point $g^{\tau _0}_{i_0,r}$. Since $i_0\in \mathbb{Z }_r, \tau _0\in \mathcal{G }_d$ are arbitrary, the Eq. (3.7) holds for all Gauss points in $\mathcal{G }_d$. By the same reasoning, (3.7) holds for all Gauss points in $\mathcal{G }_b$. The statement of the lemma is proved. $\square$

In the next lemma, we show that $\Pi$ is a bounded operator from the trial space to the test space. To this end, we let $a=x_0< x_1<\cdots <x_m=b,\ c=y_0< y_1<\cdots <y_n=d$ be distinct points in $[a, b]$ and $[c,d]$ such that $\mathcal{P }=\{\tau _{k,l}|k\in \mathbb{Z }_m, l\in bZ_n\}$ where the rectangular element $\tau _{k;l}=[x_{k-1},x_k]\times [y_{l-1},y_l]$.

Lemma 3.5

If $\mathcal{P }$ is shape regular, then for any $v_\mathcal{P }\in U_\mathcal{P }^r$,

$$\begin{aligned} |\Pi v_\mathcal{P }|_{\mathcal{P }^{\prime }}\lesssim | v_\mathcal{P }|_1, \end{aligned}$$

(3.9)

where the hidden constant depends only on $r$.

Proof

By the definition of the semi-norm $|\cdot |_{\mathcal{P }^{\prime }}$, we have

$$\begin{aligned} |\Pi v_\mathcal{P }|^2_{\mathcal{P }^{\prime }}=\sum _{\tau \in \mathcal{P }}\sum _{E\in \mathcal{E }_{{P}^{\prime }}, E\cap \tau \not =\emptyset } h_E^{-1}\int \limits _{E\cap \tau } \left[ \Pi v_\mathcal{P }\right] _E^2ds. \end{aligned}$$

(3.10)

Therefore, to prove (3.9), we only to prove that for all $\tau \in \mathcal{P }$,

$$\begin{aligned} \sum _{E\in \mathcal{E }_{P^{\prime }}, E\cap \tau \not =\emptyset } \left[ \Pi v_\mathcal{P }\right] _E^2\lesssim | v_\mathcal{P }|^2_{1,\tau }. \end{aligned}$$

(3.11)

Noticing $\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}\in Q_{r-1}(\tau )$ for $\tau =\tau _{k,l}$, we have

$$\begin{aligned} \sum _{i\in \mathbb{Z }_r} \lfloor \Pi v_\mathcal{P }\rfloor _{g^\tau _{i,j}}&= A^\tau _{y,j}\sum _{i\in \mathbb{Z }_r} A^\tau _{x,i} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y }(g^\tau _{i,j})=A^\tau _{y,j}\int \limits _{x_{k-1}}^{x_{k}}\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y }(x, g^\tau _{y,j})dx\\&= A^\tau _{y,j}\frac{\partial v_\mathcal{P }}{\partial y }(x_k, g^\tau _{y,j})-A^\tau _{y,j}\frac{\partial v_\mathcal{P }}{\partial y }(x_{k-1}, g^\tau _{y,j}). \end{aligned}$$

On the other hand, by (3.4), we have

$$\begin{aligned} \sum _{i\in \mathbb{Z }_r} \lfloor \Pi v_\mathcal{P }\rfloor _{g^\tau _{i,j}}=[\Pi v_\mathcal{P }]_{E^{\tau ,x}_{r,j}}-[\Pi v_\mathcal{P }]_{E^{\tau ,x}_{0,j}}. \end{aligned}$$

Then,

$$\begin{aligned}{}[\Pi v_\mathcal{P }]_{E^{\tau _{k,l},x}_{r,j}}-[\Pi v_\mathcal{P }]_{E^{\tau _{k,l},x}_{0,j}} = A^{\tau _{k,l}}_{y,j}\frac{\partial v_\mathcal{P }}{\partial y }(x_k, g^{\tau _{k,l}}_{y,j})-A^{\tau _{k,l}}_{y,j}\frac{\partial v_\mathcal{P }}{\partial y }(x_{k-1}, g^{\tau _{k,l}}_{y,j}). \end{aligned}$$

(3.12)

We note that for all $k$,

$$\begin{aligned}{}[\Pi v_\mathcal{P }]_{E^{\tau _{k-1,l},x}_{r,j}}=[\Pi v_\mathcal{P }]_{E^{\tau _{k,l},x}_{0,j}}, \end{aligned}$$

Moreover since $\frac{\partial v_\mathcal{P }}{\partial y}$ is continuous across the edge of $\tau _{k,l}\cap \tau _{k-1,l}$, we have

$$\begin{aligned} A^{\tau _{k-1,l}}_{y,j}\frac{\partial v_\mathcal{P }}{\partial y }(x_k, g^{\tau _{k-1,l}}_{y,j})=A^{\tau _{k,l}}_{y,j}\frac{\partial v_\mathcal{P }}{\partial y }(x_{k}, g^{\tau _{k,l}}_{y,j}). \end{aligned}$$

Then (3.12) can be rewritten as

$$\begin{aligned}{}[\Pi v_\mathcal{P }]_{E^{\tau _{k+1,l},x}_{0,j}}-[\Pi v_\mathcal{P }]_{E^{\tau _{k,l},x}_{0,j}}=A^{\tau _{k+1,l}}_{y,j} \frac{\partial v_\mathcal{P }}{\partial y }(x_{k}, g^{\tau _{k,l}}_{y,j})-A^{\tau _{k,l}}_{y,j}\frac{\partial v_\mathcal{P }}{\partial y }(x_{k-1}, g^{\tau _{k,l}}_{y,j}). \end{aligned}$$

(3.13)

Since $v_\mathcal{P }=0$ and $\Pi v_\mathcal{P }=0$ on $\partial \Omega$, we have

$$\begin{aligned} \frac{\partial v_\mathcal{P }}{\partial y }(g^{\tau _{k,l}}_{x,r+1}, g^{\tau _{k,l}}_{y,j})=0, [\Pi v_\mathcal{P }]_{E^{\tau _{k,l},x}_{r,j}}=0. \end{aligned}$$

Then by (3.13), for all $\tau =\tau _{k,l}\in \mathcal{P }, j\in \mathbb{Z }_r$, we have

$$\begin{aligned} \left[ \Pi v_\mathcal{P }\right] _{E^{\tau , x}_{0,j}}=A^\tau _{y,j}\frac{\partial v_\mathcal{P }}{\partial y }(g^\tau _{x,0}, g^\tau _{y,j}). \end{aligned}$$

(3.14)

Therefore, by the inverse inequality and shape regularity of $\mathcal{P }$, and the fact that $A^\tau _{y,j}\sim h_\tau$, we have

$$\begin{aligned} \left| [\Pi v_\mathcal{P }]_{E^{\tau , x}_{0,j}}\right|&\le h_\tau \left\| \frac{\partial v_\mathcal{P }}{\partial y }(\cdot , g^\tau _{y,j})\right\| _{L^\infty (x_{k-1},x_k)}\\&\lesssim h_\tau (h^\tau )^{-\frac{1}{2}}\left\| \frac{\partial v_\mathcal{P }}{\partial y }(\cdot , g^\tau _{y,j})\right\| _{L^2(x_{k-1},x_k)}\\&\lesssim h_\tau ^{\frac{1}{2}}\left\| \frac{\partial v_\mathcal{P }}{\partial y }(\cdot , g^\tau _{y,j})\right\| _{L^2(x_{k-1},x_k)}. \end{aligned}$$

For $i\in \mathbb{Z }_r$,

$$\begin{aligned}{}[\Pi v_\mathcal{P }]_{E^{\tau , x}_{i,j}}&= [\Pi v_\mathcal{P }]_{E^{\tau , x}_{0,j}}+\sum _{i^{\prime }=1}^i\lfloor \Pi v_\mathcal{P }\rfloor _{g^\tau _{i^{\prime },j}}\\&= [\Pi v_\mathcal{P }]_{E^{\tau , x}_{0,j}}+A^\tau _{y,j}\sum _{i^{\prime }=1}^i A^\tau _{x,i^{\prime }} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y }(g^\tau _{i^{\prime },j}), \end{aligned}$$

and by the inverse inequality and the fact that $A^\tau _{x,i}\sim h_\tau$,

$$\begin{aligned} \left| \sum _{i^{\prime }=1}^i A^\tau _{x,i^{\prime }} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y }(g^\tau _{i^{\prime },j})\right|&\lesssim h_\tau \left\| \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y }(\cdot , g^\tau _{y,j})\right\| _{L^\infty (x_{k-1},x_k)}\\&\lesssim h_\tau ^{\frac{1}{2}}\left\| \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y }(\cdot , g^\tau _{y,j})\right\| _{L^2(x_{k-1},x_k)}\\&\lesssim h_\tau ^{-\frac{1}{2}}\left\| \frac{\partial v_\mathcal{P }}{\partial y }(\cdot , g^\tau _{y,j})\right\| _{L^2(x_{k-1},x_k)}, \end{aligned}$$

Therefore for all $i\in \mathbb{Z }^0_r$, there holds

$$\begin{aligned} \left| [\Pi v_\mathcal{P }]_{E^{\tau , x}_{i,j}}\right| \lesssim h_\tau ^{\frac{1}{2}}\left\| \frac{\partial v_\mathcal{P }}{\partial y }(\cdot , g^\tau _{y,j})\right\| _{L^2(x_{k-1},x_k)}. \end{aligned}$$

Consequently,

$$\begin{aligned} \sum _{i\in \mathbb{Z }_r^0}\left| [\Pi v_\mathcal{P }]_{E^{\tau , x}_{i,j}}\right| ^2 \lesssim h_\tau \int \limits _{x_{k-1}}^{x_k}\left| \frac{\partial v_\mathcal{P }}{\partial y }(x, g^\tau _{y,j})\right| ^2 dx. \end{aligned}$$

(3.15)

Since $\int \nolimits _{x_{k-1}}^{x_k}\left( \frac{\partial v_\mathcal{P }}{\partial y }(x, \cdot )\right) ^2dx$ is a polynomial (w.r.t $y$) of degree less than $2r-1$, we have

$$\begin{aligned} \sum _{j\in \mathbb{Z }_r}A^\tau _{y,j} \int \limits _{-1}^1 \left( \frac{\partial v_\mathcal{P }}{\partial y }(x, g^\tau _{y,j})\right) ^2dx = \int \limits _{y_{l-1}}^{y_l}\int \limits _{x_{k-1}}^{x_k} \left( \frac{\partial v_\mathcal{P }}{\partial y }(\xi , \eta )\right) ^2d\xi d\eta =\left\| \frac{\partial v_\mathcal{P }}{\partial y }\right\| _{L^2(\tau )}^2. \end{aligned}$$

Noticing (3.15) and the fact that $A^\tau _{y,j}\sim h_\tau$, we obtain

$$\begin{aligned} \sum _{i\in \mathbb{Z }_r^0, j\in \mathbb{Z }_r}\left( [\Pi v_\mathcal{P }]_{E^{\tau , x}_{i,j}}\right) ^2\lesssim \left\| \frac{\partial v_\mathcal{P }}{\partial y }\right\| _{L^2(\tau )}^2. \end{aligned}$$

Similarly,

$$\begin{aligned} \sum _{i\in \mathbb{Z }_r, j\in \mathbb{Z }^0_r}\left( [\Pi v_\mathcal{P }]_{E^{\tau , y}_{i,j}}\right) ^2\lesssim \left\| \frac{\partial v_\mathcal{P }}{\partial x}\right\| _{L^2(\tau )}^2. \end{aligned}$$

Recall $\mathcal{E }_{\mathcal{P }^{\prime }}\cap \tau =\{E^{\tau ,y}_{i,j} \big |i\in \mathbb{Z }_r, j\in \mathbb{Z }^0_r\}\cup \{E^{\tau ,x}_{i,j}\big |i\in \mathbb{Z }^0_r, j\in \mathbb{Z }_r\}$, we obtain

$$\begin{aligned} \sum _{E\in \mathcal{E }_{\mathcal{P }^{\prime }}\cap \tau } \left( [\Pi v_\mathcal{P }]_E\right) ^2 \lesssim |v_\mathcal{P }|^2_{1,\tau }. \end{aligned}$$

That is, (3.11) is verified. The inequality (3.9) then follows. $\square$

With the help of $\Pi$, we obtain a bilinear form $a_\mathcal{P }(\cdot ,\Pi \cdot )$ which is defined only on the trial space $\mathcal{U }_\mathcal{P }^r$. We next show the coercivity of $a_\mathcal{P }(\cdot ,\Pi \cdot )$. An essential idea in the proof is to express $a_\mathcal{P }(\cdot ,\Pi \cdot )$ as a Gauss quadrature of some finite element bilinear form.

Theorem 3.6

If $\alpha$ is piecewise constant with respect to $\mathcal{P }$, then

$$\begin{aligned} a_\mathcal{P } (v_\mathcal{P } ,\Pi v_\mathcal{P } )\ge \alpha _0|v_\mathcal{P } |_1^2,\quad \forall v_\mathcal{P }\in U^r_\mathcal{P }. \end{aligned}$$

(3.16)

Proof

We define two functions for all $(x,y)\in \Omega$ by

$$\begin{aligned} v^1(x,y)=\int \limits _c^y \alpha (x,y^{\prime })\frac{\partial v_\mathcal{P }}{\partial x}(x,y^{\prime }) dy^{\prime },\quad v^2(x,y)=\int \limits _a^x \alpha (x^{\prime },y)\frac{\partial v_\mathcal{P }}{\partial y}(x^{\prime },y) dx^{\prime }. \end{aligned}$$

A straightforward calculation yields that

$$\begin{aligned} a_\mathcal{P }(v_\mathcal{P },\Pi v_\mathcal{P }) = -\sum _{\tau \in \mathcal{P }}\sum _{i,j\in \mathbb{Z }_r}\lfloor \Pi v_\mathcal{P } \rfloor _{g^{\tau }_{i,j}}\left( v^1(g^\tau _{i,j})+ v^2(g^\tau _{i,j})\right) . \end{aligned}$$

Noticing that (3.7) holds for all $g^\tau _{i,j}\in \mathcal{G },$ we obtain

$$\begin{aligned} a_\mathcal{P }(v_\mathcal{P },\Pi v_\mathcal{P })&= I_1+I_2, \end{aligned}$$

where

$$\begin{aligned} I_1=-\sum _{\tau \in \mathcal{P }}\sum _{i,j\in \mathbb{Z }_r} A^\tau _{x,i}A^\tau _{y,j} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^\tau _{i,j}) v^1(g^\tau _{i,j}), \end{aligned}$$

and

$$\begin{aligned} I_2=-\sum _{\tau \in \mathcal{P }}\sum _{i,j\in \mathbb{Z }_r} A^\tau _{x,i}A^\tau _{y,j} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^\tau _{i,j}) v^2(g^\tau _{i,j}). \end{aligned}$$

We next estimate $I_1$. To this end, for all $\tau =\tau _{k,l}\in \mathcal{P }, i\in \mathbb{Z }_r$, we denote by

$$\begin{aligned} Err _{\tau , i}=\int \limits _{y_{l-1}}^{y_l}\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^\tau _{x,i},y)v^1(g^\tau _{x,i}, y)dy-\sum _{j\in \mathbb{Z }_r} A^\tau _{y,j} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^\tau _{x,i},y)v^1(g^\tau _{x,i}, g^\tau _{y,j}) \end{aligned}$$

the error of the Gauss quadrature of the function $\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^\tau _{x,i},\cdot )v^1(g^\tau _{x,i}, \cdot )$ in the interval $[y_{l-1},y_l]$. Moreover, let

$$\begin{aligned} Res =\sum _{\tau \in \mathcal{P }}\sum _{i\in \mathbb{Z }_r}A^\tau _{x,i} Err_{\tau ,i}. \end{aligned}$$

With this notation,

$$\begin{aligned} I_1&= -\sum _{\tau \in \mathcal{P }}\sum _{i\in \mathbb{Z }_r}A^\tau _{x,i}\int \limits _{y_{l-1}}^{y_l}\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^\tau _{x,i},y)v^1(g^\tau _{x,i}, y)dy+ Res \end{aligned}$$

Since $\alpha$ is a constant in each $\tau \in \mathcal{P }$, and for any given $y\in [y_{l-1}, y_l]$,

$$\begin{aligned} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(\cdot ,y)v^1(\cdot , y)\in \mathbb{P }_{2r-2}([x_{k-1}, x_k]) \end{aligned}$$

Then

$$\begin{aligned} \sum _{i\in \mathbb{Z }_r}A^\tau _{x,i}\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^\tau _{x,i},y)v^1(g^\tau _{x,i}, y)=\int \limits _{x_{k-1}}^{x_k} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(x,y)v^1(x, y)dx. \end{aligned}$$

Consequently,

$$\begin{aligned} I_1&= -\sum _{\tau \in \mathcal{P }}\int \limits _{y_{l-1}}^{y_l}\int \limits _{x_{k-1}}^{x_k} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(x,y)v^1(x, y)dx dy+ Res \nonumber \\&= -\int \limits _{c}^{d}\int \limits _{a}^{b} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(x,y)v^1(x, y)dx dy+ Res \nonumber \\&= \int \limits _{c}^{d}\int \limits _{a}^{b}\alpha (x,y)\left( \frac{\partial v_\mathcal{P }}{\partial x}(x, y)\right) ^2dydx+ Res , \end{aligned}$$

(3.17)

where we have used integration by parts in the last equality.

We next estimate $Res$. Using the fact that $\alpha$ is a constant $\tau$, we have

$$\begin{aligned} \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^\tau _{x,i},\cdot )v^1(g^\tau _{x,i}, \cdot )\in \mathbb{P }_{2r}([y_{l-1},y_l]). \end{aligned}$$

Then for all $y\in [y_{j-1},y_j]$,

$$\begin{aligned} \frac{\partial ^{(2r)}}{\partial y^{(2r)}}\left( \frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y}(g^\tau _{x,i},\cdot )v^1(g^\tau _{x,i}, \cdot )\right) =\alpha (2r)!\frac{r}{r+1} a_{\tau ,i}^2 \ge 0. \end{aligned}$$

where $a_{\tau ,i}$ is the leading coefficient of the polynomial $\frac{\partial v_\mathcal{P }}{\partial x}(g^\tau _{x,i},y)$ in $\tau$. Consequently,

$$\begin{aligned} Err _{\tau , i}\ge 0, \forall \tau \in \mathcal{P }, i\in \mathbb{Z }_r, \end{aligned}$$

and thus

$$\begin{aligned} Res \ge 0. \end{aligned}$$

In summary,

$$\begin{aligned} I_1\ge \alpha _0\int \limits _a^b\int \limits _c^d\left( \frac{\partial v_\mathcal{P }}{\partial x}(x, y)\right) ^2dydx. \end{aligned}$$

(3.18)

By the same arguments,

$$\begin{aligned} I_2\ge \alpha _0\int \limits _c^d\int \limits _a^b\left( \frac{\partial v_\mathcal{P }}{\partial y}(x, y)\right) ^2dxdy. \end{aligned}$$

(3.19)

Combining (3.18) and (3.19), the inequality (3.16) follows. $\square$

Remark 3.7

We can extend the above result to the case that $\alpha =\left( \begin{array}{ll}\alpha _{11}&{}\alpha _{12}\\ \alpha _{21}&{}\alpha _{22}\end{array}\right)$ is a positive definite matrix where $\alpha _{ij},1\le i,j\le 2$ are piecewise constants with respect to $\mathcal{T }_h$. In fact, in this case, we have

$$\begin{aligned} a_\mathcal{P }(v_\mathcal{P },\Pi v_\mathcal{P })&= -\sum _{\tau \in \mathcal{P }}\sum _{i,j\in \mathbb{Z }_r}\lfloor \Pi v_\mathcal{P } \rfloor _{g^{\tau }_{i,j}}\left( v^1(g^\tau _{i,j})+ v^2(g^\tau _{i,j})\right) =I_1+I_2, \end{aligned}$$

with

$$\begin{aligned} v^1(x,y)=\int \limits _c^y \left( \alpha _{11}\frac{\partial v_\mathcal{P }}{\partial x}+\alpha _{12}\frac{\partial v_\mathcal{P }}{\partial y}\right) (x,y^{\prime }) dy^{\prime }, \end{aligned}$$

and

$$\begin{aligned} v^2(x,y)=\int \limits _a^x \left( \alpha _{21}\frac{\partial v_\mathcal{P }}{\partial x}+\alpha _{22}\frac{\partial v_\mathcal{P }}{\partial y}\right) (x^{\prime },y) dx^{\prime }. \end{aligned}$$

By the same arguments in the proofs of Theorem 3.6, we obtain

$$\begin{aligned} I_1&\ge -\int \limits _c^d\int \limits _a^b\frac{\partial ^2 v_\mathcal{P }}{\partial x\partial y} v^1(x,y) dxdy\\&= \int \limits _c^d\int \limits _a^b\frac{\partial v_\mathcal{P }}{\partial x} \left( \alpha _{11}\frac{\partial v_\mathcal{P }}{\partial x}+\alpha _{12}\frac{\partial v_\mathcal{P }}{\partial y}\right) dxdy. \end{aligned}$$

Similarly,

$$\begin{aligned} I_2\ge \int \limits _c^d\int \limits _a^b\frac{\partial v_\mathcal{P }}{\partial y} \left( \alpha _{21}\frac{\partial v_\mathcal{P }}{\partial x}+\alpha _{22}\frac{\partial v_\mathcal{P }}{\partial y}\right) dxdy. \end{aligned}$$

Consequently,

$$\begin{aligned} a_\mathcal{P }(v_\mathcal{P },\Pi v_\mathcal{P })\ge \int \limits _a^b\int \limits _c^2 ({\bigtriangledown }v_\mathcal{P })^T \alpha {\bigtriangledown }v_\mathcal{P } dxdy. \end{aligned}$$

The inequality (3.16) follows from the positive definitness of $\alpha$.

Summarizing the above two lemmas, we obtain the following inf-sup property.

Theorem 3.8

Let $\mathcal{P }$ be a shape regular and quasi-uniform partition with the meshsize $h$. If the coefficient $\alpha$ is piecewise constant with respect to $\mathcal{P }$, then the inf-sup property

$$\begin{aligned} \inf _{v_\mathcal{P }\in U^r_\mathcal{P }}\sup _{w_{\mathcal{P }^{\prime }} \in V_{\mathcal{P }^{\prime }} } \frac{a_\mathcal{P } (v_\mathcal{P } ,w_{\mathcal{P }^{\prime }} )}{|v_\mathcal{P } |_1 |w_{\mathcal{P }^{\prime }}|_{\mathcal{P }^{\prime }}}\gtrsim 1 \end{aligned}$$

(3.20)

holds for all $h$. If $\alpha$ is piecewise continuous with respect to $\mathcal{P }$, then (3.20) holds when the meshsize $h$ is sufficiently small.

Proof

When $\alpha$ is piecewise constant, by (3.16) and (3.9), for any $v_\mathcal{P }\in U^r_\mathcal{P }$,

$$\begin{aligned} \sup _{w_{\mathcal{P }^{\prime }}\in V_{\mathcal{P }^{\prime }}} \frac{a_\mathcal{P }(v_\mathcal{P }, w_{\mathcal{P }^{\prime }})}{|w_{\mathcal{P }^{\prime }}|_{\mathcal{P }^{\prime }}} \ge \frac{a_\mathcal{P }(v_\mathcal{P },\Pi v_\mathcal{P })}{|\Pi v_\mathcal{P }|_{\mathcal{P }^{\prime }}}\ge \frac{\alpha _0|v_\mathcal{P }|_1^2}{|\Pi v_\mathcal{P }|_{\mathcal{P }^{\prime }}}\gtrsim |v_\mathcal{P }|_{1}. \end{aligned}$$

The inf-sup condition (3.20) is proved.

When $\alpha$ is only piecewise continuous, let

$$\begin{aligned} \bar{\alpha }(x,y)=\frac{1}{|\tau |}\int \limits _\tau \alpha (x,y)dxdy, \quad \forall (x,y)\in \tau \in \mathcal{P } \end{aligned}$$

and denote the piecewise modulus of continuity of $\alpha$ by

$$\begin{aligned} m_\mathcal{P }(\alpha ,h)=\sup \left\{ \big |\alpha (\mathbf{x}_1)-\alpha (\mathbf{x}_2)\big |:\big |\mathbf{x}_1-\mathbf{x}_2\big |\le h,\quad \forall \mathbf{x}_1, \mathbf{x}_2\in \tau , \quad \forall \ \tau \in \mathcal{P } \right\} . \end{aligned}$$

The fact that $\alpha$ is piecewise continuous implies that $m_\mathcal{P }(\alpha ,h)$ converges to 0 when $h$ goes to 0. Since $\bar{\alpha }$ is piecewise constant, by Lemma 3.6,

$$\begin{aligned} \bar{a}_\mathcal{P }(v_\mathcal{P },\Pi v_\mathcal{P }) := \sum _{E\in \mathcal{E }_{\mathcal{P }^{\prime }}}[\Pi v_\mathcal{P }]\int \limits _E \bar{\alpha }\frac{\partial v}{\partial \mathbf{n}}ds\ge \alpha _0 |v_\mathcal{P }|^2_1. \end{aligned}$$

On the other hand, by the same arguments in Theorem 3.1, we have

$$\begin{aligned} \left| a_\mathcal{P }(v_\mathcal{P },\Pi v_\mathcal{P })-\bar{a}_\mathcal{P }(v_\mathcal{P },\Pi v_\mathcal{P })\right| \lesssim m_\mathcal{P }(\alpha ,h)|v_\mathcal{P }|^2_1, \end{aligned}$$

Then when $h$ is sufficiently small,

$$\begin{aligned} a_\mathcal{P }(v_\mathcal{P },\Pi v_\mathcal{P })\ge \left( \alpha _0-cm_\mathcal{P }(\alpha ,h)\right) \big |v_\mathcal{P } \big |^2_{1,\Omega }\ge \frac{\alpha _0}{2}\big |v_\mathcal{P }\big |^2_{1,\Omega }. \end{aligned}$$

The inf-sup condition (3.20) is proved. $\square$

3.3 $H^1$ Error Estimate

We begin with some preparations. First, by the inverse inequality,

$$\begin{aligned} \big |v_\mathcal{P }\big |_\mathcal{P }\sim \big |v_\mathcal{P }\big |_1,\quad \forall v_\mathcal{P }\in U_\mathcal{P }^r. \end{aligned}$$

With this equivalence, we deduce from the inf-sup condition (3.20) that

$$\begin{aligned} \inf _{v_\mathcal{P }\in U_\mathcal{P }^r}\sup _{w_{\mathcal{P }^{\prime }} \in V_{\mathcal{P }^{\prime }} } \frac{a_\mathcal{P } (v_\mathcal{P } ,w_{\mathcal{P }^{\prime }} )}{|v_\mathcal{P } |_\mathcal{P } |w_{\mathcal{P }^{\prime }}|_{\mathcal{P }^{\prime }}}\ge c_0, \end{aligned}$$

(3.21)

where the constant $c_0=c_0(r)$ depends only on $r$.

Let $u_I\in U^r_\mathcal{P }$ be the interpolation of $u$ that satisfies

$$\begin{aligned} u_I(P)= u(P), \quad \forall P\in \mathcal{N }_L. \end{aligned}$$

Note that similar interpolations have been used in the literature for superconvergence analysis, see, e.g., [41, 42] for the one-dimensional situation.

We are now ready to present our main result.

Theorem 3.9

Let $u\in \ H_0^1(\Omega )\cap H_\mathcal{P }^{2}(\Omega )$ be the solution of (2.1) and (2.2), $u_\mathcal{P }$ the solution of (2.5). Then for sufficiently small $h$,

$$\begin{aligned} \big |u-u_\mathcal{P }\big |_\mathcal{P }\le \frac{M}{c_0} \inf _{v_\mathcal{P }\in U_{\mathcal{P }}}\big |u-v_\mathcal{P }\big |_\mathcal{P }. \end{aligned}$$

(3.22)

Consequently, if $u\in H^{r+1}(\Omega )$,

$$\begin{aligned} |u-u_\mathcal{P }|_{1}\lesssim h^r|u|_{r+1}, \end{aligned}$$

(3.23)

where the hidden constant is independent of the mesh size $h$.

Proof

By (3.2), (3.3) and the inf-sup condition (3.21), for all $v_\mathcal{P }\in U_{\mathcal{P }}$, there holds

$$\begin{aligned} \big |u-u_\mathcal{P }\big |_\mathcal{P }\le \big |u-v_\mathcal{P }\big |_\mathcal{P }+\big |v_\mathcal{P }-u_\mathcal{P }\big |_\mathcal{P } \le \left( 1+\frac{M}{c_0}\right) \big |u-v_\mathcal{P }\big |_\mathcal{P }. \end{aligned}$$

Using a technique in Xu and Zikatanov [38], the constant $1+\frac{M}{c_0}$ in the above inequality can be reduced to $\frac{M}{c_0}$. That is, (3.22) holds.

We conclude from the definition of $|\cdot |_\mathcal{P }$ and (3.22) that

$$\begin{aligned} |u-u_\mathcal{P }|_1\le |u-u_\mathcal{P }|_\mathcal{P }\lesssim \inf \limits _{v_\mathcal{P }\in U^r_\mathcal{P }}|u-v_\mathcal{P }|_\mathcal{P }. \end{aligned}$$

Note that

$$\begin{aligned} \inf \limits _{v_\mathcal{P }\in U^r_\mathcal{P }}|u-v_\mathcal{P }|_\mathcal{P }\le |u-u_I|_{1}+h|u-u_I|_{2}, \end{aligned}$$

where $u_I$ is the Lagrange interpolation of $u$ at the Lobatto points in the trial space $U^r_\mathcal{P }$. By the standard approximation theory, we obtain the estimate (3.23). $\square$

3.4 Superconvergence and $L^2$ Error Estimates

We first present a superconvergence result and then use it to establish our $L^2$ error estimate.

Theorem 3.10

Assume that $u\in H_0^1(\Omega )\cap H^{r+2}(\Omega )$ is the solution of (2.1)–(2.2), and $u_\mathcal{P }$ is the solution of the FV scheme (2.5). Then for all $w_{\mathcal{P }^{\prime }}\in V_{\mathcal{P }^{\prime }}$,

$$\begin{aligned} |a_\mathcal{P }(u-u_I,w_{\mathcal{P }^{\prime }})|\lesssim h^{r+1}|u|_{r+2,\mathcal{P }}|w_{\mathcal{P }^{\prime }}|_{\mathcal{P }^{\prime }}, \end{aligned}$$

(3.24)

where $|u|_{r+2,\mathcal{P }}=\left( \sum \nolimits _{\tau \in \mathcal{P }}|u|^2_{r+2,\tau }\right) ^{\frac{1}{2}}$. Consequently,

$$\begin{aligned} |u_I-u_\mathcal{P }|_1\lesssim h^{r+1}|u|_{r+2,\mathcal{P }}. \end{aligned}$$

(3.25)

Proof

We can derive the following inequality by the standard superconvergence argument, see, e.g., [43], for all $\tau \in \mathcal{P }, i,j\in \mathbb{Z }_p$,

$$\begin{aligned} \left\| \frac{\partial (u-u_{I})}{\partial x}(g^\tau _{x,i},\cdot )\right\| _{L^\infty [g^\tau _{y,j},g^\tau _{y,j+1}]}, \left\| \frac{\partial (u-u_{I})}{\partial y}(\cdot ,g^\tau _{y,j})\right\| _{L^\infty [g^\tau _{x,i},g^\tau _{x,i+1}]} \lesssim h^r|u|_{r+2,1,\tau },\nonumber \\ \end{aligned}$$

(3.26)

It follows from (3.1) that

$$\begin{aligned} \big |a_p(u-u_I,w_p)|&\le \Vert \alpha \Vert _\infty |w_p|_p \left( \sum _{E\in \mathcal{E }_p} h_E\int \limits _E \left( \frac{\partial (u-u_I)}{\partial \mathbf{n}}\right) ^2ds\right) ^{\frac{1}{2}}\\&\lesssim h^{r+1}|w_p|_p|u|_{r+2,\mathcal{P }}, \end{aligned}$$

where in the last step we have used (3.26) and the fact $|u|_{r+2,1,\tau }\lesssim h^{\frac{1}{2}}|u|_{r+2,\tau }$

We next show (3.25). By the inf-sup condition (3.20),

$$\begin{aligned} |u_I-u_p|_1\lesssim \sup \limits _{w_p\in V_p} \frac{a_p(u_p-u_I,w_p)}{|w_p|_p} =\sup \limits _{w_p\in V_p}\frac{a_p(u-u_I,w_p)}{|w_p|_p}. \end{aligned}$$

Combining the above inequality with (3.24), we derive (3.25). $\square$

As a direct consequence of the superconvergence result (3.25), we have the following $L^2$ estimate.

Theorem 3.11

Assume that $u\in H_0^1(\Omega )\cap H^{r+2}(\Omega )$ is the solution of (2.1)–(2.2), and $u_\mathcal{P }$ is the solution of the FV scheme (2.5), then there holds

$$\begin{aligned} \Vert u-u_\mathcal{P }\Vert _{0}\lesssim h^{r+1}\Vert u\Vert _{r+2}. \end{aligned}$$

(3.27)

Proof

By the triangle inequality,

$$\begin{aligned} \Vert u-u_\mathcal{P }\Vert _0\le \Vert u-u_I\Vert _0+\Vert u_\mathcal{P }-u_I\Vert _0 \end{aligned}$$

where $u_I$ is the interpolation of $u$ given in the previous subsection.

Since $u_I=u_\mathcal{P }=0$ on $\partial \Omega$, we have by the Poincaré inequality that

$$\begin{aligned} \Vert u_\mathcal{P }-u_I\Vert _0\lesssim |u_\mathcal{P }-u_I|_1 \lesssim h^{r+1}|u|_{r+2}. \end{aligned}$$

Moreover,

$$\begin{aligned} \Vert u-u_I\Vert _0\lesssim h^{r+1}\Vert u\Vert _{r+1}\le h^{r+1}\Vert u\Vert _{r+2}. \end{aligned}$$

Then we have (3.27). $\square$

Remark 3.12

In the above $L^2$ error estimate, we do not need to use the so-called Aubin–Nitsche techniques.

Remark 3.13

Comparing with most results in the literature for lower-order FVM, our concern here is higher-order method. To the best of our knowledge, the superconvergence result and even optimal convergence result for the arbitrary order of the FVM in our paper has not been reported in the literature. Apparently, some regularity assumption has to be made in order to realize the high-order convergence rate. Of course, the restrictive global regularity assumption makes the method less practical. However, it is a common practice to apply local mesh refinement and adaptive procedure to overcome this difficulty.

Remark 3.14

Regarding the Remark 3.7, all the results in Theorems 3.8–3.11 can be extended to the general case that $\alpha$ is a positive definite piecewise continuous matrix.

4 Numerical Results

In this section, we present a numerical example to validate the theoretical results proved in previous sections. We consider (2.1)–(2.2) with $\alpha =1$ and $\Omega =[0,1]^2$. We choose the right-hand side function

$$\begin{aligned} f(x,y)=2\pi ^2\sin \pi x\sin \pi y, \quad (x,y)\in [0,1]^2 \end{aligned}$$

which allows the exact solution

$$\begin{aligned} u(x,y)={ \sin \pi x}\sin \pi y, \quad (x,y)\in [0,1]^2. \end{aligned}$$

We use FV schemes (2.5) with $r=2,3,4,5$ to compute FVM approximate solutions of $u$. The partition $\mathcal{P }_j,\,j=1,\ldots ,6$, are obtained by uniformly refining the unite square $[0,1]^2$. For simplicity, we write $u_j$, instead of $u_{\mathcal{P }_j}$, as the finite volume solution $u_{\mathcal{P }_j}\in U^r_{\mathcal{P }_j}$. Moreover, we denote by $h_j$ the meshsize of $\mathcal{P }_j$.

The numerical results are demonstrated in Figs. 5, 6, 7, and 8, respectively. In these figures, the horizontal coordinate always indicate the quantity $-{ \log h_j}$, while the vertical coordinate present the logarithm of errors. We depict $h_j^{r}$ by the solid curve with ‘$\Box$’ and depict $h_j^{(r+1)}$ by the dash line. We depict $|u-u_j|_{H^1}$ by the solid curve with ‘$\star$’, $\Vert u-u_j\Vert _{L^2}$ by the solid curve with ‘$\triangle$’, and $|u_I-u_j|_{H^1}$ by the solid curve with ‘$*$’. We observe that $|u-u_j|_{H^1}$ decays with the convergence rate $h_j^{r}$ which supports our theory (3.23). We also observe that both $\Vert u-u_j\Vert _{L^2}$ and $|u_I-u_j|_{H^1}$ decay with $h_j^{(r+1)}$ which support our $L^2$ estimate (3.27) and superconvergene result (3.25), respectively.

Fig. 5

$r=2$

Fig. 6

$r=3$

Fig. 7

$r=4$

Fig. 8

$r=5$

5 Conclusions and Future Works

The design and analysis of high-order FV schemes are challenging tasks. This paper is the second one in its series that attempts to set up a mathematical foundation for a family of high order FV schemes. In a previous work [9], we studied convergence and superconvergence properties of FV schemes of any order for the one-dimensional elliptic equations. In this article, we only report our results for rectangular meshes. In a forthcoming paper [40], we extend our results for the rectangular mesh to general quadrilateral meshes with rather loose mesh conditions.

The higher dimensional case is fundamentally different from, and much more complicated than the one dimensional case. We would like to stress that the proof in the current paper is not a simple generalization of the one dimensional situation. The traditional tensor-product does not apply.

We also would like to mention that the emphases of the rectangular mesh and general arbitrary quadrilateral mesh papers are different. In the current rectangular paper, the emphasis is on arbitrary order instead of a case-by-case study for quadratic, cubic, etc.; in the quadrilateral paper, the emphasis is on the nearly arbitrary mesh. The main difficulty is that for unstructured meshes, we are unable to determine the ordering, and the situation is much more complicated. The analysis involves a lot of tedious topological and geometrical discussions. Moreover, for an arbitrary quadrilateral mesh, the transformation from the reference square to an arbitrary quadrilateral is no longer an affine mapping. As a consequence, the integrand in the transferred bilinear form are not polynomials anymore. We have to take into account of residual of the numerical quadrature. Special care and new design must be taken for the analysis of FVM on a general arbitrary quadrilateral mesh.