Obtaining a reduced kinetic mechanism for Methyl Butanoate

Abstract

The computational treatment of detailed kinetic reaction mechanisms for combustion is expensive, especially in the case of biodiesel fuels. In this way, great efforts in the search of techniques for the development of reduced kinetic mechanisms have been observed. As Methyl Butanoate (MB, $C_3H_7COOCH_3$) is an essential model frequently used to represent the ester group of reactions in saturated methyl esters of large chain, this paper proposes a reduction strategy and uses it to obtain a reduced kinetic mechanism for the MB. The reduction strategy consists in the use of artificial intelligence to define the main chain and produce a skeletal mechanism, apply the traditional hypotheses of steady-state and partial equilibrium, and justify these assumptions through an asymptotic analysis. The main advantage of the strategy employed here is to reduce the work required to solve the system of chemical equations by two orders of magnitude for MB, since the number of reactions is decreased in the same order.

1 Introduction

Energy is important for all people and combustion is one of the most widely used energy conversion processes. For this reason, researchers have explored computational methods to develop practical combustion models, especially concerning the reduction of the emission of pollutants into the atmosphere [1]. Chemical kinetic modelling has become an important tool for interpreting and understanding combustion phenomena [2], leading to the development of many detailed and reduced reaction mechanisms for the combustion of different chemical compounds.

Even today, fuels are predominantly derived from oil and coal, whose combustion leads to environmental pollution, greenhouse gas emissions and problems with energy security [3]. But the high global demand of energy and the economical and environmental constraints led to the search for renewable sources of energy, such as biodiesel.

Biodiesels are usually produced by transesterification of soybean and rapeseed oils with methanol [4, 5]. Biodiesel is an oxigenated fuel containing about 10–15$\%$ oxygen by weight. Due to extra oxygen atoms, lower $\textit{CO}$ emissions can be obtained, producing a cleaner combustion than ordinary diesel [6]. Extra oxygen also reduces particulate matter and hydrocarbon emissions.

Typical biodiesel fuels consist of mixtures of saturated and unsaturated methyl esters containing extensive carbon chains [7, 8], and such complexity and the size of their constituent molecules lead to a limited study of direct detailed kinetic modeling. For example, there is a detailed chemical kinetic reaction mechanism for soy and rapeseed biodiesel fuels in which more than 4800 species and 20,000 reactions are involved [9]. Methyl oleate (MO, $C_{19}H_{36}O_2$) generated by the EXGAS software would have more than 6000 species among 50,000 reactions, making simulation of biodiesel fuels difficult [10]. The number of radicals and isomers increases with the size and asymmetry of the molecule. The number of possible reactions and species grows nonlinearly [5].

Biodiesel derived from soybean or rapeseed oil is composed of some principal fatty acid methyl esters: methyl oleate, methyl linoleate, methyl palmitate, methyl stereate and methyl linolenate. It has energy density, cetane number, stoichiometric air–fuel ratio and heat of vaporization comparable to mineral diesel.

Biodiesel can be used in existing diesel engines without significant changes in their design, and with reduced emissions of pollutants. Unsaturated oxygenated fuels produce more NOx than saturated oxygenated fuels due to the higher adiabatic flame temperature [11]. Long ignition delay increases NOx formation [10]. For biodiesel, total NOx increases about 10$\%$ compared to that of diesel fuel combustion [12]. Most of the thermal NOx is formed after the end of the combustion. Thermal NOx formation can often be decoupled from the main combustion reaction mechanism [13].

Combustion of biofuels in the diesel engine reduces the production of particle matter, unburned hydrocarbons, sulphur oxydes, volatic organic compounds and carbon monoxide [10]. The main advantages of biodiesel compared to petrodiesel are:

• is sulphur free,

• increases the ignition quality and the lubricity of the petrodiesel, when mixed with it,

• has a higher flash point, which means it is easy to handle. On the other hand, biodiesel has some disadvantages in relation to petrodiesel: it,

• has poorer properties at low temperature, creating problems in cold climates,

• has higher viscosity, making it difficult to atomize the fuel spray,

• is less stable to exposure to air and temperature and can accelerate engine corrosion.

Methyl esters of lower chains than methyl butanoate (MB, $C_3H_7COOCH_3$, $C_5H_{10}O_2$) can not be used as biodiesel surrogates. MB contains the essential chemical structure of large chain fatty acids [14]. However, the carbon chain length of MB is much smaller than typical biodiesel fuels, facilitating numerical simulation. Larger chain methyl esters, including MB, are prone to form two major intermediates, $CH_2O$ and $C_2H_4$. They exhibit reactivity similar to that of n-alkanes of similar size [10, 15].

Fuels such as methyl butanoate, n-heptane ($nC_7H_{16}$) and methyl decanoate (MD, $C_{11}H_{22}O_2$) have similar chemical reactivity at high temperature. Both, methyl butanoate and n-heptane exhibit similar resistance to extinction. Methyl decanoate reasonably predicts the molar fraction and reactivity of most species of biodiesel with substantial decrease in computational time. Only esters with long-aliphatic main chains exhibit the cool flame behavior, which is a characteristic of biodiesels.

Brakora et al. [16] constructed a biodiesel reaction mechanism of two components composed of MB and n-heptane. Ng et al. [17] developed a compact reaction mechanism for biodiesel–diesel composed by Methyl Crotonate MC (representing the unsaturated methyl ester), MB (representing the saturated methyl ester) and n-heptane (representing the straight chain hydrocarbons).

Herbinet developed a model for MD combining the proposed mechanism for n-heptane, iso-octane and MB [10]. The combustion behavior of other saturated methyl esters is similar to that of MD [18].

Reduced mechanisms for blends of biofuels can be developed by combining the reduced mechanisms of single (isolated) components [14]. Species having a peak concentration less than $10^{-7}$ can be eliminated from the mechanism, since their concentration is insignificant [17].

Non-important species can be identified with the methods of principal component analysis, sensitivity analysis, directed relation graph, and Jacobian analysis. Additional reduction can be achieved using lumping of isomers, time-scale analysis, intrinsic low dimensional manifold, computational singular perturbation, among other methods [19].

Computational simulations with detailed kinetic mechanisms are complicated because of the existence of highly reactive radicals. The greater number of reactions in the combustion mechanisms of biodiesel generally limits the possibility of a complete validation of their mechanisms and their direct applicability [4]. The investigations of kinetics of smaller molecular species, namely surrogate fuels, which may behave kinetically similar to the constituints of actual biodiesel, have been preferred [20]. Consequently, the oxidation of various esters has been analyzed by many researches.

Due to the existence of highly reactive radicals and fast reactions in the detailed mechanisms, the associated system of governing equations is stiff. One solution to this problem is the reduction of variables, whose purpose is to replace the differential equations by algebraic relations.

The reduction strategy proposed in this paper to obtain a reduced mechanism for MB consists of defining the main chain by the use of artificial intelligence, applying the hypotheses of partial equilibrium and steady-state, and justify the assumptions through an asymptotic analysis.

The mechanism of methyl butanoate ($C_{5}H_{10}O_{2}$) provides a useful first guideline of kinetic rules to construct mechanisms for larger esters [4].

2 Mathematical tools for reduced mechanisms

For a set of $n_{r}$ elementary reactions, involving $n_{s}$ species, the rate of production $w_{S_{j}}=dS_{j}/dt$ of species $S_{j}$ is [21, 22]

$$\begin{aligned} w_{S_{j}}= \sum _{i = 1}^{n_{r}}\left( \nu _{ji}^{\prime \prime }-\nu _{ji}^{\prime }\right) w_{i}, \end{aligned}$$

(1)

where $w_{i}$ is the reaction rate i given by

$$\begin{aligned} w_{i}=k_{fi} \prod _{j = 1}^{n_{s}} \left[ S_{j}\right] ^{\nu _{ji}^{\prime }} - k_{ri} \prod _{j = 1}^{n_{s}} \left[ S_{j}\right] ^{\nu _{ji}^{\prime \prime }}, \end{aligned}$$

(2)

with $[S_{j}]=c_{j}$ representing the concentration of the species j and $k_{fi}$ and $k_{ri}$ the specific rates of reaction i (forward and backward, respectively).

Thus, a chemical kinetic problem can be written as

$$\begin{aligned} \frac{d\mathbf c }{dt} = \mathbf f (\mathbf c , \mathbf k ), \text {with}&\mathbf c (0) = \mathbf c _{0} , \end{aligned}$$

(3)

where $\mathbf {\text {c}}(t)$ is the concentration of species, $k=AT^n e^{-Ea/(RT)}$ the specific reaction rate of a given reaction [23, 24], A the frequency factor, T the temperature (in Kelvins), n the temperature exponent, Ea the activation energy (in cal / mol) and R the gas constant (in cal / (molK)).

3 Numerical formulation

The mixture fraction is a useful variable in diffusion flame analysis, and represents the ratio between the mass fraction of fuel in the unburned mixture to the mass fraction in the original fuel stream. This variable plays a role similar to scalar G in premixed combustion. The mixture fraction, $Z= Y_{F,u}/Y_{F,1}$, measures the mixture of reactants and is mainly related to large flow scales [25]. It can be written as

$$\begin{aligned} Z = \frac{\upsilon Y_F - Y_{O_2} + Y_{O_2,2}}{\upsilon Y_{F,1} + Y_{O_2,2}}, \end{aligned}$$

(4)

where $\upsilon = (\upsilon _{O_2}W_{O_2})/(\upsilon _{F} W_F)$, $Y_{O_2,2}$ is the mass fraction of $\mathrm {O}_2$ in the oxidant stream, and $W_i$ the molecular weight of the species i.

Consider a jet diffusion flame in which the fuel, supplied from a round nozzle with diameter d and output velocity $u_0$, mixes with the surrounding air by convection and diffusion. The jet flame is chosen because it represents the class of nonpremixed flames.

For this case, we have a problem governed by the equations of momentum, mass fraction of species and energy. The Favre filtering becomes convenient to write the equations for turbulent flows [26]. This average helps to avoid terms such as $\rho 'u'$, which comes from the time-average method. Therefore, the set of Favre averaged equations is given by

$$\begin{aligned}&\frac{\partial \overline{\rho }\widetilde{v}_i}{\partial t} + \frac{\partial (\overline{\rho } \widetilde{v_i} \widetilde{v}_j)}{\partial x_j} = - \frac{\partial \overline{p}}{\partial x_i} + \frac{\partial }{\partial x_j}\left( \frac{1}{Re} \sigma _{ij}\right) + \widetilde{S}_{v_i}, \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\partial \overline{\rho }\widetilde{Y}_i}{\partial t} + \frac{\partial (\overline{\rho } \widetilde{v_j} \widetilde{Y}_i)}{\partial x_j} = \frac{\partial }{\partial x_j}\left( \overline{\rho \mu _T} \frac{\partial \widetilde{Y}_i}{ \partial x_j}\right) + \widetilde{\dot{w_i}}+ \widetilde{S}_{Y_i}, \end{aligned}$$

(6)

$$\begin{aligned}&\frac{\partial \overline{\rho }\widetilde{h}}{\partial t} + \frac{\partial (\overline{\rho } \widetilde{v_j} \widetilde{h})}{\partial x_j} = \frac{\partial }{\partial x_j} \left( \overline{\rho \mu _T} \frac{\partial \widetilde{h}}{\partial x_j} \right) + \widetilde{S}_{h}, \end{aligned}$$

(7)

where $\overline{\rho }$ is the averaged density, $\widetilde{v}$ the Favre averaged velocity, $\widetilde{Y_i}$ the Favre averaged mass fraction of species i, $\widetilde{\dot{w_i}}$ the reaction rate of the species i, $\bar{\mu }_T$ the eddy viscosity, $\widetilde{h}$ the Favre averaged enthalpy.

The source terms $\widetilde{S}_{u_i}$, $\widetilde{S}_{Y_i}$ and $\widetilde{S}_h$ consider the overall effects of droplets for MB, and are given by [27]

$$\begin{aligned}&\widetilde{S}_{v_i} = - \frac{1}{V} \sum _{i=1}^{N} \left( f_1 \frac{m_d}{\tau _d} \left( u_i - u_d\right) + \frac{d m_d}{d t} u_{d,i}\right) \end{aligned}$$

(8)

$$\begin{aligned}&\widetilde{S}_{Y_i} = - \frac{1}{Y_{F,u} V} \sum _{i=1}^{N} \frac{d m_d}{d t} \end{aligned}$$

(9)

$$\begin{aligned}&\widetilde{S}_{h} = - \frac{1}{V} \sum _{i=1}^{N} \left( \frac{1}{2 E_c} \frac{d}{d t} \left( m_d u_{d,i} u_{d,i}\right) + Q_d + \frac{d m_d}{d t} h_{V,s} \right) \end{aligned}$$

(10)

where V is the cell volume, N the number of droplets, $m_d$ the mass of droplet, $\tau _d$ the droplet response time, $\rho _d$ the droplet density, $d_d$ the droplet diameter, $u_{d,i}$ the droplet velocity, $Y_{F,u}$ the fuel mass fraction in the unburned mixture, $E_c$ the number of Eckert, $Q_d$ the heat transfer by convection and $h_{V,s}$ the enthalpy of the vapor on the surface of the droplet. The lagrangian equations for the droplets of MB are given by:

$$\begin{aligned}&\frac{d m_d}{d t} = -\frac{S_h}{3 S_c} \frac{m_d}{\tau _d} ln\left( 1+B_M\right) \end{aligned}$$

(11)

$$\begin{aligned}&\frac{d u_{d,i}}{d t} = -\frac{f_1}{\tau _d}\left( u_i-u_{d,i}\right) + g_i \end{aligned}$$

(12)

$$\begin{aligned}&\frac{d T_d}{d t} = -\frac{Q_d}{m_d C_{P_d}} + \frac{L_v}{m_d C_{P_d}} \frac{d m_d}{d t} \end{aligned}$$

(13)

where $f_1$ is a correction factor due to Stokes drag, $S_h$ the Sherwood number, $S_c$ the Schmidt number, $B_M$ the mass transfer number, $g_i$ the acceleration of gravity, $C_{P_d}$ the specific heat of the liquid droplet, $L_V$ the latent heat of vaporization at $T_d$.

The following considerations were made to simplify the system of equations:

• The mean viscous tensor $\left( \overline{\tau }_{j,i} \right)$ was neglected when compared to the Reynolds stress tensor $(\text{ whose } \text{ components } \text{ are } \overline{\rho } \widetilde{u^{\prime \prime } v^{\prime \prime }})$;

• The molecular transport terms in the mass fraction and temperature equations $(\overline{\rho {\mu } \mathbf {\nabla } Y_i} \text{ and } ~ \overline{\rho \mu \mathbf {\nabla } h} \text{, } \text{ respectively })$ were neglected when compared to the turbulent transport terms $(\overline{\rho } \widetilde{v^{\prime \prime } Y^{\prime \prime }_{i}} \text{ and } \overline{\rho } \widetilde{v^{\prime \prime } h^{\prime \prime }})$;

• The Reynolds stress and the turbulent transport terms were modeled using the gradient hypothesis: $\overline{\rho }\widetilde{v^{\prime \prime }_i v^{\prime \prime }_j} = - \overline{\rho } \mu _T \frac{\partial \widetilde{v_i}}{\partial x_j}$, $\overline{\rho } \widetilde{v^{\prime \prime }_i Y^{\prime \prime }_i} = - \overline{\rho } {\mu _T} \frac{\partial {\widetilde{Y}_i}}{\partial x_j}$, $\overline{\rho } \widetilde{v^{\prime \prime }_i h^{\prime \prime }} = - \rho \mu _T \frac{\partial {\widetilde{h}}}{\partial x_j}$.

The set of equations was solved numerically. A central finite difference scheme was adopted for spatial derivatives of first and second orders. A nonuniform structured mesh was used to concentrate sufficient points at the exit of the injector and along the centerline of the burner.

$$\begin{aligned} \left. \left( \frac{\partial f}{\partial x}\right) \right| _{(i,j,k)}&= \frac{ f_{(i+1,j,k)} - f_{(i-1,j,k)} }{2 \Delta x} \text {,} \end{aligned}$$

(14)

$$\begin{aligned} \left. \left( \frac{\partial f}{\partial y}\right) \right| _{(i,j,k)}&= \frac{ f_{(i,j+1,k)} - f_{(i,j-1,k)} }{2 \Delta y} \text {,} \end{aligned}$$

(15)

$$\begin{aligned} \left. \left( \frac{\partial ^2 f}{\partial y^2}\right) \right| _{(i,j,k)}&= \frac{ f_{(i,j+1,k)} - 2 f_{(i,j,k)} + f_{(i,j-1,k)} }{\Delta y^2} \text {,} \end{aligned}$$

(16)

and in a similar way in other directions. A section of the mesh is shown in Fig. 1.

Fig. 1

Sketch of the mesh used in the numerical simulation of the burner

This set of equations can be summarized as:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial y}{\partial t}&= F(y) \\ y(t_0)&= y_0 \end{aligned} \qquad y = \left( \widetilde{\rho },\widetilde{v_i},\widetilde{Y}_k,\widetilde{h}\right) ^T. \right. \end{aligned}$$

(17)

Detailed kinetic systems for biodiesel surrogates generally have significant stiffness due to the difference between the time scales of the reactive species. This causes difficulties in the convergence of purely explicit numerical methods, because rigidity imposes severe limitations on the time-step size [28]. The eigenvalues of the Jacobian matrix for F characterize the stability of the system. Generally, a system is considered stiff when its eigenvalues are very different in magnitude [29].

In this way, the system of equations (Eq. 17) was separated into two parts, one part of high rigidity g(y), and another part of low stiffness f(y),

$$\begin{aligned} \frac{\partial y}{\partial t} = f(y) + g(y)\text {,} \end{aligned}$$

(18)

where f(y) corresponds to the flow (advection and diffusion), while g(y) corresponds to the terms of chemical origin. The term g(y) has high rigidity due to the different time scales of the various reactions involved in the mechanism.

For the integration of the system of equations, the Rosenbrock method for g(y) and the Runge–Kutta–Fehlberg for f(y) were chosen. The Rosenbrock method is a semi-implicit Runge–Kutta method, defined as [30]:

$$\begin{aligned}&\left\{ \begin{aligned} \frac{dy}{dt}&= G(y) \\ y(t_0)&= y_0 \text {,} \end{aligned} \right. \end{aligned}$$

(19)

$$\begin{aligned}&\begin{aligned} y_{n+1}&= y_{n} + h \sum \limits _{i=1}^{s} {\omega _i k_i} \text {,} \\ k_i&= G\left( y_{n} + h \sum \limits _{j=1}^{i-1}{\alpha _{ij}k_{j}}\right) + h \left. \frac{\partial G}{\partial y}\right| _{\left( y_n + \sum \limits _{j=1}^{i-1}{\beta _{ij}k_{j}}\right) } \sum \limits _{j=1}^{i} \gamma _{ij} k_j \text {,} \end{aligned} \end{aligned}$$

(20)

where $\omega _i$, $\alpha _{ij}$, $\beta _{ij}$ and $\gamma _{ij}$ are constants defined by the method, whose values are determined according to the order of consistency and stability desired.

To solve this problem, a four-stage, four-order Rosenbrock method developed by Bui and Bui [31] was used. The implementation considers $\gamma _{ij} = c \phantom {.} \delta _{i,j}$ and $\beta _{ij} = 0$, where $\delta _{i,j}$ is the Kronecker delta. Thus, the system can be written according to:

$$\begin{aligned}&y_{n+1} = y_{n} + h \sum \limits _{i=1}^4{\omega _i k_i}\end{aligned}$$

(21)

$$\begin{aligned} \begin{aligned} k_1&= {A_n}^{-1} G\left( y_n\right) \\ k_2&= {A_n}^{-1} G\left( y_n + h \alpha _{21} k_1 \right) \\ k_3&= {A_n}^{-1} G\left( y_n + h\left( \alpha _{31} k_1 + \alpha _{32} k_2 \right) \right) \\ k_4&= {A_n}^{-1} G\left( y_n + h\left( \alpha _{41} k_1 + \alpha _{42} k_2 + \alpha _{43} k_3 \right) \right) \\ A_n&= \left[ I - \left. c h \frac{\partial G}{\partial y}\right| _{y_n} \right] \end{aligned} \end{aligned}$$

(22)

where I corresponds to the identity matrix. The constants $a_{ij}$, $\omega _i$ and c have their values set out in Table 1.

Table 1 Rosenbrock method parameters [31]

Unlike the implicit Runge–Kutta method, which requires the resolution of a nonlinear system at each stage of integration, the Rosenbrock procedure defined in (21) requires only the resolution of a system of linear equations for each step, a procedure simpler compared to purely implicit methods [32].

To solve the low stiffness part of Eq. (18), f(y), the Runge–Kutta–Fehlberg method (RKF45) was applied. This method provides two different order approaches for the solution, 4th and 5th orders, where the higher-order approach uses all calculated coefficients in the lowest order. This method is given by:

$$\begin{aligned} \begin{aligned} y_{n+1}&= y_n + h \sum \limits _{j=1}^{6} \omega _ik_i + \mathcal {O} \left( h^4\right) \\ y_{n+1}^{*}&= y_n + h \sum \limits _{j=1}^{6} \omega _i^{*} k_i + \mathcal {O} \left( h^5\right) \end{aligned} \end{aligned}$$

(23)

where

$$\begin{aligned} \begin{aligned} k_1&= f\left( y_n \right) \\ k_2&= f\left( y_n + h \alpha _{21} k_1 \right) \\ k_3&= f\left( y_n + h \left( \alpha _{31} k_1 + \alpha _{32} k_2\right) \right) \\ k_4&= f\left( y_n + h \left( \alpha _{41} k_1 + \alpha _{42} k_2 + \alpha _{43} k_3\right) \right) \\ k_5&= f\left( y_n + h \left( \alpha _{51} k_1 + \alpha _{52} k_2 + \alpha _{53} k_3 + \alpha _{54} k_4\right) \right) \\ k_6&= f\left( y_n + h \left( \alpha _{61} k_1 + \alpha _{62} k_2 + \alpha _{63} k_3 + \alpha _{64} k_4+ \alpha _{65} k_4\right) \right) \end{aligned} \end{aligned}$$

(24)

and the local error can be estimated as:

$$\begin{aligned} \epsilon = \left| y_{n+1} - y_{n+1}^{*}\right| = \sum \limits _{i=1}^{6} h \left( \omega _{i} - \omega _{i}^{*}\right) k_i \end{aligned}$$

(25)

The coefficients used in RKF45 are given in Table 2.

Table 2 Parameters used in the Runge–Kutta–Fehlberg method [33]

3.1 Artificial neural networks (ANNs)

The right side of the differential equations for chemical kinetics

$$\begin{aligned} \widetilde{\dot{w}_i} = \frac{d \widetilde{Y}_i}{d t} = f \end{aligned}$$

(26)

is often a quasi-linear function of the parameters to be estimated [34].

Artificial Neural Networks (ANNs) can be used as an alternative to look-up tables during numerical simulation (in LES) of combustion with reduced computational time and memory required [35]. The goal is to teach the network to associate the response with the various types of input data. The main disadvantage of the look-up (LUT) tables, as well as ISAT, In-Situ Adaptive Tabulation, and ILDM, Intrinsic Low Dimension Manifold, is the rapid growth of computational memory with model reactions [36]. The scheme of a generic ANN architecture for chemical kinetic calculations is given in Fig. 2.

Fig. 2

Schematic representation of an ANN for chemical kinetic calculations

The main problem associated with ANN simulations is the generation of the dataset that covers the chemical state of interest [37]. Often the input and output data are scaled or standardized to vary between zero and 1. However ANNs can not predict the absolute zero value, which can be bypassed by choosing a small enough value, below which the reaction rates are considered void.

About 10–20$\%$ of the thermochemical data is randomly selected to be used in the network test, while the remaining is used for training. A complex part of the learning algorithm is determining which input contributed most to an incorrect output, and how this can be corrected.

Training data should be entered randomly to prevent the network from memorizing a specific data set, to make the procedure of general use. The ANN receives as input data the temperature and mass fraction of the species and generates the rate of reaction of the species involved, as quoted by Zhou et al. [38].

There is no theoretical limit to the number of intermediate layers, but one or two [37] are often sufficient. Several configurations with a large number of intermediate layers have been tested, but four layers, one input layer, two intermediate layers, and one output layer, were sufficient to solve complex mechanisms.

The back-propagation algorithm for multi-layer ANNs is used, because it is the most popular. The algorithm is based on the descending gradient procedure and consists of two parts:

• the input is propagated forward;

• the error is propagated backwards.

The difference between the output of the last layer and the desired output is back-propagated to the previous layers, scaled by the derivative of the transfer function. The transfer function of the last layer (linear, for example) may be different from that used in the rest of the network (often the sigmoid, because it has a good level of noise immunity and has a continuous derivative), in order to accelerate the training process.

3.1.1 Back-propagation algorithm

The basic learning procedure is given by:

• 1. Initialize the weights $w_ {ij}$ connecting nodes using small random values;

• 2. Provide some input data $V_i ^ k$ and corresponding output values, $V_i ^ t$, where k corresponds to the layer, i to the node number, and t is the desired output value;

• 3. Propagate the signal forward on the network using

  $$\begin{aligned} \mathrm{net}_j ^ k = \sum _i w_{ij} ^ k V_i ^{k-1} + \beta _j \end{aligned}$$

  (27)

  and

  $$\begin{aligned} V_i ^ k = F \left( \mathrm \mathrm{{net}}_i ^ k\right) , \end{aligned}$$

  (28)

  where $w_{ij}$ are the weights of the connections between the nodes i and j, $V_i^{k-1}$ is the signal of node i and layer $(k-1)$, $\beta$ is the limit value (or bias) of node j and F is the transfer function (usually a sigmoid), $F (\mathrm {net}_i ^ k) = \left( {1 + exp (-\mathrm {net}_i ^ k)}\right) ^{-1}$;

• 4. Obtain the $\dfrac{\partial E}{\partial w_{ij}}$ values for the output layer, that is

  $$\begin{aligned} \frac{\partial E}{\partial w_{ij}^k} = - \left( V_i ^ t - V_i ^ k\right) F^{\prime }\left( \mathrm {net}_i ^ k\right) V_j^{k-1}, \end{aligned}$$

  (29)

  The error function is given by

  $$\begin{aligned} E = \frac{1}{2} \sum _i \left( V_i ^ t - V_i ^ k\right) ^ 2 \end{aligned}$$

  (30)

  and $F^{\prime }(\mathrm {net}_i ^ k) = F (\mathrm {net}_i ^ k) [1-F (\mathrm {net}_i ^ k)]$;

• 5. Obtain $\dfrac{\partial E}{\partial w_{ij}}$ of the previous layers propagating the error

  $$\begin{aligned} \dfrac{\partial E}{\partial w_{ij}^{k-1}} = \left( \sum _m \delta _m^{k} w_{mi}^{k} \right) F^{\prime }\left( \mathrm {net}_i ^{k-1}\right) V_j^{k-2} \text {;} \end{aligned}$$

  (31)

  where

  $$\begin{aligned} \delta _m^k = \left\{ \begin{aligned} - \left( V_m ^ t - V_m ^ k\right) F^{\prime }\left( \mathrm {net}_m ^ k\right) \text {,} \qquad ~~~\text { if k is an output layer} \\ \sum _n \delta _n^{k+1} w_{nm}^{k+1} F^{\prime }\left( \mathrm {net}_m ^ k\right) \text {,} \qquad \text { if k is a hidden layer} \end{aligned} \right. \end{aligned}$$

  (32)

• 6. Use $\dfrac{\partial E}{\partial w_{ij}}$ to recalculate the weights of the connections as:

  $$\begin{aligned} w_{ij} ^ {new} = w_{ij} ^\mathrm{{old}} + \eta \dfrac{\partial E}{\partial w_{ij}}, \end{aligned}$$

  (33)

  where $\eta$ corresponds to the global learning coefficient, which is constant for all iterations;

• 7. Go back to step 2 and repeat the procedure until the convergence;

• 8. Repeat for other examples (datasets).

The back-propagation algorithm is based on the principle of error correction. The basic idea of the descending gradient rule is to find a distribution of weights between the connections, which provides minimal global error [35]. The use of differences among values (increments) increases the sensitivity of the network [36].

In addition, ANNs can be incorporated into LES simulations to decrease computational time by using them in sub-grid models. The neural network can be used as a sub-grid in both chemical kinetics and turbulence in reactive flows.

4 Obtaining a reduced mechanism for MB

Mechanism reduction is a process of removing some reactions from the complete mechanism to achieve certain objectives, such as appropriate temperature and species concentration profiles [11].

Methyl butanoate, MB ($C_5H_{10}O_2$), was one of the first fuels to be proposed to emulate the reaction kinetics of biodiesel [20]. However, methyl butanoate cannot be considered as an appropriate surrogate for biodiesel for low temperatures. But molecules such as MB and MC ($C_5H_8O_2$) elucidate the effect of oxygenation on combustion [11], and models for large mechanisms can be contructed based on smaller mechanisms due to their hierarchical structure. Therefore, MB is an essential model to represent reactions of ester group in large saturated methyl esters [39].

The balance equations for the 40 species of the skeletal mechanism of 75 reactions shown in Tables 3, 4 and 5 which comes from the use of the artificial intelligence, are:

• 1. $L\left( C_5H_{10}O_2 \right) = -\,w_{1}-w_{2}-w_{3}-w_{4}-w_{5}$

• 2. $L\left( CO_2 \right) = w_{1}+w_{8}+w_{13}+w_{14}+w_{28}+w_{40}-w_{42}+w_{64}+w_{66}$

• 3. $L\left( nC_3H_7 \right) = w_{1}+w_{3}+w_{4}-w_{17}-w_{18}$

• 4. $L\left( CH_3 \right) = w_{1}+w_{8}+w_{11}+w_{13}+w_{39}-w_{42}-w_{52}-w_{54}$

• 5. $L\left( CH_2CO \right) = w_{2}+w_{7}+w_{10}+w_{12}+w_{15}-w_{39}-w_{40}-w_{41}$

• 6. $L\left( CH_3O \right) = w_{2}+w_{7}+w_{10}+w_{12}+w_{14}+w_{15}+w_{16}-w_{44}+w_{50}+2w_{52}-w_{57}-w_{65}$

• 7. $L\left( C_2H_5 \right) = w_{2}-w_{22}$

• 8. $L\left( CH_3OCO \right) = w_{3}+w_{9}+w_{42}+w_{45}+w_{46}+w_{47}+w_{48}-w_{49}-w_{50}-w_{51}+w_{65}$

• 9. $L\left( H \right) = -\,w_{4}-w_{5}+w_{6}-w_{11}-w_{12}-w_{16}+w_{17}+w_{22}+2w_{28}-w_{30}-w_{39}-w_{45}-w_{51}+w_{59}-w_{61}+w_{66}-w_{69}-w_{70}-w_{71}+w_{72}+w_{74}-w_{75}$

• 10. $L\left( CH_3OCHO \right) = w_{4}-w_{43}-w_{44}-w_{45}-w_{46}-w_{47}+w_{51}$

• 11. $L\left( C_5H_9O_2 \right) = w_{5}-w_{6}-w_{7}$

• 12. $L\left( H_2 \right) = w_{5}+w_{30}+w_{45}+w_{61}-w_{72}-w_{74}$

• 13. $L\left( C_5H_8O_2 \right) = w_{6}-w_{8}-w_{9}-w_{10}-w_{11}-w_{12}$

• 14. $L\left( C_2H_4 \right) = w_{7}+w_{12}+w_{14}-w_{23}$

• 15. $L\left( C_3H_5 \right) = w_{8}+w_{9}$

• 16. $L\left( OH \right) = -\,w_{10}-w_{14}-w_{15}+w_{19}+w_{20}+w_{21}-w_{23}-w_{25}-w_{31}+w_{32}-w_{36}+w_{37}-w_{41}-w_{43}-w_{47}+w_{49}-w_{54}-w_{55}-w_{56}+w_{60}-w_{63}+w_{64}-w_{66}-w_{67}+w_{69}+2w_{70}+w_{71}+w_{72}+2w_{73}-w_{74}$

• 17. $L\left( CH_3CHO \right) = w_{10}+w_{22}-w_{35}-w_{36}-w_{37}-w_{38}$

• 18. $L\left( C_4H_6O_2 \right) = w_{11}-w_{13}-w_{14}-w_{15}-w_{16}$

• 19. $L\left( C_2H_3 \right) = w_{13}+w_{20}+w_{23}-w_{24}+w_{34}$

• 20. $L\left( CH_2O \right) = w_{15}+w_{20}+w_{57}+w_{59}-w_{60}+w_{62}$

• 21. $L\left( C_2H_3CHO \right) = w_{16}+w_{21}-w_{31}-w_{32}-w_{33}$

• 22. $L\left( C_3H_6 \right) = w_{17}+w_{18}-w_{19}$

• 23. $L\left( O \right) = -\,w_{19}-w_{22}-w_{26}-w_{32}-w_{37}-w_{40}+w_{58}-w_{60}+w_{71}-w_{72}-w_{73}$

• 24. $L\left( C_3H_5(a) \right) = w_{19}-w_{20}-w_{21}$

• 25. $L\left( H_2O \right) = w_{23}+w_{25}+w_{29}+w_{31}+w_{36}+w_{43}+w_{47}+w_{54}+w_{55}+w_{56}+w_{63}+w_{67}+w_{69}-w_{73}+w_{74}$

• 26. $L\left( O_2 \right) = -\,w_{18}-w_{21}-w_{24}-w_{27}-w_{28}-w_{29}-w_{35}-w_{53}-w_{57}-w_{58}+w_{62}-w_{68}-w_{71}-w_{75}$

• 27. $L\left( HO_2 \right) = w_{18}-w_{20}+w_{24}-w_{33}+w_{35}-w_{38}-w_{46}-w_{49}+w_{57}-w_{62}-w_{64}+w_{67}+2w_{68}-w_{70}+w_{75}$

• 28. $L\left( C_2H_2 \right) = w_{24}-w_{25}$

• 29. $L\left( C_2H \right) = w_{25}-w_{26}-w_{27}-w_{53}$

• 30. $L\left( CO \right) =w_{26}+w_{27}+w_{29}+w_{34}+w_{39}+w_{41}+w_{49}+w_{50}+w_{53}+w_{61}+w_{63}-w_{64}-w_{65}-w_{66}$

• 31. $L\left( CH \right) = w_{26}+w_{30}+w_{55}-w_{58}$

• 32. $L\left( HCO \right) = w_{27}+w_{53}+w_{58}+w_{60}-w_{61}-w_{62}-w_{63}$

• 33. $L\left( CH_2 \right) = -\,w_{28}-w_{29}-w_{30}+w_{40}+w_{54}-w_{55}$

• 34. $L\left( C_2H_3CO \right) = w_{31}+w_{32}+w_{33}-w_{34}$

• 35. $L\left( H_2O_2 \right) = w_{33}+w_{38}+w_{46}-w_{67}-w_{68}-w_{69}$

• 36. $L\left( CH_3CO \right) = w_{35}+w_{36}+w_{37}+w_{38}$

• 37. $L\left( CH_2OH \right) = w_{41}+w_{56}-w_{59}$

• 38. $L\left( CH_2OCHO \right) = w_{43}+w_{44}-w_{48}$

• 39. $L\left( CH_3OH \right) = w_{44}-w_{56}$

• 40. $L\left( CH_3O_2 \right) = w_{49}-w_{52}$

Table 3 MB skeletal mechanism—part I

Table 4 MB skeletal mechanism—part II

Table 5 MB skeletal mechanism—part III

Table 6 MB reduced mechanism

Table 6 shows the reduced mechanism for MB; the main intermediate species are contained in this mechanism.

The following species were considered to be in steady state: $nC_3H_7$, $CH_3$, $CH_2CO$, $C_2H_5$, $C_5H_9O_2$, $C_3H_5$, $CH_3CHO$, $C_2H_3$, $C_2H_3CHO$, $C_3H_6$, $HO_2$, O, $C_3H_5(a)$, $C_2H$, CH, $CH_2$, $C_2H_3CO$, $H_2O_2$, $CH_3CO$, $CH_2OH$, $CH_2OCHO$, $CH_3O_2$.

For the eliminated species the algebraic relations are:

• $nC_3H_7$: $w_{18}=w_1+w_3+w_4-w_{17}$

• $CH_3$: $w_{54}=w_1+w_8+w_{11}+w_{13}+w_{39}-w_{42}-w_{52}$

• $CH_2CO$: $w_{41}= w_2+w_7+w_{10}+w_{12}+w_{15}-w_{39}-w_{40}$

• $C_2H_5$: $w_{22}= w_2$

• $C_5H_9O_2$: $w(7)= w_5-w_6$

• $C_3H_5$: $w(9)= -\,w_8$

• $CH_3CHO$: $w_{38}=w_{10}+w_{22}-w_{35}-w_{36}-w_{37}$

• $C_2H_3$: $w_{34}= -\,w_{13}-w_{20}-w_{23}+w_{24}$

• $C_2H_3CHO$: $w_{33}= w_{16}+w_{21}-w_{31}-w_{32}$

• $C_3H_6$: $w_{19}= w_{17}+w_{18}$

• $HO_2$: $w_{70}= w_{18}-w_{20}+w_{24}-w_{33}+w_{35}-w_{38}-w_{46}-w_{49}+w_{57}-w_{62}-w_{64}+w_{67}+2w_{68}+w_{75}$

• O: $w_{73}= -\,w_{19}-w_{22}-w_{26}-w_{32}-w_{37}-w_{40}+w_{58}-w_{60}+w_{71}-w_{72}$

• $C_3H_5(a)$: $w_{21}= w_{19}-w_{20}$

• $C_2H$: $w_{53}= w_{25}-w_{26}-w_{27}$

• CH: $w_{58}= w_{26}+w_{30}+w_{55}$

• $CH_2$: $w_{55}= -\,w_{28}-w_{29}-w_{30}+w_{40}+w_{54}$

• $C_2H_3CO$: $w_{33}= -\,w_{31}-w_{32}+w_{34}$

• $H_2O_2$: $w_{69}= w_{33}+w_{38}+w_{46}-w_{67}-w_{68}$

• CH3CO: $w_{38}= -\,w_{35}-w_{36}-w_{37}$

• $CH_2OH$: $w_{59}= w_{41}+w_{56}$

• $CH_2OCHO$: $w_{48}= w_{43}+w_{44}$

• $CH_3O_2$: $w_{52}= w_{49}$

After some algebraic operations, the reduced mechanism rates result in:

• $w_{I}=w_1+w_2+w_3+w_4+w_5$

• $w_{II}=w_{I}-w_6+w_{10}+w_{11}+w_{12}$

• $w_{III}=w_{II}-w_{11}+w_{13}+w_{14}+w_{15}+w_{16}$

• $w_{IV}=w_{III}-w_4+w_{43}+w_{44}+w_{45}+w_{46}+w_{47}-w_{51}$

• $w_{V}=w_{III}-w_5+w_6-w_{12}-w_{14}+w_{23}$

• $w_{VI}=w_{V}-w_{24}+w_{25}$

• $w_{VII}=w_{IV}-w_3+w_8-w_{42}-w_{43}-w_{44}-w_{45}-w_{47}+w_{49}+w_{50}+w_{51}-w_{65}$

• $w_{VIII}=w_{VII}-w_{44}+w_{56}$

• $w_{IX}=w_{VIII}-w_2-w_5+w_6-w_{10}-w_{12}-w_{14}-w_{15}-w_{16}+w_{44}-4w_{49}-w_{50}+w_{57}+w_{65}$

• $w_{X}=+w_{IX}-w_2-w_5+w_6-w_{10}-w_{12}-2w_{15}-w_{20}+w_{39}+w_{40}-w_{56}-w_{57}+w_{60}-w_{62}$

• $w_{XI}=w_{X}-w_1-w_8-w_{11}-w_{13}-w_{25}+w_{28}+w_{29}-w_{39}-w_{40}+w_{42}+w_{49}-w_{60}+w_{61}+w_{62}-w_{63}$

• $w_{XII}=w_1+w_8+w_{13}+w_{14}+w_{28}+w_{40}-w_{42}+w_{64}+w_{66}$

• $w_{XIII}=-w_{II}-w_{VI}-w_{1}-w_{8}-w_{11}-w_{13}-w_{17}-w_{20}+w_{24}+w_{25}+2w_{28}+2w_{29}+2w_{30}+w_{35}-w_{39}-w_{40}-w_{42}+w_{49}+w_{57}-w_{62}+w_{68}+w_{71}+w_{75}$

• $w_{XIV}=w_{III}-w_{VI}-w_{IX}-w_{XI}-w_{XII}+3w_{XIII}+w_{5}+w_{30}+w_{45}+w_{61}-w_{72}+w_{74}$

5 Stiffness of differential equations

Stiffness in differential equations occurs when the rates of change of two or more dependent variables of the same system differ by a great proportion. The numerical solution of stiff systems of equations is difficult and time consuming (and therefore, costly) because stiffness imposes severe step-size limitations on the numerical method [28].

The eigenvalues of the Jacobian matrix can characterize the stability of the system. Generally, the system is stiff when the eigenvalues differ considerably in magnitude.

A commonly used variable for analyzing the stiffness of a system is the stiffness ratio given by

$$\begin{aligned} S = \frac{\text {max}|\text {Re}(\lambda _i)|}{\text {min}|\text {Re}(\lambda _i)|} \text {,} \end{aligned}$$

(34)

where $\lambda _i$ corresponds to the eigenvalues of the local Jacobian Matrix.

The stiffness ratio does not take into account the integration interval $[t_0,t_f]$. A small value of S could contribute to raising stiffness if the interval is too long.

Another variable used to characterize stiffness is the dimensionless stiffness index

$$\begin{aligned} S = \frac{T}{\tau } \text {,} \end{aligned}$$

(35)

where T is the time scale used and $\tau = -\, \left[ \text {Re}(\lambda )\right] ^{-1}$, with $\lambda$ being the eigenvalue with the largest negative real part (spectral radius).

The skeletal mechanism used to develop the reduced mechanism strongly influences the stiffness of the latter [40].

6 Numerical results

To build a burner one can surround a high velocity jet of fuel with a lower speed annular pilot flame. Consider the burner as shown in Fig. 3. The duct has a cylindrical cross section with $D_e=1$ (dimensionless, equivalent to 30 cm) and a cylindrical tube that injects fuel with $d=0.025$ (or 7.5 mm); the coflow tube has a diameter $D=1.068~d$ and the length of the burner is $L=11~D_e$. Through the coflow tube fuel is injected with the same composition of the jet, however with 1/50 speed of the main jet. The number of grid points was taken as $199\times 51 \times 51$ in directions (x, y, z), respectively; x corresponds to the axial direction.

Fig. 3

Sketch of a jet diffusion flame

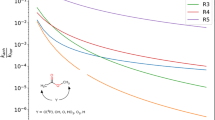
Figure 4 shows the results for the mass fractions of $\mathrm {C_5H_{10}O_2}$ and $\mathrm {O_2}$ on the left side, while on the right side of the same figure are shown the molar fractions of $\mathrm {CO_2}$, $\mathrm {CO}$ and $\mathrm {OH}$ along the domain of the mixture fraction. These products have their maximum values close to the stoichiometric surface of the flame ($Z \approx 0.1$), where there are ideal conditions for burning. This graph shows that fuel consumption as well as oxidizer comsumption are close to the Burke–Schumann solution.

To compare the numerical results with the data available in the literature, we used the work of Niemann et al. [41], in which the authors simulated a diffusion flame of MB with the same initial conditions applied in this study. The results obtained are in accordance with those presented by Niemann et al.

Fig. 4

Numerical result for the mass fractions of $\mathrm {MB}$ and $\mathrm {O_2}$ on the left size, and molar fractions of $\mathrm {CO_2}$, $\mathrm {CO}$ and $\mathrm {OH}$ on the right side to the flame of MB

Fig. 5

Temperature for MB flame

Figure 5 shows the temperature of the flame in the mixture fraction space. The adiabatic flame temperature for the MB is approximately $2000 \mathrm {K}$, which is in agreement with the results obtained in this simulation.

7 Conclusions

The present paper provides a new reduced kinetic mechanism for MB diffusion flames. In addition, we propose the use of Artificial Intelligence to the prefered path of combustion setting. Starting with a detailed mechanism, a skeletal mechanism of 75 steps and a reduced mechanism of fourteen steps were developed for the methyl butanoate. Using the steady-state assumption, wich is justified by the asymptotic analysis, provided the final level of reduction.

Often, the skeletal mechanisms found in the literature have number of species that vary between 50 and 150 and the number of reactions between 120 and 900. Such mechanisms are still too big for CFD simulations on small computers. In addition, the reactions of the ester group often include species like MP2D ($C_4H_6O_2$), MP2DMJ ($C_4H_5O_2$), $C_2H_3CO$, $CH_3OCO$, $C_2H_3$, $CH_3O$, $CH_3$, CO and $CO_2$, whose reactions were selected using artificial intelligence in this work. That’s because, with increasing temperature, the ester group begins to be consumed, and the consumption of $CH_3OCO$ dominates the early formation of $CO_2$ during the oxidation of methyl esters [42].

The main advantage of using reduced mechanism is the decrease of the computational cost to solve the system of differential equations, two orders of magnitude for the MB, as the number of reactions is reduced in the same order. In addition, the rate constants of the chemical reactions were kept unchanged in the reduction process.