1 Introduction

The viscosity of normal liquid 3He has been the topic of many previous experimental investigations [1–4]. Many measurements have been made with semi-circular vibrating wire resonators which can be conveniently modelled as straight cylinders.

The viscous drag on a straight cylindrical wire oscillating in a classical fluid was first calculated by Stokes [5]. The Stokes theory neglects the non-linear term in the Navier-Stokes equation. This is a reasonable approximation for most experimental conditions except at low frequencies of oscillation. The calculations give precise values for the frequency shift and for the frequency width of the wire resonance in terms of the Stokes functions k and k′. These are functions of the parameter γ=a/δ where a is the wire radius and δ is the viscous penetration depth given by

$$ \delta = \sqrt{\frac{\eta}{\rho \pi f}} $$
(1)

where η and ρ are the viscosity and density of the fluid, respectively, and f is the frequency of the wire motion. The Stokes functions are generally quite complex and there is no simple analytic form except in the limit of large γ, corresponding to high frequencies or low viscosity. Below we present measurements of the viscosity of normal liquid 3He using a quartz tuning fork and we show that tuning forks can be used as simple and convenient thermometers for quantum fluids.

For many years quartz tuning forks have been used in scanning probe microscopy [6]. Tuning forks/cantilevers have been used in classical fluids [7] to determine fluid viscosity and density. Over the past decade, quartz tuning fork techniques have been developed for studying quantum fluids at low temperatures [8, 9].

The geometry of tuning forks is more complicated than that of a vibrating wire, and there is no precise theory for the viscous drag. However, a simple phenomenological theory has been suggested [9] which incorporates an undetermined geometrical factor. Once this factor is known, e.g. by using some fixed calibration point, then the tuning fork can be used to determine the fluid viscosity. Alternatively, if the temperature-dependent viscosity is known, then the tuning fork can be used as a thermometer.

Vibrating wire thermometry has been widely used in liquid 3He, particularly in the superfluid phase at low temperatures [10, 11]. Vibrating wires are sensitive and precise, however tuning forks have some advantages. Unlike a vibrating wire, a tuning fork does not require a magnetic field and its properties are quite insensitive to the magnetic field. Quartz tuning forks of varying sizes can be bought very cheaply and are readily available. Tuning forks are also easy to operate, they have small intrinsic losses (low vacuum damping) and are quite robust. Furthermore, the tuning fork behaviour can be modelled with a simple analytic formula as described below.

2 Experimental Details

The quartz tuning fork has prongs of length L=2.3 mm, width W=100 μm and thickness T=220 μm. It is mounted in a Lancaster-style nuclear cooling cell [12] which is cooled a dilution refrigerator [13]. The thermal link between the cell and the mixing chamber of the dilution refrigerator is provided by high purity annealed silver wires of 1 mm diameter.

The experimental cell also contains various wires and grids for experiments in superfluid 3He. At very low temperatures, thermal quasiparticles in superfluid 3He-B become highly ballistic, and the damping on a vibrating wire at low velocities is determined by Andreev reflection from the superfluid back-flow around the wire [14, 15]. Previous measurements with this cell have shown that the same mechanism dominates for tuning forks [16]. Here, we discuss measurements at higher temperatures in normal liquid 3He.

For temperatures above 40 mK, thermometry was provided by a thick-film ruthenium oxide (RoX) chip resistor, which had a resistance of 1.496 kΩ at room temperature. This was previously calibrated against a calibrated Lakeshore thermometer. The RoX thermometer was fixed to a silver foil with a small quantity of Stycast 1266, and was thermally connected to the mixing chamber by a high purity 1 mm annealed silver wire. The resistance of the RoX thermometer was measured using a 4-wire resistance bridge, with low pass RC-filters on each lead to minimize self-heating from noise and electrical pick-up. The measurements were made whilst sweeping the temperature slowly to ensure good thermal equilibrium between the cell and the RoX thermometer. The temperature was varied by adjusting the circulation rate of the refrigerator.

Below 40 mK, electrical noise influences the temperature of the RoX thermometer which starts to saturate below around 20 mK. For thermometry below 40 mK we use a 125 μm tantalum vibrating wire resonator which is located in the cell close to the tuning fork. The vibrating wire thermometry is based on measurements of Carless, Hall and Hook (CHH) who used a similar vibrating wire to measure the viscosity liquid 3He at low temperatures [4].

2.1 Viscosity Measurements with a Tuning Fork

There have been many recent studies of the behaviour of tuning forks in quantum fluids at low temperatures [16–23]. The working principles and measurements procedures are well documented [24]. Here we give a brief outline relevant to viscosity measurements.

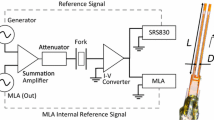
The fork is driven by an AC voltage supplied by a waveform generator. Attenuators are used to obtain the low voltage amplitudes needed for viscosity measurements. The voltage produces a driving force on the prongs due to the piezoelectric properties of quartz. The resulting motion of the prongs generates an electric current which is proportional to the tip velocity of the prongs. The constant of proportionality is known as the fork constant, a, which can be inferred indirectly from electrical measurements or directly from optical measurements of the prong motion [25].

Viscous drag produces damping on the tuning fork motion. The damping is found from the frequency width of the resonance. To measure this, the frequency of the driving voltage is swept through the resonant frequency. The response of the fork is measured using a custom current-to-voltage converter [26] and a phase-sensitive lock-in amplifier to record both the in-phase and the out-of-phase (quadrature) components. The resulting line-shape is fitted to the ideal Lorentzian response expected for a linear oscillator, with some background currents which arise from the capacitance of the circuit and electrical pick-up [24]. In practice the fits to the data are excellent, providing accurate values for the resonant frequency and the width of the resonance, Δf 2, measured from the half-height points of the in-phase response.

Neglecting the small vacuum damping, we assume that the frequency width of the resonance due to viscous drag can be written as [9]

$$ \varDelta f_2= \frac{1}{2}\sqrt{ \frac{\rho(T) \eta(T) f_l(T)}{\pi}} C S \frac{(f_l(T)/f_{vac})^2}{m_{vac}} $$
(2)

where f l (T) is the resonant frequency of the tuning fork in the liquid, f vac is the resonant frequency measured in vacuum at 4.2 K, S=L(2T+2W) is the surface area of each prong (neglecting the end), C is a geometrical constant and the effective mass in vacuum is [22]

$$ m_{vac} = 0.25\rho_q LW\mathrm{T} $$
(3)

where ρ q =2659 kgm−3 is the density of quartz.

For the fluid density, ρ(T), we use ρ(T)=m 3/V m (T) where m 3=3.016 g is the molar mass of 3He and the molar volume V m (T) is tabulated by Wilks [27] (V m ≈36.91 cm3 at low temperatures).

We note that Eq. (2) is analogous to Stokes theory for an oscillating cylinder in the limiting case of a small viscous penetration depth δ≪W. This condition is met reasonably well over our full temperature range 6 mK–1.8 K with δ=6 μm at 1 K and δ=27 μm at 6 mK. We expect that Eq. (2) will not be valid for much larger values of the viscous penetration depth.

3 Results

Below we use Eq. (2) to infer the viscosity of normal liquid 3He and compare with previous measurements. The resonant frequency of the tuning fork at 4.2 K in vacuum was found to be f vac =32705 Hz. To determine the geometrical constant C we need to use some reference point. For this we assume that the viscosity at low temperatures is the same as that measured by CHH using a vibrating wire resonator [4]. From this we find that C=0.60.

Now we have all the necessary parameters, we can extract values for the viscosity over the full temperature of our measurements. This is shown in Fig. 1 where we plot the ηT 2 (in SI units) versus temperature T. It is most convenient to plot the data in this form since according to Fermi liquid theory ηT 2 should tend towards a constant at low temperatures.

Fig. 1
figure 1

Values of ηT 2 versus temperature T. Open circles show our data obtained with the quartz tuning fork. Solid circles show early data of Betts et al. [1, 2]. The long dashed line at low temperatures shows the empirical fit to the data of CHH taken with a vibrating wire resonator [4] (this was used to determine the fork geometrical constant C). The short dashed line at higher temperature shows the empirical fit to the data of Black et al. [3] which also used a vibrating wire resonator. The solid line gives a simple polynomial fit to our data over the full temperature range (Color figure online)

Full size image

We compare our data with early measurements of Betts et al. [1, 2], shown as solid symbols in the figure, and with the fitted expression describing the measurements of Black et al. [3]:

$$ \eta_{Black}{T}^2= 10^{-7} \bigl(2.21+ 26.3\,T^{5/3} \bigr), $$
(4)

shown by the short dashed line which extends from around 50 mK upwards. For completeness the short dashed line in the figure shows the fitted expression to the CHH data below 16 mK given by [4]:

$$ \eta_{CHH}{T}^2= 10^{-7} \frac{1}{ (0.468 + 0.0383\,T^{-2})} . $$
(5)

Note that the above expression has been corrected to account for the improved temperature scale later provided by Greywall [28]. The comparison is shown a little more clearly in the inset which shows an expanded view of the low temperature data. Note that ηT 2 is almost constant in the temperature interval shown in the inset and the CHH data is forced to agree with our data in this range since this was used this to determine the geometrical constant C as discussed above.

Our data for ηT 2 fits quite well to a 5th order polynomial given by

$$ \eta T^2\! =\bigl(2.03 + 4.74\,{T} + 28.22\,{T}^2\! - 24.74~{T}^3\! + 22.40\,{T}^4\! - 6.92 \,{T}^5\bigr) \times \!10^{-7}. $$
(6)

This is show by the solid line in the figure which extends over the full temperature range from 6 mK to 1.8 K.

4 Discussion

Our viscosity data shown in the figure, are seen to be in good agreement with the previous measurements of Black et al. [3]. Also, there is good consistency with the CHH data [4] which we used to calibrate the tuning fork by determining the constant C in Eq. (2). This shows that tuning forks are well described by Eq. (2), at least when the viscous penetration depth is small compared to the fork dimensions. This allows tuning fork to be used as viscometers provided that the constant C is known or, perhaps more usefully, they can be used as thermometers in liquid 3He and other quantum fluids over a wide range of temperatures.

Mechanical resonators measure directly the temperature of the fluid via the fluid viscosity and they introduce negligible heat leaks. This gives an enormous advantage over conventional thermometers which rely on making thermal contact with the fluid since at very low temperatures thermal boundary resistances become extremely large. Tuning forks are particularly easy to use, they are relatively compact and can be purchased at very low cost. The forks can also be custom made for specific applications [22]. A disadvantage of using tuning forks over vibrating wires is that they introduce an empirical geometrical constant, C. However, this constant can be found from a single calibration point and one would expect it to have similar values for forks with similar geometries. We note that in previous work [9] with a larger tuning fork (L = 3.12 mm) a value of C=0.57 was obtained in liquid 3He.