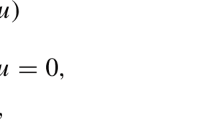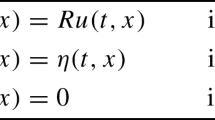Solving inverse optimal control problems via value functions to global optimality

Abstract

In this paper, we show how a special class of inverse optimal control problems of elliptic partial differential equations can be solved globally. Using the optimal value function of the underlying parametric optimal control problem, we transfer the overall hierarchical optimization problem into a nonconvex single-level one. Unfortunately, standard regularity conditions like Robinson’s CQ are violated at all the feasible points of this surrogate problem. It is, however, shown that locally optimal solutions of the problem solve a Clarke-stationarity-type system. Moreover, we relax the feasible set of the surrogate problem iteratively by approximating the lower level optimal value function from above by piecewise affine functions. This allows us to compute globally optimal solutions of the original inverse optimal control problem. The global convergence of the resulting algorithm is shown theoretically and illustrated by means of a numerical example.

1 Introduction

The aim of the inverse problem considered in this paper is the determination of finitely many parameters in the cost function of a given optimal control problem of a linear (partial) differential equation such that the resulting optimal state and control minimize a given superordinate functional, e.g. the distance to given data functions, see Example 2.1. In the context of human locomotion, similar inverse problems of ordinary differential equations are considered in [2, 3, 28].

Due to their structure, the inverse problems of interest turn out to be so-called bilevel optimal control problems, i.e. hierarchical optimization problems with two decision levels where at least one decision maker has to solve an optimal control problem, see e.g. the monographs [4, 7, 10, 32] and [19, 25, 33, 34] for detailed introductions to bilevel programming and optimal control (of ordinary as well as partial differential equations), respectively. Some more applications of bilevel optimal control can be found in [12, 17, 22, 24] while necessary optimality conditions are the subject in e.g. [5, 26, 27, 35, 36]. First steps regarding inverse optimal control of partial differential equations were carried out recently, see [16, 20]. Therein, the authors heavily exploit the uniqueness of the lower level solution for any fixed upper level variable and the properties of the associated solution operator. Note that optimal control problems with variational inequality constraints like the optimal control of the obstacle problem can be interpreted as bilevel optimal control problems as well, see [15] and the references therein.

To the best of our knowledge, there mainly exist methods for the numerical handling of inverse optimal control problems of ordinary differential equations, see e.g. [2, 3, 17, 18]. These algorithms focus on the replacement of the lower level optimal control problem by means of optimality conditions. This, however, is a delicate approach since the resulting surrogate problem is not necessarily equivalent to the original bilevel programming problem anymore, see [8], where the authors deal with this issue in the finite-dimensional situation. Furthermore, there is an uncomfortable lack of convergence results.

In this paper, we will strike a different path to derive necessary optimality conditions and to state an algorithm which can be used to solve a special class of inverse optimal control problems of (partial) differential equations. For that purpose, the optimal value function of the parametric optimal control problem (OC(x)) is used. The idea of utilizing value functions in hierarchical programming dates back to [30]. Here, we first exploit the aforementioned optimal value function in order to transfer the given hierarchical model (IOC) into an equivalent single-level program. Although the resulting nonconvex surrogate problem does not satisfy standard constraint qualification, see Lemma 5.1 and Example 5.1, necessary optimality conditions of Clarke-stationarity-type can be derived via a relaxation approach, see Theorem 5.2. In our setting, the lower level value function is convex which allows us to compute an upper approximation which is piecewise affine. This idea is taken from [9]. Afterwards, we can decompose the obtained surrogate problem into finitely many convex optimal control problems which enables us to solve the relaxed surrogate problem globally. In an iterative way, the upper approximation of the lower level value function is improved, see Algorithm 1 for details. Finally, it is shown that the proposed algorithm converges to a global solution of the underlying inverse optimal control problem, see Theorem 6.1.

The remaining parts of the paper are organized as follows: In Sect. 2, the precise problem statement is presented. Afterwards, we clarify our notation and comment on some preliminary results in Sect. 3. Section 4 is dedicated to the study of the properties of the lower level optimal value function. In Sect. 5, we transfer the original inverse optimal control problem into an equivalent single-level optimal control problem by exploiting the aforementioned optimal value function. Furthermore, we discuss the properties of the resulting surrogate problem. Using a relaxation approach, necessary optimality conditions for (IOC) are derived for the special setting where $U_{\text {ad}}$ is a box-constrained set in $L^2(\varOmega )$. Finally, we present a solution algorithm in Sect. 6. Its global convergence is shown theoretically. An illustrative example is included in order to visualize the obtained theory. Some concluding remarks and perspectives of future research are presented in Sect. 7.

2 Problem statement

We consider the parametric optimal control problem (also called lower level problem)

whose parameters $x\in \mathbb {R}^n$ have to be identified in the superordinate upper level optimization problem

$$\begin{aligned} \begin{aligned} F(x,y,u)&\,\rightarrow \,\min \limits _{x,y,u}\\ x&\,\in \,S\\ (y,u)&\,\in \,\varPsi (x). \end{aligned} \end{aligned}$$

(IOC)

Therein, $\varPsi :\mathcal {\mathbb {R}}^n\rightrightarrows {\mathcal {Y}}\times {\mathcal {U}}$ denotes the solution set mapping of the parametric optimization problem (OC(x)) and $S\subset \mathbb {R}^n$ is a nonempty polytope, i.e. a compact polyhedron.

Before we comment on the inverse optimal control problem (IOC) in more detail, we state the fundamental assumptions of this paper.

Assumption 2.1

Let ${\mathcal {Y}}$, ${\mathcal {M}}$, and ${\mathcal {U}}$ be Hilbert spaces. Furthermore, the objective functional $F:\mathbb {R}^n\times {\mathcal {Y}}\times {\mathcal {U}}\rightarrow \mathbb {R}$ is assumed to be continuously Fréchet differentiable and convex. The set $S\subset \mathbb {R}^n$ is a nonempty polytope. Moreover, we fix an isomorphism ${\mathtt {A}}\in {\mathbb {L}}\left[ {\mathcal {Y}},{\mathcal {Y}}^\star \right]$ as well as continuous linear operators ${\mathtt {B}}\in {\mathbb {L}}\left[ {\mathcal {U}},{\mathcal {Y}}^\star \right]$, ${\mathtt {C}}\in {\mathbb {L}}\left[ {\mathcal {Y}},{\mathcal {M}}\right]$, ${\mathtt {P}}\in {\mathbb {L}}\left[ \mathbb {R}^n,{\mathcal {M}}\right]$, and ${\mathtt {Q}}\in {\mathbb {L}}\left[ \mathbb {R}^n,{\mathcal {U}}\right]$. The set of feasible controls $U_{\text {ad}}\subset {\mathcal {U}}$ is assumed to be nonempty, closed, and convex. Finally, the regularization parameter $\sigma >0$ is fixed.

Due to these assumptions, the lower level objective function $f:\mathbb {R}^n\times {\mathcal {Y}}\times {\mathcal {U}}\rightarrow \mathbb {R}$ is continuous and (jointly) convex.

Next, we present a specific setting of the data which shows the close relationship of (IOC) and inverse control.

Example 2.1

Here, we comment on the inverse optimal control of Poisson’s equation. Therefore, let $\varOmega \subset \mathbb {R}^d$ be a bounded domain and choose the spaces ${\mathcal {Y}}:=H^1_0(\varOmega )$ as well as ${\mathcal {M}}={\mathcal {U}}:=L^2(\varOmega )$. For some observed state $y_{\text {o}}\in L^2(\varOmega )$ and some observed control $u_{\text {o}}\in L^2(\varOmega )$, we consider the tracking-type objective

$$\begin{aligned} \forall (x,y,u){\in }\mathbb {R}^n\times H^1_0(\varOmega )\times L^2(\varOmega ):\quad F(x,y,u):=\tfrac{1}{2}\left\| y-y_\text{ o }\right\| _{L^2(\varOmega )}^2 +\tfrac{1}{2}\left\| u-u_{\text {o}}\right\| _{L^2(\varOmega )}^2. \end{aligned}$$

We set $S:=\varDelta ^n$ where $\varDelta ^n$ represents the standard simplex, i.e.

$$\begin{aligned} \varDelta ^n:=\left\{ x\in \mathbb {R}^n\,\Bigg |\,x\ge 0,\,\sum _{i=1}^nx_i=1\right\} . \end{aligned}$$

Furthermore, let ${\mathtt {C}}$ be the continuous embedding $H^1_0(\varOmega )\hookrightarrow L^2(\varOmega )$ and let ${\mathtt {Q}}$ be the zero operator. For fixed form functions $f_1,\dots ,f_n\in L^2(\varOmega )$, we define ${\mathtt {P}}\in {\mathbb {L}}\left[ \mathbb {R}^n,L^2(\varOmega )\right]$ by means of

$$\begin{aligned} \forall x\in \mathbb {R}^n:\quad {\mathtt {P}}[x]:=\sum _{i=1}^nx_if_i, \end{aligned}$$

i.e. the objective of the lower level problem (OC(x)) takes the following form:

$$\begin{aligned} \mathbb {R}^n\times H^1_0(\varOmega )\times L^2(\varOmega )\ni (x,y,u)\mapsto \tfrac{1}{2}\left\| y-\sum \nolimits _{i=1}^nx_if_i\right\| _{L^2(\varOmega )}^2 +\tfrac{\sigma }{2}\left\| u\right\| _{L^2(\varOmega )}^2\in \mathbb {R}. \end{aligned}$$

The operator ${\mathtt {B}} \in {\mathbb {L}}\left[ L^2(\varOmega ),H^{-1}(\varOmega )\right]$, where $H^{-1}(\varOmega )$ denotes the dual space of $H^1_0(\varOmega )$, is the canonical embedding, i.e., the adjoint of ${\mathtt {C}}$. Finally, ${\mathtt {A}} \in {\mathbb {L}}\left[ H_0^1(\varOmega ), H^{-1}(\varOmega )\right]$ equals the negative Laplace operator, i.e., we have $\left\langle {\mathtt {A}}[y], v\right\rangle _{H_0^1(\varOmega )} = \int _\varOmega \nabla y(\omega ) \cdot \nabla v(\omega ) \, \mathrm {d}\omega$ for all $y,v \in H_0^1(\varOmega )$.

In [26], the author studies a bilevel programming problem which is closely related to (IOC) in terms of necessary optimality conditions. Exploiting the fact that under the postulated assumptions, (OC(x)) possesses a unique optimal solution for any instance of the parameter $x\in \mathbb {R}^n$, the bilevel program is transferred into a single-level problem by inserting the solution mapping of the lower level problem into the upper level objective. It is shown that the lower level solution mapping is directionally differentiable as long as $U_{\text {ad}}$ is polyhedric or, more general, if the projection onto $U_{\text {ad}}$ is directionally differentiable in the sense of Haraux, see [14]. Thus, the author is capable of deriving necessary optimality conditions for the bilevel programming problem via its implicit reformulation. However, the necessary constraint qualifications may fail to hold in the special setting (IOC) since the upper level variable is finite dimensional while the lower level variables are in general not.

Here, we want to use the so-called optimal value function $\varphi :\mathbb {R}^n\rightarrow \mathbb {R}$ of the parametric optimization problem (OC(x)) defined by

$$\begin{aligned} \forall x\in \mathbb {R}^n:\quad \varphi (x):=\min \left\{ \tfrac{1}{2}\left\| {\mathtt {C}}[y]-{\mathtt {P}}[x]\right\| _{{\mathcal {M}}}^2+\tfrac{\sigma }{2}\left\| u-{\mathtt {Q}}[x]\right\| _{{\mathcal {U}}}^2\,\Bigg | \begin{aligned}&{\mathtt {A}}[y]-{\mathtt {B}}[u]=0\\&u\in U_{\text {ad}} \end{aligned} \right\} \end{aligned}$$

in order to solve problem (IOC) globally. It is well known that the surrogate optimization problem

$$\begin{aligned} \begin{aligned} F(x,y,u)&\,\rightarrow \,\min \limits _{x,y,u}\\ x&\,\in \,S\\ f(x,y,u)-\varphi (x)&\,\le \,0\\ {\mathtt {A}}[y]-{\mathtt {B}}[u]&\,=\,0\\ u&\,\in \,U_{\text {ad}}, \end{aligned} \end{aligned}$$

(OVR)

is equivalent to the model problem (IOC), see [7]. Utilizing value functions in bilevel programming dates back to [30].

3 Notation and preliminaries

3.1 Notation

In this paper, we equip $\mathbb {R}^n$, the space of all real vectors with $n\in {\mathbb {N}}$ components, with the Euclidean norm $\left| \cdot \right| _{2}$. The Euclidean inner product of two vectors $x,y\in \mathbb {R}^n$ is denoted by $x\cdot y$. The sets $\mathbb {R}^+_0$ and $\mathbb {R}^-_0$ represent the nonnegative and nonpositive real numbers, respectively. For some arbitrary Banach space ${\mathcal {X}}$, $\left\| \cdot \right\| _{{\mathcal {X}}}$ denotes its norm. The set ${\mathbb {B}}_{\mathcal {X}}^\varepsilon ({\bar{x}})$ is the closed $\varepsilon$-ball around ${\bar{x}}\in {\mathcal {X}}$ w.r.t. the norm in ${\mathcal {X}}$. Let ${\mathcal {X}}^\star$ be the (topological) dual of ${\mathcal {X}}$. Then, $\left\langle \cdot , \cdot \right\rangle _{{\mathcal {X}}}:{\mathcal {X}}^\star \times {\mathcal {X}}\rightarrow \mathbb {R}$ expresses the associated dual pairing. For some set $A\subset {\mathcal {X}}$, ${\text {conv}}\,A$, ${\text {cone}}\, A$, ${\text {cl}}\,A$, ${\text {int}}\,A$, and $\partial A$ denote the convex hull of A, the smallest cone containing A, the closure of A, the interior of A, and the boundary of A, respectively. Furthermore, we define the polar cone of A by means of

$$\begin{aligned} A^\circ := \left\{ x^\star \in {\mathcal {X}}^\star \,\Bigg |\, \forall x\in A:\,\left\langle x^\star , x\right\rangle _{{\mathcal {X}}}\le 0 \right\} . \end{aligned}$$

Note that $A^\circ$ is a nonempty, closed, convex cone. Now, assume that A is convex and fix a point ${\bar{x}}\in A$. We define the radial cone, the tangent (or Bouligand) cone, and the normal cone (in the sense of convex analysis) to A at ${\bar{x}}$ via

$$\begin{aligned} {\mathcal {R}}_A({\bar{x}}):={\text {cone}}(A-\{{\bar{x}}\}),\qquad {\mathcal {T}}_A({\bar{x}}):={\text {cl}}\,{\mathcal {R}}_A({\bar{x}}),\qquad {\mathcal {N}}_A({\bar{x}}):={\mathcal {T}}_A({\bar{x}})^\circ . \end{aligned}$$

Note that ${\mathcal {N}}_A({\bar{x}})=(A-\{{\bar{x}}\})^\circ$ holds.

For some other Banach space ${\mathcal {Y}}$, ${\mathbb {L}}\left[ {\mathcal {X}},{\mathcal {Y}}\right]$ is the Banach space of all bounded, linear operators mapping from ${\mathcal {X}}$ to ${\mathcal {Y}}$. For some operator ${\mathtt {F}}\in {\mathbb {L}}\left[ {\mathcal {X}},{\mathcal {Y}}\right]$, ${\mathtt {F}}^\star \in {\mathbb {L}}\left[ {\mathcal {Y}}^\star ,{\mathcal {X}}^\star \right]$ denotes its adjoint. If ${\mathcal {X}}$ and ${\mathcal {Y}}$ are Hilbert spaces, then ${\mathtt {F}}^\star \in {\mathbb {L}}\left[ {\mathcal {Y}},{\mathcal {X}}\right]$ can also denote the so-called Hilbert space adjoint of ${\mathtt {F}}$ (which is obtained from the usual adjoint operator by identifying the spaces ${\mathcal {X}}$ and ${\mathcal {Y}}$ with their respective dual spaces via the associated Riesz isomorphisms). The operators ${\mathtt {O}}\in {\mathbb {L}}\left[ {\mathcal {X}},{\mathcal {Y}}\right]$ and ${\mathtt {I}}_{\mathcal {X}}\in {\mathbb {L}}\left[ {\mathcal {X}},{\mathcal {X}}\right]$ represent the zero-operator (which maps all elements of ${\mathcal {X}}$ to the zero in ${\mathcal {Y}}$) and the identity operator of ${\mathcal {X}}$, respectively. For Banach spaces ${\mathcal {X}}_1,\dots ,{\mathcal {X}}_n$ and ${\mathcal {Y}}_1,\dots ,{\mathcal {Y}}_m$ as well as operators ${\mathtt {F}}_{i,j}\in {\mathbb {L}}\left[ {\mathcal {X}}_j,{\mathcal {Y}}_i\right]$, $i=1,\dots ,m$, $j=1,\dots ,n$, we define the associated product operator in ${\mathbb {L}}\left[ {\mathcal {X}}_1\times \dots \times {\mathcal {X}}_n,{\mathcal {Y}}_1\times \dots \times {\mathcal {Y}}_m\right]$ by

$$\begin{aligned} \begin{bmatrix} {\mathtt {F}}_{1,1}&\dots&{\mathtt {F}}_{1,n}\\ \vdots&\vdots \\ {\mathtt {F}}_{m,1}&\dots&{\mathtt {F}}_{m,n} \end{bmatrix} \begin{pmatrix} x_1\\ \vdots \\ x_n \end{pmatrix} := \begin{pmatrix} \sum \nolimits _{j=1}^n{\mathtt {F}}_{1,j}[x_j]\\ \vdots \\ \sum \nolimits _{j=1}^n{\mathtt {F}}_{m,j}[x_j] \end{pmatrix} \end{aligned}$$

for all $(x_j)_{j=1}^n\in {\mathcal {X}}_1\times \dots \times {\mathcal {X}}_n$. For a Hilbert space ${\mathcal {H}}$, an operator ${\mathtt {G}}\in {\mathbb {L}}\left[ {\mathcal {H}},{\mathcal {H}}^\star \right]$ is called elliptic (or coercive) if there is a constant $\alpha >0$ such that

$$\begin{aligned} \forall x\in {\mathcal {H}}:\quad \left\langle {\mathtt {G}}[x], x\right\rangle _{{\mathcal {H}}}\ge \alpha \left\| x\right\| _{{\mathcal {H}}}^2 \end{aligned}$$

Recall that a mapping $J:{\mathcal {X}}\rightarrow {\mathcal {Y}}$ is called Fréchet differentiable at ${\bar{x}}\in {\mathcal {X}}$ if there exists an operator $J'({\bar{x}})\in {\mathbb {L}}\left[ {\mathcal {X}},{\mathcal {Y}}\right]$, which satisfies

$$\begin{aligned} \lim \limits _{\left\| d\right\| _{{\mathcal {X}}}\searrow 0} \frac{\left\| J({\bar{x}}+d)-J({\bar{x}})-J'({\bar{x}})[d]\right\| _{{\mathcal {Y}}}}{\left\| d\right\| _{{\mathcal {X}}}} =0. \end{aligned}$$

In case of existence, $J'({\bar{x}})$ is called the Fréchet derivative of J at ${\bar{x}}$. If the mapping ${\mathcal {X}}\ni x\mapsto J'(x)\in {\mathbb {L}}\left[ {\mathcal {X}},{\mathcal {Y}}\right]$ is well-defined and continuous in a neighborhood of ${\bar{x}}$, then J is said to be continuously Fréchet differentiable at ${\bar{x}}$.

Finally, we would like to mention that for an arbitrary domain $\varOmega \subset \mathbb {R}^d$, $L^2(\varOmega )$ is used to represent the usual Lebesgue space of (equivalence classes of) measurable, square-integrable functions. As usual, $H^1_0(\varOmega )$ denotes the closure of $C^\infty _0(\varOmega )$, the set of all arbitrarily often continuously differentiable functions with compact support in $\varOmega$, w.r.t. the common $H^1$-Sobolev norm, see [1] for details. We use $H^{-1}(\varOmega ):=H^1_0(\varOmega )^\star$ for its dual.

3.2 Preliminary results

Now, we take a look at the optimization problem

$$\begin{aligned} \begin{aligned} j(x)&\,\rightarrow \,\min \limits _{x}\\ J(x)&\,\in \,C \end{aligned} \end{aligned}$$

(P)

where $j:{\mathcal {X}}\rightarrow \mathbb {R}$ as well as $J:{\mathcal {X}}\rightarrow {\mathcal {Y}}$ are continuously Fréchet differentiable mappings between Banach spaces ${\mathcal {X}}$ and ${\mathcal {Y}}$ while $C\subset {\mathcal {Y}}$ is a nonempty, closed, convex set. A feasible point ${\bar{x}}\in {\mathcal {X}}$ of (P) satisfies the so-called Karush-Kuhn-Tucker (KKT for short) conditions if the following holds:

$$\begin{aligned} \exists \lambda \in {\mathcal {N}}_C(J({\bar{x}})):\quad j'({\bar{x}})+J'({\bar{x}})^\star [\lambda ]=0. \end{aligned}$$

If ${\bar{x}}$ is a locally optimal solution of (P) which fulfills Robinson’s constraint qualification, i.e. the condition

$$\begin{aligned}J'({\bar{x}})[{\mathcal {X}}]-{\mathcal {R}}_C(J({\bar{x}}))={\mathcal {Y}},\end{aligned}$$

is satisfied, then the KKT-conditions are valid, see [6, Theorem 3.9]. In the absence of Robinson’s constraint qualification, this result does not hold in general. Further information on constraint qualifications and necessary optimality conditions addressing optimization problems in Banach spaces can be found in [6, 31, 38].

In order to show the equivalence of certain constraint qualifications of Robinson-type in the setting of product structures, the following lemma will be useful. Similar results can be found in [26, Lemma 3.4, Corollary 3.5].

Lemma 3.1

Let Banach spaces ${\mathcal {X}}_1$, ${\mathcal {X}}_2$, ${\mathcal {Y}}_1$, and ${\mathcal {Y}}_2$ as well as sets $U\subset {\mathcal {X}}_2$ and $V\subset {\mathcal {Y}}_1$ be given. Moreover, let ${\mathtt {A}}\in {\mathbb {L}}\left[ {\mathcal {X}}_1,{\mathcal {Y}}_1\right]$, ${\mathtt {B}}\in {\mathbb {L}}\left[ {\mathcal {X}}_2,{\mathcal {Y}}_1\right]$, ${\mathtt {C}}\in {\mathbb {L}}\left[ {\mathcal {X}}_1,{\mathcal {Y}}_2\right]$, and ${\mathtt {D}}\in {\mathbb {L}}\left[ {\mathcal {X}}_2,{\mathcal {Y}}_2\right]$ be linear operators such that ${\mathtt {C}}$ is an isomorphism. We consider the following conditions:

$$\begin{aligned}&\begin{bmatrix}{\mathtt {A}}&{\mathtt {B}}\\{\mathtt {C}}&{\mathtt {D}}\end{bmatrix} \begin{pmatrix}{\mathcal {X}}_1\\ U\end{pmatrix} -\begin{pmatrix}V\\ \{0\}\end{pmatrix} =\begin{pmatrix}{\mathcal {Y}}_1\\ {\mathcal {Y}}_2\end{pmatrix}, \end{aligned}$$

(1a)

$$\begin{aligned}&\bigl ({\mathtt {A}}\circ {\mathtt {C}}^{-1} \circ (-{\mathtt {D}})+{\mathtt {B}}\bigr )[U]-V={\mathcal {Y}}_1. \end{aligned}$$

(1b)

Then, (1a) and (1b) are equivalent.

Proof

We show both implications separately.

“$\Longrightarrow$”: Assume that (1a) is valid and choose $y\in {\mathcal {Y}}_1$. Then, we find $x\in {\mathcal {X}}_1$, $u\in U$, and $v\in V$ such that ${\mathtt {A}}[x]-{\mathtt {B}}[u]-v=y$ and ${\mathtt {C}}[x]+{\mathtt {D}}[u]=0$ are valid. Observing $x=({\mathtt {C}}^{-1}\circ (-{\mathtt {D}}))[u]$, we obtain $({\mathtt {A}}\circ {\mathtt {C}}^{-1}\circ (-{\mathtt {D}})+{\mathtt {B}})[u]-v=y$. Consequently, (1b) holds.

“$\Longleftarrow$”: Next, we suppose that (1b) is valid and choose $y_1\in {\mathcal {Y}}_1$ as well as $y_2\in {\mathcal {Y}}_2$ arbitrarily. Due to the validity of (1b), we find ${\tilde{u}}\in U$ and ${\tilde{v}}\in V$ such that

$$\begin{aligned} ({\mathtt {A}}\circ {\mathtt {C}}^{-1}\circ (-{\mathtt {D}})+{\mathtt {B}})[{\tilde{u}}] -{\tilde{v}}=y_1-({\mathtt {A}}\circ {\mathtt {C}}^{-1})[y_2] \end{aligned}$$

holds true. Let us set ${\tilde{x}}:={\mathtt {C}}^{-1}[y_2-{\mathtt {D}}[{\tilde{u}}]]$. Then, we have ${\mathtt {C}}[{\tilde{x}}]+{\mathtt {D}}[{\tilde{u}}]=y_2$ and

$$\begin{aligned} \begin{aligned} {\mathtt {A}}[{\tilde{x}}]+{\mathtt {B}}[{\tilde{u}}]-{\tilde{v}}&=({\mathtt {A}}\circ {\mathtt {C}}^{-1})[y_2] +\bigl ({\mathtt {A}}\circ {\mathtt {C}}^{-1}\circ (-{\mathtt {D}})\bigr )[{\tilde{u}}] +{\mathtt {B}}[{\tilde{u}}]-{\tilde{v}}\\&=({\mathtt {A}}\circ {\mathtt {C}}^{-1})[y_2] +y_1-({\mathtt {A}}\circ {\mathtt {C}}^{-1})[y_2] =y_1. \end{aligned} \end{aligned}$$

This shows that (1a) holds. $\square$

4 Properties of the lower level optimal value function

The following result follows by standard arguments which are, nevertheless, included for the readers convenience.

Lemma 4.1

There are Lipschitz continuous functions $\psi ^y:\mathbb {R}^n\rightarrow {\mathcal {Y}}$ and $\psi ^u:\mathbb {R}^n\rightarrow {\mathcal {U}}$ which satisfy $\varPsi (x)=\{(\psi ^y(x),\psi ^u(x))\}$ for all $x\in \mathbb {R}^n$, i.e. the solution set mapping of (OC(x)) is single-valued and Lipschitz continuous.

Proof

Let us first introduce the control-to-observation operator ${\mathtt {S}}:= {\mathtt {C}}\circ {\mathtt {A}}^{-1}\circ {\mathtt {B}}\in {\mathbb {L}}\left[ {\mathcal {U}},{\mathcal {M}}\right]$ of the lower level optimal control problem (OC(x)). Eliminating the state variable y, the so-called reduced formulation of (OC(x)) is given by

$$\begin{aligned} \begin{aligned} \tfrac{1}{2}\left\| {\mathtt {S}}[u]-{\mathtt {P}}[x]\right\| _{{\mathcal {M}}}^2 +\tfrac{\sigma }{2}\left\| u-{\mathtt {Q}}[x]\right\| _{{\mathcal {U}}}^2&\,\rightarrow \, \min \limits _u\\ u&\,\in \, U_{\text {ad}}. \end{aligned} \end{aligned}$$

Observing that its objective function is continuous, convex, and coercive for any choice of x while its feasible set is nonempty, closed, and convex, standard arguments show that the reduced problem possesses a unique optimal solution $\psi ^u(x)$ for each $x\in \mathbb {R}^n$. Defining $\psi ^y:={\mathtt {A}}^{-1}\circ {\mathtt {B}}\circ \psi ^u$, we can deduce $\varPsi (x)=\{(\psi ^y(x),\psi ^u(x))\}$.

It is easily seen that the globally optimal solution $\psi ^u(x)$ of the reduced problem is the uniquely determined solution of the following variational inequality of the first kind:

$$\begin{aligned} \text {find }u\in U_{\text {ad}}:\quad \left\langle ({\mathtt {S}}^\star \circ {\mathtt {S}}+ \sigma {\mathtt {I}}_{\mathcal {U}})[u], v-u\right\rangle _{{\mathcal {U}}}\ge \left\langle ({\mathtt {S}}^\star \circ {\mathtt {P}}+\sigma {\mathtt {Q}})[x], v-u\right\rangle _{{\mathcal {U}}} \quad \forall v\in U_{\text {ad}}. \end{aligned}$$

Noting that the operator ${\mathtt {S}}^\star \circ {\mathtt {S}}+\sigma {\mathtt {I}}_{\mathcal {U}}$ is elliptic with constant $\sigma >0$ it follows that

$$\begin{aligned} \begin{aligned} \forall x,x'\in \mathbb {R}^n:\quad \left\| \psi ^u(x)-\psi ^u(x')\right\| _{{\mathcal {U}}}&\le \sigma ^{-1}\left\| ({\mathtt {S}}^\star \circ {\mathtt {P}}+\sigma {\mathtt {Q}})[x-x']\right\| _{{\mathcal {U}}}\\&\le \sigma ^{-1}\left\| {\mathtt {S}}^\star \circ {\mathtt {P}}+\sigma {\mathtt {Q}}\right\| _{{\mathbb {L}}\left[ \mathbb {R}^n,{\mathcal {U}}\right] } \left| x-x'\right| _{2}, \end{aligned} \end{aligned}$$

see [23, Theorem II.2.1]. Thus, $\psi ^u$ is Lipschitz continuous. Exploiting the representation $\psi ^y={\mathtt {A}}^{-1}\circ {\mathtt {B}}\circ \psi ^u$, the Lipschitz continuity of $\psi ^y$ follows immediately. $\square$

As a consequence of Lemma 4.1, the continuity of F, and the compactness of $S\subset \mathbb {R}^n$, we obtain the following corollary from Weierstraß’ famous theorem.

Corollary 4.1

The inverse optimal control problem (IOC) possesses a globally optimal solution.

Note that in the remaining parts of the paper, we will exploit the notion of $\psi ^y:\mathbb {R}^n\rightarrow {\mathcal {Y}}$ and $\psi ^u:\mathbb {R}^n\rightarrow {\mathcal {U}}$ as introduced in Lemma 4.1.

In the following, we study the properties of the optimal value function $\varphi$ in more detail. First, we show that $\varphi$ is a convex function. The essentials of the proof date back to [11, Proposition 2.1].

Lemma 4.2

The optimal value function $\varphi$ is convex.

Proof

Obviously, the function f is convex w.r.t. all variables. Defining

$$\begin{aligned} M:=\left\{ (y,u)\in {\mathcal {Y}}\times U_{\text {ad}}\,|\,{\mathtt {A}}[y]-{\mathtt {B}}[u]=0\right\} , \end{aligned}$$

we easily see that

$$\begin{aligned} \forall x\in \mathbb {R}^n:\quad \varphi (x)=\min \limits _{y,u}\{f(x,y,u)\,|\,(y,u)\in M\} \end{aligned}$$

is valid. Clearly, M is convex.

Choose ${\tilde{x}},x'\in \mathbb {R}^n$ as well as $\alpha \in [0,1]$ arbitrarily. Let us fix the corresponding lower level solutions $({\tilde{y}},{\tilde{u}}):=(\psi ^y({\tilde{x}}),\psi ^u({\tilde{x}}))$ and $(y',u'):=(\psi ^y(x'),\psi ^u(x'))$. The joint convexity of f as well as the obvious fact $\alpha M+(1-\alpha )M=M$ lead to

$$\begin{aligned} \begin{aligned}&\varphi (\alpha {\tilde{x}}+(1-\alpha )x') =\min \limits _{y,u}\{f(\alpha {\tilde{x}}+(1-\alpha )x',y,u)\,|\,(y,u)\in M\}\\&\quad =\min \limits _{y^1,y^2,u^1,u^2} \{f(\alpha ({\tilde{x}},y^1,u^1)+(1-\alpha )(x',y^2,u^2))\,|\,(y^1,u^1),(y^2,u^2)\in M\}\\&\quad \le \min \limits _{y^1,y^2,u^1,u^2} \{\alpha f({\tilde{x}},y^1,u^1)+(1-\alpha )f(x',y^2,u^2)\,|\,(y^1,u^1),(y^2,u^2)\in M\}\\&\quad =\alpha f({\tilde{x}},{\tilde{y}},{\tilde{u}})+(1-\alpha )f(x',y',u')\\&\quad =\alpha \varphi ({\tilde{x}})+(1-\alpha )\varphi (x'). \end{aligned} \end{aligned}$$

This completes the proof. $\square$

For later purposes, we formulate the KKT-system of the lower level problem (OC(x)) for a feasible point $(y,u)\in {\mathcal {Y}}\times {\mathcal {U}}$ of (OC(x)) for fixed parameter $x\in \mathbb {R}^n$:

$$\begin{aligned} f_y'(x, y, u) + \mathtt {A}^\star [p] = \mathtt {C}^\star [\mathtt {C}[y]-\mathtt {P}[x]]+\mathtt {A}^\star [p]&= 0, \end{aligned}$$

(2a)

$$\begin{aligned} f_u'(x, y, u) - \mathtt {B}^\star [p] + \lambda = \sigma (u-\mathtt {Q}[x])-\mathtt {B}^\star [p] +\lambda&=0, \end{aligned}$$

(2b)

$$\begin{aligned} \lambda&\in \mathcal {N}_{U_{\text {ad}}}(u). \end{aligned}$$

(2c)

It is easily seen that for fixed $x\in \mathbb {R}^n$, $y:=\psi ^y(x)$, and $u:=\psi ^u(x)$, the Lagrange multipliers $p\in {\mathcal {Y}}$ and $\lambda \in {\mathcal {U}}^\star$ are uniquely determined. Thus, we introduce mappings $\phi ^p:\mathbb {R}^n\rightarrow {\mathcal {Y}}$ and $\phi ^\lambda :\mathbb {R}^n\rightarrow {\mathcal {U}}^\star$ which assign to each $x\in \mathbb {R}^n$ the respective Lagrange multipliers p and $\lambda$ which characterize the associated lower level solution (y, u). Clearly, $\phi ^p$ and $\phi ^\lambda$ are Lipschitz continuous since $\psi ^y$ and $\psi ^u$ are Lipschitz continuous, see Lemma 4.1.

The next lemma shows the differentiability of $\varphi$. We note that this result follows partially from [6, Theorem 4.13]. However, we included a proof for the reader’s convenience.

Lemma 4.3

The optimal value function $\varphi$ is continuously Fréchet differentiable. At a given point ${\bar{x}}\in \mathbb {R}^n$, the associated Fréchet derivative is given as follows:

$$\begin{aligned} \varphi '({\bar{x}}) = \mathtt {P}^\star [\mathtt {P}[{\bar{x}}]-\mathtt {C}[\psi ^y({\bar{x}})]] +\sigma \mathtt {Q}^\star [\mathtt {Q}[{\bar{x}}]-\psi ^u({\bar{x}})] . \end{aligned}$$

Proof

Fix a reference point ${\bar{x}}\in \mathbb {R}^n$ and choose $x \in \mathbb {R}^n$ arbitrarily. For brevity, we will use the notation

$$\begin{aligned} {\bar{y}}&:= \psi ^y({\bar{x}}),&{\bar{u}}&:= \psi ^u({\bar{x}}),&{\bar{\lambda }}&:= \phi ^\lambda ({\bar{x}}),\\ y&:= \psi ^y(x),&u&:= \psi ^u(x),&\lambda&:= \phi ^\lambda (x). \end{aligned}$$

We exploit that f is a quadratic functional and that the functions $\psi ^y$ and $\psi ^u$ are Lipschitz continuous. Thus, we obtain

$$\begin{aligned} \varphi (x) - \varphi ({\bar{x}})&= f(x, y, u) - f({\bar{x}}, {\bar{y}}, {\bar{u}})\\&= f'_x(\cdot ) \, (x - {\bar{x}}) + f'_y(\cdot ) \, (y - {\bar{y}}) + f'_u(\cdot ) \, (u - {\bar{u}}) + \mathcal {O}(\left| x - {\bar{x}}\right| _{2}^2). \end{aligned}$$

Here, $(\cdot )$ abbreviates the argument $({\bar{x}}, {\bar{y}}, {\bar{u}})$. By utilizing the optimality conditions of (OC(x)), we have

$$\begin{aligned} \mathtt {B}^\star [(\mathtt {A}^{-1})^\star [ f'_y(\cdot ) ]] + f'_u(\cdot ) + {\bar{\lambda }} = 0. \end{aligned}$$

Together with $y - {\bar{y}} = \mathtt {A}^{-1}[\mathtt {B}[u - {\bar{u}}]]$, this yields

$$\begin{aligned} \varphi (x) - \varphi ({\bar{x}})&= f'_x(\cdot ) \, (x - {\bar{x}}) + \left\langle -{\bar{\lambda }}, u - {\bar{u}}\right\rangle _{\mathcal {U}} + \mathcal {O}(\left| x - {\bar{x}}\right| _{2}^2). \end{aligned}$$

Finally, we observe

$$\begin{aligned} 0 \le \left\langle -{\bar{\lambda }}, u - {\bar{u}}\right\rangle _{\mathcal {U}} \le \left\langle \lambda -{\bar{\lambda }}, u - {\bar{u}}\right\rangle _{\mathcal {U}} \le C \left| x - {\bar{x}}\right| _{2}^2 \end{aligned}$$

due to the definition of the normal cone and the Lipschitz continuity of $\psi ^u$ as well as $\phi ^\lambda$. Together with the straightforward computation of $f'_x(\cdot )$, this yields

$$\begin{aligned} \varphi '({\bar{x}}) = f'_x(\cdot ) = \mathtt {P}^\star [\mathtt {P}[{\bar{x}}]-\mathtt {C}[\psi ^y({\bar{x}})]] +\sigma \mathtt {Q}^\star [\mathtt {Q}[{\bar{x}}]-\psi ^u({\bar{x}})] \end{aligned}$$

and the proof is completed. $\square$

5 The optimal-value-reformulation

5.1 On the lack of regularity

Exploiting Lemma 4.3, we know that the optimal-value-reformulation (OVR) of (IOC) is an optimization problem with continuously Fréchet differentiable data. However, (OVR) is still a challenging problem due to the following observation.

Lemma 5.1

Robinson’s CQ is violated at each feasible point of (OVR).

Proof

We fix an arbitrary feasible point $({\bar{x}},{\bar{y}},{\bar{u}})\in \mathbb {R}^n\times {\mathcal {Y}}\times {\mathcal {U}}$ of (OVR). In order to show the lemma’s assertion, it is sufficient to construct a nontrivial singular Lagrange multiplier, see [6, Proposition 3.16(i)].

Let us consider the smooth optimization problem

$$\begin{aligned} \begin{aligned} f(x,y,u)-\varphi (x)&\,\rightarrow \,\min \limits _{x,y,u}\\ {\mathtt {A}}[y]-{\mathtt {B}}[u]&\,=\,0\\ u&\,\in \,U_{\text {ad}}. \end{aligned} \end{aligned}$$

(3)

By definition of the optimal value function $\varphi$, its infimal value is given by 0. The feasibility of $({\bar{x}},{\bar{y}},{\bar{u}})$ for (OVR) yields $f({\bar{x}},{\bar{y}},{\bar{u}})-\varphi ({\bar{x}})=0$, i.e. $({\bar{x}},{\bar{y}},{\bar{u}})$ is a globally optimal solution of (3). Obviously, Robinson’s CQ is satisfied at each feasible point of problem (3). Thus, we find $p\in {\mathcal {Y}}$ and $\eta \in {\mathcal {U}}^\star$ which satisfy

$$\begin{aligned} \begin{aligned}&0=f'_x({\bar{x}},{\bar{y}},{\bar{u}})-\varphi '({\bar{x}}),\\&0=f'_y({\bar{x}},{\bar{y}},{\bar{u}})+{\mathtt {A}}^\star [p],\\&0=f'_u({\bar{x}},{\bar{y}},{\bar{u}})-{\mathtt {B}}^\star [p]+\eta ,\\&\eta \in {\mathcal {N}}_{U_{\text {ad}}}({\bar{u}}). \end{aligned} \end{aligned}$$

Thus, $(0,1,p,\eta )\in \mathbb {R}^n\times \mathbb {R}\times {\mathcal {Y}}\times {\mathcal {U}}^\star$ is a nonvanishing singular Lagrange multiplier for (OVR) at $({\bar{x}},{\bar{y}},{\bar{u}})$. Since $({\bar{x}},{\bar{y}},{\bar{u}})$ was an arbitrarily chosen feasible point of (OVR), the proof is completed. $\square$

In [37], the authors try to overcome this well-known drawback of the optimal-value-reformulation of finite-dimensional bilevel programming problems by penalizing the violation of the constraint $f(x,y,u)-\varphi (x)\le 0$ in the objective function. There exist several situations where this penalization is exact (e.g. if the lower level problem is fully linear) and, consequently, the KKT-conditions of the optimal-value-reformulation may serve as necessary optimality conditions for the original bilevel programming problem. However, in our situation, the lower level problem (OC(x)) is quadratic (and possibly infinite dimensional). In the following example, we show that even in the finite-dimensional setting, it is not promising to rely on the KKT-conditions of (OVR).

Example 5.1

We consider the state-reduced bilevel programming problem

$$\begin{aligned} \begin{aligned} x^2-u&\,\rightarrow \,\min \limits _{x,u}\\ x&\,\in \,[0,1]\\ u&\,\in \,\mathop {{\text {argmin}}}\limits _u\{(u-x)^2\,|\,u\ge 0\}. \end{aligned} \end{aligned}$$

The lower level solution operator and the lower level optimal value function are given as stated below:

$$\begin{aligned} \forall x\in \mathbb {R}:\quad \psi ^u(x)={\left\{ \begin{array}{ll}0&{}\text {if }x< 0\\ x&{}\text {if }x\ge 0\end{array}\right. } \qquad \varphi (x)={\left\{ \begin{array}{ll}x^2&{}\,\text {if }x<0\\ 0&{}\text {if }x\ge 0.\end{array}\right. } \end{aligned}$$

One can easily check that the globally optimal solution of the bilevel programming problem is given by $({\bar{x}},{\bar{u}})=(\tfrac{1}{2},\tfrac{1}{2})$. On the other hand, the KKT-conditions of the associated optimal-value-reformulation at $({\bar{x}},{\bar{u}})$ are given by

$$\begin{aligned} \begin{aligned}&0=1+\kappa +0\cdot \rho ,\\&0=-1+0\cdot \rho +\eta ,\\&\kappa \in {\mathcal {N}}_{[0,1]}(\tfrac{1}{2})=\{0\},\\&\rho \ge 0,\\&\eta \in {\mathcal {N}}_{{\mathbb {R}}^+_0}(\tfrac{1}{2})=\{0\} \end{aligned} \end{aligned}$$

and cannot be satisfied.

5.2 Relaxing the optimal value constraint

The violation of Robinson’s CQ at all the feasible points of (OVR) is caused by the constraint $f(x,y,u)-\varphi (x)\le 0$ which is, in fact, fulfilled with equality for all feasible points due to the definition of the optimal value function. Thus, a nearby idea to overcome this problem is given by considering the relaxed problem

for a sequence of positive relaxation parameters $\{\varepsilon _k\}_{k\in \mathbb {N}}$ converging to zero as $k\rightarrow \infty$. In the results below, we discuss the features of this relaxation approach.

Lemma 5.2

Fix $k\in \mathbb {N}$. Then, Robinson’s CQ is valid at each feasible point of (OVR$(\varepsilon _k)$).

Proof

Let $({\bar{x}},{\bar{y}},{\bar{u}})\in \mathbb {R}^n\times {\mathcal {Y}}\times {\mathcal {U}}$ be a feasible point of (OVR$(\varepsilon _k)$). We consider two cases.

Case 1$f({\bar{x}},{\bar{y}},{\bar{u}})-\varphi ({\bar{x}})=\varepsilon _k$. Suppose on the contrary that Robinson’s CQ is violated at $({\bar{x}},{\bar{y}},{\bar{u}})$. Then, we have

$$\begin{aligned} \begin{bmatrix} f'_x({\bar{x}},{\bar{y}},{\bar{u}})-\varphi '({\bar{x}})&f'_y({\bar{x}},{\bar{y}},{\bar{u}})&f'_u({\bar{x}},{\bar{y}},{\bar{u}})\\ {\mathtt {O}}&{\mathtt {A}}&-{\mathtt {B}} \end{bmatrix} \begin{pmatrix} {\mathcal {R}}_{S}({\bar{x}})\\ {\mathcal {Y}}\\ {\mathcal {R}}_{U_{\text {ad}}}({\bar{u}}) \end{pmatrix} - \begin{pmatrix} {\mathbb {R}}^{-}_0\\ \{0\} \end{pmatrix} \ne \begin{pmatrix} \mathbb {R}\\ {\mathcal {Y}}^\star \end{pmatrix}. \end{aligned}$$

Exploiting the fact that ${\mathtt {A}}$ is a bijection, this leads to

$$\begin{aligned} \begin{bmatrix} f'_x({\bar{x}},{\bar{y}},{\bar{u}})-\varphi '({\bar{x}})&f'_y({\bar{x}},{\bar{y}},{\bar{u}})\circ \bar{{\mathtt {S}}}+f'_u({\bar{x}},{\bar{y}},{\bar{u}}) \end{bmatrix} \begin{pmatrix} {\mathcal {R}}_{S}({\bar{x}})\\ {\mathcal {R}}_{U_{\text {ad}}}({\bar{u}}) \end{pmatrix} -\mathbb {R}^-_0 \ne \mathbb {R}\end{aligned}$$

where $\bar{{\mathtt {S}}}:={\mathtt {A}}^{-1}\circ {\mathtt {B}}\in {\mathbb {L}}\left[ {\mathcal {U}},{\mathcal {Y}}\right]$ is the solution operator of the state equation, see Lemma 3.1. The latter is only possible if

$$\begin{aligned} \bigl (f'_y({\bar{x}},{\bar{y}},{\bar{u}})\circ \bar{{\mathtt {S}}} +f'_u({\bar{x}},{\bar{y}},{\bar{u}})\bigr ) [{\mathcal {R}}_{U_{\text {ad}}}({\bar{u}})]\subset \mathbb {R}^+_0 \end{aligned}$$

is valid. Clearly, this is a first order optimality condition for the optimization problem

$$\begin{aligned} \begin{aligned} f({\bar{x}},\bar{{\mathtt {S}}}[u],u)&\,\rightarrow \,\min \limits _u\\ u&\,\in \,U_{\text {ad}}. \end{aligned} \end{aligned}$$

Noting that f is convex while $\bar{{\mathtt {S}}}$ is linear, the objective function of this optimization problem is convex in u. Consequently, ${\bar{u}}$ solves this problem globally. Due to the definition of $\bar{{\mathtt {S}}}$, we have ${\bar{u}}=\psi ^u({\bar{x}})$ and $\bar{{\mathtt {S}}}[{\bar{u}}]={\bar{y}}=\psi ^y({\bar{x}})$. As a result, $f({\bar{x}},{\bar{y}},{\bar{u}})-\varphi ({\bar{x}})=0$ is valid. This, however, contradicts $f({\bar{x}},{\bar{y}},{\bar{u}})-\varphi ({\bar{x}})=\varepsilon _k>0$.

Case 2$f({\bar{x}},{\bar{y}},{\bar{u}})-\varphi ({\bar{x}})<\varepsilon _k$. The condition

$$\begin{aligned} \begin{bmatrix} f'_x({\bar{x}},{\bar{y}},{\bar{u}})-\varphi '({\bar{x}})&f'_y({\bar{x}},{\bar{y}},{\bar{u}})\circ \bar{{\mathtt {S}}}+f'_u({\bar{x}},{\bar{y}},{\bar{u}}) \end{bmatrix} \begin{pmatrix} {\mathcal {R}}_{S}({\bar{x}})\\ {\mathcal {R}}_{U_{\text {ad}}}({\bar{u}}) \end{pmatrix} -\mathbb {R}= \mathbb {R}\end{aligned}$$

is trivially satisfied. Thus, Lemma 3.1 shows that

$$\begin{aligned} \begin{bmatrix} f'_x({\bar{x}},{\bar{y}},{\bar{u}})-\varphi '({\bar{x}})&f'_y({\bar{x}},{\bar{y}},{\bar{u}})&f'_u({\bar{x}},{\bar{y}},{\bar{u}})\\ {\mathtt {O}}&{\mathtt {A}}&-{\mathtt {B}} \end{bmatrix} \begin{pmatrix} {\mathcal {R}}_{S}({\bar{x}})\\ {\mathcal {Y}}\\ {\mathcal {R}}_{U_{\text {ad}}}({\bar{u}}) \end{pmatrix} - \begin{pmatrix} \mathbb {R}\\ \{0\} \end{pmatrix} = \begin{pmatrix} \mathbb {R}\\ {\mathcal {Y}}^\star \end{pmatrix} \end{aligned}$$

is valid as well. However, the latter equals Robinson’s CQ for (OVR$(\varepsilon _k)$) at $({\bar{x}},{\bar{y}},{\bar{u}})$. $\square$

Lemma 5.3

For each $k\in \mathbb {N}$, the surrogate problem (OVR$(\varepsilon _k)$) possesses an optimal solution.

Proof

Let $\{(x_l,y_l,u_l)\}_{l\in \mathbb {N}}$ be a minimizing sequence of (OVR$(\varepsilon _k)$), i.e.

$$\begin{aligned} \lim \limits _{l\rightarrow \infty }F(x_l,y_l,u_l)=\alpha _k \end{aligned}$$

where $\alpha _k\in \mathbb {R}\cup \{-\infty \}$ denotes the infimal value of (OVR$(\varepsilon _k)$).

Obviously, $\{x_l\}_{l\in \mathbb {N}}\subset S$ is bounded. Using the feasibility of $(x_l,y_l,u_l)$ to (OVR$(\varepsilon _k)$), we obtain

$$\begin{aligned} \forall l\in \mathbb {N}:\quad \left\| u_l-{\mathtt {Q}}[x_l]\right\| _{{\mathcal {U}}} \le \sqrt{\tfrac{2}{\sigma }(\varphi (x_l)+\varepsilon _k)} \end{aligned}$$

which yields

$$\begin{aligned} \forall l\in \mathbb {N}:\quad \left\| u_l\right\| _{{\mathcal {U}}}\le \sqrt{\tfrac{2}{\sigma }(\varphi (x_l)+\varepsilon _k)} +\left\| {\mathtt {Q}}[x_l]\right\| _{{\mathcal {U}}}. \end{aligned}$$

Since $\{x_l\}_{l\in \mathbb {N}}$ is bounded while $\varphi$ is continuous, see Lemma 4.3, $\{u_l\}_{l\in \mathbb {N}}$ is bounded as well. Furthermore, we have $y_l=({\mathtt {A}}^{-1}\circ {\mathtt {B}})[u_l]$ for each $l\in \mathbb {N}$, i.e. the continuity of ${\mathtt {A}}^{-1}\circ {\mathtt {B}}\in {\mathbb {L}}\left[ {\mathcal {U}},{\mathcal {Y}}\right]$ and the boundedness of $\{u_l\}_{l\in \mathbb {N}}$ yield the boundedness of $\{y_l\}_{l\in \mathbb {N}}$. Thus, the sequence $\{(x_l,y_l,u_l)\}_{l\in \mathbb {N}}$ is bounded and, therefore, possesses a weakly convergent subsequence (w.l.o.g. we do not relabel this sequence) with weak limit point $({\bar{x}},{\bar{y}},{\bar{u}})$ since ${\mathcal {Y}}$ and ${\mathcal {U}}$ are Hilbert spaces while $\mathbb {R}^n$ is finite dimensional. Particularly, we have $x_l\rightarrow {\bar{x}}$. The closedness of S and the convexity and closedness of $U_{\text {ad}}$ lead to ${\bar{x}}\in S$ and ${\bar{u}}\in U_{\text {ad}}$. Furthermore, ${\mathtt {A}}[{\bar{y}}]-{\mathtt {B}}[{\bar{u}}]=0$ follows from the linearity and continuity of the operators ${\mathtt {A}}$ and ${\mathtt {B}}$. Since f is convex and continuous, it is weakly lower semicontinuous. Furthermore, $\varphi$ is continuous. This yields

$$\begin{aligned} f({\bar{x}},{\bar{y}},{\bar{u}})-\varphi ({\bar{x}})\le & {} \liminf \limits _{l\rightarrow \infty } f(x_l,y_l,u_l)-\lim \limits _{l\rightarrow \infty }\varphi (x_l)\\= & {} \liminf \limits _{l\rightarrow \infty } \bigl (f(x_l,y_l,u_l)-\varphi (x_l)\bigr ) \le \varepsilon _k, \end{aligned}$$

i.e. $({\bar{x}},{\bar{y}},{\bar{u}})$ is feasible to (OVR$(\varepsilon _k)$).

Finally, since F is convex and continuous, it is weakly lower semicontinuous as well and we obtain

$$\begin{aligned} F({\bar{x}},{\bar{y}},{\bar{u}})\le \liminf \limits _{l\rightarrow \infty }F(x_l,y_l,u_l)=\alpha _k. \end{aligned}$$

Combining this observation with the feasibility of $({\bar{x}},{\bar{y}},{\bar{u}})$ to (OVR$(\varepsilon _k)$), we obtain that it is a global solution of this problem. This completes the proof. $\square$

Lemma 5.4

Fix $k\in \mathbb {N}$. Let $(x,y,u)\in \mathbb {R}^n\times {\mathcal {Y}}\times {\mathcal {U}}$ be a feasible point of (OVR$(\varepsilon _k)$) and set ${\bar{y}}:=\psi ^y(x)$ as well as ${\bar{u}}:=\psi ^u(x)$. Then, we have

$$\begin{aligned} \left\| u-{\bar{u}}\right\| _{{\mathcal {U}}}\le \sqrt{2\varepsilon _k/\sigma }, \qquad \left\| y-{\bar{y}}\right\| _{{\mathcal {Y}}}\le C\sqrt{2\varepsilon _k/\sigma } \end{aligned}$$

where $C>0$ is a constant independent of k, x, y, and u.

Proof

Exploiting the fact that ${\mathcal {U}}$ and ${\mathcal {M}}$ are Hilbert spaces while (y, u) is feasible to (OC(x)) and $({\bar{y}},{\bar{u}})$ is optimal for (OC(x)), we obtain

$$\begin{aligned} \sigma \left\| u-{\bar{u}}\right\| _{{\mathcal {U}}}^2= & {} \sigma \left\| u-{\mathtt {Q}}[x]\right\| _{{\mathcal {U}}}^2 -2\left\langle u-{\bar{u}}, \sigma ({\bar{u}}-{\mathtt {Q}}[x])\right\rangle _{{\mathcal {U}}} -\sigma \left\| {\bar{u}}-{\mathtt {Q}}[x]\right\| _{{\mathcal {U}}}^2\\\le & {} \sigma \left\| u-{\mathtt {Q}}[x]\right\| _{{\mathcal {U}}}^2 -2\left\langle u-{\bar{u}}, \sigma ({\bar{u}}-{\mathtt {Q}}[x])\right\rangle _{{\mathcal {U}}} -\sigma \left\| {\bar{u}}-{\mathtt {Q}}[x]\right\| _{{\mathcal {U}}}^2 +\left\| {\mathtt {C}}[y]-{\mathtt {C}}[{\bar{y}}]\right\| _{{\mathcal {M}}}^2\\= & {} \sigma \left\| u-{\mathtt {Q}}[x]\right\| _{{\mathcal {U}}}^2 -2\left\langle u-{\bar{u}}, \sigma ({\bar{u}}-{\mathtt {Q}}[x])\right\rangle _{{\mathcal {U}}} -\sigma \left\| {\bar{u}}-{\mathtt {Q}}[x]\right\| _{{\mathcal {U}}}^2\\&+\left\| {\mathtt {C}}[y]-{\mathtt {P}}[x]\right\| _{{\mathcal {M}}}^2 -2\left\langle {\mathtt {C}}[y-{\bar{y}}], {\mathtt {C}}[{\bar{y}}]-{\mathtt {P}}[x]\right\rangle _{{\mathcal {M}}} -\left\| {\mathtt {C}}[{\bar{y}}]-{\mathtt {P}}[x]\right\| _{{\mathcal {M}}}^2\\= & {} 2\bigl (f(x,y,u)-\varphi (x)\bigr ) -2\bigl (\underbrace{f'_y(x,{\bar{y}},{\bar{u}})[y-{\bar{y}}] +f'_u(x,{\bar{y}},{\bar{u}})[u-{\bar{u}}]}_{\ge 0}\bigr )\\\le & {} 2\bigr (f(x,y,u)-\varphi (x)\bigr )\le 2\varepsilon _k \end{aligned}$$

which yields the first formula. The second one follows from $y - {\bar{y}} = ({\mathtt {A}}^{-1}\circ {\mathtt {B}})[u - {\bar{u}}]$ with $C:=\left\| {\mathtt {A}}^{-1}\circ {\mathtt {B}}\right\| _{{\mathbb {L}}\left[ {\mathcal {U}},{\mathcal {Y}}\right] }$. $\square$

Theorem 5.1

For each $k\in \mathbb {N}$, let $({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\in \mathbb {R}^n\times {\mathcal {Y}}\times {\mathcal {U}}$ be a globally optimal solution of (OVR$(\varepsilon _k)$). Then, the sequence $\{({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\}_{k\in \mathbb {N}}$ possesses a convergent subsequence whose limit point is a globally optimal solution of (OVR) and, thus, of (IOC). Moreover, each accumulation point of $\{({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\}_{k\in \mathbb {N}}$ is a globally optimal solution of (OVR).

Proof

Since $\{{\bar{x}}_k\}_{k\in \mathbb {N}}\subset S$ is bounded, it possesses a convergent subsequence (w.l.o.g. we use the same index again) with limit point ${\bar{x}}$ which lies in S since this set is closed. Let us set ${\bar{y}}:=\psi ^y({\bar{x}})$ and ${\bar{u}}:=\psi ^u({\bar{x}})$. Obviously, $({\bar{x}},{\bar{y}},{\bar{u}})$ is feasible to (OVR).

Using Lemma 5.4, we find a constant $C>0$ such that

$$\begin{aligned} \forall k\in \mathbb {N}:\quad \left\| {\bar{u}}_k-\psi ^u({\bar{x}}_k)\right\| _{{\mathcal {U}}} \le \sqrt{2\varepsilon _k/\sigma }\qquad \left\| {\bar{y}}_k-\psi ^y({\bar{x}}_k)\right\| _{{\mathcal {Y}}}\le C\sqrt{2\varepsilon _k/\sigma } \end{aligned}$$

holds. That is why we obtain

$$\begin{aligned} \begin{aligned} 0\le \lim \limits _{k\rightarrow \infty }\left\| {\bar{u}}_k-{\bar{u}}\right\| _{{\mathcal {U}}}&\le \lim \limits _{k\rightarrow \infty }\left( \left\| {\bar{u}}_k-\psi ^u({\bar{x}}_k)\right\| _{{\mathcal {U}}} +\left\| \psi ^u({\bar{x}}_k)-\psi ^u({\bar{x}})\right\| _{{\mathcal {U}}}\right) \\&\le \lim \limits _{k\rightarrow \infty }\left( \sqrt{2\varepsilon _k/\sigma } +L^u\left| {\bar{x}}_k-{\bar{x}}\right| _{2}\right) =0 \end{aligned} \end{aligned}$$

where $L^u>0$ denotes the Lipschitz constant of $\psi ^u$, see Lemma 4.1. Particularly, $\{{\bar{u}}_k\}_{k\in \mathbb {N}}$ converges to ${\bar{u}}$. Similarly, we can show that $\{{\bar{y}}_k\}_{k\in \mathbb {N}}$ converges to ${\bar{y}}$.

Now, let $(x,y,u)\in \mathbb {R}^n\times {\mathcal {Y}}\times {\mathcal {U}}$ be feasible to (OVR). Then, it is feasible to (OVR$(\varepsilon _k)$) for all $k\in \mathbb {N}$ which yields

$$\begin{aligned} \forall k\in \mathbb {N}:\quad F({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\le F(x,y,u). \end{aligned}$$

Noting that $\{({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\}_{k\in \mathbb {N}}$ converges strongly to $({\bar{x}},{\bar{y}},{\bar{u}})$ while F is continuous, we obtain $F({\bar{x}},{\bar{y}},{\bar{u}})\le F(x,y,u)$. Since $({\bar{x}},{\bar{y}},{\bar{u}})$ is feasible to (OVR), it must be a globally optimal solution of this problem.

We can reprise the above arguments in order to show that each accumulation point of the sequence $\{({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\}_{k\in \mathbb {N}}$ is a globally optimal solution of (OVR). $\square$

If, for some $k\in \mathbb {N}$, a globally optimal solution of (OVR$(\varepsilon _k)$) is feasible to (IOC), then it is a globally optimal solution of the latter problem as well since its feasible set is smaller than the feasible set of (OVR$(\varepsilon _k)$).

In the upcoming Sect. 5.3, we show how the above theory can be used to derive necessary stationarity conditions for local minimizers of the inverse optimal control problem (IOC).

5.3 Derivation of stationarity conditions

We intent to derive stationarity conditions for (IOC). However, we will only consider the case where ${\mathcal {U}}:=L^2(\varOmega )$ holds for a bounded domain $\varOmega \subset \mathbb {R}^d$ equipped with Lebesgue’s measure and $U_{\text {ad}}$ is given as stated below:

$$\begin{aligned} U_{\text {ad}}:= \{ u\in L^2(\varOmega ) \mid u_a(\omega )\le u(\omega )\le u_b(\omega ) \text { f.a.a. }\omega \in \varOmega \}. \end{aligned}$$

Therein, $u_a,u_b:\varOmega \rightarrow [-\infty ,\infty ]$ are measurable functions such that $U_{\text {ad}}$ is nonempty.

First, we will formulate the desired stationarity conditions.

Definition 5.1

We say that a feasible point $({\bar{x}}, {\bar{y}}, {\bar{u}})\in \mathbb {R}^n\times {\mathcal {Y}}\times L^2(\varOmega )$ of (OVR) is weakly stationary, W-stationary for short, if there exist multipliers ${\bar{p}}\in {\mathcal {Y}}$, ${\bar{\lambda }}\in L^2(\varOmega )$, ${\bar{z}}\in \mathbb {R}^n$, ${\bar{w}}\in L^2(\varOmega )$, ${\bar{\mu }}\in {\mathcal {Y}}$, ${\bar{\rho }}\in {\mathcal {Y}}$, and ${\bar{\xi }}\in L^2(\varOmega )$ which satisfy

$$\begin{aligned} F'_x({\bar{x}},{\bar{y}},{\bar{u}}) -\bigl ({\mathtt {P}}^\star \circ {\mathtt {C}}\bigr )[{\bar{\mu }}] -\sigma {\mathtt {Q}}^\star [{\bar{w}}] +{\bar{z}}&=0, \end{aligned}$$

(4a)

$$\begin{aligned} F'_y({\bar{x}},{\bar{y}},{\bar{u}}) +\bigl ({\mathtt {C}}^\star \circ {\mathtt {C}}\bigr )[{\bar{\mu }}] +{\mathtt {A}}^\star [{\bar{\rho }}]&=0, \end{aligned}$$

(4b)

$$\begin{aligned} F'_u({\bar{x}},{\bar{y}},{\bar{u}}) +\sigma {\bar{w}}-{\mathtt {B}}^\star [{\bar{\rho }}] +{\bar{\xi }}&=0, \end{aligned}$$

(4c)

$$\begin{aligned} {\mathtt {A}}[{\bar{\mu }}] -{\mathtt {B}}[{\bar{w}}]&=0, \end{aligned}$$

(4d)

$$\begin{aligned} {\bar{z}}&\in {\mathcal {N}}_S({\bar{x}}), \end{aligned}$$

(4e)

$$\begin{aligned} {\mathtt {C}}^\star [{\mathtt {C}}[{\bar{y}}]-{\mathtt {P}}[{\bar{x}}]] +{\mathtt {A}}^\star [{\bar{p}}]&= 0, \end{aligned}$$

(4f)

$$\begin{aligned} \sigma ({\bar{u}}-{\mathtt {Q}}[{\bar{x}}]) -{\mathtt {B}}^\star [{\bar{p}}]+{\bar{\lambda }}&=0, \end{aligned}$$

(4g)

$$\begin{aligned} {\bar{\lambda }}&\le 0\qquad \text {a.e. on }I^{b-}({\bar{u}}), \end{aligned}$$

(4h)

$$\begin{aligned} {\bar{\lambda }}&\ge 0\qquad \text {a.e. on }I^{a+}({\bar{u}}), \end{aligned}$$

(4i)

$$\begin{aligned} {\bar{\xi }}&=0\qquad \text {a.e. on }I^{a+}({\bar{u}})\cap I^{b-}({\bar{u}}), \end{aligned}$$

(4j)

$$\begin{aligned} {\bar{w}}&=0\qquad \text {a.e. on}\; \{\omega \in \varOmega \mid {\bar{\lambda }}(\omega )\ne 0\}. \end{aligned}$$

(4k)

If these multipliers additionally satisfy the condition

$$\begin{aligned} {\bar{\xi }}{\bar{w}}\ge 0\qquad \text {a.e. on }\varOmega , \end{aligned}$$

(5)

then $({\bar{x}},{\bar{y}},{\bar{u}})$ is said to be Clarke-stationary, C-stationary for short.

Here, the measurable sets $I^{a+}({\bar{u}}),I^{b-}({\bar{u}})\subset \varOmega$ are given by

$$\begin{aligned} I^{a+}({\bar{u}}):=\{\omega \in \varOmega \mid u_a(\omega )<{\bar{u}}(\omega )\}, \qquad I^{b-}({\bar{u}}):=\{\omega \in \varOmega \mid {\bar{u}}(\omega )<u_b(\omega )\}, \end{aligned}$$

and these sets are well-defined up to subsets of $\varOmega$ possessing measure zero.

Note that (4f)–(4i) are the KKT-conditions for the lower level problem (OC(x)) for the fixed parameter $x={\bar{x}}$. Obviously, these conditions are always satisfied for a feasible point of (OVR). The remaining conditions (4a)–(4e), (4j), and (4k) can be interpreted as the weak stationarity conditions of the equilibrium problem

$$\begin{aligned} \begin{aligned} F(x,y,u)&\,\rightarrow \,\min \limits _{x,y,u,p,\lambda }\\ x&\,\in \,S\\ {\mathtt {A}}[y]-{\mathtt {B}}[u]&\,=\,0\\ {\mathtt {C}}^\star [{\mathtt {C}}[y]-{\mathtt {P}}[x]]+{\mathtt {A}}^\star [p]&\,=\,0\\ \sigma ({{u}}-{\mathtt {Q}}[x])-{\mathtt {B}}^\star [p]+\lambda&\,=\,0\\ u&\,\in \,U_{\text {ad}}\\ \lambda&\,\in {\mathcal {N}}_{U_{\text {ad}}}(u), \end{aligned} \end{aligned}$$

(6)

which results from (IOC) replacing the implicit constraint $(y,u)\in \varPsi (x)$ by the lower level feasibility and optimality conditions.

We will derive the system of W-stationarity by using the KKT-conditions of (OVR$(\varepsilon _k)$) and observing the behaviour of the system as k tends to infinity. For a fixed $k\in \mathbb {N}$, let $(x_k,y_k,u_k)\in \mathbb {R}^n\times {\mathcal {Y}}\times L^2(\varOmega )$ be a globally optimal solution of (OVR$(\varepsilon _k)$). Due to Lemma 5.2, we know that the point $(x_k,y_k,u_k)$ satisfies the KKT-conditions of (OVR$(\varepsilon _k)$). Thus, there exist multipliers $z_k\in \mathbb {R}^n$, $\alpha _k\in \mathbb {R}$, $p_k\in {\mathcal {Y}}$, and $\lambda _k\in L^2(\varOmega )$ which solve the system

$$\begin{aligned} F'_x(x_k,y_k,u_k)+z_k +\alpha _k \bigl ( {\mathtt {P}}^\star [{\mathtt {P}}[x_k]-{\mathtt {C}}[y_k]] +\sigma {\mathtt {Q}}^\star [{\mathtt {Q}}[x_k]-u_k] -\varphi '(x_k) \bigr ) =0,&\end{aligned}$$

(7a)

$$\begin{aligned} F'_y(x_k,y_k,u_k) +\alpha _k {\mathtt {C}}^\star [{\mathtt {C}}[y_k]-{\mathtt {P}}[x_k]] +{\mathtt {A}}^\star [p_k] =0,&\end{aligned}$$

(7b)

$$\begin{aligned} F'_u(x_k,y_k,u_k) +\alpha _k\sigma (u_k-{\mathtt {Q}}[x_k]) -{\mathtt {B}}^\star [p_k] +\lambda _k =0,&\end{aligned}$$

(7c)

$$\begin{aligned} z_k \in {\mathcal {N}}_S(x_k),&\end{aligned}$$

(7d)

$$\begin{aligned} \lambda _k \in {\mathcal {N}}_{U_{\text {ad}}}(u_k),&\end{aligned}$$

(7e)

$$\begin{aligned} 0 \le \alpha _k \perp f(x_k,y_k,u_k)-\varphi (x_k) -\varepsilon _k \le 0.&\end{aligned}$$

(7f)

Recall that $\psi ^y:\mathbb {R}^n\rightarrow {\mathcal {Y}}$ and $\psi ^u:\mathbb {R}^n\rightarrow L^2(\varOmega )$ are the solution functions of the lower level (OC(x)), while $\phi ^p:\mathbb {R}^n\rightarrow {\mathcal {Y}}$ and $\phi ^\lambda :\mathbb {R}^n\rightarrow L^2(\varOmega )$ denote the associated Lagrange multiplier mappings defined via the KKT-system (2), see Sect. 4 for details.

Lemma 5.5

For each $k\in \mathbb {N}$, let $(x_k,y_k,u_k)\in \mathbb {R}^n\times {\mathcal {Y}}\times L^2(\varOmega )$ be a global minimizer of (OVR$(\varepsilon _k)$) and let $(z_k,\alpha _k,p_k,\lambda _k)\in \mathbb {R}^n\times \mathbb {R}\times {\mathcal {Y}}\times L^2(\varOmega )$ be the respective Lagrange multipliers from (7). We assume w.l.o.g. that $\{(x_k,y_k,u_k)\}_{k\in \mathbb {N}}$ converges to a globally optimal solution $({\bar{x}},{\bar{y}},{\bar{u}})\in \mathbb {R}^n\times {\mathcal {Y}}\times L^2(\varOmega )$ of (IOC), see Theorem 5.1. Then, there exist ${\bar{z}}\in \mathbb {R}^n$, ${\bar{w}}\in L^2(\varOmega )$, ${\bar{\rho }}\in {\mathcal {Y}}$, ${\bar{\xi }}\in L^2(\varOmega )$, and ${\bar{\mu }}\in {\mathcal {Y}}$ such that the convergences

$$\begin{aligned} \alpha _k(u_k-\psi ^u(x_k)) \rightharpoonup {\bar{w}},&\end{aligned}$$

(8a)

$$\begin{aligned} \alpha _k(y_k-\psi ^y(x_k)) \rightharpoonup {\bar{\mu }},&\end{aligned}$$

(8b)

$$\begin{aligned} p_k-\alpha _k\phi ^p(x_k) \rightharpoonup {\bar{\rho }},&\end{aligned}$$

(8c)

$$\begin{aligned} \lambda _k-\alpha _k\phi ^\lambda (x_k) \rightharpoonup {\bar{\xi }},&\end{aligned}$$

(8d)

$$\begin{aligned} z_k \rightarrow {\bar{z}}\,\,&\end{aligned}$$

(8e)

hold along a subsequence. Moreover, the limits ${\bar{z}}$, ${\bar{w}}$, ${\bar{\xi }}$, ${\bar{\mu }}$, and ${\bar{\rho }}$ satisfy the conditions (4a)–(4e).

Proof

Exploiting the introduced notation, we notice that

$$\begin{aligned} {\mathtt {C}}^\star [{\mathtt {C}}[\psi ^y(x_k)]-{\mathtt {P}}[x_k]]+{\mathtt {A}}^\star [\phi ^p(x_k)]&= 0, \end{aligned}$$

(9a)

$$\begin{aligned} \sigma (\psi ^u(x_k)-{\mathtt {Q}}[x_k])-{\mathtt {B}}^\star [\phi ^p(x_k)] +\phi ^\lambda (x_k)&=0, \end{aligned}$$

(9b)

$$\begin{aligned} \phi ^\lambda (x_k)&\in {\mathcal {N}}_{U_{\text {ad}}}(\psi ^u(x_k)) \end{aligned}$$

(9c)

is valid for each $k\in \mathbb {N}$. Let us focus on (8a). Multiplying (9a) and (9b) with $\alpha _k$ and subtracting these equations from (7b) and (7c) yields

$$\begin{aligned}&F'_y(x_k,y_k,u_k)+{\mathtt {A}}^\star [p_k] +\alpha _k ({\mathtt {C}}^\star \circ {\mathtt {C}})[y_k-\psi ^y(x_k)] -\alpha _k{\mathtt {A}}^\star [\phi ^p(x_k)] =0, \end{aligned}$$

(10a)

$$\begin{aligned}&F'_u(x_k,y_k,u_k)-{\mathtt {B}}^\star [p_k] +\lambda _k +\alpha _k\sigma (u_k-\psi ^u(x_k))\nonumber \\&\qquad \quad \qquad \qquad \qquad \qquad \qquad \qquad \,+\alpha _k({\mathtt {B}}^\star [\phi ^p(x_k)] -\phi ^\lambda (x_k))=0. \end{aligned}$$

(10b)

Testing (10a) with $y_k-\psi ^y(x_k)$ gives us

$$\begin{aligned} \begin{aligned}&\left\langle F'_y(x_k,y_k,u_k)+{\mathtt {A}}^\star [p_k-\alpha _k\phi ^p(x_k)], y_k-\psi ^y(x_k)\right\rangle _{{\mathcal {Y}}}\\&\quad =-\alpha _k\left\langle ({\mathtt {C}}^\star \circ {\mathtt {C}})[y_k-\psi ^y(x_k)], y_k-\psi ^y(x_k)\right\rangle _{{\mathcal {Y}}}=-\alpha _k\left\| {\mathtt {C}}[y_k-\psi ^y(x_k)]\right\| _{{\mathcal {M}}}^2\le 0, \end{aligned} \end{aligned}$$

and, therefore,

$$\begin{aligned} \begin{aligned}&\left\langle {\mathtt {B}}^\star [p_k-\alpha _k\phi ^p(x_k)], u_k-\psi ^u(x_k)\right\rangle _{L^2(\varOmega )}\\&\quad =\left\langle {\mathtt {B}}[u_k-\psi ^u(x_k)], p_k-\alpha _k\phi ^p(x_k)\right\rangle _{{\mathcal {Y}}}\\&\quad =\left\langle {\mathtt {A}}[y_k-\psi ^y(x_k)], p_k-\alpha _k\phi ^p(x_k)\right\rangle _{{\mathcal {Y}}}\\&\quad =\left\langle {\mathtt {A}}^\star [p_k-\alpha _k\phi ^p(x_k)], y_k-\psi ^y(x_k)]\right\rangle _{{\mathcal {Y}}}\\&\quad \le \left\langle -F'_y(x_k,y_k,u_k), y_k-\psi ^y(x_k)]\right\rangle _{{\mathcal {Y}}}\\&\quad =\left\langle -F'_y(x_k,y_k,u_k), ({\mathtt {A}}^{-1}\circ {\mathtt {B}})[u_k-\psi ^u(x_k)]\right\rangle _{{\mathcal {Y}}}\\&\quad \le C_1 \left\| u_k-\psi ^u(x_k)\right\| _{L^2(\varOmega )} \end{aligned} \end{aligned}$$

holds for a constant $C_1>0$ that is independent of k. If we use this after testing (10b) with $u_k-\psi ^u(x_k)$, we obtain

$$\begin{aligned} \begin{aligned}&\sigma \alpha _k\left\| u_k-\psi ^u(x_k)\right\| _{L^2(\varOmega )}^2\\&\quad = \left\langle {\mathtt {B}}^\star [p_k-\alpha _k\phi ^p(x_k)]-F'_u(x_k,y_k,u_k)+\alpha _k\phi ^\lambda (x_k)-\lambda _k, u_k-\psi ^u(x_k)\right\rangle _{L^2(\varOmega )}\\&\quad \le \left\langle {\mathtt {B}}^\star [p_k-\alpha _k\phi ^p(x_k)]-F'_u(x_k,y_k,u_k), u_k-\psi ^u(x_k)\right\rangle _{L^2(\varOmega )}\\&\quad \le C_1 \left\| u_k-\psi ^u(x_k)\right\| _{L^2(\varOmega )} +\left\langle F_u(x_k,y_k,u_k), u_k-\psi ^u(x_k)\right\rangle _{L^2(\varOmega )}\\&\quad \le C_2 \left\| u_k-\psi ^u(x_k)\right\| _{L^2(\varOmega )} \end{aligned} \end{aligned}$$

for a constant $C_2>0$ that is independent of k. Here, the first inequality follows from $\alpha _k\ge 0$, $\phi ^\lambda (x_k)\in {\mathcal {N}}_{U_{\text {ad}}}(\psi ^u(x_k))$, and $\lambda _k\in {\mathcal {N}}_{U_{\text {ad}}}(u_k)$. From above, it follows that $\alpha _k(u_k-\psi ^u(x_k))$ is bounded in $L^2(\varOmega )$. Hence, we can extract a weakly convergent subsequence and denote its weak limit by ${\bar{w}}\in L^2(\varOmega )$ in order to satisfy (8a).

Due to ${\mathtt {A}}[y_k-\psi ^y(x_k)]={\mathtt {B}}[u_k-\psi ^u(x_k)]$, we obtain (8b) and (4d) from (8a). Since F is continuously Fréchet differentiable, it follows from (10a) that ${\mathtt {A}}^\star [p_k-\alpha _k\phi ^p(x_k)]$ converges weakly. Since ${\mathtt {A}}$ is continuously invertible, the sequence $\{p_k-\alpha _k\phi ^p(x_k)\}_{k\in \mathbb {N}}$ is weakly convergent as well. Thus, defining ${\bar{\rho }}$ as its weak limit yields (8c) and (4b). Using the newly obtained convergence in (10b), we get that $\lambda _k-\alpha _k\phi ^\lambda (x_k)$ converges weakly in $L^2(\varOmega )$. The weak limit ${\bar{\xi }}$ satisfies (8d) and (4c).

It remains to show the convergence of $z_k$. Using Lemma 4.3, we obtain

$$\begin{aligned} {\mathtt {P}}^\star [{\mathtt {P}}[x_k]-{\mathtt {C}}[y_k]]+\sigma {\mathtt {Q}}^\star [ {\mathtt {Q}}[x_k]-u_k]-\varphi '(x_k) = ({\mathtt {P}}^\star \circ {\mathtt {C}})[\psi ^y(x_k)-y_k] +\sigma {\mathtt {Q}}^\star [\psi ^u(x_k)-u_k]. \end{aligned}$$

Then, the previous convergences and (7a) imply (8e) and (4a). Finally, (4e) follows from $x_k\rightarrow {\bar{x}}$ and $z_k\rightarrow {\bar{z}}$ due to the properties of the normal cone. $\square$

Lemma 5.6

We consider the setting of Lemma 5.5. Then, the multipliers ${\bar{\xi }},{\bar{w}}\in L^2(\varOmega )$ satisfy (4j) and (4k).

Proof

We start with proving (4j). W.l.o.g., we assume that $\{u_k\}_{k\in \mathbb {N}}$ and $\{\psi ^u(x_k)\}_{k\in \mathbb {N}}$ converge pointwise almost everywhere to ${\bar{u}}$ (otherwise, we select a subsequence with that property). Due to $\lambda _k\in {\mathcal {N}}_{U_{\text {ad}}}(u_k)$ and $\phi ^\lambda (x_k)\in {\mathcal {N}}_{U_{\text {ad}}}(\psi ^u(x_k))$, we have

$$\begin{aligned} \lambda _k-\alpha _k\phi ^\lambda (x_k)=0 \quad \text {a.e. on}\quad \left\{ \omega \in \varOmega \,\Bigg |\, \begin{aligned}&u_a(\omega )< u_k(\omega )< u_b(\omega )\\&u_a(\omega )<\psi ^u(x_k)(\omega )< u_b(\omega ) \end{aligned}\right\} \end{aligned}$$

for all $k\in \mathbb {N}$. Thus, the pointwise convergence of $\{u_k\}_{k\in \mathbb {N}}$ and $\{\psi ^u(x_k)\}_{k\in \mathbb {N}}$ implies that $\lambda _k-\alpha _k\phi ^\lambda (x_k)\rightarrow 0$ holds almost everywhere on $I^{a+}({\bar{u}})\cap I^{b-}({\bar{u}})$. Since $\{\lambda _k-\alpha _k\phi ^\lambda (x_k)\}_{k\in \mathbb {N}}$ converges weakly in $L^2(\varOmega )$ and pointwise almost everywhere on a subset, the limits must coincide on that subset, i.e. ${\bar{\xi }}=0$ holds almost everywhere on $I^{a+}({\bar{u}})\cap I^{b-}({\bar{u}})$.

We continue with proving (4k). If $\{\alpha _k\}_{k\in \mathbb {N}}$ has a bounded subsequence, this already implies ${\bar{w}}=0$ and (4k). Thus, we only need to consider the situation $\alpha _k\rightarrow \infty$. The continuity of $\phi ^\lambda$ implies $\phi ^\lambda (x_k)\rightarrow {\bar{\lambda }}$ in $L^2(\varOmega )$. Combining this with (8d) yields the convergence $\alpha _k^{-1}\lambda _k\rightarrow {\bar{\lambda }}$ in $L^2(\varOmega )$.

Now, let $G\subset \varOmega$ be an arbitrary measurable set and let $\chi _G\in L^\infty (\varOmega )$ denote the corresponding characteristic function which equals 1 on G and vanishes otherwise. The inequalities below follow immediately from the definition of the normal cone:

$$\begin{aligned} \begin{aligned} \left\langle \alpha _k^{-1}\lambda _k, \alpha _k\chi _G(u_k-\psi ^u(x_k))\right\rangle _{L^2(\varOmega )}&\ge 0,\\ \left\langle \phi ^\lambda (x_k), \alpha _k\chi _G(u_k-\psi ^u(x_k))\right\rangle _{L^2(\varOmega )}&\le 0. \end{aligned} \end{aligned}$$

Using the strong convergence to ${\bar{\lambda }}$ and the weak convergence to ${\bar{w}}$ yields

$$\begin{aligned} \left\langle {\bar{\lambda }}, \chi _G{\bar{w}}\right\rangle _{L^2(\varOmega )} =0. \end{aligned}$$

Since $G\subset \varOmega$ was an arbitrary measurable set, this implies (4k). $\square$

In the next lemma, we show that condition (5) holds under an additional assumption.

Lemma 5.7

We consider the setting of Lemma 5.5. If one of the operators ${\mathtt {B}}$ or ${\mathtt {C}}$ is compact, then the resulting multipliers ${\bar{\xi }},{\bar{w}}\in L^2(\varOmega )$ additionally satisfy the condition (5).

Proof

In this proof, we will only consider subsequences such that the convergences in Lemma 5.5 hold. Let $G\subset \varOmega$ be an arbitrary measurable set and $\chi _G\in L^\infty (\varOmega )$ the associated characteristic function.

Our first goal is to show

$$\begin{aligned} \left\langle {\mathtt {B}}^\star [p_k-\alpha _k\phi ^p(x_k)], \alpha _k\chi _G(u_k- \psi ^u(x_k))\right\rangle _{L^2(\varOmega )} \rightarrow \left\langle {\mathtt {B}}^\star [{\bar{\rho }}], \chi _G{\bar{w}}\right\rangle _{L^2(\varOmega )}. \end{aligned}$$

(11)

If, on the one hand, ${\mathtt {B}}$ is compact, then (11) follows immediately from (8a), (8c), and the definition of the adjoint. If, on the other hand, ${\mathtt {C}}$ is compact, then we obtain the strong convergence $\alpha _k({\mathtt {C}}^\star \circ {\mathtt {C}})[y_k-\psi ^y(x_k)] \rightarrow ({\mathtt {C}}^\star \circ {\mathtt {C}})[{\bar{\mu }}]$. Using (10a), this implies the strong convergence $p_k-\alpha _k\phi ^p(x_k)\rightarrow {\bar{\rho }}$ and (11) follow.

Now, we can combine (11) with (4c), (10b), and the sequential weak lower semi-continuity of $w\mapsto \left\langle \sigma w, \chi _Gw\right\rangle _{L^2(\varOmega )}$ which yields

$$\begin{aligned} \begin{aligned} \left\langle -{\bar{\xi }}, \chi _G{\bar{w}}\right\rangle _{L^2(\varOmega )}&=\left\langle F'_u({\bar{x}},{\bar{y}},{\bar{u}})+\sigma {\bar{w}}-{\mathtt {B}}^\star [{\bar{\rho }}], \chi _G{\bar{w}}\right\rangle _{L^2(\varOmega )}\\&\le \lim _{k\rightarrow \infty } \left\langle F'_u(x_k,y_k,u_k)-{\mathtt {B}}^\star [p_k-\alpha _k\phi ^p(x_k)], \alpha _k\chi _G(u_k-\psi ^u(x_k))\right\rangle _{L^2(\varOmega )}\\&\qquad +\liminf _{k\rightarrow \infty } \left\langle \sigma \alpha _k(u_k-\psi ^u(x_k)), \alpha _k\chi _G(u_k-\psi ^u(x_k))\right\rangle _{L^2(\varOmega )}\\&= \liminf _{k\rightarrow \infty } \left\langle -(\lambda _k-\alpha _k\phi ^\lambda (x_k)), \alpha _k\chi _G(u_k-\psi ^u(x_k))\right\rangle _{L^2(\varOmega )} \le 0. \end{aligned} \end{aligned}$$

Here, the last inequality follows from $\lambda _k\in {\mathcal {N}}_{U_{\text {ad}}}(u_k)$ and $\phi ^\lambda (x_k)\in {\mathcal {N}}_{U_{\text {ad}}}(\psi ^u(x_k))$. Since $G\subset \varOmega$ is an arbitrary subset, the pointwise condition in the claim follows. $\square$

Now, we are in a position to state the final result of this section.

Theorem 5.2

Let $({\bar{x}},{\bar{y}},{\bar{u}})\in \mathbb {R}^n\times {\mathcal {Y}}\times L^2(\varOmega )$ be a locally optimal solution of (IOC). Then, $({\bar{x}},{\bar{y}},{\bar{u}})$ is a W-stationary point of (IOC).

If, additionally, one of the operators ${\mathtt {B}}$ or ${\mathtt {C}}$ is compact, then $({\bar{x}},{\bar{y}},{\bar{u}})$ is already a C-stationary point of (IOC).

Proof

First, we note that due to Lemma 4.1, ${\bar{x}}$ is a locally optimal solution of

$$\begin{aligned} \begin{aligned} F(x,\psi ^y(x),\psi ^u(x))&\,\rightarrow \,\min \limits _x\\ x&\,\in \,S. \end{aligned} \end{aligned}$$

Let $\varepsilon >0$ be the associated radius of local optimality w.r.t. the 1-norm. Then, ${\bar{x}}$ is the unique globally optimal solution of the regularized problem

$$\begin{aligned} \begin{aligned} F(x,\psi ^y(x),\psi ^u(x))+\tfrac{1}{2}\left| x-{\bar{x}}\right| _{2}^2&\,\rightarrow \,\min \limits _x\\ x&\,\in \,S\cap {\mathbb {B}}^\varepsilon _1({\bar{x}}) \end{aligned} \end{aligned}$$

where ${\mathbb {B}}^\varepsilon _1({\bar{x}}):=\{x\in \mathbb {R}^n\,|\,\left| x-{\bar{x}}\right| _{1}\le \varepsilon \}$ is the closed $\varepsilon$-ball around ${\bar{x}}$ w.r.t. the 1-norm. Consequently, $({\bar{x}},{\bar{y}},{\bar{u}})$ is the unique global minimizer of

$$\begin{aligned} \begin{aligned} F(x,y,u)+\tfrac{1}{2}\left| x-{\bar{x}}\right| _{2}^2&\,\rightarrow \,\min \limits _{x,y,u}\\ x&\,\in \,S\cap {\mathbb {B}}^\varepsilon _1({\bar{x}})\\ (y,u)&\,\in \,\varPsi (x). \end{aligned} \end{aligned}$$

(12)

Now, we are in a position to apply Lemmas 5.5,  5.6, and 5.7 to (12) which allows us to infer that $({\bar{x}},{\bar{y}},{\bar{u}})$ is a W- or even (under the additional compactness of ${\mathtt {B}}$ or ${\mathtt {C}}$) C-stationary point of (12).

Noting that the first-order derivative of $x\mapsto \tfrac{1}{2}\left| x-{\bar{x}}\right| _{2}^2$ vanishes at ${\bar{x}}$ while ${\bar{x}}$ is an interior point of ${\mathbb {B}}^\varepsilon _1({\bar{x}})$, the W- and C-stationarity conditions of (12) and (IOC) at the point $({\bar{x}},{\bar{y}},{\bar{u}})$ coincide. This shows the theorem’s assertion. $\square$

We finish this section with two brief remarks. First, we comment on the compactness of ${\mathtt {B}}$ and ${\mathtt {C}}$. Afterwards, the actual strength of the derived necessary optimality conditions is discussed.

Remark 5.1

Let us consider the setting of Example 2.1. Therein, we fixed a bounded domain $\varOmega \subset \mathbb {R}^d$ and set ${\mathcal {M}}={\mathcal {U}}:=L^2(\varOmega )$ as well as ${\mathcal {Y}}:=H^1_0(\varOmega )$. Furthermore, ${\mathtt {C}}$ was chosen to be the natural embedding of $H^1_0(\varOmega )$ into $L^2(\varOmega )$ which is known to be compact, see [1, Theorem 6.3].

Next, assume that ${\mathtt {A}}\in {\mathbb {L}}\left[ H^1_0(\varOmega ),H^{-1}(\varOmega )\right]$ is an elliptic operator while ${\mathtt {B}}$ is given by

$$\begin{aligned} \forall u\in L^2(\varOmega )\,\forall z\in H^1_0(\varOmega ):\quad \left\langle {\mathtt {B}}[u], z\right\rangle _{H^1_0(\varOmega )}:=\int \limits _\varOmega u(\omega )z(\omega )\mathrm d\omega . \end{aligned}$$

Thus, ${\mathtt {B}}$ equals the natural embedding of $L^2(\varOmega )$ into $H^{-1}(\varOmega )$ which is compact since the adjoint embedding $H^1_0(\varOmega )\hookrightarrow L^2(\varOmega )$ is compact.

Consequently, in the standard setting of elliptic optimal control, the operators ${\mathtt {B}}$ and ${\mathtt {C}}$ are compact. Thus, due to Theorem 5.2, each locally optimal solution of the associated program (IOC) is a C-stationary point.

Remark 5.2

In the setting where ${\mathcal {Y}}:=\mathbb {R}^m$ and and ${\mathcal {U}}:=\mathbb {R}^p$ hold while the controls have to satisfy standard box-constraints at the lower level stage, the equilibrium problem (6) is a so-called mathematical program with complementarity constraints with affine data. Due to [13, Theorem 3.9], each local minimizer of this optimization problem is a so-called Mordukhovich-stationary point, and this is a stronger stationarity concept than Clarke-stationarity, see [13, Sect. 2]. As a consequence, the locally optimal solutions of the associated inverse optimal control problem are Mordukhovich-stationary points.

It remains a question of future research whether it is possible to extend the results from Theorem 5.2 to (pointwise) Mordukhovich-stationarity in the $L^2$-setting. Related issues w.r.t. other equilibrium-type optimal control problems are discussed in [15, 16].

6 Computing globally optimal solutions

The major drawback of Theorem 5.1 w.r.t. its applicability is the fact that the optimal value function $\varphi$ is only implicitly known and, consequently, it is not clear how to solve the relaxed problems (OVR$(\varepsilon _k)$) at any iterate of a potential algorithm.

Due to the convexity of $\varphi$, see Lemma 4.2, we note that the optimal-value-reformulation (OVR) of (IOC) is a so-called DC-program where DC is the classical abbreviation for Difference of Convex Functions. This structure allows the construction of algorithms which can be used to find the global minimizers of (IOC), see [21, Sect. 5] and the references therein. However, the fact that $\varphi$ is only implicitly known may induce some essential difficulties again when trying to adapt those methods directly. On the other hand, we note that the concavity of (OVR) only appears within the constraint $f(x,y,u)-\varphi (x)\le 0$ and only w.r.t. the variable x.

In order to exploit this observation for the construction of a suitable solution algorithm, we approximate the convex optimal value function $\varphi$ from above using a piecewise affine function $\xi$ which exactly interpolates $\varphi$ at an increasing number of points from S. Thus, we formulate a relaxed surrogate problem associated with (OVR) which is different from (OVR$(\varepsilon _k)$). Since $\xi$ is piecewise affine, our approach allows us to decompose the resulting surrogate problems into finitely many convex subproblems which are easy to solve. This idea is used in [9, Sect. 4] and [10, Sect. 3.6.2] to solve finite-dimensional bilevel programming problems with fully convex lower level problem.

6.1 The algorithm and its convergence properties

Let $X:=\{x^1,\dots ,x^m\}\subset \mathbb {R}^n$ be a nonempty set such that $S\subset {\text {int}}\,{\text {conv}}\,X$ holds true. The convexity of $\varphi$ yields

$$\begin{aligned} \forall x\in {\text {conv}}\,X:\quad \varphi (x) \le \min \limits _\mu \left\{ \sum \nolimits _{i=1}^m\mu _i\varphi (x^i)\, \Bigg | \,\mu \in \varDelta ^m,\,\sum \nolimits _{i=1}^m\mu _ix^i=x \right\} =:\xi _X(x). \end{aligned}$$

Obviously, $\xi _X:{\text {conv}}\,X\rightarrow \mathbb {R}$ is the optimal value function of a fully convex linear parametric optimization problem and, thus, convex and piecewise affine, see [29, Theorem 6.7, Theorem 6.9]. These properties also follow from the observation

$$\begin{aligned} {\text {epi}}\,\xi _X={\text {conv}}\{(x^i,\varphi (x^i))\,|\,i=1,\dots ,m\}+\{0\}\times \mathbb {R}^+_0 \end{aligned}$$

where ${\text {epi}}\,\xi _X$ represents the epigraph of $\xi _X$. Particularly, there exists a finite partition $\{R_X^j\}_{j=1}^{r(X)}$ of ${\text {conv}}\,X$ into so-called regions of stability such that $\xi _X$ is affine on every set $R_X^j$, $j=1,\dots ,r(X)$.

Note that for each $i=1,\dots ,m$, we have $\xi _X(x^i)=\varphi (x^i)$, i.e. $\xi _X$ interpolates $\varphi$ exactly at all the points in X. This observation gives rise to the formulation of Algorithm 1.

Below, we comment on some features of Algorithm 1.

Remark 6.1

Similar as in Lemma 5.3 it is possible to show that (OVR$(X_k)$) possesses a global solution for each $k\in \mathbb {N}$. As mentioned above, at each iteration $k\in \mathbb {N}$, we can decompose S into $r(k)\in \mathbb {N}$ regions of stability on which $\xi _{X_k}$ is affine, respectively. Thus, (OVR$(X_k)$) can be decomposed into r(k) convex subproblems which can be solved by exploiting standard methods.

Remark 6.2

For arbitrarily chosen $k,k'\in \mathbb {N}$ satisfying $k\le k'$, we have

$$\begin{aligned} \forall x\in S:\quad \varphi (x)\le \xi _{X_{k'}}(x)\le \xi _{X_k}(x). \end{aligned}$$

In order to analyze the qualitative properties of Algorithm 1, we need the following lemma.

Lemma 6.1

Let $X_1\subset \mathbb {R}^n$ be a finite set satisfying $S\subset {\text {int}}\,{\text {conv}}\,X_1$. Then, there is a constant $L>0$ such that $\xi _X$ is Lipschitz continuous on the set S with modulus L for each set $X\subset \mathbb {R}^n$ which is the union of $X_1$ and some finite subset of S.

Proof

By definition of $\varphi$, $\xi _X$, and $\xi _{X_1}$ the following relations are obvious:

$$\begin{aligned} \forall x\in {\text {conv}}\,X_1:\quad 0\le \varphi (x)\le \xi _{X}(x)\le \xi _{X_1}(x). \end{aligned}$$

Since $\xi _{X_1}$ is continuous on the compact set ${\text {conv}}\,X_1$, its maximal value $M\ge 0$ is well-defined and an upper bound for all the real numbers $|\xi _X(x)|$ such that $x\in {\text {conv}}\,X_1$ holds.

Since we have $S\subset {\text {int}}\,{\text {conv}}\,X_1$, there is some $\varepsilon >0$ such that $S+{\mathbb {B}}^\varepsilon _2(0)\subset {\text {conv}}\,X_1$ holds true. Here, ${\mathbb {B}}^\varepsilon _2(0)$ denotes the closed $\varepsilon$-ball in $\mathbb {R}^n$ around 0 w.r.t. the Euclidean norm.

For $x,y\in S$ satisfying $x\ne y$, we define

$$\begin{aligned} z:=x+\frac{\varepsilon }{\left| x-y\right| _{2}}(x-y),\qquad \alpha :=\frac{\left| x-y\right| _{2}}{\varepsilon +\left| x-y\right| _{2}} \end{aligned}$$

By construction, we have $z\in S+{\mathbb {B}}^\varepsilon _2(0)\subset {\text {conv}}\,X_1$ and $x=(1-\alpha )y+\alpha z$. Noting that $\xi _X$ is convex, we obtain $\xi _X(x)\le \xi _X(y)+\alpha (\xi _X(z)-\xi _X(y))$ which yields the estimate $\xi _X(x)-\xi _X(y)\le \alpha |\xi _X(z)-\xi _X(y)|\le 2\alpha M$. Thus, we obtain

$$\begin{aligned} \xi _X(x)-\xi _X(y) \le 2M\frac{\left| x-y\right| _{2}}{\varepsilon +\left| x-y\right| _{2}} \le \frac{2M}{\varepsilon }\left| x-y\right| _{2}. \end{aligned}$$

Interchanging the roles of x and y yields that $\xi _X$ is Lipschitz continuous on S with Lipschitz modulus $L:=\tfrac{2M}{\varepsilon }$. Note that neither M nor $\varepsilon$ depend on the precise choice of X. Thus, the proof is complete. $\square$

The next example shows that the requirement $S\subset {\text {int}}\,{\text {conv}}\,X_1$ in Lemma 6.1 cannot be relaxed.

Example 6.1

Let us assume that $n = 2$ and $\varphi (x) = x_2^2$ hold. Further, we set

$$\begin{aligned} X_1 := \left\{ (1,-1), (1,1), (0,0)\right\} , \qquad S := {\text {conv}}\,X_1. \end{aligned}$$

Now, we consider an increasing sequence $\{\theta _k\}_{k\in \mathbb {N}} \subset (0,1)\subset \mathbb {R}$ with $\theta _k\rightarrow 1$. For all $k\in \mathbb {N}$, let us define $X_k := X_1 \cup \bigcup _{i = 1}^{k-1} \{(\theta _i, 0)\}\subset \mathbb {R}^2$. Then, it can be checked that

$$\begin{aligned} \xi _{X_k}(x) = \max \left\{ x_2, -x_2, \frac{x_1 - \theta _{k-1}}{1 - \theta _{k-1}}\right\} \end{aligned}$$

is valid. In particular, the Lipschitz constant of $\xi _{X_k}$ on S is given by $(1 - \theta _{k-1})^{-1}$. Clearly, this term is not bounded as $k \rightarrow \infty$.

Now, we are well prepared to study the qualitative properties of Algorithm 1.

Theorem 6.1

Either, Algorithm 1 terminates after a finite number of steps producing a globally optimal solution, or it computes a sequence $\{({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\}_{k\in \mathbb {N}}$ of globally optimal solutions of (OVR$(X_k)$). This sequence possesses a convergent subsequence whose limit point $({\bar{x}},{\bar{y}},{\bar{u}})$ is a globally optimal solution of (OVR) and, thus, of (IOC). Moreover, each accumulation point of $\{({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\}_{k\in \mathbb {N}}$ is a globally optimal solution of (OVR).

Proof

The feasible set of (OVR$(X_k)$) is larger than the feasible set of (OVR) for each $k\in \mathbb {N}$, Thus, if $({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)$ is feasible to (OVR) for some $k\in \mathbb {N}$, then this point must be a globally optimal solution of this problem.

Suppose that the algorithm does not terminate. Clearly, the sequence $\{{\bar{x}}_k\}_{k\in \mathbb {N}}$ is bounded. The feasibility of $({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)$ to (OVR$(X_k)$) and Remark 6.2 yield

$$\begin{aligned} \forall k\in \mathbb {N}:\quad \left\| {\bar{u}}_k\right\| _{{\mathcal {U}}} \le \sqrt{\tfrac{2}{\sigma }\xi _{X_1}({\bar{x}}_k)} +\left\| {\mathtt {Q}}[{\bar{x}}_k]\right\| _{{\mathcal {U}}}. \end{aligned}$$

Since $\{{\bar{x}}_k\}_{k\in \mathbb {N}}$ is bounded while $\xi _{X_1}$ is continuous on S, $\{{\bar{u}}_k\}_{k\in \mathbb {N}}$ is bounded. From the relation ${\bar{y}}_k=({\mathtt {A}}^{-1}\circ {\mathtt {B}})[{\bar{u}}_k]$ for each $k\in \mathbb {N}$ and the continuity of ${\mathtt {A}}^{-1}\circ {\mathtt {B}}\in {\mathbb {L}}\left[ {\mathcal {U}},{\mathcal {Y}}\right]$, $\{{\bar{y}}_k\}_{k\in \mathbb {N}}$ is bounded as well. Consequently, $\{({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\}_{k\in \mathbb {N}}$ is bounded and, therefore, possesses a weakly convergent subsequence (without relabeling) with weak limit $({\bar{x}},{\bar{y}},{\bar{u}})$. Particularly, we have ${\bar{x}}_k\rightarrow {\bar{x}}$. The closedness of S and the closedness and convexity of $U_{\text {ad}}$ yield ${\bar{x}}\in S$ and ${\bar{u}}\in U_{\text {ad}}$. Furthermore, ${\mathtt {A}}[{\bar{y}}]-{\mathtt {B}}[{\bar{u}}]=0$ follows from the linearity and continuity of ${\mathtt {A}}$ and ${\mathtt {B}}$. Let $L>0$ be the Lipschitz constant of $\xi _{X_k}$ on S which, due to Lemma 6.1, does not depend on k. Since f is convex and continuous, it is weakly lower semicontinuous. Furthermore, $\varphi$ is continuous by means of Lemma 4.3. Due to the construction of the algorithm, we have $\xi _{X_k}({\bar{x}}_{k-1})=\varphi ({\bar{x}}_{k-1})$ for each $k\in \mathbb {N}$ which yields

$$\begin{aligned} \begin{aligned} \varphi ({\bar{x}})\le f({\bar{x}},{\bar{y}},{\bar{u}})&\le \liminf \limits _{k\rightarrow \infty } f({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\\&\le \limsup \limits _{k\rightarrow \infty } f({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\\&\le \limsup \limits _{k\rightarrow \infty }\xi _{X_k}({\bar{x}}_k)\\&\le \limsup \limits _{k\rightarrow \infty } \bigl (\xi _{X_k}({\bar{x}}_{k-1})+L\left| {\bar{x}}_k-{\bar{x}}_{k-1}\right| _{2}\bigr )\\&=\limsup \limits _{k\rightarrow \infty } \bigl (\varphi ({\bar{x}}_{k-1})+L\left| {\bar{x}}_{k}-{\bar{x}}_{k-1}\right| _{2}\bigr )=\varphi ({\bar{x}}). \end{aligned} \end{aligned}$$

Therefore, $({\bar{x}},{\bar{y}},{\bar{u}})$ is feasible to (OVR). Moreover, the sequence of lower level function values $\{f({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\}_{k\in \mathbb {N}}$ converges to $f({\bar{x}},{\bar{y}},{\bar{u}})$. Combining this with the weak lower semicontinuity of the functionals given by $\mathbb {R}^n\times {\mathcal {Y}}\ni (x,y)\mapsto \tfrac{1}{2}\left\| {\mathtt {C}}[y]-{\mathtt {P}}[x]\right\| _{{\mathcal {M}}}^2\in \mathbb {R}$ and $\mathbb {R}^n\times {\mathcal {U}}\ni (x,u)\mapsto \tfrac{1}{2}\left\| u-{\mathtt {Q}}[x]\right\| _{{\mathcal {U}}}^2\in \mathbb {R}$ yields

$$\begin{aligned} \begin{aligned} f({\bar{x}},{\bar{y}},{\bar{u}})&=\tfrac{1}{2}\left\| {\mathtt {C}}[{\bar{y}}]-{\mathtt {P}}[{\bar{x}}]\right\| _{{\mathcal {M}}}^2 +\tfrac{\sigma }{2}\left\| {\bar{u}}-{\mathtt {Q}}[{\bar{x}}]\right\| _{{\mathcal {U}}}^2\\&\le \liminf \limits _{k\rightarrow \infty } \tfrac{1}{2}\left\| {\mathtt {C}}[{\bar{y}}_k]-{\mathtt {P}}[{\bar{x}}_k]\right\| _{{\mathcal {M}}}^2 +\liminf \limits _{k\rightarrow \infty } \tfrac{\sigma }{2}\left\| {\bar{u}}_k-{\mathtt {Q}}[{\bar{x}}_k]\right\| _{{\mathcal {U}}}^2\\&\le \liminf \limits _{k\rightarrow \infty } \tfrac{1}{2}\left\| {\mathtt {C}}[{\bar{y}}_k]-{\mathtt {P}}[{\bar{x}}_k]\right\| _{{\mathcal {M}}}^2 +\limsup \limits _{k\rightarrow \infty } \tfrac{\sigma }{2}\left\| {\bar{u}}_k-{\mathtt {Q}}[{\bar{x}}_k]\right\| _{{\mathcal {U}}}^2\\&= \lim \limits _{k\rightarrow \infty } \left( \tfrac{1}{2}\left\| {\mathtt {C}}[{\bar{y}}_k]-{\mathtt {P}}[{\bar{x}}_k]\right\| _{{\mathcal {M}}}^2 +\tfrac{\sigma }{2}\left\| {\bar{u}}_k-{\mathtt {Q}}[{\bar{x}}_k]\right\| _{{\mathcal {U}}}^2 \right) \\&= f({\bar{x}},{\bar{y}},{\bar{u}}). \end{aligned} \end{aligned}$$

That is why we have $\left\| {\bar{u}}_k-{\mathtt {Q}}[{\bar{x}}_k]\right\| _{{\mathcal {U}}}\rightarrow \left\| {\bar{u}}-{\mathtt {Q}}[{\bar{x}}]\right\| _{{\mathcal {U}}}$. Recalling ${\bar{u}}_k-{\mathtt {Q}}[{\bar{x}}_k]\rightharpoonup {\bar{u}}-{\mathtt {Q}}[{\bar{x}}]$ and the fact that ${\mathcal {U}}$ is a Hilbert space, we already have $u_k-{\mathtt {Q}}[{\bar{x}}_k]\rightarrow {\bar{u}}-{\mathtt {Q}}[{\bar{x}}]$. Since ${\bar{x}}_k\rightarrow {\bar{x}}$ and, thus, ${\mathtt {Q}}[{\bar{x}}_k]\rightarrow {\mathtt {Q}}[{\bar{x}}]$ holds true, we obtain the strong convergence ${\bar{u}}_k\rightarrow {\bar{u}}$ in ${\mathcal {U}}$. Applying the operator $\mathtt {A}^{-1}\circ {\mathtt {B}}$, the convergence ${\bar{y}}_k\rightarrow {\bar{y}}$ in ${\mathcal {Y}}$ follows.

Pick an arbitrary feasible point $(x,y,u)\in \mathbb {R}^n\times {\mathcal {Y}}\times {\mathcal {U}}$ of (OVR). By construction, we have

$$\begin{aligned} \forall k\in \mathbb {N}:\quad F({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\le F(x,y,u). \end{aligned}$$

Since F is continuous while $\{({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\}_{k\in \mathbb {N}}$ converges strongly to $({\bar{x}},{\bar{y}},{\bar{u}})$, we obtain

$$\begin{aligned} F({\bar{x}},{\bar{y}},{\bar{u}}) =\lim \limits _{k\rightarrow \infty }F({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\le F(x,y,u). \end{aligned}$$

This shows that $({\bar{x}},{\bar{y}},{\bar{u}})$ is a globally optimal solution of (OVR) and, consequently, for (IOC).

The above arguments can be reprised in order to show that each accumulation point of the sequence $\{({\bar{x}}_k,{\bar{y}}_k,{\bar{u}}_k)\}_{k\in \mathbb {N}}$ is a globally optimal solution of (OVR). $\square$

Next, we present a counterexample which shows that Theorem 6.1 will not necessarily hold if we only require $S \subset {\text {conv}}\,X_1$ in Algorithm 1.

Example 6.2

We consider a finite-dimensional version of (IOC). In particular, we investigate the upper level problem

$$\begin{aligned} \begin{aligned} F(x,u) := \tfrac{100}{2} \, \left( x_1 - u + \tfrac{1}{\sqrt{2}}\right) ^2 + x_1 + \tfrac{1}{2} x_2^2&\,\rightarrow \,\min \limits _{x,u}\\ x&\,\in \, S := {\text {conv}}\,X_1\\ u&\,\in \,\varPsi (x), \end{aligned} \end{aligned}$$

(13)

in which $\varPsi :\mathbb {R}^2 \rightrightarrows \mathbb {R}$ is the solution map of the (state-reduced) lower level problem

$$\begin{aligned} \begin{aligned} f(x,u) := x_2^2 + (x_1 - u)^2&\,\rightarrow \,\min \limits _{u}\\ u&\,\in \,[0,2]. \end{aligned} \end{aligned}$$

(14)

The set $X_1$ is chosen as in Example 6.1. It is clear that $\varPsi (x) = \{x_1\}$ and $\varphi (x) = x_2^2$ hold for all $x \in S$. Thus, the unique global solution of (13) is given by ${\bar{x}} := (0,0)$ and ${\bar{u}} := 0$.

Now, we will check that the sequence $\{({\bar{x}}_k, {\bar{u}}_k)\}_{k\in \mathbb {N}}$ generated by Algorithm 1 (adapted to the problem at hand, cf. [9]) is recursively given by

$$\begin{aligned} {\bar{x}}_k = \left( \frac{100^2 \, (1-({\bar{x}}_{k-1})_1)}{2 \, (100 + 2\, (1-({\bar{x}}_{k-1})_1))^2} + ({\bar{x}}_{k-1})_1, 0\right) , \quad {\bar{u}}_k = ({\bar{x}}_k)_1 + \sqrt{\frac{({\bar{x}}_k)_1 - ({\bar{x}}_{k-1})_1}{1 - ({\bar{x}}_{k-1})_1}} \end{aligned}$$

with initial data ${\bar{x}}_0 = 0$. The convergences ${\bar{x}}_k \rightarrow (1,0)$ and ${\bar{u}}_k \rightarrow 1 + \tfrac{\sqrt{2}}{2}$ can be checked. This limit point is not a feasible point of (13).

In order to check that the algorithm produces the above iterates, we consider the subproblem

$$\begin{aligned} \begin{aligned} \tfrac{100}{2} \, \left( x_1 - u + \tfrac{1}{\sqrt{2}}\right) ^2 + x_1 + \tfrac{1}{2} x_2^2&\,\rightarrow \,\min \limits _{x,u}\\ x&\,\in \, S := {\text {conv}}\,X_1\\ u&\,\in \, [0,2] \\ x_2^2 + (x_1 - u)^2&\,\le \, \xi _X(x) \end{aligned} \end{aligned}$$

(15)

with $X := X_1 \cup \{(\alpha , 0)\}$ where $\alpha \in [0,1)$. As in Example 6.1, we find

$$\begin{aligned} \xi _X(x) = {\left\{ \begin{array}{ll} \frac{x_1 - \alpha }{1-\alpha } &{} \text {if } x \in {\text {conv}}\{ (\alpha ,0), (1,-1), (1,1) \}, \\ x_2 &{} \text {if } x \in {\text {conv}}\{ (\alpha ,0), (0,0), (1,1) \}, \\ -x_2 &{} \text {if } x \in {\text {conv}}\{ (\alpha ,0), (0,0), (1,-1) \}. \end{array}\right. } \end{aligned}$$

Thus, (15) can be decomposed into three convex problems and, due to symmetry, we have to solve two of them. The first problem is

$$\begin{aligned} \begin{aligned} \tfrac{100}{2} \, \left( x_1 - u + \tfrac{1}{\sqrt{2}}\right) ^2 + x_1 + \tfrac{1}{2} x_2^2&\,\rightarrow \,\min \limits _{x,u}\\ x&\,\in \, {\text {conv}}\{ (\alpha ,0), (1,-1), (1,1) \} \\ u&\,\in \, [0,2] \\ x_2^2 + (x_1 - u)^2&\,\le \, \frac{x_1 - \alpha }{1-\alpha }. \end{aligned} \end{aligned}$$

It can be checked (e.g. via the KKT-conditions) that its unique solution is given by

$$\begin{aligned} {\tilde{x}}(\alpha ) := \left( \frac{100^2 \, (1-\alpha )}{2 \, (100 + 2\, (1-\alpha ))^2} + \alpha , 0\right) , \quad {\tilde{u}}(\alpha ) := {\tilde{x}}(\alpha )_1 + \sqrt{\frac{{\tilde{x}}(\alpha )_1 - \alpha }{1 - \alpha }}. \end{aligned}$$

(16)

Moreover, the objective value can be bounded from above by

$$\begin{aligned} F\left( \left( \tfrac{1+\alpha }{2}, 0\right) , \tfrac{1+\alpha }{2}+\tfrac{1}{\sqrt{2}}\right) =\tfrac{1+\alpha }{2}<1. \end{aligned}$$

The second subproblem for (15) is

$$\begin{aligned} \begin{aligned} \tfrac{100}{2} \, \left( x_1 - u + \tfrac{1}{\sqrt{2}}\right) ^2 + x_1 + \tfrac{1}{2} x_2^2&\,\rightarrow \,\min \limits _{x,u}\\ x&\,\in \, {\text {conv}}\{ (\alpha ,0), (0,0), (1,1) \} \\ u&\,\in \, [0,2] \\ x^2_2+(x_1-u)^2&\,\le \, x_2. \end{aligned} \end{aligned}$$

The last constraint implies

$$\begin{aligned} u \le x_1 + \sqrt{x_2 - x_2^2} \le x_1 + \tfrac{1}{2}. \end{aligned}$$

Thus, for a feasible point (x, u) of this second subproblem, we can bound the objective by

$$\begin{aligned} F(x,u) \ge \tfrac{100}{2} \, \left( x_1 - u + \tfrac{1}{\sqrt{2}}\right) ^2 \ge \tfrac{100}{2} \, \left( \tfrac{1}{\sqrt{2}} - \tfrac{1}{2}\right) ^2 \ge \tfrac{100}{2} \, \left( \tfrac{1}{5}\right) ^2 = 2. \end{aligned}$$

Hence, the global solution of (15) is given by (16).

Now, the problem solved by Algorithm 1 in step k is precisely (15) with $\alpha = ({\bar{x}}_{k-1})_1$, see also the calculation in Example 6.1.

Finally, we mention that Example 6.2 shows that [9, Theorem 4.3] does not hold as stated. In the proof, the authors claim that $\xi _{X_k}$ possesses the same Lipschitz constant as $\varphi$ on S, but this is not true, see also Example 6.1.

6.2 A numerical example

Now, we are going to present a numerical example of an inverse optimal control problem with a PDE constraint. This will illustrate the performance of Algorithm 1. We will use an example where the reduced upper level objective function $x \mapsto F(x, \psi ^y(x), \psi ^u(x))$ has multiple local minimizers and is not differentiable at the global minimum.

The problem under investigation is very similar to Example 2.1. First, we fix the domain $\varOmega :=(-1,1)\times (-1,1)$ and set $n:=2$, ${\mathcal {Y}}:=H_0^1(\varOmega )$, and ${\mathcal {M}}={\mathcal {U}}:=L^2(\varOmega )$. Moreover, we define $f_1, f_2 \in L^2(\varOmega )$ via

$$\begin{aligned} \begin{aligned} f_1(\omega )&:=10\,\exp (-5(\omega _1-0.7)^2-5\,(\omega _2-0.3)^2),\\ f_2(\omega )&:=10\,\exp (-10(\omega _1+0.4)^2-10\,(\omega _2-0.5)^2) \end{aligned} \end{aligned}$$

for all $\omega =(\omega _1,\omega _2)\in \varOmega$ and choose $\sigma :=0.01$ for the regularization parameter. Let us set

$$\begin{aligned} S:={\text {conv}}\{(0,0),(1,0),(0,1)\}. \end{aligned}$$

In order to construct a nonsmooth and nonconvex example, we first set ${\tilde{x}}:=(0.3,0.3)$ and define ${\tilde{u}}\in L^2(\varOmega )$ to be the unique solution of the optimal control problem without control constraints

$$\begin{aligned} \begin{aligned} \tfrac{1}{2}\left\| y-{\tilde{x}}_1f_1-{\tilde{x}}_2f_2\right\| _{L^2(\varOmega )}^2 +\tfrac{\sigma }{2}\left\| u\right\| _{L^2(\varOmega )}^2&\,\rightarrow \,\min \limits _{y,u}&\\ -\varDelta y-u&\,=\,0 \quad&\text {on }\varOmega&\\ y&\,=\,0 \quad&\text {on }\partial \varOmega .&\end{aligned} \end{aligned}$$

(17)

Actually, we do not solve (17) but its finite element discretization. For the discretization, we use piecewise linear finite elements (with mesh size 0.1) for the state y and the control u. In order to obtain a coefficientwise projection formula (for problem (19) below), we use mass lumping for the control variables.

Next, we define the lower and upper bounds $u_a,u_b\in L^2(\varOmega )$ by

$$\begin{aligned} \forall \omega \in \varOmega :\quad u_a(\omega ):=\min \{{\tilde{u}}(\omega ),2\},\qquad u_b(\omega ):=\max \{{\tilde{u}}(\omega ),3\} \end{aligned}$$

These bounds will be used in the lower level problem in order to get a nonsmooth and nonconvex example.

Now, we consider the inverse optimal control problem

$$\begin{aligned} \begin{aligned} \tfrac{1}{2}\left\| y-0.2\,f_1-0.3\,f_2\right\| _{L^2(\varOmega )}^2+ (0.1,0.3)^\top x&\,\rightarrow \,\min \limits _{x,y,u} \\ x&\,\in \, S\\ (y,u)&\,\in \,\varPsi (x) \end{aligned} \end{aligned}$$

(18)

where $\varPsi :\mathbb {R}^2\rightrightarrows H^1_0(\varOmega )\times L^2(\varOmega )$ denotes the solution map of the parametric optimal control problem

$$\begin{aligned} \begin{aligned} \tfrac{1}{2}\left\| y-x_1f_1-x_2f_2\right\| _{L^2(\varOmega )}^2+\tfrac{\sigma }{2}\left\| u\right\| _{L^2(\varOmega )}^2&\,\rightarrow \,\min \limits _{y,u}&\\ -\varDelta y-u&=0 \quad&\text {on }\varOmega&\\ y&=0 \quad&\text {on }\partial \varOmega&\\ u_a \le u&\le u_b \quad&\text {a.e. on }\varOmega .&\end{aligned} \end{aligned}$$

(19)

For problem (19), we use the same discretization as for (17).

We give some comments concerning the construction of this problem. Since ${\tilde{u}}$ is the optimal solution of problem (17), and since $u_a \le {\tilde{u}} \le u_b$ holds almost everywhere on $\varOmega$ (by choice of the bounds), it is also the solution of the lower level problem (19) for $x = {\tilde{x}}$. Moreover, since ${\tilde{u}}$ is even the solution of (17), the bounds in (19) are only weakly active, i.e., the multipliers corresponding to these bounds are zero. Thus, we could expect that the function $x \mapsto \psi ^u(x)$ is only directionally differentiable in ${\tilde{x}}$. Finally, the objective function in the upper level problem (18) is chosen such that ${\tilde{x}}$ really becomes a global minimizer.

For convenience, we denote the reduced objective function of the upper level problem by

$$\begin{aligned} \gamma (x) := F(x,\psi ^y(x),\psi ^u(x)). \end{aligned}$$

We can see in Fig. 1 that this construction yields a nonsmooth reduced objective function $\gamma$ with a global minimizer at ${\bar{x}} = {\tilde{x}}=(0.3,0.3)$. Moreover, $\gamma$ is nonsmooth at ${\bar{x}}$ and has further local minimizers at (0, 0) and approximately (0.36, 0).

Fig. 1

The reduced objective function $\gamma$ (left) and cross sections of $\gamma$ (right). (Color figure online)

We initialize the algorithm with the choice

$$\begin{aligned} X_1:=\left\{ \left( -\tfrac{1}{2},-\tfrac{1}{2}\right) ,\left( \tfrac{3}{2},0\right) ,\left( 0,\tfrac{3}{2}\right) \right\} \end{aligned}$$

in order to guarantee $S\subset {\text {int}}\,{\text {conv}}\,X_1$. Then, we run 1000 iterations of Algorithm 1. Because we solve a relaxed optimization problem in each iteration, we obtain (increasing) lower bounds on the optimal value of the bilevel problem (18). On the other hand, calculating $\gamma ({\bar{x}}_k)$ yields upper bounds. Since ${\bar{x}}_k$ is the solution of the relaxed problem, the true value $\gamma ({\bar{x}}_k)$ can be quite large. Therefore, we denote by ${\hat{x}}_k$ the best known point of $\gamma$ in iteration k, i.e.,

$$\begin{aligned} {\hat{x}}_k := \mathop {{\text {argmin}}}\limits _{x \in \{ {\bar{x}}_1,\ldots ,{\bar{x}}_k\}} \gamma (x). \end{aligned}$$

This yields a decreasing upper bound $\gamma ({\hat{x}}_k)$.

The convergence of these lower and upper bounds, as well as the difference between both bounds can be seen in Fig. 2a. Moreover, we present the triangulation of ${\text {conv}}\,X_1$ given by the regions of stability at iteration $k=50$ in Fig. 3. Recall that the nodes of this triangulation are given by the set $X_k := X_1 \cup \bigcup _{j = 1}^{k-1}\{{\bar{x}}_j\}$. Finally, we record the Euclidean distances $\left| {\bar{x}}_k-{\bar{x}}\right| _{2}$ and $\left| {\hat{x}}_k-{\bar{x}}\right| _{2}$ in Fig. 2b, and one can believe that ${\bar{x}}_k\rightarrow {\bar{x}}$ holds as predicted by Theorem 6.1.

Fig. 2

Errors. (Color figure online)

Fig. 3

Triangulation given by $X_{50}$

From these results, we can see that the convergence of the algorithm is comparatively slow. Particularly, we have to solve several auxiliary convex problems in each iteration [to obtain the global solution of (OVR$(X_k)$)]. This is, however, the expectable price we have to pay for the guaranteed convergence towards a global minimizer.

It is possible to improve the performance of the algorithm by reducing the curvature of the value function $\varphi$. This can be done by using the modified function

$$\begin{aligned} {\tilde{f}}(x,y,u) := f(x,y,u)- \tfrac{1}{2} x^\top \mathtt {H}x \end{aligned}$$

instead of f as the objective function of the lower level problem (OC(x)). Here, we exploit the matrix

$$\begin{aligned} \mathtt {H}:= \mathtt {P}^\star \circ \mathtt {P}+ \sigma \, \mathtt {Q}^\star \circ \mathtt {Q}-(\mathtt {P}^\star \circ \mathtt {S}+\sigma \, \mathtt {Q}^\star ) \circ (\mathtt {S}^\star \circ \mathtt {S}+\sigma \, \mathtt {I}_\mathcal {U})^{-1} \circ (\mathtt {S}^\star \circ \mathtt {P}+\sigma \, \mathtt {Q}) \end{aligned}$$

where $\mathtt {S}:=\mathtt {C}\circ \mathtt {A}^{-1}\circ \mathtt {B}$ is the control-to-observation operator of (OC(x)). Note that this transformation does neither change the lower level solution mapping $\varPsi$ nor the overall (local and global) solutions of the superordinate bilevel optimization problem. Although ${\tilde{f}}$ is no longer (jointly) convex on $\mathbb {R}^n\times {\mathcal {Y}}\times {\mathcal {U}}$, it can be shown that it is convex on the subspace

$$\begin{aligned} \bigl \{ (x,y,u) \in \mathbb {R}^n\times {\mathcal {Y}}\times {\mathcal {U}} \;\bigm |\; {\mathtt {A}}[y]-{\mathtt {B}}[u]=0 \bigr \} . \end{aligned}$$

Since the feasible set of the lower level problem is contained in this subspace, this is sufficient for our purposes. Due to the reduced curvature of the resulting optimal value function ${\tilde{\varphi }}$, its approximation by piecewise affine functions is much simpler. In Fig. 4a, we can see that the error of the upper and lower bounds converges faster compared to the case without curvature reduction in Fig. 2a. Likewise, the distances $\left| {\bar{x}}_k-{\bar{x}}\right| _{2}$ and $\left| {\hat{x}}_k-{\bar{x}}\right| _{2}$ converge faster as well, see Fig. 4b (cf. Fig. 2b).

Fig. 4

Errors with curvature reduction. (Color figure online)

7 Conclusions

In this paper, a certain class of inverse optimal control problems has been studied. Using the optimal value function $\varphi$ of the associated parametric optimal control problem, we were able to derive necessary optimality conditions of Clarke-stationarity-type in the setting where the controls are chosen from a standard box-constrained set in $L^2(\varOmega )$. At the moment, it is not clear whether this result can be extended to (pointwise) Mordukhovich-stationarity. Afterwards, a global solution algorithm for the problem class of interest which exploits an iteratively refined piecewise affine upper approximation of $\varphi$ has been suggested. Its convergence properties have been investigated theoretically and illustrated by means of an example from PDE control. Finally, we demonstrated that it is possible to speed up our algorithm by reducing the curvature of $\varphi$.

Clearly, the computational realization of Algorithm 1 heavily exploits the finite-dimensional setting of the upper level variable x. In the future, it needs to be investigated if some of our ideas can be carried over to the infinite-dimensional situation. The most difficult part in Algorithm 1 is the global solution of the nonconvex relaxed surrogate problems. While this can be done by decomposing the problem into finitely many convex optimization problems in the presence of a finite-dimensional upper level variable, it is not clear how this issue can be handled in the infinite-dimensional situation. Thus, it seems to be a nearby topic of future research to study the settings where these surrogate problems are solved only locally or to some kind of stationarity.