Filter-based DIRECT method for constrained global optimization

Abstract

This paper presents a DIRECT-type method that uses a filter methodology to assure convergence to a feasible and optimal solution of nonsmooth and nonconvex constrained global optimization problems. The filter methodology aims to give priority to the selection of hyperrectangles with feasible center points, followed by those with infeasible and non-dominated center points and finally by those that have infeasible and dominated center points. The convergence properties of the algorithm are analyzed. Preliminary numerical experiments show that the proposed filter-based DIRECT algorithm gives competitive results when compared with other DIRECT-type methods.

1 Introduction

In this paper, constrained global optimization (CGO) problems are addressed by proposing the integration of a filter methodology, as outlined in [19], into a DIRECT-type method to globally solve nonsmooth and nonconvex constrained optimization problems. The mathematical formulation of the problem is:

$$\begin{aligned}{}\begin{array}[c]{rlll} \underset{x \in \varOmega }{\min } &{} f(x) \\ \text{ subject } \text{ to } &{} h(x) = 0 \\ &{}g(x) \le 0 \\ \end{array} \end{aligned}$$

(1)

where $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$, $h:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^m$ and $g:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^p$ are nonlinear continuous functions and $\varOmega =\{x\in {\mathbb {R}}^n: -\infty< l_i \le x_i \le u_i < \infty , i=1,\ldots ,n\}$. The feasible set of points that satisfy all the constraints is denoted by $F = \varLambda \cap \varOmega$ where $\varLambda = \{x\in {\mathbb {R}}^n: h(x) = 0 \text{ and } g(x) \le 0\}$. Differentiability and convexity are not assumed and therefore many local minima may exist in F. The most used and popular framework to solve problem (1) considers a penalty term, which depends on a constraint violation measure and is combined with the objective function to give the so-called penalty function. The penalty term aims to penalize f when a candidate solution, $\bar{x}$, is infeasible, i.e., when $\bar{x} \notin F$. Penalty functions require the use of a positive penalty parameter that aims to balance function and constraint violation values. Setting an initial value for the penalty parameter and tuning its values throughout the iterative process are important issues that should be addressed in the algorithm, since the performance is greatly affected by their values. In some cases, the optimal solution of the problem is attained only when the penalty parameter approaches infinity. With exact penalty functions, there exists a positive threshold such that for all parameter values smaller than that threshold the CGO and an equivalent bound constrained (or unconstrained) problem have the same global minimizers. An exact penalty approach combined with the DIRECT algorithm (for solving the bound constrained global optimization subproblems) that uses the derivatives of the involved functions for the penalty parameter updating is proposed in [11]. Later, the authors in [12] use the exact penalty framework presented in [11] and enrich the global search activity of DIRECT by using a derivative-free local search algorithm, in a multistart framework, to speed the convergence, as well as, a derivative-free strategy for the penalty parameter updating. Augmented Lagrangian functions are penalty functions for which a finite penalty parameter value is in general sufficient to guarantee convergence to the solution of the constrained problem [2]. Augmented Lagrangians for CGO problems have been implemented and their convergence properties have been derived. For example, in [4], the exact $\alpha$-branch-and-bound method is used to find approximate global solutions to the subproblems. In [5], the global convergence to a minimum is guaranteed using a nonmonotone penalty parameter tuning and gradient-based approaches for solving the bound constrained subproblems.

The use of the filter method to guarantee sufficient progress towards feasible and optimal solutions of nonlinear constrained optimization has its origin in [19]. The filter technique has been used since then in the context of a variety of problems, nonlinear optimization [38], complementarity problems [44], nonlinear equations [22], inexact line search [29], trust region [43], nonmonotone strategies [42, 44], to name a few. Filter with stochastic methods are new ideas recently proposed [24, 37, 39]. The issue concerned with the use of the filter method in the context of derivative-free optimization has not been frequently addressed [1, 7, 8, 15, 28, 36].

In this paper, we aim to integrate the filter methodology into a DIRECT-type method algorithm for solving CGO problems. The derivative-free and deterministic global optimizer DIRECT [27] is a partition-based algorithm [34] that identifies potential optimal hyperrectangles and divides them further to produce finer and finer partitions of the hyperrectangles [17, 18, 21, 26, 30, 33]. It has been shown that the set of points sampled by the DIRECT algorithm is dense in the search space [27]. Consequently, if f is continuous in a neighborhood of the global minimum, the DIRECT algorithm can sample a point that is arbitrarily near the global minimum. This guaranteed convergence makes it a reliable and interesting derivative-free global optimizer. In the present study, the use of the filter set aims to give priority to the selection (for further division) of hyperrectangles with feasible center points that are more promising relative to the objective function, followed by the selection of hyperrectangles with infeasible and non-dominated center points, promising with respect to the constraint violation measure. Finally, the most promising hyperrectangles with infeasible and dominated center points are selected by means of the constraint violation measure. The dimensions for further division are selected based on a particular order that favors feasible trial points, and infeasible and non-dominated trial points, against infeasible and dominated trial points.

The remainder of the paper proceeds as follows. Section 2 introduces the DIRECT method, the filter set methodology, presents the new filter-based DIRECT algorithm and its convergence properties. Section 3 contains the results of all the numerical experiments and the conclusions are summarized in Sect. 4.

2 Filter-based DIRECT

The DIRECT (DIviding RECTangles) algorithm has been originally proposed to solve bound constrained global optimization (BCGO) problems,

$$\begin{aligned}{}\begin{array}[c]{rl} \underset{x \in \varOmega }{\min } &{} f(x) \\ \end{array} \end{aligned}$$

(2)

where f is assumed to be a continuous function, by producing finer and finer partitions of the hyperrectangles generated from $\varOmega$ [27]. The algorithm is a modification of the standard Lipschitzian approach, in which f must satisfy the Lipschitz condition

$$\begin{aligned} |f(x_1) - f(x_2)| \le K \Vert x_1 - x_2\Vert \, \text{ for } \text{ all } \, x_1, x_2 \in \varOmega , \end{aligned}$$

where the Lipschitz constant $K > 0$ is viewed as a weighting parameter that indicates how much emphasis to place on global versus local search. DIRECT is known as a global optimizer since it is able to explore potentially optimal regions to converge to the global optimum and to avoid being trapped in local optima. It is a deterministic method that does not require any derivative information or the value of the Lipschitz constant [23]. It searches (locally and globally) by dividing all hyperrectangles that satisfy the following criteria, defining a potentially optimal hyperrectangle (POH):

Definition 1

Given the partition $\{ H^i: i \in I \}$ of $\varOmega$, let $\epsilon$ be a positive constant and let $f_{\min }$ be the current best function value. A hyperrectangle j is said to be potentially optimal if there exists some rate-of-change constant $\hat{K} > 0$ such that

$$\begin{aligned} \begin{array}{rl} f(c_j) - \hat{K} d_j &{} \le f(c_i) - \hat{K} d_i, \, \text{ for } \text{ all } \, i \in I\\ f(c_j) - \hat{K} d_j &{} \le f_{\min } - \epsilon |f_{\min }| \end{array} \end{aligned}$$

(3)

where $c_j$ is the center and $d_j$ is a measure of the size of the hyperrectangle j.

In [27], $d_j$ is the distance from $c_j$ to its vertices. The use of $\hat{K}$ intends to show that it is not the Lipschitz constant. The second condition in (3) aims to prevent the algorithm from searching locally a region where very small improvements are obtained. However, the results in the literature show that DIRECT is fairly insensitive to the setting of the balance parameter $\epsilon$, and good results are obtained for values ranging from $10^{-3}$ to $10^{-7}$ [27]. The parameter $\epsilon$ also prevents the hyperrectangle with best function value from being a POH. Identifying the set of POH can be regarded as a problem of finding the extreme points on the lower right convex hull of a set of points in the plane [27]. A 2D-plot can be used to identify the set of POH. The horizontal axis corresponds to the size of hyperrectangle and the vertical axis corresponds to the f value at the center of hyperrectangle. Further details concerning the DIRECT algorithm are available in [16, 20, 23]. In [27], the DIRECT algorithm for solving the BCGO problem is described by the six main steps presented in Algorithm 2.1.

2.1 DIRECT-type methods

Partition-based algorithms search for the global optima by using sequences of partitions of the region $\varOmega$ [34]. At each iteration, some sets are chosen to be further partitioned according to different criteria. Some criteria rely on a priori knowledge of the objective function, and others use a selection strategy that does not require any a priori knowledge on the objective function [25]. The DIRECT algorithm and some of its variants are particular cases of a partition-based algorithm (PBA) for GO [32]. Given any accuracy, a PBA can guarantee to find a solution that is sufficiently near the global optimum of problem (2). It is efficient, in the sense that it finds the regions of local minima in a few iterations. However, it requires the sampling of a dense set of points to obtain a solution. Moreover, the computational effort greatly increases as the accuracy increases.

In [34], PBA are explored and two new strategies for selecting the hyperrectangles (for further partitioning) are presented. A partition strategy that does not require any knowledge about the objective function, although it exploits information on the objective function gathered during the iterative process is proposed. The main difference between the therein called partition-based on estimation (PBE) algorithm and the DIRECT methods [18, 21, 26, 27] is that PBE iteratively estimates the global minimum value rather than the Lipschitz constant.

The robust DIRECT (RDIRECT) algorithm presented in [31] uses a bilevel strategy into a modified DIRECT algorithm to overcome the difficulty related to the slow convergence to achieve a high degree of accuracy. Since the second condition in (3) causes the original DIRECT to be sensitive to the additive scaling of the objective function (as shown in [18]), the robust version of DIRECT, meaning that it is insensitive to linear scaling of the objective function, relies on the following definition of POH:

Definition 2

[31] Given $\epsilon > 0$ and the index set of the hyperrectangles I. Let $f_{\min }$ be the known minimal function value, and $c_i$, $d_i$ be the center and the size of the ith hyperrectangle. Denote $f_{cc}$ as any convex combination of the objective function values gathered during previous iterations by RDIRECT. If there is a constant $\hat{K} > 0$, such that the following inequalities hold,

$$\begin{aligned} \begin{array}{rl} f(c_j) - \hat{K} d_j &{} \le f(c_i) - \hat{K} d_i, \, \text{ for } \text{ all } \, i \in I\\ f(c_j) - \hat{K} d_j &{} \le f_{\min } - \epsilon |f_{\min } - f_{cc}|, \end{array} \end{aligned}$$

(4)

then the jth hyperrectangle is a POH.

The convex combination is given by

$$\begin{aligned} f_{cc} = \sum _{k=1}^{k_f} \alpha _k f(c_k) \, \text{ with } \, \alpha _k \in [0,1] \, \text{ and } \, \sum _{k=1}^{k_f} \alpha _k=1 \end{aligned}$$

where $\{ f(c_k)\}_{k=1}^{k_f}$ are the gathered f values. Possible choices for $f_{cc}$ include the maximal value, the minimal value, the average or the median value of the gathered f values [31]. To improve the inefficient behavior of the PBA, the authors in [32] combine the PBA with a multigrid algorithm. The work in [33] applies a multigrid approach to the robust version of DIRECT algorithm [31], obtaining a multilevel robust DIRECT (MrDIRECT) algorithm. Although additional parameters are required by this new version, the authors show that the MrDIRECT is insensitive to the parameters.

Efficient and robust global optimization algorithms balance global and local search capabilities. A DIRECT-type algorithm that is strongly biased towards local search is presented in [21]. The authors state that the algorithm does well for small problems with a single global minimizer and only a few local minimizers. It is common knowledge that DIRECT gets quickly close to the global optimum but requires a lot more of computational effort to reach a high accuracy solution. To overcome this inconvenience, Jones in [26] suggests the use of a local optimizer by alternating between running DIRECT in the usual way and using a local search algorithm starting from the solution produced by DIRECT. In fact, DIRECT can be considered a good technique to select starting points for a local search method. The local optimizer aims to reduce the value of $f_{\min }$ which, by affecting the selection of hyperrectangles, improves the global search capability. At the same time, choosing a larger value of $\epsilon$ will directly improve the global search [33].

The DIRECT version presented in [26] has been extended to handle nonlinear inequality constraints by using an auxiliary function that combines information on the objective and constraint functions. The value of the auxiliary function is zero at the global minimizer and is positive at any point that has $f > f^{*}$ or is infeasible, where $f^*$ is the global minimum. The main idea relies on modifying the method for the selection of the hyperrectangles. The paper also addresses the use of integer variables.

Recently, two DIRECT-type algorithms with interesting ideas about the partition and selection of hyperrectangles appear for the scientific community [10, 35]. The authors in [10] propose a DIRECT-type algorithm for BCGO problems and a DIRECT-type bilevel approach for CGO. Their convergence properties are established. In theory, the lower level feasibility problem, by minimizing a penalty function, is solved and then at the upper level, the minimum of f is obtained among all the solutions of the lower level problem. At each iteration, the algorithm makes use of a derivative-free algorithm for non-smooth constrained local optimization ($\hbox {DFN}_{\mathrm{con}}$ in [14]) starting from the center points of all identified POH for f which are a subset of the POH for $\theta$ (the penalty function of the general constraints), with the aim of improving $f_{\min }$. Since DIRECT is good at locating promising regions of the search region $\varOmega$, although its efficiency deteriorates as the dimension and the ill-conditioning of the objective function increase [35], the authors in [35] propose DIRECT-type algorithms enriched by the efficient use of derivative-free local searches combined with nonlinear transformations of the feasible domain and, possibly, of the objective function.

2.2 The filter methodology

Given an approximation to the solution of the CGO problem (1), $x^{(k)}$, at iteration k, equality and inequality constraint violation is measured by the non-negative function $\theta : {\mathbb {R}}^n \rightarrow {\mathbb {R}}_+$,

$$\begin{aligned} \theta (x^{(k)})=\Vert h(x^{(k)})\Vert _1 + \Vert g(x^{(k)})_+\Vert _1 \end{aligned}$$

(5)

where $g_+ \in {\mathbb {R}}^p$ is defined componentwise by $\max \{0,g_i\}$. The filter paradigm for solving a constrained optimization problem reformulates the problem (1) into the bound constrained bi-objective optimization problem

$$\begin{aligned} \begin{array}{rl} \underset{x \in \varOmega }{\min } &{} \left( \theta (x), f(x)\right) . \\ \end{array} \end{aligned}$$

(6)

The filter method is an efficient methodology that builds a region of prohibited points, known as dominated points, while minimizing the constraint violation, $\theta$, and the objective function, f. The concept of dominance arises from the multi-objective optimization area. According to [19], the used definition is the following.

Definition 3

A point x, or the corresponding pair $(\theta (x),f(x))$, is said to dominate y, or the corresponding pair $(\theta (y),f(y))$, denoted by $x \prec y$, if and only if

$$\begin{aligned} \theta (x) \le \theta (y) \, \text{ and } \, f(x) \le f(y), \end{aligned}$$

with at least one inequality being strict.

A filter ${\mathscr {F}}$ is a finite set of pairs $(\theta (x),f(x))$, none of which is dominated by any of the others, and the corresponding points x are said to be non-dominated points.

The main ideas addressed by a filter methodology are the following.

• (i) The filter is initialized by ${\mathscr {F}}=\{(\theta ^U, -\infty )\}$ where $\theta ^U$ is an upper bound on the acceptable constraint violation.

• (ii) Slightly stronger convergence properties are obtained [6] when an envelope is added around the filter, so that a point $x^{(k)}$, or the corresponding pair $(\theta (x^{(k)}),f(x^{(k)}))$, at iteration k, is acceptable to the filter if, for all $x^{(l)}$ such that $(\theta (x^{(l)}),f(x^{(l)})) \in {\mathscr {F}}^{(k)}$,

  $$\begin{aligned} \theta (x^{(k)}) \le \beta \theta (x^{(l)}) \text{ or } f(x^{(k)}) \le f(x^{(l)}) - \gamma \theta (x^{(k)}) \end{aligned}$$

  (7)

  where $\beta , \gamma >0$ are constants.

• (iii) When a point is added to the filter, all the dominated points are removed from the filter.

• (iv) When the constraint violation becomes sufficiently small, only a sufficient reduction is enforced on f,

  $$\begin{aligned} f(x^{(k)}) \le f(x^{(k-1)}) - \alpha \varDelta ^{(k)} \end{aligned}$$

  where $\alpha \in (0,1)$ and $\varDelta ^{(k)} > 0$ tends to zero as k increases.

As described in the next section, our algorithm implements some specific ideas from the filter methodology.

2.3 Filter-based DIRECT algorithm

For solving the CGO (1), the authors in [10] define two problems. The feasibility problem aims to minimize a penalty function subject to the bound constraints and the optimality problem minimizes the objective function on the set of all the solutions to the feasibility problem. While in [10], a bilevel approach is used, where the lower level problem is the feasibility problem and the upper level is the optimality problem, our proposal minimizes constraint violation $\theta$ and objective function f simultaneously, at the same level, using a filter set methodology.

In the context of the bi-objective problem (6), to extend the concept of the “Selection” step, where the indices of the hyperrectangles which are promising are identified, in the sense that both $\theta$ and f are to be minimized, a definition of POH with respect to the function $\theta$ is required. The definition presented in [10] is adopted.

Definition 4

Given the partition $\{ H^i: i \in I_k \}$ of $\varOmega$, let $\epsilon$ be a positive constant. A hyperrectangle j is said to be potentially optimal w.r.t. the function $\theta$ if there exists some constant $\hat{K}^j > 0$ such that

$$\begin{aligned} \begin{array}{rl} \theta (c_j) - \dfrac{\hat{K}^j}{2} \Vert u^j - l^j\Vert &{} \le \theta (c_i) - \dfrac{\hat{K}^j}{2} \Vert u^i - l^i\Vert , \, \text{ for } \text{ all } \, i \in I_k \\ \theta (c_j) - \dfrac{\hat{K}^j}{2} \Vert u^j - l^j\Vert &{} \le \theta _{\min } - \epsilon \theta _{\min } \end{array} \end{aligned}$$

(8)

where $c_j$ is the center of the hyperrectangle j and $\theta _{\min } = \min _{i \in I_k} \theta (c_i)$.

The filter-based DIRECT algorithm for solving the CGO problem is described in Algorithm 2.2.

In the herein presented filter method, the identification of dominated and non-dominated points is crucial when they are infeasible. To identify the non-dominated points we modify the sufficient decrease conditions shown in (7) and require only improvement in either $\theta$ or f for a point to be acceptable to the filter, i.e., we use only the dominance conditions.

Furthermore, another specific property of our algorithm is related to the feasible points not being added to the filter [1]. In Algorithm 2.2, points are added to ${\mathscr {F}}$ as they are generated. Each time a trial point is generated and the corresponding f and $\theta$ values are evaluated, the algorithm updates the filter. Whether a point is acceptable to the filter will depend on when it is generated. This temporal property can cause the so called ‘blocking entries’ (in particular, of infeasible points that are very near to feasibility). If the feasible points were added to the filter, any infeasible point x with $\theta (x) < \theta (x^{(l)})$ (for all $x^{(l)}$ such that $(\theta (x^{(l)}),f(x^{(l)})) \in {\mathscr {F}}^{(k)}$ and $\theta (x^{(l)})>0$) and $f(x) > f(x^{F})$, (where $(\theta (x^{F}),f(x^{F}))\in {\mathscr {F}}^{(k)}$ and $\theta (x^{F})=0$), would not be acceptable to the filter. To avoid the problem of ‘blocking entries’, our filter contains only infeasible points. This strategy aims to make the filter less conservative. However, the feasible point with the least function value found so far is separately maintained and will only be used to filter other feasible points.

Thus, using this filter methodology, the “Selection” step of the algorithm defines three separate sets of indices in the partition of $H^k$:

• the set $I_k^{F}$ which corresponds to hyperrectangles with feasible center points, relative to the general equality and inequality constraints, i.e., the center points that in practice satisfy $\theta (c_j) \le \theta _{\mathrm{feasible}}$, for a sufficiently small positive tolerance $\theta _{\mathrm{feasible}}$;

• the set $I_k^{I-ND}$ which corresponds to hyperrectangles with center points that are infeasible and non-dominated points;

• the set $I_k^{I-D}$, corresponding to hyperrectangles that have infeasible and dominated center points,

where $I_k = I_k^{F} \cup I_k^{I-ND} \cup I_k^{I-D}$ and $I_k^{F} \cap I_k^{I-ND} = I_k^{F} \cap I_k^{I-D} = I_k^{I-ND} \cap I_k^{I-D} = \emptyset$. We note that, at iteration k, at least one of these sets is non-empty. Namely, one of the following cases can occur: $I_k^F \ne \emptyset$ and $I_k^{I-ND}= I_k^{I-D}= \emptyset$; $I_k^{I-ND} \ne \emptyset$ and $I_k^F = I_k^{I-D} = \emptyset$; or $I_k^{I-ND}\ne I_k^{I-D} \ne \emptyset$ and $I_k^F=\emptyset$; or $I_k^F \ne I_k^{I-ND} \ne I_k^{I-D} \ne \emptyset$.

To identify the set of POH, the three sets are handled separately. Our strategy is the following. If there are hyperrectangles with feasible center points, i.e., $I_k^{F} \ne \emptyset$, the objective function values at the center points are used to define the convex hull and POH w.r.t. f are identified. On the other hand, if there are hyperrectangles with infeasible and non-dominated center points ($I_k^{I-ND} \ne \emptyset$) then the constraint violation function $\theta$ is used instead, and POH w.r.t. $\theta$ are identified. Further, if $I_k^{I-D} \ne \emptyset$, meaning that hyperrectangles with infeasible and dominated center points do exist, then the constraint violation function $\theta$ is used and POH w.r.t. $\theta$ are identified. We note that handling $I_k^{I-ND}$ and $I_k^{I-D}$ separately to construct the convex hull, POH with only non-dominated center points are identified when handling $I_k^{I-ND}$, while POH with only dominated center points are found when using $I_k^{I-D}$.

If this separation of hyperrectangles with infeasible center points was not made, meaning that the sets $I_k^{I-ND}$ and $I_k^{I-D}$ of hyperrectangles with infeasible center points are combined into one set, only one set of POH w.r.t $\theta$ is identified. At a certain iteration, POH with infeasible non-dominated and dominated center points will probably exist in the convex hull w.r.t. $\theta$. This is illustrated in Fig. 1a, b, c and d which contain the sample points produced on iterations 7, 9, 15 and 34 (the last one) respectively, when solving Problem 5 available in [3]. The horizontal axis shows the sizes of the hyperrectangles and the vertical axis corresponds to the $\theta$ values of their centers. Infeasible non-dominated points are marked with ‘+’ (blue) and infeasible dominated points are marked with ‘$\times$’ (red). The selected POH of the convex hull are identified by a black circle. POH with non-dominated center points are the ones with smallest sizes mostly.

Fig. 1

Sets $I_k^{I-ND}$ and $I_k^{I-D}$ combined into one set -‘$+$’ (blue): non-dominated point; ‘$\times$’ (red): dominated point. a Based on $I_k^{I-ND} \cup I_k^{I-D}$, POH on iteration 7. b Based on $I_k^{I-ND} \cup I_k^{I-D}$, POH on iteration 9. c Based on $I_k^{I-ND} \cup I_k^{I-D}$, POH on iteration 15. d Based on $I_k^{I-ND} \cup I_k^{I-D}$, POH on iteration 34. (Color figure online)

Since the separation of the sets $I_k^{I-ND}$ and $I_k^{I-D}$ aimed to promote the exploration of the non-dominated infeasible region in an expeditious manner, we show in the next section that keeping these sets separate gives better results than using them combined into a single one.

When dividing the hyperrectangles in the “Division” step, the filter-based DIRECT algorithm uses the following definition of “preference point” by dimension and “preference order”.

Definition 5

The rules to define “preference point” by dimension for dividing hyperrectangles are the following. A pool is created according to the properties feasibility/infeasibility and non-dominance/dominance of each trial point generated by dimension, $t_i$ for $i=1,2$:

• if both trial points are feasible, the one with smallest f value is selected for the pool;

• if one trial point is feasible and the other is infeasible, the feasible point is selected for the pool;

• if both trial points are infeasible and non-dominated (or both dominated), the one with smallest $\theta$ value is selected for the pool;

• if both trial points are infeasible and only one is non-dominated, the non-dominated point is selected for the pool, whatever its $\theta$ value.

After the rules for a “preference point” by dimension being established, the “preference order” for division of the hyperrectangles is as follows (favoring dimensions with feasible “preference points” against infeasible ones). Starting with the dimensions that were selected by the feasibility property, first divide along the dimension m such that $f_m = \min f(t_i)$ and then continue dividing until the dimension with the highest $f(t_i)$. Then, using the dimensions that were selected by the infeasibility property, first divide along the dimension m such that $\theta _m = \min \theta (t_i)$ and then continue dividing until the dimension with the highest $\theta (t_i)$.

For the purpose of evaluating the algorithm’s performance on test problems, we will note the number of function evaluations when the algorithm finds a feasible point that is sufficiently close to the known globally optimal function value. In particular, the algorithm stops at iteration k when an approximate solution $x^{(k)}$ satisfying

$$\begin{aligned} \theta (x^{(k)}) \le \eta _1 \, \text{ and } \, \dfrac{\left| f(x^{(k)}) - f^*\right| }{\max \{1, \left| f^*\right| \}} \le \eta _2 \end{aligned}$$

(9)

is found, for sufficiently small tolerances $\eta _1, \eta _2 >0$, where $f^*$ is the best known solution to the problem. However, if conditions (9) are not satisfied, the algorithm is allowed to run until a target value of number of iterations, $NI_{\max }$, (or a target value of function evaluations) is reached.

2.4 Convergence properties

Borrowing the ideas presented in [10], we show that the filter-based DIRECT algorithm, as described by Algorithm 2.2, satisfies the everywhere dense convergence property. We present the proposition for the more general case, i.e., all three types of hyperrectangles exist in the partition $H^k$ of $\varOmega$, $k>1$, since the others are particular cases.

Proposition 1

Consider the filter-based DIRECT algorithm, as described by Algorithm 2.2, which selects

$$\begin{aligned} O_k^{F} =&\{i \in I_k^{F}: H^i \text{ is } \text{ POH } \text{ w.r.t. } f \} \end{aligned}$$

(10a)

$$\begin{aligned} O_k^{I-ND} =&\{i \in I_k^{I-ND}: H^i \text{ is } \text{ POH } \text{ w.r.t. } \theta \}\end{aligned}$$

(10b)

$$\begin{aligned} O_k^{I-D} =&\{i \in I_k^{I-D}: H^i \text{ is } \text{ POH } \text{ w.r.t. } \theta \} \end{aligned}$$

(10c)

where $I_k = I_k^{F} \cup I_k^{I-ND} \cup I_k^{I-D}$ and $I_k^{F} \cap I_k^{I-ND} = I_k^{F} \cap I_k^{I-D} = I_k^{I-ND} \cap I_k^{I-D} = \emptyset$, then

• (i) All the sequences of sets/hyperrectangles $\{ H^{i_k}\}$ produced by the algorithm are strictly nested, namely for every $\{ H^{i_k}\}$ there exists a point $\bar{x} \in \varOmega$ such that

  $$\begin{aligned} \bigcap _{k=0}^\infty H^{i_k} = \{\bar{x}\}. \end{aligned}$$

• (ii) For every $\bar{x} \in \varOmega$, the algorithm produces a strictly nested sequence of sets/hyperrectangles $\{ H^{i_k}\}$ such that

  $$\begin{aligned} \bigcap _{k=0}^\infty H^{i_k} = \{\bar{x}\}. \end{aligned}$$

Proof

Let $s^i = \Vert u^i - l^i\Vert$ be the diagonal length of the hyperrectangle $H^i$ for all $i \in I_k$ and let

$$\begin{aligned} s^{\max }_F = \max _{i \in I_k^{F}} s^i, \,\, s^{\max }_{I-ND} = \max _{i \in I_k^{I-ND}} s^i \, \text{ and } \, s^{\max }_{I-D} = \max _{i \in I_k^{I-D}} s^i \end{aligned}$$

be the three largest diagonal lengths in the three sets of the partition. Denote by $I_{\max }^F = \{i \in I_k^{F}: s^i = s^{\max }_F\}$, $I_{\max }^{I-ND}= \{i \in I_k^{I-ND}: s^i = s^{\max }_{I-ND}\}$ and $I_{\max }^{I-D} = \{i \in I_k^{I-D}: s^i = s^{\max }_{I-D}\}$ the subsets of indices of hyperrectangles with the largest diagonal lengths in the three sets of the partition. Let $O_k=O_k^F \cup O_k^{I-ND} \cup O_k^{I-D}$ and $I_{k,\max }=I_{\max }^F \cup I_{\max }^{I-ND} \cup I_{\max }^{I-D}$.

According to the Proposition 2 in [34], the convergence properties (i) and (ii) of our algorithm follow by showing that for all k, $I_{\max }^F \cap O_k^F \ne \emptyset$, $I_{\max }^{I-ND} \cap O_k^{I-ND} \ne \emptyset$ and $I_{\max }^{I-D} \cap O_k^{I-D} \ne \emptyset$.

Let the three sets of indices $\bar{I}_{\max }^F, \bar{I}_{\max }^{I-ND}, \bar{I}_{\max }^{I-D}$ be defined by

$$\begin{aligned} \bar{I}_{\max }^F= & {} \{j \in I_{\max }^F: f(c_j) = \min _{i \in I_{\max }^F} f(c_i) \} \\ \bar{I}_{\max }^{I-ND}= & {} \{j \in I_{\max }^{I-ND}: \theta (c_j) = \min _{i \in I_{\max }^{I-ND}} \theta (c_i) \} \\ \bar{I}_{\max }^{I-D}= & {} \{j \in I_{\max }^{I-D}: \theta (c_j) = \min _{i \in I_{\max }^{I-D}} \theta (c_i) \} \end{aligned}$$

For any $l \in \bar{I}_{\max }^F$, it is sufficient to choose a positive $\hat{K}_1^l$ such that

$$\begin{aligned} \hat{K}_1^l > 2 \max \left\{ \dfrac{f(c_l) - f_{\min } + \epsilon |f_{\min }|}{s^l}, \max _{j \in I_k^{F}\setminus I_{\max }^F} \dfrac{f(c_l) - f(c_j)}{s^l -s^j} \right\} \end{aligned}$$

to obtain $l \in O_k^{F}$ (as defined in (10a)) so that $\bar{I}_{\max }^F = O_k^{F} \cap I_{\max }^F \ne \emptyset$.

Similarly, let $l \in \bar{I}_{\max }^{I-ND}$ be such that $\theta (c_l) \le \theta (c_i)$ for all $i \in \bar{I}_{\max }^{I-ND}$. By choosing a positive $\hat{K}^l_2$ such that

$$\begin{aligned} \hat{K}_2^l > 2 \max \left\{ \dfrac{\theta (c_l)-\theta _{\min } + \epsilon \theta _{\min }}{s^l}, \max _{j \in I_k^{I-ND}\setminus I_{\max }^{I-ND}} \dfrac{\theta (c_l) - \theta (c_j)}{s^l -s^j} \right\} \end{aligned}$$

to obtain $l \in O_k^{I-ND}$ (as defined in (10b)) so that $\bar{I}_{\max }^{I-ND} = O_k^{I-ND} \cap I_{\max }^{I-ND} \ne \emptyset$.

The same is true for $l \in \bar{I}_{\max }^{I-D}$ such that $\theta (c_l) \le \theta (c_i)$ for all $i \in \bar{I}_{\max }^{I-D}$, where a positive $\hat{K}_3^l$ is chosen such that

$$\begin{aligned} \hat{K}_3^l > 2 \max \left\{ \dfrac{\theta (c_l)-\theta _{\min } + \epsilon \theta _{\min }}{s^l}, \max _{j \in I_k^{I-D}\setminus I_{\max }^{I-D}} \dfrac{\theta (c_l) - \theta (c_j)}{s^l -s^j} \right\} \end{aligned}$$

to obtain $l \in O_k^{I-D}$ (as defined in (10c)) so that $\bar{I}_{\max }^{I-D} = O_k^{I-D} \cap I_{\max }^{I-D} \ne \emptyset$.

Therefore, for all k we have that $O_k \cap I_{k,\max } \ne \emptyset$, which concludes the proof. $\square$

3 Numerical experiments

This section aims to present, analyze and compare the results produced by the proposed filter-based DIRECT algorithm with other DIRECT-based algorithms, implemented in the Matlab™ (Matlab is a registered trademark of the MathWorks, Inc.) programming language. Unless otherwise stated, the parameter values for the algorithm are set as follows: $\epsilon = 10^{-4}$, $\eta _1 = 10^{-4}$, $\eta _2 = 10^{-4}$ and $\theta _{\mathrm{feasible}} = 10^{-4}$.

We illustrate the performance of our algorithm on two small problems. First, we use a two-variable problem, known as ‘Gomez #3’ problem (used in [26] to illustrate the performance of the therein proposed DIRECT version), with global optimum value $f^*=-\,0.9711$, occurring at $(0.109, -\,0.623)$ to show the effectiveness of Algorithm 2.2:

$$\begin{aligned} \begin{array}{rl} \underset{-\,1\le x_1,x_2 \le 1}{\min } &{} f(x_1,x_2) = \left( 4-2.1 x_1^2+ \frac{x_1^4}{3}\right) x_1^2 + x_1 x_2 +(-\,4 + 4 x_2^2) x_2^2 \\ \text{ subject } \text{ to } &{} -\sin (4\pi x_1) + 2 \sin ^2(2\pi x_2) \le 0.\\ \end{array} \end{aligned}$$

Our filter-based DIRECT algorithm finds a solution within 1% of the known optimum after 219 function evaluations (9 iterations) and a solution within 0.01% after 733 function evaluations (18 iterations). In [26], it is mentioned that the function evaluations required in both runs are 89 and 513 respectively. The center points sampled by our algorithm in both runs are shown in Figs. 2a and 3a respectively. The points marked with ‘$\times$’ (red) are infeasible and the points marked with ‘+’ (blue) are feasible. The global minimum is displayed by a black circle. We show in Figs. 2b and 3b the behavior of $f_{\min }$ (the function value of the best solution to the problem found so far) as a function of function evaluations. The constraint violation value is zero along the iterative process.

Fig. 2

Run stopping with a solution within 1% of $f^*$. a ‘+’ (blue): feasible point; ‘$\times$’ (red): infeasible point. b Behavior of $f_{\min }$ as a function of function evaluations. (Color figure online)

Fig. 3

Run stopping with a solution within 0.01% of $f^*$. a ‘+’ (blue): feasible point; ‘$\times$’ (red): infeasible point. b Behavior of $f_{\min }$ as a function of function evaluations. (Color figure online)

We now take Problem 8 available in [3] and show in the Fig. 4a all the sampled center points of hyperrectangles generated by our algorithm when the sets $I_k^{I-ND}$ and $I_k^{I-D}$ are analyzed separately. Figure 4b shows the pairs ($\theta$, f) corresponding to the center points of the hyperrectangles: dominated points are marked with ‘$\times$’ (red); non-dominated points (or filter points) are marked with ‘+’ (blue). Based on the stopping conditions shown in (9), the algorithm converges in 23 iterations and 881 function evaluations to the global solution $-\,118.700976$ (global minimum displayed by a black circle). On the other hand, Fig. 5a, b show the center points of the hyperrectangles and the corresponding pairs ($\theta$, f) of dominated and non-dominated points, when the sets $I_k^{I-ND}$ and $I_k^{I-D}$ are combined into a single set. The global solution $-\,118.688470$ is reached after 67 iterations and 3317 function evaluations. As it is illustrated in the figures, one advantage of using these separate infeasible sets is the gain in computational effort when exploring the infeasible region.

Fig. 4

The sets $I_k^{I-ND}$ and $I_k^{I-D}$ are analyzed separately. a ‘$+$’ (blue): feasible point; ‘$\times$’ (red): infeasible point. b ‘$+$’ (blue): non-dominated point; ‘$\times$’ (red): dominated point. (Color figure online)

Fig. 5

$I_k^{I-ND}$ and $I_k^{I-D}$ are combined into a single set. a ‘$+$’ (blue): feasible point; ‘$\times$’ (red): infeasible point. b ‘$+$’ (blue): non-dominated point; ‘$\times$’ (red): dominated point. (Color figure online)

In the remaining numerical experiments, two sets of CGO problems are used. The first set contains 20 problems, with n ranging from 2 to 6 and $m+p$ ranging from 1 to 12 (details in [3]). The second set contains 82 problems, with $n \le 10$, belonging to the GLOBALLib collection of the COCONUT project [41]. They are the same problems used for the results in Tables 1 and 2 of the report [9] (with the exception of problem ex736 due to a misprint in the definition).

The results shown in Table 1—relative to the first set of problems—aim to show the effectiveness of Algorithm 2.2 (the sets $I_k^{I-ND}$ and $I_k^{I-D}$ are analyzed separately) when compared with the variant where the sets are combined into a single set. This experiment analyzes the quality of the solutions produced by both algorithms when they stop with $NI_{\max }= 20$ and $NI_{\max }= 50$ iterations. In the table, $|f_{\mathrm{glob}} - f^*|$ is used to check the proximity of the objective function value of the obtained solution, $f_{\mathrm{glob}}$, to the best known optimal solution ($f^*$ taken from [3]) and $V_{\mathrm{glob}}$ is the constraint violation, where $V_{\mathrm{glob}} = \max \{ \Vert h(x)\Vert _{\infty }, \Vert g(x)_+\Vert _{\infty }\}$. When $NI_{\max }= 20$, we conclude that Algorithm 2.2 produces better errors on 11 problems, larger errors on three and tie values on six problems. On the other hand, when $NI_{\max }= 50$, Algorithm 2.2 gives better errors on 11 problems, larger errors on four and tie values on five. However, as far as constraint violation is concerned, there are 10 ties and six wins for the Algorithm 2.2 when $NI_{\max }= 20$, and nine ties, one win when $NI_{\max }= 50$. Thus, the variant nearness to the optimal solution mostly is the approach that relies on the separate analysis of the sets $I_k^{I-ND}$ and $I_k^{I-D}$.

Table 1 Comparison based on the quality of the solutions

Table 2 Comparison between the filter-based DIRECT (Algorithm 2.2), the EPGO in [11] and the DF-EPGO in [12]

Using the same set of problems, but now using the stopping conditions in (9), the results produced by Algorithm 2.2 are compared with those of [11], where an exact penalty based algorithm (EPGO) uses the DIRECT algorithm to solve the BCGO problems. In Table 2, $f_{\mathrm{glob}}$ and $V_{\mathrm{glob}}$ have the same meaning of the previous table, NF is the number of function evaluations and k is the number of DIRECT iterations required to reach the listed solution. $NI_{\max }$ is set to 120 or 200 (depending on the problem). Problems 1, 2(a)–2(d), 5, 9, 13, 14 and 16 have been reformulated by some algebraic manipulation aiming to reduce the number of variables and equality constraints. Furthermore, Problems 3(b) and 8 had their constraints normalized. These procedures are common practice when the problem is hard to solve due to having many equality constraints or different equality and inequality constraints scaling.

The results available in [12], an exact penalty approach that relies on DIRECT to solve the BCGO problems, are also included in the comparison. For a fair comparison, the results selected for the table correspond to the version denoted by DF-EPGO, which does not include the local search phase (Table 1 in [12]). We note here that the values of NF are not provided in the cited paper. Apart from the obtained solutions to the Problems 1, 2(a)–2(c) and 6, the others are similar in the three algorithms. A simplistic analysis allows us to conclude that our algorithm produces the best $f_{\mathrm{glob}}$ on five problems and the second best on four problems; EPGO produces the best solution on five problems and the second best on another six; and DF-EPGO produces the best solution on nine problems and the second best on another nine. Problem 15 is a tie.

Fig. 6

Performance profiles: filter-based DIRECT algorithm, $\hbox {DIRECT}+\hbox {DFN}_{\mathrm{con}}$ (local disabled) and DF-EPGO. a Metric $\dfrac{\left| f_{\mathrm{glob}} - f^*\right| }{\max \{1, \left| f^*\right| \}}$. b Metric $V_{\mathrm{glob}}$

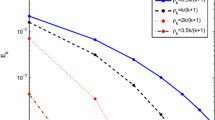
The results relative to the second set of problems are compared with those obtained by a two-level derivative-free DIRECT-type algorithm ($\hbox {DIRECT}+\hbox {DFN}_{\mathrm{con}}$) published in [10]. The results therein published, as well as those available in the report [9], correspond to a version that is enriched with a derivative-free local search procedure (the $\hbox {DFN}_{\mathrm{con}}$ proposed in [14]). We have downloaded the code in Fortran 90 (double precision), available in http://www.iasi.cnr.it/~liuzzi/ ¹ and disabled the local search for a more fair comparison. The 82 problems were also coded in Fortran 90. The results reported in [12] (Table 3 in the cited paper) that correspond to the algorithm DF-EPGO without the local search phase are also included in this comparison. The comparisons are made by using a graphical procedure to visualize the performance differences among the results produced by the three algorithms, in relative terms on the 82 problems, known as performance profiles [13]. Each plot reports (on the vertical axis) the percentage of problems solved with each algorithm that is within a certain threshold, $\tau$, (on the horizontal axis) of the best result. The performance profiles of the values of the relative gap (as defined in (9)) are shown in the Fig. 6a. Figure 6b corresponds to the metric $V_{\mathrm{glob}}$. The higher the percentage the better. A higher value for $\tau =1$ means that the corresponding algorithm achieves the lowest relative gap value (or the smallest $V_{\mathrm{glob}}$) mostly. Although we have imposed on our algorithm the limit on the number of hyperrectangles, $500 n (m+p)$ as shown in [9], the conditions referred to in (9) are also used. It is possible to conclude that, regarding the relative gap, filter-based DIRECT produces the best results in about 40% of the problems, i.e., the probability that filter-based DIRECT gives the best result on a given problem is 0.4. Similarly, the probability that the $\hbox {DIRECT}+\hbox {DFN}_{\mathrm{con}}$ (local disabled) gives the best result on a problem is about 0.1 and the probability that the DF-EPGO gives the best result on a problem is 0.56. When the profiles for $V_{\mathrm{glob}}$ are analyzed, we may conclude that the probability that the filter-based DIRECT algorithm gives the best result is about 0.33, while the probability that the $\hbox {DIRECT}+\hbox {DFN}_{\mathrm{con}}$ (local disabled) gives the best result on a given problem is about 0.65. The corresponding probability for DF-EPGO is 0.42.

4 Conclusions

In this paper, a filter-based DIRECT method for solving nonsmooth and nonconvex CGO problems is proposed. With the filter methodology, we aim to minimize the constraint violation and the objective function values simultaneously. In the DIRECT context, the filter methodology gives priority to the selection of hyperrectangles with feasible center points, followed by those with infeasible and non-dominated center points and finally by those that have infeasible and dominated center points. To define the convex hull and the POH, the hyperrectangles with infeasible center points are analyzed separately depending on the non-dominance/dominance property, which in turn are addressed separately from those with feasible centers. During hyperrectangles division, special rules to define a “preference point” by dimension and a “preference order” are proposed. The convergence properties of the algorithm are analyzed. The reported results show that the filter-based DIRECT method is able to compete with other DIRECT-type methods.

A future idea to pursue is concerned with a new strategy that aims to progressively discard a portion of the infeasible region of being explored since it is unlikely that the search may return back to the feasible region from that part of the space. To improve the solution accuracy, a local search procedure will be incorporated in the algorithm.