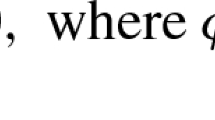Bounded Lagrange multiplier rules for general nonsmooth problems and application to mathematical programs with equilibrium constraints

Abstract

In this paper, a general optimization problem is considered to investigate the conditions which ensure the existence of Lagrangian vectors with a norm not greater than a fixed positive number. In addition, the nonemptiness and boundedness of the multiplier sets together with their exact upper bounds is characterized. Moreover, three new constraint qualifications are suggested that each of them follows a degree of boundedness for multiplier vectors. Several examples at the end of the paper indicate that the upper bound for Lagrangian vectors is easily computable using each of our constraint qualifications. One innovation is introducing the so-called bounded Lagrangian constraint qualification which is stated based on the nonemptiness and boundedness of all possible Lagrangian sets. An application of the results for a mathematical program with equilibrium constraints is presented.

1 Introduction

In this section, we briefly discuss the main idea of this paper. Consider the following general optimization problem:

$$\begin{aligned} \hbox {minimize }f(x)\hbox { subject to }F(x)\in \varLambda ,\quad x\in \varOmega . \end{aligned}$$

(1)

It is assumed that $\varLambda \subseteq Y$ and $\varOmega \subseteq X$ are closed subsets in Asplund spaces, and that $F:X\longrightarrow Y$ and $f:X\longrightarrow \mathbb {R}$ are Lipschitz near $\bar{x}\in F^{-1}(\varLambda )\cap \varOmega$. For each function $g:X\longrightarrow \mathbb {R}$ which is Lipschitz near $\bar{x}\in \mathrm{dom}\,g$, and all $(z^*,y^*)\in N(\bar{x};\varOmega )\times N(F(\bar{x});\varLambda )$, we say that $(z^*,y^*)$ is a Lagrange multiplier vector for $\bar{x}$ with respect to g iff

$$\begin{aligned} -z^* \in \partial g(\bar{x}) + D^*_N F(\bar{x})(y^*) \end{aligned}$$

where $\partial g(\bar{x})$ and $D^*_N F(\bar{x})$ are the Mordukhovich subdifferential and the normal coderivative of g and F at $\bar{x}$ (see Sect. 2). The set of all Lagrange multipliers of $\bar{x}$ with respect to g is denoted by $\varLambda (\bar{x};g)$. In this paper, we will answer the following two questions:

• 1. Under what conditions can we ensure that there exists Lagrangian vectors with a norm not greater than a specified positive number?

• 2. What conditions can characterize the nonemptiness and boundedness of the multiplier sets $\varLambda (\bar{x};g)$ together with their exact upper bounds as well?

Gauvin in [1] considered a nonlinear program with inequality and equality constraints where all functions are continuously differentiable on $\mathbb {R}^n$. He proved that the Mangasarian–Fromowitz constraint qualification MFCQ [2] is an equivalent condition for boundedness and nonemptiness of the set of Lagrangian multipliers. The authors in [3] investigated a problem similar to (1), where $\varOmega$ is closed and convex, $\varLambda$ is a closed convex cone, f is differentiable and F is continuously differentiable. They proposed a regularity assumption which was “almost” equivalent to the existence of a non-empty and weakly compact set of Lagrange multipliers. Shortly after that an equivalent condition was presented in [4] for nonemptiness and boundedness of the multiplier set of a nonlinear problem with locally Lipschitz objective and inequality constraint functions and continuously differentiable equality constraint functions. The other work in this subject was done by Pappalardo [5]. He presented a nonsmooth version of MFCQ, in the sense of Clarke, for a Lipschitz optimization problem with equality and inequality constraints and proved that his constraint qualification is equivalent to the nonemptiness and boundedness of the multiplier set. Then Jourani in [6] gave conditions, in terms of the Clarke subdifferential, ensuring the nonemptiness and the boundedness of the Lagrange multiplier sets for problem (1), assuming that $\varOmega$ and $\varLambda$ are proper sets and the functions are locally Lipschitz at the point of question. In [7], the authors discussed the conditions required to guarantee the non-emptiness and the boundedness of certain subsets of the set of Lagrange multipliers for an inequality and equality constrained vector minimization problem. Subsequently Dutta et al. [8] considered an especial extension of problem in (1) on $\mathbb {R}^n$. Instead of the constraint $F(x)\in \varLambda$, they added the term $\rho (F(x))$ to the objective function, where $\rho :\mathbb {R}^n\longrightarrow \mathbb {R}\cup \{+\infty \}$ was a proper lower semicontinuous function. Then they proposed a modification of MFCQ and proved its equivalence to the nonemptiness and boundedness of the multiplier set.

An overall review shows that, in all the papers mentioned above, a suitable form of MFCQ has been proposed as a characterization for the nonemptiness and boundedness of the multiplier set. However, it is clear that an exact upper bound is not provided via the MFCQ. In this paper, we suggest three new constraint qualifications that each of them follows a degree of boundedness for the multiplier vectors. Each constraint qualification involves a positive modulus which, together with the Lipschitzian constant of the objective function, provides us an upper bound for the Lagrange multipliers. Several examples indicate that the upper bound for Lagrangian vectors is easily computable using each of our constraint qualifications. One innovation is introducing the so-called bounded Lagrangian constraint qualification (BLCQ) which is stated based on the nonemptiness and boundedness of all possible Lagrangian sets. Although the concept of the Lagrange multiplier vector intrinsically depends on the objective function, but it will be seen that (BLCQ) is completely free from the objective function and can be characterized only by the intrinsic features of the constraint system. Among our new constraint qualifications, there is specifically the so-called regularity constraint qualification (RCQ). It is worth mentioning that (RCQ) is equivalent to (MFCQ), but with a difference that (RCQ) provides us an exact upper bound for the multiplier set. It is well known that the bound is not provided with the classical technique to derive KKT conditions via the MFCQ.

Next let us present the approach to derive our constraint qualifications. Alongside the constraint $F(x)\in \varLambda$ in problem (1), the multifunction $M:Y\overrightarrow{\longrightarrow }X$ may be defined as

$$\begin{aligned} M(y):=\{x\in X:F(x)+y\in \varLambda \}. \end{aligned}$$

It will be seen that the regularity and stability properties of M plays a key role in our work. Let us now recall some of the prominent stability properties formulated for set-valued mappings. A set-valued mapping $M:Y\overrightarrow{\longrightarrow }X$ between metric spaces is said to be Lipschitz-like (or have Aubin property [9–11]) at some point $(\bar{y},\bar{x})$ of its graph with constant $L>0$ if there exist neighborhoods V, U of $\bar{y},\bar{x}$, respectively, such that

$$\begin{aligned} M(y)\cap { U}\subset M(y')+Ld(y,y'){\mathbb {B}}_{X}\quad \hbox { for\,all}\,y,y'\in { V}, \end{aligned}$$

(2)

where ${\mathbb {B}}_{X}$ denotes the closed unit ball of X. Fixing one of the y-parameters as $\bar{y}$ in the definition of the Lipschitz-like property yields the concept of calmness [12] of M at $(\bar{y}, \bar{x})$:

$$\begin{aligned} M(y)\cap { U}\subset M(\bar{y})+Ld(y,\bar{y}){\mathbb {B}}_{X}\quad \hbox {for\,all}\,y\in V. \end{aligned}$$

(3)

Obviously, Lipschitz-like property implies calmness, whereas the converse is not necessarily true. The infimum of the values of L for which (2, 3) holds (for some associated neighborhoods U and V ) is called the Lipschitz (calmness) modulus of M at $(\bar{y}, \bar{x})$.

Parallel to these stability notions, two regularity concepts can be defined for multifunctions. Explicitly, the multifunction $G:X\overrightarrow{\longrightarrow }Y$ is metrically regular [13–15] at $(\bar{x},\bar{y})\in \mathrm{gph}\,G$ with constant $L>0$ if there exist neighborhoods V, U of $\bar{y},\bar{x}$, respectively, such that

$$\begin{aligned} d_{ G ^{-1}(y)}(x) \le Ld_{G(x)}(y) \quad \hbox {for\,all}\,(x,y)\in U\times V. \end{aligned}$$

(4)

Fixing one of the y-parameters as $\bar{y}$ in the above leads to the notion of metric subregularity [16] of G at $(\bar{x},\bar{y})$:

$$\begin{aligned} d_{ G ^{-1}(\bar{y})}(x) \le Ld_{G(x)}(\bar{y}) \quad \hbox {for\,all}\, x\in U. \end{aligned}$$

(5)

Metric subregularity clearly follows from metric regularity, but the converse does not necessarily happen.

It is well known that $M:Y\overrightarrow{\longrightarrow }X$ is Lipschitz-like around $(\bar{y}, \bar{x})\in \mathrm{gph}\,M$ if and only if its inverse $M^{-1}:X\overrightarrow{\longrightarrow }Y$ is metrically regular around $(\bar{x}, \bar{y}) \in \mathrm{gph}\,M^{-1}$ with the same constant (see [17, Theorem 1.49]). Similar result holds for the metric subregularity and calmness (see [18]). In our approach, we focus on providing an exact amount for the positive scalar L in the above notions. The paper is organized as follows. Section 2 contains basic definitions and preliminaries from variational analysis and generalized differentiation broadly used in formulations and proofs of the main results in the subsequent sections. Based on a detailed study on the nonsmooth calculus of the multifunction M in Sect. 3, we introduce new regularity conditions each of them insuring the Lipschitz-like or calmness of M. Sect. 4 deals with problem (1) and establishes new constraint qualifications and necessary optimality results with bounded Lagrange multiplier vectors for this problem. Finally in Sect. 5, we apply the results of previous sections to a mathematical program with equilibrium constraints. We also present several examples illustrating our results.

2 Preliminaries

In this section, we define some basic constructions and results from variational analysis and generalized differentiation needed in what follows. All these are taken from the book by Mordukhovich [17], where the reader can find more details, discussions, and references.

Our notation is basically standard; cf. [17]. As usual, $\Vert \cdot \Vert$ stands for the norm of Banach space X and $\langle \cdot ,\cdot \rangle$ signifies for the canonical pairing between X and its topological dual $X^*$ with the symbol $\mathop {\longrightarrow }\limits ^{w^*}$ indicating the convergence in the weak$^*$ topology of $X^*$ and the symbol ${\mathrm {cl}}^*$ standing for the weak$^*$ topological closure of a set. For any $x \in X$ and $\delta > 0$, denote by ${\mathbb {B}}(x;\delta )$ the closed ball centered at x with radius $\delta$ while $\mathbb {B}$ and $\mathbb {B}^*$ stands for the closed unit balls in X and $X^*$, respectively. For given function $f:\mathbb {R}^n\longrightarrow \mathbb {R}$, the function $f^+:\mathbb {R}^n\longrightarrow \mathbb {R}$ is defined by $f^+(x):=\max \{f(x),0\}.$ Recall that the symbol

$$\begin{aligned} \begin{array}{ll} \displaystyle \mathop {\mathrm{Lim}\,\mathrm{sup}}_{x\rightarrow \bar{x}}F(x):=\Big \{x^*\in X^*\Big |&{}\exists \;\hbox { sequences }\;x_k\rightarrow \bar{x}\;\hbox { and }\;x^*_k\mathop {\rightarrow }\limits ^{w^*}x^*\\ &{}\hbox {with }\;x^*_k\in F(x_k)\quad \hbox {for\,all}\;k\in \mathbb {N}\Big \} \end{array} \end{aligned}$$

(6)

stands for the sequential Painlevé-Kuratowski upper/outer limit of a set-valued mapping $F:X\longrightarrow X^*$ in the norm topology of X and weak$^*$ topology of $X^*$.

A Banach space X is Asplund, or it has the Asplund property, if every convex continuous function $\phi :U \longrightarrow \mathbb {R}$ defined on an open convex subset U of X is Fréchet differentiable on a dense subset of U. Note that this class includes all reflexive Banach spaces. The class of Asplund spaces possesses many useful properties and is stable under Cartesian products and linear isomorphisms. A crucial topological property of duals to Asplund spaces is that the dual unit ball is weak$^*$ sequentially compact (see [19, Theorem 3.5]).

Since all the spaces under consideration are Asplund, which is our standing assumption, we adapt the given definitions and properties to this case referring the reader to the first two chapters of [17] for the corresponding modifications in arbitrary Banach spaces.

First let us present some of the basic concepts of generalized differentiation. We start with normals to sets , then proceed to coderivatives of set-valued mappings, and then to subdifferentials of extended-real-valued functions. Given a nonempty set $\varOmega \subset X$, define the Fréchet normal cone to $\varOmega$ at $\bar{x}\in \varOmega$ by

$$\begin{aligned} \widehat{N}(\bar{x};\varOmega ):=\displaystyle \Big \{x^*\in X^*\;:\;\limsup _{x\mathop {\rightarrow }\limits ^{\varOmega }\bar{x}}\frac{\langle x^*,x-\bar{x}\rangle }{\Vert x-\bar{x}\Vert }\le 0\Big \}, \end{aligned}$$

(7)

where the symbol $x\mathop {\rightarrow }\limits ^{\varOmega }\bar{x}$ signifies that $x\rightarrow \bar{x}$ with $x\in \varOmega$. Letting for convenience $\widehat{N}(x;\varOmega )=\emptyset$ if $x\notin \varOmega$ and employing the outer limit (6) to $\widehat{N}(\cdot ;\varOmega )$, define the Mordukhovich normal cone to $\varOmega$ at $\bar{x}\in \varOmega$ as follows:

$$\begin{aligned} N(\bar{x};\varOmega ):=\mathop {\mathrm{Lim}\,\mathrm{sup}}_{x\rightarrow \bar{x}}\widehat{N}(x;\varOmega ). \end{aligned}$$

(8)

Both constructions (7) and (8) reduce to the classical normal cone when $\varOmega$ is a convex set.

Each set-valued mapping $F\overrightarrow{\longrightarrow }Y$ is uniquely associated with its graph

$$\begin{aligned} \mathrm{gph}\,F:=\big \{(x,y)\in X\times Y:\;y\in F(x)\big \}, \end{aligned}$$

in the product space $X \times Y$ . F is said to be positively homogeneous if its graph is a cone in $X \times Y$. The norm of a positively homogeneous set-valued mapping F is defined by $\Vert F\Vert := \sup \{\Vert y\Vert : y \in F(x)\hbox { and }\Vert x\Vert \le 1\}.$

Now let us define the coderivative constructions for a multifunction F used in this paper. The Fréchet coderivative of F at $(\bar{x},\bar{y})\in \mathrm{gph}\,F$ is given by

$$\begin{aligned} \widehat{D}^*F(\bar{x},\bar{y})(y^*):=\big \{x^*\in X^*:(x^*,-y^*)\in \widehat{N}\big ((\bar{x},\bar{y});\mathrm{gph}\,F\big )\big \},\quad y^*\in Y^*, \end{aligned}$$

(9)

and the normal coderivative of F at the reference point is defined by

$$\begin{aligned} D^*_N F(\bar{x},\bar{y})(y^*):=\big \{x^*\in X^*:\;(x^*,-y^*)\in N\big ((\bar{x},\bar{y});\mathrm{gph}\,F\big )\big \},\quad y^*\in Y^*. \end{aligned}$$

(10)

We also need the following modification of the normal coderivative (10) called the mixed coderivative of F at $(\bar{x},\bar{y})$ and defined by

$$\begin{aligned} \begin{array}{ll} D^*_M F(\bar{x},\bar{y})(y^*):=\Big \{&{}x^*\in X^*:\exists \;(x_k,y_k)\mathop {\rightarrow }\limits ^{\mathrm{\small gph}\,F}(\bar{x},\bar{y}),\; x_k^*\mathop {\rightarrow }\limits ^{w^*}x^*,\\ &{}y^*_k\mathop {\rightarrow }\limits ^{\Vert \cdot \Vert }y^*\;\hbox { with }\;(x^*_k,-y^*_k)\in \widehat{N}\big ((x_k,y_k);\mathrm{gph}\,F\big )\Big \}, \end{array} \end{aligned}$$

(11)

where $\mathop {\rightarrow }\limits ^{\Vert \cdot \Vert }$ stands for the norm convergence in the dual space; we usually omit the symbol $\Vert \cdot \Vert$ indicating the norm convergence simply by “$\rightarrow$” and also skip $\bar{y}=f(\bar{x})$ in the coderivative notation if $F=f:X\rightarrow Y$ is a single-valued mapping. It follows from the definitions for general mappings $F: X \overrightarrow{\longrightarrow }Y$ that

$$\begin{aligned} \widehat{D}^*F(\bar{x},\bar{y})(y^*)\subseteq D^*_M F(\bar{x},\bar{y})(y^*)\subseteq D^*_N F(\bar{x},\bar{y})(y^*), \end{aligned}$$

for any $y^*\in Y^*$, and that all the three multifunctions are positively homogeneous in $y^*$.

Considering the function $f:X\longrightarrow \overline{\mathbb {R}}$ which is lower semi continuous (l.s.c.) around $\bar{x}\in \mathrm{dom}\,f:=\{x\in X|f(x)<\infty \}$, the presubdifferential or Fréchet subdifferential of f at $\bar{x}$ is defined by

$$\begin{aligned}\widehat{\partial }f(\bar{x}):=\left\{ x^*\in X^*:\liminf _{x\longrightarrow \bar{x}}\frac{f(x)-f(\bar{x})-\left<x^*,x-\bar{x}\right>}{\Vert x-\bar{x}\Vert }\ge 0 \right\} , \end{aligned}$$

and the Mordukhovich or limiting subdifferential of f at $\bar{x}$ is given by

$$\begin{aligned} \partial f(\bar{x}):=\displaystyle \mathop {\mathrm{Lim}\,\mathrm{sup}}_{x\mathop {\longrightarrow }\limits ^{f}\bar{x}}\widehat{\partial }f(x). \end{aligned}$$

Among the most important ingredients of variational analysis and generalized differentiation in infinite-dimensional spaces are the so-called “normal compactness” properties of sets and mappings, which are automatic in finite dimensions while playing a crucial role in infinite-dimensional variational analysis and applications. In this paper, we need the following general versions of such properties defined in the products of Asplund spaces, which are well known to be also Asplund. Given a set $\varOmega \subset \prod _{j=1}^m X_j$ and an index set $J\subset \{1,\ldots ,m\}$, we say that $\varOmega$ is partially sequentially normally compact (PSNC) at $\bar{x}\in \varOmega$ with respect to $\{X_j|\;j\in J\}$ iff for any sequences $x_k\mathop {\rightarrow }\limits ^{\varOmega }\bar{x}$ and $x^*_k=(x^*_{1k},\ldots , x^*_{mk})\in \widehat{N}(x_k;\varOmega )$ one has

$$\begin{aligned} \left. \begin{array}{l} x^*_{jk}\mathop {\rightarrow }\limits ^{w^*}0,\;j\in J,\;\\ \Vert x^*_{jk}\Vert \rightarrow 0,\;j\in \{1,\ldots ,m\}\setminus J\end{array}\right\} \Longrightarrow \Vert x^*_{jk}\Vert \rightarrow 0,\quad j\in J,\quad \hbox { as }\;k\rightarrow \infty . \end{aligned}$$

In the extreme case of $J=\{1,\ldots ,m\}$, both PSNC properties defined above do not depend on the product structure and reduce to the so-called sequential normal compactness (SNC) property of $\varOmega$ at $\bar{x}$.

Given a set-valued mapping $F:X\longrightarrow 2^Y$, we associate it with the graphical set $\mathrm{gph}\,F$ that belongs to the product space $X\times Y$. Thus the PSNC/SNC properties of the graph in the above senses induce the corresponding properties of F. In this vein, we say that F is PSNC at $(\bar{x},\bar{y})\in \mathrm{gph}\,F$ iff its graph is PSNC at this point with respect to X.

Let us now recall two auxiliary results of nonsmooth calculus in Asplund spaces from [17]. Let $S: X \overrightarrow{\longrightarrow }Y$ and $\bar{x}\in \mathrm{dom}\,S:=\{x\in X|S(x)\ne \emptyset \}$. Given $\bar{y}\in S(\bar{x})$, we say that S is inner semicontinuous at $(\bar{x},\bar{y})$ iff for each sequence $x_k \longrightarrow \bar{x}$ with $x_k \in \mathrm{dom}\,S$, there is a sequence $y_k \in S(x_k)$ such that $y_k \longrightarrow \bar{y}$ as $k \longrightarrow +\infty$. Also, S is inner semicompact at $\bar{x}$ iff for any sequence $x_k\longrightarrow \bar{x}$ there is a sequence $y_k \in S(x_k)$ that contains a convergent subsequence as $k\longrightarrow \infty$. Clearly, the inner semicontinuity of S at $(\bar{x}, \bar{y})$ implies the inner semicompactness of S at $\bar{x}$, which may be substantially weaker than the inner semicontinuity. The first result explains normal and mixed coderivatives of compositions of set-valued mappings between Asplund spaces via their corresponding coderivatives.

Theorem 2.1

[17, Theorem 3.13] (chain rules for coderivatives) Let $G: X\overrightarrow{\longrightarrow }Y$ , $F: Y \overrightarrow{\longrightarrow }Z$, $\bar{z}\in (F \circ G)(\bar{x}):=\{z\in Z|\exists y\in G(\bar{x})\hbox { such that }z\in G(y)\}$, and

$$\begin{aligned} S(x, z) := G(x) \cap F^{-1}(z) = \{y \in G(x)| z \in F(y)\} . \end{aligned}$$

Given $\bar{y}\in S(\bar{x}, \bar{z})$, assume that S is inner semicontinuous at $(\bar{x}, \bar{z}, \bar{y})$, that the graphs of F and $G^{-1}$ are locally closed around the points $(\bar{y}, \bar{z})$ and $(\bar{x}, \bar{y})$, respectively, that either F is PSNC at $(\bar{y}, \bar{z})$ or $G^{-1}$ is PSNC at $(\bar{y}, \bar{x})$, and that the mixed qualification condition

$$\begin{aligned} D^*_M F(\bar{y}, \bar{z})(0) \cap (- D^*_MG^{-1}(\bar{y}, \bar{x})(0)) = \{0\}, \end{aligned}$$

is fulfilled. Then, the following assertion holds for both coderivatives $D^* = D^*_N$ and $D^* = D^*_M$ for all $z^*\in Z^*$:

$$\begin{aligned} D^*(F \circ G)(\bar{x}, \bar{z})(z^*) \subset D^*_NG(\bar{x}, \bar{y}) \circ D^*F(\bar{y}, \bar{z})(z^*) . \end{aligned}$$

The second theorem from [17] provides conditions for the preservation of the metric regularity of set-valued mappings under their general composition.

Theorem 2.2

Let $\bar{z}\in (F \circ G)(\bar{x})$, where $G: X \overrightarrow{\longrightarrow }Y$ and $F: Y \overrightarrow{\longrightarrow }Z$ are set-valued mappings between Asplund spaces. Assume that the graphs of G and $F^{-1}$ are locally closed near $\bar{x}$ and $\bar{z}$, respectively, and that the following conditions hold:

• 1. The set-valued mapping $(x, z)\mapsto G(x) \cap F^{-1}(z)$ is inner semicompact around $(\bar{x}, \bar{z})$.

• 2. For every $\bar{y}\in G(\bar{x})\cap F^{-1}(\bar{z})$ both mappings G and F are locally metrically regular around $(\bar{x}, \bar{y})$ and ($\bar{y}, \bar{z})$, respectively.

Then $F\circ G$ is locally metrically regular around $(\bar{x}, \bar{z})$.

3 Lipschitzian properties of a general constraint system

The focus in this section is on the stability and regularity properties of a class of multifunctions between Asplund spaces of the type

$$\begin{aligned} M(y):=\{x\in X:F(x)+y\in \varLambda \}, \end{aligned}$$

(12)

where $\varLambda \subseteq Y$ is a closed subset and $F:X\longrightarrow Y$ is locally Lipschitz near some point $\bar{x}\in F^{-1}(\varLambda )$. As will be seen later, this multifunction plays an important role in our main results. First, let us take a closer look at this class and carefully examine some of their variational properties. To this end, we support the following two theorems. The first one which is named by the Mordukhovich criterion, lists some pointbased characterizations for Lipschitz-like property.

Theorem 3.1

[17, Theorem 4.10] Let $M:Y\overrightarrow{\longrightarrow }X$ be a set-valued mapping between Asplund spaces that is assumed to be closed-graph around $(\bar{y},\bar{x})\in \mathrm{gph}\,M$. Then the following properties are equivalent:

• 1. M is Lipschitz-like around $(\bar{y},\bar{x})$.

• 2. M is PSNC at $(\bar{y},\bar{x})$ and $\Vert D^*_M M(\bar{y},\bar{x})\Vert <\infty$.

• 3. M is PSNC at $(\bar{y},\bar{x})$ and $D^*_M M(\bar{y},\bar{x})(0) = \{0\}$.

Moreover, in this case one has the estimates

$$\begin{aligned} \Vert D^*_M M(\bar{y},\bar{x})\Vert \le {\mathrm {lip}}\, M(\bar{y},\bar{x})\le \Vert D^*_N M(\bar{y},\bar{x})\Vert , \end{aligned}$$

where

$$\begin{aligned} {\mathrm {lip}}\, M(\bar{y},\bar{x}):=\inf \{L > 0|(2) \hbox { holds for } L \}. \end{aligned}$$

The upper estimate holds if ${\mathrm {dim}}\, Y < \infty$.

The second theorem provides us an upper estimate for the constant of metric subregularity of $M^{-1}$. Letting ${\mathrm {subreg}}\,G(\bar{x},\bar{y}) := \inf \{L > 0| (5) \text{ holds } \text{ for } L\}$, one has,

Theorem 3.2

[20, Theorem 3.1.] Let X and Y be Asplund spaces and $G : X \overrightarrow{\longrightarrow }Y$ be a closed multifunction and $(\bar{x},\bar{y})\in \mathrm{gph}\,G$. Then

$$\begin{aligned} {\mathrm {subreg}}\,G(\bar{x}, \bar{y}) \le \inf _{\varepsilon >0}\sup \{ \Vert \hat{D}^* G^{-1}(y,x)\Vert :x \in {\mathbb {B}}(\bar{x}; \varepsilon ) \setminus G ^{-1}(\bar{y}), y \in G(x) \cap {\mathbb {B}}(\bar{y}; \varepsilon ) \} . \end{aligned}$$

In our first result we show that there are clear relationships between the Fréchet and normal coderivatives of M and the corresponding constructions of F and $\varLambda$.

Theorem 3.3

For each $y^*\in Y^*$ and any $(x,y)\in \mathrm{gph}\,M^{-1}$ the following equation holds:

$$\begin{aligned} \hat{D}^*M^{-1}(x,y)(y^*)=\left\{ \begin{array}{ll} \hat{D}^*F(x)(-y^*) &{}\quad \hbox {if } y^*\in -\hat{N}(F(x)+y;\varLambda ), \\ \emptyset &{}\quad \hbox {otherwise}. \\ \end{array}\right. \end{aligned}$$

Proof

Suppose that $G:Y\overrightarrow{\longrightarrow }Y$ is defined by $G(y):=\varLambda -y$. It is easy to see that $M=F^{-1}\circ G$. On the other hand we have $G=G^{-1}$, and thus, $M^{-1}=G\circ F$. Assume that for given spaces X and Y and a nonempty subset $\varOmega \subset X$ the indicator mapping $\varDelta : X \overrightarrow{\longrightarrow }Y$ of $\varOmega$ relative to Y is given by

$$\begin{aligned} \varDelta (x;\varOmega )=\left\{ \begin{array}{ll} \{0\}\subset Y &{}\quad \hbox {if }x\in \varOmega , \\ \emptyset &{}\quad \hbox {otherwise.} \\ \end{array}\right. \end{aligned}$$

Applying now the above notion and letting $A+\emptyset =\emptyset$, we define the multifunction $\varPhi :X\times Y\overrightarrow{\longrightarrow }Y$ by

$$\begin{aligned} \varPhi (x,y):=G(y)+\varDelta ((x,y);\mathrm{gph}\,F). \end{aligned}$$

Let us then prove that for each $(x,y)\in \mathrm{gph}\,M^{-1}$ and all $y^*\in Y^*$

$$\begin{aligned} \hat{D}^*M^{-1}(x,y)(y^*)=\{x^*\in X^*|(x^*,0)\in \hat{D}^*\varPhi (x,F(x),y)(y^*)\}. \end{aligned}$$

(13)

Observing that $(x',y'',y')\in \mathrm{gph}\,\varPhi$ if and only if $y''=F(x')$, $(x',y')\in \mathrm{gph}\,M^{-1}$, and the fact that the Fréchet normal cone is invariant with respect to equivalent norms we get

$$\begin{aligned}&\frac{1}{L+1}\limsup \nolimits _{\begin{array}{l} \scriptstyle {(x',y')\longrightarrow (x,y)} \\ \scriptstyle {y'\in (G\circ F)(x')} \\ \end{array}}\frac{\langle x^*,x'-x\rangle -\langle y^*,y'-y\rangle }{\Vert (x',y')-(x,y)\Vert }\\&\quad \le \limsup \nolimits _{\begin{array}{l} \scriptstyle {(x',y'',y')\longrightarrow (x,F(x),y)} \\ \scriptstyle {y'\in \varPhi (x',y'')} \\ \end{array}} \frac{\langle (x^*,0,-y^*),(x',y'',y')-(x,F(x),y)\rangle }{\Vert (x',y'',y')-(x,F(x),y)\Vert }\\&\quad =\limsup \nolimits _{\begin{array}{l} \scriptstyle {(x',y'',y')\longrightarrow (x,F(x),y)} \\ \scriptstyle {y''=F(x'),y'\in G(y'')} \\ \end{array}} \frac{\langle x^*,x'-x\rangle -\langle y^*,y'-y\rangle }{\Vert (x',y'',y')-(x,F(x),y)\Vert }\\&\quad \le \limsup \nolimits _{\begin{array}{l} \scriptstyle {(x',y')\longrightarrow (x,y)} \\ \scriptstyle {y'\in (G\circ F)(x')} \\ \end{array}}\frac{\langle x^*,x'-x\rangle -\langle y^*,y'-y\rangle }{\Vert (x',y')-(x,y)\Vert }, \end{aligned}$$

where $L>0$ is the Lipschitz constant of F near x. The above immediately implies the equation in (13). On the other hand, we see that

$$\begin{aligned} \varPhi (x,y)=\psi (x,y)+\varPsi (x,y), \end{aligned}$$

where $\psi (x,y):=-y$ and $\varPsi (x,y):=\varLambda +\varDelta ((x,y);\mathrm{gph}\,F)$. By using [17, Theorem 1.62], we conclude that

$$\begin{aligned} \hat{D}^*\varPhi (x,F(x),y)(y^*)=(0,-y^*)+\hat{D}^*\varPsi ((x,F(x)),y+F(x))(y^*). \end{aligned}$$

The above together with (13) yields

$$\begin{aligned} (x^*,y^*)\in \hat{D}^*\varPsi ((x,F(x)),y+F(x))(y^*). \end{aligned}$$

Taking a closer look at the multifunction $\varPsi$, we observe that

$$\begin{aligned} \varPsi (x,y)=\varLambda +\varDelta ((x,y);\mathrm{gph}\,F)=\left\{ \begin{array}{ll} \varLambda &{}\quad \hbox {if } (x,y)\in \mathrm{gph}\,F, \\ \emptyset &{}\quad \hbox {otherwise.} \\ \end{array}\right. \end{aligned}$$

Putting all above together,we obtain $\mathrm{gph}\,\varPsi =\mathrm{gph}\,F\times \varLambda$ and also,

$$\begin{aligned}&(x^*,y^*,-y^*) \in \hat{N}((x,F(x)),F(x)+y);\mathrm{gph}\,F\times \varLambda ) \\&\quad =\hat{N}((x,F(x));\mathrm{gph}\,F)\times \hat{N}(F(x)+y;\varLambda ). \end{aligned}$$

The latter inclusion means that $x^*\in \hat{D}^*F(x)(-y^*)$ and $-y^*\in \hat{N}(F(x)+y;\varLambda )$ and completes the proof of theorem. $\triangle$ $\square$

The following corollary is a direct consequence of Theorem 3.3 and we present it here without proof.

Corollary 3.1

For both coderivatives $D^* = D^*_N$ and $D^* = D^*_M$ for all $y^*\in Y^*$ and any $(x,y)\in \mathrm{gph}\,M^{-1}$one has

$$\begin{aligned} D^*M^{-1}(x,y)(y^*)=\left\{ \begin{array}{ll} D^*F(x)(-y^*) &{}\quad \hbox {if } y^*\in - N(F(x)+y;\varLambda ), \\ \emptyset &{}\quad \hbox {otherwise}. \\ \end{array}\right. \end{aligned}$$

In the next result we easily derive a regularity property for M that is likely to be undiscovered.

Theorem 3.4

If F is Lipschitz around $\bar{x}$, then M is metrically regular at $(0,\bar{x})\in \mathrm{gph}\,M$, and particularly, $D^*_MM^{-1}(\bar{x},0)(0)=\{0\}$ and $M^{-1}$ is PSNC at $(\bar{x},0)$.

Proof

Suppose that the multifunction $G:Y\overrightarrow{\longrightarrow }Y$ is defined as in the proof of Theorem 3.3 and consider the representations $M=F^{-1}\circ G$ and $M^{-1}=G\circ F$. Defining the multifunction $S:X\times Y\overrightarrow{\longrightarrow }Y$ by $S(x,y):=G(y)\cap \{F(x)\}$, we can easily compute that

$$\begin{aligned} S(x,y)=\left\{ \begin{array}{ll}\{F(x)\}&{}\quad \hbox {if } F(x)+y\in \varLambda ,\\ \emptyset &{}\quad \hbox {otherwise.}\end{array}\right. \end{aligned}$$

Due to the continuity of F, S is inner semicontinuous at $(\bar{x},0,F(\bar{x}))$(and specially inner semicompact at $(\bar{x},0)$).

Let us show that $G=G^{-1}$ is Lipschitz-like at each point of its graph with modulus 1. For given $y,y'\in Y$ and $w\in G(y)$, one has $w+y\in \varLambda$ and if $w':=w+y-y'$, then $w'\in G(y')$ and $\Vert w-w'\Vert =\Vert y-y'\Vert$. Hence we have $G(y)\subseteq G(y')+\Vert y-y'\Vert {\mathbb {B}}_Y$. Now using [17, Theorem 4.10] we deduce that for any point $(\bar{y},\bar{w})\in \mathrm{gph}\,G$, $G=G^{-1}$ is PSNC and $D^*_MG(\bar{y},\bar{w})(0)=\{0\}$. On the other hand, since F and $G=G^{-1}$ are Lipschitz-like around $\bar{x}$ and $(0,F(\bar{x}))$, $F^{-1}$ and $G=G^{-1}$ are metrically regular near corresponding points by [17, Theorem 1.49]. Now using Theorem 2.2 together with [17, Theorems 1.49 and 4.10], the proof is completed. $\square$

4 Necessary optimality conditions for a general optimization problem

In this section we focus our attention on problem (1). Our main goal is to establish new necessary optimality results with bounded Lagrange multiplier vectors for the problem in (1). First let us consider the following supplementary problem:

$$\begin{aligned} \hbox {minimize } \phi (x, y) \hbox { subject to } y \in S(x), \quad x \in \varOmega , \end{aligned}$$

(14)

where $S: X \overrightarrow{\longrightarrow }Y$ and $\phi : X \times Y \longrightarrow \mathbb {R}$. To establish our main result in this section, we need to recall the following theorem from [17].

Theorem 4.1

[21, Theorems 5.33 and 5.34] Let $(\bar{x}, \bar{y})$ be a local optimal solution to (14). Assume that the sets $\mathrm{gph}\,S$ and $\varOmega$ are locally closed around $(\bar{x}, \bar{y})$ and $\bar{x}$, respectively. Assume also that either S is PSNC at $(\bar{x}, \bar{y})$ or $\varOmega$ is SNC at $\bar{x}$, and that the mixed qualification condition

$$\begin{aligned} D^*_M S(\bar{x}, \bar{y})(0)\cap (- N(\bar{x};\varOmega ) ) = \{0\}, \end{aligned}$$

is fulfilled. Assume also that $\phi$ is locally Lipschitzian around $(\bar{x}, \bar{y})$. Then there is $(x^*, y^*)\in \partial \phi (\bar{x}, \bar{y})$ such that

$$\begin{aligned} - x^* \in D^*_N S(\bar{x}, \bar{y})(y^*) + N(\bar{x};\varOmega ) . \end{aligned}$$

In the sequel, we turn our attention to the following specific type of multifunction M:

$$\begin{aligned} \widetilde{M}(z,y):=\{x\in X:(x+z,F(x)+y)\in \varOmega \times \varLambda \},~~~~\forall (z,y)\in X\times Y. \end{aligned}$$

(15)

The first lemma in this section shows that the calmness of $\widetilde{M}$ at the point $((0,0),\bar{x})$ enables us to transform locally the general problem in (1) into an especial form of the problem in (14).

Lemma 4.1

Let $\bar{x}$ be a local optimal solution to problem (1). Assume that f is Lipschitz continuous around $\bar{x}$ with constant $l_f$ and that the mapping $\widetilde{M}$ in (12) is calm at $((0,0),\bar{x})$ with modulus l . Then there are neighborhoods $\mathscr {V}$ of $\bar{x}$ and $\mathscr {U}$ of $0\in Y$ such that $(\bar{x}, (0,0)) \in X\times X\times Y$ solves the penalized problem

$$\begin{aligned} \hbox { minimize } \phi (x,(z, y)):= & {} f(x) + \nu \Vert (z,y)\Vert \hbox { subject to } (z,y)\in \widetilde{M}^{-1}(x)\cap [({\mathscr {V}}-\bar{x})\times {\mathscr {U}}],\\&\quad x\in \varOmega \cap {\mathscr {V}}, \end{aligned}$$

provided that $\nu > l_f.l$.

Proof

Taking $\varepsilon >0$ such that $\nu >l_f(l+\varepsilon )$, since $\widetilde{M}$ is calm at $((0,0),\bar{x})$ with modulus l, there are neighborhoods $\mathscr {V}$ of $\bar{x}$ and $\mathscr {U}$ of 0 such that for some $\hat{x}\in \widetilde{M}(0,0)$ one has the estimate

$$\begin{aligned} \Vert x-\hat{x}\Vert \le (l+\varepsilon )\Vert (z,y)\Vert ,\hbox { whenever } x\in M(z,y)\cap \mathscr {V}, (z,y)\in ({\mathscr {V}}-\bar{x})\times {\mathscr {U}}. \end{aligned}$$

Using this and the Lipschitz continuity of f with constant $l_f$, we get

$$\begin{aligned}\begin{array}{ll} f(\bar{x}) &{} \le f(\hat{x})=f(x)+(f(\hat{x})-f(x)) \\ &{} \le f(x)+l_f\Vert \hat{x}-x\Vert \le f(x)+l_f(l+\varepsilon )\Vert (z,y)\Vert \\ &{} \le f(x)+\nu \Vert (z,y)\Vert , \\ \end{array} \end{aligned}$$

whenever $(z,y)\in \widetilde{M}^{-1}(x)\cap [({\mathscr {V}}-\bar{x})\times {\mathscr {U}}]$, $x\in \varOmega \cap {\mathscr {V}}$. $\square$

We continue by the the following lemma which adapts the results of previous section to the multifunction $\widetilde{M}$ in (15).

Lemma 4.2

Consider the mapping $\widetilde{F}:X\longrightarrow X\times Y$ defined by

$$\begin{aligned} \widetilde{F}(x):=(x,F(x)),~~~~~\forall x\in X, \end{aligned}$$

where $F:X\longrightarrow Y$ is a mapping between Asplund spaces. For each $x\in X$ and $(x^*,z^*,y^*)\in X^*\times X^*\times Y^*$, the following assertions hold true:

• 1. If $x^*\in \hat{D}^*\widetilde{F}(x)(z^*,y^*)$, then one has $x^*-z^*\in \hat{D}^*F(x)(y^*)$.

• 2. If $x^*\in D^*_N\widetilde{F}(x)(z^*,y^*)$, then one has $x^*-z^*\in D^*_NF(x)(y^*)$.

Proof

• 1. Using the definition of Fréchet coderivative, we get

  $$\begin{aligned} \limsup _{(x',x',F(x'))\longrightarrow (x,x,F(x))} \frac{\langle (x^*,-z^*,-y^*),(x',x',F(x'))-(x,x,F(x))\rangle }{\Vert (x',x',F(x'))-(x,x,F(x))\Vert }\le 0.\\ \end{aligned}$$

  But the above easily implies that

  $$\begin{aligned} \limsup _{(x',F(x'))\longrightarrow (x,F(x))} \frac{\langle (x^*-z^*,-y^*),(x',F(x'))-(x,F(x))\rangle }{\Vert (x',F(x'))-(x,F(x))\Vert }\le 0, \end{aligned}$$

  which completes the proof of part 1.

• 2. Using the definition of normal coderivative together with the assertion of part 1, we can choose sequences $x_k\in X$ and $(x^*_k,z^*_k,y^*_k)\in X^*\times X^*\times Y^*$ satisfying $x_k\longrightarrow \bar{x}$, $(x^*_k,z^*_k,y^*_k)\mathop {\longrightarrow }\limits ^{w^*}(x^*,z^*,y^*)$ and for each k, $x^*_k-z^*_k\in \hat{D}^*F(x_k)(y^*_k)$. The latter immediately yields $x^*-z^*\in D^*_NF(x)(y^*)$ and ends the proof of the lemma. $\square$

Lemma 4.3

Suppose that $\varOmega \subset X$ is a closed subset in Asplund space X. Consider the multifunction $G:X\overrightarrow{\longrightarrow }X$ defined by $G(z):=\varOmega -z$ for each $z\in X$ and take $(\bar{z},\bar{z}')\in \mathrm{gph}\,G$. Then $\bar{z}+\bar{z}'\in \varOmega$ and the following assertions hold true:

• 1. If $(z^*,x^*)\in \widehat{N}((\bar{z},\bar{z}');\mathrm{gph}\,G)$, then $z^*=x^* \in \widehat{N}(\bar{z}+\bar{z}';\varOmega )$.

• 2. If $(z^*,x^*)\in N((\bar{z},\bar{z}');\mathrm{gph}\,G)$, then $z^*=x^* \in N(\bar{z}+\bar{z}';\varOmega )$.

• 3. $D^*_NG(\bar{z},\bar{z}')(0)=\{0\}$.

Proof

It is sufficient to prove part 1. The proof of other parts is immediate from part 1. Using the definition of Fréchet normals, we get:

$$\begin{aligned} \limsup _{\scriptstyle {(z,z')\mathop {\longrightarrow }\limits ^{gph G}(\bar{z},\bar{z}')}}\frac{\langle z^*,z-\bar{z}\rangle +\langle x^*,z'-\bar{z}'\rangle }{\Vert (z-\bar{z},z'-\bar{z}')\Vert }\le 0. \end{aligned}$$

The definition of G immediately gives us some $x,\bar{x}\in \varOmega$ satisfying $x=z+z'$ and $\bar{x}=\bar{z}+\bar{z}'$. Thus the above inequality can be written as

$$\begin{aligned} \limsup _{\scriptstyle {(z,x-z)\mathop {\longrightarrow }\limits ^{gph G}(\bar{z},\bar{x}-\bar{z})}}\frac{\langle z^*-x^*,z-\bar{z}\rangle +\langle x^*,x-\bar{x}\rangle }{\Vert (z-\bar{z},(x-z)-(\bar{x}-\bar{z}))\Vert }\le 0. \end{aligned}$$

(16)

Taking arbitrary sequence $x\mathop {\longrightarrow }\limits ^{\varOmega }\bar{x}$, one has $(\bar{z},x-\bar{z})\in \mathrm{gph}\,G$, thus the limit in (16) implies that

$$\begin{aligned} \limsup _{x\mathop {\longrightarrow }\limits ^{\varOmega }\bar{x}}\frac{\langle x^*,x-\bar{x}\rangle }{\Vert x-\bar{x}\Vert }\le 0, \end{aligned}$$

hence $x^*\in \widehat{N}(\bar{z}+\bar{z}';\varOmega )$. On the other hand for any given $v\in X$ with $\Vert v\Vert =1$ and $\varepsilon \downarrow 0$, we have $(\bar{z}+\varepsilon v,\bar{x}-\bar{z}-\varepsilon v)\mathop {\longrightarrow }\limits ^{\mathrm{gph}\,G}(\bar{z},\bar{x}-\bar{z})$. Using again (16), we deduce that $\langle z^*-x^*,v\rangle \le 0$. Since v was chosen arbitrarily, we get $z^*=x^*$ and the proof is completed. $\square$

In the following we present new constraint qualifications for the constraint system: “$x\in \varOmega$ subject to $F(x)\in \varLambda$.”As will be seen later, each of these constraint qualifications leads to a certain type of Lipschitzian properties for the multifunction $\widetilde{M}$ in (15).

Definition 4.1

Let $\bar{x}\in \varOmega \cap F^{-1}(\varLambda )$. We say that

• 1. the regularity constraint qualification (RCQ) holds at $\bar{x}$ iff, there is a positive real number c such that the following implication holds:

  $$\begin{aligned} \left. \begin{array}{l} y^*\in N(F(\bar{x});\varLambda ) \\ z^*\in N(\bar{x};\varOmega )\\ x^*-z^*\in D^*_NF(\bar{x})(y^*) \end{array} \right\} \Longrightarrow c\Vert (z^*,y^*)\Vert \le \Vert x^*\Vert . \end{aligned}$$

  (17)

• 2. the semi-regularity constraint qualification 1 (sRCQ1) holds at $\bar{x}$ iff, there are positive scalars $\delta ,c$ such that for all $(z,y,x)\in \mathrm{gph}\,\widetilde{M}\cap [{\mathbb {B}}((0,0);\delta )\times {\mathbb {B}}(\bar{x};\delta )]\setminus \{(0,0,\bar{x})\}$ the following implication holds:

  $$\begin{aligned} \left. \begin{array}{l} y^*\in \hat{N}(F(x)+y;\varLambda ) \\ z^*\in \hat{N}(x+z;\varOmega )\\ x^*-z^*\in \hat{D}^*F(x)(y^*) \end{array} \right\} \Longrightarrow c\Vert (z^*,y^*)\Vert \le \Vert x^*\Vert . \end{aligned}$$

  (18)

• 3. the semi-regularity constraint qualification 2 (sRCQ2) holds at $\bar{x}$ iff, there is neighborhood $\mathscr {U}$ of $\bar{x}$ together with the positive scalar c such that for all $x\in {\mathscr {U}}\setminus (\varOmega \cap F^{-1}(\varLambda ))$,

  $$\begin{aligned} c\Vert x-\bar{x}\Vert \le d_{\varOmega }(x)+d_{\varLambda }(F(x)). \end{aligned}$$

The next theorem shows that each of our new constraint qualifications ensures a degree of stability for $\widetilde{M}$. The important point about these constraint qualifications is that they can also provide an exact upper bound for the constant of the Lipschitzness of $\widetilde{M}$. This property makes them suitable for deriving bounded Lagrange multiplier rules.

Theorem 4.2

Let $\bar{x}\in \varOmega \cap F^{-1}(\varLambda )$.

• 1. If $\varOmega$ and $\varLambda$ are SNC at $\bar{x}$ and $F(\bar{x})$ and (RCQ) holds at $\bar{x}$, then $\widetilde{M}$ is Lipschitz-like at $((0,0),\bar{x})$ with a modulus smaller than $c^{-1}$.

• 2. If (sRCQ1) holds at $\bar{x}$, then $\widetilde{M}$ is calm at $((0,0),\bar{x})$ with a modulus smaller than $c^{-1}$.

• 3. If (sRCQ2) holds at $\bar{x}$, then $\widetilde{M}$ is calm at $((0,0),\bar{x})$ with a modulus smaller than $c^{-1}$.

Proof

• 1. Due to [17, Theorem 4.10], it is sufficient to prove that $\widetilde{M}$ is PSNC at $((0,0),\bar{x})$ and $\Vert D^*_N\widetilde{M}((0,0),\bar{x})\Vert \le c^{-1}$. Considering the map $\widetilde{G}:X\times Y\overrightarrow{\longrightarrow }X\times Y$ given by $\widetilde{G}(z,y):=(\varOmega \times \varLambda )-(z,y)$, it is easy to show that that $\widetilde{M}=\widetilde{F}^{-1}\circ \widetilde{G}$. The SNC property of $\varOmega$ and $\varLambda$ at $\bar{x}$ and $F(\bar{x})$ together with Lemma 4.3(1) clearly implies that $\widetilde{G}$ is SNC at $(0,0,\bar{x},F(\bar{x}))\in \mathrm{gph}\,\widetilde{G}$. Furthermore, from Lemma 4.3(3) we get for each $((\bar{x},\bar{y}),(\bar{z},\bar{w}))\in \mathrm{gph}\,\widetilde{G}$,

  $$\begin{aligned} D^*_N\widetilde{G}((\bar{x},\bar{y}),(\bar{z},\bar{w}))(0,0)=\{(0,0)\}. \end{aligned}$$

  Thus according to [17, Theorem 3.95] $\widetilde{M}$ is PSNC at the point of question. Now taking $(z^*,y^*)\in D^*_N\widetilde{M}((0,0),\bar{x})(x^*)$ and using corollary 3.1, we deduce that $z^*\in -N(\bar{x};\varOmega )$, $y^*\in -N(F(\bar{x});\varLambda )$ and $-x^*\in D^*\widetilde{F}(\bar{x})((-z^*,-y^*)$. Noting the definition of limiting normals together with an easy application of Lemma 4.2 leads to $-x^*+z^*\in D^*F(\bar{x})(y^*)$. Then the (RCQ) at $\bar{x}$ implies that $\Vert (z^*,y^*)\Vert \le c^{-1}\Vert x^*\Vert$ and completes the the proof of part 1.

• 2. The proof of this part is immediate from Theorems 3.2 and 3.3 together with Lemma 4.2.

• 3. The proof of this part is easy and omitted. $\square$

Applying now Lemma 4.1 together with Theorems 4.1 and 4.2, we readily arrive at the following theorem which plays a key role in our main results.

Theorem 4.3

Let $\bar{x}$ be a local optimal solution to problem (1) and denote the Lipschitz constant of f around $\bar{x}$ by $l_f$. Assume also that one of the following conditions holds:

• 1. $\varOmega$ and $\varLambda$ are SNC at $\bar{x}$ and $F(\bar{x})$ and (RCQ) holds at $\bar{x}$ with constant c.

• 2. (sRCQ1) is satisfied at $\bar{x}$ with constant c.

• 3. (sRCQ2) is satisfied at $\bar{x}$ with constant c.

Then for any $\nu > l_f.c^{-1}$ there is $(z^*,y^*)\in N(\bar{x};\varOmega )\times N(F(\bar{x});\varLambda )$ with $\Vert (z^*,y^*)\Vert \le \nu$ such that

$$\begin{aligned} -z^* \in \partial f(\bar{x}) + D^*_N F(\bar{x})(y^*). \end{aligned}$$

Proof

From the viewpoint of necessary optimality conditions the penalized optimization problem in Lemma 4.1 can be equivalently written as :

$$\begin{aligned} \hbox { minimize } f(x)+\nu \Vert (z,y)\Vert \hbox { subject to } (z,y)\in \widetilde{M}^{-1}(x), \quad x\in X, \end{aligned}$$

which is an especial form of problem (14). At the same time, we observe by Theorem 3.4 that $D^*_M\widetilde{M}^{-1}(\bar{x},(0,0))(0)=\{0\}$ and $\widetilde{M}^{-1}$ is PSNC at $(\bar{x},0)$. In addition to all this, we know by Theorem 4.2 that $\widetilde{M}$ is calm at $((0,0),\bar{x})$ with modulus smaller than $c^{-1}$. Thus all the assumptions of Theorem 4.1 are satisfied. Now adapting the result of this theorem to the above problem and then using the subdifferential sum rule of [17, Theorem 2.33(c)] for $f(x)+\nu \Vert (z,y)\Vert$, we get for some $(z^*,y^*)\in \nu {\mathbb {B}}_{X^*\times Y^*}$,

$$\begin{aligned} 0 \in \partial f(\bar{x}) + D^*_N \widetilde{M}^{-1}(\bar{x},(0,0) )(-z^*,-y^*). \end{aligned}$$

The coderivative representation of Corollary 3.1 follows that $(z^*,y^*)\in N(\bar{x};\varOmega )\times N(F(\bar{x});\varLambda )$, and $(- \partial f(\bar{x}))\cap D^*_N\widetilde{F}(\bar{x})(z^*,y^*)\ne \emptyset$. Using now the second assertion of Lemma 4.2, we get immediately that $-z^* \in \partial f(\bar{x}) + D^*_N F(\bar{x})(y^*)$ and end the proof. $\square$

At this point of our work, we are going to introduce a general definition for the Lagrange multiplier vectors of the constraint system of problem (1). Furthermore, we define for the first time a new constraint qualification which is stated based on the boundedness of all multiplier sets that may exist. As will be seen later, this constraint qualification is completely independent from the objective function and can be characterized only by the properties of constraint system.

Definition 4.2

We say that the bounded Lagrangian constraint qualification (BLCQ) holds at $\bar{x}$ with constant $l>0$ iff, for all the functions $g:X\longrightarrow \mathbb {R}$ which are locally Lipschitz near $\bar{x}$ with constant $l_g$ and attain their local minimum over the feasible region of problem (1) at $\bar{x}$, the set $\varLambda (\bar{x};g)$ is nonempty and bounded by $l.l_g$.

We observed above that each of our new constraint qualifications ensures the existence of bounded Lagrange multiplier vectors. The following theorem illustrates the relationship between (RCQ) and (sRCQ1) and (BLCQ).

Theorem 4.4

Take $\bar{x}\in F^{-1}(\varLambda )\cap \varOmega$ and suppose that $\varOmega$ and $\varLambda$ are SNC at $\bar{x}$ and $F(\bar{x})$. Then the following assertions hold:

• 1. (RCQ) is satisfied at $\bar{x}$ with constant c if and only if (BLCQ) holds at $\bar{x}$ with constant $c^{-1}$.

• 2. If (BLCQ) holds at $\bar{x}$ with constant $c^{-1}$, then (sRCQ1) is satisfied at $\bar{x}$ with constant c.

Proof

• 1. Suppose that (RCQ) holds at $\bar{x}$ with constant $c>0$ and consider the function $g:X\longrightarrow \mathbb {R}$ which is locally Lipschitz near $\bar{x}$ with constant $l_g$. Suppose also that $\bar{x}$ is a minimal point for g over $F^{-1}(\varLambda )\cap \varOmega$. Then obviously, $\varLambda (\bar{x};g)\ne \emptyset$. Now take arbitrarily $(z^*,y^*)\in \varLambda (\bar{x};g)$. Then $z^*\in N(\bar{x};\varOmega )$, $y^*\in N(F(\bar{x});\varLambda )$ and clearly we can find $x^*\in \partial g(\bar{x})$ such that $-x^*-z^*\in D^*_NF(\bar{x})(y^*)$. The later in turn gives us by (RCQ) and the Lipschitzness of g near $\bar{x}$ that $\Vert (z^*,y^*)\Vert \le c^{-1}\Vert x^*\Vert \le c^{-1}.l_g$. Conversely, assume that (BLCQ) holds at $\bar{x}$ with constant $c^{-1}$. Taking now $z^*\in N(\bar{x};\varOmega )$, $y^*\in N(F(\bar{x});\varLambda )$ and $x^*\in D^*_NF(\bar{x})(y^*)+z^*$ and defining the function $g:X\longrightarrow \mathbb {R}$ by $g(x):=\langle x^*,\bar{x}-x\rangle +\Vert x^*\Vert \Vert \bar{x}-x\Vert$, we can easily see that g is locally Lipschitz near $\bar{x}$ with constant $\Vert x^*\Vert$. Clearly, $\bar{x}$ is a global minimal for g on X. Further, one has $-x^*\in \partial g(\bar{x})=\{-x^*\}+{\mathbb {B}}(0;\Vert x^*\Vert )$, and thus, $(z^*,y^*)\in \varLambda (\bar{x};g)$. Using then (BLCQ) we get $\Vert (z^*,y^*)\Vert \le c^{-1}\Vert x^*\Vert$, and thus, (RCQ) is satisfied at $\bar{x}$ with constant c.

• 2. Assume that (BLCQ) holds at $\bar{x}$ with constant $c^{-1}$ and suppose by contrary that we can choose sequences $x_k\longrightarrow \bar{x}$, $(z_k,y_k)\mathop {\longrightarrow }\limits ^{X\times Y}(0,0)$ such that $x_k+z_k\in \varOmega$ and $F(x_k)+y_k\in \varLambda$ together with sequences $z^*_k\in \widehat{N}(x_k+z_k;\varOmega )$ and $y^*_k\in \widehat{N}(F(x_k)+y_k;\varLambda )$ and $x^*_k\in \hat{D}^*F(x_k)(y^*_k)+z^*_k$ such that for each $k\in \mathbb {N}$, $k\Vert x^*_k\Vert <\Vert (z^*_k,y^*_k)\Vert$. Defining $\tilde{x}^*_k:=\frac{x^*_k}{\Vert (z^*_k,y^*_k)\Vert }$, $\tilde{z}^*_k:=\frac{z^*_k}{\Vert (z^*_k,y^*_k)\Vert }$ and $\tilde{y}^*_k:=\frac{y^*_k}{\Vert (z^*_k,y^*_k)\Vert }$, then, $\tilde{z}^*_k\in \widehat{N}(x_k+z_k;\varOmega )$, $\tilde{y^*_k}\in \widehat{N}(F(x_k)+y_k;\varLambda )$ and $\tilde{x^*_k}\in \hat{D}^*F(x_k)(\tilde{y^*_k})+\tilde{z}^*_k$ and $\Vert \tilde{x^*_k}\Vert <\frac{1}{k}\Vert {(\tilde{z}^*_k,\tilde{y}^*_k)}\Vert =\frac{1}{k}$. Since $\{\tilde{z}^*_k\}$ and $\{\tilde{y}^*_k\}$ are bounded and X and Y are Asplund, we can assume without generality that $\tilde{x^*_k}\mathop {\longrightarrow }\limits ^{w^*}\tilde{x}^*\in X^*$ and $\tilde{y^*_k}\mathop {\longrightarrow }\limits ^{w^*}\tilde{y}^*\in Y^*$. Obviously $\tilde{x^*_k}\mathop {\longrightarrow }\limits ^{\Vert \cdot \Vert }0$ and the SNC property of $\varOmega$ and $\varLambda$ at $\bar{x}$ and $F(\bar{x})$ immediately implies that $\Vert (\tilde{z}^*,\tilde{y}^*)\Vert =\gamma >0$, , and thus, $\tilde{z}^*\in N(\bar{x};\varOmega )$, $\tilde{y}^*\in N(F(\bar{x});\lambda )$ and $0\in D^*_NF(\bar{x})(\tilde{y}^*)+\tilde{z}^*$. If we define $g(x)\equiv 0$, then g is Lipschitz with constant $l_g=0$ which attains its global minimum at $\bar{x}$ and $(\tilde{z}^*,\tilde{y}^*)\in \varLambda (\bar{x};g)$. While the latter together with (BLCQ) gives us $0<\gamma =\Vert (\tilde{z}^*,\tilde{y}^*)\Vert \le l.0=0$ and completes the proof by contradiction. $\square$

The following example illustrates a situation that none of the constraint qualifications of Theorem 4.3 holds.

Example 4.1

Consider the following problem

$$\begin{aligned}\begin{array}{cc} \min &{} f(x_1,x_2):=x_1-x_2 \\ s.t. &{} F(x_1,x_2):=x_1^2+x_2\in \varLambda :=(-\infty ,0], \\ &{} (x_1,x_2)\in \varOmega :=\mathbb {R}\times \{0\}. \end{array} \end{aligned}$$

Obviously $\bar{x}=(0,0)$ is the unique feasible point. However there is no $\lambda \in \mathbb {R}_+$ satisfying

$$\begin{aligned} 0\in (1,-1)+\lambda (0,1)+N((0,0);\varOmega ). \end{aligned}$$

Indeed, none of the constraint qualifications of Theorem 4.3 holds at $\bar{x}$. It is sufficient to show that sRCQ1 and sRCQ2 are not satisfied at $\bar{x}$. If we take $(x_{1k},x_{2k}):=(\frac{1}{k},0)$, then $\{(x_{1k},x_{2k})\}$ is a sequence of infeasible points converging to $\bar{x}$. Taking $(z_{1k},z_{2k},y_k):=(0,0,-\frac{1}{k^2})$, then $(z_{1k},z_{2k},y_k,x_{1k},x_{2k})\in \mathrm{gph}\,\widetilde{M}$ and we get for $\lambda _k:=1\in N(g(x_{1k},x_{2k})+y_k;\varLambda )$ and $z^*_k=(0,\frac{1}{k}-1)\in \widehat{N}((x_{1k},x_{2k})+(z_{1k},z_{2k});\varOmega )$,

$$\begin{aligned} (x_{1k}^*,x_{2k}^*):=\left( \frac{2}{k},\frac{1}{k}\right) \in \lambda _k\widehat{\partial }g(x_{1k},x_{2k})+\widehat{N}((x_{1k},x_{2k})+(z_{1k},z_{2k});\varOmega ), \end{aligned}$$

while $\frac{k}{3}\Vert (x_{1k}^*,x_{2k}^*)\Vert <\Vert (\lambda _k,z^*_k)\Vert$. Thus sRCQ1 is not fulfilled at $\bar{x}$. An easy computation for the same sequence $\{(x_{1k},x_{2k})\}$, gives us

$$\begin{aligned} \Vert (x_{1k},x_{2k})\Vert >\frac{k}{2}[F^+(x_{1k},x_{2k})+d_{\varOmega }(x_{1k},x_{2k})], \end{aligned}$$

which implies that sRCQ2 does not hold at $\bar{x}$.

Remark 4.1

It is a well-known fact that finite dimensional spaces belong to the class of Asplund spaces. Thus the results of this section obviously hold in finite dimensional spaces as well. Moreover, we present for the first time conditions that provide exact upper bounds for Lagrangian vectors. Thus it appears that our results are new even in finite dimensions.

It is also noteworthy that various types of optimization problems can be locally written as (1). A prominent example of such a problem is a mathematical program with equilibrium constraints (MPEC) which will be discussed in the next section. Furthermore, any standard nonlinear problem with equality, inequality and set constraints can be formulated as problem (1). This means that our results are applicable for standard nonlinear problems.

As previously mentioned, the majority of work that has been done in this area has focused on a suitable form of MFCQ as a characterization for the nonemptiness and boundedness of the multipliers set. Here we present an adaptation of this constraint qualification for problem (1) and compare it with our new constraint qualifications.

Definition 4.3

Let $\bar{x}\in \varOmega \cap F^{-1}(\varLambda )$. We say that the Mangasarian Fromovitz constraint qualification (MFCQ) holds at $\bar{x}$ iff, the following implication holds:

$$\begin{aligned} \left. \begin{array}{l} y^*\in N(F(\bar{x});\varLambda ) \\ z^*\in D^*_NF(\bar{x})(y^*)\cap (-N(\bar{x};\varOmega ))\\ \end{array} \right\} \Longrightarrow \Vert (z^*,y^*)\Vert =0. \end{aligned}$$

(19)

Theorem 4.5

Take $\bar{x}\in F^{-1}(\varLambda )\cap \varOmega$. Then the following assertions hold:

• 1. If $\varOmega$ and $\varLambda$ are SNC at $\bar{x}$ and $F(\bar{x})$, then (RCQ)$\Longrightarrow$(MFCQ)$\Longrightarrow$(sRCQ1).

• 2. If X and Y are finite dimensional, then (RCQ)$\Longleftrightarrow$(MFCQ).

Proof

• 1. The proof of (RCQ)$\Longrightarrow$(MFCQ) is trivial. Suppose that (sRCQ1) is not satisfied at $\bar{x}$. Then similar to the proof of part 2. of Theorem 4.4, we can find some $\tilde{z}^*\in N(\bar{x};\varOmega )$, $\tilde{y}^*\in N(F(\bar{x});\varLambda )$ such that $0\in D^*_NF(\bar{x})(\tilde{y}^*)+\tilde{z}^*$ and $\Vert (\tilde{z}^*,\tilde{y}^*)\Vert \ne 0$. Thus (MFCQ) does not hold at $\bar{x}$.

• 2. Suppose that X and Y are finite dimensional and that (RCQ) is not satisfied at $\bar{x}$. Thus there is a sequence $(x^*_k,z^*_k,y^*_k)\in X^*\times X^*\times Y^*$ such that $\Vert x^*_k\Vert =1$, $z^*_k\in N(\bar{x};\varOmega )$, $y^*_k\in N(F(\bar{x});\varLambda )$, $x^*_k-z^*_k\in D^*_NF(\bar{x})(y^*_k)$ and $\Vert (z^*_k,y^*_k)\Vert >k$. Defining

  $$\begin{aligned} \tilde{x}^*_k:=\frac{x^*_k}{\Vert (z^*_k,y^*_k)\Vert },\tilde{z}^*_k:=\frac{z^*_k}{\Vert (z^*_k,y^*_k)\Vert },\tilde{y}^*_k:=\frac{y^*_k}{\Vert (z^*_k,y^*_k)\Vert }, \end{aligned}$$

  we get $\tilde{x}^*_k\longrightarrow 0$, and we can assume without loss of generality that $(\tilde{z}^*_k,\tilde{y}^*_k)\longrightarrow (\tilde{z}^*,\tilde{y}^*)\ne 0$. Since the limiting normal cone is closed in finite-dimensional spaces, we directly deduce that $\tilde{y}^*\in N(F(\bar{x});\varLambda )$ and $\tilde{z}^*\in (D^*_NF(\bar{x})(y^*)\cap (-N(\bar{x};\varOmega ))$. Thus (MFCQ) does not hold at $\bar{x}$ and complete the proof of theorem. $\square$

It is worth mentioning that the assertion 2. of the above theorem fails to be true in infinite dimensions, even in the case of the simplest Hilbert space $l^2$. The following example illustrates this fact.

Example 4.2

Consider the following constraint system:

$$\begin{aligned} F(x)\in \varLambda ,~~~~x\in \varOmega , \end{aligned}$$

where $F:l^2\longrightarrow l^2$ is defined by $F(x):=-x$, $\varLambda :=\{x\in l^2:x_1\le 0\}$ and

$$\begin{aligned} \varOmega :=\{s(e_1 - ke_k) + t( ke_1 - e_m): m> k > 1, s, t \ge 0\} \cup \{te_1: t \ge 0\}, \end{aligned}$$

where $\{e_1,e_2,\ldots \}$ is the sequence of orthonormal vectors in $l^2$. In [17, Example 1.7], it is proved that for each $k>2$, $e_1 + \frac{1}{k} e_k \in N(0;\varOmega )$ and $e_1\notin N(0;\varOmega )$. If taking $y^*_k:=e_1\in N(0;\varLambda )$, $z^*_k:=e_1 + \frac{1}{k} e_k\in N(0;\varOmega )$ and $x^*_k:=\frac{1}{k} e_k$, we get $x^*_k-z^*_k\in D^*_NF(0)(y^*_k)$ and

$$\begin{aligned} k\Vert x^*_k\Vert =1<\Vert (z^*_k,y^*_k)\Vert , \end{aligned}$$

which implies that (RCQ) does not hold at $\bar{x}=0$. On the other hand since $e_1\notin N(0;\varOmega )$, it is easy to see that for each $y^*\in N(0;\varLambda )\setminus \{0\}$,

$$\begin{aligned} D^*_NF(0)(y^*)\cap (-N(0,\varOmega ))=\emptyset , \end{aligned}$$

and also,

$$\begin{aligned} D^*_NF(0)(0)\cap (-N(0,\varOmega ))=\{0\}. \end{aligned}$$

Thus (MFCQ) is satisfied at $\bar{x}$.

Remark 4.2

In the case that X and Y are finite dimensional, F is continuously differentiable and $\varOmega =X$, (MFCQ) and (RCQ) are written as follows:

$$\begin{aligned} \begin{array}{l@{\quad }l} \mathbf{MFCQ:}&{} \left. \begin{array}{l} y^*\in N(F(\bar{x});\varLambda ) \\ 0=\nabla F(\bar{x})^Ty^*\\ \end{array} \right\} \Longrightarrow y^*=0. \end{array} \end{aligned}$$

(20)

$$\begin{aligned} \begin{array}{l@{\quad }l} \mathbf{RCQ:}&\exists c>0:\quad \forall y^*\in N(F(\bar{x});\varLambda ):\quad c\Vert y^*\Vert \le \Vert \nabla F(\bar{x})^Ty^*\Vert . \end{array} \end{aligned}$$

(21)

Note that condition (20) is similar to the MFCQ stated in [22] for a general mathematical program. If $\varLambda = \mathbb {R}^m_-$, this condition reduces to the following classical MFCQ,

$$\begin{aligned} \left. \begin{array}{l} y^*\in \mathbb {R}^m_+,\\ 0= F(\bar{x})^Ty^*,\\ 0=\nabla F(\bar{x})^Ty^*,\\ \end{array} \right\} \Longrightarrow y^*=0, \end{aligned}$$

which by Theorem 4.5, is equivalent to the following condition:

$$\begin{aligned} \exists c>0:~~~ \hbox { for all }y^*\in \mathbb {R}^m_+\hbox { with }0= F(\bar{x})^Ty^*:~~~c\Vert y^*\Vert \le \Vert \sum _{i=1}^my^*_i\nabla F_i(\bar{x})\Vert . \end{aligned}$$

Finally in this section, we present several examples illustrating our new constraint qualifications and the relationships between them. By the results of Theorems 4.4 and 4.5, under the SNC property of $\varOmega$ and $\varLambda$ at $\bar{x}$ and $F(\bar{x})$, we can obtain the following diagram of implications:

$$\begin{aligned} {\mathrm {BLCQ}}\Longleftrightarrow {\mathrm {RCQ}}\Longrightarrow {\mathrm {MFCQ}}\Longrightarrow {\mathrm {sRCQ1}}. \end{aligned}$$

Our first example shows that the above right implication does not hold in the opposite direction. This example also indicates that sRCQ2 generally does not imply RCQ.

Example 4.3

Consider the following nonlinear system;

$$\begin{aligned}\begin{array}{l} F(x_1,x_2):=|x_1|\le 0 \\ (x_1,x_2)\in \mathbb {R}^2. \end{array} \end{aligned}$$

We show that (sRCQ1) holds at (0, 0), and at the same time, (RCQ) is not fulfilled at this point. Since $\partial F(0,0)=[-1,1]\times \{0\}$, it is easy to see that for all $\lambda >0$, $(0,0)\in \lambda \partial F(0,0)$, and thus, (RCQ) can not hold at (0, 0). On the other hand for each $(x_1,x_2)\in \mathbb {R}^2$ with $x_1\ne 0$, one has

$$\begin{aligned} \widehat{\partial }F(0,0)=\left\{ \begin{array}{ll} \{(-1,0)\} &{}\quad if\,x_1<0, \\ \{(1,0)\} &{}\quad if\,x_1>0 . \end{array} \right. \end{aligned}$$

Thus if $(x'_1,x'_2)\in \widehat{\partial }(\lambda F)(x_1,x_2)$, then $|\lambda |=\Vert (x'_1,x'_2)\Vert$ which shows that (sRCQ1) holds at (0, 0) with $c=1$. We can show also that (sRCQ2) does not hold at this point. For all $c,\delta >0$, if $\varepsilon :=\frac{c\delta }{2\sqrt{1+c^2}}$ and $x:=(\varepsilon ,\frac{\varepsilon }{c})$, then $\Vert x\Vert <\delta$ and

$$\begin{aligned} F^+(x)=\varepsilon <\varepsilon \sqrt{1+c^2}=c\Vert x\Vert . \end{aligned}$$

The following three examples show, on the whole, that there is not any direct relation between sRCQ2 and RCQ or sRCQ1.

Example 4.4

Consider the following nonlinear system:

$$\begin{aligned}\begin{array}{l} F_1(x_1,x_2):=|x_1|\le 0 \\ F_2(x_1,x_2):=\sin (\Vert (x_1,x_2)\Vert )\le 0 \\ (x_1,x_2)\in \mathbb {R}^2. \end{array} \end{aligned}$$

For sufficiently small positive real numbers $\varepsilon$ it can be proved that $\sin \varepsilon \ge \frac{1}{2}\varepsilon$. Thus for all $(x_1,x_2)$ in a suitable neighborhood of the null vector we get:

$$\begin{aligned} 0\le \frac{1}{2}\Vert (x_1,x_2)\Vert \le \sin (\Vert (x_1,x_2)\Vert )=F_2^+(x_1,x_2). \end{aligned}$$

Thus it is easy to see that (sRCQ2) is satisfied at (0, 0) with $c=\frac{1}{2}$. Now let us show that (RCQ) does not hold for this system at (0, 0). An easy calculation gives us

$$\begin{aligned} \partial F_1(0,0)=[-1,1]\times \{0\}\hbox { and }\partial F_2(0,0)={\mathbb {B}}((0,0);1). \end{aligned}$$

The above especially implies that for all $(\lambda _1,\lambda _2)\in \mathbb {R}^2_+$, $(0,0)\in \lambda _1\partial F_1(0,0)+\lambda _2\partial F_2(0,0)$, which violates (RCQ). (sRCQ1) is not also satisfied at this point since, for sufficiently small $\delta >0$ and for all $\lambda >0$, $x=(0,\delta )$ is an infeasible point and we have

$$\begin{aligned} (0,\cos \delta )\in \widehat{\partial }(\lambda F_1)(x)+\widehat{\partial }F_2(x). \end{aligned}$$

Fixing $\delta$ and taking limit as $\lambda \longrightarrow \infty$, we deduce that (sRCQ1) can not hold at (0, 0).

Example 4.5

Consider the following nonlinear system:

$$\begin{aligned}\begin{array}{l} F_1(x_1,x_2):=x_1\le 0 \\ F_2(x_1,x_2):=\sin (x_2)-\frac{1}{2}|x_2|\le 0 \\ (x_1,x_2)\in \mathbb {R}^2. \end{array} \end{aligned}$$

We show that for the above system (RCQ) holds at (0, 0) with $c=\frac{1}{2}$. Observing that

$$\begin{aligned} \partial F_1(0,0)=(1,0)\hbox { and }\partial F_2(0,0)=\Big \{\big (0,\frac{1}{2}\big ),\big (0,\frac{3}{2}\big )\Big \}, \end{aligned}$$

if we take

$$\begin{aligned} (x_1,x_2)\in \lambda _1\partial F_1(0,0)+\lambda _2\partial F_2(0,0), \end{aligned}$$

then one has $x_1=\lambda _1$ and $x_2\in \{\frac{\lambda _2}{2},\frac{3\lambda _2}{2}\}$, which straightly implies that

$$\begin{aligned} \frac{1}{2}\Vert (\lambda _1,\lambda _2)\Vert \le \Vert (x_1,x_2)\Vert . \end{aligned}$$

We can prove that (sRCQ1) is also satisfied at (0, 0) with $c=\frac{1}{4}$. It is sufficient to show that for each infeasible point $(x_1,x_2)$ near (0, 0) with $x_2\ne 0$ the following condition holds:

$$\begin{aligned} (x'_1,x'_2)\in \widehat{\partial }(\lambda _1 F_1)(x_1,x_2)+\widehat{\partial }(\lambda _2 F_2)(x_1,x_2)\Longrightarrow \frac{1}{4}\Vert (\lambda _1,\lambda _2)\Vert \le \Vert (x'_1,x'_2)\Vert . \end{aligned}$$

To do so, observe that the left side of the above implies that

$$\begin{aligned}(x'_1,x'_2)=\left\{ \begin{array}{ll} (\lambda _1,\lambda _2(\cos (x_2)-\frac{1}{2})&{}\quad if\,x_2>0 \\ (\lambda _1,\lambda _2(\cos (x_2)+\frac{1}{2})&{}\quad if\,x_2<0 , \end{array} \right. \end{aligned}$$

thus for sufficiently small $|x_2|$, $\frac{1}{4}\Vert (\lambda _1,\lambda _2)\Vert \le \Vert (x'_1,x'_2)\Vert$. We can show also that (sRCQ2) does not hold at (0, 0). For all $c,\delta >0$, if $\varepsilon :=\frac{c\delta }{2\sqrt{1+c^2}}$ and $x:=(\varepsilon ,-\frac{\varepsilon }{c})$, then $\Vert x\Vert <\delta$ and

$$\begin{aligned} F_1^+(x)+F_2^+(x)=\varepsilon <\varepsilon \sqrt{1+c^2}=c\Vert x\Vert . \end{aligned}$$

Example 4.6

consider the following nonlinear system;

$$\begin{aligned} \begin{array}{l} F(x_1,x_2):=x_1\le 0 \\ (x_1,x_2)\in \mathbb {R}^2. \end{array} \end{aligned}$$

Obviously (RCQ) and (sRCQ1) hold for this system at (0, 0) with $c=1$. Now let us show that (sRCQ2) is not satisfied at (0, 0). For any given $\delta ,c>0$, if we choose $\alpha$ such that $\frac{1}{\sqrt{1+\alpha ^2}}<c$, and take $\varepsilon :=\frac{\delta }{2\sqrt{1+\alpha ^2}}$ and $x:=(\varepsilon ,\alpha \varepsilon )$, then $\Vert x\Vert \le \delta$ and $F^+(x)=\varepsilon <c\Vert x\Vert =c\sqrt{1+\alpha ^2}\varepsilon$.

5 Application to nonsmooth mathematical programs with equilibrium constraints

In this section we consider a special class of optimization problems known as Mathematical Programs with Equilibrium Constraints (MPECs) (see [23–25]). A specific feature of these problems is the presence of “equilibrium constraints” of the type $y \in F(x)$, where F(x) often represents the solution map to a “lower-level” problem of parametric optimization. MPECs naturally appear in various aspects of hierarchical optimization and equilibrium theory as well as in many practical applications, especially those related to mechanical and economic modelling. Note that most MPECs, are basically different from standard nonlinear problems with equality and inequality constraints. For instance the Mangasarian-Fromovitz constraint qualification is not satisfied for these problems.

The goal in this section is applying the results obtained in the previous sections to derive bounded necessary optimality conditions for local solutions to the following case of MPECs:

$$\begin{aligned} \begin{array}{ccc} \text {min}\quad f(z) &{} &{} \\ \text {s.t}\quad &{}g(z)\le 0, &{}h(z)=0, \\ &{}G(z)\ge 0 , &{} H(z)\ge 0,\\ &{} &{} G(z)^{T}H(z)=0,\\ &{}z\in \varOmega , \end{array} \end{aligned}$$

(22)

where $f:X\longrightarrow {\mathbb {R}}$, $g:X\longrightarrow {\mathbb {R}}^m$, $h:X\longrightarrow {\mathbb {R}}^p$, $G:X\longrightarrow {\mathbb {R}}^l$, and $H:X\longrightarrow {\mathbb {R}}^l$ are locally Lipschitz functions defined on the Asplund space X and $\varOmega \subseteq X$ is a closed set. We can write the program (22) in the following general form:

$$\begin{aligned} \begin{array}{rl} \text {minimize}&{}f(z)\\ \text {subject to}&{} F(z)\in \varLambda ,\\ &{}z\in \varOmega ,\end{array} \end{aligned}$$

(23)

where for some $n\in {\mathbb {N}}$, $\varLambda \subseteq {\mathbb {R}}^n$ is a nonempty closed (possibly nonconvex) set and $f:X\longrightarrow {\mathbb {R}}$ and $F:X\longrightarrow {\mathbb {R}}^n$ are locally Lipschitz functions around $\bar{z}\in F^{-1}(\varLambda )\cap \varOmega$ defined on Asplund space X. To show this, consider a local minimizer $\bar{z}$ of (22). Then from complementarity term in (22), it is clear that either $G_i(\bar{z})$, or $H_i(\bar{z})$, or both must be zero. To distinguish among these cases, we divide the indices of G and H into three sets:

$$\begin{aligned} \begin{array}{c} \alpha :=\alpha (\bar{z}):=\{i:G_{i}(\bar{z})=0,H_{i}(\bar{z})>0\}, \\ \beta :=\beta (\bar{z}):=\{i:G_{i}(\bar{z})=0,H_{i}(\bar{z})=0\}, \\ \gamma :=\gamma (\bar{z}):=\{i:G_{i}(\bar{z})>0,H_{i}(\bar{z})=0\}.\\ \end{array} \end{aligned}$$

(24)

Also, suppose that

$$\begin{aligned} {\mathscr {I}}_g:={\mathscr {I}}_g(\bar{z}):=\{i=1,2, \ldots , m|g_i(\bar{z})=0\}, \end{aligned}$$

(25)

is the index set of active components of g at $\bar{z}$. Next we define the function F in (23) utilizing these sets:

$$\begin{aligned} F(z):=(g_{{\mathscr {I}}_g}(z),h(z),G_{\alpha }(z),G_{\beta }(z),H_{\beta }(z),H_{\gamma }(z)). \end{aligned}$$

(26)

Finally, we define the closed $\varLambda$ as follows:

$$\begin{aligned} \varLambda :={\mathbb {R}}^{|{\mathscr {I}}_g|}\times 0_p\times 0_{|\alpha |}\times {\mathscr {C}} \times 0_{|\gamma |}, \end{aligned}$$

(27)

where

$$\begin{aligned} {\mathscr {C}}:=\{(a,b)\in {\mathbb {R}}^{|\beta |}\times {\mathbb {R}}^{|\beta |}|~a\ge 0,b\ge 0,a^Tb=0\}. \end{aligned}$$

Remark 5.1

The definition of the general form (23) depends on the solution $\bar{z}$ of the program (22). Therefore, local equivalence refers to the fact that the feasible regions of the programs (22) and (23) are equal for a whole neighborhood of the local minimizer $\bar{z}$, that was used to define (23).

We proceed with stating some stationary and constraint qualification conditions for MPEC (22) that are suitable for our aim.

Definition 5.1

We say that

• 1. $\bar{z}$ is a bounded M-stationary point iff there exists a positive scalar $k_0$ such that for all $\nu \ge k_0$, one can find $z^*\in N(\bar{z};\varOmega )$ together with the vector $\lambda =(\lambda ^g,\lambda ^h,\lambda ^G,\lambda ^H)\in {\mathbb {R}}^m\times {\mathbb {R}}^p\times {\mathbb {R}}^l\times {\mathbb {R}}^l$ such that $\Vert (z^*,\lambda )\Vert \le \nu$ and

  $$\begin{aligned}&-z^*\in \partial f(\bar{z})+\sum _{i=1}^{m}\lambda _i^g\partial g(\bar{z})+\sum _{i=1}^{p}\lambda _i^h\partial h_i(\bar{z})\nonumber \\&\quad -\sum _{i=1}^{l}\left[ \lambda _i^G\partial G_i(\bar{z})+\lambda _i^H\partial H_i(\bar{z})\right] ,\nonumber \\&\qquad \lambda ^g\ge 0,g(\bar{z})^T\lambda ^g=0, \lambda _{\gamma }^G=0,\lambda _{\alpha }^H=0,\nonumber \\&\qquad (\lambda _i^G>0\wedge \lambda _i^H>0)\vee \lambda _i^G\lambda _i^H=0,\forall i\in \beta . \end{aligned}$$

  (28)

• 2. the regularity constraint qualification (RCQ) holds at $\bar{z}$ iff, there is a positive real number c such that the following implication holds:

  $$\begin{aligned} \left. \begin{array}{l} z^*\in N(\bar{z};\varOmega )\\ x^*-z^*\in \sum _{i=1}^{m}\lambda _i^g\partial g(\bar{z})+\sum _{i=1}^{p}\lambda _i^h\partial h_i(\bar{z})\\ ~~~~~~~~~~~~~~-\sum _{i=1}^{l}[\lambda _i^G\partial G_i(\bar{z})+\lambda _i^H\partial H_i(\bar{z})]\\ \lambda ^g\ge 0, g(\bar{z})^T\lambda ^g=0, \lambda _{\gamma }^G=0,\lambda _{\alpha }^H=0,\\ (\lambda _i^G>0\wedge \lambda _i^H>0)\vee \lambda _i^G\lambda _i^H=0,\forall i\in \beta . \end{array} \right\} \Longrightarrow c\Vert (z^*,\lambda _g,\lambda _h,\lambda _G,\lambda _H)\Vert \le \Vert x^*\Vert . \end{aligned}$$

  (29)

• 3. the semi-regularity constraint qualification (sRCQ) holds at $\bar{z}$ iff, there are positive scalars $\delta ,c$ such that for each infeasible point $z\in {\mathbb {B}}(\bar{z};\delta )$ and for any $x\in {\mathbb {B}}(0;\delta )\cap (\varOmega -z)$ the following implication holds:

  $$\begin{aligned} \left. \begin{array}{l} z^*\in \widehat{N}(z+x;\varOmega )\\ x^*-z^*\in \widehat{\partial }\left( \sum _{i=1}^{m}\lambda _i^g g+\sum _{i=1}^{p}\lambda _i^h h_i\right. \\ \left. ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~-\sum _{i=1}^{l}[\lambda _i^G G_i+\lambda _i^H H_i]\right) (z),\\ \lambda ^g\ge 0, g(z)^T\lambda ^g=0, \lambda _{\gamma }^G=0,\lambda _{\alpha }^H=0,\\ (\lambda _i^G>0\wedge \lambda _i^H>0)\vee \lambda _i^G\lambda _i^H=0,\forall i\in \beta ,\\ \lambda :=(\lambda _g,\lambda _h,\lambda _G,\lambda _H). \end{array} \right\} \Longrightarrow c\Vert (z^*,\lambda )\Vert \le \Vert x^*\Vert . \end{aligned}$$

  (30)

Now we are ready to establish bounded necessary optimality conditions for the program (22).

Theorem 5.1

Let $\bar{z}$ be a local optimal point for MPEC (22) where X is an Asplund space and all the functions are locally Lipschitz around $\bar{z}$. Also assume that one of the following conditions holds:

• 1. $\varOmega$ is SNC and (RCQ) is satisfied at $\bar{z}$.

• 2. (sRCQ) is satisfied at $\bar{z}$.

Then $\bar{z}$ is a bounded M-stationary point.

Proof

If we define the function F and the set $\varLambda$ as in (26) and (27), then it is easy to see that $\bar{z}$ is an optimal solution of the problem in (23). On the other hand, a direct calculation shows that the constraint qualification (RCQ) or (sRCQ) for $\bar{z}$ as a feasible point of MPEC (22) implies the condition (RCQ) or (sRCQ1) for this point as a feasible point of (23). Thus the result follows from parts 1 and 2. of Theorem 4.3. $\square$

Remark 5.2

In [26], necessary optimality conditions was derived for local solutions to MPEC (22). In this paper analogous to [26], after reformulating (22) in general form (1), the new constraint qualifications are defined based on the stability properties of the corresponding multifunction M in (12). The major advantage of the present approach over the previous works is to provide exact upper bounds for the Lagrange multiplier vectors. It is unprecedented in an MPEC context to the best of our knowledge.

Example 5.1

Consider the following constraint system:

$$\begin{aligned} G(x):=x_1\ge 0,~~~H(x):=\max \{x_1,x_2\}\ge 0,~~~G(x)H(x)=0,~~~x=(x_i)_{i=1}^{\infty }\in l^2. \end{aligned}$$

Obviously $\bar{z}:=0$ is feasible for the above system. Let us show that (RCQ) holds at $\bar{z}$. An easy computation shows that $\partial G(0)=\{e_1\}$ and $\partial H(0)={\mathrm {conv}}\,\{e_1,e_2\}$. Thus if $x^*\in -\lambda ^G\partial G(0)-\lambda ^H\partial H(0)$, then for some $\alpha \in [0,1]$,

$$\begin{aligned} \Vert x^*\Vert ^2=|-\lambda ^G-\alpha \lambda ^H|^2+|(1-\alpha )\lambda ^H|^2. \end{aligned}$$

Clearly if $\lambda ^H=0$, then $\Vert x^*\Vert =\Vert (\lambda ^G,\lambda ^H)\Vert$, and if $\lambda ^G=0$, then

$$\begin{aligned} \Vert x^*\Vert ^2=|\lambda ^H|^2[\alpha ^2+(1-\alpha )^2]>\frac{1}{4}|\lambda ^H|^2=\frac{1}{4}\Vert (\lambda ^G,\lambda ^H)\Vert ^2. \end{aligned}$$

Also if $\lambda ^G>0$ and $\lambda ^H>0$, then

$$\begin{aligned} \Vert x^*\Vert ^2=|\lambda ^G|^2+2\alpha \lambda ^G\lambda ^H+|\lambda ^H|^2[\alpha ^2+(1-\alpha )^2]>|\lambda ^G|^2+\frac{1}{4}|\lambda ^H|^2>\frac{1}{4}\Vert (\lambda ^G,\lambda ^H)\Vert ^2. \end{aligned}$$

Hence (RCQ) holds at $\bar{z}$ with constant $\frac{1}{2}$.

6 Conclusion

The paper concerns constraint qualifications that insure the existence of Lagrangian vectors with a norm not greater than a specified positive number. Three new constraint qualifications are suggested that each of them follows a degree of boundedness for multiplier vectors. Each constraint qualification provides us an upper bound for the Lagrange multipliers. The several examples indicate that the upper bound is easily computable using each of our constraint qualifications. An interesting application to mathematical programs with equilibrium constraints is presented.

It is notable that we state the constraint qualifications and necessary optimality conditions within the framework of the Mordukhovich calculus. This certainly allows us to deal with a much wider range of problems. Several examples are given to illustrate the application of our results for nonsmooth and nonconvex mathematical problems. From the numerical viewpoint, these examples specially show that our approach is practically calculable and does not cause any difficulty. Consequently, it can be hoped that our results may be useful in providing new efficient tools and methods for various types of nonsmooth constrained optimization problems.