Global Threshold Dynamics of an Infection Age-Space Structured HIV Infection Model with Neumann Boundary Condition

Abstract

This paper aims to the investigation of the global threshold dynamics of an infection age-space structured HIV infection model. The model is formulated in a bounded domain involving two infection routes (virus-to-cell and cell-to-cell) and Neumann boundary conditions. We first transform the original model to a hybrid system containing two partial differential equations and a Volterra integral equation. By appealing to the theory of fixed point problem together with Picard sequences, the well-posedness of the model is shown by verifying that the solution exists globally and the solution is ultimately bounded. Under the Neumann boundary condition, we establish the explicit expression of the basic reproduction number. By analyzing the distribution of characteristic roots of the associated characteristic equation in terms of the basic reproduction number, we achieve the local asymptotic stability of the steady states. The global asymptotic stability of the steady states is established by the technique of Lyapunov functionals, respectively. Numerical simulations are performed to validate our theoretical results.

1 Introduction

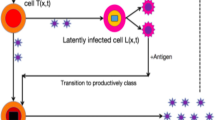
Inspired by the classical works of Ho et al. [17] and Perelson et al. [30], the dynamical properties of differential equations modelling the with-in host viral dynamics have obtained much attention (see, e.g., [6, 13, 19, 23, 24, 33, 39, 45, 49]). It has been widely recognized that some typical features of viral dynamics, such as, time delays, infection age structure, and spatial heterogeneity should be taken into account in studying with-in host dynamics, which may give us new insights into the interactions among uninfected target T cells, infected T cells, and free virus particles. Let T(t), u(t, a) and V(t) be the concentrations of uninfected target T cells, infected T cells of infection age a and the free virus particles at time t, respectively. Here the infection age is defined by the time since infection began and the infection-age structure is used to demonstrate the mechanisms that the death rate and virus production rate of infected T cells should be infection-age-dependent, denoted by $\theta (a)$ and p(a), respectively. The following initial-boundary-value problem was studied in Nelson et al. [28],

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\text {d}T(t)}{\text {d}t}=h -d T(t)-\beta _1T(t)V(t), \\ \displaystyle \left( \frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right) u(t,a)=-\theta (a)u(t,a),\\ \displaystyle \frac{\text {d}V(t)}{\text {d}t}=\int _0^\infty p(a)u(t,a)\text {d}a-cV(t),\\ \displaystyle u(0,t)=\beta _1T(t)V(t),\\ \displaystyle T(0) = T_0, u(0, a) = u_0(a),\ \text{ and }\ V(0) = V_0, \end{array}\right. \end{aligned}$$

(1.1)

where h and d are the constant recruitment rate and the natural death rate of uninfected cells; $\beta _1$ is the infection rate; c is the clearance rate of virions. In [28], the local dynamics of the model was achieved for some special cases and the time to reach the peak viral level are illustrated by numerical simulations. To evaluate the roles of a distinct combination of therapies, Rong et al. [13, 33] took the model (1.1) as a basis and adapted it incorporating three different classes of drugs. The global dynamics of model (1.1) was completely solved in Huang et al. [19] by the technique of Lyapunov functionals. Model (1.1) also be used as a basic framework to investigate the dynamics of hepatitis B or C virus in Qesmi et al. [32].

As pointed in [3, 7, 31, 48], the variant infectivity in different ages may arise from the heterogeneous structure of the infected T cells. In recent years, more and more works have been devoted to investigating the effects of cell-to-cell infection routes in lymphoid tissues (via formation of virological synapses) on viral dynamics [11, 18, 37, 38]. The cell-to-cell infection routes have been recognized as important factors in virus spread (see, e.g., [6, 23, 39, 45, 49]). Lai and Zou [23] formulated the distributed delay differential equations, and investigated the global stability of equilibrium of the model. Wang et al. [40] further extended the model (1.1) to the following model:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\text {d} T(t)}{\text {d} t}=h-dT(t)-\beta _1T(t)V(t,x)-\beta _2T(t)\int _0^{+\infty }\ q(a)u(t,a)\mathrm{d}a,\\ \displaystyle \left( \frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right) u(t,a)=-\theta (a)u(t,a),\\ \displaystyle \frac{\text {d} V(t)}{\text {d} t}= \int _0^{+\infty }p(a)u(t,a)\mathrm{d}a -c V(t),\\ \displaystyle u(t,0)=\beta _1T(t)V(t)+\beta _2T(t)\int _0^{+\infty }q(a)u(t,a)\mathrm{d}a, \end{array}\right. \end{aligned}$$

(1.2)

where $\beta _2$ and q(a) measure the infection rate and the infectivity between uninfected target T cells and infected T cells, respectively. The global threshold dynamics of (1.2) in terms of the basic reproduction number was achieved by solid analysis. Subsequently, by incorporating the logistic growth for target T cells, the oscillations via local Hopf bifurcation was studied in [45, 46, 49]. Shu et al. [39] gave the complete analysis on HIV infection model involving nonlinear target-cell dynamics and nonlinear incidences, and studied global dynamics in the aspect of global threshold dynamics and oscillations via global Hopf bifurcation. Cheng et al. [6] proposed an age-structured HIV infection model in the form of a two-compartment model and analyzed the global attractivity of the equilibria by the perturbation theory. Zhang and Liu [50] investigated the Hopf bifurcation of a delayed infection-age structured HIV infection model by appealing to the theory of integrated semigroup with the non-dense domain. Wu and Zhao [43] studied the effects of drug resistance by formulating an infection-age HIV model involving a drug-sensitive strain and a drug-sensitive strain, and revealed that the efficacy of antiretroviral drug treatments becomes weaker arising from the presence of cell-to-cell route.

However, ordinary differential equations modeling of viral infection assumed that the intracellular reaction occurs simultaneously. As argued in [12], the HIV spread and replication in lymphoid tissues are affected by the tissue architecture and composition. The results in [25] revealed that the dynamics of HIV in vivo may mainly be affected by different physiological environments, especially, in the early stage of infection.

Due to the complexity of the physiological environment and the tissue architectures of lymphoid tissues, the spatial aspects of the tissues should be taken into account on viral dynamics. Very recently, Ren et al. [34] considered a reaction-diffusion within-host HIV model in a heterogeneous environment. Let t and x be the time and location variables, respectively. We denote by T(t, x), $T^*(t, x)$, and V(t, x) the densities of uninfected target T cells, infected T cells, and the free virus particles, associated with diffusion rates $D_1(x)$, $D_2(x)$, and $D_3(x)$, respectively. The model formulated in [34] is the following form,

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial T}{\partial t}-\nabla \cdot [D_1(x)\nabla T]=\ h(x) -d(x)T-\beta _1(x)TV-\beta _2(x)TT^*,\ x\in \Omega ,\ t>0,\\ \displaystyle \frac{\partial T^*}{\partial t}- \nabla \cdot [D_2(x)\nabla T^*]=\ \beta _1(x)TV+\beta _2(x)TT^*-r(x)T^*,\ x\in \Omega ,\ t>0,\\ \displaystyle \frac{\partial V}{\partial t}-\nabla \cdot [D_3(x)\nabla V]=\ N(x)T^*-c(x)V,\ x\in \Omega ,\ t>0,\\ \displaystyle \frac{\partial T}{\partial \nu }=\frac{\partial T^*}{\partial \nu }=\frac{\partial V}{\partial \nu }=0,\quad x\in \partial \Omega ,\ t>0, \end{array}\right. \end{aligned}$$

(1.3)

where $\Omega$ is the spatial domain. $\nu$ is the outward normal vector to $\partial \Omega$. The space-dependent parameters h(x), d(x), $\beta _i(x)\ (i=1,2)$, r(x), N(x) and c(x) (the biological meaning can be found in [34]) are strictly positive, and uniformly bounded functions on $\overline{\Omega }$. In the bounded domain, the authors obtained the global threshold type result in terms of the basic reproduction number, while in the unbounded domain, the existence of traveling wave solutions and the minimum wave speed was established. Furthermore, the authors also found that the minimum wave speed and the asymptotic spreading speed are affected by the diffusion of cells and cell-to-cell infection route.

Recently, the infection age-space structured models have attracted wide attentions, which are spent on understanding the effects of the time since infection and the spatial heterogeneity on the transmission of infectious diseases. In 2009, Ducrot and Magal [8] studied the traveling wave problem for a diffusive SIR model with infection age. As a continuous study of [8], Ducrot and Magal [9] further considered the external supplies in the age-space structured SIR model, and they found that the model admits a traveling wave connecting the two different steady states. Until recently, Chekroun and Kuniya [4] proposed an infection age-space structured SIR model on a bounded domain. After reformulating the model into a hybrid system of one diffusive equation and one Volterra integral equation, the threshold-type results for the disease extinction and persistence in one-dimensional domain were studied. Later on, Yang et al. [47] made an attempt to extend the methods and ideas used in [4], and proposed a spatial spreading of brucellosis model in a continuous bounded domain. Some basic mathematical arguments, including the existence, uniqueness of the solution and threshold dynamics were successfully addressed.

The stability analysis of infection-free and infection steady state has witnessed an important and fundamental approach for understanding viral dynamics. We also mention that the global asymptotic stability of the constant equilibrium of (1.3) was achieved in the spatially homogeneous environment without considering the infection-age structure, and the infection-age structured model (1.2) was investigated with two infection routes but without considering the spatial aspects of the lymphoid tissues. Thus, we adopt the features of (1.3) and (1.2), and continue to consider the global threshold-type results of the model involving the following aspects:

• In the early stage of infection, uninfected target T cells, infected T cells, and the free virus particles disperse at the target tissues (bounded domain) $\Omega \subset \mathbb {R}^n$ according to the Fickian diffusion or Brownian motion associated with the Neumann boundary condition and constant diffusion coefficients $d_1>0$, $d_2>0$ and $d_3>0$, respectively.

• With infection age a, we use u(t, a, x) to denote the concentration of infected T cells. Based on model (1.2), the dynamics of infected cells is governed by

  $$\begin{aligned} \left( \frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right) u(t,a,x)=d_2\Delta u(t,a,x)-\theta (a)u(t,a,x), \end{aligned}$$

  (1.4)

  where $\theta (a)\in L_+^\infty (0,+\infty )$ is the natural mortality of infected cells. Further, we assume that $\theta (a)>\theta _{\min }$ for some positive number $\theta _{\min }$. The free virus particles are produced at the rate $\int _0^{+\infty }p(a)u(t,a,x)\mathrm{d}a$, where $p(a)\in L_+^\infty (0,+\infty )$ is the age-specific per capita viral production rate of infected cells. In fact, the functional form of the viral production kernel, p(a), is unknown and remains to be determined experimentally. Here we give an example that capture features of the biology:

  $$\begin{aligned} p(a) = \left\{ \begin{array}{ll} \displaystyle P_{\text {max}}(1-e^{-\beta (a-a_1)}),\ a>a_1,\\ \displaystyle 0,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text {else}, \end{array}\right. \end{aligned}$$

  where $P_{\text {max}}$ is the maximum production rate, because cellular resources will ultimately limit how rapidly virions can be produced. $\beta$ controls how rapidly the saturation level is reached. $a_1$ is the delay in viral production. This kernel can mimic either a very rapid increase to maximal production or a slow increase to maximal production depending on the value of $\beta$. We refer the readers to [28] for more details.

• We measure the virus interference during infection as saturation effect. Thus, uninfected target T cells are contacted by free virus particles at the rate $\beta _1T\frac{V}{1+\alpha V}$, where $\alpha$ is a half-saturation constant. As to the cell-to-cell transmission mechanism, we use the bilinear mechanism

  $$\begin{aligned} \beta _2T\int _0^{+\infty }\ q(a)u(t,a,x)\mathrm{d}a \end{aligned}$$

  to account for the sustaining interactions between uninfected target T cells and infected T cells through the formation of the virological synapses, as it accounts for about 60% of viral infection [22]. Here, $q(a)\in L_+^\infty (0,+\infty )$. Hence, we adopt

  $$\begin{aligned} u(t,0,x)=\beta _1T\frac{V}{1+\alpha V}+\beta _2T\int _0^{+\infty }q(a)u(t,a,x)\mathrm{d}a. \end{aligned}$$

  (1.5)

• To make things not too complicated (as model involving the two infection routes and spatial diffusion have already made the problem very challenging), we adopt the recruitment rate h, natural death rates of cells (d and b) and the clearance rate of virus particles c as constant. Biologically, there exist $0<a_1<a_2<+\infty$ such that $q(a)>0$ and $p(a)>0$, for all $a\in (a_1,a_2)$. Moreover, we give the following hypothesis: (H) Assume that $\lim _{a\rightarrow \infty }u(t,a,x) = 0$, which means that all the biological individuals cannot survive all the time.

Therefore, we arrive at the following reaction-diffusion and infection-age structured HIV infection model,

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial T}{\partial t}=d_1 \Delta T+h-dT-u(t,0,x),\\ \displaystyle \left( \frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right) u(t,a,x)=d_2\Delta u(t,a,x)-\theta (a)u(t,a,x),\\ \displaystyle u(t,0,x)=\beta _1T\frac{V}{1+\alpha V}+\beta _2T\int _0^{+\infty }q(a)u(t,a,x)\mathrm{d}a,\\ \displaystyle \frac{\partial V}{\partial t}=d_3 \Delta V+ \int _0^{+\infty }p(a)u(t,a,x)\mathrm{d}a -c V,\\ \displaystyle T(0,x)=\phi _1(x),\ u(0,a,x)=\phi _2(a,x),\ V(0,x)=\phi _3(x),\ a\ge 0,\ x\in \overline{\Omega }, \end{array}\right. \end{aligned}$$

(1.6)

with the following boundary condition

$$\begin{aligned} \frac{\partial T}{\partial \nu }=\frac{\partial u(t,a,x)}{\partial \nu }=\frac{\partial V}{\partial \nu }=0,\ x\in \partial \Omega ,\ t>0. \end{aligned}$$

(1.7)

For mathematical considerations, denote by $\mathbb {X}:=C(\overline{\Omega },\mathbb {R})$ the continuous functions space equipped with the norm $\left| \cdot \right| _\mathbb {X}$. Denote by $\mathbb {Y}:=L^1(\mathbb {R}_+,\mathbb {X})$ the integrable functions space equipped with the norm $\left| \varphi \right| _\mathbb {Y}:=\int _0^{+\infty }\left| \varphi (a)\right| _\mathbb {X}\mathrm{d}a,~\varphi \in \mathbb {Y}$. Let $\mathbb {X}^+$ and $\mathbb {Y}^+$ be the positive cones of $\mathbb {X}$ and $\mathbb {Y}$, respectively.

Suppose that $T_i(t)\ (i=1,2,3):\ \mathbb {X} \rightarrow \mathbb {X},\ t \ge 0$, are the strongly continuous semigroups corresponding to the operators, $d_i\Delta \ (i=1,2,3)$ with Neumann boundary condition. It is well-known that

$$\begin{aligned} (T_i(t)\phi )(x) = \int _\Omega \Gamma _i(t, x, y)\phi (y)\mathrm{d}y,\ t \ge 0,\ \phi \in \mathbb {X}, \end{aligned}$$

where $\Gamma _i(t, x, y)\ (i = 1,2,3)$ is the Green function of $d_i\Delta \ (i=1,2,3)$ subject to the Neumann boundary condition. By the arguments as those in [36, Corollary 7.2.3] and [29, Theorem 1.5], $T_i(t)\ (i=1,2,3):\ \mathbb {X}\rightarrow \mathbb {X},\ t \ge 0$, is strongly positive and compact. Further, $T(t) = (T_1(t),T_2(t),T_3(t)):\ \mathbb {X}^3 \rightarrow \mathbb {X}^3,\ t \ge 0$, forms a strongly continuous semigroup.

System (1.6) can be reformulated by the method of characteristics (see, e.g., [14, 15, 44]). In the following, we give the details for this issue. Define $U_c(x,t) = u(t,t+c,x)$ with $c\in \mathbb {R}$, one has that

$$\begin{aligned} \frac{\partial }{\partial t}U_c(x,t) = d_2 \Delta U_c(x,t) - \delta (t+c) U_c(x,t),\ \ \text {for}\ \ t\ge t_c, \end{aligned}$$

with Neumann boundary condition

$$\begin{aligned} \frac{\partial U_c}{\partial \nu }=0,\ x\in \partial \Omega ,\ t\ge t_c, \end{aligned}$$

where $t_c = \max \{0,c\}$. It follows from [15] that

$$\begin{aligned} U_c(x,t) = e^{\int _{t_c}^t \delta (\tau +c)\text {d} \tau }\int _\Omega \Gamma _2(t-t_c,x,y)U_c(t_c,y)\text {d}y. \end{aligned}$$

If $a>t$, then $t_c=0$. Hence we have

$$\begin{aligned} u(t,a,x) =&\ e^{\int _{t_c}^t \delta (\tau +a-t)\text {d} \tau }\int _\Omega \Gamma _2(t,x,y)U_c(0,y)\text {d}y\\ =&\ e^{\int _{t_c}^t \delta (\tau +a-t)\text {d} \tau }\int _\Omega \Gamma _2(t,x,y)u(c,0,y)\text {d}y\\ =&\ e^{\int _{a-t}^t \delta (\tau )\text {d} \tau }\int _\Omega \Gamma _2(t,x,y)u(a-t,0,y)\text {d}y\\ =&\ \frac{\pi (a)}{\pi (a-t)}\int _\Omega \Gamma _2(t,x,y)\phi _2(a-t, y)\mathrm{d}y, \end{aligned}$$

where $\pi (a)=e^{-\int _0^a\theta (\sigma )\mathrm{d}\sigma }$.

If $t>a$, then $t_c=t-a$. With a similar argument as above, we can obtain that

$$\begin{aligned} u(t,a,x) = \pi (a) \int _\Omega \Gamma _2(a,x,y)u(t-a,0,y)\mathrm{d}y. \end{aligned}$$

Hence, u(t, a, x) can be solved as

$$\begin{aligned} u(t,a,x)= \left\{ \begin{array}{ll} \displaystyle \pi (a) \int _\Omega \Gamma _2(a,x,y)u(t-a,0,y)\mathrm{d}y,&{}\ t> a, \\ \displaystyle \frac{\pi (a)}{\pi (a-t)}\int _\Omega \Gamma _2(t,x,y)\phi _2(a-t, y)\mathrm{d}y,&{}\ t\le a. \end{array}\right. \end{aligned}$$

(1.8)

Note that

$$\begin{aligned} u(0,a,x)=\phi _2(a,x)=\int _\Omega \Gamma _2(0,x,y)\phi _2(a, y)\mathrm{d}y,\ \forall t<a. \end{aligned}$$

(1.9)

Substituting (1.8) into (1.6) gives the following hybrid system containing two reaction-diffusion equations (T and V) and a Volterra integral equation (for simplicity, we denote u(t, 0, x) as u(t, x)),

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial T}{\partial t}=d_1 \Delta T+h-u(t, x)-dT,\\ \displaystyle u(t, x)= \beta _1T\frac{V}{1+\alpha V}+\beta _2T(\mathbf{F} _1+\mathbf{F} _2),\\ \displaystyle \frac{\partial V}{\partial t}=d_3 \Delta V+ \mathbf{F} _3+\mathbf{F} _4 -cV,\\ \displaystyle T(0,x)=\phi _1(x), ~u(0,x)=\beta _1\phi _1(x)\frac{\phi _3(x)}{1+\alpha \phi _3(x)}+\beta _2\phi _1(x)\mathbf{F} _2(0,x),\ V(0,x)=\phi _3(x),\ x\in \overline{\Omega }, \end{array}\right. \end{aligned}$$

(1.10)

where

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \mathbf{F} _1=\int _0^tq(a)\pi (a)\int _\Omega \Gamma _2(a,x,y)u(t-a ,y)\mathrm{d}y\mathrm{d}a,\\ \displaystyle \mathbf{F} _2=\int _t^{+\infty }q(a)\frac{\pi (a)}{\pi (a-t)}\int _\Omega \Gamma _2(t,x,y)\phi _2(a-t, y)\mathrm{d}y\mathrm{d}a,\\ \displaystyle \mathbf{F} _3=\int _0^tp(a)\pi (a)\int _\Omega \Gamma _2(a,x,y)u(t-a ,y)\mathrm{d}y\mathrm{d}a,\\ \displaystyle \mathbf{F} _4=\int _t^{+\infty }p(a)\frac{\pi (a)}{\pi (a-t)}\int _\Omega \Gamma _2(t,x,y)\phi _2(a-t, y)\mathrm{d}y\mathrm{d}a. \end{array}\right. \end{aligned}$$

(1.11)

The main goal of the current paper is to rigorously investigate the global threshold type results of (1.6). In Sect. 2, Theorem 2.2 tell us that (1.10) has a unique nonnegative solution defined on $[0,\infty )\times \overline{\Omega }$, and the solution is ultimately bounded in $\mathbb {X}^+\times \mathbb {Y}^+\times \mathbb {X}^+$. Thus it comes naturally to investigate system (1.10) in a bounded domain. Section 3 is spent on defining the basic reproduction number (BRN). Our result in Lemma 3.1 indicates that the next generation operator (NGO) $\mathcal {L}$ is strictly positive, bounded, and compact, which is proved by the Ascoli-Arzela theorem. Thus one can get the specific expression of BRN $\mathfrak {R}_0$ by appealing to Krein-Rutman theorem, where $\mathfrak {R}_0$ is the only positive eigenvalue of $\mathcal {L}$, corresponding to which, there is a positive eigenvector. Further, once $\mathfrak {R}_0 > 1$, (1.6) has a unique space-independent infection equilibrium $\hat{E}=(\hat{T}, \hat{u}(a), \hat{V})$ (see Lemma 3.2). In Sect. 4, Theorem 4.1 below indicates that $\mathfrak {R}_0$ works perfectly in determining the local dynamics for infection-free steady state $E_0$ and space-independent infection equilibrium $\hat{E}$ by checking the distribution of characteristic root of Eq. (4.5). More specifically, if $\mathfrak {R}_0 < 1$, $E_0$ is locally asymptotically stable (LAS), while $\hat{E}$ is LAS if $\mathfrak {R}_0 > 1$. Section 5 is devoted to the study of the persistence of infection in the system (1.10) for $\mathfrak {R}_0> 1$, where the strong persistence is implied by the weak persistence. In Sect. 6, the global attractivity of $E_0$ and $\hat{E}$ are obtained by the technique of Lyapunov functionals. Lastly, the numerical simulations are performed to reinforce the theoretical findings.

2 Well-Posedness of the Model

This section aims to verify that the solution of (1.10) exists globally. We first prove the following result.

Theorem 2.1

For any $(\phi _1, \phi _2, \phi _3)\in \mathbb {X}^+\times \mathbb {Y}^+\times \mathbb {X}^+$, system (1.10) with (1.11) admits a unique nonnegative solution (T, u, V) on $[0,t_{\text {max}})$, where $t_{\text {max}}\in \mathbb {R}_+^*$.

Proof

Let $\mathbb {Y}_{t_{\text {max}}}:=C([0,t_{\text {max}}],\mathbb {X})$, associated with the following norm in $\mathbb {Y}_{t_{\text {max}}}$,

$$\begin{aligned} \left\| v\right\| _{\mathbb {Y}_{t_{\text {max}}}}=\sup _{0\le t\le t_{\text {max}}}\left\| v(t,\cdot )\right\| _\mathbb {X},\ v\in \mathbb {Y}_{t_{\text {max}}}. \end{aligned}$$

For $(t,x)\in [0,t_{\text {max}})\times \overline{\Omega }$, solving T and V from (1.10) yields that

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle T= \breve{\mathbf{F }}+\int _0^t e^{-d(t-a)} \int _\Omega \Gamma _1(t-a,x,y) [h-u(a,y)] \mathrm{d}y\mathrm{d}a,\\ \displaystyle V= \tilde{\mathbf{F }}+\int _0^t e^{-c(t-a)} \int _\Omega \Gamma _3(t-a,x,y) [F_3(a,y)+F_4(a,y)] \mathrm{d}y\mathrm{d}a,\\ \end{array}\right. \end{aligned}$$

(2.1)

where $\breve{\mathbf{F }}=e^{-d t}\int _\Omega \Gamma _1(t,x,y)\phi _1(y)\mathrm{d}y$ and $\tilde{\mathbf{F }}=e^{-c t}\int _\Omega \Gamma _3(t,x,y)\phi _3(y)\mathrm{d}y$. Putting T and V into u equation, we get that for $(t,x)\in [0,t_{\text {max}})\times \overline{\Omega }$,

$$\begin{aligned} u(t,x)=&\ \left[ \breve{\mathbf{F }}+\int _0^t e^{-d(t-a)} \int _\Omega \Gamma _1(t-a,x,y) [h-u(a,y)] \mathrm{d}y\mathrm{d}a\right] \nonumber \\&\times \left[ \beta _1\frac{(\tilde{\mathbf{F }}+\int _0^t e^{-c(t-a)} \int _\Omega \Gamma _3(t-a,x,y) [\mathbf{F} _3(a,y)+\mathbf{F} _4(a,y)]\mathrm{d}y\mathrm{d}a)}{1+\alpha (\tilde{\mathbf{F }}+\int _0^t e^{-c(t-a)} \int _\Omega \Gamma _3(t-a,x,y) [\mathbf{F} _3(a,y)+\mathbf{F} _4(a,y)]\mathrm{d}y\mathrm{d}a)} +\beta _2(\mathbf{F} _1+\mathbf{F} _2)\right] \nonumber \\ \le&\ \left[ \breve{\mathbf{F }}+\int _0^t e^{-d(t-a)} \int _\Omega \Gamma _1(t-a,x,y) [h-u(a,y)] \mathrm{d}y\mathrm{d}a\right] \times \bigg [\beta _2(\mathbf{F} _1+\mathbf{F} _2)\\&\ +\beta _1(\tilde{\mathbf{F }}+\int _0^t e^{-c(t-a)} \int _\Omega \Gamma _3(t-a,x,y) [\mathbf{F} _3(a,y)+\mathbf{F} _4(a,y)]\mathrm{d}y\mathrm{d}a) \bigg ]\nonumber \\ :=&\ \mathcal {F}(u)(t,x).\nonumber \end{aligned}$$

(2.2)

In what follows, we shall utilize the Banach-Picard fixed point theorem to verify that the operator $\mathcal {F}:\ \mathbb {Y}_{t_{\text {max}}}\rightarrow \mathbb {Y}_{t_{\text {max}}}$ admits a fixed point, that is, system (1.10) admits a unique local solution. For the simplicity of notations, we denote

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \overline{\mathbf{F }}_1= \breve{\mathbf{F }}+\int _0^t e^{-d(t-a)} \int _\Omega \Gamma _1(t-a,x,y) h\mathrm{d}y\mathrm{d}a,\\ \displaystyle G_1(u)= -\int _0^t e^{-d(t-a)} \int _\Omega \Gamma _1(t-a,x,y) u(a,y)\mathrm{d}y\mathrm{d}a,\\ \displaystyle G_2(u)=\beta _2\int _0^tq(a)\pi (a)\int _\Omega \Gamma _2(a,x,y)u(t-a ,y)\mathrm{d}y\mathrm{d}a,\\ \displaystyle G_3(u)=\beta _1\int _0^t e^{-c(t-b)} \int _\Omega \Gamma _3(t-b,x,y)\int _0^bp(a)\pi (a)\int _\Omega \Gamma _2(a,y,z)u(b-a ,z)\mathrm{d}z\mathrm{d}a\mathrm{d}y\mathrm{d}b,\\ \displaystyle \overline{\mathbf{F }}_2=\beta _2\mathbf{F} _2(t,x)+\beta _1\tilde{\mathbf{F }}+\beta _1\int _0^t e^{-c(t-a)} \int _\Omega \Gamma _3(t-a,x,y) \mathbf{F} _4(a,y)\mathrm{d}y\mathrm{d}a. \end{array}\right. \end{aligned}$$

In these settings, $\mathcal {F}$ can be rewritten as

$$\begin{aligned} \begin{aligned} \mathcal {F}u=[\overline{\mathbf{F }}_1+G_1(u)][G_2(u)+G_3(u)+\overline{\mathbf{F }}_2]. \end{aligned} \end{aligned}$$

Hence, by selecting two functions $u_1$ and $u_2$ in $\mathbb {Y}_{t_{\text {max}}}$ and set $\tilde{u}:=u_1-u_2$, we have

$$\begin{aligned}&\ \mathcal {F}u_1-\mathcal {F}u_2\\&\quad =\ \overline{\mathbf{F }}_1 G_2(\tilde{u})+G_1(u_1)G_2(\tilde{u})+G_2(u_2)G_1(\tilde{u}) +\overline{\mathbf{F }}_1 G_3(\tilde{u})+G_1(u_1)G_3(\tilde{u})+G_3(u_2)G_1(\tilde{u})\\&\qquad +\overline{\mathbf{F }}_2 G_1(\tilde{u})\\&\quad \le \ |(\overline{\mathbf{F }}_1+G_1(u_1))(\overline{G}_2+\overline{G}_3)+(G_2(u_2)+G_3(u_2)+\overline{\mathbf{F }}_2)\overline{G}_1|\left| u_1-u_2\right| _{\mathbb {Y}_{t_{\text {max}}}}, \end{aligned}$$

where

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \overline{G}_1= -\int _0^t e^{-d(t-a)} \int _\Omega \Gamma _1(t-a,x,y) \mathrm{d}y\mathrm{d}a,\\ \displaystyle \overline{G}_2=\beta _2\int _0^tq(a)\pi (a)\int _\Omega \Gamma _2(a,x,y)\mathrm{d}y\mathrm{d}a,\\ \displaystyle \overline{G}_3=\beta _1\int _0^t e^{-c(t-b)} \int _\Omega \Gamma _3(t-b,x,y)\int _0^{b}p(a)\pi (a)\int _\Omega \Gamma _2(a,y,z)\mathrm{d}z\mathrm{d}a\mathrm{d}y\mathrm{d}b. \end{array}\right. \end{aligned}$$

Let

$$\begin{aligned} \tilde{L}(t_{\text {max}}):=\sup \limits _{0\le t\le t_{\text {max}}}\left| (\overline{\mathbf{F }}_1+G_1(u_1))(\overline{G}_2+\overline{G}_3)+(G_2(u_2)+G_3(u_2)+\overline{\mathbf{F }}_2)\overline{G}_1\right| _\mathbb {X}. \end{aligned}$$

We can choose sufficiently small $0<t_{\text {max}}\ll 1$ such that $\tilde{L}(t_{\text {max}})<1$. Hence, we can get the following inequality,

$$\begin{aligned} \left| \mathcal {F}u_1-\mathcal {F}u_2\right| _{\mathbb {Y}_{t_{\text {max}}}}\le \tilde{L} (t_{\text {max}})\left| u_1-u_2\right| _{\mathbb {Y}_{t_{\text {max}}}}, \end{aligned}$$

which means that $\mathcal {F}$ is a strict contraction in $\mathbb {Y}_{t_{\text {max}}}$. This confirms the assertion that the system (1.10) admit a unique local solution on $[0,t_{\text {max}})$.$\square$

We next establish the positivity of the solution.

Proposition 2.1

For any $(\phi _1, \phi _2, \phi _3)\in \mathbb {X}^+\times \mathbb {Y}^+\times \mathbb {X}^+$ and $(t,x)\in [0,t_{\text {max}})\times \overline{\Omega }$, we have

$$\begin{aligned} T(t,x)>0,\ V(t,x)\ge 0\ \text{ and }\ u(t,x)\ge 0. \end{aligned}$$

Proof

By (1.9), we know that if $\phi _2\in \mathbb {Y}^+$, then

$$\begin{aligned} u(0,x)=\beta _1\phi _1(x)\frac{\phi _3(x)}{1+\alpha \phi _3(x)}+\beta _2\phi _1(x)\int _0^\infty q(a)\phi _2(a,x)\mathrm{d}a\ge 0, \ \forall x\in \overline{\Omega }. \end{aligned}$$

Define the following positive linear operator $\Phi _i\ (i=1,2): \mathbb {Y}\rightarrow \mathbb {Y}$ as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \Phi _1(\varphi )(t,x):=\int _0^tq(a)\pi (a)\int _\Omega \Gamma _2(a,x,y)\varphi (t-a,y)\mathrm{d}y\mathrm{d}a, ~\varphi \in \mathbb {Y},\\ \displaystyle \Phi _2(\varphi )(t,x):=\int _0^tp(a)\pi (a)\int _\Omega \Gamma _2(a,x,y)\varphi (t-a,y)\mathrm{d}y\mathrm{d}a,~\varphi \in \mathbb {Y}, \end{array}\right. \end{aligned}$$

(2.3)

in the sense that $\Phi _i(\mathbb {Y}^+)\subset \mathbb {Y}^+$ as $\Gamma _2(a,x,y)>0$. It follows that

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial T}{\partial t}>d_1 \Delta T- \left[ \beta _2(\Phi _1(u)+\mathbf{F} _2)+\frac{\beta _1}{\alpha }+d\right] T,&{}\ t\in [0,t_{\text {max}}),\ x\in \Omega ,\\ \displaystyle \frac{\partial T}{\partial \nu }=0,&{}\ t\in [0,t_{\text {max}}),\ x\in \partial \Omega . \end{array}\right. \end{aligned}$$

(2.4)

Due to the fact that for any $(t,x)\in [0,t_{\text {max}})\times \overline{\Omega }$, $\beta _2(\Phi _1(u)+F_2)+\frac{\beta _1}{\alpha }+d$ is continuous and bounded, we have that $T(t,x)>0$, by the standard strong maximum principle.

Next we shall show the positivity of u(t, x). If there exist $(t_1,x_1)\in [0,t_{\text {max}})\times \overline{\Omega }$ such that

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle u(t,x)\ge 0,&{}\ t\in [0,t_1)\ \mathrm{and~}\ x\in \Omega ;\\ \displaystyle u(t,x_1)=0,&{}\ t=t_1\ \mathrm{and}\ x_1\in \Omega ;\\ \displaystyle u(t+\varepsilon ,x_1)<0,&{}\ t=t_1,\ x_1\in \Omega \ \mathrm{and}\ 0<\varepsilon \ll 1. \end{array}\right. \end{aligned}$$

Thus,

$$\begin{aligned} u(t_1+\varepsilon ,x_1)=&\ \beta _1T(t_1+\varepsilon ,x_1)\frac{V(t_1+\varepsilon ,x_1)}{1+\alpha V(t_1+\varepsilon ,x_1)}+\beta _2T(t_1+\varepsilon ,x_1)\\&\ \times \left( \int _0^{t+\varepsilon }q(a)\pi (a)\int _\Omega \Gamma _2(a,x,y)u(t+\varepsilon -a ,y)\mathrm{d}y\mathrm{d}a+\mathbf{F} _2(t_1+\varepsilon ,x_1)\right) . \end{aligned}$$

Moreover, it follows from the third equation of (1.10) that

$$\begin{aligned} V(t) = \int _0^t e^{-c(t-s)}\int _\Omega [\mathbf{F} _3(s,y)+{} \mathbf{F} _4(s,y)]\Gamma _3(t-s,x,y)\text {d} y \text {d} s+e^{-ct}\int _\Omega \Gamma _3(t,x,y)\phi _3(y)\text {d} y. \end{aligned}$$

Hence,

$$\begin{aligned} V(t_1+\varepsilon ) \ge \int _0^{t_1+\varepsilon } e^{-c(t+\varepsilon -s)}\int _\Omega \mathbf{F} _3(s,y)\Gamma _3(t_1+\varepsilon -s,x,y)\text {d} y \text {d}s. \end{aligned}$$

Note that

$$\begin{aligned} \mathbf{F} _3(s,y)=\int _0^s p(a)\pi (a)\int _\Omega \Gamma _2(a,x,y)u(s-a ,y)\mathrm{d}y\mathrm{d}a\ge 0,\ \ s\in (0,t_1+\varepsilon ), \end{aligned}$$

for small enough $\varepsilon$. Together with $\mathbf{F} _1\ge 0$, $\mathbf{F} _2\ge 0$, we have $u(t_1+\varepsilon ,x_1)\ge 0$ for small enough $\varepsilon$, which results in a contradiction. By some similar arguments as above, we can conclude that $V(t,x)\ge 0$. This completes the proof.$\square$

We next show the solution of (1.10) exists globally.

Theorem 2.2

For any $(\phi _1, \phi _2, \phi _3)\in \mathbb {X}^+\times \mathbb {Y}^+\times \mathbb {X}^+$, then (1.10) admits a unique nonnegative solution (T, u, V) on $[0,\infty )\times \overline{\Omega }$. Furthermore, the solution of (1.10) is ultimately bounded.

Proof

In fact, by Proposition 2.1, we know that T equation of system (1.10) satisfies

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial T}{\partial t}<d_1 \Delta T+h-dT,&{}\ t\in [0,t_{\text {max}}),\ x\in \Omega , \\ \displaystyle \frac{\partial T}{\partial \nu }=0, &{}\ t\in [0,t_{\text {max}}),\ x\in \Omega , \end{array}\right. \end{aligned} \end{aligned}$$

(2.5)

which implies that $\frac{h}{d}$ is the upper solution of T(t, x). We confirm that for any $(t,x)\in [0,t_{\text {max}})\times \overline{\Omega }$, $u(t,x)<+\infty$. If it is not true, we suppose that there exists $(t^*, x^*)\in [0,t_{\text {max}})\times \Omega$ satisfying $\lim _{t\rightarrow {t^*-0}}u(t,x^*)=+\infty$. Hence, $\lim _{t\rightarrow {t^*-0}}\partial _t T(t,x^*)=-\infty$, which results in the contradiction to the positivity of T (see in Proposition 2.1). Hence, $u(t, x) <\infty$. We are now ready to confirm the boundedness of V(t, x). Let $p^+=\text {ess.sup}_{a\in \mathbb {R}_+}p(a)<+\infty$. Since

$$\begin{aligned} \mathbf{F} _3+\mathbf{F} _4 \le&\ p^+\int _0^\infty \pi (a)\int _\Omega \Gamma _2(a,x,y)u(t-a ,y)\mathrm{d}y\mathrm{d}a\\&\ + p^+\int _0^\infty \frac{\pi (a+t)}{\pi (a)}\int _\Omega \Gamma _2(t,x,y)\phi _2(a, y)\mathrm{d}y\mathrm{d}a :=\mathbf{M} _u, \end{aligned}$$

it follows that

(2.6)

Hence, V never blow up in $t\in [0,t_{\text {max}}),\ x\in \Omega$. Consequently, we arrive at the assertion that the solution of (1.10) exists globally in $\mathbb {X}^+\times \mathbb {Y}^+\times \mathbb {X}^+$. After passing to some similar arguments as before if necessary, we can confirm that for any $(\phi _1, \phi _2, \phi _3)\in \mathbb {X}^+\times \mathbb {Y}^+\times \mathbb {X}^+$ and a sufficiently large positive number $\mathbf{M} _\infty$,

$$\begin{aligned} 0<\limsup \limits _{t\rightarrow \infty }(T(t,x), u(t,x), V(t,x)) \le \mathbf{M} _\infty . \end{aligned}$$

In fact, solving the T-equation of (2.1) gets

$$\begin{aligned} \begin{aligned} T\le&\ h\int _0^t e^{-d(t-a)} \int _\Omega \Gamma _1(t-a,x,y) \mathrm{d}y\mathrm{d}a+e^{-d t}\int _\Omega \Gamma _1(t,x,y)\phi _1(y)\mathrm{d}y\\ \le&\ \frac{h}{d}(1-e^{-dt})+e^{-dt}\parallel \phi _1\parallel _\mathbb {X}<\infty . \end{aligned} \end{aligned}$$

(2.7)

By taking the limit $t\rightarrow \infty$ in (2.6) and (2.7), we immediately get

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }T(t,x)\le \frac{h}{d}\ \text{ and }\ \limsup \limits _{t\rightarrow \infty }V(t,x)\le \mathbf{M} _v. \end{aligned}$$

This together with $u(t,x)<+\infty$ immediately gives the ultimate boundedness of the solution in $\mathbb {X}^+\times \mathbb {Y}^+\times \mathbb {X}^+$.

Since c is a constant, we have

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial V(t,x)}{\partial t}>d_3 \Delta V(t,x) -cV(t,x),&{}\ t\in [0,t_{\text {max}}),\ x\in \Omega ,\\ \displaystyle \frac{\partial V(t,x)}{\partial \nu }=0,&{}\ t\in [0,t_{\text {max}}),\ x\in \partial \Omega .\\ \end{array}\right. \end{aligned}$$

(2.8)

By the standard strong maximum principle, we get that $V(t,x)>0$. This completes the proof.$\square$

3 Basic Reproduction Number

Following the classical theory in [10, 42], in this section, we shall define the basic reproduction number $\mathfrak {R}_0$ of model (1.10). Obviously, (1.10) always exists an infection-free steady state $E_0=(T_0,0,0)$ with $T_0=\frac{h}{d}$. We are now ready to define the next generation operator for model (1.10) on $\mathbb {X}^+\times \mathbb {Y}^+\times \mathbb {X}^+$. We consider the following linear sub-system of model (1.10) at disease-free equilibrium $E_0$.

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \left( \frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right) u(t,a,x)=d_2\Delta u(t,a,x)-\theta (a)u(t,a,x),\\ \displaystyle u(t,0,x)=\beta _1T_0V+\beta _2T_0\int _0^{+\infty }q(a)u(t,a,x)\mathrm{d}a,\\ \displaystyle \frac{\partial V}{\partial t}=d_3 \Delta V+ \int _0^{+\infty }p(a)u(t,a,x)\mathrm{d}a -c V. \end{array}\right. \end{aligned}$$

(3.1)

Firstly, we have

$$\begin{aligned} V(t) = \int _0^t e^{-c(t-s)}\int _\Omega \mathbf{R} _1(s,y)\Gamma _3(t-s,x,y)\text {d} y \text {d} s+e^{-ct}\int _\Omega \Gamma _3(t,x,y)\phi _3(y)\text {d} y, \end{aligned}$$

where

$$\begin{aligned} \mathbf{R} _1(t,x) = \int _0^{+\infty }p(a)u(t,a,x)\mathrm{d}a. \end{aligned}$$

Recall that $u(t,x): = u(t,0,x)$. This combines with (1.8) gives that

$$\begin{aligned}&u(t,x) = \beta _2 T_0 \left( \int _0^t q(a)\pi (a)\int _\Omega \Gamma _2(a,x,y) u(t-a,y)\text {d}y\text {d}a + \mathbf{R} _2(t,x)\right) \\&+ \beta _1 T_0 \left( \int _0^t e^{-c(t-a)}\int _\Omega \Gamma _3(t-a,x,y)\int _0^a p(s)\pi (s)\int _\Omega \Gamma _2(s,y,z)u(a-s,z)\text {d}z\text {d}s\text {d}y\text {d}a+ \mathbf{R} _3(t,x)\right) , \end{aligned}$$

where

$$\begin{aligned} \mathbf{R} _2(t,x) = \beta _2 T_0 \int _0^\infty q(a+t)\int _\Omega \Gamma _2(a+t,x,y) \phi _2(a,y)\frac{\pi (a+t)}{\pi (a)}\text {d}y\text {d}a \end{aligned}$$

and

$$\begin{aligned} \mathbf{R} _3(t,x) = \beta _1 T_0 \int _0^t e^{-c(t-a)}\Gamma _3(t-a,x,y)\int _a^\infty p(s)\frac{\pi (s)}{\pi (a-s)}\int _\Omega \Gamma _2(s,y,t)\phi _2(s-a,t)\text {d}z\text {d}s\text {d}y\text {d}a. \end{aligned}$$

Similar to [47], the next generation operator $\mathcal {L}$ can be evaluated as follows,

$$\begin{aligned} \mathcal {L}[\varphi ](x) =&\ \beta _2 T_0 \int _0^\infty q(a)\pi (a)\int _\Omega \Gamma _2(a,x,y) \varphi (y)\text {d}y\text {d}a\nonumber \\&\ + \beta _1 T_0\int _0^\infty \int _0^t e^{-c(t-a)}\int _\Omega \Gamma _3(t-a,x,y)\int _0^a p(s)\pi (s)\nonumber \\&\qquad \int _\Omega \Gamma _2(s,y,z)\varphi (z)\text {d}z\text {d}s\text {d}y\text {d}a\text {d}t\nonumber \\ =&\ \beta _2 T_0 \int _0^\infty q(a)\pi (a)\int _\Omega \Gamma _2(a,x,y) \varphi (y)\text {d}y\text {d}a\nonumber \\&\ + \beta _1 T_0\int _0^\infty e^{-ca}\int _\Omega \Gamma _3(a,x,y)\int _0^a p(s)\pi (s)\int _\Omega \Gamma _2(s,y,z)\varphi (z)\text {d}z\text {d}s\text {d}y\text {d}a, \end{aligned}$$

(3.2)

for any $\varphi \in \mathbb {X}$. Following the classical theory in [10, 42], the basic reproduction number $\mathfrak {R}_0$ is defined by the spectral radius of $\mathcal {L}$, i.e., $\mathfrak {R}_0:=r(\mathcal {L})$.

As to $\mathcal {L}$, we have the following result.

Lemma 3.1

Let $\mathcal {L}$ be defined by (3.2). The next generation operator $\mathcal {L}$ is strictly positive, bounded, and compact.

Proof

Obviously, the next generation operator $\mathcal {L}$ is positive. Due to the properties of $\Gamma _2$ and $\Gamma _3$, we denote by $\{\varphi _n\}_{n\in \mathbb {N}}$ the bounded sequence in $\mathbb {X}$, which satisfies $|\varphi _n|_\mathbb {X}\le \mathbb {K}$, for some $\mathbb {K}>0$. Let $\{\psi _n\}_{n\in \mathbb {N}}=\mathcal {L}\varphi _n$. It then follows that

$$\begin{aligned} \begin{aligned} \Vert \psi _n(x)\Vert _{\mathbb {X}}\le&\ \beta _2\frac{h}{d}\int _0^{+\infty }q(a)\pi (a)\int _\Omega \Gamma _2(a,x,y)\mathrm{d}y\mathrm{d}a\Vert \varphi _n\Vert _\mathbb {X}\\&\ +\beta _1 T_0\int _0^\infty e^{-ca}\int _\Omega \Gamma _3(a,x,y)\int _0^a p(s)\pi (s)\text {d}s\text {d}y\text {d}a\Vert \varphi _n\Vert _\mathbb {X}\\ \le&\beta _2\frac{h}{d}\int _0^{+\infty }q(a)\pi (a)\mathrm{d}a\mathbb {K}+\beta _1 T_0\int _0^\infty e^{-ca}\int _\Omega \Gamma _3(a,x,y)\int _0^a p(s)\pi (s)\text {d}s\text {d}y\text {d}a\mathbb {K}, \end{aligned} \end{aligned}$$

for all $x\in \Omega$, which gives the uniform boundedness of $\{\psi _n\}_{n\in \mathbb {N}}$. By the Ascoli-Arzela theorem, we are now ready to verify that $\{\psi _n\}_{n\in \mathbb {N}}$ is equi-continuous. Taking any $x, \tilde{x}\in \Omega$ with $|x-\tilde{x}|\le \delta$. Direct calculation gives

$$\begin{aligned} |\psi _n(x)-&\psi _n(\tilde{x})|_{\mathbb {X}} \le \beta _2\frac{h}{d}\int _0^{+\infty }q(a)\pi (a) \int _\Omega |\Gamma _2(a,x,y)-\Gamma _2(a,\tilde{x},y)|\varphi _n( y)\mathrm{d}y\mathrm{d}a\\&\ + \beta _1 T_0\int _0^\infty e^{-ca}\int _\Omega |\Gamma _3(a,x,y)-\Gamma _3(a,\tilde{x},y)|\int _0^a p(s)\pi (s)\int _\Omega \Gamma _2(s,y,z)\varphi (z)\text {d}z\text {d}s\text {d}y\text {d}a. \end{aligned}$$

Denote $q^+=\text {ess.sup}_{a\in \mathbb {R}_+}q(a)<+\infty$ and $p^+=\text {ess.sup}_{a\in \mathbb {R}_+}p(a)<+\infty$. From the properties of $\Gamma _i(a, x, y),\ (i=2,3)$, we can select $\epsilon >0$ such that $|\Gamma _2(a,x,y)-\Gamma _2(a,\tilde{x},y)|\le \frac{\epsilon }{T_0\mathbb {K}\mid \Omega \mid q^+\beta _2}$ and $|\Gamma _3(a,x,y)-\Gamma _3(a,\tilde{x},y)|\le \frac{c\epsilon }{ T_0\mathbb {K}\mid \Omega \mid p^+\beta _1}$ for all $y\in \Omega$, where $|\Omega |$ is the volume of $\Omega$. For such $\epsilon$ and $\delta$, we immediately have

$$\begin{aligned} \left| \psi _n(x)-\psi _n(\tilde{x})\right| _{\mathbb {X}}\le \epsilon , \end{aligned}$$

that is, $\{\psi _n(x)\}_{n\in \mathbb {N}}$ is equi-continuous. Thus, the next generation operator $\mathcal {L}$ is compact. This proves Lemma 3.1.$\square$

Generally speaking, it is not east to get the spectral radius of the next generation operator $\mathcal {L}$, if not impossible, so that we can not get further information on dynamical properties of (1.10). By Lemma 3.1 combined with the Krein-Rutman theorem [1, Theorem 3.2], we know that the basic reproduction number is the only positive eigenvalue of $\mathcal {L}$, corresponding to which, there is a positive eigenvector. Substituting $\varphi (x) \equiv \phi ^* > 0$ ($\phi ^*$ is a constant) into (3.2) and using $\int _\Omega \Gamma _i(\cdot , x, y)\mathrm{d}y = 1,\ (i=2,3)$,

$$\begin{aligned} \mathcal {L} \phi ^* = \beta _2\frac{h}{d}\int _0^\infty q(a)\pi (a)\mathrm{d}a\phi ^*+\frac{\beta _1 h}{cd}\int _0^\infty p(a)\pi (a)\mathrm{d}a\phi ^*. \end{aligned}$$

Hence, $\mathfrak {R}_0=r(\mathcal {L})$ is given by

$$\begin{aligned} \mathfrak {R}_0=\ \beta _2T_0Q+\frac{\beta _1 }{c}T_0P, \end{aligned}$$

(3.3)

where

$$\begin{aligned} Q=\int _0^\infty q(a)\pi (a)\mathrm{d}a\ \text{ and }\ P=\int _0^\infty p(a)\pi (a)\mathrm{d}a. \end{aligned}$$

We should mention that with the assumption that all parameters of (1.10) are spatially homogeneous, $E_0$ is constant equilibrium. It is crucial to (3.2) that the next generation operator $\mathcal {L}$ does have a positive constant eigenvector, which in turn implies that $\mathfrak {R}_0$ can be explicitly characterized by a positive constant (see also in [4, 5]).

Denote by $\hat{E}$ the space-independent infection equilibrium of (1.10), if it exists. Then it satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle h-\hat{u}(0)-d\hat{T}=0,\\ \displaystyle \frac{\text {d} \hat{u}(a)}{\text {d} a}= -\theta (a)\hat{u}(a),\\ \displaystyle \hat{u}(0)=\beta _1\hat{T}\frac{\hat{V}}{1+\alpha \hat{V}}+\beta _2\hat{T}\int _0^{+\infty }q(a)\hat{u}(a)\mathrm{d}a,\\ \displaystyle \int _0^{+\infty }p(a)\hat{u}(a)\mathrm{d}a -c\hat{V}=0. \end{array}\right. \end{aligned}$$

(3.4)

From the second equation of (3.4), one has that

$$\begin{aligned} \hat{u}(a)=\hat{u}(0)e^{-\int _0^a \theta (s)\text {d}s}=\hat{u}(0)\pi (a). \end{aligned}$$

Furthermore, from the first and forth equations of (3.4), we have

$$\begin{aligned} \hat{T}=\frac{h-\hat{u}(0)}{d}\ \ \ \text{ and }\ \ \ \hat{V}=\frac{1}{c}\int _0^\infty p(a)\hat{u}(a)\text {d}a=\frac{1}{c}\int _0^\infty p(a)\hat{u}(0)\pi (a)\text {d}a=\frac{P}{c}\hat{u}(0). \end{aligned}$$

(3.5)

Now, we can see that $\hat{T}$, $\hat{V}$ and $\hat{u}(0)$ can be written as terms of $\hat{u}(0)$. Putting $\hat{T}$ and $\hat{V}$ into the third equation of (3.4) gives

$$\begin{aligned} \Upsilon (\hat{u}(0))=a_0(\hat{u}(0))^2+a_1\hat{u}(0)+a_2, \end{aligned}$$

(3.6)

where $a_0=\alpha \beta _2PQ$, $a_1=c\beta _2Q+\beta _1P+\alpha dP-\alpha \beta _2hQP$ and $a_2=cd-\beta _1hQ-c\beta _2hQ=cd[1-\mathfrak {R}_0]$. Since $a_0>0$, it has $\Upsilon (\pm \infty )=+\infty$. In the case that $\mathfrak {R}_0\le 1$, we know that $\Upsilon (0)\ge 0$ and

$$\begin{aligned} \Upsilon '(\hat{u}(0))=2a_0\hat{u}(0)+a_1. \end{aligned}$$

Since $\mathfrak {R}_0\le 1$, that is, $c\beta _2hQ + \beta _1hP\le cd$, thus we can conclude that

$$\begin{aligned} c\beta _2Q+\beta _1P+\alpha dP-\alpha \beta _2hQP>\alpha P( d-\beta _2hQ)\ge 0, \end{aligned}$$

we have that $\Upsilon '(\hat{u}(0))>0$ for any $\hat{u}(0)\ge 0$ when $\mathfrak {R}_0\le 1$. It follows that Eq. (3.6) has no positive root, which in turn implies that (1.10) has no space-independent infection equilibrium $\hat{E}$. In the case that $\mathfrak {R}_0\ge 1$, we know that $\Upsilon (0) = a_2 < 0$. From the properties of the quadratic function $\Upsilon (\hat{u}(0))$, (3.6) admits a unique positive root $\hat{u}(0)$.

In summary, we have the following result.

Lemma 3.2

If $\mathfrak {R}_0 > 1$, (1.6) has a unique space-independent infection equilibrium $\hat{E}=(\hat{T}, \hat{u}(a), \hat{V})$, which is unique and defined by (3.5).

4 Dynamics for the System

This section is paid to the local and global asymptotic stability of $E_0$ and $\hat{E}$.

4.1 Local Dynamics

We are now ready to establish the local asymptotic stability of $E_0$ and $\hat{E}$. Let $E^*=(T^*,u^*(a),V^*)$ be $E_0$ or $\hat{E}$ of (1.6), we linearize (1.6) around $E^*$ yields

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial T}{\partial t}=d_1 \Delta T-dT-T^*\left( \frac{\beta _1V}{(1+\alpha V^*)^2}+\beta _2\int _0^{+\infty }\ q(a)u(t,a,x)\mathrm{d}a\right) \\ \displaystyle -T\left( \frac{\beta _1 V^*}{1+\alpha V^*}+\beta _2\int _0^{+\infty }\ q(a)u^*(a)\mathrm{d}a\right) ,\\ \displaystyle \left( \frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right) u(t,a,x)=d_2\Delta u(t,a,x)-\theta (a)u(t,a,x),\\ \displaystyle \frac{\partial V}{\partial t}=d_3 \Delta V+ \int _0^{+\infty }p(a)u(t,a,x)\mathrm{d}a -cV,\\ \displaystyle u(t,0,x)=T^*\left( \frac{\beta _1V}{(1+\alpha V^*)^2}+\beta _2\int _0^{+\infty }\ q(a)u(t,a,x)\mathrm{d}a\right) \\ \displaystyle +T\left( \frac{\beta _1 V^*}{1+\alpha V^*}+\beta _2\int _0^{+\infty }\ q(a)u^*(a)\mathrm{d}a\right) ,\\ \displaystyle \frac{\partial T}{\partial \nu }=\frac{\partial u(t,a,x)}{\partial \nu }=\frac{\partial V}{\partial \nu }=0. \end{array}\right. \end{aligned}$$

(4.1)

By a classical parabolic theory [2], we denote by $\zeta _j (j = 1, 2, \cdots )$ with $0 = \zeta _0< \zeta _1< \zeta _2 <\cdots$ the eigenvalues of $-\Delta$ subject to (1.7). Assume that the following parabolic problem with the homogeneous Neumann boundary condition

$$\begin{aligned} \left\{ \begin{array}{ll}\displaystyle \frac{\partial U(t,x)}{\partial t}=\Delta U(t,x),\\ \displaystyle \frac{\partial U(t,x)}{\partial \nu }=0, \end{array}\right. \end{aligned}$$

has the exponential solution in the form of $U(t, x) = e^{\eta t}z(x), ~z(x) \in X_i$. Further from the exponential Ansatz (see, e.g., [27, Theorem 3.1]), we have that $\Delta z(x) = -\zeta _iz(x)$. We substitute $T = e^{\eta t}\phi (x)$, $u(t, a, x) = e^{\eta t}\varphi (a, x)$, $V =e^{\eta t}\psi (x)$ into (4.1), obtaining that

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \eta \phi (x)=-d_1\zeta _i \phi (x)-d\phi (x)-T^*\left( \frac{\beta _1\psi (x)}{(1+\alpha V^*)^2}+\beta _2\int _0^{+\infty }\ q(a)\varphi (a, x)\mathrm{d}a\right) \\ \displaystyle -\phi (x)\left( \frac{\beta _1V^*}{1+\alpha V^*}+\beta _2\int _0^{+\infty }\ q(a)u^*(a)\mathrm{d}a\right) ,\\ \displaystyle \eta \varphi (a, x) +\frac{\partial \varphi (a, x)}{\partial a} =-d_2\zeta _i \varphi (a, x)-\theta (a)\varphi (a, x),\\ \displaystyle \eta \psi (x)=-d_3 \zeta _i \psi (x)+ \int _0^{+\infty }p(a)\varphi (a, x)\mathrm{d}a -c \psi (x),\\ \displaystyle \varphi (0, x)=T^*\left( \frac{\beta _1\psi (x)}{(1+\alpha V^*)^2}+\beta _2\int _0^{+\infty }\ q(a)\varphi (a, x)\mathrm{d}a\right) \\ \displaystyle +\phi (x)\left( \frac{\beta _1 V^*}{1+\alpha V^*}+\beta _2\int _0^{+\infty }\ q(a)u^*(a)\mathrm{d}a\right) . \end{array}\right. \end{aligned}$$

(4.2)

Combined with the second and fourth equation of (4.2), we get that

$$\begin{aligned}\varphi (a,x)=\varphi (0,x)\hat{\pi }(a)e^{-\eta a},\ \text{ with }\ \hat{\pi }(a)=\pi (a)e^{-d_2\zeta _ia}. \end{aligned}$$

We next claim that $\eta \ne -(d_1\zeta _i+d)$ and $\eta \ne -(d_3\zeta _i+c)$. In fact, if $\eta =-(d_1\zeta _i+d)$, together with the first equation of (4.2), imply that $\varphi (0, x) = 0$. Hence, by the third equation of (4.2), $\eta =-(d_3\zeta _i+c)$, which results in a contradiction. $\eta \ne -(d_3\zeta _i+c)<0$ can be proved in a similar way. This claim together with the first and third equation of (4.2) imply that

$$\begin{aligned} \phi (x)=-\frac{\varphi (0,x)}{\eta +d_1\zeta _i+d}\ \mathrm{and}\ \psi (x)=\frac{\varphi (0,x)\widehat{P}(\eta )}{\eta +d_3\zeta _i+c}, \end{aligned}$$

(4.3)

where $\widehat{P}(\eta ):=\int _0^\infty p(a)\hat{\pi }(a)e^{-\eta a}\mathrm{d}a$. Plugging (4.3) into the fourth equation of (4.2) yields

$$\begin{aligned}&\ \left( 1+\frac{\beta _1V^*}{(\eta +d_1\zeta _i+d)(1+\alpha V^*)}+\frac{\beta _2\int _0^{+\infty } q(a)u^*(a)\mathrm{d}a}{\eta +d_1\zeta _i+d}\right) \varphi (0,x)\nonumber \\&\quad =\ T^*\left( \beta _2\widehat{K}(\eta ) +\frac{\beta _1\widehat{P}(\eta )}{(\eta +d_3\zeta _i+c)(1+\alpha V^*)^2}\right) \varphi (0,x), \end{aligned}$$

(4.4)

where $\widehat{K}(\eta ):=\int _0^\infty q(a)\hat{\pi }(a)e^{-\eta a}\mathrm{d}a$. Canceling $\varphi (0,x)$ on both sides of (4.4), we conclude that

$$\begin{aligned}&1+\frac{\beta _1V^*}{(\eta +d_1\zeta _i+d)(1+\alpha V^*)}+\frac{\beta _2\int _0^{+\infty } q(a)u^*(a)\mathrm{d}a}{\eta +d_1\zeta _i+d}\nonumber \\&\quad =T^*\left( \beta _2\widehat{K}(\eta ) +\frac{\beta _1\widehat{P}(\eta )}{(\eta +d_3\zeta _i+c)(1+\alpha V^*)^2}\right) . \end{aligned}$$

(4.5)

In what follows, we pay attention to analyze the characteristic roots of (4.5).

Theorem 4.1

If $\mathfrak {R}_0 < 1$, $E_0$ is locally asymptotically stable, while $\hat{E}$ is locally asymptotically stable if $\mathfrak {R}_0 > 1$.

Proof

Let us first prove the local stability of $E_0$. In this case, (4.5) can be simplified to

$$\begin{aligned} 1=\frac{h}{d}\left( \beta _2\widehat{K}(\eta ) +\frac{\beta _1\widehat{P}(\eta )}{\eta +d_3\zeta _i+c}\right) . \end{aligned}$$

(4.6)

Suppose by contrary that (4.6) admits a real positive root $\eta >0$. We directly have

$$\begin{aligned} \frac{h}{d}\left| \left( \beta _2\widehat{K}(\eta ) +\frac{\beta _1\widehat{P}(\eta )}{\eta +d_3\zeta _i+c}\right) \right| \le \mathfrak {R}_0. \end{aligned}$$

If $\mathfrak {R}_0<1$, the above inequality leads to a contradiction to (4.6). Hence, all the real roots of (4.6) are negative.

Let $\eta = m \pm ni$ (with $m \ge 0$ and $n > 0$) be a pair of complex roots of (4.6). After passing elementary analysis, we directly have

$$\begin{aligned} \begin{aligned} 1=&\frac{h}{d}\left( \frac{\beta _1(m+c+d_3\zeta _i)\int _0^\infty p(a)\hat{\pi }(a)e^{-ma}\cos (na)\mathrm{d}a-\beta _1n\int _0^\infty p(a)\hat{\pi }(a)e^{-ma}\sin (na)\mathrm{d}a}{(m+c+d_3\zeta _i)^2+n^2}\right. \\&\left. +\beta _2\int _0^\infty q(a)\hat{\pi }(a)e^{-ma}\cos (na)\mathrm{d}a\right) \le \mathfrak {R}_0. \end{aligned} \end{aligned}$$

This contradicts with $\mathfrak {R}_0 < 1$. This proves the assertion that $E_0$ is LAS.

We next prove the local stability of $\hat{E}$. If $\eta = m+ni$ with $m \ge 0$, the left-hand side of (4.5) satisfies

$$\begin{aligned}&\ \left| 1+\frac{\beta _1\hat{V}}{(\eta +d_1\zeta _i+d)(1+\alpha \hat{V})}+\frac{\beta _2\int _0^{+\infty }\ q(a)\hat{u}(a)\mathrm{d}a}{\eta +d_1\zeta _i+d}\right| \nonumber \\&\quad =\ \frac{\sqrt{[(m+d_1\zeta _i+d)(1+\alpha \hat{V})+\Xi ]^2+n^2(1+\alpha \hat{V})^2}}{\sqrt{[(m+d_1\zeta _i+d)^2+n^2](1+\alpha \hat{V})^2}}>1, \end{aligned}$$

(4.7)

where $\Xi =\beta _1\hat{V}+\beta _2\int _0^{+\infty }q(a)\hat{u}(a)\mathrm{d}a(1+\alpha \hat{V})$. However, the right-hand side of (4.5) satisfies

$$\begin{aligned}&\ \hat{T}\left| \beta _2\widehat{K}(\eta ) +\frac{\beta _1\widehat{P}(\eta )}{(\eta +d_3\zeta _i+c)(1+\alpha \hat{V})^2}\right| \le \hat{T}\left| \beta _2\widehat{K}(\eta ) +\frac{\beta _1\widehat{P}(\eta )}{(\eta +d_3\zeta _i+c)(1+\alpha \hat{V})}\right| \nonumber \\&\quad \le \ \frac{\hat{T}}{\hat{u}(0)}\left| \beta _2Q+\frac{\beta _1c\hat{V}}{(\eta +d_3\zeta _i+c)(1+\alpha \hat{V})}\right| \le \frac{\hat{T}}{\hat{u}(0)}\left| \beta _2\int _0^\infty q(a)\pi (a)da+\beta _1\frac{\hat{V}}{(1+\alpha \hat{V})}\right| =1. \end{aligned}$$

(4.8)

Comparing (4.7) and (4.8), we conclude that all roots of (4.5) have negative real parts if $\mathfrak {R}_0>1$. This proves the assertion that $\hat{E}$ is LAS if $\mathfrak {R}_0>1$.$\square$

4.2 Persistence of Infection When $\mathfrak {R}_0>1$

In this subsection, we are concerned with the uniform persistence of (1.10) for $\mathfrak {R}_0> 1$. Considering a semiflow associated with system (1.10), and replacing $u(t-a, 0, y)$ in (1.8) by $u(t-a, y)$ for short, we have the following result (see also in [35, Section 9.4]).

Lemma 4.1

Let $(\phi _1, \phi _2, \phi _3)\in \mathbb {X}^+ \times \mathbb {Y}^+\times \mathbb {X}^+$. For all $t\ge 0$ and $x\in \Omega$, system (1.10) admits a continuous semiflow defined by $\Theta (t, \phi _1, \phi _2, \phi _3):=(T(t,\cdot ), u(t,\cdot ,\cdot ), V(t,\cdot ))\in \mathbb {X}^+ \times \mathbb {Y}^+\times \mathbb {X}^+$.

Proof

For any $r, t, a\ge 0$ and $x\in \Omega$, let

$$\begin{aligned} T_r(t,x)=T(r+t,x),\ u_r(t,x)=u(r+t,x),\ V_r(t,x)= V(r+t,x),\ u_r(t,a,x)=u(r +t,a,x). \end{aligned}$$

Hence, we have

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial T_r(t,x)}{\partial t}=d_1\Delta T_r(t,x)+h- u_r(t,x)-dT_r(t,x),\\ \displaystyle \frac{\partial V_r(t,x)}{\partial t}=d_3\Delta V_r(t,x)+\int _0^{+\infty }p(a)\pi (a)\int _\Omega \Gamma _2(a,x,y)u_r(t-a,a,y)\mathrm{d}y\mathrm{d}a-cV(t,x), \end{array}\right. \end{aligned}$$

(4.9)

with $T_r(0,x)=T(r ,x)$ and $V_r(0,x)= V(r,x)$, and

$$\begin{aligned} \displaystyle u_r(t, x)= \beta _1T_r(t,x)\frac{V_r(t,x)}{1+\alpha V_r(t,x)}+\beta _2T_r(t,x)\int _0^{+\infty }q(a)u_r(t,a,x)\mathrm{d}a. \end{aligned}$$

(4.10)

This together with (1.8) implies that for $x\in \Omega$,

$$\begin{aligned} u_r(t,a,x)= \left\{ \begin{array}{ll} \displaystyle \pi (a)\int _\Omega \Gamma _2(a,x,y)u_r(t-a, y)\mathrm{d}y,&{}\ a<r+t,\\ \displaystyle \frac{\pi (a)}{\pi (a-r-t)}\int _\Omega \Gamma _2(r+t,x,y)\phi _2(a-r-t, y)\mathrm{d}y,&{}\ a\ge r+t. \end{array}\right. \end{aligned}$$

(4.11)

After passing elementary calculation, we have

$$\begin{aligned} u_r(0,a-t,x)= \left\{ \begin{array}{ll} \displaystyle \pi (a-t)\int _\Omega \Gamma _2(a-t,x,y)u_r(t-a, y)\mathrm{d}y, ~~~~~ &{}a\in [t,r+t),\\ \displaystyle \frac{\pi (a-t)}{\pi (a-r-t)}\int _\Omega \Gamma _2(r ,x,y)\phi _2(a-r-t, y)\mathrm{d}y, ~~~~~ &{}a\ge r+t. \end{array}\right. \end{aligned}$$

On the other hand,

$$\begin{aligned}&\frac{\pi (a)}{\pi (a-t)}\int _\Omega \Gamma _2( t,x,y)u_r(0,a-t,y)\mathrm{d}y\\&=\left\{ \begin{array}{ll} \displaystyle \pi (a)\int _\Omega \Gamma _2(a ,x,y)u_r(t-a, y)\mathrm{d}y, &{} a\in [t,r+t),\\ \displaystyle \frac{\pi (a)}{\pi (a-r-t)}\int _\Omega \Gamma _2(r+t ,x,y)\phi _2(a-r-t, y)\mathrm{d}y, &{} a\ge r+t\text{. } \end{array}\right. \end{aligned}$$

Combined with (4.11), we directly have

$$\begin{aligned} u_r(t,a ,x) = \left\{ \begin{aligned} \displaystyle&\pi (a)\int _\Omega \Gamma _2(a ,x,y)u_r(t-a, y)\mathrm{d}y, ~~~~~&t-a>0,\\ \displaystyle&\frac{\pi (a)}{\pi (a-t)}\int _\Omega \Gamma _2(t ,x,y)u_r(0,a- t, y)\mathrm{d}y, ~~~~~&a-t\ge 0. \end{aligned}\right. \end{aligned}$$

(4.12)

It then follows from (4.9), (4.10) and (4.12) that for all $r\ge 0$ and $t\ge 0$,

$$\begin{aligned} \Theta (t, T(r,\cdot ), u_r(t,\cdot ,\cdot ), V(r,\cdot )) =(T_r(t ), u_r(t,\cdot ), V_r(t ))=\Theta (r+t, \phi _1, \phi _2, \phi _3). \end{aligned}$$

This completes the proof.$\square$

Let

$$\begin{aligned}&\mathbb {D}:=\left\{ (\phi _1, \phi _2, \phi _3)\in \mathbb {X}^+ \times \mathbb {Y}^+\times \mathbb {X}^+: \beta _1\phi _1\frac{\phi _3}{1+\alpha \phi _3}\right. \\&\left. \quad +\beta _2\phi _1\int ^{+\infty }_0q(a)\phi _2(a,x)\mathrm{d}a>0\ \text{ for } \text{ some }\ x\in \Omega \right\} . \end{aligned}$$

The following result implies that the solution of (1.10) is uniformly weak $|\cdot |_\mathbb {X}$-persistence (see also in [5, Lemma 6.1] and [4, Lemma 5.2]).

Lemma 4.2

If $\mathfrak {R}_0 > 1$ and $(\phi _1, \phi _2, \phi _3) \in \mathbb {D}$, then

$$\begin{aligned} \limsup _{t\rightarrow +\infty }|u(t,\cdot )|_\mathbb {X}>\varepsilon _1 \end{aligned}$$

holds for a sufficiently small constant number $\varepsilon _1> 0$.

Proof

Since $\mathfrak {R}_0 > 1$, choosing a sufficiently small number $\varepsilon > 0$ such that

$$\begin{aligned} \begin{aligned} \frac{h-\varepsilon }{d}\left( \beta _2\int _0^{\infty }q(a)\pi (a)\mathrm{d}a +(\beta _1-\varepsilon )\int _0^{\infty }e^{-cs}\mathrm{d}s\int _0^{\infty }p(a)\pi (a)\mathrm{d}a\right) >1. \end{aligned} \end{aligned}$$

(4.13)

If there exists $t_1>0$ such that

$$\begin{aligned} \mid u(t,x)\mid _\mathbb {X}\le \varepsilon ,\ \text{ for } \text{ all }\ t\ge t_1,\ x\in \Omega , \end{aligned}$$

then, by (4.13), we can choose a small $\lambda >0$ and $t_2>t_1$ such that $\tilde{\mathfrak {R}}>1$, where

$$\begin{aligned} \begin{aligned} \tilde{\mathfrak {R}}:=\frac{h-\varepsilon }{d}(1-e^{-d\tilde{s}})\left( \beta _2\int _0^{\infty }q(a)\pi (a)e^{-\lambda a}\mathrm{d}a +(\beta _1-\varepsilon )\int _0^ \infty e^{-cs}e^{-\lambda s }\mathrm{d}s \int _0^{\infty }p(a)\pi (a)e^{-\lambda a}\mathrm{d}a \right) , \end{aligned} \end{aligned}$$

(4.14)

and $\tilde{s}=t_2-t_1$. By using this $\varepsilon$,

$$\begin{aligned} \frac{\partial T}{\partial t} \ge d_1\Delta T+h-\varepsilon -dT,\ t>t_2,\ x\in \Omega . \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} \displaystyle T&\ge e^{-d(t-t_1)}\int _\Omega \Gamma _1(t-t_1,x,y)T(t_1,y)\mathrm{d}y+\frac{h-\varepsilon }{d}\left( 1-e^{-d(t-t_1)}\right) \\&\ge \frac{h-\varepsilon }{d}\left( 1-e^{-d\tilde{s}}\right) ,\ \text{ for } \text{ all }\ t>t_2,\ x\in \Omega . \end{aligned} \end{aligned}$$

Similarly,

$$\begin{aligned} \begin{aligned} \displaystyle V&\ge \int _0^te^{-c(t-s)}\int _\Omega \Gamma _3(t-s,x,y)\int _0^\infty p(a)u(s,a,y)\mathrm{d}a\mathrm{d}y\mathrm{d}s \\&\ge \int _0^te^{-cs}\int _\Omega \Gamma _3(s,x,y)\int _0^{t-s} p(a)\pi (a)\int _\Omega \Gamma _2(a,y,z)u(t-s-a,z)\mathrm{d}z\mathrm{d}a\mathrm{d}y\mathrm{d}s \end{aligned} \end{aligned}$$

holds for all $t>t_2,\ x\in \Omega$. Not that the incidence function $f(V)=\beta _1\frac{V}{1+\alpha V}$ satisfies $f(0)=0$, $f'(V)=\frac{\beta _1}{(1+\alpha V)^2}>0$ and $f''(V)=\frac{-2\alpha \beta _1}{(1+\alpha V)^3}<0$. Due to the fact that $\lim \limits _{V\rightarrow 0} \frac{f(V)}{V}=f'(0)$, there exists a $\hat{\varrho }$ such that

$$\begin{aligned} f(V)\ge \left( f'(0)-\varepsilon \right) V,\ \forall \ \Vert V\Vert <\hat{\varrho }. \end{aligned}$$

Using the fact $\varepsilon _1=\min \{\hat{\varrho },\varepsilon \}$, together with Lemma 4.1, we take $t_2=0$ (and thus, $t_1=-\tilde{s}$) by taking $T(t_2,x)$, $V(t_2,x)$ and $u(t_2,a,x)$ as a new initial condition. Hence,

$$\begin{aligned} \begin{aligned} \displaystyle u(t,x)&\ge \frac{h-\varepsilon }{d}\left( 1-e^{-d\tilde{s}}\right) \left( \beta _2\int _0^tq(a)\pi (a) \int _\Omega \Gamma _2(a,x,y)u(t-a,y)\mathrm{d}y\mathrm{d}a\right. \\&\quad \left. +\left( \beta _1-\varepsilon \right) \int _0^te^{-cs}\int _\Omega \Gamma _3(s,x,y)\int _0^{t-s} p(a)\pi (a)\int _\Omega \Gamma _2(a,y,z)u(t-s-a,z)\mathrm{d}z\mathrm{d}a\mathrm{d}y\mathrm{d}s\right) . \end{aligned} \end{aligned}$$

(4.15)

Obviously, for all $x\in \Omega$, $\int _0^\infty e^{-\lambda t}u(t,x)\mathrm{d}t<\infty$. Define $u(t,\hat{x})=\min _{x\in \Omega } u(t,x)$. Taking Laplace transform on both sides of (4.15), we get

$$\begin{aligned}&\ \int _0^\infty e^{-\lambda t}u(t,\hat{x})\mathrm{d}t\\&\quad \ge \frac{h-\varepsilon }{d}\left( 1-e^{-d\tilde{s}}\right) \left( \beta _2\int _0^\infty e^{-\lambda t}\int _0^tq(a)\pi (a) \int _\Omega \Gamma _2(a,\hat{x},y)u(t-a,y)\mathrm{d}y\mathrm{d}a\mathrm{d}t\right. \\&\qquad \left. +\left( \beta _1-\varepsilon \right) \int _0^\infty e^{-\lambda t}\int _0^te^{-cs}\int _\Omega \Gamma _3(s,\hat{x},y)\int _0^{t-s} p(a)\pi (a)\right. \\&\left. \qquad \qquad \int _\Omega \Gamma _2(a,y,z)u(t-s-a,z)\mathrm{d}z\mathrm{d}a\mathrm{d}y\mathrm{d}s\mathrm{d}t\right) \\&\quad \ge \frac{h-\varepsilon }{d}\left( 1-e^{-d\tilde{s}}\right) \left( \beta _2\int _0^\infty q(a)\pi (a)\int _a^\infty e^{-\lambda t} \int _\Omega \Gamma _2(a,\hat{x},y)u(t-a,y)\mathrm{d}y\mathrm{d}t\mathrm{d}a\right. \\&\left. +\left( \beta _1-\varepsilon \right) \int _0^\infty e^{-cs}\int _s^\infty e^{-\lambda t}\right. \\&\left. \qquad \qquad \int _\Omega \Gamma _3(s,\hat{x},y)\int _0^{t-s}p(a)\pi (a)\int _\Omega \Gamma _2(a,y,z)u(t-s-a,z)\mathrm{d}z\mathrm{d}a\mathrm{d}y\mathrm{d}t\mathrm{d}s\right) . \end{aligned}$$

After passing elementary calculations, we obtain

$$\begin{aligned}&\ \int _0^\infty e^{-\lambda t}u(t,\hat{x})\mathrm{d}t\\&\quad \ge \frac{h-\varepsilon }{d}\left( 1-e^{-d\tilde{s}}\right) \left( \beta _2\int _0^\infty q(a)\pi (a)e^{-\lambda a}\int _\Omega \Gamma _2(a,\hat{x},y) \int _0^\infty e^{-\lambda (t-a)}u(t,y)\mathrm{d}t \mathrm{d}y\mathrm{d}a\right. \\&\qquad \left. +\left( \beta _1-\varepsilon \right) \int _0^\infty e^{-cs}e^{-\lambda s}\int _0^\infty e^{-\lambda t}\int _\Omega \Gamma _3(s,\hat{x},y)\right. \\&\qquad \left. \int _0^ tp(a)\pi (a)\int _\Omega \Gamma _2(a,y,z)u(t-a,z)\mathrm{d}z\mathrm{d}a\mathrm{d}y\mathrm{d}t\mathrm{d}s\right) \\&\quad \ge \frac{h-\varepsilon }{d}\left( 1-e^{-d\tilde{s}}\right) \left( \beta _2\int _0^\infty q(a)\pi (a)e^{-\lambda a}\int _\Omega \Gamma _2(a,\hat{x},y) \int _0^\infty e^{-\lambda t}u(t,y)\mathrm{d}t \mathrm{d}y\mathrm{d}a\right. \\&\qquad \left. +\left( \beta _1-\varepsilon \right) \int _0^\infty e^{-cs}e^{-\lambda s}\int _0^\infty p(a)\pi (a) e^{-\lambda a}\int _\Omega \Gamma _3(s,\hat{x},y)\right. \\&\qquad \left. \int _0^\infty e^{-\lambda t}\int _\Omega \Gamma _2(a,y,z)u(t,z)\mathrm{d}z\mathrm{d}t\mathrm{d}y\mathrm{d}a\mathrm{d}s\right) . \end{aligned}$$

Consequently, we obtain that

$$\begin{aligned}&\ \int _0^\infty e^{-\lambda t}u(t,\hat{x})\mathrm{d}t\\&\quad \ge \frac{h-\varepsilon }{d}\left( 1-e^{-d\tilde{s}}\right) \left( \beta _2\int _0^\infty q(a)\pi (a)e^{-\lambda a}\int _\Omega \Gamma _2(a,\hat{x},y)\right. \\&\qquad \left. \int _0^\infty e^{-\lambda t}u(t,y)\mathrm{d}t \mathrm{d}y\mathrm{d}a\right. \\&\qquad \left. +\left( \beta _1-\varepsilon \right) \int _0^\infty e^{-cs}e^{-\lambda s}\int _0^\infty p(a)\pi (a) e^{-\lambda a}\int _\Omega \Gamma _3(s,\hat{x},y)\right. \\&\qquad \left. \int _\Omega \Gamma _2(a,y,z)\int _0^\infty e^{-\lambda t}u(t,z)\mathrm{d}t\mathrm{d}z\mathrm{d}y\mathrm{d}a\mathrm{d}s\right) \\&\quad \ge \tilde{\mathfrak {R}}\int _0^\infty e^{-\lambda t}u(t,\hat{x})\mathrm{d}t, \end{aligned}$$

which is a contradiction with (4.14). This proves Lemma 4.2.$\square$

By the arguments similar to those in [4, Proposition 5.3] and [16, Theorem 1], we arrive at the below assertion on the strong $|\cdot |_X$-persistence.

Proposition 4.1

Suppose that $\mathfrak {R}_0 > 1$. For any $(\phi _1, \phi _2, \phi _3) \in \mathbb {D}$, there exists a sufficiently small number $\epsilon _2 > 0$ such that

$$\begin{aligned} \liminf _{t\rightarrow +\infty }|u(t, \cdot )|_X>\epsilon _2. \end{aligned}$$

With the help of Proposition 4.1, we show the following result.

Proposition 4.2

If $\mathfrak {R}_0>1$, system (1.6) is uniformly strongly persistent, namely, there exists a positive value $\varepsilon$ such that for any solution with the initial condition in $\mathbb {D}$

$$\begin{aligned} \liminf _{t\rightarrow \infty ,x\in \Omega }T(t,x)>\varepsilon ,\ \liminf _{t\rightarrow \infty ,x\in \Omega }u(t,a,x)>\varepsilon ,\ \liminf _{t\rightarrow \infty ,x\in \Omega }V(t,x)>\varepsilon , \end{aligned}$$

for $(a, x)\in \mathbb {R}_+\times \Omega$.

Proof

By Proposition 4.1, there exists positive constants $\eta$ and $T_0$ such that $u(t,a,x)\ge \eta \pi (a)$ for $t\ge T_0$. Then there exists a sufficiently small constant $\eta _0$ such that $u(t,a,x)\ge \eta \pi (a) - \eta _0$. It follows from the third equation of (1.6) that

$$\begin{aligned} \frac{\partial V}{\partial t}\ge d_3 \Delta V+ H -c V \end{aligned}$$

where $H = \int _0^\infty p(a) (\eta \pi (a) - \eta _0) \text {d} a$. Hence,

$$\begin{aligned} V(t,x) \ge H \int _0^t e^{-ca}\int _\Omega \Gamma _3(a,x,y)\text {d}a\text {d}y = \frac{H}{c}(1-e^{-ct}). \end{aligned}$$

Thus, there exists $\eta _1$ and $T_2>T_1$ such that $V(t,x)\ge \varepsilon _1$. Lastly, by the positivity of T(t, x) and choose $\eta = \min \{\eta _0,\eta _1\}$, we finish the proof.$\square$

4.3 Global Attractivity of Steady States

This subsection is spent on the global asymptotic stability of $E_0$ and $\hat{E}$. Combined with local asymptotic stability and global attractivity of equilibria, we shall confirm that both $E_0$ and $\hat{E}$ are globally asymptotically stable. The global attractivity of $E_0$ and $\hat{E}$ is achieved by the technique of Lyapunov functionals.

Theorem 4.2

Suppose that $\mathfrak {R}_0 < 1$, then $E_0$ is globally asymptotically stable.

Proof

Let $g(\alpha ) = \alpha -1 -\ln \alpha ,\ \alpha \in \mathbb {R}^+$. Then $g(\alpha )\ge 0$ for all $\alpha \in \mathbb {R}^+$ and the equality holds if and only if $\alpha =1$.

Define a Lyapunov function $L_{E_0}(t):\ \mathbb {D}\rightarrow \mathbb {R}$:

$$\begin{aligned} L_{E_0}(t)=\int _\Omega [L_T(t,x)+L_u(t,x)+L_V(t,x)]\mathrm{d}x, \end{aligned}$$

where $L_T=T_0g(\frac{T}{T_0})$, $L_u=\int _0^\infty \Psi (a)u(t,a,x)\mathrm{d}a$ and $L_V=\frac{\beta _1T_0}{c}V$. The function $\Psi (a)$ is nonnegative and integrable. We define $\Psi (a)$ as

$$\begin{aligned} \Psi (a)=\int _a^\infty \left( \beta _1T_0\frac{p(\theta )}{c}+\beta _2T_0q(\theta )\right) \frac{\pi (\theta )}{\pi (a)}\mathrm{d}\theta . \end{aligned}$$

Obviously, we have the following properties for $\Psi (a)$,

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \Psi '(a)=-\left( \beta _1T_0\frac{p(a)}{c}+\beta _2T_0q(a)\right) +\theta (a)\Psi (a),\\ \displaystyle \Psi (0)=\mathfrak {R}_0. \end{array}\right. \end{aligned}$$

(4.16)

We first calculate the derivative of $L_T(t, x)$ along the solution of system (1.6), obtaining that

$$\begin{aligned} \frac{\partial L_T}{\partial t} =&\ d_1\frac{(T-T_0)\Delta T}{T}-d\frac{(T-T_0)^2}{T}+\left[ \beta _1T_0\frac{V}{1+\alpha V}\right. \nonumber \\&\ \left. +\beta _2T_0\int _0^{+\infty }\ q(a)u(t,a,x)\mathrm{d}a\right] -u(t,0,x). \end{aligned}$$

(4.17)

By (1.8), we rewrite $L_u(t, x)$ as

$$\begin{aligned} L_u =&\ \int _0^t\Psi (t-a)\pi (t-a)\int _\Omega \Gamma _2(t-a,x,y)u(a,0,y)\mathrm{d}y\mathrm{d}a\\&\ +\int _0^\infty \Psi (a+t)\frac{\pi (a+t)}{\pi (a)}\int _\Omega \Gamma _2(t,x,y)\phi _2(a,y)\mathrm{d}y\mathrm{d}a. \end{aligned}$$

It then follows that

$$\begin{aligned} \frac{\partial L_u}{\partial t}=&\ \Psi (0)\int _\Omega \Gamma _2(0,x,y)u(t,0,y)\mathrm{d}y+ \int _0^t\frac{\partial \Psi (t-a)}{\partial t}\pi (t-a)\int _\Omega \Gamma _2(t-a,x,y)u(a,0,y)\mathrm{d}y\mathrm{d}a\nonumber \\&\ -\int _0^t \theta (t-a) \Psi (t-a)\pi (t-a)\int _\Omega \Gamma _2(t-a,x,y)u(a,0,y)\mathrm{d}y\mathrm{d}a\nonumber \\&\ +\int _0^t\Psi (t-a)\pi (t-a)\int _\Omega \frac{\partial \Gamma _2(t-a,x,y)}{\partial t}u(a,y)\mathrm{d}y\mathrm{d}a\nonumber \\&\ +\int _0^\infty \frac{\partial \Psi (t+a)}{\partial t}\frac{\pi (t+a)}{\pi (a)}\int _\Omega \Gamma _2(a+t,x,y)\phi _2(a,y)\mathrm{d}y\mathrm{d}a\\&\ -\int _0^\infty \theta (t+a) \Psi (t+a)\frac{\pi (t+a)}{\pi (a)}\int _\Omega \Gamma _2(a+t,x,y)\phi _2(a,y)\mathrm{d}y\mathrm{d}a\nonumber \\&\ +\int _0^\infty \Psi (t+a)\frac{\pi (t+a)}{\pi (a)}\int _\Omega \frac{\partial \Gamma _2(a+t,x,y)}{\partial t}\phi _2(a,y)\mathrm{d}y\mathrm{d}a.\nonumber \end{aligned}$$

(4.18)

It follows from [21] that the Green function $\Gamma _2$ satisfies $\int _\Omega \Gamma _2(0,x,y)u(t,0,y)\mathrm{d}y = u(t,0,x)$ and $\frac{\partial \Gamma _2}{\partial t} = d_2\Delta u(t,a,x)$. On the other hand, it follows from (1.8) that

$$\begin{aligned}&\int _0^t\Psi _t(t-a)\pi (t-a)\int _\Omega \Gamma _2(t-a,x,y)u(a,0,y)\mathrm{d}y\mathrm{d}a \\&\quad + \int _0^\infty \Psi _t(t+a)\frac{\pi (t+a)}{\pi (a)}\int _\Omega \Gamma _2(t,x,y)\phi _2(a,y)\mathrm{d}y\mathrm{d}a\\&\quad =\int _0^t\Psi '(a)\pi (a)\int _\Omega \Gamma _2(a,x,y)u(t-a,0,y)\mathrm{d}y\mathrm{d}a \\&\quad + \int _t^\infty \Psi '(a)\frac{\pi (a)}{\pi (a-t)}\int _\Omega \Gamma _2(t,x,y)\phi _2(a-t,y)\mathrm{d}y\mathrm{d}a\\&\quad = \int _0^\infty \Psi '(a) u(t,a,x)\text {d}a \end{aligned}$$

where $\Psi _t(t-a): = \frac{\partial \Psi (t-a)}{\partial t}$ and $\Psi '(a):=\frac{\partial \Psi (a)}{\partial a}$. Same arguments with the other terms of (4.18), we have

$$\begin{aligned} \frac{\partial L_u}{\partial t}= \Psi (0)u(t,0,x)+\int _0^\infty [\Psi '(a)-(\theta (a)-d_2\Delta )\Psi (a)]u(t,a,x)\mathrm{d}a. \end{aligned}$$

(4.19)

Further, we calculate the derivative of $L_V$, obtaining that

$$\begin{aligned} \begin{aligned} \frac{\partial L_V}{\partial t}=\frac{\beta _1T_0}{c}d_3\Delta V +\frac{\beta _1T_0}{c}\int _0^\infty p(a)u(t,a,x)\mathrm{d}a-\beta _1T_0V. \end{aligned} \end{aligned}$$

(4.20)

Finally, we integrate the equation (4.17), (4.19) and (4.20) over $\Omega$, obtaining that

$$\begin{aligned} \begin{aligned} \frac{d L_{E_0}(t)}{d t}=&\ \int _\Omega \bigg [d_1\frac{(T-T_0)\Delta T}{T}-d\frac{(T-T_0)^2}{T}+[\beta _1T_0\frac{V}{1+\alpha V}+\beta _2T_0\int _0^{+\infty }\ q(a)u(t,a,x)\mathrm{d}a]\\&\ -u(t,0,x)+\Psi (0)u(t,0,x)+\int _0^\infty [\Psi '(a)-(\theta (a)-d_2\Delta )\Psi (a)]u(t,a,x)\mathrm{d}a\\&+\frac{\beta _1T_0}{c}d_3\Delta V +\frac{\beta _1T_0}{c}\int _0^\infty p(a)u(t,a,x)\mathrm{d}a-\beta _1T_0V\bigg ]\mathrm{d}x\\ =&\ -d_1T_0\int _\Omega \frac{\Vert \nabla T\Vert ^2}{T^2}\mathrm{d}x-d\int _\Omega \frac{(T-T_0)^2}{T}\mathrm{d}x\\&\qquad +\int _\Omega (\Psi (0)-1)u(t,0,x)\mathrm{d}x-\int _\Omega \frac{T_0\beta _1\alpha V^2}{1+\alpha V}\text {d}x\\&+\int _\Omega \int _0^\infty \left[ \beta _1T_0\frac{p(a)}{c}+\beta _2T_0q(a)+\Psi '(a)-(\theta (a)-d_2\Delta )\Psi (a)\right] u(t,a,x)\mathrm{d}a\mathrm{d}x. \end{aligned} \end{aligned}$$

Here we have used $\int _\Omega \Delta T \text {d}x=0$ and $\int _\Omega \frac{\Delta T}{T} \text {d}x= \int _\Omega \frac{\Vert \nabla T\Vert ^2}{T^2}\text {d}x$. With the help of (4.16), one arrives at

$$\begin{aligned} \begin{aligned}&\frac{\text {d} L_{E_0}(t)}{\text {d} t}=\ -d_1\int _\Omega \frac{\Vert \nabla T\Vert ^2}{T^2}\mathrm{d}x-d\int _\Omega \frac{(T-T_0)^2}{T}\mathrm{d}x\\&\quad -\int _\Omega \beta _1T_0\frac{\alpha V^2}{1+\alpha V}\text {d}x+\int _\Omega (\mathfrak {R}_0-1)u(t,0,x)\mathrm{d}x. \end{aligned} \end{aligned}$$

As a result, with the help of [41, Theorem 4.2], $E_0$ is globally attractive in $\mathbb {D}$ if $\mathfrak {R}_0 < 1$.$\square$

Now we are ready to confirm that $\hat{E}$ is globally attractive in $\mathbb {D}$, where $\hat{E}$ is the space-independent infection equilibrium of (1.10). We first show the following lemma.

Lemma 4.3

The infection steady state $(\hat{T}, \hat{u}(a), \hat{V})$ satisfies

$$\begin{aligned} \begin{aligned} \frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^{\infty }&p(a)\hat{u}(a) \left[ 1-\frac{(1+\alpha \hat{V})TV\hat{u}(0)}{(1+\alpha V)\hat{T}\hat{V}u(t,0,x) }\right] \mathrm{d}a \ \\&+\beta _2\hat{T}\int _0^{\infty }q(a)\hat{u}(a)\left[ 1-\frac{Tu(t,a,x)\hat{u}(0)}{\hat{T}\hat{u}(a)u(t,0,x) }\right] \mathrm{d}a \ =0. \end{aligned} \end{aligned}$$

Proof

By the forth equation of (3.4), we have

$$\begin{aligned}&\ \frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^{\infty }p(a)\hat{u}(a)\text {d}a + \beta _2\hat{T}\int _0^{\infty }q(a)\hat{u}(a)\text {d}a\\&\quad =\ \beta _1\hat{T}\frac{\hat{V}}{1+\alpha \hat{V}}+\beta _2\hat{T}\int _0^{+\infty }q(a)\hat{u}(a)\mathrm{d}a\\&\quad =\ \hat{u}(0). \end{aligned}$$

On the other hand, using the fact that

$$\begin{aligned} u(t,0,x)=\beta _1T\frac{V}{1+\alpha V}+\beta _2T\int _0^\infty q(a)u(t,a,x)\mathrm{d}a, \end{aligned}$$

we have

$$\begin{aligned}&\ \frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^{\infty }p(a)\hat{u}(a) \frac{(1+\alpha \hat{V})TV\hat{u}(0)}{(1+\alpha V)\hat{T}\hat{V}u(t,0,x) }\mathrm{d}a +\beta _2\hat{T}\int _0^{\infty }q(a)\hat{u}(a)\frac{Tu(t,a,x)\hat{u}(0)}{\hat{T}\hat{u}(a)u(t,0,x) }\mathrm{d}a\\&\quad =\ \left( \frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^{\infty }p(a)\hat{u}(a) \frac{(1+\alpha \hat{V})TV}{(1+\alpha V)\hat{T}\hat{V}}\mathrm{d}a +\beta _2\hat{T}\int _0^{\infty }q(a)\hat{u}(a)\frac{Tu(t,a,x)}{\hat{T}\hat{u}(a)}\mathrm{d}a\right) \frac{\hat{u}(0)}{u(t,0,x)}\\&\quad =\ \hat{u}(0). \end{aligned}$$

This finishes the proof. $\square$

Theorem 4.3

Suppose that $\mathfrak {R}_0 >1$ and initial data $(\phi _1, \phi _2, \phi _3) \in \mathbb {D}$, then $\hat{E}$ is globally asymptotically stable.

Proof

In this proof, we first give some notations,

$$\begin{aligned} \begin{aligned}&\bar{L}_T(t,x)=G[T(t,x),\hat{T}],\\&\bar{L}_u(t,x)=\int _0^\infty \Psi _1(a)G[u(t,a,x),\hat{u}(a)]\mathrm{d}a,\\&\bar{L}_V(t,x)=\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}G[V(t,x),\hat{V}], \end{aligned} \end{aligned}$$

where

$$\begin{aligned} G[m,n](t,x)=m-n-n\ln \frac{m}{n}, \end{aligned}$$

and

$$\begin{aligned} \Psi _1(a)=\int _a^\infty \left( \frac{\beta _1 \hat{T}p(\theta )}{c(1+\alpha \hat{V})}+\beta _2 \hat{T}q(\theta )\right) \frac{\pi (\theta )}{\pi (a)}\mathrm{d}\theta . \end{aligned}$$

Define a Lyapunov functional as

$$\begin{aligned} L_{\hat{E}}(t)=\int _\Omega [\bar{L}_T(t,x)+\bar{L}_u(t,x)+\bar{L}_V(t,x)]\mathrm{d}x. \end{aligned}$$

We calculate the derivative of $\bar{L}_T$, together with $h= d\hat{T}+\hat{u}(0)$, obtaining that

$$\begin{aligned} \frac{\partial \bar{L}_T}{\partial t}=\left( 1-\frac{\hat{T}}{T}\right) d_1\Delta T-d\frac{(T-\hat{T})^2}{T}+\left( 1-\frac{\hat{T}}{T}\right) (\hat{u}(0)-u(t,0,x)). \end{aligned}$$

Next, we deal with $\bar{L}_u$, clearly,

$$\begin{aligned} \frac{\partial \bar{L}_u}{\partial t}=&\ \int _0^\infty \Psi _1(a)\left[ 1-\frac{\hat{u}(a)}{u(t,a,x)}\right] \frac{\partial u(t,a,x)}{\partial t}\text {d}a\\ =&\ \int _0^\infty \Psi _1(a)\left[ 1-\frac{\hat{u}(a)}{u(t,a,x)}\right] \left( d_2 \Delta u(t,a,x)-\theta (a)u(t,a,x) - \frac{\partial u(t,a,x)}{\partial a}\right) \text {d}a. \end{aligned}$$

Note that

$$\begin{aligned}&\ \hat{u}(a) \frac{\partial }{\partial a}\left( \frac{u(t,a,x)}{\hat{u}(a)}-1-\ln \frac{u(t,a,x)}{\hat{u}(a)}\right) \\ =&\ \hat{u}(a) \left( 1- \frac{\hat{u}(a)}{u(t,a,x)}\right) \left( \frac{u_a(t,a,x)\hat{u}(a) - u(t,a,x)\hat{u}_a(a)}{\hat{u}^2(a)}\right) \\ =&\ \left( 1- \frac{\hat{u}(a)}{u(t,a,x)}\right) \frac{\partial u(t,a,x)}{\partial a} + \left( 1- \frac{\hat{u}(a)}{u(t,a,x)}\right) \theta (a)u(t,a,x), \end{aligned}$$

here we have used the fact that $\hat{u}_a(a) = -\theta (a) \hat{u}(a)$. Further, direct calculation yields

$$\begin{aligned} {\Psi _1}'(a)\hat{u}(a) + \Psi _1(a)\hat{u}'(a) = - \left( \frac{\beta _1 \hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2 \hat{T}q(a)\right) \hat{u}(a). \end{aligned}$$

Using integration by parts, one has

$$\begin{aligned}&\ \int _0^\infty \Psi _1(a)\left( 1- \frac{\hat{u}(a)}{u(t,a,x)}\right) \frac{\partial u(t,a,x)}{\partial a}\text {d}a\\&\quad =\ \int _0^\infty \Psi _1(a)\hat{u}(a) \frac{\partial }{\partial a}\left( \frac{u(t,a,x)}{\hat{u}(a)}-1-\ln \frac{u(t,a,x)}{\hat{u}(a)}\right) \text {d}a\\&\qquad \ - \int _0^\infty \Psi _1(a)\left( 1- \frac{\hat{u}(a)}{u(t,a,x)}\right) \theta (a)u(t,a,x)\text {d}a\\&\quad =\ \Psi _1(a)\hat{u}(a) \left( \frac{u(t,a,x)}{\hat{u}(a)}-1-\ln \frac{u(t,a,x)}{\hat{u}(a)}\right) \bigg |_{a=0}^{a=\infty }\\&\qquad - \int _0^\infty \left( \frac{u(t,a,x)}{\hat{u}(a)}-1-\ln \frac{u(t,a,x)}{\hat{u}(a)}\right) \left( {\Psi _1}'(a)\hat{u}(a) + \Psi _1(a)\hat{u}'(a)\right) \text {d}a\\&\qquad \ - \int _0^\infty \Psi _1(a)\left( 1- \frac{\hat{u}(a)}{u(t,a,x)}\right) \theta (a)u(t,a,x)\text {d}a\\&\quad =\ \lim _{a\rightarrow \infty }\Psi _1(a) \hat{u}(a) g\left( \frac{u(t,a,x)}{\hat{u}(a)}\right) - \Psi _1(0) \hat{u}(0) g\left( \frac{u(t,0,x)}{\hat{u}(0)}\right) \\&\qquad \ +\int _0^\infty \hat{u}(a) \left[ \frac{\beta _1\hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2\hat{T}q(a) \right] g\left( \frac{u(t,a,x)}{\hat{u}(a)}\right) \text {d}a\\&\qquad +\int _0^\infty \hat{u}(a) \theta (a)\Psi _1(a)g\left( \frac{u(t,a,x)}{\hat{u}(a)}\right) \text {d}a\\&\qquad - \int _0^\infty \Psi _1(a)\left( 1- \frac{\hat{u}(a)}{u(t,a,x)}\right) \theta (a)u(t,a,x)\text {d}a\\&=\quad \ \lim _{a\rightarrow \infty }\Psi _1(a) \hat{u}(a) g\left( \frac{u(t,a,x)}{\hat{u}(a)}\right) - \Psi _1(0) \hat{u}(0) g\left( \frac{u(t,0,x)}{\hat{u}(0)}\right) \\&\ \qquad +\int _0^\infty \hat{u}(a) \left[ \frac{\beta _1\hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2\hat{T}q(a) \right] g\left( \frac{u(t,a,x)}{\hat{u}(a)}\right) \text {d}a\\&\qquad - \int _0^\infty \Psi _1(a)\left( 1- \frac{\hat{u}(a)}{u(t,a,x)}\right) \theta (a)u(t,a,x)\text {d}a, \end{aligned}$$

where g(x) was defined in the proof of Theorem 4.2. By hypothesis (H), we know that

$$\begin{aligned} \lim _{a\rightarrow \infty }\Psi _1(a) \hat{u}(a) g\left( \frac{u(t,a,x)}{\hat{u}(a)}\right) = 0. \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} \frac{\partial \bar{L}_u}{\partial t}=&\ \int _0^\infty \left( \frac{\beta _1\hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2\hat{T}q(a)\right) \left[ \hat{u}(a)-u(t,a,x)+\hat{u}(a)\ln \frac{u(t,a,x)}{\hat{u}(a)}\right] \mathrm{d}a\\&+\int _0^\infty \Psi _1(a)\left[ 1-\frac{\hat{u}(a)}{u(t,a,x)}\right] d_2\Delta u(t,a,x)\mathrm{d}a+\Psi _1(0)G[u(t,0,x),\hat{u}(0)]. \end{aligned} \end{aligned}$$

We further have the derivative of $\bar{L}_V$ as follows:

$$\begin{aligned} \frac{\partial \bar{L}_V}{\partial t} =&\ \frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})} \frac{\partial }{\partial t}\left[ V - \hat{V} - \hat{V} \ln \frac{V}{\hat{V}}\right] \\ =&\ \frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\left( 1-\frac{\hat{V}}{V}\right) \frac{\partial V}{\partial t}\\ =&\ \left( 1-\frac{\hat{V}}{V}\right) \left( \frac{d_3\beta _1\hat{T}}{c(1+\alpha \hat{V})}\Delta V+ \frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^\infty p(a)u(t,a,x)\mathrm{d}a-\frac{\beta _1\hat{T}V}{1+\alpha \hat{V}}\right) . \end{aligned}$$

By denoting $\hat{L}=\bar{L}_T+\bar{L}_u+\bar{L}_V$, we directly have

$$\begin{aligned} \begin{aligned} \frac{\partial \hat{L}}{\partial t} =&\ \left( 1-\frac{\hat{T}}{T}\right) d_1\Delta T-d\frac{(T-\hat{T})^2}{T}+\int _0^\infty \Psi _1(a)\left[ 1-\frac{\hat{u}(a)}{u(t,a,x)}\right] d_2\Delta u(t,a,x)\mathrm{d}a\\&\ +\left( 1-\frac{\hat{V}}{V}\right) \frac{d_3\beta _1\hat{T}}{c(1+\alpha V)}\Delta V+\Xi (t,x), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \Xi (t,x) =&\left( 1-\frac{\hat{T}}{T}\right) (\hat{u}(0)-u(t,0,x))\\&\ +\int _0^\infty \left( \frac{\beta _1\hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2\hat{T}q(a)\right) \left[ \hat{u}(a)-u(t,a,x)+\hat{u}(a)\ln \frac{u(t,a,x)}{\hat{u}(a)}\right] \mathrm{d}a\\&\ +\Psi _1(0)\hat{u}(0)\left( \frac{u(t,0,x)}{\hat{u}(0)}-1-\ln \frac{u(t,0,x)}{\hat{u}(0)}\right) \\&\ +\left( 1-\frac{\hat{V}}{V}\right) \left( \frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^\infty p(a)u(t,a,x)\mathrm{d}a-\frac{\beta _1\hat{T}V}{1+\alpha \hat{V}}\right) . \end{aligned}$$

Recall that

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle u(t,0,x)=\beta _1T\frac{V}{1+\alpha V}+\beta _2T\int _0^\infty q(a)u(t,a,x)\mathrm{d}a,\\ \displaystyle \hat{u}(0)=\beta _1\hat{T}\frac{\hat{V}}{1+\alpha \hat{V}}+\beta _2\hat{T}\int _0^\infty q(a)\hat{u}(a)\mathrm{d}a. \end{array}\right. \end{aligned}$$

Furthermore, by the forth equation of (3.4), we have

$$\begin{aligned} \beta _1 \hat{T} \frac{\hat{V}}{1+\alpha \hat{V}} = \int _0^\infty \frac{\beta _1 \hat{T}}{c(1+\alpha \hat{V})}p(a) \hat{u}(a)\text {d}a. \end{aligned}$$

Moreover, since

$$\begin{aligned} \Psi _1(0)=\int _0^\infty \left( \frac{\beta _1 \hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2 \hat{T}q(\theta )\right) \pi (a)\mathrm{d}a, \end{aligned}$$

and recall that $\hat{u}(a) = \hat{u}(0)\pi (a)$, we have

$$\begin{aligned}&\Psi _1(0)\hat{u}(0)\left( \frac{u(t,0,x)}{\hat{u}(0)}-1-\ln \frac{u(t,0,x)}{\hat{u}(0)}\right) \\&\quad =\int _0^\infty \left( \frac{\beta _1 \hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2 \hat{T}q(a)\right) \hat{u}(0) \pi (a)\left( \frac{u(t,0,x)}{\hat{u}(0)}-1-\ln \frac{u(t,0,x)}{\hat{u}(0)}\right) \mathrm{d}a\\&\quad =\int _0^\infty \left( \frac{\beta _1 \hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2 \hat{T}q(a)\right) \hat{u}(a)\left( \frac{u(t,0,x)}{\hat{u}(0)}-1-\ln \frac{u(t,0,x)}{\hat{u}(0)}\right) \mathrm{d}a. \end{aligned}$$

It then follows that

$$\begin{aligned} \Xi (t,x) =&\ \beta _1\hat{T}\frac{\hat{V}}{1+\alpha \hat{V}}+\beta _2\hat{T}\int _0^\infty q(a)\hat{u}(a)\mathrm{d}a -\beta _1T\frac{V}{1+\alpha V}-\beta _2T\int _0^\infty q(a)u(t,a,x)\mathrm{d}a\\&\ -\beta _1\hat{T}\frac{\hat{V}}{1+\alpha \hat{V}}\frac{\hat{T}}{T}-\beta _2\hat{T}\int _0^\infty q(a)\hat{u}(a)\mathrm{d}a\frac{\hat{T}}{T} +\beta _1\hat{T}\frac{V}{1+\alpha V}+\beta _2\hat{T}\int _0^\infty q(a)u(t,a,x)\mathrm{d}a\\&\ +\int _0^\infty \left( \frac{\beta _1\hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2\hat{T}q(a)\right) \left[ \hat{u}(a)-u(t,a,x)+\hat{u}(a)\ln \frac{u(t,a,x)}{\hat{u}(a)}\right] \mathrm{d}a\\&\ +\int _0^\infty \left( \frac{\beta _1 \hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2 \hat{T}q(a)\right) \hat{u}(a)\left( \frac{u(t,0,x)}{\hat{u}(0)}-1-\ln \frac{u(t,0,x)}{\hat{u}(0)}\right) \mathrm{d}a\\&\ +\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^\infty p(a)u(t,a,x)\mathrm{d}a-\frac{\beta _1\hat{T}V}{1+\alpha \hat{V}}\\&\ - \frac{\hat{V}}{V}\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^\infty p(a)u(t,a,x)\mathrm{d}a + \frac{\beta _1\hat{T}\hat{V}}{1+\alpha \hat{V}}\\ =&\ \beta _2\hat{T}\int _0^\infty q(a)\hat{u}(a)\left[ 1-\frac{\hat{T}}{T}-\ln \frac{u(t,a,x)}{u(t,0,x)}\right] \mathrm{d}a\\&\ +\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^\infty p(a)\hat{u}(a)\left[ 2-\frac{\hat{T}}{T}-\frac{V}{\hat{V}}+\frac{V(1+\alpha \hat{V})}{\hat{V}(1+\alpha V)}-\frac{\hat{V}u(t,a,x)}{V\hat{u}(a)} +\ln \frac{u(t,a,x)}{u(t,0,x)}\right] \mathrm{d}a. \end{aligned}$$

Note that

$$\begin{aligned}&\ \int _0^\infty \left( \frac{\beta _1 \hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2 \hat{T}q(a)\right) \hat{u}(a)\frac{u(t,0,x)}{\hat{u}(0)}\text {d}a\\ =&\ \int _0^\infty \left( \frac{\beta _1 \hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2 \hat{T}q(a)\right) \hat{u}(a)\text {d}a\frac{u(t,0,x)}{\hat{u}(0)}\\ =&\ u(t,0,x)\\ =&\ \beta _1T\frac{V}{1+\alpha V}+\beta _2T\int _0^\infty q(a)u(t,a,x)\mathrm{d}a, \end{aligned}$$

and using the zero trick in Lemma 4.3, one has that

$$\begin{aligned} \Xi (t,x) =&\ \beta _1\hat{T}\frac{\hat{V}}{1+\alpha \hat{V}}+\beta _2\hat{T}\int _0^\infty q(a)\hat{u}(a)\mathrm{d}a\\&\ -\beta _1\hat{T}\frac{\hat{V}}{1+\alpha \hat{V}}\frac{\hat{T}}{T}-\beta _2\hat{T}\int _0^\infty q(a)\hat{u}(a)\mathrm{d}a\frac{\hat{T}}{T} +\beta _1\hat{T}\frac{V}{1+\alpha V}\\&\ +\int _0^\infty \left( \frac{\beta _1\hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2\hat{T}q(a)\right) \hat{u}(a)\ln \frac{u(t,a,x)}{\hat{u}(a)}\mathrm{d}a\\&\ -\int _0^\infty \left( \frac{\beta _1 \hat{T}p(a)}{c(1+\alpha \hat{V})}+\beta _2 \hat{T}q(a)\right) \hat{u}(a)\ln \frac{u(t,0,x)}{\hat{u}(0)}\mathrm{d}a\\&\ -\frac{\beta _1\hat{T}V}{1+\alpha \hat{V}} - \frac{\hat{V}}{V}\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^\infty p(a)u(t,a,x)\mathrm{d}a + \frac{\beta _1\hat{T}\hat{V}}{1+\alpha \hat{V}}\\&\ +\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^{\infty }p(a)\hat{u}(a) \left[ 1-\frac{(1+\alpha \hat{V})TV\hat{u}(0)}{(1+\alpha V)\hat{T}\hat{V}u(t,0,x) }\right] \mathrm{d}a \ \\&\ +\beta _2\hat{T}\int _0^{\infty }q(a)\hat{u}(a)\left[ 1-\frac{Tu(t,a,x)\hat{u}(0)}{\hat{T}\hat{u}(a)u(t,0,x) }\right] \mathrm{d}a\\ =&\ \beta _2\hat{T}\int _0^\infty q(a)\hat{u}(a)\left[ 2-\frac{Tu(t,a,x)\hat{u}(0)}{\hat{T}\hat{u}(a)u(t,0,x) }-\frac{\hat{T}}{T}+\ln \frac{u(t,a,x)}{\hat{u}(a)}+\ln \frac{\hat{u}(0)}{u(t,0,x)}\right] \mathrm{d}a\\&\ +\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^\infty p(a)\hat{u}(a)\left[ 2-\frac{\hat{T}}{T}-\frac{V}{\hat{V}}+\frac{V(1+\alpha \hat{V})}{\hat{V}(1+\alpha V)}-\frac{\hat{V}u(t,a,x)}{V\hat{u}(a)} \right] \mathrm{d}a\\&\ +\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^{\infty }p(a)\hat{u}(a) \left[ 1-\frac{(1+\alpha \hat{V})TV\hat{u}(0)}{(1+\alpha V)\hat{T}\hat{V}u(t,0,x) }+\ln \frac{u(t,a,x)}{\hat{u}(a)}+\ln \frac{\hat{u}(0)}{u(t,0,x)}\right] \mathrm{d}a\\&\ +\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^{\infty }p(a)\hat{u}(a) \left[ 1-1+\frac{1+\alpha V}{1+ \alpha \hat{V}}-\frac{1+\alpha V}{1+ \alpha \hat{V}}\right] \mathrm{d}a\\&\ +\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^{\infty }p(a)\hat{u}(a) \left[ \ln \frac{T}{\hat{T}}+\ln \frac{\hat{T}}{T}+\ln \frac{V}{\hat{V}}+\ln \frac{\hat{V}}{V}\frac{1+\alpha V}{1+ \alpha \hat{V}}+\ln \frac{1+ \alpha \hat{V}}{1+\alpha V}\right] \mathrm{d}a. \end{aligned}$$

Clearly, the last two terms of the above equation is zero, where we have used the fact that $\ln \frac{a}{b} + \ln \frac{b}{a} = 0$. We then have

$$\begin{aligned} \frac{\partial \hat{L}}{\partial t}= & {} \ \left( 1-\frac{\hat{T}}{T}\right) d_1\Delta T-d\frac{(T-\hat{T})^2}{T}\nonumber \\&\ +\int _0^\infty \Psi _1(a)\left[ 1-\frac{\hat{u}(a)}{u(t,a,x)}\right] d_2\Delta u(t,a,x)\mathrm{d}a+\left( 1-\frac{\hat{V}}{V}\right) \frac{d_3\beta _1\hat{T}}{c(1+\alpha \hat{V})}\Delta V\nonumber \\&\ -\beta _2\hat{T}\int _0^\infty q(a)\hat{u}(a)\left[ g\left( \frac{\hat{T}}{T}\right) +g\left( \frac{Tu(t,a,x)\hat{u}(0)}{\hat{T}\hat{u}(a)u(t,0,x) }\right) \right] \mathrm{d}a\nonumber \\&\ -\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^\infty p(a)\hat{u}(a)\left[ g\left( \frac{\hat{T}}{T}\right) +g\left( \frac{\hat{V}u(t,a,x)}{V\hat{u}(a)}\right) \right. \nonumber \\&\ \left. +g\left( \frac{1+\alpha V}{1+\alpha \hat{V}}\right) +g\left( \frac{(1+\alpha \hat{V})TV\hat{u}(0)}{(1+\alpha V)\hat{T}\hat{V}u(t,0,x) }\right) \right] \mathrm{d}a\nonumber \\&\ +\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _0^\infty p(a)\hat{u}(a)\left[ -1+\frac{1+\alpha V}{1+\alpha \hat{V}}+\frac{V(1+\alpha \hat{V})}{\hat{V}(1+\alpha V)}-\frac{V}{\hat{V}}\right] \mathrm{d}a.\nonumber \\ \end{aligned}$$

(4.21)

Consequently, we integrate (4.21) over $\Omega$, obtaining that

$$\begin{aligned} \frac{\text {d} L_{\hat{E}}(t)}{\text {d} t}=&\ -d_1\hat{T}\int _\Omega \frac{\Vert \nabla T\Vert ^2}{T^2}\mathrm{d}x-d\int _\Omega \frac{(T-\hat{T})^2}{T}\mathrm{d}x-\frac{d_3\beta _1\hat{T}\hat{V}}{c(1+\alpha \hat{V})}\int _\Omega \frac{\Vert \nabla V\Vert ^2}{V^2}\mathrm{d}x\\&\ -d_2\int _0^\infty \Psi _1(a)\hat{u}(a)\int _\Omega \frac{\Vert \nabla u(t,a,x)\Vert ^2}{u^2(t,a,x)}\mathrm{d}x\mathrm{d}a\\&\ -\beta _2\hat{T}\int _\Omega \int _0^\infty q(a)\hat{u}(a)\left[ g\left( \frac{\hat{T}}{T}\right) +g\left( \frac{Tu(t,a,x)\hat{u}(0)}{\hat{T}\hat{u}(a)u(t,0,x) }\right) \right] \mathrm{d}a\mathrm{d}x\\&\ -\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _\Omega \int _0^\infty p(a)\hat{u}(a)\left[ g\left( \frac{\hat{T}}{T}\right) +g\left( \frac{\hat{V}u(t,a,x)}{V\hat{u}(a)}\right) \right. \\&\ \left. +g\left( \frac{1+\alpha V}{1+\alpha \hat{V}}\right) +g\left( \frac{(1+\alpha \hat{V})TV\hat{u}(0)}{(1+\alpha V)\hat{T}\hat{V}u(t,0,x) }\right) \right] \mathrm{d}a\mathrm{d}x\\&\ -\frac{\beta _1\hat{T}}{c(1+\alpha \hat{V})}\int _\Omega \int _0^\infty p(a)\hat{u}(a)\frac{\alpha (V-\hat{V})^2}{\hat{V}(1+\alpha V)(1+\alpha \hat{V})}\mathrm{d}a\mathrm{d}x\\ \le&\ 0, \end{aligned}$$

where $g(\alpha ) = \alpha -1 -\ln \alpha \ge 0$, for $\alpha \in \mathbb {R}^+$. Note that each term of $\frac{\text {d} L_{\hat{E}}(t)}{\text {d} t}$ is non-negative, Hence, due to the terms contain $(T-\hat{T})^2$ and $(V-\hat{V})^2$, we must have $\frac{\text {d} L_{\hat{E}}(t)}{\text {d} t} =0$ holds if and only if $T = \hat{T}$, $V =\hat{V}$. Moreover, since $g(\alpha )=0$ if and only if $\alpha =1$, then $\frac{\text {d} L_{\hat{E}}(t)}{\text {d} t} =0$ means that

$$\begin{aligned} \frac{\hat{T}}{T}=\frac{\hat{V}u(t,a,x)}{V\hat{u}(a)}=\frac{1+\alpha V}{1+\alpha \hat{V}}=\frac{(1+\alpha \hat{V})TV\hat{u}(0)}{(1+\alpha V)\hat{T}\hat{V}u(t,0,x)}=\frac{Tu(t,a,x)\hat{u}(0)}{\hat{T}\hat{u}(a)u(t,0,x)}=1. \end{aligned}$$

Inserting $T = \hat{T}$ and $V =\hat{V}$ into the above relation, give us $u(t, a, x) = \hat{u}(a)$. With the help of [41, Theorem 4.2], together with Theorem 4.1, we confirm that $\hat{E}$ is globally asymptotically stable if $\mathfrak {R}_0>1$. This proves Theorem 4.3. $\square$

5 Numerical Simulation

To support and validate the global threshold type result of (1.10), we perform numerical simulations in the cases of the 1-dimensional and 2-dimensional domain. We first consider the spatially 1-dimensional case and fix $\Omega = (0, 1)$. We artificially set

$$\begin{aligned} h = 1,\ d = 0.1,\ b = 0.2,\ \alpha = 1,\ c = 0.1,\ d_1 = d_2=d_3=0.0002,\ p = q=1,\ \theta = 0.1. \end{aligned}$$

(5.1)

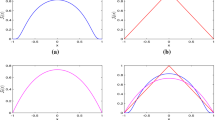
If we take $\beta _1 = \beta _2=0.0026$, then $\mathfrak {R}_0 = 0.95335 < 1$. From Theorem 4.2, $E_0$ is globally attractive. Figure 1a–c demonstrate that the density of uninfected target T cells approaches a positive level, the densities of infected T cells and the free virus particles decay to zeros as time evolves. The spatial distributions of infected T cells gradually enlarge with higher prevalence but decays as time evolves (see Fig. 1d).

Fig. 1

The time evolution of the densities of uninfected target T cells, infected T cells (with $U(t,x)=\int _0^{\infty }u(t,a,x)\text {d}a$) and the free virus particles of system (1.6) with (5.1) and $\beta _1 = \beta _2=0.0026$ ($\mathfrak {R}_0=0.95335 < 1$). The initial data is $\phi _1(x)=10,\ \phi _2(a,x)=e^{-b\times a-\int _0^a \theta (s)\text {d}s} (x-0.3)(0.7-x)$, and $\phi _3(x)=0$

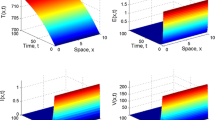
If we take $\beta _1 = \beta _2=0.003$, then $\mathfrak {R}_0 = 1.100021$. Theorem 4.3 ensures that $\hat{E}$ is globally attractive. From Fig. 2a–c, the densities of uninfected target T cells, the densities of infected T cells and the free virus particles go towards some positive distributions as time evolves. We have seen from Fig. 2d that the spatial distributions of infected T cells gradually enlarge with higher prevalence as time evolves.

Fig. 2

The time evolution of the densities of uninfected target T cells, infected T cells (with $U(t,x)=\int _0^{\infty }u(t,a,x)\text {d}a$) and the free virus particles of system (1.6) with (5.1) and $\beta _1 = \beta _2=0.003$ ($\mathfrak {R}_0=1.100021>1$). The initial data is $\phi _1(x)=10,\ \phi _2(a,x)=e^{-b\times a-\int _0^a \theta (s)\text {d}s} (x-0.3)(0.7-x)$, and $\phi _3(x)=0$

We next consider the spatially 2-dimensional case and fix $\Omega = (0, 1)\times (0,1)$. We artificially set the parameters the same as in (5.1). In Fig. 3, we see from Theorem 4.2 that $E_0$ is globally attractive. Figure 3a demonstrates that the density of uninfected target T cells approaches a positive level. Figure 3b, c demonstrate that the densities of infected T cells and the free virus particles decay to zeros as time evolves. In Fig. 4, we see from Theorem 4.3 that $\hat{E}$ is globally attractive, that is, the densities of uninfected target T cells, the densities of infected T cells and the free virus particles converges to some positive distributions as time evolves.

Fig. 3

The time evolution of the densities of uninfected target T cells, infected T cells (with $U(t,x)=\int _0^{\infty }u(t,a,x)\text {d}a$) and the free virus particles of system (1.6) with (5.1), $\Omega = (0, 1)\times (0,1)$ and $\beta _1 = \beta _2=0.0026$ ($\mathfrak {R}_0=0.95335 < 1$). The initial data is $\phi _1(x,y)=10,\ \phi _2(a,x,y)=e^{-b\times a-\int _0^a \theta (s)\text {d}s}(x-0.3)(0.7-x)(y-0.3)(0.7-y)$, and $\phi _3(x,y)=0$

Fig. 4

The time evolution of the densities of uninfected target T cells, infected T cells (with $U(t,x)=\int _0^{\infty }u(t,a,x)\text {d}a$) and the free virus particles of system (1.6) with (5.1), $\Omega = (0, 1)\times (0,1)$ and $\beta _1 = \beta _2=0.003$ ($\mathfrak {R}_0=1.100021>1$). The initial data is $\phi _1(x,y)=10,\ \phi _2(a,x,y)=e^{-b\times a-\int _0^a \theta (s)\text {d}s}(x-0.3)(0.7-x)(y-0.3)(0.7-y)$, and $\phi _3(x,y)=0$

6 Discussion

The stability analysis of infection-free and infection steady state has witnessed an important and fundamental approach for understanding viral dynamics. This paper is spent on the global threshold type dynamics of an infection age-space structured HIV infection model involving two infection routes. The formulated model is inspired from previous models (1.3) and (1.2), where global threshold dynamics of (1.3) is obtained in a spatially homogeneous case and global threshold dynamics of (1.2) is obtained without considering the spatial aspects of the lymphoid tissues. The formulated model also extend models in [19, 23, 28, 40] in spatial aspects. In a bounded domain, we investigated the model (1.6) under the Neumann boundary condition. We first transform the system into a hybrid system containing two reaction-diffusion equations and a Volterra integral equation. By appealing to the Banach-Picard fixed point theorem, we have proved the well-posedness of the system (1.10), that is, the solution of (1.10) exists globally, and it is ultimately bounded. Following the classical theory in [10, 42], the basic reproduction number $\mathfrak {R}_0$ is defined by the spectral radius of $\mathcal {L}$. We should mention that with the assumption that all parameters of (1.10) are spatially homogeneous, $E_0$ is constant. It is crucial to (3.2) that the next generation operator $\mathcal {L}$ does have a positive constant eigenvector, which in turn implies that basic reproduction number $\mathfrak {R}_0$ can be explicitly characterized by a positive constant (see also in [4, 5]).

The global threshold dynamics in terms of basic reproduction number $\mathfrak {R}_0$ is investigated by determining the local and global asymptotic stability of $E_0$ and $\hat{E}$ (see Theorems 4.2 and 4.3). The methods used here are standard but not trivial. We also proved the strong $|\cdot |_\mathbb {X}$-persistence of (1.10) with $\mathfrak {R}_0>1$, which is implied by the uniformly weak $|\cdot |_\mathbb {X}$-persistence (see (Proposition 4.1)). The global attractivity of $E_0$ and $\hat{E}$ are achieved by the technique of Lyapunov functional. Biologically, the HIV infection can be controlled with eradication and persistence in terms of basic reproduction number $\mathfrak {R}_0$ as time evolves. Finally, numerical simulations in the 1-dimensional and 2-dimensional domain are carried out to validate our main results.