Dynamics and Chaos in the Elliptic Isosceles Restricted Three-Body Problem with Collision

Abstract

The elliptic isosceles restricted three-body problem (EIR3BP) with collision is defined as follows: two point masses $m_1= m_2$ move along a degenerate elliptic collision orbit under their gravitational attraction, then describe the motion of a third massless particle moving on a plane perpendicular to their line of motion and passing through the center of mass of the primaries. By symmetry, the component of the angular momentum of the massless particle along the direction of the line of the primaries is conserved. We fixed it to a non-zero value in order to avoid total collision, and perform the reduction to one and a half degrees of freedom. We prove that the flow defined by the EIR3BP is complete and if a solution escapes to infinity when time $t \rightarrow \pm \infty$, then it is parabolic or hyperbolic. A description of the parabolic orbits is given and they are asymptotic to a degenerate periodic orbit at infinity. We verify that the unstable and stable manifolds $P^{u,s}$ of this periodic orbit at infinity are differentiable (in fact, $C^{\infty }$) at the origin and analytic outside. For sufficiently large angular momentum, we prove that $P^{u}$ and $P^{s}$ intersect a surface of section $\Sigma$ in simple closed curves $\gamma ^{u,s}$ having two points of intersection and we show that $\gamma ^{u}$ and $\gamma ^{s}$ have a transversal intersection at these points. We prove that there exists a subset of $\Sigma$ where the Poincaré map is topologically conjugate to a Bernoulli shift, in particular this shows the existence of a very complicated dynamic (chaotic dynamic) in the EIR3BP.

1 Introduction

The elliptic isosceles restricted three body problem (EIR3BP) with collision is defined as follows: Two equal point masses $m_1= m_2$ move under Newton’s law of gravitational attraction in a collision elliptic orbit parametrized by $\rho (t)$ on the z-axis. A third massless particle moves on a plane (x, y) passing through the center of mass of the primaries and perpendicular to their line of motion. Thus the equations of motion for the massless particle are

$$\begin{aligned} \begin{array}{rl} \ddot{x} &{}= -\frac{x}{\left( x^2 + y^2 + \frac{\rho ^{2}(t)}{4}\right) ^{3/2}}\\ \ddot{y} &{}= - \frac{y}{\left( x^2 + y^2 + \frac{\rho ^{2}(t)}{4}\right) ^{3/2}}, \end{array} \end{aligned}$$

(1)

where $\rho (t) = 1-\cos E$ is the distance between the primaries and E is eccentric anomaly. The problem consists in describing the dynamics of the massless particle. Of course the primaries collide successively, but since it is a Keplerian motion its regularized motions are completely understood. In order to avoid total collision we fix the z-component of its angular momentum to a fixed constant $c\ne 0$.

Some restricted problems related to our problem have been studied: If c were taken as zero and the initial conditions of the third particle be given towards the line of the primaries we get the isosceles restricted three body problem with collision studied in [1, 9]. In [12], periodic solutions are obtained numerically. The present problem is also related to the Sitnikov problem in the following aspect: in the latter the primaries move along elliptic orbits of eccentricity e; in [11] parabolic orbits are studied when e is close to zero, when the problem becomes integrable. Our case is far from this in the sense that we are considering $e=1$. The fixed non zero value of c prevents total collision to happen and permits focusing on the existence of bounded motions without collisions (of the massless particle), the dynamics is not less complex though.

In a preliminary work [4] the dynamics of this problem in the finite part, was studied; more precisely, it was shown the existence of symmetric periodic solutions. In this paper we focus on solutions which perform large excursions far from the line of primaries. More precisely we study the set of parabolic orbits in which the massless particle escapes to infinity with asymptotic velocity zero. A complete description of the parabolic orbits is given and we prove they are asymptotic to a degenerate periodic orbit at infinity. Using [2, 3, 10] we are able to verify that the unstable and stable manifolds $P^{u,s}$ of this periodic orbit at infinity are $C^{\infty }$ at the origin and analytic outside. Next, considering a sufficiently large angular momentum we prove that $P^{u}$ and $P^{s}$ intersect a surface of section $\Sigma$ in simple closed curves $\gamma ^{u,s}$ having two points of intersection and we show numerically that $\gamma ^{u}$ and $\gamma ^{s}$ have transversal intersection at these points. Our approach is maintained analytically most of the time, and we just could not give an analytic proof of the transversality of the manifolds $P^u$ and $P^s$, but we present numerical work which sustains its transversality. The main technical difficulty in order to prove analytically the transversal intersection of the invariant manifolds along two homoclinic orbits is that there is not an adequate “small parameter” which would help in using perturbation theory, for example, the Melnikov method. On the other hand, in our approach we cannot prove the boundedness for all time of the coefficient of the series (see Eq. 23) which define $P^{u}$ and $P^{s}$. Finally, we prove that there exists a subset of $\Sigma$ where the Poincaré map is topologically conjugate to a Bernoulli shift, in particular this show the existence of a very complicated dynamics (chaotic dynamics) in the EIR3BP.

The structure of the paper is as follows. In Sect. 2 we state the non-autonomous equations of motion in Cartesian and polar coordinates. In Sect. 3 the problem is reduced by the z-component of the angular momentum and the monotonicity of the time variation of the Hamiltonian is proved in successive intervals of time. We prove that the solutions are defined for all time so the flow is complete. Then individual solutions escaping to infinity are completely classified. In order to study long time and global behavior of bounded solutions, in Sect. 4 we study bounded solutions with large excursions to infinity. We study the parabolic orbits, and its stable and unstable manifolds using McGehee’s and Fontich arguments. In Sect. 5 we prove that for c large enough, these manifold intersects along two homoclinic orbits; we prove numerically the transversality along them.

In Sect. 6, the Poincaré map associated with the surface of section is shown to contain a full shift as a subsystem as a consequence of a theorem of Moser. Section 7 presents some numerical explorations which support the hypothesis of transversality assumed in Sect. 5 and 6 to build up the main construction for the symbolic dynamics. We also show some orbits of the EIR3BP. Finally, in “Appendix” we exhibit several important results in order to make the paper self contained.

There are several results in the literature related with the problem of transversality of the invariant parabolic manifolds in the restricted three body problem. In [8] the authors study the restricted circular three body problem. They use the mass ratio of the primaries as the perturbed parameter. So, using classical perturbation theory they prove the transversality of the invariant parabolic manifolds. More recently in [7] the transversality of the invariant manifolds is proved for all values of the mass ratio. They have used the Jacobi constant as a parameter since their system is conservative. In [6] the tetrahedral four-body problem is considered. In this work the authors prove the existence of a symbolic dynamics. The transversal intersection of the invariant manifolds is given numerically, since they do not have a small parameter which would help in using perturbation theory.

2 Statement of the Problem

Parameterizing the distance between the primaries, and the time as a function of the eccentric anomaly, we arrive that

$$\begin{aligned} \rho= & {} a(1-\cos E), \end{aligned}$$

(2)

$$\begin{aligned} nt= & {} E-\sin E, \end{aligned}$$

(3)

where $n=2\pi /T$ is the mean motion and T is the period. Both are related through Kepler’s third law $a^3 n^2=1$. In what follows we will take $a=n=1$, which amount to take the maximum distance among the primaries as 2, and the period equal to $T=2\pi$. Let (x, y) be the coordinates of the test particle in the plane perpendicular to the line of motion of the primaries (see Fig. 1). It is evident from the form of Eq. (1), that the z-component of the angular momentum of the massless particle $c= y \dot{x}- x \dot{y}$ is a constant of the motion. Throughout this work we will suppose that $c \ne 0$. Next, using this symmetry, we can reduce the equations introducing polar coordinate as usual $x= r \cos \theta$, $y= r \sin \theta$, and then system (1) becomes

$$\begin{aligned} \begin{array}{rl} \frac{d^2 r}{d t^2} &{}= - \frac{r}{\left( r^2 + \frac{\rho ^{2}(t)}{4}\right) ^{3/2}}+ \frac{c^2}{r^3},\\ \frac{d \theta }{d t}&{}= \frac{c}{r^2}. \end{array} \end{aligned}$$

(4)

Note that since $c \ne 0$ our problem is different from the Sitnikov (elliptic case) problem (see details in [11]). In fact, here we have the parameter c and we do not have the parameter associated with the eccentricity, which is very useful when we use perturbation theory. On the other hand, we have a singularity associated to $r=0$.

Fig. 1

The elliptic isosceles restricted three body problem with collision

The second equation in (4) can be solved by means of quadrature, that is,

$$\begin{aligned} \theta (t)= \displaystyle \int _0^t \frac{c}{r^2(s)} ds+ \theta _0, \end{aligned}$$

(5)

and so (4) becomes the reduced system. It is a $2\pi$-periodic Hamiltonian system with Hamiltonian function

$$\begin{aligned} H(r,p_r,t) = \frac{p_r^2}{2} + \frac{c^2}{2 \, r^2} - \frac{1}{\sqrt{r^2 + \frac{\rho ^{2}(t)}{4}}}, \end{aligned}$$

(6)

where $p_r=\dot{r}$ is the conjugate momentum to r. The corresponding equations of motion are

$$\begin{aligned} \begin{array}{rl} \frac{dr}{dt} &{}= p_{r}\\ \frac{dp_{r}}{dt}&{}= -\dfrac{r}{\left( r^2 +\frac{\rho (t)^2}{4}\right) ^{3/2}}+ \dfrac{c^2}{r^3}. \end{array} \end{aligned}$$

(7)

The previous equations of motion can also be expressed in terms of the eccentric anomaly as an independent variable as follows

$$\begin{aligned} \begin{array}{rl} \frac{dr}{dE} &{}= (1-\cos E)p_r\\ \frac{dp_r}{dE} &{}= (1-\cos E)\left( -\frac{r}{\left( r^2+\frac{(1-\cos E)^2}{4}\right) ^{3/2}}+\frac{c^2}{r^3}\right) . \end{array} \end{aligned}$$

(8)

Although the system (8) has critical points whenever $\cos E=1$, the inverse transformation of the Kepler equation (3), namely $t=t(E)$ constitutes an uniformization parameter and system (7) the regularized system. Also for numerical computations to be explained in Sect. 7, Eq. (8) is better suitable for this purpose.

3 Completeness of the Flow

Let us derive some general properties of the flow associated to the system (7). A straightforward computation gives us.

Lemma 1

The derivative of the Hamiltonian function H along the solutions of the system (7) is given by

$$\begin{aligned} \frac{dH}{dt}=\frac{\partial H}{\partial t}=\frac{\rho (t) \dot{\rho }(t)}{4(r^2 + \frac{\rho (t)^2}{4})^{3/2}}. \end{aligned}$$

In particular, by the previous result

$$\begin{aligned} \frac{dH}{dt}= \left\{ \begin{array}{lll} {<}0 &{} \quad \text{ if } &{} \quad \dot{\rho }(t) < 0,\\ {>}0 &{} \quad \text{ if } &{} \quad \dot{\rho }(t) > 0. \end{array}\right. \end{aligned}$$

The following propositions show that the infinitesimal body never crosses the line of the primaries if $c\ne 0$. In particular, triple collision does not occur for finite time.

Proposition 1

If $c\ne 0$, and   there  exists  $\lim _{t \rightarrow t^{*}} r(t)$,   then  for no sequence $\{t_k\}$ converging to $t^*,$ with $t^*$ a constant, results $\lim _{k \rightarrow \infty } r(t_k)=0.$

Proof

Firstly we observe that of the expression (6) and of $\lim _{k \rightarrow \infty } r(t_k)=0$ it follows that

$$\begin{aligned} \lim _{k\rightarrow \infty }r(t_k) \left( H(t_k)-\frac{p_r (t_k)^{2}}{2}\right) \ge \lim _{k\rightarrow \infty } \left( \frac{c^2}{2r(t_k)}-1\right) = +\infty . \end{aligned}$$

So,

$$\begin{aligned} \lim _{k \rightarrow \infty } H(t_k)=+\infty . \end{aligned}$$

We can assume that the sequence $\{t_k\}$ is monotone and, for definiteness, increasing. Then, since

$$\begin{aligned} \dfrac{dH}{dt}=\dfrac{\rho \dot{\rho }}{4\left( r^2+\frac{\rho ^2}{4}\right) ^{3/2}}, \end{aligned}$$

we have the existence of a constant d and $\epsilon > 0$ depending of $t^*$ such that $\frac{dH}{dt}(t)\le d$ for $t\in (t^*-\epsilon , t^*)$ in contradiction with the divergence of $H(t_k)$ established above. $\square$

The following result complements the previous proposition and shows that neither asymptotically non-triple collision occur.

Proposition 2

If $c \ne 0$, r(t) is defined for all t and there exists $\lim _{t \rightarrow \pm \infty } r(t)$, then $\lim _{t \rightarrow \pm \infty } r(t) \ne 0.$

Proof

Suppose that $c\ne 0$ and $\lim _{t\rightarrow \pm \infty }r(t)=0$. From (4) and the obvious inequality

$$\begin{aligned} \begin{array}{l} - \frac{r}{\left( r^2 + \frac{\rho (t)^2}{4}\right) ^{3/2}} + \frac{c^2}{r^3}\ge -\frac{1}{r^2} + \frac{c^2}{r^3} \end{array} \end{aligned}$$

it follows

$$\begin{aligned} \frac{d^2 r}{d t}\ge \frac{1}{r^3}(-r+c^2). \end{aligned}$$

Therefore, $\lim _{t\rightarrow \pm \infty }\frac{d^2 r}{d t^2}= +\infty$ and there exists a time $t_{1}$ such that $\frac{d^2 r}{d t}\ge k$ for all $t\ge t_{1}$, for some $k\in {\mathbb {R}}^+$. Integrating both sides we get $r(t) \ge \frac{k}{2}t^2 + bt + d$, where b, $d \in {\mathbb {R}}$ are constant. Thus $r(t)\rightarrow \infty$ as $t\rightarrow \pm \infty$, which contradicts $\lim _{t\rightarrow \pm \infty }r(t)=0$. $\square$

Remark 1

The last two propositions say that if $c \ne 0$ then any solution is free of total collisions either in finite or infinite time. This result is well known in the general three-body problem when the total angular momentum is different from zero (see [13]).

The next theorem shows that any solution of the system (7) is defined for all time, i.e., the flow is complete.

Theorem 1

If $c \ne 0$ then the maximal interval $(\omega _{-}, \omega _{+})$ of existence of solutions of (7) is $(-\infty , +\infty )$.

Proof

Let $(\omega _{-}, \omega _+)$ be the maximal interval of existence of a solution $(r(t),p_{r}(t))$ of (7). Suppose on the contrary, that the solutions are not defined for all time. Let $\xi \equiv \sqrt{r^2 + p_{r}^{2}}$. Then, for $t^{*}$ a constant, either (i) $\lim _{t\rightarrow t^{*}}r(t)=0$, or (ii) $\lim _{t\rightarrow t^{*}}\xi (t)= +\infty$. The case (i) is ruled out by Proposition 1 and, in this way, there are $\delta >0, \tau >0$ such that

$$\begin{aligned} r(t)\ge \delta , \quad \text{ for }\, \, t\in (t^*-\tau , t^{*}). \end{aligned}$$

Thus, since the righthand side of (7) is Lipshitzian for $r\ge \delta$, the existence of the limit $lim_{t\rightarrow t^*}(r(t), \theta (t))$ and the solution of (7) can be continued past $t^{*}$ establishing $\omega _{+}=+\infty$.

In the case (ii) we can suppose that $\lim _{t\rightarrow t^{*}} r(t)= +\infty$, because if $\lim _{t \rightarrow t^{*}} p_{r}(t)=\pm \infty$ then $\lim _{t \rightarrow t^{*}}r(t)= \infty$. In fact, if $\lim _{t \rightarrow t^{*}} p_{r}(t)=\pm \infty$ and $\lim _{t \rightarrow t^{*}}r(t)= r^{*}$, for some $r^{*}\in {\mathbb {R}}$, we have from the second equation in (7) that $\lim _{t \rightarrow t^{*}}\dot{p}_r(t)$ is constant so, $p_r(t)$ remains bounded as $t\rightarrow t^{*}$, which is a contradiction. Let us suppose then that $\lim _{t \rightarrow t^{*}}r(t)= +\infty$. Again by the second equation in (7) it follows that $\lim _{t\rightarrow t^{*}}\ddot{r}(t)=0$. Therefore $\dot{r}(t)$ remains bounded as $t \rightarrow t^{*}$ and then r(t) remains bounded as $t\rightarrow t^{*}$. This is a contradiction. The result for $\omega _{-}$ is proved in an analogous way. $\square$

4 The Flow Near Infinity

Let us now study solutions escaping to infinity, so we need the following definition.

Definition 1

A solution $(r(t), \dot{r}(t))$ of the system (7) is called an escaping solution if it is defined for all $t>0$ and $\lim _{t\rightarrow \infty }r(t)=\infty$. An escaping solution is called parabolic, if

$$\begin{aligned} \lim _{t\rightarrow \infty } \dot{r}(t)= 0. \end{aligned}$$

and it is called hyperbolic if

$$\begin{aligned} \lim _{t\rightarrow \infty }\dot{r}(t)= p^*, \end{aligned}$$

where $p^*$ is a finite positive value.

Proposition 3

Any escaping solution of (7) with $c \ne 0$ is parabolic or hyperbolic.

Proof

Suppose that $r(t)\rightarrow \infty$ as $t\rightarrow \infty$; from (4) we have that

$$\begin{aligned} \ddot{r}(t)= & {} - \frac{r(t)}{\left[ r^2(t)+ \frac{\rho ^2(t)}{4}\right] ^{3/2}}+\frac{c^2}{r^3(t)}\\= & {} - \frac{1}{r^2(t)} \frac{1}{[1+ \left( \rho (t)/2r(t)\right) ^2]^{3/2}}+ \frac{c^2}{r^3(t)} \sim -\frac{1}{r^2(t)}, \end{aligned}$$

since $\rho (t)$ remains bounded. Then $\ddot{r}(t) \rightarrow 0^-$ as $t \rightarrow \infty$, and so $\dot{r}(t)$ is decreasing as t goes to infinity. It follows that $\lim _{t\rightarrow \infty }\dot{r}(t)= p^*$ exists and there are two possibilities: Either $p^*=-\infty$ or is a finite number. In the first case, there exists $t_1\in {\mathbb {R}}$ such that $\dot{r}(t)<-1$ for all $t>t_1$. So, there exists $t_2$ with $r(t_2)=0$ in contradiction with the Proposition 1. Therefore, $\lim _{t \rightarrow +\infty } \dot{r}(t)=p^*$, a real number. If $p^*<0$ then there exists $t_1>0$ such that $\dot{r}(t)<p^*/2$ for $t>t_1$. Integrating it yields $r(t)<r(t_1)+p^*/2 t$, in particular r(t) vanishes for some $t>t_1$, again contradicting Proposition 1. $\square$

From the previous proposition and Eq. (6) we arrive at the following result.

Corollary 1

Along any escaping solution of (7) with $c \ne 0$, $\displaystyle \lim _{t\rightarrow +\infty } 2H(t)= p^{*2}$.

Next, we are going to study escaping solutions, and in this approach let us use McGehee’s coordinates [10], that is, we make the change of variables

$$\begin{aligned} r= \frac{2}{u^2},\quad {\dot{r}}= v. \end{aligned}$$

(9)

So $u \rightarrow 0$ corresponds to $r \rightarrow +\infty$, and Eq. (7) assumes the form

$$\begin{aligned} \begin{array}{rl} \dot{u}&{}= -\frac{1}{4} u^3 v\\ \dot{v}&{}= \frac{1}{4} u^4 \left( -\frac{1}{\left[ 1+\frac{u^4 \rho ^2(t)}{16}\right] ^{3/2}}+ \frac{c^2}{2} u^2\right) , \end{array} \end{aligned}$$

(10)

together with the differential equation

$$\begin{aligned} \dot{E}= \frac{1}{1- \cos E}, \end{aligned}$$

which is consequence of (3). The origin $(u, v)= (0,0)$ is an equilibrium point of the system (10) contained in the invariant plane $u=0$. The set

$$\begin{aligned} N_{\infty }= \{(u, v, E) \ / \ u=0 \} \end{aligned}$$

is called the infinity manifold, and clearly it is invariant by the flow of system (10). Moreover, the flow extends analytically to it. We are interested in studying solutions that escape parabolically to infinity, that is, solutions such that $(u,v)\rightarrow (0,0)$ as $t\rightarrow \infty$. It is known that the set of initial conditions of such solutions form a variety which we denote by stable parabolic manifold, see [10]. Using the McGehee or, more recently, Baldomá et al. [2, 3] notations, the stable parabolic manifold (locally) is defined by the set $P^s= {\mathcal {A}}^+({\mathcal {P}}, {\mathcal {B}})$, where

$$\begin{aligned} {\mathcal {A}}^+({\mathcal {P}}, {\mathcal {B}})= & {} \left\{ (u, v) \in {\mathcal {B}} \ / \ {\mathcal {P}}^k(u, v) \in {\mathcal {B}}, \forall \, k>0, \, {\mathcal {P}}^k(u, v) \rightarrow (0, 0), \, \text{ as }\, k \rightarrow +\infty \right\} ,\\ {\mathcal {B}}= & {} {\mathcal {B}}(\beta , \delta )=\left\{ (u,v)\in {\mathbb {R}}^2 \ / \ 0\le u\le \delta , |v|\le \beta \, u\right\} \end{aligned}$$

where ${\mathcal {P}}$ denotes the Poincaré map or first return map associated to the periodic orbit $(u,v)=(0,0)$, which will study in the next proposition. The variable u is considered positive in order to avoid ambiguity in the transformation (9). The existence of this set ${\mathcal {B}}$ is guaranteed in [10].

In the next proposition we determine an approximation of the Poincaré map associated to system (10). Some preliminary results are described in Sect. 1.

Proposition 4

The Poincaré map ${\mathcal {P}}$ defined in a neighborhood ${\mathcal {U}}$ of the periodic orbit $(u,v)=(0,0)$ is given by the diffeomorphism

$$\begin{aligned} {\mathcal P}(u,v)=\left( u - \frac{\pi }{2} u^3\left[ v+ r_1(u,v)\right] , v -\frac{\pi }{2} u^3 \left[ u-\frac{c^2}{2} u^3 -\frac{45}{192} u^5+ r_2(u,v)\right] \right) , \end{aligned}$$

(11)

where $r_1$ and $r_2$ are real analytic functions in the variables u, v and of order two in these variables.

Proof

We are going to apply the analysis given in Sect. 1 in order to calculate the Poincaré map ${\mathcal P}$ around the $2\pi$-periodic orbit $(u, v, t)=(0, 0, t)$ of the differential system

$$\begin{aligned} \begin{array}{rl} \frac{du}{dt}=&{} \frac{1}{4} u^3 v\\ \frac{dv}{dt}=&{} -\left[ \frac{u^4}{4}- \frac{c^2}{8}u^6 - \frac{3}{128}u^8\rho ^2(t)+ \frac{15}{8192}u^{12}\rho ^4(t) + {\mathcal {O}}(u^{16}) \right] \\ \frac{dt}{dt}=&{} 1, \end{array} \end{aligned}$$

(12)

which is obtained using Taylor’s series in (10) around the point $u=0$. We denote the flow of (12) by $\varphi (t, u, v)= (\varphi _1(t, u, v), \varphi _2(t, u, v), \varphi _3(t, u, v))$, where $\varphi _3(t, u, v)=t$, and so $\sigma (\alpha )= 2\pi$. Clearly the time of return is $\sigma (\alpha )= 2\pi$. Thus, following the notation of Sect. 1 we have that $\frac{\partial ^n {\mathcal {P}}}{\partial \alpha ^n}= \frac{\partial ^n \varphi (\sigma (\alpha ), \alpha )}{\partial \alpha ^n}$ and then the Poincaré map is given by

$$\begin{aligned} \begin{array}{ll} {\mathcal {P}}(u, v)=&{} \alpha _{0} + \frac{\partial \varphi }{\partial u}(\alpha _0, \sigma (\alpha _0))u + \frac{\partial \varphi }{\partial v}(\alpha _0, \sigma (\alpha _0))v \\ &{} +\,\frac{1}{2!}\left[ \frac{\partial ^2\varphi }{\partial u^2}(\alpha _0, \sigma (\alpha _0))u^2 + 2 \frac{\partial ^2\varphi }{\partial u\partial v(\alpha _0, \sigma (\alpha _0))uv}+ \frac{\partial ^2\varphi }{\partial v^2}(\alpha _0, \sigma (\alpha _0))v^2\right] \\ &{} +\,\frac{1}{3!}\left[ \frac{\partial ^3 \varphi }{\partial u^3}(\alpha _0, \sigma (\alpha _0))u^3 + 3\frac{\partial ^3\varphi }{\partial u^2 \partial v}(\alpha _0, \sigma (\alpha _0))u^2v \right. \\ &{} \left. \quad \qquad +\, 3\frac{\partial ^3 \varphi }{\partial u \partial v^2}(\alpha _0, \sigma (\alpha _0)) u v^2 + \frac{\partial ^3\varphi }{\partial v^3}(\alpha _0, \sigma (\alpha _0))v^3\right] \\ &{} +\, \frac{1}{4!} \left[ \frac{\partial ^4 \varphi }{\partial u^4}(\alpha _0, \sigma (\alpha _0))u^4 + 4\frac{\partial ^4\varphi }{\partial u^3 \partial v}(\alpha _0, \sigma (\alpha _0))u^3v+ 6\frac{\partial ^4 \varphi }{\partial u^2 \partial v^2}(\alpha _0, \sigma (\alpha _0)) u^2 v^2\right. \\ &{} \left. \quad \qquad +\, 4\frac{\partial ^4\varphi }{\partial u \partial v^3}(\alpha _0, \sigma (\alpha _0)) u v^3+ \frac{\partial ^4\varphi }{\partial v^4}(\alpha _0, \sigma (\alpha _0))v^4 \right] + {\mathcal {O}}((\alpha - \alpha _0)^5). \end{array} \end{aligned}$$

(13)

We take the initial condition $\alpha _0= (0, 0)$ which is a point of the periodic solution (0, 0, t) and thus it is a fixed point of ${\mathcal {P}}$. As $\dfrac{\partial \varphi }{\partial \alpha }(t,\alpha _0 )\mid _{t=0}= I$, we have that $\dfrac{\partial \varphi _1}{\partial u}(t, \alpha _0)=1$ and $\dfrac{\partial \varphi _2}{\partial v}(t, \alpha _0)=1$. On the other hand, we know that $\dfrac{\partial ^2 \varphi }{\partial \alpha ^2}(t, \alpha _0)$ is a solution of

$$\begin{aligned} \dot{Y}= Df(\varphi (t, \alpha _0))Y + B(t). \end{aligned}$$

(14)

In this case $B(t)= D^2f(\varphi (t, \alpha _0))\frac{\partial \varphi }{\partial x}(t,\alpha _0)^2$, because $D^2f(\varphi (t, \alpha _0))\equiv 0$. Note that since $Df(\varphi (t, \alpha _0))$ $\equiv 0$, it follows that $\dfrac{\partial ^2\varphi }{\partial \alpha ^2}(t, \alpha _0)$ $= \dfrac{\partial ^2\varphi }{\partial \alpha ^2}(t, \alpha _0)\mid _{t=0}\equiv 0.$ In particular, we have that $\dfrac{\partial ^2\varphi }{\partial \alpha ^2}(\sigma (\alpha _0), \alpha _0) = \dfrac{\partial ^2\varphi }{\partial \alpha ^2}(2\pi , \alpha _0)\equiv 0.$

Continuing the process we obtain that $\dfrac{\partial ^3 \varphi }{\partial \alpha ^3}(t, \alpha _0)$ is a solution of (14) where now $B(t)= D^3f(\varphi (t, \alpha _0))\frac{\partial \varphi }{\partial \alpha }(t, \alpha _0)^3 +D^2f(\varphi (t, \alpha _0))(\frac{\partial \varphi }{\partial \alpha }(t, \alpha _0), \frac{\partial ^2\varphi }{\alpha ^2}(t, \alpha _0))\equiv 0$, because the matrices $D^3f(\varphi (t, \alpha _0)), D^2f(\varphi (t, \alpha _0))$ are identically null. Since $Df(\varphi (t, \alpha _0))\,\equiv \,0$, we have that $\dfrac{\partial ^3 \varphi }{\partial \alpha ^3}(t, \alpha _0)= \dfrac{\partial ^3 \varphi }{\partial \alpha ^3}(t, \alpha _0)\mid _{t=0}\,\equiv \,0$. So, $\dfrac{\partial ^3\varphi }{\partial \alpha ^3}(2\pi , \alpha _0)\equiv 0.$

In the fourth step, we know that $\dfrac{\partial ^4 \varphi }{\partial \alpha ^4}(t, \alpha _0)$ is a solution of Eq. (14) where $B(t)= D^4f(\varphi (t, \alpha _0))\frac{\partial \varphi }{\partial \alpha }(t, \alpha _0)^4$, because all the other terms are zero. We know that $Df(\varphi (t, \alpha _0))$ is identically null, so in order to find $\dfrac{\partial ^4 \varphi }{\partial \alpha ^4}(t, \alpha _0)$ it is sufficient to integrate the equation

$$\begin{aligned} \frac{d}{dt}\frac{\partial ^4 \varphi }{\partial \alpha ^4}(t, \alpha _0)= D^4f(\varphi (t, \alpha _0))\frac{\partial \varphi }{\partial \alpha }(t, \alpha _0)^4, \end{aligned}$$

where in the matrix $D^4f(\varphi (t, \alpha ))$ we have

$$\begin{aligned} \begin{array}{rlrlrlrlrl} \frac{\partial ^4f_1}{\partial u^4}= 0, &{} \quad \frac{\partial ^4f_1}{\partial u^3\partial v}=-\frac{3}{2}, &{} \quad \frac{\partial ^4f_1}{\partial u^2\partial v^2}= 0, &{} \quad \frac{\partial ^4f_1}{\partial u \partial v^3}= 0, \quad \frac{\partial ^4f_1}{\partial v^4}= 0, \\ \frac{\partial ^4f_1}{\partial v^3\partial u }= 0, &{} \quad \frac{\partial ^4f_1}{\partial v^2\partial u^2}=0, &{} \quad \frac{\partial ^4f_2}{\partial u^3 \partial v}= 0, &{} \quad \frac{\partial ^4f_2}{\partial u^2\partial v^2}= 0, \quad \frac{\partial ^4f_2}{\partial u \partial v^3}= 0, \\ \frac{\partial ^4f_2}{\partial v^4}\!=\! 0, &{} \quad \frac{\partial ^4f_2}{\partial v^3 \partial u}\!=\! 0, &{} \quad \frac{\partial ^4f_1}{\partial v\partial u^3}\!=\! -\frac{3}{2},\ &{} \quad \frac{\partial ^4f_2}{\partial u^4}\!=\!-6 + \frac{360}{8}c^2u^2+ \frac{5040}{128}u^4\rho ^2(t){+} {\mathcal {O}}(u^8). \end{array} \end{aligned}$$

So, $\dfrac{\partial ^4 \varphi }{\partial \alpha ^4}(\sigma (\alpha _0),\alpha _0 )$ reduces to

$$\begin{aligned} \begin{array}{rl} \dfrac{\partial ^4 \varphi }{\partial \alpha ^4}(\sigma (\alpha _0),\alpha _0 )=&{} \left( 0,\dfrac{\partial ^4 \varphi _2}{\partial u^4}(\sigma (\alpha _0),\alpha _0 )\right) u^4 + 4\left( \dfrac{\partial ^4 \varphi _1}{\partial u^3 \partial v}(\sigma (\alpha _0),\alpha _0 ),0\right) u^3v\\ =&{} (-12\pi u^3v,-12\pi u^4). \end{array} \end{aligned}$$

In the fifth step, we observe that $\dfrac{\partial ^5 \varphi }{\partial \alpha ^5}(t, \alpha _0)$ is solution of Eq. (14) with $B(t)= D^5f(\varphi (t, \alpha _0))\frac{\partial \varphi }{\partial \alpha }(t, \alpha _0)^5 + 10D^4f(\varphi (t, \alpha _0))\left( \left( \frac{\partial \varphi }{\partial \alpha }(t, \alpha _0)\right) ^3\,, \frac{\partial ^2 \varphi }{\partial \alpha ^2}(t, \alpha _0)\right) + \,\text{ other } \text{ terms }$. Observe that the matrix $D^5f(\varphi (t, \alpha _0))$ is given by

$$\begin{aligned} \begin{array}{rlrlrlrlrl} \frac{\partial ^5f_1}{\partial u^5}= 0, &{} \quad \frac{\partial ^5f_1}{\partial u^4\partial v}= 0, &{}\quad \frac{\partial ^5f_1}{\partial u^3\partial v^2}= 0, &{} \quad \frac{\partial ^5f_1}{\partial u \partial v^4}=0, \quad \frac{\partial ^5f_1}{\partial v^5}=0,\\ \frac{\partial ^5f_1}{\partial v^4\partial u }=0, &{}\quad \frac{\partial ^5f_1}{\partial v^3\partial u^2}=0, &{} \quad \frac{\partial ^5f_1}{\partial v\partial u^4}=0, &{}\quad \frac{\partial ^5f_2}{\partial u^4 \partial v}=0, \quad \frac{\partial ^5f_2}{\partial u^3\partial v^2}=0,\\ \frac{\partial ^5f_2}{\partial u \partial v^4}\!=\!0, &{}\quad \frac{\partial ^5f_2}{\partial v^5}\!=\!0, &{} \quad \frac{\partial ^5f_2}{\partial v^4 \partial u}\!=\!0, &{} \quad {\frac{\partial ^5f_2}{\partial u^5}\big |}_{\alpha _0}\!=\! \left[ {\frac{720}{8}c^2u {+} \frac{630}{4}u^3\rho (t)^2 {+} {\mathcal {O}}(u^7)}\right] \big |_{\alpha _0}\!=\!0 \\ \end{array} \end{aligned}$$

Since $D^5f(\varphi (t, \alpha _0))$ is a null matrix and $D^4f(\varphi (t, \alpha _0))\left( \left( \frac{\partial \varphi }{\partial \alpha }(t, \alpha _0)\right) ^3\,, \frac{\partial ^2 \varphi }{\partial \alpha ^2}(t, \alpha _0)\right)$ is not null, it follows that $\dfrac{\partial ^5\varphi }{\partial \alpha ^5}(t, \alpha _0)$ is given by the integral solution of the equation

$$\begin{aligned} \frac{d}{dt}\frac{\partial ^5 \varphi }{\partial \alpha ^5}(t, \alpha _0)= 10D^4f(\varphi (t, \alpha _0))\left( \frac{\partial \varphi }{\partial \alpha }(t, \alpha _0)^3\,, \frac{\partial ^2 \varphi }{\partial \alpha ^2}(t, \alpha _0)\right) . \end{aligned}$$

In the sixth step, we have that $\dfrac{\partial ^6 \varphi }{\partial \alpha ^6}(t, \alpha )$ is given by the integral of the equation

$$\begin{aligned} \begin{array}{rl} \frac{d}{dt}\frac{\partial ^6 \varphi }{\partial \alpha ^6}(t, \alpha _0)&{}= D^6f(\varphi (t, \alpha _0))\left( \frac{\partial \varphi }{\partial \alpha }(t, \alpha _0)\right) ^6 \\ &{}\quad +\, 10D^4f(\varphi (t, \alpha _0))\frac{\partial }{\partial \alpha }\left( \left( \frac{\partial \varphi }{\partial \alpha }(t, \alpha _0)\right) ^3 \, \frac{\partial ^2 \varphi }{\partial \alpha }(t, \alpha _0)\right) \\ &{}\quad +\,6D^4f(\varphi (t, \alpha _0))\left( \frac{\partial \varphi }{\partial \alpha }(t, \alpha _0)\, \frac{\partial }{\partial \alpha }\left( \left( \frac{\partial \varphi }{\partial \alpha }(t, \alpha _0)\right) ^2\, \frac{\partial ^2 \varphi }{\partial \alpha }(t, \alpha _0)\right) \right) \\ &{}\quad +\, 4D^4f(\varphi (t, \alpha _0))\left( \frac{\partial \varphi }{\partial \alpha }(t,\alpha _0)\right) ^3\frac{\partial ^3\varphi }{\partial \alpha ^3}(t, \alpha _0) \\ &{}\quad +\, D^4f(\varphi (t, \alpha _0))\left( \frac{\partial \varphi }{\partial \alpha }(t,\alpha _0)\right) ^2\left( \frac{\partial ^2\varphi }{\partial \alpha ^2}(t, \alpha _0)\right) ^2. \end{array} \end{aligned}$$

Observe that in $D^6f(\varphi (t, \alpha ))$ the unique non identically null term is $\dfrac{\partial ^6f_2}{\partial u^6}=\dfrac{720}{8}c^2 + \frac{1890}{4}u^2\rho (t)^2 + {\mathcal {O}}(u^6)$. So $D^6f(\varphi (t, \alpha _{0}))$ only has the nonzero component $\dfrac{\partial ^6f_2}{\partial u^6}(t, \alpha _{0})=\dfrac{720}{8}c^2$.

At the seventh step, we have that, $\dfrac{\partial ^7 \varphi }{\partial \alpha ^7}(t, \alpha _0)$ is solution of the equation (14) where in this case B(t) have nonzero terms that coming from $D^4f(\varphi (t, \alpha _0))$ and $D^6f(\varphi (t, \alpha _0))$. The matrix $D^7f(\varphi (t, \alpha ))$ has only the nonzero term $\dfrac{\partial ^7f_2}{\partial u^7}= \frac{3780}{4}u\rho (t)^2 + {\mathcal {O}}(u^5)$. So $D^7f(\varphi (t, \alpha _{0}))\equiv 0$.

In the eighth step, $\dfrac{\partial ^8 \varphi }{\partial \alpha ^8}(t, \alpha _0)$ is solution of Eq. (14) where B(t) has nonzero terms coming from $D^4f(\varphi (t, \alpha _0)),$ $D^6f(\varphi (t, \alpha _0))$ and $D^8f(\varphi (t, \alpha _0)).$ The matrix $D^8f(\varphi (t, \alpha ))$, only has the non-null term $\dfrac{\partial ^8f_2}{\partial u^8}= \frac{3780}{4}\rho (t)^2 +{\mathcal {O}}(u^4)$. Thus, $D^8f(\varphi (t, \alpha _{0}))$ has only the component $\dfrac{\partial ^8f_2}{\partial u^8}(t, \alpha _{0})=\frac{3780}{4}\rho (t)^2$. In this way, we have

$$\begin{aligned} \dfrac{\partial ^8 \varphi }{\partial \alpha ^8}(\sigma (\alpha _0), \alpha _0)=\dfrac{\partial ^8 \varphi }{\partial \alpha ^8}(2\pi , \alpha _0)= \left( 0, \, \, \, \frac{3780}{4}\int _{0}^{2\pi }\rho (\tau )^2 d\tau \right) u^8. \end{aligned}$$

Replacing $\rho ^2(t)= [1-\cos E(t)]^2$ by its Fourier series, which is given by $\dfrac{5}{2}+ \displaystyle \sum _{\alpha =1}^{\infty } a_\alpha \cos {\alpha t}$, we have that

$$\begin{aligned} \begin{array}{rl} \dfrac{\partial ^8 \varphi }{\partial \alpha ^8}(\sigma (\alpha _0), \alpha _0) &{}= \left( 0, \,\, \frac{3780}{4}\displaystyle \int _{0}^{2\pi }\left[ \frac{5}{2}+ \sum _{\alpha =1}^{\infty } a_\alpha \cos {\alpha t}\right] d\tau \right) u^8\\ &{}= (0,\, \, 4725\pi )u^8. \end{array} \end{aligned}$$

Thus, using (13) we arrive to

$$\begin{aligned} {\mathcal {P}}(u,v)=\left( u - \frac{\pi }{2} u^3\ [v+ r_1(u,v)], v -\frac{\pi }{2} u^3\ \left[ u - \frac{c^2}{2} u^3 - \frac{45}{192} u^5+ r_2(u,v)\right] \right) , \end{aligned}$$

where $r_1$ and $r_2$ are real analytic functions in the variables u, v and of order two in these variables. This concludes the proof of the proposition. $\square$

It is clear that the equilibrium point (0, 0) is degenerate for the system (10) since the differential of the Poincaré map at (0, 0) is the identity matrix. As $\rho (t)= 1-\cos E(t)$ is $2\pi$ periodic in t, this critical point can be seen as a $2\pi$-periodic orbit in the extended phase space $\{(u,v,t) \in {\mathbb {R}}^3 \mid u \ge 0\}$. The next theorem guarantees that $P^s$ is a one dimensional manifold which is a real analytic arc.

Theorem 2

There exist a convex open set $V=(0,r)$ such that $P^s={\mathcal {A}}^+({\mathcal {P}}, {\mathcal {B}}(\beta , r))$ is the graph of an analytic function $\varphi : (0, r) \rightarrow {\mathbb {R}}$, that is, $P^s \cap ({\mathcal {U}} \cap V)= \{(u, v) \ / \ v= \varphi (u), \, u \in (0, r)\}$. Moreover, the function $\varphi$ is $C^{\infty }$ at 0.

Proof

We will use the notation considered in Theorems 7 and 8 (see “Differentiability of the Invariant Manifolds $P^{u,s}$ at the Origin” in Appendix and Refs. [2, 3]). Firstly, since we are interested in the solution close to $u=0$ we write system (10) around the point $u=0$ so we obtain the system

$$\begin{aligned} \begin{array}{rl} \dot{u} &{}= -\frac{1}{4} u^3 v\\ \dot{v} &{}= -\frac{1}{4} u^4 + \frac{c^2}{8} u^6+ O(u^8). \end{array} \end{aligned}$$

(15)

In order to prove the first part of the theorem we will prove that the Poincaré map ${\mathcal {P}}$ defined in (11) satisfies conditions (H1)–(H4) of Theorem 7. In order to apply this theorem, the map ${\mathcal {P}}$ is not yet in a suitable form, so we make the change of variables

$$\begin{aligned} u=\frac{ x+ y}{2}, \quad v= \frac{x-y}{2}, \end{aligned}$$

thus the system (15) is equivalent to

$$\begin{aligned} \begin{array}{rl} \dot{x} &{}= -\frac{1}{32} (x+y)^3 x+\frac{c^2}{512} (x+y)^ 6+ O((x+y)^8)\\ \dot{y} &{}= \frac{1}{32} (x+y)^3 y- \frac{c^2}{512} (x+y)^ 6+ O((x+y)^8). \end{array} \end{aligned}$$

(16)

Then the map ${\mathcal {P}}$ becomes

$$\begin{aligned} F(x, y)= (x+p(x,y)+ r_1(x, y), y+ q(x, y)+ r_2(x, y)) \end{aligned}$$

(17)

where

$$\begin{aligned} \begin{array}{rl} p(x,y)=&{} -\frac{\pi }{16} (x+y)^3 x,\\ q(x,y)=&{} \frac{\pi }{16} (x+y)^3 y,\\ r_1(x, y)=&{} o(\Vert (x,y)\Vert ^4),\\ r_2(x, y)=&{} o(\Vert (x,y)\Vert ^4). \end{array} \end{aligned}$$

(18)

Thus $N_p= N_q= 4$. Since $1+ D_x p(x, 0)= 1-\frac{\pi }{4} x^3 < 1$, then (H1) follows. As $D_x q(x, y)= \frac{3 \pi }{16} (x+y)^2 y$ and $D_y q(x,0)= \frac{\pi }{16} x^3 > 0$, so we have verified (H2). Now, we observe that $x+ p(x, 0)= x- \frac{\pi }{16} x^4$, then $dist(x+p(x, 0), [r, +\infty )) \ge \frac{\pi }{16} x^4$, therefore (H3) holds. Now, we observe that $|1+ D_xp(x, 0)|+ |1-\frac{1}{4} D_xp(x, 0)|= 2- \frac{3\pi }{16} x^3< 2$, and then H4 is true. So we have proved the first part of the theorem, that is, there exists a one-dimensional stable invariant manifold of the origin, which, for $r>0$ small enough, can be expressed as the graph of an analytic function $y= \tilde{\varphi } (x)$.

In order to prove the second part of the theorem, we will apply Theorem 8 given in “Differentiability of the Invariant Manifolds $P^{u,s}$ at the Origin” in Appendix. It is clear that in our case $m=1$, the map F is analytic, in particular is $C^{\infty }$, so $k= \infty$. Also, $F(0, 0)= (0, 0)$ and $DF (0, 0) = Id$. We verify that $N= M = 4$, $\frac{\partial F^1}{\partial x^4}(0, 0)= - \frac{3 \pi }{2} < 0$, and $\frac{\partial ^4 F^2}{\partial x^3 \partial y}(0, 0)= \frac{3 \pi }{8} > 0$. Then all the assumptions of Theorem 8 are satisfied, hence there are a $C^{\infty }$ map $K: [0, r) \rightarrow {\mathbb {R}}^2$ and a polynomial $R: {\mathbb {R}} \rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} F \circ K= K \circ R. \end{aligned}$$

(19)

Let $K= (K_1, K_2)$. As $\frac{\partial K_1}{\partial x}(0) = 1 \ne 0$ by the inverse function theorem we have that in a small neighborhood of $x=0$ there is $K_1^{-1}$. Thus from (19) we have

$$\begin{aligned} F_1(K_1(x), K_2(x))= & {} K_1(R(x)), \end{aligned}$$

(20)

$$\begin{aligned} F_2(K_1(x), K_2(x))= & {} K_2(R(x)), \end{aligned}$$

(21)

then by (20)

$$\begin{aligned} K_1^{-1} (F_1(K_1(x), K_2(x)))= R(x), \end{aligned}$$

and by substituting it in (21), we arrive to

$$\begin{aligned} K_2 \circ K_1^{-1} \circ F_1 = F_2. \end{aligned}$$

(22)

On the other hand, points in the $Graph(\tilde{\varphi })$, are characterized by

$$\begin{aligned} \tilde{\varphi } \circ F_1= F_2. \end{aligned}$$

In [2] is proved that the function $\varphi$ is locally unique, therefore $\tilde{\varphi }= K_2 \circ K_1^{-1}$ and so we conclude that $\tilde{\varphi }$ is $C^{\infty }$ at $x=0$.

It remains to transform the invariant manifold to the original variables. The variable u is a function of x, since $u= \frac{x+y}{2}= \frac{x+ \tilde{\varphi }(x)}{2}= h(x)$. We observe that h is an analytic function in (0, r) and is $C^{\infty }$ at $x=0$. Furthermore, $Lip (h) \le \frac{1+ Lip (\tilde{\varphi })}{2} < 1$, therefore, there is an analytic function $\overline{\varphi }$ such that $x= \overline{\varphi }(u)$ (see details in [2]), and then the stable invariant manifold of the point (0, 0) can be represented as the graph of

$$\begin{aligned} v= \varphi (u):= \frac{1}{2} \left[ \overline{\varphi }(u)-\tilde{\varphi }(\overline{\varphi }(u))\right] \end{aligned}$$

where $u \in (0, u_0)$. In conclusion, we have proved that $\varphi$ is analytic in $(0, u_0)$ and $\varphi$ is $C^{\infty }$ at $u=0$. $\square$

The existence of an unstable parabolic manifold, denoted by $P^u$, can be obtained immediately by considering the inverse of the Poincaré map. More precisely, this manifold corresponds to the orbits that were captured parabolically, that is, solutions such that $(u,v)\rightarrow (0,0)$ as $t\rightarrow -\infty$. According [10], we must have

$$\begin{aligned} P^u= {\mathcal {A}}^-({\mathcal {P}}, {\mathcal {B}})= \{(u, v) \in {\mathcal {B}} \ / \ {\mathcal {P}}^{-k}(u, v) \in {\mathcal {B}}, \forall k>0, \, {\mathcal {P}}^{-k}(u, v) \rightarrow (0, 0), \, \text{ as }\, k \rightarrow +\infty \}. \end{aligned}$$

Thus, in order to prove the existence of an unstable manifold of the periodic point (0, 0) for the system (10), we only need to perform the change given by $t\rightarrow -t$ and $(u, v, E) \rightarrow (u, -v, -E)$, because the system (10) is invariant under the symmetry $(u,v,t) \rightarrow (u,-v,-t)$. In these new variables the dominant terms of this system do not change and therefore we can use the same arguments as for the stable manifold and conclude that there exists a one-dimensional unstable manifold associated to the periodic point (0, 0) with the same properties about the differentiability.

Remark 2

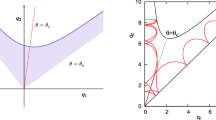
In order to clarify some geometrical aspects of the behavior of the invariant manifold, we are going to denote the critical point (0, 0) in the slice time $\Pi _{\tau }$ by $p_{\tau }$, according to Fig. 2. We know that it can be seen as a $2\pi$-periodic orbit, namely, $\Gamma (t)$, in the extended phase space $\{(u,v,t) \in {\mathbb {R}}^3 \mid u \ge 0\}$. It follows that the invariant manifold associated to $\Gamma (t)$, $P^s_{\Gamma (t)}$, is constituted by curves parametrized by t in this phase space. In fact, by Theorem 2, the stable manifold associated to critical point $p_{\tau }$, $P^s_{p_{\tau }}$, is the graph of the function $\varphi$, that is, $P^s_{p_{\tau }}$ is given by (u, v) where $v=\varphi (u), u\in (0,r)$ with r sufficiently small. So, in the extended phase space, it follows that $P^s_{\Gamma (t)}$ is given locally by $v=\displaystyle \sum _{n\ge 0}b_n(t)u^{n}$, where $\displaystyle \sum _{n\ge 0}b_n(\tau )u^{n}=\varphi (u)$ with $\tau$ in the interval $[0,2\pi )$ .

Fig. 2

The Fig. a represents the behaviour of the manifolds near to infinite on a time slice $\Pi _{\tau }=\{(u,v,t)| t=\tau \}$, for c very small and figure b for c sufficiently large. The figures on the right describe the geometry of the stable and unstable manifolds associated to the periodic orbit $\Gamma (t)$, both in the extended phase space and on the slice time

If we assume that the local stable manifold $P^{s}_{\Gamma (t)}$ is given by $v= -{\mathcal {G}}(u,-t)$, then since the system (10) is invariant under the symmetry $(u,v,t) \rightarrow (u,-v,-t)$, the equation of the local unstable manifold $P^{u}_{\Gamma (t)}$ is $v= {\mathcal {G}}(u,t)$, where

$$\begin{aligned} v= {\mathcal {G}}(u,t)= \sum _{n \ge 0} b_n(t) u^n, \end{aligned}$$

(23)

and the terms $b_n(t)$ can be computed by comparing coefficients.

Proposition 5

The points (u, v, t) of the local unstable manifold $P^{u}_{\Gamma (t)}$ are given by the graph of $v = {\mathcal {G}}(u,E)$, where

$$\begin{aligned} {\mathcal {G}}(u,E)= & {} - u+ b_3(E) u^3 + b_5(E) u^5 + b_7(E)u^7+ b_8(E)u^8+b_9(E) u^9 \nonumber \\&+ \, b_{11}(E)u^{11}+b_{12}(E)u^{12}+b_{13}(E)u^{13}+ b_{14}(E)u^{14}+O(u^{15}), \end{aligned}$$

(24)

and the non-zero coefficients up to order 14 are

$$\begin{aligned} \begin{array}{ll} b_3(E)&{}=\frac{c^2 }{8}, \quad b_5(E) = \frac{1}{128}\left( c^4+5\right) , \quad b_7(E) = \frac{\left( c^6+5 c^2\right) }{1024}\\ b_8(E) &{}=-\frac{(15 \sin (E)-9 \sin (2 E)+\sin (3 E))}{512}, \quad b_9(E) =-\frac{\left( -5 c^8-30 c^4+164\right) }{32{,}768}\\ b_{11}(E)&{}= -\frac{\left( 1404 \cos (E)-612 \cos (2 E)+ 132 \cos (3 E)- 9 \cos (4 E)-915\right) }{16{,}384}\\ b_{12}(E) &{}= -\frac{-519 \sin (E) +825 \cos (E)\sin (E)-432 \cos ^2(E)\sin (E) +150 \cos ^3(E)\sin (E) - 24 \cos ^4(E)\sin (E)}{65{,}536}\\ b_{13}(E) &{}= -\frac{3355 c^2 - 5148 c^2 \cos (E) + 2244 c^2 \cos (2E) - 484 c^2\cos (3E) + 33c^2 \cos (4E) }{393{,}216}\\ b_{14}(E) &{}= -\frac{(77{,}616+ 342 c^2-21 c^{10}-150 c^6)E+(-126{,}000 - 342 c^2+21 c^{10} + 150 c^6)\sin (E) + 33{,}120\sin (2E)}{262{,}144}\\ &{}\quad -\,\frac{-7080 \sin (3E)+ 900\sin (4E)}{262{,}144}+\frac{27 \sin (5E)}{163{,}840} \end{array} \end{aligned}$$

(25)

and $t=E-\sin {E}$. Here we call the attention for the dependence of the coefficients $b_{j}$ on the parameter c. By symmetry the points of the local stable manifold $P^{s}_{\Gamma (t)}$ satisfy $v= -{\mathcal {G}}(u,-E)$.

Proof

In “Computation of the Coefficients $b_j$ in (23)” of the Appendix, we give details about the process of obtention of the coefficients $b_n(E)$ recursively. $\square$

The following proposition describes the unstable manifold $P^{u}_{\Gamma (t)}$ as a graph of a function $u = {\mathcal {F}}(v,E)$ and is obtained by straightforward inversion of the series (24). The stable manifold $P^s_{\Gamma (t)}$ is obtained as the graph of $u = {\mathcal {F}}(-v,-E)$.

Proposition 6

The points (u, v, t) of the local unstable manifold $P^{u}_{\Gamma (t)}$ are given by the graph of $u = {\mathcal {F}}(v,E)$, where

$$\begin{aligned} {\mathcal {F}}(v,E)= & {} - v+ a_3(E) v^3 + a_5(E) v^5 + a_7(E)v^7+ a_8(E)v^8+a_9(E) v^9+a_{10}(E)v^{10}\nonumber \\&+a_{11}(E)v^{11}+a_{12}(E)v^{12}+ a_{13}(E)v^{13}+a_{14}(E)v^{14}+ O(v^{15}) \end{aligned}$$

(26)

and the non-zero coefficients up to order 14 are

$$\begin{aligned} \begin{array}{rl} a_3( E)&{}= -\frac{c^2}{8}, \quad a_5(E)= \frac{\left( -7c^4-5\right) }{128}, \quad a_7(E)=\frac{\left( -33 c^6-45 c^2\right) }{1024}\\ a_8(E)&{}=\frac{-15 \sin (E)+9 \sin (2 E)-\sin (3E)}{512}, \quad a_9(E)= \frac{-715 c^8 -1430 c^4-86}{32{,}768}\\ a_{10}(E)&{}= \frac{11 c^2\left( 15 \sin (E)-9 \sin (2 E)+ \sin (3 E)\right) }{4096}\\ a_{11}(E)&{}= \frac{-1048 c^{10}- 2750 c^6 -633 c^2 - 9984 \sin ^6(E/2)+ 2304\cos (E)\sin ^6(E/2)}{65{,}536}\\ a_{12}(E)&{}=\frac{(328 + 2730 c^4 + (64 - 780 c^4)\cos (E) - 63\cos (2E) + 6 \cos (3E))\cos (E/2) \sin ^3(E/2)}{16{,}384}\\ a_{13}(E)&{}= \frac{(-63 (-65 + 1817 c^4 + 4000 c^8 + 1233 c^{12}) + 117{,}760 c^2 (-13 + 3\cos (E)) \sin ^6(E/2))}{6{,}291{,}456}\\ a_{14}(E)&{}=\frac{(-3{,}104{,}640 - 13{,}680 c^2 + 6000 c^6 + 840 c^{10})E - 60 \sin (E)(-84{,}000 + 2997 c^2 + 8175 c^6 + 14 c^{10})}{10{,}485{,}760} \\ &{} \quad + \, \frac{900\sin (2E) (-1472 + 105 c^2 + 323 c^6) + (283{,}200 + 8250 c^2 - 32{,}300 c^6) \sin (3E)}{10{,}485{,}760} \\ &{} \quad + \, \frac{(- 36{,}000 - 5625 c^2) \sin (4E) + (1728 + 450 c^2) \sin (5E)}{10{,}485{,}760} \end{array} \end{aligned}$$

(27)

where $t=E-\sin {E}$.

For simplicity, in the following sections, we do not distinguish the stable and unstable manifolds associated to the periodic orbit $\Gamma (t)$ with those associated to the critical point $p_{\tau }$. In both cases we will use the same symbol. The reader can distinguish the two cases by the context.

5 Transversality of the Stable and Unstable Manifolds

In this section we will characterize the intersection of the global stable and unstable manifolds, $P^{u,s}$, obtained from the local ones by saturating the flow. For brevity we still denote them by the same symbol. Consider the annular section

$$\begin{aligned} \Sigma = \{(r, \dot{r},t)\mid r>0, \dot{r}=0, t\in {\mathbb {R}}\;\text{ mod } (2\pi )\}. \end{aligned}$$

(28)

We will show that $P^{u}$ (and $P^{s}$) meets $\Sigma$ forwards (backwards) for the first time, in a simple closed curve $\gamma _u$ ($\gamma _s$). But before that note that

Proposition 7

$\Sigma$ is transversal to the flow associated the system (7), excepting for a differentiable closed curve around the origin.

Proof

Since $\Sigma$ is defined by the equation $\dot{r}=0$, the transversality can fail whenever $\ddot{r}=0$. Let us write this equation as a polynomial with time-dependent coefficients

$$\begin{aligned} 0=r^8 -c^4 \left( r^2+\rho ^2/4\right) ^3 =k^4-c^4 k^3 -\frac{3}{4} c^4 k^2 \rho ^2-\frac{3}{16}c^4 k \rho ^4 -\frac{1}{64} c^4\rho ^6\equiv p(k,t),\ \end{aligned}$$

(29)

where $k=r^2$. For any fixed value of t, p(k, t) is a polynomial in k which by the Descartes signs rule, has exactly one positive root, which we will denote by k(t). Since the coefficients of the polynomial are $2\pi$-periodic, $0= p(k(t+2\pi ),t+2\pi )=p(k(t+2\pi ),t)$, and as $p(k(t),t)=0$, then by the uniqueness $k(t+2\pi )= k(t)$. Thus, except for the closed curve $r(t)=k(t)^{1/2}$, $t\in {\mathbb {R}}\;\text{ mod } (2\pi )$, the flow is transversal to $\Sigma$. Furthermore, the curve k(t) such that $p(k,t)=0$ is differentiable. In fact, a direct computation yields the resultant of the polynomial p(k, t) and its derivative $\frac{\partial p}{\partial k}(k,t)$ to be $27c^4+ 64\rho ^2$, which does not vanish for any real $\rho$, therefore all the roots are simple, that is, $\frac{\partial p}{\partial k}(k,t)\ne 0$ for k such that $p(k,t)=0$. By the implicit function theorem the curve k(t) is differentiable. $\square$

Observe that $p(k,t)<0$, if and only if, $\ddot{r}>0$ and $p(k,t)>0$, if and only if, $\ddot{r}<0$. Thus $\Sigma$ is divided in two components $\Sigma _{+}$ and $\Sigma _{-}$ by the curve $r(t)=k(t)^{1/2}$, $t\in {\mathbb {R}}(\text{ mod } 2\pi )$ where

$$\begin{aligned} \Sigma _{+}= \{(r, \dot{r},t)\mid r>0, \dot{r}=0 , p(r^2,t)<0,t\in {\mathbb {R}}(\text{ mod } 2\pi )\} \end{aligned}$$

(30)

and $\Sigma _{-}$ is defined similarly but with the inequality $p(r^2,t)>0$, instead. Then whenever a solution $(r(t),\dot{r}(t))$ crosses $\Sigma ^{+}$ (resp. $\Sigma ^{-}$), we have $\ddot{r}(t)>0$ (resp. $\ddot{r}(t)<0$). From (29) it follows that $p(0,t)<0$ therefore the component $\Sigma _{+}$ contains the origin $r=\dot{r}=0$, $t\in {\mathbb {R}}(\text{ mod } 2\pi )$ in its closure.

Lemma 2

The system (4) does not admit solutions $(r(t), \dot{r}(t))$ such that r(t) is constant.

Proof

The proof follows by inspecting Eq. (4). $\square$

Proposition 8

Let the angular momentum be taken large enough, namely

$$\begin{aligned} c> \frac{1}{3^{1/4}}\approx 0.7598356\ldots \end{aligned}$$

Then if r(t) is a parabolic solution of (4), that is, $r(t)\rightarrow \infty$ and $\dot{r}(t)\rightarrow 0$ as $t\rightarrow \infty$, then there exists a largest finite value $t_{-1}$, such that $\dot{r}(t_{-1})=0$. Moreover $\ddot{r}(t_{-1})>0$.

Proof

From (4) it follows that for large r, $\ddot{r}<0$. Since $r(t)\rightarrow \infty$ as $t\rightarrow \infty$ we have $\ddot{r}(t)<0$ and $\dot{r}(t)>0$ for large t. We follow such a solution backwards in time. It cannot happen that $\ddot{r}(t)<0$ for all t, since in that case r(t) would be concave downwards and it would imply that r(t) vanishes for some t, contrary to Proposition 1. Therefore there exists a first $t_{-2}$ (backwards in time) such that $\ddot{r}(t_{-2})=0$, with $\dot{r}(t_{-2})>0$, so at least in a small interval $(t_{-2}-\epsilon ,t_{-2})$ (for $\epsilon >0$ sufficiently small), $\dot{r}(t)>0$. Suppose that r(t) is increasing with $\dot{r}(t)>0$ for all $t \in (-\infty , t_{-2})$. So, since $r(t)\ge 0$, that is, r(t) is bounded from below and, by Proposition 2, $\lim _{t\rightarrow \pm \infty }r(t)\ne 0$, it follows that $\lim _{t\rightarrow -\infty }r(t)=r^*$ exists and is a positive quantity. The last condition says that in the x–y Cartesian plane, the solution winds towards a circle of radius $r^*$ backwards in time. Let us prove that this assertion leads to a contradiction. Consider the suspension of (4)

$$\begin{aligned} \frac{d^2r}{dt^2}= & {} -\frac{r}{(r^2+\rho ^2/4)^{3/2}}+\frac{c^2}{r^3} \\ \frac{dt}{dt}= & {} 1 (\text{ mod } 2\pi ) \end{aligned}$$

and take a small transversal section $\Sigma =(r^*-\delta ,r^*+\delta )$ to the circle of radius $r^*$; that is, an annulus in the extended phase space $\Sigma \times {\mathbb {R}}(\text{ mod } 2\pi )$. Then along the above mentioned solution, the backwards first return map associated to this section defines a sequence $(r_n,t_n)$ such that $r_n\rightarrow r^*$. Passing to a subsequence if necessary we can suppose that $t_n\rightarrow t^*\in {\mathbb {R}}(\text{ mod } 2\pi )$. By continuity of the return map, the solution through $(r^*,t^*)$ is a periodic orbit which projects into the circle of radius $r^*$. By the previous lemma, the system (4) does not admit such a solution, and we get a contradiction.

Thus $\dot{r}$ cannot be positive for all $t<t_{-2}$ and therefore there exists a maximal $t_{-1}$, $t_{-1}<t_{-2}$ such that $\dot{r}(t_{-1})=0$. Let us show that $\ddot{r}(t_{-1})>0$; if $\ddot{r}(t_{-1})<0$ then $t_{-1}$ would be a local maximum, but since $r(t)\rightarrow \infty$ as $t\rightarrow \infty$ by Rolle’s Theorem there would be a $t_{-1}'>t_{-1}$ such that $\dot{r}(t_{-1}')=0$ contrary to the definition of $t_{-1}$. Let us show that $\ddot{r}(t_{-1})=0$ also leads to a contradiction: Multiply (4) by $\dot{r}$ to get and then integrate from $t_{-1}$ to a large positive $t_0$,

$$\begin{aligned}&\begin{array}{c} \frac{d}{dt}\left( \frac{1}{2}\dot{r}^2\right) = -\frac{c^2}{2}\frac{d}{dt} \left( \frac{1}{r^2}\right) - \frac{r\dot{r}}{\left( r^2+\frac{\rho ^2}{4}\right) ^{3/2}}\\ \end{array}\\&\quad \begin{array}{c} \frac{1}{2}(\dot{r}^2(t_0)- \dot{r}^2(t_{-1}))= - \frac{c^2}{2}\left( \frac{1}{r(t_0)^2}-\frac{1}{r(t_{-1})^2}\right) -\int _{t_{-1}}^{t_0}\frac{r\dot{r}}{\left( r^2+\frac{\rho ^2}{4}\right) ^{3/2}} dt. \end{array} \end{aligned}$$

Taking the limit as $t_0\rightarrow \infty$, we get

$$\begin{aligned} 0= \frac{c^2}{2}\left( \frac{1}{r_{-1}^2}\right) -\int _{t_{-1}}^{\infty }\frac{r\dot{r}}{\left( r^2+\frac{\rho ^2}{4}\right) ^{3/2}} dt\quad \text{ or } \quad \frac{c^2}{2r_{-1}^2}= \int _{t_{-1}}^{\infty }\frac{r\dot{r}}{\left( r^2+\frac{\rho ^2}{4}\right) ^{3/2}} dt, \end{aligned}$$

(31)

where we have used the shorthand $r_{-1}=r(t_{-1})$. The last integral can be estimated as follows: since $\dot{r}(t)>0$ for $t\in (t_{-1},\infty )$ and $\rho =1-\cos (E)\le 2$

$$\begin{aligned} \int _{r_{-1}}^{\infty }\frac{ r}{\left( r^2+1\right) ^{3/2}} dr \!=\!\int _{t_{-1}}^{\infty }\frac{r\dot{r}}{\left( r^2+1\right) ^{3/2}} dt \!\le \! \int _{t_{-1}}^{\infty }\frac{r\dot{r}}{\left( r^2+\frac{\rho ^2}{4}\right) ^{3/2}} dt \!\le \! \int _{t_{-1}}^{\infty }\frac{\dot{r}}{r^2} dt\!=\! \int _{r_{-1}}^{\infty }\frac{1}{r^2} dr. \end{aligned}$$

Computing the integrals at the extremes of the above inequalities and using (31) we have

$$\begin{aligned} \frac{1}{\sqrt{r_{-1}^2+1}} < \frac{c^2}{2r_{-1}^2}< \frac{1}{r_{-1}}, \end{aligned}$$

from which it follows that

$$\begin{aligned} r_{-1}\ge \frac{c^2}{2},\quad \text{ and }\quad r_{-1}^4- \frac{c^4}{4}\left( r_{-1}^2+1 \right) \le 0. \end{aligned}$$

The left-hand side of the last inequality is a quadratic polynomial in $k=r_{-1}^2$ with real roots

$$\begin{aligned} k=\frac{c^4}{8}\pm \frac{c^2}{2}\sqrt{1+\frac{c^4}{16}}. \end{aligned}$$

Choosing the positive root, it yields the estimate

$$\begin{aligned} \frac{c^2}{2}\le r_{-1}\le \frac{c}{\sqrt{2}}\sqrt{\frac{c^2}{4}+ \sqrt{1+\frac{c^4}{16}}}. \end{aligned}$$

(32)

Now the polynomial (29) can be expressed as the equality

$$\begin{aligned} k^3(k-c^4)= c^4\rho ^2 \left( \frac{3}{4}k^2+\frac{3}{16}k\rho ^2+\frac{1}{64}\rho ^4\right) . \end{aligned}$$

(33)

The left hand side vanishes for $k=0,c^4$ and is negative in $(0,c^4)$; the right hand side is nonnegative within this interval, therefore the positive root lies in the interval $[c^4,\infty )$. But

$$\begin{aligned} \frac{c^4}{8}+ \frac{c^2}{2}\sqrt{1+\frac{c^4}{16}}< c^4 \end{aligned}$$

for

$$\begin{aligned} c> \frac{1}{3^{1/4}}\approx 0.7598356\ldots \end{aligned}$$

Thus we conclude that for $r_{-1}$ within the bound (32), $k=r_{-1}^2$ cannot be a solution of (33) or a root of (29) so $\ddot{r}(t_{-1})\ne 0$. Therefore $\ddot{r}(t_{-1})> 0$. $\square$

Theorem 3

Let the angular momentum be taken large enough, namely

$$\begin{aligned} c > \frac{1}{3^{1/4}}\approx 0.7598356\ldots \end{aligned}$$

Then the global stable (unstable) manifolds $P^{s}$ ($P^{u}$) intersect the section $\Sigma$ backwards (forwards) for the first time, in a simple closed curve $\gamma ^{s}$ ($\gamma ^{u}$) contained in the component $\Sigma _{+}$. Both curves enclose the origin and intersect at least in two points located at $t=0$ and $t=\pi$.

Proof

By Proposition 6 follows that the local stable manifold associated to the periodic orbit $\Gamma (t)$ is a cylinder, given by the equation $u={\mathcal {F}}(-v, -E(t))$. Observe that for v sufficiently small we have that $u={\mathcal {F}}(-v, -E(t))\approx v$.

Consider the plane $v\!=\!v_0 >0$ with $v_0$ sufficiently small (that is $\{(u, v_0, E)| u>0, E \in [0,2\pi )\}$), it follows that the intersection of the local stable manifold, $u\!=\!{\mathcal {F}}(-v, -E(t))\approx v$, with $v\!=\!v_0$, given by $u\!=\!{\mathcal {F}}(-v_0, -E(t))\approx v_0$, is a circle $\gamma '^{s}$ since $E\in S^1$, $t\in S^1$. Note that $\gamma '^{s}$ can be explicitly parametrized as follows: $t \rightarrow (u(t),v_0, t)$, where $u(t)\!=\! {\mathcal {F}}(-v_0,-E(t))\approx v_0$ and $t\in S^1$, see Fig. 3 (left). On the other hand, by definition, $\gamma '^s$ consists of solutions such that $r(t)\rightarrow \infty$, $\dot{r}(t)\rightarrow 0$ as $t\rightarrow \infty$ (that is $\gamma '^s$ consists of points of the solutions that go to infinity with zero radial velocity). So, for each $(u(t), v_0, t)\approx (v_0, v_0, t)$ in $\gamma '^{s}$, that is, for each $(v_0, v_0, t_0)$ with $t_0\in [0, 2\pi )$ we following the corresponding solution backwards in time along the flow yields a cylinder which, by Proposition 8, intersects the section $\Sigma _{+}$ for the first time $t_{-1}$, in a simple closed curve $\gamma ^s$, since the variable $t_0\in {\mathbb {R}} (\text{ mod } 2\pi )$ gives an explicit parametrization, see Fig. 3 (right). We use the following parametrization in order to exhibit that it encircles the origin of the section $\Sigma _{+}$: Let $t_{-1}$ denote, as in the proof of the previous proposition, the first time such that $\dot{r}(t_{-1})\!=\!0$, and let $r_{-1}\!=\!r(t_{-1})$, then the curve $\gamma ^s$ can be parameterized as $\xi +i\eta \!=\!r_{-1}e^{i t_{-1}}$; since $r(t_{-1})>0$, it encircles the origin. Observe that $t_{-1}\!=\! t_{-1}(t_0)$. By a similar argument, the unstable manifold $P^u$ intersects for the first forward time the section $\Sigma$ in a closed curve $\gamma ^u$ which encircles the origin. Using coordinates $\xi +i\eta \!=\! r \cos t+ i r \sin t$, for the section $\Sigma$, the symmetry $(r, p_r, t) \rightarrow (r, -p_r, -t)$ becomes $t\rightarrow -t$, that is, a reflection with respect to the $\xi$-axis. Since both $\gamma ^{s,u}$ encircle the origin, they intersect at least in two points along the $\xi$-axis. Furthermore, since the coefficients in (26) depend on t in that way, it follows that $\gamma ^{s,u}$ intersect at least in the points located at $t\!=\!0$ and $t\!=\!\pi$. See Figs. 9 and 10 (left) for the numerical description of the curve $\gamma ^{s}$ and $\gamma ^u$ on the section $\Sigma$ for different values of c. $\square$

Fig. 3

The parametrization of the curve ${\gamma '}^{s}$

We will make explicit the additional transversality hypothesis, obtained numerically.

Theorem 4

The parabolic stable and unstable manifolds $P^s$, $P^u$ intersect transversally along the homoclinic orbit $t_{-1}=0$, for c large enough. For $t_{-1}=\pi$ there is also a transversal intersection with a small intersection angle (see Figs. 9 and 10 (right) for the numerical description of the transversal intersection of $P^u$ and $P^s$ along the homoclinic orbit on the section $\Sigma$ for different values of c).

Remark 3

This result is consistent with numerical explorations performed for a wide range of values of the parameter c, details of this fact are given in Appendix, “Transversal Intersection of the Invariant Manifolds $P^{u,s}$” section.

In the next section, we are going to explore dynamical consequence of the transversal intersection of the stable and unstable manifolds. Also, we describe the solutions near the critical escape velocity and show that there is a set of orbits to which one can associate any sequence of integers (i.e., the symbolic dynamics).

6 Symbolic Dynamics

Given a point $(r_0, \dot{r}_0, t_0) \in \Sigma _+$, where $r_0=r(t_0)$ and $\dot{r}_0=\dot{r}(t_0)$, then $\dot{r}_0=0$ and $\ddot{r}(t_0)>0$. In according to the ideas given in [11], we define a mapping $\phi$ on part of the plane $\Sigma _+$ by following a solution $(r(t), \dot{r}(t))$ of (7) with initial condition $r(t_0)=r_0, \dot{r}(t_0)=0$ until its first intersection with section $\Sigma _+$, say $t_1>t_0$, if it exists, and set $r_1=r(t_1)$. In this way, the mapping $\phi$ is given by

$$\begin{aligned} \begin{array}{cccc}\phi : &{}\Omega \subset \Sigma _+&{} \rightarrow &{} \Sigma _+\\ &{}(r_0,t_0)&{}\rightarrow &{} (r_1, t_1).\end{array} \end{aligned}$$

(34)

If there is not $t_1$ with this property we set $t_1=\infty$. We described the initial values $(r_0, t_0)$ in polar coordinates on a plane $\Sigma _+$, being $t_0$ representing the angle and $r_0$ the radius.

We now discuss where this map is defined and we characterize its complement. Let $D_0$ denote the set of points in $\Sigma _+$ for which a finite $t_1>t_0$ exists and we add to $D_0$ the point $(0, t_0)$. Thus, $D_0$ represents the initial values of the orbits which return to $\dot{r}=0$.

Lemma 3

For $(r_0, t_0)$ outside $D_0$ the corresponding solutions escape.

Proof

Let r(t) be the solution of (7) satisfying

$$\begin{aligned} r(t_0)=r_0,\quad {\dot{r}}(t_0)=0, \quad {\ddot{r}}(t_0)>0 \end{aligned}$$

and $t_1=\infty$, so $\dot{r}(t)>0$ for $t>t_0$. Observe that it is not possible that $\dot{r}(t)<0$ for $t>t_0$. In fact, if this occurs we will have or $\lim _{t\rightarrow t^*}r(t)=0$ for $t^*$ finite or $\lim _{t\rightarrow \infty }r(t)=0$, contracting Propositions 1 and 2. Thus, r is monotonically increasing for $t>t_0$ and so

$$\begin{aligned} r(t)\rightarrow \infty \, \, as \, \, t \rightarrow \infty . \end{aligned}$$

In fact, since $\dot{r}(t)>0$ for $t > t_0$, it follows that r(t) is an increasing function for all $t > t_0$, in particular there exists

$$\begin{aligned} \displaystyle \lim _{t\rightarrow \infty }r(t) \end{aligned}$$

and it can be finite or infinite. We will assume that $\displaystyle \lim _{t\rightarrow \infty }r(t)= \gamma \ge r_0 >0$, with $\gamma \in {\mathbb {R}}$. Then by Eq. (7) we have that $\ddot{r}(t)$ is bounded as $t\rightarrow \infty$. Then by Lemma¹ $\dot{r}(t) \rightarrow 0$ as $t \rightarrow \infty$. In conclusion, it follows that $(r(t), \dot{r}(t))$ is an equilibrium point, which is a contradiction. Therefore,

$$\begin{aligned} \displaystyle \lim _{t\rightarrow \infty }r(t)= \infty . \end{aligned}$$

Moreover, again by (7), follows that $\ddot{r}<0$ for $t\!>\!tilde{t}$ for some $\tilde{t}>t_0$. So, the function $\dot{r}$ is monotonically decreasing for $t\!>\!tilde{t}$, so $\dot{r}(\infty )=\lim _{t\rightarrow \infty }\dot{r}\ge 0$ exists. Recall, see Proposition 3, that one refers to a hyperbolic orbit if $\dot{r}(\infty )>0$ and to a parabolic orbit if $\dot{r}(\infty )=0.$ Thus, for $(r_0, t_0)$ outside $D_0$ the corresponding solutions escape which are parabolic or hyperbolic. $\square$

Let $D_0'$ be the complement of $D_0$. By the previous lemma, we have seen that $D_0'$ corresponds to parabolic and hyperbolic orbits. The hyperbolic orbits form an open set in $D_0'$ and since $D_0'$ is closed (since $D_0$ is an open set) it follows that $\partial D_0$ is contained in $D_0'$ and consists of parabolic orbits; thus $\partial D_0=\gamma ^s$. In a similar way we define $D_1$ as the set of initial conditions $(r_0,\dot{r}_0,t_0)$ with $\dot{r}_0 = \dot{r}(t_0)=0$ and $\ddot{r}(t_0)>0$ such that there exists $t_{-1}<t_0$ such that $\dot{r}(t_{-1})=0$ and $\ddot{r}(t_{-1})>0$. Its complement $D_1'$ consists of escaping hyperbolic or parabolic orbits for $t\rightarrow -\infty$ and $\partial D_1=\gamma ^{u}$.

The proof of the following theorem follows the same lines as in the Sitnikov problem, see [11, Theorem 3.6, p. 92], and depends solely on the structure of the parabolic orbits given by Theorem 4 (that is, there exists a transversal intersection of the stable and unstable manifolds), so we will not repeat these arguments.

Theorem 5

There exists a set $S\subset D_0$ which is invariant under the Poincaré map $\phi$ given in (34) such that its restriction to S is conjugate to the full shift in an infinite number of symbols.

We give a brief description of the symbolic dynamics involved, i.e., we described the dynamical consequence derived of the Theorem 5: Given $(r_0,\dot{r}_0,t_0)\in D_0$ consider the sequences of consecutive times $t_n$ such that $\dot{r}(t_n)=0,$ ordered according to $t_n < t_{n+1}$. Define the sequence of integers

$$\begin{aligned} a_{n}= \left[ \dfrac{t_n- t_{n-1}}{2\pi }\right] \end{aligned}$$

where $[\quad ]$ denote integer part; thus $a_{n}\in {\mathbb {N}} \cup \{\infty \}$ measures the number of binary collisions of the primaries between consecutive closest approaches of the infinitesimal to the line of primaries: $\dot{r}(t_{n})=0$ and $\ddot{r}(t_n)>0$.

For each initial condition on the invariant set S we associate the sequence of integers $(a_n)$ where we agree that in the case $a_n=\infty$ the sequence finishes and we add the symbol $\infty$. In this way the kind of sequences is of the following type:

• 1. $( \ldots , a_{-1}, a_{0}, a_{1}, \ldots )$,   with $a_{n} \in {\mathbb {N}}$ for all $n \in {\mathbb {Z}}$. This succession corresponds to the orbits of the infinitesimal which perform an infinite number of closest approaches to the line of primaries in the past and in the future and the sequence $(a_n)$ codifies the number of collisions of the primaries between closest approaches.

• 2. $( \infty , a_{k}, a_{k+1} \ldots )$,  with $k\le 0,$ and $a_{n}\in {\mathbb {N}}$ for all $n\in {\mathbb {Z}}$ such that $n>k-1$. This case corresponds to the orbits of the infinitesimal ejected from infinity and remains oscillating performing closest approaches to the line of primaries. This can be labeled as capture orbits.

• 3. $( \ldots , a_{l-2}, a_{l-1}, \infty )$,  with $l\ge 1$ and $a_{n}\in {\mathbb {N}}$ for all $n\in {\mathbb {Z}}$ such that $n<l$. This case corresponds to escaping orbits of the infinitesimal in the future which perform closest approaches to the line of primaries in the past.

• 4. $( \infty , a_{k-1}, \ldots , a_{l-1}, \infty ),$  with $k\le 0,\, l\ge 1$ and $a_{n}\in {\mathbb {N}}$ for all $n\in {\mathbb {Z}}$ such that $k < n < l$. This case corresponds to the orbits of the infinitesimal coming from infinity oscillates a finite number of times and escape to infinity.

The following theorem is a consequence of Theorem 5 and its proof follows the same arguments as in [11, p. 97].

Theorem 6

There exists an integer $\hat{b}>0$ such that any sequence $a=(a_n)$ with $a_n\ge \hat{b}$ corresponds to a solution of (7).

Proof

According to [11, p. 97], given an initial condition in $D_0(\delta )$ ² the return time to $\dot{r}=0$ has a lower bound, $\hat{b}$, depending on $\delta$. In this way, given an arbitrary sequence $s=(\cdots s_{-1}, s_0, s_1, \cdots )$ of one of the four kinds described above, follows that it corresponds to an orbit for which the integral part $\left[ \dfrac{t_n-t_{n-1}}{2\pi }\right]$ of the return time is prescribed as an sequence $a_n= s_n+[c]$. In this case, $\hat{b}=[c]$. For more details see [11]. $\square$

Observe that the above theorem allows also to find infinitely many periodic orbits by choosing periodic sequences. Note that these sequences are as the first kind above $( \ldots , a_{-1}, a_{0}, a_{1}, \ldots )$,   with $a_{n} \in {\mathbb {N}}$ for all $n \in {\mathbb {Z}}$ an periodic sequence.

7 Numerical Exploration

In this section we present some numerical explorations of the ERI3BP. In Fig. 4 or in Fig. 5 we present a typical phase portrait of the Poincaré map, which is of short period since the time is defined by consecutive passages of the primaries through the aphelio, that is, when the time satisfies $\cos (E)=-1$ which corresponds to the maximal distance between the primaries. In Fig. 6 the path for the same initial condition used for the Poincaré map in Fig. 4 is shown in the $p_r$–r and in the x–y planes. These orbits appear in the kind of sequences 1 described in Sect. 6. Fig. 7 is shown for $c=0.5$. In Fig. 8 the homoclinic orbit corresponding to the crossing with $E=\pi$ is shown in the x–y plane.

Fig. 4

Poincaré map, described in the $p_r$–r plane, associated with the section $E=\pi (\text{ mod } 2\pi )$ corresponding to a maximal distance among the primaries. The angular momentum is $c=0.1$. A zoom of the last plot is given below

Fig. 5

Zooms of Fig. 4

Fig. 6

The paths in the $p_r$–r plane (left) and in the original x–y plane (center). A zoom of the last plot (right). The angular momentum is $c=0.1$

Fig. 7

The paths in the $p_r$–r plane (left) and in the original x–y plane (center). A zoom of the last plot (right). The angular momentum is $c=0.5$

Fig. 8

The homoclinic parabolic orbit corresponding to the crossing $E=\pi$ (aphelium of the primaries) for $c=0.2$

Appendix

1.1 Transversal Intersection of the Invariant Manifolds $P^{u,s}$

Fig. 9

Curves $\gamma ^{u,s}$ for $c=1$ (left) in $\xi \, \eta$-plane. Details of the transversal crossing (right)

We take the initial conditions on the unstable manifold of the parabolic orbits, given by the series $u = {\mathcal {F}}(v,E)$, described in (26). We have computed numerically the first intersection of $P^{u,s}$ with the section $\Sigma$, solving in backward time system (7). We denote by $\gamma ^{u,s}$ this first intersection. In Figs. 9 and 10 they are represented in the plane $\xi +i\eta =r_{-1} e^{i E_{-1}}$ and are obtained through the Mathematica program (we use the subroutines Runge–Kutta pairs of orders 2(1) through 9(8) with quadruple precision and starting step size equal to 0.0125) as follows: using the approximation in order 14 to the unstable manifold $P^u$ given by (26) we choose 100 equally spaced values for the eccentric anomaly E on the interval $[0,2\pi )$. We take $v=-0.1$, so the corresponding values of $u= {\mathcal {F}}(v,E)$ are calculated. In this way, we have the initial conditions $(u_i, v_i)=({\mathcal {F}}(-0.1, E_i), -0.1)$, $i=0, \ldots , 100$. Through the change of coordinates (9) each initial condition is transformed to initial conditions for the system (7) ($(r_i, p_{r_i})=(2/u_i^2, -0.1), i=0, \ldots , 100$) and then the solution is followed numerically up to its first intersection with $\Sigma ^{+}$ ($p_r=0$ with $\dot{p_r}>0$); with the values of $r_{-1}$ and $E_{-1}$ at an intersection, the point $\xi +i\eta = r_{-1} e^{i E_{-1}}$ is computed and plotted. Figures 9 and 10 describe these points in the $\xi -\eta$ plane for $c=1$ and $c=0.5$. The dashed circles in pink in the Figs. 9 and 10 are the circles whose radii are determined by the lower and upper bounds in inequality (32).

Fig. 10

Curves $\gamma ^{u,s}$ for $c=0.5$ (left). details of the transversal crossing (right)

1.2 Differentiability of the Invariant Manifolds $P^{u,s}$ at the Origin

In order to make the paper self-contained, we include here the main results in [2, 3] for convenience of the reader.

We consider the map $F: U \subset {\mathbb {R}}^{n+m} \rightarrow {\mathbb {R}}^{n+m}$ of the form

$$\begin{aligned} F(x, y)= (x+ p(x, y)+ r_1(x, y), y+ q(x, y)+ r_2(x, y)), \end{aligned}$$

(35)

where p(x, y), q(x, y) are homogeneous polynomials of degree $N_p$ and $N_q$ respectively, with $N_p, N_q \ge 2$, $r_1(x,y)$ of order $o(\Vert (x,y)\Vert ^{N_p})$, $Dr_1(x,y)$ of order $o(\Vert (x,y)\Vert ^{N_{p}-1})$, $r_2(x,y)$ of order $o(\Vert (x,y)\Vert ^{N_q})$, $Dr_2(x,y)$ of order $o(\Vert (x,y)\Vert ^{N_{q}-1})$. We introduce the projections $\pi ^1(x, y)= x$, and $\pi ^2(x, y)= y$. Given a subset $V \subset {\mathbb {R}}^n$ we define

$$\begin{aligned} W^s_V= \{(x, y) \in U \ / \ \pi ^1 F^k(x, y) \in V, k \ge 0, \, F^k(x, y) \rightarrow (0, 0), \, \text{ as }\, k \rightarrow +\infty \} \end{aligned}$$

and its local version

$$\begin{aligned} W^s_{V, r}\!=\! \{(x, y) \in U \ / \ \pi ^1 F^k(x, y) \!\in \! V \cap B(0, r), k \ge 0, \, F^k(x, y) \rightarrow (0, 0), \, \text{ as }\, k \rightarrow +\infty \}. \end{aligned}$$

We will assume that there exists a set $V\subset U$ and $r, \rho >0$ such that

• (H1)   The polynomial p satisfies $sup_{x\in V^{1}(\rho )}\Vert Id+D_xp(x,0)\Vert <1.$

• (H2)   The polynomial q satisfies $D_xq(x,0)=0$ for $x\in V^{1}(\rho )$ and $sup_{x\in V^{1}(\rho )}\Vert Id-D_{y}q(x,0)\Vert <1.$

• (H3)   There exists $A>0$ such that for all $x \in V(r)$, $dist(x+p(x,0), V(r)^{c})\ge A\Vert x\Vert ^{N_p}$.

• (H4)   For all $x \in V^{1}(\rho ), \Vert Id+D_{x}p(x,0)\Vert +\Vert Id-\frac{1}{N_p}D_xp(x,0)\Vert <2$, where $V(r)=\{x\in V| \Vert x\Vert <r\}$ and $V^{1}(\rho )=\{\rho \, x/\Vert x\Vert | x\in V(r)\}$.

Theorem 4.1 in [2] states the following.

Theorem 7

Let F be an analytic map of the form (35). Assume that there exists a convex open set $V \subset {\mathbb {R}}^n, 0\in \partial V$ and $r, \rho >0$ such that hypotheses H1–H4 hold. Then $W^{s}_{V,r}$ is the graph of a real analytic function

$$\begin{aligned} \varphi : V(r)\rightarrow {\mathbb {R}}^m. \end{aligned}$$

In the two-dimensional case, if $n=1$ and $m=1$, V can be taken as the intervals (0, r) or $(-r , 0)$. When $V= (0, r)$ the corresponding invariant set $W^s_{V, r}$ corresponds to $P^s= {\mathcal {A}}(F, {\mathcal {U}})$ given according to the notation in [10] with ${\mathcal {U}}={\mathcal {B}}(\beta , r)$ and the set $V^{1}(\rho )$ above is given by $V^{1}(\rho )=[0,r]$ .

It is important to observe that as was discussed in [2, p. 59], $\varphi$ is differentiable at 0 and $D\varphi (0)=0$. On the other hand, as $\varphi$ is analytic we can prove that $D \varphi (x) \rightarrow 0$ as $x \rightarrow 0^+$, so $\varphi$ is of class $C^1$ at the origin. In [3] the authors give information about the degree of differentiability of $\varphi$ at $x=0$. Below we state the theorem that guarantees such information.

Theorem 8

Let $F= (F^1, F^2) : U \subset {\mathbb {R}}^{1+m} \rightarrow {\mathbb {R}}^{1+m}$ be a $C^r$ map, $r \ge 2$ or $r= \infty$, such that $F(0, 0)=0$, $DF(0, 0)= Id$,

$$\begin{aligned} D^j F^1(0, 0)= & {} 0, \quad \text{ for }\quad 2 \le j \le N-1, \end{aligned}$$

(36)

$$\begin{aligned} D^j F^2(0, 0)= & {} 0, \quad \text{ for }\quad 2 \le j \le M-1, \end{aligned}$$

(37)

and

$$\begin{aligned} \frac{\partial ^N F^1}{\partial x^N}(0, 0) < 0, \quad \frac{\partial ^M F^2}{\partial x^M}(0, 0) = 0, \end{aligned}$$

(38)

for some $2 \le N, M \le r$. In the case when $M \le N$ we also assume that

$$\begin{aligned} Spec \frac{\partial ^M F^2}{\partial x^{M-1} \partial y}(0, 0) \subset \{z \in {\mathbb {C}} \ / \ Re z >0 \}. \end{aligned}$$

(39)

Let $L= min (N, M)$ and $\eta = 1+ N-L$. We assume that $r > 2 N-1$. Then there exist a $C^p$ map $K: [0, t_0) \subset {\mathbb {R}} \rightarrow {\mathbb {R}}^{1+m}$, with $p=[(r-N+1)/ \eta ]-1$, of class $C^r$ in $(0, t_0)$ and a polynomial $R : {\mathbb {R}} \rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} F \circ K= K \circ R. \end{aligned}$$

(40)

Moreover, $K(t)= (t, 0)+ O(t^2)$ and $R(t)=t+ d_N t^N+ O(t^{2N-1})$ with $d_N= \frac{\partial ^N F^1}{\partial x^N}(0, 0)$.

1.3 Computation of the Coefficients $b_j$ in (23)

We use the eccentric anomaly as the independent variable and observe that $t=E-\sin {E}$, so $\frac{dt}{dE}=\rho$. Differentiating $v= {\mathcal {G}}(u,E)=\sum _{n=0}^{\infty } b_n(E)u^n$, we get

$$\begin{aligned} \frac{\partial v}{\partial E}=\frac{\partial {\mathcal {G}}}{\partial u}\frac{\partial u}{\partial E}+\frac{\partial {\mathcal {G}}}{\partial E}. \end{aligned}$$

Substituting (15) in the previous equation and using that $\frac{dt}{dE}=1-\cos E=\rho$, we get

$$\begin{aligned} \begin{array}{ll} -\frac{\rho }{4}u^4\sum \nolimits _{n\ge 0}\left( \begin{array}{c}\!-3/2\\ \!n\end{array}\right) \frac{\rho ^{2n}u^{4n}}{16^n}\!+\!\frac{\rho c^2}{8}u^6 = - \frac{\rho }{4}\left( \sum \nolimits _{n\ge 1}nb_nu^{n+2}\right) \left( \sum \nolimits _{n\ge 0}b_nu^{n}\right) \!+\! \sum \nolimits _{n\ge 0}b_n'u^{n}\\ -\frac{\rho }{4}\sum \nolimits _{n\ge 0}\left( \begin{array}{c}-3/2\\ n\end{array}\right) \frac{\rho ^{2n} u^{4(n+1)}}{16^n}+\frac{\rho c^2}{8}u^6 = -\frac{\rho }{4}\sum \nolimits _{n\ge 3}c_n u^n+ \sum \nolimits _{n\ge 0}b_n'u^{n}, \end{array} \end{aligned}$$

where $'$ means derivative with respect to E and the coefficients $c_n$ are obtained from the formula for the Cauchy product:

$$\begin{aligned} \begin{array}{rl} c_n&{}= \displaystyle \sum _{k+l=n, k\ge 3, l\ge 0} (k-2) b_{k-2}b_l \\ &{} = \displaystyle \sum _{l=0}^{n-3} (n-l-2)b_{n-l-2} b_l\\ &{} = (n-2)b_{n-2}b_0+ (n-3)b_{n-3}b_1 + \cdots +b_1b_{n-3}. \end{array} \end{aligned}$$

In this way the equation can be written as

$$\begin{aligned} -\frac{\rho }{4}\sum _{\begin{array}{c}n\ge 4,\\ n\equiv 0 (\text{ mod } 4) \end{array}}\left( \begin{array}{c}-3/2\\ \frac{n-4}{4}\end{array}\right) \frac{\rho ^ {\frac{n-4}{2}}u^{n}}{16^{\frac{n-4}{4}}}+\frac{\rho c^2}{8}u^6 =- \frac{\rho }{4}\sum _{n\ge 3}c_n u^n+\sum _{n\ge 0}b_n'u^{n}. \end{aligned}$$

(41)

The first equations read $b_0'=0,\, b_1'=0,\, b_2'=0$. Then it follows that $b_0=b_0^{(0)},\, b_1=b_1^{(0)},\, b_2=b_2^{(0)}$ are constant. The following equations up to the seventh order are:

$$\begin{aligned} b_3'-\frac{\rho }{4}c_3= 0, \quad b_4'-\frac{\rho }{4}c_4= - \frac{\rho }{4}, \quad b_5'-\frac{\rho }{4}c_5= 0, \quad b_6'-\frac{\rho }{4}c_6= \frac{\rho c^2}{8}, \quad b_7'-\frac{\rho }{4}c_7 = 0. \end{aligned}$$

and for $n\ge 8$,

$$\begin{aligned} b_n' = \left\{ \begin{array}{ll}\frac{\rho }{4}c_n -\frac{1}{4}\frac{1}{16^{\frac{n}{4}-1}}\left( \begin{array}{c}-3/2\\ \frac{n}{4}-1\end{array}\right) \rho ^{\frac{n}{2}-1},&{} \quad n\equiv 0 (\text{ mod } 4)\\ \frac{\rho }{4}c_n &{} \quad \text{ otherwise }. \end{array}\right. \end{aligned}$$

(42)

or equivalently, $b_n'$ is given by the following relations:

$$\begin{aligned} \begin{array}{ll} \!\!\frac{\rho }{4}\left[ (n\!-\!2)(b_{n-2}b_0+ \cdots + b_{\frac{n}{2}}b_{\frac{n}{2}-2})\!+\! \frac{n-2}{2}b_{\frac{n-2}{2}}^2\right] \!-\!\frac{1}{4}\frac{1}{16^{\frac{n}{4}-1}}\!\left( \begin{array}{c}\!-3/2\!\!\\ \!\frac{n}{4}\!-\!1\!\!\end{array}\right) \rho ^{\frac{n}{2}-1},&{} \quad n\equiv 0 (\text{ mod } 4),\\ \!\!\frac{\rho }{4}\left[ (n-2)(b_{n-2}b_0+ \cdots + b_{\frac{n}{2}}b_{\frac{n}{2}-2})+ \frac{n-2}{2}b_{\frac{n-2}{2}}^2\right] ,&{} \quad n \not \equiv (\text{ mod } 4) \, \text{ and }\, n\, \, \text{ is }\, \, \text{ even },\\ \!\!\frac{\rho }{4}\left[ (n-2)(b_{n-2}b_0+ \cdots + b_{\frac{n-1}{2}}b_{\frac{n-3}{2}})\right] ,&{} \quad n \not \equiv (\text{ mod } 4) \, \text{ and }\, n\, \, \text{ is }\, \, \text{ odd }. \end{array}\nonumber \\ \end{aligned}$$

(43)

The computation of the coefficients $b_n(E)$ is done recursively. In fact, suppose that for $n\ge 0$ the coefficients $b_0(E), b_1(E),\ldots , b_{n-3}(E)$ are known. We take the corresponding nth equation in (43) and impose the condition on the coefficient $b_n(E)$ to be periodic. Taking the average on both sides of (43) we get the equation for the constant term of $c_n$ (and thus for the constant term of $b_{n-2}$ which will be denoted by $b_{n-2}^{(0)}$),

$$\begin{aligned} \frac{1}{\pi }\int _0^{2\pi } \rho (E)c_n(E)\,dE=\frac{1}{\pi }\frac{1}{16^{\frac{n}{4}-1}} \left( \begin{array}{c}-3/2\\ \frac{n}{4}-1\end{array}\right) \int _0^{2\pi } \rho ^{\frac{n}{2}-1}(E)\,dE . \end{aligned}$$

(44)

The integral on the right hand side can be computed in terms of the Gamma function:

$$\begin{aligned} \frac{1}{\pi }\int _{0}^{2\pi }\rho ^n(E)\,dE=\frac{2^{n+1} \Gamma (n+\frac{1}{2})}{\sqrt{\pi }\Gamma (n+1)}. \end{aligned}$$

Using the functional relationship for the $\Gamma$ function

$$\begin{aligned} \Gamma (z)\Gamma \left( z+\frac{1}{2}\right) =2^{1-2z}\sqrt{\pi }\Gamma (2z), \end{aligned}$$

we get

$$\begin{aligned} \frac{2^{n+1}\Gamma \left( n+\frac{1}{2}\right) }{\sqrt{\pi }\Gamma (n+1)}= & {} \frac{2^{n+1}\Gamma (n)\Gamma \left( n+\frac{1}{2}\right) }{\sqrt{\pi } \Gamma (n)\Gamma (n+1)}\\= & {} \frac{2^{n+1} 2^{1-2n}\Gamma (2n)}{\Gamma (n)\Gamma (n+1)}\\= & {} \frac{2^{2-n}(2n-1)!}{(n-1)!n!}. \end{aligned}$$

In summary

$$\begin{aligned} \frac{1}{\pi }\int \rho \,c_n\,dE =\frac{1}{16^{\frac{n}{4}-1}}\left( \begin{array}{c}-3/2\\ \frac{n}{4}-1\end{array}\right) \frac{2^{3-\frac{n}{2}}(n-3)!}{\left( \frac{n}{2}-2\right) !\left( \frac{n}{2}-1\right) !} \end{aligned}$$

(45)

whenever $n\ge 8$ and $n\equiv 0 (\text{ mod } 4)$, zero otherwise.

Since the right-hand side of Eq. (43) is known, and the left-hand side contains the constant term $b_{n-2}^{(0)}$ and known quantities that are derived from the integration of known coefficients, namely,

$$\begin{aligned} \frac{1}{\pi }\int _0^{2\pi } (1-\cos {E})\left( (n-2)b_{n-2}b_0+(n-3)b_{n-3} b_1+\cdots b_1 b_{n-3}\right) \,dE, \end{aligned}$$

then it can be solved for $b_{n-2}^{(0)}$. The full form of $b_{n-2}(E)$ can be obtained by integrating the $(n-2)$th equation

$$\begin{aligned} b_{n-2}'-\frac{\rho }{4}c_{n-2} = r h s \end{aligned}$$

where rhs, for $n-2 \equiv 0 \, (mod\, 4)$, is known and depends only on the integration of the trigonometric polynomial coming from some power of $\rho$ and in turn can be expressed in terms of Hypergeometric functions. Note that rhs is zero otherwise. $\square$

1.4 Preliminary of Proposition 4

First we will introduce some preliminary results. Let

$$\begin{aligned} \dot{x} = f(t, x) \end{aligned}$$

(46)

be a system of ordinary differential equations, where f(t, x) is of class $C^{r}$ and $x \in {\mathcal {U}}$ with ${\mathcal {U}} \subset {\mathbb {R}}^{n}$ open. Let $\varphi (t, x) = \varphi _{t}(x)$ be a solution of (46) with initial condition $\varphi (0, x) = \varphi _ {0}(x) = x$, and, $\dot{\varphi }_{t}(x) = f(t, \varphi _{t}(x))$. Since f is of class $C^r$, $\varphi _{t}(x)$ is of class $C^r$ and we can obtain the variational equations by differentiating the relation $\dot{\varphi }_{t}(x) = f(t, \varphi _{t}(x))$ with respect to the variable x and interchanging the order of differentiation. Thus, the first variational equation is given by

$$\begin{aligned} \frac{d}{dt}\frac{\partial \varphi _{t}(x)}{\partial x}= Df(\varphi _{t}(x))\frac{\partial \varphi _{t}(x)}{\partial x}, \end{aligned}$$

with initial condition ${\dfrac{\partial \varphi _{t}(x)}{\partial x}}\Big |_{t=0}= I$, where Df is the Jacobian matrix of f and I is $n\times n$ identity matrix.

The variational equations of higher order are obtained similarly. We present them here second and third orders.

$$\begin{aligned} \frac{d}{dt}\frac{\partial ^{2}\varphi _{t}(x)}{\partial x^2}= D^{2}f(\varphi _{t}(x)) \left( \frac{\partial \varphi _{t}(x)}{\partial x}\right) ^2 + Df(\varphi _{t}(x))\frac{\partial ^{2}\varphi _{t}(x)}{\partial x^2}, \end{aligned}$$

with ${\dfrac{\partial ^2\varphi _{t}(x)}{\partial x^2}}\Big |_{t=0} =0$ and

$$\begin{aligned} \begin{array}{rl} \frac{d}{dt}\frac{\partial ^{3}\varphi _{t}(x)}{\partial x^3}=&{} D^{3}f(\varphi _{t}(x)) \left( \frac{\partial \varphi _{t}(x)}{\partial x}\right) ^3 + D^{2}f(\varphi _{t}(x))\left( \frac{\partial ^2 \varphi _{t}(x)}{\partial x^2},\frac{\partial \varphi _{t}(x)}{\partial x}\right) \\ &{} +\, Df(\varphi _{t}(x))\frac{\partial ^{3}\varphi _{t}(x)}{\partial x^3}, \end{array} \end{aligned}$$

with $\dfrac{\partial ^{3}\varphi _{t}(x)}{\partial x^3}\Big |_{t=0}=0.$

In order to know the derivatives of the flow $\varphi _ {t} (x)$ with respect to the initial conditions $\alpha$ of a periodic orbit we use the variational equations. In fact, we are going to study the flow around a periodic orbit through the Poincaré map defined in a cross section of this orbit.

Let $\Xi$ be a cross section of the periodic orbit defined by initial condition $\alpha _{0}\in \Xi$ and let $\sigma = \sigma (\alpha )$ be the time that the orbit spends to the first return to $\Xi$. We can assume without loss of generality that $\sigma (\alpha )$ is defined for all $\alpha \in \Xi$, because we can take $\Xi$ so small as needed, and by the theorem of continuous dependence on the initial conditions follows the assertion. If we start with the initial condition $\alpha _{1} \in \Xi$, we define the Poincaré map ${\mathcal {P}}: \Xi \rightarrow \Xi$ as

$$\begin{aligned} {\mathcal {P}}(\alpha _{1})=\alpha _{2}= \varphi (\sigma (\alpha _{1}), \alpha _{1}), \end{aligned}$$

with $\alpha _2 \in \Xi .$ So, we write the Poincaré map in the following way

$$\begin{aligned} {\mathcal {P}}(\alpha )= \varphi (\sigma (\alpha ), \alpha ). \end{aligned}$$

Calculating the first derivative with respect to initial conditions of the Poincaré map we obtain

$$\begin{aligned} \frac{\partial {\mathcal P}}{\partial \alpha }= \frac{\partial \varphi }{\partial \sigma }\frac{\partial \sigma }{\partial \alpha } + \frac{\partial \varphi }{\partial \alpha }, \end{aligned}$$

where $\frac{\partial \varphi }{\partial \alpha }$ is obtained by the first variational equation. For the second derivative, we have the expression

$$\begin{aligned} \frac{\partial ^2 {\mathcal {P}}}{\partial \alpha ^{2}}= \frac{\partial ^2 \varphi }{\partial \alpha ^2}+ \frac{\partial ^2 \varphi }{\partial \sigma \partial \alpha }\frac{\partial \sigma }{\partial \alpha }+ \frac{\partial \varphi }{\partial \sigma }\frac{\partial ^2 \sigma }{\partial \alpha ^2}, \end{aligned}$$

where $\frac{\partial ^2 \varphi }{\partial \sigma \partial \alpha }$ and $\frac{\partial ^2 \varphi }{\partial \alpha ^2}$ are given by the first and second variational equations respectively. Continuing on this way we obtain the Taylor development of ${\mathcal {P}}$ around a fixed point $\alpha _{0} \in \Xi$

$$\begin{aligned} {\mathcal {P}}(\alpha )= \alpha _0 + \left( {\frac{\partial {\mathcal {P}}}{\partial \alpha }}\Big |_{\alpha = \alpha _0}\right) (\alpha - \alpha _0) + \frac{1}{2!}\left( {\frac{\partial ^2 {\mathcal {P}}}{\partial \alpha ^2}}\Big |_{\alpha = \alpha _0}\right) (\alpha - \alpha _0)^2 + {\mathcal {O}}((\alpha - \alpha _0)^3). \end{aligned}$$

See more details see [5].