Abstract
We consider scalar reaction-diffusion equations with non-dissipative nonlinearities generating global semiflows which exhibit blow-up in infinite time. This type of equations was only recently approached and the corresponding dynamical systems are known as slowly non-dissipative systems. The existence of unbounded solutions, referred to as grow-up solutions, requires the introduction of some objects interpreted as equilibria at infinity. By extending known results, we are able to obtain a complete decomposition of the associated non-compact global attractor. The connecting orbit structure is determined based on the Sturm permutation method, which yields a simple criterion for the existence of heteroclinic connections.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the following scalar reaction-diffusion equation
where \(f(x,u,u_{x})=bu+g(x,u,u_{x})\) and \(g:[0,\pi ]\times \mathbb {R}^{2}\rightarrow \mathbb {R}\) is a bounded \(C^{2}\) function. This implies, from standard theory (see, for instance, [1, 16, 19]), that we are provided with a local solution semigroup defined by \(u(t,\cdot )=S(t)u_{0}\) for \(t\ge 0\) and initial condition \(u_{0}\) in an adequate phase space. By the comparison principle if \(b<0\) this semigroup is dissipative, therefore possessing a compact global attractor, i.e., a nonempty compact invariant set attracting every bounded subset of the state space, see for instance [2, 16]. Also, due to the existence of a Lyapunov function [22, 30], the semigroup \(S(t)\) has a gradient-like behavior and, consequently, the attractor is composed of the equilibria and the heteroclinic orbits connecting them. When \(b>0\) the semigroup is no longer dissipative but we still obtain a non-compact global attractor defined as the nonempty minimal set attracting all bounded sets of the state space. In [6, 7], Ben-Gal has considered this problem for the case \(f=f(u)\) and described the non-compact global attractor in terms of bounded equilibria, equilibria at infinity, and their heteroclinic connecting orbits. In addition, the heteroclinic connectivity was described in terms of previously known blocking principles involving the Morse indices of equilibria and the zero numbers of the differences between equilibrium solutions, see for example [3, 4, 12]. In this paper we consider the general case \(f=f(x,u,u_{x})\) and describe the heteroclinic connectivity by means of a permutation introduced in [11] and used extensively for the characterization and equivalence of global attractors, as we can see for instance in [12–14, 29].
Our main result, contained in Theorem 2, describes a simple criterion for the existence of heteroclinic connections on the non-compact global attractor. A permutation of all the equilibria, both bounded and at infinity, allows for the description of the connecting orbit structure in terms of an adjacency notion introduced in [29].
This paper is organized as follows. In Sect. 2 we introduce the class of slowly non-dissipative equations. We also present preliminary results that lead to the existence of grow-up solutions, and provide the definition of non-compact global attractor. In Sect. 3 we obtain the asymptotic behavior of grow-up solutions and introduce the concept of equilibria at infinity. We then prove that, under nondegeneracy conditions, the set of equilibria is non-empty.
In Sect. 4 the heteroclinic connections with the equilibria at infinity are considered. The theory of inertial manifolds is used here to obtain the exact limits of the grow-up solutions. Also, the connecting orbit structure within infinity is described.
The main goal of Sect. 5 is to obtain a permutation associated with Eq. (1) characterizing the non-compact global attractor. We define the suspension of any given meander permutation and consider suspensions of the usual permutation related to (1), obtained from the ordering of the equilibrium points according to their values at \(x=0\) and \(\pi \). The permutation obtained from the suspensions is then proved to be realizable by a dissipative equation and is then associated with the non-dissipative Eq. (1).
In Sect. 6 we prove our main result. First, the Morse indices and zero numbers of the equilibria of the dissipative equation are calculated. Then, a correspondence between the equilibria of the non-dissipative Eq. (1) and the equilibria of the dissipative equation is made in such a way that the nodal properties are preserved. We prove that the permutation derived from the suspensions determines the heteroclinic connections in the non-compact global attractor, which is then characterized in terms of the adjacency notion.
2 Set-Up and Preliminary Results
We consider the Hilbert space \(X=L^{2}([0,\pi ])\) with norm \(\Vert \cdot \Vert \). Moreover, we denote by \(A\) the sectorial operator \(-\partial _{xx}-bI\). We know that \(-A\) generates the analytic semigroup \(e^{-tA}\), [19, 25]. For \(A_{1}=A+bI\), the fractional power spaces
for each \(\alpha \ge 0\), are well defined with the graph norm \(\Vert x\Vert _{\alpha }:=\Vert A_{1}^{\alpha }x\Vert , x\in X^{\alpha }\).
We assume that \(g=g(x,u,p):[0,\pi ]\times \mathbb {R}^{2}\rightarrow \mathbb {R}\) is a bounded \(C^{2}\) function, globally Lipschitz in \((u,p)\), i.e., there exist positive constants \(L_{1}\) and \(L_{2}\) such that
Moreover, to control the decay behavior of the number of zeros of solutions at infinity needed in Sect. 4, we assume that \(L_{2}<1\). On \(X^{\alpha }\), with \(\alpha >\frac{3}{4}\), the Nemitskii operator of \(g\) defined by
takes values in \(X\) and is globally bounded and Lipschitz in \(u\in X^{\alpha }\). We take \(\alpha >\frac{3}{4}\) so that \(X^{\alpha }\subset C^{1}\). The solution semigroup \(S(t)\) is then defined in the underlying space \(X^{\alpha }\) for \(t\ge 0\),
The dynamical system generated by Eq. (1) is dissipative if there is a fixed large ball in the state space which attracts all the solutions. A dynamical system is fast non-dissipative if for at least one initial condition the corresponding solution exhibits a blow-up in finite time. A recently introduced class of systems called slowly non-dissipative consists of all systems for which global existence and uniqueness is guaranteed for every initial condition, but some solutions blow-up in infinite time. See [5].
Since \(g\) is bounded, the dynamical system generated by (1) is globally defined. Indeed, \(\Vert S(t)u_{0} \Vert _{\alpha }\) is bounded for each \(0<t<\infty \) and \(\alpha \in (3/4,1)\). If \(t(u_{0})\) denotes the maximal time of existence of the solution through \(u_{0}\), then it follows from [19] that \(t(u_{0})=+\infty \) for all \(u_{0}\in X^{\alpha }\). This implies that a finite-time blow-up does not take place and the dynamical system obtained is either dissipative or slowly non-dissipative.
We consider an orthonormal basis \(\{\varphi _{j}(x)\}_{j\in \mathbb {N}_{0}}\) in \(L^{2}([0,\pi ])\) comprised of eigenfunctions of the operator \(A\) with Neumann boundary conditions, i.e., \(\varphi _{j}(x)=\sqrt{\frac{2}{\pi }}\cos jx\) for \(j=1,2,\dots \) and \(\varphi _{0}(x)=\sqrt{\frac{1}{\pi }}\). We further denote by \(\lambda _{j}\) the corresponding eigenvalues, which are given by \(\lambda _{j}=j^{2}-b\) for each \(j\in \mathbb {N}_{0}\).
Lemma 1
If \(b>0\) then the dynamical system generated by Eq. (1) is slowly non-dissipative.
Proof
We consider the eigenspaces \(E_{j}\) of \(A\) associated with each eigenvalue \(\lambda _{j}\). Using the \(L^2\)-eigenprojections any solution \(u(t,x)\) of (1) is represented by
where \(\hat{u}_{j}(t)=\langle u(t,\cdot ),\varphi _{j}(\cdot )\rangle _{L^{2}}\) with the inner product in \(L^{2}([0,\pi ])\). Applying the \(E_{j}\)-projection to Eq. (1) we obtain
which, by selfadjointness of \(A\), implies
If we write \(\langle g(x,u,u_{x}),\varphi _{j}(x)\rangle _{L^{2}}=\langle G(u)(x),\varphi _{j}(x)\rangle _{L^{2}}\), where \(G(u)\) is the Nemitskii operator for \(g(u)\), and denote
we finally obtain from (3),
We notice that if \(b>0\) then \(\lambda _{j}=j^{2}-b<0\) at least for \(j=0\). Then the general solution of the linear non-homogeneous ODE (4) has the form \(\hat{u}_{j}(t)=\hat{u}_{j}^{p}(t)+\hat{u}_{j}^{h}(t)\), where \(\hat{u}_{j}^{p}(t)\) is a particular solution of (4) and \(\hat{u}_{j}^{h}(t)\) is a solution of the corresponding homogeneous equation. As a particular solution we take \(\hat{u}_{j}^{p}(t)=\int _{\infty }^{t}e^{-\lambda _{j}(t-s)}\hat{g}_{j}(s)ds\) and the solution with initial condition \(\hat{u}_{j}(0) = \int _{\infty }^{0}e^{\lambda _{j}s}\hat{g}_{j}(s)ds+\hat{u}_{j}^{h}(0)\), is given by
Since \(G(u)\) is bounded in \(L^{2}\) we have that \(\hat{g}_{j}(t)\) is uniformly bounded for all \(j\in \mathbb {N}_{0}\). Consequently, the particular solution \(\hat{u}_{j}^{p}(t)\) is uniformly bounded for all \(j\in \mathbb {N}_{0}\) such that \(\lambda _{j}<0\). On the other hand, whenever \(\lambda _{j}\) is strictly negative and \(\hat{u}_{j}^{h}(0)\ne 0\), then \(\hat{u}_{j}^{h}(t)=\hat{u}_{j}^{h}(0)e^{-\lambda _{j}t}\) grows exponentially as \(t\) goes to infinity.
From the Fourier decomposition using the eigenprojections we conclude that the \(L^2\)-norm of a solution \(u(t,x)\) of (4) is \(\Vert u(t,\cdot )\Vert ^2 = \sum _{i=0}^{\infty } (\hat{u}_{i}(t))^2\). Since we have \(\lambda _j<0\) at least for \(j=0\), if we take an initial condition \(u_{0}\) such that \(\hat{u}_{0}^{h}(0) \ne 0\), then \(\hat{u}_{0}(t)\rightarrow \infty \) as \(t\rightarrow \infty \). Thus, the corresponding solution \(u(t,x)\) for such an initial condition exhibits infinite-time blow-up. \(\square \)
This proof also shows that if \(u(t,\cdot )\) is a grow-up solution then at least one mode \(\hat{u}_{j}(t)\) for \(j\le \sqrt{b}\) will grow-up to infinity with \(t\), since all the remaining modes \(\hat{u}_{l}(t)\) for \(l>\sqrt{b}\) must remain bounded. In fact, in this case \(\lambda _{l}=l^{2}-b>0\) and, writing the general solution of (4) as
where \(\hat{u}_{l}(0)=\langle u_{0}(\cdot ),\varphi _{l}(\cdot )\rangle _{L^{2}}\), we obtain
using the uniform bound \(\Gamma \) for \(\hat{g}_{l}\).
Despite the non-dissipativity of Eq. (1), we can still guarantee the existence of a Lyapunov functional given in the form
where \(H(x,u,p)\) is a smooth function on \([0,\pi ]\times \mathbb {R}^{2}\) with \(H_{pp}>0\) (see [22, 30]). The functional \(V\) satisfies
Solutions \(u(t,\cdot ) \in X^{\alpha }\) which are unbounded in time are called grow-up solutions. In order to begin the discussion regarding the asymptotic behavior of these unbounded solutions of Eq. (1), we recall the next lemma derived in [6].
Lemma 2
Consider the Eq. (1) with \(b>0\). Then the solution \(u(t,\cdot )\) either converges to some bounded equilibrium as \(t\) goes to infinity or \(u(t,\cdot )\) is a grow-up solution.
The proof follows from an application of LaSalle’s invariance principle [15] to the Lyapunov functional (7). One immediate consequence of these two lemmas is that there does not exist a global attractor for the semigroup \(S(t)\). We then present the following definition of non-compact global attractor introduced in [6].
Definition 1
A non-compact global attractor for the Eq. (1) is a non-empty minimal set in \(X^{\alpha }\) attracting all bounded sets of \(X^{\alpha }\).
3 Non-compact Global Attractor
Next we consider a grow-up solution and its normalized trajectory in order to obtain a description of the explicit behavior of grow-up solutions. We recall the following lemma obtained in [6].
Lemma 3
Let \(b>0\), \(b\ne n^{2}\) for \(n\in \mathbb {N}\). Consider a grow-up solution \(u(t,\cdot )\) of (1) and its normalized trajectory \(\frac{u(t,\cdot )}{\Vert u(t,\cdot )\Vert }\). Then, there is \(m<\sqrt{b}\) such that \(\frac{u(t,\cdot )}{\Vert u(t,\cdot )\Vert }\) converges to \(\varphi _{m}^{\iota }\) in \(L^{2}\), where \(\varphi _{m}^{\iota }=\iota \varphi _{m}\) and \(\iota \in \{ +1,-1 \}\). Moreover, a necessary and sufficient condition for the rescaled trajectory to converge to \(\varphi _{m}^{\iota }\) in \(L^{2}\) is that
and the sign of \(\varphi _{m}^{\iota }(0)\) should be the same as \(u(t,0)\) for all \(t\in (T,\infty )\), for some \(T>0\).
Proof
Again we let \(u(t,x)=\sum _{j=0}^{\infty }\hat{u}_{j}(t)\varphi _{j}(x)\), and we remark that \(|\hat{u}_{j}(t)| \le c/j^2\) for all \(j>\sqrt{b}\), since these modes decay. By Lemma 1 at least one mode \(\hat{u}_{m}(t)\) for some \(m<\sqrt{b}\) will grow-up to infinity with \(t\). If \(\hat{u}_{m}\) is the only infinitely growing mode, then
for all \(l \ne m\). If, on the other hand, \(u(t,\cdot )\) has more than one infinitely growing mode, let \(\hat{u}_{m}\) denote the one with the lowest subscript. Reasoning as in (5) we see that the growth to infinity of a mode \(\hat{u}_{i}\) is determined by the term \(\hat{u}_{i}^{h}(0)e^{-\lambda _{i}t}\). Hence the mode \(\hat{u}_{m}(t)\) grows exponentially faster than any other growing mode \(\hat{u}_{i}(t)\), \(m<i<\sqrt{b}\), and we still have
Then we obtain (8) and, from a zero number stabilization argument, we conclude that the rescaled solution \(\frac{u(t,\cdot )}{\Vert u(t,\cdot )\Vert }\) converges to either \(\varphi _{m}\) or \(-\varphi _{m}\). The sign condition on \(u(t,0)\) for all \(t\in (T,\infty )\) then implies that the limit is \(\varphi _{m}^{\iota }=\iota \varphi _{m}\).
Conversely, from
we conclude that
which implies (8). The \(L^{2}\) convergence of the rescaled trajectory to \(\varphi _{m}^{\iota }\) then implies that \(u(t,0)\) has the same sign of \(\varphi _{m}^{\iota }(0)\) for all \(t\in (T,\infty )\). \(\square \)
As we are interested in the limiting objects at infinity, we are particularly concerned with the modes with \(j\le \sqrt{b}\). In [18] Hell used Poincaré projections in Hilbert space to study the grow-up solutions interpreted as heteroclinic orbits to points at infinity. Using this approach we show that the projections to infinite norm of the equilibria of the linear equation \(u_{t}=u_{xx}+bu\) play the role of equilibria at infinity for the given nonlinear Eq. (1). Following [18] we consider the Poincaré projection of the space \(X^{\alpha }\times \{1\}\) onto the infinite dimensional upper hemisphere
where \(\langle u,v \rangle _{\alpha }=\langle A_{1}^{\alpha }u,A_{1}^{\alpha }v \rangle _{L^{2}}\) is the inner product in \(X^\alpha \). The hyperplane \(X^\alpha \times \{1\}\) is tangent to the unit sphere in \(X^{\alpha }\times \mathbb {R}\). The Poincaré projection is defined in the following way: for a given point \(M\) on the hyperplane, the straight line through \(M\) and the center of the unit sphere \((0,0)\) intersects the sphere at two antipodal points, one on the upper hemisphere and one in the lower. The Poincaré projection of \(M\), which will be denoted by \(\mathcal {P}(M)\), is defined as the intersection point on the upper hemisphere. As \(M\) goes to infinity on \(X^{\alpha }\times \{1\}\), \(\mathcal {P}(M)\) goes to the boundary of \(\mathcal {H}\), that is, the equator of the unit sphere \(\mathcal {H}_{e} := \{ (\chi ,0)\in X^\alpha \times \mathbb {R}:\langle \chi ,\chi \rangle _\alpha = 1 \}\). By examining the Eq. (1) on \(X^\alpha \) transformed by the projection \(\mathcal {P}\), Hell has obtained the equilibrium points on the equator
for all \(j\in \mathbb {N}_{0}\).
Because the infinity of \(X^{\alpha }\) is projected onto the equator \(\mathcal {H}_{e}\) and \(\Phi _{j}^{\pm }\) are equilibrium points on \(\mathcal {H}_{e}\), we define objects \(\Phi _{j}^{\infty ,\pm }\) at infinity as
and refer to these as equilibria at infinity. However, we have only a finite number of equilibria at infinity. This follows from Lemma 3 and from the fact that the eigenmodes with \(j>\sqrt{b}\) remain bounded for any grow-up solution. The set of equilibria at infinity is given precisely by
where \([\cdot ]\) denotes the integer part.
We decompose the global attractor as
where \(\mathcal {A}^{c}_{f}\) is the maximal compact invariant subset contained in some sufficiently large ball \(B \subset X^\alpha \) and \(\mathcal {A}^{\infty }_{f}\) is an unbounded subset. The bounded subset is composed of the set of solutions in \(\mathcal {A}_{f}\) which remain bounded in the state space \(X^{\alpha }\) for \(t \ge 0\). Therefore, we may apply the standard theory for dissipative equations and conclude that the bounded subset \(\mathcal {A}^{c}_{f}\) is composed of the set of bounded equilibria \(E^{c}_{f}\) and their connecting heteroclinic orbits (see [16]). The unbounded subset \(\mathcal {A}^{\infty }_{f}\) contains the set of equilibria at infinity \(E^{\infty }_{f}\) and the subset of grow-up solutions.
In the sequel we want to prove that \(E^{c}_{f}\) is non-empty. The bounded equilibria \(v\in E^{c}_{f}\) of Eq. (1) are the solutions of the ODE boundary value problem
We then associate with (10) the initial value problem
We remark that the set of solutions \(u=u(x,u_{0}),v=v(x,u_{0})\) of (11) defines the two-dimensional manifold in \([0,\pi ]\times \mathbb {R}^{2}\)
Under the setting of Eq. (1), all trajectories of the initial value problem (11) are guaranteed to exist for all \(x\in [0,\pi ]\). Also let the section curve of \(L\) at \(x=\pi \) be denoted by \(\gamma \), i.e.,
The intersection points of \(\gamma \) with the plane \(v=0\) correspond to the equilibria of (1) (see [11, 28]).
We next show that under appropriate conditions Eq. (1) has at least one stationary solution. The assertion is already known if (1) is dissipative, as it follows from a series of results derived in [17, 20, 30]. In which concerns non-dissipative equations in the form (1), according to Matano, no satisfactory result was obtained except for the case \(f(x,u,u_{x})=f(u)\), see [21, Remark 4.6]. Also, this state of affairs does not seem to have changed much in the last 30 years. Then, in the next lemma we address this matter and consider non-dissipative equations in the general form (1), under the nondegeneracy condition \(b\ne n^{2}\).
Lemma 4
If the dynamical system generated by Eq. (1) is
-
(i)
dissipative (i.e., with \(b<0\)), or
-
(ii)
slowly non-dissipative (i.e., with \(b>0\)) and \(b\ne n^{2}\) for \(n\in \mathbb {N}\),
then the set of equilibria \(E^{c}_{f}\) is not empty.
Proof
To verify the non-emptiness of \(E^{c}_{f}\) we prove that \(\gamma \) intersects the plane \(v=0\). We address the slowly non-dissipative case \((ii)\). We rewrite (11) in the form
and introduce the change to polar coordinates
with \(\rho (0,u_{0})=u_{0}\) and \(\theta (0,u_{0})=0\). This corresponds to the well-known Prüfer transformation normally used in Sturm-Liouville eigenvalue problems to prove Sturm comparison theorem. From (13) and (14), we obtain
This implies (for \(\rho \ne 0\))
Since \(g\) is uniformly bounded, given \(\delta >0\) there exists \(\hat{R}>0\) large enough such that \(|\rho (x,u_0)|>\hat{R}\) implies
Moreover, we have
for all \(x \in [0,\pi ]\) and some positive constant \(C\). From (17) we conclude that, for a given \(\hat{R}>0\), if \(|\rho (0,u_0)|\) is sufficiently large, then \(|\rho (x,u_0)|>\hat{R}\) uniformly on \([0,\pi ]\). Therefore, if \(|\rho (0,u_0)|\) is sufficiently large, we have
Thus, from (16) we have
and, since \(\theta (0,u_0)=0\), we obtain \(|\theta (\pi ,u_0)-\sqrt{b}\pi | < \delta \pi \). Letting \(\varepsilon =\delta \pi \), we finally obtain that for a given \(\varepsilon >0\) there exists \(R>0\) such that \(|\rho (0,u_0)|>R\) implies
As \(|\rho (\pi ,u_0)|\) grows with \(|\rho (0,u_0)|=|u_{0}|\) and \(b\ne n^{2}\) for \(n\in \mathbb {N}\), we conclude from (18) that for both \(u_0>R\) and \(u_0<-R\) the curve \(\gamma \) is asymptotic to a straight line with inclination angle \(\sqrt{b}\pi \), therefore going from one (upper or lower) semiplane of \(\{(x,u,v):x=\pi \}\) to the other. Hence, the continuous curve \(\gamma \) must intersect the plane \(v=0\), which implies that \(E^{c}_{f}\) is not empty.
For the proof of \((i)\) we refer the reader to [17, 20, 30]. \(\square \)
4 Heteroclinics to Infinity
In the sequel we let \(b>0\) and \(b\ne n^{2}\) for \(n\in \mathbb {N}\). From the proof of Lemma 4 this implies that all the solutions of (10) have their values contained in a bounded subset of the phase plane \((u,u_x)\). In addition, we also make the generic assumption that all bounded equilibria \(v \in E^{c}_{f}\) are hyperbolic. Hyperbolicity of \(v\in E^{c}_{f}\) means that \(\lambda =0\) is not an eigenvalue of the linearization of (10) at \(v\)
with Neumann boundary conditions. Hence, from here on we deal with only a finite set \(E^{c}_{f}=\{v_{1},\dots ,v_{n}\}\).
As usual, the Morse index \(i(v)\) of the hyperbolic \(v\in E^{c}_{f}\) denotes the number of strictly positive eigenvalues of (19), alias, the dimension of the unstable manifold of \(v\), \(W^{u}(v)\).
The nondegeneracy condition \(b \ne n^{2}\) in Lemma 4 corresponds to the hyperbolicity of the equilibria at infinity, as we can see in [18] and [7]. This concept is related to the projected equation obtained on the equator \(\mathcal {H}_{e}\) from which we find the equilibria at infinity.
We intend to determine the bounded equilibria connecting to infinity as well as the exact limit of the grow-up solutions. In order to do that, it is necessary to work in higher norms than the \(L^{2}\)-norm. This is due to the fact that the \(L^{2}\)-norm is insufficient for determining the exact limiting object at infinity since the \(L^2\)-norm alone does not prevent the zero number to drop at \(t=\infty \). As it was observed in [5], despite the fact that the influence of the bounded nonlinearity \(g\) must decrease as the norm of \(u(t,\cdot )\) grows to infinity, we are unable to study the limit in the \(X^{\alpha }\) norm. To obtain the limits in \(C^{1}\), we appeal to the theory of inertial manifolds. We have the following result from Miklavčič [24] for the existence of an inertial manifold for Eq. (1).
Lemma 5
Consider the Eq. (1) with \(g\) satisfying the inequality (2) for some positive constants \(L_{1}<+\infty \) and \(L_{2}<1\). Then there exists an inertial manifold \(\mathcal {M}\) for Eq. (1) and \(\mathcal {M}\) contains the non-compact global attractor \(\mathcal {A}_{f}\). Moreover, \(\mathcal {M}\) is Lipschitz continuous with values in \(C^{1}\).
In the dissipative case and for \(f=f(u)\) Brunovskỳ [8] used the inertial manifold to show that the global attractor is the graph of a \(C^1\) smooth function over a subset of a finite dimensional linear space of dimension equal to the maximal Morse index of the equilibria in the attractor. Later Brunovskỳ and Tereščák [9] extended the existence result of the inertial manifold to the case of \(f=f(x,u,u_x)\) with a small Lipschitz constant \(L_2<\varepsilon \). Finally, Miklavčič [24] obtained this existence result for the case \(L_2<1\). Using these results, Matano and Nakamura [23, Theorem E] extended the smooth graph result of Brunovskỳ to the case of \(f=f(u,u_x)\) with \(L_2<1\) (under periodic boundary conditions).
The next lemma determines the limiting object at infinity by just requiring information on the zero number of the grow-up solution.
Lemma 6
Let \(v\) be a hyperbolic equilibrium for Eq. (1) and \(u(t,\cdot )\) a grow-up solution in the unstable manifold of \(v\), \(W^{u}(v)\), with
for all \(t\in (T,\infty )\) for some \(T>0\). Then
where \(\varphi _{m}^{\iota } = \iota \varphi _{m}\) and \(\iota = \mathrm{sign }(u(t,0)-v(0))\) for \(t \in (T,\infty )\).
Proof
From the existence of the inertial manifold \(\mathcal {M}\) we have that \(\mathcal {M}=\mathrm{graph }[\Psi ]\) where
is a Lipschitz mapping with values in \(C^{1}\), and we decompose \(u(t,\cdot )\) as \(u(t,\cdot )=p(t,\cdot )+q(t,\cdot )\) where
We know that all modes \(\hat{u}_{j}(t)\) with \(j>\sqrt{b}\) remain bounded and also, from Lemma 3, it follows that
for some integer \(i\) with \(i<\sqrt{b}\).
The mapping \(\Psi \) is uniformly bounded in \(C^{1}\), thus \(q(t,\cdot )\) remains bounded as \(p(t,\cdot )\) grows to infinity along with \(u(t,\cdot )\). As a result, we have that
and
Since \(p(t,\cdot )\) and \(\varphi _{i}^{\iota }(\cdot )\) are both in the finite-dimensional subspace \(P_{N}D(A)\), due to norm equivalence in finite dimension it follows that
Finally, since \(\Vert u\Vert \) grows up to infinity as \(t\rightarrow \infty \), we must have
for all \(t>T\). This implies that \(i=m\) and \(\iota =\mathrm{sign }(u(t,0)-v(0))\) for all \(t\in (T,\infty )\). \(\square \)
This lemma asserts that the zero number \(z(u(t,\cdot )-v(\cdot ))\) of a grow-up solution \(u \in W^u(v)\) can only drop at finite times \(t<T\) (thus excluding the disturbing possibility \(t=\infty \)), hence explicitly identifying the equilibrium at infinity to which the grow-up solution connects to.
For dissipative equations with Dirichlet boundary conditions, Brunovskỳ and Fiedler have constructed the \(y\)-map which is an important tool for describing the heteroclinic connections on the global attractor, see [3]. For each initial condition \(u_0\) in the unstable manifold of a hyperbolic equilibrium \(v\), \(y(u_0)\) determines the zero number \(z(u(t,\cdot )-v(\cdot ))\) of the corresponding shifted solution and the sign of \(u(t,0)-v(0)\). An extended form of the \(y\)-map was designed by Ben-Gal [5, 6] to deal with slowly non-dissipative equations with Neumann boundary conditions. For any hyperbolic equilibrium \(v\) and any positive integer \(m<i(v)\), the surjectiveness of the \(y\)-map (see [3, Lemma 2.2]) implies the existence of a solution \(u(t,\cdot )\) in \(W^u(v)\) with \(z(u(t,\cdot )-v(\cdot ))=m\) for all \(t>0\).
Given an equilibrium \(v\in E^{c}_{f}\), we say that \(v\) has a heteroclinic connection to the object at infinity \(\Phi ^{\infty }\in \{\Phi _{j}^{\infty ,\pm }: j=0,\dots ,[\sqrt{b}]\}\) if there exists a grow-up solution \(u(t,\cdot )\) satisfying
where \(\varphi \in \{\varphi _{j}^{\pm }\}_{j\in \mathbb {N}}\) and \(\varphi \) corresponds to the equilibrium \(\Phi \in \{\Phi _{j}^{\pm }\}_{j\in \mathbb {N}}\) on the sphere at infinity which is the projection of \(\Phi ^{\infty }\).
We define the zero number of \(\Phi _{j}^{\infty ,\pm }\) as
and
Also, we let
and
Under the above setting, we postulate
We notice that the zero numbers of the objects at infinity \(\{\Phi _{j}^{\pm }\}_{j\in \mathbb {N}}\) are consistent in the sense that the zero numbers of the corresponding heteroclinic orbits do not drop at \(t=\infty \) and the eigenfunctions \(\{\pm \varphi _{j}\}_{j\in \mathbb {N}}\) only have simple zeros.
The next definition adapts to the equilibria at infinity the notion of adjacency first introduced in [29].
Definition 2
Let \(v\in E^{c}_{f}\) and let \(\Phi ^{\infty } \in \{\Phi _{j}^{\infty ,\pm }: j=0,\dots ,[\sqrt{b}]\}\) denote an equilibrium at infinity with \(z(\Phi ^{\infty }-v)=m\), for some \(m\in \mathbb {N}\). We say that \(v\) and \(\Phi ^{\infty }\) are \(m\)-adjacent if there does not exist \(w\in E^{c}_{f}\) with \(z(\Phi ^{\infty }-w)=z(v-w)=m\) and
-
(i)
\(v(0) < w(0) < \Phi ^{\infty }(0)\), if \(v(0) < \Phi ^{\infty }(0)\),
-
(ii)
\(\Phi ^{\infty }(0) < w(0) < v(0)\), if \(\Phi ^{\infty }(0) < v(0)\).
With this adjacency definition we address the heteroclinic connectivity of finite equilibria to objects at infinity via grow-up solutions.
Lemma 7
(Infinite Blocking Lemma) Let \(v \in E^{c}_{f}\) be a hyperbolic equilibrium and let \(\Phi ^{\infty } \in \{\Phi _{j}^{\infty ,\pm }: j=0,\dots ,[\sqrt{b}]\}\) denote an equilibrium at infinity with \(z(\Phi ^{\infty }-v)=m\). If \(v\) and \(\Phi ^{\infty }\) are not \(m\)-adjacent, then \(v\) does not have any heteroclinic connection to the object \(\Phi ^{\infty }\) at infinity.
Proof
First notice that (21) implies that \(m \le [\sqrt{b}]\). Assume that there exists a grow-up solution \(u(t,\cdot )\) connecting \(v\) to \(\Phi ^{\infty }\). Since \(v\) and \(\Phi ^{\infty }\) are not \(m\)-adjacent, there exists \(w\in E^{c}_{f}\) such that
and
Then \(\tilde{u}=u-w\) is a trajectory from \(v-w\) to \(\Phi ^{\infty }-w\) satisfying \(\tilde{u}_{t} = \tilde{u}_{xx}+b\tilde{u}+\tilde{g}(x,\tilde{u},\tilde{u}_{x})\) with \(\tilde{g}(x,\tilde{u},\tilde{u}_{x}) := g(x,w+\tilde{u},w_{x}+\tilde{u}_{x})-g(x,w,w_{x})\). By Lemma 6 we conclude that there exists \(T>0\) such that \(z(u(t,\cdot )-w(\cdot ))=m\) for all \(t>T\). Since (26) holds, the value of \(w(0)\) lies between \(u(t,0)\) and \(v(0)\), increasing the value of \(t\) if necessary. Thus
Moreover, by the nonincreasing property of \(z(\tilde{u}(t,\cdot ))\) we have that \(z(v-w) \ge z(u(t,\cdot )-w)\). On the other hand, by (25)
However, since \(v(0)-w(0)\) and \(u(t,\cdot )-w(0)\) have opposite signs and \(\tilde{u}(t,0) \ne 0\) for all non-dropping times, we must have some dropping time before \(T\) and \(z(v-w) > z(u(t,\cdot )-w)\) which is a contradiction. \(\square \)
The next lemma ensures the existence of connections whenever they are not blocked.
Lemma 8
(Infinite Liberalism Lemma) Let \(v\in E^{c}_{f}\) be a hyperbolic equilibrium, let \(m\) denote an integer such that \(0 \le m \le i(v)-1\), and let \(\Phi ^{\infty }\in \{\Phi _{j}^{\infty ,\pm }: j=0,\dots ,[\sqrt{b}]\}\) denote an equilibrium at infinity with \(z(\Phi ^{\infty }-v)=m\). If \(v\) and \(\Phi ^{\infty }\) are \(m\)-adjacent, then \(v\) has a heteroclinic connection to the object \(\Phi ^{\infty }\) at infinity.
Proof
Using the \(y\)-map we obtain an initial condition \(u_{0}\in W^{u}(v)\) such that the corresponding solution \(u(t,\cdot )\) satisfies
for all \(0\le t<\infty \), with \(\mathrm{sign }(u(t,0)-v(0)) = \iota := \mathrm{sign }(\Phi ^{\infty }(0))\). For more details see [5, 6, 26]. We show first that there does not exist any bounded equilibrium \(w\) of (1) such that \(u(t,\cdot )\) converges to \(w\) as \(t\) goes to infinity.
Let us assume that \(\lim _{t\rightarrow \infty } u(t,\cdot ) = w\) for some equilibrium \(w\in E^{c}_{f}\). Then, as the zero number of the shifted solution \(u-v\) is nonincreasing
must be less than or equal to \(m\). Suppose \(z(w-v)<m\). This would imply that the zero number of the shifted solution drops at infinity and we show why this is not possible. Let
Since \(\tilde{w} \not \equiv 0\), it follows that \(\tilde{w}\) has only simple zeros, as it solves the ODE
Therefore, any solution in a sufficiently small neighborhood of \(\tilde{w}\) must also have only simple zeros. It implies that \(z(u(t,\cdot )-v(\cdot ))\) is constant over some small neighborhood of \(t=\infty \) and, thus,
for all very large \(t\). However, in this case \(z(u(t,\cdot )-v(\cdot ))\) would have to drop at some finite time as \(u(t,\cdot )\) converges to \(w\), which is a contradiction. Therefore, if \(v\) connects to \(w\) via \(u(t,\cdot )\) then \(z(w-v)=m\). Since \(\mathrm{sign }(u(t,0)-v(0))=\iota \) for all \(0 \le t < \infty \), the sign of \(u(t,0)-v(0)\) remains always positive or negative in forward time. Then, \(\mathrm{sign }(w(0)-v(0))=\iota \). However, there does not exist any bounded equilibrium \(w\) fulfilling these conditions, i.e,
since \(v\) and \(\Phi ^{\infty }\) are \(m\)-adjacent.
Since \(u(t,\cdot )\) cannot converge to any bounded equilibrium, by Lemma 2 we conclude that \(\lim _{t\rightarrow \infty } \Vert u(t,\cdot )\Vert = \infty \) and thus \(u(t,\cdot )\) is a grow-up solution. Finally, it was proven in Lemma 6 that in this case the normalized trajectory \(\frac{u(t,\cdot )}{\Vert u(t,\cdot )\Vert }\) converges in the \(C^{1}\)-norm to the eigenfunction \(\varphi _{m}^{\iota }\). This means that \(v\) has a heteroclinic connection to the object \(\Phi _{m}^{\infty ,\iota }\) at infinity. Since \(z(\Phi ^{\infty })=z(\Phi ^{\infty }-v)=m\) and \(\mathrm{sign }(\Phi ^{\infty }(0))=\iota \), it follows from (20) and (22) that \(\Phi ^{\infty }=\Phi _{m}^{\infty ,\iota }\). \(\square \)
The connecting orbit structure within infinity was obtained in [18]. The intra-infinite heteroclinics are namely the following:
with \(i,j\in \{ 1,\dots ,[\sqrt{b}]\}\).
5 Suspension
In this section we obtain a permutation related to Eq. (1) in the sense of [11]. We begin by recalling some facts which hold true in the dissipative case.
Let \(h\) be a function such that the dynamical system induced by
is dissipative. Assume also that all the equilibria are hyperbolic. We denote by \(E_{h}=\{w_{1},\dots ,w_{N}\}\) the set of equilibria of Eq. (28) ordered by their values at \(x=0\),
Let \(\sigma _{h} \in S(N)\) denote the permutation defined by the reordering at \(x=\pi \),
This permutation corresponds to the ordering of the points of intersection of the plane \(v=0\) with the curve \(\gamma _{h}\) defined for the stationary equation for (28) as in (12). Permutations related in this way to a Jordan curve like \(\gamma _{h}\) (in the Poincaré sphere) are called meander permutations.
We say that a permutation \(\sigma \in S(N)\) is a dissipative permutation if \(\sigma (1)=1\) and \(\sigma (N)=N\). Given any \(\sigma \in S(N)\) we also define the vector \((i_{j}(\sigma ))_{1 \le j \le N}\) by
for \(j=1,\dots ,N-1\). Then \(\sigma \) is called a Morse permutation if \(i_{j}(\sigma )\ge 0\) for all \(1\le j\le N\). We say that the permutation \(\sigma \) is realizable by a dissipative Eq. (28) if \(\sigma =\sigma _{h}\), with \(\sigma _{h}\) defined in (29). A permutation that is realizable by a dissipative equation is referred to as a Sturm permutation. The motivation for these definitions is the realization result obtained in [13] and recalled in Theorem 1 further below in this section.
For each equilibrium \(w_{j}\in E_{h}\), the Morse index \(i(w_{j})\) coincides with \(i_{j}(\sigma _{h})\). That is to say that
This is shown in [27]. The indices \(i_{j}(\sigma _{h})\) can alternatively be written as
with empty sums denoting zero (see [12]). For dissipative equations with only hyperbolic equilibria, the number of equilibria \(N\) is odd and the permutation defined in (29) is a dissipative Morse meander permutation. Moreover, a permutation \(\sigma \) associated to dissipative systems satisfies (31) and we have \(i(w_{1})=i(w_{N})=0\).
As a consequence of (1) being non-dissipative we see in the next lemma that the Morse indices \(i(v_{1})\) and \(i(v_{n})\) are both different from zero.
The equilibria in \(E^{c}_{f}=\{v_{1},\dots ,v_{n}\}\) are ordered by their values at \(x=0\). We denote by \(\overline{\theta }=\overline{\theta }(x,u_{0})\) the solution of the differential equation
where
This \(\overline{\theta }=\overline{\theta }(\cdot ,u_{0})\) corresponds to the angle swept by the unit vector tangent to the \(x\)-section of \(L\) along the solution \((u(\cdot ,u_{0}),v(\cdot ,u_{0}))\), as obtained from the linearization of (28), with \(u_0\) corresponding to the initial value of problem (11). We also denote by \(s(u_{0}):=(\pi ,u(\pi ,u_{0}),v(\pi ,u_{0}))\) the point in the section curve \(\gamma \) corresponding to the initial condition \(u_{0}\). Then \(\overline{\theta }(\pi ,u_{0})\) can also be read as the angle swept clockwise by the unit vector tangent to \(\gamma \) at \(s(u_{0})\) as \(s(u_{0})\) describes \(\gamma \), with \(u_{0}\) going from \(-\infty \) to \(\infty \) (see [27, 28]). Finally, let \(u_{0}^{j}\) be the initial value satisfying \(u_{0}^{j}=v_{j}(0)\) for the equilibrium \(v_{j}\). Then, the Morse index of \(v_{j}\) is given by \(i(v_{j})=1+[\overline{\theta }(\pi ,u_{0}^{j})/\pi ]\). See [27, 28].
Lemma 9
Assume that all equilibria of (1) are hyperbolic. Then the Morse index of the minimal and maximal equilibria, \(v_{1}\) and \(v_{n}\), are given by
Proof
As already mentioned, the Morse index of an equilibrium \(v_j\) is given by \(i(v_j)=1+[\overline{\theta }(\pi ,u_0^j)/\pi ]\) for all \(j=1,\dots ,n\), where \(u_{0}^{j}=v_{j}(0)\). The equilibria \(v_{1}\) and \(v_{n}\) being hyperbolic implies that \(\overline{\theta }(\pi ,u_{0}^{1}),\overline{\theta }(\pi ,u_{0}^{n}) \ne m \pi \), for all \(m\in \mathbb {N}\) (see [27]). In the following we show that \([\overline{\theta }(\pi ,u_{0}^{j})/\pi ] = [\sqrt{b}]\) for \(j=n\), the case \(j=0\) being similar.
Let \(u=u(x,u_{0}), v=v(x,u_{0})\) denote the solutions of (11) and let \(\theta (\pi ,u_{0})\) be the angle swept clockwise by the position vector \((u(x,u_{0}), v(x,u_{0}))\) as \(x\) runs from \(x=0\) to \(x=\pi \). We have seen in the proof of Lemma 4 that \(\theta (x,u_{0})\) satisfies (16) and \(\lim _{|u_0|\rightarrow \infty }\theta (\pi ,u_{0})=\sqrt{b}\pi \) (see (18)). This limit does not depend on the bounded nonlinearity \(g\), hence it does not change if \(g\) is modified by an adequate cut-off outside a large subset of \([0,\pi ]\times \mathbb {R}^2\). Let \(C_1>0\) denote a bound on the solutions \(u=u(x,u_{0}), v=v(x,u_{0})\) of (11) with \(u_0 \in [u_0^1,u_0^n]\),
Also, let \(C_2>0\) denote a bound for the solutions \(u\in \mathcal {A}^c_f\) on the compact global attractor of (1), which as we recall is in \(X^\alpha \subset C^1\),
Then, for an open neighborhood \(D \subset \mathbb {R}^2\) of the set
we define a \(C^2\) function \(\tilde{g}\) compactly supported in \([0,\pi ] \times D\) such that
for all \(|u|,|v| \le \max \{C_1,C_2\}\) and \(x \in [0,\pi ]\). The dynamical system generated by (1) with \(g\) replaced by \(\tilde{g}\) is non-dissipative and it possesses a noncompact global attractor
where \(\tilde{f}(x,u,p)=bu+\tilde{g}(x,u,p)\) and \(\mathcal {A}^c_{\tilde{f}}\) is the maximal compact invariant set. Then, in view of (36) we have that \(\mathcal {A}^c_f\subset \mathcal {A}^c_{\tilde{f}}\) and the replacement of \(g\) by \(\tilde{g}\), assumed from here on, does not affect the Morse indices of any equilibria. In fact, this replacement does not change the section curve \(\gamma \) for \(u_0\in [ u_0^1,u_0^n ]\).
If \(|u_0|\) is sufficiently large, then \((u(x,u_{0}), v(x,u_{0})) \notin D\) and we have that \(\tilde{g}(x,u(x,u_{0}), v(x,u_{0})) = 0\) for all \(x\in [0,\pi ]\). In this case, since \(\overline{\theta }=\overline{\theta }(x,u_0)\) satisfies (33) and \(q_0(x,u_{0}) \equiv q_1(x,u_{0})\equiv 0\) we conclude that \(\overline{\theta }_x(x,u_0) = \sqrt{b}\). Therefore \(\overline{\theta }(\pi ,u_0) = \sqrt{b}\pi \) for large values of \(|u_0|\) and
for \(r>u_0^n\) large. Then, let \(\gamma _n\) denote the arc of the section curve \(\gamma \) between the points \((u_0^n,0)\) and \((u(\pi ,r),v(\pi ,r))\),
Also, let \(\overline{\gamma }_n\) denote the horizontal line segment between the points \((u_0^n,0)\) and \((u(\pi ,r),0)\),
and finally let \(\overline{\overline{\gamma }}_n\) denote the vertical line segment between \((u(\pi ,r),0)\) and \((u(\pi ,r),v(\pi ,r))\),
We then define the closed curve \(\Gamma _n = \gamma _n \cup \overline{\gamma }_n \cup \overline{\overline{\gamma }}_n\). Since \(v_n\) is the equilibrium with maximal initial value \(u_0\), the curve \(\gamma _n\) intersects the horizontal axis only at \((u(\pi ,u_0),0)\), hence \(\gamma _n \cap \overline{\gamma }_n = \emptyset \) is empty. Moreover, for \(r\) sufficiently large we also have \(\gamma _n \cap \overline{\overline{\gamma }}_n = \emptyset \) by (18). We therefore conclude that \(\Gamma _n\) is a Jordan curve, i.e., a piecewise differentiable simple and closed curve. It then follows from (37) and the turning tangent theorem ([10]) applied to \(\Gamma _n\) that
This implies
and using (37) we have \([\overline{\theta }(\pi ,u_0^n)/\pi ] = [\sqrt{b}]\) as required. \(\square \)
As a consequence of this lemma, the dynamical system generated by Eq. (1) is non-dissipative for \(b>0\) and \(i(v_{1})=i(v_{n})=k\) with \(k:=1+ [\sqrt{b}]\) strictly positive. Then, if dissipative properties are not verified, we do not expect the Morse indices of the equilibria to satisfy (32). In spite of this fact, we want to obtain the Morse indices of the equilibria \(v_{j}\in E^{c}_{f}\) in terms of an associated permutation defined in an analogous manner as for dissipative equations.
We similarly define for Eq. (1) a permutation \(\sigma _{f}\in S(n)\) by ordering the equilibria in \(E^c_f\) firstly at \(x=0\) and then according to their values at \(x=\pi \). The permutation \(\sigma _{f}\) can also be defined from the corresponding section curve \(\gamma =\gamma _{f}\) obtained for (1), as we can see in [28]. Therefore \(\sigma _{f}\) is a meander permutation.
For this permutation \(\sigma =\sigma _{f} \in S(n)\) we define the vector \((i_{j}(\sigma ))_{1\le j\le n}\) by
for \(j=1,\dots ,n-1\). We next verify that the dimension of the unstable manifold of the equilibrium \(v_{j}\), which we are denoting by \(i(v_{j})\), coincides with \(i_{j}(\sigma _{f})\) for all \(1 \le j \le n\).
Lemma 10
Let \(k=1+[\sqrt{b}]\). If \(\sigma =\sigma _{f}\in S(n)\) denotes the meander permutation corresponding to the section curve \(\gamma =\gamma _{f}\) of (1) and \((i_{j}(\sigma _{f}))_{1 \le j \le n}\) is the vector defined by (38), then
Proof
It was established in [27] that the Morse indices \(i(v_{j})\) of the equilibria \(v_{j}\in E^{c}_{f}\) are determined in terms of the curve \(\gamma \) defined in (12). As already mentioned, the relation is given by
where \(\bar{\theta }\) is the solution of (33). We now want to write (40) explicitly in terms of \(\sigma _{f}\).
Since \(\bar{\theta }(\pi ,v_{j}(0))\) can also be read as the angle swept clockwise by the unit vector tangent to \(\gamma \) at \(s(u_{0})=(\pi ,u(\pi ,u_{0}),p(\pi ,u_{0}))\), with \(p=u_{x}\), as \(u_{0}\) goes from \(-\infty \) to \(v_{j}(0)\), we obtain from (40) that
with \(c_j\in \{-1,+1\}\). From the alternative definition of \(\bar{\theta }(\pi ,v_{j}(0))\) in terms of \(\gamma _{f}\) and from (40), one obtains that
where \(p_{u_{0}}\) denotes the derivative of \(p\) with respect to \(u_{0}\). It follows from the definition of \(\sigma _{f}\) that
We also have the relation
Moreover, the following inequalities hold
As a result, the alternation rule
follows from (43). Equivalently we have
From (42) and (44) we therefore conclude that
that is,
for all \(1 \le j \le n\), which compares with (38) as we wanted to prove. \(\square \)
Remark that by (34) and (39) we have \(i_{1}(\sigma _{f})=i_{n}(\sigma _{f})=k\). In the sequel, we present the definition of suspension of a permutation \(\sigma \in S(n)\).
Definition 3
Let \(\sigma \in S(n)\) denote a meander permutation and \(k\) a positive integer. We define the suspension \(\hat{\sigma }^{k}\) of the permutation \(\sigma \) as the permutation \(\hat{\sigma }^{k}\in S(n+2)\) which satisfies:
-
(i)
\(\hat{\sigma }^k(j) = \sigma (j-1)+1\), for \(j \in \{2,\dots ,n+1\}\); and
-
(ii)
if \(k\) is odd
$$\begin{aligned} \hat{\sigma }^k(1)=1 \text{ and } \hat{\sigma }^k(n+2)=n+2, \end{aligned}$$and if \(k\) is even
$$\begin{aligned} \hat{\sigma }^k(1) = n+2 \text{ and } \hat{\sigma }^k(n+2) = 1. \end{aligned}$$
It is clear that \(\hat{\sigma }^{k}\) is a meander permutation. For this permutation we define the vector \((i_{j}(\hat{\sigma }^{k}))_{1\le j\le n+2}\) by (38) with \(k\) replaced by \(k-1\). That is,
and
for \(j=1,\dots ,n+1\). For an illustration of a permutation suspension see Fig. 1 further below in Sect. 6.
From (46) we conclude that after \(k\) suspensions of \(\sigma _{f}\) one obtains a meander permutation \(\hat{\sigma }^{1}_{f}\in S(n+2k)\) with a vector \((i_{j}(\hat{\sigma }^{1}_{f}))_{1\le j\le n+2k}\) satisfying
Indeed, since \(\hat{\sigma }_{f}^{j}\) is the suspension of \(\hat{\sigma }_{f}^{j+1}\) and \(i_{1}(\hat{\sigma }_{f}^{j})=j-1\), for \(1 \le j \le k\), it follows that \(i_{1}(\hat{\sigma }_{f}^{1})=0\). In order to prove that \(i_{n+2k}(\hat{\sigma }_{f}^{1})=0\) we show that \(i_{n+2}(\hat{\sigma }^{k})=k-1\) which implies the former equality by reverse induction on \(k\). By (47) we have
Hence, it follows that
since \(1<(\hat{\sigma }^{k})^{-1}(n+1)<n+2\). We next prove that \(i_{n+1}(\hat{\sigma }^{k})=k\). For that we need to verify the following
If \(j=1\), we have from (47)
Suppose now that \(i_{j}(\hat{\sigma }^{k})=i_{j-1}(\sigma )\) for \(j \le n-1\). Then
We thus conclude inductively that (50) holds and, consequently, \(i_{n+1}(\hat{\sigma }^{k})=i_{n}(\sigma )=k\). By (49) this implies \(i_{n+2}(\hat{\sigma }^{k})=k-1\) and completes (48).
It is clear that \(\hat{\sigma }_{f}^{1} \in S(N)\) with \(N=n+2k\). Moreover, for all \(j\in \{1,\dots ,k\}\cup \{n+k+1,\dots ,n+2k\}\), the permutation \(\hat{\sigma }_{f}^{1}\) satisfies
Furthermore, by \((i)\) of Definition 3, \(\hat{\sigma }_{f}^{1}\) and \(\sigma _{f}\) are related by
For an illustration of a sequence of \(k\) suspensions see Fig. 2 of Sect. 6.
The next step is to verify the existence of a function \(h\) realizing the permutation \(\hat{\sigma }_{f}^{1}\). To do that we recall the following result
Theorem 1
[13] There exists a \(C^{2}\) function \(h\) realizing the permutation \(\sigma \in S(N)\) if, and only if, \(N\) is odd and \(\sigma \) is a dissipative Morse meander permutation.
We know that \(\hat{\sigma }_f^1 \in S(N)\) is a meander permutation which is dissipative since \(N=n+2k\) is odd and \(\hat{\sigma }_f^1(1) = 1, \hat{\sigma }_f^1(N)=N\) by (51). Moreover, the vector \((i_j(\hat{\sigma }_f^1))_{1 \le j \le N}\) defined in (30) satisfies
for all \(j=1,\dots ,N\). Indeed, it follows from (48) that (53) holds for \(j=1\) and \(j=N\). If \(j\in \{k+1,\dots ,k+n\}\), we have from (50) that
for \(l=1,\dots ,n\). Lastly, if \(j\in \{ 2,\dots ,k\}\cup \{n+k+1,\dots ,n+2k-1\}\) we invoke (30) and use (51). This yields
if \(j\in \{1,\dots ,k-1\}\cup \{n+k+1,\dots ,n+2k-1\}\), which is equivalent to
and to
Then, by recalling that \(i_{1}(\hat{\sigma }_{f}^{1}) = i_{n+2k}(\hat{\sigma }_{f}^{1}) = 0\), it follows that
for \(j=1,\dots ,k\). Therefore, \(\hat{\sigma }_{f}^{1}\) is a Morse permutation. We are then able to apply Theorem 1 and ensure the existence of a function \(h\) realizing \(\hat{\sigma }_{f}^{1}\).
Let \(D\subset \mathbb {R}^{2}\) be the large open set defined in (35). Our aim is to change \(f\) outside \([0,\pi ]\times D\) in such a way that the modified semiflow coincides with the original one on the bounded subset \(\mathcal {A}_f^c\) of \(\mathcal {A}_f\). We let \(h\) be such that
This ensures the existence of a large ball \(B\subset X^\alpha \subset C^1\) where the semiflow generated by (1) coincides with the semiflow generated by
We will define \(h\) for \((x,u,p)\) outside \([0,\pi ] \times D\) in such a way that the dynamical system induced by (57) is dissipative. Hence (57) will possess a compact global attractor \(\mathcal {A}_{h}\). Nevertheless, we can decompose \(\mathcal {A}_{h}\) into a maximal compact invariant subset \(\mathcal {A}_{h}^{c}\) contained in \(B\) and its complement, that is,
We notice that the set \(E^{c}_{f}\) of equilibria of (1) coincides with the subset of equilibria of Eq. (57) that are contained in \(B\). This follows directly from the fact that \(h=f\) on \(B\). As a consequence, the set of all equilibria of (57) is decomposed as follows
The subset \(\mathcal {A}_{h}^{c}\subset B\) is the set of all orbits that never leave \(B\). Therefore, \(\mathcal {A}_{h}^{c}\) is composed of the set \(E^{c}_{f}\) of equilibria in \(B\) and their heteroclinic orbits, which coincides with the definition of \(\mathcal {A}^{c}_{f}\). In this way, we have \(\mathcal {A}^{c}_{f}=\mathcal {A}_{h}^{c}\).
Also let \(\hat{D}\subset \mathbb {R}^{2}\) be a larger set containing \(D\). We require that
for some constant \(c<0\). To define the function \(h\) on the remaining portion of the domain \([0,\pi ]\times \mathbb {R}^2\) we appeal to the permutation \(\hat{\sigma }^1_f\). We use the fact that \(\hat{\sigma }^1_f\) is realizable by a function \(h\) and then verify that, in Theorem 1, it is possible to choose \(h\) satisfying the requirements (56) and (58). In this way, we have defined a cut-off function \(h\) that coincides with \(f\) on the large ball \(B\) containing the bounded subset \(\mathcal {A}_f^c\) and such that the corresponding semiflow is dissipative.
Before imposing on \(h\) the requirements (56) and (58) we remark that, on both meanders \(\gamma =\gamma _{f}\) and \(\gamma _{h}\), the arcs joining the intersection points with the \(u\)-axis can be isotopically transformed into semicircles. Therefore, we are allowed to work with meanders \(\gamma \) in canonical form, i.e., essentially composed of semicircle arcs (see [13]).
The first requirement (56) is quite simple since we notice that \(\gamma _{f}\) and \(\gamma _{h}\) share the same permutation on the set \(E^{c}_{f}\). The second requirement (58) follows from the realization results of canonical meanders by boundary value problems (see [11, 13]), and the condition that for \(|u|\) sufficiently large the projection \((u,p)\mapsto (u,0)\) is a local diffeomorphism. We also have that the canonical meander \(\gamma _{h}\), outside the semicircles shared with \(\gamma _{f}\), is composed of semicircles corresponding to the suspensions \(\hat{\sigma }^{k}_{f},\hat{\sigma }^{k-1}_{f},\dots ,\hat{\sigma }^{1}_{f}\). The realization of the canonical meander \(\gamma _h\) by second order boundary value problems then completes the definition of the smooth function \(h\) on the missing set \([0,\pi ]\times (\hat{D} {\setminus } D)\).
Therefore, the requirements (56) and (58) on \(h\) imply that the dynamical system induced by (57) is dissipative and preserves the equilibria in \(E^{c}_{f}\) and the heteroclinic connections between them.
6 Connecting Orbit Structure
The aim of this section is to prove our main result, Theorem 2, presented next. This theorem provides a simple criterion for the existence of heteroclinic connections between the equilibria in \(E_{f}\).
Theorem 2
Let \(u\) and \(v\) be equilibria in \(E_{f}\) satisfying \(z(u-v)=m\), with the extended interpretation of the zero number for the equilibria at infinity given by (20) and (21). Then there exists a heteroclinic connection between \(u\) and \(v\) if, and only if, they are \(m\)-adjacent. Moreover, if the equilibria \(v\) and \(w\) are connected, then the one with higher Morse index is the source of the connection.
Let \(E_{h}=\{ w_{1},w_{2},\dots ,w_{N} \}\) be the set of equilibria of (57). The permutation \(\sigma _{h}=\hat{\sigma }_{f}^{1}\) being Sturm implies that the Morse indices \(i(w_{j})\) can be obtained in terms of \(\sigma _{h}\) as in (32). Also, the intersection numbers \(z(w_{j}-w_{m})\) are given explicitly in terms of \(\sigma _{h}\), for all \(j,m\in \{1,\dots ,N\}\), as we can see in [11, 12, 28] and as it is presented in the next Proposition. We may equivalently use the recursions formulae in [12, Proposition 2.1].
Proposition 1
Under the above setting and considering the Sturm permutation \(\sigma _{h}\in S(N)\), for \(1\le m<l\le N\), the Morse indices are given by
and the intersection numbers by
where empty sums denote zero.
We collect in the following lemmas the results previously obtained from \(\hat{\sigma }_{f}^{1}\) for the Morse indices \(i(w_{j})\), \(w_{j}\in E_{h}\). Lemmas 11 and 12 follow respectively from (55) and (54).
Lemma 11
The Morse indices of the exterior equilibria in \(E_{h}\), i.e., the equilibria \(w_{j} \in E_{h}\) with \(j\in \{1,\dots ,k\}\cup \{n+k+1,\dots ,n+2k\}\), satisfy:
and
Lemma 12
The Morse indices of the interior equilibria in \(E_{h}\), i.e., the equilibria \(w_{j} \in E_{h}\) with \(j\in \{k+1,\dots ,k+n\}\), satisfy:
The previous lemma displays the relation between the Morse indices \(i(w_{j})\) of \(w_{j} \in E_{h}\) and the Morse indices \(i(v_{l})\) of \(v_{l} \in E^{c}_{f}\), and is also a direct consequence of (56).
Regarding the information on the zero numbers contained on the permutation \(\sigma _{h}\) we have two results. In Lemma 13 we present the zero numbers of the differences between the \(k\) first/last equilibria and the remaining \(n\) middle equilibria in \(E_{h}\), i.e., the number of intersections between the exterior and the interior equilibria. In Lemma 14 we obtain the zero number results for the \(n\) middle equilibria \(w_{j} \in E_{h}\), i.e., the interior equilibria.
Lemma 13
For any \(1 \le l \le n\), the following holds
Proof
By [12, Proposition 2.1] we are also provided with the following expressions
In order to prove the first statement of the lemma, we claim that for any \(1 \le j \le k\) we have
Indeed, from (62) we obtain
for all \(1 \le j \le k\) and \(2 \le l \le n\). But, since
we have
and conclude from (65) that
for all \(1 \le j \le k\) and \(2 \le l \le n\). In particular, this shows (64).
It is then sufficient to compute \(z(w_{k+1}-w_{j})\). For that, using (62) we write
for \(2 \le m \le k-j\) and \(1 \le j \le k\). We further notice that by (51) we have
Then, we obtain
for \(2 \le m \le k-j\). Also, for \(m=k+1-j\) we have from (62)
which, by (66) implies that \(z(w_{k+1}-w_{j})=z(w_{k}-w_{j})\). Therefore we conclude that (67) holds for \(2\le m\le k+1-j\).
Hence, using (67) iteratively from \(m=k+1-j\) to \(m=2\) we obtain
Thus, by (61) and Lemma 11 we conclude that \(z(w_{k+1}-w_{j})=j-1\). Therefore, (64) implies (59) for \(1 \le l \le n\).
To ensure (60), we first prove that
for all \(1 \le l \le n\). We remark that for \(l=n\) the above sum is empty, which means that \(i(w_{k+n})=k\) as expected. In order to prove (68), we first notice that \(z(w_{n+2k}-w_{k+l})=0\) by (63), and
by Proposition 1. These equalities imply
since \((-1)^{n+2k}\mathrm{sign }(\sigma _{h}^{-1}(n+2k)-\sigma _{h}^{-1}(k+l)) = -1\) by (51). Noticing that, again by (51), the last \((k-1)\) terms of the sum in (69) add-up to
we conclude that
which shows (68).
We are then able to obtain (60) using (68). From Proposition 1 we have
for \(1 \le l \le n\) and \(0 \le j \le k-1\). Again by (51) we obtain
and the last \((k-j-1)\) terms of the sum in (70) add-up to
By (68) this yields
Then (60) holds for \(1 \le l \le n\). \(\square \)
The next result on the zero numbers of the differences between interior equilibria in \(E_{h}\), follows immediately from (56). It provides the obvious relation between the zero numbers of the differences between equilibria \(w_{j} \in E_{h}\) with \(k+1 \le j \le k+n\) and the zero numbers of the differences between equilibria \(v_{l} \in E^{c}_{f}\).
Lemma 14
For all \(1 \le m < l \le n\), the following holds:
The following lemma establishes expressions for these zero numbers in terms of the permutation \(\sigma _{f}\).
Lemma 15
For any \(1 \le m < l \le n\), the zero number \(z(v_{l}-v_{m})\) is given by
Proof
From Proposition 2, using Lemmas 14 and 12, we have
Then, recalling that \(\sigma _h=\hat{\sigma }^1_f\) we obtain from (52)
If we let \(j=\sigma _f(r)\) for \(r\in \{1,\dots ,n\}\) we have that \(j\in \{1,\dots ,n\}\), and taking inverse permutations we rewrite (74) as
This implies the following equalities
for all \(m\) and \(j\) in \(\{1,\dots ,n\}\). By substitution into (73) this yiels (72) as wanted. \(\square \)
Remarkably, Lemmas 11 and 13 lead to the following convenient relations:
for \(0 \le j \le k-1\), and
for \(0 \le j \le k-1\) and \(1 \le l \le n\), that is, for all bounded equilibria \(v_l \in E^{c}_{f}\) and all equilibria at infinity \(\Phi _{j}^{\infty ,\pm }\). Moreover, as seen in Lemmas 12 and 14, the Morse indices and zero numbers for the differences between interior equilibria \(w_{j} \in E_{h}\), with \(j\in \{k+1,\dots ,k+n\}\), coincide with the corresponding Morse indices and zero numbers for the equilibria \(v_{l}\in E^{c}_{f}\).
Under the dissipative setting of Eq. (28), we recall from [29] the adjacency notion and the associated heteroclinic connection result.
Definition 4
Consider any two different equilibria \(w_{r}\) and \(w_{s}\) in \(E_{h}\) with \(z(w_{r}-w_{s})=m\) and \(w_{s}(0)<w_{r}(0)\). We say that \(w_{r}\) and \(w_{s}\) are \(m\)-adjacent if there does not exist any other equilibrium \(w \in E_{h}\) satisfying
and
Theorem 3
[29] Let \(w_{r}\) and \(w_{s}\) be any two different equilibria in \(E_{h}\) with \(z(w_{r}-w_{s})=m\). Then there exists a heteroclinic connection between \(w_{r}\) and \(w_{s}\) if, and only if, they are \(m\)-adjacent.
We know that the bounded subset \(\mathcal {A}_{f}^{c}\) of \(\mathcal {A}_{f}\) coincides with the subset \(\mathcal {A}_{h}^{c}\subset \mathcal {A}_{h}\), where \(\mathcal {A}_{h}^{c} \subset B\) and \(\mathcal {A}_{h}=\mathcal {A}_{h}^{c}\cup \{\mathcal {A}_{h}{\setminus }\mathcal {A}_{h}^{c}\}\). In particular, the equilibrium \(w_{k+l}\in E_{h}\) coincides with the equilibrium \(v_{l} \in E_{f}\), for any \(l\in \{1,\dots ,n\}\). Moreover, the heteroclinic connections in \(\mathcal {A}_{h}^{c}\) between the equilibria \(w_{k+l}\) are identical to the heteroclinic connections in \(\mathcal {A}_{f}^{c}\) between the equilibria \(v_{l}\). All of these facts follow from (56). We thus conclude that the connections on \(\mathcal {A}_{f}^{c}\) are given as in Theorem 3, i.e., there is a heteroclinic connection between \(v_{l}\) and \(v_{m}\) if, and only if, \(v_{l}\) and \(v_{m}\) are adjacent. Then \(\sigma _{h}\) determines the connecting orbit structure on \(\mathcal {A}_{f}^{c}\).
Proof of Theorem 2
After the previous observation we are only concerned with the connections involving the equilibria at infinity. The case of intra-infinite heteroclinic connections (27) is simple to verify from the adjacency rules, since there are neither infinite nor exterior blockings. Then suppose that an interior equilibrium \(w_{k+l}=v_{l}\), for some \(l\in \{1,\dots ,n\}\), has a heteroclinic connection to the exterior equilibrium \(w_{j}\), for some \(j\in \{1,\dots ,k\}\). We thus know, from Lemma 13, that
Since \(w_{k+l}\) connects to \(w_{j}\), we conclude from Theorem 3, that there does not exist any equilibrium \(w\in E_{h}\) satisfying
and
We want to see that the equilibrium \(v_{l}=w_{k+l}\) connects to the equilibrium in \(E_{f}\) corresponding to \(w_{j}\), that is, the equilibrium at infinity \(\Phi _{j-1}^{\infty ,-}\). Assume by contradiction that this is not the case. Then, it follows from Lemma 8 that there exists an equilibrium \(v\in E_{f}^{c}\) satisfying
and
Which leads to a contradiction because \(v=w_{k+m}\) for some \(m\in \{1,\dots ,n\}\) and, then, \(v\) could not satisfy (77) and (78) since there does not exist \(w\in E_h\) satisfying (75) and (76). We thus conclude that the heteroclinic connections to infinity in \(\mathcal {A}_{f}\) are also given as in Theorem 3, that is to say that the permutation \(\sigma _{h}\) determines the heteroclinic connections to infinity in \(\mathcal {A}_{f}\).
Moreover, heteroclinic orbits run in the direction of decreasing Morse indices, (see [12]). These observations conclude the proof of the theorem. \(\square \)
To illustrate the permutation suspension procedure we consider the following non-dissipative nonlinearity \(f=f(u)\),
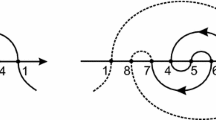
In this case we have \(k=1+[\sqrt{10}]=4\). The meander \(\gamma _f\) was numerically obtained in [7]. The set \(E_f\) has \(n=9\) equilibria, and the canonical form of the meander \(\gamma _f\) is depicted in Fig. 1 below.
In this case we have
and the Morse indices computed from (38) are given by
Then, the suspension process described in Definition 3 applied to \(\sigma _f\) yields
The sucessive application of this suspension procedure leads to
and finally,
This corresponds to the permutation \(\sigma _h=\hat{\sigma }_f^1\) and the canonical form of the meander \(\gamma _h\) is depicted in Fig. 2.
The total number of equilibria in \(E_h\) is \(N=17\), which correspond to 9 interior and 8 exterior equilibria, and the corresponding Morse indices are given by
References
Amann, H.: Global existence for semilinear parabolic systems. J. Reine Angew. Math. 360, 47–83 (1985)
Babin, A.V., Vishik, M.: Attractors of evolution equations. Studies in Mathematics and its Applications, vol. 25. North-Holland Publishing Co., Amsterdam (1992)
Brunovskỳ, P., Fiedler, B.: Connecting orbits in scalar reaction diffusion equations. Dynamics Reported, vol. 1, pp. 57–89. Dynam. Report. Ser. Dynam. Systems Appl., vol. 1. Wiley, Chichester (1988)
Brunovskỳ, P., Fiedler, B.: Connecting orbits in scalar reaction diffusion equations II. The complete solution. J. Differ. Equ. 81(1), 106–135 (1989)
Ben-Gal, N.: Grow-up solutions and heteroclinics to infinity for scalar parabolic PDEs. Thesis (Ph.D.), Brown University (2010)
Ben-Gal, N.: Non-compact global attractors for slowly non-dissipative PDEs I: the asymptotics of bounded and grow-up heteroclinics. Preprint (2011)
Ben-Gal, N.: Non-compact global attractors for slowly non-dissipative PDEs II: the connecting orbit structure. Preprint (2011)
Brunovskỳ, P.: The attractor of the scalar reaction diffusion equation is a smooth graph. J. Dynam. Differ. Equ. 2(3), 293–323 (1990)
Brunovskỳ, P., Tereščák, I.: Regularity of invariant manifolds. J. Dynam. Differ. Equ. 3(3), 313–337 (1991)
do Carmo, M.P.: Differential Geometry of Curves and Surfaces. Prentice-Hall Inc, Englewood Cliffs (1976)
Fusco, G., Rocha, C.: A permutation related to the dynamics of a scalar parabolic PDE. J. Differ. Equ. 91(1), 111–137 (1991)
Fiedler, B., Rocha, C.: Heteroclinic orbits of semilinear parabolic equations. J. Differ. Equ. 125(1), 239–281 (1996)
Fiedler, B., Rocha, C.: Realization of meander permutations by boundary value problems. J. Differ. Equ. 156(2), 282–308 (1999)
Fiedler, B., Rocha, C.: Orbit equivalence of global attractors of semilinear parabolic differential equations. Trans. Am. Math. Soc. 352(1), 257–284 (2000)
Hale, J.K.: Dynamical systems and stability. J. Math. Anal. Appl. 26(1), 39–59 (1969)
Hale, J.K.: Asymptotic behavior of dissipative systems. Mathematical Surveys and Monographs, vol. 25. American Mathematical Society, Providence (1988)
Hale, J.K., Massatt, P., Asymptotic behavior of gradient-like systems. Dynamical Systems, II (Gainesville, 1981), pp. 85–101. Academic Press, New York (1982)
Hell, J.: Conley index at infinity. Topol. Methods Nonlinear Anal. 42(1), 137–167 (2013)
Henry, D.: Geometric theory of semilinear parabolic equations. Lecture Notes in Mathematics, vol. 840. Springer, Berlin (1981)
Matano, H.: Convergence of solutions of one-dimensional semilinear parabolic equations. J. Math. Kyoto Univ. 18(2), 221–227 (1978)
Matano, H.: Asymptotic behavior and stability of solutions of semilinear diffusion equations. Publ. Res. Inst. Math. Sci. 15(2), 401–454 (1979)
Matano, H.: Asymptotic behavior of solutions of semilinear heat equations on \({S}^1\). Nonlinear Diffusion Equations and their Equilibrium States, II (Berkeley, CA, 1986). Math. Sci. Res. Inst. Publ., vol. 13. Springer, New York (1988)
Matano, H., Nakamura, K.: The global attractor of semilinear parabolic equations on \({S}^1\). Discrete Contin. Dynam. Syst. 3(1), 1–24 (1997)
Miklavčič, M.: A sharp condition for existence of an inertial manifold. J. Dynam. Differ. Equ. 3(3), 437–456 (1991)
Pazy, A. Semigroups of linear operators and applications to partial differential equations. Applied Mathematical Sciences, vol. 44. Springer, New York (1983)
Pimentel, J.: Asymptotic behavior of slowly non-dissipative systems. Thesis (Ph.D.)-Instituto Superior Técnico—Universidade de Lisboa (2014)
Rocha, C.: Generic properties of equilibria of reaction-diffusion equations with variable diffusion. Proc. R. Soc. Edinburgh: Sect. A 101(1–2), 45–55 (1985)
Rocha, C.: Properties of the attractor of a scalar parabolic PDE. J. Dynam. Differ. Equ. 3(4), 575–591 (1991)
Wolfrum, M.: A sequence of order relations: encoding heteroclinic connections in scalar parabolic PDE. J. Differ. Equ. 183(1), 56–78 (2002)
Zelenyak, T.I.: Stabilization of solutions of boundary value problems for a second order parabolic equation with one space variable. Differ. Equ. 4(1), 17–22 (1968)
Acknowledgments
This work was partially supported by FCT/Portugal through the project PEst-OE/EEI/LA0009/2013. The first author was supported by SFRH/BD/51389/2011 (FCT/Portugal), and GDE/246318/2012-0 (CNPq-Brazil). The authors also acknowledge the useful comments of the referee.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Pimentel, J., Rocha, C. A Permutation Related to Non-compact Global Attractors for Slowly Non-dissipative Systems. J Dyn Diff Equat 28, 1–28 (2016). https://doi.org/10.1007/s10884-014-9414-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-014-9414-x