Robust multiobjective portfolio optimization: a set order relations approach

Abstract

We consider Markowitz’s portfolio optimization problem that heavily suffers from uncertainties of input parameters. And based on set order relations, uncertain portfolio optimization problem at various extreme cases is modelled as robust multiobjective formulations. At first, borrowing set order relations, three concepts of set less ordered efficiency are defined for multiobjective portfolio optimization problems with uncertainties. Subsequently, following from Ben-Tal and Nemirovski (Math Oper Res 23(4):769–805, 1998; Oper Res Lett 25:1–13, 1999), several multiobjective robust counterparts are introduced, and tackled by multiobjective particle swarm optimization approach. As such, the properties of the obtained (robust) efficient solutions are further characterized. Finally, the empirical researches from the real stock market show that (robust) efficient solutions based on set order relations are highly advisable for the investors.

1 Introduction

It is well known that Markowitz’s mean–variance portfolio optimization problem (see Markowitz 1952, 1959) is strongly sensitive to the perturbations from input parameters (i.e., the expected return and the covariance of returns), which causes that the optimization results are seriously unreliable. To this end, there are various ways to manage these uncertain parameters. For example, sensitivity analysis treats uncertainties of the parameters after an optimal solution is obtained. It belongs to a post-optimization method (see Saltelli et al. (2000)). Moreover, stochastic optimization assumes that uncertainties of the parameter whose probability distribution is known are of a stochastic nature (see Birge and Louveaux 2011). Conversely, robust optimization, which is employed in the present paper, requires the uncertain parameters lying in some uncertain set without any distribution assumptions. It transforms the uncertain optimization problems to the deterministic ones by robust counterpart (see Ben-Tal and Nemirovski 1998, 1999).

Although robust counterpart is conveniently achieved at the worst case of all the realizations over the uncertain set, it is worth mentioning that the resulting optimization solutions are very conservative without consideration of the different extreme cases. Therefore, besides the worst case, this paper still investigates the other cases where the corresponding robust counterparts handle with uncertainties in the portfolio optimization problem, to provide the related portfolio strategies with the different statuses of the stock market, which is research focus of this paper. At same time, set order relations have been extensively studied to treat uncertain parameters in (robust) multiobjective optimization problems at different extreme cases (see Kuroiwa 1998, 1999; Schöttle and Werner 2006, 2009; Ehrgott et al. 2014; Chen and Zhou 2018). Even so, there are still lots of theoretical and practical issues to be further investigated, for instance, at various extreme cases robust counterparts of uncertain portfolio optimization problem and their computational cost, the properties of robust efficient solutions and portfolio performance in real stock market. These issues constitute the main contents of this study.

Thus, borrowing the idea of robust counterpart and the concepts of set order relations, for uncertain portfolio optimization problem this paper build the corresponding robust counterpart to the various extreme cases over uncertain set. Meanwhile, considering the computational cost of various robust counterparts (especially, with complex constraints), they will be maintained their multiobjective characteristic and solved by multiobjective optimization approach. Roughly speaking, main contributions of this paper are as follows:

• Lower robust counterpart is for the first time introduced for uncertain multiobjective portfolio optimization problems via the idea of robust counterpart developed by Ben-Tal and Nemirovski (1998, 1999) and the concepts of set ordered relations.

• Multiple relationships between robust efficient frontiers and nominal efficient frontier are roundly studied, and new knowledge obtained: upper robust efficient frontier lies on the right side of lower robust efficient frontier; and nominal efficient frontier lies between them.

• Through the investigation for robust efficiency loss and some inherent parameters in the optimization problem, some new discoveries are achieved at: robust efficiency loss is negatively related to the number of assets in a portfolio. Moreover, it is positively linked to the radius and negatively to the scaling factor of the ellipsoid uncertain set.

• Portfolio performance of various efficient solutions is also for the first time demonstrated in real stock market, and some new findings provided for the investors: at the bear market, the investment strategies of alternative robust efficient solutions can produce the fewest the return loss of portfolio with the lowest risk. And, investment strategies of lower robust efficient solutions generate the highest returns compared to the other efficient solutions at the bull market. Also, at the steady market nominal efficient solutions provide the relatively superior performance. But, the portfolio performance of upper robust efficient solutions is very disappointed at any market.

In addition, despite studying portfolio optimization problems, our methodology based on set order relations can also be applied to any uncertain multiobjective optimization problem. Naturally, it is also helpful to other optimization problems in the economics field.

The remainder of this paper is organized as follows. Section 2 introduces necessary concepts and basic theories of (deterministic and uncertain) multiobjective optimization (Sect. 2.1) and robust optimization (Sect. 2.2). A robust multiobjective portfolio optimization based on set order relations is described in Sect. 3 where four kinds of concepts of set order relations are presented in detail. In light of set order relations, the approaches to finding robust efficient solutions for uncertain multiobjective portfolio optimization problems are introduced in Sect. 4; and multiobjective particle swarm optimization solver is introduced for computing (robust) efficient solutions. Sect. 5 illustrates some basic properties of (robust) efficient solutions and portfolio performance in the real stock market. Finally, we present conclusions in Sect. 6.

2 Preliminaries

2.1 Multiobjective optimization

Firstly, without a loss of generality, assume that a multiobjective optimization is written as

$$ \begin{aligned} \hbox{min} \;f(x) = (f_{1} (x), \ldots ,f_{q} (x)) \hfill \\ \quad \;\,{\text{s}} . {\text{t}} .\quad x \in {\mathcal{X}} \hfill \\ \end{aligned} $$

(2.1)

where $f:{\mathbb{R}}^{n} \to {\mathbb{R}}^{q}$ is the vector-valued function composed of $q$ objective components. The function is simultaneously minimized over a set of feasible solutions $x$ (composed of a set of vectors). ${\mathcal{X}} \subseteq {\mathbb{R}}^{n}$ is the feasible region. The class of multiobjective optimization is referred to as a deterministic multiobjective optimization (DMO) without uncertain parameters. It is always used as an ideal model for real-world optimization.

Remark 2.1

Actually, Markowitz’s mean–variance portfolio is a multiobjective optimization problem, which has two objective components. Suppose that a portfolio of n risky assets is considered; the portfolio weighted vector $x \in {\mathbb{R}}_{ + }^{n}$ is subject to $\sum\nolimits_{i = 1}^{n} {x_{i} } = 1$. Naturally, the mean–variance portfolio optimization problem can be written by

$$ \begin{aligned} &\hbox{min} \;f(x) = (f_{1} (x),f_{2} (x)) \hfill \\ &{\text{s}} . {\text{t}} .\;\,\sum\limits_{i = 1}^{n} {x_{i} } = 1 \hfill \\ &\quad \,m_{i} \le x_{i} \le M_{i} ,\quad i = 1, \ldots ,n \hfill \\ \end{aligned} $$

(2.2)

In (2.2), $f_{1} (x) = x^{T} \widehat{\Sigma }x$ is one objective component measuring the risk of portfolio; $f_{2} (x) = - \hat{\mu }^{T} x$ is the other objective component measuring the return of portfolio. And the parameters of $\hat{\mu }$ and $\hat{\varSigma }$ are assumed to be accurately computed by $\hat{\mu }_{i} = E[R_{i} ]$ and $\hat{\varSigma }_{ij} = E[(R_{i} - \hat{\mu }_{i} )(R_{j} - \hat{\mu }_{j} )]$; here, $R_{i}$ is the return on asset $i, i = 1, \ldots ,n$. $M_{i}$ ($m_{i}$) which denotes the maximum (minimum) proportion invested on $A_{i}$; here, the constraint is called budget constraint (90% for maximum proportion and 10% for minimum proportion in the following sections).The resulting portfolio optimization problem is referred to as the nominal mean–variance (NMV) portfolio optimization problem. The efficient solutions obtained by NMV portfolio optimization problem are called nominal efficient solutions, whose efficient set is denoted by ${\mathcal{X}}_{nmv}$. Additionally, the constraints in NMV portfolio optimization problem are consistent with those of the other portfolio optimization problems mentioned in the next sections.

However, uncertainty can emerge anywhere in the real world (e.g., the preceding expected returns $\hat{\mu }$ possibly varying in a set of scenarios called an uncertainty set (${\mathcal{U}} \subseteq {\mathbb{R}}^{p}$).As such, a multiobjective optimization problem with uncertain parameters is referred to as an uncertain multiobjective optimization (UMO) problem. UMO is written as

$$ {\mathcal{P}}({\mathcal{U}}): = (P(\zeta ),\zeta \in {\mathcal{U}}) $$

(UMO)

defined as a family of parameterized problems

$$ \begin{aligned} &P(\zeta ) \hbox{min} f(x,\zeta ) = (f_{1} (x,\zeta ), \ldots ,f_{q} (x,\zeta )) \hfill \\ & {\text{s}} . {\text{t}} . x \in {\mathcal{X}} \hfill \\ \end{aligned} $$

where $f: {\mathcal{X}} \times {\mathcal{U}} \to {\mathbb{R}}^{q}$ and ${\mathcal{X}} \subseteq {\mathbb{R}}^{n}$.

Remark 2.2

In the context of Markowitz’s mean–variance portfolio, when the parameters of the expected return and the covariance matrix are considered to be uncertain rather than accurate, they are denoted by $\zeta = (\mu ,\varSigma )$ than by $(\hat{\mu },\hat{\varSigma })$.Further, assume the covariance matrix $\varSigma \in {\mathbb{S}}_{ + }^{n}$ and expected return $\mu \in {\mathbb{R}}^{n}$. Then, the objective function of (2.2) is replaced by $\hbox{min} f(x) = (f_{1} (x,\zeta ),f_{2} (x,\zeta ))$. The resulting multiobjective portfolio optimization problem is referred to as the uncertain mean–variance (UMV) portfolio optimization problem. In addition, we note that the geometry of the uncertainty set ${\mathcal{U}}$ is crucial to optimize UMV portfolio optimization problem. In the existing literature, there are some of uncertainty sets which are employed in the uncertain optimization problem. However, the ellipsoidal uncertainty set (see Ben-Tal et al. 2009; Schöttle and Werner 2006, 2009) is highlighted to have a good nature. So, in the present paper, we will employ and introduce it as follows:

$$ {\mathcal{U}}_{\delta } (\hat{\mu },\hat{\varSigma }): = \left\{ (\mu ,\varSigma ) \in {\mathbb{R}}^{n} \times {\mathbb{S}}_{ + }^{n} : || \mu - \hat{\mu }|| + c || \varSigma - \hat{\varSigma }|| \le \delta \right\} $$

(2.3)

where $(\hat{\mu },\hat{\varSigma })$ is the centre of an ellipsoid set (i.e., nominal values), and $\delta$ is its radius.

Multiobjective (portfolio) optimization problems have been described. Subsequently, the concepts of their efficient solutions will be presented.

Due to an absence of total ordering on ${\mathbb{R}}^{q}$, the solution vectors of the multiobjective optimization function $f(x)$ must be defined based on partial ordering relations. In the present paper, ordering relations, i.e., ≦, ≤ and < , are applied (see Ehrgott 2005). Their meanings are described as follows: $x,y \in {\mathbb{R}}^{q}$

• $x{ \leqq }y: \Leftrightarrow y_{i} \in \left[ {x_{i} ,\;\infty } \right)$ for all $i = 1, \ldots ,q$.

• $x \le y : \Leftrightarrow y_{i} \in \left[ {x_{i} , \infty } \right)$ for all $i = 1, \ldots ,q,\;{\text{and}}\; x \ne y$.

• $x < y: \Leftrightarrow y_{i} \in ( x_{i} , \infty )$ for all $i = 1, \ldots ,q$.

The notation $[././.]$ is used to shorten the text. The cones ${\mathbb{R}}_{{ \leqq }}^{q}$,${\mathbb{R}}_{ \le }^{q}$ and ${\mathbb{R}}_{\text{ < }}^{q}$ are defined as ${\mathbb{R}}_{{[{ \leqq }/ \le /\text{ < }]}}^{q} : = \{ x \in {\mathbb{R}}^{q} ,x [{ \leqq }/ \le /\text{ < }] 0\}$. Similarly,${\mathbb{R}}_{[\geqq/\geqslant/>]}^{q} : = \{x \in {\mathbb{R}}^{q},x [{\geqq}/\geqslant/>]0\}$.

The goal of multiobjective optimization problems is to obtain all efficient solutions in the feasible region ${\mathcal{X}}$. In the following, we define efficient solutions obtained by partial ordering relations.

Definition 2.3

(Efficient solutions) For a feasible solution $x \in {\mathcal{X}}$, when $x$ is called efficient, then there is no $x^{\prime} \in {\mathcal{X}}\backslash \{ x\}$ such that $f(x^{\prime}) \le f(x)$.

Analogously, replacing ≤ with ≦ or < , strictly efficient or weakly efficient can be defined. Then, $x$ is [strictly/./weakly] efficient

$$ \Leftrightarrow f(x) \subseteq f(x^{\prime}) - {\mathbb{R}}_{{[{\geqq}/\geqslant/>]}}^{q} \;{\text{or}}\; f(x) + {\mathbb{R}}_{{[{\geqq}/{\geqslant}/>]}}^{q} \supseteq f(x^{\prime}) $$

(2.4)

This relationship grasps the meaning of robustly efficient as it is used in the following section.

2.2 Robust optimization

Robust optimization, ideal approach for disposing uncertainties in multiobjective optimization problems, have recently attracted more interests from researchers and practitioners. We refer the readers to Ben-Tal et al. (2009) and Bertsimas et al. (2011) for specific information on it. In particular, Ben-Tal has conducted extensive researches in robust optimization and its application, where the robust counterpart has been introduced. Robust counterpart attempts to transform uncertain optimization problem into deterministic one based on the worst case of all the realizations (i.e., scenarios) over an entire uncertainty set. As such, the resulting robust optimization problem can ensure that the solutions obtained are still efficient.

For the UMO problem, uncertainty of the parameters is eliminated at the worst-case scenario. Then, the resulting optimization problem is dealt with by the deterministic multiobjective approaches. Borrowing from the ideology of (P*) (see Ben-Tal and Nemirovski 1998, 1999) and of (RP_u) (see Fliege and Werner 2014), the robust counterpart of UMO problem can be given by:

$$ \mathop {\hbox{min} }\limits_{x \in \chi } \mathop {\hbox{max} }\limits_{{\zeta \in {\mathcal{U}}}} f(x,\zeta ) = \mathop {\hbox{min} }\limits_{x \in \chi } ( \mathop {\hbox{max} }\limits_{{\zeta \in {\mathcal{U}}}} f_{1} (x,\zeta ), \ldots ,f_{q} (x,\zeta )). $$

(RMO)

The goal of RMO problem is to discover all solutions that can remain efficient even at the worst-case scenario. That is, the obtained solution $x$ satisfies $f(x)\subseteq f(x^{\prime})- {\mathbb{R}}_{\geqslant}^{q}$ for any other solution $x^{\prime}$. According to Ehrgott, Ide and Schöbel (2014), such solutions in RMO problem are also referred to as minmax robust efficiency. Similarly, the strictly and weakly efficient solutions are referred to as minmax robust strictly efficiency and weakly efficiency, respectively.

Remark 2.4

For the UMV portfolio optimization problem, its robust counterpart at the worst case is given by

$$ \begin{aligned} \mathop {\hbox{min} }\limits_{x \in \chi } \mathop {\hbox{max} }\limits_{{\zeta \in U_{\delta } (\hat{\mu },\hat{\varSigma })}} f(x,\zeta ) & = \mathop {\hbox{min} }\limits_{x \in \chi } \mathop {\hbox{max} }\limits_{{(\mu ,\varSigma ) \in U_{\delta } (\hat{\mu },\hat{\varSigma })}} \left( \begin{aligned} x^{T} \varSigma x \hfill \\ - \mu^{T} x \hfill \\ \end{aligned} \right) \\ & = \mathop {\hbox{min} }\limits_{x \in \chi } \left( \begin{aligned} x^{T} \hat{\varSigma }x + \frac{\delta }{c}||x||^{2} \hfill \\ - \hat{\mu }^{T} x + \delta ||x|| \hfill \\ \end{aligned} \right) \\ \end{aligned} $$

(RMVminmax)

where the ellipsoid uncertainty set ${\mathcal{U}}_{\delta } (\hat{\mu },\hat{\varSigma })$ is same with ellipsoid uncertainty set used by Ben-Tal et al. (2009).

3 Set order relations for robust multiobjective portfolio optimization

Set order relations, as originate from set-valued optimization, investigate the relationship of optimization solutions and their efficiency via comparing multiple objective function values taken as a set of vector. Their researches and applications have been increasingly emerged in multiobjective optimization filed, especially with uncertain parameters (see Ehrgott et al. 2014; Kuroiwa 1998, 1999; Ide et al. 2014; Ide and Köbis 2014; Khan et al. 2014).

Set order relations include four kinds of relations corresponding different extreme cases over parameter set (here, it is the ellipsoid uncertainty set), that is, upper set less ordered relation at the worst case, lower set less ordered relation at the best case, alternative set less ordered relation at the intersection case and set less ordered relation at the union case, respectively. At each extreme case the optimization solutions of multiobjective optimization problem can be obtained. Actually, the optimization solutions of RMV_minmax are achieved at the worst case of set order relations. However, at long time ago Keynes confirmed that for the stock market containing multiple extreme cases, long-period prediction only considering one extreme case is not accurate. Contrarily, it should be divided into multiple successive sub-periods prediction corresponding different extreme cases (see Keynes 1936). His proposal can be just accomplished through set order relations.

To this end, firstly, the basic theory of set order relations is introduced as follows.

3.1 Upper set less ordered relation and upper set less ordered efficiency

Definition 3.1

(Upper set less ordered relation) For two arbitrary sets ${\mathcal{X}},{\mathcal{Y}} \subset {\mathbb{R}}^{q}$, the upper set less ordered relation ${ \preccurlyeq }_{s}^{u}$ w.r.t ${\mathbb{R}}_{{[{\geqq}/{\geqslant}/>]}}^{q}$ should satisfy

$$ {\mathcal{X} \preccurlyeq }_{s}^{u} {\mathcal{Y}} \Leftrightarrow {\mathcal{X}} \subseteq {\mathcal{Y}} - {\mathbb{R}}_{{[{ \geqq }/ \ge / > ]}}^{q} ( \Leftrightarrow \forall x \in {\mathcal{X}} \exists y \in {\mathcal{Y}}:x[{ \leqq }/ \le / < ]y) $$

(3.1)

It is clear that upper set less ordered relation only focuses on the worst case of all possible scenarios of UMO problem.

Definition 3.2

(Upper set less ordered efficiency) If a feasible solution $x \in {\mathcal{X}}$ is called upper set less ordered [strictly/./weakly] efficient for an UMO problem, then there is not $x^{\prime} \in {\mathcal{X}}\backslash \{ x\}$ such that $f_{{\mathcal{U}}} (x^{\prime}) { \preccurlyeq }_{s}^{u} f_{{\mathcal{U}}} (x)$ w.r.t ${\mathbb{R}}_{{[{\geqq}/{\geqslant}/>]}}^{q}$. So, it holds that

$$ \nexists x^{\prime} \in {\mathcal{X}\backslash }\{ x\} : f_{{\mathcal{U}}} (x^{\prime}) \subseteq f_{{\mathcal{U}}} (x) - {\mathbb{R}}_{{[{ \geqq }/ \ge / > ]}}^{q} $$

(3.2)

Obviously, upper set less ordered efficiency of a feasible solution is equivalent to its minmax robust efficiency described in the Sect. 2.2, i.e., $f_{{\mathcal{U}}} (x^{\prime}) { \preccurlyeq }_{s}^{u} f_{{\mathcal{U}}} (x)$ w.r.t ${\mathbb{R}}_{{[{\geqq}/{\geqslant}/>]}}^{q}$. In addition, for the convenient description, upper set less ordered efficiency and minmax robust efficiency are all written as upper robust efficiency; and their corresponding efficient solutions are also written as upper robust efficient solutions. Simultaneously, upper robust [strictly/./weakly] efficient solutions are denoted by $urse$, $ure$ and $urwe$, respectively; similarly, their corresponding solutions sets are denoted by ${\mathcal{X}}_{urse}$, ${\mathcal{X}}_{ure}$ and ${\mathcal{X}}_{urwe}$, respectively.

Lemma 3.3

For an UMV portfolio optimization problem, the following relationships hold

$$ {\mathcal{X}}_{urwe} \subseteq {\mathcal{X}}_{ure} \subseteq {\mathcal{X}}_{urse} . $$

Remark 3.4

In fact, for an UMV portfolio optimization problem, it is not allowed that the portfolio weighted vector is complete zero, i.e., none of assets are invested. As such, the relationship satisfies ${\mathcal{X}}_{urwe} = {\mathcal{X}}_{ure}$. Additionally, robust strictly efficient solutions also reveal that the investment strategies of the investors are risk averse.

3.2 Lower set less ordered relation and lower set less ordered efficiency

The descriptions of lower set less ordered relation and its efficiency are introduced as follows, see Kuroiwa (1998), Ide and Köbis (2014).

Definition 3.5

(Lower set less ordered relation) For two arbitrary sets ${\mathcal{X}},{\mathcal{Y}} \subset {\mathbb{R}}^{q}$, lower set less ordered relation ${ \preccurlyeq }_{s}^{l}$ w.r.t. ${\mathbb{R}}_{{[{\geqq}/{\geqslant}/>]}}^{q}$ should satisfy

$$ {\mathcal{X} \preccurlyeq }_{s}^{l} {\mathcal{Y}} \Leftrightarrow {\mathcal{X}} + {\mathbb{R}}_{{[{ \geqq }/ \ge / > ]}}^{q} \supseteq {\mathcal{Y}} ( \Leftrightarrow \forall y \in {\mathcal{Y}} \exists x \in {\mathcal{X}}:x[{ \leqq }/ \le / < ]y) $$

(3.3)

From the definition of lower set less ordered relation, it is easily observed that lower set less ordered relation is just the opposite of upper set less ordered relation. That is, the former focus on the best case of all the possible realizations in uncertainty set rather than the worst case.

Definition 3.6

(Lower set less ordered efficiency) If a feasible solution $x \in {\mathcal{X}}$ is called lower set less ordered [strictly/./weakly] efficient for an UMO problem, then there is not $x^{\prime} \in {\mathcal{X}}\backslash \{ x\}$ such that $f_{{\mathcal{U}}} (x^{\prime}) { \preccurlyeq }_{s}^{l} f_{{\mathcal{U}}} (x)$ w.r.t. ${\mathbb{R}}_{{[{\geqq}/{\geqslant}/>]}}^{q}$. So, it holds that

$$ \nexists x^{\prime} \in {\mathcal{X}\backslash }\{ x\}: f_{{\mathcal{U}}} (x^{\prime}) + {\mathbb{R}}_{{[{ \geqq }/ \ge / > ]}}^{q} \supseteq f_{{\mathcal{U}}} (x) $$

(3.4)

Contrary to upper set less ordered efficiency, lower set less ordered efficiency is identical with minmin robust efficiency rather than minmax robust efficiency. In the same way, for the convenient description, lower set less ordered efficiency and minmin robust efficiency are all written as lower robust efficiency; and their corresponding efficient solutions are also written as lower robust efficient solutions. At same time, lower robust [strictly/./weakly] efficient solutions are denoted by $lrse$, $lre$ and $lrwe$, respectively; analogously, their linked solutions sets are also denoted by ${\mathcal{X}}_{lrwe}$, ${\mathcal{X}}_{lre}$ and ${\mathcal{X}}_{lrse}$, respectively.

Lemma 3.7

For an UMO problem, the following relationships hold

$$ {\mathcal{X}}_{lrwe} \subseteq {\mathcal{X}}_{lre} \subseteq {\mathcal{X}}_{lrse} . $$

Remark 3.8

For an UMV portfolio optimization problem, the following relationship also satisfies:

${\mathcal{X}}_{lrwe} = {\mathcal{X}}_{lre}$. And, lower robust strictly efficient solutions reveal that the investment strategies of the investors are risk affine.

3.3 Alternative set less ordered relation and alternative set less ordered efficiency

The third concept in the set ordered relation family is alternative set less ordered relation and its corresponding efficiency. It is composed of a combination of upper set less ordered relation and lower set less ordered relation, see Ide and Köbis (2014), Ide et al. (2014). It is described as follows:

Definition 3.9

(Alternative set less ordered relation) For two arbitrary sets ${\mathcal{X}},{\mathcal{Y}} \subset {\mathbb{R}}^{q}$, ${\mathcal{X}}$ dominates ${\mathcal{Y}}$ w.r.t. alternative set less ordered relations (denoted as ${ \preccurlyeq }_{s}^{a}$) and w.r.t. ${\mathbb{R}}_{{[{\geqq}/{\geqslant}/>]}}^{q}$, which should satisfy

$$ \Leftrightarrow (\forall x \in {\mathcal{X}} \exists y \in {\mathcal{Y}}:x[{ \leqq }/ \le / < ]y) or (\forall y \in {\mathcal{Y}} \exists x \in {\mathcal{X}}:x[{ \leqq }/ \le / < ]y) $$

(3.5)

In terms of the meanings of alternative set less ordered relations, it is obvious that alternative set less ordered relation focuses on the worst case and the best case of all the possible realizations in uncertainty set. And alternative set less ordered efficiency is given as follows.

Definition 3.10

(Alternative set less ordered efficiency) If a feasible solution $x \in {\mathcal{X}}$ is called alternative set less ordered [strictly/./weakly] efficient for an UMO problem, then there is not $x^{\prime} \in {\mathcal{X}}\backslash \{ x\}$ such that $f_{{\mathcal{U}}} (x^{\prime}) { \preccurlyeq }_{s}^{a} f_{{\mathcal{U}}} (x)$. So, it holds

$$ \nexists x^{\prime} \in {\mathcal{X}\backslash }\{ x\} {:}\, f_{{\mathcal{U}}} (x^{\prime}) + {\mathbb{R}}_{{[{ \geqq }/ \ge / > ]}}^{q} \supseteq f_{{\mathcal{U}}} (x) or f_{{\mathcal{U}}} (x^{\prime}) \subseteq f_{{\mathcal{U}}} (x) - {\mathbb{R}}_{{[{ \geqq }/ \ge / > ]}}^{q} $$

(3.6)

It is clear that a feasible solution is alternative set less ordered efficiency, which is upper set less ordered efficiency as well as lower set less ordered efficiency. Thus, alternative set less ordered efficiency is equivalent to minmax robust efficiency and minmin robust efficiency. For the convenient description, alternative set less ordered efficiency is written as alternative robust efficiency; and its related efficient solutions are also written as alternative robust efficient solutions. Meanwhile, alternative robust [strictly/./weakly] efficient solutions are denoted by $arse$, $are$ and $arwe$, respectively; equally, their corresponding solutions sets are also denoted by ${\mathcal{X}}_{arse}$,${\mathcal{X}}_{are}$ and ${\mathcal{X}}_{arwe}$, respectively.

Lemma 3.11

For an UMO problem, the following relationships satisfy

$$ {\mathcal{X}}_{arwe} \subseteq {\mathcal{X}}_{are} \subseteq {\mathcal{X}}_{arse} . $$

Remark 3.12

For an UMV portfolio optimization problem, the following relationship holds:${\mathcal{X}}_{arwe} = {\mathcal{X}}_{are}$ And alternative robust efficient solutions suggest that the investment strategies of the investors are based on the worst case and the best case. So, Ide and Köbis (2014) suggest that alternative robust efficient solutions are good choices for the investors.

Lemma 3.13

Given an UMV portfolio optimization problem, the following statements hold:

• If short selling is limited, then ${\mathcal{X}}_{urse} = {\mathcal{X}}_{ure}$ and ${\mathcal{X}}_{lrse} = {\mathcal{X}}_{lre}$.

• If ${\mathcal{X}}_{urse} \cap {\mathcal{X}}_{lrse} = \emptyset$, then ${\mathcal{X}}_{arwe} = {\mathcal{X}}_{are} = {\mathcal{X}}_{arse} = \emptyset$.

• If $|{\mathcal{X}}_{arwe} | = 1$, then $|{\mathcal{X}}_{arse} | = \emptyset$.

  where $|\cdot|$ expresses the number of the set.

3.4 Set less ordered relation

Set less ordered relation is another simple combination of upper set less ordered relation and lower set less ordered relation (see Young 1931; Nishnianidze 1984; Eichfelder and Jahn 2012; Ide and Köbis 2014).

Definition 3.14

(Set less ordered relation) For two arbitrary sets ${\mathcal{X}},{\mathcal{Y}} \subset {\mathbb{R}}^{q}$, ${\mathcal{X}}$ dominates ${\mathcal{Y}}$ w.r.t. set less ordered relations (denoted as ${ \preccurlyeq }_{s}$) and w.r.t.${\mathbb{R}}_{{[{\geqq}/{\geqslant}/>]}}^{q}$, which should be satisfied by

$$ \Leftrightarrow (\forall x \in {\mathcal{X}} \exists y \in {\mathcal{Y}}{:}\,x[{ \leqq }/ \le / < ]y) \,\,and \,\,(\forall y \in {\mathcal{Y}} \exists x \in {\mathcal{X}}:x[{ \leqq }/ \le / < ]y) $$

(3.7)

Set less ordered efficiency can be given as follows:

Definition 3.15

(Set less ordered efficiency) If a feasible solution $x \in {\mathcal{X}}$ is called set less ordered [strictly/./weakly] efficient for an UMO problem, then there is not $x^{\prime} \in {\mathcal{X}}\backslash \{ x\}$ such that $f_{{\mathcal{U}}} (x^{\prime}) { \preccurlyeq }_{s} f_{{\mathcal{U}}} (x)$ w.r.t. ${\mathbb{R}}_{{[{\geqq}/{\geqslant}/>]}}^{q}$.So, it holds that

$$ \nexists x^{\prime} \in {\mathcal{X}\backslash }\{ x\} {:}\, f_{{\mathcal{U}}} (x^{\prime}) + {\mathbb{R}}_{{[{ \geqq }/ \ge / > ]}}^{q} \supseteq f_{{\mathcal{U}}} (x)\,\, and\,\, f_{{\mathcal{U}}} (x^{\prime}) \subseteq f_{{\mathcal{U}}} (x) - {\mathbb{R}}_{{[{ \geqq }/ \ge / > ]}}^{q} $$

(3.8)

It is evident that a feasible solution which is said to be set less ordered efficiency may be upper set less ordered efficiency or lower set less ordered efficiency.

Remark 3.16

For an UMV portfolio optimization problem, it is trivial to seek for the efficient solutions which are set less ordered efficiency. Thus, we do not consider it in the following sections.

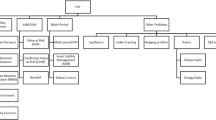
From Definitions 3.1–3.14, the relationships among set order relation can be depicted in Fig. 1.

Fig. 1

The relationships among set order relation

Upper set less ordered relation and lower set less ordered relation concentrate on two quite differently extreme cases in the uncertain set. They can provide robust efficient solutions. Moreover, alternative set less ordered relation is interested in the intersection of them. It can supply better choices for the investors.

4 Computing robustly efficient solutions for uncertain multiobjective portfolio optimization

In the above descriptions several kinds of robust efficient solutions are analyzed based on set order relation. Then, how to obtain these robust efficient solutions will be given in the followings.

4.1 Robust multiobjective portfolio formulations

In order to obtain upper/lower/alternative robust efficient solutions, robust multiobjective formulations are proposed based on Ben-Tal and Nemirovski (1998, 1999).

• (a) Computing upper robust efficient solutions

According to Definitions 3.1 and 3.2, it is evident that upper robust efficiency is equivalent to minmax robust efficiency (see Fliege and Werner 2014; Ehrgott et al. 2014). This relationship tells the fact of computing upper robust efficient solutions for UMV portfolio optimization problems via RMV_minmax. So, upper robust counterpart can be given as

$$ \begin{aligned} \min_{{x \in {\mathcal{X}}}} \max_{\zeta = (\mu ,\varSigma )} f(x,\zeta ) & = \min_{{x \in {\mathcal{X}}}} \max_{{(\mu ,\varSigma ) \in U_{\delta } (\hat{\mu },\hat{\varSigma })}} \left( \begin{aligned} x^{T} \varSigma x \hfill \\ - \mu^{T} x \hfill \\ \end{aligned} \right) \\ & = \min_{{x \in {\mathcal{X}}}} \left( \begin{aligned} x^{T} \hat{\varSigma }x + \frac{\delta }{c}||x||^{2} \hfill \\ - \hat{\mu }^{T} x + \delta ||x|| \hfill \\ \end{aligned} \right) \\ \end{aligned} $$

(RMV-upper)

RMV-upper produces the efficient solutions which are upper robust efficient solutions.

• (b) Computing lower robustly efficient solutions

According to Definitions 3.5 and 3.6, it is easily fund that lower robust efficiency is contrary to upper robust efficiency. For this reason, in borrowing the idea of robust counterpart for UMO problem (see Ehrgott et al. (2014)), lower robust efficient solutions are achieved by constructing lower robust counterpart for UMO which is analytically given by

$$ \begin{aligned} \min_{{x \in {\mathcal{X}}}} \min_{\zeta = (\mu ,\varSigma )} f(x,\zeta ) & = \min_{{x \in {\mathcal{X}}}} \min_{{(\mu ,\varSigma ) \in U_{\delta } (\hat{\mu },\hat{\varSigma })}} \left( \begin{aligned} x^{T} \varSigma x \hfill \\ - \mu^{T} x \hfill \\ \end{aligned} \right) \\ & = \min_{{x \in {\mathcal{X}}}} \left( \begin{aligned} x^{T} \hat{\varSigma }x - \frac{\delta }{c}||x||^{2} \hfill \\ - \hat{\mu }^{T} x - \delta ||x|| \hfill \\ \end{aligned} \right) \\ \end{aligned} $$

(RMV-lower)

Unlike to RMV-upper, RMV-lower employs to minimize the function with uncertain parameter $\zeta$ taking the value at the best case (i.e., the best scenario) and the optimization variable $x$ fixed while reducing uncertainty in the optimization problem. And the efficient solutions obtained by RMV-lower are lower robust efficient solutions.

• (c) Computing alternative robustly efficient solutions

In light of Definitions 3.9 and 3.10, alternative robust efficient solutions are associated with upper robust efficient solutions and lower robust efficient solutions. That is, alternative robust efficient solutions are gained by

$$ {\mathcal{X}}_{arse} = {\mathcal{X}}_{urse} \cap {\mathcal{X}}_{lrse} $$

(RMV-alternative)

• (d) Computing nominally efficient solutions

For the sake of comparing upper/lower/alternative robust efficient solutions to nominal efficient solutions, here, NMV portfolio optimization problem is re-written as

$$ \min_{{x \in {\mathcal{X}}}} \left( \begin{aligned} x^{T} \hat{\varSigma }x \hfill \\ - \hat{\mu }^{T} x \hfill \\ \end{aligned} \right) $$

(NMV)

4.2 Multiobjective particle swarm optimization solver

In Sect. 4.1, we give the corresponding (robust) multiobjective formulation for obtaining upper/lower/alternative/nominal (robust) efficient solutions. In terms of solving these complex formulations, there are many means of finding robustly efficient solutions to uncertain multiobjective portfolio optimization problems. In operations research and management engineering fields in particular, various scalarization methods are extensively developed and applied to identify efficient solutions (e.g., weighted sum scalarization and ε-constraint scalarization for the identification of robustly efficient solutions (see Schöttle and Werner 2009; Ehrgott et al. 2014) and max-ordering scalarization for lower robustly efficient solutions (see Ide and Köbis 2014; Köbis 2014). These scalarization methods compute the set of upper/lower robustly efficient solutions dependent on the special set Λ or ε (see Ehrgott et al. 2014); additionally, the computational cost is also dependent on the problem structure of the single-objective optimization. To this end, we wish to introduce a popular approach: multiobjective particle swarm optimization (MOPSO) for multiobjective optimization problems (see Coello et al. 2002, 2004). MOPSO involves the use of a stochastic and parallel search algorithm. In disposing of sophisticated multiobjective optimization problems with high dimension variables, complex constraints and multiple objective functions, it exhibits remarkably fast convergence and rapid parallel processing and is easily applied. MOPSO methods have been compared to other solvers (see Coello et al. 2002; Mishra et al. 2014, etc.). MOPSO has been widely used as a prevalent solver of complex optimization problems (see Wang and Liang 2008; Rabbani et al. 2010; Halassi 2016, etc.).

We now introduce the main steps of MOPSO for uncertain multiobjective portfolio optimization problems as follows:

• Method: MOPSO for NMV, RMV-UPPER, RMV-LOWER and RMV-ALTERNAL

Input: :

A set of parameters from a robust multiobjective portfolio formulation: $\hat{\sum },\hat{\mu },\delta ,c$; from robustly efficient solution sets: $X_{NMV} = X_{URMV} = X_{LRMV} = X_{ARMV} = \emptyset$ and from the set of parameters of MOPSO: the size of the population Max, maximum iteration numbers MaxIter, the inertia weight ω, and learning factors c₁ and c₂.

Step 1: :

Initialization

• (a) Initialize the population (initialize the stochastic position x(i) of each particle representing portfolio vectors of the multiobjective portfolio optimization problem).

• (b) Initialize the speed v(i) of each particle (= 0).

Step 2: :

Evaluate the fitness of each particle (objective functions are (NMV), (RMV-UPPER), and (RMV-LOWER))

Step 3: :

Store the optimal position of each particle representing nondominated solutions of the repository gbest

Step 4: :

Build hypercubes of search spaces explored and locate particles while using them as a coordinate system in which each particle’s coordinates are defined based on its objective functions

Step 5: :

Initialize the historical optimal memory pbest of each particle to travel through the entire search space (initially pbest(i) = x(i))

Step 6: :

WHILE MaxIter has not been exceeded DO

• (a) Update the speed of each particle according to the following expression:

  $$ v\left( i \right) = \omega \cdot v\left( i \right) + Rand_{1} \cdot \left( {pbest\left( i \right) - x\left( i \right)} \right) + Rand_{2} \cdot \left( {gbest\left( h \right) - x\left( i \right)} \right) $$

  (where Rand₁ is a random number in the range [0, 1] and Rand₂).

• (b) Update the position of each particle according to the following expression:

  $$ x\left( i \right) = x\left( i \right) + v\left( i \right) $$

• (c) Prevent particles in the search space from extending beyond their boundaries to prevent new solutions from violating the constraints.

• (d) Evaluate the fitness value of each particle according to its objective functions.

• (e) Update global optimal particles in the gbest alongside the geographical representation of these particles in the hypercubes.

• (f) IF the current position of the particle is better than its historical optimal position pbest(i), THEN pbest(i) = x(i).

• (g) Proceed to Step 6.

END WHILE

X_NMV= gbest (obtained from (NMV)), X_URMV= gbest (obtained from (RMV-UPPER)), X_LRMV= gbest (obtained from (RMV-LOWER)), and X_ARMV (obtained from (RMV-ALTERNAL)).

Output: :

$X_{NMV} ,X_{URMV} ,X_{LRMV} \;{\text{and}}\;X_{ARMV} .$

5 Illustrations of robust multiobjective portfolio efficient solutions

We present two examples to demonstrate the influence of set order relations on a multiobjective portfolio optimization problem. Firstly, a simple example is used to identify the relationships between robust efficiency loss based on set order relation and three fixed parameters of the optimization problem; then, a practical example from the real stock market is used to illustrate the performance of the mean–variance portfolio optimization problem based on set order relation.

5.1 A simple example

At first, assume there are $n = 5$ assets to be invested; their nominal parameters (i.e., expected returns and volatilities) are shown in the following:

$$ \begin{aligned} \hat{\mu } & = (0.050,0.055,0.060,0.065,0.070)^{T} , \\ \hat{\sigma } & = (0.100,0.125,0.150,0.175,0.200)^{T} . \\ \end{aligned} $$

The correlation coefficients of pairwise returns are given by $\hat{\rho } = 0.5$; and the feasible region of portfolio weighted vectors is denoted as ${\mathcal{X}} = \{ x \in {\mathbb{R}}_{ + }^{n} |x^{T} 1 = 1\}$. Further, for uncertain parameter $(\mu ,\varSigma )$, we use the preceding ellipsoid uncertain set whose parameter values are set by $\delta = 0.0075$ and $c = 2$ (see Fliege and Werner 2014).

The results of NMV, RMV-upper, RMV-lower and RMV-alternative are illustrated in Fig. 2. Furthermore, we set the number of assets to 3, 10 and 20 as is shown in Figs. 3, 4 and 5, respectively. From Figs. 2, 3, 4, and 5, it is evident that upper/lower/alternative robust efficient frontiers are closer to the nominal efficient frontier with an increasing of the number of assets. Simultaneously, it also illustrates that increasing the number of assets in the portfolio can improve risks and revenues of RMV-upper and RMV-lower. That is, with the number of assets in the portfolio increases, upper/lower/alternative robust efficiency loss decreases. Such explicitly implies that robust efficiency loss is negatively related to the number of assets in the portfolio. Here, there are two assumptions which need be pointed out: all of the correlation coefficients of pairwise returns are fixed (i.e., $\hat{\rho } = 0.5$); and all expected returns are positive. Whether or not the above results remain unchanged when these assumptions changed requires further investigation.

Fig. 2

Efficient frontier when the number of assets is $n = 5$

Fig. 3

Efficient frontier when the number of assets is $n = 3$

Fig. 4

Efficient frontier when the number of assets is $n = 10$

Fig. 5

Efficient frontier when the number of assets is $n = 20$

Next, the influences of two parameters $(\delta ,c)$ in the ellipsoid uncertain set are investigated on the efficient frontier and robust efficiency loss. We take $(\delta ,c) = (0.0075,2)$ as the reference value (see Fliege and Werner 2014), and keep the number of assets $n = 5$ unchanged. Then, the case of $\delta = 0.075$ and the value $c$ unchanged is illustrated in Fig. 6.

Fig. 6

$\delta = 0.075$ and $c = 2$

Oppositely, the case of $c = 20$ and $\delta$ unchanged is depicted in Fig. 7. Alternatively, when $\delta$ and $c$ are simultaneously decreased (i.e., $\delta = 0.00075$ and $c = 0.2$) or simultaneously enlarged (i.e., $\delta = 0.075$ and $c = 20$), the changes drastically occur (see Figs. 8 and 9, respectively).

Fig. 7

$\delta = 0.0075$ and $c = 20$

Fig. 8

$\delta = 0.00075$ and $c = 0.2$

Fig. 9

$\delta = 0.075$ and $c = 20$

Comparisons of Figs. 2, 6, and 9 show that the radius of ellipsoid uncertainty set heavily affects upper robust efficient frontier. That is, with the increase of the radius, upper robust efficient frontier will be farther from the nominal efficient frontier (i.e., upper robust efficiency loss becomes larger); meanwhile, the length of upper robust efficient frontier gets shorter (i.e., the number of upper robust efficient solutions becomes rarer). Such implies that upper robust efficiency loss is positively related to the radius of ellipsoid uncertainty set. Furthermore, lower/alternative robust efficient frontier is sensitive to the scaling factor of ellipsoid uncertainty set. In other words, lower/alternative robust efficient frontier is closer to the nominal efficient frontier with the increase of the scaling factor. Such suggests that lower/alternative efficiency loss is negatively linked with the scaling factor. Additionally, the number of alternative robust efficient solutions decreases while the radius increases.

5.2 A practical example based on real market data

In this section, we will investigate the performance of upper/lower/alternative robust efficient solutions via the data from the real stock market; and the performance of MOPSO is also compared to the state-of-art solvers, namely NSGA-II (see Deb et al. 2000) and SPEA2 (see Zitzler et al. 2001).

We randomly select the daily close prices of 10 stocks from the Chinese stock market denoted as S1… S10. These data cover January 1, 2006 to December 31, 2010; and the entire period is also divided into three sub-periods: a bull market from January 1, 2006 to October 31, 2007, a bear market from November 1, 2007 to October 31, 2008, and a steady market from November 1, 2008 to December 31, 2010 (descriptive statistics are shown Table 3 of the Appendix). For a bull market, we use 315 observations from January 1, 2006 to April 30, 2007 for our in-sample analysis and 121 observations from May 1, 2007 to October 31, 2007 for our out-of-sample analysis. Likewise, for a bear market, we use 160 observations from November 1, 2007 to June 30, 2008 for our in-sample analysis and 83 observations from July 1, 2008 to October 31, 2008 for our out-of-sample analysis. For a steady market, we use 306 observations from November 1, 2008 to January 31, 2010 for our in-sample analysis and 221 observations from February 1, 2010 to December 31, 2010 for our out-of-sample analysis.

Each sub-period in-sample efficient frontier of RMV-upper/RMV-lower/RMV-alternative and NMV is shown in Figs. 10, 11, 12, respectively. It is evident that upper robust efficient frontier varies considerably at each sub-period. Especially, the number of lower robust efficient solutions is extremely rare, which is contrary to the results obtained in Sect. 5.1. The reason is that in the real stock market the correlation coefficients of pairwise returns are not fixed; however, they are invariable and non-negative (i.e., $\hat{\rho } = 0.5$) in Sect. 5.1. Such further suggests that lower robust efficient solutions are sensitive to the correlation coefficients of pairwise returns. On the aspect of robust efficiency loss, lower robust efficiency loss is larger than upper robust efficiency loss. Additionally, from Lemmas 3.3, 3.7, 3.11 and 3.13, upper/lower/alternative robust weak efficient solutions are trivial in the real stock.

Fig. 10

Robust efficient frontier for a bull market

Fig. 11

Robust efficient frontier for a bear market

Fig. 12

Robust efficient frontier for a steady market

Now, we still use the data from the real stock market to test the computing performance; at same time, NMV, RMV-upper and RMV-lower are chosen as test functions. For each of them, their running parameters are completely same in population size, number of iterations and repository that are 100,300 and 50, respectively; about the implications of these running parameters, the interesting readers can refer to the related literature.

The figures from Figs. 13, 14, and 15 show that SPEA2, MOPSO and NSGA-II produce efficient frontiers by solving NMV, RMV-upper and RMV-lower, respectively. And the average running time of the three algorithms are seen in Table 1. Furthermore, to satisfy more practical needs, cardinality constraints are imposed on the above test functions with the original constraints unchanged. Cardinality constraints contain the limitations of the number of stock invested in portfolio (here, 9 for the maximum number and 2 for the minimum number). The resulting functions become quadratic mixed-integer optimization problems (denoted by NMV-qmi, RMV-upper-qmi and RMV-lower-qmi, respectively). The results obtained by three algorithms via solving these complex functions are indicated in Table 1 and Figs. 16, 17, and 18.

Fig. 13

Efficient frontiers produced by SPEA2, MOPSO and NSGA-II for NMV

Fig. 14

Efficient frontiers produced by SPEA2, MOPSO and NSGA-II for RMV-upper

Fig. 15

Efficient frontiers produced by SPEA2, MOPSO and NSGA-II for RMV-lower

Table 1 The average running time (in s) for SPEA 2, MOPSO and NSGA-II

Fig. 16

Efficient frontiers produced by SPEA2, MOPSO and NSGA-II for NMV-qmi

Fig. 17

Efficient frontiers produced by SPEA2, MOPSO and NSGA-II for RMV-upper-qmi

Fig. 18

Efficient frontiers produced by SPEA2, MOPSO and NSGA-II for RMV-lower-qmi

It is obvious that MOPSO occupies competitive advantages in the average running time and the quality of efficient solutions compared to the other algorithms. Also, the number of efficient solutions obtained by NMV-qmi, RMV-upper-qmi and RMV-lower-qmi is less than the one by NMV, RMV-upper and RMV-lower, respectively. But, in the shape of efficient frontiers the whole difference is not greater.

Next, in order to investigate the portfolio performance of the out-of-example analysis, we arbitrarily select one or more solutions from nominal/upper/lower/alternative (robust) efficient solutions set obtained by NMV-qmi, RMV-upper-qmi, RMV-lower-qmi and RMV-alternative-qmi (composed of the intersection of RMV-upper-qmi and RMV-lower-qmi). This procedure need successively test each efficient solution in their corresponding solution set, i.e., ${\mathcal{X}}_{nmv}$, ${\mathcal{X}}_{urse}$, ${\mathcal{X}}_{lrse}$ and ${\mathcal{X}}_{arse}$. Then, for each constructed portfolio by the selected efficient solution, out-of-sample returns are computed at each sub-period; portfolio performance of the out-of-sample is given in Table 2. There is not an efficient solution that is repeatedly selected at the three sub-periods. This result does not fully coincide with the conclusions of Ide and Köbis (2014) and Ide et al. (2014). Because of the sacrifice of robust efficiency loss, lower robust efficient solutions construct the investment strategy that can provide the returns of portfolio as high as 0.09% at the bull market. However, at the same market the investment strategy of upper robust efficient solutions produce the negative returns of portfolio owing to their too conservative. At the steady market, the investment strategy of nominal efficient solutions seem to be very well, its loss of portfolio returns being the fewest (− 0.04%) but the highest risk (6.71%). as well, at the bear market the portfolio returns generated by lower robust efficient solutions is same with those by alternative robust efficient solutions; but the risk of the former is 1.69% higher than that of the latter. Such conclusion is just as Ide and Köbis (2014) suggested.

Table 2 Portfolio performance of the out-of-sample period for the investment strategies from various different efficient solutions

We now describe the tendency curves of cumulative returns for these efficient solutions at each sub-period (see Figs. 19, 20 and 21). From these curves the above observations can be also confirmed. For example, at the steady market and at the earlier stage of the bear market, investment strategies of alternative robust efficient solutions perform the best. But, at this time lower robust efficient solutions fail to be popular by the investors. Inversely, at the bull market they are very attractive in that they can produce better outcomes than the other solutions at the tendency of the stock market being optimistic. Meanwhile, at the steady market all robust efficient solutions are inferior to nominal efficient solutions.

Fig. 19

Cumulative returns for the bull market. NMV represents the cumulative returns from NMV portfolio optimization problem with budget and cardinality constraints; similarly, RMV-upper represents the cumulative returns from RMV-upper portfolio optimization problem with budget and cardinality constraints; RMV-lower represents the cumulative returns from RMV-lower portfolio optimization problem with budget and cardinality constraints; RMV-alternative represents the cumulative returns from RMV-alternative portfolio optimization problem with budget and cardinality constraints; hereinafter

Fig. 20

Cumulative returns for a steady market

Fig. 21

Cumulative returns for a bear market

The above results are originated from our definitions for efficient solution based on set order relations. In the other words, set order relations define the efficient solutions which are more suitable for the different market situations (i.e., bull market, steady market, or bear market). Thus, according to the tendency of stock market, the investors can select the suitable efficient solutions and construct portfolio strategy to enhance the returns of portfolio and reduce the risk.

6 Conclusions

To deal with uncertainties of input parameters in Markowitz’s portfolio optimization problem, for the first time we have roundly studied robust counterparts of several extreme cases via the concept of set order relations and the idea of robust counterpart introduced by Ben-Tal and Nemirovski (1998, 1999). Simultaneously, considering the computational cost of robust counterparts with complex constraints, we employ multiobjective optimization approach (i.e., MOPSO) to obtain (robust) efficient solutions. Their portfolio performance and basic properties in real stock market are further investigated. And some important results are observed as follows.

At the aspect of the properties of (robust) efficient solutions and the inherent parameters, we construct a numerical experiment in gist of Fliege and Werner (2014) but more complex. The aim is to roughly discovery the dynamic relationships between (robust) efficient solutions and the inherent parameters through the numerical experiments rather than through the mathematic derivations. Our experimental results illustrate that the size of assets in a portfolio and the parameters (i.e., the radius and scaling factor) in ellipsoid uncertainty set significantly influence on robust efficient frontier and robust efficiency loss. For example, the increase of the radius will lead to upper robust efficient frontier gradually becoming shorter as well as the increase of robust efficiency loss. Conversely, robust efficiency loss will reduce due to increase the scaling factor and/or the size of assets.

At the other aspect of portfolio performance of (robust) efficient solutions, a compromising of the inherent parameters is achieved at according to the preceding numerical experiment. Finally, the practical example tells such fact that the investment strategies of upper/lower/alternative/nominal (robust) efficient solutions have their own advantages in the real stock market. Generally speaking, at the bull market lower efficient solutions can bring about more the returns of portfolio, compared to the other efficient solutions. Simultaneously, the investment strategies of alternative robust efficient solutions are desirable with the lowest risk at the bear market. However, at the steady market nominal efficient solutions’ investment strategies behave very well. Surprisely, portfolio performance of upper robust efficient solutions is exceptionally poor at any market.

These significant outcomes further explain that in the real stock market each of (robust) efficient solutions can be recommended to construct the advisable portfolio according to the status of stock market (i.e., bull market, bear market, or steady market). Evidently, the introduction of set order relations to uncertain mean–variance portfolio optimization problem is highly meaningful. Additionally, it is also pointed out that MOPSO is a desirable solver for the sophisticated portfolio optimization problems.

Appendix

See Table 3.

Table 3 Descriptive statistics of stock returns