Solving the maximum vertex weight clique problem via binary quadratic programming

Abstract

In recent years, the general binary quadratic programming (BQP) model has been widely applied to solve a number of combinatorial optimization problems. In this paper, we recast the maximum vertex weight clique problem (MVWCP) into this model which is then solved by a probabilistic tabu search algorithm designed for the BQP. Experimental results on 80 challenging DIMACS-W and 40 BHOSLIB-W benchmark instances demonstrate that this general approach is viable for solving the MVWCP problem.

1 Introduction

Given an undirected graph $G=(V,E)$ with vertex set V and edge set E, a clique is a set of vertices $C\subseteq V$ such that every pair of distinct vertices of C is connected with an edge in G, i.e., the subgraph generated by C is complete. The maximum clique problem (MCP) is to find a clique of maximum cardinality. An important generalization of the MCP, known as the maximum vertex weight clique problem (MVWCP), arises when each vertex i in G is associated with a positive weight $w_{i}$. The MVWCP aims to find a clique of G with the maximum $\sum _{i\in {C}} w_{i}$. It is clear that the MCP is a special case of the MVWCP with $w_{i}=1$ for each vertex.

The MCP is computationally difficult given that its associated decision problem is known to be NP-complete (Garey and Johnson 1979). As a generalization of the MCP, the MVWCP has at least as the same computational complexity as the MCP. Like the MCP, the MVWCP has important applications in many domains like computer vision, pattern recognition and robotics (Ballard and Brown 1983).

To solve these clique problems, a variety of solution algorithms have been reported in the literature. Examples of exact methods based on the general Branch-and-Bound (B&B) or Branch-and-Cut methods for the MCP (or its equivalent maximum stable set problem) can be found in Carraghan and Pardalos (1990), Konc and Janĕzi c̆ (2007), Li and Quan (2010), Macreesh and Prosser (2013), Östergård (2002), Rebennack et al. (2011), Rebennack et al. (2012), Segundo et al. (2011), and Tomita and Kameda (2007). For the MVWCP, some exact algorithms are tightly related to the corresponding algorithms designed for the MCP (Babel 1994; Östergård 2001) while other B&B based methods can be found in Warren and Hicks (2006). On the other hand, a number of heuristic algorithm have also been proposed to find sub-optimal solutions to the MVWCP, including an augmentation algorithm (Manninno and Stefanutti 1999), a distributed computational network algorithm (Bomze et al. 2000), a trust region technique algorithm (Busygin 2006), a phased local search algorithm (Pullan 2008), a multi-neighborhood tabu search algorithm (Wu et al. 2012), and a breakout local search algorithm (Benlic and Hao 2013). For an updated recent review of algorithms for these clique problems, the reader is referred to Wu and Hao (2015).

During the past decade, binary quadratic programming (BQP) has emerged as a unified model for numerous combinatorial optimization problems, such as max-cut (Kochenberger et al. 2013; Wang et al. 2013), set partitioning (Lewis et al. 2008), set packing (Alidaee et al. 2008), generalized independent set (Kochenberger et al. 2007) and maximum edge weight clique (Alidaee et al. 2007). A review of the additional applications and the reformulation procedures can be found in Kochenberger et al. (2004, 2014). Using the BQP model to solve the targeted problem has the advantage of directly applying an algorithm designed for the BQP rather than resorting to a specialized solution method. Moreover, this approach proves to be competitive for several problems compared to specifically designed algorithms (Alidaee et al. 2007; Kochenberger et al. 2013; Lewis et al. 2008; Wang et al. 2013).

There exists several studies on the application of the BQP model to solve the classic MCP (Kochenberger et al. 2014; Pajouh et al. 2013; Pardalos and Rodgers 1992). However, for the more general MVWCP, no computational study has been reported in the literature using the BQP model. In this paper, we investigate for the first time the application of the BQP model to the MVWCP and solve the resulting BQP problem with the probabilistic tabu search algorithm (BQP-PTS) designed for the BQP (Wang et al. 2013). Experimental results on 80 challenging DIMACS-W and 40 BHOSLIB-W instances demonstrate that this general BQP approach with the PTS algorithm performs quite well in terms of solution quality at the price of more computing time for some benchmark instances.

The rest of this paper is organized as follows. Section 2 illustrates how to transform the MVWCP into the form of the BQP. Section 3 presents our probabilistic tabu search algorithm to solve the transformed BQP model. Section 4 report the computational results and comparisons with other state-of-the-art algorithms in the literature. The paper concludes with Sect. 5.

2 Transformation to the BQP model

2.1 Linear model for the MVWCP

Given an undirected graph $G=(V,E)$ with vertex set V and edge set E, each vertex associated with a positive weight $w_{i}$, the binary linear programming model for the MVWCP can be formulated as follows (Sengor et al. 1999):

$$\begin{aligned} \begin{array}{rl} Max&{} f(x) = \sum \limits _{i=1}^{n} w_{i}x_{i}\\ \text {subject to:}&{} x_{i}+x_{j} \le 1, \ \forall \{v_{i},v_{j}\}\in \overline{E}\\ &{} x_{i}\in \{0,1\}, i\in \{1,\ldots ,n\} \end{array} \end{aligned}$$

(1)

where $n=|V|$, $x_i$ is the binary variable associated to vertex $v_i$, $\overline{E}$ denotes the edge set of the complementary graph $\overline{G}$.

Notice that if $w_i=1$ ($i\in \{1,\ldots ,n\}$), Eq. (1) turns into the linear model of the classic maximum clique problem.

2.2 Nonlinear BQP alternative

The linear model of the MVWCP can be recast into the form of the BQP by utilizing the quadratic penalty function $g(x)=Px_{i}x_{j}$ ($x_{i}$ is binary, $i\in \{1,\ldots ,n\}$) to replace the inequality constraint of the MVWCP where P is a negative penalty scalar. Since the inequality constraint $x_{i}+x_{j} \le 1$ implies that $x_{i}$ and $x_{j}$ cannot receive value 1 at the same time, the infeasibility penalty function g(x) will equal to 0 if the inequality constraint is satisfied; otherwise g(x) will take a large penalty value 2P. To construct the nonlinear BQP model, each inequality constraint is replaced by the penalty function g(x) which is added to the linear objective of Eq. (1) and the nonlinear BQP model can be formulated as follows:

$$\begin{aligned} \begin{array}{ll} Max&{} xQx = \sum \limits _{i=1}^{n} w_{i}x_{i}+\sum \limits _{i=1}^{n}\sum \limits _{j=1,j \ne i}^{n} w_{ij}x_{i}x_{j}\\ &{}x_{i}\in \{0,1\}, i\in \{1,\ldots ,n\} \end{array} \end{aligned}$$

(2)

where $w_{ij}=P$ if $\{v_{i},v_{j}\} \in \overline{E}$ and 0 otherwise.

This formulation is one of many nonlinear reformulations of the MVWCP and has been studied in previous work like Horst et al. (1995). The quadratic function will have the same objective value as the linear form subject to all penalty items equaling to 0, indicating that all constraints are satisfied. According to Eq. (2), any violated constraint, i.e., for each $\{v_{i},v_{j}\} \in \overline{E}$, in a solution will add a penalty value 2P to the objective value. Thus, simply setting $|P| > 0.5\sum _{i=1}^{i}w_{i}$, where each linear objective function coefficient $w_{i}>0$, will enable an infeasible solution to get a large penalty value. Actually it suffices to set a smaller $|P|>0.5w^{m}$ ($w^{m}$ is the maximal value among all $w_{i},\ i \in \{1,\ldots , n\}$). Under this setting, a good decision for improving an infeasible solution would be to remove vertices associated with violated constraints, making constraints gradually reduced and finally an infeasible solution become feasible. Consider that the quadratic penalty function should be negative under the case of a maximal objective, we select $P=-1000$ for the MVWCP benchmark instances tested in our experiments. With this choice, for any optimal solution x of problem (2), $g(x)=0$ holds. In other words, the subgraph constructed by the variables with the assignment of 1 in the optimized solution x forms a clique. An illustrative example of this transformation is given in Appendix. Since Eq. (2) corresponds to the well-known BQP model, any algorithm designed for solving the BQP can be readily used to solve the MVWCP. In our case, we apply a probabilistic tabu search algorithm described in the next section.

3 Probabilistic tabu search algorithm

Metaheuristics are often used to solve hard optimization problems, such as quasi-human based heuristics (He and Huang 2010; Wu et al. 2002), variable neighborhood search (Hansen and Mladenović 2001), ant colony algorithm (Dorigo 1997), probabilistic tabu search (Glover 1989; Xu et al. 1996), etc. In this paper, we solve the MVWCP directly in the nonlinear BQP form as expressed in Eq. (2) by adapting our previous probabilistic tabu search algorithm (BQP-PTS) designed for the BQP (Wang et al. 2013). BQP-PTS is a multistart procedure, consisting of a greedy probabilistic solution construction phase and a sequel tabu search phase to optimize the objective function. These two phases proceed iteratively until a stopping condition is satisfied. Below we summarize the main ingredients of the BQP-PTS algorithm.

3.1 Greedy probabilistic construction of initial solutions

We construct a new solution for the general BQP model according to a greedy probabilistic construction heuristic. The construction procedure consists of two phases: one is to adaptively and iteratively select some variables to receive the value 1; the other is to assign the value 0 to the remaining variables. The pseudo-code of this construction procedure is shown in Algorithm 1.

First, the partial solution is set to be empty and all the variables of the problem instance are put into the set of the remaining variables VS. At each iteration we construct a candidate list CL such that CL is a subset of VS and each variable in CL has a positive objective function increment OFI. Then we choose one variable from CL with a probability of 1 / |CL| and assign it with the value 1. This variable with its assignment value is added into the partial solution and is removed from VS. This process continues until CL becomes empty. The last step is to assign the remaining variables in VS with value 0.

To quickly compute the objective function increment OFI, we maintain a vector IV, with each entry $IV_{i}$ recording the objective function increment when putting a variable $x_{i}$ with the value 1 into the partial solution. Initially, IV is computed as $w_{i}$ since the initial partial solution is empty. Once a variable $x_{s}$ joins into the partial solution, then each such entry $IV_{i}$ with its corresponding variable belonging to the set of the remaining variables VS is updated as $IV_{i} = IV_{i} + 2w_{si}$. Because of this additional vector, the complexity of this construction procedure is bounded by $O(n)^2$.

Although this strategy is much simpler than that used in the original algorithm (Wang et al. 2013), it was experimentally demonstrated to be effective. Notice that seen from the side of the MVWCP, CL is the set of vertices which form a clique with those in the partial solution. This strategy of constructing an initial solution is consistent with many specific maximum clique algorithms in the literature.

3.2 Tabu search

For each initial solution generated by the greedy probabilistic construction, we apply an extended version of the tabu search algorithm described in Wang et al. (2013) to further improve its quality. The tabu search algorithm in Wang et al. (2013) uses a simple one-flip move (flipping the value of a single variable $x_{i}$ to its complementary value $1-x_{i}$) to conduct the neighborhood search. Here we not only exploit the one-flip move but also incorporate a two-flip move (flipping the values of a pair of variables ($x_{i},x_{j}$) to their corresponding complementary values ($1-x_{i},1-x_{j}$)) (Glover and Hao 2010). The above two types of moves constitute the neighborhood structures N1 and N2.

One drawback of an N2 move is the amount of time it consumes. Considerable effort is required to evaluate all the two-flip moves because the neighborhood structure N2 generates $n(n-1)/2$ solutions at each iteration. To overcome this obstacle, we employ an instance of the Successive Filter candidate list strategy of Glover and Laguna (1997) by restricting our attention to moves in N2 that can be obtained as follows. The first step is to examine all the one-flip moves of the current solution x, and if any of these moves is improving we go ahead and select it. But if no one-flip move is improving, we limit attention to one-flip moves that produce an objective function value no worse than $f(x) + 2P$, where f(x) is the objective function value of x. (Recall that we are maximizing and the penalty P is negative. This implies that the candidate one-flip moves can violate at most a single additional constraint beyond those violated by x, since a single constraint is penalized as $Px_{ij} + Px_{ji}$ and hence incurs a penalty of 2P.) Finally, only the one-flip moves that pass this filtering criterion are allowed to serve as the source of potential two-flip moves.

Tabu search typically introduces a tabu list to assure that solutions visited within a certain number of iterations, called the tabu tenure, will not be revisited (Glover and Laguna 1997). In the present study, each time a variable $x_i$ is flipped, this variable enters into the tabu list and cannot be flipped for the next TabuTenure iterations. For the neighborhood structure N1, our tabu search algorithm then restricts consideration to variables not forbidden by the tabu list. For the neighborhood structure N2, we consider a move to be non-tabu only if both variables associated with this move are not in the tabu list and only such moves are considered during the search process. According to preliminary experiments, we set $TabuTenure(i)=7+rand(5)$ where rand(5) produces a random integer from 1 to 5.

For each iteration in our tabu search procedure, a non-tabu move is chosen according to the following rules: (1) if the best move from N1 leads to a solution better than the best solution obtained in this round of tabu search, we select the best move from N1, thus bypassing consideration of N2; (2) if no such move in N1 exists, we select the best move from the combined pool of N1 and N2. A simple aspiration criterion is applied that permits a move to be selected in spite of being tabu if it leads to a solution better than the current best solution. The tabu search procedure stops when the best solution cannot be improved within a given number $\mu$ of moves and we call this number the improvement cutoff. According to a preliminary experiment on parameter tuning, $\mu$ is set to be 5000 for all the instances except for san instances for which $\mu = 10$. In fact, it was observed that for some san instances, it is more effective to restart the search than to make long tabu iterations.

In order to quickly calculate the gains of performing a move, we maintain a vector $\varDelta$ which is initialized as follows:

$$\begin{aligned} \varDelta _{i}={\left\{ \begin{array}{ll} w_{i}+\sum \nolimits _{j=1, j \ne i}^{n} 2w_{ij}x_{j} \ \ (x_{i} = 0) \\ w_{i}-\sum \nolimits _{j=1, j \ne i}^{n} 2w_{ij}x_{j} \ \ (x_{i} = 1) \\ \end{array}\right. } \end{aligned}$$

(3)

Then if a move corresponding to a one-flip move $x_{i}$ is performed, then we update the set of variables affected by this move using the following scheme (Glover and Hao 2010):

$$\begin{aligned} \varDelta _{k} = {\left\{ \begin{array}{ll} -\varDelta _{k} \ \ (k = i) \\ \varDelta _{k} - 2w_{ik} \ \ (k \ne i, x_{k} = x_{i}) \\ \varDelta _{k} + 2w_{ik} \ \ (k \ne i, x_{k} = 1- x_{i}) \\ \end{array}\right. } \end{aligned}$$

(4)

If a move corresponding to a two-flip move ($x_{i}, x_{j}$) from the neighborhood N2 is performed, then we update the set of variables affected by this move using the following scheme (Glover and Hao 2010):

$$\begin{aligned} \varDelta _{k} ={\left\{ \begin{array}{ll} -\varDelta _{k} - 2w_{ij} \ \ (k = i \ or \ k = j) \\ \varDelta _{k} - 2w_{ik} + 2w_{jk}\ \ (k \ne i, k \ne j, x_{k} = x_{i}, x_{k} = 1- x_{j}) \\ \varDelta _{k} + 2w_{ik} - 2w_{jk}\ \ (k \ne i, k \ne j, x_{k} = x_{j}, x_{k} = 1- x_{i}) \\ \end{array}\right. } \end{aligned}$$

(5)

Given the fact that the BQP-PTS algorithm is designed for the general BQP model (instead of the MVWCP model studied in the paper), the above presentation of BQP-PTS does not refer to the MVWCP. However, it is possible to give an interpretation of some operators used by BQP-PTS related to the MVWCP. For instance, the one-flip move for the BQP model can be considered as moving a single vertex in or out the current solution (clique). On the other hand, such an interpretation will change depending on the target problem under consideration.

4 Experimental results

4.1 Benchmark instances

We used two sets of benchmark instances for our computational assessments. The first set concerns 80 DIMACS-W instances proposed in Pullan (2008), which were adapted from the well-known DIMACS instances¹ for benchmark purpose to evaluate maximum clique algorithms. The second set is composed of 40 BHOSLIB-W instances,² which were adapted from the BHOSLIB benchmarks with hidden optimum solutions (Benlic and Hao 2013). The weighting method is to allocate weights to vertices according to the following scheme: for each vertex i, $w_i$ is set equal to $i\,mod\,200+1$, which enables us to exactly replicate the instances without difficulty.

The DIMACS benchmarks comprise the following families of graphs: Random graphs (Cx.y and DSJCx.y of size x and density 0.y), Steiner triple graphs (MANNx with up to 3321 nodes and 5,506,380 edges), Brockington graphs with hidden optimal cliques (brockx_1, brockx_2, brockx_3, brockx_4 of size x), Gen random graphs with a unique known optimal solution (genx_p0.9_z of size x), Hamming and Johnson graphs stemming from the coding theory, Keller graphs based on Keller’s conjecture on tilings using hypercubes (with up to 3361 verices and 4,619,898 edges), P-hat graphs (p_hatx-z of size x), San random graphs (sanx_y_z of size x and density 0.y) and Sanr random graphs (sanrx-z with size x and density z). The BHOSLIB-W benchmarks have sizes ranging from 450 vertices and 17,794 edges up to 1534 vertices and 127,011 edges.

4.2 Experimental protocol

Our probabilistic tabu search algorithm for the BQP model was programmed in C++ and compiled using GNU GCC on a PC with Pentium 2.83 GHz CPU and 2 GB RAM. We used the CPU clocks as the stop condition of our algorithm. Given the stochastic nature of BQP-PTS, each problem instance was independently solved 100 times.

For the DIMACS-W benchmarks, the time limit for a single run was set as follows: 1 min for instances of hamming, gen, c-fat, johnson, p_hat, sanr, keller except keller6 and mann_a9; 5 min for instances of brock, dsjc, san and C families except C2000.5, C2000.9, C4000.5; 60 min for C2000.5, C2000.9 and keller6; 600 min for C4000.5, mann_a27, mann_a45, mann_a81. For the BHOSLIB benchmarks, the time limit was set as 60 min.

4.3 Experimental results

In this section, we verify the effectiveness of our BQP approach with the BQP-PTS algorithm on the 80 DIMACS-W instances and 40 BHOSLIB-W instances. Furthermore, we compare this general BQP approach with three recent and powerful heuristics which are specially dedicated to the MVWCP: the PLS$_W$ algorithm (Pullan 2008), the multi-neighborhood tabu search algorithm MN/TS (Wu et al. 2012) and the breakout local search BLS (Benlic and Hao 2013).

Table 1 Computational comparisons of the BQP-PTS approach with the PLS, MS/TS and BLS algorithms on the set of DIMACS-W instances

Table 2 Computational comparisons of the BQP-PTS approach with the MS/TS and BLS algorithms on the set of BHOSLIB-W instances

Table 1 presents the experimental results for the DIMACS-W benchmarks, where the columns under headings of BQP-PTS, PLS$_W$, MN/TS and BLS list respectively the best solution values Best obtained by each algorithm, number of times to reach Best over 100 runs Succ., and the average CPU time Time (in seconds) to reach Best. Notice that an entry with ${<}\epsilon$ signifies the average CPU time was less than 0.01 second and NA signifies the results are unavailable. The solution values inferior to the best known ones are marked in bold.

From Table 1, we observe that BQP-PTS obtains 76 best solutions for the evaluated 80 instances, better than 67 of PLS$_W$ and competitive with 77 of MN/TS and 78 of BLS. For the 2 failed cases, BQP-PTS achieves the second best solutions. In addition, BQP-PTS has a success rate of 100 % to reach the best solutions for 64 instances, 12 more than PLS$_W$ but 4 and 5 less than MN/TS and BLS, respectively. Finally, BQP-PTS reaches the best known results within a reasonable time (less than 30 min) for most instances, except for 7 instances of C and MANN families. The long computing time for these instances could be attributed to their difficulty (in fact, the reference MVWCP heuristics also need longer time to attain their best solutions for these instances than for other instances). In particular, PLS$_W$ can only attain its indicated best values for some of these C and MANN instances (as well as some other instances) under a long and relaxed time condition (indicated by ‘–’ in Table 1). Moreover, unlike the dedicated MVWCP algorithms which incorporate problem specific implementation to ensure their search efficiency, BQP-PTS, as a general solver, does not benefit from such advantages.

Table 2 shows the results of the BQP-PTS approach compared to those of the MN/TS and BLS algorithms for the BHOSLIB-W benchmarks (the PLS$_W$ algorithm does not report results for the BHOSLIB-W benchmarks). Table 2 lists the best solution values Best, number of times hitting Best over 100 runs Succ., the average solution values and the average CPU time Time (in seconds) to reach Best for each algorithm. From Table 2, we observe that BQP-PTS is able to attain the best known results for all the 40 instances as BLS does while MN/TS misses two best values (frb56-25-2 and frb56-25-5). In addition, BQP-PTS has a success rate of 100 % to reach the best known results for 22 instances, better than MN/TS for 8 instances and BLS for 14 instances. Moreover, BQP-PTS obtains better average solution values than MN/TS and BLS for 32 and 26 instances, while requiring slightly more computing time, particularly compared to MN/TS.

Finally, we also evaluated our BQP-PTS approach for the (unweighted) maximum clique instances. Without bothering to show tabulated results, we observed that BQP-PTS was able to attain the best known results for 77 of 80 DIMACS instances except for C2000.9 (79 vs 80), MANNa_45 (344 vs 345), MANNa_81 (1098 vs 1100) and for all the 40 BHOSLIB instances. Such a performance can be considered as quite good even compared to the best performing MCP algorithms presented in the recent review (Wu and Hao 2015). However, our BQP-PTS algorithm requires more computing time than specific MCP algorithms, in particular when it is applied to solve some very difficult instances.

5 Conclusion

We recast the maximum vertex weight clique problem (MVWCP) into the binary quadratic programming (BQP) model, which was solved by a probabilistic tabu search algorithm. Experiments on two sets of challenging DIMACS-W and BHOSLIB-W benchmarks indicate that this general BQP approach is viable for solving the MVWCP problem. In particular, without incorporation of domain specific knowledge, this approach was able to attain the best known results for 76 out of 80 DIMACS-W instances and for all the 40 BHOSLIB-W instances within reasonable computing times. For the conventional maximum clique problem, the BQP approach achieved similar performances by attaining the best known results for 77 out of 80 DIMACS instances and for all the 40 BHOSLIB instances. However, our BQP approach is more time consuming than specific algorithms especially for some very difficult instances and some parameters need to be tuned to achieving its best performance. These computational outcomes demonstrate that the general BQP model constitutes an interesting alternative to solve these clique problems without calling for specific heuristics.

For future consideration, it would be interesting to explore using the probabilistic tabu search design not only within the restart part of our method, but also periodically within the improving part of our method which currently consists of a relatively simple form of tabu search. Another interesting research line is to investigate automatic parameter tuning techniques to obtain a general and parameter free BQP solver.

Appendix

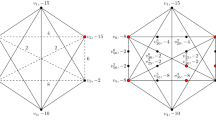
To illustrate the transformation from the MVWCP to the BQP, we consider the following graph (see Fig. 1):

Fig. 1

A graph sample

Its linear formulation according to Eq. (1) is:

$$\begin{aligned} \begin{aligned} Max \ \ f(x)=2x_{1}+3x_{2}+4x_{3}+5x_{4}+2x_{5}+3x_{6} \\ \text {s.t.}\ \ \ \ x_1+x_3 \le 1;\ \ \ \ \ \ \ \ \ \ x_1+x_4 \le 1; \\ x_1+x_6 \le 1;\ \ \ \ \ \ \ \ \ \ x_2+x_4 \le 1;\\ x_2+x_6 \le 1;\ \ \ \ \ \ \ \ \ \ x_3+x_5 \le 1;\\ x_3+x_6 \le 1;\ \ \ \ \ \ \ \ \ \ x_5+x_6 \le 1. \end{aligned} \end{aligned}$$

(6)

Choosing the scalar penalty $P=-15$, we obtain the following BQP model:

$$\begin{aligned} Max\quad f(x)= & {} 2x_{1}+3x_{2}+4x_{3}+5x_{4}+2x_{5}+3x_{6}-30x_{1}x_{3}-30x_{1}x_{4}\nonumber \\&-30x_{1}x_{6}-30x_{2}x_{4}-30x_{2}x_{6}-30x_{3}x_{5}-30x_{3}x_{6}-30x_{5}x_{6} \end{aligned}$$

(7)

which can be re-written as:

$$\begin{aligned} \left( \begin{array}{c} x_1\ x_2 \ x_3 \ x_4 \ x_5 \ x_6 \end{array}\right) \times \left( \begin{array}{cccccc} 2 &{}0 &{}-15 &{}-15 &{}0 &{}-15 \\ 0 &{}3 &{}0 &{}-15 &{}0 &{}-15 \\ -15 &{}0 &{}4 &{}0 &{}-15 &{}-15 \\ -15 &{}-15 &{}0 &{}5 &{}0 &{}0 \\ 0 &{}0 &{}-15 &{}0 &{}2 &{}-15 \\ -15 &{}-15 &{}-15 &{}0 &{}-15&{}3 \\ \end{array}\right) \times \left( \begin{array}{c} x_1 \\ x_2\\ x_3\\ x_4\\ x_5\\ x_6 \\ \end{array}\right) \end{aligned}$$

(8)

Solving this BQP problem yields $x_3=x_4=1$ (all other variables equal zero) and the optimal objective function value is 9.