Independent sets in some classes of $S_{i, j, k}$-free graphs

Abstract

The maximum weight independent set (MWIS) problem on graphs with vertex weights asks for a set of pairwise nonadjacent vertices of maximum total weight. In 1982, Alekseev (Comb Algebraic Methods Appl Math 132:3–13, 1982) showed that the M(W)IS problem remains NP-complete on H-free graphs, whenever H is connected, but neither a path nor a subdivision of the claw. We will focus on graphs without a subdivision of a claw. For integers $i, j, k \ge 1$, let $S_{i, j, k}$ denote a tree with exactly three vertices of degree one, being at distance i, j and k from the unique vertex of degree three. Note that $S_{i,j, k}$ is a subdivision of a claw. The computational complexity of the MWIS problem for the class of $S_{1, 2, 2}$-free graphs, and for the class of $S_{1, 1, 3}$-free graphs are open. In this paper, we show that the MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair)-free graphs, by analyzing the structure of the subclasses of this class of graphs. This also extends some known results in the literature.

1 Introduction

For notation and terminology not defined here, we follow Brandstädt et al. (1999). Let $P_n$ and $C_n$ denote respectively the path, and the cycle on n vertices. If ${\mathcal {F}}$ is a family of graphs, a graph G is said to be ${\mathcal {F}}$-free if it contains no induced subgraph isomorphic to any graph in ${\mathcal {F}}$.

In a graph G, an independent set is a subset of mutually nonadjacent vertices. The maximum independent set (MIS) problem asks for an independent set of G with the maximum cardinality. The maximum weight independent set (MWIS) problem asks for an independent set of total maximum weight in the given graph G with vertex weight function w on V(G). The M(W)IS problem is well known to be NP-complete in general and hard to approximate; it remains NP-complete even on restricted classes of graphs (Corneil 1985; Poljak 1974). On the other hand, the M(W)IS problem is known to be solvable in polynomial time on several graph classes such as: chordal graphs (Frank 1976); $P_4$-free graphs (Corneil et al. 1985); perfect graphs (Grötschel et al. 1981); and $2K_2$-free graphs (Farber 1989).

In 1982, Alekseev (1982) showed that the M(W)IS problem remains NP-complete on H-free graphs, whenever H is connected, but neither a path nor a subdivision of the claw.

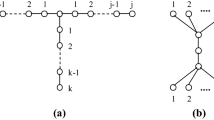
In this paper, we will focus on graphs without a subdivision of a claw. For integers $i, j, k \ge 1$, let $S_{i, j, k}$ denote a tree with exactly three vertices of degree one, being at distance i, j and k from the unique vertex of degree three. The graph $S_{1,1,1}$ is called a claw and $S_{1, 1, 2}$ is called a chair or fork. Also, note that $S_{i,j, k}$ is a subdivision of a claw.

Minty (1980) showed that the MWIS problem can be solved in polynomial time for $S_{1, 1,1}$-free graphs (or claw-free graphs), and Lozin and Milanič (2008) showed that the MWIS problem can be solved in polynomial time for $S_{1, 1,2}$-free graphs (or fork-free graphs). However, for larger $i + j + k$, the complexity status of the MWIS problem in $S_{i,j,k}$-free graphs is open. In particular, the class of $P_6$-free graphs, the class of $S_{1, 2, 2}$-free graphs, and the class of $S_{1, 1, 3}$-free graphs constitute the minimal classes, defined by forbidding a single connected subgraph on six vertices, for which the computational complexity of M(W)IS problem is unknown. Also, it is known that there is an $n^{O(\log ^2n)}$-time, polynomial-space algorithm for MWIS on $P_6$-free graphs (Lokshtanov et al. 2016). This implies that MWIS on $P_6$-free graphs is not NP-complete, unless all problems in NP can be solved in quasi-polynomial time. On the other hand, MWIS is shown to be solvable in polynomial time for several subclasses of $S_{i,j,k}$-free graphs, for $i+j+k \ge 5$ such as: ($P_6, S_{1,2,2}$, co-chair)-free graphs (Karthick and Maffray 2016); ($S_{1, 1, 3}$, banner)-free graphs (Karthick and Maffray 2015; $S_{1, 2, 2}$, bull)-free graphs (Karthick and Maffray 2015; $S_{1, 1, 3}$, bull)-free graphs (Karthick and Maffray 2016), and some classes of planar/subcubic $S_{i, j, k}$-free graphs (Alekseev and Malyshev 2009; Malyshev 2013). It is also known that the MIS problem can be solved in polynomial time for some subclasses of $S_{i, j, k}$-free graphs such as: $S_{1,2,k}$-free planar graphs and $S_{1,k,k}$-free graphs of low degree (Lozin and Milanič 2007), and $S_{2,2,2}$-free sub-cubic graphs (Lozin et al. 2015); and see Gerber et al. (2004), Le et al. (2015a, b) for several other subclasses. See Fig. 1 for some of the special graphs used in this paper.

Fig. 1

Some special graphs

In this paper, we follow the approach developed recently by Brandstädt and Giakoumakis (2015), which combines modular decomposition and clique separator decomposition, we show that the MWIS problem can be efficiently solved in the class of ($S_{1, 2, 2}, S_{1, 1,3}$, co-chair)-free graphs by analyzing the structure of the subclasses of this class of graphs. In particular, we first show that the MWIS problem can be efficiently solved in the class of ($S_{1, 2, 2}, S_{1, 1,3}$, diamond)-free graphs (Sect. 4). Using this result, we show that the MWIS problem can be efficiently solved in the class of ($S_{1, 2,2}, S_{1, 1,3}$, co-chair)-free graphs (Sect. 5). These results extends some known results for the MWIS problem in the literature such as for: $P_4$-free graphs, ($P_5$, diamond)-free graphs (Arbib and Mosca 2002), and ($P_5$, co-chair)-free graphs (Karthick 2014). A preliminary version (extended abstract) of this paper is appearing in Karthick (2016).

While the MWIS problem in co-chair-free graphs is well known to be NP-complete (Poljak 1974), note that the class of $S_{1, 1, 3}$-free graphs and the class of $S_{1, 2, 2}$-free graphs extend the class of $P_4$-free graphs, the class of claw-free graphs, the class of fork-free graphs and the class of $P_5$-free graphs. It is also known recently that the MWIS problem in $P_5$-free graphs can be solved in polynomial time (Lokshtanov et al. 2014).

2 Notation and terminology

Let G be a finite, undirected and simple graph with vertex-set V(G) and edge-set E(G). We let $|V(G)| = n$ and $|E(G)| = m$. For a vertex $v \in V(G)$, the neighborhood N(v) of v is the set $\{u \in V(G) \mid uv \in E(G)\}$, and the closed neighborhood N[v] is the set $N(v) \cup \{v\}$. The neighborhood N(X) of a subset $X \subseteq V(G)$ is the set $\{u \in V(G){\setminus } X : u$ $\text{ is } \text{ adjacent } \text{ to } \text{ a } \text{ vertex } \text{ of } X\}$. Given a subgraph H of G and $v \in V(G){\setminus } V(H)$, let $N_H(v)$ denote the set $N(v) \cap V(H)$, and for $X \subseteq V(G){\setminus } V(H)$, let $N_H(X)$ denote the set $N(X) \cap V(H)$. For any two subsets $S, T\subseteq V(G)$, we say that S is complete to T if every vertex in S is adjacent to every vertex in T.

A hole is a chordless cycle $C_k$, where $k \ge 5$. An odd hole is a hole $C_{2k+1}$, where $k \ge 2$.

The k-apple is the graph obtained from a chordless cycle $C_k$ of length $k\ge 4$ by adding a vertex that has exactly one neighbor on the cycle.

The diamond is the graph $K_4 -e$ with vertex-set $\{v_1, v_2, v_3, v_4\}$ and edge-set $\{v_1v_2, v_2v_3, v_3v_4, v_4v_1, v_1v_3\}$.

The co-chair is the graph with vertex-set $\{v_1, v_2, v_3, v_4, v_5\}$ and edge-set $\{v_1v_2, v_2v_3, v_3v_4, v_4v_1, v_1v_3, v_4v_5\}$; it is the complement graph of the chair/fork graph (see Fig. 1).

A vertex $z \in V(G)$ distinguishes two other vertices $x, y \in V(G)$ if z is adjacent to one of them and nonadjacent to the other. A set $M\subseteq V(G)$ is a module in G if no vertex from $V(G) {\setminus } M$ distinguishes two vertices from M. The trivial modules in G are $V(G), \emptyset$, and all one-vertex sets. A graph G is prime if it contains only trivial modules. Note that prime graphs on at least four vertices are connected.

A class ${\mathcal {G}}$ of graphs is hereditary if every induced subgraph of a member of ${\mathcal {G}}$ is also in ${\mathcal {G}}$. We will use the following theorem by Lozin and Milanič (2008).

Theorem 1

(Lozin and Milanič 2008) Let ${\mathcal {G}}$ be a hereditary class of graphs. If there is a constant $p \ge 1$ such that the MWIS problem can be solved in time $O(|V(G)|^p)$ for every prime graph G in ${\mathcal {G}}$, then the MWIS problem can be solved in time $O(|V(G)|^p + |E(G)|)$ for every graph G in ${\mathcal {G}}$. $\Box$

Let ${\mathcal {C}}$ be a class of graphs. A graph G is nearly ${\mathcal {C}}$ if for every vertex v in V(G) the graph induced by $V(G) {\setminus } N[v]$ is in ${\mathcal {C}}$. Let $\alpha _w(G)$ denote the weighted independence number of G. Obviously, we have:

$$\begin{aligned} \alpha _w(G)= & {} \max \{w(v) + \alpha _w(G{\setminus } N[v]) \mid v \in V(G)\}. \end{aligned}$$

(1)

Thus, whenever MWIS is solvable in time $T:= O(f(n))$ on a class ${\mathcal {C}}$, then it is solvable on nearly ${\mathcal {C}}$ graphs in time $O(n\cdot T)$ (Brandstädt and Hoáng 2007).

A clique in G is a subset of pairwise adjacent vertices in G. A clique separator (or clique cutset) in a connected graph G is a subset Q of vertices in G which induces a complete graph, such that the graph induced by $V(G) {\setminus } Q$ is disconnected. A graph is an atom if it does not contain a clique separator.

We will also use the following theorem given in Karthick and Maffray (2015).

Theorem 2

(Karthick and Maffray 2015) Let ${\mathcal {C}}$ be a class of graphs such that MWIS can be solved in time O(f(n)) for every graph in ${\mathcal {C}}$ with n vertices. Then in any hereditary class of graphs whose all atoms are nearly $\mathcal C$ the MWIS problem can be solved in time $O(n^2\cdot f(n))$. $\square$

The following notation will be used several times in the proofs. Given a graph G, let v be a vertex in G and H be an induced subgraph of $G{\setminus } N[v]$ such that v has no neighbor in H. Let $t=|V(H)|$. Then we define the following sets:

$$\begin{aligned} Q_{\ }= & {} \text{ the } \text{ component } \text{ of } G{\setminus } (V(H)\cup N(V(H))) \hbox { that contains }v, \\ A_i= & {} \{x \in V(G) {\setminus } V(H) : |N_H(x)| = i\} \ (1 \le i \le t), \\ A_i^+= & {} \{x \in A_i \mid N(x) \cap Q \ne \emptyset \}, \\ A^-_i= & {} \{x \in A_i \mid N(x) \cap Q = \emptyset \}, \\ A^+= & {} A^+_1\cup \cdots \cup A^+_t \ \text{ and } \ A^- = A^-_1\cup \cdots \cup A^-_t. \end{aligned}$$

So, $N(H) = A^+ \cup A^-$. Note that, by the definition of Q and $A^+$, we have $A^+ = N(Q)$. Hence, $A^+$ is a separator between H and Q in G.

3 Preliminary lemmas

In this section, we derive some preliminary lemmas which are needed for the later sections. See Fig. 2 for the graphs $H_i, i \in \{1, 2, \ldots , 8\}$.

Fig. 2

Graphs $H_i, i \in \{1, 2, \ldots , 8\}$ used in Lemma 1

Lemma 1

Let $G = (V, E)$ be a prime co-chair-free graph. Then G is $(H_1, H_2, H_3)$-free. Further, (i) if G is $S_{1, 2,2}$-free, then G is $(H_4, H_5)$-free, and (ii) if G is $S_{1, 1, 3}$-free, then G is $(H_4, H_6,$ $H_7, H_8)$-free.

Proof

Suppose to the contrary that G contains an induced subgraph which is isomorphic to $H_i$, for some $i \in \{1, 2, \ldots , 8\}$ (as shown in Fig. 2). Since G is prime, $\{a_1, a_2\}$ is not a module in G, so there exists a vertex $x \in V {\setminus } V(H_i)$ such that (up to symmetry) $xa_1 \in E$ and $xa_2 \notin E(G)$. Then since $\{x, a_1, b_1, b_2, a_2\}$ does not induce a co-chair in G, x has a neighbor in $\{b_1, b_2\}$.

If x is adjacent to both $b_1$ and $b_2$, then since $\{x, b_1, b_2, a_2, b_3\}$ does not induce a co-chair in $G, xb_3 \in E$, and then since $\{x, b_1, b_2, a_2, b_4\}$ does not induce a co-chair in $G, xb_4 \notin E$. But, then $\{x, a_1, b_1, b_3, b_4\}$ induces a co-chair in G, which is a contradiction. Therefore, x is adjacent to exactly one of $b_1, b_2$.

Suppose that $i \ne 7, 8$. We may assume (up to symmetry) that $xb_1 \in E$ and $xb_2 \notin E$. Since $\{x, a_1, b_1, b_2, b_4\}$ does not induce a co-chair in $G, xb_4 \notin E$, and then since $\{x, a_1, b_1, b_3, b_4\}$ does not induce a co-chair in $G, xb_3 \notin E$. Now, we prove a contradiction as follows:

• $i = 1$: Since $\{x, a_1, a_2, b_3, p\}$ does not induce a co-chair in $G, xp \in E$. But, now $\{x, a_1, b_3, b_4, p\}$ induces a co-chair in G, which is a contradiction. Thus, G is $H_1$-free.

• $i = 2$: Since $\{x, a_1, b_1, p, b_4\}$ does not induce a co-chair in $G, xp \in E$. But, now $\{x, b_1, p, a_2, b_3\}$ induces a co-chair in G, which is a contradiction. Thus, G is $H_2$-free.

• $i = 3$: Since $\{x, a_1, b_1, b_2,t\}$ does not induce a co-chair in $G, xt \notin E$, and then since $\{x, a_1, b_1, p, t\}$ does not induce a co-chair in $G, xp \in E$. Then since $\{x, b_1, p, a_2, q\}$ does not induce a co-chair in $G, xq \in E$. But, now $\{b_1, x, a_1, q, b_4\}$ induces a co-chair in G, which is a contradiction. Thus, G is $H_3$-free.

• $i = 4$: Since $\{x, a_1, b_1, b_2, p\}$ does not induce a co-chair in $G, xp \notin E$. But, then either $\{x, a_1, b_3, b_4, p, a_2\}$ induces an $S_{1, 2,2}$ in G or $\{x, a_1, b_3, b_4, p, b_2\}$ induces an $S_{1, 1, 3}$ in G, a contradiction. Thus, G is $H_4$-free.

• $i = 5$: Since $\{x, b_1, a_2, b_3, b_4, p\}$ does not induce an $S_{1, 2, 2}$ in $G, xp \in E$. But, now $\{x, p, a_2, b_3,$ $b_4, b_2\}$ induces an $S_{1, 2, 2}$ in G, which is a contradiction. Thus, G is $H_5$-free.

• $i = 6$: Since $\{x, a_1, b_1, b_2, p\}$ does not induce a co-chair in $G, xp \notin E$. But, now $\{x, b_1, a_2, b_3,$ $b_4, p\}$ induces an $S_{1, 1, 3}$ in G, which is a contradiction. Thus, G is $H_6$-free.

Suppose that $i = 7$. Note that x is adjacent to exactly one of $b_1, b_2$. Then as earlier, we have $xb_3 \notin E$ and $xb_4 \notin E$ (otherwise, in both the cases, G induces a co-chair). Now, if $xb_1 \in E$ and $xb_2 \notin E$, then since $\{x, b_1, a_2, b_3, b_4, p\}$ does not induce an $S_{1, 1, 3}$ in $G, xp \in E$. But, now $\{p, x, b_1, a_1, b_3\}$ induces a co-chair in G, which is a contradiction. Next, if $xb_2 \in E$ and $xb_1 \notin E$, then since $\{x, a_1, b_2, b_1, p\}$ does not induce a co-chair in $G, xp \in E$. But, now $\{b_4, b_3, a_1, x, p, a_2\}$ induces an $S_{1, 1, 3}$ in G, which is a contradiction. Thus, G is $H_7$-free.

Suppose that $i = 8$. Again, as earlier, we have $xb_3 \notin E$ and $xb_4 \notin E$ (otherwise, G induces a co-chair). Now, if $xb_1 \in E$ and $xb_2 \notin E$, then since $\{x, a_1, b_1, b_2, p\}$ does not induce a co-chair in $G, xp \in E$. Also, since $\{x, a_1, b_1, b_2, t\}$ does not induce a co-chair in $G, xt \notin E$, and then since $\{x, a_1, b_1, q, t\}$ does not induce a co-chair in $G, xq \in E$. But, now $\{a_2, b_1, q, x, p\}$ induces a co-chair in G, which is a contradiction. Next, if $xb_2 \in E$ and $xb_1 \notin E$, then since $\{x, b_2, p, b_3, b_4, b_1\}$ does not induce an $S_{1, 1, 3}$ in $G, xp \in E$. Also, since $\{x, a_1, b_1, b_2, t\}$ does not induce a co-chair in $G, xt \notin E$, and then since $\{x, a_1, b_2, q, t\}$ does not induce a co-chair in $G, xq \in E$. But, now $\{p, x, b_2, q, t\}$ induces a co-chair in G, which is a contradiction. Thus, G is $H_8$-free.

This completes the proof of Lemma 1. $\square$

Fig. 3

Graphs twin-$C_5, H^*$ and $C_5^*$

Lemma 2

Let $G = (V, E)$ be a prime (5-apple, $C_5^*$, diamond)-free graph. Then G is twin-$C_5$-free (see Fig. 3).

Proof

Suppose to the contrary that G contains an induced twin-$C_5$, say H, as shown in Fig. 3. Since G is prime, $\{v_2, v_2'\}$ is not a module in G, so there exists a vertex x in $V {\setminus } V(H)$ such that (up to symmetry) $xv_2' \in E$ and $xv_2 \notin E$. Then since $\{v_2', v_1, v_3, v_4, v_5, x\}$ does not induce a 5-apple in $G, xv_i \in E$, for some $i \in \{1, 3, 4, 5\}$. If $xv_1 \in E$, then since G is diamond-free, $xv_3, xv_5 \notin E$. Then since $\{v_1, v_2, v_3, v_4, v_5, x\}$ does not induce a 5-apple in $G, xv_4 \in E$, but then $\{v_1, v_2', v_3, v_4, v_5, x\}$ induces a $C_5^*$ in G, which is a contradiction. A similar contradiction arises if we assume $xv_3 \in E$. So, we may assume that $xv_1, xv_3 \notin E$. Then since G is 5-apple-free, $xv_4\in E$ and $xv_5 \in E$. Now, $\{v_1, v_2', v_3, v_4, v_5, x\}$ induces a $C_5^*$ in G, which is a contradiction. So, G is twin-$C_5$-free. $\square$

Lemma 3

(Karthick 2014) If $G = (V, E)$ is a prime (co-chair, gem)-free graph, then G is diamond-free.

4 ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond)-free graphs

In this section, we show that the MWIS problem can be efficiently solved in the class of ($S_{1, 2, 2}, S_{1, 1,3}$, diamond)-free graphs by analyzing the atomic structure of the subclasses of this class of graphs.

4.1 ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond, 5-apple, $C_5^*$)-free graphs

Theorem 3

Let $G= (V, E)$ be a prime ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond, 5-apple, $C_5^*$)-free graph. If G contains an odd hole $C_{2k+1}$, then G is claw-free.

Proof

Since G is prime, it is connected, and by Lemma , G is twin-$C_5$-free. Let C denotes a shortest odd hole $C_{2k+1}$ in G with vertices $v_1, v_2, \ldots , v_{2k+1}$ and edges $v_iv_{i+1}, v_{2k+1}v_1 \in E$, where $i \in \{1, 2, \ldots , 2k\}$ with $k \ge 2$. Then the following claim holds.

Claim 3.1

If $x \in V(G) {\setminus } V(C)$ has a neighbor on C, then there exists an i such that $N(x) \cap V(C) = \{v_i, v_{i+1}\}$.

Proof of Claim 3.1

If $k = 2$, since G is (5-apple, $C_5^*$, twin-$C_5$, diamond)-free, the claim holds. So, suppose that $k \ge 3$. To prove the claim, we prove the following:

(1):

There exists an i such that $xv_i, xv_{i+1} \in E$ and $xv_{i-1}, xv_{i+2} \notin E$.

(2):

Either $|N(x) \cap V(C)| = 2$ or $|N(x) \cap V(C)| = 4$. Moreover, there exists an i such that $N(x) \cap V(C) = \{v_i, v_{i+1}\}$ (if $|N(x) \cap V(C)| = 2$), and $N(x) \cap V(C) = \{v_i, v_{i+1}, v_j, v_{j+1}\}$, for some $j \in \{i+3, i+4, \ldots , i+2k-2\}$ (if $|N(x) \cap V(C)| = 4$).

Since x has a neighbor on C, we may assume that x is adjacent to $v_{i}$ on C. If (1) does not hold, then $xv_{i+1}, xv_{i-1} \notin E$. Then since $\{v_{i-2}, v_{i-1}, v_{i}, v_{i+1},$ $v_{i+2}, x\}$ does not induce an $S_{1, 2, 2}$ in G, we have either $xv_{i-2} \in E$ or $xv_{i+2} \in E$. We may assume, up to symmetry, that $xv_{i-2} \in E$. Then since $\{v_{i+3}, v_{i+2},$ $v_{i+1}, v_i, v_{i-1}, x\}$ does not induce a $C_5$ or an $S_{1, 1, 3}$ in G, we have $xv_{i+2} \in E$. Then since $\{v_{i+1}, v_{i+2}, x, v_{i-2},$ $v_{i-1}, v_{i-3}\}$ does not induce an $S_{1, 1, 3}$ in $G, xv_{i-3} \in E$. Then since G is diamond-free, $\{v_{i+3}, v_{i-3},$ $x, v_i, v_{i+1}, v_{i-1}\}$ induces an $S_{1, 1, 3}$ in G (if $k = 3$) or $\{v_{i-4}, v_{i-3}, x, v_i, v_{i+1}, v_{i-1}\}$ induces an $S_{1, 1, 3}$ in G (if $k \ge 4$), a contradiction. So (1) holds.

By (1), we have $\{v_i, v_{i+1}\} \subseteq N(x) \cap V(C)$ and $xv_{i-1}, xv_{i+2} \notin E$. Further, if there exists an index $j \in \{i+3, i+4, \ldots , i+2k-1\}$ such that $xv_j \in E$ and $xv_{j-1} \notin E$, then $xv_{j+1} \in E$ (for, otherwise, $\{v_{i-1}, v_i, v_{i+1}, v_{i+2}, x\} \cup \{v_{j-1}, v_j, v_{j+1}\}$ induces an $S_{1, 1, 3}$ in G). Now, if x is adjacent to a vertex $v_t$ on C, where $t \notin \{i-1, i, i+1, i+2, j-1, j, j+1, j+2\}$, then either a diamond or an $S_{1, 2, 2}$ is an induced subgraph of G, which is a contradiction. Hence $N(x) \cap V(C) = \{v_i, v_{i+1}\}$ or $N(x) \cap V(C) = \{v_i, v_{i+1}, v_j, v_{j+1}\}$, for some $j \in \{i+3, i+4, \ldots , i+2k-2\}$. So (2) holds.

Further, if $|N(x) \cap V(C)| = 4$, then G contains an odd hole $C'$ shorter than C, which is a contradiction to the choice of C. $\Diamond$

To prove the theorem, we suppose for contradiction that G contains an induced claw, say K with vertex-set $\{a, b, c, d\}$ and edge-set $\{ab, ac, ad\}$. By Claim 3.1, K cannot have more than two vertices on C. Also, at most one vertex in $\{b, c, d\}$ belongs to C. Now we have following cases (the other cases are symmetric):

• (1) $V(K) \cap V(C) = \{a, d\}$: Let y be the other neighbor of a on C. Then by Claim 3.1, $by, cy \in E$. But, now $\{a, b, c, y\}$ induces a diamond in G, which is a contradiction.

• (2) $V(K) \cap V(C) = \{a\}$: We may assume (wlog.) that $a = v_1$. Then by Claim 3.1, at least two vertices in $\{b, c, d\}$ are adjacent either to $v_2$ or to $v_{2k+1}$, say b and c are adjacent to $v_2$. Then $\{a, v_2, b, c\}$ induces a diamond in G, which is a contradiction.

• (3) $V(K) \cap V(C) = \{d\}$: We may assume (wlog.) that $d = v_1$. Then by Claim 3.1, up to symmetry, we may assume $av_2 \in E$. Suppose that $k =2$. Then since G is ($S_{1, 1, 3}$, 5-apple, diamond)-free, both b and c have neighbors in C. To avoid a diamond in G and by Claim 3.1, we assume (wlog.) that $bv_3, bv_4, cv_4, cv_5 \in E$. But, now $\{d=v_1, a, b, v_4, v_5, c\}$ induces a $C_5^*$ in G, which is a contradiction. So, suppose that $k \ge 3$. Then since G is diamond-free, $bv_2, cv_2 \notin E$. We claim that either $bv_3 \in E$ or $cv_3 \in E$. Otherwise, since $\{v_4, v_3, v_2, a, b, c\}$ does not induce an $S_{1, 1, 3}$ in G, either $bv_4 \in E$ or $cv_4 \in E$. But, now $\{v_4, v_3, v_2, a, b, c\}$ will induce a $C_5$ in G, which is a contradiction to the fact that $k \ge 3$ and the choice of C. Thus, we may assume that $bv_3 \in E$. Then by Claim 3.1, $bv_4 \in E$. Then $cv_3 \notin E$ (for, otherwise, by Claim 3.1, $cv_4 \in E$, but then $\{v_3, v_4, b, c\}$ induces a diamond in G), and hence $cv_4 \notin E$ (for, otherwise, $\{a, c, v_4, v_3, v_2\}$ induces a $C_5$ in G). Now, $\{v_5, v_4, b, a, c\}$ induces a $C_5$ in G (if $cv_5 \in E$) or $\{v_5, v_4, b, a, d(= v_1), c\}$ induces an $S_{1, 1, 3}$ in G (if $cv_5 \notin E$), a contradiction.

• (4) $V(K) \cap V(C) = \emptyset$ and a vertex of K has a neighbor on C: Assume a has neighbors on C, say $v_1$ and $v_2$. Then to avoid an induced claw intersecting C, both $v_1$ and $v_2$ have exactly two neighbors among b, c, d. We may assume (wlog.) that $v_1$ is adjacent to b and c. But, now $\{v_1, a, b, c\}$ induces a diamond in G, which is a contradiction. So, assume that a has no neighbor on C. Assume (wlog.) that b has a neighbor on C. By Claim 3.1, we may assume that $N(b) \cap V(C) = \{v_1, v_2\}$. Now, $v_2$ is adjacent to either c or d (for, otherwise, either $\{v_3, v_2, b, a, c, d\}$ will induce an $S_{1, 1, 3}$ or $\{v_3, v_2, b, a, c\}$ will induce a $C_5$ or $\{v_3, v_2, b, a, d\}$ will induce a $C_5$ in G). Assume that $cv_2 \in E$. Since G is diamond-free, $cv_1 \notin E$ and by Claim 1, $cv_3 \in E$. Thus, $N(c) \cap V(C) = \{v_2, v_{3}\}$. By similar arguments, we see that $N(d) \cap V(C) = \{v_1, v_{2k+1}\}$. Now, $\{v_4, v_3, c, a, b ,d\}$ induces an $S_{1, 1, 3}$ in G, which is a contradiction.

• (5) $V(K)\cap V(C) = \emptyset$ and no vertex of K has a neighbor on C: Since G is connected, there exists an $i \in \{1, 2, \ldots , 2k+1\}$ and a path $v_i = u_1-u_2-\cdots -u_t-a$, say P connecting $v_i$ and a in G (where $t \ge 2$) and with $u_2$ has a neighbor on C. By the choice of P, no vertex of this path has a neighbor on C except $u_2$. By Claim 3.1, either $u_2v_{i+1} \notin E$ or $u_2v_{i-1} \notin E$. Assume that $u_2v_{i+1} \notin E$. Now, $u_t \ne b, c, d$ (for, otherwise (wlog.) if $u_t = b$, then $\{v_{i+1}, v_i = u_1, u_2, \ldots , u_t = b, a, c, d\}$ induces an $S_{1, 1, 3}$ in G). Then since G is diamond-free, at least two vertices in $\{b, c, d\}$ are not adjacent to $u_t$, say b and c. Then $\{v_{i+1}, v_i = u_1, u_2, \ldots , u_t, a, b, c\}$ induces an $S_{1, 1, 3}$ in G, which is a contradiction.

Hence G is claw-free, and this completes the proof of the theorem. $\square$

Theorem 4

The MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond, 5-apple, $C_5^*$)-free graphs.

Proof

Let G be an ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond, 5-apple, $C_5^*$)-free graph. If G is odd-hole-free, then G is (odd-hole, diamond)-free. Since MWIS in (odd-hole, diamond)-free graphs can be solved in polynomial time (Brandstädt and Mosca 2015), MWIS can be solved in polynomial time for G. Next, suppose that G contains an odd-hole. If G is prime, then by Theorem 3, G is claw-free. Since MWIS in claw-free graphs can be solved in polynomial time (Minty 1980), MWIS can be solved in polynomial time for G. The time complexity is the same when G is not prime, by Theorem 1. $\square$

4.2 ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond, 5-apple)-free graphs

Theorem 5

Let $G = (V, E)$ be an ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond, 5-apple)-free graph. Then G is nearly $C_5^*$-free.

Proof

Let us assume on the contrary that there is a vertex $v \in V(G)$ such that $G{\setminus } N[v]$ contains an induced $C_5^*$, say H, with vertices named as in Fig. 3. Let C denotes the 5-cycle induced by the vertices $\{v_1, v_2, v_3, v_4, v_5\}$ in H. For $i \in \{1, 2, \ldots , 6\}$, we define sets $A_i, A_i^+, A^+$, and Q as in the last paragraph of Sect. 2. To prove the theorem, it is enough to show that $A^+ = \emptyset$. Assume to the contrary that $A^+ \ne \emptyset$, and let $x \in A^+$. Then there exists a vertex $z \in Q$ such that $xz \in E$. Then since G is (5-apple, diamond)-free, $|N_H(x) \cap V(C)| \in \{0, 2, 3\}$. Now:

• (i) If $|N_H(x) \cap V(C)|= 0$, then since $x\in N(H), xv_6 \in E$. But then $\{z, x, v_6, v_1,$ $v_2, v_5\}$ induces an $S_{1, 1, 3}$ in G, which is a contradiction.

• (ii) If $|N_H(x) \cap V(C)|= 2$, and if $N_H(x) \cap V(C) = \{v_i, v_{i+2}\}$, for some $i \in \{1, 2, 3, 4, 5\}, i \mod 5$, then $\{z, x, v_{i+2}, v_{i+3}, v_{i+4}, v_{i}\}$ induces a 5-apple in G, which is a contradiction.

• (iii) If $|N_H(x) \cap V(C)|= 2$, and if $N_H(x) \cap V(C) = \{v_i, v_{i+1}\}$, for some $i \in \{1, 2, 3, 4, 5\}, i \mod 5$, then since $\{z, x\} \cup V(H)$ does not induce a diamond or an $S_{1, 1, 3}$ in G, we have $i \ne 3$. Again, since G is diamond-free, $xv_6 \notin E$. But, then $\{z, x\} \cup V(H)$ induces a subgraph of G in which either $S_{1, 1, 3}$ or $S_{1, 2, 2}$ is an induced subgraph, which is a contradiction.

• (iv) If $|N_H(x) \cap V(C)|= 3$, then since G is diamond-free, $N_H(x) \cap V(C) = \{v_i, v_{i+1}, v_{i+3}\}$, for some $i \in \{1, 2, 3, 4, 5\}, i \mod 5$. Then since G is diamond-free, $i \ne 3$ and $xv_6 \notin E$. But, then $\{z, x\} \cup V(H)$ induces a subgraph of G in which either $S_{1, 1, 3}$ or $S_{1, 2, 2}$ is an induced subgraph, which is a contradiction.

These contradictions show that $A^+ = \emptyset$, and hence G is nearly $C_5^*$-free. $\square$

Theorem 6

The MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond, 5-apple)-free graphs.

Proof

Let G be an ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond, 5-apple)-free graph. Then by Theorem , G is nearly $C_5^*$-free. Since MWIS in ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond, 5-apple, $C_5^*$)-free graphs can be solved in polynomial time (by Theorem ), by the consequence given below Eq. (1) in Sect. 2, MWIS in ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond, 5-apple)-free graphs can be solved in polynomial time. $\square$

4.3 ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond)-free graphs

Theorem 7

Let $G = (V, E)$ be an $S_{1, 2, 2}, S_{1, 1, 3}$, diamond-free graph. Then every atom of G is nearly 5-apple-free.

Proof

Let $G'$ be an atom of G. We want to show that $G'$ is nearly 5-apple-free, so let us assume on the contrary that there is a vertex $v \in V(G')$ such that $G'{\setminus } N[v]$ contains an induced 5-apple H with vertex-set $\{v_1, v_2, v_3, v_4, v_5, v_6\}$ and edge-set $\{v_1v_2, v_2v_3, v_3v_4,$ $v_4v_5, v_5v_1, v_1v_6\}$. Let C denotes the 5-cycle induced by the vertices $\{v_1, v_2, v_3, v_4, v_5\}$ in H. For $i\in \{1, 2, \ldots , 6\}$, we define sets $A_i, A_i^+, A^+$, and Q, with respect to G, v and H, as in the last paragraph of Sect. 2. Then, we immediately have the following:

Claim 7.1

If $x \in N(H)$, then $|N_H(x) \cap V(C)| \le 3$. In particular, if $x \in A^+$, then $|N_H(x) \cap V(C)| = 3$, and hence there exists an index $j \in \{1, 2, \ldots , 5\}$, vertex index arithmetic modulo 5, such that $N_H(x) \cap V(C) = \{v_j, v_{j+1}, v_{j+3}\}$. $\Diamond$

So, we have:

Claim 7.2

$A_1^+ = A_2^+ = A_5^+ = A_6^+ = \emptyset$.

Claim 7.3

If $x \in A_3^+$, then $N_H(x)$ is equal to $\{v_1, v_3, v_4\}$.

Proof of Claim 7.3

Suppose not. Then by Claim 7.1, there exists an index $j \in \{1, 2, 4, 5\}, j \mod 5$, such that $N_H(x) = \{v_j, v_{j+1}, v_{j+3}\}$. Since $x \in A_3^+, xv_6 \notin E$, and there exists a vertex z in Q such that $xz \in E$. Now, if $N_H(x) = \{v_1, v_2, v_4\}$, then $\{v_6, v_1, x, v_4, v_3, z\}$ induces an $S_{1, 2, 2}$ in G, and if $N_H(x) =\{v_2, v_3, v_5\}$, then $\{v_6, v_1, v_5, x, v_3, z\}$ induces an $S_{1, 1, 3}$ in G, a contradiction. Since the other cases are symmetric, the claim follows. $\Diamond$

Claim 7.4

$|A_3^+| = 1$.

Proof of Claim 7.4

Suppose not. Let $x, y \in A_3^+$. By Claim 7.3, $N_H(x) = N_H(y) = \{v_1, v_3, v_4\}$. Now, if $xy \in E$, then $\{v_4, x, y, v_1\}$ induces a diamond in G, and if $xy \notin E$, then $\{v_4, x, y, v_3\}$ induces a diamond in G, a contradiction. $\Diamond$

Claim 7.5

If $x \in A_4^+$, then $N_H(x)$ is equal to $\{v_1, v_3, v_4, v_6\}$.

Proof of Claim 7.5

Suppose not. Then by Claim 7.1, there exists an index $j \in \{1, 2, 4, 5\}, j \mod 5$, such that $N_H(x) \cap V(C) = \{v_j, v_{j+1}, v_{j+3}\}$. Since $x \in A_4^+, xv_6 \in E$ and there exists a vertex z in Q such that $xz \in E$. Now, if $N_H(x) \cap V(C) = \{v_1, v_2, v_4\}$, then $\{v_6, v_1, v_2, x\}$ induces a diamond in G, and if $N_H(x) \cap V(C) =\{v_2, v_3, v_5\}$, then $\{v_1, v_6, x, v_3, v_4, z\}$ induces an $S_{1, 2, 2}$ in G, a contradiction. Since the other cases are symmetric, the claim follows. $\Diamond$

Claim 7.6

$|A_4^+| = 1$.

Proof of Claim 7.6

Suppose not. Let $x, y \in A_4^+$. By Claim 7.5, $N_H(x) = N_H(y) = \{v_1, v_3, v_4, v_6\}$. Now, if $xy \in E$, then $\{v_4, x, y, v_3\}$ induces a diamond in G, a contradiction and if $xy \notin E$, then $\{v_3, v_4, x, y\}$ induces a diamond in G, a contradiction. $\Diamond$

Claim 7.7

At most one of $A_3^+$ or $A_4^+$ is empty.

Proof of Claim 7.7

Suppose not. Let $x \in A_3^+$ and $y \in A_4^+$. By Claim 7.3, $N_H(x) = \{v_1, v_3, v_4\}$, and by Claim 7.5, $N_H(y) = \{v_1, v_3, v_4, v_6\}$. Now, if $xy \in E$, then $\{v_3, x, y, v_1\}$ induces a diamond in G, a contradiction, and if $xy \notin E$, then $\{v_3, v_4, x, y\}$ induces a diamond in G, a contradiction. $\Diamond$

Now, by Claim 7.2, $A^+ = A_3^+ \cup A_4^+$, and by Claims 7.4, 7.6 and 7.7, $A^+$ is a clique. Since $A^+$ is a separator between H and Q in G, we obtain that $V(G')\cap A^+$ is a clique separator in $G'$ between H and $V(G')\cap Q$ (which contains v). This is a contradiction to the fact that $G'$ is an atom. $\square$

Theorem 8

The MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond)-free graphs.

Proof

Let G be an ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond)-free graph. Then by Theorem 7, every atom of G is nearly 5-apple-free. Since MWIS in ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond, 5-apple)-free graphs can be solved in polynomial time (by Theorem 6), MWIS in ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond)-free graphs can be solved in polynomial time, by Theorem 2. $\square$

5 ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair)-free graphs

In this section, we show that the MWIS problem can be efficiently solved in the class of ($S_{1, 2, 2}, S_{1, 1,3}$, co-chair)-free graphs by analyzing the atomic structure of the subclasses of this class of graphs.

5.1 ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair, gem)-free graphs

Theorem 9

The MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair, gem)-free graphs.

Proof

Let G be an ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair, gem)-free graph. First suppose that G is prime. Then by Lemma 3, G is diamond-free. Since the MWIS problem in ($S_{1, 2, 2}, S_{1, 1, 3}$, diamond)-free graphs can be solved in polynomial time (by Theorem 8), MWIS can be solved in polynomial time for G, by Theorem 1. Then the time complexity is the same when G is not prime, by Theorem 1. $\square$

5.2 ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair, $H^*$)-free graphs

Theorem 10

Let $G = (V, E)$ be a prime ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair, $H^*$)-free graph. Then every atom of G is nearly gem-free (see Fig. 3 for the graph $H^*$).

Proof

Let $G'$ be an atom of G. We want to show that $G'$ is nearly gem-free, so let us assume on the contrary that there is a vertex $v \in V(G')$ such that the anti-neighborhood of v in $G'$ contains an induced gem H. Let H have vertex set $\{v_1, v_2, v_3, v_4, v_5\}$ and edge set $\{v_1v_2, v_2v_3, v_3v_4, v_1v_5, v_2v_5,$ $v_3v_5, v_4v_5\}$. For $i\in \{1, 2, \ldots , 5\}$, we define sets $A_i, A_i^+, A_i^-$, and Q, with respect to G, v and H, as in the last paragraph of Sect. 2. Then we have the following properties:

Claim 10.1

Every vertex x in N(H) satisfies either $v_5\in N(x)$ or x has at least one neighbor in $\{v_2, v_3\}$. In particular, (i) if $x \in A_1$, then $N_H(x) =\{v_5\}$, and (ii) if $x \in A_2$, then $N_H(x) \in \{ \{v_2, v_3\}, \{v_2, v_5\}, \{v_3, v_5\}, \{v_1, v_3\},$ $\{v_2, v_4\}\}$.

Proof of Claim 10.1

Suppose to the contrary that $xv_5\notin E$ and x has no neighbor in $\{v_2, v_3\}$. Then, up to symmetry, we have $xv_1\in E$, and so $\{x, v_1, v_2, v_3, v_5\}$ induces a co-chair in G, a contradiction. $\Diamond$

Let $B^*$ denote the set $\{x \in A_2 : N_H(x) = \{v_1, v_3\}\} \cup \{x \in A_2 : N_H(x) = \{v_2, v_4\}\}$.

Claim 10.2

$A_2^+ = A_3^+ = A_4^+ = \emptyset$.

Proof of Claim 10.2

Assume the contrary and let $x \in A_2^+\cup A_3^+\cup A_4^+$. There is a vertex z in Q such that $xz \in E$. First suppose that $xv_5 \notin E$. Then by Claim 10.1, x has at least one neighbor in $\{v_2, v_3\}$. Now, if $\{v_2, v_3\} \subseteq N_H(x)$, then $\{v_5, v_2, v_3, x, z\}$ induces a co-chair in G, which is a contradiction. So, we may assume that x has exactly one neighbor in $\{v_2, v_3\}$, say $xv_2 \in E$ and $xv_3 \notin E$. Since $x\in A_i^+$ ($i \ge 2$), either $xv_1 \in E$ or $xv_4 \in E$. But, then either $\{v_5, v_1, v_2, x, z\}$ induces a co-chair in G, or $\{v_5, v_2, v_3, v_4, x ,z\}$ induces a $H^*$ in G, respectively, a contradiction. So, suppose that $xv_5 \in E$. Then it follows that there is a clique $\{p,q,r\}\subset V(H)$ such that $xp, xq\in E$ and $xr\notin E$. Then $\{z, x, p, q, r\}$ induces a co-chair in G, a contradiction. $\Diamond$

Claim 10.3

For each $i\in \{2,\ldots ,5\}, A_5^+$ is complete to $A^-_i$.

Proof of Claim 10.3

Assume the contrary. Let $x \in A_5^+$ and $y \in A^-_i$ be such that $xy \notin E$. Since $x \in A_5^+$, there exists $z \in Q$ such that $xz \in E$. Now, if $y \in (\bigcup _{i =2}^5 A^-_i){\setminus } B^*$, then there exist vertices $p,q \in V(H)$ such that $pq \in E$ and $yp, yq\in E$. Then $\{z, x, p, q, y\}$ induces a co-chair in G, a contradiction. So, $y \in B^*$. But, now, $\{x, v_4, v_5, v_1, y\}$ induces a co-chair in G, a contradiction. $\Diamond$

Claim 10.4

$A_5^+$ is a clique.

Proof of Claim 10.4

Assume the contrary. Then $G[A_5^+]$ has a co-connected component X of size at least 2. Since G is prime, X is not a module in G in G, so there is a vertex z in $V(G){\setminus } X$ that distinguishes two vertices x and y of X, and since X is co-connected we can choose x and y non-adjacent. Clearly $z\notin H$ and $z\notin A_5^+$. So either (i) z has no neighbor in H, or (ii) $z \in A^-$ and so, by Claim 10.3 (since $\{z\}$ is not complete to $A_5^+$), $z \in A^-_1$, or (iii) $z \in A^+$ and so, by Claim 10.2, $z \in A^+_1$. In either of these three cases, by Claim 10.1, we see that $\{z, x, y, v_1, v_2\}$ induces a co-chair in G, a contradiction. $\Diamond$

Let $B = A_2^- \cup A_3^- \cup A_4^- \cup A_5^-$.

Claim 10.5

If $A_1^+\ne \emptyset$, then $\{v_5\}$ is complete to B.

Proof of Claim 10.5

Assume on the contrary that there is a vertex $x \in B$ such that $xv_5\notin E(G)$. Since $A_1^+ \ne \emptyset$, there is a vertex $a \in A_1^+$ and a vertex $z \in Q$ such that $az \in E(G)$. Recall that $N_H(a)=\{v_5\}$, by Claim 10.1. Now, if there exists vertices $p, q \in \{v_1, v_2, v_3, v_4\}$ such that $pq \in E$ and $xp, xq \in E$, then since $\{x, p, q, v_5, a\}$ does not induce a co-chair in $G, xa \in E$. But, then $\{z, a, x, v_5, p, q\}$ induces a $H^*$ in G, a contradiction. So, we may assume that $N_H(x) \cap \{v_1, v_2, v_3, v_4\}$ is an independent set. Hence by Claim 10.1, $N_H(x)$ is either $\{v_1, v_3\}$ or $\{v_2, v_4\}$. We may assume, up to symmetry, that $N_H(x) = \{v_1, v_3\}$. Then since $\{z, a, v_5, v_1, x, v_4\}$ does not induce an $S_{1, 2, 2}$ in $G, xa \in E$. But, then $\{z, a, x, v_3, v_2, v_4\}$ induces an $S_{1, 1, 3}$ in G, a contradiction. $\Diamond$

Claim 10.6

There is no edge between $A_1^+$ and B.

Proof of Claim 10.6

Assume the contrary, and let $a \in A_1^+$ and $b \in B$ be such that $ab \in E$. Since $a \in A_1^+$, there exists $y \in Q$ such that $ay \in E$. Since $b \in B$, by Claim 10.5 there exists an index j ($j \in \{1, \ldots , 4\}$) such that $bv_5, bv_j \in E$. Then $\{y, a, b, v_5, v_j\}$ induces a co-chair in G, which is a contradiction. $\Diamond$

Claim 10.7

If $a \in A_1^+, b \in B$, and $x \in A_1^-$, then $\{a, b, x\}$ does not induce a path in G.

Proof of Claim 10.7

Assume the contrary. Since $a \in A_1^+$, there exists a vertex $z \in Q$ such that $az \in E$. By Claim  10.6, $ab \notin E$. Thus, by the assumption, $ax \in E$ and $xb \in E$. Also, by Claims 10.1 and 10.5, we have $av_5, xv_5 \in E$ and $bv_5 \in E$. But, now $\{z, a, x, b, v_5\}$ induces a co-chair in G, which is a contradiction. $\Diamond$

Suppose that $A_1^+ = \emptyset$. Then $A^+ = A_5^+$, which is a clique by Claim 10.4. Since $A^+$ is a separator in G between H and Q, it follows that $V(G')\cap A^+$ is a clique separator in $G'$ between H and $V(G')\cap Q$ (which contains v); this is a contradiction to the fact that $G'$ is an atom. Therefore $A_1^+ \ne \emptyset$. Now, Claims 10.1 and 10.2 imply that $N(v_4) \subseteq \{v_3, v_5\}\cup B\cup A_5^+$, and Claims 10.4, 10.6, and 10.7 imply that $A_5^+ \cup \{v_2, v_3, v_5\}$ is a clique separator between $\{v_4\}$ and Q in G. Hence $V(G')\cap (A_5^+ \cup \{v_2, v_3, v_5\})$ is a clique separator between $\{v_4\}$ and $V(G')\cap Q$ in $G'$, again a contradiction to the fact that $G'$ is an atom. $\square$

Theorem 11

The MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair, $H^*$)-free graphs.

Proof

Let G be an ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair, $H^*$)-free graph. First suppose that G is prime. By Theorem , every atom of G is nearly gem-free. Since the MWIS in ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair, gem)-free graphs can be solved in polynomial time (by Theorem 9), MWIS in ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair, $H^*$)-free graphs can be solved in polynomial time, by Theorem 2. Then the time complexity is the same when G is not prime, by Theorem 1. $\square$

5.3 ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair)-free graphs

Theorem 12

Let $G= (V, E)$ be a prime ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair)-free graph. Then every atom of G is nearly $H^*$-free.

Proof

Let $G'$ be an atom of G. We want to show that $G'$ is nearly $H^*$-free, so let us assume on the contrary that there is a vertex $v \in V(G')$ such that the anti-neighborhood of v in $G'$ contains an induced $H^*$ as shown in Fig. 3. For $i\in \{1, \ldots , 6\}$, we define sets $A_i, A_i^+, A_i^-$, and Q, with respect to G, v and H, as in the last paragraph of Sect. 2. Then we have the following properties:

Claim 12.1

$A_1 = \emptyset$.

Proof of Claim 12.1

Suppose to the contrary that $A_1 \ne \emptyset$, and let $x \in A_1$. Then: (i) If $N_{H^*}(x)$ is either $\{v_1\}$ or $\{v_3\}$, then $\{x\} \cup V(H^*)$ induces a graph which is isomorphic to $H_7$ in G, a contradiction to Lemma 1. (ii) If $N_{H^*}(x)$ is either $\{v_2\}$ or $\{v_4\}$, then $\{x, v_1, v_2, v_3, v_4\}$ induces a co-chair in G, which is a contradiction. (iii) If $N_{H^*}(x) = \{v_5\}$, then $\{x\} \cup V(H^*)$ induces a graph which is isomorphic to $H_6$ in G, a contradiction to Lemma 1. (iv) If $N_{H^*}(x) = \{v_6\}$, then $\{x\} \cup V(H^*)$ induces a graph which is isomorphic to $H_4$ in G, a contradiction to Lemma 1. So, the claim holds. $\Diamond$

Claim 12.2

If $x \in A_2$, then $N_{H^*}(x) \in \{\{v_1, v_2\}, \{v_1, v_4\}, \{v_1, v_5\}, \{v_1, v_6\},$ $\{v_2, v_3\}, \{v_3, v_4\},$ $\{v_3, v_5\}, \{v_3, v_6\}, \{v_5, v_6\}\}$.

Proof of Claim 12.2

For, otherwise if $N_{H^*}(x) \in \{\{v_1, v_3\}, \{v_2, v_5\}, \{v_2, v_6\},$ $\{v_4, v_5\}, \{v_4, v_6\}\}$, then $\{x, v_1, v_2, v_3, v_4\}$ induces a co-chair in G, which is a contradiction, and if $N_{H^*}(x)$ is $\{v_2, v_4\}$, then $\{x\} \cup V(H^*)$ induces a graph which is isomorphic to $H_5$ in G, a contradiction to Lemma 1. So, the claim holds. $\Diamond$

Claim 12.3

$A_2^+ = \emptyset$.

Proof of Claim 12.3

Suppose to the contrary that $A_2^+ \ne \emptyset$, and let $x \in A_2^+$. Then there is a vertex z in Q such that $xz \in E$. We use Claim 12.2 to show a contradiction to our assumption as follows: Now, if $N_{H^*}(x) \in \{\{v_1, v_2\}, \{v_1, v_4\}, \{v_2, v_3\}, \{v_3, v_4\}\}$, then it follows that there is a clique $\{p,q,r\}\subset V(H^*)$ such that $xp, xq \in E$ and $xr\notin E$. But, then $\{z, x, p, q, r\}$ induces a co-chair in G, which is a contradiction. Next, if $N_{H^*}(x) \in \{\{v_1, v_5\},$ $\{v_1, v_6\}, \{v_3, v_5\}, \{v_3, v_6\}\}$, then $\{z, x, v_1, v_3, v_5, v_6\}$ induces an $S_{1, 2, 2}$ in G, which is a contradiction. Finally, if $N_{H^*}(x)$ is $\{v_5, v_6\}$, then $\{v_1, v_2, v_3,$ $v_4, v_5, x, z\}$ induces a graph which is isomorphic to $H_4$ in G, a contradiction to Lemma 1. So, $A_2^+ = \emptyset$, and the claim holds. $\Diamond$

Claim 12.4

If $x \in A_3$, then $N_{H^*}(x) \in \{\{v_1, v_2, v_4\}, \{v_1, v_3, v_5\}, \{v_1, v_5, v_6\}, \{v_2, v_3, v_4\}, \{v_2,$ $v_4,$ $v_6\},$ $\{v_3, v_5, v_6\}\}$.

Proof of Claim 12.4

Suppose the contrary. Now, if $v_6 \in N_{H^*}(x)$, then since $x \in A_3, |N_{H^*}(x) \cap \{v_1, v_2, v_3, v_4\}| \in \{1, 2\}$. If $|N_{H^*}(x) \cap \{v_1, v_2, v_3, v_4\}| = 2$, then it follows that there is a clique $\{p, q, r\}\subset \{v_1, v_2, v_3, v_4\}$ such that $xp, xq \in E$ and $xr\notin E$. But, then $\{v_6, x, p, q, r\}$ induces a co-chair in G, which is a contradiction. So, $|N_{H^*}(x) \cap \{v_1, v_2, v_3, v_4\}| = 1$, and hence $v_5 \in N_{H^*}(x)$. Since $x \in A_3$ and by our contrary assumption, either $v_2 \in N_{H^*}(x)$ or $v_4 \in N_{H^*}(x)$. But, then $\{v_1, v_2, v_3, v_4, x\}$ induces a co-chair in G, which is a contradiction. So, we may assume that $v_6 \notin N_{H^*}(x)$. Now, (i) if $N_{H^*}(x)$ is $\{v_1, v_2, v_3\}$, then $\{x, v_1, v_3, v_4, v_5\}$ induces a co-chair in G, (ii) if $N_{H^*}(x)$ is $\{v_2, v_3, v_5\}$, then $\{x, v_2, v_3, v_5, v_6\}$ induces a co-chair in G, and (iii) if $N_{H^*}(x)$ is $\{v_1, v_2, v_5\}$, then $\{x, v_1, v_2, v_5, v_6\}$ induces a co-chair in G, which are contradictions. Finally, if $N_{H^*}(x)$ is $\{v_2, v_4, v_5\}$, then $\{x\} \cup V(H^*)$ induces a graph which is isomorphic to $H_1$ in G, a contradiction to Lemma 1. Hence the claim is proved. $\Diamond$

Claim 12.5

If $x \in A_3^+$, then $N_{H^*}(x)$ is either $\{v_1, v_5, v_6\}$ or $\{v_3, v_5, v_6\}$.

Proof of Claim 12.5

For, otherwise, by Claim 12.4, $N_{H^*}(x) \in \{\{v_1, v_2, v_4\},$ $\{v_1, v_3, v_5\}, \{v_2, v_3,$ $v_4\}, \{v_2, v_4, v_6\}\}$. Since $x\in A_3^+$, there is a vertex z in Q such that $xz \in E$. Now, if $N_{H^*}(x) \in \{\{v_1, v_2, v_4\},$ $\{v_1, v_3, v_5\}, \{v_2, v_3, v_4\}\}$, then it follows that there is a clique $\{p,q,r\}\subset V(H^*)$ such that $xp, xq \in E$ and $xr\notin E$. But, then $\{z, x, p, q, r\}$ induces a co-chair in G, which is a contradiction. Next, if $N_{H^*}(x)$ is $\{v_2, v_4, v_6\}$, then $\{v_1, v_2, v_3, v_4, v_6, x, z\}$ induces a graph which is isomorphic to $H_6$ in G, a contradiction to Lemma 1. So the claim is proved. $\Diamond$

Let $B_3'$ denotes the set $\{x \in A_3^+ \mid N_{H^*}(x) = \{v_1, v_5, v_6\}\}$ and let $B_3''$ denotes the set $\{x \in A_3^+ \mid N_{H^*}(x) = \{v_3, v_5, v_6\}\}$.

Claim 12.6

$B_3'$ and $B_3''$ are cliques in G.

Proof of Claim 12.6

Suppose to the contrary that there exists vertices $x, y \in B_3'$ such that $xy \notin E$. Since $x\in A_3^+$, there exists a vertex z in Q such that $xz \in E$. Now, if $yz \in E$, then $\{z, x, y, v_5, v_6, v_1, v_3\}$ induces a graph which is isomorphic to $H_5$ in G, which contradicts Lemma 1, and if $yz \notin E$, then $\{v_5, v_6, x, y, z\}$ induces a co-chair in G, which is a contradiction. Hence, $B_3'$ is a clique in G. Similarly, $B_3''$ is also a clique in G. $\Diamond$

Claim 12.7

At most one of $B_3'$ or $B_3''$ is non-empty.

Proof of Claim 12.7

Suppose the contrary, and let $x \in B_3'$ and $y \in B_3''$. Then since $\{x, y, v_1, v_5, v_6\}$ does not induce a co-chair in $G, xy \in E$. Since $x\in A_3^+$, there exists a vertex z in Q such that $xz \in E$. Now, if $yz \in E$, then $\{v_2, v_5, x, y, z\}$ induces a co-chair in G, which is a contradiction, and if $yz \notin E$, then $\{z, x, y, v_3, v_2, v_4\}$ induces an $S_{1, 1, 3}$ in G, which is a contradiction. Hence the claim. $\Diamond$

Claim 12.8

$A_4^+ = \emptyset$.

Proof of Claim 12.8

Suppose to the contrary that $A_4^+ \ne \emptyset$ and let $x \in A_4^+$. There is a vertex z in Q such that $xz \in E$. Now, if x is adjacent to all the vertices in $\{v_1, v_2, v_3, v_4\}$, then $\{z, x, v_1, v_2, v_4, v_5, v_6\}$ induces a graph which is isomorphic to $H_7$ in G, a contradiction to Lemma 1. So, we may assume that x is non-adjacent to at least one vertex in $\{v_1, v_2, v_3, v_4\}$. Also, since $x \in A_4^+, x$ is adjacent to at least two vertices in $\{v_1, v_2,$ $v_3, v_4\}$. Now, if $N_{H^*}(x)$ is $\{v_2, v_4, v_5, v_6\}$, then $\{x, v_1, v_2, v_5, v_6\}$ induces a co-chair in G, a contradiction, and in all the other cases, there is a clique $\{p,q,r\}\subset V(H^*)$ such that $xp, xq \in E$ and $xr\notin E$. But, then $\{z, x, p, q, r\}$ induces a co-chair in G, which is a contradiction. $\Diamond$

Claim 12.9

$A_5^+ = \emptyset$.

Proof of Claim 12.9

Suppose to the contrary that $A_5^+ \ne \emptyset$ and let $x \in A_5^+$. Then there is a vertex z in Q such that $xz \in E$. Suppose x is adjacent to all the vertices in $\{v_1, v_2, v_3, v_4\}$. Further, if x is adjacent to $v_5$, then $\{x, v_2, v_3, v_5, v_6\}$ induces a co-chair in G, which is a contradiction, and if x is adjacent to $v_6$, then $\{x\} \cup V(H^*)$ induces a graph which is isomorphic to $H_2$ in G, a contradiction to Lemma 1. So, we may assume that x is non-adjacent to exactly one vertex in $\{v_1, v_2, v_3, v_4\}$. Then, there is a clique $\{p,q,r\}\subset V(H^*)$ such that $xp, xq \in E$ and $xr\notin E$. But, then $\{z, x, p, q, r\}$ induces a co-chair in G, which is a contradiction. $\Diamond$

Claim 12.10

$A_3^+$ is complete to $A_6^+$.

Proof of Claim 12.10

Suppose to the contrary that there exist vertices $x \in A_3^+$ and $y \in A_6^+$ such that $xy \notin E$. Then by Claim 12.5, $N_{H^*}(x)$ is either $\{v_1, v_5, v_6\}$ or $\{v_3, v_5, v_6\}$. Then either $\{v_3, y, v_5, v_6, x\}$ or $\{v_1, y, v_5, v_6, x\}$ induces a co-chair in G, a contradiction. $\Diamond$

Claim 12.11

For each $i\in \{2,\ldots , 6\}, A_6^+$ is complete to $A^-_i$.

Proof of Claim 12.11

Assume the contrary. Let $x \in A_6^+$ and $y \in A^-_i$ be such that $xy \notin E$. Since $x \in A_6^+$, there exists $z \in Q$ such that $xz \in E$. Now, if there exists vertices $p, q \in V(H^*)$ such that $pq \in E$ and $py, qy \in E$, then $\{z, x, p, q, y\}$ induces a co-chair in G, which is a contradiction. So, we assume that $N_{H^*}(y)$ is an independent set. Then by the above claims on $A_i^+, i \ge 2$, we have $N_{H^*}(y) \in \{\{v_1, v_5\}, \{v_1, v_6\}, \{v_3, v_5\}, \{v_3, v_6\}, \{v_2, v_4, v_6\}\}$. Now, if $N_{H^*}(y) \in \{\{v_1, v_5\}, \{v_3, v_5\}\}$, then $\{z, x, y\} \cup V(H^*)$ induces a graph which is isomorphic to $H_8$ in G, a contradiction to Lemma 1. So, $N_{H^*}(y) \in \{\{v_1, v_6\}, \{v_3, v_6\}, \{v_2, v_4, v_6\}\}$. But, then $\{v_1, v_4, v_5, x, y\}$ induces a co-chair in G (if $N_{H^*}(y) = \{v_1, v_6\})$, and $\{v_3, v_4, v_5, x, y\}$ induces a co-chair in G (if $N_{H^*}(y) = \{v_3, v_6\})$, which are contradictions. Finally, if $N_{H^*}(y) = \{v_2, v_4, v_6\}$, then $\{z, x, y\} \cup V(H^*)$ induces a graph which is isomorphic to $H_3$ in G, a contradiction to Lemma 1. $\Diamond$

Claim 12.12

$A_6^+$ is a clique.

Proof of Claim 12.12

Suppose the contrary. Then $G[A_6^+]$ has a co-connected component X of size at least 2. Since G is prime, X is not a non-trivial module in G, so there is a vertex z in $V(G){\setminus } X$ that distinguishes two vertices x and y of X, and since X is co-connected we can choose x and y non-adjacent. We may assume (wlog.) that $xz \in E$ and $yz \notin E$. Clearly $z\notin V(H^*)$ and $z \notin A_6^+$. By Claims 12.1 and 12.11, $z \notin A^-$, and by Claims 12.1, 12.3, 12.8, 12.9, and 12.10, we have $z \notin A^+$. Hence, z has no neighbor in $H^*$, and we see that $\{z, x, y, v_1, v_2\}$ induces a co-chair in G, a contradiction. $\Diamond$

By Claims 12.1, 12.3, 12.8, and 12.9, we have $A^+ = A_3^+ \cup A_6^+$, which is a clique by Claims 12.6, 12.7, 12.10, and 12.12. Since $A^+$ is a separator in G between $H^*$ and Q, it follows that $V(G')\cap A^+$ is a clique separator in $G'$ between $H^*$ and $V(G')\cap Q$ (which contains v); this is a contradiction to the fact that $G'$ is an atom. $\square$

Theorem 13

The MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair)-free graphs.

Proof

Let G be an ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair)-free graph. First suppose that G is prime. By Theorem , every atom of G is nearly $H^*$-free. Since the MWIS problem in ($S_{1, 2, 2}, S_{1, 1, 3}, H^*$, co-chair)-free graphs can be solved in polynomial time (by Theorem ), MWIS can be solved in polynomial time for G, by Theorem 2. Then the time complexity is the same when G is not prime, by Theorem 1. $\square$

6 Conclusion

The computational complexity of the M(W)IS problem for $S_{1, 2, 2}$-free graphs, and for $S_{1, 1, 3}$-free graphs are open. However, M(W)IS is known to be solvable in polynomial time for subclasses of $S_{i,j,k}$-free graphs (Gerber et al. 2004; Karthick and Maffray 2015, 2016; Le et al. 2015a, b). In this paper, using graph decomposition techniques, we showed that the MWIS problem can solved in polynomial time for ($S_{1, 2, 2}, S_{1, 1, 3}$, co-chair)-free graphs. This extends some known results in the literature. Note that the class of $S_{1, 2, 2}$-free graphs, and the class of $S_{1, 1, 3}$-free graphs include: $P_4$-free graphs, claw-free graphs, $P_5$-free graphs, and fork-free graphs (or chair-free graphs) for which the MWIS is known to be solved efficiently by various techniques (see Corneil et al. 1985; Lokshtanov et al. 2014; Lozin and Milanič 2008; Minty 1980; Sbihi 1980).