Independent Sets in Classes Related to Chair-Free Graphs

Abstract

The Maximum Weight Independent Set (MWIS) problem on graphs with vertex weights asks for a set of pairwise nonadjacent vertices of maximum total weight. MWIS is known to be NP-complete in general, but solvable in polynomial time in classes of $S_{i,j,k}$-free graphs, where $S_{i,j,k}$ is the graph consisting of three induced paths of lengths i, j, k with a common initial vertex. The complexity of the MWIS problem for $S_{1, 2, 2}$-free graphs, and for $S_{1, 1, 3}$-free graphs are open. In this paper, we show that the MWIS problem can solved in polynomial time for ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair)-free graphs, by analyzing the structure of the subclasses of this class of graphs. This extends some known results in the literature.

1 Introduction

Let G be a finite, undirected and simple graph with vertex-set V(G) and edge-set E(G). We let $|V(G)| = n$ and $|E(G)| = m$. Let $P_n$ and $C_n$ denote respectively the path, and the cycle on n vertices. If $\mathcal {F}$ is a family of graphs, a graph G is said to be $\mathcal {F}$ -free if it contains no induced subgraph isomorphic to any graph in $\mathcal {F}$. A class of graphs $\mathcal {G}$ is hereditary if every induced subgraph of a member of $\mathcal {G}$ is also in $\mathcal {G}$. For notation and terminology not defined here, we follow [5].

In a graph G, an independent (or stable) set is a subset of mutually nonadjacent vertices in G. The Maximum Independent Set (MIS) problem asks for an independent set in the given graph G with maximum cardinality. The Maximum Weight Independent Set (MWIS) problem asks for an independent set of total maximum weight in the given graph G with vertex weight function w on V(G). The M(W)IS problem is well known to be NP-complete in general and hard to approximate; it remains NP-complete even on restricted classes of graphs [9, 35]. Alekseev [1] showed that the M(W)IS problem remains NP-complete on H-free graphs, whenever H is connected, but neither a path nor a subdivision of the claw ($K_{1, 3}$). On the other hand, the M(W)IS problem is known to be solvable in polynomial time on many graph classes such as: chordal graphs [12]; $P_4$-free graphs [10]; perfect graphs [14]; $2K_2$-free graphs [11]; $P_3 \cup P_2$-free graphs [28]; claw-free graphs [31, 36]; chair-free graphs (or fork-free graphs) [24]; apple-free graphs [6]; and $P_5$-free graphs [21].

Fig. 1.

Some special graphs.

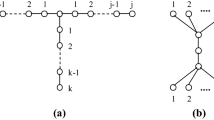
For integers $i, j, k \ge 0$, $S_{i,j,k}$ is the graph consisting of three induced paths of lengths i, j, k with a common initial vertex. The graph $S_{0,1,2}$ is isomorphic to $P_4$ and the graph $S_{0,2,2}$ is isomorphic to $P_5$. The graph $S_{1,1,1}$ is called a claw and the graph $S_{1, 1, 2}$ is called a chair or fork. Also, note that $S_{i,j, k}$ is a subdivision of a claw, if $i, j, k \ge 1$. See Fig. 1 for some of the special graphs used in this paper.

As mentioned earlier, the complexity status of the MWIS problem in the graphs classes defined by a single forbidden induced subgraph of the form $S_{i,j,k}$ was solved for the case $i + j + k \le 4$. However, for larger $i + j + k$, the complexity of MWIS in $S_{i,j,k}$-free graphs is open. In particular, the class of $P_6$-free graphs, the class of $S_{1, 2, 2}$-free graphs, and the class of $S_{1, 1, 3}$-free graphs constitute the minimal classes, defined by forbidding a single connected subgraph on six vertices, for which the computational complexity of the M(W)IS problem is open. It is known that there is an $n^{O(\log ^2n)}$-time, polynomial-space algorithm for MWIS on $P_6$-free graphs [22]. This implies that MWIS on $P_6$-free graphs is not NP-complete, unless all problems in NP can be solved in quasi-polynomial time. On the other hand, MWIS is shown to be solvable in polynomial time for several subclasses of $S_{i,j,k}$-free graphs, for $i+j+k \ge 5$ such as: subclasses of $P_6$-free graphs [3, 16, 29, 32–34]; subclasses of $S_{1, 2, 2}$-free graphs [17, 18]; and subclasses of $S_{1, 1, 3}$-free graphs [17]. It is also known that the MIS problem can be solved in polynomial time for some subclasses of $S_{i, j, k}$-free graphs such as: $S_{1,2,k}$-free planar graphs and $S_{1,k,k}$-free graphs of low degree [23], and $S_{2,2,2}$-free sub-cubic graphs [27]; and see [13, Table 1] for several other subclasses.

Graph decompositions techniques such as clique separator decomposition [37, 38] and modular decomposition [30] play a crucial role in structural graph theory and in designing efficient graph algorithms. Recently, using this technique, MWIS is shown to be solvable in polynomial time for some hereditary graph classes [3, 4, 6, 15, 17, 18, 26], and these results improve several results published in various papers.

A hole is a chordless cycle $C_k$, where $k \ge 5$. An odd hole is a hole $C_{2k+1}$, where $k \ge 2$. The k-apple is the graph obtained from a chordless cycle $C_k$ of length $k\ge 4$ by adding a vertex that has exactly one neighbor on the cycle. The diamond is the graph $K_4 -e$ with vertex-set $\{v_1, v_2, v_3, v_4\}$ and edge-set $\{v_1v_2, v_2v_3, v_3v_4, v_4v_1, v_1v_3\}$. The co-chair is the graph with vertex-set $\{v_1, v_2, v_3, v_4, v_5\}$ and edge-set $\{v_1v_2,$ $v_2v_3, v_3v_4, v_4v_1, v_1v_3, v_4v_5\}$; it is the complement graph of the chair/fork graph (see Fig. 1).

A set $M\subseteq V(G)$ is a module if every vertex in $V(G) \setminus M$ is adjacent to either all vertices of M or to none of them. A graph G is prime if its only modules have size 0, 1 or n.

Lozin and Milanič [24], using modular decomposition techniques [30], showed the following:

Theorem 1

([24]). Let $\mathcal {G}$ be a hereditary class of graphs. If there is a constant $p \ge 1$ such that the MWIS problem can be solved in time $O(|V(G)|^p)$ for every prime graph G in $\mathcal {G}$, then the MWIS problem can be solved in time $O(|V(G)|^p + |E(G)|)$ for every graph G in $\mathcal {G}$. $\Box$

Let $\mathcal {C}$ be a class of graphs. A graph G is nearly $\mathcal {C}$ if for every vertex v in V(G) the graph induced by $V(G) \setminus N[v]$ is in $\mathcal {C}$. Let $\alpha _w(G)$ denote the weighted independence number of G. Obviously, we have:

$$\begin{aligned} \alpha _w(G)= & {} \max \{w(v) + \alpha _w(G\setminus N[v]) \mid v \in V(G)\}. \end{aligned}$$

(1)

Thus, whenever MWIS is solvable in time T on a class $\mathcal {C}$, then it is solvable on nearly $\mathcal {C}$ graphs in time $n\cdot T$.

A clique in a graph G is a subset of pairwise adjacent vertices in G. A clique separator (or clique cutset) in a connected graph G is a subset Q of vertices in G which induces a complete graph, such that the graph induced by $V(G) \setminus Q$ is disconnected. A graph is an atom if it does not contain a clique separator.

In [17], Karthick and Maffray showed the following.

Theorem 2

([17]). Let $\mathcal C$ be a class of graphs such that MWIS can be solved in time O(f(n)) for every graph in $\mathcal C$ with n vertices. Then in any hereditary class of graphs whose all atoms are nearly $\mathcal C$ the MWIS problem can be solved in time $O(n^2\cdot f(n))$. $\Box$

In this paper, using the above framework, we first show that the MWIS problem can be efficiently solved in the class of ($S_{1, 2, 2}$, $S_{1, 1,3}$, diamond)-free graphs (Sect. 2). Using this, we show that the MWIS problem can be efficiently solved in the class of ($S_{1, 2, 2}$, $S_{1, 1,3}$, co-chair)-free graphs by analyzing the structure of the subclasses of this class of graphs (Sect. 3). These results extend some known results for the MWIS problem in the literature such as: $P_4$-free graphs [10], ($P_5$, diamond)-free graphs [2], and ($P_5$, co-chair)-free graphs [7, 15].

Fig. 2.

Graphs $H^*$ and $C_5^*$.

2 ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond)-free graphs

Our analysis of the (atomic) structure of subclasses of ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond)-free graphs enables us to prove that the MWIS problem can be efficiently solved in the class of ($S_{1, 2, 2}$, $S_{1, 1,3}$, diamond)-free graphs.

2.1 ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond, 5-apple, $C_5^*$)-free graphs

Theorem 3

Let $G= (V, E)$ be a prime ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond, 5-apple, $C_5^*$)-free graph. If G contains an odd hole $C_{2k+1}$ with $k \ge 2$, then G is claw-free (see Fig. 2 for the graph $C_5^*$).

Theorem 4

The MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond, 5-apple, $C_5^*$)-free graphs.

Proof

Let G be an ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond, 5-apple, $C_5^*$)-free graph. If G is odd-hole-free, then G is (odd-hole, diamond)-free. Since MWIS in (odd-hole, diamond)-free graphs can be solved in polynomial time [8], MWIS can be solved in polynomial time for G. Suppose that G is prime and contains an odd-hole. Then by Theorem 3, G is claw-free. Since MWIS in claw-free graphs can be solved in polynomial time [31], MWIS can be solved in polynomial time for G. Then the time complexity is the same when G is not prime, by Theorem 1. $\Box$

2.2 ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond, 5-apple)-free graphs

Theorem 5

Let $G = (V, E)$ be an ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond, 5-apple)-free graph. Then G is nearly $C_5^*$-free.

Proof

Let us assume to the contrary that there is a vertex $v \in V(G)$ such that $G\setminus N[v]$ contains an induced $C_5^*$, say H, with vertices named as in Fig. 2. Let C denotes the 5-cycle induced by the vertices $\{v_1, v_2, v_3, v_4, v_5\}$ in H. For $i \in \{1, 2, \ldots , 6\}$, we define the following:

$$\begin{aligned} Q_{\ }= & {} \text{ the } \text{ component } \text{ of } G\setminus (V(H)\cup N(V(H))) \text{ that } \text{ contains } \text{ v }, \\ A_i= & {} \{x \in V(G) \setminus V(H) \mid |N_H(x)| = i\}, \\ A_i^+= & {} \{x \in A_i \mid N(x) \cap Q \ne \emptyset \}, \\ A^-_i= & {} \{x \in A_i \mid N(x) \cap Q = \emptyset \}, \\ A^+= & {} A^+_1\cup \cdots \cup A^+_6 \ \text{ and } \ A^- = A^-_1\cup \cdots \cup A^-_6. \end{aligned}$$

So, $N(H) = A^+ \cup A^-$. Note that, by the definition of Q and $A^+$, we have $A^+ = N(Q)$. Hence $A^+$ is a separator between H and Q in G.

To prove the theorem, it is enough to show that $A^+ = \emptyset$. Assume to the contrary that $A^+ \ne \emptyset$, and let $x \in A^+$. Then there exists a vertex $z \in Q$ such that $xz \in E$. Then since G is (5-apple, diamond)-free, $|N_H(x) \cap V(C)| \in \{0, 2, 3\}$. Now:

• (1) If $|N_H(x) \cap V(C)|= 0$, then since $x\in N(H)$, $xv_6 \in E$. But then $\{z, x, v_6, v_1,$ $v_2, v_5\}$ induces an $S_{1, 1, 3}$ in G, which is a contradiction.

• (2) If $|N_H(x) \cap V(C)|= 2$, and if $N_H(x) \cap V(C) = \{v_i, v_{i+2}\}$, for some $i \in \{1, 2, 3, 4, 5\}$, $i \mod 5$, then $\{z, x, v_{i+2}, v_{i+3}, v_{i+4}, v_{i}\}$ induces a 5-apple in G, which is a contradiction.

• (3) If $|N_H(x) \cap V(C)|= 2$, and if $N_H(x) \cap V(C) = \{v_i, v_{i+1}\}$, for some $i \in \{1, 2, 3, 4, 5\}$, $i \mod 5$, then since $\{z, x\} \cup V(H)$ does not induce a diamond or an $S_{1, 1, 3}$ in G, we have $i \ne 3$. Again, since G is diamond-free, $xv_6 \notin E$. But, then $\{z, x\} \cup V(H)$ induces either an $S_{1, 1, 3}$ or an $S_{1, 2, 2}$ in G, which is a contradiction.

• (4) If $|N_H(x) \cap V(C)|= 3$, then since G is diamond-free, $N_H(x) \cap V(C) = \{v_i, v_{i+1}, v_{i+3}\}$, for some $i \in \{1, 2, 3, 4, 5\}$, $i \mod 5$. Then since G is diamond-free, $i \ne 3$ and $xv_6 \notin E$. But, then $\{z, x\} \cup V(H)$ induces either an $S_{1, 1, 3}$ or an $S_{1, 2, 2}$ in G, which is a contradiction.

These contradictions show that $A^+ = \emptyset$, and hence G is nearly $C_5^*$-free. $\Box$

Theorem 6

The MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond, 5-apple)-free graphs.

Proof

Let G be an ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond, 5-apple)-free graph. Then by Theorem 5, G is nearly $C_5^*$-free. Since MWIS in ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond, 5-apple, $C_5^*$)-free graphs can be solved in polynomial time (by Theorem 4), MWIS in ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond, 5-apple)-free graphs can be solved in polynomial time (by the consequence given below Eq. (1)). $\Box$

2.3 ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond)-free graphs

Theorem 7

Let $G = (V, E)$ be an ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond)-free graph. Then every atom of G is nearly 5-apple-free.

Theorem 8

The MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond)-free graphs.

Proof

Let G be an ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond)-free graph. Then by Theorem 7, every atom of G is nearly 5-apple-free. Since MWIS in ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond, 5-apple)-free graphs can be solved in polynomial time (by Theorem 6), MWIS in ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond)-free graphs can be solved in polynomial time, by Theorem 2. $\Box$

3 ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair)-free graphs

Our analysis of the (atomic) structure of subclasses of ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair)-free graphs enables us to prove that the MWIS problem can be efficiently solved in the class of ($S_{1, 2, 2}$, $S_{1, 1,3}$, co-chair)-free graphs.

3.1 ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair, gem)-free graphs

We use the following lemma given in [15].

Lemma 1

([15]). If $G = (V, E)$ is a prime (co-chair, gem)-free graph, then G is diamond-free.$\Box$

Theorem 9

The MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair, gem)-free graphs.

Proof

Let G be an ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair, gem)-free graph. First suppose that G is prime. Then by Lemma 1, G is diamond-free. Since the MWIS problem in ($S_{1, 2, 2}$, $S_{1, 1, 3}$, diamond)-free graphs can be solved in polynomial time (by Theorem 8), MWIS can be solved in polynomial time for G, by Theorem 1. Then the time complexity is the same when G is not prime, by Theorem 1. $\Box$

3.2 ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair, $H^*$)-free graphs

Theorem 10

Let $G = (V, E)$ be a prime ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair, $H^*$)-free graph. Then every atom of G is nearly gem-free (see Fig. 2 for the graph $H^*$).

Theorem 11

The MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair, $H^*$)-free graphs.

Proof

Let G be an ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair, $H^*$)-free graph. First suppose that G is prime. By Theorem 10, every atom of G is nearly gem-free. Since the MWIS in ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair, gem)-free graphs can be solved in polynomial time (by Theorem 9), MWIS in ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair, $H^*$)-free graphs can be solved in polynomial time, by Theorem 2. Then the time complexity is the same when G is not prime, by Theorem 1. $\Box$

3.3 ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair)-free graphs

Theorem 12

Let $G= (V, E)$ be a prime ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair)-free graph. Then every atom of G is nearly $H^*$-free.

Theorem 13

The MWIS problem can be solved in polynomial time for ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair)-free graphs.

Proof

Let G be an ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair)-free graph. First suppose that G is prime. By Theorem 12, every atom of G is nearly $H^*$-free. Since the MWIS problem in ($S_{1, 2, 2}$, $S_{1, 1, 3}$, $H^*$, co-chair)-free graphs can be solved in polynomial time (by Theorem 11), MWIS can be solved in polynomial time for G, by Theorem 2. Then the time complexity is the same when G is not prime, by Theorem 1. $\Box$

4 Conclusion

The complexity of the M(W)IS problem for $S_{1, 2, 2}$-free graphs, and for $S_{1, 1, 3}$-free graphs are open. However, M(W)IS is known to be solvable in polynomial time for subclasses of $S_{i,j,k}$-free graphs [13, 17–20, 23, 25, 27]. In this paper, using graph decomposition techniques, we showed that the MWIS problem can solved in polynomial time for ($S_{1, 2, 2}$, $S_{1, 1, 3}$, co-chair)-free graphs. This extends some known results in the literature. Note that the class of $S_{1, 2, 2}$-free graphs, and the class of $S_{1, 1, 3}$-free graphs include: $P_4$-free graphs, claw-free graphs, $P_5$-free graphs, and fork-free graphs (or chair-free graphs) for which the MWIS is known to be solved efficiently by various techniques (see [10, 21, 24, 31, 36]).