A lower bound for the adaptive two-echelon capacitated vehicle routing problem

Abstract

Adaptive two-echelon capacitated vehicle routing problem (A2E-CVRP) proposed in this paper is a variant of the classical 2E-CVRP. Comparing to 2E-CVRP, A2E-CVRP has multiple depots and allows the vehicles to serve customers directly from the depots. Hence, it has more efficient solution and adapt to real-world environment. This paper gives a mathematical formulation for A2E-CVRP and derives a lower bound for it. The lower bound is used for deriving an upper bound subsequently, which is also an approximate solution of A2E-CVRP. Computational results on benchmark instances show that the A2E-CVRP outperforms the classical 2E-CVRP in the costs of routes.

1 Introduction

In modern logistics, the capacitated vehicle routing problem (CVRP) which was introduced by Dantzig and Ramser (1959) has economic significance. However, the classical vehicle problem could not describe the complicated real-world environments, and hence researchers introduce many variants of CVRP, for example, the two-echelon vehicle routing problem (2E-CVRP) which was described by Feliu et al. (2007). In the classical 2E-CVRP, the customer demands are firstly delivered from the depot to satellites, then from satellites to customers. The depot and satellites both have homogenous vehicle fleets. The goal of 2E-CVRP is to find a set two-level routes of minimum total cost, in which first-level routes are from the depot to satellites, and second-level routes are from satellites to customers.

The integer linear program formulation of 2E-CVRP could be divided into the vehicle flow formulation and the set-partitioning based formulation which were detailed by Toth and Vigo (2001). Jepsen et al. (2013) proposed a vehicle flow formulation of 2E-CVRP and presented a branch-and-cut algorithm to solve it. Baldacci et al. (2013) used the ng-route relaxation which was proposed by Baldacci et al. (2011) to derive a lower bound on the set-partitioning based formulation of 2E-CVRP, and then used the lower bound and the q-route relaxation which was proposed by Christofideds et al. (1981) to generate approximately exact solutions.

There is much work concerning on solving 2E-CVRP which are mainly considered in deterministic environment, and formulated in form of integer linear program. Because CVRP is NP-hard, 2E-CVRP also cannot be solved in polynomial time. Therefore, approximation algorithms such as those described by Das (2011) and heuristic algorithms (Ghannadpour et al. 2014; Li et al. 2014; Zhang et al. 2014) are employed. Approximation algorithms could ensure a limited ratio for the solutions, however, it is also difficult to find good approximation ratio for CVRP. As proved by Wøhlk (2008), finding a 3/2-approximation for the Capacitated Arc Routing Problem (CARP) is NP-hard, and it goes worse when the edges do not satisfy the triangle inequality. Because each CARP instance could be transformed to CVRP, finding 3/2-approximation for CVRP is also NP-hard. To deal with large scale instances, heuristic algorithms are largely be developed, such as the cutting plane method described by Baldacci et al. (2008) and the column generation method described by Baldacci and Mingozzi (2009), in which the lower and upper bounds influence the performance ratio significantly.

In order to find a much more efficient solution for handling CVRP and let the problem adapt real-world environment, this paper extends 2E-CVRP and introduces a new model, i.e., the adaptive two-echelon capacitated vehicle routing problem (A2E-CVRP), in which there are multiple depots, such as airports, train stations and sea ports, and these depots could deliver the demands directly to the nearby customers, rather than transport them to satellites firstly. Because of this adaptive nature, A2E-CVRP generalizes the classical 2E-CVRP, and theoretically, its optimum route set has less cost than that of 2E-CVRP.

This paper introduces a mathematical formulation for A2E-CVRP. We derive a lower bound based on the method proposed by Baldacci et al. (2013), and then use it to derive an upper bound which is also an approximate solution of A2E-CVRP. In the computational results, we show that both the lower and the upper bounds of A2E-CVRP are smaller than those of the classical 2E-CVRP. Besides, the lower and the upper bounds could be further used to generate solutions closer to optimality. Based on the computational results on benchmark instances, the A2E-CVRP outperforms the classical 2E-CVRP in the costs of routes.

The remaining part of this paper is organized as below. In Sect. 2, we describe the A2E-CVRP in detail and give its mathematical formulation. Sections 3 and 4 describe the lower bound and the algorithm for generating the lower and upper bounds. To reduce the length of the paper, the proof of the lower and upper bounds is not included. Computation results are listed in Sect. 5, and some conclusive remarks are given in Sect. 6. Besides, the proof of the theorems in this paper could be found in the e-companion of this paper.

2 Problem introduction and mathematical formulation

The map of A2E-CVRP is an undirected complete graph G(N, E), which is abstract from some real-world logistics environments. The vertex set $N = N_D \cup N_S \cup N_C$, and edge set E consists of all the edges connecting the vertices in N, where $N_D$ represents the depot sets, $N_S$ represents the satellites set, and $N_C$ is the customer set.

Each customer $i \in N_C$ has a positive integer demand $q_i$, and each edge in E has a routing cost, which is commonly the road length. Each depot $d \in N_D$ can deliver the demand (${\le }B_d^1$) to satellites by $m_d^1$ homogeneous vehicles of load capacity $Q_1$, and each $k \in N_S \cup N_D$ can deliver the demand (${\le }B_k^2$) to customers by $m_k^2$ homogeneous vehicles of load capacity $Q_2$. $B_d^1 \le m_d^1 Q_1$ and $B_k^2 \le m_k^2 Q_2$ always hold.

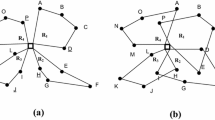
The dynamic process of A2E-CVRP is illustrated in Fig. 1. The squares, triangles and circles represent depots, satellites and customers respectively. The solid lines represent the first-level routes, which deliver demands from depots to satellites. The dashed lines represent the second-level routes, which deliver demands from satellites to customers. The bold solid lines represent the adaptive routes, which deliver demands from depots directly to customers. Our goal is to find a set consisting of the kind of routes with the minimum routing costs.

Fig. 1

The dynamic process of A2E-CVRP

The linear program formulation of A2E-CVRP is give below. Let $M_d$ be the index set of each first-level routes dr of cost $g_{dr}$ starting from depot d, and $\mathscr {M}_{sd}$ be the subset of $\mathscr {M}_d$, in which dr must visit satellite s. Furthermore, let $\mathscr {R}_k$ be the index set of each second-level (or adaptive) routes kl of cost $c_{kl}$ starting from satellite (or depot) k, and $\mathscr {R}_{ik}$ be the subset $\mathscr {R}_k$, in which kl must visit customer i. Finally, let $w_{kl}$ be the total demand that is delivered by a second-level or adaptive route kl.

The decision variables $x_{kl}$ and $y_{dr}$ equal 1 if and only if the corresponding routes are selected in the optimum solution, and 0 otherwise. The decision variable $q_{srd}$ denotes the demand that is delivered by the first-level route r starting from depot d and visiting satellite s.

$$\begin{aligned} z(F) = \min \sum _{d \in N_D} \sum _{r \in \mathscr {M}_d} g_{dr} y_{dr} + \sum _{k \in N_S \cup N_D} \sum _{l \in \mathscr {R}_k} c_{kl} x_{kl} \end{aligned}$$

s.t.

$$\begin{aligned}&\sum _{k \in N_S \cup N_D} \sum _{l \in \mathscr {R}_{ik}} x_{kl} = 1, \quad i \in N_C \end{aligned}$$

(1)

$$\begin{aligned}&\sum _{l \in \mathscr {R}_k} x_{kl} \leqslant m_k^2, \quad k \in N_S \cup N_D \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{l \in \mathscr {R}_k} x_{kl} w_{kl} \leqslant B_k^2, \quad k \in N_S \cup N_D \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{d \in N_D} \sum _{r \in \mathscr {M}_{sd}} q_{srd} = \sum _{l \in \mathscr {R}_s} x_{sl} w_{sl}, \quad s \in N_S \end{aligned}$$

(4)

$$\begin{aligned}&\sum _{r \in \mathscr {M}_{d}} y_{dr} \leqslant m_d^1, \quad d \in N_D \end{aligned}$$

(5)

$$\begin{aligned}&\sum _{s \in R_{dr}} q_{srd} \leqslant Q_1, d \in N_D, \quad r \in \mathscr {M}_{d} \end{aligned}$$

(6)

$$\begin{aligned}&\sum _{r \in \mathscr {M}_d} \sum _{s \in R_{dr}} q_{srd} \leqslant B_d^1, \quad d \in N_D \end{aligned}$$

(7)

$$\begin{aligned}&x_{kl} \in \{ 0, 1 \}, \quad l \in \mathscr {R}_k, \; k \in N_S \cup N_D \end{aligned}$$

(8)

$$\begin{aligned}&y_{dr} \in \{ 0, 1 \}, \quad r \in \mathscr {M}_d, \; d \in N_D \end{aligned}$$

(9)

$$\begin{aligned}&q_{srd} \in \mathbb {Z}^+ , \quad s \in N_S, \; r \in \mathscr {M}_d, \; d \in N_D \end{aligned}$$

(10)

The second-level and adaptive constraints are given by (1)–(3). (1) Ensures each customer is visited exactly once. (2) Ensures that a depot or satellite uses at most all its own second-level vehicles. (3) Ensures a depot or satellite will not supply demands beyond its service ability. The first-level constraints are (5)–(7). (5) Ensures a depot uses at most all its own first-level vehicles. (6) Ensures a first-level vehicle will not deliver demands beyond its load capacity. (7) Ensures a depot will not supply demands beyond its service ability. Constraint (4) connects the first-level and second-level routes, that is to say, the demands received by a satellite must equal to those it delivered. Constraints (8)–(10) describes the decision variables.

3 The lower bound of A2E-CVRP

The lower bound is formulated in Theorems 1 and 3. Theorem 1 relaxes the model of A2E-CVRP in a lagrangian fashion, and subsequently, Theorem 3 relaxes the formulation in Theorem 1 to improve the effectiveness in running time.

3.1 Lower bound z(RF)

Theorem 1 firstly introduces the dual variables $\lambda _i \in \mathbb {R}, \; i \in N_C$ of constraint (1) and $\mu _k \in \mathbb {R}^-, k \in N_S \cup N_D$ of constraint (2), and then defines the marginal routing cost $\beta _{ik}$ for the second-level or adaptive route kl which serves customer $i \in N_C$.

$$\begin{aligned} \sum _{i \in N_C} \alpha _{ikl} \beta _{ik} \leqslant c_{kl} - \sum _{i \in N_C} \alpha _{ikl} \lambda _i - \mu _k, \quad l \in \mathscr {R}_k, \; k \in N_S \cup N_D \end{aligned}$$

(11)

$\alpha _{ikl}$ means the number of times that customer $i \in N_C$ is visited by route kl. $\xi _{ik}$ equals 1 if and only if the demand of customer $i \in N_C$ is delivered from k. The relaxation RF is given as below.

$$\begin{aligned} z( RF ( \beta , \; \lambda , \; \mu ))= & {} \min \sum _{k \in N_S \cup N_D} \sum _{i \in N_C} \xi _{ik} \beta _{ik} + \sum _{d \in N_D} \sum _{r \in \mathscr {M}_d} y_{dr} g_{dr}\\&+\,\sum _{i \in N_C} \lambda _i + \sum _{k \in N_S \cup N_D} \mu _k m_k^2 \end{aligned}$$

s.t.

$$\begin{aligned}&\sum _{k \in N_S \cup N_D} \xi _{ik} = 1, \quad i \in N_C \end{aligned}$$

(12)

$$\begin{aligned}&\sum _{i \in N_C} \xi _{ik} q_i \leqslant B_k^2, \quad k \in N_C \cup N_D \end{aligned}$$

(13)

$$\begin{aligned}&\sum _{d \in N_D} \sum _{r \in \mathscr {M}_{sd}} q_{srd} = \sum _{i \in N_C} \xi _{is} q_i, \quad s \in N_S \end{aligned}$$

(14)

$$\begin{aligned}&\quad (5){-}(7), \; (9) \; and \; (10) \nonumber \\&\xi _{ik} \in \{ 0, 1 \}, \quad i \in N_C, \quad k \in N_S \cup N_D. \end{aligned}$$

(15)

Theorem 1

$z(RF(\beta , \; \lambda , \; \mu ))$ is a lower bound of z(F), for any $\beta _{ik}$ defined in (11), $\lambda _i \in \mathbb {R}$ and $\mu _k \in \mathbb {R}^-$.

Corollary 1

Let z(UB) be an upper bound of z(F). For any $\beta _{ik}$ defined in (11), $\lambda _i \in \mathbb {R}$ and $\mu _k \in \mathbb {R}^-$, define the reduced cost as below.

$$\begin{aligned} \tilde{c}_{kl} = c_{kl} - \sum _{i \in N_C} \alpha _{ikl} (\beta _{ik} + \lambda _i) - \mu _k \geqslant 0, \quad l \in \mathscr {R}_k, \; k \in N_S \cup N_D \end{aligned}$$

(16)

Then, any optimum solution of the mathematical formulation of A2E-CVRP cannot contain a second-level or adaptive route whose reduced cost $\tilde{c}_{kl} \geqslant z(UB) - z(RF(\beta , \; \lambda , \; \mu ))$.

Theorem 2

Let z(LF) be the optimum solution of the linear relaxation of A2E-CVRP, then the following inequality holds.

$$\begin{aligned} \max _{(\beta , \; \lambda , \; \mu )} z(RF{(\beta , \; \lambda , \; \mu )} ) \geqslant z(LF). \end{aligned}$$

3.2 Lower bound $z(\overline{RF})$

The lower bound $z(\overline{RF}(\beta , \; \lambda , \; \mu ))$ is the solution of the linear program $\overline{RF}(\beta , \; \lambda , \; \mu )$. In the optimum solution, $\xi _{krw}$ equals 1 if and only if the first-level route dr deliver demand w, and $\xi _{krw}$ equals 1 if and only if the depot d deliver demand w by using its adaptive vehicles.

$$\begin{aligned} z(\overline{RF}(\beta , \; \lambda , \; \mu ))= & {} \min \sum _{d \in N_D} \sum _{r \in \mathscr {M}_d} \sum _{w \in W_{dr}} (g_{dr} + \phi _{drw}) \xi _{drw} + \sum _{d \in N_D} \sum _{w \in W_d} \phi _{dw} \xi _{dw}\\&+\,\sum _{i \in N_C} \lambda _i + \sum _{k \in N_D \cup N_D} \mu _k m_k^2 \end{aligned}$$

s.t.

$$\begin{aligned}&\sum _{d \in N_D} \sum _{r \in \mathscr {M}_d} \sum _{w \in W_{dr}} w \xi _{drw} + \sum _{d \in N_D} \sum _{w \in W_d} w \xi _{dw} = q_{tot} \end{aligned}$$

(17)

$$\begin{aligned}&\sum _{r \in \mathscr {M}_d} \sum _{w \in W_{dr}} \xi _{drw} \leqslant 1, \; \sum _{w \in W_d} \xi _{dw} \leqslant 1, \quad d \in N_D,r \in \mathscr {M}_d \end{aligned}$$

(18)

$$\begin{aligned}&\xi _{drw} \in \{0, \; 1 \}, \quad d \in N_D; \; r \in \mathscr {M}_d \; and \; w \in W_{dr} \end{aligned}$$

(19)

$$\begin{aligned}&\xi _{dw} \in \{0, \;1 \}, \quad d \in N_D; \; r \in \mathscr {M}_d \; and \; w \in W_{dr} \end{aligned}$$

(20)

The $\phi _{drw}$ and $\phi _{dw}$ are detailed as below.

$$\begin{aligned} \phi _{drw} = \min \sum _{i \in N_C} \left( \min _{s \in R_{dr}} \beta _{is}\right) z_i, \quad \phi _{dw} = \min \sum _{i \in N_C} \beta _{id} z_i \end{aligned}$$

s.t.

$$\begin{aligned}&\sum _{i \in N_C} q_i z_i = w \end{aligned}$$

(21)

$$\begin{aligned}&0 \leqslant z_i \leqslant 1, \quad i \in N_C \end{aligned}$$

(22)

$\phi _{drw}$ is a lower bound of the second-level route costs for delivering some demand w from the satellites $R_{dr}$, which are visited by the first-level route $r \in \mathscr {M}_d$; $\phi _{dw}$ is a lower bound of the adaptive route costs for delivering some demand w from the depot d.

Theorem 3

$z(\overline{RF}(\beta , \; \lambda , \; \mu )) \leqslant z(F)$, for any $\beta _{ik}$ defined in (11), $\lambda _i \in \mathbb {R}$ and $\mu _k \in \mathbb {R}^-$.

Corollary 2

Let z(UB) be an upper bound of z(F). Then, any optimum solution of the mathematical formulation of A2E-CVRP cannot contain a second-level or adaptive route whose reduced cost $\tilde{c}_{kl} > z(UB) - z(\overline{RF}(\beta , \; \lambda , \; \mu )).$

3.3 The smaller range of demand

The demand range $W_{dr}$ and $W_d$ could be reduced as blow, so that the computation for the lower bound could speed up.

$$\begin{aligned} W_{dr}= & {} \{ w \in \mathbb {Z}^+: w_{dr}^{min} \leqslant w \leqslant w_{dr}^{max}\} , \; { where}\\ W_d^{min}= & {} \max \{0, \; q' \}, \; and \; w_{dr}^{max} = \min \{Q_1, \sum _{s \in R_{dr}} B_s^2, \; B_d^1, \; q_{tot} \}, \; { where}\\ q'= & {} q_{tot} - q_{a} - q'_{1st} - q''_{1st}, \; { where}\\ q_{a}= & {} \sum _{d \in N_D} B_d^2, \; q'_{1st} = \min \left\{ \sum _{d \in N_D \setminus \{ d \}}B_d^1, \; \sum _{s \in N_S} B_s^2 \right\} ,\\&q''_{1st} = \min \left\{ B_d^1, \; \max \{0, \; m_d^1 - 1) \right\} \\ W_{d}= & {} \left\{ w \in \mathbb {Z}^+: w_{d}^{min} \leqslant w \leqslant w_{d}^{max}\right\} , \; { where}\\ W_d^{min}= & {} \max \{0, \; q' \}, \; and \; w_d^{max} = \min \{ B_d^2, \; q_{tot} \}, \; { where}\\ q'= & {} q_{tot} - q_{1st} - q_{a}, \quad q_{1st} = \min \left\{ B_d^1, \; \sum _{s \in N_S} B_s^2 \right\} , \quad q_{a'} = \sum _{d \in N_D \setminus \{ d \}} B_d^2 . \end{aligned}$$

4 The algorithm for the bounds

This section details the algorithm for generating the lower and upper bounds as below, which generalizes the algorithm proposed by Baldacci et al. (2013). Especially for computing the upper bound (UB), we directly use the corresponding procedure described by Baldacci et al. (2013), by abandoning its improvement stage. Our computational results show that it still generates approximate solutions within toleration. Besides, we compute UB each time when the micro iteration is finished to improve the upper bound.

• 1. Initialization

  • $\overline{\mathscr {R}}_k = \{(k,i,k) \}, \; k \in N_S \cup N_D$

  • $\lambda _i = 0, i \in N_C$

  • $\mu _k = 0, \; k \in N_S \cup N_D$

  • $LB = 0 \; and \; UB = \infty$

• 2. Iteration (Macro times)

  • (1) Iteration (Micro times)

    • (i) Set $z^*=0$

    • (ii) Compute $\beta _{ik}, \; i \in N_C, \; k \in N_S \cup N_D$ by routes set $\overline{\mathscr {R}}_k$ and Theorem 4.

    • (iii) Compute $z(\overline{RF})$ as described in Sect. 4.2

      • Set $z^* = z(\overline{RF})$ once $z(\overline{RF}) > z^*$, and

      • Set $\beta ^* = \beta , \lambda ^* = \lambda , \mu ^* = \mu$

    • (vi) Compute $\lambda$ and $\mu$ by the subgradient method, which is described in Sect. 4.2.

  • (2) Compute UB

  • (3) Update $\overline{R}_k = \overline{R}_k \cup \mathscr {N}_k, \;where \; \mathscr {N}_k = \hat{R}_k \setminus \bar{R}_k$.

    • If each $\mathscr {N}_k = \emptyset$ and $z^* > LB$, then $LB = z^*$.

4.1 Computing $\beta _{ik}$

We define the marginal cost $\beta _{is}$ and $\beta _{id}$ for each satellite and each depot respectively, whose computing formulas are combined into (23) in Theorem 4. Because only a subset $\bar{\mathscr {R}}_k \subseteq \hat{\mathscr {R}}_k$ could be used for computing $z^* = z(\overline{RF})$, $\beta _{ik}$ is valid only if both the second-level routes and the adaptive routes are not generated, and so does $z^* = z(\overline{RF})$. The routes are generated in form of ng-routes (Baldacci et al. 2011).

Theorem 4

Let $\hat{\mathscr {R}}_k \supseteq \mathscr {R}_k$ be the index set of second-level or adaptive (nonnecessarily elementary) routes, a feasible $\beta _{ik}$ satisfying (11) could be computed as below.

$$\begin{aligned} \hat{\beta }_{ik} = q_i \cdot \min _{l \in \hat{\mathscr {R}}_{ik}} \left\{ \frac{c_{kl} - \sum _{i \in N_C} \alpha _{ikl} \lambda _i - \mu _k}{\sum _{i \in N_C} \alpha _{ikl} q_i} \right\} , \quad k \in N_S \cup N_D, \; i \in N_S . \end{aligned}$$

(23)

4.2 Generating $z(\overline{RF})$

The solution $z(\overline{RF})$ is generated by solving the following integer program. Here, $h_d^1(w)$ is the minimum cost of depot d, whose delivering demand is w. $h_d^1(w)$ equals to the sum of the costs of its first-level routes and some lower bound $\phi _{drw}$ on the correspondingly second-level routes. $h_d^A(w)$ is the minimum cost of depot d, whose demand is w and delivered by its adaptive routes. Contraint (24) ensures that all the delivered demands equal to the total demands, and Contraint (25) ensures that a depot must deliver exactly one certain demand by its first-level routes or adaptive routes. Finally, $\rho _{dw}^1$ and $\rho _{dw}^A$ are the decision variables. This integer program could be solved within time toleration by CPLEX (2012) or even by pure enumeration, because the number of all the depots is a small constant in the environment of real-world logistics.

$$\begin{aligned} h = \min \sum _{d \in N_D} h_d^1(w) \cdot \rho _{dw}^1 + \sum _{d \in N_D} h_d^A(w) \cdot \rho _{dw}^A \end{aligned}$$

s.t.

$$\begin{aligned}&\sum _{d \in N_D} w \cdot \rho _{dw}^1 + \sum _{d \in N_D} w \cdot \rho _{dw}^A = q_{tot} \end{aligned}$$

(24)

$$\begin{aligned}&\sum _{w \in W_{dr}} \rho _{dw}^1 \leqslant 1, \; \sum _{w \in W_d} \rho _{dw}^A \leqslant 1 = q_{tot} , \quad d \in N_D \end{aligned}$$

(25)

$$\begin{aligned}&\rho _{dw}^1 \in \{0, 1 \}, \quad d \in N_D \end{aligned}$$

(26)

$$\begin{aligned}&\rho _{dw}^A \in \{0, 1 \}, \quad d \in N_D \end{aligned}$$

(27)

In the right side of the objective function, $h_d^A(w)$ and $h_d^1(w)$ are the vectors of the results by solving (28) and the dynamic program (29) respectively.

$$\begin{aligned} h_d^A(w)= & {} \phi _{dw}, \quad d \in \mathscr {N}_d \end{aligned}$$

(28)

$$\begin{aligned} h_d^1(w)= & {} \min _{0 \leqslant w' \leqslant \min \{w, w_{dr}^{max}\}} h_d^1(r-1, w'). \end{aligned}$$

(29)

4.3 Searching direction

The procedure for computing the searching direction in the subgradient method is given as below. In our experiments, the length of search step e is set to a constant 1.0. However, the best value e varies among different instances. A good way to set the value is adopting the changeable length, i.e., e is set to a small value firstly, then is increased when $z(\overline{RF})$ increases slowly and reduced when $z(\overline{RF})$ increases quickly.

• (1) Input

  • optimum solution of $\overline{RF}$: $\xi _{krw}$ and $\xi _{kw}$

  • optimum solution of $\phi _{krw}$ and $\phi _{kw}$: $z_i$

• (2) Computation

  • Obtain route sets $\tilde{\mathscr {R}}_k = \{ l(i,k) \}$ and $\tilde{\mathscr {R}}_d = \{ l(i,d) \}$

    • (i) (a) init $\tilde{\mathscr {R}}_k = \emptyset , \; k \in N_S$

      • (b) and $l(i,d) = 0, i \in N_C, d \in N_D$

    • (ii) (a) for each first-level route dr, such that $\xi _{drw} = 1$,

      • get $\bar{k}(i) = \{k | \min _{k \in R_{dr}} \beta _{ik} \}, i \in V(d,r,w)$

      • set $l(i, \bar{k}(i)) =$ the route corresponding to $\beta _{ik}, i \in V(d,r,w)$

      • for each $i \in V(d,r,w)$, get $\tilde{\mathscr {R}}_{k(i)} = \tilde{\mathscr {R}}_{k(i)} \cup \{ l(i, k(i)) \}$

    • (b) for each depot d, such that $\xi _{dw} = 1$,

      • get $\bar{d}(i) = \{d \}, i \in V(d,w)$

      • set $l(i, \bar{d}(i)) =$ the route corresponding to $\beta _{id}, i \in V(d,w)$

      • for each $i \in V(d,w)$, get $\tilde{\mathscr {R}}_{d(i)} = \tilde{\mathscr {R}}_{d(i)} \cup \{ l(i, d(i)) \}$

• (3) Output

  • $\lambda _i = \lambda _i - \epsilon \cdot \gamma \cdot (\alpha _{iS} + \alpha _{iD} - 1)$

  • $\mu _{k} = \min \{ 0, \; \mu _{k} = \epsilon \cdot \gamma \cdot (\delta _k - m_k) \}$

  • $\mu _{d} = \min \{ 0, \; \mu _{d} = \epsilon \cdot \gamma \cdot (\delta _d - m_d) \}$

  • $\alpha _{iS} = \sum _{s \in N_S} \sum _{l \in \tilde{\mathscr {R}}_s} \alpha _{isl} \cdot \tilde{x}_{sl}, \quad i \in N_C$

  • $\alpha _{iD} = \sum _{d \in N_D} \sum _{l \in \tilde{\mathscr {R}}_d} \alpha _{idl} \cdot \tilde{x}_{dl}, \quad i \in N_C$

  • $\delta _s = \sum _{l \in \tilde{\mathscr {R}}_s} \tilde{x}_{sl}, \quad s \in N_S$

  • $\delta _d = \sum _{l \in \tilde{\mathscr {R}}_d} \tilde{x}_{dl}, \quad s \in N_D$

  • $\tilde{x}_{sl} = \sum _{i \in N_C: l(i, s) = l} ( \alpha _{isl} \cdot q_i) / \left( \sum _{i \in N_C} \alpha _{isl} \cdot q_i\right) , \quad l \in \tilde{\mathscr {R}}_s, \quad s \in N_S$

  • $\tilde{x}_{dl} = \sum _{i \in N_C: l(i, d) = l} ( \alpha _{idl} \cdot q_i) / \left( \sum _{i \in N_C} \alpha _{idl} \cdot q_i\right) , \quad l \in \tilde{\mathscr {R}}_d, \quad d \in N_D$

  • $r = \frac{0.2\overline{RF}(\beta ,\lambda ,\mu )}{{\sum _{i \in N_C} (\alpha _{iS} + \alpha _{iD} - 1)^2 + \sum _{s \in N_S} (\delta _{s} - m_s)^2 + \sum _{d \in N_D} (\delta _{d} - m_d)^2}} .$

5 Computational results

The algorithm for computing the lower and upper bounds are coded in Matlab, with CPLEX (2012) for solving linear programs and mix-integer programs. The experiments are performed on the environment of Inter Core i5-3470 CPU (3.20GHz), 4 GB RAM Memory and Window 7 operation system. The data sets are from Set 1, Set 2 and Set 3 which are used by Baldacci et al. (2013). The computational results are detailed in Tables 1 and 2. In practice, the parameter Macro is set to 50, Micro is set to 5, e is set to 0.1, and |Ni| is set to 12 for instances in Set 1. For Set 2, Macro is set to 15, Micro is set to 20, e is set to 0.1, and |Ni| is set to 21.

Table 1 shows the results of instances from Set 1, each of which has 1 depot, 2 satellites and 13 customers. The “Solution” column lists the solution of A2E-CVRP. The “z(F)” sub-column shows the optimum costs computed directly by CPLEX (2012). The “$n_u/n_s$” sub-column shows the numbers of the used and total satellites in the optimum solutions. In “$N^{1st}{-}N^{2nd}{-}N^a$” sub-column, the numbers from left to right denote the numbers of the first-level routes, second-level routes and adaptive routes respectively used by the optimum solutions. In the “Lower Bound” column, “LB” shows the lower bound computed by our algorithm, and “LB/z” shows the percentages of the lower bounds on the corresponding optimum solutions. The “Comparison” column shows the solution of classical 2E-CVRP. The “z1(F)” sub-column shows the optimum solutions of 2E-CVRP, the “SC” sub column shows the save costs, i.e., $z1(F) - z(F)$, and the “SC/z1” sub-column shows the percentages of the saved costs on z1(F). The bold results in the column of Lower Bound show the exact solutions. The bold results in the column of Comparison show that the saved costs become large when the satellites are located far away from the depot.

Table 1 Computational results on the instances of set 1

Table 2 shows the results of all the instances with 22 customers from Set 2 and 3. When the customer number goes up to 20, the computing time of generating all possible routes is beyond toleration. So, we use the algorithm for computing UB described in Sect. 4 to output approximate solutions. The “Bounds” column shows the lower bounds and upper bounds on the instances, and the LB/UB shows the percentages. The “Comparison” shows the comparison to the computational results of Baldacci et al. (2013), in which “z1(F)” and “LD1” denote the solutions and lower bounds computed by their algorithm DP1. The “SC” sub-column denotes the saved costs, which equal to z1(F) minus UB. The “SC/z1” sub-column shows the percentages of SC on z1(F). The italic results show that there are two solutions which are worse than the compared ones.

Table 2 Computational results on the instances of n22 instances of set 2 and set 3

Figure 2 shows the comparison of the results in Table 1. The lower bounds, z(F) and z1(F) are shown in forms of dashed line, solid line and dotted line respectively. The X-axis shows the instance numbers and the Y-axis show the costs. It is easy to see that z(F) is always lower than z1(F), which demonstrates that the solution of A2E-CVRP is always better than that of classical 2E-CVRP. The z(F) becomes lower and lower than z1(F), when the satellites are located further away from depots. Besides, the lower bounds generated by our algorithm are close to z(F), and there are 22 results out of 66 which are equal to z(F).

Fig. 2

Comparison of the results in Table 1

Figure 3 shows the comparison of the results in Table 2. The lower bounds, upper bounds and z1(F) are showed in forms of dashed line, solid line and dotted line respectively. The meaning of X-axis and the Y-axis is same as that in Fig. 2. The computational results show that the upper bounds are smaller than the optimum solutions of classical 2E-CVRP. There are only two exceptions in the instances, whose lower bounds are close to the optimum solutions of the corresponding 2E-CVRP.

Fig. 3

Comparison of the results in Table 2

6 Conclusions

In this paper, we described the mathematical formulation of the adaptive two echelon vehicle routing problems. Then, a lower bound of A2E-CVRP is given, after which the upper bound could be generated as an approximate solution. The solution of A2E-CVRP is better than that of 2E-CVRP both in theory and our computational experiments.

Tables 1 and 2 show that the saved costs become large when the satellites are located far away from the depot. Besides, the lower bound and upper bound could be further used to derive algorithm for generating solutions closer to the optimality, such as that described by Baldacci et al. (2013) or some branch and bound methods.

Appendices

Appendix 1: Proofs of Theorem 1 and Corollary 1

Consider an optimal solution $(\bar{x}, \bar{y}, \bar{q})$ of cost $\bar{z}(F)$, and we define

$$\begin{aligned} J_{k}= & {} \{l\in R_{k}:\bar{x}_{kl}=1\},\quad k\in N_{S}\cup N_{D}\\ L_{k}= & {} \{r\in M_{d}:\bar{y}_{dr}=1\}, \quad d\in N_{D}\\ \bar{V}_{k}= & {} \{i\in R_{kl}:l\in J_{k}\},\quad k\in N_{S}\cup N_{D}\\ \bar{N}_{S}= & {} \{i\in R_{r}:r \in L_{k}:k\in N_{D}\\ \bar{N}_{D}= & {} \left\{ d \in N_{D}:\sum \limits _{l\in R_{d}}\bar{x}_{dl}\geqslant 1\right\} \end{aligned}$$

Let $z(RF(\beta ,\lambda ,\mu ))$ be the optimal cost, of a valid group of $(\beta ,\lambda ,\mu )$. So, from (11), we have

$$\begin{aligned} \tilde{c}_{kl}=c_{kl}-\sum \limits _{i\in N_{c}}\alpha _{ikl}\cdot (\beta _{ik}+\lambda _{i})-\mu _{k}\geqslant 0, \quad k\in N_{S}\cup N_{D},\quad l\in R_{k} \end{aligned}$$

Then

$$\begin{aligned} \sum \limits _{k\in \bar{N}_{S}\cup \bar{N}_{D}}\sum \limits _{l\in J_{k}}\tilde{c}_{kl}=\sum \limits _{k\in \bar{N}_{S}\cup \bar{N}_{D}}\sum \limits _{l\in J_{k}}c_{kl}-\sum \limits _{k\in \bar{N}_{S}\cup \bar{N}_{D}}\sum \limits _{l\in J_{k}}\sum \limits _{i\in N_{c}}\alpha _{ikl}\cdot (\beta _{ik}+\lambda _{i})-\sum \limits _{k\in \bar{N}_{S}\cup \bar{N}_{D}}\sum \limits _{l\in J_{k}}\mu _{k} \end{aligned}$$

(30)

and obviously,

$$\begin{aligned}&\sum \limits _{l\in J_{k}}\sum \limits _{i\in N_{c}}\alpha _{ikl}\cdot (\beta _{ik}+\lambda _{i})=\sum \limits _{i\in \bar{V}_{k}}(\beta _{ik}+\lambda _{i}), k\in \bar{N}_{S}\cup \bar{N}_{D} \end{aligned}$$

(31)

$$\begin{aligned}&\sum \limits _{k\in \bar{N}_{S}\cup \bar{N}_{D}}\sum \limits _{l\in J_{k}}\mu _{k} =\sum \limits _{k\in \bar{N}_{S}\cup \bar{N}_{D}}|J_{k}|\cdot \mu _{k} \geqslant \sum \limits _{k\in \bar{N}_{S}\cup \bar{N}_{D}}m^{2}_{k}\cdot \mu _{k} \end{aligned}$$

(32)

move (31), (32) into (30), we get

$$\begin{aligned}&\sum \limits _{k\in \bar{N}_{S}\cup \bar{N}_{D}}\sum \limits _{l\in J_{k}}\tilde{c}_{kl}=\sum \limits _{k\in \bar{N}_{S}\cup \bar{N}_{D}}\sum \limits _{l\in J_{k}}c_{kl}+\sum \limits _{d\in N_{d}}\sum \limits _{r\in M_{d}}y_{dr}\cdot g_{dr}\nonumber \\&\quad -\,\left( \sum \limits _{d\in N_{d}}\sum \limits _{r\in M_{d}}y_{dr}\cdot g_{dr}+\sum \limits _{k\in \bar{N}_{S}\cup \bar{N}_{D}}\sum \limits _{i\in \bar{V}_{k}}(\beta _{ik} +\lambda _{i})+\sum \limits _{k\in \bar{N}_{S}\cup \bar{N}_{D}}m^{2}_{k}\cdot \mu _{k}\right) \end{aligned}$$

(33)

In (33), the left side $\geqslant 0$, the first and the second terms of the right side $=\,\bar{z}(F)$, and the remaining terms of the right side = the cost $\tilde{z}(RF(\alpha ,\beta ,\gamma ))$ of feasible solution of

$$\begin{aligned} \tilde{y}= & {} \bar{y}\\ \xi _{ik}= & {} 1, \; i\in \bar{V}_{k},\; k\in \bar{N}_{S}\cup \bar{N}_{D};\; 0, \; otherwise\\ \tilde{q}= & {} \bar{q} \end{aligned}$$

so,

$$\begin{aligned} \sum _{k\in \bar{N}_{S}\cup \bar{N}_{D}}\sum _{l\in J_{k}}\tilde{c}_{kl}\leqslant \bar{z}(F)-z(RF(\beta ,\lambda ,\mu )) \end{aligned}$$

(34)

and

$$\begin{aligned} \bar{z}(F)-z(RF(\beta ,\lambda ,\mu ))\geqslant 0 \end{aligned}$$

It is obvious that corollary 1 hold by (34).

Appendix 2: Proof of Theorem 2

$$\begin{aligned} z(dual\;LF)= & {} max\sum \limits _{i\in N_{c}}u_{i}+\sum \limits _{k\in N_{S}\cup N_{D}}m^{2}_{k}\cdot \upsilon _{k}+\sum \limits _{k\in N_{S}\cup N_{D}}B^{2}_{k}\cdot \sigma _{k}+\sum \limits _{d\in N_{D}}m^{1}_{d}\cdot \eta _{d}\nonumber \\&+\,\sum \limits _{d\in N_{d}}\sum \limits _{d\in N_{D}}\sum \limits _{r\in M_{d}}\vartheta _{dr} \end{aligned}$$

s.t.

$$\begin{aligned}&\sum \limits _{i\in R_{sl}}\mu _{i}+\upsilon _{s}+w_{sl}\cdot \sigma _{s}-\omega _{sl}\cdot \alpha \leqslant c_{sl},\quad s\in N_{s},l\in R_{s} \end{aligned}$$

(35)

$$\begin{aligned}&\sum \limits _{i\in R_{dl}}\mu _{i}+\upsilon _{d}+\omega _{d}l\cdot \sigma _{d}\leqslant c_dl, \quad d\in N_{D},l\in R_{k} \end{aligned}$$

(36)

$$\begin{aligned}&\eta _{d}-Q_{1}\cdot \omega _{dr}+\vartheta _{dr}\leqslant g_{dr}, \quad d\in N_{d},r\in M_{d} \end{aligned}$$

(37)

$$\begin{aligned}&\alpha _{i}+\omega _{dr}\leqslant 0, \quad i\in N_{s},d\in N_{d},r\in M_{id} \end{aligned}$$

(38)

$$\begin{aligned}&\mu \in \mathbb {R}, \upsilon _{k},\sigma _{k},\alpha _{k},\eta _{k}, \omega _{kr},\vartheta _{kr}\leqslant 0 . \end{aligned}$$

(39)

1.1 Construct $(\beta ,\lambda ,\mu )$ satisfying (11)

Firstly, let

$$\begin{aligned} \mu _{k}= & {} \upsilon ^{*}_{k},\quad k\in N_{S}\cup N_{D}\\ \beta _{is}= & {} \mu ^{*}_{i}+q_{i}(\sigma ^{*}_{s}-\alpha ^{*}_{s}), \quad i\in N_{c},s\in N_{S}\\ \beta _{id}= & {} u^{*}_{i}+q_{i}\cdot \sigma _{d}^{*},\quad i\in N_{c},d\in N_{D}\\ \lambda _{i}= & {} 0,\quad i\in N_{c} \end{aligned}$$

By the definition of $a_{ikl}$, it’s obvious that

$$\begin{aligned} \mathop {\sum }\limits _{i \in {N_c}} {a_{ikl}} \cdot {q_i} = {w_{kl}},k \in {N_S}\mathop \cup {N_D},\quad l \in {{\mathscr {R}}_k} \end{aligned}$$

then, we have

$$\begin{aligned} \mathop {\sum }\limits _{i \in {N_c}} {a_{ikl}} \cdot {\beta _{\mathrm{{ik}}}} = \mathop {\sum }\limits _{i \in {N_c}} {a_{ikl}} \cdot u_\mathrm{{i}}^* + {w_{kl}} \cdot \sigma _\mathrm{{k}}^* - {w_{kl}} \cdot \alpha _\mathrm{{k}}^*,\quad s \in {N_S},l \in {{\mathscr {R}}_k} \end{aligned}$$

and

$$\begin{aligned}&\mathop {\sum }\limits _{i \in {N_c}} {a_{idl}} \cdot {\beta _{\mathrm{{id}}}} = \mathop {\sum }\limits _{i \in {N_c}} {a_{idl}} \cdot u_\mathrm{{i}}^* + {w_{dl}} \cdot \sigma _\mathrm{{d}}^*,\;\;\;\;d \in {N_D},l \in {{\mathscr {R}}_d}\\&\mathop {\sum }\limits _{i \in {N_c}} {a_{ikl}} \cdot {\beta _{\mathrm{{ik}}}} \le {c_{kl}} - v_\mathrm{{k}}^*,\;\;\;\;k \in {N_S}\mathop \cup \nolimits ^ {N_D},l \in {{\mathscr {R}}_k} \end{aligned}$$

1.2 Prove $max_{(\beta ,\lambda ,\mu )}\geqslant z(RF(\beta ,\lambda ,\mu ))\geqslant z(dual LF)$

For $\mu$ and $\upsilon$

Let $(\xi ^{*},y^{*},q^{*})$ be the optimal solution of $z(RF(\beta ,\lambda ,\mu ))$. By definition $(\beta ,\lambda ,\mu )$, we have

$$\begin{aligned} z\left( {RF\left( {\beta ,\lambda ,\mu } \right) } \right)= & {} \mathop {\sum }\limits _{s \in {N_s}} \mathop {\sum }\limits _{i \in {N_c}} (u_\mathrm{{i}}^* + {q_\mathrm{{i}}} \cdot \left( {\sigma _\mathrm{{s}}^* - \alpha _\mathrm{{s}}^*} \right) ) \cdot \xi _{is}^* + \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{i \in {N_c}} (u_\mathrm{{i}}^* + {q_\mathrm{{i}}} \cdot \sigma _\mathrm{{d}}^*) \cdot \xi _{id}^*\\&+\, \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} y_{dr}^* \cdot {g_{dr}} + \mathop {\sum }\limits _{i \in {N_c}} {\lambda _i} + \mathop {\sum }\limits _{k \in {N_s}\mathop \cup \nolimits ^ {N_D}} v_\mathrm{{k}}^* \cdot m_k^2\\= & {} \mathop {\sum }\limits _{i \in {N_c}} u_\mathrm{{i}}^* \cdot \left( \mathop {\sum }\limits _{s \in {N_s}} \xi _{is}^*\right) \mathrm{{ + }}\mathop {\sum }\limits _{s \in {N_s}} \sigma _\mathrm{{s}}^* \cdot \left( \mathop {\sum }\limits _{i \in {N_c}} {q_\mathrm{{i}}}\xi _{is}^*\right) \\&-\, \mathop {\sum }\limits _{s \in {N_s}} \alpha _\mathrm{{s}}^* \cdot \left( \mathop {\sum }\limits _{i \in {N_c}} {q_\mathrm{{i}}}\xi _{is}^*\right) \\&+\, \mathop {\sum }\limits _{i \in {N_c}} u_\mathrm{{i}}^* \cdot \left( \mathop {\sum }\limits _{d \in {N_D}} \xi _{id}^*\right) + \mathop {\sum }\limits _{d \in {N_D}} \sigma _\mathrm{{d}}^* \cdot \left( \mathop {\sum }\limits _{i \in {N_c}} {q_\mathrm{{i}}}\xi _{id}^*\right) \\&+\, \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} y_{dr}^* \cdot {g_{dr}} + \mathop {\sum }\limits _{k \in {N_s}\mathop \cup {N_D}} v_\mathrm{{k}}^* \cdot m_k^2 \end{aligned}$$

By (12), we have

$$\begin{aligned} \mathop {\sum }\limits _{i \in {N_c}} u_\mathrm{{i}}^* \cdot \left( \mathop {\sum }\limits _{k \in {N_s}\mathop \cup {N_D}} \xi _{ik}^*\right) = \mathop {\sum }\limits _{i \in {N_c}} u_\mathrm{{i}}^* \end{aligned}$$

For $\eta$ and $\vartheta$

By (37), we have

$$\begin{aligned} \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} {g_{dr}} \cdot {y^*}_{dr}\geqslant & {} \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} {\eta ^*}_d \cdot {y^*}_{dr} - \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} {Q_1} \cdot {\omega ^*}_{dr} \cdot {y^*}_{dr} \\&+ \,\mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} {\vartheta ^*}_{dr} \cdot {y^*}_{dr} \end{aligned}$$

Then, because $\eta ^*_{d}\leqslant 0$, and by (13), we have

$$\begin{aligned} \mathop {\sum }\limits _{d \in {N_D}} \left( {\eta ^*}_d \cdot \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} {y^*}_{dr}\right) \ge \mathop {\sum }\limits _{d \in {N_D}} {\eta ^*}_d \cdot m_d^1 \end{aligned}$$

and because $\vartheta ^*_d\leqslant 0$, we have

$$\begin{aligned} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} {\vartheta ^*}_d \cdot {y^*}_{dr} \geqslant \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} {\vartheta ^*}_d \end{aligned}$$

For $\sigma$

From above, we have

$$\begin{aligned} z \left( {RF\left( {\beta ,\lambda ,\mu } \right) } \right)\geqslant & {} \mathop {\sum }\limits _{i \in {N_c}} u_\mathrm{{i}}^* + \mathop {\sum }\limits _{s \in {N_s}} \sigma _\mathrm{{s}}^* \cdot \left( \mathop {\sum }\limits _{i \in {N_c}} {q_\mathrm{{i}}}\xi _{is}^*\right) -\mathop {\sum }\limits _{s \in {N_S}} \alpha _\mathrm{{s}}^* \cdot \left( \mathop {\sum }\limits _{i \in {N_c}} {q_\mathrm{{i}}}\xi _{is}^*\right) \\&+\, \mathop {\sum }\limits _{i \in {N_c}} u_\mathrm{{i}}^* \cdot \left( \mathop {\sum }\limits _{d \in {N_D}} \xi _{id}^*\right) + \mathop {\sum }\limits _{d \in {N_D}} \sigma _\mathrm{{d}}^* \cdot \left( \mathop {\sum }\limits _{i \in {N_c}} {q_\mathrm{{i}}}\xi _{id}^*\right) + \mathop {\sum }\limits _{d \in {N_D}} {\eta ^*}_d \cdot m_d^1\\&-\, \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} {Q_1} \cdot {\omega ^*}_{dr} \cdot {y^*}_{dr} + \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} {\vartheta ^*}_{dr} \!+\! \mathop {\sum }\limits _{k \in {N_S}\mathop \cup {N_D}} v_\mathrm{{k}}^* \cdot m_k^2 \end{aligned}$$

Because $\sigma ^*_d\leqslant 0$ and by (13), we have:

$$\begin{aligned} \mathop {\sum }\limits _{k \in {N_S}\mathop \cup {N_D}} \sigma _\mathrm{{k}}^* \cdot \left( \mathop {\sum }\limits _{i \in {N_c}} {q_\mathrm{{i}}}\xi _{ik}^*\right) \ge \mathop {\sum }\limits _{k \in {N_S}\mathop \cup {N_D}} \sigma _\mathrm{{k}}^* \cdot B_k^2 \end{aligned}$$

For $\alpha$ and $\omega$

By (14), we have

$$\begin{aligned} \mathop {\sum }\limits _{s \in {N_s}} \alpha _\mathrm{{s}}^* \cdot \left( \mathop {\sum }\limits _{i \in {N_c}} {q_\mathrm{{i}}}\xi _{is}^*\right)= & {} \mathop {\sum }\limits _{s \in {N_s}} \alpha _\mathrm{{s}}^* \cdot \left( {\mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_{sd}}} q_{srd}^*} \right) \\= & {} \mathop {\sum }\limits _{s \in {N_s}} \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_{sd}}} \alpha _\mathrm{{s}}^* \cdot q_{srd}^* \\= & {} \mathop {\sum }\limits _{i \in {N_s}} \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_{id}}} \alpha _\mathrm{{i}}^* \cdot q_{srd}^* \end{aligned}$$

Because $\omega ^*_{kr}\leqslant 0$, and by (6), we have:

$$\begin{aligned} \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} ( - {\omega ^*}_{dr}{y^*}_{dr}{Q_1})\geqslant & {} \mathop {\sum }\limits _{\mathrm{{d}} \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} \left( - {\omega ^*}_{dr}\mathop {\sum }\limits _{i \in {R_{dr}}} q_{srd}^*\right) \\= & {} \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_d}} \mathop {\sum }\limits _{i \in {R_{dr}}} ( - {\omega ^*}_{dr} \cdot q_{srd}^*)\\= & {} \mathop {\sum }\limits _{d \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_{id}}} \mathop {\sum }\limits _{i \in {N_S}} ( - {\omega ^*}_{dr} \cdot q_{srd}^*) \\= & {} \mathop {\sum }\limits _{i \in {N_S}} \mathop {\sum }\limits _{k \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_{ik}}} ( - {\omega ^*}_{kr} \cdot q_{jrk}^*) \end{aligned}$$

and because (38), we have

$$\begin{aligned}&- \mathop {\sum }\limits _{k \in {N_s}} \alpha _\mathrm{{k}}^* \cdot \left( \mathop {\sum }\limits _{i \in {N_c}} {q_\mathrm{{i}}}\xi _{ik}^*\right) - \mathop {\sum }\limits _{k \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_k}} {Q_1} \cdot {\omega ^*}_{kr} \cdot {y^*}_{kr}\\&\quad \geqslant \, - \mathop {\sum }\limits _{i \in {N_s}} \mathop {\sum }\limits _{k \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_{ik}}} \alpha _\mathrm{{i}}^* \cdot q_{irk}^*\\&\qquad +\, \mathop {\sum }\limits _{i \in {N_s}} \mathop {\sum }\limits _{k \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_{ik}}} ( - {\omega ^*}_{kr} \cdot q_{jrk}^*)\\&\quad = \, - \mathop {\sum }\limits _{i \in {N_s}} \mathop {\sum }\limits _{k \in {N_D}} \mathop {\sum }\limits _{r \in {{\mathscr {M}}_{ik}}} (\alpha _\mathrm{{i}}^* + {\omega ^*}_{kr}) \cdot q_{jrk}^*\\&\quad \geqslant \,0 \end{aligned}$$

Finally, by all above, we get $z(RF(\beta ,\lambda ,\mu ))\geqslant z(dual LF)$

Appendix 3: Proofs of Theorem 3 and Corollary 2

We define the optimum solution of ${\phi _{krw}: z_i^*(d,r,w), \; i \in N_C}$. Let $V\left( {d,r,w} \right) = \{ i \in N_C: z_i^*(d,r,w) > 0\}$ be the set of supplied customers, and $\xi _{krw} = 1$ if and only if route $r \in {{\mathscr {M}}_d}$ delivers demand w in the optimum solution.

Step 1: Prove $\zeta _{krw}$ defined by $(\bar{\xi }, \bar{y}, \bar{q})$ is a feasible solution

Let $(\bar{\xi }, \bar{y}, \bar{q})$ be an optimum solution of $z(RF(\beta , \lambda , \mu ) )$, and we define $\overline{\mathscr {M}}_d = \{r \in \mathscr {M}_d: \bar{y}_{dr} = 1\}, \; \overline{V}_d = \{i \in N_C: \bar{\xi }_{dr} = 1\}$. For any $r \in {{\mathscr {M}}_d}$, define $\bar{w}_{dr} = \sum _{s \in R_{dr}} \bar{q}_{srd}$. For all $\bar{\zeta }_{drw}$, set $\bar{\zeta }_{drw} = 1$, when $r \in {\overline{{\mathscr {M}}}_d}$ and $w = \bar{w}_{dr}$; set $\bar{\zeta }_{drw} = 0$, when $r \in {\overline{{\mathscr {M}}}_d}$ but $w \ne \bar{w}_{dr}$; set $\bar{\zeta }_{drw} = 0$, when $d \in {{\mathscr {M}}_d \setminus \overline{{\mathscr {M}}}_d}$. For $\overline{N}_D = \{d \in N_D: \sum _{i \in N_C} q_i \cdot \bar{\xi }_{id} > 0 \}$, we define $\bar{w}_d = \sum _{i \in N_C} q_i \cdot \bar{\xi }_{id}$. For all $\bar{\zeta }_{dw}$, set $\bar{\zeta }_{dw} = 1, \; when \; d \in {\overline{N}_D}$ and $w \ne \bar{w}_d$; set $\bar{\zeta }_{dw} = 0, \; when \; d \in {N_D \setminus \overline{N}_D}$.

Its’ obvious that $\zeta _{drw}$ satisfies (18), now we prove that $\bar{\zeta }_{drw}$ satisfies (17). By (14), we have

$$\begin{aligned} \sum _{d \in {N_D}} \sum _{i \in {N_c}} {\bar{\xi }_{id}} \cdot {q_i} + \sum \limits _{s \in {N_S}} \sum _{d \in {N_D}} \sum _{r \in {{\mathscr {M}}_{sk}}} {\bar{q}_{srd}} = \sum _{k \in {N_S} \cup {N_D}} \sum _{i \in {N_c}} {\bar{\xi }_{ik}} \cdot q_i . \end{aligned}$$

By ${\bar{q}_{srd}}, \; when \; r \in \mathscr {M}_d \setminus \overline{\mathscr {M}}_d, \, s \in N_S$, ${\bar{q}_{srd}} = 0, \; when \; r \in \overline{\mathscr {M}}_d, \; s \in N_S \setminus R_{dr}$, and the definition of $\bar{w}_{dr}$ and $\bar{\zeta }_{drw}$, we have

$$\begin{aligned} \sum _{s \in {N_S}} \sum _{d \in {N_D}} \sum _{r \in {{\mathscr {M}}_{sd}}} {\bar{q}_{srd}} = \sum _{\mathrm{{d}} \in {N_D}} \sum _{r \in \overline{\mathscr {M}}_d} \sum _{s \in {R_{dr}}} {\bar{q}_{srd}} = \sum _{d \in {N_D}} \mathop \sum _{r \in {{\mathscr {M}}_d}} \sum _{w \in {W_{dr}}} w \cdot {\bar{\zeta }_{drw}} \end{aligned}$$

and

$$\begin{aligned} \sum _{d \in {N_D}} \sum _{w \in {W_d}} w \cdot {\bar{\zeta }_{dw}} = \sum _{d \in {N_D}} \sum _{i \in {N_c}} {\bar{\xi }_{id}} \cdot {q_i}. \end{aligned}$$

By (12), we have

$$\begin{aligned} \sum _{s \in {N_S}} \sum _{i \in {N_c}} {\bar{\xi }_{is}} \cdot {q_i} = \sum _{i \in {N_c}} \left( {q_i} \cdot \sum _{s \in {N_S}} {\bar{\xi }_{is}}\right) \end{aligned}$$

and

$$\begin{aligned} \sum _{k \in {N_S} \cup {N_D}} \sum _{i \in {N_c}} {\bar{\xi }_{ik}} \cdot {q_i} = \sum _{i \in {N_c}} \left( {q_i} \cdot \sum _{k \in {N_S} \cup {N_D}} {\bar{\xi }_{ik}}\right) = \sum _{i \in {N_c}} {q_i} = {q_{tot}}. \end{aligned}$$

From the above 4 equations, we prove $\bar{\zeta }_{drw}$ satisfies (17).

Step 2: Prove $\theta _{ikr}$ defined by $(\bar{\xi }, \bar{y}, \bar{q})$ is a feasible solution

For $i \in N_C$, we define $\theta _{ikr}$. When $s \in N_S, \; r \in \mathscr {M}_d$ and $\mathscr {M}_{sd} = M_{sd}$,

$$\begin{aligned} {\theta _{isrd}} = \left\{ {\begin{array}{ll} 0, &{}\quad if \quad {\bar{\xi }_{is}} = 0\\ \frac{{{\bar{q}_{srd}}}}{{ \sum _{d \in {N_D}} \sum _{r \in {\overline{\mathscr {M}}_{sd}}} {\bar{q}_{srd}}}}, &{} \quad if \quad \bar{\xi }_{is} = 1 \end{array}} \right. \end{aligned}$$

When $d \in N_D$,

$$\begin{aligned} {\theta _{id}} = \left\{ {\begin{array}{ll} 0, &{}\quad if \quad {\bar{\xi }_{id} = 0}\\ 1, &{}\quad if \quad \bar{\xi }_{id} = 1 \end{array}} \right. \end{aligned}$$

Then, for $d \in N_D, r \in \overline{\mathscr {M}}_d, \; w = \bar{w}_{dr}$, we define $\bar{z}_i (r, \bar{w}_{dr}) = \sum _{s \in R_{dr}} \theta _{isrd}$ , and for $d \in N_D, \; w = \bar{w}_d$, we define $\bar{z}_i (\bar{w}_{d}) = \theta _{id}$. It’s obvious that $0 \leqslant z_i \leqslant 1$, now we prove $\bar{z}_i$ satisfies the constraint $\sum _{i \in N_C} q_i \cdot z_i = w$.

Part 1

For $d \in N_D, r \in \overline{\mathscr {M}}_d, \; w = \bar{w}_{dr}$, we have

$$\begin{aligned} \sum _{i \in {N_C}} {q_i} \cdot {\bar{z}_i}\left( {r,{\bar{w}_{dr}}} \right) = \sum _{i \in {N_C}} {q_i} \cdot \sum _{s \in {R_{dr}}} {\theta _{isrd}}. \end{aligned}$$

By the definition of $\theta _{isrd}$, it is easy to have

$$\begin{aligned} \sum _{i \in {N_C}} {q_i} \cdot \sum _{s \in {R_{dr}}} {\theta _{isrd}}= & {} \sum _{i \in {N_C}} \sum _{s \in {R_{dr}}} {q_i} \cdot {\theta _{isrd}} = \sum _{s \in {R_{dr}}} \sum _{i \in {\overline{V}_s}} {q_i} \cdot {\theta _{isrd}} \\= & {} \sum _{s \in {R_{dr}}} \left( \sum _{i \in {\overline{V}_s}} {q_i}\right) \cdot \frac{{{\bar{q}_{srd}}}}{{\sum _{d \in {N_D}} \sum _{r \in {\overline{\mathscr {M}}_{sd}}} {\bar{q}_{srd}}}}. \end{aligned}$$

Since $\sum _{d \in {N_D}} \sum _{r \in {\overline{\mathscr {M}}_{sd}}} {\bar{q}_{srd}} = \sum _{i \in {\overline{V}_s}} {q_i}$, we have

$$\begin{aligned} \sum _{s \in {R_{dr}}} \left( \sum _{i \in {\overline{V}_s}} {q_i}\right) \cdot \frac{{{\bar{q}_{srd}}}}{{\sum _{d \in {N_D}} \sum _{r \in {\overline{\mathscr {M}}_{sd}}} {\bar{q}_{srd}}}} = \sum _{s \in {R_{dr}}} {\bar{q}_{srd}} = {\bar{w}_{dr}}. \end{aligned}$$

From the above 3 equations, we get

$$\begin{aligned} \sum _{i \in {N_C}} {q_i} \cdot {\bar{z}_i}\left( {r,{\bar{w}_{dr}}} \right) = {\bar{w}_{dr}}. \end{aligned}$$

Part 2

For $d \in N_D, \; w = \bar{w}_d$, by the definition of $\theta _{id}$, it is easy to have

$$\begin{aligned} \sum _{i \in {N_C}} {q_i} \cdot {\bar{z}_i}\left( {r,{\bar{w}_{d}}} \right) = \sum _{i \in {N_C}} {q_i} \cdot {\theta _{id}} = \sum _{i \in {\overline{V}_C}} {q_i} \cdot {\theta _{id}} = {\bar{w}_{d}}. \end{aligned}$$

Step 3: Prove $z(RF({\beta }, {\lambda }, {\mu })) \geqslant z(\overline{RF}(\bar{\beta }, \bar{\lambda }, \bar{\mu }))$

By the definition of $\theta _{isrd}$ and $\theta _{id}$ , it is easy to know that, when i is served by $s \in N_S, \bar{\xi }_{is} = \sum _{d \in N_D} \sum _{r \in \overline{\mathscr {M}}_{sk}} \theta _{isrd}$; When i is served by $d \in N_D, \; \bar{\xi }_{id} = \theta _{id}$. So, we have

$$\begin{aligned} \bar{z}(RF({\beta }, {\lambda }, {\mu }))= & {} \min \sum _{k \in {N_S} \cup {N_D}} \sum _{i \in {N_c}} {\bar{\xi }_{ik}} \cdot {\beta _{ik}} + \sum _{d \in {N_D}} \sum _{r \in {{\mathscr {M}}_d}} {\bar{y}_{dr}} \cdot {g_{dr}} \\&+\, \sum _{i \in {N_c}} {\lambda _i} + \sum _{k \in {N_s} \cup {N_D}} {\mu _k} \cdot m_k^2\\= & {} \min \sum _{s \in {N_S}} \sum _{i \in {N_c}} {\bar{\xi }_{ik}} \cdot {\beta _{is}} + \sum _{d \in {N_D}} \sum _{i \in {N_c}} {\bar{\xi }_{id}} \cdot {\beta _{id}} + \sum _{d \in {N_D}} \sum _{r \in {{\mathscr {M}}_d}} {\bar{y}_{dr}} \cdot {g_{dr}} \\&+\, \sum _{i \in {N_c}} {\lambda _i} + \sum _{k \in {N_s} \cup {N_D}} {\mu _k} \cdot m_k^2\\= & {} \min \sum _{s \in {N_S}} \sum _{i \in {N_c}} \left( {{\sum _{d \in {N_D}} \sum _{r \in {\overline{\mathscr {M}}_{sd}}} {\theta _{srd}}}}\right) \cdot {\beta _{is}} + \sum _{d \in {N_D}} \sum _{r \in {\overline{{\mathscr {M}}}_d}} {g_{dr}} \\&+\, \sum _{d \in {N_D}} \sum _{i \in {N_C}} {\bar{\theta }_{id}} \cdot {\beta _{id}} + \sum _{i \in {N_c}} {\lambda _i} + \sum _{k \in {N_s} \cup {N_D}} {\mu _k} \cdot m_k^2 \end{aligned}$$

It’s obvious that:

$$\begin{aligned} \sum _{s \in {N_s}} \sum _{i \in {N_c}} \left( {\sum \limits _{d \in {N_D}} \sum _{r \in {\overline{\mathscr {M}}_{sd}}} {\theta _{isrd}}} \right) \cdot {\beta _{is}}= & {} \sum _{s \in {N_s}} \sum _{i \in {N_c}} \sum _{d \in {N_D}} \sum _{r \in {\overline{\mathscr {M}}_{sd}}} {\theta _{isrd}} \cdot {\beta _{is}}\\= & {} \sum _{d \in {N_D}} \sum _{i \in {N_c}} \sum _{s \in {N_s}} \sum _{r \in {\overline{\mathscr {M}}_{sd}}} {\theta _{isrd}} \cdot {\beta _{is}}.\\= & {} \mathop \sum _{d \in {N_D}} \sum _{i \in {N_c}} \sum _{r \in {\overline{\mathscr {M}}_d}} \sum _{s \in {R_{dr}}} {\theta _{isrd}} \cdot {\beta _{is}} \\= & {} \sum _{d \in {N_D}} \sum _{r \in {\overline{\mathscr {M}}_d}} \left( \sum _{i \in {N_c}} \sum _{s \in {R_{dr}}} {\theta _{isrd}} \cdot {\beta _{is}}\right) . \end{aligned}$$

By ${\bar{z}_i} (r, \bar{w}_{dr}) = \sum _{s \in {R_{dr}}} {\theta _{isrd}}, \; \bar{z}_i(\bar{w}_d ) = \theta _{id} = \bar{\xi }_{id}$, and the definition of $\zeta _{drw}$ and $\zeta _{dw}$, we have

$$\begin{aligned} \sum _{i \in {N_c}} \sum _{s \in {R_{dr}}} {\beta _{is}} \cdot {\theta _{isrd}}\ge & {} \sum _{i \in {N_c}} \left( { {\min }_{s \in {R_{dr}}} {\beta _{is}}} \right) \cdot \left( { \sum _{s \in {R_{dr}}} {\theta _{isrd}}} \right) \\= & {} \sum _{i \in {N_c}} \left( { {\min }_{s \in {R_{dr}}} {\beta _{is}}} \right) \cdot {\bar{z}_i}(r, \bar{w}_{dr}) = {\bar{\phi }_{dr{\bar{w}_{dr}}}} \end{aligned}$$

and

$$\begin{aligned} \sum _{i \in {N_c}} \sum _{s \in {R_{dr}}} {\beta _{id}} \cdot {\theta _{id}} = \sum _{i \in {N_C}} {\bar{z}_i}(\bar{w}_{d}) \cdot \beta _{id} = {\bar{\phi }_{d{\bar{w}_{d}}}}, \end{aligned}$$

so,

$$\begin{aligned} \bar{z}(RF({\beta }, {\lambda }, {\mu })) \geqslant \min \sum _{d \in {N_D}} \sum _{r \in {{\mathscr {M}}_d}} ({\bar{\phi }_{dr{\bar{w}_{dr}}}} + g_{dr})+ {\bar{\phi }_{d{\bar{w}_{d}}}} + \sum _{i \in {N_c}} {\lambda _i} + \sum _{k \in {N_s} \cup {N_D}} {\mu _k} \cdot m_k^2. \end{aligned}$$

Finally, we conclude that

$$\begin{aligned} {z}(RF({\beta }, {\lambda }, {\mu })) = \bar{z}(RF({\beta }, {\lambda }, {\mu })) \geqslant \bar{z}(\overline{RF}({\beta }, {\lambda }, {\mu })) \geqslant {z}(\overline{RF}({\beta }, {\lambda }, {\mu })). \end{aligned}$$