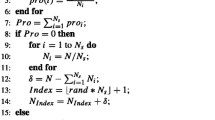Modified differential evolution with self-adaptive parameters method

Abstract

The differential evolution algorithm (DE) is a simple and effective global optimization algorithm. It has been successfully applied to solve a wide range of real-world optimization problem. In this paper, the proposed algorithm uses two mutation rules based on the rand and best individuals among the entire population. In order to balance the exploitation and exploration of the algorithm, two new rules are combined through a probability rule. Then, self-adaptive parameter setting is introduced as uniformly random numbers to enhance the diversity of the population based on the relative success number of the proposed two new parameters in a previous period. In other aspects, our algorithm has a very simple structure and thus it is easy to implement. To verify the performance of MDE, 16 benchmark functions chosen from literature are employed. The results show that the proposed MDE algorithm clearly outperforms the standard differential evolution algorithm with six different parameter settings. Compared with some evolution algorithms (ODE, OXDE, SaDE, JADE, jDE, CoDE, CLPSO, CMA-ES, GL-25, AFEP, MSAEP and ENAEP) from literature, experimental results indicate that the proposed algorithm performs better than, or at least comparable to state-of-the-art approaches from literature when considering the quality of the solution obtained.

1 Introduction

Many real-world problems may be formulated as optimization problems with variables in continuous domains. In the past decade, we have viewed different kinds of evolutionary algorithms advanced to solve optimization problems, such as genetic algorithm (GA), particle swarm optimization algorithm (PSO), estimation of distribution algorithms (EDA), ant colony optimization (ACO), simulated annealing (SA), biogeography based optimization (BBO), differential evolution (DE), artificial bee colony (ABC), and cuckoo search algorithm (CS) (Suman 2004; Horn et al. 1994; Zhang and Muhlenbein 2004; Clerc and Kennedy 2002; Dorigo et al. 1996; Simon 2008; Storn and Price 1997; Yang and Deb 2009).

Recently, differential evolution algorithm (Storn and Price 1997) has been proposed as a simple and powerful population-based stochastic optimization method, which is originally motivated by the mechanism of the natural selection. This algorithm searches solutions using three basic operators: mutation, crossover and greedy selection. Mutation is used to generate a mutation vector by adding differential vectors obtained from the difference of several randomly chosen parameter vectors to the parent vector. After that, crossover operation generates the trial vector by combining the parameters of the mutation vector with the parameters of a parent vector selected from the population. Finally, according to the fitness value, selection operation determines which of the vectors should be chosen for the next generation by implementing a one-to-one completion between the generated trail vectors and the corresponding parent vectors. In order to accelerate the convergence speed and avoid trapping in the local optima, several variations of DE have been proposed to enhance the performance of the standard DE recently. Moreover, DE has been proved to be quite efficient when solving real-world problems. Similar with other evolutionary algorithms, DE also has many disadvantages. For example, while the global exploration ability is considered adequate, its local exploitation ability is regarded weak and its convergence velocity is too low. In the other aspects, the performance of the DE algorithm is sensitive to the mutation strategy and respective control parameters such as the population size, crossover rate and scale factor. The best setting for the control parameter is different for different problems. Therefore, in order to successfully solve a complex problem, the parameter setting and the mutation strategy are very important (Das and Suganthan 2011).

In fact, the performance of the conventional DE algorithm highly depends on the mutation and crossover operations. Being fascinated by the prospect and potential of DE, recently, many researches are working on the improvement of DE, and many variants of the new algorithm are presented. A brief overview of these algorithms is proposed in this section.

Brest et al. (2006) proposed a self adaptive parameter setting in differential evolution algorithm in order to avoid the manual parameter setting of $F$ and CR. The parameter control technique is based on the self adaptation of two parameters associated with the evolutionary process. The main goal here is to product a flexible DE, in terms of control parameters $F$ and CR. The result shows that the algorithm with self adaptive control parameter setting is better than, or at least comparable to, the standard DE algorithm and other evolutionary algorithms from literature.

Rahnamayan et al. (2008) proposed the opposition based Differential evolution (ODE) employing the logic based on the opposition points in order to enhance search properties of DE and test a wide portion of the decision space. The ODE algorithm consists of a DE framework and two opposition based components: the first after the initial sampling and the second after the survivor selection scheme.

Liu and Lampinen (2005) introduced a new version of the differential evolution algorithm with control parameters, called the fuzzy adaptive differential evolution algorithm. The algorithm uses the fuzzy logic controllers to adapt the parameters.

Qin et al. (2009) proposed a self adaptive DE algorithm (SaDE), in which both trail vector generation strategies and their associated control parameter values were gradually self-adaptive by learning from their previous experiences in generating promising solutions. This method does not use any particular learning strategy, nor any specific setting for the control parameters $F$ and CR. From the results, we can conclude that SaDE is more effective in obtaining better quality solution, which are more stable with the relatively smaller standard deviation and higher success rate.

Zhang and Sanderson (2009) proposed a novel algorithm, named JADE, to improve the performance of the differential evolution algorithm by proposing a novel mutation strategy “DE/current-to-pbest/1” and then the self adaptive parameters were used to update the parameters. Experiment results show that JADE is better than, or at least comparable to other algorithms in terms of the solutions.

Ghosh et al. (2011) proposed an effective adaptation technique which suggested a novel automatic tuning method for the scale factor and crossover rate of population members in DE. This technique is proposed based on their objective function values. Comparison with the best-known and expensive variants of DE over fourteen well-known numerical benchmarks and a real-life engineering problem reflects the superiority of proposed parameter tuning scheme in terms of the accuracy, convergence speed, and robustness.

Das et al. (2009) described a family of improved variants of the DE/target-to-best/1/bin scheme, which utilized the concept of the neighborhood of each population member. In order to balance the exploration and exploitation of the algorithm, a new hybrid mutation strategy is proposed. The local mutation model was the explorative mutation operator and the global mutation model is the exploitative mutation operator. Experiment results showed that the algorithm was better than other algorithms on a test suite of 24 test problems and two real-life problems.

Wang et al. (2011a) proposed a new composite differential evolution algorithm, which was improved by combining several effective trial vector generation strategies with some suitable control parameter settings. This algorithm used three trail generator methods and three different parameter settings. CoDE has been tested on all the CEC2005 test problems. Experimental results showed that the CoDE algorithm was very competitive.

In other aspects, some studies on hybrid algorithms for DE found that the performance of hybrid DE algorithms have a better solution quality with in a given number of objective function evaluations. Therefore, there has been an increasing interest in combining DE with other algorithms. Gong et al. (2010) proposed a hybrid DE with BBO namely DE/BBO, for the global numerical optimization problem. The algorithm combines the exploration of DE with the exploitation of BBO effectively. The experimental results show that the algorithm can obtain the high quality of the final solutions and the high convergence rate. Sun et al. (2004) proposed a combination of DE algorithms and the estimation of distribution algorithm (EDA), in which new promising solution was created by DE/EDA. This algorithm used a probability model to determine promising regions in order to focus the search process on those areas. The presented experimental results showed that the DE/EDA outperformed DE and EDA. Noman and Iba (2008) proposed a crossover-based adaptive local search operation for enhancing the performance of standard differential evolution algorithm; this algorithm combined the DE with fittest individual refinement (FIR). The FIR scheme accelerated DE by applying a fixed-length crossover-based in the neighborhood of the best solution in each generation. Gong et al. (2008) proposed an improved version of DE, namely orthogonal based DE. This algorithm employed the two level orthogonal crossovers to improve the performance of DE. The results indicated that orthogonal based DE is able to find the optimal or close-to-optimal in all cased. Omran et al. (2007) proposed the barebones differential evolution that is a new, almost parameter-free optimization algorithm that is a hybrid of the barebones particle swarm optimization and differential evolution. DE was used to mutate for each individual, the attractor associated with that particle, defined as a weighted average of its personal and neighborhood best positions. Neri and Tirronen (2009) proposed the scale factor local search differential evolution. This algorithm was a differential evolution based memetic algorithm which employs, within a self adaptive scheme, two local search algorithms. These local search algorithms aimed at detecting a value of the scale factor corresponding to an offspring with a high performance. A statistical analysis of the optimization results has been included in order to compare the results in terms of final solution detected and convergence speed. Yang et al. (2008) proposed the neighborhood search differential evolution. In this algorithm, the scale factor was adjusted by the sampling value from probability distributions, and the mutation was updated by a logic inspired by evolutionary programming.

Practically, based on the analysis of the above introduction, it can easy to see that the control parameters and the new mutation strategy are the major modifications. However, compared with these two parts, the new mutation strategy seems little to enhance the local search ability of DE or to overcome the convergence rate of the algorithms. Then, proposing the new control parameters and the new mutation model are still an open challenge direction of research. Therefore, in this paper, we propose a new differential evolution algorithm which uses a new self adaptive crossover rate depending on the success rate of the crossover probability. In order to balance the exploration and exploitation of the algorithm, a probability rule is used to combine two different mutation rules to enhance the diversity of the population and the convergence rate of the algorithm. In other aspect, our algorithm has a very simple structure and thus it is easy to implement. To verify the performance of MDE, 16 benchmark functions chosen from literature are employed. Compared with other evolution algorithms from literature, experimental results indicate that the proposed algorithm performs better than, or at least comparable to state-of-the-art approaches from literature when considering the quality of the solution obtained.

2 Basic algorithm

2.1 Differential evolution algorithm

Differential Evolution (DE) is a fairly novel population based search heuristic which is simple to implement and requires little parameter tuning compared to other search heuristics in continuous space. Different from other algorithms, DE uses distance and direction information from the current population to guide the search process. The crucial idea behind DE is a scheme for producing trial vectors according to the manipulation of target vector and difference vector. If the trail vector yields a worse fitness than a predetermined population member, the newly trail vector will be accepted and compared in the following generation. Sometimes, when handling the single problem and multi-objective problem, the algorithm is superior to other algorithms, such as genetic algorithm and particle swarm optimization. The logic of standard differential evolution algorithm can be described as follows:

As can be seen in pseudo-code, DE can be summarized into three major steps: mutation, crossover and selection. In the beginning of the algorithm, the algorithm begins with a randomly initiated population which generates NP*$D$ matrix with uniform probability distribution random values. We can generate the $j$th component of the $i$th vector as

$$\begin{aligned} x_{j,i,0} =x_{j,\min } +rand_{i,j} [0,1]\cdot (x_{j,\max } -x_{j,\min } ) \end{aligned}$$

(1)

where $rand_{i,j} [0,1]$ is a uniformly distribution random number between 0 and 1. $i = 1,{\ldots },\, NP$ and $j=1,{\ldots },D$. $x_{j,\max }$ and $x_{j,\min }$ are the upper bound and lower bound of the $j$th column, respectively.

After initialization, mutation vectors $V_{i,G}$ are generated according to each population member or target vector $X_{i,G}$ in current population. In the standard DE algorithm, five different mutation strategies can be used with one or two different crossover methods, which are listed in the followings:

“DE/rand/1/bin”

$$\begin{aligned} V_{i,G} =X_{r_1 ,G} +F\cdot (X_{r_2 ,G} -X_{r_3 ,G} ) \end{aligned}$$

“DE/best/1/bin”

$$\begin{aligned} V_{i,G} =X_{best,G} +F\cdot (X_{r_1 ,G} -X_{r_2 ,G} ) \end{aligned}$$

“DE/current-to-best/1/bin”

$$\begin{aligned} V_{i,G} =X_{i,G} +F\cdot (X_{best,G} -X_{i,G} )+F\cdot (X_{r_1 ,G} -X_{r_2 ,G} ) \end{aligned}$$

“DE/best/2/bin”

$$\begin{aligned} V_{i,G} =X_{best,G} +F\cdot (X_{r_1 ,G} -X_{r_2 ,G} )+F\cdot (X_{r_3 ,G} -X_{r_4 ,G} ) \end{aligned}$$

“DE/rand/2/bin”

$$\begin{aligned} V_{i,G} =X_{r_1 ,G} +F\cdot (X_{r_2 ,G} -X_{r_3 ,G} )+F\cdot (X_{r_4 ,G} -X_{r_5 ,G} ) \end{aligned}$$

(2)

where $r_1 ,r_2 ,r_3 ,r_4 ,r_5 \in [1,\ldots ,NP]$ are randomly chosen integers, and $r_1 \ne r_2 \ne r_3 \ne r_4 \ne r_5 \ne i$. $F$ is a mutation control parameter which affects the disturbance added by the weight of different vectors. $X_{best,G}$ is the best individual with the best fitness in the current population at generation $G$. In this paper, we use the “DE/rand/1/bin” mutation method to generate the offspring vector in the basic DE algorithm.

In the crossover operation, a recombination of the offspring vector $V_{i,G}$ and the parent vector $X_{i,G}$ produces a trail vector $U_{i,G} =[u_{1,i,G} ,u_{2,i,G} ,u_{3,i,G} ,\ldots ,u_{D,i,G}]$. Usually the binomial crossover is accepted, which is defined as follows:

$$\begin{aligned} u_{j,i,G} =\left\{ {\begin{array}{l} v_{j,i,G} ,(rand_j [0,1]\le CR)\,or\,(j=j_{rand}) \\ x_{j,i,G} ,otherwise \\ \end{array}} \right. \end{aligned}$$

(3)

where $j=[1,\ldots ,D];rand_{i,j} [0,1]$ is a random number between (0,1);$j_{rand} =[1,\ldots ,D]$ is the randomly chosen index, CR is the crossover rate and $v_{j,i,G}$ is the difference vector of the $j$th particle in the $i$th dimension at the $G$th iteration, and $u_{j,i,G}$ denotes the trail vector of the $j$th individual in the $i$th dimension at the $G$th iteration.

Selection operation is used to choose the next population (i.e. $G=G+1$) between the trail population and the target population. The selection operation can be described as follows:

$$\begin{aligned} X_{i,G+1}&= U_{i,G} ,\quad \hbox {If}\, f(U_{i,G} )\le f(X_{i,G})\nonumber \\&= x_{i,G} ,\quad \hbox {If}\, f(U_{i,G} )>f(X_{i,G} ) \end{aligned}$$

(4)

3 Modified differential evolution algorithm

In order to apply the differential evolution algorithm to more complex optimization problems, the further improvement in performance is necessary. In this paper, we introduce an efficient algorithm named modified differential evolution algorithm (MDE) to get the global optimization solution of high quality for the numerical optimization problems. In this section, we will use two mutation rules: DE/rand/2/bin and DE/rand to pbest/1/bin (Zhang and Sanderson 2009). These rules are used alternately through a probability rule. In the standard DE, scale factor $F$ and crossover rate CR are set to the fixed constant for the process of the algorithm. However, it is easy to make the algorithm trap into the local solution and lead to convergence premature of the DE algorithm. Hence, in this section, to enable all solutions to get rid of the stagnation easily, an adaptive strategy of modifying the scale factor, crossover rate and the relative success number of the two new proposed parameters in a previous period is proposed. Overall, in this paper, three modifications are proposed in order to balance the exploration and exploitation of the DE algorithm.

3.1 Modified mutation strategy

Global exploration and local exploitation are two important aspects in developing an effective evolutionary algorithm. The first is to find every region of the search space and the second denotes the ability to converge to the optimal solution as fast as possible. The mutation strategy plays a vital role in the search capability and the convergence rate. As mentioned above, there are many strategies proposed in DE (Yang and Deb 2009), each one has its own characterize. However, to our best knowledge, different optimization problems require different mutation strategies depending on the nature of the problems and available computation resources. DE/rand/2/bin is the mutation strategy that has been the most successful and widely used scheme in the literature. From this mutation strategy, it can be seen that five vectors are selected at random from the current population. Hence, it can conclude that the basic DE/rand/2/bin mutation strategy can maintain the population diversity and global search ability. However, it suffers for weak local exploitation ability, and its convergence rate is still lower when the optimal solution is reached. In Zhang and Sanderson (2009), this paper indicates that DE/current-to pbest/1/bin can maintain the diversity of the population and the convergence rate. In this strategy, an optional external archive is used and it can utilize historical data to provide information of the progress direction. The archive provides the information about the progress direction and it can enhance the diversity of the population. In this paper, because we don’t use the external archive, the random vector will be added to the DE/current-to pbest/1/bin. The DE/rand-to pbest/1/bin can be described as follows:

“DE/rand-to-best/1/bin”

$$\begin{aligned} V_{i,G} =X_{r_1 ,G} +F\cdot (X_{_{best,G} }^p -X_{r_1 ,G} )+F\cdot (X_{r_2 ,G} -X_{r_3 ,G} ) \end{aligned}$$

(5)

where $X_{_{best,G} }^p$ is randomly chosen as one of the top 100p% in the current population, and $p\in [0,1]$. This process explores the region according to the $X_{_{best,G} }^p$. Moreover, it can maintain the diversity of the population and enhance the convergence rate of the algorithm at the same time. From the new mutation strategy, we can find that this new strategy has two benefits. Firstly, the randomly vectors are instead of the current individual in the original mutation strategy in Zhang and Sanderson (2009). It can enhance the diversity of the population. Secondly, the pbest individual is selected as the new mutation process that exploits the feasible region according to $X_{_{best,G} }^p$. Consequently, this new mutation strategy has the better local search ability and it can enhance the diversity of the population. In this paper, this new mutation strategy is combined into the original DE algorithm and it is integrated into the basic mutation strategy DE/rand/2/bin through some probability rules. The framework of this new mutation strategy can be described as follows:

$$\begin{aligned}&If\hbox { rand}\le \omega \hbox { then}\nonumber \\&\quad \quad V_{i,G} =X_{r_1 ,G} +F\cdot (X_{_{best,G} }^p -X_{r_1 ,G} )+F\cdot (X_{r_2 ,G} -X_{r_3 ,G} ) \nonumber \\&else \nonumber \\&\quad \quad V_{i,G} =X_{r_1 ,G} +rand\cdot (X_{r_2 ,G} -X_{r_3 ,G} )+F\cdot (X_{r_4 ,G} -X_{r_5 ,G}) \nonumber \\&end\, if \end{aligned}$$

(6)

As can be seen in formula 6, $rand$ returns a real number between 0 and 1 with uniform random probability. $\omega$ is the probability value which determines to select the mutation rule. It can observe that for each individual, only one of the two strategies can be used for the process of generating the trail vector. Therefore, the value of $\omega$ is very important. In this paper, we consider three different schemes for the selection and adaptation of $\omega$ to determine the mutation rule. We can describe them in the following:

• (1) Random probability rule: in this scheme, the value of the $\omega$ of each individual is made to vary as a uniformly distributed random number in (0, 1), i.e. $\omega \in [0,1]$. Such a choice may enhance the diversity of the population. However, it will make the convergence speed slower.

• (2) Linear increment rule: $\omega$ is linearly increased from 0 to 1:

  $$\begin{aligned} \omega =\frac{\hbox {G}}{\hbox {Gmax}} \end{aligned}$$

  (7)

Where rand is a real number between 0 and 1 with a uniform random probability distribution and $G$ is the current generation. Gmax is the maximum generation number. Based on the modified search strategy, it can find that one of the two strategies is used for producing the current individual relative to a uniformly distributed random value within the range (0, 1). For each individual, if the random real number is smaller than (G/Gmax), then the DE/rand-to pbest/1/bin is used. Otherwise, the DE/rand/2/bin is used. For these rules, the probability of selecting one of these two new search strategies is a function of the generation number. The value of (G/Gmax) increases zero to one in order to balance exploration and the exploitation. In fact, in the beginning, two different strategies are selected to produce the offspring. From the (G/Gmax), the probability of selecting the DE/rand/2/bin is greater than the probability of the DE/rand-to pbest/1/bin. This process causes exploration. Then, as the generation increases, the two new search methods may be used with the same probability. This process directs the search. In the last, two search strategies are still used. However, in the opposite, the probability of selecting the DE/rand-to-pbest/1/bin is greater than the probability of the DE/rand/2/bin. Finally, it enhances the exploitation. Hence, based on the linear decreasing probability rule and two new search methods, the algorithm can balance the exploitation and exploration in the search space.

• (3) Exponential increment rule: the value of $\omega$ increases from zero to one in an exponential fashion inspired by the paper (Das et al. 2009):

  $$\begin{aligned} \omega =\hbox {e}xp\left( {\frac{G}{G_{\max } }\cdot \ln (2)} \right) -1 \end{aligned}$$

  (8)

Compared with the linear increment rule, this scheme increases the number of running the DE/rand/2/bin and reduces the number of running the DE/rand-to pbest/1/bin. In other words, this scheme is slower in the exploitation and faster in the exploration. The method of selecting the mutation rule is the same as the linear increment rule.

3.2 Randomized scale factor

The scale factor is a very important control parameter that controls the amplification of the differential variation between two individuals. In the original DE algorithm, the value of $F$ is kept as a constant value. Small values of $F$ lead to the premature convergence, and high values of $F$ slow down the search. To our knowledge, there is no optimal value of the $F$ that can solve all complex benchmark problems. However, from the formula 6, we can find that if the value of $F$ is always the same value, and the diversity of the population is lost as all the individuals are calculated by the same scale factor. Hence, the scale factor must be a positive value for the search process. In order to solve this drawback of keeping the $F$ constant, we generate the value of $F$ as two Gaussian distributions. Gaussian distribution is used because it gets most of the numbers within unity due to its short tail property. Moreover, the random numbers generated are not bound within any limit, this is because larger values of scale parameter ‘$F$’ will assist the solution space to easily escape from large plateaus or suboptimal peaks, thereby minimizing the chances to trap to local optima. It can be described as follows:

$$\begin{aligned} \begin{array}{l} If\, \hbox { rand()}\le \hbox {rand() then} \\ \qquad F=\left| {\hbox {Gaussian(0.3,0.3)}} \right| \\ else \\ \qquad F=\left| {\hbox {Gaussian(0.7,0.3)}} \right| \\ end\, if \\ \end{array} \end{aligned}$$

(9)

where $F=\left| {\hbox {Gaussian(0.3,0.3)}} \right|$ is a random number with the range (0.6, 1.2) and $F=\left| {\hbox {Gaussian(0.7,0.3)}} \right|$ is a random number with the range (0.2, 1.6). This range ensures both the exploitation tendency and exploration ability.

3.3 Self adaptive crossover rate

The crossover operation aims to construct an offspring by mixing components of the current element and of that generated by mutation operator. The crossover rate reflects the probability with which the trail individual inherits the actual individual’s genes. Small values of CR in exploratory move parallel to a small number of axes of the search space, while large values of CR move at angles to the search spaces’ axes. Additionally, at the early stage of the search, the diversity of the population is large and the variance of the population is large. Hence, the CR needs to a small value in order to avoid exceeding the level of diversity and this can reduce the convergence rate. Then, after some generations, the population will become similar. In this stage, in order to advance the diversity and increase the convergence speed, the value of CR must be a large value. The paper (Montgomery and Chen 2010) also suggests that many existing adaptive DE techniques will be likely unable to find and exploit both low and high values of CR will avoid the value which adversely affect algorithm performances. Moreover, for different problems, they need different value of parameters; some problems need to enhance the diversity and the convergence speed. In other aspects, some problems need to smaller value to avoid the exceeding level of diversity that may result in premature convergence and slow the convergence rate. Therefore, based on the above analysis and discussions, and in order to balance the exploration and exploitation of the algorithm, in this paper, we propose a statistical learning strategy which selects the evolution method for each individual according to the relative success ratio of selecting one of two new parameters in the previous periods. Two new parameters settings can be described as follows:

$$\begin{aligned} (1)\, CR_1 \in [0.05,0.15]; (2)\, CR_2 \in [0.85,1] \end{aligned}$$

(10)

Based on two new parameter settings, the first one can increase the possibility stagnation and slow down the search process. The second one can advance diversity and increase the convergence speed. In the beginning of the algorithm, we generate the value of parameter $CR$ using the first one for each individual. Then we design a new label $l$ to store the success ratio of two new parameters. In each generation, we generate the $CR$ according to the two new parameters. If the $CR$ is generated by using the first one, we will set the label $l_i^2 = 1$, otherwise if the $CR$ is generated by using the second one, we will set the label $l_i^2=2$. Then after generating the offspring individuals, we calculate the individual and compare it with the previous individuals. If the $CR$ is generated by using the first one with the better solution, we will set the label $l_i^1 = 1$, otherwise, we will set the label $l_i^1 = 2$. And then, we calculate the number of the success ratio. According to the success ratio, we can generate the new CR value. The method can be described as follows:

From the procedure, we can find that the parameter success1 and success2 are important for the algorithm. The sucess1 denotes the success number of using the first parameter setting in a learning period. The success2 denotes the success number of using the second parameter setting in a learning period. For the evolutionary process, if the individual using the first parameter setting is superior to the previous generation, the $l_i^1$ will be set one, otherwise it will be set zero. In the final of every generation, the summation of label $l_i^1$ for different parameter settings will be calculated. Then, we compare success1 and success2. If the sucess1 is larger than the success2, it denotes the first parameter setting can perform better than second parameter setting. We will add the probability of selecting the first parameter setting. Otherwise, it represents that the second parameter setting is very efficient. We also reduce the probability of selecting the first parameter setting, and then add the probability of selecting the second parameter setting.

3.4 Boundary constraints

The modified differential evolution algorithm assumes that the whole population should be in an isolated and finite space. During the searching process, if there are some individuals that may move out of bounds of the space, the original algorithm will stop them on the boundary. In other words, the individual will be assigned a boundary value. The disadvantage is that if there are too many individuals on the boundary, and especially when there exists some local minima on the boundary, the algorithm will lose its population diversity to some extent. In order to tackle this problem, we proposed the following repair rule:

$$\begin{aligned} x_i =\left\{ {\begin{array}{lll} 2^{*} x_{\min } -x_i &{}\hbox { if }\quad x_i <x_{\min } \\ 2^{*} x_{\max } -x_i &{}\hbox { if }\quad x_i >x_{\max } \\ x_i &{}\hbox { otherwise} \\ \end{array}} \right. \end{aligned}$$

(11)

where $x_{\max }$ and $x_{\min }$ are the upper bound and lower bound of each dimension for every individual, respectively.

3.5 Modified differential evolution with self adaptive parameter setting

In this section, we will propose a modified differential evolution with self adaptive parameter settings. Firstly, we use a new mutation rule based on the DE/rand/2/bin and DE/rand-to-pbest/1/bin to generate the trail vector. The new mutation rule is used through the probability model. The proposed mutation rule maintains the diversity of the population and enhances the diversity of the population. Secondly, both operations diversify the population and improve the convergence speed, and the parameter adaptation automatically updates the control parameter according to the success ration of the two parameter settings in the learning period. In addition, the MDE has a very simple structure and thus it is easy to implement and not enhance any complexity. This method can overcome the lack of the exploitation of the original DE algorithm. The Algorithm 3 can be described as follows:

4 Performance evaluation

To evaluate the performance of our algorithm, we apply it to 16 standards benchmark functions (Li et al. 2013; Mallipeddi et al. 2010). These functions have been widely used in the literature. The first four functions are unimodal functions. The following 12 functions are multimodal test functions. Among them, for the function f03, the generalized Rosenbrock’s function is a multimodal function when D$>$3. For these functions, the number of the local minima increases exotically with the problem dimension. So far, these problems have been widely used as benchmarks for researches with different methods by many researchers. Definitions of the benchmark problems are described as follows:

• (1) Shifted sphere function

  $f_1 (x)=\sum _{i=1}^D {z_i^2 } , z=\mathrm{X}-\mathrm{O}, o=[o_1 ,o_2 ,\ldots ,o_D ]:$ the shift global optimum.

• (2) Shifted Schwefel’s problem 1.2

  $f_2 (x)=\sum _{i=1}^D {\left( {\sum _{j=1}^i {z_i } } \right) } ^{2}, z=\mathrm{X}-\mathrm{O}, \quad o=[o_1 ,o_2 ,\ldots ,o_D ]:$ the shift global optimum.

• (3) Rosebrock’s function

  $f_3 (x)=\sum _{i=1}^{D-1} {[100(x_{i+1} -x_i^2 )^{2}+(x_i -1)^{2}]} ,$

• (4) Shifted Schwefel’s problem 1.2 with noise in fitness

  $f_4 (x)=\sum _{i=1}^D {\left( {\sum _{j=1}^i {z_i } } \right) } ^{2}(1+0.4\left| {N(0,1)} \right| ), z=\mathrm{X}-\mathrm{O}, \quad o=[o_1 ,o_2 ,\ldots ,o_D ]:$ the shift global optimum.

• (5) Shifted Ackley’s function

  $f_5 (x)=-20\exp (-0.2\sqrt{\frac{1}{D}\sum _{i=1}^D {z_i^2 } })-\exp (\frac{1}{D}\sum _{i=1}^D {\cos 2\pi z_i}), z=\mathrm{X}-\mathrm{O}, \quad o=[o_1 ,o_2 ,\ldots ,o_D ]:$ the shift global optimum.

  +20+e

• (6) Shifted rotated Ackley’s function

  $f_5 (x)=-20\exp (-0.2\sqrt{\frac{1}{D}\sum _{i=1}^D {z_i^2 } })-\exp (\frac{1}{D}\sum _{i=1}^D {\cos 2\pi z_i}) , z=M(\mathrm{X}-\mathrm{O}), \quad cond(M)=1, o=[o_1 ,o_2 ,\ldots ,o_D ]:$ the shift global optimum.

  +20+e

• (7) Shifted Griewank’s function

  $f_7 (x)=\frac{1}{400}\sum _{i=1}^D {z_i^2 } -\prod _{i=1}^D {\cos (\frac{z_i }{\sqrt{i}})} +1, z=\mathrm{X}-\mathrm{O}, \quad o=[o_1 ,o_2 ,\ldots ,o_D ]:$ the shift global optimum.

• (8) Shifted rotated Griewank’s function

  $f_8 (x)=\frac{1}{400}\sum _{i=1}^D {z_i^2 } -\prod _{i=1}^D {\cos (\frac{z_i }{\sqrt{i}})} +1, z=M(\mathrm{X}-\mathrm{O}), cond(M)=3, \quad o=[o_1 ,o_2 ,\ldots ,o_D ]:$ the shift global optimum.

• (9) Shifted Rastrigin’s function

  $f_9 (x)=\sum _{i=1}^D {[z_i^2 -10\cos (2\pi z_i )+10]}, z=\mathrm{X}-\mathrm{O}, o=[o_1 ,o_2 ,\ldots ,o_D ]:$ the shift global optimum.

• (10) Shifted rotated Rastrigin’s function

  $f_{10} (x)=\sum _{i=1}^D {[z_i^2 -10\cos (2\pi z_i )+10]}, z=M(\mathrm{X}-\mathrm{O}), cond(M)=2, o=[o_1 ,o_2 ,\ldots ,o_D ]:$ the shift global optimum.

• (11) Shifted rotated Rastrigin’s function

  $$\begin{aligned} f_{10} (x)&= \sum _{i=1}^D {[z_i^2 -10\cos (2\pi z_i )+10]},\\ y_i&= \left\{ {\begin{array}{ll} z_i &{}\left| {z_i } \right| <1/2 \\ round(z_i )/2&{} \left| {z_i } \right| <1/2 \\ \end{array}} \right. \hbox {for}\,\, i=1,2,\ldots ,D \end{aligned}$$

  $z=\mathrm{X}-\mathrm{O}, o=[o_1 ,o_2 ,\ldots ,o_D ]:$ the shift global optimum.

• (12) Schwefel’s function

  $$\begin{aligned} f_{12} (x)=418.9828\times D-\sum _{i=1}^D {x_i \sin (\left| {x_i } \right| ^{1/2})}. \end{aligned}$$

• (13) Penalty 1’s function

  $$\begin{aligned} f_{13} (x)&= \frac{\pi }{D}\{10\sin ^{2}(\pi y_i )+\sum \limits _{i=1}^{D-1} {(y_i -1)} ^{2}[1+10\sin ^{2}(\pi y_i +1)]+(yD-1)^{2}\\&+\sum \limits _{i=1}^D {u(x_i ,10,100,4)} \}\\ y_i&= 1+\frac{x_i +1}{4} \quad u(x_i ,a,k,m)=\left\{ {\begin{array}{l} k(x_i -a)^{m} \\ 0 \\ k(-x_i -a)^{m} \\ \end{array}} \right. \begin{array}{l} x_i >a \\ -a<x_i <a \\ x_i <-a \\ \end{array} \end{aligned}$$

• (14) Penalty 2’s function

  $$\begin{aligned} f_{14} (x)&= 0.1\{10\sin ^{2}(\pi y_i )+\sum _{i=1}^{D-1} {(y_i -1)^{2}[1+10\sin ^{2}(\pi y_i +1)]} +(yD-1)^{2}\}\\&+\sum _{i=1}^D {u(x_i ,10,100,4)} \end{aligned}$$

• (15) Composition function 1 (CF1)

  The function $f_{15} (x)$ (CF1) is composed by using 10 sphere functions; the global optimum is easy to find the global solution.

• (16) Composition function 6 (CF6)

The function $f_{16} (x)$(CF6) is composed by using 10 different benchmark functions, i.e. 2 rotated Rastrigin’s functions, 2 rotated Weierstress functions, 2 rotated Griewank’s functions, 2 rotated Ackley’s functions and 2 rotated Sphere functions.

Based on these functions, the shift and rotated functions make the optimum is very difficult to be found. Where $\vec {o}$ denotes the position of the shifted optima. M is a rotation matrix and $cond(M)$ is the condition number of the matrix. The global optimum, search ranges and initialization ranges of the test functions are presented in Table 1.

Table 1 Global optimum, search ranges and initialization ranges of the test functions

4.1 Experimental setup

In order to evaluate the effectiveness and efficiency of MDE, we have chosen a suitable set of value and don’t have made any effort in finding the best parameter settings because of this algorithm is a self adaptive method. In this experiment, we set the number of individuals in all algorithms to be 50. The algorithm is coded in MATLAB 7.9, and experiments are made on a Pentium 3.2 GHz Processor with 4.0 GB of memory. The above benchmark functions f1 to f16 are tested in 10-dimension and 30-dimension. The maximum number of function evaluations is set to 100,000 for 10D problems and 300,000 for 30D problems. For all test functions, the algorithms carry out 50 independent runs. The real numbers +, $\approx$, - denote that the modified differential evolution algorithm is superior to, equal to or inferior to other algorithms.

4.2 Effect of different $\omega$ value

In this section, we compared with three different probability rules including the random probability rule, linear increment rule and exponential increment rule. The experiment results are listed in Table 2. From Table 2, it is interesting to see that there is always one or more version of MDE that outperforms the standard DE with the DE/rand/1/bin scheme. This reflects the effectiveness of the incorporation of the hybrid mutation rule in DE. From the results, we also can find that the time-varying $\omega$ is better than the random probability rule. It notes that the random probability rule is also better than the original algorithm. Compared with two increment rules, the results show that the linear increment rule is better than the exponential increment rule. Therefore, in this paper, we use the linear increment rule as the final model to form a judicious tradeoff between the exploration and exploitation which is the key for the success of the MDE.

Table 2 Comparison between different $\omega$ on 30D problems

Table 3 Comparison between MDE and various classical DE methods on 10D problems

Table 4 Comparison between MDE and various classical DE methods on 30D problems

4.3 Comparison of the original DE algorithm with different parameters

In this section, we compare our method with six different DE/rand/1/bin including DE/rand/1/bin with (F = 0.8, CR = 0.9), DE/rand/1/bin with (F = 0.9, CR = 0.1), DE/rand/1/bin with (F = 0.9, CR = 0.9), DE/rand/1/bin with (F = 0.5, CR = 0.3), DE/rand/1/bin with (F = 0.5, CR = 0.9), and DE/rand/1/bin with (F = 0.7, CR = 0.3). The results (mean, standard deviation values) of this experiment are presented in Tables 3 and 4 for 10D and 30D, respectively. The “$-$” denotes our algorithm is better than other algorithms. And the “+” and “$\approx$” denote our algorithm is inferior to, equal to other algorithms. This comparison is between these DE algorithms with different parameter settings with our algorithm MDE. In Tables 3 and 4, we can find that no single parameter setting is adopted for all problems. For 10D problem presented in Table 3, it can be observed that MDE is inferior to, equal to and superior to the differential evolution with different parameter settings in 11, 29, and 56 problems, respectively out of the total 96 cases. Therefore, the MDE is always either better or equal. Moreover, as can be seen in this table, we can find the DE/rand/1/bin with (F = 0.9, CR = 0.1) and DE/rand/1/bin with (F = 0.5, CR = 0.3) are better than other classical DE algorithms. For the 30D problems presented in Table 4, it can observed that MDE is inferior to, equal to and superior to the different methods in 1, 21, and 74 problems, respectively out of the total 96 cases. From this table, the results of MDE are statistically significantly better as compared to all other algorithms considered here. Obviously, it can be concluded that MDE is superior to its entire algorithm in all these 16 test functions in terms of average and standard deviation values. In this table, for the function f04, the DE/rand/1/bin with (F = 0.5, CR = 0.9) can give the best solution than the MDE algorithm. For the 10D and 30D problem, we can find that the performance of all these algorithms is very similar. The significant difference is that the performance of MDE is not affected in a worse way along with the growth of the search space dimensionality. Therefore, it can conclude that MDE is better than the DE algorithm with different parameter settings. This result indicates that MDE has the greater robustness than DE with different parameter settings on the majority of functions.

Table 5 Comparison between MDE and various state-of-the-art DE methods on 10D problems

Table 6 Comparison between MDE and various state-of-the-art DE methods on 30D problems

Table 7 Comparison between MDE with CLPSO, CMA-ES, and GL-25 algorithms on 10D problems

Table 8 Comparison between MDE with CLPSO, CMA-ES, and GL-25 algorithms on 30D problems

4.4 Comparison of MDE with state-of-art DE variants

In this section, we compare MDE with six other DE variants including ODE (Rahnamayan et al. 2008), OXDE (Wang et al. 2011b), SaDE (Qin et al. 2009), JADE (Zhang and Sanderson 2009), jDE (Brest et al. 2006), and CoDE (Wang et al. 2011a). The mean and standard deviation values are presented in Tables 5 and 6 for 10D and 30D problems, respectively. To compare the performance of different algorithms, the results are labeled by the “$-$”, “+” and “$\approx$”. Out of the five algorithms used for comparison, the MDE is statistically better than other algorithms that use the label “$-$”. From the results, it can be seen that MDE can perform better than other algorithms in most of the cases. For the 10D problems in Table 5, among these algorithms used for comparison, OXDE is weaker in performance. But, it can provide the best solution for the function f16 compared with other algorithms. For the unimodal function f01–f04, MDE can obtain the two better solutions than other algorithms except the f03. For f04, ODE and JADE can give the better solution than other algorithms. For multimodal functions f08–f16 with many local minima, the final results are more important because of this function can reflect the algorithm’s ability to escape from the poor local optima and obtain the near-global optimum. The MDE provides better solutions for some functions except f06, f08, f10, and f16. For these four functions, the optimal solution can be obtained by the ODE, SaDE, JADE, jDE and CoDE. For f06, SaDE can give the better results. For f08 and f10, JADE gives the best solution. All in all, it can be observed that MDE is inferior to, equal to, superior to compared algorithm in 10, 41, and 45 cases, respectively out of the 96 cases. For the dimensional 30, the experimental results of 50 independent runs are summarized in Table 6. From the Table 6, we can find that MDE is able to find the optimal or near-optimal solution with small deviations for these 12 functions including f02, f04, f10 and f16. For the f02 and f10, JADE can give the best solutions. For f04, ODE can perform better than other algorithms. jDE can perform better than MDE in the f16 function. In general, the performance of MDE is highly competitive with other algorithms, especially for the high-dimensional problems.

Table 9 Comparison between MDE and different EP on 10D problems

Table 10 Comparison between MDE and different EP on 30D problems

Table 11 Comparison between MDE and MDE with different version on 30D problem

4.5 Comparison of MDE with other state-of-art algorithm variants

In order to evaluate the effectiveness and efficiency of MDE, we compare its performance with CLPSO (Liang et al. 2006), CMA-ES (Hansen and Ostermeier 2001), and GL-25 (Garcia-Martinez et al. 2008). Liang et al. proposed a new particle swarm optimization-CLPSO. A particle used the personal historical best information of all the particles to update its velocity. Hansen and Ostermeier proposed a very efficient and famous evolution strategy. Garcia-Martinez et al. proposed a hybrid real-coded genetic algorithm which combines the global and local search. Each method was run 50 times on each test function. Table 7 summarizes the experimental results for 10 dimensional. As can be seen in Table 7, MDE significantly outperforms CLPSO, CMA-ES, and GL-25. MDE performs better than CLPSO, CMA-ES, and GL-25 on 12, 15, and 11 out of 16 test function, respectively. CLPSO is superior to, equal to MDE on 5 test functions. CMA-ES performs superior to MDE on one test functions. GL-25 is superior to, equal to MDE on 4 test functions. For the 30D, the results are shown in Table 8 in terms of the mean, standard deviation of the solutions obtained in the 50 independent runs by each algorithm. From the Table 8, we can find that the MDE provides better solutions than other algorithms. From the results, it can observed that MDE is inferior to, equal to, superior to compared algorithms in 1, 4, and 43 cases, respectively out of the 48 cases. The results demonstrate good performance of MDE in solving these problems.

4.6 Comparison of MDE, AFEP, MSAEP and ENAEP

In the experiment, we compare the performance of MDE and AFEP, MSAEP and ENAEP (Mallipeddi et al. 2010). AFEP is an adaptive evolutionary programming which presents empirical studies carried out to evaluate the performance of different constraint handling methods on constrained real-parameter optimization. MSAEP presents a mixed strategy evolutionary programming algorithm that employs the Gaussian, Cauchy, Lévy, and single-point mutation operators. The results of the MSAEP show that the mixed strategy performs equally well or better than the best of the four pure strategies, for all of the benchmark problems. ENAEP enables us to benefit from different mutation operators with different parameter values whenever they are effective during different stages of the search process. Experimental results show that the algorithm is very effective. The experimental results are given in Tables 9 and 10 for different algorithms at dimension 10D and 30D. For 10D, the performance of MDE is significantly superior to all evolutionary algorithms for all functions except f08 and f16 according to the experimental results is shown in Table 9. For f08 and f16, MSAEP slightly performs better than MDE. All in all, from the results, it can be observed that MDE is inferior to, equal to, superior to the compared algorithms on 4, 0, and 44 cases. For the 30D, as can be seen in Table 10, we can conclude that the performance of all other algorithms is very similar to that on the 10-deminsional benchmark functions. The significant difference is that the performance of MDE is not affected in a worse way with the increase of the dimensional. Hence, we can also conclude that the self adaptive method and the new search method can enhance the ability to accelerate DE, and especially for the higher dimensionality.

Fig. 1

The success rate of one of the two parameter settings for f01-f08

Fig. 2

The success rate of one of the two parameter settings for f09-f16

4.7 A parametric study on MDE

In this section, in order to investigate the impact of the problem modifications, some experiments are conducted. Three different versions of MDE algorithm have been tested and compared against the proposed ones.

• Version 1: to study the effect of the proposed modifications for the self adaptive parameter with the basic mutation DE/rand/1/bin strategy. This version denotes the MDE1.

• Version 2: to study the effect of the proposed modifications for the new mutation rule with the basic parameter setting (F = 0.5; CR = 0.9). This version denotes the MDE2.

• Version 3: modified differential evolution algorithm with self adaptive parameters method

In order to evaluate the final solution quality produced by all algorithms, the performance of these three different versions of MDE algorithms are investigated based on the 30D functions. The results of the MDE algorithm against its versions and the standard DE algorithm are summarized in Table 11. As can be seen in Table 11, we can find that the self adaptive parameter settings can enhance the standard DE effectively. Then the new mutation rule can enhance the results based on the multimodal functions. Accordingly, the main benefits of the proposed modification can balance between the exploration and exploitation ability through the evolutionary process. Figures 1 and 2 show the success rate of one of the two parameter settings for all functions. As can be seen in figures, the value of CR1 performs better than the functions f01, f05–f09, f11 and f13–f16. For f02, f03, and f12, CR2 is the winner compared with the CR1. For f04 and f10, they have the similar effect for the final results. All in all, the self adaptive method is very suitable for solving these global problems.

5 Conclusions

The performance of DE depends on the selected mutation strategy and its associated parameter values. In this paper, we propose a modified differential evolution with the self adaptive parameter settings for solving unconstrained global real-parameter optimization problems in the continuous domain. In our paper, the proposed algorithm proposes two mutation rules based on the rand and best individuals among the entire population. In order to balance the exploitation and exploration of the algorithm, the new rules are combined with the two mutation strategies through a probability rule. Then, a self adaptive parameter is introduced as uniform random numbers to enhance the diversity of the population based on the relative success ratio of the new proposed parameter setting in a previous period. In other aspect, our algorithm has a very simple structure and thus it is easy to implement. To verify the performance of MDE, 16 benchmark functions chosen from literature are employed. The results show that the proposed MDE algorithm clearly outperforms the standard DE with six different parameter settings. Compared with some evolution algorithms from the literature, we find our algorithm is superior to or at least highly competitive with these algorithms.

In this paper, we only consider the global optimization. The algorithm can be extended to solve other problems such as constrained optimization problems.