The effect of background flow shear on the topographic Rossby wave

Abstract

Due to the ubiquitous steep continental shelf slope in the East China Sea, topographic Rossby waves are very common when the Kuroshio Current flows along the slope, and of great importance in the water and energy exchange between the open ocean and coastal sea. To examine the structural characteristics of topographic Rossby wave, we use stretching transform of time and space and perturbation method to get the analytic solution of potential vorticity equation with topography. For a given background flow v = v₀ + δx, the effect of background flow shear is discussed. The main conclusions are drawn that background flow shear is required for the existence of solitary Rossby waves; for flow shear δ < 0 (δ > 0), anticyclonic (cyclonic) solitary Rossby waves exist and their zonal structure tilts eastward (westward); the phase speed of solitary Rossby waves is related to the amplitude and flow shear intensity; solitary Rossby waves are non-dispersive waves, and the width of solitary waves is inversely proportional to the intensity of the flow shear. Furthermore, these theoretical results are used to explain the propagation speeds and distributions of eddies along the Kuroshio Current in the East China Sea. In addition, these results could be applied to other areas with similar meridional current and topography.

1 Introduction

Topographic Rossby waves are induced by cross-isobathic motions as fluid columns are stretched and compressed over sloping topography (Pedlosky 1987; Oey and Lee 2002). The existence of special topography and the strong western boundary current is conducive to the generation of Rossby waves and eddies (Louis et al. 1982; Oey and Lee 2002; Kamidaira et al. 2016; Ribbe et al. 2018). These eddies are different from the surrounding coastal water due to their biological and physical characteristics, and have been observed in all western boundary current regions.

The Kuroshio Current is one of the world’s major western boundary currents. It plays an important role in the meridional transport of warm and salty tropical water northward, and influences the regional climatic system of the East China Sea (Yang et al. 2011; Xu et al. 2011; Sasaki et al. 2012). In the East China Sea, Kuroshio flows northeastward along the 200 m isobath of the continental shelf break approximately 150–200 km away from the Ryukyu Island (Qiu 2001). These geographical configurations are preferable conditions for the emergence of island wakes and associated eddy shedding, and the development of submesoscale eddy through baroclinic and barotropic instability due to the Kuroshio fronts and topographic shear (Kamidaira et al. 2016). The width of the Kuroshio frontal eddy is about 40 km, and its phase speed is about 30 ${\text{cm}}\;{\text{s}}^{ - 1}$ (Yanagi et al. 1998). In classical topographic Rossby wave theory, the shallow topography is in right hand of the Rossby wave along the propagation direction, so the observed phase speed of the eddy is smaller than the velocity of Kuroshio. The eddy-related processes are essential to the lateral transport of material within the area between the Kuroshio and the islands. Numerical results show a predominance of submesoscale anticyclonic eddies over cyclonic eddies in this area (Kamidaira et al. 2016). However, East China Sea around the Kuroshio has preferable conditions to maintain positive relative vorticity in terms of the classical topographic Rossby wave theory, centrifugal instability, and cyclonic ageostrophic instability, so the anticyclonic eddies are mainly affected by other factors. An energy conversion analysis relevant to the eddy-generation mechanisms revealed that a combination of both the shear instability due to the Kuroshio and the topography and baroclinic instability around the Kuroshio front jointly provoke these near-surface anticyclonic eddies, as well as the subsurface cyclonic eddies that are shed around the shelf break. Using drifter data and high-resolution model output, Liu et al. (2017) found that oceanic eddies are asymmetrically distributed across the Kuroshio in the East China Sea: predominant cyclonic (anticyclonic) eddies are on the western (eastern) sides of Kuroshio. The generation mechanism of these submesoscale eddies is speculated to be related to the horizontal velocity shear of the Kuroshio when it flows northeastward along the shelf break in the East China Sea. Figure 1 shows topography and sea surface flow field in the East China Sea. However, the eddies’ generation mechanism and spatial structure characteristics remain absent. Chelton and Schlax (1996) pointed out that the theory for free, linear Rossby waves is an incomplete description of the observed oceanic waves. Observed characteristics of isolated anomalies were found to be broadly consistent with nonlinear quasi-geostrophic theory, which suggests the importance of nonlinear dynamics (Chelton et al. 2007, 2011; Shi et al. 2018).

Fig. 1

Characteristics of topography and surface current in the East China Sea. a Sea surface flow derived from mean absolute dynamic topography (ADT) averaged over the period 2000–2012, and topography is color shaded. b Sea surface height and geostrophic current on September 5, 2008. Black dotted circles indicate cyclonic eddies, and yellow dotted circles indicate anticyclonic eddies. The topography data are extracted from ETOPO5 (https://www.ngdc.noaa.gov/mgg/global/). The altimeter products with a daily temporal resolution and 1/4° × 1/4° spatial resolution were produced by DUACS and distributed by AVISO (ftp://ftp.aviso.altimetry.fr/) (color figure online)

This paper aims to study the background flow shear effects on the topographic Rossby wave in the nonlinear regime. Based on the potential vorticity equation, and using scale transformations and the perturbation expansions method (Long 1964; Boyd 1980; Ono 1981; Shi et al. 2015, 2018; Lu et al. 2018; Yang et al. 2018; Zhang and Yang 2019), a nonlinear model and its corresponding asymptotic solution are derived in this paper. Using the asymptotic solution, the influences of background flow shear on the spatial structure, propagation speed, and wave width of solitary Rossby wave are discussed in detail. As an example, the characteristics of the eddies on both sides of the Kuroshio in the East China Sea are studied.

2 Methodology

Figure 2a gives the topographic slope and Kuroshio path in the East China Sea, where Kuroshio flows mainly along the steep shelf break. The schematic Fig. 2b shows a model, which describes the typical topography and background flow features in shelf break.

Fig. 2

Model schematic. a Topographic slope and Kuroshio path in the East China Sea. b Model schematic

Considering the bottom slope effect is much greater than the $\beta$ effect, the non-dimensional potential vorticity equation with the topographic effect is (Pedlosky 1987):

$$\frac{\partial }{\partial t}(\nabla^{2} \psi - F\psi ) + J(\psi ,\nabla^{2} \psi ) + J(\psi ,h) = 0,$$

(1)

where $F = L^{2} /R_{d}^{2}$, $L$ is a characteristic length scale of the motion, $R_{d}$ is the Rossby deformation radius, $\psi$ is the stream function, and

$$h = H_{0} - \beta_{h} x,$$

(2)

which represents topography with east–west slope (assume $\beta_{h} > 0$). Substitution of (2) into (1) yields

$$\frac{\partial }{\partial t}(\nabla^{2} \psi - F\psi ) + J(\psi ,\nabla^{2} \psi ) + \beta_{h} \frac{\partial \psi }{{\partial y}} = 0.$$

(3)

The horizontal velocity can be obtained from:

$$u_{g} = - \frac{\partial \psi }{{\partial y}},\;\;\;v_{g} = \frac{\partial \psi }{{\partial x}}.$$

The boundary conditions for Eq. (3) are:

$$\frac{\partial \psi }{{\partial y}} = 0\;{\text{at}}\;x = 0,\;1.$$

(4)

The background stream function is given by:

$$\varphi_{0} (x) = \int v (x)dx.$$

(5)

We take the total stream function $\psi$ as a disturbance stream $\varepsilon \varphi$ pre-imposed on the meridional flow $v$:

$$\psi = \varphi_{0} (x) + \varepsilon \varphi = \int v (x)dx + \varepsilon \varphi ,$$

(6)

where $\varepsilon$ represents the Rossby number, which is a small parameter. Substitution of (6) into (1) yields:

$$\varepsilon \frac{\partial }{\partial t}(\nabla^{2} \varphi - F\varphi ) + \varepsilon v\frac{\partial }{\partial y}\nabla^{2} \varphi + \varepsilon (\beta_{h} - v_{xx} )\frac{\partial \varphi }{{\partial y}} + \varepsilon^{2} J(\varphi ,\nabla^{2} \varphi ) = 0.$$

(7)

To balance the nonlinearities and dispersions, we introduce the following small scales:

$$Y = \varepsilon^{1/2} (y - c_{0} t),T = \varepsilon^{3/2} t,$$

(8)

where $c_{0}$ is the linear Rossby wave phase speed, which can be determined by solving the eigenvalue problem below. Based on the multiple scale method, the disturbance stream function has the form of

$$\varphi = \varphi_{1} + \varepsilon \varphi_{2} + \ldots = A(Y,T)\psi_{1} (x) + \varepsilon B(Y,T)\psi_{2} (x) + \ldots$$

Using the method reported in our previous paper (Shi et al. 2018), we readily obtain the following eigenvalue equation for $\psi_{1} (x)$:

$$\frac{{\partial^{2} \psi_{1} }}{{\partial x^{2} }} + \frac{{\beta_{h} - \nu_{xx} + Fc_{0} }}{{v - c_{0} }}\psi_{1} = 0,$$

(9)

$$\psi_{1} = 0\;{\text{at}}\;x = 0,\;1.$$

(10)

Solving (9) with boundary condition (10), the eigenvalue $c_{0}$ and zonal structure $\psi_{1}$ can be determined. The amplitude $A(Y,T)$ satisfies the equation:

$$\frac{\partial A}{{\partial T}} + a_{1} A\frac{\partial A}{{\partial Y}} + a_{2} \frac{{\partial^{3} A}}{{\partial Y^{3} }} = 0,$$

(11)

where

$$\begin{aligned} a_{0} = & - \int_{0}^{1} {\frac{{\beta_{h} - v_{xx} + Fv}}{{(v - c_{0} )^{2} }}\psi_{1}^{2} dx,} \, \\ a_{1} = & \frac{1}{{a_{0} }}\int_{0}^{1} \,\frac{{\psi_{1}^{3} }}{{v - c_{0} }}\mathop {\left( {\frac{{\beta_{h} - v_{xx} + Fc_{0} }}{{v - c_{0} }}} \right)}\nolimits_{x} dx, \\ a_{2} = & \frac{1}{{a_{0} }}\int_{0}^{1} \,\psi_{1}^{2} dx. \\ \end{aligned}$$

(12)

Equation (11) also has been obtained by Benney (1966), Yamagata (1982), Redekopp (1977), and Shi et al. (2018). However, the influences of background flow shear on the spatial structure, propagation velocity, and wave width of topographic solitary Rossby wave have not been studied.

3 Background flow effects

Considering the background flow shear ($v_{x} \ne 0$), the analytical solution of eigenvalue equations [Eqs. (9) and (10)] is difficult to find, but it can be solved using the asymptotic analytical method. The present analysis assumes that the typical background shear flow in continental shelf break has the following form:

$$v = \overline{v} + \delta \left( {x - \frac{1}{2}} \right) = \overline{v} - \frac{1}{2}\delta + \delta x = v_{0} + \delta x,\;\;v_{0} = \overline{v} - \frac{1}{2}\delta ,\;\delta < < 1.$$

(13)

To solve the eigenvalue equations [Eqs. (9) and (10)], we assume that:

$$\left\{ \begin{aligned} \psi_{1} & = \varphi^{0} + \delta \varphi^{1} + \cdots \\ c_{0} & = \overline{{c_{0} }} + \delta \overline{{c_{1} }} + \cdots \\ \end{aligned} \right..$$

(14)

Similar to the manipulations shown in the (Shi et al. 2018) except that the planetary $\beta$ effect is replaced by topography variation, we obtain the solution as follows:

$$\left\{ \begin{aligned} \psi_{1} = & \sin n\pi x + \delta \frac{1}{4}\frac{n\pi }{{\overline{v} - \overline{{c_{0} }} }}\left[ {\left( {x - x^{2} } \right)cosn\pi x + \frac{x}{n\pi }sinn\pi x} \right] + O(\delta^{2} ) \\ c_{0} = & \overline{v} - \frac{{\beta_{h} + F\overline{v}}}{{(n\pi )^{2} + F}} + O(\delta^{2} ). \\ \end{aligned} \right.$$

(15)

These equations indicate that the zonal structure of solitary wave (eddy) is asymmetry due to the influence of background flow shear.

Substituting (13) and (15) into (12) and omitting the $O(\delta^{2} )$ term gives:

$$\begin{aligned} a_{1} = & \frac{4}{3}\frac{{(1 - ( - 1)^{n} )n\pi }}{{\beta_{h} + F\overline{v}}}\delta , \\ a_{2} = & - \frac{{\beta_{h} + F\overline{v}}}{{((n\pi )^{2} + F)^{2} }}. \\ \end{aligned}$$

(16)

Using Jacobi elliptic function expansion methods and Eq. (8), the cnoidal wave solution of (11) is:

$$A(y,t) = A_{0} \mathop {{\text{cn}}}\nolimits^{2} \left\{ {\varepsilon^{{\tfrac{1}{2}}} \sqrt {\frac{{A_{0} a_{1} }}{{12a_{2} m^{2} }}} \left[ {y - \left( {c_{0} + \frac{{A_{0} a_{1} }}{3}\left( {2 - \frac{1}{{m^{2} }}} \right)\varepsilon } \right)t - \frac{{Y_{0} }}{\sqrt \varepsilon }} \right],m} \right\}.$$

(17)

Here, $m$ represents the modulus of Jacobi elliptic function which measures the relative importance of nonlinearity to dispersion, $A_{0}$ is the amplitude of the wave, $\varepsilon^{{ - \frac{1}{2}}} \sqrt {\frac{{12a_{2} m^{2} }}{{A_{0} a_{1} }}}$ is the width of the wave, and $c_{0} + \frac{{A_{0} a_{1} }}{3}\left( {2 - \frac{1}{{m^{2} }}} \right)\varepsilon$ is the phase speed of the wave. The solution implies the wave maintains its shape while propagating at a constant velocity. The width of the solitary Rossby wave is:

$$w\; = \,\varepsilon^{{ - \frac{1}{2}}} \sqrt {\frac{{12a_{2} m^{2} }}{{A_{0} a_{1} }}} \; = \;\frac{{3m\left| {\beta_{h} \; + \;F\overline{\nu }} \right|}}{{\left( {n^{2} \pi^{2} \; + \;F} \right)\sqrt \varepsilon }}\frac{1}{{\sqrt {\left( {1 - \left( { - 1} \right)^{n} } \right)n\pi \sqrt { - A_{0} \delta } } }},$$

(18)

which indicates that the width of the solitary wave is inversely proportional to the flow shear strength $|\delta |$, and that it has ${\text{sign}}(A_{0} ) = - {\text{sign}}(\delta )$. If the background flow shear is positive ($\delta > 0$), there is cyclonic solitary Rossby wave ($A_{0} < 0,\;n = 1$), if it is negative ($\delta < 0$), there is anticyclonic solitary Rossby wave ($A_{0} > 0,\;n = 1$). The phase speed of the solitary Rossby wave is:

$$c = c_{0} + \frac{{A_{0} a_{1} }}{3}\left( {2 - \frac{1}{{m^{2} }}} \right)\varepsilon ,$$

(19)

which is related to the amplitude and flow shear intensity. The nonlinear effect can make the velocity of solitary Rossby wave slower or faster than the linear Rossby wave, that is determined by the value of $m$. Under long-wave approximation ($m \to 1$), nonlinear effect reduces the speed of Rossby wave.

4 Results and discussion

The present analysis focuses on the shelf break of the East China Sea and takes $n = 1$. It is noteworthy that $n$ must be an odd number in Eq. (16); otherwise, a solitary Rossby wave cannot exist. The typical values of parameters for topographic Rossby wave are $V = 1\;{\text{m}}\;{\text{s}}^{ - 1} ,\;L = 4 \times 10^{5} \;{\text{m}},\;R_{d} = 4 \times 10^{5} \;{\text{m}},\;\beta_{h} = 1,\;|A_{0} | = 1,\;\varepsilon = 0.2,\;\delta = - 0.2$.

Figure 3a gives the zonal structure of Rossby wave using (15). When $\delta < 0$, the zonal structure tilts eastward, and when $\delta > 0$, the zonal structure tilts westward. When $\delta = 0$, which degenerates to linear Rossby wave, the zonal structure has east–west symmetry. Figure 3b and c describes the amplitude $A$ in (17) of Rossby wave with different values of $m\;(\delta = - 0.2)$ and $\delta \;(m = 0.9)$, when $Y_{0} = 0,\;t = 0$ and $|A_{0} | = 1$. Here, $m$ denotes the modulus of the cnoidal waves (17), which is a free parameter ranged from 0 to 1 and also measures the relative importance of nonlinearity to dispersion, and we assume that $m = 0.9$. If $m \to 0$, the cnoidal waves convert into cosine waves, and if $m \to 1$, the cnoidal waves turn into solitary wave. When the flow shear is negative ($\delta < 0$), anticyclonic solitary Rossby wave occurs ($A > 0$). When the flow shear is positive ($\delta > 0$), cyclonic solitary Rossby wave occurs ($A < 0$). When $\delta = 0$, the model reduces to the linear model and either anticyclonic or cyclonic solitary Rossby waves exist (the amplitude can be arbitrary). In the width solution, it is worth noting that the bigger the $A_{0}$ is, the smaller the width is. It means that this solution permits strong solitary wave with a small diameter. Moreover, it is interesting to note that the width of the solitary wave is proportional to the bottom slope $\beta_{h}$ and $\overline{v}$. The width of the solitary Rossby wave is also related to the flow shear; the weaker the flow shear, the larger the width of the solitary Rossby wave. Figure 3d illustrates the flow shear and amplitude effects on phase speed using (19), where the phase speed is scaled with $V$. Relative to the background flow, Rossby wave propagates southward with shallower water on the right hand in the Northern Hemisphere. Both flow shear and amplitude effects reduce the phase speed of Rossby wave. For a given flow shear ($\delta \ne {0}$), the phase speed is inversely proportional to the amplitude ($|A_{0} |$), and the greater the shear, the more significant the effect of amplitude on the phase speed. If $\delta = 0$, the model degenerates into the linear model and the phase speed is not related to amplitude. For a given amplitude, the phase speed is inversely proportional to the strength of the background flow shear ($|\delta |$), and the maximum value of phase speed is obtained when $\delta = 0$, which is exactly the result of the linear model. Figure 3e depicts the characters of solitary Rossby waves along background shear flow. It is worth noting that the existence of solitary wave is essentially due to the background flow shear. If the influence of the topographic effect is neglected, the theoretical results are still valid, and the topography only affects the velocity and width of the waves.

Fig. 3

Characteristics of solitary Rossby wave when n = 1. a Zonal structure Ψ₁ with different values of δ. b Amplitude A with different values of m(δ = − 0.2). c Amplitude A with different values of δ(m = 0.9). d Phase speed of Rossby wave with different values of A₀ and δ. e Background flow shear effects on solitary Rossby waves

The above discussion shows the background flow shear has a significant impact on the topographic Rossby wave. Consideration of the nonlinear effects shows that the solitary Rossby wave exists with properties that are quite different from linear Rossby wave but consistent with observations. If background flow shear is positive (negative), cyclonic (anticyclonic) solitary Rossby wave exist and their zonal structure tilts westward (eastward), which is consistent with the observations that the asymmetrical distribution of eddies across the Kuroshio in the East China Sea: cyclonic (anticyclonic) eddies are mainly concentrated on the western (eastern) sides of Kuroshio (Liu et al. 2017). This structural feature of the eddy facilitates the material exchange between the Kuroshio and shelf. Kamidaira et al. (2016) conducted numerical experiment for the area around the Ryukyu Islands. The results showed that eddies are generated due to the interactions between Kuroshio and local topography, including the ridge of the island to the east and the continental shelf break to the west, along which the Kuroshio persistently flows. The near-surface anticyclonic negative vorticity on the eastern side of the Kuroshio and the subsurface cyclonic positive vorticity on the western side are generated via the combination of shear instability and baroclinic instability, both of which are evidently influenced by the Kuroshio. In addition, the phase speed of the solitary Rossby wave is smaller than that predicted by linear Rossby wave theory; larger amplitude solitary Rossby wave has slower northward phase speed. Topography and nonlinear effects cause the Rossby wave to propagate southward relative to the background flow, so the observed Rossby wave velocity is smaller than the velocity of Kuroshio. Previous studies have shown that the velocity of the eddies is about $0.3\;{\text{m}}\;{\text{s}}^{ - 1}$, which is much smaller than the Kuroshio velocity ($\sim 1\;{\text{m}}\;{\text{s}}^{ - 1}$). The observations also confirm the property of non-dispersive, because the eddies retain their shapes as they propagate and the energy at every wavenumber propagates at the same speed. The solitary wave generation mechanism is most likely due to the instability of the background currents. The width of solitary wave is inversely related to the background current shear strength. If the shear is strong, it will produce small solitary wave, such as the eddies distributed across the Kuroshio in the East China Sea. The characteristics of the topographic Rossby waves are significantly different from those of the planetary Rossby waves in the ocean (Shi et al. 2018). The nonlinear effect increases the speed of westward planetary Rossby waves in the subtropical countercurrent zone. However, the nonlinear effect reduces the speed of northward topographic Rossby waves along the continental shelf break of the East China Sea. The effects of background flow shear on solitary Rossby waves are summarized in Fig. 3.

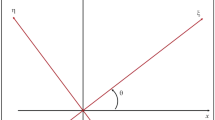
To further verify the theoretical results, we analyze the characteristics of Rossby waves along Kuroshio Current using Radon transform. Radon transform can be used to objectively study the propagation speeds of the ocean Rossby waves (Chelton and Schlax 1996; Challenor et al. 2001). The essential method is to convert the (x, t) coordinates to (θ, z) coordinates (see Fig. 4), and then calculates the waves energy in different θ directions using $\int {P^{2} (\theta ,z)} dz$. The θ corresponding to the maximum value of the wave energy is the main direction of wave propagation. The formula $c = \Delta x/\Delta t\tan (\theta - \pi /2)$ can be used to calculate the Rossby waves speed, where $\Delta x$ is the spatial resolution and $\Delta t$ is the temporal resolution.

Fig. 4

Schematic of the Radon transform of a longitude-time section

The sea surface height, sea-level anomaly, and velocity data with daily temporal resolution and $1/4^{{\text{o}}} \times 1/4^{{\text{o}}}$ spatial resolution, used in this section, were produced by DUACS and distributed by AVISO (ftp://ftp.aviso.altimetry.fr/). Figure 5a describes sea surface height and velocity in the East China Sea, and the velocity and corresponding gradient along LS section are shown in Fig. 5b. Two sections (LE06 and LE04) along eastern side of the Kuroshio are selected to calculate wave speed. LE06 and LE04 indicate the flow velocity of 0.6 m s⁻¹ and 0.4 m s⁻¹, respectively. We apply Radon transform to the sea-level anomaly data along LE06 and LE04 sections (see Fig. 6). From Fig. 6c and f, the θ corresponding to the maximum energy are 90.70° and 90.79°. Using the formula $c = \Delta x/\Delta t\tan (\theta - \pi /2)$, where $\Delta x = 500{\text{m}}$ and $\Delta t = 86400{\text{s}}$, the wave speeds along LE06 and LE04 are 0.47 m s⁻¹ and 0.41 m s⁻¹, respectively. From Eq. (19), the difference between the background current velocity and waves speed is closely related to the background current velocity and wave intensity. The stronger the waves intensity and the faster the background flow velocity are, the larger the difference. The wave speed along LE04 is 0.41 m s⁻¹, which is close to the background velocity 0.4 m s⁻¹. However, the wave speed along LE06 is 0.47 m s⁻¹, which is much smaller than the background velocity 0.6 m s⁻¹. The maximum energy in Fig. 6c is larger than that in Fig. 6f, that means that the wave intensity along LE06 is greater than LE04. All the above results indicate that the background flow has an important influence on the spatial structure, intensity, and propagation speed of the topographic Rossby waves.

Fig. 5

Sea surface height and flow velocity in the East China Sea averaged from 2000 to 2012. a Sea surface height in the East China Sea. The blue contours indicate the flow velocity; the blue dotted lines indicate the sections for calculating the propagation speed of the sea-level anomaly signal; the solid black line indicates the section for calculating the flow velocity. b The flow velocity and corresponding gradient along LS section (start from northwest point) (color figure online)

Fig. 6

Processes of calculating the Rossby waves phase speed along LE06 and LE04 using Radon transform. Hovmöller diagram of sea-level anomaly a of LE06 and d of LE04. After Radon transform b of LE06 and e of LE04. Rotational angle-spectral energy map c) of LE06 and f of LE04

5 Conclusions

To understand the eddy distribution pattern on both sides of the Kuroshio Current, we derived an asymptotic solution of the potential vorticity equation describing topography Rossby waves, using the method of multiple scales perturbation theory. For a background meridional flow $v = v_{0} + \delta x$, the effects of flow shear on the zonal structure, width, and phase speed of solitary Rossby waves were studied.

Background flow shear is the condition for the existence of solitary Rossby waves. For flow shear $\delta < 0$ ($\delta > 0$), anticyclonic (cyclonic) solitary Rossby waves exist and their zonal structure tilts eastward (westward). The phase speed of solitary Rossby waves is related to the amplitude and flow shear intensity. Topography and nonlinear effects cause the Rossby waves to propagate southward relative to the background flow with shallower water on the right hand of the observer looking in the direction of the wave propagation. Solitary Rossby waves are non-dispersive waves, and the width of solitary Rossby waves is inversely proportional to the intensity of the flow shear ($|\delta |$).

In the theoretical analysis, the distribution of eddies across the Kuroshio in the East China Sea is mainly influenced by topography, nonlinearity, and Kuroshio Current shear. The observed wave speed derived from sea-level anomaly data is much smaller than the background flow velocity and can be interpreted, at least qualitatively, by the theoretical results. In addition, centrifugal instability, cyclonic ageostrophic instability, baroclinic, and barotropic instability due to the Kuroshio fronts and topographic shear have important effects on the development of eddies, which needs further research.