1 Introduction

Turbulent processes in the oceanic mixed layer are of crucial importance in regulating the temperature and velocity fields in the upper ocean, thus controlling atmosphere–ocean interactions leading to climate changes. Accurate parameterization of subgrid-scale upper ocean processes must therefore be incorporated into oceanic general circulation models and/or coupled atmosphere–ocean general circulation models.

Second-order turbulence closure models, for example, the Mellor–Yamada closure model (Mellor and Yamada 1974, 1982) and its modified versions have been widely incorporated into atmospheric and oceanic general circulation models. The Mellor–Yamada closure model, however, has been criticized for underestimation of mixing intensity leading to a warm sea surface temperature bias (Martin 1985; Large and Crawford 1995) and a high relative humidity bias in the atmospheric boundary layer (Sun and Ogura 1980; Turton and Brown 1987). This deficiency motivated a number of studies attempting to improve the Mellor–Yamada closure model by incorporating data from field observations and laboratory experiments (e.g., Galperin et al. 1988; Mellor 2001), although the available data were somewhat limited to be reflected in the formulation of each turbulent quantity.

The performance of second-order turbulence closure models in reproducing the atmospheric and oceanic mixed layer processes can be more accurately evaluated through large eddy simulation (LES) studies that directly derive each turbulent quantity. Moeng and Wyngaard (1986, 1989) carried out LES and showed the importance of buoyancy effects in parameterizing several turbulent quantities in the convectively driven atmospheric boundary layers. Nakanishi (2001) and Nakanishi and Niino (2004, 2006, 2009) carried out a series of LES studies of the atmospheric boundary layers to develop a turbulence closure model which has improved the shortcomings of the Mellor–Yamada closure model, for example, insufficient growth of the convective boundary layer; the improved model has been incorporated into meso-scale weather prediction models (Saito et al. 2007; Wang et al. 2011) and atmospheric general circulation models (Watanabe et al. 2010). LES has also been used to reproduce several upper ocean processes (Skyllingstad and Denbo 1995; McWilliams et al. 1997; Wang et al. 1998; Skyllingstad et al. 2000; Noh et al. 2004; Sullivan et al. 2007), the results of which have sometimes been used to assess parameterized turbulent quantities for the oceanic mixed layer processes (Large and Gent 1999; Skyllingstad et al. 2000; Umlauf and Burchard 2005; Noh et al. 2011).

In this study, we evaluate the performance of the two second-order turbulence closure models of Mellor and Yamada (1982) (MY) and Nakanishi and Niino (2009) (NN) in reproducing the development of the oceanic mixed layer by inertially rotating wind stress forcing. We first perform LES for the resonant inertial response of the upper ocean; the excited large amplitude near-inertial oscillations lead to enhanced vertical shear causing strong turbulent mixing in the upper ocean, thus having dominant effects on sea surface temperature (Price et al. 1978; Shay et al. 1992; Large and Crawford 1995; Skyllingstad et al. 2000; Zedler et al. 2002; Furuichi et al. 2008). Using our LES results as a reference, we next evaluate the performance of MY and NN. Special attention is directed to examining whether or not NN, the performance of which has been shown in the atmospheric boundary layer, can also reproduce the characteristic feature in oceanic mixed layer processes, namely, the evolution of turbulence associated with the enhancement of wind-induced inertial shear.

2 Numerical models

2.1 LES

The experimental design of LES in this study is essentially the same as that described by Skyllingstad et al. (2000), who successfully reproduced a typical resonant inertial response of the upper ocean to a traveling storm observed during the Ocean Storms Experiment (Large and Crawford 1995). The filtered governing equations are given by:

$$ \left( {\frac{\partial }{\partial t} + \user2{u} \cdot \nabla } \right)\user2{u} + \user2{f} \times \user2{u} = - \nabla \left( {\frac{p}{{\rho_{0} }}} \right) - \frac{{g\rho^{'} }}{{\rho_{0} }}{\hat{\user2{z}}} + {\text{SGS}}, $$
$$ \left( {\frac{\partial }{\partial t} + \user2{u} \cdot \nabla } \right)\theta = {\text{SGS}}, $$
$$ \nabla \cdot \user2{u} = 0 $$

where u = (u, v, w) is the three-dimensional velocity vector, θ is the potential temperature, f = f \( {\hat{\user2{z}}} \) is the Coriolis parameter with \( {\hat{\user2{z}}} \) the upward unit vector, p is the pressure, g is the acceleration due to gravity, ρ 0 is the reference density, and ρ′ is the density perturbation (hereafter, primed variables denote the resolved perturbations from the horizontal average in LES). The subgrid-scale turbulent processes (denoted by SGS) are parameterized using the filtered structure function approach of Ducros et al. (1996), because it has been confirmed to perform well in reproducing the observed development of the oceanic mixed layer under strong wind forcing (Skyllingstad et al. 2000). For simplicity, the salinity is assumed to be constant (32.8 psu) and no surface heat flux is applied. The effects of the Langmuir circulation (Craik and Leibovich 1976) and of surface wave breaking on the development of the oceanic mixed layer are also ignored because they are likely to be much smaller than the effect of resonant wind stress forcing (Skyllingstad et al. 2000; Noh et al. 2004). Throughout this study, the local inertial frequency at 45°N (f 45) is assumed.

A cyclic boundary condition is used at the lateral boundaries, whereas a rigid boundary condition is used at both the top and bottom. To eliminate the effects of reflected waves from the bottom rigid boundary, a sponge layer is introduced within 15 m of the bottom. To solve the governing equations, we use a Fourier expansion in the horizontal directions and a centered finite difference in the vertical direction with the fourth-order Runge–Kutta time stepping method.

The wind stress forcing τ is prescribed as:

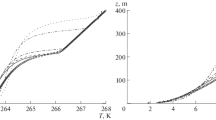
$$ \varvec{\tau}= \left( {\tau_{x} , \tau_{y} } \right) = A_{0} \sin^{2} \left( {\pi t/t_{d} } \right)\left( {\cos \omega t, - \sin \omega t} \right) $$

where ω represents a constant angular rotation rate, A 0 = 1.4 Nm−2 is the maximum wind stress, and t d = 24 h is the storm duration. We carry out two kinds of LES with ω = f 45 (resonant case, Fig. 1a) and ω = 0 s−1 (off-resonant case) to see how the evolution of the oceanic mixed layer is linked with resonant inertial oscillations. The initial background temperature field is horizontally uniform and mimics the typical stratification in the North Pacific during fall (Fig. 1b), whereas the initial turbulent velocity field is assumed to be a superposition of small random perturbations having the horizontal average of kinetic energy q 20 exp(z/H) with q 20  = 10−10 m2 s−2 and H = 20 m. The model domain is 200 m in the horizontal and 108 m in the vertical with a grid resolution Δx = Δy = Δz = 0.8 m, much higher than used by Skyllingstad et al. (2000) (2 m). The numerical simulations are carried out for 24 h with a time step of 0.5 s.

Fig. 1
figure 1

a Time series of wind stress forcing for ω = f 45. b Vertical structure of initial temperature profile

Full size image

It should be noted that the results of LES, in particular, the turbulent heat flux and the energy dissipation rate, might be affected by grid resolution. To see the sensitivity of the calculated results to grid resolution, therefore, an additional LES is carried out for the resonant case using Δx = Δy = Δz = 0.5 m for 12 h.

2.2 One-dimensional turbulence closure models

In this study, we evaluate a simplified Level 2.5 version of MY (Mellor 2001, 2003) and the Level 2.5 version of NN (Nakanishi and Niino 2009). Because these turbulence closure models have already been described in detail by the above authors, only a brief description is given below.

The turbulence closure models express turbulent fluxes as:

$$ UF = \langle w^{*} u^{*} \rangle = - qlS_{\text{M}} \frac{\partial U}{\partial z},\quad VF = \langle w^{*} v^{*} \rangle = - qlS_{\text{M}} \frac{\partial V}{\partial z},\quad HF = \langle w^{*} \theta^{*} \rangle = - qlS_{\text{H}} \frac{\partial \Uptheta }{\partial z}, $$
(1)

where 〈〉 denotes ensemble average, U and V are the ensemble-averaged horizontal velocities, Θ is the ensemble-averaged potential temperature, u *, v *, w *, and θ * are the turbulent components of velocity and temperature, respectively, q 2/2 is the turbulent kinetic energy, l is the turbulent length scale, and S M and S H are the stability functions.

The stability functions S H and S M in MY are given by

$$ S_{\text{H}} = \frac{{A_{2} \left( {1 - 6A_{1} /B_{1} } \right)}}{{1 - \left( {3A_{2} B_{2} + 18A_{1} A_{2} } \right)G_{\text{H}} }}, $$
(2a)
$$ S_{\text{M}} = \frac{{\left( {18A_{1}^{2} + 9A_{1} A_{2} } \right)S_{\text{H}} G_{\text{H}} + A_{1} \left( {1 - 3C_{1} - 6A_{1} /B_{1} } \right)}}{{1 - 9A_{1} A_{2} G_{\text{H}} }}, $$
(2b)

where

$$ G_{\text{H}} = - \frac{{l^{2} }}{{q^{2} }}N^{2}, $$

N is the buoyancy frequency, and (A 1, A 2, B 1, B 2, C 1) = (0.92, 0.74, 16.6, 10.1, 0.08) are the closure constants. Note that q and l are obtained by solving the prognostic equations:

$$ \frac{{\partial (q^{2}) }}{\partial t} + \frac{\partial }{\partial z}\left\{{ - qlS_{q}\frac{{\partial (q^{2}) }}{\partial z}} \right\} = 2\left [{qlS_{\text{M}} \left\{ {\left( {\frac{\partial U}{\partial z}} \right)^{2} + \left( {\frac{\partial V}{\partial z}} \right)^{2} } \right\} - qlS_{\text{H}} N^{2} - \frac{{q^{3} }}{{B_{1} l}}} \right], $$
(3)
$$ \frac{{\partial (q^{2}l) }}{\partial t} + \frac{\partial }{\partial z}\left\{ { - ql S_{q}\frac{{\partial (q^{2} l)}}{\partial z}} \right\} = E_{1} l\left[ {qlS_{\text{M}} \left\{ {\left( {\frac{\partial U}{\partial z}} \right)^{2} + \left( {\frac{\partial V}{\partial z}} \right)^{2} } \right\} - E_{3} qlS_{\text{H}} N^{2} } \right] - \frac{{Wq^{3} }}{{B_{1} }}, $$
(4)

where W is a “wall proximity” function, and (E 1, E 3) = (1.8, 1.0) are additional non-dimensional constants, and we assume S q  = 0.41S M following Mellor (2003).

In another turbulence closure model NN, the closure constants (A 1, A 2, B 1, B 2, C 1, C 2, C 3, C 5) = (1.18, 0.665, 24.0, 15.0, 0.137, 0.75, 0.352, 0.2) are introduced taking into account the buoyancy effects on the pressure-covariance terms (Moeng and Wyngaard 1986, 1989) and the stability functions S H and S M are given by:

$$ S_{\text{H}} = \alpha_{\text{c}} A_{2} \frac{{\phi_{1} + 3C_{1} \phi_{4} }}{{\phi_{1} \phi_{3} + \phi_{2} \phi_{4} }}, $$
(5a)
$$ S_{\text{M}} = \alpha_{\text{c}} A_{1} \frac{{\phi_{2} - 3C_{1} \phi_{3} }}{{\phi_{1} \phi_{3} + \phi_{2} \phi_{4} }}, $$
(5b)

where

$$ \begin{aligned} \phi_{1} & = 1 - 9\alpha_{\text{c}}^{2} A_{1} A_{2} \left( {1 - C_{2} } \right)G_{\text{H}},\quad \phi_{2} = \phi_{5} + 9\alpha_{\text{c}}^{2} A_{2}^{2} \left( {1 - C_{2} } \right)\left( {1 - C_{5} } \right)G_{\text{H}},\\ \phi_{3} & = \phi_{5} - 12\alpha_{\text{c}}^{2} A_{1} A_{2} \left( {1 - C_{2} } \right)G_{\text{H}},\quad \phi_{4} = 6\alpha_{\text{c}}^{2} A_{1}^{2} G_{\text{M}}, \\ \alpha_{\text{c}} & = \min \left( {q/q_{2},1} \right), \\ \end{aligned} $$

with

$$ \phi_{5} = 1 - 3\alpha_{\text{c}}^{2} A_{2} B_{2} \left( {1 - C_{3} } \right)G_{\text{H}}, $$
$$ G_{\text{M}} = \frac{{l^{2} }}{{q^{2} }}\left[ {\left( {\frac{\partial U}{\partial z}} \right)^{2} + \left( {\frac{\partial V}{\partial z}} \right)^{2} } \right], $$

and q 22 /2 the turbulent kinetic energy given by the Level 2 model. In addition, the formulation of S q is modified as S q  = 3S M .

Another important difference between MY and NN is in the formulation of turbulent length scale: instead of using Eq. 4, we prescribe the turbulent length scale in NN by taking into account the effect of stable stratification such as:

$$ l^{ - 1} = l_{\text{S}}^{ - 1} + l_{\text{T}}^{ - 1} + l_{\text{B}}^{ - 1} $$
(6)

where

$$ l_{\text{S}} = - \kappa z,\quad l_{\text{T}} = 0.23\frac{{\int_{ - D}^{0} {\left( { - qz} \right){\text{d}}z} }}{{\int_{ - D}^{0} {q{\text{d}}z} }},\quad l_{\text{B}} = \left\{ \begin{gathered} q/N\quad N^{2} > 0 \hfill \\ \infty \quad N^{2} \le 0 \hfill \\ \end{gathered} \right. $$

with κ = 0.41 the von Kármán constant. Because no surface heat flux is applied in this study, the expression for the turbulent length scale can be simplified from its original version by dropping the newly introduced terms which depend on the Monin–Obukhov length scale.

Each turbulence closure model is incorporated into a simple one-dimensional numerical model with uniform 2-m resolution. With the same initial conditions as used in LES for the turbulent velocity field (q 2 = q 20 exp(z/H) with q 20  = 10−10 m2 s−2 and H = 20 m) and the background temperature field (Fig. 1b), the one-dimensional numerical model is forced by each of the resonant and off-resonant wind forcing. The results are then compared with the corresponding LES to check the performance of each turbulence closure model.

3 Results and discussion

3.1 Results of LES

Figure 2a–f depicts the results from LES with Δx = Δy = Δz = 0.8 m for the resonant case showing the time series of potential temperature (θ, contour) and the resolved turbulent heat flux (w′θ′, shade) in an x–z cross section (a–c) and the time-depth sections of the horizontally averaged temperature and velocity fields (d–f). Negative turbulent heat flux is gradually enhanced as a result of strong vertical mixing in the thermocline (Fig. 2a–c). Consequently, the bottom of the thermocline deepens and the sea surface temperature drops by 1.3°C (Fig. 2d). It is also found that the velocity fields develop and extend downward in response to the resonant wind stress forcing (Fig. 2e, f), which leads to enhancement of vertical shear at the base of the oceanic mixed layer causing strong entrainment. Figure 2g shows the time series of the horizontally averaged sea surface temperature obtained from the resonant and off-resonant LES, demonstrating that the resonant wind stress forcing produces much more rapid evolution of the oceanic mixed layer. Overall behavior of the oceanic mixed layer shown in Fig. 2 is consistent with previous observations and numerical experiments (Large and Crawford 1995; Crawford and Large 1996; Skyllingstad et al. 2000).

Fig. 2
figure 2

Results from LES. a–c Vertical cross sections of the temperature (color contour; interval is 0.4°C) and the resolved turbulent heat flux (shade) along y = 0 m for the resonant case. d–f Time-depth sections of the horizontally averaged temperature (contour interval 0.4°C) and zonal and meridional velocities (contour interval 0.2 ms−1) for the resonant case. g Time series of the horizontally averaged sea surface temperature for the two cases

Full size image

To assess the turbulence closure models, we use the vertical profiles of total turbulent heat flux calculated using:

$$ HF_{\text{LES}} = \overline{{w^{\prime } \theta^{\prime } }} + HF_{\text{SGS}}, $$

where the overbar denotes the horizontal average and HF SGS is the contribution from the subgrid-scale parameterization. Figure 3 shows the vertical profiles of HF LES for the resonant case and those of HF SGS, both at t = 12 h and 18 h (t = 12 h) for a grid resolution of 0.8 (0.5) m. The effect of subgrid-scale parameterization is minor (at most 15% of the total turbulent heat flux) and the total turbulent heat flux is fairly independent of grid resolution. Furthermore, comparison of the calculated results using grid resolution of 0.8 m and 0.5 m for each turbulent quantity shown later (Fig. 5) indicates that the turbulent kinetic energy can be calculated without taking into account the subgrid-scale contributions (discussed in the Sect. 3.2) and the conclusion presented here is not subject to grid resolution.

Fig. 3
figure 3

Vertical profiles of horizontally averaged total turbulent heat flux for the resonant case from LES using Δ = 0.8 m (black lines) and Δ = 0.5 m (gray lines, only for t = 12 h). The dash–dotted lines denote the contributions from the subgrid-scale parameterization

Full size image

3.2 Comparison of LES with turbulence closure models

Figure 4 shows the time-depth sections of the temperature and velocity fields and the time variations of the sea surface temperature for the resonant case, both obtained from MY and NN, which should be compared with the corresponding results from LES. Although MY and NN both reproduce the enhancement of inertial oscillations in response to the resonant wind stress forcing, the drop of the sea surface temperature is underestimated by 25% in MY and overestimated by 15% in NN.

Fig. 4
figure 4

Results obtained from turbulence closure models for the resonant case. a–c Time-depth sections of temperature (contour interval 0.4°C) and zonal and meridional velocities (contour interval 0.2 ms−1) obtained from MY. d–f As in a–c but from NN. g Comparison of the sea surface temperature obtained from LES (gray solid line) with those obtained from MY (black dashed line) and NN (black solid line)

Full size image

Figure 5 shows the vertical profiles of N 2, q 2, and B 1 l at t = 12 h and 18 h for the resonant case obtained from LES (gray lines), MY (red lines), and NN (blue lines), respectively, all of which are associated with the turbulent heat and momentum fluxes (Eqs. 1, 2a, 2b, 5a, 5b). In particular, the turbulent quantities from LES are calculated using:

$$ q^{2}_{\text{LES}} = \overline{{u^{\prime } u^{\prime } + v^{\prime } v^{\prime } + w^{\prime } w^{\prime } }} = \overline{{u_{i}^{\prime } u_{i}^{\prime } }},\quad \left[ {B_{1} l} \right]_{\text{LES}} = \frac{{q^{3}_{\text{LES}} }}{{\left| {\varepsilon_{\text{LES}} } \right|}},\quad \varepsilon_{\text{LES}} = - \overline{{\frac{{X_{\text{m}} }}{2}\left( {\frac{{\partial u_{j}^{\prime } }}{{\partial x_{i} }} + \frac{{\partial u_{i}^{\prime } }}{{\partial x_{j} }}} \right)^{2} }}, $$

where the subscripts i and j denote the x, y, z directions, and ε LES is the energy dissipation with X m the eddy viscosity calculated in LES (Nakanishi and Niino 2009; Skyllingstad et al. 2000).

Fig. 5
figure 5

Time variations of vertical profiles of N 2, q 2, and B 1 l obtained from LES (gray lines), MY (red lines), and NN (blue lines), respectively, for the resonant case. The green lines denote the results obtained from the slightly modified NN (see text). In the upper panels, the results of the additional LES using a nearly half grid resolution (0.5 m) are shown (light gray lines). Note that the result of LES for B 1 l below the base of the oceanic mixed layer which rapidly increases with depth has not been used in this analysis

Full size image

The calculated values of q 2LES and [B 1 l]LES can be used to assess the turbulence closure models, except [B 1 l]LES below the base of the oceanic mixed layer (defined as the depth at which N 2 becomes maximum; Fig. 5) which rapidly increases with depth as ε LES approaches zero. We can see that the discrepancies in the vertical profiles of N 2, q 2, and B 1 l found between MY and LES are significantly reduced between NN and LES except for B 1 l.

To identify the parameters responsible for the discrepancies between LES, MY, and NN, we first compare the vertical profiles of S H/B 1 for the resonant case obtained by incorporating the turbulent quantities from LES (Fig. 5) into Eq. 1 (i.e. [S H/B 1]LES = −HF LES/(q LES [B 1 l]LES ∂θ LES /∂z)) with those obtained by incorporating the turbulent quantities from LES into Eq. 2a ([S H/B 1]MY) and Eq. 5a ([S H/B 1]NN). The results are shown in Fig. 6 where we can see that, compared with Eq. 2a, Eq. 5a yields a vertical profile of S H/B 1 closer to that from LES. This implies the performance of the stability functions is improved by taking into account the buoyancy effects on the pressure-covariance terms.

Fig. 6
figure 6

Comparison of the vertical profiles of S H/B 1 for the resonant case obtained by incorporating the turbulent quantities from LES (Fig. 5) into Eq. 1 (i.e. [S H/B 1]LES = −HF LES/(q LES [B 1 l]LES ∂θ LES /∂z), gray lines), Eq. 2a ([S H/B 1]MY, black dash-dotted lines), and Eq. 5a ([S H/B 1]NN, black solid lines)

Full size image

Next, the vertical profiles of [B 1 l]LES are compared with those obtained by incorporating the turbulent quantities from LES into Eq. 6 ([B 1 l]NN). Figure 7 shows that, in contrast with the stability functions, the difference between [B 1 l]NN (black thin lines) and [B 1 l]LES (gray lines) becomes evident below z = −20 m.

Fig. 7
figure 7

Comparison of the vertical profiles of B 1 l obtained from LES for the resonant case ([B 1 l]LES, gray lines) with those obtained by incorporating the turbulent quantities from LES (Fig. 5) into Eq. 6 ([B 1 l]NN, black thin lines) and the modified version of Eq. 6 where the buoyancy length scale is reduced by about half ([B 1 l]NNmod, black thick lines). Note that [B 1 l]LES below the base of the oceanic mixed layer which rapidly increases with depth has not been used in this analysis

Full size image

This motivates us to carry out an additional numerical experiment slightly modifying NN such that the buoyancy length scale l B (Eq. 6) is reduced by approximately half (l B = 0.53q/N) as suggested by Galperin et al. (1988, 1989) who took into account the relationship between the temperature variance and the Ozmidov length scale (Dillon 1982) and the results of the laboratory experiments on decaying turbulence in stratified fluids (Dickey and Mellor 1980). We can obtain the vertical profile of B 1 l closer to that of [B 1 l]LES by incorporating the turbulent quantities from LES into the modified version of Eq. 6 mentioned above ([B 1 l]NNmod, black thick lines in Fig. 7). Furthermore, incorporating [B 1 l]NNmod thus obtained and other turbulent quantities from LES into Eq. 5a yields the vertical profile [S H/B 1]NNmod which agrees well with that from LES (i.e. [S H/B 1]LESmod = −HF LES/(q LES [B 1 l]NNmod ∂θ LES /∂z)) except below the base of the oceanic mixed layer (Fig. 8). As a result, this slight modification leads to accurate predictions of vertical profiles of N 2, q 2, and B 1 l (green lines in Fig. 5) and hence the development of the oceanic mixed layer (Fig. 9).

Fig. 8
figure 8

Comparison of the vertical profiles of S H/B 1 for the resonant case obtained by incorporating [B 1 l]NNmod (black thick lines in Fig. 7) and other turbulent quantities from LES into Eq. 1 (i.e. [S H/B 1]LESmod = −HF LES/(q LES [B 1 l]NNmod ∂θ LES /∂z), gray lines) and Eq. 5a ([S H/B 1]NNmod, black lines)

Full size image
Fig. 9
figure 9

a Time-depth section of temperature for the resonant case (contour interval 0.4°C) obtained from the modified NN where the buoyancy length scale l B is reduced by about half (l B = 0.53q/N). b Comparison of the sea surface temperature obtained from LES with that obtained from the modified NN

Full size image

Finally, we evaluate the performance of MY, NN, and the modified NN for the off-resonant case. Figures 10 and 11 show the time variations of the temperature field and the vertical profiles of N 2, q 2, and B 1 l, where we can recognize the same features as found for the resonant case; the discrepancies in the vertical profiles of N 2, q 2, and B 1 l between MY and LES are reduced between NN and LES and much more between the modified NN and LES (Fig. 11). The underestimate (overestimate) of the decrease of sea surface temperature in MY (NN) can be suitably corrected by using the modified NN (Fig. 10).

Fig. 10
figure 10

a–d Time-depth sections of the temperature (contour interval 0.4°C) and e time variations of the sea surface temperature obtained from LES, MY, NN, and the modified NN, respectively, for the off-resonant case

Full size image
Fig. 11
figure 11

Time variations of vertical profiles of N 2, q 2, and B 1 l obtained from LES (gray lines), MY (red lines), NN (blue lines), and the modified NN (green lines), respectively, for the off-resonant case. Note that the result of LES for B 1 l below the base of the oceanic mixed layer which rapidly increases with depth has not been used in this analysis

Full size image

4 Conclusion

In this study, by comparison with results from LES, we have found that the development of the oceanic mixed layer caused by resonant wind stress forcing (i.e. strong entrainment at the base of the oceanic mixed layer and accompanying decrease of sea surface temperature) is underestimated by the second-order turbulence closure model of Mellor and Yamada (1982) (MY) and somewhat overestimated by the second-order turbulence closure model of Nakanishi and Niino (2009) (NN). Considering that the stability functions in NN perform better than those in MY in reproducing the vertical structure of turbulent heat flux, we have modified NN by reducing the buoyancy length scale l B (Eq. 6) by approximately half (l B = 0.53q/N) and found that the discrepancy can be much diminished. The turbulent length scale and the stability functions both reflecting the effect of density stratification have thus been found to be essential in simulating the resonant inertial response of the oceanic mixed layer to strong wind stress forcing.

This study is relevant to the numerical modeling of the upper ocean response at mid latitudes where near-inertial oscillations are efficiently excited (Watanabe and Hibiya 2002; Alford 2003; Zhai et al. 2007, 2009; Komori et al. 2008; Furuichi et al. 2008). Needless to say, the results of LES should be compared with those of other oceanic mixed layer models (Price et al. 1986; Large et al. 1994; Kantha and Clayson 1994, 2004; Noh and Kim 1999; Umlauf and Burchard 2005; Huang et al. 2011) in more realistic situations by taking into account convection, surface wave breaking, and Langmuir turbulence. Each of the improved oceanic mixed layer models should be incorporated into oceanic general circulation models to check its performance in terms of the large-scale ocean dynamics (Ezer 2000; Kara et al. 2008).