Characterization of fibril dynamics on three timescales by solid-state NMR

Abstract

A multi-timescale analysis of the backbone dynamics of HET-s (218–289) fibrils is described based on multiple site-specific R ₁ and R _1ρ data sets and S ² measurements via REDOR for most backbone ¹⁵N and ¹³Cα nuclei. ¹⁵N and ¹³Cα data are fitted with motions at three timescales. Slow motion is found, indicating a global fibril motion. We further investigate the effect of ¹³C–¹³C transfer in measurement of ¹³Cα R ₁. Finally, we show that it is necessary to go beyond the Redfield approximation for slow motions in order to obtain accurate numerical values for R _1ρ.

Introduction

Obtaining atomic-resolution structures of proteins has become an important component of protein studies, in order to understand the correlation between structure and function. However, proteins exhibit motions on multiple timescales, making a static structure an incomplete picture. Molecular motion plays a critical role in the behavior of proteins: slow motions may indicate large-scale rearrangement of a protein, for example, as a result of a signaling process, or binding of substrates to enzymes. Faster motions are indicative of more localized motion, giving insight into local protein flexibility. Site-specific characterization of protein motions across multiple timescales complements atomic-resolution structure, giving information about both slow, concerted motions and fast, local motions. NMR spectroscopy is an ideal technique to study motion across many timescales; exchange spectroscopy (Jeener et al. 1979), relaxation-dispersion experiments (McConnell 1958), and spin–lattice relaxation (Allerhand et al. 1971) cover motions with correlation times from ~1 s to ~1 ps.

Site-specific analysis of protein dynamics utilizing solid-state NMR can typically provide information on up to 2–3 timescales of motion (Zinkevich et al. 2013), each characterized by a timescale and an amplitude, although in principle it is possible to use more complex analyses. To perform site-specific analysis of dynamics, the following measurements are commonly combined: (1) measurement of incompletely-averaged anisotropic interactions (typically one-bond dipolar couplings), (2) measurement of several longitudinal relaxation-rate constants (typically R ₁ or NOE), and (3) measurement of transverse relaxation times (typically R _1ρ or CSA-dipole cross-correlated cross-relaxation; Chevelkov et al. 2007a; Krushelnitsky et al. 2010; Lewandowski et al. 2010; Skrynnikov 2007). Both R ₁ and R _1ρ measurements can be attributed to modulation of some ¹H–X coupling and/or CSA of nucleus X at various timescales (R ₁ typically provides information for τ _c < 100 ns and R _1ρ for τ _c > 10 ns, see SI Figure 1), whereas incompletely averaged dipolar couplings provide the total amplitude of motion (characterized by its order parameter, S ²) of the ¹H–X coupling. Therefore, one can characterize protein dynamics by collecting some or all of these parameters site specifically and then fitting them to a dynamic model.

To date, a variety of studies have investigated dynamics information using solid-state NMR. Chevelkov et al. combined solution and solid-state NMR data to investigate nanosecond motion with the extended model-free approach (Chevelkov et al. 2007b; Clore et al. 1990). Chevelkov et al. (2009) and Schanda et al. (2010) used the extended model-free approach in solid-state NMR, obtaining information on two timescales of motion, with correlation times in the nano- and picosecond ranges. Zinkevich et al. (2013) pushes this approach towards its limit, using combined R _1ρ, R ₁, and S ² measurements for ¹H–¹⁵N spin pairs, and fitting up to three motions to the data (amplitudes were determined for three motions, although correlation times could only be determined for two of three motions for many residues), while also considering temperature dependence to calculate the activation energy of the motions, utilizing the Arrhenius relationship. Lamley et al. utilize measurements acquired from both ¹⁵N and ¹³C′, and combined the data for analysis (Lamley et al. 2015). Other studies utilize only one or two of these measurements, thus allowing a characterization of motion on only a single timescale of interest. For example, Ma et al. (2014) utilize only R _1ρ (in this case, R _1ρ resulting from fluctuation of the isotropic chemical shift) for characterization of slow conformational exchange (on the order of 2900 s⁻¹) in ubiquitin and Good et al. (2014) studied collective motion in Anabaena Sensory Rhodopsin using S ² of backbone dipole couplings and ¹⁵N R _1ρ measurements. Solid-state NMR data may also be utilized in conjunction with molecular-dynamics simulations, lending insight into the interpretation of experimental parameters (Lange et al. 2009; Ma et al. 2015; Mollica et al. 2012; Xue and Skrynnikov 2014).

We present a study of dynamics in the fibrils formed by HET-s (218–289), which is the prion-forming domain of the HET-s protein from Podospora anserina, responsible for a programmed cell death reaction, known as heterokaryon incompatibility (Glass and Kaneko 2003; Saupe 2000). HET-s (218–289) is an ideal representative for amyloid proteins, due to a high degree of local order (Siemer et al. 2006), a lack of polymorphism, and a well defined structure (Van Melckebeke et al. 2010; Wasmer et al. 2008), simplifying analysis. HET-s (218–289) is also an important model amyloid for drug design (Herrmann et al. 2015; Schütz et al. 2011). A cartoon of the HET-s (218–289) fibril structure is shown in Fig. 1. We have characterized the dynamics in HET-s (218–289) fibrils using site-specific dynamics analysis of backbone ¹H–¹⁵N and ¹Hα–¹³Cα spin pairs, including measurements of S ², R ₁, and R _1ρ. A more complete discussion of the biological significance of our findings will be presented elsewhere. Here, we discuss relaxation theory with particular emphasis on importance of ¹³C–¹³C transfer in ¹³Cα R ₁ measurements, problems arising for measurement and calculation of R _1ρ, experimental methods including choice of samples and modifications to the REDOR sequence for measurement of ¹Hα–¹³Cα couplings, and finally data analysis with a discussion of potential pitfalls. Although our discussion is directed by particular challenges that arose when applying dynamics analysis to HET-s (218–289) fibrils, many of the conclusions are broadly applicable to the study of proteins dynamics in general by solid-state NMR.

Fig. 1

Schematic representation of the HET-s (218–289) backbone structure in the context of amyloid fibrils (adapted from Van Melckebeke et al. 2011; Wasmer et al. 2008). Each protein monomer forms two turns of a β solenoid which are shown separately here, with the following color-code: white: hydrophobic, blue: positively charged, red: negatively charged, green: polar

Theory and practical aspects of relaxation measurements

Summary of relaxation formalism

Redfield relaxation theory (Redfield 1957) lays a widely-utilized basis for calculating relaxation parameters. In solids the relaxation-rate constants depend on the orientation of individual crystallites relative to the external magnetic field, and in fact those rates will change throughout the rotor period (Torchia and Szabo 1982). This orientation and deterministic time dependence of the relaxation-rate constants makes the data evaluation more complicated than for solution-state studies. Given the limited signal-to-noise ratio of experimental relaxation-data measurements and the limited spread of the magnitude of the rate constants due to crystallite orientations, often single-exponential decays are assumed, where the rate constant of the single exponential is approximated by the average of the rate constants (Giraud et al. 2005). The Lipari–Szabo model-free approach (Lipari and Szabo 1982), gives a simple procedure to calculate the average relaxation-rate constants from model-independent order parameters (S ²) and correlation times (τ _c). In this case, (1 − S ²) is related to the amplitude of motion of the anisotropic interaction (usually dipole or CSA), although the exact physical interpretation of S ² is not determined without specifying a model (see SI Section 1.1 for the definition of S ² for two models).

The extended model-free approach (Clore et al. 1990) gives the spectral-density function for two motions, one fast and one slow, characterized by $S_{\text{f}}^{2}$, τ _f and $S_{\text{s}}^{2}$, τ _s, respectively, as

$$J(\omega ) = \frac{2}{5}\left( {1 - S_{\text{f}}^{2} } \right)\frac{{\tau_{\text{f}} }}{{1 + (\omega \tau_{\text{f}} )^{2} }} + \frac{2}{5}S_{\text{f}}^{2} \left( {1 - S_{\text{s}}^{2} } \right)\frac{{\tau_{\text{s}} }}{{1 + (\omega \tau_{\text{s}} )^{2} }}.$$

(1)

The effects of the two motions are cumulative, but the contributions of the slow motion are scaled by the presence of the fast motion. Here, we have assumed that the two correlation times are separated by at least one order of magnitude so that the calculation of an effective correlation time for the fast motion is not required. From the spectral density, one can calculate R ₁ relaxation-rate constants of spin I induced by fluctuation of a dipolar coupling as

$$R_{1}^{\text{IS}} = \left( {\frac{{\delta^{\text{IS}} }}{4}} \right)^{2} \left( {J(\omega_{I} - \omega_{S} ) + 3J(\omega_{I} ) + 6J(\omega_{I} + \omega_{S} )} \right)$$

(2)

where $\delta^{\text{IS}} = - 2\frac{{\mu_{0} }}{4\pi }\frac{{\gamma_{I} \gamma_{S} \hbar }}{{r_{\rm IS}^{3} }}$ is the anisotropy of the dipolar-coupling tensor, and ω _Ι and ω _S are the nuclear Larmor frequencies. The R ₁ relaxation of spin I induced by a chemical-shift anisotropy (ω _I σ _zz = 2Δσ/3) is given by

$$R_{1}^{\text{CSA}} = \frac{3}{4}\left( {\omega_{I} \sigma_{zz} } \right)^{2} J(\omega_{I} ).$$

(3)

The total R ₁ relaxation-rate constant is then given by the sum

$$R_{1} = R_{1}^{\text{IS}} + R_{1}^{\text{CSA}} .$$

(4)

Similarly, it is possible to calculate expressions for R _1ρ, while accounting for the effects of both MAS and the applied RF field (Haeberlen and Waugh 1969; Kurbanov et al. 2011) using

$$R_{1\rho }^{\text{IS}} = \frac{1}{2}R_{1}^{\text{IS}} + \left( {\frac{{\delta^{\text{IS}} }}{4}} \right)^{2} \left( {3J(\omega_{S} ) + \frac{1}{3}J(\omega_{1} - 2\omega_{\text{r}} ) + \frac{2}{3}J(\omega_{1} - \omega_{\text{r}} ) + \frac{2}{3}J(\omega_{1} + \omega_{\text{r}} ) + \frac{1}{3}J(\omega_{1} + 2\omega_{\text{r}} )} \right),$$

(5)

$$R_{1\rho }^{\text{CSA}} = \frac{1}{2}R_{1}^{\text{CSA}} + \frac{1}{6}\left( {\omega_{\text{I}} \sigma_{zz} } \right)^{2} \left( {\frac{1}{2}J(\omega_{1} - 2\omega_{\text{r}} ) + J(\omega_{1} - \omega_{\text{r}} ) + J(\omega_{1} + \omega_{\text{r}} ) + \frac{1}{2}J(\omega_{1} + 2\omega_{\text{r}} )} \right),$$

(6)

$$R_{1\rho } = R_{1\rho }^{\text{IS}} + R_{1\rho }^{\text{CSA}} .$$

(7)

Here, ω _r and ω ₁ are the MAS frequency and RF field strength (nutation frequency) applied to the I spin, respectively, assuming that RF irradiation is applied on-resonance. Note that we will discuss the validity of the R _1ρ equations in “Transverse relaxation (R _1ρ) and the violation of the Redfield approximation” section.

Measurement of multiple R ₁ values at different Larmor frequencies and/or R _1ρ values at different spinning frequencies and rf-field strengths can in some cases be sufficient to determine both the timescale (τ _c) and amplitude (S ²) of a motion or even multiple motions. However, depending on the correlation time of a given motion, it may be difficult to determine these parameters accurately because their fit values can be strongly correlated. In this case, when using the model-free approach, one can determine the total S ² independent of the correlation time by directly measuring the magnitude of the incompletely-averaged dipolar coupling of the spin pair in question. In this case, the observed dipole coupling is related to S ² by its ratio to the rigid-limit dipole coupling (calculated using the vibration-averaged bond distance):

$$S^{2} = \left( {{{\delta_{\text{obs}}^{\text{IS}} } \mathord{\left/ {\vphantom {{\delta_{\text{obs}}^{\text{IS}} } {\delta_{\text{rigid}}^{\text{IS}} }}} \right. \kern-0pt} {\delta_{\text{rigid}}^{\text{IS}} }}} \right)^{2}$$

(8)

If motions on multiple time scales are present, then the S ² determined by direct measurement of the dipolar coupling will be the product of all order parameters of the different motions acting on the dipole coupling.

$$S^{2} = S_{ 1}^{2} \cdot S_{ 2}^{2} \cdot \ldots$$

(9)

Note that if the timescale of a motion is slower than the recoupling rate of the experiment used to measure S ², then this motion will not be observed via the order parameter. For a ¹H–¹³C one-bond dipole coupling (δ = 44.8 kHz), this means that sensitivity of the recoupling experiment to slow motions will begin to degrade for correlation times of tens of microseconds.

In order to utilize the above equations, one must be able to assume that the spin of interest (¹³Cα or ¹⁵N in our case) is only affected by R ₁ or R _1ρ relaxation from the dipole coupling to the bonded ¹H and its own CSA. Couplings to other nuclei are weak enough that their effect on relaxation-rate constants is usually negligible. R ₁ measurements can be distorted because of cross relaxation to the bonded ¹H, which results in a coupled system of relaxation equations. However in solid-state NMR, ¹H inversion rates, which are typically induced by proton spin diffusion, are sufficiently fast to decouple the system of equations. Proton-driven spin-diffusion (PDSD) between ¹³C nuclei (Ernst and Meier 1998) does have real potential to distort ¹³Cα R ₁ measurements, and the extent of this effect remains a contentious issue in dynamics measurement in solid-state NMR.

¹³C spin-diffusion and NOE in R ₁ measurements

Effects of ¹³C–¹³C magnetization transfer can be investigated with an exchange model, given by

$$\frac{d}{dt}\left[ {\begin{array}{*{20}c} {\left\langle {I_{1z} } \right\rangle } \\ {\left\langle {I_{2z} } \right\rangle } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - R_{1}^{(1)} - k} & k \\ k & { - R_{1}^{(2)} - k} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left\langle {I_{1z} } \right\rangle - M_{0} } \\ {\left\langle {I_{2z} } \right\rangle - M_{0} } \\ \end{array} } \right]$$

(10)

where k is the rate constant for exchange of longitudinal magnetization between spins 1 and 2 and $R_{1}^{(1)}$ and $R_{1}^{(2)}$ are the respective relaxation-rate constants (Giraud et al. 2007). The eigenvalues of the matrix give the following characteristic rate constants,

$$\lambda_{ \pm } = \frac{{R_{1}^{(1)} + R_{1}^{(2)} }}{2} + k \pm \frac{{\sqrt {(R_{1}^{(1)} - R_{1}^{(2)} )^{2} + 4k^{2} } }}{2}.$$

(11)

Two limiting cases for magnetization exchange then arise, the first when $2k \gg \left| {R_{1}^{(1)} - R_{1}^{(2)} } \right|$, and the second with $2k \ll \left| {R_{1}^{(1)} - R_{1}^{(2)} } \right|$, with Eq. (11) simplifying to

$$\begin{array}{*{20}l} {2k \gg \left| {R_{1}^{(1)} - R_{1}^{(2)} } \right|:} \hfill & {\lambda_{ + } = \frac{{R_{1}^{(1)} + R_{1}^{(2)} }}{2} + 2k,} \hfill & {\lambda_{ - } = \frac{{R_{1}^{(1)} + R_{1}^{(2)} }}{2}} \hfill \\ {2k \ll \left| {R_{1}^{(1)} - R_{1}^{(2)} } \right|:} \hfill & {\lambda_{ + } = R_{1}^{(1)} + k,} \hfill & {\lambda_{ - } = R_{1}^{(2)} + k} \hfill \\ \end{array} .$$

(12)

In the former case, magnetization on both spins 1 and 2 decays bi-exponentially, with a combination of the two R ₁ rates. Since the rates are averaged together, it is very difficult to determine reliable dynamics data in this situation. In the latter case, magnetization decays mono exponentially, with rates of $R_{1}^{(1)} + k$ and $R_{1}^{(2)} + k$, for spin 1 and 2, respectively. Then if k is sufficiently small compared to R ₁, it is possible to obtain reliable dynamics data.

It has been shown that by spinning at 60 kHz MAS, signal decay is mono exponential and coupled spins (Cα and Cβ, Cα and C’) show distinct relaxation rates, giving clear indication that the limit $2k \ll \left| {R_{1}^{(1)} - R_{1}^{(2)} } \right|$ is well satisfied (Lewandowski et al. 2010). However, being in this limit does not necessarily require that $R_{1} \gg k$. Investigations of the SH3 protein at 50 kHz MAS show severe changes in measured R ₁ relaxation rates when measuring a uniformly ¹³C labeled sample, as compared to a sample prepared such that most ¹³C have only ¹²C neighbors, using a sample grown with 2-¹³C glycerol (Asami et al. 2015). Larger R ₁ rates in the uniformly ¹³C labeled sample are then most likely attributed to ¹³C–¹³C transfer, indicating that rates measured in this sample are not very reliable for dynamics analysis.

We have used a partially protonated, uniformly ¹³C labeled sample in this study for ¹³Cα R ₁ measurements, and so it is critical that we verify that the rates obtained are primarily due to relaxation induced by the ¹Hα–¹³Cα dipole coupling and the ¹³Cα CSA-as opposed to ¹³C–¹³C polarization transfer. It is possible to estimate the rate of spin-diffusion for a pair of ¹³C spins from the ratio of cross-peak intensity to diagonal peak intensity in a ¹³C PDSD spectrum (Giraud et al. 2007; Lewandowski et al. 2010) and one can in fact, put bounds on the spin-diffusion rate constant. For example, for a Cα–Cβ pair, where we assume that $R_{1}^{\alpha }\, < \, R_{1}^{\beta }$, it can be demonstrated that $I_{\beta \alpha } /I_{\beta \beta } \ge k_{\alpha \beta } \tau \ge I_{\alpha \beta } /I_{\alpha \alpha }$, where $I_{\beta \alpha }$ is the cross peak for which magnetization begins on Cβ and ends on Cα, and τ is the length of the PDSD mixing (see SI Section 1.2 for further discussion). Figure 2 shows a ¹³C PDSD spectrum obtained at 60 kHz MAS with 1 s mixing, using the sample for which ¹³Cα R ₁ will be measured. Traces are drawn through the most intense cross peaks, and the ratio of cross peak to diagonal peak is indicated. From these ratios, it is possible to put bounds on the spin-diffusion rates. It is also possible to obtain some additional information when no cross peak is visible, if a diagonal peak is well-resolved and by assuming the cross-peak amplitude is less than twice the spectrum root mean squared amplitude (RMS), thus allowing upper bounds to be placed on the spin-diffusion rates. Several bounds obtained this way are given in Table 1.

Fig. 2

¹³C–¹³C PDSD spectrum with 1 s mixing. Traces are shown through the most prominent cross-peaks, and the ratio of the cross peak intensity to the diagonal peak intensity is indicated. The rate constant of magnetization transfer between the Cα and Cβ is bounded by (I _αβ/I _αα) < k _αβ τ < Ι _βα/Ι _ββ (here, τ = 1 s). Also shown is the Cα–CO region, where peaks resulting from ¹³C–¹³C ΝΟΕ transfer are visible

Table 1 Bounds on Cα–Cβ spin-diffusion rates

One first notes that the cross peaks identified (260T, 261T, and 241L) are the residues with the 1st, 7th, and 3rd smallest chemical-shift difference between Cα and Cβ, respectively. This seems unlikely to be coincidence, since a smaller chemical-shift difference will typically lead to more efficient spin diffusion (Ernst and Meier 1998). Peaks for which the spin-diffusion rate was bounded only by the diagonal peak intensity and the spectrum RMS show also low upper bounds to the ¹³C–¹³C transfer rate. Aside from 260T, and 261T, the bounds on the rates here indicate that measurement of ¹³Cα R ₁ rates should be dominated by relaxation processes and not by ¹³C–¹³C transfer as can be seen by comparison to the R ₁ rate constants reported in the results section.

This raises the question why we are able to get relatively good results for measurement of ¹³Cα R ₁ in uniformly ¹³C labeled HET-s (218-289), whereas Asami et al. (2015) do not for uniformly ¹³C labeled SH3. A simple answer can be that we spin at 60 kHz MAS, as compared to Asami et al. who spin at 50 kHz. To test this, we compare median values of ¹³Cα R ₁ for our sample at 50 kHz and at 60 kHz MAS, and find rates of 0.29 and 0.21 s⁻¹, a nearly 40 % increase in the measured rate at 50 kHz. Furthermore, when spinning to 65 kHz, the median rate is 0.20 s⁻¹; this relatively small change between 60 and 65 kHz suggests that contributions from spin-diffusion are mostly quenched above 60 kHz. Plots of the residue specific rate constants are given in SI Figure 3.

Nonetheless, spinning to 60 kHz MAS may not always be sufficient to remove all ¹³C–¹³C transfer. Very weak Cα–C′ cross peaks appear in Fig. 2, which is unexpected due to the large chemical-shift difference (Asami et al. observe similar results for SH3). For comparison, we measure a fully-protonated sample of uniformly ¹³C labeled MLF under the same conditions (60 kHz MAS), and find that there are no Cα–C′ cross peaks (see SI Figure 4). The most likely explanation for appearance of Cα–C′ cross peaks in the sample of HET-s but not in MLF is that slower motion (ns-μs) in HET-s induces ¹³C–¹³C NOE (Kaiser 1963; Solomon 1955), whereas MLF has very little motion in this timescale to induce an NOE, although note that the protonation level is different in the MLF sample. This complicates the question as to whether ¹³C–¹³C transfer can be eliminated by faster spinning. NOE transfers due to microsecond (or slower) motions can in fact be reduced by faster spinning, however NOE transfers due to faster motion cannot be, and so the approach of preparing samples which do not have neighboring ¹³C may be the only viable approach if the NOE contribution is significant (Asami et al. 2015). However, NOE transfer does not appear to be a severe problem in our case, based on cross-peak analysis. Nonetheless, this study will have some systematic distortion of the ¹³C R ₁ measurements due to potential additional ¹³C–¹³C relaxation pathways.

Transverse relaxation (R _1ρ) and the violation of the Redfield approximation

The ability to fit both R ₁ and R _1ρ data using the model-free approach allows one to utilize the extended model-free analysis to fit both slow and fast correlation times. Here, we investigate potential problems that may arise when utilizing the above listed equations for R _1ρ [Eqs. (5)–(7)]. We begin by examining the behavior of R _1ρ as a function of the correlation time, because at some point Redfield theory will no longer be valid when the correlation time becomes too long. In order to investigate the range for which Eq. (5) is valid, we have used stochastic Liouville simulations (Abergel and Palmer 2003; Kubo 1963; Schneider and Freed 1989) of a dipole-coupled, two-spin system (without CSA) undergoing a two-site hop (Wittebort and Szabo 1978), where the opening angle between the two sites is 5°, and determined its R _1ρ for a wide range of correlation times, as shown in Fig. 3. The simulation is performed in the laboratory frame of reference, which employs the full untruncated dipolar-coupling Hamiltonian, and, therefore, gives numerically accurate results for the complete range of timescales. This calculation is compared to R _1ρ calculated based on Eq. (5), involving the Redfield approximation. In addition, R _1ρ is also calculated from a stochastic Liouville simulation in the rotating frame using the high-field truncated rotating-frame Hamiltonian. The calculation based on Eq. (5) is in very good agreement with the stochastic Liouville simulation in the laboratory frame for τ _c < 320 ns. However, for longer correlation times, the calculation deviates from the exact simulation, and at the maximum deviation it is 1.65 times larger than the correct R _1ρ value. To understand this failure, one must note that the Redfield approximation assumes that the magnetization does not evolve significantly within the correlation time of the motion (Redfield 1957). The calculated T _1ρ (T _1ρ = 1/R _1ρ) is orders of magnitude longer than the correlation time, τ _c, meaning that relaxation will not change the magnetization significantly within τ _c. However, coherent behavior may also cause evolution of the magnetization. Since a perfect spin-lock cannot be obtained, some evolution of magnetization will occur due to the dipole coupling to the ¹H. In SI Figure 5, we show how this evolution affects the amount of magnetization along the x-axis, and see that it causes an oscillation with a rate on the order of the rotor frequency. Therefore, although the magnetization refocuses periodically, the assumptions taken in Redfield theory can fail as the correlation time approaches the rotor frequency.

Fig. 3

Comparison of R _1ρ calculation methods. Here, we calculate R _1ρ for a ¹H–¹³C spin system with δ ^IS/2π = 46.6 kHz, ω _r/2π = 60 kHz, and ω ₁/2π = 35 kHz, undergoing a hopping motion between two orientations, separated by 5°. The correlation time of this motion is swept. A simulation is performed in the lab-frame (black, dotted line), in the rotating frame (blue line), and a calculation is done using the model-free approach, with Eq. (5) (red line). The lab-frame simulation is numerically exact over the entire range of correlation times

In contrast, the rotating-frame simulations that use the high-field approximation are in good agreement with the laboratory-frame simulation for τ _c > 3.2 ns. Therefore, we calculate R _1ρ based on Redfield theory using equations Eqs. (5) and (6) for τ _c < 320 ns, but use the stochastic Liouville simulations in the rotating frame for longer correlation times. In principle one could also use the laboratory-frame simulation for all timescales, but this is much more computationally expensive as discussed in SI Section 1.7. Note that the motional models that we eventually use include multiple timescales. In this case, only one motion has τ _c > 320, and so R _1ρ is determined via simulation for this motion, and R _1ρ contributions due to faster motions are determined using Eqs. (5) and (6), and all contributions to R _1ρ are simply added together.

Calculating R _1ρ based on Redfield theory using Eqs. (5) and (6) can still return qualitative results for slow motions, but particular care should be taken when fitting multiple timescales, as amplitude (S ²) errors in the slow timescale can propagate to the fast timescale if the total amplitude of motion is characterized with S ² measurements. Further, when comparing results from different nuclei, one may find disagreement in the resulting timescales.

When measuring R _1ρ, one must also avoid the presence of coherent contributions to the decay of the spin-locked magnetization; in particular one must avoid the vicinity of the HORROR (ω ₁ = ω _r/2; Nielsen et al. 1994) and rotary-resonance (ω ₁ = ω _r, ω ₁ = 2ω _r; Oas et al. 1988) conditions. In principle, however, R _1ρ measured near the rotary-resonance condition may contain valuable information. This is because motions with long correlation times have little effect on the spectral-density function, J(ω), except when ω is near to zero [see Eq. (1)]. Therefore, in order to obtain information on slow motions, ideally one measures R _1ρ under conditions that sample J(ω) near zero. From (5) and (6), we see that the condition ω ≈ 0 is met when ω ₁ ≈ ω _r or ω ₁ ≈ 2ω _r, which is coincident with the rotary-resonance conditions. Therefore, one cannot sample J(0) exactly, but it is possible to work near this condition, as long as appropriate caution is taken and the coherent contributions to the decay can be neglected (see below).

In order to investigate measurement of R _1ρ near rotary resonance, we perform several simulations (see SI Section 1.8 for details). The blue traces in Fig. 4 show signal intensity for a single spin pair at a particular powder orientation and an ensemble average near the rotary resonance condition, in A and B respectively. The intensity corresponds to x-magnetization on the ¹³C spin. As one sees, oscillation due to the proximity to rotary resonance is periodically refocused for individual spin-pairs (Fig. 4a, blue trace). For a powder average, some initial loss occurs since the spin pairs do not oscillate at the same frequency, but the total signal quickly equilibrates and only a very slow decay is observed at later times. However, if the ¹H spin flips during the oscillation, then individual spin pairs do not refocus, as shown in Fig. 4a, red trace. The net result is that the ensemble- and powder-averaged signal decays towards zero, as shown in Fig. 4b, red trace.

Fig. 4

Signal intensity as a function of time near the rotary-resonance condition. Here, a ¹H–¹³C spin pair is simulated (δ ^IS/2π = 46.6 kHz, no CSA), with ω _r/2π = 60 kHz, and ω ₁/2π = 48 kHz. a A single spin pair is considered (with Euler angles α = 0°, β = 65°, γ = 0°), without (blue) and with flips (red) of the ¹H. The flip positions are marked by dotted lines. b An ensemble average is considered, without ¹H flips (blue) and with ¹H flips at a rate of 20 s⁻¹ (red)

To further illustrate this, we show a picture in Fig. 5 for an example of signal decay, based on a static experiment. Then, there is no rotary resonance condition, but there is an effective field that depends on the spin-locking field and the dipole coupling- as well as the state of the ¹H spin. Magnetization oscillates around the initial effective field (labeled as ‘before flip’. Note that one measures the projection of magnetization onto the x-axis). Then, after some time the ¹H flips, moving the effective field (labeled as ‘after flip’). The effect this has on the magnetization depends when the ¹H flips. Two extreme cases are shown. In the first case, magnetization has returned exactly to its starting location when the ¹H flip occurs. This causes the magnetization to begin to oscillate from the x-axis to below the xy-plane, instead of above it, and so the projection of magnetization on the x-axis is unaffected. In the second case, the ¹H flip occurs when the magnetization is 180° away from its starting position around the effective field. This results in the magnetization taking a much wider trajectory around the new effective field, and the projection of the magnetization on the x-axis is reduced. Repeated flips like this will further deplete the magnetization on the x-axis. Of course, all cases in between these extremes will also occur, and will be averaged over the ensemble of spins. In the MAS case, the effective field is time dependent, although the analogy stands. Furthermore, the deviation of the trajectory of magnetization from the spin-locking field increases as rotary resonance is approached, therefore increasing the signal dephasing. This leads to faster R _1ρ dephasing due to ¹H flips.

Fig. 5

Illustration of ¹³C or ¹⁵N magnetization trajectory in response to ¹H spin flips. The field resulting from the dipole coupling (red), the field from the spin lock (green), and the resulting effective field (blue) are shown as solid lines. In black, the trajectory that the magnetization takes from the x-axis around the effective field is shown. After a ¹H flip, the direction of the field from the dipole coupling and also the effective field are changed (dotted lines). The trajectory of magnetization is shown after the flip for the case that the magnetization is along the x-axis when the flip occurs (case 1), and for the case that the magnetization has rotated 180° around the effective field when the flip occurs (case 2). The first case results in no observable change of the projection of magnetization along the x-axis, but the second case reduces the projection

The rate of magnetization decay due to ¹H flips depends both on the proximity to the rotary-resonance condition and on the rate that ¹H flips occur, which in turn depends on the MAS frequency, ¹H density, and to some extent on the spin-lock strength applied to the heteronucleus (a major source of ¹H flips is proton spin diffusion, see Grommek et al. (2006) and Takegoshi et al. (2003) for the dependency of spin diffusion on fields applied to other nuclei). However, the ¹H flip rate can be measured (see “Experiments” section), and, therefore, this contribution can be calculated and compensated for in the data-evaluation process. Note that this is only possible because the contribution to R _1ρ from ¹H inversion (ΔR ^{(1H inver)}_1ρ ) is approximately additive to other R _1ρ contributions, such that

$$R_{1\rho }^{{ ( {\text{exp)}}}} \approx R_{1\rho }^{{ ( {\text{stoch)}}}} + \Delta R_{1\rho }^{{(1{\text{H \;inver}})}} .$$

(13)

We verify this via simulations that include both a stochastic motion and ¹H inversions, and compare the resulting R _1ρ to simulations including only stochastic motion and only ¹H inversion (see SI Figure 6). Figure 6 shows this contribution to R _1ρ as a function of ¹H flip rate, at the experimental conditions used in this study. Note the greater contributions seen for ¹Hα–¹³Cα spin pairs compared to ¹H–¹⁵N spin pairs. The site-specific corrections for our experimental data are given for ¹⁵N in Fig. 7 and for ¹³Cα in SI Figure 7.

Fig. 6

Calculated ΔR _1ρ rates as a function of the ¹H flip rate. The ω ₁ and ω _r values chosen are those used in our experiments for ¹³C and ¹⁵N. ω _r/2π = 60 kHz for all curves except for the red line in (a), for which ω _r/2π = 40 kHz

Fig. 7

¹H flip rate and R _1ρ correction. a We show the measured ¹H flip rate for each spin-lock and spinning frequency, matching the conditions used for measurement of ¹⁵N R _1ρ relaxation. The rates shown in (a) are then used in (b) to calculate ΔR ^{(1H inver)}_1ρ , the correction of the measured R _1ρ rate. The different experimental conditions are shown, with a different colored bar for each measurement condition, following the color code shown in (b)

To emphasize the importance of contributions to R _1ρ from ¹H inversion, we illustrate how potential problems arise using a simple model simulation. For ¹⁵N, let us assume a motion with τ _c = 3 ns and an S ² = 0.810, and for ¹³Cα we assume a motion with τ _c = 3 ns and S ² = 0.880. We will also assume a ¹H frequency of 850 MHz, for ¹⁵N we assume the anisotropy of the dipolar coupling to the ¹H is δ = 22.9 kHz and the CSA is Δσ = 150 ppm, and for ¹³C the coupling is δ = 46.6 kHz and the CSA is Δσ = 30 ppm. If we use Eq. (7), we calculate for all values of ω ₁ and ω _r a ¹⁵N R ^(stoch)_1ρ value of 2.0 s⁻¹ and a ¹³Cα R ^(stoch)_1ρ of 4.0 s⁻¹. However, the typical ¹H inversion rates measured in this study fall in the range of 10–20 s⁻¹, although the full range is quite a bit broader (Fig. 7, SI Figure 7). Assuming, for both ¹⁵N and ¹³Cα, a ¹H inversion rate of 20 s⁻¹, different values of R _1ρ are obtained depending on the simulation conditions. The predicted rates (R ^(stoch)_1ρ  + ΔR ^(1H inver)_1ρ ) as a function of the parameters are plotted as colored bars in Fig. 8a for ¹⁵N and in Fig. 8b for ¹³Cα. The rate constants obtained for ¹⁵N R _1ρ are all greater than 2.0 s⁻¹, and those obtained for ¹³Cα R _1ρ are all greater than 4.0 s⁻¹, with increasing deviation from R ^(stoch)_1ρ as the rotary-resonance condition is approached.

Fig. 8

Misinterpretation of R _1ρ caused by ¹H inversion but interpreted as slow molecular motion. a We take the ¹⁵N experimental settings for ω ₁ and ω _r, and use simulation to predict R _1ρ relaxation rates for a motion with τ _c = 3 ns and S ² = 0.810 and for a ¹H inversion rate of 20 s⁻¹ (colored bars). The simulated rates are then fitted to a model that only considers motion (no ¹H inversion), using simulation of a slow motional, two-site hop with τ _c = 6.3 μs and S ² = 0.998 (black dots). b We do the same for our ¹³Cα experimental settings, this time for a motion with τ _c = 3 ns and S ² = 0.880 and for a ¹H inversion rate of 20 s⁻¹ (colored bars). We also fit to a simulation of a slow motional, two-site hop model, in this case with τ _c = 5.0 μs and S ² = 0.997 (black dots). The fit is not as good, due to the usage of a different MAS frequency for the last data point

The problem becomes clear when one tries to fit these simulated R _1ρ rates to a motional model without considering the contribution by the ¹H inversion. In this case, one finds that the R _1ρ can be reasonably well fit to a motional model with only a single motion, as shown in Fig. 8a, b (black dots). For ¹⁵N, the fit to a single motion yields a correlation time of 6.3 μs and S ² = 0.998, and for ¹³Cα the correlation time is 5.0 μs and S ² = 0.997. Thus, the assumed motion with a 3 ns correlation time and a relatively low order parameter has now been fitted to a single, microsecond motion with a much higher order parameter—a severe failure of the analysis. To avoid such a misinterpretion when using experimental data, it is important to either avoid experimental conditions that have a large contribution to the measured R _1ρ from ¹H inversion (ΔR _1ρ), or measure the ¹H inversion rate and correct for the effect. It is also worth noting that for ¹³Cα, where one of the simulation conditions involves a different MAS frequency, the fit to incorrect motion is much worse, so that acquiring R _1ρ at both different spin-locking frequencies and different MAS frequencies can help differentiate between true motion and magnetization decay induced by ¹H inversion.

Experimental methods

Sample preparation

Measurement of dynamics data in the solid state requires minimization of undesired coherent interactions, so that measured relaxation rates on the X-nucleus can be attributed primarily to stochastic modulation of the X-CSA, and H–X dipole coupling of the bonded ¹H. This is, in part, achieved by partial deuteration of the sample to be measured. An additional benefit to sample deuteration is that it improves resolution in the ¹H dimension, making it possible improve sensitivity with ¹H detection (Agarwal et al. 2014).

Therefore, samples were prepared to yield uniformly ¹³C, ¹⁵N labeled HET-s, with partial deuteration. Samples for measurement of both ¹H–¹⁵N and ¹Hα–¹³Cα dynamics were prepared by recombinant expression of histidine-tagged HET-s (218–289) in Escherichia coli BL21 in M9 minimal medium (Balguerie et al. 2003). Uniformly labeled ²H, ¹³C glucose was the sole carbon source, and ¹⁵NH₄Cl was the sole nitrogen source. In the case of the sample for the study of ¹H–¹⁵N dynamics, the growth solvent is pure D₂O, but fibrilization is performed in pure H₂O to yield a sample only protonated at exchangeable sites. For the sample for the study of ¹Hα–¹³Cα dynamics, the growth solvent is 75 % D₂O and 25 % H₂O, and fibrilization is performed in D₂O. This growth medium yields 25 % protonation at the Hα position, and limited protonation at other positions (Asami et al. 2010, 2012; Lundström et al. 2009). Fibrilization in D₂O eliminates protonation at exchangeable sites. Details of sample preparation, purification, and fibrilization are given in SI Section 2.1.

Experiments

In order to precisely determine dynamics on multiple timescales, the direct order parameter S ², three R ₁, and five R _1ρ measurements (including ¹H flip-rate measurements for R _1ρ correction) were acquired site specifically for the dynamics of both ¹Hα–¹³Cα and ¹H–¹⁵N vectors. The experiments are summarized in Table 2. All experiments were acquired using MAS at 60 kHz, unless otherwise noted, using a Bruker Advance III HD console (400, 500, and 850 MHz Larmor frequencies) and a 1.3 mm triple-resonance (¹H, ¹³C, ¹⁵N) probe. Sample temperature was 23.3 ± 0.3 °C, determined by referencing the supernatant water shift to DSS (Böckmann et al. 2009). Two-dimensional ¹H–¹⁵N and ¹Hα–¹³Cα correlation experiments were used to obtain site resolution, where detection was performed on the ¹H nucleus in order to maximize signal to noise. This required assigning the ¹H resonances, which was done using the existing N, Cα, Cβ, and C′ assignment (Siemer et al. 2006; Van Melckebeke et al. 2010); the details of the assignment will be provided elsewhere.

Table 2 Experiments and parameters

The pulse sequences used to measure dynamics data are shown in Fig. 9. All sequences use an initial adiabatic cross-polarization step (Hediger et al. 1995) to the heteronucleus of interest to boost the initial polarization (¹⁵N or ¹³Cα) and water suppression using a modified MISSISSIPPI sequence (Zhou and Rienstra 2008; π/2 pulses are inserted after each saturation period). Magnetization is then transferred back to ¹H from the heteronucleus, and signal is detected on ¹H. Detailed experimental parameters are provided in SI Section 2.2.

Fig. 9

Pulse sequences for 2D experiments to measure dynamics data. a, b R ₁ and R _1ρ measurement sequences, respectively, where τ is incremented to obtain relaxation curves. c Measures the ¹H flip rate, under the same conditions as the R _1ρ measurements. d The shifted-REDOR sequence, which is used to measure ¹H–¹⁵N residual dipole couplings. The * indicates the pulse that could be replaced with a selective pulse for selective REDOR. e The REDOR sequence that is used to measure ¹Hα–¹³Cα couplings by frequency-selecting the ¹Hα resonances. For both (d) and (e), XY-16 phase cycling (Gullion et al. 1990) is used to compensate pulse error (with mirroring of phases around the center of the REDOR period), and n is incremented to obtain REDOR curves. S ₀ reference curves are obtained by omitting all ¹H π-pulses during the dephasing period

In both R ₁ and R _1ρ sequences, magnetization is allowed to decay, either as longitudinal magnetization for R ₁ measurements (Fig. 9a), or as spin-locked magnetization for R _1ρ (Fig. 9b). The sequence shown in Fig. 9c measures the ¹H flip rate required for the correction of the R _1ρ data. Since initially the net magnetization is roughly equal at all sites, it is necessary to first perform the indirect dimension so that polarization is unequal for the different ¹H, allowing polarization transfer between them. This also means that signal gains due to spin-diffusion from different sites appear as cross-peaks, and so do not distort the measurement of ¹H flip rate on the peaks of interest (assuming separation between the cross peaks and the peaks of interest). Note that an RF-field is applied to the heteronucleus during measurement of the ¹H flip rate. This field needs to match that used during the corresponding R _1ρ measurement, because couplings to ¹³C or ¹⁵N spins assist ¹H spin-diffusion, and so fields applied to those spins may change the spin-diffusion rates (Grommek et al. 2006; Takegoshi et al. 2001). Because a major source of ¹H flips is spin-diffusion, it is possible to observe bi-exponential (or multi-exponential) behavior when measuring the ¹H flip rate, due to build up of magnetization on neighboring ¹H’s. In this case, it is not yet clear whether one can correct the R _1ρ to account for ¹H spin-diffusion. However, if spin-diffusion does not result in significant buildup on neighboring ¹H’s (due to sufficiently fast R ₁ or diffusion to more distant protons, for example), then nearly monoexponential behavior is seen, as was observed in our experiments (see SI Figure 17 for plots of the ¹H behavior), and we can perform the R _1ρ correction. One must also be careful that new cross-peaks do not overlap peaks of interest, and therefore distort the extracted ¹H flip rate- although we also did not encounter this problem.

The REDOR sequence is used to measure the ¹H–¹⁵N and ¹Hα–¹³Cα dipolar couplings (Gullion and Schaefer 1989b) because of its robustness against RF inhomogeneity and incorrect settings of the RF field strength (Schanda et al. 2011). The scaling factor of the standard REDOR sequence (Jaroniec et al. 2000) is too large for the measurement of one-bond dipole couplings at fast MAS frequencies. This problem can be overcome by shifted-time REDOR, where the pulses in the center of the rotor period are shifted in order to reduce the effective recoupling strength [mirror-symmetric REDOR (Gullion and Schaefer 1989a)], as shown in Fig. 9d. We use this sequence for obtaining ¹H–¹⁵N order parameters.

Measuring ¹Hα–¹³Cα order parameters is more challenging, because our isotope-labeling scheme leads to some residues protonated at the ¹Hα position as well as at the ¹Hβ position. Frequency-selective REDOR (Jaroniec et al. 2001) can be used to only recouple H–C couplings for which the H resonance is within a given frequency range, making it possible to exclude most Hβ–Cα couplings. However, frequency-selective REDOR is not compatible with mirror-symmetric shifted REDOR shown in Fig. 9d. The reason for this is that frequency-selective REDOR uses a selective pulse on the ¹H channel in the center of the REDOR period, which replaces the first pulse after the center of the sequence (marked with a * in Fig. 9d). Then, the ¹H–X dipole couplings of protons that are inverted by the selective pulse are refocused by the frequency-selective REDOR sequence, whereas dipole couplings of protons that are not inverted by the selective pulse are not refocused, because the second half of the REDOR period reverses the recoupling achieved in the first half of the REDOR period. When one uses the mirror-symmetric shifted REDOR shown in Fig. 9d, however, one finds that if the first pulse after the center of the REDOR period (marked with a *) is removed, recoupling is still achieved- although the rate of recoupling is not the same as if the pulse is included. Therefore, even if a selective pulse is used, the dipole couplings to protons that are not inverted with a selective pulse are also recoupled but with a smaller scaling factor. To resolve this, we have modified the REDOR sequence as shown in Fig. 9e. In fact, the sequence used here is very similar to the mirror asymmetric sequences presented in (Gullion and Schaefer 1989a), because the first and second half of the sequence are identical without mirroring. Therefore, if the ¹H is not inverted in the center of the sequence, the recoupling achieved in the first half of the sequence is reversed in the second half, making it possible to use selective REDOR. One does need to be careful, however, since not all Hβ chemical shifts are well separated from the Hα chemical shifts.

Note that although the π-pulses in our sequence are immediately next to each other, we still have recoupling. When using fast MAS, in our case 60 kHz, strong π-pulses still take up a significant part of the rotor period (e.g. two 150 kHz π-pulses take 40 % of the rotor period). Therefore, two π-pulses placed immediately next to each other in the center of the rotor period significantly reduce the effective dipole coupling during that period, and so the dipole coupling is no longer completely averaged by MAS (see SI Figure 8 for calculation of a time-trace). For the selective pulse, we use a Q3 pulse (Emsley and Bodenhausen 1992), with bandwidth set to cover the ¹Hα chemical shift range (at a ¹H frequency of 850 MHz, this resulted in a 1376 μs pulse, 3.2 kHz bandwidth- defined by the width where at least 50 % inversion occurs). We utilize XY-16 phase cycling (Gullion et al. 1990) as in the shifted REDOR sequence. We check that the measured ¹Hα–¹³Cα dipole couplings are not strongly scaled by our sequence, a serious problem for dynamics analysis resulting from radio-frequency (RF) inhomogeneities, which has been investigated in detail for ¹H–¹⁵N dipole couplings (Haller and Schanda 2013). We check for scaling by refitting our REDOR data set with a uniform scaling factor multiplied by the measured dipole couplings, and optimizing that scaling factor to best-fit the data. Ultimately, we scaled our dipole couplings up by a factor of 1.012, a relatively small amount.

Data analysis

Each dynamic parameter measurement is acquired as a series of 2D experiments, where the value of either τ, or n for REDOR experiments, is incremented (see Fig. 9). We then extract the amplitude for each cross peak in all spectra. This yields time-dependent intensities for each resonance (selected measurements given in SI Figures 17–21), which are then fitted to determine relaxation-rate constants and scaled dipolar couplings, and finally the acquired dipolar couplings and relaxation rates are fitted to a dynamic model. The details of each step are presented in this chapter.

Spectrum fitting

A significant amount of overlap of resonances in both 2D ¹H–¹⁵N and ¹H–¹³C spectra make extraction of accurate amplitudes for each residue difficult using either peak maxima or peak integration (see SI Figure 9). Therefore, we have developed an automated spectrum-fitting routine, using MATLAB (The MathWorks 2013). For our purposes, it is critical to have precise fitting of the spectra; in particular, peak shapes must be as accurate as possible. Incorrect shapes result either in fitting of incorrect amplitudes of neighboring peaks due to the overlap, or one must add extra peaks to fit out these extra errors leading to over-fitting, and, therefore, introducing additional noise into the extracted data.

In order to have optimal results, we fit the experimental spectrum using peak shapes that are calculated based on acquisition and processing parameters; in particular acquisition time, apodization function, and zero-filling are used to generate accurate peak shapes. The type of signal decay is user specified in each dimension (Gaussian, exponential, or some mixture), and we vary the type of decay to further improve fitting. A more complete description of this program will be presented in a separate publication.

In order to extract intensities from 2D spectra, we begin by generating a reference fit for each of the two data series: one for Hα–Cα 2D spectra and one for H–N 2D spectra. The resulting fits are shown in SI Figure 9 where the experimental and fitted spectra are shown along with several traces to show the fit quality. The program determines number of peaks, peak positions, line widths, and intensities for the reference fits. Then for each data series, the number of peaks and the peak positions are fixed for all consecutive fits. However, the line widths are re-optimized, to account for different magnetic fields, and other smaller variations in experimental conditions. Once the line widths are re-optimized for a data series, then each spectrum in the series is fitted by only allowing the intensities to vary. By fixing as many parameters as possible, the influence that overlap of neighboring peaks has on the measured intensities is minimized. Note that this method makes the quality of the initial fits critical, and in general makes spectrum phasing and referencing very important. Examples of the resulting time traces are given in SI Figures 17–21.

Parameter and error determination

After intensities are extracted from the 2D spectra, it is necessary to determine relaxation rates or partially-averaged dipolar couplings from the data. For all relaxation rates except ¹⁵N R _1ρ, the intensity data is fitted to a mono-exponential decay

$$I_{k} = A\exp ( - R\tau_{k} ),$$

(14)

where R = R ₁ or R _1ρ, and A accounts for the differences in intensities for different resonances. We also use this formula to extract the rate of ¹H inversion from experimental data, and furthermore for extracting R _1ρ values from simulations. When fitting ¹⁵N R _1ρ, we have to fit the data to a bi-exponential function:

$$I_{k} = \frac{A}{2}\left( {\exp ( - R_{a} \tau_{k} ) + \exp ( - R_{b} \tau_{k} )} \right)$$

(15)

This is a result of significant contributions from CSA/dipole cross-correlated cross relaxation to the spin-locked two-spin term (2I_xS_z) leading to a bi-exponential decay of the magnetization. Another way of looking at this is that the two lines of the ¹⁵N multiplett (I_xS_α and I_xS_β) decay with two different relaxation-rate constants. However, ¹H inversion causes these two rates to partially average, and in the limit of fast flipping, R _a = R _b. Therefore, the ratio of R _a to R _b changes for different residues, but the average of these two rates is independent of the flip rate and we report R _1ρ = (R _a + R _b)/2. Note that this is the rate predicted by Redfield theory [see Eq. (7)], and if we compare to a stochastic Liouville simulation, we may also take the average of the bi-exponential fit of the simulated curve.

REDOR data consists of two data sets: S curves, which give dephasing due to coupling between the ¹H and the heteronucleus, and S ₀ curves, which have the ¹H π pulses omitted (note that S and S ₀ here should not be confused with the order parameter, S ²). The length of our dephasing period is relatively short (600 μs for ¹Ηα–¹³Cα, 1.33 ms for ¹⁵N), so that the decay of the S ₀ curve is linear in this range. Therefore, we only acquire a few S ₀ spectra, using linear regression to fit the S ₀ to a straight line so that for a particular residue,

$$S_{0,k} = m\tau_{k} + b.$$

(16)

Then the REDOR curve is given by

$$I_{k} = \frac{{S_{0,k} - S_{k} }}{{S_{0,k} }},$$

(17)

and the intensities I _k are fit to amplitudes determined by simulating the appropriate pulse sequence in SIMPSON (Bak et al. 2000) with a two-spin system, where the order parameter (S ² = (δ ^IS_obs /δ ^IS_rigid )²) is varied to achieve a fit. For ¹Hα–¹³Cα REDOR curves, the simulated amplitudes are also fitted with an additional scaling factor (I ^fit _k  = AI ^sim _k ). Imperfect inversion of the ¹Hα by the selective pulse (Fig. 9e) decreases the dephasing amplitude, although otherwise does not significantly impact the shape of the dephasing curve. The additional scaling factor accounts for this.

For all parameters, it is also necessary to know the error of the measurement. We obtain a standard deviation by bootstrapping our data (Efron and Tibshirani 1993): first, we obtain a best fit of the data to the model, and then assume that

$$I_{{{ \exp },k}} = I_{{{\text{model}},k}} + \varepsilon_{k} ,$$

(18)

where ε _k is the error at data point k. Then, a bootstrapped data set is generated using

$$I_{{{\text{bootstrap}},k}} = I_{{{\text{model}},k}} + \varepsilon_{m} ,$$

(19)

where ε _m is a randomly selected error (with replacement) from the ε _k of the original fit. The bootstrapped intensities are then refit, to obtain a new value of the parameter of interest (R ₁, R _1ρ, S ²). The bootstrapping process is repeated 100 times, and the standard deviation of the fitted parameters obtained from the bootstrapped data is taken to obtain the measurement standard deviation (σ). The advantage of using a bootstrap to determine error is that it inherently includes all sources of error occurring within a given data set. This then includes spectral noise, as well as other experimental variations- such as instrumental instabilities and temperature variation within a data set. It will not include variations that occur between data sets, however, and so we must take care to control sample quality, temperature, etc.

Fitting to a dynamic model

For each ¹Hα–¹³Cα and ¹H–¹⁵N spin pair, we have several experimental parameters (R ₁, R _1ρ, and S ²), which must be fitted to a dynamic model that is characterized by multiple amplitudes (S ²) and timescales (τ) of motion. Then, we can compare the experimental parameters to those calculated from the dynamic model using a χ ²-statistic as follows:

$$\chi_{\nu }^{2} = \frac{{\left( {S_{ \exp } - S_{\text{calc}} } \right)^{2} }}{{\left( {\sigma (S)} \right)^{2} }} + \sum\limits_{k = 1}^{{N_{{R_{1} }} }} {\frac{{\left( {R_{1,k}^{ \exp } - R_{1,k}^{\text{calc}} } \right)^{2} }}{{\left( {\sigma (R_{1,k} )} \right)^{2} }}} + \sum\limits_{k = 1}^{{N_{{R_{1\rho } }} }} {\frac{{\left( {R_{1\rho ,k}^{ \exp } - R_{1\rho ,k}^{\text{calc}} } \right)^{2} }}{{\left( {\sigma (R_{1\rho ,k} )} \right)^{2} }}} .$$

(20)

Equation (20) contains the calculated values for all experiments, the experimental values, and the experimental standard deviation. ν is the degrees of freedom of the χ ² distribution, given by the number of experimental parameters ($N_{{R_{1} }} + N_{{R_{1\rho } }} + 1$) minus the number of fit parameters. Minimizing the value of χ ² by varying the dynamic model parameters then returns a fit to the dynamic model that favors the more precisely measured parameters. We report the reduced-χ ² in later figures, which is given by χ ²/ν. We additionally estimate the 68 % confidence interval for each parameter, by finding the range on that parameter for which χ ² < χ ²_min  + 1, where χ ²_min is the minimized value of χ ² (Clifford 1973). Details of the error analysis and the χ ² minimization are given in Section 3.2 of the SI.

When fitting experimental parameters to dynamic models, we will use either two or three timescales of motion. If a motion has a correlation time longer than 320 ns, R _1ρ will be calculated using stochastic-Liouville simulations in the rotating frame, otherwise it will be calculated using Redfield theory [Eq. (7)]. R ₁ is always calculated using Redfield theory [Eq. (4)], because slow motions with correlation times longer than 320 ns will have a negligible contribution to R ₁. We assume for all calculations or simulations a ¹Ηα–¹³Cα bond distance of 1.105 Å, a ¹H–¹⁵N bond distance of 1.02 Å, a ¹³Cα CSA of 20 ppm (although this is almost negligible), and a ¹⁵N CSA of Δσ = 170 ppm. The ¹³Cα CSA is assumed to be axially symmetric and collinear with the ¹Hα–¹³Cα dipole coupling. The ¹⁵N CSA is assumed to have an asymmetry of η = 0.4 (Wylie et al. 2006), and Euler angles of (α = 30°, β = 25°, γ = 0°; Hou et al. 2010).

Results and discussion

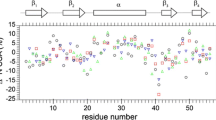
We begin investigating the HET-s dynamics by fitting both data sets (¹⁵N and ¹³Cα) independently to dynamic models. Previously, it has been shown that when incorporating both R ₁ and R _1ρ at multiple external fields and multiple spin-locking strengths (and spin-locking frequency offsets), that a three-timescale fit provides a statistically significant, better fit of the relaxation data (Zinkevich et al. 2013). Therefore, we will investigate both two- and three-timescale fits for our results. We begin by fitting the ¹⁵N and ¹³Cα data sets to models that incorporate two timescales of motion, and, therefore, four fit parameters (S ²_f , τ _f, S ²_s , τ _s). Figure 10 shows the site-specific slow correlation times resulting from this fit (note that for some glycine residues, the two Hα yield different chemical shifts and can be analyzed separately, and so here and throughout the paper two values appear for these residues). The results indicate that there is slow motion detected throughout the HET-s (218–289) fibril. Furthermore, timescales of ~10 μs indicate concerted motions of at least several atoms or more (Henzler-Wildman and Kern 2007). In fact, the narrow distribution of timescales for ¹Hα–¹³Cα and ¹H–¹⁵N suggests that the entire molecule may see a single, slow motion- similar to results of a recent study on crystalline Ubiquitin (Ma et al. 2015). Since a concerted motion should have approximately the same correlation time for all residues, we will require that all residues are fitted to the same slow correlation time, τ _s. This has the added benefit that we reduce the number of parameters required to fit our data.

Fig. 10

Slow timescales (τ _s) determined using a 4-parameter fit (S ²_f , τ _f, S ²_s , τ _s) for both ¹Hα–¹³Cα and ¹H–¹⁵N dynamics, shown in (a) and (b), respectively. We only show the slow timescale, to illustrate that the distribution is rather narrow, in particular for ¹Hα–¹³Cα, and similar for both spins, an argument that this is likely to be a single, concerted motion

To find τ _s, its value is varied and the complete experimental data set is refit at each value, by optimizing the remaining parameters, which are S ²_s , τ _f, and S ²_f if a two-timescale model is used, and S ²_s , τ _i, S ²_i , τ _f, and S ²_f if a three-timescale model is used (s, i, and f indicate slow, intermediate and fast). Then the reduced-χ ² (sum of χ ² for all residues, divided by total number of measured parameters minus number of fit parameters) is calculated at each value of τ _s to determine the best value for each model. This is done both for ¹⁵N and ¹³Cα data sets, and for both two-timescale and three-timescale models, and plotted against the slow correlation time, τ _s, shown in Fig. 11a, b, respectively. As one sees, the best reduced-χ² value for both nuclei is found when using the three-timescale model. For the two-timescale model, the best fit value of τ _s was found to be 6.2 and 4.1 μs for ¹Η–¹⁵N and ¹Hα–¹³Cα slow motion, respectively. For the three timescale model, τ _s was found to be 14.7 and 8.7 μs, for ¹H–¹⁵N and ¹Hα–¹³Cα motion, respectively.

Fig. 11

Statistical comparison of two- and three-timescale models for ¹⁵N and ¹³Cα. a The reduced–χ ² (calculated over all residues) for the two-timescale model for both ¹⁵N and ¹³Cα data as a function of the slow correlation time, τ _s, which is set to be the same for all residues. b The reduced-χ ² for the three-timescale model for both ¹⁵N and ¹³Cα data as a function of τ _s. c The residue specific difference of the AIC parameter for the two- and three-timescale models for ¹⁵N, and d the difference for ¹³Cα, where positive values indicate that the three-timescale model better fits the data

To further investigate the choice of model, we evaluate the residue-specific fit quality with the Akaike Information Criterion (AIC; Abdullah et al. 2013; Akaike 1974). This allows comparison of two models to determine which better fits the data, while also accounting for the number of fitting parameters being used.

$$AIC = N\ln \left( {\chi^{2} /N} \right) + 2K.$$

(21)

Here, N is the number of experimental parameters (3R ₁, 5 R _1ρ, and 1 S ² yields N = 9), χ ² is as given in (20), and K is the number of fitting parameters (3 or 5 depending on whether we use the two- or three-timescale model, noting that we do not count the slow correlation time, τ _s, since it is fitted against the full data set and does not significantly contribute to the degrees of freedom of an individual residue). The model for which the AIC parameter is smaller is then considered to be the better model, while taken into account both fit quality and number of fit parameters. The results for ¹⁵N and ¹³Cα analysis are shown in Fig. 11c, d, respectively, where the difference in the AIC for the two-timescale model and the three-timescale model is plotted against the residue number (positive values indicate that the three-timescale model is better).

The three-timescale model fits the majority of residues better for both data sets. In Fig. 12 the fit is given for ¹H–¹⁵N motion and in Fig. 13 the fit is given for ¹Hα–¹³Cα, with comparison of calculated and experimental data in Figs. 14 and 15. We find that nearly all of the residues for which the two-timescale is the better-fit model have either S ²_i or S ²_f close to one in the corresponding three-timescale model, indicating very little motional contribution from the intermediate or fast motion. Because the contributions of one of the three correlation times are minimized, the model is reduced to a form that is very similar to the two-timescale model. Also, the amplitudes and correlation times of the remaining motions are very similar to those in the two-timescale models (see Fig. 16, SI Figure 10). These correlations first indicate that use of the bootstrap method to evaluate error on experiment parameters, and subsequent usage of those errors to evaluate χ ² via (20), gives reliable evaluation of model quality. Also, it allows us to rely only on the three-timescale model, since it results in a fit that is similar to the two-timescale model where the AIC parameter favors that model. A side effect of the minimal contribution of one of the motions to the three-timescale model is that it can cause a sharp increase in the error of the corresponding correlation time, since one must be able to measure significant changes in the experimental parameters to be able to accurately characterize the correlation time.

Fig. 12

Fit parameters for ¹H–¹⁵N dynamics using a three-timescale model. a The residue specific fast motional amplitude (S ²_f ). b The fast motional timescale (τ _f), plotted logarithmically. c, d The intermediate motional timescale (τ _i), and amplitude (S ²_i ). e The slow motional amplitude (S ²_s ), using a correlation time of τ _s = 14.7 μs. f The reduced-χ ² of the fit. a–e Error bars, which approximate a 68 % confidence interval for the parameter

Fig. 13

Fit parameters for ¹Hα–¹³Cα dynamics using a three-timescale model. a The residue specific fast motional amplitude (S ²_f ). b The fast motional timescale, plotted logarithmically. c, d The intermediate motional amplitude (S ²_i ) and timescale (τ _i), respectively. c We highlight fibril core residues pointing outward in grey (excluding those between β-sheets—see Fig. 1). e The slow motional amplitude (S ²_s ), using a correlation time of τ _s = 8.7 μs. d The reduced-χ ² of the fit. a–e Error bars, which approximate a 68 % confidence interval for the parameter

Fig. 14

Experimental parameters for ¹H–¹⁵N dynamics fitted to a three-timescale model. a–e Measured R _1ρ for different spin-locking strengths (bars), versus values calculated from the fitted model (black dots). f–h R ₁ measurements and calculated values for different magnetic fields. i Measured versus calculated S ², measured with shifted REDOR. All measurements also include error bars, indicating one standard deviation on the measurement data, determined via bootstrapping

Fig. 15

Experimental parameters for ¹Hα–¹³Cα dynamics fitted to a three-timescale model. a–e Measured R _1ρ for different spin-locking strengths and MAS frequencies (bars), versus values calculated from the fitted model (black dots). f–h R ₁ measurements and calculated values for different magnetic fields. i Measured versus calculated S ². All measurements also include error bars, indicating one standard deviation on the measurement data, determined via bootstrapping

Fig. 16

Fit parameters for ¹Hα–¹³Cα dynamics using a two-timescale model. a The residue specific fast motional amplitude (S ²_f ). b The fast motional timescale, plotted logarithmically. c The slow motional amplitude (S ²_s ), using a correlation time of τ _s = 6.2 μs. d The reduced-χ ² of the fit. In (c), we highlight fibril core residues pointing outward in grey (excluding those between β-sheets—see Fig. 1). a–c Error bars, which approximate a 68 % confidence interval for the parameter

The results of fitting of relaxation data can depend critically on the model chosen. For example, when fitting ¹Ηα–¹³Cα data to a three-timescale model, we note that a trend emerges: the S ²_i is correlated to the position of the side-chain, where residues that point into the fibril core have higher values of S ²_i (less motion) and those that point outwards towards the solvent have lower values (more motion). Interestingly, when ¹³Cα data is fitted to a two-timescale model, the same trend emerges, but for values of S ²_s , which is assumed to be a global motion, as shown in Fig. 16. This represents a critical failure of model-free fitting: a motion that is residue-dependent becomes part of the fit of a global motion. A model that is too simple can easily mix two separate motions into one timescale of the model, yielding data that is impossible to interpret reasonably. A similar problem arises when analyzing ¹H–¹⁵N dynamics with only a two-timescale model, where most of the nanosecond range motion is omitted entirely from the fit (see SI Figure 10). Both situations demonstrate that determination of the best model via statistical tests is important. However even then, a smaller or lower quality data set may not have the information content to satisfy a more complex model, and so statistical tests would indicate a simpler model is a better fit. This does not mean that the simpler model adequately describes the dynamic behavior, only that the data is insufficient to support a more complex model. This can result in a fit that combines physically distinct motions into a single motion and correlation time. Then the physical meaning of those motions may be obscured and the resulting fit parameters can be distorted.

Our analysis shows a discrepancy in the best-fit slow correlation times for the analysis of ¹⁵N and ¹³Cα data, yielding correlation times of 14.7 and 8.7 μs, respectively. Although not orders of magnitude apart, the difference is surprising since we postulate that a single, global motion is responsible for the measurement of a microsecond timescale, and so ideally the correlation times would be in full agreement. One potential reason for the difference is that we do not fully account for coherent effects in R _1ρ measurements. We do note that, in particular for ¹³Cα data, coherent effects are expected to produce notably different trends for R _1ρ than motion, as was shown in Fig. 8. There, R _1ρ that is calculated as a result of coherent effects (¹H-flipping) for spin-lock strengths of 25 kHz and MAS of 40 kHz, and spin-lock strength of 48 kHz and 60 kHz fit poorly to the dynamic model. Therefore, to check that coherent effects are not contributing significantly to our fit of slow motion, we re-fit ¹Hα–¹³Cα dynamics data while excluding R _1ρ data measured with 25/40 kHz, and 48/60 kHz spin-lock/MAS frequencies, and then predict those data points. The result is shown in SI Figure 13, where we see that most points are very well predicted-indicating that the motional model is reasonable and unlikely to be the result of coherent effects on the R _1ρ. An additional consideration is that since the source of the microsecond motion is not yet clear, it is possible that the model-free approach does not adequately describe it, and so modeling of ¹³C versus ¹⁵N slow dynamics could result in slightly different fitted timescales.

When studying slow motions, it is useful to notice that the slow correlation time of a global motion, τ _s, and the site specific slow order parameters, S ²_s can be fairly well determined only based on R _1ρ data. In this case, one may fit the R _1ρ data while only modeling a single, slow timescale. We do so, and plot the reduced-χ ² for all residues as a function of τ _s in Fig. 17a, obtaining the best fits for τ _s = 6.2 μs for ¹H–¹⁵N and τ _s = 4.1 μs for ¹Hα–¹³Cα data. These are identical to the rate constants found for the two-timescale model using the full data set. This is because when fitting the full data set for the two-timescale model, the fast timescale is usually in the picosecond range of motion, and so has little effect on the calculated R _1ρ. Similarly, the microsecond motion has no effect on the calculated R ₁ values, and since the S ²_s are very near to one, it also does not contribute significantly to the total order parameter. The resulting residue specific values for S ²_s are also very similar to those determined using the two-timescale model, as shown in Fig. 18 (see SI Figure 14 for fit of the data). However, there is a systematic overestimation of the S ²_s determined using only R _1ρ as compared to using the full data set. This is because fast motion reduces the effective dipole coupling, such that the slower motion does not induce as much relaxation, requiring larger motions to account for the same R _1ρ rate constants [see Eq. (1)]; when fitting only R _1ρ, one does not determine the faster motions and, therefore, it is impossible to account for the scaling.

Fig. 17

Calculation of the slow correlation time, τ _s, using only R _1ρ data. a The reduced-χ ² calculated for all residues as a function of the slow correlation time for both ¹H–¹⁵N data and ¹Hα–¹³Cα data. The model includes only one slow motion. b The reduced-χ ² calculated for all residues, but the model includes both a slow timescale, and an intermediate timescale. The correlation times and order parameters are not fitted for the intermediate timescale-only a contribution to the R _1ρ from intermediate timescale motion is fitted, which is independent of MAS and spin-lock frequency

Fig. 18

S ²_s determined for ¹H–¹⁵N and ¹Hα–¹³Cα motion using only R _1ρ data. Colored dots show S ²_s for which only R _1ρ data was fitted to a single, slow motion, with a correlation time of 6.2 μs for ¹⁵N data and 4.1 μs for ¹³Cα data. Grey dots show S ²_s determined while fitting the full data set to a two-timescale model, showing that usually fitting to the full data set predicts a lower S ²_s (larger motion)

Alternatively, R _1ρ values may be fitted to a slow timescale, and an intermediate (ns) timescale. In this case, the contribution of the intermediate timescale to R _1ρ will be the same for all experimental conditions [see Eqs. (1), (5), and (6)], where the dependence of R _1ρ on the MAS and field strength vanishes for sufficiently short correlation times). Then, it will be impossible to characterize the intermediate timescale with S ²_i and τ _i, but the data can nonetheless be fitted with a constant contribution to all R _1ρ measurements for a given residue due to the intermediate timescale motion (R _1ρ offset). We perform this fit, for various values of τ _s, and plot the reduced-χ ² for each in Fig. 17b, obtaining best fits for τ _s = 18.5 μs for ¹H–¹⁵N and τ _s = 7.0 μs for ¹Hα–¹³Cα motion. The values are very similar to those found for the three-timescale model, although no longer identical (as compared to 14.7 and 8.7 μs). Values of S ²_s are also similar, although again biased because scaling of the relaxation by faster motions is not accounted for (see SI Figure 15, and SI Figure 16 for fit of the data). Some differences emerge because the intermediate (ns) motion affects all measured parameters (R ₁, R _1ρ, and S ²). Then, influence of R ₁ and S ² on the intermediate motion affects its contribution to calculation of R _1ρ, resulting in minor changes to the calculated slow correlation time. Ultimately, the extraction of information on slow, microsecond motion from only R _1ρ data is complicated by contributions to R _1ρ from intermediate motion. However, if the slow motion is global, the fact that all residues can be fitted to one correlation time makes a reasonable analysis possible, whereas determination of residue-specific slow correlation times and amplitudes along with contributions to R _1ρ from intermediate timescale motion would be extremely difficult.

Conclusions

The combined use of R ₁, R _1ρ, and S ² data for both ¹Hα–¹³Cα and ¹H–¹⁵N has been shown to be a powerful addition to dynamics analysis, and allows the descriptions of the dynamics by three timescales of motion, representative of a slow, global motion, intermediate, and fast motion. Measurement of similar slow motion on both nuclei gives further evidence of the presence of a slow motion, whereas nanosecond and picosecond motions showed differences in trends between ¹Hα–¹³Cα and ¹H–¹⁵N, indicating that they provide information on different motions. Of course a three-timescale model is still a rather crude description of the complex dynamics of a protein fibril but the three-timescale fit of both ¹H–¹⁵N and ¹Hα–¹³Cα motion pushes the limits of the information content of our dynamics data, although is supported by statistics that show that most residues are better fit with a three-timescale model. Our ability to separate three timescales relies heavily on the fact that it was possible to use a single slow-motion correlation time for all residues, reducing the number of parameters being fitted for each residue.

Having a sufficiently complex model to represent the protein motion is critical. In our case, if only two timescales are used to describe ¹Hα–¹³Cα motion, then slow and intermediate motion of ¹Hα–¹³Cα are interpreted as a single motion, and the physical meaning of both motions becomes highly convoluted, since features of both motions are mixed together into a single parameter set. Similarly, when ¹H–¹⁵N motion is fitted to a two-timescale model, most nanosecond timescale motion is excluded from the resulting model. One may use statistical tests to verify that a more complex model is supported by the data, as we have done with the AIC parameter, but when the statistical test supports usage of a simpler model, it does not prove that the real motion is well described by the simpler model. It then may be necessary to improve the experimental data set to obtain a good description of the real motion. In our case, most of the residues for which the simpler, two-timescale model was favored by the AIC parameter, the three-timescale model also indicated that one motion contributed only slightly to the dynamics behavior, giving good agreement between results of model fitting and statistical analysis. Of course similar errors may be introduced into our three-timescale model as additional timescales certainly exist but cannot be characterized by present day experiments.

We were able to obtain evidence of global motion in the HET-s fibril, with similar slow correlation times (τ _s) for both ¹H–¹⁵N and ¹Hα–¹³Cα models. Fitting of slow motion on both nuclei with similar correlation times shows that the slow motion is unlikely to be an experimental artifact. The ability to make a direct comparison of the slow motion relies on the fact that it is a global motion, and so should be highly correlated. Still, combining data from multiple nuclei can be worthwhile, as shown by Lamley et al., where the motion of the peptide plane can be modeled from combined ¹⁵N and ¹³C′ (backbone carbonyl) data (Lamley et al. 2015). This is not true for ¹H–¹⁵N and ¹Hα–¹³Cα that is not global, since the bonds to ¹³Cα do not lie in the peptide plane. Therefore, whereas combination of ¹⁵N relaxation and ¹³C’ motion may be used to more accurately characterize the concerted peptide plane motion, combination of ¹⁵N and ¹³Cα relaxation can highlight different motions. Of course, all nuclei can be combined to investigate global motions, and it is possible for a single local motion (several nuclei) to be observed on both the ¹⁵N and ¹³Cα nuclei, although in our study, ¹⁵N and ¹³Cα motions were not strongly correlated.

If motional parameters acquired from different nuclei are compared as a means for model verification, or analyzed in concert, it becomes critical that the model used to calculate R _1ρ is correct. Approximations in the R _1ρ calculation can still yield qualitative results for a single type of nucleus but the degree of error will vary for different types of nuclei. Therefore, one should rely on more accurate simulations rather than Redfield-theory based methods for slow motions particularly when multiple nuclei are being used. Furthermore, it is important to account for magnetization decay induced by ¹H inversion, both in order to maintain agreement between different nuclei and additionally to avoid misinterpreting such ¹H inversion induced magnetization decay as slow motion. Although many of the errors that we have corrected here are relatively small, the errors can accumulate, making the additional effort required for an accurate analysis worthwhile.