The nature and quality of professional development (PD) of teachers of mathematics has been the focus of much attention in the USA (Borko 2004; Hill 2004, 2010; Wilson and Berne 1999). Recent policy documents recommend that PD for teachers should clearly focus on subject matter knowledge, connect closely to the work of teaching, and dynamically integrate teacher learning and practice within the content of PD (e.g., Blank and Nina de las Alas 2009; Conference Board of the Mathematical Sciences 2012; Marrongelle et al. 2013). Less attention has been paid to who provides this PD and what prepares these leadersFootnote 1 to do so effectively (Elliott et al. 2009a; Even 2014; Kazemi et al. 2009). International reviews document that formalized professional development opportunities for leaders are exceptions rather than the norm (Even 2008; Jaworski and Huang 2014; Jensen et al. 2016). Instead leader practice is assumed to develop through continuous interactions with and reflections on PD experiences and may or may not involve intentional mentoring or leader development opportunities (Jaworski and Huang 2014; Zaslavsky and Leikin 2004).

Researchers investigating professional development suggest that facilitators play a crucial role in fostering productive teacher learning (Banilower et al. 2006; Bell et al. 2010; Cobb and Jackson 2011; Schifter and Lester 2005). Evidenced in this research is the importance of leaders in guiding the content of PD to support teacher learning of mathematics needed for teaching. However, leaders typically have little to no preparation for supporting teacher learning (Borko et al. 2014; Even 2008; 2014; Jackson et al. 2015). Thus, it is not surprising that there is a scarcity of research on leader learning. As a result, we lack research-based principles to guide the design of leader preparation. The Researching Mathematics Leader Learning (RMLL) was a 5-year research and development project investigating what leaders learn about cultivating mathematically rich professional development environments for K-12 teachers.

Our project was designed around videocases of mathematics professional development. In this article, we examine how our use of these videocases aided leader noticing of the work required to facilitate mathematics PD. We address two interrelated research questions:

  1. 1.

    How did our framing of videocases advance or hinder leaders’ pedagogical reasoning around facilitating mathematics PD?

  2. 2.

    In what ways did leaders attend to teacher learning goals and notice the work facilitators do to support teacher learning?

Based on the findings from this study, we offer a set of design principles for leader professional development. Our aim is to contribute to the limited research on leader learning and preparation and to advance future leader research.

Theoretical Perspectives on Leader Learning

We draw on professional noticing (Mason 2002; Sherin et al. 2011) to consider leaders’ pedagogical reasoning around facilitation. In this section, we review how noticing has been characterized and advanced in teacher education. This literature grounds our use of noticing to conceptualize and analyze leader learning. We contend that sharpening leader noticing is a critical step toward preparing leaders to enact PD aimed at developing mathematical knowledge for teaching.

According to van Es and Sherin (2002), teacher noticing is comprised of three interrelated components: (a) identifying what is important or noteworthy about a classroom situation; (b) using what one knows about the context to reason about classroom events; and (c) making connections between the specifics of classroom interactions and the broader principles of teaching and learning they represent (p. 573). We adapted this definition to support and investigate leader noticing, replacing students in classrooms with teachers in professional development settings.

Although the development of noticing is conceptualized in various ways depending on the research focus, (i.e., teachers’ attention to student thinking, equity, or classroom lessons more broadly), there is general agreement on a number of indicators of advanced noticing. These indicators include: specificity in recalling details; supporting statements with evidence; moving beyond description or evaluation to interpretation; offering alternative explanations; and exploring relationships between teacher–student interactions and student learning (McDuffie et al. 2014; Santagata and Angelici 2010; Sherin and van Es 2009; van Es and Sherin 2008).

As Jaworski (1990) and others point out, a critical factor in promoting productive teacher discussions is the ability to maintain a focus on evidence-based interpretations and avoid premature judgments or evaluation. Evaluation leads to classifying and explaining away events, closing down opportunities for teachers to consider mathematical ideas deeply or reason pedagogically (Coles 2013; Jaworski 1990; van Es and Sherin 2008). In contrast, holding multiple interpretations of events opens possibilities for one to consider the implications of various actions and act differently (Mason 2011). Likewise, we consider leaders’ ability to refrain from evaluative comments and to instead imagine alternatives as a critical step toward enacting new facilitation practices.

Numerous studies have demonstrated how teacher noticing can be advanced through collaborative analysis of practice, typically through the use of video (McDuffie, et al. 2014; Star and Strickland 2008; Sherin and van Es 2009; van Es 2011). For example, van Es and Sherin (2008) and Sherin and van Es (2009) detailed the development of teachers’ selective attention to and knowledge-based reasoning around student thinking through participation in researcher-facilitated video clubs. Collectively, the research on using video to support teacher noticing highlights the importance of establishing clear goals, analytic frameworks, and specific prompts to guide discussion (e.g., Goldsmith and Seago 2011; Santagata 2011). Together with skillful facilitation, such supports can direct teachers to mathematically important elements of the video and scaffold teacher noticing (McDuffie et al. 2014; van Es and Sherin 2008).

We hypothesized that leader noticing could be honed in ways that support pedagogical reasoning around facilitation. Specifically, we were interested in how changes in our framework for leader development and the resulting changes in the prompts and tasks we used with our videocases shaped leader noticing in three ways: (a) accounting for the mathematical work of the facilitator and teachers in the videocase; (b) linking the mathematical work to goals for teacher learning; and (c) reasoning around the facilitator’s work in advancing those learning goals.

Leader knowledge and skills

Our aims for leader noticing were informed by research on the knowledge and skills needed to facilitate PD. Here, we build on an international review in a recent themed issue of ZDM (Jaworski and Huang 2014) along with a synthesis of what Even (2014) has termed “pioneering work” in leader PD. This body of work includes first-person accounts of becoming a mathematics teacher educator or leader (e.g., Coles 2013; Tzur 2001), reflections on the demands of leaders using prepared mathematics professional development curricula (e.g., Davenport and Ebby 2000; Schifter and Lester 2005; Stein et al. 1999), and the limited studies involving formal preparation of PD leaders (e.g., Campbell and Malkus 2014; Elliott 2005; Even 2005; Jaworski 2001; Zaslavsky and Leikin 2004). These studies are helpful in illuminating the dynamic and demanding work of facilitators and the tensions they navigate in pursuing learning goals with teachers.

Only recently have studies of leaders moved beyond descriptions of general competencies (e.g., expertise in teaching, knowledge of mathematical content, skills of leading, and ability to foster reflection on teaching) to begin to articulate specific knowledge and skills leaders need to facilitate teacher learning. Across this work, leader knowledge is often conceptualized as an extension of the knowledge needed for teaching (Campbell and Malkus 2014; Jaworski and Huang 2014). Leaders’ strong grasp of the content and effective facilitation skills are recognized as key to challenging the thinking of adults and moving mathematical conversations in productive directions (Borko et al. 2008; Even 2005).

A foundational study of leader learning, the MANOR project, highlights the extension of knowledge needed for teaching. Conceptualized by Israeli researchers, Even, Robinson, and Carmeli (2003) and Even (2005), MANOR sought not only to develop knowledge of mathematics content, teaching, and learning (knowledge also needed by teachers of mathematics), but also to develop knowledge and practice specific to leading PD. This included knowledge of current views of teacher learning, mentoring, and the work practices of teachers.

A more recent study by Borko and colleagues, supporting facilitators to implement the problem-solving cycle (iPSC) (Borko et al. 2014; Koellner et al. 2011), further articulates what content knowledge and facilitation skills for leaders might entail. Borko and colleagues reported that leaders implementing the iPSC were challenged to facilitate mathematical discussions in which teachers critically examined the affordances of different representations and solution strategies. They concluded that in order to support teacher learning, leaders needed to draw on mathematical knowledge for professional development. They posit that such knowledge entails three domains—specialized content knowledge, pedagogical content knowledge, and learning community knowledge (Borko et al. 2014). These three domains are in use when leaders facilitate mathematical goals for teacher learning in PD.

Borko et al.’ (2014) and Even et al.’ (2003, 2005) research helps us understand the domains of leader knowledge needed to enact quality PD. However, they and others acknowledge that how leaders become skilled in putting this knowledge into use is less understood (Jackson et al. 2015). In order for leaders to develop their knowledge base, leaders need opportunities to notice facilitation skills and resources at play in PD. In particular, they need to notice the entailments of facilitation such as how a facilitator pursues teacher learning goals within the complex interactional work of PD.

Design framework for leader professional development

The aim of our leader development work was to support leaders in learning how to facilitate robust opportunities for teachers’ mathematical learning, particularly in leading discussions of mathematical tasks with teachers. Our two-phase research and development design allowed us to construct a set of seminars for leaders, enact the seminar design with two groups of leaders in geographically distinct locations, analyze these data, and construct a second set of seminars for a third group of leaders. This section details our design considerations across the two phases of our 5-year project.

In Phase I, two constructs, adapted from classroom research to professional development, guided our design of leader PD: sociomathematical norms and a set of practices for orchestrating productive mathematical discussions. The first component of the design framework was adapted from Yackel and Cobb’s (1996) attention to normative ways of guiding learners’ social and mathematical interactions. We distinguished social norms in PD, the general ways teachers engage with one another, from sociomathematical norms in PD, the specific ways teachers engage in mathematical work (Elliott et al. 2009b; Kazemi et al. 2007). Sociomathematical norms included negotiating what counted as a sufficient mathematical explanation in PD settings and considering how mathematical representations were used. We framed our discussion of videocases of professional development with leaders by asking them to identify the sociomathematical norms for explanation that seemed to be in place. Our work with this construct recognized that leaders need to be cognizant of the tensions that may exist between teachers’ typical engagement in mathematics PD and practices that foster deep understandings of mathematics (Ball and Cohen 1999; Forman 2004).

The second component of the design framework was adapted from the classroom research of Stein et al. (2008) in which they identified five practices for orchestrating mathematically productive discussions with students. Similar to the teacher’s role in classrooms, we contend that leaders should also be strategic and thoughtful in how they anticipate, monitor, select, and sequence teachers’ sharing of their solutions. Here, we conjectured that the five practices would be useful skills for leaders to enact in PD to support teacher engagement in mathematically productive discussion.

Prior to designing a second set of seminars, we analyzed Phase I data to determine how seminar constructs supported leaders’ sense-making around facilitation and leaders’ ability to negotiate mathematical reasoning while facilitating PD. Content analyses of fieldnotes constructed from video records and observations of seminar discussions, transcripts of interviews from a sample of leaders, and observations of leaders’ facilitation revealed that although leaders found the constructs useful for learning to lead mathematically rich discussions, they faced tensions related to making PD relevant for teachers and were challenged to identify clear, attainable, goals for working on mathematics tasks with their colleagues (Elliott et al. 2009a). To prepare leaders to meet these challenges, we needed to better specify goals for teacher learning and design opportunities for leaders to (a) intentionally experience pursuing mathematical ideas important for teacher learning and (b) see how teacher learning needs are different than student needs.

Thus, in Phase II we added a third construct in order to better attend to the purposes for doing mathematical work in PD. We drew on Ball, Thames and Phelps’ (2008) mathematical knowledge for teaching (MKT) framework and focused on one aspect of it—specialized content knowledge (SCK). Ball and colleagues explain that teachers draw on SCK when they analyze a task and its possible solution methods, consider the reasoning that might underlie correct and incorrect solutions, and evaluate the affordances and drawbacks of various representations and the connections among them. For example, teachers, like other professionals, can compute an answer to a multiplication problem. Doing so successfully requires common content knowledge. Specialized knowledge of multiplication needed for teaching includes such things as knowing the various meanings of multiplication (e.g., as equal groups, as area), linking written symbols to representations for both whole number and fraction multiplication, recognizing common student errors, and knowing the similarities and differences among various strategies (e.g., partial products, estimating and compensating, proportional reasoning). SCK is important for enhancing teachers’ classroom instruction because teachers draw on this knowledge when planning, teaching, and responding to students’ ideas (see Ball et al. 2008 for an elaboration). It follows then that leaders’ capacity to cultivate teachers’ specialized knowledge of mathematics has everything to do with leaders’ ability to know what mathematical understandings to press for with teachers (Neubrand 2008).

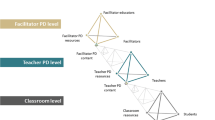
In our revised framework (see Fig. 1), we put the three constructs in relation to one another. The framework first points to naming the mathematical goal for teacher learning and identifying a suitable task for attaining that goal. The attainment of the goal is made possible by the way norms for mathematical reasoning are negotiated in intentionally orchestrated discussions. This revised framework places sociomathematical norms for mathematical reasoning and the five practices for orchestrating discussions in service of attaining subject matter learning goals for teachers. The addition of SCK as a third design construct resulted in changes in the way we engaged leaders in the mathematics prior to the videocase and to the prompts we used to guide leaders’ discussion of the videocase. To illustrate these changes and how the framework informed the leader professional development design, we discuss the activities of one videocase, Janice’s method, within the methodology section of the paper.

Fig. 1
figure 1

Framework for doing mathematics in professional development

Full size image

Methodology

Using a quantitative and qualitative methodology, data analysis for this article draw on a large corpus of data from the two phases of the leader project including both video records and text-based artifacts. To investigate how our framing of videocases advanced or hindered leaders’ pedagogical reasoning and document how leaders’ noticed the work of the PD facilitator, our two research questions, we examined six seminars across the two phases of our design. Before detailing this analysis, we provide background information on the participants and seminar content.

Participants

Across two phases of research, we engaged 72 leaders in videocase-based seminars to support their ability to plan for and facilitate mathematical tasks in professional development. Participants included those with formalized leadership roles (e.g., designated coaches or mathematics specialists) as well as those who volunteered, or were identified by administrators, as informal leaders in a department or school. The common attribute among all those we define as leaders is that each was responsible for leading professional development sessions with teachers. Phase I consisted of two research sites. One site included leaders from elementary and middle grades (n = 13) from one large district. These leaders had little experience facilitating PD, but all had responsibilities as leaders in the district. The other site included K-12 leaders (n = 24) from several districts. One-third of these leaders had four or more years of facilitation experience, and the majority also had classroom teaching responsibilities. In Phase II of the project, we worked with K-12 leaders (n = 35) from three districts. Phase II participants took on a range of leadership roles including district level teachers on special assignment, elementary mathematics coaches and practicing teachers who took on leadership responsibilities at either the district or building level. Similar to the combined Phase I population, approximately one-fourth of Phase II leaders had 1–4 years of experience facilitating PD, while the majority had little to no prior facilitation experience.

Prior to engaging in Leader Seminars, we administered a mathematical knowledge for teaching assessment based on measures developed by the learning mathematics for teaching (LMT) project (http://sitemaker.umich.edu/lmt/people). This assessment was designed with the support of the LMT staff to highlight the content areas germane to the leader seminars. Our intent was not to measure change or growth in leaders’ MKT (hence there was no post-assessment); but rather, it was to provide additional means to compare background experiences and resources across the three groups of leaders. Leader scores in both phases were quite widespread, with a range of 6 to 31 correct out of 32 possible items in Phase I and a range of 6 to 29 in Phase II. The average scores were also similar with means of 18 and 19 and medians of 19 and 16 in Phase I and Phase II, respectively.Footnote 2 In short, leader groups across the two phases were comparable in terms of mathematical background and the range of teaching and leading experience.

Seminar content

Leaders participated in a series of three or four two-day seminars across an academic year (a total of six days in Phase I and eight days in Phase II). In Phase I, the leader PD curriculum was designed around a set of previously published leader videocases that served as a focal point for the design team to collaboratively create seminar plans (Carroll and Mumme 2007). These plans were used across both sites. Two design team members, who brought extensive experience and knowledge of leading mathematics teacher and leader PD to the project, each took responsibility for facilitating the three sessions at one of the two research sites in Phase I. In Phase II, the PD curriculum was redesigned using a portion of the Phase I materials and supplemented with new videocases and written cases of teacher professional development. Phase II was co-facilitated by the same two facilitators.

Each seminar followed a purposeful progression of events centered on select videocases of PD. We chose videocases as a vehicle for leader development because they provide vivid, authentic images of the complex work of facilitating mathematical discussions with teachers (Borko et al. 2008; Janík and Seidel 2009; Seago and Goldsmith 2006). Presented as objects of inquiry, we used the videocases to create opportunities for leaders to unpack teachers’ mathematical thinking, facilitator actions, and the interaction between the two. The videocases consisted of short, subtitled clips (5 to 10 min in duration) showing a leader managing a discussion of teachers’ solutions to a mathematics task. Accompanying materials included transcripts, copies of teacher work, and other relevant resources (adapted from Carroll and Mumme 2007).

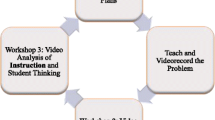
Each seminar included repeated cycles of activity beginning with leaders working on the mathematics task used in the PD videocase. Leaders then viewed and discussed the videocase, first with a focus on what mathematical explanations were shared, which reflected our intent for leaders to be clear on the mathematics available in the videocase. In a second viewing, leaders were asked to consider how participants in the videocase engaged in sharing explanations in order to focus on group norms and issues of facilitation. Finally, leaders engaged in a variety of connecting to practice activities designed to encourage further reflection around the videocase and help leaders apply newly gained insights to their own facilitation of PD. Between seminars, leaders facilitated PD, often using tasks from the leader project, and reflected on their facilitation experiences during the following seminarFootnote 3 (see Fig. 2).

Fig. 2
figure 2

Project seminar design around videocases

Full size image

In Phase I, leaders engaged in six videocases, while Phase II consisted of six videocases and two written PD cases (see Table 1 for a list of videocases). Because we revised our framework to specify teacher learning goals that attend to SCK, different videocases were needed in Phase II of the project. The one exception was Janice’s method, a videocase used in the first seminar of Phase I and in the final seminar of Phase II. Because Janice’s method was the only videocase viewed by participants in both Phase I and Phase II,Footnote 4 we use this case to illustrate the revisions we made in Phase II to attend to mathematical learning goals for teachers. These revisions included not only changing how we engaged leaders in the mathematics prior to viewing, but also refining discussion prompts to more tightly focus on mathematical knowledge of subtraction at play in the videocase.

Table 1 PD videocases by seminar
Full size table

Comparing Phase I and II framing of Janice’s method

In preparation for viewing the videocase, leaders first engaged in a mathematics task. In Phase I, leaders were simply directed to solve 92 − 56 mentally and share their solution methods—the same task as teachers in the videocase. We revised the mathematics task in Phase II to better attend to the SCK ideas embedded in whole number subtraction (see Table 2 for task description). Our intent was to engage leaders in considering different interpretations of subtraction (e.g., take away vs. difference) and to consider how these interpretations might be represented on a number line. We posited that this would provide a productive mathematical lens for leaders to interpret the videocase. After discussing their mathematical work in both small and whole group, leaders viewed the associated videocase.

Table 2 Comparison of Phase I and II mathematics tasks for Janice’s method
Full size table

Janice’s method videocaseFootnote 5 is from a workshop with K-5 teachers focused on developing computational fluency with subtraction. Participants were asked to compute 92 − 56 mentally. In the videocase clip, a teacher named Janice answered 36 and shared her strategy. In explaining that she rounded 92 down to 90 and 56 up to 60, she said, “I know 90 is 2 from 92, so I put 2 plus the 4 that I needed to add to 56 to get 60, which equals 6. And add 30 and 6 together will give you that 36.” The facilitator asked Janice, “Why did you add the 2 and the 4?” Janice answered by saying that she needed to “recover” the 2 and the 4. A conversation ensued about what Janice meant by the term recover. The case contains a number of mathematical issues that could be unpacked. These include the use of a number line to represent a distance interpretation of subtraction, compensation strategies for both removal and distance interpretations of subtraction, and the role of context in understanding these strategies.

The prompts used to frame the first videocase discussions are given in Table 3. In Phase I, leaders were prompted to describe Janice’s method and make connections among the explanations the facilitator and other teachers provided for the method. Leaders in Phase II were also asked to discuss explanations that were offered. However, leaders were further pressed to symbolically represent specific explanations (i.e., a procedural explanation of “minusing a minus,” a contextual example, and a number line model) and discuss the underlying interpretations or models of subtraction evoked in these explanations. These more focused discussion prompts were designed to situate leaders in SCK terrain—considering models and interpretations of subtraction. The final prompt reflects our efforts to support leaders to identify mathematical learning goals for teachers.

Table 3 Comparing Phase I and II prompts for the first viewing of the videocase
Full size table

A side-by-side comparison of Phase I and II prompts for the second videocase discussion, provided in Table 4, again demonstrates how our additional emphasis on SCK influenced our seminar design work. Across both phases, the intent of the second videocase viewing was for leaders to attend to sociomathematical norms and consider these in relation to purpose. Prompts in Phase II, however, focused more directly on how Casilda (videocase facilitator) was or was not supporting productive norms and advancing mathematical learning goals.

Table 4 Comparing Phase I and II prompts for the second viewing of the videocase
Full size table

The more explicit prompts for Janice’s method shown here are representative of how, in Phase II, we first engaged leaders in SCK ideas that might need to be unpacked in a videocase. Leaders were then prompted to consider the videocase facilitator’s moves in relation to developing norms and supporting teacher learning of those mathematical ideas.

Data sources

Data sources for this article include video and fieldnote records of leader discussions and the artifacts produced by leaders and provided for them during seminars and used in discussions. Two cameras were used to capture the whole and small group discussions. The small groups on camera were rotated throughout the seminar series to ensure that a range of grade levels and experience were represented. Seminar artifacts, including handouts, posters of mathematical solutions created by leaders, and mathematical work recorded in journals or co-constructed during small and whole group discussions, were examined in conjunction with video and fieldnote analyses.

Data analysis

In our initial analysis of Phase I, mentioned earlier, we did not employ a noticing framework, but instead focused our qualitative analysis on leaders’ uptake of seminar constructs as evidenced in leader interviews, fieldnotes from seminar discussions and from our observations of leaders’ PD facilitation. For this article, we re-analyzed data from three seminars within each phase, early, midway, and at the end of the series, to investigate our first research question on how the framing of the videocases advanced or hindered leaders’ reasoning around facilitation. Within these seminars, we examined the small group discussion after the second viewing of each videocase, which centered on how the videocase facilitator and teachers collectively engaged in mathematics. This allowed us to examine ways leaders attended to learning goals and noticed facilitation work to support teacher learning, our second research question.

We used Studiocode© (Studiocode Business Group 2012), a qualitative video analysis software, to analyze leader discussions. Each discussion was first chunked into idea units (Jacobs and Morita 2002). An idea unit was defined by a segment of leader dialog with an identifiable focus. We started a new idea unit when there was a distinct shift in the focus, for example, when leaders’ discussion of a videocase moved from investigating the types of questions the facilitator asked to consider a particular mathematical explanation a teacher provided. The average length of an idea unit was slightly over 2 min, with a range from 30 s to 4 min. To develop reliability in identifying idea units, the research group first collectively discussed verbal cues in leader discussions that denoted changes in actor and topic and chunked a selection of data into idea units. Next researchers were paired to identify and agree upon idea units within a full discussion. An average of 80 % agreement was obtained upon initial segmenting of data. Researchers reconciled disagreements on idea units prior to coding the data.

Each idea unit was coded according to actor, topic, and stance (Sherin and van Es 2009). Actor codes designated whom the leaders focused on (e.g., videocase facilitator, videocase teachers, teachers in general, themselves). Topic codes were used to note what leaders attended to as they discussed how the group was interacting (e.g., PD pedagogy, norms, classroom teaching) and whether these topics reflected, either implicitly or explicitly, seminar constructs of SCK, sociomathematical norms, or the five practices. Consistent with Sherin and van Es (2009), stance codes captured whether leaders were describing, evaluating, or interpreting events in the videocase. To distinguish between positive and negative judgments of videocase events, we coded idea units in which leaders seemed to be taking an evaluative stance as either approve or disapprove. We added the stance code speculate when leaders were taking an inquiry stance in their interpretation by framing comments as wonderings rather than declarative statements. We also added the stance code extend to denote instances when leaders were extending beyond the videocase to consider other settings or to rehearse alternative facilitation moves. Thus, our final coding scheme resulted in five stance codes: approve, disapprove, describe, interpret, speculate, and extend (see “Appendix” for full list of codes). Together, these actor, topic, and stance codes were designed to capture both what and how leaders noticed. Because of our coding decisions and the nature of leader conversations, an idea unit always consisted of a single actor, but could contain multiple topic and stance codes.

Two researchers coded each discussion. Disagreements were resolved through discussion or by consulting a third researcher to reach consensus on all coding. The final, agreed upon, coded timelines for Phase I and II small group conversations were then uploaded into a database to identify patterns within and across the leader seminars.

Studiocode database and matrix features allowed us to calculate the frequency of actor, topic, and stance codes as well as the number of idea units coded with the same combinations of codes. Using Boolean searches of the data matrix, combinations of actor and high-frequency codes were identified (e.g., videocase facilitator in combination with PD pedagogy and purpose). We calculated the percentage of codes per total idea units and constructed tables to highlight patterns and compare across small group discussions in Phase I and II. Graphical representations from these data are presented in “Findings” section.

The matrix function also supported qualitative analysis by collecting idea units coded with a single or combination of codes. Instances of video clips with particular codes were grouped and watched in succession to identify themes. For example, in our earlier work, we learned that leaders had difficulty articulating a mathematical learning goal for teachers (Elliott et al. 2009a). We were especially interested in leaders’ focus on videocase facilitator moves in relation to a mathematical goal. Examination of idea units coded with videocase facilitator as actor and topic codes of PD pedagogy and purpose led to the identification of several themes discussed in findings section.

Findings

In this section, we address how our framing of the videocases advanced or hindered leaders’ pedagogical reasoning around mathematics PD. Recall, we are interested in how changes in our framework for leader PD and resulting changes in prompts and tasks shaped leader noticing in relation to the facilitator’s work to advance goals for teacher learning. The purpose of this analysis is not to compare individual leader learning outcomes from Phase I and II, but rather to gain insights into leader learning and preparation.

Our analysis indicates that Phase II leader discussions were more focused on the work of the facilitators in advancing teacher learning than Phase I leader discussions. To substantiate this claim and define what we mean by more focused discussions, we first present quantitative results from our coding of leader activity across Phase I and II. These frequency displays of actor, topic, and stance codes within leaders’ conversations illustrate shifts in the general nature of videocase discussions from Phase I to Phase II. We present and interpret these shifts to answer our first research question regarding the way our framing of videocases advanced or hindered leaders’ pedagogical reasoning. To address our second research question, we then present themes that emerged from our qualitative analysis of Phase II data to further illustrate how leaders were attending to teacher learning goals and noticing aspects of facilitation in these more focused discussions.

Quantitative analysis of leader noticing

To facilitate comparisons across phases, the quantitative results are organized around our three coding categories of actor, topic, and stance with totals for each phase. A table with statistics for individual videocases is provided in “Appendix.” As detailed below, discussions in Phase I were spread among actor codes, lacked a clear topical focus, and were predominantly coded as an interpretative stance. We saw Phase I discussions to be wide ranging. In Phase II discussions, a higher percentage of idea units centered on the videocase facilitator as actor and topic codes of PD pedagogy, norms, and purpose. We take this as evidence that discussions were more focused on facilitator’s moves in relation to norms and goals.

Actor

Figure 3 shows percentages of actor codes for Phase I and II. In Phase I, leaders’ attention was spread out among various actors. In Phase I, approximately half of the idea units were focused on videocase facilitator or teachers, with greater attention to teachers. In the remaining idea units, actor codes were almost equally distributed across the whole PD group, other actors (e.g., students, colleagues in their building), and the leaders themselves. We interpreted this spread to indicate that the focus of small group discussions was diffuse and more attention was paid to teachers than to facilitators.

Fig. 3
figure 3

Distribution of actor codes in Phase I and II discussions

Full size image

In Phase II, almost 75 % of idea units focused on the videocase facilitator or teachers with more than half of those idea units centered on videocase facilitator. In the remaining idea units, leaders were focused on the entire professional development group (8 %), other actors (8 % e.g., students or their colleagues), and facilitators in general (6 %). These data indicate that in Phase II, leader noticing was more often linked to the facilitator.

Topic

Analysis of topic codes further supports our claim that leader noticing in Phase II centered more tightly on facilitation. As shown in Fig. 4, we found a rather even focus (14–23 % of idea units) on topics such as PD pedagogy, purpose, professional norms, and classroom teaching in Phase I.Footnote 6 Moreover, there was no consistent trend in topical focus over the course of the seminars. In fact, a topical focus on the videocase facilitator’s purpose, which appeared in 17 % of idea units in seminar I, diminished over time. These data in particular corroborated findings from our earlier research that our seminars were not successful in helping leaders elaborate the purposes of doing mathematics with teachers in PD (Elliott et al. 2009a).

Fig. 4
figure 4

Distribution of selected topic codes in Phase I and II discussions

Full size image

Topic codes in Phase II show a dramatic shift toward the pedagogy being enacted by the facilitator with 46 % of idea units coded as PD pedagogy and 32 % of idea units coded as purpose. These statistics are mirrored in Janice’s method where only 7 % of idea units were coded as PD pedagogy and 17 % of idea units were coded as purpose in Phase I. In Phase II discussions of Janice’s method, these numbers increased to 44 % for PD pedagogy and 31 % for purpose. This suggests that the leaders noticed the work the facilitator does to engage teachers as well as the rationale for this work.

The interactive work of facilitators and teachers is also captured in our coding of norms. In Phase II, professional norms were discussed in 30 % of idea units and sociomathematical norms were explicitly discussed in 16 % of the idea units, nearly double the percentages from Phase I. Finally, there was a substantial decrease in topic codes such as classroom teaching, K-12 students, and curriculum from Phase I to Phase II. In other words, leaders in Phase II spent less time talking about issues tangential to the case (e.g., stories of their own students or a particular curriculum) and more time considering the facilitator–teacher interactions. We take this as further evidence that leaders maintained a focus on PD pedagogy and the work a facilitator does to support teacher learning.

Stance

Looking at overall percentages for stance codes, Fig. 5, there were no substantial differences between Phase I and Phase II. In both phases, leaders took an interpretive stance the majority of the time. Although, there was a considerable increase in extend/rehearse codes with only 3 % in Phase I compared with 24 % in Phase II.

Fig. 5
figure 5

Distribution of stance codes in Phase I and II discussions

Full size image

Examining stance across the seminars in Phase II revealed a different story. While 44 % of idea units in In & Out Tables,Footnote 7 the first videocase, were coded as describe, there were no instances of describe in either of the later two videocases we analyzed. Moreover, there was a substantial decline in evaluative comments, those coded as praise/approve or disapprove. Approve codes decreased from 28 % in In & Out Tables to only 6 % in Janice’s method and there were no instances coded as disapprove. In Phase I, 17 % of the idea units in Janice’s method were coded as praise/approve and there was no comparable change in stance codes across the seminar series. We take this shift in the nature of the discussion, from describing or evaluating toward interpreting and imagining alternatives, as an indicator of more productive noticing in Phase II.

Summary of quantitative results

Our first research question asks how our framing of videocases advanced or hindered leaders’ pedagogical reasoning about mathematics PD. We considered this question as we examined our quantitative data, recognizing that our constructs for designing leader PD shifted across the two phases. Recall, in Phase II we added a third construct focused on specialized content knowledge (SCK) (Ball et al. 2008) that resulted in changes in the mathematics tasks we gave leaders and a refinement of the videocase prompts (see Tables 2, 3, and 4 for an example). These changes were intended to focus leaders’ attention on the mathematical work of the facilitator and teachers in relation to goals for teacher learning and the facilitator’s role in advancing those goals.

Our analysis of Phase I data suggests that the constructs and videocase prompts resulted in more diffuse discussion of actors and topics. In contrast, quantitative results demonstrate that Phase II small group discussions were more centered on the videocase facilitator and teacher as actors with PD pedagogy, purpose, and norms as the most common topics. Leaders typically adopted an interpretive stance with increased instances of extending or rehearsing in the videocase discussions. In short, leader discussions in Phase II focused on the work of facilitation and features we hypothesize are central to the development of pedagogical reasoning about leading PD.

Qualitative analysis of leader noticing

We claim from the quantitative data that leader discussions in Phase II were focused in productive ways. To illustrate what those more focused discussions entailed, we present three interrelated themes that were revealed in our qualitative analysis of Phase II discussions. These themes provide a context for considering design principles for leader PD.

First, leaders noticed the work the facilitator does to pursue a mathematics goal for teacher learning in PD. Second, leaders noticed multiple mathematical goals that could be pursued. The capacity to simultaneously hold multiple interpretations of a videocase enabled leaders to explore hypothetical moves in relation to PD goals. And finally, leaders noticed that a key purpose of PD should be to support teacher learning—and in particular, to support the development of SCK. In the following sections, we use excerpts from leader discussions in Phase II to elaborate each of these themes.

Leaders noticed the work the facilitator does to pursue a mathematics goal for teacher learning

As demonstrated in the quantitative results above, Phase II leaders attended to the videocase facilitator over half of the time, whereas in Phase I leaders demonstrated a dual focus on videocase facilitators and teachers. To explore how Phase II leaders were reasoning about the facilitator, we examined idea units coded with videocase facilitator as actor in combination with topic codes of PD pedagogy and/or purpose. In Phase I, small groups connected their noticing of the videocase facilitator to PD pedagogy 29 % of the time. In contrast, 65 % of the idea units coded as videocase facilitator were also coded with PD pedagogy in Phase II. Moreover, 41 % of those idea units coded as videocase facilitator and PD pedagogy were also coded with purpose.

Our examination of PD pedagogy and purpose codes uncovered that leaders noticed the mathematical trajectory evidenced in videocases and identified specific facilitation moves that advanced that agenda. For example, in small group discussions around the first videocase, In & Out Tables, leaders attended to where and how the videocase facilitator, Brian, stepped in to ask guiding questions or reiterate teacher ideas to conclude that the facilitator had a clear agenda and “knows exactly what he wants out of the conversation.” Further, leaders speculated on what Brian might have done to maintain this focus after a videocase teacher makes a comment about grading that the leaders interpreted as unrelated to Brian’s mathematical purpose. Leaders wondered whether the facilitator had some “back pocket” questions or prompts for teachers to explore.

In the Halving and Doubling videocaseFootnote 8 discussions during seminar two, leaders also noted the facilitator’s role in pursuing a mathematical goal by pointing to specific statements and actions as evidence of the facilitator’s intentional planning. Prior to engaging in this videocase, leaders were introduced to practices for sharing teacher work (adapted from Stein et al. 2008) and were prompted to discuss where they saw evidence that Becca (the videocase facilitator) may have used the practices. In response, leaders in one group noted how the videocase facilitator monitored, selected, and sequenced teacher work in order to make connections to an array model that demonstrated the Halving and Doubling conjecture.

Barb: I was struck by how she (Becca) did the connecting and she led from one thing to another. On line 93 she said ‘I kept talking to your group because you had the array of 6 by 10 and I was trying to figure out a way to talk about it.’ Then she saw the other drawing and she was explaining why she had them come up. So that connecting the teachers’ work, that last practice that was talked about, and the way that she had them share those different examples allowed them to see those connections.

In this exchange, Barb points to the transcript to highlight how the videocase facilitator elicited a particular mathematical representation, the array model, in order to make mathematical connections. Barb asserts that the videocase facilitator moves, linking two groups’ explanations, provided further support that the videocase facilitator was pursuing a particular mathematical goal.

Leaders in this group continued to narrate Becca’s purposeful use of the five practices to make connections among representations. This led them to wonder what would have happened if the videocase teachers had not generated visual models. Their discussion extended to consider the work a facilitator might do to introduce a solution or support teachers to develop productive models of the operation.

In short, leaders’ noticed the work the facilitator does to pursue a mathematics goal for teachers. This includes intentionally planning PD with that mathematical goal in mind. Further, leaders were imagining a range of facilitation moves necessary to maintain a focus on this goal. This final point is connected to our second claim.

Leaders noticed multiple goals that could be pursued

The second theme emerged from further analysis of leaders’ stance. Leader conversations coded with extend or speculate accounted for 38 % of idea units in which videocase facilitator was the actor. Over half of those instances were also coded with purpose, indicating that leaders were inferring mathematical goals and suggesting alternative moves in relation to these goals.

Within the videocase activities, leaders were not explicitly given the videocase facilitator’s goals. Instead, leaders were prompted to speculate on purpose in relation to specific facilitator comments and questions or on the interactions between the videocase facilitator and teachers more generally (see Table 4 for an example). As a result, leaders recognized a range of purposes that could be pursued within a task. This capacity to simultaneously hold multiple interpretations of the videocase enabled leaders to explore hypothetical moves in relation to PD goals.

To illustrate what this reasoning sounded like, we share an excerpt from Janice’s method. Leaders spent considerable time discussing the videocase facilitator’s purpose and interpreted the majority of facilitation moves as attempts to clarify Janice’s method and hone in on what was happening when Janice had to account for the shift of four units from 56. Recall, in the videocase Janice solved the mental subtraction problem 92 − 56 by rounding 92 down to 90 and 56 up to 60. She then added both the 2 and 4 back to 30 to “recover the difference.” In this excerpt, leaders in one small group questioned whether there was enough evidence in the videocase to make a strong claim that Casilda (the videocase facilitator) was explicitly trying to work on models of subtraction.

Opal: So you think her goal was just being able to articulate what you’re doing?

Jack: No. I think the goal was to look at the mathematics of that particular example. And I don’t think the goal was necessarily to have Janice do the work, but just to help everybody understand why it was two plus four.

Maria: I got the sense that Casilda’s purpose was to highlight the difference as opposed to the take away. That’s what I was thinking.

Leaders began by advancing a number of potential purposes a facilitator might pursue in Janice’s subtraction strategy. These ranged from general goals for mathematical explanation (being able to articulate the method clearly) to mathematical ideas particular to subtraction (i.e., why does this compensation method work). When Maria poses that the facilitator could be working to distinguish two meanings for subtraction leaders go back to the case searching for evidence of facilitator moves that might support that goal.

Opal: But I would have thought if her goal was to highlight difference versus take away [models] there would have been some more explicit language to help with that, like ‘this was the difference’ or ‘we took away.’ I wasn’t sure what her purpose was. My assumption generally when you’re subtracting two-digit numbers is to unpack the regrouping. But I don’t have evidence that that was being done.

Jack: I think it may not have been such a specific goal as you’re suggesting. I think that it might have been just to help teachers understand why you can add the two and the four to get the right answer. That it’s not just a fluke.

Maria: She started right from the beginning, ‘why would you add the two and the four?’ ‘what do you mean about recovery?’ ‘So you still had that two somewhere, you still had that four somewhere.’ ‘What happened to the difference?’ That’s why I kept feeling like she was trying to solidify that idea.

This excerpt is encouraging in a number of ways. Our preparation for viewing the videocase intentionally oriented leaders to consider models of subtraction. Yet, they did not simply conclude that the videocase facilitator was working with that same intention. Instead, they wondered what Casilda might have said or done if that was indeed her aim. Rather than evaluating the facilitation moves, or interpreting them in a narrow way, leaders drew upon their own mathematical work prior to viewing the videocase, together with specific evidence from the case, to reason about a range of goals that may be pursued with the task. From there, they were able to speculate, as Opal is doing above, on the mathematics that would need to be made more explicit for teachers depending on the goal (i.e., using the language of “difference” or “taking away” if one wanted to highlight different meanings of subtraction).

Not only did leaders notice and interpret videocase facilitator moves in relation to a range of mathematical goals, they also took up opportunities to consider alternative pedagogical moves in support of these goals. Across Phase II discussions, we heard leaders wonder about other ways to draw out the intended mathematics or questions a facilitator might ask to get teachers to dig into particular solution methods. These discussions opened opportunities for leaders to imagine alternative facilitation moves to advance teacher learning. For example, in the Halving and Doubling discussion referenced earlier, leaders speculated on what they might do to elicit visual models. Leaders discussed preparing models in advance and imagined questions they may pose to press teachers to consider different representations.

As theorized in the noticing literature (Mason 2002), the ability to hold multiple interpretations and consider a range of possible responses can prepare one to interact in future situations. We posit that leaders’ increased awareness of mathematical learning goals for teachers and the facilitator’s role in advancing these goals is a first step toward enacting PD that supports the development of SCK. We elaborate this further in discussing our final theme.

Leaders noticed that a key purpose of PD should be to support teacher learning: and in particular, to support the development of SCK

The final theme that PD should support the development of teachers’ SCK emerged from leaders noticing that not all mathematical ideas shared by videocase teachers were of equivalent worth. As the seminar series evolved, leaders were better able to articulate the mathematics available in a task and ideas that might advance teachers’ understanding of the mathematics needed for teaching.

Leaders were linking facilitator moves to mathematical goals as early as the first seminar. However, when asked about the facilitator’s purpose in the first videocase, In & Out Tables, before we had provided SCK language, the conversations stayed at a more general level. For example, in the small group discussions described earlier, leaders all agreed that Brian, the facilitator, had a mathematical agenda, but other than noting it was not about grading, leaders did not articulate what that agenda might have been. In the final seminar discussions, leaders were better able to articulate specific mathematical ideas. We recognize that some of this could have been due to the nature of the tasks themselves, (i.e., the subtraction in Janice’s method might have been more accessible and thus easier to detail). Given that we did not hear similar mathematical discussions in Janice’s method during Phase I, we contend that leaders were better positioned to notice and name the mathematics due to our framework revision to attend to SCK.

We highlight an example from Janice’s method to demonstrate how by the end of the seminar series some leaders were attending to SCK goals for teachers. As in the small group exchange shared in the previous section, this group is also responding to the prompt, “What might be Casilda’s purpose in this discussion?” The discussion begins with Pat wondering why the facilitator would choose to unpack Janice’s method in such depth.

Pat: Do you think maybe she (Casilda) doesn’t understand what Janice said? So she’s seeking clarification because…

Barb: I thought that the first time through, but the second time watching it I am wondering whether she was just trying to make sure that everybody knew exactly where those numbers were coming from and maybe working on that idea of developing that norm of explaining and justifying. Trying to draw out deeper conversation. We talked a little bit about Janice’s language and how it could have been confusing so I was wondering if Casilda was purposefully being very basic about the questions to draw out that discussion about where those numbers come from and what they mean.

In contrast to some of the conversations in Phase I in which leaders were concerned about what Janice herself may or may not have understood, leaders considered what the teacher group needed to understand about this particular method of subtraction. Barb’s comments, that Casilda might be trying to draw out a “deeper conversation” about where the numbers come from and what the numbers mean, suggest that there is important mathematics here for teachers to understand.

Henry then turned to the transcript to label facilitation moves to support Barb’s claim that Casilda wanted everyone to understand the mathematical ideas underlying Janice’s method. In noting Casilda’s specific comments and questions, both Henry and Barb were attending to the role the facilitator played in advancing particular SCK goals, in this case unpacking compensation strategies for subtraction and examining different representations.

In a final excerpt from this small group, Barb highlights how the facilitator is able to acknowledge another teacher’s methods while still pursuing the mathematical goal of making sense of the two and the four in Janice’s method.

Barb: So on line 95 – it’s interesting here because they had gotten into that 2 minus, minus 4 kind of thing (a method presented by Chris, a videocase teachers). Casilda wrote it down, but she seemed to move away from that really quickly. ‘So let’s think on that, but what I really want to know is, did Janice explain why she added back the two?’ Casilda moved the discussion back to what they were talking about. And it helped boil down to that the question was really about the four. I like the way she moved it back in a way that went back to the key question for them.

Barb acknowledges the facilitator’s skill at recording Chris’ method and quickly moving the conversation back to unpacking what is happening with the 4 in Janice’s Method. In the process, she is indicating that Chris’s explanation of “minus a minus” was not necessarily productive in terms of deepening teachers’ understanding of key relationships underlying compensation strategies. In fact, both small groups on camera during Janice’s method noted how the minus a minus explanation was insufficient.

In response to the prompt, “How are Casilda’s purpose and norms tied to SCK?” leaders in the other small group described the mathematical knowledge that the facilitator needed to not only know herself, but also communicate to the teachers with whom she was working.

Maria: One illustration is that if she had let Chris just be done, everybody had their great “aha” that it was “minus a negative four” that is at that procedural level. But it’s that SCK that she (the videocase facilitator) had to understand the deeper… you know to be able to represent it other than symbolically and somehow get that across. That is kind of what goes into that specialized knowledge.

Jack: The SCK is knowing going into this problem that you can manipulate the different parts and that by manipulating the different parts it causes a change in the difference.

Maria and Jack are suggesting not only that the purpose of PD is SCK, but that it is the leader’s responsibility to understand the SCK in order to “get that across” or pursue it with teachers. These statements are echoed by researchers who propose that facilitators must have an understanding of different solution methods and representations that goes beyond the procedural level (Borko et al. 2014; Schifter and Lester 2005).

These discussions indicate how some leaders saw that a key purpose for doing mathematics in PD is to advance teachers’ MKT and in particular SCK. We find it promising that leaders were noting facilitation moves that pushed teachers beyond serial sharing (i.e., presenting ideas in rapid succession with little discussion or connections), toward unpacking ideas behind a particular method more deeply. We contend that these types of conversations, while difficult, are necessary to support the development of SCK.

Summary of qualitative results

Themes emerging from our qualitative analysis uncover ways in which leaders attended to learning goals and noticed the work facilitators do to support teacher learning (our second research question). Overall, leader discussions centered on the mathematics of the videocase and facilitation moves that kept teacher conversation focused on unpacking a particular representation or solution method. Importantly, leaders moved beyond merely describing events and were interpreting them in relation to mathematical goals and making connections to broader PD facilitation strategies. These conversations are particularly salient given our goal to support leaders’ ability to advance the mathematical thinking of a group of teachers. By linking facilitation moves to mathematical purposes, we believe leaders are better prepared to notice and act upon mathematical opportunities that arise in PD.

Discussion

This study demonstrates how the framing and use of videocases can advance leader learning. Our revised framework for leader PD and videocase prompts shaped leader noticing in relation to: (a) accounting for the mathematical work of the facilitator and teachers in the videocase; (b) linking the mathematical work to goals for teacher learning; and (c) reasoning around the facilitator’s work in advancing those learning goals. Earlier analysis of leader discussions and case leader facilitation of PD suggested that in Phase I we did not fully support leaders’ understanding of how learning goals for teachers differ from those for students. Nor did we focus on what facilitation toward a specific mathematics goal would entail (Elliott et al. 2009a). Our analysis suggests that leader discussions in Phase I were diffuse, uncovering potential reasons why leaders did not notice goals and facilitation. Phase II data show leader discussions were more focused on facilitation practices in relation to goals for teacher learning.

Across the Phase II seminar series, leaders’ talk became more explicit about the mathematical terrain within the videocases. In early seminars, leaders noticed more generally how the videocase facilitator directed teacher conversations by selecting which contributions to pursue. Midway in the series, leaders used the five practices as a lens for viewing videocases and noticed the videocase facilitator’s explicit rationale for connecting contributions. In the final seminar, leaders noticed the facilitator’s attempts to explore multiple representations to understand compensation methods of subtraction. While leaders were able to recognize that there was a mathematics goal as early as the first seminar, the mathematics was underspecified and not distinguished from content for students. Across the seminar series leaders developed their noticing related to articulating mathematical goals for teacher learning and imagining moves a facilitator might make to press on those goals. We posit that such noticing supports pedagogical reasoning about facilitation that will enable leaders to enact PD practices to build teachers’ SCK.

In their work with a select group of mathematics coaches, Jackson et al. (2015) found that while coaches were able to design experiences based on long-term goals for teachers, they were less adept at pressing on teachers’ thinking during PD to advance these goals. While we do not offer data in this article about leaders in-the-moment facilitation with teachers, we find it promising that leaders in our project were able to notice and imagine facilitation moves that would press on specific mathematics. We contend that productive noticing is a first step toward enacting new practices (Mason 2011; Sherin and van Es 2009).

Researchers (e.g., Borko et al. 2014; Jackson et al. 2015; Jaworski and Huang 2014) are just beginning to investigate what leaders of PD need to know and be able to do to advance teacher learning. This study contributes to this emerging knowledge base on facilitation by providing insights into leader learning and preparation. In the following section, we summarize our own learning and advance a set of design principles for preparing PD leaders. These design principles exist within a framework that acknowledges the importance of norms and practices for productive teacher discussion. Our intent is to explicate ways to further support leaders’ understanding of the SCK construct and the role of SCK in advancing teacher learning.

Design principles for leader PD

Our own understanding of preparing PD leaders has evolved across the design and analysis of this project. Based on our work with over seventy leaders in a variety of settings, we make the following related assertions. First, leaders need to identify mathematical learning goals for teachers, which are different than learning goals for K-12 students. The use of videocases in leader PD should help leaders identify the learning terrain for teachers as distinct from students. Second, if leaders can articulate mathematical learning goals for teachers, they are better positioned to notice and enact facilitation practices to orchestrate discussion and cultivate norms that support the attainment of those goals.

Given these assertions, we propose an initial set of design principles for professional development of mathematics leaders:

  1. 1.

    Centering leaders’ mathematical work on clear learning goals for teachers allows for differentiating teachers’ and students’ learning needs.

  2. 2.

    When tasks for leaders explicitly target SCK goals leaders are better able to identify the mathematical ideas important for teaching.

  3. 3.

    Purposeful facilitation of videocases that exemplify instances when mathematical goals for teachers are being pursued support leaders’ attention to the pedagogical and mathematical work of facilitating teacher learning.

Design principle #1: center leaders’ mathematical work on clear learning goals for teachers

Leader PD should provide examples of teacher learning goals and include explicit discussion of how those differ from student learning goals. We offer an example related to the subtraction task in Janice’s method to illustrate what we mean by distinguishing between student and teacher learning goals. A learning goal for students might be stated as: “Students are able to correctly solve a two-digit subtraction problem that requires regrouping, and model the solution on a number line.” A learning goal for teachers might be: “Teachers recognize which interpretations of subtraction are easier to model on a number line and are able to explain various compensation strategies used to solve subtraction problems.” The purpose for students to use different representations (here a number line) is to build their conceptual understanding of mathematical concepts such as place value and the operation of subtraction. The purpose for teachers is to support students in developing this understanding. This requires that teachers have facility with a wide range of methods that students might use as well as an understanding of the affordances and constraints of different definitions or meanings of subtraction in relation to these models and representations.

Our focus on specialized content knowledge for teaching has been particularly useful for articulating mathematical goals for teacher learning (Ball et al. 2008; Suzuka et al. 2009). In revising seminars for Phase II, we elaborated goals for both mathematical practices (e.g., making correspondences between visual models and symbolic representations, generalizing, justifying) and mathematical content (e.g., the meaning of operations, interpreting models for subtraction). The articulated mathematics goals provided a clear aim for leaders’ mathematical work and discussion. Because these were new constructs for leaders, we saw our Phase II leader group make progress on expressing the import of SCK. However, our data also reveal that leaders need support in understanding this purpose and, more importantly, in identifying SCK goals across content areas.

Design principle #2: design tasks for leaders that explicitly target SCK goals

Tasks for teachers in PD to advance teachers’ mathematical learning may not be the same as tasks given to students. Tasks should engage the specialized knowledge of mathematics unique to teaching. In selecting and modifying tasks for Phase II seminars, we considered how the tasks provided opportunities to unpack key mathematical ideas, encouraged multiple representations and connections across these representations, and required justification—ideas previously identified as characteristics of SCK tasks (see Suzuka et al. 2009).

In addition to tweaking student or teacher tasks to meet these criteria, we found that framing discussions with specific prompts tied directly to teacher learning goals led to productive SCK discussions. For example, rather than leaving it to chance that leaders would explore the difference model of subtraction or the affordances and constraints of number line representations in Janice’s method, we crafted discussion prompts with these goals in mind. As given in Table 3, the prompts moved from the general question “what connections do you notice among the explanations,” in Phase I, to the more specific, “how would you represent each explanation symbolically” and “what models of subtraction do they represent,” in Phase II.

Leaders need to know how to specify purposes for doing mathematics in ways that develop teachers’ SCK and identify tasks and discussion prompts that immerse teachers in SCK. As a result of our Phase II revisions, we have made significant progress in our own thinking about the type of work in which we want to engage leaders and in writing more specific prompts to get there.

Design principle #3: provide videocases (or other artifacts of practice) that exemplify instances when mathematical goals for teachers are being pursued and facilitate analysis of the videocase to make the work of the PD leader explicit

Mathematical tasks and videocases are valuable tools that can support leader learning by capturing the complexity of facilitator–teacher interactions, and allowing for in-depth reflection from multiple perspectives. To capitalize on learning opportunities, the choice of video and the ways in which it is facilitated matter (Brophy 2004; Seago 2004). Video used in leader PD that includes rich mathematical discussion (e.g., elaborating on definitions, meanings of operations or representational use) can advance leaders’ thinking around the mathematics teachers are learning.

As a field we lack robust images of PD that might support the development of SCK. Such work entails sharing different strategies not just for the sake of seeing multiple methods, but also for the purpose of interrogating these methods in relation to mathematics needed in teaching. For example, teachers might explore commonalities and differences in various models and meanings of operations or what particular representations make visible mathematically. Previous research on mathematics PD has found that this is not the typical way in which teachers engage in mathematics in PD (Hill and Ball 2004; Loveless et al. 2005; Wilson and Berne 1999).

Thus, we found ourselves critically evaluating the videocases we used in Phase I and being creative in how we engaged leaders in representations of PD practice in Phase II. One alternative in Phase II included showing shorter segments from the videocase and engaging leaders in discussion of potential next steps or questions a facilitator might pose to teachers given a particular learning goal. We also incorporated new video resources and written cases, from published PD materials and written by the research team, to highlight not only the specific mathematics but also how teachers might engage in the mathematics to develop SCK.

In addition to images of teachers engaging productively in mathematics, leaders also need to see the interactive work of a facilitator supporting teachers to take up mathematics central to advancing SCK. We posit that cases that illustrate the complex, highly relational facilitation that occurs when exploring the underlying meanings of operations, pressing for justifications based on generalized reasoning rather than steps in how a solutions is formed, or examining the limitations and affordances of various representations will provide leaders with new images of high-quality mathematics PD. Leader discussions of these cases would be guided by a purposeful set of prompts that focus on the work the facilitator does to pursue mathematical goals for teachers.

Conclusion

Mathematics leaders’ capacity to design and lead high-quality PD for teachers is critical to supporting teacher learning at scale (Borko et al. 2014; Jackson et al. 2015). This study was intended to fill the research gap on leader learning and preparation. Our research demonstrates how we made progress on honing leader noticing across our two-phase design. Initially, we put less emphasis on the preparation work and relied on the videocases themselves to orient leaders to facilitation moves for orchestrating productive mathematical discussion and cultivating sociomathematical norms that promote teacher learning. Now we see the initial mathematical preparation and identification of specific mathematical learning goals for teachers as more critical in developing leaders’ knowledge.

Policy documents offering recommendations for teacher professional development highlight the importance of continued research on preparing leaders with expertise in facilitating teacher learning (Desimone 2009; Marrongelle, et al. 2013). We offer design principles for leader PD that not only highlight the need for robust norms and facilitation practices, but also foreground principles for learning to facilitate teacher learning of specialized mathematics for teaching. We make note of the fact that videocases of teachers engaged in PD were the cornerstone of our leader development work. We anticipate that different models of PD for leaders (e.g., repeated lesson study cycles) might yield additional insights. Operating under design principles that attend to sociomathematical norms, orchestrating productive discussion and advancing SCK, future research might pursue how leader groups differentially participate in leader PD and take up these ideas to inform their facilitation of teacher PD. Such work can support refinements and additions to the design principles we have offered.