Introduction

Teaching mathematics for conceptual understanding is a fundamental goal of mathematics teacher education (National Council of Teachers of Mathematics [NCTM] 2000; National Research Council [NRC] 2001). Such teaching is complex (Hiebert et al. 1997; Putnam et al. 1992), and teachers may need a certain kind of knowledge to teach mathematics for conceptual understanding effectively (Ball et al. 2005a; Hiebert et al. 2007), including deep conceptual understanding of the mathematics (Ball et al. 2005b). However, having deep conceptual understanding may be insufficient knowledge for recognizing conceptual understanding of particular learning goals in children’s mathematical work. Teachers need to be able to assess whether their students are learning what is intended, and teacher educators need to provide experiences which help prospective teachers (PSTs) develop this ability. But what kinds of experiences should they provide? Are there certain contexts in which conceptual understanding alone is sufficient preparation for analyzing student understanding?

PSTs have attended to student thinking productively under certain conditions (Jacobs and Philipp 2004; Jansen and Spitzer 2009; Morris 2006; Philipp 2008). Jacobs and Philipp’s (2004) work demonstrated that teacher educators’ use of a questioning framework enhanced PSTs’ conversations about student work and focused their attention on children’s mathematical thinking and its role in instruction. Specifically, questions that (a) prepared teachers to understand children’s thinking, (b) encouraged teachers to deeply explore children’s thinking, and (c) helped teachers identify instructional moves to extend children’s thinking, proved to be valuable. Additionally, Morris’ (2006) work demonstrated that PSTs analyzed instruction with respect to student learning and used their analyses to make productive revisions to instruction. When PSTs analyzed a mathematics lesson with the belief that there was a problem (i.e., the children did not learn the mathematics), PSTs attended to critical elements of the lesson, including student thinking and mathematical content.

The goal of this study is twofold: to examine the role conceptual understanding (hereafter “content knowledge”Footnote 1) plays in PSTs’ ability to recognize children’s conceptual understanding of mathematics, and, when content knowledge proves insufficient, to examine the effects of an intervention aimed at supporting PSTs in recognizing evidence of children’s conceptual understanding of mathematics. Prior research demonstrated that PSTs benefited from activities in which they were asked to distinguish between student responses that did and did not provide relevant information about students’ understanding (Morris 2006). Further, PSTs often accepted a set of procedural steps as evidence of conceptual understanding (Spitzer et al. 2011). One conjecture from this latter work is that PSTs may have lacked sufficient content knowledge to distinguish between responses indicating procedural knowledge and those indicating conceptual understanding. This work also suggested that PSTs often attended to irrelevant evidence when making claims about student learning, for example citing teacher explanations as evidence of students’ learning (Morris 2006). Building on this work, this study examines the role content knowledge plays in PSTs’ ability to recognize evidence of children’s conceptual understanding. Further, an intervention was designed to include examples in which children used correct procedures and in which they included irrelevant evidence that could be mistaken for evidence of understanding.

Conceptual understanding and procedural knowledge

Before proceeding, it is important to provide a definition of conceptual understanding:

Knowledge that is rich in relationships. It can be thought of as a connected web of knowledge, a network in which the linking relationships are as prominent as the discrete pieces of information. Relationships pervade the individual facts and propositions so that all pieces of information are linked to some network. (Hiebert and Lefevre 1986, 3–4)

Conceptual understanding is often described in contrast to procedural knowledge, which can be defined as “a familiarity with the individual symbols of the system and with the syntactic conventions for acceptable configuration of symbols … [or] consist[ing] of rules or procedures for solving mathematical problems” (Hiebert and Lefevre 1986, pp. 7–8). For this study, procedural knowledge is considered specifically with respect to algorithms where knowledge of relationships is primarily sequential: a step in a procedure is connected to the next step.

In this study, children’s or PSTs’ responses that only describe the steps of a procedure are considered “calculational explanations” (Thompson et al. 1994), which are opaque with regard to the subject’s conceptual understanding. Part of the purpose of this study is to determine whether PSTs attribute conceptual understanding to children who provide such calculational explanations, which only show evidence of procedural knowledge.

Children’s or PSTs’ responses demonstrating conceptual understanding reflect a conceptual orientation toward mathematics (Thompson et al. 1994) such that their explanations are driven by “an image of a system of ideas and ways of thinking … focused on a rich conception of situations, ideas and relationships among ideas” (pp. 6–7, emphasis in original) and tend to go beyond descriptions of steps in a problem to include reasons for the steps. Further, children’s or PSTs’ responses demonstrating conceptual understanding may not refer to algorithmic steps at all but may instead directly describe mathematical concepts by connecting numeric symbols to the quantities represented by the symbols (e.g., “6/7” is 6 pieces where each piece is 1/7 of one whole).

Methods

Fifty-four PSTs from a university in the mid-Atlantic region of the United States volunteered to participate in this study. All of the students were enrolled in a 4-year undergraduate program for elementary school teacher education. PSTs’ mathematics preparation within this program consists of three mathematics content courses followed by one or two mathematics methods courses. Participants were recruited from the first of the three mathematics content courses.

The course

This course focused on developing PSTs’ mathematical understanding of key number and operation topics, in the context of whole numbers and decimals, typically developed with early grades children. This course was also designed to introduce PSTs to children’s learning of mathematics using video clips of children solving problems, at times asking PSTs to make conclusions about those children’s mathematical understanding.

Of relevance to this study, the first lesson of the course required PSTs to read Chapter 4 of Adding it Up (NRC 2001), which described five strands of mathematical proficiency: conceptual understanding, procedural fluency, strategic competence, adaptive reasoning, and productive disposition. As part of this lesson, PSTs watched two video clips of children who struggle with algorithms but demonstrate conceptual understanding while using manipulatives (Philipp and Cabral 2005). PSTs were asked how they might respond to the children as a teacher, with the goal of the subsequent discussion focused on articulating definitions of conceptual understanding, procedural knowledge, and adaptive reasoning. PSTs were also encouraged to note that having conceptual understanding of a mathematical concept does not imply that one has procedural knowledge, and vice versa. Besides this initial activity, the lesson plans for the course do not explicitly use these terms, nor is there any subsequent work engaging PSTs in recognizing evidence of conceptual understanding. Only the intervention tasks subsequently addressed this idea.

The intervention

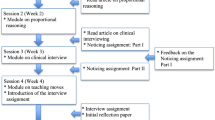
The intervention consisted of two components with in-class activities and homework assignments. For the first component, PSTs watched a first-grade lesson on place value for homework in the preparation for class (Annenberg Media 2007). In this video lesson, the teacher introduced children to the concept of place value with a place value mat (a box of one color on the left, labeled tens, and a box of another color on the right, labeled ones). The teacher led the class in activities in which they exchanged 10 ones for a ten, and students also worked at centers collecting groups of ten with various manipulatives. The teacher in the lesson did much of the initial explaining, raising the question of whether the children understood the connection between the numeric symbols and the amount of tens and ones or were following the procedure modeled for them by their teacher. Later in the lesson, numerous children offered their ideas, providing an opportunity to compare and contrast evidence of conceptual understanding. A primary goal of this initial activity was to support PSTs’ recognition of the kinds of evidence needed to make a claim that a child has conceptual understanding of a mathematical idea.

The following class day, PSTs were instructed to focus on two specific children in the video and to “record what these two children know and what evidence there is for that knowledge.” These two children were selected because, in each case, much of the meaning-making was done by the teacher as opposed to seeing evidence of the children’s mathematical understanding. Next, instructors asked PSTs to discuss their hypotheses about the children’s understanding in groups and reach a consensus about what each child understands and what evidence can support their claims. A whole class discussion followed, with instructors highlighting that good teacher explanations do not mean that students understand, and sometimes activities meant to give conceptual understanding can become proceduralized in practice. Then, PSTs analyzed the lesson again, focusing on evidence regarding the mathematical understanding of two different students. In each case, some evidence of conceptual understanding was demonstrated by the children, yet the children also followed the steps the teacher modeled, raising the question of whether the children were demonstrating conceptual understanding or procedural knowledge.

For the second component of the intervention, PSTs examined nine typical children’s solutions to the problem 63.7 + 49.8. These included a mixture of procedurally and conceptually based solutions with both correct and incorrect answers, correct and incorrect use of procedures, and some responses providing evidence of a child’s conceptual understanding of decimal addition. A sample of three response cards is provided in Table 1.

Table 1 Children’s responses to 63.7 + 49.8
Full size table

Prospective teachers’ examined the various children’s solutions and discussed what each child knew about the addition of decimal quantities. Next, PSTs sorted the children’s responses according to two categories of their choosing (e.g., correct vs. incorrect solution, common algorithm vs. nonstandard algorithm). In the subsequent class discussion, PSTs volunteered their criteria, shared the way they sorted children’s response cards, and presented a rationale for their sorting. Instructor comments during this time were focused on supporting PSTs in distinguishing between children’s procedural responses and those demonstrating conceptual understanding and whether a certain feature of a child’s response, like the use of appropriate vocabulary or a diagram, was sufficient evidence to suggest conceptual understanding. Finally, PSTs individually sorted the nine children’s solutions one additional time based on the criterion, “Which of the students do you think have a good understanding of rebundling when two numbers are added together?” PSTs were asked to explain their decision about whether to include a child’s response in this category using evidence from the response cards. PSTs discussed their responses in groups and in a whole class discussion and attempted to reach consensus on where to place children’s responses for this criterion.

The intervention was implemented over three class periods with all students enrolled in three sections of the course during weeks 10 and 11 of this 14-week course (which met twice per week). The second, third, and fourth authors on this paper were the instructors of these three sections. In order to maximize the fidelity of implementation of the intervention, these three course instructors and the first author met regularly to discuss the implementation, and all four members of the research team observed one another’s classrooms during the intervention. A fourth section of twenty PSTs served as a control group and did not participate in any aspect of this intervention.

Instruments

Two researcher-designed instruments across three content areas were used in this study. The first, administered prior to the intervention, aimed to elicit PSTs’ content knowledge and the second, a pre- and post-intervention instrument, aimed to examine PSTs’ ability to recognize evidence of children’s conceptual understanding of mathematics.

Content knowledge instrument

The content knowledge instrument (see Appendix 1) was designed around three specific mathematics tasks representing three different content areas: subtraction of decimals with rebundling (solve 63.3 − 29.5), comparison of fractions (circle the larger fraction, 5/6 or 6/7), and multiplication of fractions (solve 5/6 × 3/8). Subtraction of decimals was content-covered in the course, whereas multiplication and comparison of fractions were not. Mathematics problems that elementary school students would be expected to be able to solve were specifically selected. Follow-up questions were also included with each task (e.g., “Explain your thinking.”) in the hope that these additional prompts would support PSTs in either rationalizing procedural solutions or considering alternative ways to solve problems, which, in turn, might provide evidence of conceptual understanding. PSTs were also prompted to write story problems in some cases as this could illuminate their understanding of important mathematical concepts (Barlow and Drake 2008; English 1998; Luo 2009). While some story problems written to accompany a task may not provide evidence of PSTs’ content knowledge (e.g., a PST might write a story problem for decimal subtraction that provides evidence of their understanding of subtraction but not of their understanding of regrouping), together, these combinations of prompts could support eliciting PSTs’ mathematical content knowledge as they provide PSTs multiple opportunities to demonstrate their thinking.

Recognizing conceptual understanding instrument

The instrument examining PSTs’ ability to recognize evidence of children’s conceptual understanding provided PSTs with three distinct types of children’s responses for each content area (see Appendix 2): (a) one with evidence of conceptual understanding, (b) one with features commonly associated with conceptual understanding but with insufficient evidence of conceptual understanding (hereafter “responses with conceptual features”), and (c) one successfully using a standard procedure accompanied by a calculational explanation. The features referred to in (b) included particular “conceptual” vocabulary (such as “unbundle” and “rebundle” rather than “borrow” and “carry”) and diagrams, which were used throughout the course to illustrate concepts. Category (b) was used to see whether PSTs would equate vocabulary or diagram usage with conceptual understanding. Also, for each of these three sets of children’s responses, PSTs were asked to, “Compare and contrast the children’s responses to one another with respect to their understanding of ______.” Looking to comparison of fractions content as a model (see Appendix 2), Frank’s response demonstrates conceptual understanding, Darren’s response uses a conceptual feature (a diagram), but does not provide evidence of conceptual understanding of comparison of fractions, and Erin’s response demonstrates procedural knowledge but not conceptual understanding.

Interviews and focus groups

To examine PSTs’ evaluations of children’s mathematical understanding further, all PSTs were asked to participate in either individual interviews or focus group sessions. Of the 54 PSTs in the study, six PSTs (11%) participated in individual interviews and 17 PSTs (31%) participated in focus group sessions. The same questions were asked in each setting. Focus groups consisted of four to eight students, and the interviewer posed questions to the whole group. Focus group participants listened to one another’s responses and talked to one another during the sessions. The questions posed in each setting asked PSTs to describe what they looked for as evidence of student understanding and to consider what factors make it easier or harder to recognize student understanding.

Data analysis

Data for all measures were analyzed through a constant comparative process (Glaser and Strauss 1967) with the goal of identifying PSTs’ content knowledge and their characterizations of children’s mathematical understanding. For each instrument, at least two authors independently coded each participant’s response, compared analyses, and reached consensus for any disagreements.

Content knowledge instrument analysis

Prospective teachers’ responses to the content knowledge instrument were coded holistically. For each of the three main tasks (see Appendix 1), responses to the tasks and to all of the follow-up prompts were considered together for evidence of conceptual understanding. Then, the entire task was given one of four codes: good evidence, some evidence, or no evidence of conceptual understanding, or evidence of a misconception. If at least one response to the main task or a follow-up prompt revealed good evidence of conceptual understanding and there were no misconceptions evident, the entire task for that PST was coded as good evidence. If no responses were coded as being good evidence but at least one response was coded as having some evidence of conceptual understanding (and no evidence of a misconception), then the entire task was coded as some evidence, and so forth. In the following paragraphs, we provide examples of each of the four codes from the comparing fractions content area.

For comparing 5/6 and 6/7, a response demonstrating good evidence of the relative size of fractions demonstrated that equal-sized wholes were necessary to compare fractions and had a method for comparing the pieces within the wholes. For instance, the following was coded as good evidence of conceptual understanding: “6/7 is a larger fraction than 5/6 because with 6/7, the whole is broken into more pieces. Thus, each piece is smaller. If one takes 5 of the larger pieces it will be less than 6 of the smaller pieces, because the remaining piece left for 6/7 would be smaller.”

Some evidence of conceptual understanding meant that a portion of the concept was inadequately described. The PST response in Fig. 1 serves as an example. In this response, the PST’s explanation about the size of the pieces seems to demonstrate conceptual understanding, but then the PST comes to an erroneous conclusion about the relationship between 5/6 and 6/7. She claims that since sixths are bigger than sevenths, 5/6 is bigger than 6/7. So while some conceptual understanding is apparent, we did not consider this to be good evidence of conceptual understanding.

Fig. 1
figure 1

Example of some evidence of understanding the relative size of fractions

Full size image

A third possibility was that PSTs demonstrated no evidence of conceptual understanding. These responses included PSTs’ procedural responses that gave no indication of conceptual understanding. One PST stated, “Multiply both denominators by some number so that they equal each other. Then multiply each numerator with the number that you multiplied its denominator by. The larger numerator will be the larger fraction.” This PST did not provide any evidence of conceptual understanding when responding to the follow-up prompts, so for this task, the PST was assigned a code of no evidence of conceptual understanding.

Finally, the code evidence of a misconception was assigned when the PST demonstrated a clear misunderstanding of a mathematical concept, such as not using the same-sized whole when comparing the fractions (see Fig. 2).

Fig. 2
figure 2

Evidence of a PST misconception

Full size image

Recognizing conceptual understanding instrument analysis

To analyze PSTs’ ability to recognize children’s conceptual understanding of mathematics, the four authors independently coded each PST response for each of the three types of children’s responses (demonstrating conceptual understanding, demonstrating procedural knowledge, and responses with conceptual features) within each of the three content areas (subtraction of decimals, comparison of fractions, and multiplying fractions). Thus, each PST had nine responses coded (one for each cell in Appendix 2). Close attention was paid to PSTs’ descriptions of the children’s mathematical work and to whether PSTs’ descriptions recognized and/or distinguished between conceptual understanding and procedural knowledge. Codes were developed reflecting whether PSTs said that the child understood, did not understand, that there was not enough information to say, or that made no mention of the child’s understanding but instead referred to the child’s “explanation,” “method,” or “steps.” Most often, PSTs did not use the term conceptual understanding, and the codes were constructed to reflect the language of the PSTs. PST data were discarded if the pre- or post-instrument was left blank, or if the PST simply restated what the child did, making no evaluation of the child’s understanding or method.

Sometimes, inferences about what PSTs meant were required; efforts were made to err on the conservative side. For instance, when describing procedural responses, occasionally, PSTs would claim that the child “knows the procedure” or “understands the steps.” Was the PST saying that the child only knew the steps and did not have conceptual understanding? Or was this another way of saying that the child understands? To support the effect of the intervention, the former could have been accepted. Therefore, these kinds of statements were equated with statements that indicated clearly that the child understood the concept. This decision is also supported by Spitzer et al.’s (2011) finding that PSTs tended to attribute conceptual understanding to procedural solutions. Of course, PSTs used the word “understands” in a variety of ways. In order to get some sense of what they meant by “understands,” we looked at the type of responses they chose to label as providing evidence of understanding. For example, when PSTs said Erin “understands,” we could infer that they were conflating procedural and conceptual understanding, but if they were careful to say that Erin knows what to do but may not understand completely, we could infer they were differentiating between different kinds of knowledge.

Interview and focus group transcript analysis

Transcripts from individual interviews and focus groups were analyzed through a constant comparative process (Glaser and Strauss 1967) to identify recurring themes, including those related to PSTs’ characterizations of children’s mathematical understanding and what they considered sufficient evidence for their characterizations. The first author made initial conjectures from the existing data record, then continually revisited and revised those hypotheses in subsequent analyses. In the interest of brevity, the themes that emerged from this analysis are not reported within this paper. Instead, PSTs’ responses are used to inform the discussion.

Results

The results are presented in two primary sections. The first section presents findings related to the role content knowledge played in PSTs’ ability to recognize evidence of children’s conceptual understanding of mathematics. The second section presents findings related to the effect of the intervention on PSTs’ ability to analyze children’s responses with conceptual features and those demonstrating procedural knowledge.

PSTs’ content knowledge

Analysis of PSTs’ responses on the Content Knowledge Instrument shows that, for the subtraction of decimals content, all of the PSTs (100%) demonstrated some evidence of conceptual understanding. When asked to solve 63.3 − 29.5 and address follow-up prompts, most PSTs successfully used a standard procedure and demonstrated their knowledge of place value concepts in their explanations. Further, all PSTs’ were able to write a correct story problem for children. This result is not entirely surprising, given that this is content covered in the course.

With respect to PSTs’ knowledge of comparison of fractions concepts, most PSTs (≈60%) demonstrated some evidence of conceptual understanding, about one-fourth (≈27%) demonstrated evidence of a misconception, and about one-fifth (≈18%) showed no evidence of understanding or misunderstanding. Analysis of PSTs’ knowledge of multiplication of fractions concepts, however, showed that most PSTs (≈75%) demonstrated evidence of a misconception, particularly by writing inappropriate multiplication story problems for children. The other one-fourth of PSTs’ demonstrated some evidence of conceptual understanding of multiplication of fractions.

PST content knowledge and analysis of children’s work

Results from the Recognizing Conceptual Understanding Instrument pre-assessment are organized first by the three response types (demonstrating conceptual understanding, containing conceptual features, and demonstrating procedural knowledge). Within each of these categories, differences that arise between content areas are addressed.

Content knowledge and responses demonstrating conceptual understanding

For each child’s response that demonstrated conceptual understanding (“Frank,” “Alicia,” “Brad,” Appendix 2), a correct PST response was one that evaluated the child’s response as demonstrating conceptual understanding or as noting that there is not enough information. A response stating that the child does not understand, uses a confusing or poor method, or does not explain their thinking well, was considered an incorrect evaluation. Analysis of PSTs’ initial evaluations of children’s responses demonstrating conceptual understanding with respect to their content knowledge suggests that PSTs’ content knowledge did seem to support their analyses for the comparison of fractions but did not play a role in the multiplication of fractions content area. A claim cannot be substantiated for the subtraction of decimals content because there was too little variation in PSTs’ knowledge.

For the comparison of fractions content, content knowledge did support PSTs’ in recognizing evidence of children’s conceptual understanding (χ2 = 7.924, df = 2, p = 0.0190). Most PSTs that demonstrated some evidence of conceptual understanding of comparison of fractions (73%) appropriately labeled a conceptually sound child’s response as such (e.g., “Frank understands that 7/8 is larger than 6/7. … He does understand that 7/8 is closer to one whole than 6/7 is.”). Whereas most PSTs that demonstrated evidence of a misconception about comparison of fractions (80%) labeled a conceptually sound child’s response as representative of a lack of understanding. These PSTs’ argued, for example, “Frank sees that 1/7 is smaller than 1/6 but does not see that when it is 6/7 that it is still smaller than 5/6” (emphasis added).

It is not clear whether content knowledge supported PSTs’ analysis of children’s responses demonstrating conceptual understanding of subtraction of decimals. A chi-squared test is not possible as all PSTs demonstrated some evidence of content knowledge. It is worth noting that most PSTs (82%) correctly identified a child’s response demonstrating conceptual understanding as such.

For the multiplication of fractions content, however, content knowledge did not support PSTs in recognizing evidence of conceptual understanding in children’s responses (χ2 = 0.148, df = 1, p = 0.7007). While all of the PSTs that showed some evidence of conceptual understanding of multiplication of fractions appropriately labeled a child’s response demonstrating conceptual understanding of multiplication of fractions as such, almost all of the PSTs that demonstrated evidence of a misconception about multiplication of fractions (91%) also appropriately labeled the child’s response.

Content knowledge and responses with conceptual features

This section addresses the role of content knowledge in supporting PSTs’ analyses of children’s responses constructed with certain features commonly associated with conceptual understanding (e.g., diagram, vocabulary) but where the child’s response also did not demonstrate conceptual understanding (“Darren,” “Brad,” “Indigo,” Appendix 2). Analysis of PSTs’ pre-intervention evaluations of children’s responses with conceptual features suggests that PSTs’ content knowledge did seem to support their analyses for comparison of fractions but did not play a role in the multiplication of fractions content area. Again, a claim cannot be substantiated for the subtraction of decimals content but patterns are noted.

For the comparison of fractions content area, the child’s response included a feature often associated with conceptual understanding (a diagram), but the child also demonstrates a misconception (the child used different-sized wholes to compare the fractions). An appropriate PST evaluation needed to have some recognition of this misconception. Inappropriate evaluations indicated that the child understood the relative size of the two fractions. Results suggest that content knowledge supported PSTs’ in recognizing the misconception in the child’s response (χ2 = 8.809, df = 2, p = 0.0175). Of the PSTs that showed some evidence of understanding comparison of fractions, most (93%) described the child’s response exhibiting a misconception as evidence the child lacks understanding. PSTs wrote things like, “Darren doesn’t use much of his knowledge of fractions. He simply draws a picture and determines since 6 is greater than 5, then that must be the answer. He shows no understanding of what a fraction means.” However, for the PSTs’ that demonstrated evidence of a misconception about comparison of fractions, nearly half (46%) stated the child understood the mathematics.

For the subtraction of decimals content area, there was no misconception in the child’s solution. Instead, the conceptual feature was the use of “rebundling” language, which was used throughout the course. An appropriate evaluation was considered to be one which indicated that there was not enough evidence to say whether the child understood. While a chi-squared test cannot be used to ascertain significance, it is worth noting that about one-half of these PSTs characterized this child’s response inappropriately as demonstrating evidence the child understands (28%) or does not understand (19%).

For the multiplication of fractions content, the child’s solution again had a conceptual feature in that it described a diagram. In this case, it lacked essential details about the solution (why does the child draw a line through the boxes?). An appropriate response would indicate that more information would be needed to know whether the child understood. A chi-squared test (χ2 = 0.740, df = 2, p = 0.6906) reveals that content knowledge did not support PSTs’ in analyzing responses with conceptual features. Regardless of content knowledge, most of the PSTs evaluated the child’s response as demonstrating conceptual understanding (60%) or a lack of understanding (29%), while a few noted that more evidence was needed (11%).

Content knowledge and analysis of procedural responses

For PSTs’ initial analyses of responses demonstrating procedural knowledge, since evidence of conceptual understanding was not present, an appropriate response was considered to be one which indicated that more information would be needed to know whether the child understood. In all three content areas, data analysis suggests that content knowledge did not support PSTs’ in analyzing children’s procedural responses. In all three content areas, PSTs tended to consider responses demonstrating procedural knowledge as evidence of conceptual understanding.

In the subtraction of decimals content (“Gary,” Appendix 2), even though all PSTs’ exhibited some evidence of conceptual understanding of subtraction of decimals, about half (48%) characterized Gary’s response as evidence of conceptual understanding, saying things like, “Gary understood the need to rebundle so that he could subtract correctly and understood how to explain his work.” About one-fourth of PSTs (26%) suggested the response was evidence Gary did not have conceptual understanding. Only one-fourth of PSTs indicated that more information was needed to decide whether Gary had conceptual understanding of subtraction of decimals content. As before, a chi-squared test is not helpful here. More compelling evidence is that half of the PSTs demonstrating good content knowledge seemed to see Gary’s explanation as evidence of conceptual understanding.

Similarly, in the comparison of fractions content, most of the PSTs (79%) that demonstrated some evidence of conceptual understanding of comparison of fractions assessed the child’s response demonstrating procedural knowledge as evidence the child has conceptual understanding and most of the PSTs (77%) that demonstrated evidence of a misconception about comparison of fractions also assessed the response in this way. A chi-squared test (χ2 = 5.242, df = 4, p = 0.2634) reveals that content knowledge did not support PSTs’ in their analysis of children’s procedural responses for comparison of fractions. The same is true for the multiplication of fractions content (χ2 = 1.405, df = 2, p = 0.4954), where most of the PSTs (60%) that demonstrated some evidence of conceptual understanding of multiplication of fractions concepts stated that the procedural response was evidence the child understands the mathematics and most of the PSTs (68%) that demonstrated evidence of a misconception about multiplication of fractions also characterized procedural responses in this way.

Summary

Analysis of PSTs’ content knowledge shows that all PSTs’ demonstrated some evidence of conceptual understanding of subtraction of decimals, most demonstrated some evidence of conceptual understanding of comparison of fractions, but few demonstrated evidence of conceptual understanding of multiplication of fractions. Regardless of content knowledge, before the intervention in all three content areas, most PSTs recognized children’s responses demonstrating conceptual understanding as such and most characterized children’s procedural responses as evidence of conceptual understanding. Additionally, content knowledge seemed to support PSTs’ analyses of responses with conceptual features for the comparison of fractions content only—which was also the only content area where the child’s solution revealed a misconception.

Effect of intervention

This section examines the effect of an intervention on PSTs’ analyses of children’s responses with conceptual features and those with procedural solutions. For PSTs’ analyses of children’s responses demonstrating conceptual understanding, PSTs came in able to recognize children’s responses demonstrating conceptual understanding as such and maintained that ability after the intervention in all three content areas. The same is true for their analysis of the one response with clear evidence of a misconception. They had more trouble recognizing situations in which more evidence would be needed to say that a child understood, such as when only evidence of procedural knowledge is present or when conceptual features are included and no misconception is demonstrated. This section examines the pre- and post-intervention results to see whether the intervention had an effect on PSTs’ ability to analyze children’s responses with conceptual features and procedural solutions where more information would be needed to make claims about understanding. For this analysis, the following four categories based on changes on the Recognizing Evidence of Conceptual Understanding Instrument are used: growth, moderate growth, no effect, and intervention unsuccessful.

Growth was defined as PSTs moving away from associating conceptual understanding with responses having conceptual features or procedural solutions to noting that more evidence is needed to assess whether the child understands the mathematics. For example, one PST initially evaluated a procedural response as “Erin’s process of solving is more advanced, by finding a common denominator it shows her understanding of fractions.” After the intervention, the PST said, “Erin knows exactly what needs to be done to solve the problem. It is unclear if she knows why she has to do it, though.” This was considered growth because the PST took a more critical perspective regarding evidence of Erin’s understanding, indicating that it is “unclear” if Erin truly understands the procedure she carries out.

Moderate growth was characterized by PSTs moving away from suggesting that a response containing conceptual features or demonstrating procedural knowledge was evidence of conceptual understanding to suggest instead that these responses were evidence of a lack of understanding. For example, if a PST moved away from the same initial response presented above to stating, “Erin is showing her work using LCD … I don’t think she has a good understanding of fraction sizes because she just uses LCD to find the answer,” it was considered moderate growth. This was considered moderate growth because the intervention did indeed move students away from thinking responses with conceptual features or procedural explanations (i.e., no evidence of conceptual understanding) were evidence of conceptual understanding and supported PSTs in becoming more critical of these responses for conceptual learning goals, which might be considered an intermediate step in PSTs’ growth (see Spitzer et al. 2011).

If there was no change on PSTs’ appropriate evaluations of procedural responses (i.e., there is not enough information to tell), these data were considered representative of a ceiling effect and were coded no effect. Data labeled no effect were not used in the analysis of the effect of the intervention. If, however, there was no change in PSTs’ inaccurate evaluations of responses with conceptual features or procedural solutions, then the intervention was considered unsuccessful. The intervention was also considered unsuccessful if PSTs initially noted that there was not enough evidence to determine whether the child understood, only to move away from that idea.

The next section examines the effect of the intervention in each of the three content areas with respect to PSTs’ evaluations of children’s responses containing conceptual features, then with respect to responses demonstrating procedural knowledge.

Effect of intervention, responses with conceptual features by content area

In the subtraction of decimals (χ2 = 8.69, df = 2, p = 0.011) and multiplication of fractions (χ2 = 7.57, df = 2, p = 0.023) content areas, there was significant change in PSTs’ pre- and post-intervention analyses of children’s responses with conceptual features. Analysis of comparison of fractions is not considered here because the child’s response demonstrated a misconception.

For the analyses of responses with conceptual features in the subtraction of decimals content, the intervention supported 92% of the PSTs that initially characterized the child’s response with conceptual features as evidence of conceptual understanding to instead argue that it is evidence of a lack of understanding (moderate growth) or there is not enough information to decide (growth). However, the intervention was only somewhat effective in supporting PSTs in moving away from characterizing responses with conceptual features as evidencing a lack of understanding. Only 38% of PSTs with this initial response showed growth (moving to “not enough evidence”). After the intervention, across all responses, 61% of PSTs still characterized the child’s response as evidence of a lack of understanding.

In the same response category but moving to the multiplication of fractions content, we see the intervention was somewhat successful in that 32% of PSTs that initially characterized the child’s response with conceptual features as evidence of conceptual understanding moved to instead argue that it is evidence of lack of understanding (moderate growth) or there is not enough information to decide (growth) and 50% of the PSTs that initially characterized the child’s response with conceptual features as evidence of a lack of understanding moved to argue that there was not enough information to decide (growth). Although there is more room for growth in this content area, responses overall moved from 65% to 58% of PSTs saying that the child understands, showing a smaller positive effect.

One possible explanation for the difference with respect to PSTs’ post-intervention analyses of children’s responses with conceptual features is PSTs’ content knowledge. Recall that 100% of PSTs demonstrated some evidence of content knowledge of subtraction of decimals, whereas 75% of PSTs demonstrated evidence of a misconception about multiplication of fractions. A chi-squared test reveals a statistically significant difference (χ2 = 21.400, df = 2, p = 0.000) between PSTs’ post-intervention analyses of responses with conceptual features for the subtraction of decimals content and multiplication of fractions content.

Effect of intervention, procedural responses by content area

As with the previous response type, there was significant change in PSTs’ pre- and post-intervention analyses of children’s procedural responses for the subtraction of decimals (χ2 = 21.061, df = 2, p = 0.000) and multiplication of fractions (χ2 = 7.556, df = 2, p = 0.0229) content.

For the analyses of procedural responses in the comparison of fractions content area, there was not significant change in PSTs’ characterization of procedural responses. Most PSTs (69%) came in assessing the procedural response as evidence of conceptual understanding and all of these PSTs maintained that assessment after the intervention. In addition, five PSTs (10%) that initially felt the child’s response was evidence that the child did not have conceptual understanding and one PST (2%) that initially felt there was not enough evidence to tell whether the child understood, moved to stating that the child demonstrated conceptual understanding (intervention unsuccessful). Thus, after the intervention, 82% of PSTs characterized the procedural response of finding a common denominator to compare fractions as evidence of a child’s conceptual understanding of mathematics.

For the analyses of procedural responses in the subtraction of decimals content area, the intervention was successful in that almost all (95%) of the of the PSTs that initially said that the procedural response was evidence of the child’s conceptual understanding moved to instead note that it is evidence of a lack of understanding (moderate growth) or there is not enough information to decide (growth). On the other hand, with respect to characterizing procedural responses as evidence of a lack of understanding, 91% of the PSTs that initially characterized children’s thinking in this way maintained that assessment after the intervention (intervention unsuccessful). Overall, responses moved from 84% of PSTs saying the child understands to 5% saying the child understands—a positive effect. At the same time, within this growth, after the intervention, 66% of PSTs felt that procedural responses around subtractions of decimals suggested that the child lacked conceptual understanding of the mathematics.

For the analyses of procedural responses for multiplication of fractions, of the 75% of PSTs who initially described the procedural response as evidence of conceptual understanding, just 50% had the same response after the intervention (moderate growth and growth). Of those PSTs moving away from suggesting the procedural response was evidence of conceptual understanding, the majority of those (60%) moved to noting that there was not enough evidence to tell whether the child understands the mathematical idea.

Effect of intervention and control group comparison

Did the control group students have similar results, suggesting that the significant changes documented above are not due to the intervention, but due to the course? Given that the control group students were chosen by convenience sampling, it was important to ascertain whether this group differed from the students in the experimental group in significant ways. Analysis of the initial assessment of children’s responses by the control group against the initial assessment by the experimental group shows that no statistically significant difference exists between the two groups (see Appendix 3). Further, analysis of the control group’s assessment of responses with conceptual features and procedural responses in all three content areas showed no statistically significant gains from pre- to post-test for control group students. Thus, results presented above seem to be due to the intervention.

Summary of effect of intervention

Results suggest that the intervention was successful in moving PSTs away from evaluating responses with conceptual features and procedural solutions as evidence of conceptual understanding for the subtraction of decimals content. While notable numbers of PSTs also moved away from evaluating such responses as evidence of conceptual understanding for the multiplication of fractions content, many PSTs still saw these responses as evidence of conceptual understanding after the intervention. This was also true for the analyses of procedural responses in the comparison of fractions content. Further, in the areas where there was growth in PSTs’ analyses of children’s mathematical work, we also saw that PSTs tended to become critical of children’s responses, suggesting that responses with conceptual features or procedural solutions were evidence that the child did not understand the mathematics.

Discussion

This study contributes to the field’s understanding of the role content knowledge might play in PSTs’ ability to recognize evidence of children’s conceptual understanding of mathematics, particularly demonstrating that content knowledge is necessary, but not sufficient. Further, the results of this study illuminate some experiences which, coupled with a deep exploration of the mathematical content, show promise for supporting PSTs’ ability to recognize evidence of children’s conceptual understanding of mathematics.

Role of content knowledge

The results of this study suggest that content knowledge alone is insufficient in supporting PSTs’ ability to recognize evidence of children’s conceptual understanding of mathematics. Regardless of content knowledge, in all three content areas (before intervention), PSTs’ characterized children’s responses demonstrating conceptual understanding as such. When children’s responses demonstrated procedural knowledge or contained conceptual features, PSTs again characterized such responses as evidence of conceptual understanding.

One explanation for these results may be that content knowledge alone does not support PSTs in looking beyond surface features contained in children’s responses. Put differently, PSTs may have attended to irrelevant evidence (i.e., a feature), which is consistent with Morris’ (2006) findings. These features seem to include explanations of diagrams, explanations using “conceptual” language, and correct explanations of procedures (standard algorithms).

For the children’s responses demonstrating conceptual understanding, in the case where content knowledge was not shown to be a factor in PSTs’ analyses (multiplication of fractions) and where it is uncertain the role content knowledge might play (subtraction of decimals), the children’s responses contained conceptual features in addition to evidence the child has conceptual understanding. Alicia’s response regarding the multiplication of fractions describes a diagram and Hilary’s response regarding subtraction of decimals uses “rebundling” language (see Appendix 2). This raises questions about the extent to which PSTs attended to these conceptual features rather than evidence of conceptual understanding. It seems PSTs’ pre-intervention analyses of children’s responses align with previous research findings in that PSTs may have been attending to irrelevant evidence (Morris 2006) and that they tended to consider responses that demonstrated procedural knowledge as evidence of conceptual understanding (Spitzer et al. 2011).

Additionally, PSTs’ interview and focus group responses suggest they might be projecting their own understandings and experiences onto their analyses in ways that make the analysis of procedural responses particularly difficult (this was evident in five of six interviewees and all three focus groups). This was true both when PSTs were equating procedural responses with conceptual understanding or with a lack of conceptual understanding. For example, one PST reflected,

In my mind, they’re the same thing [good method and conceptual understanding] because fully understanding is also like my understanding … That’s the way I was taught, yeah … because I understand what she’s doing and I was taught the same way so when she does the lowest common denominator I’m like, oh, that’s what I did, too.

In this interview, the PST believes that she understands fully and equates her understanding with the understanding demonstrated by the child. In other cases, PSTs referenced their own experiences to describe why they evaluated a child’s procedural response as evidence the child does not understand. One PST stated, for example:

I think that my friends who did it themselves and understood it were able to understand it, whereas when I just copied what the teacher did and tried to memorize the exact steps that they did, a lot of times it wasn’t, like I really like had no idea what happened in that certain class.

This PST believes that a procedural response is evidence of a lack of understanding, because in her experience, those were the kinds of responses she gave when she had little conceptual understanding. These interviews suggest that previous experiences with mathematical procedures may make it difficult for PSTs to evaluate procedural solutions, especially in a class in which many of their notions about algorithms are being challenged.

As noted, results of this study suggest that content knowledge alone is insufficient to explain patterns in the results, and that PSTs likely need additional types of experiences to support the development of their ability to recognize evidence of children’s conceptual understanding of mathematics. Future research could examine the effects of an intervention that supports PSTs’ in reflection and discussion about their own experiences and that explicitly discusses the tendency of teachers to project their own understanding into their analyses of children’s thinking.

Yet content knowledge did seem to support PSTs’ analyses of children’s responses in two cases. Looking more closely at these cases can further inform how to support PSTs’ ability to recognize evidence of children’s conceptual understanding of mathematics. In the first case, PSTs’ content knowledge about comparison of fractions seemed to support them in analyzing the response demonstrating conceptual understanding (see “Frank” in Appendix 2). The PSTs that demonstrated content knowledge tended to recognize that this response demonstrated conceptual understanding, whereas the PSTs that demonstrated a misconception about comparison of fractions tended to argue that Frank’s response demonstrated evidence of a lack of understanding. One reason content knowledge might emerge as a factor here and not in PSTs’ analyses of children’s responses demonstrating conceptual understanding in the other content areas may be because PSTs with content knowledge draw on it in all cases, whereas PSTs that evidence misconceptions do not as easily recognize conceptual understanding (Also, in Frank’s case, the response does not include any surface features, or “clues” about conceptual understanding.). In all cases where PSTs analyzed children’s responses demonstrating conceptual understanding, PSTs with content knowledge recognized these responses as such. For PSTs that have demonstrated misconceptions about comparison of fractions, they instead argue that Frank lacks understanding and many noted that they were confused by Frank’s explanation. PSTs noted things like, “Frank’s response is unclear and confusing,” or “I don’t understand Frank’s reasoning.” This suggests both that if PSTs are provided with children’s responses that do not have conceptual features, they draw on their content knowledge to analyze children’s thinking and that activities that support PSTs in distinguishing between features of problems that do and do not provide evidence of children’s conceptual understanding may prove useful. This study’s intervention aimed to support PSTs in this way, and those results are considered in the next section.

In the second case, PSTs’ content knowledge of comparison of fractions seemed to support their ability to analyze a child’s response exhibiting a misconception. This seems similar to the result of Morris’s (2006) work with PSTs’ analyses of video-taped mathematics lessons with respect to children’s learning. Morris found that when PSTs were told a lesson was problematic, they more closely attended to what students were doing and were better able to analyze the lesson by developing claims about connections between teaching and learning. In this study, although PSTs were not told something was problematic about a child’s thinking, perhaps when a child’s response was perceived as different from a normal, expected response (one with a clear and complete explanation), PSTs were prompted to take a closer look at the child’s thinking. In turn, this closer look may have supported PSTs in drawing on their content knowledge to analyze children’s responses. This implies that in other instances not viewed as deviating from the norm, PSTs did not draw on their content knowledge. Perhaps this explains, in part, why content knowledge was not always related to PSTs’ analyses of children’s responses demonstrating conceptual understanding or procedural knowledge, as these were perceived as more “clear” by PSTs. Responses from two PSTs in their interviews shed light on this possibility for further investigation. One PST noted, “[this response] was all wording, none of it was numbers, so I really had to look more deep into it,” suggesting that only in certain cases might a response prompt deeper analysis. Another PST reflected that when determining whether a student understands a particular mathematical idea, she looks for whether “they make it very clear exactly what they were thinking and then they just end the problem … a student who just simply stated exactly what they were thinking, that’s when I understood exactly how they solved it and how they did it.”

Effect of intervention

Given that content knowledge is insufficient in supporting PSTs’ ability to recognize evidence of children’s conceptual understanding of mathematics, can an intervention improve this skill? These results suggest that the intervention supported PSTs in moving away from labeling children’s responses with conceptual features and those demonstrating procedural knowledge as evidence of conceptual understanding. This result was more pronounced in the subtraction of decimals content but was notable in the multiplication of fractions content area (and statistically significant in both), suggesting a relatively short intervention can produce significant improvement in PSTs’ analyses of children’s responses. When considering PSTs’ content knowledge in the light of these results, it is noticeable that the intervention was particularly effective in supporting PSTs’ analyses in the content aligned with the course, subtraction of decimals.

At the same time, a few caveats should be considered regarding claims that can be made about the effect of this intervention. First, though this intervention was successful in moving PSTs’ away from suggesting procedural responses or responses with conceptual features were evidence of conceptual understanding, many of these PSTs after the intervention instead argued that such responses were evidenced the child lacked understanding. This was true for both types of responses in the subtraction of decimals content area and for the procedural responses within the multiplication of fractions content area. This is still considered moderate growth in that PSTs’ moved away from thinking responses with conceptual features or procedural explanations (i.e., responses providing no evidence of conceptual understanding) were evidence of conceptual understanding and became more critical of these responses for conceptual learning goals, which might be considered an intermediate step in PSTs’ growth. This result mirrors the results of Spitzer et al. (2011) who found in their study of PSTs’ analysis of children’s mathematical thinking that PSTs displayed an “increased tendency to doubt students’ understanding rather than doubting the quality of evidence for making decisions” (p. 18).

Though this study has a similar result, one contribution this study makes with respect to this finding is that PSTs’ content knowledge does not seem to support them in avoiding these overly critical tendencies. More work is needed to consider how to further support PSTs’ in their analysis of children’s thinking. As mentioned previously, perhaps this overly critical stance is a reflection of PSTs’ drawing on their experiences and projecting those onto their analyses of children’s mathematical thinking. Research is needed that considers how best to support PSTs’ reflection and discussion about their experiences and the role those play in their analyses of children’s mathematical thinking. This research might also include a greater number of task responses for children to demonstrate that across multiple pieces of evidence, (a) a child has procedural knowledge and conceptual understanding, (b) a child has procedural knowledge but seems to lack conceptual understanding, and (c) a child has procedural knowledge but there is no information about conceptual understanding. Perhaps having these specific, different responses will support PSTs in moving away from assuming it will be like their own situation, and it may support PSTs in recognizing that procedural responses may reflect conceptual understanding or lack of understanding, or neither.

A second caveat specifically relates to PSTs’ improved the ability to analyze children’s responses containing conceptual features. In the multiplication of fractions content area, while the intervention supported many PSTs in moving away from considering such responses as evidence of conceptual understanding, after the intervention, 58% of PSTs still viewed Brad’s response (see Appendix 2) describing the use of a diagram but not containing sufficient evidence of conceptual understanding as evidence of conceptual understanding. This was not the case for PSTs’ analyses of responses with conceptual features in the subtraction of decimals content (as just described, PSTs after the intervention characterized these responses as evidence of a lack of understanding). One reason why the intervention may have been less successful in supporting PSTs’ analyses of children’s responses with conceptual features in the multiplication of fractions content area may have been due to PSTs’ content knowledge of multiplication of fractions. A statistically significant difference exists between PSTs’ analyses of responses with conceptual features in the subtraction of decimals content and multiplication of fractions content (χ2 = 21.4, df = 2, p = 0.000) and 100% of PSTs demonstrated some evidence of conceptual understanding of subtraction of decimals, while 75% of PSTs demonstrated evidence of a misconception about multiplication of fractions. When examining the children’s responses, perhaps PSTs’ knowledge of subtraction of decimals allowed them to “see through” the conceptual features of the child’s explanation and recognize the lack of evidence of conceptual understanding (i.e., the “rebundling” language did not adequately describe the relationship between the places). Perhaps content knowledge about fraction multiplication would have similarly supported the PSTs in seeing past the conceptual feature in the child’s response. It is important to note that subtraction with decimals was a focus of the course and was much closer to the content covered in the intervention, while multiplication of fractions was not discussed during the course. Thus, while content knowledge alone cannot account for PSTs’ ability to evaluate children’s responses with conceptual features, it seems that content knowledge does play an important role.

A third caveat specifically relates to PSTs’ improved ability in analyzing children’s responses, demonstrating procedural knowledge in that the intervention was not successful for the comparison of fractions content area. Though most PSTs demonstrated some evidence of conceptual understanding of comparison of fractions, after the intervention, they still considered the procedural response of finding a common denominator to compare fractions evidence of conceptual understanding of mathematics. This was not the case in their analyses of procedural responses in the subtraction of decimals or multiplication of fractions content areas. One possibility for this result may be related to the question children were asked to respond to. A child’s response “comparing” two fractions may require a higher level of cognitive demand as opposed to a question asking a child to compute (i.e., subtract or multiply). A procedural response for a more complicated mathematical task, comparing, might suggest a level of existing conceptual understanding. A more appropriate, comparable task with respect to level of cognitive demand may have been to show a child’s procedure for finding an equivalent fraction. Future research should investigate how the level of cognitive demand of tasks relates to PSTs’ ability to analyze responses to those tasks.

Finally, it is important to point out that since the post-intervention instruments were completed immediately following the intervention, there may be an immediacy impact influencing the results. While a delayed post-test was administered 4 months after the course ended in an attempt to determine whether the effects of the intervention were retained long term, only 25% of the sample participated (n = 14), making the numbers too small to warrant claims. There were some promising trends within these data in that at least half of the PSTs provided desired analyses of children’s conceptual understanding of mathematics for responses containing conceptual features or procedural explanations in all three content areas on the delayed post-test, but more research is needed to examine the long-term effect of this intervention.

Conclusion

This study suggests that content knowledge is necessary but insufficient in supporting PSTs’ ability to recognize evidence of children’s conceptual understanding of mathematics. Deep explorations of mathematical concepts should be supplemented with experiences evaluating children’s mathematical thinking, particularly using examples that highlight the differences between evidence of procedural knowledge and evidence of conceptual understanding. These interventions, even if relatively short, may support PSTs in moving away from attributing conceptual understanding to procedural responses or those containing conceptual features but no evidence of conceptual understanding. While the intervention did prove significant, the fact that even after the intervention, many PSTs considered procedural responses or those containing conceptual features as evidence of conceptual understanding shows room for further growth.

These results also suggest that teacher education programs should engage PSTs in such analyses early on, perhaps simultaneously with their content knowledge development. Mathematics teacher education programs need not be structured such that PSTs’ must develop some pre-requisite amount of content knowledge before engaging in analyzing children’s understanding of mathematics.

Evaluating student understanding is an essential skill for teaching with which PSTs need experience. Learning to tell the difference between evidence of conceptual understanding and procedural knowledge and between features that provide evidence of conceptual understanding and those that do not are particularly persistent challenges, in no small part because of PSTs’ own experiences as learners of mathematics and their subsequent beliefs about what it means to know mathematics. This paper serves to reveal the challenge and complexity of this work and acknowledges that while the intervention constitutes a step toward building a knowledge base for teacher education, more refining is necessary.