How do mathematics teacher educators go about designing good mathematical tasks? In order to address this question, it would also be prudent to address what is meant by ‘good’ tasks. This, in turn, requires us to acknowledge that, within teacher education, mathematical tasks are used to achieve a variety of diverse goals. As teacher educators we have the dual responsibility of preparing mathematics teachers, both mathematically and pedagogically. In this paper, we first explore the rich and varied ways in which mathematical tasks can, and are, used to fulfil this dual responsibility. We then focus on the way tasks can be designed (and refined) for the purposes of promoting mathematical understanding. This process is then exemplified through the tale of one task that has been developed (and is still being developed) for this purpose.

Using mathematical tasks

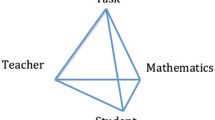
The use of mathematical tasks within mathematics teacher education can serve many purposes. As teacher educators, we use tasks to access mathematical content as well as to highlight and exemplify issues pertaining to mathematical pedagogy. These goals are not attained ex nihilo, however. As educators, we guide the attainment of these goals through the skilful crafting of tasks as well as through the skilful use of these tasks within our classrooms. That is, we use our knowledge of mathematics and pedagogy to produce understanding of mathematics and pedagogy within our prospective teachers. This creates a complex environment in which the goals of our practice take on the form of our practice. This complexity can be unravelled, somewhat, by disaggregating our knowledge of mathematics and use of pedagogy from the mathematical and pedagogical understandings we wish to instil within our students. Such a disaggregation of the mathematics from the pedagogy allows us to examine our use of mathematical tasks in teacher education from a number of different perspectives – highlighted in the 2 × 2 array presented in Figure 1. The content of the four cells can be read as the “The use of x to promote understanding of Y ”.

Fig. 1
figure 1

 

Full size image

mM: The use of mathematics to promote understanding of Mathematics

According to Schoenfeld (1982), one of the characteristics of a good problem is that it should serve as an introduction to important mathematical ideas. By definition, any use of mathematical tasks should access some mathematical idea. Somewhat more challenging is the use of mathematical tasks to access specific mathematical ideas (or as Schoenfeld states – important ideas). Such a use requires a deep and diverse understanding of the mathematics that is embedded within the task – we refer to this knowledge as task knowledge (TK).

pM: The use of pedagogy to promote understanding of Mathematics

However, having a good mathematical task and good task knowledge may not be enough. Using mathematical tasks to access mathematical concepts may also require the skilful orchestration of classroom dynamics. Similar to Schulman’s (1986) ideas regarding pedagogical content knowledge (PCK), pedagogical task knowledge (PTK) is imperative here. We need not only to be aware of the mathematics embedded within the task (TK), but must also be able to liberate this mathematics from the task. As such, teachers must have an in-depth understanding of the mathematical knowledge of their students, as individuals and as a collective. Further, they need an understanding of how to mobilize this knowledge for their students’ learning.

mP: The use of mathematics to promote understanding of Pedagogy

Mathematical tasks (as already mentioned) can be, and are, also used to access issues pertaining to the pedagogy of mathematics (Ball, 1996, 1988; Feiman-Nemser & Featherstone, 1992; Fosnot, 1989; Mosenthal & Ball, 1992). As elaborated upon in the introductory paper in this SI, mathematical tasks provide a context within which to explore issues such as: the nature of mathematics, assessment, constructivism, social constructivism, group work, and so on. Knowing the limitation of a task in this regard is imperative. So too is knowledge of how the task will ‘move’ within a classroom context. For example, a task that naturally causes students to retreat into their own thoughts is not a good task for modeling the dynamics of group work.

pP: The use of pedagogy to promote understanding of Pedagogy

However, simply being aware of the pedagogical limitations and affordances of a given mathematical task is, again, not enough. As teacher educators we must be able to orchestrate the emergence of the affordances from within the tasks. In particular, this will require knowledge of the embedded pedagogical affordances within the context of the task, as well as an ability to liberate and mobilize these affordances within the dynamic context of the classroom.

Having an explicit understanding of how and why mathematical tasks are used in teacher education gives us insight into what qualities a ‘good’ task must have. However, it does not automatically provide us with the ability to design ‘good’ tasks. Although ‘good’ tasks are inseparable from their intended use and the intended goals, they are also inseparable from the context (the milieu) in which they are used. As such, the designing of ‘good’ tasks requires an interface between the theoretical and the practical, between the intended and the actual, between the task and the student. In what follows we present such a dynamic interface in the form of a recursive process, used to design ‘good’ mathematical tasks. This process is constructed on the ideas presented in the aforementioned usage-goal framework.

Designing ‘good’ mathematical tasks

For us, the process of designing mathematical tasks is a recursive process that applies as well to the creation of entirely new tasks as it does to the adaptation (or refinement) of already existing tasks. This recursive process consists of four stages: predictive analysis, trial, reflective analysis, and adjustment.

Predictive analysis is what is done in the absence of the experience of using a new (or newly adjusted) task within a teacher education context. In this phase, our personal experiences with solving the task as well as our experiences using similar tasks with preservice teachers aids us in predicting the affordances that the task may access. These predictions are imperative because they not only inform us of the possible mathematical and pedagogical affordances but also how best to liberate these affordances during a trial period within a classroom context. After the trial the task is reflectively analysed for the mathematical and pedagogical affordances that the task, as designed and implemented, actually accesses. This is an important phase within the recursive process because this is when we may see either new affordances or realize the inaccessibility of the predicted affordances. Either one of these cases will require a rethinking of the tasks (mM/mP) and/or its implementation (pM/pP). This rethinking is done within the adjustment phase and the whole process starts over. After each iteration of this recursive process our knowledge of the affordances of the task are expanded and refined, as is our understanding of how best to liberate these affordances.

The initial iteration of this recursive process is worth discussing. What is often the case is that our own approach to the task initially impedes our ability to see different interpretations and solutions. The first trial phase of the process is very useful in this regard. It not only allows us to see a great variety of interpretations and solutions, but also helps us to see to what extend our own methods are accessible to our audience. With this new information in hand we have to decide which affordances to pursue – our initial predicted ones and/or the newly revealed ones. In either case, an adjustment to the task and/or the delivery of the task is often necessary.

The tale to be told

In this section we examine more closely the aforementioned recursive process of predictive analysis, trial, reflective analysis, and adjustment used in designing ‘good’ tasks. We do this using narrative to tell the stories of a single task called the Pentomino Problem. Given the space limitations we focus on the design aimed at accessing mathematical affordances, and mention pedagogical affordances only briefly. The Pentomino Problem is a task that has gone through many cycles of the recursive process and, although not yet complete, the task has reached a point where it can be described as ‘good’. The story of this task comes from its use over several years within a number of different sections of an elementary mathematics method course, each section enrolling between 25 and 40 students. Each iteration involved a different group of students enrolled in a different section of the course. In each iteration students had about 8 weeks to complete the task outside of class time. This particular task has been used both in practice and in research to explore issues pertaining to the belief structures of pre-service teachers with respect to the nature of mathematics and what it means to learn and teach mathematics (Liljedahl, 2007), the creative process of problem solving (Liljedahl, 2005), and the elementary number theory concepts embedded in the task (Liljedahl, 2006).

Iteration I

The initial version of the Pentomino Problem can be seen in Figure 2.

Fig. 2
figure 2

 

Full size image

The initial mathematical analysis of this task produced an elegant solution that combined a number of concepts from elementary number theory, decimal representation of numbers, and modulo arithmetic. Consider a pentomino placed somewhere on the hundreds chart. Now consider the cell within this pentomino with the smallest value (this will be the uppermost left cell in the pentomino). If this is given the value of x then the four remaining cells can be expressed as having the values x + a 1 , x + a 2 , x + a 3 , and x + a 4 , where a i represents the numerical distance from x (a i  > 0). When considering the remainder in division by 5 of the sum of these five values (5x + a 1  + a 2  + a 3  + a 4 ) then x is quickly seen to be irrelevant. That is, the position of the pentomino does not change the remainder. Further, if a i is decomposed into its vertical (v i ) and horizontal (h i ) displacement from x (a i  = 10v i + h i ) then it becomes apparent that the vertical displacements of each of the remaining four cells do not contribute to the remainder in division by 5. What does contribute to the remainder, however, are the horizontal displacements. That is, the remainder will be the sum of h 1 , h 2 , h 3 , and h 4 modulo 5.

Given that this task was to be used with a group of preservice elementary school teachers with limited mathematical experiences, it was predicted that the aforementioned concepts pertaining to elementary number theory and to modulo arithmetic would emerge naturally but without formal language. As such, this task was seen as a way of exposing the students to specific mathematical concepts through having them work on a mathematical task (mM). However, what happened was quite different from what was predicted.

The students were given the task as shown in Figure 2 and asked to submit individual solutions. The most common solution to the task was a table that displayed each pentomino in each of its orientationsFootnote 1 along with its remainder. The efficiency of these tables relied on the fact that position doesn’t matter. However, this fact was arrived at through observation rather than through the predicted analysis. This is nicely summarized in Rebecca’s comments:

Right away we figured out that the position doesn’t matter. This was a huge relief to us because the problem suddenly went from something that seemed completely undoable to something that we could manage.

Iteration II

Clearly adjustments to the task were necessary. The students’ heavy reliance on observation in the first trial was seen both as a weakness and strength – a weakness because it seemed to prevent them from seeing the mathematics that underpinned their observations and as a strength because it allowed them to recognize some of the important patterns in the task. As such, it was decided that the task needed refinement. In particular, the sentence “Look for, and explain , patterns that will help you to solve this problem” was added to the task instructions. This can be seen as a mathematical refinement to the task (mM), as the requirement to explain invites students to engage more thoroughly with the embedded mathematical content.

The addition had both the predicted result as well as an unpredicted result. The predicted result was that the students continued to construct tables, but this time they began to access the mathematics that underpinned some of the observations that they were making. This is exemplified in Dave’s comments:

We realized right away that the remainder was the same no matter where we put the shape. It took a lot longer to figure out why this was so. It wasn’t until we got a hint from the instructor that we started thinking about moving the shape just slightly. If we take a shape, say the L, and we put it on the chart so that it covers the 25, 35, 45, 46, and 47 then the sum will be 198. If we now move the L one square to the right then the numbers that are covered will be 26, 36, 46, 47, and 48. We just increased each of the numbers by 1. So, the new total is now 203, 5 more than it was before. But this doesn’t matter, because when we divide by 5 we still have a remainder of 3. Likewise, if we move the L down then the numbers that are now covered will be 35, 45, 55, 56, and 57. Basically, we increased each of the numbers by 10, for a total of 50. Adding 50 to a number doesn’t change the remainder because 5 goes into 50.

The unpredicted result was that, like Dave, the students were extending their observations with mathematical explanations. Dave’s observations were typical of the students in this trial in that he saw the pentomino shapes holistically, as opposed to being comprised of individual cells each of which contributed to the remainder. As a result, he based his mathematical explanation on how the sum of the five cells changed with position and along with it, how the remainder changed (or didn’t change).

Other unpredicted results in this trial were frequent observations of patterns pertaining to symmetry and ‘balance’. That is, the students observed that even those shapes that are symmetrical about a vertical axis (c.f. ) have no remainder, and those shapes that are only ‘equally weighted’ or ‘balanced’ on both sides of a vertical axis (c.f. ) also have no remainder. Both of these observations are seen in the words of Veronica:

When we looked at the pentominoes that had no remainder the first thing we noticed was that from the midpoint of the shape there was always an equal number of blocks on each side. Sometimes the shapes were symmetrical like the +, the U and the T. Other times the shapes were not symmetrical like the Z. We decided that all of these shapes were somehow balanced and the blocks must cancel each other out and make a remainder of zero.

Although patterns were observed, the reasons as to why these patterns emerge were not well explained. As mentioned above, we attribute this lack of explanation to the students’ holistic treatment of the pentominoes, which allows them to see patterns but does not easily allow them to explain the patterns.

Iteration III

Given the holistic treatment of the pentominoes in the previous iteration it was decided that somehow the students needed to get away from using the tables. As such, both the task itself and the implementation were adjusted. The task was modified very slightly by not providing the total number of different pentominoes. This change was made as part of the move from having the students working on the tasks individually to having them work on the task in groups of three to five students. This was further facilitated through an introductory activity in which the students, working in groups, were asked to determine exactly how many pentomino shapes there were. The second adjustment was to replace the request to “Look for, and explain , patterns that will help you to solve this problem” with a request to find the remainder quickly. This was made in order to get the students past the relatively inelegant solution that relied on a table. This emphasis on speed was further accentuated through repeated demonstrations by the instructor of almost instantaneous calculations of remainders of random pentominoes placed in random orientations and positions on the hundreds chart. These changes in general and the changes in implementation in particular can be seen as a use of pedagogy to access the mathematics embedded within the task (pM).

The task, in its new form, was used with a new population of preservice elementary school teachers. The changes to both the task and the implementation of the task had the desired effect. The reliance on the table seen in the first two iterations, although not eliminated, did not become the terminal point of the solution – it was deemed by the groups not to be quick enough. In fact, the emphasis on quickly along with the aforementioned demonstration of quickly had a profound effect on the students’ efforts on the problem. There was a pervasive sense that regardless of the speed of their current solution, there was always a quicker solution just over the horizon. This provided impetus to continue looking for more elegant solutions, and in turn led to the observations of many more unpredicted properties and, in turn, to the use of several unpredicted strategies.

Although the position does not matter, orientation does. The observation that symmetrical (c.f. ) and balanced (c.f. ) pentominoes have no remainder was accompanied by observations that reflection and 1800 rotation of pentominoes produces fives-compliment remainders (c.f. has r = 3 and has r = 2) and that remainders of pentominoes can be seen both as excesses and deficits (c.f. has r = 2 and r = −3). Again, these observations were either not explained at all or were not well explained. And again, this can be attributed to the holistic treatment of the pentominoes. However, also emerging from this group of students’ work was the observation that the remainder of a sum can be calculated by considering how each addend contributes to the remainder. This observation was seen in three different strategies, all of which involved the renumbering of the hundreds chart, as shown in Figure 3.

Fig. 3
figure 3

(a) Considering the Ones Digit Only (b) Considering the Remainders (c) Considering the Deficit Remainders

Full size image

All the groups recognized that the tens digit of each cell did not contribute to the remainder. This was well explained as “adding 10’s doesn’t change the remainder when dividing by 5.” As a result, many groups chose to renumber the hundreds chart using only the ones digit (see Figure 3a). This renumbering was often accompanied by a placement of the pentominoes in the left most columns (since position does not matter). A more sophisticated observation was the recognition that the remainder in division of a sum by 5 can be found from the sum of the remainders of the individual addends. This resulted in a renumbering of the chart using remainders of each cell (see Figure 3b). This renumbering was again accompanied by the strategic placement of pentominoes in the left most columns. Finally, some students combined the previous renumbering of the grid with their understanding of remainder as possibly being deficit (i.e. a remainder of 3 is the same as a deficit of 2). This resulted in a renumbering of the chart as seen in Figure 3c and was again accompanied by the strategic placement of pentominoes. The groups who came to the solution of renumbering the chart as in figure 3c had no difficulties explaining their observations pertaining to symmetry, balance, and reflective and rotational complements. This is nicely demonstrated in Angela’s comments:

We noticed in the remainder zero group that there are always the same number of squares on the left as on the right. We now see that these cancel each other out because the ones on the right have a positive remainder and the ones on the left have a negative remainder.

Iteration IV

The observation that the remainder in division of a sum can be found from the sum of the remainders of the individual addends is an important mathematical concept that, although present in the previous iteration, we felt needed – as a pedagogical consequence of their work – to become more common among the students. As such, the task was again modified in its delivery. In this iteration it was decided to allocate some time for in-class interaction within the 8-weeks period of students’ work on the task outside the class. In particular, the students were given square tiles to use while working on the task in class. This was accompanied by a request to make a pentomino with remainder zero first, and then using this pentomino as a base move only one tile to produce a new pentomino, and predict its remainder. This process was then repeated and complexities added. This pedagogical adjustment to the task was done in order to facilitate the liberation of the pentominoes from the hundreds chart and to aid the students in seeing how each individual cell may contribute to the remainder of the pentomino as a whole. Again, this adjustment to the task had predicted and unpredicted results.

The predicted result was that the groups uniformly developed a strategy for dynamically calculating the remainder of any pentomino. This is exemplified in Colleen’s solution:

figure h

Gary suggested that we start with the I, which we know has a remainder of zero. Then we give each step away from our starting position a value of 1 or –1 depending on which direction it moves. So, to get the remainder for the stairway we move one block to the left (−1) and two blocks to the right (+2). So, the remainder will be +1.

The unpredicted result was that many of the groups explained this strategy in terms of changes to the dividend.

There was also uniformity in the evolution of solution strategies in this iteration. These solution strategies are summarized in a flowchart in Figure 4, which was constructed to show both the strategies that emerged for each group as well as the order that the strategies emerged. That is, each group proceeded through the solution strategies from top to bottom with the possible omission of strategy two and/or four. For more details on this flowchart and/or the strategies that emerged from this task see Liljedahl (2005).

Fig. 4
figure 4

Flowchart of the Evolution of Strategies

Full size image

Pedagogical affordances

Although the aforementioned exemplification of the task design process focused solely on the mathematical affordances – mM and pM – that have been sought, and sometimes attained, that is not to say that the Pentomino Problem has been used only for this purpose. From the very beginning this task was also used for the pedagogical affordances it offered. In the early iterations the task was used as a way of providing the students with experiences that were, for many, absent from their mathematical biographies – experiences with exploring mathematics and mathematical relationships, working on one task for an extended period of time, perseverance, and discovery. With subsequent iterations the task has become a context through which to examine general mathematical and pedagogical issues around group work, journaling, assessment, and what it means to teach and learn mathematics. In some cases these affordances emerge out of the students’ engagement with the task (c.f. exploration, discovery, perseverance). In other cases the affordances emerge out of the administering of the task, including task presentation and debrief (c.f. group work, journaling, assessment). As such, these affordances, and the way they are liberated, fit respectively into the mP and pP categories of the usage-goal framework.

With both mathematical and pedagogical affordances, there are more adjustments to be made and more affordances to be attained. Considering specific mathematical aspects, we are designing prompts and variations that will support further engagement with modular arithmetic and encourage the use of standard algebraic notation as a tool for explaining ideas or proving assertions. Our pedagogical goals are far-reaching in that we wish to influence preservice teachers’ understanding of what it means to teach and learn mathematics. The Pentomino Problem is just a tale of one task in this journey.

Conclusion

As teacher educators we use mathematical tasks all the time, for a variety of goals. While agreeing with the distinction drawn by Christiansen & Walther (1986, see Introductory paper) between task and activity, the task-related activity which takes place is highly dependent on how the task is presented, on teacher-learner interactions during the activity, and on how the work is debriefed. The usage-goal framework presented in the initial section of this paper gives us a way to think more explicitly about how and why we are using these mathematical tasks with our students. The framework also provides the foundation upon which to design a ‘good’ mathematical task and how to refine the design to make a good task even better.

In this paper we examined the recursive process of designing tasks that not only speaks to what it means for a task to be good (vis-à-vis the usage-goal framework), but also what sorts of explicit attention to the process is necessary in order to construct tasks from our predicted and reflective experiences in using mathematics tasks with preservice teachers. As we enter into this recursive process, we become attuned not only to the mathematical or pedagogical affordances that are contained within a task, but also to how best to liberate those affordances. That is, with each iteration of the design process our task knowledge (TK) becomes simultaneously more diverse and more refined. Similarly, each experience with implementing the task gives us greater pedagogical task knowledge (PTK). As such, the “goodness” of the task is determined by the affordances embedded and liberated in the task-activity, activity that is enriched by our TK and PTK.