Exploration of structural, optical, dielectric properties and curve fittings of Yb³⁺-substituted β-type hexagonal ferrites

Abstract

The rare-earth element Yb³⁺-substituted β-ferrites KFe_11−xYb_xO₁₇ with composition (x = 0, 0.02, 0.06 and 0.1) have been synthesized by sol–gel auto combustion method and sintered at 950 °C. X-ray diffraction (XRD) analysis divulged the formation of single phase β-hexagonal ferrites structure for the whole series. The crystallite size varied in the range of 26–43 nm for all samples. FTIR spectra showed absorption bands at different wave numbers which also confirmed the single phase of the samples. The samples had high dielectric constant, dielectric loss, and tangent loss values at lower frequencies while these values declined with increase in frequency. This dielectric behavior of the samples had been explained on the basis of Maxwell–Wagner and Koop’s model. The dielectric constant results were fitted theoretically by using Debye function which indicated the involvement of more than one ion in dielectric relaxation process. The AC conductivity increased with the increase of frequency and the nonlinear fitting of AC conductivity was obtained through Jonscher’s power law that followed conduction model exactly. The semicircle of cole–cole plots adumbrated the contribution of both grains and grain boundaries to the resistive and capacitive behavior of the material.

1 Introduction

Hexagonal ferrites are considered as fundamental materials owing to their various technological applications in stealth technology, isolators, filters, sensors and transformers etc.[1]. Various studies on hexagonal ferrites exhibited many properties due to high saturation magnetization, low/high coercivity, high electrical resistivity as well as good dielectric losses, high permittivity and permeability [2]. Hexagonal ferrites are categorized into R, M, W, U, X, Y, Z, and β type on the basis of their structural parameters and chemical formulas [3]. Among all these hexagonal ferrites, the Potassium (K)-based β ferrites had taken much interest due to their applications for humidity sensor [4] and cathode active material for Li batteries [5] and due to its ionic and electronic conductivity it can be used for industries, fuel cells, electrode materials, and batteries as well [6]. K-β ferrite has hexagonal unique structure because it contains Alkali layer and spinel blocks with stacking patterns “SSAS*S*A*”, whereas * represents the 180° rotation of block along the c-axis with γ-Fe₂O₃ as shown in Fig. 1.The Iron occupies the spinel block on tetrahedral and octahedral sites. It also contains alkali layer which occupy the conduction and mirror plane. The mirror plane consists of two oxygen ions: one is connected to spinel block while other is connected to conduction plane. The conduction plane consists of three different sites named as BR (Beeverse Ross), aBR (Anti-Beeverse Ross) and mO (Mid-Oxygen) sites. Potassium ion K⁺ migrates within conduction plane and can easily be drifted due to less energy difference among conduction sites. At room temperature, initially, the K⁺ ion occupies the BR sites, but can migrate to aBR site because of greater thickness of Alkali layer [7]. This motion of K⁺ ions from BR sites to aBR sites may help in the ionic conductivity of the material. It is evident that the properties of pure β ferrite can be changed by introducing the divalent and/or trivalent elements in pure ferrites [8, 9]. The trivalent rare-earth element Yb³⁺ was chosen to substitute in pure ferrites for present investigation. Sol–gel auto combustion method was used to synthesize the samples in current research work because of inexpensive precursor materials that are required to synthesize materials, narrow size distribution, phase development, and advantage for chemically homogenous microstructure [3].

Fig. 1

KFe₁₁O₁₇ β- ferrites crystal structure of unit cell. The figure at left side shows the existence of tetrahedral and octahedral sites and the occupation of these sites by different ions within unit cell of β- ferrites. The right side figures (b, c) show the upper view of unit cell which elucidate ionic arrangements and the bonding between different ions within unit cell of β- ferrites

The intention was to synthesize single phase K-based β-type hexagonal ferrites by using sol–gel auto combustion technique at low sintering temperature and to explore the effect of Yb³⁺ substitution on structural, dielectric, and FTIR properties of β-type hexagonal ferrites.

2 Experimental procedure

Hexagonal $\beta$-ferrite with chemical composition KFe_11−xYb_xO₁₇ (x = 0, 0.02, 0.06, 0.1) were synthesized through sol–gel auto combustion technique. The chemicals such as Potassium Hydroxide KOH (Sigma Aldrich, ≥ 85%), Ytterbium Nitrate Yb (NO₃)₂.6H₂O (Sigma Aldrich, 99.9%), Iron Nitrate Fe(NO₃)₃.9H₂O (Sigma Aldrich, ≥ 99.95%), and Citric Acid HOC(COOH)(CH₂COOH)₂ (Sigma Aldrich, ≥ 99.5%) were used as precursor materials. The mixtures of all the aforementioned salts were dissolved in 300 ml ultrapure deionized water in separate beakers for each concentration. The beakers were placed on the hot plate where the magnetic stirrer was used for smooth mixing purpose. The Ammonium hydroxide (NH₄OH) was added up drop by drop to maintain the pH level between 7 and 8. With the addition of ammonium hydroxide, the color of the solution turned into yellow. The sample was continuously stirred at 80 °C for 2–3 h till the brown gel was obtained. The ignition of brown gel was done by increasing temperature of hot plate up to 350 °C. The dried gel was grinded in a mortal pestle to obtain very fine and fluffy powder of brownish color. After sintering at 950 °C for 3 h, the required phase of Beta hexagonal ferrites was successfully achieved. The color of sintered powder was turned into wine red. The powder samples were brought in compact pellet form by applying the 40KN force via hydraulic press.

The structural properties were measured by Bruker D8 advance X-ray diffractometer. The Precision multiferroic II ferroelectric (P-PMF) ferroelectric meter was used to measure electrical polarization properties. The frequency-dependent dielectric properties in the frequency range of 20 Hz to 20 MHz were measured by Wanyer impedance analyzer with model # 6500 B series at room temperature. The FTIR spectra were recorded from Shimadzu IR tracer 100 in the wave number range of 4000–400 cm⁻¹.

3 Results and discussions

3.1 Structural analysis

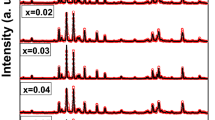
Materials exhibit distinct characteristics on the basis of its structural behavior. The XRD patterns of all KFe_11−xYb_xO₁₇ (x = 0, 0.02, 0.06, 0.1) K-beta hexagonal ferrites are depicted in Fig. 2. The single phase for all the samples can be observed from XRD patterns. It is worth to note that the intensities of peaks altered with the substitution of Yb contents. Consequently, some peaks disappeared from XRD patterns with Yb contents. The peaks at 2θ value 26.0 and 51.52 disappeared from XRD patterns of all Yb-substituted samples while the peak (306) at 2θ = 57.67 also disappeared from the last concentration x = 0.1. The peaks width was observed to increase with the substitution of Yb³⁺ ions which specify that these beta ferrites are composed of fine particle and this broadening of peaks also indicated the decrement in density and increase in surface-to-volume ratio of particles in material [10]. The X-rays diffraction (XRD) patterns reveal the basic information regarding crystal structure, unit cell volume, dislocation density, bond, and position of atoms within the unit cell. The lattice parameters a, c, and c/a were calculated by using following equation:

$$ {\text{Sin}}^{2} \theta \, = \, \lambda^{2} /3a^{2} \left( {h^{2} + hk + k^{2} } \right) \, + \, \left( {\lambda^{2} /4c^{2} } \right) \, l^{2} $$

(1)

Fig. 2

XRD patterns of all samples of KFe_11−xYb_xO₁₇ (x = 0.0, 0.02, 0.06, 0.1) β-ferrites

The unit cell volume of the prepared specimen (beta hexagonal ferrites) was calculated by using following equation;

$$ V = \, a^{2} c \, \left( {\sin \, 120^\circ } \right) $$

(2)

where d_hkl indicates the spacing between planes and h, k, and l show miller indices.

All the diffraction peaks were well indexed and corresponds to the K-beta hexagonal ferrites. The values of lattice parameters, c/a, and unit cell volume are given in Table. I. The calculated values of miller indices (hkl) were well matched with JCPD Card # 01–087-1546 which confirmed single phase hexagonal crystal structure of space group P6₃/mmc without any impurity phase. The lattice parameters “a” and “c” changed due to Yb³⁺ ions substitution in pure hexagonal ferrites and the unit cell volume calculated for all sample exhibited an increasing trend due to Yb³⁺ cations substitution.

Debye-Scherrer formula was used to find the crystalline size of synthesized sample which is described as;

$$ D = \frac{0.94 \lambda }{{\beta \cos \theta }} $$

(3)

where 0.94 is a shape constant, $\lambda$ is a wavelength of x-ray source, β is full width half maximum (FWHM) which represents the peak width at half maximum, and $\theta$ represents Bragg’s angle (degrees) of incident X-rays.

The crystallite size varied in the range of 26.0–43.0 nm for all samples and the values are given in Table 1. This can be attributed to the difference in the ionic radii of core and substituted elements. As Yb³⁺ ions (0.85 Å) have larger ionic radii than Fe⁺³ ions (0.64 Å), the bond length between ions is altered and the plan axis also changed which enhances the unit cell volume. This difference in ionic radii of ions produces the lattice strain within unit cell which results in lattice expansion and the lattice parameters and crystallite size got changed [11]. As the crystallite size of the prepared samples is less than 50 nm, it may be used in high-density recording media to get desirable signal-to-noise ratio [12].

Table 1 The values of lattice parameters a, c and c/a, unit cell volume, crystallite size, and dislocation density of KFe_11−xYb_xO₁₇ (x = 0.1, 0.02, 0.06, 0.0) β-ferrites for all concentrations

The dislocation density was calculated by using following formula;

$$ \rho = \frac{1}{{S^{2} }} $$

(4)

The dislocation density helps to find the number of the dislocations in a unit volume of crystalline sample. The values of dislocation density are given in Table 1 and the variation in the values of dislocation density with Yb³⁺ substitutions can easily be observed from the table [13].

The bond length was calculated from following relation;

$$ {\text{B}}.{\text{ L }} = \sqrt {\left( {{\text{a}}^{{2}} /{3 } + \, \left( {0.{5} - {\text{u}}} \right)^{{2}} {\text{c}}^{{2}} } \right)} $$

(5)

where a and c are the lattice parameters and u is the positional parameter. Positional parameter is measured from the equation as given below;

$$ u \, = \, a^{2} / \, 3c^{2} + 0.25 $$

(a)

From above equations, the bond length was calculated for all samples. The calculated value of bond length for (x = 0.0) is 11.6 Å, while for substituted sample (x = 0.02, 0.06, 0.1), it changed to 11.29 Å, 12.18 Å, and 11.94 Å, respectively. So, it can be concluded in a manner that the bond lengths changed with Yb³⁺ substitution in pure ferrites and these values are in good agreement with unit cell volume values.

3.2 Dielectric properties

The real part of dielectric permittivity (ε′) expressed the ability of electric storage-like polarization and imaginary part (ε′) of dielectric permittivity represents the capability of electric loss-like power dissipation.

The following formula was used to calculate the real part (ε′) of dielectric permittivity;

$$ \varepsilon^{\prime} = \frac{cd}{{A\epsilon_{o} }} $$

(6)

Whereas ‘c’ and ‘d’ in Eq. (6) represent the capacitance and thickness of the prepared samples, respectively, ‘A’ is the pellet surface area and ‘ε_o’ denotes the permittivity of free space with value 8.85 × 10⁻¹² m⁻³ kg⁻¹s⁴A².

The following equation defines the loss factor of dielectric material:

$$ \varepsilon^{\prime\prime} \, = {\text{Tan}} \delta \varepsilon^{\prime} $$

(7)

where ε′ represents the dielectric constant and ε″ is the dielectric loss factor.

The variation of the dielectric constant (ε′) with applied frequency for all sample has been shown in Fig. 3a. It was observed that the dielectric constant (ε′) of pure sample (x = 0.0) has high value at low frequency as compared to the substituted samples. It is seen from dielectric (ε′) behavior that the entire samples are frequency dependent i.e., firstly increased and then declined to reach a constant value with increasing frequency. According to Maxwell and Wagner concept, there are two layers which are responsible for variant behavior of dielectric constant. The first layer has conducting nature and called as grain, while the second layer exhibits the insulating behavior and is known as grain boundary [14]. According to Koop’s theory concept, the dielectric (ε′) constant has high value at low frequency due to insulating grain boundaries while at high frequency, the grains become active which lead to the decrease in value of dielectric constant. Consequently, by increasing the frequency, the charge carriers acquire enough energy to start hopping of electrons between Fe²⁺ ↔ Fe³⁺ sites which decreases the polarization and hence the dielectric properties diminished. Moreover, some type of defects, voids, and dislocation of ions are also responsible for the maximum value of dielectric constant at lower frequency values [15]. It can be concluded that the substitution of Yb³⁺ ions enhanced the dielectric constant and ionic polarizability of the samples. The increment in dielectric constant might be due to increase in bond length that may produce more relaxation time with substitution of Yb³⁺. The experimental results of dielectric constant were compared with theoretically calculated by using Debye’s function results. The Debye equation is given as follows:

$$ \epsilon^{\prime} = \epsilon^{\prime}_{\infty } + \frac{{\left( {\epsilon^{\prime}_{0} - \epsilon^{\prime}_{\infty } } \right)}}{{\left[ {1 + \left( {\omega \tau } \right)^{{2\left( {1 - \alpha } \right)}} } \right]}} $$

(8)

Fig. 3

a Variation of dielectric constant with log frequency of KFe_11−xYb_xO₁₇ (x = 0.0, 0.02, 0.06, 0.1) β-ferrites. b Variation of dielectric constant with log frequency and Debye fitting of KFe_11−xYb_xO₁₇ (x = 0, 0.02, 0.06, 0.1) β-ferrites

where ${\epsilon }^{^{\prime}}$ shows real part of dielectric and $\epsilon^{\prime}_{\infty }$ dielectric constant at frequency of 1 MHz, dielectric constant frequency at lowest frequency 20 Hz, ω = 2 π f, τ is mean time relaxation, $\alpha$ is spreading factor of the relaxation time [16]. It was worth noting from Fig. 3b that the fitted data exactly matched the experiment data which divulge the contribution of more than one ions to relaxation time [17].

The dielectric loss factor (ε″) behavior as a function of frequency of all the samples has been plotted in Fig. 4. The loss factor is the most important part of the total energy loss in ferrites while materials which have low loss factor are better to use due to small energy loss. It was noticed that the varying trend of dielectric loss (ε″) with frequency is analogous to the dielectric constant (ε′) results. It is reported that the loss factor in ferrites material commonly imitate the conductivity of materials because the highly conducting materials possess high losses [15].

Fig. 4

Variation of dielectric loss with log f for KFe_11−xYb_xO₁₇ (x = 0.0, 0.02, 0.06, 0.1) β-ferrites

The tangent loss (δ) of any dielectric material can be calculated by the help of following formula:

$$ \tan \delta = \frac{1}{2\pi fRC} $$

(9)

Figure 5 elaborates the variation of tangent loss (δ) as a function of frequency. It can clearly be observed from Fig. 5 that the tangent loss (δ) has maximum value at lower frequency and this can be attributed to the fact that at low frequency, all the dipoles get enough time to align themselves in rotation to the applied field. Hence the interfacial polarization phenomenon takes place which results in the increment in the value of tangent loss at lower frequency [18]. While at higher frequencies, the relaxation time is very low due to which interfacial polarization will cease up and there will be no rotation of dipoles and meanwhile the phase angle will not change, and consequently, the tangent loss remains constant.

Fig. 5

Variation of tangent loss with log f of KFe_11−xYb_xO₁₇ (x = 0.0, 0.02, 0.06, 0.1) β-ferrites

The following relation is used to calculate the conductivity of material:

$$ \sigma = \sigma_{ac} + \sigma_{dc} $$

(10)

It was observed that the substituted samples have high value of conductivity than the pure sample. The 2nd factor on the right hand side of Eq. 10 is independent of frequency called DC conductivity, while the first factor is frequency dependent called AC conductivity and is calculated by following relation:

$$ \sigma_{ac} = \pi f\varepsilon^{\prime\prime}\varepsilon_{o} $$

(11)

In above relation, $\varepsilon^{\prime\prime}$ is the imaginary part of dielectric constant, while ${\varepsilon }_{o}$ represent the free space permittivity. The variation in AC conductivity with log frequency for pure (x = 0.0) and Yb³⁺-substituted samples (x = 0.02, 0.06 and 0.1) have been depicted in Fig. 6a. The AC conductivity had low value at low frequency, while it increased rapidly at higher frequency. This behavior of ac conductivity with frequency can be explained in terms of double-layer Maxwell and Wagner model. This model predicts that at low-frequency region, the grain boundaries play major role while at higher frequency region, the grains are more active and help in electron hopping process [19]. In present case, at higher frequency region, the conductivity is very high due to the reason that it includes the response of bounded charge carrier to the conductivity process [20]. It is further observed in Fig. 6a that there are two different regimes within frequency limit: plateau region which corresponds to low-frequency region where conductivity was found to be independent of frequency and dispersion region which corresponds to high-frequency region where conductivity increases with increase in frequency [21].

Fig. 6

a Variation of ac conductivity with log f of KFe_11−xYb_xO₁₇ (x = 0.0, 0.02, 0.06, 0.1) β-ferrites. b Variation of ac conductivity with f and curve fitting by using Jonscher’s power law of KFe_11−xYb_xO₁₇ (x = 0.0, 0.02, 0.06, 0.1) β-ferrites

The frequency dependence of AC conductivity is generally examined by using Jonscher’s power law [22] as shown in Fig. 6b.

$$ \sigma_{ac} = \sigma_{dc} + \, A\omega^{n} $$

(12)

where ‘’A’’ shows dispersion parameter and strength of polarizability, while ‘‘n’’ shows the dimensionless frequency exponent constituting the interaction between lattice surrounding mobile ions [23]. According to Jonscher’s power law, the origin of dispersion region in higher frequency of conductivity arises due to hopping of mobile charge carriers [24].

The variation of electric modulus (M′) with log frequency for all the samples of hexagonal $\beta$ferrites have been shown in Fig. 7. The total electrical modulus ‘M’ depends on real electrical modulus and complex modulus. This is denoted by the following equation:

$$ M_{{{\text{total}}}} = M^{\prime} + jM^{\prime\prime} $$

(13)

Fig. 7

Variation of electric modulus (M′) with log f of KFe_11−xYb_xO₁₇ (x = 0.0, 0.02, 0.06, 0.1) β-ferrites

In above equation, the first factor can be calculated from the equation given below:

$$ M^{\prime} = \frac{{\varepsilon^{\prime}}}{{\left( {\varepsilon^{{\prime}{2}} + \varepsilon^{{\prime\prime}{2}} } \right)}} $$

(14)

The 2nd factor in Eq. 10 can be calculated from the equation given below:

$$ M^{\prime\prime} = \frac{{\varepsilon^{\prime\prime}}}{{\left( {\varepsilon^{{\prime}{2}} + \varepsilon^{{\prime}{2}} } \right)}} $$

(15)

The electrical modulus shows queer behavior with changing frequency. It can be perceived from the Fig. 7 that the electric modulus exhibits a constant value at lower frequency which is due to electrode effect or ionic polarization [25], while all the samples (x = 0.0, 0.02, 0.06 and 0.1) show the maximum asymmetric behavior at higher frequency and this asymmetric behavior confirms the occurrence of space charge polarization at high-frequency region [26]. Figure 8 depicts the behavior of complex modulus M'' versus log frequency. At high frequency, the single sharp peak was observed for all samples due to maximum asymmetric trend. This trend clearly demonstrates the relaxation behavior and also is related to single polarization phenomenon of grain boundaries [27]. Consequently, the peak intensity was increased and a slight shift of peak towards low-frequency region was also observed with substitution of Yb³⁺ contents. This indicated the presence of dielectric relaxation within the material. Furthermore, the M″ graph trend at low-frequency region interpreted that the jumping of charge carriers followed the large distance and these charge carriers were limited to shorter distance at high-frequency region. This transformation of charge carriers with frequency modifications for all samples from tiny to longer range of mobility revealed the materials conductivity factor [28].

Fig. 8

Variation of complex electric modulus (M″) with log f for KFe_11−xYb_xO₁₇ (x = 0.0, 0.02, 0.06, 0.1) β-ferrites

The Cole–Cole graph of the sample KFe_11−xYb_xO₁₇ with concentration (x = 0.00, 0.02, 0.06, and 0.1) was drawn between the real part of modulus (M′) and the imaginary parts of the modulus (M″) and depicted in Fig. 9. The Cole–Cole graphs can be understood on the basis of resistivity of grains and grain boundaries of the samples. It is evident that the left side of semicircle in Cole–Cole plot at lower frequency value emerges due to resistance of grain. The central part of graph at intermediate frequency is the function of grain boundary resistance and the right side at extreme frequency indicated the combined effect of resistance of both grain and grain boundary [29]. The semicircle for each graph clearly indicated the dominant contribution of grain boundary resistance. The slight increase in the intensity of semicircle peak for the concentrations of x = 0.02 and 0.06 was noticed from the figure which attributed to the increase in grain boundary resistance for these concentrations [30].

Fig. 9

Cole–Cole plots for all concentrations of KFe_11−xYb_xO₁₇ (x = 0.0, 0.02, 0.06, 0.1) β-ferrites

The impedance is used for the better understanding of electroactive part of microstructure within the sample. Impedance is the total flow of an alternating current within the material which suffers a shift in phase angle and amplitude. Figure 10 depicts the real part (Z′) of impedance as a function of variant frequency. Impedance in terms of real and imaginary part can be calculated from the relation given as follows;

$$ Z \, = \, Z^{\prime} \, + \, jZ^{\prime\prime} $$

(16)

Fig. 10

The variation of Impedance (Z′) with log F of KFe_11−xYb_xO₁₇ (x = 0.0, 0.02, 0.06, 0.1) β-ferrites

where Z′ is resistive and Z″ is the reactive part of complex impedance. The decreasing behavior of real part (Z′) of impedance with increase in frequency can be explained on the base of conductivity of the material [31]. It is observed that at lower frequencies, the impedance (Z′) has high value which can be attributed to the effect of grain boundaries, while this effect of grain boundaries decreased with the increase of frequency [32, 33]. It is worth to note that the value of (Z′) decreased with Yb³⁺ ions substitution which confirmed the improvement in material’s conductivity at low-frequency region. The relation between imaginary (Z″) part of impedance and frequency has been given in Fig. 11. The peak shifting towards high frequencies was observed with substitution of Yb³⁺ions in pure sample which indicated the presence of relaxation process within samples [34]. The further increase of Yb³⁺ contents lowered the peaks intensity and resulted in the overall decrease in the impedance (Z″) of material.

Fig. 11

The variation of complex impedance (Z″) verses log f of KFe_11−xYb_xO₁₇ (x = 0.0, 0.02, 0.06, 0.1) β-ferrites

3.3 Fourier transforms infrared spectroscopy analysis

The Fourier transform infrared (FTIR) spectra of KFe_11−xYb_xO₁₇ (x = 0.02, 0.06 and 0.1) were recorded at room temperature in range of 400–4000 cm⁻¹ and depicted in Fig. 12. The large number of absorption bands at wave numbers 3258, 2909, 2352,1609, 1356, 1020, 496, and 416 cm⁻¹ were observed from FTIR spectra. The absorption band at wave number 416 and 496 cm⁻¹ can be attributed to the stretching vibration of Fe–O ions at tetrahedral and octahedral sites of the unit cell [35, 36]. The absorption band at wave number 2358 cm⁻¹ was due to the presence of carbon hydrogen stretching vibration [37], while the band at 2937 cm⁻¹ can be assigned to O–H bonds [38, 39]. The absorption band at 1356 cm⁻¹ was associated to metal–oxygen–metal (Fe–O–Fe) bonds [40]. The absorption bands at 1020 cm⁻¹ arose due to stretching vibration of C–O–C bond extending in the carbonyl groups which is absorbed from atmosphere [41]. The broad dip at 3258 and 1609 cm⁻¹ can be assigned to stretching vibration of H–O–H bonds of water, ascended due to moisture absorbed from atmosphere [36, 40]. The absence of any other absorption band produced due to precursor materials, residual material, or any other material confirmed the single β-hexaferrites phase of this material.

Fig. 12

FTIR spectra of all samples of KFe_11−xYb_xO₁₇ (x = 0, 0.02, 0.06, 0.1) β-ferrites

4 Conclusion

The sol–gel auto combustion method was used to synthesize the K-based KFe_11−xYb_xO₁₇ (x = 0.0, 0.02, 0.06 and 0.1) β-hexagonal ferrite at sintering temperature of 950 °C. The X-ray diffraction patterns revealed the single phase for all the prepared samples. The lattice parameters, crystallite size as well as unit cell volume were observed to be changed with substitution. The dielectric constant value was noticed to decrease with Yb³⁺ substitution while dielectric loss and tangent loss values were increased with substituted contents. The curve fitting of dielectric data was carried out by using modified Debye’s function which adumbrated the contributions of more than one ion in dielectric relaxation process within all substituted samples. The frequency-dependent AC conductivity was well explained by applying modified Jonscher’s power law which indicated that all the material had increasing trend of dispersion conductivity with the applied frequency. The Cole–Cole plot specified the major contribution of grain boundaries in materials. The FTIR spectra analysis also confirmed the existence of single hexagonal phase for all synthesized samples.