Introduction

Dynamic mechanical analysis (DMA) method has been extensively used for characterizing viscoelastic properties of polymers [1, 2], composites [3, 4] and biomaterials [5, 6]. In this method, a sinusoidal loading cycle is applied and the storage (E′) and loss (E″) moduli are calculated from the in-phase and out-of-phase components of load and displacement cycles [7, 8]. The sinusoidal loading can be applied at different frequencies and temperatures, and the entire dataset can be generated on a single specimen. However, both E′ and E″ are in frequency domain and do not have much significance in mechanical design field. Recent studies have focused on developing methods to transform this frequency domain data to time domain [9,10,11]. The time-domain data can be used to extract elastic modulus over a range of strain rates and temperatures, which has tremendous importance in engineering fields, especially for designing structures for dynamic loading conditions that can be subjected to different temperatures. Extracting the elastic modulus over a range of strain rates and temperatures from the DMA results of a single specimen eliminates the need to conduct a large number of tensile tests [12,13,14]. The predictions of this transform have been validated with data on neat polymers [9, 15], nanocomposites [16] and hollow particle-filled composites [10]. The method works by first applying the classic time–temperature superposition principle (TTS) to build the master curve for E′. This master curve is represented by an equation called master relation, which provides a relation for E′ with respect to frequency and temperature. It allows extrapolating the values beyond the frequency range covered in the DMA experiments [17]. Then, E′ is transformed to time-domain relaxation modulus E(t) using linear integral relation of viscoelasticity [9, 10]. Finally, E(t) is used to predict the stress response with certain strain history and temperature and obtain the elastic modulus with respect to strain rate and temperature [18].

Although the existing transformation method based on storage modulus has many advantages [11, 19, 20], it also has some limitations. First, the equations are set up for transforming data that show only one thermal transition peak in the DMA response. When more than one thermal transitions are present in the storage modulus, the current transformation methods find it difficult to identify and model each transition, especially if two transition are close to each other. Loss modulus is able to resolve the thermal transitions better, and an approach based on loss modulus is expected to be more robust. The difficulties increase with the number of transitions. In addition, the method becomes computationally expensive because a large number of constants need to be determined to solve the equations. Use of artificial neural network (ANN) with parallel computing may have significant benefits for developing a generalized solution for this problem. A method for developing ANN-based solution for a single thermal transition material has been demonstrated [20]. However, a generalized method demonstrating the possibility of treating complex material behaviors has not been tested. Inspired by biological neural networks, ANN is efficient at handling complex nonlinear behaviors and has a strong physical foundation for use in the materials science field [21]. ANN has been used in prediction [22,23,24] and optimization [25] of material properties.

The master relation defined with respect to temperature and frequency is used to develop the scheme for extracting elastic modulus [19]. Using temperature and frequency as the inputs, the form of the radial basis neural network (RBNN) satisfies the form of the TTS principle and enables massive computation tasks robustly [26]. Using E″ as output, the neural network can easily identify and model each thermal transition, even though the two thermal transitions are close to each other. The E′ of both strain rate sensitive and insensitive material can be divided into frequency-dependent and frequency-independent parts. Both parts can be calculated separately from E″ using Kramers–Kronig (K–K) relation [11, 27]. The properties of strain rate sensitive material are mainly contributed by the frequency-dependent part, while the properties of strain rate-insensitive material are mainly contributed by the frequency-independent part. By modeling both frequency-dependent and frequency-independent part separately, this work builds a general description of strain rate sensitive and insensitive material. It is noted that E′ has a strong dependence on temperature. It will have poor fitting results when using least square error, which is the most popular one, as the object function. In addition, it is sometimes not easy to distinguish multiple thermal transitions present in the material behavior in the storage modulus curve. Hence, the scheme in the present work relies on using loss modulus E″, which varies in a smaller range than E′ and is capable of generating better fitting results when using least square error as the object function.

The RBNN is used in the present work to build the master relation over a wide range of temperatures and frequencies. The RBNN is tested at various regulation factors and neuron numbers to find the best fitting parameters. The data are used to predict the elastic modulus of the material over a range of strain rates and temperatures. It is worth mentioning that this work is focused on building the relations between the properties obtained from different testing methodologies. Since the parameters such as materials inhomogeneity and materials quality should affect the results obtained from both testing methods, DMA and tensile tests, in a similar manner, these materials related factors are not the focus of the present study.

Materials and methods

RBNN methodology and back propagation

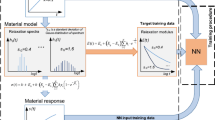
The two components of complex modulus, E′ and E″, are not independent, and their relation is discussed in section “Relations between storage and loss modulus”. The frequency range of master relation needs to be wide enough to implement the transformation. To build a master relation which can describe both strain rate sensitive and insensitive material behaviors under a wide range of temperatures and frequencies, E′ is divided into the frequency-dependent and frequency-independent parts. The master relation of E′ can be established by finding both parts individually using K–K relation. The transformation procedure is shown in Fig. 1.

Figure 1
figure 1

The procedure of radial basis neural network modeling scheme for dynamic mechanical analysis data

Full size image

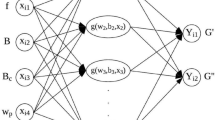
The RBNN is used to establish the master relations of E″. The frequency and temperature are chosen as the inputs of the RBNN. For multiple-layer RBNN, the mapping function between two layers can be mathematically defined as [28]

$$ E\left( x \right) = \mathop \sum \limits_{m = 1}^{N} \beta_{m} \varPhi_{m} \left( {\left\| {x - R_{m} } \right\|} \right) $$
(1)

where E(x) is the output E″, x is the vector of the input (ω and T), N is the number of basis and βm is the coefficient of basis Φm. Rm is the set of centers, which is the center set of thermal transition in this work. The contribution of each basis is determined by the distance to each basis center. The basis function is developed using the K–K relation and TTS principle. The contribution of mth neuron in the hidden layer, zm, can be expressed by

$$ z_{m} = \varPhi_{m} \left( {\alpha_{m}^{T} x - \alpha_{m0} } \right) $$
(2)

where αm is the weight vector of x and αm0 is the biased term for mth neuron. A three-layer RBNN is used, and it has two input neurons ω and T and one output neuron E″. Only one hidden layer is used, and each neuron in the hidden layer corresponds to one thermal transition. The accuracy of neural network is sensitive to the neuron number and is studied in the initial part of the analysis. To reduce the over-fitting phenomenon, a regulation term Ω(α, β) is added to the performance function as [29]

$$ \tilde{F}\left( {E^{\prime\prime};x} \right) = F\left( {E^{\prime\prime};x} \right) + \theta \varOmega \left( {\alpha ,\beta } \right) $$
(3)

where α and β are the parameters of RBNN and θ is the regulation factor. Proper regulation factor needs to be chosen to achieve a balance between over-fitting and under-fitting. The mean sum of squared errors is used as the measure of error of neural network, and L2 regulation or ridge regression is used for regulation term as

$$ F\left( {E^{\prime \prime } ;x} \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} F_{i} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left[ {E^{\prime \prime } \left( {x_{i} } \right) - \tilde{E}^{\prime \prime } \left( {x_{i} } \right)} \right]^{2} $$
(4a)
$$ \varOmega \left( {\alpha ,\beta } \right) = \frac{1}{J}\mathop \sum \limits_{j = 1}^{J} a_{j}^{2} + \frac{1}{K}\mathop \sum \limits_{k = 1}^{K} \beta_{k}^{2} $$
(4b)

where \( \tilde{E}^{\prime\prime} \) is the fitted loss modulus and E″ is the experimental loss modulus, Fi is the prediction error of ith data, N is the size of the dataset, J is the number of parameters between input layer and hidden layer and K is the number of parameters between hidden layer and output layer.

In order to train the RBNN, the DMA results of one specimen are used. The dataset contains the storage and loss modulus measurements at 860 combinations of temperatures and frequencies. The training process of RBNN starts by randomly dividing the dataset into training set, validation set and test set in 60:15:25 ratio. The corresponding sizes of training, validation and test set are 516, 129 and 215 data points, respectively. Then, the RBNN is trained by minimizing the performance function using training set. When the improvement in the performance diminishes, the training is stopped. The neural network is trained using back-propagation method to establish the master relation of E″. The weights are trained to minimize the error using gradient descent, and the change of each weight for each iteration (r) can be expressed as

$$ \alpha_{lm}^{{\left( {r + 1} \right)}} = \alpha_{lm}^{\left( r \right)} - \gamma \left[ {\frac{2}{N}\mathop \sum \limits_{i = 1}^{N} \frac{{\partial F_{i} }}{{\partial \alpha_{lm}^{\left( r \right)} }} + \theta \frac{2}{J}\alpha_{lm}^{\left( r \right)} } \right] $$
(5a)
$$ \beta_{m}^{{\left( {r + 1} \right)}} = \beta_{m}^{\left( r \right)} - \gamma \left[ {\frac{2}{N}\mathop \sum \limits_{i = 1}^{N} \frac{{\partial F_{i} }}{{\partial \beta_{m}^{\left( r \right)} }} + \theta \frac{2}{K}\beta_{m}^{\left( r \right)} } \right] $$
(5b)

where γ is the learning rate, which is kept as 0.01; βm is the weight between mth neuron and output; and αlm is the weight between lth input and mth neuron in the hidden layer. The gradient of F can be expressed as

$$ \frac{{\partial F_{i} }}{{\partial \alpha_{lm}^{\left( r \right)} }} = - \left( {E^{{\prime \prime }} \left( {x_{i} } \right) - \tilde{E}^{\prime \prime } \left( {x_{i} } \right)} \right)\beta_{m}^{\left( r \right)} x_{i} \varPhi_{m}^{{\prime }} \left( {\alpha_{m}^{T} x_{i} - \alpha_{0m} } \right) $$
(6a)
$$ \frac{{\partial F_{i} }}{{\partial \beta_{m}^{\left( r \right)} }} = - \left( {E^{{\prime \prime }} \left( {x_{i} } \right) - \tilde{E}^{{\prime \prime }} \left( {x_{i} } \right)} \right)\varPhi_{m} \left( {\alpha_{m}^{T} x_{i} - \alpha_{m0} } \right) $$
(6b)

The back-propagation process converges when the gradients of the weights are below 10−5.

Material and experiments

The virgin EVA is of grade N8038 produced by TPI Polene, Thailand. It is injection molded into DMA and tensile test specimens at 150 ˚C and 60 bar. The dimensions for DMA specimens are 60.0 × 12.7 × 2.5 mm3 (length × width × height), and the geometry of tensile test specimens conforms to ASTM D638.

A TA Instruments (New Castle, DE) Q800 DMA is used to characterize the specimens in − 150 to 60 ˚C temperature range with a temperature step of 5 ˚C. The DMA tests are conducted under dual-cantilever configuration (span length: 35 mm) with strain control mode with a maximum displacement of 25 µm. For each temperature step, the soaking time is set as 5 min to ensure thermal equilibrium. Frequency sweeps are conducted at 20 discrete frequencies logarithmically spaced between 1 and 100 Hz. The experiment is terminated when the force magnitude drops below 10−4 N. Three specimens are tested for repeatability. The profile of E′ and E” with respect to temperature is shown in Fig. 2 at 1 Hz frequency. The glass transition temperature is observed to be at − 30 ˚C in the material. The initial part of the graph also shows the presence of another peak at − 150 ˚C. In the previous studies, storage modulus is used for modeling the material response; however, thermal transitions are not reliably resolved in the storage modulus curve so the loss modulus is the better choice for modeling the material behavior for thermal transition temperatures. The three-dimensional response surfaces of E′ and E″ are shown in Fig. 3, where both temperature and frequency sweeps are conducted. Similar response surfaces will be plotted from the modeling results for comparison with the experimental results.

Figure 2
figure 2

Profile of storage and loss moduli with respect to temperature at 1 Hz frequency

Full size image
Figure 3
figure 3

Three-dimensional (3D) response surfaces of a storage modulus and b loss modulus for EVA constructed from dynamic mechanical analysis data

Full size image

An Instron 4467 universal test system is used for the time-domain viscoelastic properties at room temperature. An Instron 25-mm gage length extensometer is used to obtain the strain history data under different initial strain rates from 2.5 × 10−6 to 2.5 × 10−3 s−1. Four specimens are repeated for each strain rate, and a representative set of stress–strain curves for EVA is presented in Fig. 4.

Figure 4
figure 4

A representative set of tensile stress–strain curves for EVA at four different strain rates

Full size image

Relations between storage and loss modulus

The E′(ω) and E″(ω) are not independent and their relation at a given temperature T can be expressed as [30]

$$ E^{\prime } \left( {\omega ,T} \right) - E^{\prime } \left( {0,T} \right) = \frac{2}{\pi }\mathop \int \limits_{0}^{\infty } \frac{{\omega^{2} E^{\prime \prime } \left( {\lambda ,T} \right)}}{{\lambda \left( {\omega^{2} - \lambda^{2} } \right)}}{\text{d}}\lambda $$
(7)

where ω is the angular frequency and E′(0, T) is the E′ at frequency 0. The right side represents the difference between storage modulus at frequency 0 and ω, which can be named as ΔE′. ΔE′ is a function of frequency and temperature while E′(0, T) is frequency-independent. Using this relation, the temperature-dependent E′ can be divided into frequency-independent component E′(0, T) and frequency-dependent component ΔE′(ω, T). The E′(0, T) is simplified as E0′(T) for convenience in the following work as

$$ \Delta E^{\prime } \left( {\omega ,T} \right) = \frac{2}{\pi }\mathop \int \limits_{0}^{\infty } \frac{{E^{\prime \prime } \left( {\lambda , T} \right)\omega^{2} }}{{\lambda \left( {\omega^{2} - \lambda^{2} } \right)}}{\text{d}}\lambda $$
(8a)
$$ E_{0}^{{\prime }} \left( T \right) = E^{\prime } \left( {\omega ,T} \right) - \frac{2}{\pi }\mathop \int \limits_{0}^{\infty } \frac{{E^{\prime \prime } \left( {\lambda ,T} \right)\omega^{2} }}{{\lambda \left( {\omega^{2} - \lambda^{2} } \right)}}{\text{d}}\lambda $$
(8b)

To implement this process, E″ at wide range of frequencies and temperatures needs to be found. Taking derivative with respect to ω on both sides of Eq. 8.b:

$$ \frac{{{\text{d}}E^{\prime } \left( {\omega ,T} \right)}}{{{\text{d}}\ln \omega }} = \frac{{{\text{d}}\Delta E^{\prime } \left( {\omega ,T} \right)}}{{{\text{d}}\ln \omega }} = - \frac{4}{\pi }\mathop \int \limits_{0}^{\infty } \frac{{\lambda E^{\prime \prime } \left( {\lambda ,T} \right)}}{{\left( {\omega^{2} - \lambda^{2} } \right)^{2} }}{\text{d}}\lambda $$
(9)

The K–K relation can be found when E″ changes slowly with ω as per the following equation [27] and can be used to find the radial basis function

$$ E^{\prime \prime } \left( {\omega ,T} \right) \approx \frac{\pi }{2}\frac{{{\text{d}}E^{\prime } \left( {\omega ,T} \right)}}{{{\text{d}}\ln \omega }} $$
(10)

Zeltmann et al. [9] used sigmoid function to describe E′ for single thermal transition as

$$ E^{\prime } \left( \omega \right) = a + b\tanh \left( {c\ln \left( \omega \right) + d} \right) $$
(11)

where a, b, c and d are the parameters that need to be determined. By combining Eqs. 8 and 9, the corresponding radial basis of E″ for ith transition can be found as

$$ E^{{\prime \prime }} \left( \omega \right) = \text{sech}^{2} \left( {c \ln \left( \omega \right) + d} \right) $$
(12)

The radial basis can be expanded to temperature using TTS principle. According to TTS principle, the master relation of the instantaneous modulus does not change shape as the temperature is changed. Following TTS principle, the parameters c is constant under different temperatures and only d is a function of temperature T. The linear form is used between hidden layers and the radial basis function of E″ for ith transition can be established as

$$ E_{i}^{\prime \prime } \left( {\omega ,T} \right) = \text{sech}^{2} \left( {c_{i} \ln \left( \omega \right) + d_{i} T + e_{i} } \right) $$
(13)

where ei is the bias term for each layer. The RBNN is used to establish the material relation of E″ for multiple transitions material. The neural network can be expanded to a frequency range of 10−50 to 1050, which is large enough for Eq. 8.

The RBNN can be integrated with respect to ω to find E0′(T). It is fitted using a sigmoid function as

$$ E_{0}^{\prime } \left( T \right) = a_{0} + b_{0} \left( {T - T_{0} } \right)_{ + } + w_{0} \tanh \left( {d_{0} T + e_{0} } \right) $$
(14)

where a0, b0 and w0 are parameters to fit E0′(T), (T − T0)+ is a piecewise linear function and it can be defined as

$$ \left( {T - T_{0} } \right)_{ + } = \left\{ {\begin{array}{*{20}l} {\left( {T - T_{0} } \right) } \hfill & {T \ge T_{0} } \hfill \\ 0 \hfill & {T < T_{0} } \hfill \\ \end{array} } \right. $$
(15)

Following this method, the master relations of E′ and E″ can be found, which can describe the viscoelastic relation at a wide range of frequencies and temperatures and be used for transformation to time domain.

Transform to time domain

The frequency domain master relation of E′ can be transformed to time-domain relaxation function at a certain temperature T, E(t, T), using integral relations of viscoelasticity as [30]

$$ E\left( {t,T} \right) = \frac{2}{\pi }\mathop \int \limits_{0}^{\infty } \frac{{E^{\prime } \left( {\omega ,T} \right)}}{\omega }\sin \left( {\omega t} \right)d\omega $$
(16)

For thermal equilibrium, the stress–strain relation with specific strain history can be found using

$$ \sigma \left( {t, T} \right) = E*\dot{\varepsilon } = \mathop \int \limits_{0}^{t} E\left( {t - \tau , T} \right)\frac{{{\text{d}}\varepsilon \left( \tau \right)}}{{{\text{d}}\tau }}{\text{d}}\tau $$
(17)

where σ, ε and τ are stress, strain and time variable, respectively. For tensile test, the strain rate is assumed to be constant and the time-dependent stress history can be approximated as [30]

$$ \sigma \left( {t,T} \right) = \dot{\varepsilon }\mathop \int \limits_{0}^{t} E\left( {\tau , T} \right){\text{d}}\tau $$
(18)

Using this transformation, the stress–strain relation can be predicted and the time-domain elastic modulus can be extracted at various temperatures and strain rates.

Results and discussion

Model tuning

As the fitting results are influenced by the penalty factors θ and neuron numbers, the modeling process consists of two steps: First, RBNN is tested by mathematical experiments to determine the best training parameters; then, the parameters are used on experimental data to establish the master relation of E′ and E″ under a wide range of temperatures and frequencies.

The best training parameter is found by a mathematical experiment. A mathematical model is used to simulate the material behavior with two thermal transitions. The RBNN is trained on the simulated data to find the best parameters. The mathematical model is generated by training the RBNN using the experimental E″ without penalty factor (θ = 0). The RBNN for the mathematical model has one hidden layer containing two neurons. The training, validation and test sets are generated using the mathematical model. To test the robustness of the method, two different levels of Gaussian noises are added into training set as

$$ \tilde{E}^{\prime }_{\text{train/validation}} = \tilde{E}^{\prime } \left( {1 + \xi } \right) $$
(19)

where ξ is a Gaussian distribution with mean of 0 and the standard deviation is set at 0.05 and 0.025. Then the RBNN is trained with different penalty factors and neuron numbers using the data generated by the mathematical model. The accuracy of RBNN is found by comparing the prediction of RBNN and mathematical model, and average training and testing errors are found using root mean square error. The experiments are repeated for 500 times to find the average training and testing errors.

The RBNN is trained in the penalty factor range of 10−11 to 10−1. The errors with respect to penalty factor θ are shown in Fig. 5. The RBNN achieves the best accuracy when the penalty factor θ is around 10−5. The under-fitting problem imperils the accuracy when the penalty factor θ is more than 10−3 and the penalty factor is so large that it dominates the fitting. On the contrary, the over-fitting problem appears when the penalty factor θ is less than 10−7. The penalty factor is not strong enough to constrain the over-fitting and compromise the accuracy.

Figure 5
figure 5

The training error and testing error with respect to regulation factor θ at a 2.5% and b 5% Gaussian noises (Number of neurons = 2)

Full size image

The trend of accuracy with respect to neuron number is also investigated. The penalty factor θ is set to be 10−5 and it is trained with different neuron numbers as per the results shown in Fig. 6. The RBNN achieves the best accuracy when its neuron number equals 2, which agrees with the neuron number in the mathematical model. Similar to the trend in penalty factor, the under-fitting jeopardizes the accuracy when the neuron number is less than 2 and the RBNN is not powerful enough. The accuracy decreases when the neuron number is much larger than 2 due to over-fitting.

Figure 6
figure 6

The training error and testing error with respect to number of neurons at a 2.5% and b 5% Gaussian noises (Regulation factor θ = 10−5)

Full size image

The master relation of E″ is established using RBNN with 2 neurons and penalty factor 10−5. The average error of test set is 2.72 MPa, which is 3.89% of the average loss modulus. The response surface of predicted E″ with respect to temperature and frequency is shown in Fig. 7a, and the map of fitting error is shown in Fig. 7b. The Pearson correlation coefficient R for training set and test set is found to be 0.9897 and 0.9824, as shown in Fig. 8. The region near the thermal transition temperature, where E″ achieves the peak, shows the highest level of error. With the master relation of E″, ΔE′ and E′(0) can be calculated individually. The E′(0) and the fitting results are shown in Fig. 9 and show close matching with each other at the entire temperature range. The variation of experimental E′(0) is contributed by the error of E″.

Figure 7
figure 7

a Response surface of loss modulus fitted by RBNN. b Map of the fitting error with respect to temperature and frequency

Full size image
Figure 8
figure 8

The Pearson’s correlation coefficient R of the experimental and predicted storage modulus for a training set b test set

Full size image
Figure 9
figure 9

The frequency-independent part of storage modulus E′(0)

Full size image

Transformation to elastic modulus

The master relation of E′ can be transformed to time-domain relaxation modulus E(t,T) using Eqs. 16–18. The E(t,T) at different temperatures is shown in Fig. 10. Then the stress response with certain strain history under different temperatures can be extracted, which can be used to calculate the elastic modulus.

Figure 10
figure 10

Time-domain relaxation modulus E(t, T) with respect to frequency at different temperatures. Both increase in temperature and frequency show decrease in the relaxation modulus

Full size image

The elastic modulus is defined using 0.5% secant modulus due to nonlinear elastic response of EVA, and its response surface of EVA with respect to temperature and strain rates, predicted from the present model, is presented in Fig. 11. To evaluate the accuracy of transformation results, the elastic modulus obtained from the transform is compared with the experimentally measured modulus obtained from tensile test results shown in Fig. 12. Four experimental data points are plotted in this figure for each strain rate. Some of the values are very close and overlap with each other. The predictions achieve an average root mean square error (RMS) of 3.3% RMS and the maximum error is 4.9%, which affirms the applicability and accuracy of the present method.

Figure 11
figure 11

Response surface of predicted elastic modulus with respect to temperature and strain rate

Full size image
Figure 12
figure 12

Comparison between predicted and experimental elastic modulus values at room temperature. Four experimental data points are plotted at each strain rate but some of them overlap due to the close values

Full size image

The method can predict the elastic properties over a wide range of temperatures and strain rates from the results of DMA testing on a single specimen. It is also successful in dealing with material that has two thermal transitions in the test temperature range. A similar procedure will be applicable if there are a larger number of thermal transitions, with the possible main difference that the RBNN optimization process will result in a different parameter set for optimization. The present method eliminates the need for a large number of tensile tests. In addition, the present scheme based on artificial neural network can be effectively implemented in parallel computing to allow transforming properties of materials that have multiple thermal transitions in the test results.

Conclusions

In this work, a method is developed to transform the frequency domain DMA testing results to time-domain elastic modulus at various temperatures and strain rates. EVA is used as the study material for this work, and RBNN is used to establish the master relations of E″ at a wide range of temperatures and frequencies. With the L2 regulation factor, the RBNN is tested under various regulation factors and neuron numbers to find the best training parameters. Then E′ is divided into frequency-dependent and frequency-independent components to build a general description of strain rate sensitive and insensitive materials with multiple thermal transitions. Two parts are individually calculated from master relations of E″ using the K–K relation and then transformed to E(t,T). The E(t,T) can be used to predict the viscoelastic response with certain strain history and temperature, and the elastic properties can be extracted. To verify the accuracy of the transform, the elastic modulus predicted from the DMA transform is compared with the values obtained from experimental tensile tests. At strain rate between 10−6 and 10−2 s−1, the transformation achieves 3.3% RMS average error and 4.9% maximum error. Based on the RBNN, the process is easy to be implemented using parallel computing and is robust. The study focuses on the testing methodology, not on the material composition or microstructure, and the transform should work on any other material with multiple thermal transitions.