Introduction

The fatigue and fracture of materials have been widely investigated since last century. The linear elastic fracture mechanics (LEFM) have been a mature tool to solve many crack problems. According to LEFM, the behaviors of materials are linear elastic, so the stresses at the crack tip are singular. In fact, the material will yield and generate a PZ when the stress near the crack tip exceeds the yield limit of the material. When it is small-scale yielding, LEFM can be still applied to analyze behaviors of the materials containing cracks. For the brittle fracture and fatigue crack problem, a little plastic deformation will occur. The stress intensity factor is an important mechanical parameter to study these problems. However, PZ will increase as the external load increases. LEFM cannot be applied to solve crack problems when PZ size is relatively large and it is large-scale yielding. In this case, the mechanical parameters J integral [1] and crack tip open displacement were proposed to be the fracture criterions. There is a positive correlation among J integral, crack tip open displacement and PZ size [1,2,3,4]. So it is necessary to investigate PZ at the crack tip.

From the macroscopic point of view, PZ is predicted by the yield criterions, such as von Mises, Tresca, Hill yield criterion and so on. Considering T-stress or complete stress field, Sousa et al. [5] calculated PZ of the crack tip based on von Mises yield criterion. Vasco-Olmo et al. [6] studied the shape and size using both von Mises yield criterion and Tresca yield criterion and analyzed the influence of PZ on the crack tip shielding. Xin et al. [7] investigated PZ of the crack tip based on Hill yield criterion for orthotropic materials and isotropic materials. Nazarali and Wang [8] analyzed the effect of T-stress on PZ of the crack tip based on von Mises yield criterion. Based on the finite element method, Caputo et al. [9] investigated the effect of the loading conditions, the yield limit, the crack length and the thickness on PZ size. Chen et al. [10] analyzed the relationship between cyclic PZ size and the maximum crack opening displacement. Bouiadjra et al. [11, 12] studied the effect of micro-cracks and microcavities on PZ shape and size of the macro-crack tip. Paul [13] analyzed the influence of the inclusion on PZ of the crack tip. Based on experimental method, Korda et al. [14] observed cyclic PZ by in situ scanning electron microscope for high-strength steels. Mishra and Parida [15] studied PZ at a center crack tip in a thin sheet by the photostress coating method.

From the microscopic point of view, actually, the plastic deformation at the crack tip is due to dislocations emitted from the crack tip. Ding et al. [16], Saka and Agata [17], Goswami and Pande [18] and Ohr el al. [19,20,21,22] observed the dislocations at the crack tip by experiments. Some theoretical dislocation models were proposed to explain the micro-mechanism of PZ. Bilby et al. [23] proposed the famous BCS model that the yield zone was represented by continuously distributed dislocations along the crack line. Chang and Ohr [24] improved BCS model and proposed the dislocation-free zone model. The model considered that there was an elastic zone between the crack tip and PZ, which was observed by transmission electron microscope fracture experiments [18, 19, 22]. Lung and Xiong [25] proposed a negative dislocation model to modify BCS model. Atkinson and Kanninen [26, 27] proposed an inclined strip yield super-dislocation model. Chen and Takezono [28] and Lee and Chung [29] presented the inclined strip yield continuous dislocation model. The results [23,24,25,26] shown that these dislocation models have certain limitations to represent the shape of PZ, but they are valid to calculate PZ size and the crack tip open displacement.

It is difficult to avoid generating micro-cracks in the process of material manufacture and application. So the interaction problem between the micro-cracks and the macro-crack was widely investigated. Kachanov [30,31,32] proposed a simple solution to crack problems that the actual tractions on individual cracks were replaced approximately by the average tractions. Gong et al. [33,34,35], Horiand and Nemat-Nasser [36] and Meguid et al. [37] studied the interaction between micro-cracks and the macro-crack based on the complex potentials method. Ibbett et al. [38] investigated the effect of the particles on the crack propagation by the extended finite element method. In order to analyze complex crack problems effectively, DDT was proposed and it was introduced in detail by the book [39]. Its core idea was that the cracks and boundaries could be replaced by the continuously distributed dislocations. Based on DDT, Han and Dhanasekar [40], Zhang et al. [41] and Li et al. [42] presented the solution of a finite plane containing cracks. Jin and Keer [43] studied interaction among multiple edge cracks. Li et al. [44] considered the effect of the micro-crack on the macro-crack propagation in an infinite plane. The influence of the defects on PZ ahead of the crack tip was investigated by some researchers based on DDT, and Chang and Kotousov [45] presented a strip yield model for two collinear cracks. Hoh et al. [46] investigated the effect of a circular inclusion on the crack tip plasticity.

The fore-mentioned works investigated the interaction between the macro-crack and micro-cracks by theoretical method, but they did not consider the plasticity of the crack tip. When the plasticity was considered, they utilized only the finite element method to analyze interaction problem between the macro-crack and micro-cracks. In this way, the micro-mechanism of interaction between the micro-cracks and PZ ahead of the macro-crack tip cannot be understood clearly. In the paper, the influence of the micro-cracks on PZ of the macro-crack tip is investigated based on DDT and the Gauss–Chebyshev quadrature method. PZ is determined based on von Mises yield criterion, and the effect of the micro-crack on PZ shape and size is analyzed. On the other hand, the DDT model is established to model PZ. The dislocation density is obtained, and the influence of the micro-crack on PZ size of the macro-crack tip is analyzed.

Formulation

In the paper, PZ of the macro-crack tip in the presence of the micro-crack is determined by von Mises yield criterion and the DDT model.

PZ based on von Mises yield criterion

Problem description

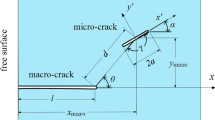
As shown in Fig. 1, an infinite plane contains an arbitrarily oriented micro-crack and a macro-crack under uniaxial tension load.

Figure 1
figure 1

An infinite plane containing a micro-crack and a macro-crack under uniaxial tension load

Full size image

The infinite plane is assumed to be elastic. The cracks can be replaced by the continuously distributed dislocations based on DDT. The problem can be equivalent to two subproblems. The first one is that an infinite plane without the cracks is subjected to remote uniaxial tension load. The second is that an infinite plane contains continuously distributed dislocations in the crack regions without external load. So the stresses at an arbitrary location can be obtained. Based on von Mises yield criterion, the yield zone can be determined. θ and α are shown in Fig. 1, and the positive values are defined in the anticlockwise direction. θ and α are called as the micro-crack orientation and the micro-crack angle, respectively.

Solution scheme

As described in “Problem description” section, the problem shown in Fig. 1 can be equivalent to two subproblems. Firstly, the solution to the second subproblem will be presented. An edge dislocation with the components of Burgers vector b x and b y is located at the position (ξ, 0) in an infinite plane. The stress components at the position (x, y) due to the dislocation can be given by

$$ \bar{\sigma }_{ij} (\xi ,x,y) = c\left[ {b_{x} G_{xij} (\xi ,x,y) + b_{y} G_{yij} (\xi ,x,y)} \right]\quad ij = xx, \, xy \, or \, yy $$
(1)

where \( c = {{2\mu } \mathord{\left/ {\vphantom {{2\mu } {\pi (\kappa + 1)}}} \right. \kern-0pt} {\pi (\kappa + 1)}} \). μ is shear modulus. κ is Kolosov’s constant and κ = (3 − v)/(1 + v) in plane stress, v being Poisson’s ratio. G(ξ, x, y) is the dislocation influence function. The first subscript on G(ξ, x, y) denotes the Burgers vector, and the last two denote the associated tractions. The expressions of G(ξ, x, y) can be obtained by the book [39].

In order to convenient statement, the macro-crack is called as crack A and the micro-crack is called as crack B. The stresses in the global coordinate system x–o–y at the point (x 1 + ξ, y 1) induced by the dislocation can be given by

$$ \bar{\sigma }_{ij} (x',y',\xi ) = c\left\{ {b_{x} G_{xij}^{AB} (x_{1} ,y_{1} ) + b_{y} G_{yij}^{AB} (x_{1} ,y_{1} )} \right\}\quad ij = xx, \, xy \, or \, yy $$
(2)

where

$$ x_{1} = d\cos \theta - \xi + x'\cos \alpha - y'\sin \alpha ;\quad y_{1} = d\sin \theta + x'\sin \alpha + y'\cos \alpha $$
(3)

The tractions in the local coordinate system x′–o′–y′ can be obtained by

$$ \bar{\sigma }_{ij} (x',y',\xi ) = c\left\{ {b_{x} G_{xij}^{AB} (x',y',\xi ) + b_{y} G_{yij}^{AB} (x',y',\xi )} \right\}\quad ij = x'y' \, or \, y'y' $$
(4)

where

$$ \begin{aligned} G_{iy'y'}^{AB} (x',y',\xi ) = G_{ixx}^{AB} (x_{1} ,y_{1} )\sin^{2} \alpha + G_{iyy}^{AB} (x_{1} ,y_{1} )\cos^{2} \alpha - G_{ixy}^{AB} (x_{1} ,y_{1} )\sin 2\alpha \hfill \\ G_{ix'y'}^{AB} (x',y',\xi ) = \left[ {G_{iyy}^{AB} (x_{1} ,y_{1} ) - G_{ixx}^{AB} (x_{1} ,y_{1} )} \right]\sin \alpha \cos \alpha + G_{ixy}^{AB} (x_{1} ,y_{1} )\cos 2\alpha \quad i = x \, or \,y \hfill \\ \end{aligned} $$
(5)

For formula (4), setting y′ = 0, the associated tractions on crack B due to the dislocation along crack A can be obtained. Setting y′ = 0, d = 0 and θ = α = 0, the associated tractions on crack A due to the dislocation along crack A can be obtained. In the same way, the associated tractions on crack A due to the dislocation along crack B can be obtained, and the associated tractions on crack B due to the dislocation along crack B can be obtained.

Numerical solution of integral equations

Based on the DDT, the micro-crack and the macro-crack can be modeled by continuously distributed dislocations. So the tractions along crack B induced by the total dislocations along crack A and crack B can be given by

$$ \begin{aligned} \bar{\sigma }_{ij}^{B} (x') =\,& c\int_{{ - a_{A} }}^{{a_{A} }} {\left[ {B_{x}^{A} (\xi )G_{xij}^{AB} (x',\xi ) + B_{y}^{A} (\xi )G_{yij}^{AB} (x',\xi )} \right]} d\xi \\ & + c\int_{{ - a_{B} }}^{{a_{B} }} {\left[ {B_{x}^{B} (\xi )G_{xij}^{BB} (x',\xi ) + B_{y}^{B} (\xi )G_{yij}^{BB} (x',\xi )} \right]} d\xi \quad ij = x'y' \, or \, y'y' \\ \end{aligned} $$
(6)

where B A(ξ) and B B(ξ) are the dislocation density of crack A and crack B, respectively. a A and a B are the half length of crack A and crack B, respectively. In the same way, the tractions components on crack A due to the total dislocations along crack B and crack A can be obtained.

The first subproblem shown is that an infinite plane without cracks is subjected to remote uniaxial tension load σ ∞. It must ensure that the crack face is traction-free, so the integral equations can be established based on the superposition principle.

$$ \begin{aligned} \sigma_{ij}^{A} (x) + \bar{\sigma }_{ij}^{A} (x) = 0\quad - a_{A} < x <\,a_{A} ;\quad ij = yy \, or \, xy \hfill \\ \sigma_{ij}^{B} (x') + \bar{\sigma }_{ij}^{B} (x') = 0\quad - a_{B} < x' <\,a_{B} ;\quad ij = y'y' \, or \, x'y' \hfill \\ \end{aligned} $$
(7)

where

$$ \sigma_{yy}^{A} (x) = \sigma^{\infty } ;\quad \sigma_{xy}^{A} (x) = 0;\quad \sigma_{y'y'}^{B} (x') = \sigma^{\infty } \cos^{2} \alpha ;\quad \sigma_{x'y'}^{B} (x') = \sigma^{\infty } \sin \alpha \cos \alpha $$
(8)

The analytical solution of singular integral Eq. (7) is difficult to obtain, but the numerical solution can be obtained by Gauss–Chebyshev quadrature method [47, 48]. The cracks are ‘singular at both ends,’ so the form of dislocation density function may be given by

$$ B(s) = {{\phi (s)} \mathord{\left/ {\vphantom {{\phi (s)} {\sqrt {(1 - s^{2} )} }}} \right. \kern-0pt} {\sqrt {(1 - s^{2} )} }} $$
(9)

where \( \phi (s) \) is an unknown function. And then Eq. (7) can be replaced approximately by a series of algebraic equations. It can be written as

$$ \begin{aligned} - \frac{\pi }{c}\sigma_{ij}^{\infty } (x) = & \frac{1}{N}\sum\limits_{I = 1}^{N} {\left\{ {a_{A} \left[ {\phi_{x}^{A} (s_{I} )G_{xij}^{AA} (t_{k} ,s_{I} ) + \phi_{y}^{A} (s_{I} )G_{yij}^{AA} (t_{k} ,s_{I} )} \right]} \right.} \\ & \left. {\quad + a_{B} \left[ {\phi_{x'}^{B} (s_{I} )G_{x'ij}^{BA} (t_{k} ,s_{I} ) + \phi_{y'}^{B} (s_{I} )G_{y'ij}^{BA} (t_{k} ,s_{I} )} \right]} \right\}\quad ij = yy \, or \, xy \\ & - \frac{\pi }{c}\sigma_{ij}^{\infty } (x') = \frac{1}{N}\sum\limits_{I = 1}^{N} {\left\{ {a_{A} \left[ {\phi_{x}^{A} (s_{I} )G_{xij}^{AB} (t_{k} ,s_{I} ) + \phi_{y}^{A} (s_{I} )G_{yij}^{AB} (t_{k} ,s_{I} )} \right]} \right.} \\ & \left. { \quad+\,a_{B} \left[ {\phi_{x'}^{B} (s_{I} )G_{x'ij}^{BB} (t_{k} ,s_{I} ) + \phi_{y'}^{B} (s_{I} )G_{y'ij}^{BB} (t_{k} ,s_{I} )} \right]} \right\} \quad ij = y'y' \, or \, x'y' \\ \end{aligned} $$
(10)

where

$$ \begin{aligned} s_{I} = \cos \left[ {{{\pi (2I - 1)} \mathord{\left/ {\vphantom {{\pi (2I - 1)} {2N}}} \right. \kern-0pt} {2N}}} \right]\quad I = 1,2, \ldots ,N \hfill \\ t_{k} = \cos \left[ {{{\pi k} \mathord{\left/ {\vphantom {{\pi k} N}} \right. \kern-0pt} N}} \right]\quad k = 1,2, \ldots ,N - 1 \hfill \\ \end{aligned} $$
(11)

The extra equations must be established to solve Eq. (10). Notice that, on the crack, there is no net dislocation.

$$ \sum\limits_{I = 1}^{N} {\phi_{x}^{A} (s_{I} )} = \sum\limits_{I = 1}^{N} {\phi_{y}^{A} (s_{I} )} = \sum\limits_{I = 1}^{N} {\phi_{x'}^{B} (s_{I} )} = \sum\limits_{I = 1}^{N} {\phi_{y'}^{B} (s_{I} )} = 0 $$
(12)

So Eq. (10) can be solved and \( \phi (s_{I} ) \) can be obtained. Further, the stress components at an arbitrary point (x, y) can be given by

$$ \begin{aligned} \sigma_{ij} (x,y) = & \frac{1}{N}c\sum\limits_{I = 1}^{N} {\left\{ {a_{A} \left[ {\phi_{x}^{A} (s_{I} )G_{xij} (x,y) + \phi_{y}^{A} (s_{I} )G_{yij} (x,y)} \right]} \right.} \\ & \left. { +\, a_{B} \left[ {\phi_{x'}^{B} (s_{I} )G_{x'ij} (x,y) + \phi_{y'}^{B} (s_{I} )G_{y'ij} (x,y)} \right]} \right\} +\, \sigma_{ij}^{\infty } \quad ij = xx, \, xy \, or \, yy \\ \end{aligned} $$
(13)

where \( \sigma_{yy}^{\infty } = \sigma^{\infty } \) and \( \sigma_{xx}^{\infty } = \sigma_{xy}^{\infty } = 0 \). PZ can be obtained by yield criterion. Considering the case of plane stress, the von Mises yield criterion is given by

$$ (\sigma_{1} - \sigma_{2} )^{2} + (\sigma_{2} )^{2} + (\sigma_{1} )^{2} = 2\sigma_{f}^{2} $$
(14)

where σ f is the yield limit and

$$ \sigma_{1,2} = \frac{1}{2}\left( {\sigma_{xx} (x,y) + \sigma_{yy} (x,y)} \right) \pm \frac{1}{2}\sqrt {\left( {\sigma_{xx} (x,y) - \sigma_{yy} (x,y)} \right)^{2} +\, 4\sigma_{xy}^{2} (x,y)} $$
(15)

Substituting Eqs. (13) and (15) into (14), the boundary of PZ can be obtained.

PZ based on the DDT model

Problem description

In the section, PZ is modeled by the distributed dislocation technique, which is called as the DDT model. As shown in Fig. 2, an infinite plane contains a finite macro-crack, a pair of symmetric micro-cracks and two plastic strips under uniaxial tension load σ ∞. The edge dislocations are emitted from the macro-crack tip. And PZ will be generated at the macro-crack tip under remote uniform tension load. In order to solve the problem, some assumptions and simplifications are made as follows:

Figure 2
figure 2

An infinite plane containing a finite macro-crack and a pair of symmetric micro-cracks under uniaxial tension load

Full size image
  1. 1.

    The material is assumed to be elastic–perfectly plastic, namely that the tensile stress σ yy in PZ is equal to the yield limit.

  2. 2.

    The plasticity at the micro-cracks tip is neglected, because PZ at the micro-cracks tip is relatively small.

  3. 3.

    The edge dislocations in PZs are distributed continuously along the line of the macro-crack.

The cracks can be replaced by the continuously distributed dislocations based on DDT. In order to narrate conveniently, PZs, the macro-crack and the micro-cracks are marked as ‘1,’ ‘2,’ ‘3,’ ‘4’ and ‘5,’ respectively, as shown in Fig. 2. The problem can be equivalent to two subproblems. The first one is that an infinite plane without the macro-crack and the micro-cracks is subjected to remote uniform tension load. The second is that an infinite plane contains continuously distributed dislocations in five regions without external load.

Solution scheme

Firstly, the solution to the second subproblem will be presented. The stresses at point (x i , 0) in region ‘i’ induced by the dislocation at location (ξ j , 0) along region ‘j’ can be given by

$$ \bar{\sigma }_{nm}^{ji} (x_{i} ) = c\left\{ {b_{{x_{j} }} G_{{x_{j} mn}}^{ji} (\xi_{j} ,x_{i} ) + b_{{y_{j} }} G_{{y_{j} mn}}^{ji} (\xi_{j} ,x_{i} )} \right\}\quad mn = xy \, or \, yy $$
(16)

Based on the principle of superposition, the stresses along region ‘i’ induced by the all dislocations in five regions can be given by

$$ \bar{\sigma }_{mn}^{i} (x_{i} ) = c\sum\limits_{j = 1}^{5} {\int_{{ - R_{j} }}^{{R_{j} }} {\left\{ {B_{{x_{j} }} (\xi_{j} )G_{{x_{j} mn}}^{ji} (\xi_{j} ,x_{i} ) + B_{{y_{j} }} (\xi_{j} )G_{{y_{j} mn}}^{ji} (\xi_{j} ,x_{i} )} \right\}} } d\xi_{j} \quad mn = xy \, or \, yy $$
(17)

where R j is the half length of the region ‘j.’ R 1 = 0.5p 1, R 2 = 0.5p 2, R 3 = a 1 and R 4 = R 5 = a 2. B(ξ j ) is the dislocation density function of the region ‘j.’ For two arbitrarily oriented and located cracks, the dislocation influence functions G(d, θ, α) have been given by “PZ based on von Mises yield criterion” section. So the dislocation influence function G ji(ξ j , x j ) in this problem can be obtained by substituting the parameters d, θ and α into d ji , θ ji and α ji . G ji(ξ j , x j ) = G ji(ξ j , x j , R j , d ji , θ ji , α ji ), and the parameters d ji , θ ji and α ji are given in Table 1.

Where p 1 is PZ size of the left tip of the macro-crack and p 2 is PZ size of the right tip. a 1 and a 2 are the half length of the macro-crack and the micro-cracks, respectively. The definition of the parameters d, θ and α is same to Fig. 1. d is the distance between the macro-crack center and the micro-crack center.

Table 1 Parameters d ji , θ ji and α ji in this model
Full size table

Numerical solution of integral equations

For the problem shown in Fig. 2, the cracks face must be ensured traction-free. And the tensile stress σ yy in PZs is equal to the yield limit. So the integral equations can be established as follows.

$$ - \frac{\pi }{c}\sigma_{mn}^{i} (x) = \frac{1}{\pi }\sum\limits_{j = 1}^{5} {\int_{{ - R_{j} }}^{{R_{j} }} {\left\{ {B_{{x_{j} }} (\xi_{j} )G_{{x_{j} mn}}^{ji} (\xi_{j} ,x_{i} ) + B_{{y_{j} }} (\xi_{j} )G_{{y_{j} mn}}^{ji} (\xi_{j} ,x_{i} )} \right\}} } d\xi_{j} \quad mn = xy \, or \, yy $$
(18)

where

$$ \begin{aligned} \sigma_{yy}^{1} (x) = \sigma_{yy}^{2} (x) = \sigma^{\infty } - \sigma_{f} ; \, \sigma_{yy}^{3} (x) = \sigma^{\infty } ;\quad \sigma_{yy}^{4} (x) = \sigma_{yy}^{5} (x) = \sigma^{\infty } \cos^{2} (\alpha ) \hfill \\ \sigma_{xy}^{1} (x) = \sigma_{xy}^{2} (x) = \sigma_{xy}^{3} (x) = 0;\quad \sigma_{xy}^{4} (x) = \sigma_{xy}^{5} (x) = \sigma^{\infty } \cos \alpha \sin \alpha \hfill \\ \end{aligned} $$
(19)

where σ ∞ and σ f are the remote tension load and the yield limit, respectively. The analytical solution of Eq. (18) is difficult to be obtained, but its numerical solution can be obtained by Gauss–Chebyshev quadrature method [47, 48]. For the macro-crack and the micro-crack, they are singular at their both ends. So the form of the dislocation density functions can be given by

$$ B_{j} (s) = {{\phi (s_{j} )} \mathord{\left/ {\vphantom {{\phi (s_{j} )} {\sqrt {(1 - s_{j}^{2} )} }}} \right. \kern-0pt} {\sqrt {(1 - s_{j}^{2} )} }}\quad j = 3,4,5 $$
(20)

For the PZs, they are bounded at their both ends. So the form of the dislocation density functions can be given by

$$ B_{j} (s) = \phi (s_{j} )\sqrt {(1 - s_{j}^{2} )} \quad j = 1,2 $$
(21)

where \( \phi (s_{j} ) \) is the unknown function. Equation (18) can be replaced approximately by a series of algebraic equations based on Gauss–Chebyshev quadrature method. It can be written as

$$ - \frac{\pi }{c}\sigma_{mn}^{i} (t_{iK} ) \quad= \sum\limits_{j = 1}^{5} {\sum\limits_{I = 1}^{N} {W_{j} R_{j} \left\{ {\phi_{{x_{j} }} (s_{jI} )G_{{x_{j} mn}}^{ji} (s_{jI} ,t_{iK} ) + \phi_{{y_{j} }} (s_{jI} )G_{{y_{j} mn}}^{ji} (s_{jI} ,t_{iK} )} \right\}} } \quad mn\,=\,xy \, or \, yy $$
(22)

where

$$ \begin{aligned} s_{1I} = s_{2I} = \cos \left[ {{{\pi I} \mathord{\left/ {\vphantom {{\pi I} {(N + 1)}}} \right. \kern-0pt} {(N + 1)}}} \right]\quad I = 1, \, 2, \ldots ,N \hfill \\ s_{3I} = s_{4I} = s_{5I} = \cos \left[ {{{\pi (2I - 1)} \mathord{\left/ {\vphantom {{\pi (2I - 1)} {2N}}} \right. \kern-0pt} {2N}}} \right]\quad I = 1, \, 2, \ldots ,N \hfill \\ t_{1K} = t_{2K} = \cos \left[ {{{\pi (2K - 1)} \mathord{\left/ {\vphantom {{\pi (2K - 1)} {(2N + 2)}}} \right. \kern-0pt} {(2N + 2)}}} \right]\quad K = 1, \, 2, \ldots ,N + 1 \hfill \\ t_{3K} = t_{4K} = t_{5K} = \cos \left[ {{{\pi K} \mathord{\left/ {\vphantom {{\pi K} N}} \right. \kern-0pt} N}} \right]\quad K = 1, \, 2, \ldots ,N - 1 \hfill \\ W_{3} = W_{4} = W_{5} = {1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-0pt} N};\quad W_{1} = W_{2} = {{(1 - s_{2}^{2} )} \mathord{\left/ {\vphantom {{(1 - s_{2}^{2} )} {(N + 1)}}} \right. \kern-0pt} {(N + 1)}} \hfill \\ \end{aligned} $$
(23)

The extra equations must be established to solve Eq. (22). Notice that there is no net dislocation on the macro-crack and the micro-cracks.

$$ \sum\limits_{I = 1}^{N} {\phi_{{x_{j} }} (s_{jI} )} = \sum\limits_{I = 1}^{N} {\phi_{{y_{j} }} (s_{jI} )} = 0 \, \quad j = 3, \, 4, \, 5 $$
(24)

So Eq. (22) can be solved. PZ size p 1 and p 2 can be obtained and \( \phi (s_{jI} ) \) can be known. Further, the dislocation density functions B(s) of PZ can be obtained by Eq. (21) where

$$ \phi (s_{j} ) = \frac{2}{N + 1}\sum\limits_{I = 1}^{N} {\left[ {\sum\limits_{h = 0}^{N - 1} {\sin \left[ {\frac{I\pi }{N + 1}} \right]\sin \left[ {\frac{I\pi }{N + 1}(h + 1)} \right]} \frac{\sin [(h + 1)\arccos (s)]}{\sin [\arccos (s)]}} \right]} \phi (s_{jI} ) $$
(25)

Results and discussion

In this section, PZ of the right macro-crack tip is only analyzed. The results of macroscopic analysis and microscopic analysis are shown as follows.

Macroscopic analysis of PZ

Comparison between theoretical and experimental results

In this section, the case is considered that an infinite plane contains only a center crack without micro-cracks under uniaxial tensile load. The comparison between theoretical and experimental results is shown in Fig. 3. The crack is located in \( - 1 \le x/a \le 1 \). The parameter a is the half length of the crack. Due to the symmetry, only the upper half part of PZ is shown.

Figure 3
figure 3

Comparison between theoretical PZ in this paper and experimental PZ

Full size image

The experimental result was obtained under the conditions of 2024-T3 Alclad specimen of size (420 × 410 × 1 mm) containing a center crack subjected to uniaxial tensile load. The crack length to sheet width ratio is 0.25. The applied stress to the yield limit ratio is 0.6. The experimental result of PZ boundary was determined based on Tresca yield criterion. Compared with the experimental conditions, the theoretical result in Fig. 3 is obtained by Tresca yield criterion. And σ ∞/σ f is also taken as 0.6.

The results show that the shape of PZ in the paper is similar to the experimental result, and the size of PZ is slightly smaller than the experimental result. So the method in the paper can be applied to predict PZ.

The effect of the micro-crack on PZ

The stress field can be obtained by Eq. (13), and PZ is determined by von Mises yield criterion. σ ∞/σ f is taken as 0.5. a is half length of the macro-crack. Half length of the micro-crack is taken as 0.1a.

The variation of PZ shape and size versus the location of the micro-crack is shown in Figs. 4 and 5. The red line denotes the boundary of PZ in the case that an infinite plane contains only the macro-crack without the micro-crack, and the thick black line denotes the boundary in the case that an infinite plane contains a micro-crack and a macro-crack.

Figure 4
figure 4

Variation of PZ versus the location of the parallel micro-crack (α = 0°)

Full size image
Figure 5
figure 5

Variation of PZ versus the location of the inclined micro-crack (α = 30°)

Full size image

In order to explain the results in Figs. 4 and 5 clearly, the case is considered that an infinite plane contains only a center crack. The contour representation of the normalized stress σ yy /σ ∞ is shown in Fig. 6. The white region denotes the stress shielding, and the gray region denotes the stress amplification.

Figure 6
figure 6

Contour representation of normalized stress σ yy /σ ∞ for a center crack in an infinite plane

Full size image

The results in Figs. 4 and 5 show that the micro-crack has a little amplification effect on PZ of the macro-crack tip when it locates in front of PZ of the macro-crack tip. This is because the macro-crack locates in the stress amplification regions of the micro-crack. As the micro-crack is close to PZ of the macro-crack tip, PZ of the macro-crack tip and the micro-crack tip will join together. PZ of the macro-crack tip increases drastically. When the micro-crack enters into PZ of the macro-crack tip, it has an obvious shielding effect on the plasticity of the macro-crack tip. This is because the macro-crack tip locates in the stress shielding regions of the micro-crack. The stress field near the macro-crack tip is relaxed by the micro-crack. When the micro-crack is behind the macro-crack tip, it decreases the width of PZ but increases the height. On the whole, in the case, the micro-crack has a little effect on PZ size of the macro-crack tip. Comparing Figs. 4 and 5, it can be observed that the micro-crack angle has a little effect on PZ of the macro-crack tip.

For LEFM, the stress field near the crack tip is obtained based on Williams [49] expansion, and the first-order term of Williams expansion is considered only. But some recent works [50,51,52,53] shown that the high-order terms of Williams expansion had a significant effect on the stress field and the crack propagation. The stress field based on DDT is the complete stress field, so the results of PZ in the paper are more precise. However, the stresses will redistribute as the plasticity generates due to stress relaxation. So PZ in this paper by the yield criterion is an approximate value.

Microscopic analysis of PZ

Comparison and analysis about PZ size

Considering the case that an infinite plane contains a center crack under uniform tensile load, the results of PZ size are obtained by different methods, as shown in Fig. 7.

Figure 7
figure 7

Comparison about PZ size obtained by different methods

Full size image

The variation of normalized PZ size p/a versus the applied stress level under remote uniform tensile load is depicted, and the comparison between the theoretical results and the experiment results is shown in Fig. 7. The results obtained by Dugdale model are same as BCS model, and the formula for calculating PZ size is given by

$$ p = a\left[ {\sec \left( {\frac{{\pi \sigma^{\infty } }}{{2\sigma_{f} }}} \right) - 1} \right] $$
(26)

The experimental results were obtained under the conditions of 2024-T3 Alclad specimen of size (420 × 410 × 1 mm) containing a center crack subjected to uniaxial tensile load. PZ size by experiments is the distance from the crack tip to the farthest point of PZ boundary.

The stresses are obtained by DDT, as shown in Fig. 6. PZ size along the crack line can be calculated based on von Mises yield criterion under plane stress condition. The results in this paper are obtained by von Mises yield criterion without considering stress relaxation, so it is smaller than other results.

The results in Fig. 7 show that the results are very close among Dugdale model, BCS model, the experiments and the DDT model. So it is reasonable that the DDT model is applied to calculate PZ size. The following results are obtained by the DDT model.

Influence of micro-cracks on dislocation distribution at the macro-crack tip

In order to view clearly, the schematic diagram of the micro-cracks and the macro-crack is shown in Fig. 8.

Figure 8
figure 8

Schematic diagram of the micro-cracks parameters

Full size image

As analyzed above, PZs are modeled as an array of continuously distributed edge dislocations. The dislocation density function can show the status of dislocation distribution in PZ, and it is plotted as follows.

The variation of normalized dislocation density versus the position x/a 1 under remote uniform tensile load for different applied stress level is depicted in Fig. 9. The other parameters are d/a 1 = 3, a 2/a 1 = 0.3, α = 0° and θ = 30°. The results show that the dislocations are in the form of inverse pileup, which is consistent with previous observations by experiments [18, 22]. The crack tip piles up a large amount of dislocations. As the applied stress increases, PZ size will increase dramatically, and the dislocations piled at the macro-crack tip will increase.

Figure 9
figure 9

Normalized dislocation density function in PZ for different applied stress level

Full size image

The variation of normalized dislocation density versus the location x/a 1 under remote uniform tensile load for different distance d/a 1 is depicted in Fig. 10. The other parameters are σ ∞/σ f  = 0.3, a 2/a 1 = 0.3, α = 0° and θ = 60°. The results show that the micro-cracks decrease PZ size. PZ size of the macro-crack tip decreases with the distance d/a 1 decreasing. In this case, the micro-cracks have a hindering effect on the dislocations omitted from the macro-crack tip.

Figure 10
figure 10

Normalized dislocation density function in PZ for different distance d/a 1

Full size image

The variation of normalized dislocation density versus the location x/a 1 under remote uniform tensile load for different micro-crack orientation θ is depicted in Fig. 11. The other parameters are σ ∞/σ f  = 0.4, a 2/a 1 = 0.3, α = 0° and d/a 1 = 3. The results show that the micro-cracks have an amplification effect on PZ size at θ = 20°, while they have a shielding effect at θ = 60° and θ = 80°. The micro-crack orientation θ has a little effect on the dislocation pileup of the macro-crack tip.

Figure 11
figure 11

Normalized dislocation density function in PZ for different micro-crack orientation θ

Full size image

The results in Figs. 9, 10 and 11 show that the dislocations are in the form of inverse pileup and the dislocation density at the both end of PZ are bounded, which is similar to dislocation distribution of the dislocation-free zone model. The dislocation density obtained by BCS model is infinite at the crack tip, which is not in conformity with the truth. So it is more proper that the DDT model is applied to analyze the dislocation distribution in PZ. However, for many materials, it is possible that several glide planes at the crack tip are activated simultaneously, and then a broad PZ is formed. In this case, the dislocations are not distributed along the line of the macro-crack, and the DDT model cannot be applied to represent the shape of PZ, but it is still valid to calculate PZ size.

Influence of the micro-crack angle on PZ size

The variation of normalized PZ size versus the micro-crack angle under remote uniform tensile load for different micro-crack orientation is depicted in Fig. 12. The other parameters are d/a 1 = 2, a 2/a 1 = 0.2 and σ ∞/σ f  = 0.4. p 0 is PZ size of the macro-crack tip without micro-cracks. The results show that the micro-cracks have a little effect on PZ size of the macro-crack tip at 60° < α < 120°. In this case, the inclination of the micro-cracks is relatively large, so the tractions on the micro-cracks face are relatively small. Hence, the micro-cracks have a little effect on the macro-crack. The effect of the micro-cracks on PZ size will get stronger as the inclination of the micro-cracks decreases at 0° < α < 60° and 120° < α < 180°.

Figure 12
figure 12

Normalized PZ size versus the micro-crack angle

Full size image

Influence of the micro-crack length on PZ size

The variation of normalized PZ size versus the micro-crack length under remote uniform tensile load for different micro-crack orientation is depicted in Fig. 13. The other parameters are d/a 1 = 2, α = 0° and σ ∞/σ f  = 0.4. The results show that the effect of the micro-cracks on PZ size of the macro-crack tip will get stronger as the micro-cracks length increases. The micro-cracks increase PZ size at θ = 15°, while they have a shielding effect on PZ size at θ > 30°.

Figure 13
figure 13

Normalized PZ size versus the micro-crack length

Full size image

Next, the amplification and shielding effect of the micro-cracks on PZ size will be analyzed in detail.

Influence of the micro-crack location (x 0/a 1, y 0/a 1) on PZ size

The variation of normalized PZ size p 2/p 0 versus the micro-crack location (x 0/a 1, y 0/a 1) under remote uniform tensile load for different micro-crack angle is depicted in Fig. 14. The macro-crack is located in \( - 1 \le x_{0} /a_{1} \le 1 \). The other parameters are a 2/a 1 = 0.2 and σ ∞/σ f  = 0.4. x 0/a 1 and y 0/a 1 are the horizontal distance and vertical distance between the macro-crack center and the micro-crack center, respectively, as shown in Fig. 8.

Figure 14
figure 14

Contour chart of normalized PZ size p 2/p 0

Full size image

The micro-cracks have an amplification effect on PZ size in the cyan regions, and they have a shielding effect on PZ size in the gray regions. The results show that the amplification and shielding regions are divided into five strip-shaped regions, which are amplification, shielding, amplification, shielding and amplification region from left to right, respectively. The size and shape of shielding and amplification regions are different for the different micro-crack angle α. Considering the case of an infinite plane containing a center crack under uniaxial tension load, as shown in Fig. 6. Figure 6 shows that the stress concentration is produced near the crack tip and the stress shielding is produced in the bottom or top of the crack face, which is the reason that there are shielding regions when the micro-cracks are located in the bottom or top of the macro-crack. There are amplification regions when the micro-cracks are located in front of or behind the macro-crack. It can be observed that the micro-cracks have a little amplification effect on PZ size at about x 0/a 1 < −1 and x 0/a 1 > 2. This is because that the distance between the micro-cracks and the macro-crack is relatively large. At about −1 < x 0/a 1 < 1 and 0.2 < y 0/a 1 < 0.6, the micro-cracks has a relatively large effect on PZ size.

Conclusion

In the paper, the problem of an infinite plane containing a macro-crack and micro-cracks is studied. PZ is determined based on macroscopic and microscopic methods. The dislocation density function in PZ is obtained. The effect of the micro-crack on PZ of the macro-crack tip is analyzed. Some conclusions can be summarized as follows.

  1. 1.

    When the micro-crack locates in front of PZ of the macro-crack tip, it has a little amplification effect on PZ of the macro-crack tip.

  2. 2.

    As the micro-crack is close to the macro-crack tip, PZ of the macro-crack tip and the micro-crack tip will join together.

  3. 3.

    When the micro-crack enters into PZ of the macro-crack tip, it has an obvious shielding effect on PZ of the macro-crack tip.

  4. 4.

    When the micro-crack is behind the macro-crack tip, it decreases the width of PZ but increases the height. On the whole, it has a little effect on PZ size.

  5. 5.

    The dislocation distribution in PZ is in the form of inverse pileup.

  6. 6.

    The effect of micro-cracks on PZ size will get stronger as the inclination of the micro-cracks decreases.

  7. 7.

    The effect of micro-cracks on PZ size will get stronger as the micro-cracks length increases.

  8. 8.

    The amplification and shielding regions are divided into five strip-shaped regions. And they appear alternately from left to right. The size and shape of the shielding and amplification regions are different for the different micro-crack angle.

The results in the paper can provide some useful information to predict the plastic behaviors in the macro-crack tip for the materials containing micro-cracks. What is more, the analysis of amplification and shielding regions is important to materials design.