Introduction

The changes in the shape and structure of a material with temperature variation have been a focus of many studies for decades. Typically, the change in geometrical parameters of a material under thermal loading is characterized by its coefficient of thermal expansion (CTE) which is normally positive for most materials, indicating that the material expands when heated and contracts when cooled. Counterintuitively, materials that exhibit negative CTE do exist. Such materials contract in at least one direction upon heating and vice versa, giving rise to a property referred to as the negative thermal expansion (NTE). Molecular materials which show NTE have been discovered and are well studied [1–10], with large negative CTEs, recorded up to −33.5 × 10−6 K−1 [4]. These materials include ceramics, zeolites and oxides such as Cu2O, ZrW2O8 and ZrV2O7 [7]. The mechanisms that govern NTE in these molecular structures mainly involve the deflections of metal–oxygen linkages in molecules with ‘bridging oxygen’ atoms [6–9], a mechanism closely related to rigid unit modes and its variants [4–6, 8–14]. Takenaka [4] has also explored other mechanisms of NTE in molecular structures. However, these mechanisms are scale dependent, operate on the nanoscale and are governed by molecular vibrations [9, 13], and thus physical modelling of the mechanism pose as a challenge.

In an excellent work by Sigmund and Torquato [15], several optimal microstructures exhibiting extreme thermal expansion were obtained from topology optimization. Vandeperre et al. [16] reported that an isosceles triangular structure with struts made of aluminium and Invar, with respective CTEs of 24 × 10−6 and 1 × 10−6 K−1, can generate CTE as low as −360 × 10−6 K−1. It was proposed that strains can be tailored through microstructural design in response to temperature as a stimulus [17]. In the work of Lakes [18], it was shown that in 2D and 3D cellular solids as well as in composites with one phase of negative bulk modulus, both high thermal expansion and high modulus can be obtained. In lieu of this, the current advancement of engineering technologies has made it possible for man-made metamaterials to be produced which exhibit extreme properties such as NTE and auxeticity or NPR (characterized by a negative Poisson’s ratio). This generates the possibility to explore a whole new dimension of engineering materials previously thought to be impossible. For a recent comprehensive review on auxetic metamaterials, refer [19] and for NTE refer [4, 20].

One of the more widely studied structures is a triangular truss-like structure which exhibits anisotropic NTE via the scale-independent ‘shortening of triangles’ mechanism [21–25]. Obviously, the extent of the NTE and the CTE of the overall structure would be highly influenced by the material properties and the dimensional parameters of each rib in the triangular cell [21]. This means that, in most cases, the overall CTE of the structure is tailorable and an arbitrary value of the CTE can be obtained through careful material selection and design. Space trusses in the form of 3D tetrahedrons, inspired from the 2D triangles, have also been shown to be capable of NTE [23, 24], while in-plane isotropic NTE has also been shown in 2D planar hexagonal, triangular and square designs based on an arrangement of the root triangular structure [25]. Some structures such as the bimetallic chiral structure [26] were also studied for its NTE on top of its auxetic properties. Wu et al. [27] provided experimental proof of occurrence of isotropic NTE in 2D anti-trichiral and anti-tetrachiral metamaterials constructed from two material ribs. A bimetallic design was explored in [28] which made use of a modified simple re-entrant structure with bimetallic curved ribs. With relation to this, the study in [22] also shows the incorporation of the triangular NTE structure into a rotating triangle auxetic, thus creating a planar structure which displays both NTE and NPR.

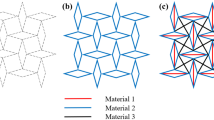
With the exception of the bimetallic design, the NTE mechanism studied in most cellular metamaterials depends on the ‘shortening of triangles’ mechanism. However, the proposed designs for the structures in most of these studies were incapable of showing any auxetic properties. The list of cellular metamaterials capable of existing NTE is till limited in the ‘menu card’ of metamaterials. As an expansion to this, the following paper explores linear NTE in a man-made cellular triangular re-entrant structure. Figure 1 shows the re-entrant triangular metamaterial microstructure analysed in this paper. Designs for dual-material triangular re-entrant structure that is potentially capable of both NTE and NPR were subsequently introduced. The occurrence of both these properties simultaneously in a structure, with their range being a modifiable to a certain capacity, allows for its extensive applications ranging from electronic sensors and actuators to composite structures with extreme mechanical and thermal load bearing capabilities. In this paper, only NTE was studied because the material modifications were performed to the existing cellular re-entrant triangular structure that evolved from topology optimization in [29] and already proven to be capable of showing NPR, without changing its intrinsic geometry. Figure 2 shows a triangular re-entrant network exhibiting NPR of about −0.8. This work is an extension to the previous NTE studies reported in the works of Lim [23, 24, 28] and Grima et al. [13, 21, 22]. The appropriate analytical study and finite element (FE) simulations were carried out to study the NTE mechanism and how the CTE of the structures changes with the change of a set of parameters.

Figure 1
figure 1

The Re-entrant triangular metamaterial microstructure used in this study and the analysed RVE to represent the periodic network

Full size image
Figure 2
figure 2

Auxetic behaviour in a re-entrant triangular metamaterial a constrained network and b auxetic response (ν ≈ −0.8) as obtained from finite element simulation using Abaqus beam elements (B31)

Full size image

Analytical modelling

The re-entrant triangular cell constructed from dual-material struts is shown in Fig. 3 along with the structural model. The geometrical parameters are illustrated in Fig. 3. In order to determine the influencing parameters and a crude trend of NTE, a simplified analytical model has been presented. Since, the cell is symmetrical about vertical axis, half of the cell was analysed. The following assumptions were made in this model

Figure 3
figure 3

Analytical representation of 2D dual-material axi-symmetric cell consisting of material 1 (in red) and material 2 (in black)

Full size image
  1. (1)

    The absence of initial internal stresses in the members.

  2. (2)

    The NTE microstructure is mainly designed for capturing NTE rather than maximizing the stiffness.

  3. (3)

    The NTE effect is mainly due to temperature-induced axial stretching/contraction of the members.

  4. (4)

    The CTE is linear only for small range of temperatures.

  5. (5)

    The pin joints are assumed frictionless.

  6. (6)

    The absence of any other external force.

The firm lines represent the initial positions of the cell and the dashed lines represent the displaced positions of the cellular struts after a temperature change ΔT. The subscripts 1 and 2 refer to the parameters of the longer and shorter (re-entrant base) chevron struts, respectively. Points A, B and C were assigned rolling contacts. Equation 1 relates the CTE α of the struts of cellular representative volumetric element (RVE) and the thermal strain in the struts due to a temperature change ΔT.

$$ \varepsilon = \alpha \Updelta T. $$
(1)

Due to a change in temperature ΔT, the lengths of the struts change depending on the expansion/contraction. The lengths after expansion/contraction can be given as

$$ L_{i}^{\prime} = L_{i} \left({1 + \alpha_{i} \Updelta T} \right)\quad \left({i = s_{1},\;s_{2}} \right). $$
(2)

The L 2 and L 1 can be correlated as

$$ L_{1} = L_{2} \frac{{\sin \theta_{2}}}{{\sin \theta_{1}}}. $$
(3)

Due to the thermal expansion/contraction of struts, the angles between the struts also change. From geometrical situation, Eq. 4 can be easily deduced:

$$ \theta_{i}^{\prime} = \sin^{- 1} \left({\frac{{\sin \theta_{i}}}{{1 + \alpha_{i} \Updelta T}}} \right). $$
(4)

Similarly, the parameters a and b can be written as

$$ a = L_{2} \cos \theta_{2}, $$
(5)
$$ b = 2L_{2} \sin \theta_{2}. $$
(6)

The dual-material cell is designed such that it exhibits NTE along Y-axis and positive thermal expansion along X-axis. Thus, the structure depicts anisotropic thermal expansion. Here we are interested in NTE which is observed along Y-axis. This will be illustrated more clearly in the next section on FE modelling. Therefore, the thermal strain in Y direction (refer Fig. 3) can be evaluated from change in height dc using Eq. 7.

$$ \varepsilon_{Y} = \frac{\rm dc}{c}, $$
(7)

where dc represents the change in dimension c of cell as projected on Y-axis. Using Eq. 8, the value of dc can be evaluated

$$ {\rm dc} = \left[{\left\{{L_{2} \left({1 + \alpha_{s2} \Updelta T} \right)\sin^{- 1} \left({\frac{{\sin \theta_{2}}}{{1 + \alpha_{s2} \Updelta T}}} \right) - L_{2} \cos \theta_{2}} \right\} - \left\{{L_{1} \left({1 + \alpha_{s1} \Updelta T} \right)\sin^{- 1} \left({\frac{{\sin \theta_{1}}}{{1 + \alpha_{s1} \Updelta T}}} \right) - L_{1} \cos \theta_{1}} \right\}} \right]. $$
(8)

From geometry, the relation for evaluating c can be derived as shown in Eq. 9.

$$ c = L_{2} \cos \theta_{2} - L_{1} \sin \theta_{1}. $$
(9)

Substituting the value of dc, c and L 1 in Eq. 7, the expression for evaluating thermal strain in Y-direction can be written as

$$ \varepsilon_{Y} = \left[{\frac{{\left\{{(1 + \alpha_{s2} \Updelta T)\cos \left[{\sin^{- 1} \left({\frac{{\sin \theta_{2}}}{{1 + \alpha_{s2} \Updelta T}}} \right)} \right] - \cos \theta_{2}} \right\} - \frac{{\sin \theta_{2}}}{{\sin \theta_{1}}}\left\{{(1 + \alpha_{s1} \Updelta T)\cos \left[{\sin^{- 1} \left({\frac{{\sin \theta_{1}}}{{1 + \alpha_{s1} \Updelta T}}} \right)} \right] - \cos \theta_{1}} \right\}}}{{\cos \theta_{2} - \left({\frac{{\sin \theta_{2}}}{{\sin \theta_{1}}}} \right)\cos \theta_{1}}}} \right]. $$
(10)

From Eqs. 1 and 10, the expression for evaluating thermal expansion (negative) in Y direction can be written as

$$ \alpha_{Y} = \frac{1}{\Updelta T}\left[{\frac{{\left\{{(1 + \alpha_{s2} \Updelta T)\cos \left[{\sin^{- 1} \left({\frac{{\sin \theta_{2}}}{{1 + \alpha_{s2} \Updelta T}}} \right)} \right] - \cos \theta_{2}} \right\} - \frac{{\sin \theta_{2}}}{{\sin \theta_{1}}}\left\{{(1 + \alpha_{s1} \Updelta T)\cos \left[{\sin^{- 1} \left({\frac{{\sin \theta_{1}}}{{1 + \alpha_{s1} \Updelta T}}} \right)} \right] - \cos \theta_{1}} \right\}}}{{\cos \theta_{2} - \left({\frac{{\sin \theta_{2}}}{{\sin \theta_{1}}}} \right)\cos \theta_{1}}}} \right]. $$
(11)

In order to calibrate the model for better prediction of values and compare it with FE modelling findings, we introduce a parameter k in Eq. 11. The parameter k covers the parameters which are difficult and tedious to include in an analytical model but can be included in FE-based models. The modified expression can be written as

$$ \alpha_{Y} = k \cdot \frac{1}{\Updelta T}\left[{\frac{{\left\{{(1 + \alpha_{s2} \Updelta T)\cos \left[{\sin^{- 1} \left({\frac{{\sin \theta_{2}}}{{1 + \alpha_{s2} \Updelta T}}} \right)} \right] - \cos \theta_{2}} \right\} - \frac{{\sin \theta_{2}}}{{\sin \theta_{1}}}\left\{{(1 + \alpha_{s1} \Updelta T)\cos \left[{\sin^{- 1} \left({\frac{{\sin \theta_{1}}}{{1 + \alpha_{s1} \Updelta T}}} \right)} \right] - \cos \theta_{1}} \right\}}}{{\cos \theta_{2} - \left({\frac{{\sin \theta_{2}}}{{\sin \theta_{1}}}} \right)\cos \theta_{1}}}} \right]. $$
(12)

It can be observed that the NTE in the Y direction depends mainly on following parameters:

  1. (i)

    the angle θ 2 of the cell,

  2. (ii)

    the dimensionless CTE of the strut (α s2ΔT), and

  3. (iii)

    the ratio of CTEs \( \left( {\frac{{\alpha_{s1} }}{{\alpha_{s2} }}} \right) \) of the struts of the cellular structure.

In order to verify and validate this, FE modelling is carried out in the following section.

Finite element modelling

Cellular structure and parameters

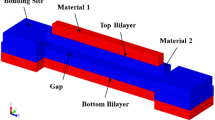
The dual-material metamaterial microstructure with re-entrant triangular structures is shown in Fig. 1. The unit cell of a symmetrical dual-material 2D triangular re-entrant structure can be simplified into a RVE as shown in Fig. 4. The cell was so designed that the ribs of the re-entrant base were of the material with a different CTE than the two chevron rods. The 2D re-entrant triangular unit cell was modelled with the geometrical parameters as shown in Fig. 4a. In this paper, a and b were taken as the vertical height and length of re-entrant base, respectively. The ratio of a to b, \( \frac{a}{b}, \) was referred to as the cell aspect ratio. The angles θ 1 and θ 2 represent the inclination of the struts with the vertical. The ribs/struts were designed to have square cross sections with sides (t × t) mm. As for the material properties, material 1 (re-entrant base material) was modelled with Young’s modulus E 1, CTE α s1 and Poisson’s ratio ν 1, while material 2 (longer chevron struts) was modelled with Young’s modulus E 2, CTE α s2 and Poisson’s ratio ν 2, where α s1 ≥ α s2. For all simulations, ν 1 = ν 2 = 0.3. The ratio of the CTEs, \( \frac{{\alpha_{s1} }}{{\alpha_{s2} }}, \) was referred to as the strut CTE ratio and the ratio of the Young’s moduli, \( \frac{{E_{1} }}{{E_{2} }}, \) was referred to as the stiffness ratio in this study. Thermal expansion of the structure is anisotropic, and the principal direction for which NTE would occur in this case for this structure was along the Y-axis. This is because of the way of design of this structure. Therefore, the CTE along this direction, α Y , was taken as a measure of NTE. The RVE was constrained using periodic boundary conditions, and as shown in Fig. 4b, green dots represent that these points are constrained to be in a straight line.

Figure 4
figure 4

Analysed 2D dual-material RVE consisting of material 1 (in red) and material 2 (in black) with a the dimensional parameters and b the regions whereby the RVE was vertically tied to the rest of the planar structure, denoted by the green circles

Full size image

Figure 5 shows a 3D RVE of the metamaterial under study. The 3D RVE maintains the dimensional parameters defined earlier for the 2D case. The only difference is that the 3D RVE consists of two 2D RVEs attached perpendicular to each other along the central axis running through the apex of each cell. Due to symmetry and periodicity, the 3D RVE will also exhibit same behaviour as 2D RVE and hence it can be analysed using 2D RVE.

Figure 5
figure 5

3D dual-material RVE consisting of material 1 (in red) and material 2 (in black) with some dimensional parameters. The RVE was simply constructed by combining two perpendicular 2D RVEs denoted by the dotted lines. The dimensional parameters from the 2D RVE carries over identically to the 3D RVE in both the Y–X and the Y–Z plane

Full size image

Simulation approach

FE simulation of a dual-material triangular re-entrant structure RVE with ribs/struts connected at the joints by welds was carried out using Simulia Abaqus CAE. The simulations were conducted on a RVE instead of on a 2D planar structure or 3D network. This is to minimize simulation time and to ease the change of dimensional parameters in between trials. The 2D RVE was constrained with periodic and symmetry boundary conditions and was simulated for a thermal load. The principal linear CTE of the structures was evaluated using Eq. 1. The thermal strain was evaluated using the change in (a − h) along the Y-direction caused by change in temperature ΔT, where ΔT ≠ 0. A positive strain in Y direction indicates an increase in height and vice versa. The FE model for evaluating thermal strains can be represented using Eq. 13.

$$ \varepsilon_{ij}^{\rm th} = \alpha \left[{T - T_{0}} \right]\delta_{ij}, $$
(13)

where δ ij is the Kronecker delta function.

Figure 6 shows the element study for the simulation of RVE. Solid elements (C3D8R) are stiff in bending and prone to locking. Therefore, they give lower values of α Y . In order to overcome these problems, very fine mesh has to be used which becomes computationally expensive. By using single layer of shell elements (S4R), appropriate values of α Y are obtained. However, shell elements also cannot effectively capture the effects of rotation and bending. When beam elements (B31) are used, the simulated values for α Y converge and reach a stable value using the least number of elements. Beam (B31) elements are shear flexible with linear interpolation. With respect to this, the computation time using beam elements was also significantly lower, making it the best choice among the three elements for further simulations. The choice of beam elements also eases the parametrization during simulations, as and when necessary. The beam elements also allow arbitrary specification of section properties such as I and A. Truss elements (T3D2) were not used as they can carry only axial loads and this will not solve our purpose. The truss elements are mainly used for design for stiffness and here our objective is to capture the NTE effect which is exhibited well by beam elements. A convergence study was also done with iterations of different numbers of elements to test the precision and accuracy of the FE modelling approach on simulations of the unit cells. This study was done to determine the suitable seed size for meshing before any of the primary simulations were carried out. In the convergence study, the number of elements was changed by varying the global seed size for meshing and halving it with each subsequent trial. Figure 7 shows the convergence plots for the re-entrant triangular RVE. From the convergence study, suitable number of elements was determined in order to obtain a converged solution.

Figure 6
figure 6

α Y , computational time and the number of elements in the RVE for a converged mesh result in a 2D triangular re-entrant unit cell for a solid elements C3D8R, b shell elements S4R and c beam elements B31

Full size image
Figure 7
figure 7

Mesh convergence study for FE analyses on a 2D triangular re-entrant RVE for a solid elements, b shell elements and c beam elements

Full size image

Results and discussion

The mechanism of NTE

Figure 8 shows a scaled up re-entrant deformation mechanism for the simulated 2D re-entrant triangle cell at different temperatures. When the structure is cooled as in Fig. 8a, the base ribs of material 1, with higher α s1, contract more than the other ribs, pushing the cell upwards and increasing its height. Conversely, the base ribs expand more than the other two when the structure is heated as in Fig. 8b. This pulls the cell downwards, decreasing the overall height. In both cases, the height of the cell changes counterintuitively with temperature, whereby a positive change in temperature results in a negative change of height and vice versa. The thermal expansion of the cell is anisotropic as the horizontal length of the cell changes positively with temperature. It can be observed that the negative CTE occurs along the Y-axis. Further analyses also ascertain that α Y is not temperature sensitive nor is it scale dependent.

Figure 8
figure 8

The mechanism of NTE in the 2D re-entrant triangle structure. The structure is depicted at a −50 °C, b room temperature, i.e. 25 °C and at c 100 °C

Full size image

Figure 9 illustrates the 3D re-entrant triangular unit cell simulated at temperatures above and below room temperature. The height of the cell decreases with an increase in temperature, and vice versa. In this structure, lateral expansion (or contraction) occurs along the two perpendicular YX and YZ planes. With an increase in temperature, the base plane (XZ) expands more and pulls the cell downwards and vice versa. The 3D cell also exhibits same behaviour as obtained from the 2D structures. It is observed that the way the values of α Y change with the geometrical and material parameters, follow the same trend both in 3D and in 2D. This is because the lateral expansion of the cell along one plane (say, YX) is exactly the same and is not constrained by the expansion of the cell along the perpendicular plane (YZ). Also, the two cells on these two planes are identical and symmetrical about the centre. The 3D structure is, in essence, two 2D structures independently and perpendicularly bonded together. It was found that the values for α Y in both cases are identical when simulated under the same parametric conditions. Consequently, the results apply to both 2D and 3D configurations of the dual-material metamaterial under investigation.

Figure 9
figure 9

The mechanism of NTE in the 3D re-entrant triangle structure. The structure is depicted at a −50 °C, b room temperature, i.e. 25 °C and at c 100 °C

Full size image

These re-entrant triangular truss alike metamaterial structures are so designed that they exhibit NTE and anisotropic thermal expansion based on stretch-dominated mechanisms. However, from Fig. 8 it seems that some buckling takes place due to thermal loading. Thus, for design purposes this needs to be taken into account. The critical buckling load of a pin end column of square section of dimensions t × t and length L, Young’s modulus E and section moment of inertia I is given by

$$ P_{\rm cr} = \frac{{\pi^{2} EI}}{{L^{2}}}. $$
(14)

For a square cross section of dimensions t × t, the area moment of inertia I is given by

$$ I = \frac{{t^{4}}}{12}. $$
(15)

Substituting Eq. 15 in Eq. 14, P cr for our problem can be written as

$$ P_{\rm cr} = \frac{{\pi^{2} Et^{4}}}{{12L^{2}}}. $$
(16)

The crippling strain corresponding to crippling load P cr can be obtained by dividing the load with cross-sectional area and Young’s modulus. Rearranging the terms we get

$$ \varepsilon_{\rm cr} = \frac{{\pi^{2} t^{2}}}{{12L^{2}}}. $$
(17)

For our problem, we can see from simulations (Fig. 8) that buckling seems to occur predominantly in longer chevron struts made of a material with CTE α s2 lower than the one of the material of re-entrant base α s1 (α s2 < α s1). Consider a specific case in which the re-entrant triangular structure has L = 4 mm and t = 0.5 mm. Substituting these values in Eq. 17, the crippling strain ϵ cr comes out to be 0.01288. Now substituting the values of α s1 = 8 × 10−6 K−1 and ϵ cr = 0.01288 in Eq. 1, the temperature difference corresponding to thermal crippling strain comes out to be ΔT = 1610 °C. Thus, it is confirmed that for given temperature changes (in Fig. 8) buckling is not occurring. The buckling type effect in Fig. 8 is just a visual effect in FE software due to scaling up. For specific design purposes, the buckling effect can be quantified by equating crippling strain to thermal strain.

Variation of NTE with geometrical parameters and material properties

As shown in “Analytical modelling” section, NTE in the Y direction depends on the angle θ 2, ratio of CTEs \( \left( {\frac{{\alpha_{s1} }}{{\alpha_{s2} }}} \right) \) of the struts of the cellular structure and the dimensionless CTE of the longer chevron strut (α s2ΔT). A number of simulations were performed to study the variation of α Y with α s2ΔT for different values of θ 2. The results of these simulations are plotted in Fig. 10. It can be observed that for this metamaterial α Y becomes more negative with decreasing values of α s2ΔT. Furthermore, α Y becomes more negative for higher values of θ 2. In order to obtain more NTE, lower values of the dimensionless CTE α s2ΔT and higher values of θ 2 are recommended.

Figure 10
figure 10

Variation of α Y with α s2ΔT in a triangular re-entrant RVE for θ 2 = {10, 20, 30, 40, 45, 50}°

Full size image

The CTE of the cellular material depends on the material properties of the constituent material of the struts. As an engineering question of what ratio of the CTEs of the struts \( \frac{{\alpha_{s1} }}{{\alpha_{s2} }} \) should be used and what values of θ 2 should be used to obtain more NTE, several FE simulations were carried out. Figure 11 shows the variation of non-dimensional α Y /α s2 with θ 2 for different values of \( \frac{{\alpha_{s1} }}{{\alpha_{s2} }}. \) It can be observed from Fig. 11 that the trend is non-linear. The α Y becomes more negative with an increase in \( \frac{{\alpha_{s1} }}{{\alpha_{s2} }} \) and θ 2. It is interesting to note that the NTE effect is not pronounced for \( \frac{{\alpha_{s1} }}{{\alpha_{s2} }} < 4. \) Thus, it is recommended that such a system will exhibit NTE for \( \frac{{\alpha_{s1} }}{{\alpha_{s2} }} > 4. \)

Figure 11
figure 11

Variation of non-dimensional α Y /α s2 with θ 2 for different CTE ratios α s1/α s2 = {1, 2, 4, 5, 6, 8}

Full size image

For structural applications, the effect of stiffness ratio \( \frac{{E_{1} }}{{E_{2} }} \) on α Y needs to be evaluated as the stiffness of the struts may influence thermal strains. Figure 12 shows the plot of α Y with α s2ΔT for different values of stiffness ratio of the struts \( \left( {\frac{{E_{1} }}{{E_{2} }}} \right). \) It can be observed that the stiffness ratio has a small effect on α Y . However, it can be seen that α Y becomes slightly more negative for higher values of the stiffness ratio \( \frac{{E_{1} }}{{E_{2} }} \) and at lower values of the dimensionless CTE α s2ΔT. In other words, the NTE effect becomes slightly more prominent as the re-entrant base material becomes stiffer relative to the longer chevron strut. However, there is no major effect of stiffness ratio on NTE. As the plots of the chosen parameters in Fig. 12 overlap each other due to close data population, this was further visualized from plot of α Y with \( \frac{{E_{1} }}{{E_{2} }} \) for different values of θ 2 (Fig. 13) keeping other parameters constant. It can be observed from Fig. 13 that for \( \frac{{E_{1} }}{{E_{2} }} > 0.2, \) the slope of the curve becomes nearly zero. It is evident now that stiffness ratio has only slight effect on α Y . Furthermore, it should be taken into account that if E 1 is too small relative to E 2, the re-entrant base material would simply deform and buckle before it is able to efficiently expand and push the entire cell out laterally.

Figure 12
figure 12

Variation of α Y with α s2ΔT in a 2D triangular re-entrant RVE for stiffness ratios, E 1/E 2 = {0.1, 0.5, 0.7, 1.0, 1.5, 2.0}

Full size image
Figure 13
figure 13

Variation of α Y with stiffness ratio, E 1/E 2 for different values of θ 2

Full size image

Comparison of analytical and finite element findings

Figure 14 shows the variation of the non-dimensional thermal expansion coefficient term α Y /α s2 with θ 2 for different values of \( \frac{{\alpha_{s1} }}{{\alpha_{s2} }} \) as obtained from analytical solution (Eq. 12) for k = 0.5. It can be observed from both Figs. 14 and 11 that the calibrated analytical model and the FE solution predict the same trend and they are in good agreement with each other. Both the figures confirm that the trend is non-linear and the effect of NTE becomes more negative for higher CTE ratios, \( \frac{{\alpha_{s1} }}{{\alpha_{s2} }}, \) and for higher values of θ 2.

Figure 14
figure 14

Variation of the non-dimensional term α Y /α s2 with θ 2 for different CTE ratios α s1/α s2 = {1, 2, 4, 5, 6, 8} as evaluated from the analytical model

Full size image

Further discussion

The deformation mechanism of the cell under thermal loading is due to the lateral stretch (or contraction) of the base of the cell with respect to the other ribs. This implies that NTE in a 2D re-entrant unit cell can also be described using the CTE of the structure along the X-axis, α X , which is calculated using Eq. 14, where b was earlier defined in Fig. 4; Δb is the change in the value of b along the X-direction under thermal loading, and ΔT is the change in temperature. Here, a positive Δb indicates that the base length of the unit cell is increasing. A positive thermal expansion in X-direction makes this structure to exhibit anisotropic thermal expansion. Thus, it is important to study how the CTE in X-direction varies with cell geometry (a/b) which are mainly governed by single parameter θ 2. For instance, Fig. 15 shows the relationship between α X and the θ 2. α X rises rapidly with θ 2 to a maximum value before decreasing gradually to a value around CTE of material 1, α s1. However, the value of α X is also not readily available (except for the case where h = 0 and α X  ≈ α s1), and is dependent on all other parameters as well.

$$ \alpha_{x} = \frac{\Updelta b}{b\Updelta T}. $$
(18)
Figure 15
figure 15

Variation of α X with θ 2 in a 2D re-entrant triangular RVE

Full size image

Figure 16 depicts a 4 × 4 planar structure comprising of 2D re-entrant triangles simulated for a thermal load of 75 °C above room temperature. The simulation demonstrates that the planar structure is equally capable of showing NTE, with negative CTEs up to −2.8 × 10−6 K−1 recorded for this set of parameters. This is in agreement with the negative CTE obtained with beam elements as in Fig. 6c. This also justifies the RVE selection and choice of beam elements to model this metamaterial.

Figure 16
figure 16

Negative thermal expansion in a 4 × 4 2D planar structure. The structure was simulated for a temperature rise to 100 °C from room temperature (25 °C)

Full size image

One aspect that needs further attention is that the CTEs are considered to be constant, leading to linear expansions. However, such trend is exhibited only up to limited temperature range. In such situations, the mean CTE will serve the purpose. Rewriting Eq. 13 in terms of mean CTE α m, we get

$$ \varepsilon_{ij}^{\rm th} = \alpha_{\rm m} \left[{T - T_{0}} \right]\delta_{ij}. $$
(19)

When temperature effects are considered, the mean CTE α m can be evaluated as

$$ \alpha_{\rm m} = \frac{{\int_{{T_{0}}}^{T} {\alpha {\rm d}T}}}{{[T - T_{0}]}}. $$
(20)

Furthermore, these metamaterial structures may behave in a drastically different manners under extreme temperature conditions such as Arctic pole (−30 °F), Antarctic pole (−129 °F), Ocean bed (−4 °C) and space (ranging from as low as −32 °F to as high as 3500 °F). Under such conditions besides the thermal coefficients, the material properties also play a crucial role. Ductile brittle transitions, embrittlement, etc., also start to play role. Together with NTE, the metallurgical aspects should be investigated in future to enforce the application of NTE materials in aviation, spacecraft, submarine and other equipment.

Importantly, the potential of tailorable CTEs in such a structure brings about contributions to the composite industry whereby composites can be made by combining the NTE phase with other components to tune the overall CTE to a specific value for a particular application, especially when zero thermal expansion is required in high thermal stress scenarios [24]. This NTE concept in cellular metamaterials is also promising in the design of voided composites which can exhibit NTE. Design of fasteners that expand on cooling will be useful in achieving tight fastening under cold industrial environments [30]. On a smaller scale, the NTE and auxetic properties can also be useful for an array of electronic applications, which include the production of micro-sensors and micro-actuators that respond to thermal stimulus. This NTE property can also be used in the dental braces which adjust their tightness over the teeth in response to the temperature. In space applications where the components are subjected to extreme thermal environments, this property can be used to counter the effects of positive thermal expansion, although, in extreme environments, metallurgical aspects of these materials will also come into effect. Inspired from [31] which mentions that thermal distortion of solar arrays of Hubble telescope caused due to extreme thermal environments makes them vibrate, the property of NTE can be useful in optics and space components to counter the effect of positive thermal expansion. Coupling the effects of NTE with ferroelectricity and magnetism can open up novel applications of NTE effect where controlled thermal expansion is desired in ferroelectric and magnetic environments [32]. Mechanoresponsive polymers [33] with NTE property at ambient temperature have potential applications in drug delivery, smart optical systems, micro-electromechanical systems, near-infrared-based macromolecular switches and motors and for thermal energy storage/conversion at ambient temperatures.

Conclusions

In this paper, NTE behaviour in a re-entrant triangular metamaterial structure was studied using analytical and FE techniques. The overall thermal expansion of the cell was anisotropic, i.e., negative along vertical axis and positive along horizontal axis. The structure was constructed from two different materials that are welded/bonded/brazed together. Abaqus beam elements (B31) were found suitable to effectively model the NTE effect in such metamaterial structures. Effectively, it was shown that the dual-material re-entrant triangle is fully capable of exhibiting NTE with tailorable CTE on top of its auxetic properties, which opens up a new range of practical applications. In all cases, the NTE effect is scale and temperature independent and occurs principally along the height of the cell. The mechanism of NTE in this cellular structure was stretch-dominated. The extent of NTE is more negative for higher values of θ 2, i.e., the inclination of the longer chevron strut with the vertical, lower values of α s2ΔT, i.e., non-dimensional CTE of the longer chevron strut and for higher values of the CTE ratio of struts \( \left( {\frac{{\alpha_{s1} }}{{\alpha_{s2} }}} \right). \) It is recommended that for such a structure to exhibit pronounced NTE effect, the CTE ratio of struts should be greater than 4, i.e., \( \frac{{\alpha_{s1} }}{{\alpha_{s2} }} > 4. \) The ratio of the Young’s moduli of the materials has negligible effect on the overall CTE of the cell. The FE prediction agrees well with the calibrated analytical model. In future research, several other metamaterial and truss structures capable of exhibiting NTE should be developed and analysed for exploiting the NTE effect in engineering applications.