Optoelectronic and thermoelectric properties of KAuX₅ (X = S, Se): a first principles study

Abstract

The electronic structure as well as optical and thermoelectric properties of the orthorhombic polychalcogenides of gold KAuX₅ (X = S, Se) compounds have been investigated using full-potential linearized augmented plane wave within the framework of the density functional theory (DFT). The local density approximation (LDA), generalized gradient approximation (GGA) by Perdew, Burke and Ernzerhof (PBE), Engel–Vosko generalized gradient approximation (EV-GGA), and the recently modified Becke–Johnson approximation (mBJ) formalism are used for the exchange correlation energy to calculate the total energy. The results show that KAuX₅ (X = S, Se) is a direct band gap semiconductor at Γ–Γ point. The total and partial density of states indicate that the states Au-d, S-p, and Se-p of both compounds have strong contributions to valence band in the energy range from −10 up to 0.0 eV. One can notice from electronic charge density that both compounds show greater iconicity and smaller covalency. Optical properties with photon incident energy up to 14.0 eV have been calculated and analyzed. Important transport properties such as Seebeck coefficients as well as thermal and electrical conductivities and effective mass are obtained and discussed in details.

Introduction

Alkali metal polychalcogenide salts in molten state have been an excellent preparation technique at intermediate temperature for the production of new polychalcogenide compounds [1, 2]. Both Au and Cu are especially among the most reactive toward polychalcogenide species (Qx 2-; Q) S, Se, Te) which give rise to several phases with an attractive feature. At present, different polychalcogenides materials (compounds of S, Se, and Te) are studied by many methods. Due to the fact that these compounds have wide range of chalcogenides properties and, as a result, it has wide area of their practical applications [3] in optoelectronics, photovoltaic and thermoelectric energy conversion, phase change memory devices, catalysis, etc.

The coinage metals comprise d¹⁰ got considerable curiosity due to its potential attractive d ¹⁰–d¹⁰ interactions which is still contentious and issue of a discussion marked [4]. The engrossing photophysical properties and photochemical of luminescent d¹⁰ compounds make them sympathetic for their expected applications in organic light emitting diode display technology [5]. Furthermore, there is electron paucity in the majority of the heteroatom-centered complexes and the gold–gold interactions give a considerable input to their stability [6]. Gold (Au) is infamous material in electrical devices packaging [7]. Cui et al. [8] comprehensively enquired the functional and mechanical stabilities of Gold nanoclusters, which also got substantial consideration because of their good photostability, high fluorescence, exceptional biocompatibility, non-toxicity, and solubility [9]. In recent time's implausible work has been made by Seryotkin et al. [10] by synthesizing gold–silver sulfoselenides from melts on heating stoichiometric mixtures of elementary compounds in evacuated quartz ampoules, which results in a series of compounds, i.e., (x = 0.25, 0.5, 0.75, 1, and 1.5). In reaction with the molten polychalcogenide salt, gold losses its mobility and melts quickly at low temperature of 190 °C [11]. In the beginning of the nineteenth century Bertholet [12] gives the description that gold dissolves in alkali steel poly sulfide melts but not in the molten sulfur. The chemical viewpoints of ternary mixtures (A = alkali metal; X = S, Se, Te) are very significant because of many phases possibilities. The strong subjectivity of gold for chalcogen atoms shows the substantiation in the described ternary compounds [13, 14], encloses long-chain polychalcogenides. Bakakin also worked on the chalcogenides and investigated thirteen chalcogenides crystal structures which are Na, Au(I), and Ag(I) in the series, with, from incorporated positions on the base of sphenoidal portrayal. New potential in crystal geometry and crystallochemical inquiry of inorganic compounds whose structures are differentiated by a moderately consistent distribution of atoms are proven as a prototype of chalcogenides [15]. Much experimentally data on the crystal structure of ternary chalcogenides depending on the elements of the IB group have been collected up to date. Although, their portrayal is usually rather eclectic, even in review (see, for example [16, 17]). Our relative analysis of 80 crystal organisations of Au(I), Ag(I), and Cu(I) mono chalcogenides with alkaline and Tl¹⁺ cations showed that all kinds can be systematized based on rod fragments as slashes from standard sphere packings: close_packed, body_centered, and primitive. Each cramming has exact steric distinctions which sway the possibility of the potential placement of atoms after cramming, based on their total sizes and the feature of chemical bonding.

From above it is clear that there is dearth information about the electronic band structures and the optical properties of KAuS₅ and KAuSe₅ compounds. Thus in this manuscript, we have comprehensively discussed the electronic band structure, charge density, effective mass, optical properties and thermoelectric properties of KAuS₅ and KAuSe₅ using full-potential linearized augmented plane-wave (FP-PLAW), as implemented in the WIEN2K computer package, within the local density approximation (LDA), generalized gradient approximation (GGA) by Perdew, Burke and Ernzerhof (PBE), Engel–Vosko generalized gradient approximation (EV-GGA), and the recently modified Becke–Johnson approximation (mBJ) exchange correlation.

Crystal structure and computational details

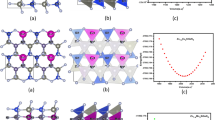
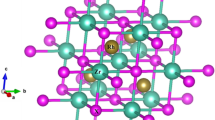
The investigated compounds KAuX ₅ (X = S, Se) have orthorhombic symmetry with space group Ibam (# 72). The crystal structure of these compounds is shown in Fig. 1. The crystallographic parameters of our investigated compounds are summarized in Table 1. The bond lengths and bond angles are given in Table 2 and 3 for both compounds in comparison with the experimental data. Now-a-days, the density functional theory (DFT) is the most accurate and successful microscopic theory in the field of computational materials science [18, 19]. WEIN2K package based on FP-LAPW method was carried out to calculate the electronic band structure, total and partial density of states, optical and thermoelectric properties of KAuX ₅ (X = S, Se). The exchange correlation potential was treated using the local density approximation of Ceperley–Alder (LDA) [20], and Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) [21], to calculate the total energy. Furthermore, to avoid the well-known LDA and GGA underestimation of the band gap, we have used the Engel–Vosko generalized gradient approximation (EVGGA) [22] and the recently modified Becke–Johnson (mBJ) approximation [23]. We have optimized the atomic positions by minimizing the forces acting on each atom. From the relaxed geometry the chemical bonding and the electronic structure can be find out and different spectroscopes can be simulated and compared with experimental data [24]. In the calculations reported here, we used plane-wave cut off parameter $R_{\text{MT}} K_{\hbox{max} } = 7$, determine the matrix size, (where R _MT is the smallest radius of all atomic Muffin-tin spheres and K _max represents the magnitude of the largest k-vector in the plane-wave expansion) and $G_{\hbox{max} } = 12\,{\text{a}}. {\text{u}}.^{ - 1}$for the Fourier charge density expansion was used. Muffin-tin (MT) spheres radii were chosen in such a way that there is no charge leakage from the core. These values were 2.17, 1.84, and 2.5 a.u., respectively, for Au, S, and K of KAuS₅ compound, while for KAuSe₅, it was 2.0 a.u. for all atoms. Inside the MT spheres the l _max is expanded up to 10, while outside it is constant. The Muffin-tin radii due to minimization of the forces the total energy of the system is stable in the range of 10⁻¹ Ry, and consider the self-consistent calculation were done to be convergent in KAuS₅ and KAuSe₅ respectively. For the structural properties, the integral over the Brillouin zone (BZ) is performed up to 170 k-points in the irreducible Brillouin zone (IBZ), using the Monkhorst–Pack special k-points approach [25].

Fig. 1

Molecular structure of, a KAuS ₅ , b KAuSe ₅

Table 1 Calculated and experimental lattice parameters and atomic positions of KAuX ₅ (X = S, Se)

Table 2 Calculated and experimental bond lengths and bond angles data of KAuS ₅

Table 3 Calculated and experimental bond length and bond angle data of KAuSe ₅

The complex dielectric function $\varepsilon = \varepsilon + i\varepsilon$ is used to derive the optical properties of the matter. The imaginary part of the dielectric function $\varepsilon_{2} \left( \omega \right)$ is obtained directly from FLAPW electronic calculations from the momentum matrix elements between the occupied and unoccupied wave functions within the selection rules. The real part $\varepsilon_{1} \left( \omega \right)$ is determined through the use of the familiar Kramers–Kronig relation [26]. All the other optical constants, such as the refractive index, optical reflectivity $R\left( \omega \right)$, energy-loss spectrum $L\left( \omega \right)$, absorption coefficient $I\left( \omega \right),$ and optical conductivity $\sigma \left( \omega \right),$ can be calculated from the values of $\varepsilon_{2} \left( \omega \right)$ and $\varepsilon_{1} \left( \omega \right)$ [27, 28].

In this analysis, we calculated thermal effects related to the charge carrier transport using the Boltzmann transport theory [29, 30] and the rigid band approach. This approach is applied to conductivity which is based on the transport distribution. The Boltzmann transport equation depicts the time evolution of the charge carrier distribution function under the action of electric/magnetic field and thermal gradient. In our calculation, we have used the full-potential linear augmented plane-wave method, to obtain the Seebeck coefficient and electrical properties related to temperature using some standard thermodynamic relations.

Result and discussion

Band structure

The electronic band structures of KAuX₅ (X = S, Se) are computed using the FP-LAPW technique within LDA-CA, GGA-PBE, EVGGA ,and mBJ as shown in Fig. 2. It is clear from these figures that the maximum of the valence band and minimum of the conduction band are located at Γ point of BZ, resulting in a direct band gap at $\left( {\Upgamma{-}\Upgamma } \right)$ for both KAuS₅ and KAuSe₅. We are interested in the bands around Fermi level, thus we concentrate at the energies between −2.0 and 4.0 eV. For lower energies the compounds show similar contribution of the core electrons. It is also obvious from these figures that these compounds show the semiconducting behavior. These figures further clear that the replacement of the S by Se in KAuX ₅ (X = S, Se) decreases the value of band gap energy. The values of the obtained band gap for these compounds using LDA-CA, GGA-PBE, EVGGA, and mBJ approximation are listed in Table 4. Following this table one can see that mBJ approach produces better band gap [31–34] than LDA, GGA, and EVGGA. Therefore we have used mBJ for further explanations of the density of states, optical and thermal properties of our investigated compounds.

Fig. 2

Calculated band structure of KAuS ₅ using a LDA, b GGA-PBE, c EVGGA, and d mBJ and of KAuSe ₅ using e LDA, f GGA-PBE, g EVGGA, and h mBJ

Table 4 Calculated Eg of KAuX ₅ (X = S, Se) using LDA, GGA-PBE, EVGGA, and mBJ

Density of states

For further explanation, we have calculated the total and partial density of states for KAuX ₅ (X = S, Se) as shown in Fig. 3. Following these figures one can see that the lowest lying valence bands of KAuS ₅ compound, which are situated in the range −15.0 to −10.0 eV arise due to the strong contributions of Au-d (0.12 electrons/state), S-s (0.38 electrons/state), K-s (0.52 electrons/state), and K-p (0.13 electrons/state) states, with small contributions of Au-s (0.042 electrons/state), Au-p (0.024 electrons/state), and S-p (0.032 electrons/state) states. While for the compound KAuSe ₅ it arise due to the strong contributions of Se-s (1.33 electrons/state), K-p (0.205 electrons/state), Au-p (0.108 electrons/state), and Au-d (0.105 electrons/state) states, with small contribution of Se-p (0.033 electrons/state), Se-d (0.021electrons/state), and Au-s (0.026 electrons/state) states. Negligible contribution of Au-f (0.0036 electrons/state) state in KAuS ₅ compound and both of Au-f and K-s (0.001 electrons/state) states in KAuSe ₅ compound is observed. The second group between −10.0 and 0.0 eV, which is below Fermi level has significant contribution from Au-d (5.8 electrons/state), S-p (1.17 electrons/state), S-s (0.43 electrons/state) states and both of K-p plus Au-s (0.54 electrons/state) states, with small contribution of Au-p (0.065 electrons/state) and Au-f (0.0036 electrons/state) states for KAuS ₅ compound, as shown in Fig. 3. While in KAuSe ₅ the states Se-p (0.82 electrons/state), Au-s (0.37 electrons/state), and Au-d (4.2 electrons/states) have strong contribution, and the states Au-p (0.039 electrons/state), Se-s (0.033 electrons/state), K-p (0.019 electrons/state), K-s (0.0045 electrons/state), Se-d (0.005 electrons/state), and Au-f (0.0023 electrons/state) states in KAuSe ₅ show very small contribution as indicated in Fig. 3. One can see from Fig. 3 that the state Au-d shows dominancy in the energy range from −10.0 to 0.0 eV in both compounds. In this region the valence bands are fully localized.

Fig. 3

Calculated total density state (DOS) and partial density of states (PDOS) of KAuX ₅ (X = S, Se) structure

It is also clear that there exists a strong hybridization between S-s and K-s states in KAuS ₅ , while for KAuSe ₅ it is between the states Au-s and Se-p which indicate the existence of covalent bonding in both compounds. The state Au-6s is hybridized with the S-3p state in KAuS ₅ compound and the state Au-6s is hybridized with Se-4p at lower conduction bands giving rise to anti-bonding $\pi^{*}$ and $\sigma^{*}$ bands. It is also clear from Fig. 3 that with replacing S by Se the DOS dispersion is shifted toward higher energy.

Electronic charge density

The 2D electronic charge density contours for (100) and (010) crystallographic planes of KAuX ₅ (X = S, Se) compounds are illustrated in Fig. 4. These planes possess all types of atoms. We examine the bonding features and total valence charge density distribution of KAuS ₅ and KAuSe ₅ . The charge density distribution around K, Au, S, and Se atoms depicts spherically symmetric concentration which shows ionic bond behavior, and in some areas of structures Au and S/Se atoms shared electron, which depict strong covalent interaction. As the electronegativity of S (2.58) and Se (2.55) atoms is greater than the K (1.0) and Au (2.2), which shows the greater accumulation of charges, near S and Se along the bond and the charge uniformly distributed around them. One can see easily from the color charge density scale that blue color (+1.00) confirms the maximum charge accumulation site.

Fig. 4

Electronic space charge density distribution contour calculated with mBJ in the (010) and (100) planes of KAuX ₅ (X = S, Se)

When S is replaced by Se, it shows a decrease in the transformation of charge between Au and S and also the bond length decreases. One can see that both compounds show greater iconicity and smaller covalency. The valence shell charge carrier (VSCC) properties change, due to the replacement of one atom by another [35]. It is also clear from the figure that the increase in the charge distribution at S and Se site is observed. It can also be seen that due to minor charge transfer from Au to S or Se, it is characterized by ionic bonding.

Effective mass

Here the parabolic effective-mass approach is calculated for KAuX ₅ (X = S, Se), which has better approach with the tight-bonding approximation. These calculations show better report of the electron hole asymmetry. The effective-mass approach appreciably decreases computation time as compared to atomistic behavior. The effective mass, also called the effective band mass m* found from band structure at each maximum points in k-space (usually at Γ point). At these points the minimum of the conduction band or maximum of the valence band was appropriate by parabolic curves as

$$ \frac{1}{{m_{i,j}^{ * } }} = \frac{2}{\hbar }\frac{{d^{2} E_{i,j} }}{{dK_{i,j}^{2} }} $$

(1)

where ħ is the plank’s constant. The heavy and light holes generated from the same band i, which is averaging over j, were determined from the following formula [36], resulting to the effective band mass

$$ m_{i}^{ * } = \left( {m_{i,h}^{{ *^{3/2} }} + m_{i,l}^{{ *^{3/2} }} } \right)^{3/2} $$

(2)

From these Eqs. (1, 2), it is abbreviated that in n-type semiconductors only electrons (majority charge carriers) contribute to electrical conductivity, because the electrons mass with the smallest energy in the conduction band find out the transport features of electrons (effective mass). The mechanism used to produce electron effective mass $m^{ * }$, when phonon induces in the direction perpendicular to the interfaces.

We should emphasize that there is a substantially decrease in the values of the carrier effective masses with using different exchange–correlation functional. These values are given in Table 5, in which the LDA shows greater values for the electron effective mass, heavy holes and light holes, then the next highest values are for GGA then EVGGA, whereas mBJ shows the lowest values, for KAuX ₅ (X = S, Se) around Γ-point, by appropriating the electronic band structure to a parabolic function given in Eq. (1).

Table 5 Calculated effective mass of KAuX₅ (X = S, Se) using LDA, GGA-PBE, EVGGA, and mBJ

Optical properties

Now let us turn our concern to the optical properties of the investigated compounds. These compounds have orthorhombic symmetry. The symmetry allows three non-zero dielectric tensor. Since mBJ produces better band gap for the investigated compounds, this inspires us to use this approach to examine the optical properties, which is essentially depending on band gap. The energy eigenvalues and electron wave function are required to calculate the frequency-dependent dielectric function. All optical spectra, specifically real $\varepsilon_{1} \left( \omega \right)$ and imaginary parts of the dielectric function $\varepsilon_{2} \left( \omega \right)$, reflectivity $R\left( \omega \right)$, refractive index $n\left( \omega \right)$, conductivity $\sigma \left( \omega \right)$, absorption coefficient $I\left( \omega \right),$ and energy-loss function $L\left( \omega \right)$ are studied. These are shown in Fig. 5. It is clear from these figures that both compounds have almost the same optical spectra. This is attributed to the fact that the characteristics of the conduction bands and the symmetries of the wave functions, which follow the selection rules and are fully reflected in the matrix moment elements, are somewhat similar.

Fig. 5

Calculated real and imaginary part of dielectric function, reflectivity, energy-loss function, optical conductivity, refractive index and absorption coefficient of KAuS ₅ and KAuSe ₅ using mBJ

The calculated average imaginary (absorptive) $\varepsilon_{2}^{\text{ave}} \left( \omega \right)$ and real (dispersive) $\varepsilon_{1}^{\text{ave}} \left( \omega \right)$ parts of the dielectric functions for both compounds using LDA, GGA, EVGGA, and mBJ are illustrated in Fig. 5(a–d). Following Fig. 5a and b, one can see that all the structure in $\varepsilon_{2}^{\text{ave}} \left( \omega \right)$ for both compounds is shifted toward higher energies by around 0.1 eV with higher magnitude especially for the spectral structure at lower energies with moving from LDA to GGA, EVGGA then to mBJ.

From the imaginary part the real part can be obtained using the Kramers–Kronig relation. The average real part $\varepsilon_{1}^{\text{ave}} \left( \omega \right)$ as illustrated in Fig. 5c and d confirms that moving from LDA to GGA, EVGGA then to mBJ leads to enhance the optical gap. This could be illuminated on the basis of Penn’s model [37]. This model suggests a relation between $\varepsilon (0)$ and $E_{\text{g}}$(band gap), which is given by the following equation:

$$ \varepsilon (0) \approx 1 + \left( {{{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } {E_{\text{g}} }}} \right. \kern-0pt} {E_{\text{g}} }}} \right)^{2} $$

(3)

It is clear from the above Eq. (3) that $\varepsilon (0)$ is inversely proportional to $E_{\text{g}}$. The compounds which have smaller band gape exhibit larger value of $\varepsilon (0)$. Gazing to the average imaginary and real parts of the calculated dielectric functions, we should accentuate that mBJ gives rise to a better band splitting, resulting in better optical transition between the occupied and unoccupied states. So for this motive we discuss the result of mBJ.

Figure 5(e, f) demonstrates the calculated imaginary part of the complex dielectric function $\varepsilon_{2}^{xx} \left( \omega \right)$, $\varepsilon_{2}^{yy} \left( \omega \right)$ and $\varepsilon_{2}^{zz} \left( \omega \right)$ for KAuX ₅ (X = S, Se). The broadening is assumed to be at 1.0 for KAuS₅ and KAuSe₅, which is typical value for the experimental accuracy. The critical points (thresholds of first fundamental absorption edge) are found to be at 2.08 and 1.41 eV for KAuS₅ and KAuSe₅, at this point the material shows high transparency. It is clear from Fig. 5(e, f) that there is a considerable anisotropy among $\varepsilon_{2}^{xx} \left( \omega \right)$, $\varepsilon_{2}^{yy} \left( \omega \right),$ and $\varepsilon_{2}^{zz} \left( \omega \right)$ along the spectral region.

The real part of frequency dependent of the dielectric function $\varepsilon_{1}^{xx} \left( \omega \right)$, $\varepsilon_{1}^{yy} \left( \omega \right),$ and $\varepsilon_{1}^{zz} \left( \omega \right)$ was determined from the imaginary part $\varepsilon_{2} \left( \omega \right)$ using the Kramers–Kronig dispersion relation. The real part of the dielectric function for both compounds is illustrated in Fig. 5(g, h). In these spectra, the static values of the real part of the dielectric $\varepsilon_{1} \left( \omega \right)$, which is the important quantity, given by the low energy limit of $\varepsilon_{1} \left( 0 \right)$. We should emphasize that we do not take phonon contribution to the dielectric screening and $\varepsilon_{1} \left( 0 \right)$ corresponds to the static optical dielectric constant. The calculated static value of dielectric constant $\varepsilon_{1} \left( 0 \right)$ is found to be equal to 4.04 (5.39), 4.88 (6.83), and 5.46 (7.61) for $\varepsilon_{1}^{xx} \left( 0 \right)$, $\varepsilon_{1}^{yy} \left( 0 \right)$ and $\varepsilon_{1}^{zz} \left( 0 \right)$, for KAuS₅ (KAuSe ₅ ). It is also clear from Fig. 5(g, h) that in inverse relation to the band gap value, the value of $\varepsilon_{1} \left( 0 \right)$for KAuS ₅ is smaller than that of KAuSe ₅ , Penn model could be used to explain it. Following these figures we noticed that the $\varepsilon_{1}^{xx} \left( \omega \right)$, $\varepsilon_{1}^{yy} \left( \omega \right),$ and $\varepsilon_{1}^{zz} \left( \omega \right)$ spectrum increases initially for both compounds, and decreases to reach negative value at the energy around 8.0 eV for KAuS₅ and 7.5 eV for KAuSe₅.

In Fig. 5(i, j) we plot the three components $R_{{}}^{xx} \left( \omega \right)$, $R_{{}}^{yy} \left( \omega \right),$ and $R_{{}}^{zz} \left( \omega \right)$ of the calculated reflectivity spectra of KAuS₅ and KAuSe₅ compounds. It is clear that the reflectivity has maximum value at about 13.5 eV originated from the interband transitions. It is obvious that these compounds possess semiconducting behavior since the reflectivity $R\left( \omega \right)$ values do not approach the unity toward zero energy. With the reflectivity value smaller than 0.1 or 10 %, the spectrum is nearly flat in the low energy region up to 9.0 eV. But at higher energy the reflectivity peaks increase rapidly with some oscillations.

The calculated electron energy-loss function $L_{{}}^{xx} \left( \omega \right)$, $L_{{}}^{yy} \left( \omega \right),$ and $L_{{}}^{zz} \left( \omega \right)$ is described in Fig. 5(k, l). It determines the energy-loss function of the fast moving electron in the material. In the spectra the main peaks are observed due to properties corresponding to a collective oscillations of the valence electrons (plasma resonance) and the frequency is called plasma frequency. In the case of interband transitions (plasmon excitations) the scattering probability for volume losses is directly linked to the energy-loss function. At low energy range we do not see any prominent peaks in these spectra. As $\varepsilon_{2} \left( \omega \right)$ has a small decrease while the magnitude of the energy-loss peaks increases at higher energy. The plasmon losses of the collective oscillations of the valence electrons and their corresponding energies are related to the density of valence electrons. For example, the reflection spectra, the trailing edges, represent the maximum peak of $L\left( \omega \right)$ are positioned at 12.3 eV for KAuS₅ and 12.85 eV for KAuSe₅. These peaks relate to the abrupt decrease of the reflectivity spectrum $R\left( \omega \right)$ and to the zero crossing of $\varepsilon_{1} \left( \omega \right)$.

The calculated optical conductivity $\sigma \left( \omega \right)$ is shown in Fig. 5(m–p), there is a relationship between optical conductivity and frequency-dependent dielectric function $\sigma \left( \omega \right)$, which is denoted by the following equation as

$$ \varepsilon \left( \omega \right) = \frac{1 + 4\pi \iota \sigma (\omega )}{\omega } $$

(4)

The electron-dipole transition momentums between occupied conduction band and the unoccupied conduction band states produce peaks in the optical conductivity spectra.

The refractive indices $n\left( \omega \right)$ of KAuS₅ and KAuSe₅ are illustrated in Fig. 5(q, r), which indicate the dispersion of electromagnetic energy when it penetrates in a crystal. There is no dispersion for the refractive index equal to unity at total energies. From $n\left( \omega \right)$ spectra we can see that at long-wavelength region the curve is fairly flat and rapid increase is observed at shorter wavelengths, showing the specific shape of dispersion curve near an electronic interband transition. The static value of the refractive indices $n_{{}}^{xx} \left( 0 \right)$, $n_{{}}^{yy} \left( 0 \right),$ and $n_{{}}^{zz} \left( 0 \right)$ is found to be at 2.01 (2.3), 2.2 (2.6), and 2.3 (2.7) for KAuS ₅ (KAuSe ₅ ), respectively. The fundamental band gap transition gives a strong increase in the value of refractive index. There exists a considerable anisotropy between the three components of the refractive indices.

We have also calculated the absorption coefficient $I_{{}}^{xx} \left( \omega \right)$, $I_{{}}^{yy} \left( \omega \right),$ and $I_{{}}^{zz} \left( \omega \right)$ for both compounds as illustrated in Fig. 5(s, t) these also show three structure as in the case of $\varepsilon_{2} \left( \omega \right)$. Both KAuS ₅ and KAuSe ₅ show that the maximum absorption occurs at higher energies. Moving toward lower energies, we find a significant decrease in $I\left( \omega \right)$ of both compounds. The threshold of the absorption spectra of both compounds (KAuS₅ and KAuSe₅) is located at 2.08 and 1.47 eV. Following Fig. 5(s, t) the absorption coefficient $I\left( \omega \right)$ of KAuS₅ shows higher absorption for all three components compared to KAuSe₅ which shows lower absorption. It is also clear that $I_{{}}^{xx} (\omega )$, $I_{{}}^{yy} (\omega ),$ and $I_{{}}^{zz} (\omega )$ of both compounds show anisotropy along the spectral region.

Thermoelectric properties

The electrical conductivities over relaxation time and Seebeck coefficient “S” of KAuX ₅ (X = S, Se) are shown in Fig. 6(a–c) plotted versus chemical potential ($\mu$) at three different temperatures. In order to discuss the thermoelectric behavior, we write the expressions for the Seeback coefficient S and electronic conductivity (σ) as follows

Fig. 6

Calculated transport coefficients of KAuX₅ (X = Se, S) as a function of chemical potential: electrical conductivity, Seeback coefficient, and thermal conductivity

$$ S = \frac{{8\pi^{2} \kappa_{\text{B}}^{2} }}{{3eh^{2} }}m^{ * } T\left( {\frac{\pi }{3n}} \right)^{3/2} $$

(5)

$$ \sigma = ne\mu, $$

(6)

where the symbols, $K_{\text{B}}$is the Boltzmann constant, e is the electronic charge, $h$ is the plank’s constant, $m^{*}$ is the effective mass, n is the carrier concentration, and $\mu$ is the carrier mobility.

In the mean time the electrons and holes carrier are restricted in the z-direction to move. They are constrained with infinite barriers to move along the x and y directions. In general, we concentrated on the zz-component of transport coefficients as shown in Fig. 6a. In between these molecules, a strong electronic interaction is found due to stacking of $\pi{-}\pi$ electrons. There is anisotropy in our investigated compounds as shown in Fig. 6(a, b). It is clear that KAuSe ₅ is a n-type semiconductor, where mobility of electron is greater than hole mobility and KAuS ₅ is a p-type semiconductor. In the former compound the valence band is comparatively flat but dispersive conduction band, which makes transport of electrons much easier in comparison to holes. The later compound is the p-type semiconductors which are also shown in Fig. 6(a, b). In the KAuS ₅ compound, the valence band is broader than KAuSe ₅ compound. So in this case, the acoustic phonons scatter the holes strongly as compared to electrons because the electrons possess smaller deformation potential constants [38] than those for holes. As a result, the electron mobility is greater than that of holes.

We also consider that the summary of the electronic contribution to thermal conductivity and electrical conductivity demonstrates the same trend due to the variation of carrier concentration. We also find that there is an increase in the electrical conductivity and decrease in the thermo power. It (thermo power) indicates peaks at specific carrier concentration. From Eq. (3) it is clear that the Seebeck coefficient depends on the effective mass i.e., heavy effect mass caused the greater value of Seebeck coefficient near the valence band maxima, especially which is related to Au-d small dispersive band. From Fig. 6(c, d) one can find the increase/decrease in the main peaks near the Fermi energy level at different temperatures for the Seebeck coefficient. The Seebeck coefficient peak for KAuS ₅ is higher than KAuSe ₅ . At temperature 300 K, the main peaks of both compounds have higher main peak, which indicates that it has larger semiconducting gap as compared to KAuS ₅ .

In general, the compounds with larger Seebeck coefficient show the large contrast of DOS and/or carriers (electrons and holes) velocities above/below the chemical potential, especially near to the band gap edges [39, 40]. While it is remarkable that the parameter (Seebeck coefficient) is very important for measuring nice thermoelectric compound with large figure of merit, but when we increase the temperature the peaks decrease.

The lattice thermal conductivities of both compounds KAuS ₅ and KAuSe ₅ are shown in Fig. 6(e, f), which show crystal-like temperature dependence. It is also clear from Fig. 6(e, f) that the thermal conductivity of KAuS ₅ is greater than the KAuSe ₅ at various temperatures. We keep $\frac{{\kappa_{\text{l}} }}{\tau } = 10^{14} \,W/mKs$ fix for all structure of both compounds. It’s main purpose to compare the structure on same level.

Here both electrons and phonons contribute to thermal conductivity. In addition to Seebeck coefficient, the electrical $\left( \sigma \right)$ and thermal conductivity $\kappa = \kappa_{\text{l}} + \kappa_{\text{e}}$, where $\kappa_{\text{l}}$ and $\kappa_{\text{e}}$ represent the lattice and electronic contributions that influence the figure of merit of thermoelectric compounds appreciably [41].

The lattice vibrations anharmonicity produce the lattice thermal conductivity and featured by the classical force fields. We calculate the lattice thermal conductivity of both compounds in the z direction, along which greater power factor is investigated.

Conclusions

In conclusion, we used the full-potential linear augmented plane-wave technique within LDA, GGA, EVGGA, and mBJ form of approximation to calculate the structural and electronic properties of the orthorhombic compounds KAuS ₅ and KAuSe ₅ at normal pressure. Our calculated band gap varies from 0.913 to 1.418 for KAuSe ₅ and from 1.605 to 2.080 for KAuS ₅ , which shows direct band gap for both compounds. Both the band structure and density of states reported that both the compounds are semiconductors. The bandwidth of the conduction bands increases replacing Se by S atom. The analysis of the electronic charge densities shows that both compounds are highly ionic semiconductors with large band gap a $\left( {\Upgamma{-}\Upgamma } \right)$ and also indicates greater ionicity and smaller covalency between Au and S, Se. The frequency dependence of dielectric function is determined, which is the critical point of the structure, and investigated to clear the optical transition. Linear optical properties i.e., energy-loss function reflectivity, refractivity, refractive index, optical conductivity, and absorption for a wide range of energy from 0 to 14 eV have been obtained from dielectric function and studied. Further, we have derived the static dielectric constant. As the Seebeck coefficient depends on the effective mass, here the calculated effective mass is enhanced in KAuSe ₅ as compared to KAuS ₅ , resulting in the reduction of the mobility of the electrons and increase in the Seebeck coefficient S [42]. So the improvement in the thermoelectric power-factor can be achieved.

Normally, small band gap energy semiconductors are good thermoelectric materials. For this reason, we investigate the thermoelectric Seebeck coefficients of both compounds. It is noted that at around 700 K, the n-type doping in the KAuS ₅ is more optimal than p-type doping than in KAuS ₅ , while KAuS ₅ contains more p-type doping than KAuSe ₅ . Finally, we established that KAuSe ₅ is fit for high thermoelectric materials than KAuS ₅ . On the basis of our results, the constant $\frac{{\kappa_{\text{l}} }}{\tau }$ approach was also studied.