Prediction on viscoelastic properties of three-dimensionally braided composites by multi-scale model

Abstract

Three-dimensional viscoelastic properties of four-step three-dimensionally (3D) braided composites are studied in this paper. Based on the three-cell division scheme, a multi-scale model for 3D braided composites is proposed. A periodic boundary condition is applied to characterize the periodic structure of 3D braided composites and yarns. Given the viscoelastic parameters of resin matrix and the elastic constants of fibers, the viscoelastic properties of yarns are obtained by the finite element method and Prony Series fitting. The three-dimensional viscoelastic constitutive relationship of interior cells is derived based upon the viscoelastic properties of yarns and resin matrix. Moreover, the viscoelasticity of 3D braided composites is studied by creep experiment. The viscoelastic deformation obtained from the multi-scale method agrees well with the experimental results. The influence of the two independent micro-structural parameters, braiding angles, and fiber volume fractions, on the viscoelastic properties of 3D braided composites is investigated in detail.

Introduction

Three-dimensionally braided composites have been widely used in many industries, such as airplanes, space structures, ships, and building structures. Their complex spatial structure of yarns significantly improves the transverse strength, shear stiffness, impact resistance, and resistance to damage, etc. In recent years, many researchers have focused their efforts on the micro-structures and elastic properties for three-dimensionally braided composites. The typical micro-structure models are the fabric geometric model [1], the fiber inclination model [2], the three-cell model [3], and the finite multi-phase element model [4], etc. The three-cell model is extensively used to predict the mechanical properties of 3D braided composites because it is able to describe the micro-structure more accurately. The elastic strain energy approach was proposed by Ma et al. [5] based on the fiber structures of four-step braided composites and the energy method. Byun et al. [6] predicted the elastic properties of three-dimensionally braided composites by using the fabric geometric model and the volume averaging method. Sun and Qiao [7] developed the fiber-inclination model, and predicted the strength of four-step braided composites based upon the transverse isotropy of unidirectional laminas and the Tsai–Wu polynomial failure criterion. Sun and Gu [8] investigated the out-of-plane and in-plane compressive failure behavior of 4-step 3D braided composites at quasi-static and high strain rates by experimental method.

Recently, the finite element method [9–12] and the multi-scale asymptotic (MSA) analysis method [13–16] were extensively applied to numerically predict the average stiffness and strength properties of 3D braided composites for their accurate prediction. Incorporating with homogenization method, Sun et al. [10] developed the incompatible displacement element and hybrid stress element to predict mechanical behaviors of braided composites. Xu and Xu [12] proposed a meso-mechanical finite element model to predict the effective elastic properties and the meso-scale mechanical response of 3D five-directional braided composites. Chen et al. [13] introduced a homogenization method and established a unit cell model to predict the elastic properties of braided composites. Yu and Cui [15] investigated tensile strength, bending strength, and torsion strength of four-step 3D braided composites through a two-scale method.

The viscoelastic deformation of many resin matrix composites is significant. The viscoelastic deformation in resin matrix composites will become more serious, when the ambient temperature increases, or the internal friction in composites under loads causes heat. Many researchers have focused their efforts on the viscoelastic behavior of polymer matrix composites. Brinson and Knauss [17] studied the time–temperature behavior of multiphase composites by the finite element analysis and dynamic correspondence principle of viscoelasticity. Koishi et al. [18] investigated the dynamic viscoelastic response of Kelvin–Voigt composites by using asymptotic homogenization method. The predicted composite properties were compared well with the limited measurements. Chung et al. [19] developed a new practical finite element approach for viscoelastic micro/macro creep problem via asymptotic homogenization, and investigated the viscoelastic properties of woven-fabric composites. Seifert et al. [20] characterized the 3D linear viscoelastic response of a plain weave composite material at elevated temperature by the finite element analysis and experimental method. Lévesque et al. [21] developed a theoretical model to predict the viscoelastic behaviors of the particle reinforced composites by the homogenization method. It is very important to study the viscoelastic properties of three-dimensionally resin matrix braided composites, since they are widely used in the long-term and variable temperature environment. Liu et al. [22, 23] investigated the viscoelastic properties of 3D braided composites by creep experiments under constant temperature and constant loads, and discussed the influence of braiding parameters on the viscoelastic behaviors. However, there is still little theoretical prediction on the viscoelastic properties of 3D braided composites.

In this paper, a multi-scale finite element model, i.e., the three-cell structure model of 3D braided composites on meso-scale and the representative volume element of yarns on micro-scale is established. Viscoelastic properties of resin matrix and yarns are derived. The three-dimensional viscoelastic constitutive relationship of four-step 3D braided composites is obtained from the multi-scale model. Moreover, the viscoelastic properties of 3D braided composites are studied by creep experiment. The viscoelastic deformation obtained from the multi-scale method is compared with the experimental results. The influence of braiding angles and fiber volume fractions on the viscoelastic properties of 3D braided composites is investigated.

Multi-scale model of 3D braided composites and periodic boundary

The complex spatial topological structure of three-dimensionally braided composites consists of three kinds of cells, i.e., interior cells, surface cells, and corner cells [24]. The viscoelastic properties of 3D braided composites are determined mainly by the interior cells which take a main proportion. Therefore, only the interior cell is considered and the viscoelastic properties of interior cells are used to represent the viscoelasticity of 3D braided composites in this study.

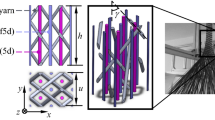
The three-cell model division of four-step 3D braided composites is shown in Fig. 1. The interior cell can be further divided into Sub-cell A and Sub-cell B, which are arranged alternately, as shown in Fig. 2.

Fig. 1

Three-cell structure division of 3D braided composites

Fig. 2

Structure of an interior cell. a A division scheme of an interior cell. b Sub-cell A. c Sub-cell B

On micro-scale, assuming that the fibers are uniformly distributed, the yarns can be regarded as unidirectional fiber composites, as shown in Fig. 3a. A periodic part of the yarn called representative volume element (RVE), as shown in Fig. 3b is analyzed. The structural parameters of RVE are described as

$$ V_{\text{yf}} = \frac{{2\pi r^{\prime 2} }}{ab} $$

(2.1)

where $b = \sqrt 3 a$, $V_{\text{yf}}$ is the fiber volume fraction of yarns, $r^{\prime}$ is radius of fibers.

Fig. 3

Micro-structure of yarns. a Cross-section. b Representative volume element (RVE)

From Figs. 1 and 3, it is shown that the interior cell of three-dimensionally braided composites and the RVE of yarns are periodically arranged in 3D braided composites and yarns, respectively. The deformation on the interfaces between unit cells should be continuous, i.e., intrusion and separation are not allowed. The processing method of the periodic boundary condition for the finite element analysis in this paper is from Xia et al. [25]. To apply the periodic boundary conditions, the mesh grids on the opposite surfaces of the unit cell are same, i.e., the number of nodes on the opposite surfaces is equal, and the corresponding nodes on the two surfaces have the same coordinates on their planes. The meshing procedure is as follows: (1) divide the surface of X ₁ = 0 to surface grids; (2) copy the grids in the surface of X ₁ = 0 to the surface of X ₁ = h _x ; (3) divide the other surfaces to surface grids by using the same method with step (1) and step (2); (4) based on the grids on the surfaces, divide the interior cell to solid grids; (5) delete the surface grids. Then the mesh grids in the opposite surfaces of the interior cell could be one-to-one correspondence. The finite element models of a representative volume element and an interior cell are established, and the periodic boundary condition is applied, as shown in Figs. 4 and 5, respectively.

Fig. 4

Finite element model of the RVE (V _yf = 85 %). a Fibers. b Resin matrix. c RVE

Fig. 5

Finite element model of an interior cell (V _f = 37 %, V _yf = 85 %, and γ = 30°). a Yarns. b Resin matrix. c An interior cell

Viscoelastic analysis by multi-scale model

Viscoelastic properties of resin matrix

The resin matrix of three-dimensionally braided composites in this section is resin ED-6 [26], whose volume deformation is linearly elastic and shear deformation is described by the standard linear viscoelastic solid model, as shown in Fig. 6. The material parameters of ED-6 are shown in Table 1.

Fig. 6

Standard linear viscoelastic solid model

Table 1 Viscoelastic constants of resin matrix (ED-6) at room temperature [26]

The relaxation modulus of resin matrix is expressed as

$$ \left[ {C_{ij} } \right] = \left[ {\begin{array}{*{20}c} {K + \frac{4}{3}Y\left( t \right)} & {K - \frac{2}{3}Y\left( t \right)} & {K - \frac{2}{3}Y\left( t \right)} & 0 & 0 & 0 \\ {K - \frac{2}{3}Y\left( t \right)} & {K + \frac{4}{3}Y\left( t \right)} & {K - \frac{2}{3}Y\left( t \right)} & 0 & 0 & 0 \\ {K - \frac{2}{3}Y\left( t \right)} & {K - \frac{2}{3}Y\left( t \right)} & {K + \frac{4}{3}Y\left( t \right)} & 0 & 0 & 0 \\ 0 & 0 & 0 & {Y\left( t \right)} & 0 & 0 \\ 0 & 0 & 0 & 0 & {Y\left( t \right)} & 0 \\ 0 & 0 & 0 & 0 & 0 & {Y\left( t \right)} \\ \end{array} } \right] $$

(3.1)

where K is volume modulus, Y(t) is shear modulus which is a function of time. Y(t) can be expressed as the first-order Prony series

$$ Y(t) = Y_{0} + Y_{1} e^{ - t/\tau } $$

(3.2)

For shear deformation, the differential constitutive equation is written as

$$ S_{ij} + p_{1} \frac{{dS_{ij} }}{dt} = q_{0} e_{ij} + q_{1} \frac{{de_{ij} }}{dt} $$

(3.3)

where $p_{1} = \frac{{\eta_{2} }}{{G_{1} + G_{2} }}$, $q_{0} = \frac{{2G_{1} G_{2} }}{{G_{1} + G_{2} }}$, $q_{1} = \frac{{2G_{1} \eta_{2} }}{{G_{1} + G_{2} }}$.

Laplacian transformation for Eq. (3.3) gives

$$ (1 + p_{1} s)\overline{{S_{ij} }} = (q_{0} + q_{1} s)\overline{{e_{ij} }} $$

(3.4)

Then

$$ P(s) = 1 + p_{1} s \, , \, Q(s) = q_{0} + q_{1} s $$

(3.5)

$$ \overline{Y} (s) = \frac{Q(s)}{sP(s)} = \frac{{q_{0} + q_{1} s}}{{s\left( {1 + p_{1} s} \right)}} $$

(3.6)

Laplacian inverse transformation for Eq. (3.6) gives

$$ \begin{gathered} Y\left( t \right) = q_{0} + (\frac{{q_{1} }}{{p_{1} }} - q_{0} )e^{{ - t/p_{1} }} \, = 2\left( {\frac{{G_{1} G_{2} }}{{G_{1} + G_{2} }} + \frac{{G_{1}^{2} }}{{G_{1} + G_{2} }}e^{{ - t/(\frac{{\eta_{2} }}{{G_{1} + G_{2} }})}} } \right) \end{gathered} $$

(3.7)

Viscoelastic properties of yarns and interior cells

Using contracted notations, the 3D creep-type viscoelastic constitutive equation at constant temperature is expressed in the form of hereditary integral as

$${\varepsilon_{i}\left(t\right)=\int_{{0^{-}}}^{t}{D_{ij}\left({t-\tau}\right)\frac{{d\sigma_{j}\left(\tau\right)}}{d\tau}d\tau}}\\\;\;{\left({i,j=1,2,\cdots,6}\right)}\\ $$

(3.8)

where D _ij (t) is creep compliance.

Because the RVE of yarns and the interior cell of 3D braided composites are structurally symmetric, their equivalent viscoelastic properties are considered to be orthotropic. In this case, a total of nine independent functions of time are necessary to characterize the viscoelastic constitutive relationship, and the creep compliance is given as follows

$$ \left[ {D_{ij} \left( t \right)} \right] = \left[ {\begin{array}{*{20}c} {D_{11} \left( t \right)} & {D_{12} \left( t \right)} & {D_{13} \left( t \right)} & 0 & 0 & 0 \\ {D_{12} \left( t \right)} & {D_{22} \left( t \right)} & {D_{23} \left( t \right)} & 0 & 0 & 0 \\ {D_{13} \left( t \right)} & {D_{23} \left( t \right)} & {D_{33} \left( t \right)} & 0 & 0 & 0 \\ 0 & 0 & 0 & {D_{44} \left( t \right)} & 0 & 0 \\ 0 & 0 & 0 & 0 & {D_{55} \left( t \right)} & 0 \\ 0 & 0 & 0 & 0 & 0 & {D_{66} \left( t \right)} \\ \end{array} } \right] $$

(3.9)

where all entities in the above matrix are functions of time, that are creep functions.

Considering a uniaxial stepped stress $\sigma_{11}^{0}$ in direction X ₁, $D_{11} (t)$, $D_{12} (t)$ and $D_{13} (t)$ are determined as

$$ D_{11} (t) = \frac{{\varepsilon_{11} (t)}}{{\sigma_{11}^{0} }}, \, D_{12} (t) = \frac{{\varepsilon_{22} (t)}}{{\sigma_{11}^{0} }}, \, D_{13} (t) = \frac{{\varepsilon_{33} (t)}}{{\sigma_{11}^{0} }} $$

(3.10)

Similarly, $D_{22} (t)$,$D_{23} (t)$ and $D_{33} (t)$ can be determined.

For a pure shear stepped stress $\sigma_{12}^{0}$ in plane X ₁ OX ₂, $D_{44} (t)$ is determined as

$$ D_{44} (t) = \frac{{\gamma_{12} (t)}}{{\sigma_{12}^{0} }} $$

(3.11)

Similarly, $D_{55} (t)$ and $D_{66} (t)$ can be determined.

Then, the relationship between the creep compliance and relaxation modulus can be expressed in terms of convolution and Laplacian transformation.

$$ L\left[ {C_{ik} \left( t \right) * D_{kj} \left( t \right)} \right] = \overline{C}_{ik} \left( s \right) \cdot \overline{D}_{kj} \left( s \right) = s^{ - 2} I_{ij} $$

(3.12)

where L denotes Laplacian transformation, * denotes convolution, $\overline{C}_{ik} \left( s \right)$ is the Laplacian transformation of C _ik (t) and $\overline{D}_{kj} \left( s \right)$is the Laplacian transformation of D _kj (t), I _ij is a unit matrix. Then,

$$ \overline{C}_{ij} \left( s \right) = s^{ - 2} I_{ik} \left[ {\overline{D}_{kj} \left( s \right)} \right]^{ - 1} $$

(3.13)

So C _ij (t) can be obtained by

$$ C_{ij} \left( t \right) = L^{ - 1} \left[ {s^{ - 2} I_{ik} \left[ {\overline{D}_{kj} \left( s \right)} \right]^{ - 1} } \right] $$

(3.14)

where L ⁻¹ denotes the Laplacian inverse transformation.

Therefore, the 3D relaxation-type viscoelastic constitutive equation at constant temperature can be expressed in the form of hereditary integral as follows

$$ \, \begin{array}{*{20}c} {\sigma_{i} \left( t \right) = \int_{{0^{ - } }}^{t} {C_{ij} \left( {t - \tau } \right)\frac{{d\varepsilon_{j} \left( \tau \right)}}{d\tau }d\tau } } \\ {\left( {i,j = 1,2, \cdots ,6} \right)} \\ \end{array} $$

(3.15)

The fibers in the study are carbon fiber T300 [26] with their elastic properties shown in Table 2. Assuming that the fiber volume fraction of yarns V _yf is 85 %, some discrete data of the entities in the creep compliance matrix are obtained from the finite element analysis and Eqs. 3.9–3.11, as shown in Fig. 7. It is shown that if errors are ignored, there should be D ₁₁(t) = D ₂₂(t), D ₁₃(t) = D ₂₃(t), D ₄₄(t) = 2(D ₁₁(t) − D ₁₂(t)) and D ₅₅(t) = D ₆₆(t), i.e., only five independent creep variables are needed to be determined.

Table 2 Elastic constants of fibers (T300) [26]

Fig. 7

Creep compliances of yarns versus time. a D ₁₁(t) and D ₂₂(t). b D ₁₂(t). c D ₁₃(t) and D ₂₃(t). d D ₃₃(t). e D ₄₄(t) and 2(D ₁₁(t) − D ₁₂(t)). f D ₅₅(t) and D ₆₆(t)

However, the entities in the creep compliance matrix are described as functions of time for determining the viscoelastic properties. Prony series is applied to fit the creep functions. The form of the first-order Prony Series is

$$ f\left( t \right) = \alpha + \beta e^{ - t/\tau } $$

(3.16)

The fitting curves and the parameters of creep functions are shown in Fig. 7 and Table 3, respectively.

Table 3 Entities in creep compliance matrix of yarns (V _yf = 85 %)

Substituting the creep compliances into formula (3.14), the relaxation modulus matrix is determined. Then, the viscoelastic constitutive relationship of yarns can be obtained from Eq. 3.8 or 3.15.

Assuming that in interior cells the fiber volume fraction V _f is 37 % and the braiding angle γ is 30°, some discrete data of the entities in the creep compliance matrix are obtained from the finite element analysis and Eqs. 3.9–3.11 based upon the viscoelastic constitutive relationship of resin matrix and yarns, as shown in Fig. 8. From the simulation results, it is shown that if errors are ignored, there should be D ₁₁(t) = D ₂₂(t), D ₁₃(t) = D ₂₃(t), and D ₅₅(t) = D ₆₆(t), i.e., only six independent creep variables are necessary to determine the viscoelastic properties of interior cells. The analytical expression of the creep compliance can be fitted by first-order Prony series (Eq. 3.16), as shown in Fig. 8. The parameters of the creep functions are shown in Table 4. The relaxation moduli matrix is determined from the creep compliances by Eq. 3.14.

Fig. 8

Creep compliances of interior cells versus time. a D ₁₁(t) and D ₂₂(t). b D ₁₂(t). c D ₁₃(t) and D ₂₃(t). d D ₃₃(t). e D ₄₄(t). f D ₅₅(t) and D ₆₆(t)

Table 4 Entities in creep compliance matrix of interior cells (V _f = 37 %, V _yf = 85 %, and γ = 30°)

Substituting the creep compliances and the relaxation moduli into Eqs. 3.8 and 3.15, respectively, the creep-type and relaxation-type viscoelastic constitutive relationships of 3D braided composites are determined.

Creep experiment of 3D braided composites

The resin matrix of the experimental specimen is Epoxy 618. Zhou and Zhang [27] obtained the creep curves of Epoxy 618 from creep experiment, as shown in Fig. 9. The length, width and thickness of the experimental specimen are 200, 22.3, and 3.45 mm, respectively. The ambient temperature is 15 °C. In the experiment, step stress (10 and 17 MPa, respectively) is applied to the specimen for 3730 s. And the average strain of the specimen in the loading direction is measured during the loading period. It is shown that the viscoelastic deformation of Epoxy 618 is significant. After 1 h of the stepped stress load, the creep strain of Epoxy 618 tends to a steady value.

Fig. 9

Creep curves of Epoxy 618 obtained from creep experiment

According to the definition of creep compliance, the creep compliance of Epoxy 618 can be obtained from the creep experimental data. In order to obtain the analytical expression of the creep compliance, the second-order Prony Series (as shown in Eq. 4.1) is applied to fit the creep compliance function.

$$ J\left( t \right) = A - Be^{{ - t/\tau_{1} }} - Ce^{{ - t/\tau_{2} }} $$

(4.1)

The fitting results are shown in Eq. 4.2 and Fig. 10.

$$ J\left( t \right) = \left( {2.978 - 0.273e^{ - t/0.595} - 0.253e^{ - t/0.0335} } \right) \times 10^{ - 10} Pa^{ - 1} $$

(4.2)

That is

$$ \left\{ {\begin{array}{*{20}c} {A = 2.978 \times 10^{ - 10} {\text{Pa}}^{ - 1} ,B = 0.273 \times 10^{ - 10} {\text{Pa}}^{ - 1} ,C = 0.253 \times 10^{ - 10} {\text{Pa}}^{ - 1} } \\ {\tau_{1} = 0.595h,\tau_{2} = 0.0335h} \\ \end{array} } \right. $$

(4.3)

Fig. 10

Creep compliance of Epoxy 618 obtained from the Prony Series fitting and creep experiment

From Fig. 10, it is shown that the fitting results agree well with the creep experimental results. Therefore, the viscoelastic properties of Epoxy 618 can be described by Eq. 4.2.

Laplacian transformation for Eq. 4.1 gives

$$ \overline{J} \left( s \right) = \frac{A}{s} - \frac{B}{{s + {1 \mathord{\left/ {\vphantom {1 {\tau_{1} }}} \right. \kern-0pt} {\tau_{1} }}}} - \frac{C}{{s + {1 \mathord{\left/ {\vphantom {1 {\tau_{2} }}} \right. \kern-0pt} {\tau_{2} }}}} $$

(4.4)

The relationship between relaxation modulus and creep compliance is

$$ \overline{J} \left( s \right) \cdot \overline{G} \left( s \right) = s^{ - 2} $$

(4.5)

Then

$$ \overline{G} \left( s \right) = \frac{1}{{\overline{J} \left( s \right)}} \cdot \frac{1}{{s^{2} }}{ = }\frac{{s^{2} + \left( {{1 \mathord{\left/ {\vphantom {1 {\tau_{1} }}} \right. \kern-0pt} {\tau_{1} }} + {1 \mathord{\left/ {\vphantom {1 {\tau_{2} }}} \right. \kern-0pt} {\tau_{2} }}} \right)s + {1 \mathord{\left/ {\vphantom {1 {\left( {\tau_{1} \tau_{2} } \right)}}} \right. \kern-0pt} {\left( {\tau_{1} \tau_{2} } \right)}}}}{{\left( {A - B - C} \right)s^{3} + \left[ {A\left( {{1 \mathord{\left/ {\vphantom {1 {\tau_{1} }}} \right. \kern-0pt} {\tau_{1} }} + {1 \mathord{\left/ {\vphantom {1 {\tau_{2} }}} \right. \kern-0pt} {\tau_{2} }}} \right) - {B \mathord{\left/ {\vphantom {B {\tau_{2} }}} \right. \kern-0pt} {\tau_{2} }} - {C \mathord{\left/ {\vphantom {C {\tau_{1} }}} \right. \kern-0pt} {\tau_{1} }}} \right]s^{2} + {{As} \mathord{\left/ {\vphantom {{As} {\left( {\tau_{1} \tau_{2} } \right)}}} \right. \kern-0pt} {\left( {\tau_{1} \tau_{2} } \right)}}}} $$

(4.6)

Substituting Eq. (4.3) into Eq. (4.6), it is obtained that

$$ \overline{G} \left( s \right) = \frac{{s^{2} + 31.538s + 50.180}}{{2.453s^{3} + 85.354s^{2} + 149.440s}} $$

(4.7)

Laplacian inverse transformation for Eq. (4.7) gives

$$ G\left( t \right) = \left( {3.358 + 0.335e^{{{{ - t} \mathord{\left/ {\vphantom {{ - t} {0.541}}} \right. \kern-0pt} {0.541}}}} + 0.385e^{{{{ - t} \mathord{\left/ {\vphantom {{ - t} {0.0303}}} \right. \kern-0pt} {0.0303}}}} } \right) \times 10^{9} Pa $$

(4.8)

Using Eq. 4.8 as the material parameter input for the finite element calculation, the viscoelastic deformation of Epoxy 618 calculated by the finite element method compares with the experimental results, as shown in Fig. 11. It is shown that the finite element results agree well with the creep experimental results. Therefore, Eq. 4.8 can be used as the material parameter for numerically simulating the viscoelastic properties of Epoxy 618.

Fig. 11

Viscoelastic deformation of Epoxy 618 obtained from the finite element analysis and creep experiment

The length, width, and thickness of the experimental specimen of 3D braided composites are 230, 30, and 5 mm, respectively. The matrix is Epoxy 618, whose viscoelastic properties are characterized by Eq. 4.8. The fiber is carbon T300, whose material parameters are listed in Table 2. The fiber volume fraction and the interior braiding angle are 45 % and 32°, respectively. The ambient temperature is 15 °C. In the experiment, step stress (120 and 160 MPa, respectively) is applied to the specimen for 9000 s. Then the stress is unloaded immediately. After that, the specimen is maintained at no load for 5400 s. The average strain of the specimen in the loading direction is measured during the experimental period.

The viscoelastic deformation of 3D braided composites with the same braiding parameters, matrix and fibers as the experimental specimen is derived from the multi-scale method. The viscoelastic deformation derived from the multi-scale method is compared with the creep experimental results, as shown in Fig. 12. It is shown that the viscoelastic deformation derived from the multi-scale method agrees well with the experimental results. The maximum error between the multi-scale prediction and experimental results is 6.31 %.

Fig. 12

Comparison of multi-scale method results and creep experimental results

Effects of braiding angles and fiber volume fractions on viscoelasticity

The interior cell of four-step 3D braided composites with 1 × 1 pattern, as shown in Fig. 2, is characterized by two independent parameters, the braiding angle γ and the fiber volume fraction V _f. In this section, the effects of braiding angles and fiber volume fractions on the viscoelastic properties are studied by the multi-scale method. Only the viscoelastic properties related to directions X ₁ and X ₃ are investigated since the viscoelastic behaviors of 3D braided composites in directions X ₁ and X ₂ are same.

The viscoelastic constitutive relationships of 3D braided composites with the same fiber volume fraction (V _f = 37 %) and different braiding angles (below 45°) are derived. The creep compliance curves are presented in Fig. 13. It is shown that with the increase of braiding angles, the creep compliances in direction X ₁, the shear creep compliances in plane X ₁ OX ₂ and the shear creep compliances in plane X ₁ OX ₃ decrease, while the creep compliances in the braiding direction X ₃ increase. With the same braiding angle increments, the decrements of creep compliances in direction X ₁ and plane X ₁ OX ₃ decrease, while the increments of creep compliances in the braiding direction X ₃ increase. It also indicates that the impact of braiding angles upon the viscoelastic properties related to the braiding direction X ₃ is much significant.

Fig. 13

Creep compliances for different braiding angles. a X ₁-direction tension (D ₁₁(t)). b X ₃-direction tension (D ₃₃(t)). c X ₁ OX ₂-plane shear (D ₄₄(t)). d X ₁ OX ₃-plane shear (D ₅₅(t))

The creep compliances with the same braiding angle (γ = 40°) and different fiber volume fractions are presented in Fig. 14. It is shown that with the increase of fiber volume fractions, the creep compliances in direction X ₁, the creep compliances in the braiding direction X ₃, the shear creep compliances in plane X ₁ OX ₂ and the shear creep compliances in plane X ₁ OX ₃ decrease. With the same fiber volume fraction increments, the decrements of creep compliances in direction X ₁, the braiding direction X ₃ and plane X ₁ OX ₃ decrease. It is also shown that the influence of fiber volume fractions on the viscoelastic behaviors related to different directions is similar.

Fig. 14

Creep compliances for different fiber volume fractions. a X ₁-direction tension (D ₁₁(t)). b X ₃-direction tension (D ₃₃(t)). c X ₁ OX ₂-plane shear (D ₄₄(t)). d X ₁ OX ₃-plane shear (D ₅₅(t))

Conclusion

In this paper, three-dimensional viscoelastic properties of 3D braided composites at constant temperature were characterized by a multi-scale model. Based on the three-cell division scheme, the multi-scale model in which the unit cell is composed of yarns and resin matrix, and the yarn is composed of fibers and resin matrix, was proposed. A periodic boundary condition was applied to the interior cell of 3D braided composites and the RVE of yarns.

On the yarn scale, given the viscoelastic parameters of resin matrix and the elastic constants of fibers, the 3D viscoelastic constitutive relationship of yarns was obtained by the finite element method and Prony series fitting. The simulation result indicates that only five independent creep functions are necessary to fully characterize the viscoelastic properties of yarns. On the interior cell scale, given the viscoelastic properties of resin matrix and yarns, the 3D viscoelastic constitutive relationship of interior cells was obtained by again the finite element method and Prony series fitting. It is shown that the equivalent viscoelastic properties of interior cells are orthotropic, and the viscoelastic responses related to directions X ₁ and X ₂ are same. Moreover, the viscoelasticity of 3D braided composites is studied by creep experiment. The viscoelastic deformation of 3D braided composites obtained from the multi-scale method agrees well with the experimental results.

Furthermore, the effects of braiding angles and fiber volume fractions on the viscoelastic behaviors of four-step 3D braided composites with 1 × 1 pattern have been investigated. When braiding angles are below 45°, with the increase of braiding angles, the viscoelastic deformation of the X ₃-direction (braiding direction) tension increases, while the viscoelastic deformations of the X ₁-direction tension, X ₁ OX ₂-plane shear and X ₁ OX ₃-plane shear decrease. The impact of braiding angles upon the viscoelastic properties related to the braiding direction X ₃ is much significant. The viscoelastic deformations of the X ₁-direction tension, X ₃-direction tension, X ₁ OX ₂-plane shear, and X ₁ OX ₃-plane shear decrease with the increase of fiber volume fractions.