Modeling and experiments in dissolutive wetting: a review

Abstract

Wetting, phase change, and reaction in high temperature systems (e.g., a liquid metal on a metal substrate) are complex phenomena that are only partially understood. These phenomena occur in joining processes, thin film processing and sintering among others. Dissolutive wetting is characterized by chemical and physical processes that span a broad range of spatial and temporal scales. While experiments are difficult to conduct, there have been a number of experimental investigations of dissolutive wetting in metal–metal systems and a short review of these studies is presented. Although limited, recently there have been studies comparing results, such as spreading rate and dissolution depth, from experiments to those from computational simulations. For dissolutive wetting in metal systems it is difficult to observe much of the spreading process experimentally. Computational models may provide better understanding of many aspects of dissolutive wetting. Models of dissolutive wetting incorporate knowledge from chemical thermodynamics, phase transformations, capillary behavior, and multi-phase transport. A number of computational models have appeared in the literature over the last 10 years. Dissolutive wetting has been studied using a broad range of approaches from molecular dynamics to continuum based models at the drop scale that include hydrodynamic transport using different levels of sophistication. We present a comprehensive review of the modeling approaches that have been used to study dissolutive wetting.

Introduction

This paper reviews the current state of knowledge of dissolutive wetting. Dissolutive wetting is a process in which a wetting liquid dissolves the substrate that it is wetting. It is one aspect of reactive wetting, a process in which chemical reaction with the substrate can involve both dissolution and the formation of reaction products at interfaces and in the bulk liquid phase. The majority of technological interest in reactive wetting arises from applications in joining processes of metals and ceramics, and as such, the physics of high-temperature capillarity plays a dominant role. The formation of reaction products at interfaces during spreading in metal–metal and metal–ceramic systems, especially in the vicinity of the contact line (triple line), presents a very complex physicochemical system. These reaction products can form in the absence of global chemical equilibrium and are sometimes transient and can even disappear altogether. Their presence at the contact line can improve wetting and when present all along the solid/liquid (S/L) interface can mediate dissolution/diffusion of the underlying substrate. The complexities associated with the presence of reaction products have generally frustrated attempts to include them realistically in theoretical models. However, under the assumption of the simplest product morphologies, their inclusion in models has resulted in illuminating theoretical predictions that corroborate experimental findings [1–8].

Dissolutive wetting involves the simplest form of reaction of liquid with the substrate and can be more readily modeled. It has consequently attracted significant recent interest from those studying reactive wetting [9–12]. Understanding dissolutive wetting would constitute a major first step in the understanding of product-forming reactive systems. There are two types of metallic systems that manifest dissolutive wetting: (1) intrinsically dissolutive systems, e.g., Bi–Sn, for which dissolution is the only liquid-substrate interaction possible, and (2) product-forming systems at temperatures exceeding the stability temperatures of all products, e.g., Si–Cu at temperatures above 859 °C [12]. Dissolution affects the dynamics of wetting locally at the contact line by changing the interfacial energies and by alteration of the contact line geometry. On the much larger length scale of the drop, dissolution creates concentration gradients to resolve the initial chemical disequilibrium. The concentration gradients extend to the contact line region where they drive flux of dissolved solute away from the contact line, enabling contact line advance [13]. The study of dissolutive wetting has largely been confined to experiments and computational modeling. Analytical study is frustrated by the nonlinearities inherent in the governing transport equations—especially for short times—and in the boundary conditions imposed at the liquid/vapor (L/V) and solid/liquid (S/L) interfaces, both of which evolve with time. Furthermore, the common intersection of these interfaces with a solid/vapor (S/V) interface forms a contact line, the conditions at which remain poorly understood. Dissolutive wetting experiments are themselves fraught with difficulties. The optical opacity of metal and ceramic material systems makes difficult the tracking of the evolution of the L/S boundary due to dissolution, and the necessity to conduct experiments in a chamber with an atmosphere carefully controlled to prevent oxidation at very high temperatures limits both manual and optical access.

The study of reactive wetting has primarily employed molten drops spreading on initially flat substrates. The spreading of drops in isothermal reactive systems is driven by mechanical and chemical forces toward complete equilibrium over a cascade of timescales ranging from sub-millisecond/millisecond to years. In the discussion that follows, we prefer to simplify this cascade into two regimes: short- and long-time spreading.

Short-time dissolutive wetting

We confine our discussion of dissolutive wetting to metal-metal systems. Spontaneous wetting may be initiated either by drop transfer or rapid melting of solid spheres; both processes have technological merit. Drop transfer delivers molten metal from a non-wettable substrate to a wettable substrate at the same temperature. Normally a complete transfer of the molten mass between surfaces occurs forming a wetting pendant drop. The rapid melting of spheres delivers molten liquid to the wettable substrate on the much slower time scale of melting. The initial wetting of the two processes is very different: drop transfer produces initial (maximum) wetting velocities of ∼1 m/s [6] while melting of spheres produces initial wetting velocities on the order of 10⁻² m/s (O(10⁻²) m/s) [14, 15]. The source of these initially large wetting velocities in molten metal wetting is the uncompensated Young force which, for metal–metal systems of very low solubilities, can be written as F _Y = γ (cos θ₀ − cos θ_D), where γ is the surface tension, and θ₀ and θ_D are the equilibrium and dynamic contact angles, respectively. F _Y is actually the force per unit length of contact line. In drop transfer, at inital contact, θ_D ≈ 180°; for low solubility systems, θ₀ ∼ 15–25° and F _Y is close to 2γ. To put the magnitude of this force in perspective, consider a drop of molten Ag with initial radius of 1 × 10⁻³ m. If the above F _Y is considered to act on one edge of a cube of equivalent volume (mass) of Ag resting on a frictionless substrate (the assumption of frictionless spreading at early time will be substantiated below), the resulting acceleration of the cube would be ∼74 m/s². The consequences of large initial velocities in dissolutive wetting are large initial Reynolds and solutal Peclet numbers, rendering the short-time transport dynamics highly nonlinear and theoretical modeling very challenging. The fluid dynamics of drop transfer, specifically the spontaneous wetting dynamics that occur when a liquid first contacts a solid, is of intrinsic interest in wetting physics.

In the rapid melting of solid spheres, a liquid drop is created in time $\tau_{\rm M}\sim R_{\rm S}^{2}/\mathcal{D},$ where R _S is the diameter of the solid sphere and $\mathcal{D}$ is the thermal diffusivity of the sphere metal (for millimetric size Sn spheres, τ_M∼ O(10⁻²) s). Large dynamic contact angles are not generated in this mode of liquid delivery and consequently, as noted above, initial spreading velocities are ∼10⁻² m/s. The initial wetting forces are resisted by viscosity as surface tension forces rapidly shape the melting mass into a spherical cap. Because melting begins at the point of initial contact, dissolution begins in the molten pool formed directly beneath the remaining solid mass. Thus, dissolutive effects on spreading exert a much earlier influence in solid sphere melting than in drop transfer.

Dimensionless parameter space for short-time dissolutive wetting

We first establish a relevant dimensionless parameter space for short-time dissolutive wetting. The relative importances of gravity and surface tension in spreading are estimated by the value of the Bond number Bo = L ²/(γ /ρg), where L is a characteristic length of the liquid domain, γ is the surface tension, ρ is the liquid density, and g is acceleration of gravity. For millimetric size liquid volumes in metal–metal systems, Bo ≪ 1 (e.g., for Sn–Bi at 250 °C and L = 0.889 mm, Bo = 9.78 × 10⁻²). Surface tension will act to restore a L/V interface deformed from spherical shape, but viscosity will resist this restoration. The relative influences of viscosity and surface tension in spreading are measured by the capillary number Ca = μ U/γ, where μ is the dynamic viscosity and U is a characteristic velocity. The most easily measured velocity scale in spontaneous wetting processes is the contact line (CL) velocity. For initial wetting in drop transfer, Ca ∼  O(10⁻³) (e.g., for Sn–Bi at 250 °C, Ca = 3.26 × 10⁻³). The smallness of both Bo and Ca is the basis of the spherical cap assumption for the liquid–vapor (L/V) interface in many theoretical and computational models. The Weber number We = ρU ² L/γ measures the relative importance of inertial to capillary forces in deposition processes where U is the speed of the drop approaching the target surface. For melting spheres, this velocity is zero and for drop transfer, the experimenter tries to make this velocity as small as possible. Thus, this is not a useful number to describe dissolutive wetting. The Reynolds number Re = ρUL/μ measures the ratio of inertial to viscous forces in a flow. For early wetting in drop transfer, Re ∼ O(10³) and its value approaches zero as wetting ceases. One can characterize the fluid dynamics of early time dissolutive wetting using Ca − Re space [16]. We note that Ca/Re = Oh ², where Oh = μ /(ρ Lγ)^1/2 is the Ohnesorge number representing the relative importances of viscous forces to inertia times surface tension forces. Oh is a natural parameter to characterize spontaneous wetting because it is independent of the CL velocity which is not an imposed velocity. Oh may be thought of as the inverse square root of the Reynolds number based on the capillary velocity V _cap = γ/μ; V _cap estimates the velocity of a L/V interface in the absence of contact line effects. The values of the Ohnesorge number for liquid metals are Oh∼ O(10⁻⁴ − 10⁻³); for Sn, Oh = 9.18 × 10⁻⁴. The transport of dissolved solute is characterized by the value of the solutal Peclet number Pe _s = UL/D where D is the diffusivity of the solute in the solvent metal. The Schmidt number Sc is defined as the ratio of the Peclet number to the Reynolds number: Sc = Pe _s/Re = ν /D. For the Sn–Bi system, Sc ∼ O(10²) and at early time, Pe _s ∼ O(10⁵) indicating the strong role of convection in the transport of solute.

Short-time dissolutive wetting kinetics and dynamics

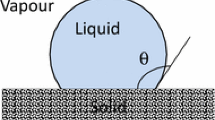
Because the literature on inert wetting is comparatively large compared to that for reactive wetting, there is natural tendency to compare and interpret the observed kinetics and dynamics of reactive wetting in terms of established results for inert wetting [17]. Of the two usual observables in both categories of wetting drops, the wetted radius r(t) and the superficial dynamic contact angle θ _T (t), the latter may differ in the two cases depending on whether dissolution extends up to the contact line (Fig. 1). As noted above, the nature of the global L/S interface, and in particular its shape in the near vicinity of the triple junction, is generally not accessible in situ in reactive wetting experiments. Conditions at the time of wetting are inferred from post-mortem analysis of quenched, cross-sectioned specimens. Notwithstanding, there is still great emphasis placed on measurements of r(t) and θ _T (t) and their comparison to inert analogs.

Fig. 1

The configuration of the triple line: a inertia-dominated regime in which the dissolving portion of the L/S interface lags the CL due to initially large CL velocities (θ_B exaggerated). b Dissolution-dominated regime in which dissolution couples the L/S interface to the CL

Using drop transfer delivery of millimetric-size water drops to perfectly wetting glass substrates imaged using a fast camera, Biance et al. [18] showed that the short-time dynamics were well described by $r(t)/R\sim (t/\sqrt{\rho R^{3}/\gamma})^{\alpha},$ where α ≈ 0.52; here R is the radius of the drop prior to transfer and r(t) is the wetted radius. This relationship was found to be valid for a temporal interval of approximately 1 ms. The wetting kinetics then began a transition (that was very apparent in the raw r(t) data) to viscously mediated spreading described by $r(t)/R\sim (t/(\mu R/\gamma))^{\alpha}$ with α = 1/10, with the crossover time $\tau \sim Oh^{-1/4}\sqrt{\rho R^{3}/\gamma}$ clearly increasing with droplet size R . The α = 1/10 result has theoretical underpinning: it is a prediction of Tanner’s law [17], valid for long-time spreading of drops. The time scales in both kinetic regimes are not unexpected. The scaling $\tau_{R}=\sqrt{\rho R^{3}/\gamma}$ (also known as the Rayleigh time) follows from seeking a nondimensional form of the relationship r = r(ρ , γ , R, t, θ₀) governing short-time wetting: the dimensionless relationship is $r/R=f(t/\sqrt{\rho R^{3}/\gamma},\theta_{0}).$ The scaling $\tau_{\rm vis}=\mu R/\gamma$ follows from seeking a nondimensional form of the relationship $r=r(\mu ,\gamma ,R,t,\theta_{0})$ governing long-time wetting: the dimensionless relationship is $r/R=g(t/(\mu R/\gamma),\theta_{0}).$ The findings of Biance et al. [18] are somewhat remarkable in that they reveal that a wetting drop of viscous liquid behaves as if it is an inviscid fluid for short times, with the main resistance to the uncompensated Young force being the inertia of the liquid. Once the liquid is moving, the viscosity begins to dominate the resistance. Given that the inertia-mediated spreading transitions to viscosity-mediated spreading, the fact that τ_R ∼  O(10⁻³) s and τ_vis ∼ O(10⁻⁵) s may at first be confusing. However, it must be remembered that τ_R and τ_vis appear in power law expressions for which r(t)/R < 1 and r(t)/R ≫ 1, respectively.

Saiz et al. [19] considered purely dissolutive binary metal systems with extremely low (<3 wt%) substrate miscibility in various solvent metals. They performed drop transfer experiments of molten Ag (θ₀ ∼ 21⁰), Au (θ₀ ∼ 24⁰), Cu (θ₀ ∼ 23⁰) and silicate glasses on poly- and single-crystalline Mo, recorded using a very fast camera. They reported that the metallic drops exhibited r(t) ∼ t ^1/2 kinetics in an inertially dominated spreading regime. They discussed a subsequent ”capillary” spreading regime but did not identify a transition to this regime in their data. In the data of Biance et al. [18], this transition was very clear. Their raw r(t) data seemed to suggest spreading cessation coincided roughly with the time of complete drop separation from the nonwetting substrate, an event that appeared to excite capillary waves on the drop surface whose presence was manifest at the contact line in the form of weakly damped (Oh ≪ 1) oscillations. The duration of spreading in Saiz et al. [19] was approximately 10–20 ms for all of the metallic systems, during which time no evidence of dissolution was found. They considered these systems as non-reactive, and the spreading as effectively that of inert liquids at high temperature.

Bird et al. [20] examined sub-millimetric drops of aqueous glycerol solutions spreading on partially wetting silicon substrates using an ultrafast camera. They used a variant of drop transfer by growing a pendant drop from a needle until it touched the target surface below it. Silicon wafers coated with various silanes produced a range of equilibrium contact angles from 0° to 180°. They found that over a temporal range of 1.5 ms, their data were well-described by the power law r(t)/R = C(t/τ _R )^α. They determined that the exponent α varied monotonically from α ≈ 0.5 for small θ₀ to α ≈ 0.3 for large θ₀. They also found that the O(1) prefactor C decreases with increasing θ₀. The transition to viscosity-mediated spreading occured at t ∼ 2−3τ _R , nominally independent of θ₀. This time was observed to correlate with the time it took a capillary wave—initiated by the large curvature (and hence pressure) change produced by initial drop contact with the wetting substrate—to propagate over the drop. These results are very significant. Fundamentally, as Bird and co-workers [20, 21] note, the presence of a contact line in partial wetting (not present in the θ₀ = 0 case, assuming the existence of a precursor film)—at which viscous stresses are divergent—might impose a viscosity-dominated resistance to spreading from t = 0 onward; hence α = 1/2 kinetics would never appear. This possibility has been dispelled. Furthermore, the present authors are not aware of any purely dissolutive metal–metal system that exhibits perfect wetting; thus the results of Bird and co-workers [20, 21] are particularly relevant to dissolutive wetting.

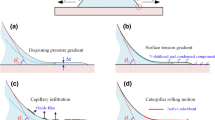
On the global scale of the drop, it is reasonable to expect the effects of dissolution to be negligible at short times. A conservative estimate (neglecting convective transport) for the amount of substrate dissolved during the inertia-dominated spreading is L _D ∼ (Dτ_R)^1/2, where D is the binary diffusion coefficient of substrate metal in the molten metal. For liquid metals, D ∼ 10⁻⁹ m²/s, and thus L _D ∼ 10⁻⁶ m. This extent of dissolved solute is small on the scale of the drop but the effects of even low concentrations of solute at the contact line are not easily quantitatively assessed. As noted above, the onset of dissolution in spreading drops is generally not observable in situ. The only in situ observations of the onset of global dissolutive effects in metal–metal systems were performed by Yin et al. [22], where drop transfer was conducted in a Hele-Shaw cell whose transparent windows allowed visualization of the evolving S/L interface (Fig. 2). These observations show no dissolution (to within the optical resolution of a video microscope) during short-time wetting and the early stages of viscosity-mediated spreading and generally corroborate the assertions of Saiz et al. [9]. At the present time, the general conjecture is that dissolution is negligible at the CL during short-time spreading and consequently the L/S interface lags the CL as illustrated in Fig. 1a. If the effects of dissolution are truly negligible for short times, then the results of Bird and co-workers [20, 21] should apply to dissolutive systems. Certainly the spreading kinetics r(t) exhibiting values of α less than 0.5 should be expected. The results of Saiz et al. [9] might merit closer examination to determine whether a subtle dependence of the power exponent on θ₀ actually results in α-values less than their observed value 0.5.

Fig. 2

Dissolution behavior of pure Sn spreading on pure Bi at 250 °C in a Hele-Shaw cell. The three images on the left were acquired using a high-speed camera at 1000 fps (The short-time regime ($\lesssim 1\, {\rm ms}$) cannot be resolved by this camera). The three images on the right were acquired using a high resolution camera at 15 fps; the L/S boundary is marked by arrows. Some images reprinted from [22] with permission from IOP Science

The sensible spreading of a drop in a dissolutive system is thought to stop when the drop arrives at a quasi-equilibrium state (final equilibrium, marked by a spherically shaped L/S interface, takes years). The value of θ ⁰_T at this quasi-equilibrium state (the superscript 0 now refers to this quasi-equilibrium state) is the appropriate equilibrium value appearing in the uncompensated Young force F _Y. When appreciable dissolution occurs and extends right up to the contact line, the expression for F _Y is more complicated [14]: $F_{\rm Y}=\gamma_{\rm SL}(t)[\gamma_{\rm SL}^{0}/\gamma_{\rm SL}(t)\cdot \cos \theta_{\rm B}^{0}-\cos \theta_{\rm B}(t)]+\gamma (t)[\gamma^{0}/\gamma (t)\cdot \cos \theta_{\rm T}^{0}-\cos \theta_{\rm T}(t)].$ However, when the spreading stops within 20 ms and before dissolution occurs as in the case of the low miscibility systems [9], what is the appropriate value of θ₀ in Young force that drives the short-time spreading? According to Saiz et al. [9], it is the value of θ₀ appearing in the work of separation expression $W_{\rm sep}=\gamma^{0}(1+\cos\theta_{0})=\gamma^{0}+\gamma_{\rm SV}^{0}-\gamma_{\rm SL}^{0}$ where γ⁰ and γ ⁰_SV are the surface energies of clean liquid and solid surfaces and γ ⁰_SL is a non-equilibrium interfacial energy (absent interdiffusion and adsorption) between the pure phases.

Long-time dissolutive wetting

Experimental observations show that drops contacting perfectly or partially wetting surfaces initially spread at very large velocities driven by surface forces and resisted primarily by inertia. This short-time spreading regime is followed by transition to viscosity-resisted spreading. The viscous regime persists until the surface forces equilibrate and spreading ceases. Experimental data for spreading in dissolutive systems do not provide as clear a picture. In dissolutive systems, surface and chemical forces must equilibrate before spreading ceases. Furthermore, because the forces at the contact line depend on the geometry of the interfaces there, and because interfacial forces are composition-dependent, the two force systems are coupled. The data of Saiz et al. [9] provide the only quantitative evidence that dissolutive systems exhibit short-time spreading kinetics. The observations of Yin [23] provide the only qualitative data that show, even for highly soluble systems, the effects of dissolution do not exert themselves until times significantly greater than the inertia-dominated short-time spreading. Therefore, at some point during the viscosity-resisted spreading regime, the effects of dissolution begin to dominate. The model of Warren et al. [13] shows that wetting/spreading occurs in the absence of an uncompensated Young force. In their model, wetting/spreading is driven solely by the concentration gradient of solute at the triple line. It is likely that both a Young force and a chemical force are operative at all times during dissolutive spreading, and that both eventually decay monotonically to zero as a quasi-equilibrium state is reached. A complete understanding of the relative magnitudes of these two forces as a function of time presently does not exist.

Highly dissolutive systems exhibit spreading times of 10² s, approximately 10⁵ times longer than short-time spreading. These times are well in excess of the times for the spreading of a drop of similar physicochemical properties on an inert (flat) substrate. The salient characteristic of long-time dissolutive spreading is the evolution of the L/S boundary to a configuration far from its original flat configuration. Experiments, as noted above, provide limited access to the evolution of this boundary and the associated concentration field. Theoretical and computational models have the potential to provide key insight into the dynamics and kinetics of this phase of wetting/spreading.

Long-time experiments of dissolutive systems

Dissolutive wetting has been studied experimentally by several researchers. Sharps et al. [24] conducted experiments on the Cu–Ag system at 782 and 900 °C to correlate wetting and spreading with reactivities of the liquid and the solid substrate. They found wetting for the dissolutive systems (e.g., Ag–Cu alloys on pure Cu) was better than for the inert systems (e.g., eutectic Ag–Cu on Cu presaturated with Ag at 782 °C). Yost and O’Toole [25] investigated the wetting behaviors of Bi–Sn alloys on Bi substrates at 240 °C. The final wetting configuration was quantified by metallographic cross-sectioning and scanning electron microscopy (SEM). They demonstrated that dissolution increases the amount of available liquid and found that the equilibrium geometry (in terms of θ ⁰_B and θ ⁰_T ) is independent of system size. Experiments were conducted on single crystal and polycrystalline Bi substrates, and it was found that grain size has minimal influence on dissolution and spreading in the Bi–Sn system.

Because of the long spreading times of the Bi–Sn system, Yin et al. [14] were able to employ rapid quenching in conjunction with metallographic cross-sectioning to assemble a snapshot sequence of the evolution of the L/S interface with time (Figs. 3, 4). They observed that the rate of spreading was dependent on the initial liquid concentration, that spreading velocity decreased monotonically with increasing Bi content and that the quasi-equilibrium value of θ ⁰_T increased monotonically with increasing Bi content. Their data clearly showed that the rate of dissolution is driven by the solute concentration difference between the solid and liquid. They observed that the L/S interface tended to meet the L/V interface at a 90° angle, except for very large (initial) Bi-content alloys (Fig. 5). These observations corroborate the computational modeling predictions of Warren et al. [13] who showed that, despite the imposition of a value θ_L = θ_T + θ_B = 35° at the triple line, the L/S and L/V interfaces appeared on a slightly coarser scale to have orthogonal orientations. This led to a region close to the triple line in which L/S interface changed curvature in order to satisfy the imposed condition on θ_L. The physical reason for the coarse scale orthogonal orientations of the two interfaces is that the L/S interface is an approximate isoconcentrate (this fact rests on the assumption that atomic processes of dissolution at the interface are much faster than bulk diffusion of the solute in the solvent metal), and this means that the solute concentration gradient must be perpendicular to this surface. But if the S/L interface adjoins the L/V interface at the contact line, then they must do so at a 90° angle; otherwise, there would be a nonzero component of the mass flux through the L/V interface which is physically inadmissible. The tendency for the interfaces to be orthogonal is mitigated when the concentration gradient is weakened; this was observed to occur by Yin et al. [23] when the initial Bi content exceeded 80 wt%. Protsenko et al. [12] took exception to the above arguments, finding a value of θ_L = 15° for pure Cu wetting Si at 1100 °C. Calculations for θ_L, based on ad hoc geometric models of the S/L interface, supported their findings of a smaller angle. In fact, they asserted that θ_L generally is equal to (numerically but not configurationally) the Young’s angle, i.e., the value of θ ⁰_T for a saturated Cu–Si solution on a flat pure Si substrate. However, some concern must be given to the condition of the drop/substrate on which they made measurements, which, by their own admission, was compromised by cracks developed during cooling and by the appearance of large Si crystals on the L/V interface. Protsenko et al. [12] also discuss the effects of solutal Marangoni convection on the spreading in dissolutive systems, owing to the solute concentration gradients that develop along the L/V interface. We defer discussion of this topic to the next section.

Fig. 3

Dissolution behavior of two Bi–Sn alloys spreading on pure Bi at 250 °C. a Eutectic 57Bi43Sn quenched at 3 s. b 80Bi20Sn quenched at 2 s. Reprinted from [14] with permission from Elsevier

Fig. 4

Sideview images of an 80Bi20Sn alloy spreading on Bi at 250 °C showing the evolution of the L/V interface. The bottom figure shows the evolution of the S/L interface determined from quenching and cross-sectioning at a typical diametral plane. Bottom figure reprinted from [14] with permission from Elsevier

Fig. 5

Contact angle versus time for 80Bi20Sn alloy spreading on Bi at 250 °C

Computational modeling of dissolutive systems

Modeling dissolutive wetting in metal/metal systems, requires accurately treating the fluid dynamics with coupled heat and mass transport, phase transformations, and interfacial phenomena at both the L/V and S/L interfaces. The physical phenomena involved in dissolutive wetting occur over a broad range of spatial and temporal scales, and the material properties of liquid metals (e.g., surface tension, viscosity) further complicate modeling efforts. As discussed earlier in this article, the dissolutive wetting process can be characterized in terms of two regimes: the short-time behavior, where capillarity is the major driving force and inertial forces dominate the very fast hydrodynamic spreading of the liquid on an essentially macroscopically inert substrate; the long-time solute dissolution-dominated regime, where local equilibrium is established at the S/L interface. This description of the dissolutive wetting process is well-evidenced in experimental studies of dissolutive wetting systems, such as, Ag on Cu [11], Cu on Si [12], and Sn on Bi [14].

Over the last 40 years there has been an extensive amount of research performed on the hydrodynamics of wetting which has greatly increased the fundamental understanding of how a liquid wets an inert surface [26–29]. Various types of mathematical models of hydrodynamic wetting and spreading have been developed. Analytical models generally rely on asymptotic methods and the lubrication approximation for the fluid motion has been widely used. For hydrodynamic spreading, the treatment of the liquid/solid/gas triple line is crucial in determining the dynamic evolution of the spreading liquid. The work of Dussan and Davis [30] elucidated the difficulty in modeling the contact line due to the shear stress singularity that results from the application of the no-slip condition on the solid up to and including the contact line. Perhaps the biggest issue in modeling wetting, inert or dissolutive, from a continuum viewpoint is the distinction between the macroscopic and microscopic behavior. Efforts to model wetting and spreading on the continuum level have led to the formulation of various relationships, both theoretical and empirical, between the speed of the contact line and the contact angle. The importance of the triple line region and the difficulties in modeling it have been thoroughly reviewed in a relatively recent book by Shikhmurzaev [31]. The book provides a comprehensive review of the literature on this topic.

A variety of modeling approaches, both analytical and computational, have been employed to gain a better understanding of the physical processes associated with dissolutive wetting, although to a much lesser extent than inert wetting. Braun et al. [32] employed lubrication theory to model drop spreading with mass transfer by including gradients in the concentration resulting from the interaction of the liquid with the substrate. The solute exchange between the liquid and substrate was treated by a mass transfer coefficient boundary condition at the solid surface. Warren et al. [13] used a vertically averaged solute transport model to study the motion of triple junction and the shape of solid–liquid interface evolution. This model primarily captures the later stage of spreading. The convective transport in the solute conservation equation is treated in an approximate manner. Later, Su et al. [33] employed this model to investigate the dynamics of axisymmetric Bi–Sn alloy drops spreading on Bi. The results are compared with the experimental data reported by Yin et al. [14], and the numerical results and experimental data agree well for alloys with a smaller Sn content, confirming the dominant role of diffusion in dissolutive wetting for certain systems. Molecular dynamics simulations [34] also have been used to explore dissolutive wetting in terms of atomic scale processes. The atomic scale modeling yields R ∼ t ^1/2.

The model of dissolutive wetting used by Warren et al. [13] and Su et al. [33] is based on an approximate treatment of the hydrodynamics. While the evolution of the S/L interface is mainly controlled by dissolution, the dissolution is controlled by both convective and diffusive transport. Thus, for a more complete model of dissolutive wetting, it is essential to couple the dissolution with an accurate model of the transport. Also in order to properly model dissolutive wetting, the dynamic behavior, and evolution of the L/V and S/L interfaces must be accurately treated computationally. The treatment of the triple line behavior, both for inert and dissolutive wetting, perhaps poses the most difficulty for computational models.

It is now becoming possible to use state-of-the-art computational techniques to obtain complex time-evolving solutions to multi-scale models of wetting phenomena both in the case of inert and dissolutive wetting. For solving moving boundary problems, explicit front tracking techniques [35], the arbitrary Lagrangian–Eulerian method [36] and implicit interface tracking techniques such as the level-set and phase-field methods offer the capability to model-specific aspects of both inert [37–39] and dissolutive wetting [40–42]. Diffuse interface (e.g., phase-field) methods have been successful in accurately capturing the complex interfacial patterns observed in phase evolution processes such as dendritic growth where both interfacial energy and kinetics play a role in determining the evolution of the phase boundary. For wetting problems, diffuse interface models require the coupling of the Navier–Stokes equations with generalized versions of the Cahn–Hilliard equation. Accurate solutions to the model equations require sophisticated numerical techniques and are computationally intensive. Diffuse interface models are developed in the framework of chemical thermodynamics and incorporate phase diagram information or equations of state for alloy systems. However, to date, the models have been limited to very small drops and computational domains, and using parameter values (e.g., viscosity, surface tension, and temperature) entirely consistent with real experimental conditions remains a challenge.

An interesting aspect of diffuse interface models is how they capture the triple line behavior. For inert wetting, the models display an effective slip that allows the contact line to move. Also, it has been found that the contact line speed is dependent on the the interface thickness [37]. There are a number of other issues associated with diffuse interface models. Because of the diffusive nature of the equations governing the movement of the interfaces, it is observed that the extent of spreading may depend not only on the static contact angle but also on the balance between convective and diffusive transport.

A more conventional methodology for dealing with moving interfaces is to treat them as sharp boundaries and track them in a Lagrangian framework using grid points. When coupled with the transport equations, the interfaces evolve according to the conservation and kinetic laws that are applied to the interfaces. The Arbitrary Lagrangian–Eulerian (ALE) method is attractive because of its capability to handle large deformation and track the motion of interface accurately. The ALE technique was developed in order to combine the advantages of both the Lagrangian and Eulerian descriptions. In the ALE approach, the nodes of the computational mesh can be moved with the continuum in a normal Lagrangian fashion, be held fixed in an Eulerian manner, or be moved in an arbitrarily specified way to provide a continuous re-zoning capability. Because of this freedom in moving the mesh, the ALE technique can handle greater distortion than purely Lagrangian algorithm and has a better resolution than a purely Eulerian description. This type of computational methodology has been successfully employed to model the motion of a liquid–vapor interface by Li et al. [43], solid–liquid interface [44–46] and the combination of the two for dissolutive wetting by Su [36].

Drop spreading simulations

As discussed in the Introduction, the experiments of Bird et al. [20] studied the very early time dynamics for an inert and partially wetting system. They found that the evolution of the drop radius followed a power law where the exponent varied monotonically with equilibrium contact angle. Carlson et al. [39] employing a diffuse interface model were able to capture this behavior for rapid wetting by accounting for nonequilibrium at the triple line. They concluded that the treatment of the triple line region that occurs naturally in the diffuse interface model leads to a local structure that accurately captures the behavior, both qualitatively and quantitatively, reported in [20]

In the case of dissolutive wetting, as discussed earlier, the model developed by Warren et al. [13], assumes that transport of solute occurs primarily by diffusion. The equations governing the flow field are not solved in this model, but the motion of the liquid and convective transport in the drop are included in an approximate manner. Conservation of mass is satisfied using a flow field that was developed from lubrication theory appropriate for thin drops. The L/V interface is treated as a spherical cap that moves due to its coupling with the dissolution front. The model formulation presented in Warren et al. provides a good starting point for analyzing the important physical processes in the long-time regime of dissolutive wetting. Some of the key assumptions of the model are that the vertical location of the contact line remains at the original height of the S/L interface, the liquid and solid densities are equal and independent of concentration, the top liquid surface is a spherical cap, the S/L interface is in local equilibrium and the Gibbs–Thomson equation is used to define the solute concentration there. They obtained a relationship, resulting from the flux boundary conditions for the liquid surface and the S/L interface at the contact line, that determines the speed of the contact line as a function of the geometrical parameters and the concentration gradient evaluated at the triple junction,

$$ \frac{{\rm d}R}{{\rm d}t}=-\frac{Dc^{\prime}}{c}\frac{\tan\theta_{\rm T}+\tan \theta_{\rm B}}{\tan \theta_{\rm B}}. $$

(1)

Here D is the solute diffusivity in the liquid, c′ is the liquid concentration gradient at the triple junction, the definitions of θ_T and θ_B are shown in Fig. 1. The contact angle in this case is the sum of θ_T and θ_B. In their model the contact angle is assumed constant. This result shows that a small downward displacement of the S/L interface (small θ_B) leads to faster horizontal movement of the triple junction.

The diffuse interface model simulations by Villanueva et al. [41] were able to capture both inert and dissolutive wetting depending on the values of the model parameters. The diffuse representation of the L/V interface includes evaporation and condensation and these mechanisms played a role in determining the spreading dynamics. In addition, the model yields a strong dependence of the wetting dynamics on the solute diffusivity. In order to treat realistic interface thicknesses (≈1 nm) the drop size was limited to 100 nm. The simulations show that the fluid flow driven by capillary forces is dominant at early time. Later as the phase change becomes the dominant driving force, the spreading velocity is three orders of magnitude smaller than the early time velocities. As the drop spreads and dissolution at the S/L interface proceeds, the liquid must move accordingly as the drop shape evolves. The relatively large Schmidt numbers for metals spreading on metal substrates point to primarily convective transport of solute within the drop. As spreading occurs, the concentration close to the contact line first increases rapidly to a maximum and then decreases more slowly to the equilibrium concentration, while the concentration at the center of the drop decreases and reaches a minimum before slowly approaching the equilibrium concentration.

The short timescale behavior for dissolutive wetting was studied by Wheeler et al. [42] using a diffuse interface model that is significantly different from the approach used in [41]. In [42], only the L/V interface is treated via Cahn–Hilliard theory coupled to the compressible flow equations. The S/L interface evolution is captured using a Cahn–Allen phase field approach that includes convective transport. In their study, a 1-μm drop diameter is used, requiring artificially thick interface representations. Even though the drop is very small, the Ohnesorge number is on the order of 10⁻³ indicating that inertial effects are significant. Their simulations exhibit the t ^−1/2 spreading rate indicative of inertial spreading. They compared the radius versus time predictions from their simulations to the data of Saiz and Tomsia [47] for the Cu–Mo system and obtained reasonable agreement.

The ALE method was employed to simulate both inert wetting and dissolutive wetting in liquid metal systems, using a fluid transport model based on the Navier–Stokes equations [36]. Simulations of inert wetting were performed to test the behavior of the numerical model and showed good agreement with published experimental data. Dissolutive wetting was studied for the isothermal spreading of a binary alloy drop on a metal substrate. For an axisymmetric drop of millimeter size, the evolutions of the liquid–vapor interface and the solid–liquid interface are determined by the ALE method in a moving frame as the drop spreads. The rate of spreading, the shape of the dissolution boundary, flow field, and concentration distribution within the drop are computed and the effect of concentration gradient on spreading kinetics is investigated. The sharp interface representation requires slip be incorporated at the triple point. A slip length on the order of the mesh size is used. For this type of model the dynamics of the spreading are never completely independent of the slip length. Nevertheless, model is capable of capturing the short-time inertial behavior as well as the longer-time dissolution-controlled spreading.

Solutal Marangoni effects

For dissolutive systems, as a result of surface tension variation with species concentration, solutal Marangoni convection may be important and can have an impact on drop spreading. The appearance of Marangoni driven films for dissolutive systems is discussed by Saiz and Tomsia [47]. Protsenko et al. [12] have shown that solutal Marangoni convection controls the spreading kinetics for the dissolutive wetting of Si by liquid Cu.

Braun et al. [32] developed a simplified model of solutal Marangoni convection in a spreading droplet. In some very recent work, Su [36] modeled the impact of solutal Maragoni convection on the spreading of a drop in a dissolutive system using the computational approach described earlier. In this study, a simple linear variation between the surface tension and the solute concentration is assumed,

$$ \gamma =\gamma_{0}\pm \gamma_{c}(c-c_{0}), $$

where γ and c are the surface tension and species concentration along the surface of liquid drop, γ₀ is the surface tension at triple junction which is constant because the concentration at triple junction is assumed to be the equilibrium concentration c ₀. In the linear model, the variation of surface tension with concentration is represented by γ _c . The variation of the surface tension with species concentration has been measured for a number of metal–metal systems. The linear model is used as an approximation for moderate concentration variation—the measured surface tension variation for most metal systems is generally nonlinear over a large range of concentration variation.

For the simulations presented here, a value for γ _c of 10 mN/m was used for concentration specified in wt%. Figure 6 shows the impact of solutal Marangoni convection on the spreading kinetics for the base model parameters. The blue dot-dash line is the result without the Marangoni effect, and the red dash line and green line are the opposing and cooperating cases. Clearly, the solutal-capillary flow influences the spreading behavior of the drop. The behavior exhibited by the model is in qualitative agreement with the results for dissolutive wetting in the Cu–Si system reported by Protsenko et al. [12].

Fig. 6

Spreading kinetics for different surface tension dependence on concentration

To better understand the behavior resulting from the solutal Marangoni effect, the flow field in the entire drop and the solute concentration in the triple junction region are presented in Figs. 7 and 8, respectively. Note that the same plotting scale is used for all three cases. Based on the nature of the flow patterns shown in Fig. 7, it is evident in the cooperating case, that due to the negative surface tension gradient along the L/V interface resulting from the concentration gradient, the convective flow is toward the triple junction which enhances the spreading. On the other hand, for the opposing case, the surface tension gradient is positive, and the Marangoni driven flow along the L/V interface is away from the triple junction and spreading is reduced. In addition for the opposing case, the convective transport of solvent along the S/L interface is enhanced resulting in more dissolution of the substrate away from the triple junction. The convective solute transport in the triple junction region is reduced in this case and dissolution is less apparent (i.e., the S/L interface remains flatter close to the triple junction). Figure 9 shows the evolution of dissolution depth at the center of the drop and the corresponding drop shape after 10 s.

Fig. 7

Flow field at 0.1 s for the different surface tension variation cases

Fig. 8

Concentration profiles close to the contact line region for the different surface tension variation cases

Fig. 9

Dissolution depth versus time for different surface tension dependence on concentration

Final equilibrium

At final equilibrium, the total contact angle θ ⁰_L depends only on the three interfacial energies at a given temperature, and is independent of the initial liquid composition, i.e., θ ⁰_L  = θ ⁰_T  + θ ⁰_B  = constant. However, it is less obvious that the values of θ ⁰_T and θ ⁰_B may individually depend on the initial composition. In this section, such dependence is derived for the Bi–Sn system as an example.

As noted several times above, the cessation of sensible spreading does not represent a final equilibrium configuration of the system. True equilibrium occurs on a time scale of years [13, 14] and is associated with the relaxation of curvature variations (and associated concentration variations) along the S/L interface This relaxation can involve changes in r(t). The final three-phase equilibrium for dissolutive systems at a given temperature requires both chemical and mechanical equilibrium. The former implies that the liquid is uniformly at the saturation composition and the latter implies that the net force vanishes on the contact line. Both the L/V and S/L interfaces must assume a constant curvature shape, so that no concentration variation exists along the interfaces. Therefore, the liquid phase is bounded by two spherically shaped interfaces forming a known volume V ⁰_dis  + V _init, assuming the volume change due to mixing is negligible. The spherical cap expressions for V _init and V ⁰_dis are

$$ V_{\rm init} = \frac{R^{3}\pi}{3\sin^{3}\theta_{\rm T}^{0}}\left(2-3\cos \theta_{\rm T}^{0}+\cos^{3}\theta_{\rm T}^{0}\right) $$

(2)

$$ V_{\rm dis}^{0} = \frac{R^{3}\pi}{3\sin^{3}\theta_{\rm B}^{0}}\left(2-3\cos \theta_{\rm B}^{0}+\cos^{3}\theta_{\rm B}^{0}\right), $$

(3)

where R = r(t→ ∞) is the equilibrium spreading radius and V ⁰_dis can be calculated from the initial alloy composition X ⁱ_Solute and the equilibrium composition X ⁰_Solute . A third equation is provided by force equilibrium at the contact line:

$$ \theta_{\rm T}^{0}+\theta_{\rm B}^{0}= {\rm constant}. $$

(4)

Equations (2), (3), and (4) then provide a complete set of equations for the unknowns R, θ ⁰_T and θ ⁰_B .

Figure 10 illustrates the solution of the equilibrium equation set for some hypothetical interfacial energies in the Bi–Sn system. The dashed lines are plots of θ ⁰_B versus θ ⁰_T from Eq. (2) and (3) for the composition range from pure Sn to 90Bi10Sn. The abscissa in the figure is the iso-concentrate of 93Bi7Sn at 250 °C and corresponds to θ ⁰_B  = 0°; thus the values of θ ⁰_T on the abscissa are possible angles for inert wetting scenarios. The solid straight line is θ ⁰_B versus θ ⁰_T from Eq. (4) with θ ⁰_T  + θ ⁰_B  = 30°. The intersections of dashed lines and the straight solid line are the solutions for θ ⁰_T and θ ⁰_B , and are clearly dependent on the initial solder alloy composition. The spreading radius R is calculated using either of Eqs. (2) or (3).

Fig. 10

Determination of equilibrium contact angles θ ⁰_T and θ ⁰_B for the Bi–Sn system. Dashed lines are from Eqs. (2) and (3). The straight solid line is from Eq. (4). The solution for θ ⁰₁ and θ ⁰₂ can be found at the intersection of the solid and the dashed lines

Conclusions and future directions

The spreading of millimetric-sized molten drops in dissolutive metal–metal systems occurs over a cascade of timescales, ranging from sub-milliseconds to essentially years for final equilibrium. The most relevant time range is conveniently divided into short- and longer-time domains. In the short-time domain, the drop at initial contact is driven by the uncompensated Young force and resisted by inertia forces. The kinetics in this domain are characterized by r(t) ∼ t ^α, where α ≤ 0.5 and the equality holds for perfectly wetting systems. Once the drop has been set in motion, viscous forces overtake inertia forces as the primary resistance to the Young force. For systems with low miscibility, spreading can terminate in less than 20 ms, before any significant dissolution can occur; subsequent dissolution requires only minor changes to achieve a final configuration. In high miscibility systems, the inertia- → viscosity-controlled spreading sequence yields to dissolution-controlled spreading which can take as long O(10²) s. These conclusions have been drawn from observation of spreading kinetics, the main observables being the superficial contact angle and the wetted radius as functions of time. Quenching and metallographic cross-sectioning enable construction of discrete-time histories of the L/V and S/L interface evolutions. Novel Hele-Shaw experiments provide qualitative real-time observation of the interface evolutions, but need further refinement and supporting theoretical analysis to provide quantitative information.

Considerable strides have been made in the last 10 years in the sophistication of models of dissolutive wetting. Computational techniques for treating complex moving boundary problems such as moving mesh approaches (e.g., ALE) and diffuse interface methods based on Cahn–Hilliard theory have been applied to simulate the dissolutive wetting and spreading drops by a number of different investigators. While no one approach today is capable of capturing the complex behavior exhibited by dissolutive wetting over the wide range of temporal and spatial scales, computational models beginning with molecular dynamics, and continuing up to large-scale multi-phase transport models have helped piece together a better understanding of the important phenomena. A review of some of the more recent studies has been presented. In addition, as an example of some recent work, the effect of solutal Marangoni convection during dissolutive wetting was demonstrated utilizing a recent computational model. The Marangoni convection is found to alter the spreading kinetics at the dissolutive wetting stage. The spreading of the drop is diminished or enhanced depending on whether the Marangoni flow opposes or coincides with the primary flow driven by the spreading. In addition, the final drop shape is found to depend on the presence of the Marangoni flow because of the resulting modified convection patterns inside of the drop.

Progress in understanding dissolutive wetting would benefit from more experimental data for different material systems. Future experiments could be of the traditional axisymmetric drop type or new wetting/spreading geometries that might be more amenable to supporting modeling. Experiments in transparent material systems in which simultaneous in situ observation of the evolution of both the L/S and L/V interfaces would be possible are highly desirable. Such experiments would constitute a significant improvement over the data obtained from opaque material systems in which temporal L/S interface data is obtained by quenching and subsequent metallographic cross-sectioning. Material systems that exhibit large solubilities would be most valuable, and experiments across the range of solubility—from inert to saturated (inert)—in a given material system must be conducted. It is now clear that wetting and spreading in dissolutive systems occur over a cascade of time scales, and experiments should include resolution of the early time wetting to assess any effects of dissolution that might be present.

The level of sophistication in computational models of dissolutive wetting will continue to evolve. As described here, the models range from molecular dynamics at one end of the spectrum to full 3-D fluid flow models including heat and mass transport. High performance computing platforms combined with adaptive finite-element solution methods enable accurate simulations of the transport on the mesoscale in dissolutive wetting systems. Computational techniques for multi-phase problems such as the ALE and level set methods are able to capture the evolving phase boundaries accurately while providing flexibility in the types of physical effects that can be modeled at the interfaces. Perhaps even more promising are the capabilities afforded by diffuse interface models which offer a means of developing models incorporating thermodynamic and kinetic effects utilizing a more physical rather than mathematical framework. However, the large range of spatial and temporal scales involved in wetting, dissolution and reaction still call for the development of more comprehensive multi-scale models that properly couple the molecular behavior at interfaces with the larger scale transport processes.