Abstract
The refinement order on partitions corresponds to the operation of merging blocks in a partition, which is relevant to image segmentation and filtering methods. Its mathematical extension to partial partitions, that we call standard order, involves several operations, not only merging, but also creating new blocks or inflating existing ones, which are equally relevant to image segmentation and filtering techniques. These three operations correspond to three basic partial orders on partial partitions, the merging, inclusion and inflating orders. There are three possible combinations of these three basic orders, one of them is the standard order, the other two are the merging-inflating and inclusion-inflating orders. We study these orders in detail, giving in particular their minimal and maximal elements, covering relations and height functions. We interpret hierarchies of partitions and partial partitions in terms of an adjunction between (partial) partitions (possibly with connected blocks) and scalars. This gives a lattice-theoretical interpretation of edge saliency, hence a typology for the edges in partial partitions. The use of hierarchies in image filtering, in particular with component trees, is also discussed. Finally, we briefly mention further orders on partial partitions that can be useful for image segmentation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper discusses partial order relations on partitions (or partial partitions) that can be relevant to the process of image segmentation or filtering. It elaborates on the first part of [26].
Let E be a set. A partition of E is a family of non-void mutually disjoint subsets of E, called blocks [17], whose union is E. We write Π(E) for the set of all partitions of E. A partial partition of E is a partition of any subset of E, it consists also of non-void mutually disjoint blocks, but their union is not necessarily equal to E. We write Π ∗(E) for the set of all partial partitions of E. Given π∈Π ∗(E), the union of all blocks of π is called the support of π and written supp(π); thus π is a partition of supp(π); the complement E∖supp(π) of the support is the background of π.
The set Π(E) is partially ordered by refinement: for π 1,π 2∈Π(E), we say that π 1 is finer than π 2, or that π 2 is coarser than π 1, and write π 1≤π 2 (or π 2≥π 1), if and only if every block of π 1 is included in a block of π 2, equivalently, every block of π 2 is a union of blocks of π 1. Then (Π(E),≤) is a complete lattice, whose least (finest) and greatest (coarsest) elements are the identity partition (whose blocks are all singletons in E) and the universal partition (with E as single block) [17].
The set Π(E) and its order ≤ are both relevant to image segmentation. We consider images as functions E→T, where T is the set of image values, and the goal of segmentation is to build from such a function F:E→T a segmentation defined as a partition π of E, such that F is in some sense “homogeneous” on each block of π. Now Soille [37] summarizes conventional requirements of image segmentation as follows:
-
1.
The segmentation method relies on a criterion that determines, for every function F and every subset A of E, whether F is homogeneous on A or not.
-
2.
Given a function F, its segmentation is a partition of E into connected blocks on which F is homogeneous; these blocks are called segmentation classes.
-
3.
Merging two or more adjacent segmentation classes, F is not homogeneous on the resulting set; in other words F cannot be homogeneous on a connected union of two or more segmentation classes.
Here Soille considers the connectivity of sets arising from an adjacency graph, but more generally we can assume that the so-called connected sets constitute a connection \(\mathcal{C}\) on \(\mathcal{P}(E)\) [21, 27, 30]. For any function F:E→T, let \(\mathcal{C}^{F}\) be the family of all \(A \in\mathcal{C}\) (i.e., A is a connected subset of E) such that F is homogeneous on A according to the criterion of item 1. By item 2, the segmentation of F is a partition π F of E whose blocks belong to \(\mathcal{C}^{F}\). Now let π′>π F be a strictly coarser partition; then the larger blocks of π′ are obtained by merging segmentation classes of π F; either the merged classes are not adjacent, and the resulting block of π′ will not be connected, or these merged classes are adjacent, but then by item 3, F will not be homogeneous on the resulting block of π′. In any case, a larger block of π′ does not belong to \(\mathcal{C}^{F}\). Therefore π F must be a maximal element, for the refinement ordering, of the family \(\varPi(E,\mathcal{C}^{F})\) of all partitions whose blocks belong to \(\mathcal{C}^{F}\).
Here we see the relevance to image segmentation of the refinement order in terms of the operation involved in the coarsening of a partition: merging blocks. We can also consider the opposite operation, involved in the refinement of a partition: splitting blocks. These two operations are well-understood and have been used for a long time, for instance in the split-and-merge approaches to image segmentation [19].
The refinement order on partitions intervenes also in connected filtering. The flat zones of a function F:E→T are the maximal connected subsets of E on which F has constant value; they constitute a partition of E, let us write it π flat (F). Now a connected filter ψ transforms F into a function ψ(F) where each flat zone is a union of flat zones of F, in other words, the partition of flat zones of ψ(F) is coarser than the one of flat zones of F: π flat (F)≤π flat (ψ(F)).
The refinement order on Π(E) extends naturally to the set Π ∗(E) of all partial partitions of E: for π 1,π 2∈Π ∗(E), we write π 1≤π 2 (or π 2≥π 1), if and only if every block of π 1 is included in a block of π 2. Following [26], we call this partial order the standard order. Then (Π ∗(E),≤) is a complete lattice, whose least and greatest elements are the empty partial partition (having no block) and the universal partition (with E as single block).
In [22] we pointed out the interest of considering partial partitions for the study of image segmentation. Let us give here several reasons:
-
Some image segmentation algorithms produce segmentation classes separated by boundaries made of pixels; this happens with some versions of the watershed algorithm, but it arises also by necessity in some connective segmentation methods [27, 32], such as the smooth and jump connections, where seeds (or points) are agglomerated on the basis of overlapping or contact, and distinct regions must be non-adjacent in order to prevent their merger. Here the regions (segmentation classes) constitute a partial partition of the space E, and the boundaries form the background (complement of the support) of that partial partition.
-
It is interesting to combine region-based segmentation (like watershed or connective segmentation) with edge detection [15]. Indeed, in region-based segmentation methods, the only edges that are preserved are those that separate distinct regions, in particular, edges that are not closed will usually disappear; one might want to preserve unclosed edges, so that they could be closed with some post-processing; furthermore, there is no guarantee that the regions will always be separated along the most salient edges. Thus one can constrain the segmentation by providing not only initial markers for the regions, but also markers for the edges that will remain outside the final regions constituting the segmentation.
-
Morphological segmentation usually works in a bottom-up way, by growing mutually disjoint regions from markers (as in the watershed), or by constructing successively the segmentation classes (in a compound segmentation paradigm, see [27, 31]). This means constructing a sequence of partial partitions that is growing for the standard order.
-
From a top-down point of view, a segmentation algorithm associates to every function F:E→T and every subset A of E a partition (or partial partition) π F(A) of A [27, 32]. This leads to the block splitting operator on Π ∗(E) that applies π F to each block of a partial partition: Π ∗(E)→Π ∗(E):ξ↦⋃ A∈ξ π F(A). This operator is anti-extensive for the standard order, and we showed in [24, 25] that for three image segmentation methodologies (connective segmentation and its compound and constrained variants) this operator is idempotent and has specific algebraic properties related to order.
Compared to the refinement order on Π(E), the standard order on Π ∗(E) shares many algebraic properties [22–25]. However it is conceptually more complex. Let π 1,π 2∈Π ∗(E) such that π 1≤π 2; thus every block of π 1 is included in a block of π 2. But contrarily to the case of the refinement order on Π(E), a block of π 2 will not necessarily be a union of blocks of π 1. When it is not itself a block of π 1, it can be obtained by one of the following operations: (a) creating a new block; (b) inflating a block of π 1; (c) merging several blocks of π 1; (d) merging and inflating several blocks of π 1. See Fig. 1. Therefore it is not appropriate to call this order on Π ∗(E) refinement, as we did in [22]; hence the new name standard order [26].
We saw above that the operation of merging blocks is relevant to image segmentation. Now the two other operations, inflating and creating blocks, are also relevant, since they are involved respectively in region growing (such as watershed) and in compound segmentation (where the segmentation classes are built successively with varying criteria [27, 31]). This suggests that the standard order is in fact a combination of three basic orders, associated to the three basic operations of merging, inflating and creating blocks. We will indeed define three primary partial order relations on Π
∗(E), the merging, inclusion and inflating orders, written ⊑, ⊆ and ⊴; all three are included in the standard order ≤. Next we will describe two secondary partial order relations obtained by combining two of the three primary orders, the merging-inflating and inclusion-inflating orders, written  and
and  ; on the other hand combining merging with inclusion, one generates the standard order.
; on the other hand combining merging with inclusion, one generates the standard order.
There are other meaningful partial order relations on Π ∗(E) that are not included in the standard order. Serra [33, 34] defined on Π ∗(E) the building order ⋐ by a kind of logical inversion of the standard order: π 1⋐π 2 if and only if every block of π 2 contains at least one block of π 1 (it may also contain or intersect other blocks of π 1). To be more precise, Serra studied in fact the partial order on \(\mathcal{P}(E)\) induced by the building order on the partial partition of connected components of a set: for \(X,Y \in \mathcal{P}(E)\), X⋐Y if and only if every connected component of Y contains a connected component of X. (NB. He also used the symbol ⪯ instead of ⋐.) Now ⋐ is a partial order relation, and it is generally unrelated to the standard order ≤, except when the partial partitions have the same support: if π 1≤π 2 and supp(π 1)=supp(π 2), then π 1⋐π 2; in particular for partitions, the building order ⋐ contains the refinement order ≤. However the building order does not constitute a lattice, and it is not easy to define operators with given order-theoretic properties (for instance, isotony).
This new order relation was motivated by the problem, encountered with many image segmentation algorithms, of “small parasitic” segmentation classes appearing along contours and transitions, where the region homogeneity criterion fails. Serra proposes to eliminate them and take as final partition the watershed or influence zones (in a Voronoi diagram) of the remaining segmentation classes corresponding to significant objects. See Fig. 2. Now both operations of first removing “parasitic” blocks and next inflating the remaining blocks, are extensive for the building order. More precisely, starting from a partial partition π 0:
-
1.
Remove “small parasitic” blocks from π 0 (through some “parasitism” and size criterion); the resulting partial partition π 1 satisfies π 0≥π 1 but π 0⋐π 1.
-
2.
Inflate the blocks of π 1 (for example by a Voronoi diagram, or through a homogeneity criterion), without creating any new block; the merging of blocks, although not excluded in theory, is not used in practice; the resulting partial partition π 2 satisfies both π 1≤π 2 and π 1⋐π 2.
Then the partial partition π 2, having fewer but bigger blocks than π 0, is “better”, a quality that is certified by the order π 0⋐π 2.
(a) The graph of a one-dimensional grey-level edge; below we show (top bar) its segmentation into connected classes with bounded slope (light grey rectangles for non-singleton classes, vertically hatched ones for groups of singleton classes); note the large number of small classes on the edge; eliminating them (middle bar), the final segmentation (bottom bar) consists of the influence zones of the two large classes. (b) From left to right: a disk B; a subset of the plane is segmented into two connected zones open by B, while the remaining points form singletons; the desired segmentation is obtained by the influence zones of the two connected open zones
Note that the example of Fig. 2(a) can be adapted to give an edge enhancement method, by considering flat zones instead of segmentation classes: “small parasitic” flat zones along the edge are removed, then the remaining large flat zones are extended to cover the removed small ones.
Let us remark that the criteria are vital: if we had removed “big non-parasitic” blocks and then inflated the remaining “small parasitic” ones, the result would be catastrophic, while the two operations would still be extensive for the building order.
Taking a critical look at Serra’s argument, we first note that the construction of π 2 from π 0 involves two restricted operations (first removing blocks, next inflating blocks), guided by two distinct criteria (first size and “parasitism”, next homogeneity or distance to the marker); in fact these two operations correspond to two restricted orders, the inverse inclusion and the inflating orders: π 0⊇π 1⊴π 2. Next, although we have a growing sequence for the building order, π 0⋐π 1⋐π 2, intuitively π 1 cannot be considered as a “good” result, since it has a smaller support than π 0; this is corroborated by the standard order that gives π 0≥π 1≤π 2. In all practical examples, the block growth of step 2 must be repeated until the blocks removed in step 1 are fully covered, in other words supp(π 2)=sup(π 0) (in fact, Serra considers that π 0 and π 2 are partitions of E).
Thus in our opinion, the building order on Π ∗(E) is too general to be meaningful. We can consider that since the two operations of first removing then inflating blocks use distinct criteria, they constitute two distinct stages in segmentation, hence they must correspond to two distinct order relations, namely the inverse inclusion and inflating orders. Another possibility is to consider the succession of the two operations as a compound operation that is successful only if the support of the initial partial partition is fully recovered. We call this compound operation apportioning: some blocks in a partial partition may be split, and their parts are merged with some remaining blocks; this includes the possibility of a block being merged with another without being split. This introduces a new partial order relation on Π ∗(E), which extends the merging order. We call it the apportioning order; it was briefly suggested in Serra’s work [33, 34], but was not pursued further. We will study it in a future paper.
We have seen that several partial order relations on Π ∗(E) can be defined by purely mathematical relations on blocks, but they become really meaningful when they correspond to certain types of operations on partial partitions that are effectively used in segmentation (or filtering), and these operations are generally guided by specific criteria.
The purpose of this paper is the detailed study, with a view on image segmentation and filtering, of these orders on partial partitions: the three basic ones (merging, inclusion and inflating orders) and their combinations (merging-inflating, inclusion-inflating and standard orders). In particular, we consider least and greatest elements, the covering relation, the length of intervals and the height of elements. Indeed, since an order on partial partitions corresponds to a type of operation in the construction of a segmentation, the height of a partial partition will correspond to its complexity in terms of elementary operations necessary to obtain it.
An important notion in morphological image segmentation is that of a hierarchy, that is, a growing sequence of segmentation partitions, starting and ending with the least and greatest partitions [12, 13]; a related concept is that of edge saliency [16], namely, specifying for each edge portion its evolution through the levels of the hierarchy. They have been studied for Π(E) with the refinement order. Following the framework of [23], where the hierarchy corresponds to an erosion from scalars to partitions, with the adjoint dilation measuring the diameter of blocks according to an ultrametric, we extend this analysis to partial partitions with the standard order. Also the notion of an edge between blocks implicitly assumes the connectedness of these blocks, and indeed one makes such an assumption in segmentation; thus we will work in the lattice of (partial) partitions with blocks belonging to a given (partial) connection. In the case of a connectivity based on an adjacency graph, we need to consider the saliency not only of the edge separating a pair of adjacent points, but also of each individual point. We also briefly discuss the relation to saliency of the basic operations of merging, creating or inflating blocks involved in the orders that we have studied. Finally, hierarchies of partial partitions with connected blocks intervene in connected filtering through the structure of the max-tree and min-tree [28, 29] (also called component tree [14]), so we consider the relevance of our new orders to this filtering approach.
This paper being very long, we have left out a topic discussed in [26]: the numerical evaluation of segmentation partitions by some function (called energy in [7, 10, 35, 36] and valuation in [26]), which has to be minimized or maximized. An example of such function is the order-theoretical height, which we determine for the orders introduced in this paper. This topic will be dealt with in a future paper.
There are also many more orders on Π ∗(E), such as the apportioning order briefly mentioned above, then its combinations with the inflating and the inclusion orders, but also orders obtained by combining one of the three basic orders with the inverse of another one. This will be discussed in yet another paper.
1.1 Paper Organization
Section 2 recalls basic facts concerning the refinement order on partitions and the standard order on partial partitions, the structure of the corresponding complete lattices, as well as their relations with connections and partial connections. It also describes some basic relations between partial partitions defined in terms of block inclusion. Section 3 studies the three basic orders (merging, inclusion and inflating) and their combinations (standard, merging-inflating and inclusion-inflating). Section 4 analyses hierarchies and saliency, with a view on image segmentation and filtering. Finally Sect. 5 concludes, summarizing our results, discussing their relevance and putting them into perspective. Appendix discusses the compatibility of all these partial order relations with local knowledge.
2 Mathematical Preliminaries
We give here our notation and recall some known mathematical facts. We will also introduce some new general results about partial partitions.
In mathematical formulas, we will write “&” for the logical “and”. Given a set A, we will write: \(\mathcal{P}(A)\) for the set of parts of A; given any subset B of A, \(\mathcal{P}(A/B)\) for the set of parts of A containing B, \(\mathcal{P}(A/B) = \{ X \mid B \subseteq X \subseteq A \}\); |A| for the cardinal of A. Given two subsets A and B of a set E, we say that A and B overlap, and write A≬B, if A∩B≠∅.
2.1 Relations and Orders
Each binary relation R is identified with the set of ordered pairs (a,b) such that aRb, so if we say that the relation S is included in the relation R, or that R contains S, this means that aSb implies aRb; similarly, the intersection (resp., union) of two relations R and S is the relation Q such that aQb iff aRb and (resp., or) aSb. This applies in particular to partial order relations.
Our terminology on orders and lattices follows [3, 4, 6]. We will consider several distinct order relations; for their notation we follow a common rule: we use some symbol for the strict order “strictly less than” (e.g., ◀), the underlined symbol for the corresponding wide order “less than or equal to” (e.g.,  ), then the mirror symbol for the inverse strict order “strictly greater than” (e.g., ▶) and the underlined mirror symbol for the inverse wide order “greater than or equal to” (e.g.,
), then the mirror symbol for the inverse strict order “strictly greater than” (e.g., ▶) and the underlined mirror symbol for the inverse wide order “greater than or equal to” (e.g.,  ). The only exception is for the building order on partial partitions, where we use ⋐ for “less than or equal to” and ⋑ for “greater than or equal to”, without any specific symbol for “strictly less than” and “strictly greater than”; indeed, we consider this order as a mathematical relation which is not really a “meaningful order”.
). The only exception is for the building order on partial partitions, where we use ⋐ for “less than or equal to” and ⋑ for “greater than or equal to”, without any specific symbol for “strictly less than” and “strictly greater than”; indeed, we consider this order as a mathematical relation which is not really a “meaningful order”.
Given a partial order relation ≤ on a set P, we call isolated any x∈P that is incomparable to any other element of P: ∀y∈P, neither y<x nor x<y holds (equivalently, x is both maximal and minimal). For x,y∈P we say that y covers x (or x is covered by y) if x<y but there is no z∈P such that x<z<y; this relation is usually written x≺y or y≻x; when we analyse the covering relation for distinct orders, we can distinguish them by using various superscripts like \(\buildrel r \over \prec\). Given x,y∈P with x≤y, the length of the interval [x,y]={z∈P∣x≤z≤y} is the supremum of all integers n with x=z 0<⋯<z n =y; when this length is finite (for instance when P is finite), it is the greatest such n, and the sequence takes the form x=z 0≺⋯≺z n =y, we call it a covering chain between x and y. When P has a least element 0, the height of x∈P is the length of the interval [0,x]. When P has no least element, but for every x∈P there exists a minimal element m such that m≤x, we call the height of x w.r.t. m the length of the interval [m,x].
The poset P is graded if there is a map g:P→Z such that for any x,y∈P, x<y ⇒ g(x)<g(y) and x≺y ⇒ g(y)=g(x)+1 [3]; more specifically, we say that P is graded by g. We have then x≺y ⇔ [x≤y & g(y)=g(x)+1]. (NB. In [6] this consequence is given as the definition, which is unsufficient, because it does not guarantee the finite length of intervals.) In a graded poset P, every interval has finite length, and P satisfies the Jordan-Dedekind chain condition, namely that all covering chains between x and y (for x<y) have the same length, which is g(y)−g(x). Furthermore, if P has a least element 0, then the height h satisfies h(x)=g(x)−g(0) for all x∈P, thus P is graded by h.
Since we will consider compound orders on partial partitions, with compound covering relations, we need to introduce compound grading functions:
Proposition 1
In a poset (P,≤), let the covering relation ≺ be the disjoint union of t relations \(\buildrel1 \over\prec, \ldots, \buildrel t \over\prec\). Consider n maps g 1,…,g t :P→Z, and let \(g = \sum_{i=1}^{t} g_{i}\). Suppose that:
-
1.
For all x,y∈P and i=1,…,t we have
$$x \buildrel i \over\prec y \implies \begin{cases} g_i(y) = g_i(x) + 1 , \\ g_j(y) = g_j(x)\quad \textit{for}\ j \ne i . \end{cases} $$
Then the following two statements are equivalent:
-
2.
Every interval in P has finite length.
-
3.
For all x,y∈P,
$$x < y \implies \begin{cases} \forall i = 1, \ldots, t, & g_i(y) \ge g_i(x) , \\ \exists i \in\{1, \ldots, t\}, & g_i(y) > g_i(x) . \end{cases} $$
When these conditions are met, we obtain the following:
-
4.
For all x,y∈P and i=1,…,t we have
$$x \buildrel i \over\prec y \iff x \le y \ \&\ \begin{cases} g_i(y) = g_i(x) + 1 , \\ g_j(y) = g_j(x)\quad \textit{for}\ j \ne i . \end{cases} $$ -
5.
In a covering chain z 0≺⋯≺z n in P, among the n coverings z ℓ−1≺z ℓ (ℓ=1,…,n), there are g i (z n )−g i (z 0) occurrences of \(z_{\ell-1} \buildrel i \over \prec z_{\ell}\) for i=1,…,t.
-
6.
P is graded by g.
Proof
When x≺y, we have \(x \buildrel i \over\prec y\) for some i, then item 1 gives g i (y)=g i (x)+1 and g j (y)=g j (x) for j≠i, hence g(y)=g(x)+1. Now for x<y, item 3 gives g(y)>g(x). Thus items 1 and 3 together imply that P is graded by g, that is, item 6.
Next, item 6 implies item 2. Let x<y; we show by induction on g(y)−g(x) that the interval [x,y] has length at most g(y)−g(x). If x≺y, then the interval [x,y] has length 1≤g(y)−g(x). Otherwise, for any z∈P such that x<z<y, we have g(x)<g(z)<g(y), and as g(z)−g(x),g(y)−g(z)<g(y)−g(x), by induction hypothesis the intervals [x,z] and [z,y] have lengths at most g(z)−g(x) and g(y)−g(z), so any chain containing z must have length at most g(z)−g(x)+g(y)−g(z); therefore the interval [x,y] has length at most g(y)−g(x).
Also, items 1 and 6 together imply item 4. The forward implication ⟹ in item 4 follows directly from item 1. Consider the reverse implication ⟸. Let i∈{1,…,t} and x,y∈P such that x≤y, g i (y)=g i (x)+1 and g j (y)=g j (x) for j≠i; thus g(y)=g(x)+1. Then x≠y, that is, x<y. If x⊀y, then x<z<y for some z∈P, and item 6 gives g(x)<g(z)<g(y), which contradicts g(y)=g(x)+1. Thus x≺y; if \(x \buildrel j \over\prec y\) for j≠i, then g i (y)=g i (x) by item 1, a contradiction. Therefore \(x \buildrel i \over\prec y\).
Now item 1 implies item 5. Let i∈{1,…,t}. In a covering chain z 0≺⋯≺z n , for ℓ=1,…,n, when \(z_{\ell-1} \buildrel i \over\prec z_{\ell}\) we get g i (z ℓ )−g i (z ℓ−1)=1, while when \(z_{\ell-1} \buildrel j \over\prec z_{\ell}\) for j≠i we get g i (z ℓ )−g i (z ℓ−1)=0; hence \(g_{i}(z_{n}) - g_{i}(z_{0}) = \sum_{\ell=1}^{n} [g_{i}(z_{\ell}) - g_{i}(z_{\ell-1})]\) counts the number of occurrences of \(z_{\ell-1} \buildrel i \over\prec z_{\ell}\).
Finally, items 2 and 5 together imply item 3. Let x<y. By item 2 there is a covering chain x=z 0≺⋯≺z n =y. By item 5, for i=1,…,t, g i (y)−g i (x) counts the number of occurrences of \(z_{\ell-1} \buildrel i \over\prec z_{\ell}\) in that chain, hence this number must always be ≥0, and it is >0 for at least one i, because n>0.
We have shown that 1 & 3 ⇒ 6, 6 ⇒ 2, 1 & 6 ⇒ 4, 1 ⇒ 5 and 2 & 5 ⇒ 3. This completes the proof that 1 & 2 ⇔ 1 & 3 ⇒ 4 & 5 & 6. □
Note that item 3 can also be written: for all x,y∈P,
When the above properties are satisfied, we will say that P is graded by (g 1,…,g t ) for \((\buildrel1 \over\prec, \ldots, \buildrel t \over\prec)\). For n=1, we obtain the classical notion of grading: items 1 and 3 mean that P is graded by g=g 1, and item 6 is redundant; now item 4 is the above-mentioned variant definition x≺y ⇔ [x≤y & g(y)=g(x)+1] from [3], which is equivalent only if we assume item 2; finally item 5 is the Jordan-Dedekind chain condition.
A quasi-order is a reflexive and transitive binary relation. Note that a non-empty intersection of quasi-orders is a quasi-order, and that the intersection of an order and a quasi-order is an order.
The set of all partial order relations on a set P is closed under non-void intersection. However, it does not constitute a lattice, because the supremum of partial order relations is not necessarily defined; for instance, there is no partial order containing both an order ≤ and its inverse ≥, because antisymmetry would fail. Nevertheless, given a fixed partial order ≤ on P, the set O(≤) of all partial order relations on P that are included in ≤ is a complete lattice (since it is closed under intersection and has a greatest element).
2.2 Partial Partitions and the Standard Order
Our notation follows [22, 23]. A partial partition of E is constituted of mutually disjoint non-void subsets of E called blocks. We write Π(E) for the set of all partitions of E, and Π ∗(E) for the set of all partial partitions of E. Thus \(\varPi^{*}(E) = \bigcup_{A\in\mathcal{P}(E)} \varPi(A)\). Write Ø for the empty partial partition (with no block); in fact, Π(∅)=Π ∗(∅)={Ø}. Set 1 ∅=0 ∅=Ø, while for any \(A \in\mathcal{P}(E) \setminus\{ \emptyset\}\), let 1 A ={A} (the partition of A into a single block) and 0 A ={{p}∣p∈A} (the partition of A into its singletons); following [17], we say that 0 A is the identity partition of A, and 1 A is the universal partition of A. For π∈Π ∗(E), the support of π, written supp(π), is the union of its blocks: supp(π)=⋃π; the complement E∖supp(π) of the support is the background of π. For π∈Π ∗(E), a transversal of π is a subset of E made by choosing one point in each block of π, in other words a set A⊆supp(π) such that |A∩B|=1 for any B∈π; a crossing of π is set A⊆supp(π) such that A∩B≠∅ for any B∈π; it necessarily contains a transversal.
The refinement order on Π(E) and the standard order on Π ∗(E) are given by the same definition: for π 1,π 2∈Π ∗(E),
Then both (Π(E),≤) and (Π ∗(E),≤) are complete lattices. Their least and greatest elements are 0 E and 1 E for Π(E), but Ø and 1 E for Π ∗(E). The reader is referred to [22] for the description of the supremum and infimum operations in these lattices; they are written ⋁ and ⋀ (or ∨ and ∧ for their binary counterparts). Note that the non-void supremum and infimum operations in Π(E) are exactly the same as in Π ∗(E), and similarly, for A⊆E, the non-void supremum and infimum operations in Π(A) and in Π ∗(A) are again the same as in Π ∗(E).
Given π 1,π 2∈Π ∗(E), let us write \(\pi_{1} \buildrel m \over\prec\pi_{2}\) and say that π 2 m-covers π 1, if π 2 is obtained by merging two blocks of π 1:
Now let us write \(\pi_{1} \buildrel s \over\prec\pi_{2}\) and say that π 2 s-covers π 1, if π 2 is obtained by adding a singleton block to π 1:
Then \(\buildrel m \over\prec\) is the covering relation on partitions, and more generally on partial partitions having a common support. On the other hand, the covering relation on partial partitions is the union \(\prec\;=\; \buildrel m \over\prec\cup\buildrel s \over \prec\) [23], in other words, π 1≺π 2 if and only if \(\pi_{1} \buildrel m \over\prec\pi_{2}\) or \(\pi_{1} \buildrel s \over \prec\pi_{2}\).
Assume now that E is finite. For any π∈Π ∗(E), we define h m (π), the m-height of π, and h s (π), the s-height of π, as follows:
Since every block has at least one point, |supp(π)|≥|π|, thus h m and h s are both non-negative integers. Now the height of π [23] is their sum:
We can now determine the grading and height in Π ∗(E) and in Π(A) (for A⊆E). Note that the height in Π ∗(E) and in Π(A) was already given in [23]:
Theorem 2
Let E be finite. Then Π ∗(E) is graded by (h m ,h s ) for \((\buildrel m \over\prec, \buildrel s \over\prec)\), that is, for any π 1,π 2∈Π ∗(E) we have:
In particular, (Π ∗(E),≤) is graded by h=h m +h s . Also h m (Ø)=h s (Ø)=0, and for π∈Π ∗(E), the height of π in Π ∗(E) is h(π).
For any A⊆E, (Π(A),≤) is graded by h m . Also h m (0 A )=0, and for π∈Π(A), the height of π in Π(A) is h m (π).
Proof
For π 1≤π 2, we have supp(π 1)⊆supp(π 2), thus h s (π 1)=|supp(π 1)|≤|supp(π 2)|=h s (π 2). Given a block C∈π 2 containing exactly k blocks B 1,…,B k ∈π 1, either k=0 and \(\sum_{i=1}^{k} (|B_{i}|-1) = 0 \le|C|-1\), or k≥1 and \(\sum_{i=1}^{k} (|B_{i}|-1) = |\bigcup_{i=1}^{k} B_{i}| -k \le|C|-1\) (because C contains the disjoint union of B 1,…,B k ). Hence \(\sum_{B \in\pi_{1} \cap\mathcal{P}(C)} (|B|-1) \le|C|-1\) anyway (here \(\pi_{1} \cap \mathcal{P}(C)\) is the set of blocks of π 1 included in C). Since π 1≤π 2, every block of π 1 is included in a unique block of π 2, so we get
Hence h m and h s are growing functions: π 1<π 2 ⇒ h m (π 1)≤h m (π 2) & h s (π 1)≤h s (π 2). Given π 1≤π 2, as h=h m +h s , we have h(π 2)=h(π 1) if and only if h m (π 2)=h m (π 1) and h s (π 2)=h s (π 1); then |supp(π 2)|=|supp(π 1)| and |π 2|=|π 1|; as supp(π 1)⊆supp(π 2), we deduce that supp(π 1)=supp(π 2). So every block of π 2 is a union of blocks of π 1, and as |π 2|=|π 1|, two blocks of π 1 may not be merged in π 2, hence π 2=π 1. Therefore π 1<π 2 ⇒ h(π 1)<h(π 2).
If \(\pi_{1} \buildrel m \over\prec\pi_{2}\), then (2) gives |supp(π 2)|=|supp(π 1)| and |π 2|=|π 1|−1, hence h m (π 2)=h m (π 1)+1 and h s (π 2)=h s (π 1). If \(\pi_{1} \buildrel s \over\prec\pi_{2}\), then (3) gives |supp(π 2)|=|supp(π 1)|+1 and |π 2|=|π 1|+1, hence h m (π 2)=h m (π 1) and h s (π 2)=h s (π 1)+1.
We have thus shown that relatively to \((\buildrel m \over\prec, \buildrel s \over\prec)\), the pair (h m ,h s ) satisfies the conditions in Proposition 1, namely item 1 and the alternate form (1) of item 3, hence Π ∗(E) is graded by (h m ,h s ) for \((\buildrel m \over\prec, \buildrel s \over \prec)\). By item 6 of the Proposition, Π ∗(E) is graded by h=h m +h s .
Obviously h m (Ø)=h s (Ø)=0. Since Ø is the least element of Π ∗(E), the height of any π∈Π ∗(E) is h(π)−h(Ø)=h(π).
Finally, let A⊆E. For π 1,π 2∈Π(A), h s (π 1)=|supp(π 1)|=|supp(π 2)|=h s (π 2). From the above we deduce that π 1<π 2⇒h m (π 1)<h m (π 2) and \(\pi_{1} \buildrel m \over\prec\pi_{2} \implies h_{m}(\pi_{2}) = h_{m}(\pi_{1}) + 1\), which means that (Π(A),≤) is graded by h m . Obviously h m (0 A )=0. Since 0 A is the least element of Π(A), the height of any π∈Π(A) is h m (π)−h m (0 A )=h m (π). □
By item 4 of Proposition 1, for any π 1,π 2∈Π ∗(E),
-
π 1≺π 2 iff π 1≤π 2 and h(π 2)=h(π 1)+1.
-
\(\pi_{1} \buildrel m \over\prec\pi_{2}\) iff π 1≤π 2, h m (π 2)=h m (π 1)+1 and h s (π 2)=h s (π 1).
-
\(\pi_{1} \buildrel s \over\prec\pi_{2}\) iff π 1≤π 2, h s (π 2)=h s (π 1)+1 and h m (π 2)=h m (π 1).
Given π,π′∈Π ∗(E) such that π≤π′, by item 2 of that Proposition, there is a covering chain between π and π′. By item 5, in such a covering chain π=π 0≺⋯≺π n =π′, among the n coverings π i ≺π i+1 (i=0,…,n−1), there are h m (π′)−h m (π) m-coverings \(\pi_{i} \buildrel m \over\prec\pi_{i+1}\) and h s (π′)−h s (π) s-coverings \(\pi_{i} \buildrel s \over\prec\pi_{i+1}\), in particular n=h(π′)−h(π).
2.3 Connections and Partial Connections
For any family \(\mathcal{C}\subseteq\mathcal{P}(E)\), let \(\varPi (E,\mathcal{C}) = \varPi(E) \cap \mathcal{P}( \mathcal{C}\setminus\{ \emptyset\} )\) and \(\varPi^{*}(E,\mathcal{C}) = \varPi^{*}(E) \cap\mathcal{P}( \mathcal{C}\setminus\{ \emptyset\})\), be the families respectively of partitions and of partial partitions, whose blocks belong to \(\mathcal{C}\) (in fact, to \(\mathcal{C}\setminus\{ \emptyset\}\)).
Let \(A \in\mathcal{P}(E)\) and \(\mathcal{B}\subseteq\mathcal {P}(A)\). Then we say [22] that A is chained by \(\mathcal{B}\) if \(\bigvee_{B \in\mathcal{B}} \mathbf{1}_{B} = \mathbf{1}_{A}\) (in particular, we must have \(\bigcup\mathcal{B}= A\)); equivalently, for any p,q∈A, there are \(B_{0}, \ldots, B_{n} \in \mathcal{B}\) (n≥0) such that p∈B 0, q∈B n and B t−1∩B t ≠∅ for all t=1,…,n; we may assume that the elements of \(\mathcal{B}\) are non-empty, because A will be chained by \(\mathcal{B}\setminus \{\emptyset\}\) anyway. Note in particular that the empty set is chained by the empty family of its subsets.
Let \(\mathcal{S}(E)\) be the set of all singletons {x}, x∈E. A partial connection on \(\mathcal{P}(E)\) is a family \(\mathcal {C}\subseteq \mathcal{P}(E)\) such that \(\emptyset\in\mathcal{C}\) and \(\forall \mathcal{B}\subseteq\mathcal{C}\), \(\bigcap\mathcal{B}\ne\emptyset\ \Rightarrow\ \bigcup\mathcal {B}\in\mathcal{C}\) (for \(\mathcal{B}= \emptyset\), we have indeed \(\bigcap\mathcal{B}= E \ne\emptyset\) and \(\bigcup \mathcal{B}= \emptyset\in\mathcal{C}\)). A connection on \(\mathcal{P}(E)\) is a partial connection \(\mathcal{C}\) such that \(\mathcal{S}(E) \subset\mathcal {C}\); in fact, for any \(\mathcal{C} \subseteq\mathcal{P}(E)\), \(\mathcal{C}\) is a partial connection if and only if \(\mathcal{C} \cup\mathcal{S}(E)\) is a connection. Given a partial connection \(\mathcal{C}\), for any \(A \in\mathcal{P}(E)\), let us write \(\mathsf{PC}^{\mathcal{C}}(A)\) for the partial partition of connected components of A according to \(\mathcal{C}\) [22].
Given a family \(\mathcal{B}\) of subsets of E, the least partial connection (resp., connection) containing \(\mathcal{B}\) is called the partial connection (resp., connection) generated by \(\mathcal {B}\) and it is written \(\mathsf{Con}^{*}(\mathcal{B})\) (resp., \(\mathsf {Con}(\mathcal{B})\)). Then \(\mathsf{Con}^{*}(\mathcal{B})\) is the set of all \(X \in\mathcal{P}(E)\) that are chained by \(\mathcal {P}(X) \cap\mathcal{B}\), while \(\mathsf{Con}(\mathcal{B}) = \mathsf{Con}^{*}(\mathcal{B}) \cup \mathcal{S}(E)\). Note that \(\mathsf{Con}^{*}(\mathcal{B}) = \mathsf{Con}^{*}(\mathcal{B}\setminus\{\emptyset\})\) and that for the empty family we get Con ∗(∅)={∅}.
Serra [32] showed that for \(\mathcal{C}\subseteq\mathcal {P}(E)\) with \(\emptyset\in\mathcal{C}\), \(\mathcal{C}\) is a connection if and only if \(\varPi(E,\mathcal{C} )\) is closed under the supremum operation of Π(E) (in particular \(\varPi(E,\mathcal{C})\) comprises the empty supremum of Π(E), that is, the least element 0 E ). Then we showed [22] that \(\mathcal{C}\) is a partial connection if and only if \(\varPi^{*}(E,\mathcal{C})\) is closed under the supremum operation of Π ∗(E) (obviously, \(\varPi^{*}(E,\mathcal {C})\) comprises the empty supremum of Π ∗(E), that is, the least element Ø). We generalize these two results as follows:
Proposition 3
Let \(\mathcal{B}\subseteq\mathcal{P}(E)\). Then:
-
1.
The subset of Π ∗(E) closed under the supremum operation generated by the partial partitions 1 B , \(B \in\mathcal{B}\), is \(\varPi ^{*}(E,\mathsf{Con}^{*}(\mathcal{B}))\).
-
2.
The subset of Π(E) closed under the supremum operation generated by the partitions 1 B ∨0 E =1 B ∪0 E∖B , \(B \in \mathcal{B}\), is \(\varPi(E,\mathsf{Con}(\mathcal{B}))\).
Proof
We can assume that the elements of \(\mathcal{B}\) are non-empty, because \(\mathsf{Con}^{*}(\mathcal{B}) = \mathsf{Con}^{*}(\mathcal{B}\setminus \{\emptyset\})\) and \(\mathsf{Con}(\mathcal{B}) = \mathsf{Con}(\mathcal{B}\setminus\{\emptyset\})\). We can also assume that \(\mathcal{B}\) is non-void, because the result holds trivially for \(\mathcal{B}= \emptyset\): we get then Con ∗(∅)={∅} and \(\mathsf {Con}(\emptyset) = \{\emptyset\} \cup\mathcal{S}(E)\), hence Π ∗(E,Con ∗(∅))={Ø} and Π(E,Con(∅))={0 E }, and both are indeed generated by the empty supremum in their respective lattices Π ∗(E) and Π(E).
1. Let \(\mathcal{X}\) be the subset of Π ∗(E) closed under supremum generated by all 1 B , \(B \in\mathcal{B}\). For any \(B \in\mathcal {B}\), \(B \in\mathsf{Con}^{*}(\mathcal{B})\), so \(\mathbf{1}_{B} \in\varPi^{*}(E,\mathsf{Con}^{*}(\mathcal{B}))\); since \(\mathsf{Con}^{*}(\mathcal{B})\) is a partial connection, \(\varPi^{*}(E,\mathsf{Con}^{*}(\mathcal{B}))\) is closed under supremum, hence \(\mathcal{X} \subseteq\varPi^{*}(E,\mathsf{Con}^{*}(\mathcal{B}))\). Conversely, let \(\pi\in \varPi^{*}(E,\mathsf{Con}^{*}(\mathcal{B}))\); for any A∈π, \(A \in\mathsf{Con}^{*}(\mathcal{B})\), so A is chained by \(\mathcal{P}(A) \cap\mathcal{B}\), that is, \(\mathbf {1}_{A} = \bigvee_{B \in\mathcal{P}(A) \cap\mathcal{B}} \mathbf{1}_{B}\); we get thus
so π is a supremum of some 1 B , \(B \in\mathcal{B}\), hence \(\pi\in \mathcal{X}\). Therefore \(\mathcal{X}= \varPi^{*}(E,\mathsf {Con}^{*}(\mathcal{B}))\).
2. Let \(\mathcal{Y}\) be the subset of Π(E) closed under supremum generated by all 1 B ∨0 E =1 B ∪0 E∖B , \(B \in\mathcal{B}\). For any \(B \in\mathcal{B}\), \(B \in\mathsf{Con}(\mathcal{B})\), and for p∈E∖B, \(\{p\} \in\mathsf{Con}(\mathcal{B})\), so \(\mathbf{1}_{B} \cup\mathbf {0}_{E \setminus B} \in \varPi(E,\mathsf{Con}(\mathcal{B}))\); since \(\mathsf{Con}(\mathcal {B})\) is a connection, \(\varPi (E,\mathsf{Con}(\mathcal{B}))\) is closed under supremum, hence \(\mathcal{Y}\subseteq \varPi(E,\mathsf{Con}(\mathcal{B}))\). Conversely, let \(\pi\in \varPi(E,\mathsf{Con}(\mathcal{B} ))\); let π 1 be the set of singleton blocks of π, and let π 2=π∖π 1 be the set of non-singleton blocks of π; for any A∈π 1, 1 A ∨0 E =0 E ; for any A∈π 2, \(A \in \mathsf{Con}^{*}(\mathcal{B})\), so \(\mathbf{1}_{A} = \bigvee_{B \in \mathcal{P}(A) \cap\mathcal{B}} \mathbf{1}_{B}\) (cf. item 1), hence \(\mathbf{1}_{A} \vee\mathbf{0}_{E} = \bigvee_{B \in \mathcal{P}(A) \cap\mathcal{B}} (\mathbf{1}_{B} \vee\mathbf{0}_{E})\); we get thus
so either π 2 is empty and π=0 E , or π is a supremum of some 1 B ∨0 E , \(B \in\mathcal{B}\); hence \(\pi\in\mathcal{Y}\) in any case. Therefore \(\mathcal{Y}= \varPi(E,\mathsf{Con}(\mathcal{B}))\). □
For example, if E is endowed with an adjacency graph and \(\mathcal {C}\) is the connection consisting of all connected subsets of E according to that graph, then \(\mathcal{C}= \mathsf{Con}(\mathcal{B})\) for the set \(\mathcal{B}\) of pairs of adjacent points of E, so \(\varPi(E,\mathcal{C})\) is generated by suprema of 1 P ∨0 E , where P is a pair of adjacent points of E. Also \(\mathcal{C}= \mathsf{Con}^{*}(\mathcal{B}\cup\mathcal{S}(E))\), where \(\mathcal {S}(E)\) is the set of singletons of E, so \(\varPi^{*}(E,\mathcal{C})\) is generated by suprema of 1 P , where P is a singleton or a pair of adjacent points of E. A particular case is when any two distinct points are adjacent in that graph, so \(\mathcal{C}= \mathcal{P}(E)\), \(\varPi(E,\mathcal{C}) = \varPi(E)\), \(\varPi ^{*}(E,\mathcal{C}) = \varPi ^{*}(E)\) and \(\mathcal{B}\) is the family of all pairs of points of E; thus every partition is a supremum of 1 P ∨0 E , where P is a pair of points of E, and every partial partition is a supremum of 1 P , where P is a singleton or a pair of points of E.
2.4 Other Relations on Partial Partitions
The standard order and its logical couterpoint given by the building order suggest several possible binary relations between partial partitions, based on the inclusion of blocks; we also consider those relating the supports of the partial partitions.
Each such binary relation will get a name; we will define it by the conditions that two partial partitions π 1,π 2 must satisfy in order for the ordered pair (π 1,π 2) to belong to that relation.
Let us start with supports. The following three relations are quasi-orders:
-
1.
Support inclusion: supp(π 1)⊆supp(π 2).
-
2.
Support containment: supp(π 1)⊇supp(π 2).
-
3.
Support equality: supp(π 1)=supp(π 2).
Next, we consider relations between two partial partitions based on the inclusion of blocks. The standard order relation π 1≤π 2, namely that every block of π 1 is included in one block of π 2, can be expressed as \(\pi_{1} \subseteq\bigcup_{B \in\pi_{2}} \mathcal{P}(B)\).
Note that by the disjointness of the blocks of a partial partition, the following relation is universally satisfied: Every block of π 1 is included in at most one block of π 2:
We define the inclusion function of π 1 in π 2 as the set \(\mathit{inc}_{\pi_{1},\pi_{2}}\) of all (B,C)∈π 1×π 2 such that B⊆C. Then (6) means that \(\mathit{inc}_{\pi _{1},\pi_{2}}\) is a partially defined function from π 1 to π 2. We have \(\mathit{inc}_{\pi_{1},\pi_{2}} \circ\mathit{inc}_{\pi_{0},\pi_{1}} \subseteq \mathit{inc}_{\pi_{0},\pi_{2}}\), which means that for B∈π 0 such that \(\mathit{inc}_{\pi_{0},\pi_{1}}(B)\) and \(\mathit{inc}_{\pi_{1},\pi _{2}}(\mathit{inc}_{\pi_{0},\pi_{1}}(B))\) are defined, then \(\mathit{inc}_{\pi_{0},\pi_{2}}(B)\) is defined and we have
but there can exist C∈π 0 such that \(\mathit{inc}_{\pi_{0},\pi_{2}}(C)\) is defined, but \(\mathit{inc}_{\pi _{0},\pi_{1}}(C)\) or \(\mathit{inc}_{\pi_{1},\pi_{2}}(\mathit{inc}_{\pi_{0},\pi_{1}}(C))\) is not defined. Now π 1≤π 2 means that the function \(\mathit{inc}_{\pi_{1},\pi_{2}}\) is totally defined, in other words it is a map π 1→π 2. For π 0≤π 1≤π 2, we have the equality \(\mathit{inc}_{\pi_{1},\pi_{2}} \circ \mathit{inc}_{\pi_{0},\pi_{1}} = \mathit{inc}_{\pi_{0},\pi_{2}}\).
The building order relation
namely that every block of π 2 contains (at least) one block of π 1, can be expressed as \(\pi_{2} \subseteq\bigcup_{B \in\pi_{1}} \mathcal{P}(E/B)\); it also means that the partially defined function \(\mathit{inc}_{\pi_{1},\pi_{2}}\) is surjective. This relation satisfies the following:
Note that ⋐ contains ⊇: when π 1⊇π 2, every block of π 2 contains itself and is a block of π 1, hence π 1⋐π 2. Also
Indeed, if \(\mathit{inc}_{\pi_{1},\pi_{2}}\) and \(\mathit{inc}_{\pi _{0},\pi_{1}}\) are maps and \(\mathit{inc}_{\pi_{1},\pi_{2}} \circ\mathit{inc}_{\pi_{0},\pi_{1}} = \mathit{inc}_{\pi_{0},\pi_{2}}\) is surjective, then the map \(\mathit{inc}_{\pi_{1},\pi_{2}}\) must be surjective. Serra [33, 34] showed the first and last sentences of the following:
Proposition 4
The building order ⋐ is a partial order relation on Π ∗(E). Furthermore,
and \(\pi_{2} \setminus\mathcal{P}(E\setminus\mathsf{supp}(\pi_{1})) \Subset\pi_{2} \cap \mathcal{P}(\mathsf{supp}(\pi_{1}))\). In particular, the restriction of the building order to partitions of a fixed set contains the refinement order: given π 1,π 2∈Π ∗(E) such that supp(π 1)=supp(π 2) and π 1≤π 2, then π 1⋐π 2.
Proof
Here \(\pi_{2} \setminus\mathcal{P}(E\setminus\mathsf{supp}(\pi_{1}))\) is the set of blocks of π 2 that overlap supp(π 1), while \(\pi_{2} \cap \mathcal{P}(\mathsf{supp}(\pi_{1}))\) is the set of blocks of π 2 that are included in supp(π 1); since blocks are non-void, \(\pi_{2} \setminus \mathcal{P}(E\setminus\mathsf{supp}(\pi_{1})) \supseteq\pi_{2} \cap \mathcal{P}(\mathsf{supp}(\pi_{1}))\), so \(\pi_{2} \setminus\mathcal{P}(E\setminus\mathsf{supp}(\pi_{1})) \Subset\pi_{2} \cap \mathcal{P}(\mathsf{supp}(\pi_{1}))\). We show (9). Let \(C \in\pi_{2} \setminus\mathcal{P}(E\setminus\mathsf{supp}(\pi_{1}))\); then C≬supp(π 1), so it must overlap a block B∈π 1, but as π 1≤π 2, there is a block C′∈π 2 such that B⊆C′; since ∅⊂C∩B⊆C∩C′, the blocks C and C′ overlap, hence we have C=C′, so B⊆C: every block of \(\pi_{2} \setminus\mathcal{P}(E\setminus\mathsf {supp}(\pi_{1}))\) contains a block of π 1.
When supp(π 1)=supp(π 2), we get
and in this case (9) gives π 1≤π 2 ⇒ π 1⋐π 2, so indeed (9) generalizes Serra’s statement. □
The remark (6) suggests the following relation:
-
singularity: every block of π 2 contains at most one block of π 1,
$$\begin{aligned} & \pi_1 \Lleftarrow\pi_2 ~(\mbox{also written } \pi_2 \Rrightarrow \pi_1) \quad \iff \\ &\quad \left\lgroup \begin{array}{@{}l@{}} \forall\, B,B' \in\pi_1, \forall\, C \in\pi_2, \\ \bigl[ B \subseteq C \ \&\ B' \subseteq C \bigr] \implies B = B' \end{array} \right\rgroup. \end{aligned}$$(10)
It means that the partially defined function \(\mathit{inc}_{\pi_{1},\pi _{2}}\) is injective. Note that when B⊆C for B∈π 1 and C∈π 2, we have B=B∩C≠∅, so B∈π 1∧π 2, hence
We have the following:
The counterpart of (8) is
Indeed, let B,B′∈π 0 and C∈π 1 such that B,B′⊆C; since π 1≤π 2, there is D∈π 2 such that C⊆D, but as B,B′⊆D and π 0⇚π 2, we must have B=B′.
Singularity itself, as well as its intersection with the building order, is not transitive:
Property 5
When |E|≥5, the intersection of the building order, the singularity and the support equality relations, is not transitive; in other words, there exist π 0,π 1,π 2∈Π ∗(E) such that π 0⋐π 1⋐π 2, supp(π 0)=supp(π 1)=supp(π 2) and π 0⇚π 1⇚π 2, but \(\pi_{0} \not\Lleftarrow\pi_{2}\).
Indeed, see Fig. 3, we partition E into 5 mutually disjoint non-void sets J,K,L,M,N, and take
Then every block of π 2 contains exactly one block of π 1, every block of π 1 contains exactly one block of π 0, but every block of π 2 is the union of two blocks of π 0.
However we have the following:
Proposition 6
The intersection of the standard order and of the singularity relation, i.e., the set of ordered pairs (π 1,π 2) such that π 1≤π 2 and π 1⇚π 2, is a partial order relation on Π ∗(E).
Proof
Obviously singularity is reflexive; hence its intersection with the standard order will also be reflexive, and that intersection will inherit the antisymmetry of that order. Let us show that this intersection is transitive. Take π 0,π 1,π 2∈Π ∗(E) such that π 0≤π 1≤π 2 and π 0⇚π 1⇚π 2; then the transitivity of the order ≤ gives π 0≤π 2, thus we have only to show that π 0⇚π 2. Since π 0≤π 1≤π 2 and π 0⇚π 1⇚π 2, both \(\mathit{inc}_{\pi_{0},\pi_{1}}\) and \(\mathit{inc}_{\pi_{1},\pi_{2}}\) are injective maps, thus the map \(\mathit{inc}_{\pi_{1},\pi_{2}} \circ\mathit{inc}_{\pi_{0},\pi _{1}} = \mathit{inc}_{\pi_{0},\pi_{2}}\) is injective, that is, π 0⇚π 2. □
In [33], Serra defined the partial order relation on \(\mathcal{P}(E)\) consisting of all ordered pairs \((X,Y) \in\mathcal {P}(E)^{2}\) such that X⊆Y and \(\mathsf{PC}^{\mathcal{C}}(X) \Lleftarrow \mathsf {PC}^{\mathcal{C}}(Y)\) (for a given partial connection \(\mathcal{C}\) on \(\mathcal{P}(E)\)). Since \(X \subseteq Y \ \Rightarrow\ \mathsf{PC}^{\mathcal{C}}(X) \le\mathsf{PC}^{\mathcal{C}}(Y)\), the property of being a partial order follows from Proposition 6.
Besides the standard and building orders, we have obtained a new partial order relation on Π
∗(E) defined in Proposition 6; it is in fact the inclusion-inflating order  that we will study in Sect. 3.2.
that we will study in Sect. 3.2.
3 The Basic Orders and Their Direct Combinations
In Sect. 3.1, we will study our basic orders: the merging, inclusion and inflating orders, all three included in the standard order. They are linked by a triangular relation. Then Sect. 3.2 will consider combinations of these basic orders, generated by the composition of two of them; these combinations are direct, in the sense that none of the basic orders is inverted w.r.t. the other. We get then the merging-inflating and inclusion-inflating orders, again included in the standard order; the standard order will also be obtained as a combination of merging and inclusion. We will rely heavily on the results of Sects. 2.2 and 2.4.
3.1 The Merging, Inclusion and Inflating Triangle
Before introducing our basic orders, we define the corresponding covering relations and heights. For π 1,π 2∈Π ∗(E), let us write \(\pi_{1} \buildrel c \over\prec\pi_{2}\) and say that π 2 c-covers π 1, if π 2 is obtained by adding a block to π 1:
Next, let us write \(\pi_{1} \buildrel i \over\prec\pi_{2}\) and say that π 2 i-covers π 1, if π 2 is obtained by inflating one block of π 1, to which one point is added:

When E is finite, for any π∈Π ∗(E), we define h c (π), the c-height of π, as its size:
Thus, see (4), h m (π)=h s (π)−h c (π) and h s (π)=h m (π)+h c (π).
The first basic order is the merging order ⊑ (we called it pure refinement order in [26]). It is defined as the intersection of the standard order and of the support equality relation:
Here every block of π 1 is included in a block of π 2, and every block of π 2 is a union of blocks of π 1: indeed, for any C∈π 2 and p∈C, as p∈supp(π 1), there is some B∈π 1 such that p∈B, and B⊆C′ for some C′∈π 2, thus p∈C∩C′, so C=C′ and p∈B⊆C. We say then that π 1 is a splitting of π 2, or that π 2 is a merging of π 1.
Theorem 7
Merging ⊑ is a partial order relation on Π ∗(E); it is included in the standard order: π 1⊑π 2 ⇒ π 1≤π 2. Further,
The poset (Π ∗(E),⊑) is the disjoint union of the complete lattices (Π(A),≤) for all \(A \in\mathcal{P}(E)\), where for distinct \(A,A' \in\mathcal{P}(E)\), elements of Π(A) and Π(A′) are mutually incomparable. The maximal and minimal elements are all 1 A and 0 A respectively, for \(A \in\mathcal{P}(E)\); every π∈Π ∗(E) majorates a unique minimal element, namely 0 supp(π). The covering relation is \(\buildrel m \over\prec\).
Let E be finite. Then (Π ∗(E),⊑) is graded by h m , that is, for any π 1,π 2∈Π ∗(E) we have
For π∈Π ∗(E), the height of π w.r.t. 0 supp(π) is h m (π).
Proof
Being the intersection of the partial order ≤ and of the quasi-order given by support equality, merging ⊑ is a partial order relation included in ≤.
If π 0≤π 1≤π 2, then supp(π 0)⊆supp(π 1)⊆supp(π 2), and if π 0⊑π 2, then supp(π 0)=supp(π 2), from which we deduce that supp(π 0)=supp(π 1)=supp(π 2), hence π 0⊑π 1⊑π 2. Therefore (18) holds.
Obviously Π ∗(E) is the disjoint union of the Π(A) for all \(A \in\mathcal{P}(E)\), and π 1⊑π 2 means that there is some \(A \in \mathcal{P}(E)\) with π 1,π 2∈Π(A) and π 1≤π 2 (for the refinement order), so the two sentences following (18) are valid. Similarly the covering relation is the one for the refinement order, that is \(\buildrel m \over\prec\).
When E is finite, the grading by h m , and the latter being the height, follow from Theorem 2. □
In the Introduction, we already argued that the refinement order on partitions is relevant to image segmentation and connected filtering. For partial partitions, the merging order is involved in split-and-merge operations in segmentation.
Our second basic order is inclusion: for π 1,π 2∈Π ∗(E), π 1⊆π 2 simply means that each block of π 1 is a block of π 2; in other words, the inclusion function \(\mathit{inc}_{\pi_{1},\pi_{2}}\) is the identity map on π 1:
Theorem 8
Inclusion ⊆ is a partial order relation on Π ∗(E); it is included in the standard order: π 1⊆π 2 ⇒ π 1≤π 2. Further,
In the poset (Π ∗(E),⊆), every non-void family {π i ∣i∈I} (I≠∅) has an infimum, given by the intersection ⋂ i∈I π i ; it has a supremum if and only if all distinct blocks in the union ⋃ i∈I π i are pairwise disjoint, and then this union is the supremum. The least element is Ø, the maximal elements are all partitions of E. For any π∈Π ∗(E), \(\mathcal{P}(\pi) \subseteq\varPi ^{*}(E)\), it is the set of minorants of π and it is closed under non-void infima and suprema. The covering relation is \(\buildrel c \over\prec\).
Let E be finite. Then (Π ∗(E),⊆) is graded by h c , that is, for any π 1,π 2∈Π ∗(E) we have
The height of any π∈Π ∗(E) is h c (π).
Proof
The first sentence is obvious. If π 0≤π 1≤π 2 and π 0⊆π 2, then for any B∈π 0, there are C∈π 1 and D∈π 2 with B⊆C⊆D, and B∈π 2; as B,D∈π 2 with B⊆D, we get B=D, and as B⊆C⊆D=B, B=C, hence B∈π 1; therefore π 0⊆π 1. Thus (19) holds.
Given a non-void family {π i ∣i∈I} (I≠∅) of partial partitions, ⋂ i∈I π i is a partial partition, it is thus their infimum for the inclusion order. If in ⋃ i∈I π i we have B∈π i and C∈π j with B≬C, then no partial partition can have both B and C as blocks, hence it cannot contain both π i and π j : the family has no supremum. On the other hand if all blocks of ⋃ i∈I π i are pairwise disjoint, then ⋃ i∈I π i is a partial partition, hence it is the supremum for the inclusion order.
For any π∈Π ∗(E), we always have Ø⊆π, so Ø is the least element. If π∉Π(E), then π⊂π∪{E∖π}, but if π∈Π(E), we cannot have π⊂π′, so the maximal elements are partitions. Obviously \(\mathcal{P}(\pi)\), ordered by inclusion, is a subset of Π ∗(E), closed under non-void infima and suprema.
When E is finite, as h c (π)=|π|, cf. (16), the statements about the grading and the height are straightforward. □
It should be noted that for π 1⊆π 2, as π 2 is obtained by adding to π 1 new blocks outside its support, |supp(π 2)|−|supp(π 1)|=|supp(π 2∖π 1)| and |π 2|−|π 1|=|π 2∖π 1|. Thus:
Comparing (19) with (18), when π 0⊆π 1≤π 2 and π 0⊆π 2, we cannot deduce that π 1⊆π 2; take for example π 0={A}, π 1={A,B} and π 2={A,C}, where ∅⊂A, ∅⊂B⊂C and A∩C=∅.
As we saw in the Introduction, the inclusion order is involved in the elimination of “parasitic” segmentation classes [33, 34], but also in the compound segmentation paradigm [27, 31], where we add to the blocks of a first segmentation those of a second segmentation of the residue. In the lattice \(\mathcal{P}(E)\), an anti-extensive operator ψ is connected if and only if for any \(X \in\mathcal{P}(E)\), the partial partition of all connected components of ψ(X) is a subset of the one of all connected components of X: \(\mathsf{PC}^{\mathcal{C}}(\psi(X)) \subseteq\mathsf{PC}^{\mathcal{C}}(X)\).
The third basic order is the inflating order ⊴, defined as the intersection of the standard and building orders and of the singularity relation:
In other words, every block of π 1 is included in a unique block of π 2 and every block of π 2 contains a unique block of π 1, the inclusion function \(\mathit{inc}_{\pi_{1},\pi_{2}}\) is a bijection between π 1 and π 2. We say then that π 1 is a deflation of π 2, or that π 2 is an inflation of π 1.
Theorem 9
Inflating ⊴ is a partial order relation on Π ∗(E); it is included in the standard order: π 1⊴π 2 ⇒ π 1≤π 2. Further,
Ø is isolated. In Π ∗(E)∖{Ø}, the minimal elements are all 0 A for \(A \in\mathcal{P}(E) \setminus\{ \emptyset\}\), while the maximal elements are all partitions of E. Given π∈Π ∗(E), the minimal elements majorated by π are the 0 A for all transversals A of π (for π=Ø, A=∅ and 0 A =Ø). The covering relation is \(\buildrel i \over\prec\).
Let E be finite. Then (Π ∗(E),⊴) is graded by h m , that is, for any π 1,π 2∈Π ∗(E) we have
For π∈Π ∗(E) and a transversal A of π, the height of π w.r.t. 0 A is h m (π).
Proof
By Propositions 4 and 6, ⋐ and ≤∩⇚ are partial orders, and ⊴ is the intersection of the two, hence it is a partial order relation included in ≤.
If π 0≤π 1≤π 2, then the maps \(\mathit{inc}_{\pi _{0},\pi_{1}} : \pi_{0} \to\pi_{1}\), \(\mathit{inc}_{\pi_{1},\pi_{2}} : \pi_{1} \to\pi_{2}\) and \(\mathit{inc}_{\pi_{0},\pi_{2}} : \pi_{0} \to\pi_{2}\) are totally defined and satisfy \(\mathit{inc}_{\pi_{1},\pi_{2}} \circ\mathit{inc}_{\pi_{0},\pi_{1}} = \mathit{inc}_{\pi_{0},\pi_{2}}\). Here π i ⊴π j (i<j) means that \(\mathit{inc}_{\pi _{i},\pi _{j}}\) is a bijection; thus if any two of \(\mathit{inc}_{\pi_{0},\pi_{1}}\), \(\mathit {inc}_{\pi_{1},\pi_{2}}\) and \(\mathit{inc}_{\pi_{1},\pi_{2}}\) are bijections, then by composition the third one will be a bijection, so we get (21).
For π≠Ø, we have no bijection between π and Ø, thus neither Ø⊴π nor π⊴Ø: Ø is isolated. In Π ∗(E)∖{Ø}, a partial partition π is minimal if and only if one cannot decrease any of its blocks, in other words all its blocks are singletons, while π is maximal if one cannot increase any of its blocks, in other words supp(π)=E. For π∈Π ∗(E) and \(A \in\mathcal{P}(E)\), we have 0 A ⊴π if and only if every point of A belongs to a block of π and every block of π contains a unique point of A, in other words A is a transversal of π.
If π 0⊲π 1⊲π 2, then π 2 is obtained from π 0 either by increasing several distinct blocks, or by increasing twice a single block, then that block increases by at least two points. Conversely if π 0⊲π 2 and π 2 is obtained from π 0 by increasing several distinct blocks, then π 1 resulting from the increase of only one of these blocks satisfies π 0⊲π 1⊲π 2; similarly, if π 2 is obtained by adding to a block of π 0 at least two points, then π 1 resulting from adding to that block only one of these points satisfies π 0⊲π 1⊲π 2. Therefore the covering relation is \(\buildrel i \over\prec\), where one block is increased by exactly one point.
Let E be finite. For π 1⊴π 2, we have π 1≤π 2, so h m (π 1)≤h m (π 2) by Theorem 2. By the bijection \(\mathit{inc}_{\pi_{1},\pi _{2}}\) we get |π 2|=|π 1|. If h m (π 2)=h m (π 1), then by (4) we get h s (π 2)=h s (π 1), so π 1=π 2 by Theorem 2. Hence π 1⊲π 2 ⇒ h m (π 1)<h m (π 2). If \(\pi_{1} \buildrel i \over\prec\pi_{2}\), then π 1⊴π 2, |π 2|=|π 1| and |supp(π 2)|=|supp(π 1)|+1, thus by (4) we get h m (π 2)=|supp(π 2)|−|π 2|=|supp(π 1)|−|π 1|+1=h m (π 1)+1. Therefore (Π ∗(E),⊴) is graded by h m . Let A be a transversal of π∈Π ∗(E); as h m (0 A )=0 by Theorem 2, the height of π w.r.t. 0 A is h m (π)−h m (0 A )=h m (π). □
Comparing (21) with (18), when π 0≤π 1≤π 2 and π 0⊴π 2, we cannot deduce that π 0⊴π 1 or π 1⊴π 2; take for example π 0={A}, π 1={A,B} and π 2={A∪B} for two disjoint non-void A and B. We will in fact obtain (30).
In the Introduction we saw that the inflating order is involved in region growing methods for segmentation, such as the watershed, or the growth of regions from seeds, guided by a homogeneity condition, see for instance [1]. The fact that Ø is isolated reflects the fact that in region growing, we need at least one marker for growing a region. Also in Serra’s method [33, 34], in the second step, eliminated “parasitic” segmentation classes are covered by inflating the remaining classes.
For homotopic reduction (or thinning) of binary images in E=Z 2, we consider two connections \(\mathcal{F}\) and \(\mathcal{B}\) for the foreground and background respectively (for instance, the ones arising from the 8- and 4-adjacencies). The topological condition is that the inclusion relation between connected components of the figure after and before reduction, and between those of the complement before and after reduction, are bijections [20]. In other words, given a figure \(F_{0} \in\mathcal{P}(E)\) and its reduction F 1, we must have
See Fig. 4, left and middle.
Left: the foreground and background are in black and light grey respectively; alternatively, the light grey connected components are the basins, and the black region is the divide. Middle: a homotopic reduction of the black foreground. Right: the connected basins grow, and the divide is reduced; compared with the homotopic reduction, we have also removed the black segment, whose points are adjacent to a single basin
In the watershed construction, we have connected basins, and the complement of their union is the divide; the divide is reduced, but its topology must not be preserved; only the connectivity of basins must be preserved. So if D 0 and D 1 are the initial and reduced divides, the condition is
NB. Since D 1⊆D 0, we have \(\mathsf{PC}^{\mathcal{F}}(D_{1}) \le \mathsf{PC}^{\mathcal{F}}(D_{0})\) anyway. A possible method is to perform a homotopic reduction of the divide until it reduces to a skeleton without any topologically simple point, and then to remove from it all points adjacent to a single basin. See Fig. 4. This approach has recently been formalized in the framework of simplicial complexes [5].
In the Introduction, we mentioned that several connective segmentation methods produce a partial partition of connected regions, and the boundaries separating them constitute the background; for some of these methods (such as the smooth connection [27, 32]), the boundaries are often thick. Thus one can apply to the segmentation background a homotopic thinning (22), or reduce it as a watershed divide (23); in both cases all segmentation classes are inflated, cf. the light grey zones in Fig. 4.
Let us now give the triangular relation linking these three orders. It means that each one can be obtained by combining the other two in some order:
Proposition 10
For any π 1,π 2∈Π ∗(E),
-
1.
If π 1⊴π 2, then there exists π∈Π ∗(E) such that π 1⊆π⊑π 2.
-
2.
If π 1⊑π 2, then there exists π∈Π ∗(E) such that π 1⊇π⊴π 2.
-
3.
If π 1≠Ø and π 1⊆π 2, then there exists π∈Π ∗(E) such that π 1⊴π⊒π 2.
See Fig. 5, top row.
Proof
Our argument is illustrated in Fig. 5, bottom row. In both items 1 and 2, if π 1=Ø, then π 2=Ø and we take π=Ø; we can thus assume that π 1≠Ø, and then π 2≠Ø.
1. Let π 1⊴π 2. For any B∈π 1, let \(f(B) = \mathit{inc}_{\pi_{1},\pi_{2}}(B) \setminus B\); thus π 2={B∪f(B)∣B∈π 1}. Take π=π 1∪{f(B)∣B∈π 1, f(B)≠∅}, we have π 1⊆π⊑π 2.
2. Let π 1⊑π 2. For any C∈π 2, choose one B∈π 1 such that B⊆C, and set f(C)=B (in other words, \(\mathit{inc}_{\pi_{1},\pi_{2}} \circ f\) is the identity on π 2). Take π={f(C)∣C∈π 2}, we have π 1⊇π⊴π 2.
3. Let π 1⊆π 2. For any C∈π 2, choose f(C)∈π 1 with the condition that when C∈π 1, f(C)=C (in other words, \(f \circ\mathit{inc}_{\pi_{1},\pi_{2}}\) is the identity on π 1). For B∈π 1, let g(B)=⋃f −1(B), the union of all C∈π 2 such that f(C)=B; as f(B)=B, B⊆g(B). Take π={g(B)∣B∈π 1}, we have π 1⊴π⊒π 2. □
3.2 Direct Combinations
We will now consider orders generated by the composition of any two basic orders. We obtain two new partial order relations, the merging-inflating
 and inclusion-inflating
and inclusion-inflating
 orders, while the standard order is generated by the merging and inclusion orders. We finally describe the lattice of order relations on Π
∗(E) generated by the three basic orders ⊑, ⊆ and ⊴. NB. The combination of one basic order with the inverse of another one will be considered in another paper.
orders, while the standard order is generated by the merging and inclusion orders. We finally describe the lattice of order relations on Π
∗(E) generated by the three basic orders ⊑, ⊆ and ⊴. NB. The combination of one basic order with the inverse of another one will be considered in another paper.
Theorem 11
The standard order is generated by inclusion followed by merging: for any π 1,π 2∈Π ∗(E), π 1≤π 2⇔∃π∈Π ∗(E), π 1⊆π⊑π 2.
Proof
If π 1⊆π⊑π 2, then π 1≤π≤π 2, hence π 1≤π 2. Suppose now that π 1≤π 2; let π′={B∖supp(π 1)∣B∈π 2, B⊈supp(π 1)} and π=π 1∪π′. Then π 1⊆π by construction; now every block of π 1∪π′ is included in a block of π 2, so π≤π 2, and supp(π)=supp(π 2), hence π⊑π 2. See Fig. 6.
□
Note that in particular inflating is generated by inclusion followed by merging, cf. item 1 of Proposition 10.
Let us now consider the two other combinations, of inflating with either merging or inclusion. First, the merging-inflating order
 (called refinement-inflating order in [26]). It is defined as the intersection of the standard and building orders:
(called refinement-inflating order in [26]). It is defined as the intersection of the standard and building orders:

In other words, every block of π 1 is included in a unique block of π 2 and every block of π 2 contains at least one block of π 1, the inclusion function \(\mathit{inc}_{\pi_{1},\pi_{2}}\) is a surjective map from π 1 to π 2.
Theorem 12
Merging-inflating
 is a partial order relation on
Π
∗(E); it is included in the standard order and it contains the merging and inflating orders:
is a partial order relation on
Π
∗(E); it is included in the standard order and it contains the merging and inflating orders:  ,
,  and
and
 . It is generated by composing merging and inflating in any order: for any
π
1,π
2∈Π
∗(E),
. It is generated by composing merging and inflating in any order: for any
π
1,π
2∈Π
∗(E),

Further,

and

Ø is isolated. In Π ∗(E)∖{Ø}, the greatest element is 1 E and the minimal elements are all 0 A for \(A \in \mathcal{P}(E) \setminus\{\emptyset\}\). Given π∈Π ∗(E), the minimal elements majorated by π are the 0 A for all crossings A of π (for π=Ø, A=∅ and 0 A =Ø). The covering relation is \(\buildrel m i \over\prec= \buildrel m \over \prec\cup\buildrel i \over\prec\).
Let E be finite. Then Π ∗(E) is graded by (−h c ,h s ) for \((\buildrel m \over\prec, \buildrel i \over\prec)\), that is, for any π 1,π 2∈Π ∗(E) we have

In particular,  is graded by
h
m
=h
s
−h
c
. For
π∈Π
∗(E) and a crossing
A
of
π, the height of
π
w.r.t. 0
A
is
h
m
(π).
is graded by
h
m
=h
s
−h
c
. For
π∈Π
∗(E) and a crossing
A
of
π, the height of
π
w.r.t. 0
A
is
h
m
(π).
Proof
Since  is the intersection of the standard and the building orders, both being order relations (see Proposition 4), it is a partial order relation included in ≤. By Proposition 4 and (17), both the building and the standard orders contain ⊑, and comparing (20) with (24),
is the intersection of the standard and the building orders, both being order relations (see Proposition 4), it is a partial order relation included in ≤. By Proposition 4 and (17), both the building and the standard orders contain ⊑, and comparing (20) with (24),  contains ⊴.
contains ⊴.
If π
1⊑π
3⊴π
2, then  , and if π
1⊴π
4⊑π
2, then
, and if π
1⊴π
4⊑π
2, then  , thus
, thus  in both cases. Suppose now that
in both cases. Suppose now that  . We will construct π
3,π
4∈Π
∗(E) such that π
1⊑π
3⊴π
2 and π
1⊴π
4⊑π
2; this is illustrated in Fig. 7.
. We will construct π
3,π
4∈Π
∗(E) such that π
1⊑π
3⊴π
2 and π
1⊴π
4⊑π
2; this is illustrated in Fig. 7.
Since π 1⋐π 2, every block C of π 2 contains a block of π 1, so C∩supp(π 1)≠∅. Let
as supp(π 1)⊆supp(π 2), we have supp(π 3)=supp(π 1), and as π 1≤π 2, we get π 1≤π 3, hence π 1⊑π 3 by (17). Now π 3≤π 2 and for any C∈π 2, C∩supp(π 1) is the unique block of π 3 included in C; hence \(\mathit{inc}_{\pi_{3},\pi_{2}}\) is a bijection, so π 3⊴π 2. Therefore π 1⊑π 3⊴π 2.
For any C∈π 2, choose one B∈π 1 such that B⊆C, and set f(C)=B (in other words, \(\mathit{inc}_{\pi_{1},\pi_{2}} \circ f\) is the identity on π 2). Let π a ={f(C)∣C∈π 2}⊆π 1 and π 0=π 1∖π a . For any C∈π 2, C∩supp(π a )=f(C), because every block of π a distinct from f(C) must be f(C′) for another C′∈π 2, so f(C′)∩C⊆C′∩C=∅; let g(C)=C∖supp(π 0); then g(C)=(C∩supp(π a ))∪(C∖supp(π 1))=f(C)∪(C∖supp(π 1)), so f(C)⊆g(C)⊆C. Let π b ={g(C)∣C∈π 2}; since f(C)⊆g(C) and f(C) is the unique block of π a included in C, hence in g(C), \(\mathit{inc}_{\pi_{a},\pi_{b}}\) is the bijection f(C)↦g(C) for all C∈π 2, so π a ⊴π b . Now supp(π b )∩supp(π 0)=∅, so π 4=π 0∪π b is a partial partition. Then π 1=π 0∪π a ⊴π 0∪π b =π 4, since \(\mathit{inc}_{\pi_{1},\pi_{4}}\) is the bijection given by f(C)↦g(C) for C∈π 2 and B↦B for B∈π 0. As π 0⊆π 1≤π 2, and g(C)⊆C for C∈π 2, we have π 4=π 0∪π b ≤π 2; now
so supp(π 4)=supp(π 0)∪supp(π b )=supp(π 2), and since π 4≤π 2, (17) gives π 4⊑π 2. Therefore π 1⊴π 4⊑π 2.
Now (25) follows from (8) and (24). If  and π
0⊴π
2, then \(\mathit{inc}_{\pi_{0},\pi_{1}}\) is a surjection, \(\mathit{inc}_{\pi_{1},\pi_{2}}\) is a map, \(\mathit{inc}_{\pi_{0},\pi _{2}} = \mathit{inc}_{\pi_{1},\pi_{2}} \circ\mathit{inc}_{\pi_{0},\pi_{1}}\) and \(\mathit{inc}_{\pi_{0},\pi _{2}}\) is a bijection; but then the surjection \(\mathit{inc}_{\pi_{0},\pi_{1}}\) must also be injective, hence it is a bijection, so π
0⊴π
1, and by (21) we deduce that π
1⊴π
2. Therefore (26) holds.
and π
0⊴π
2, then \(\mathit{inc}_{\pi_{0},\pi_{1}}\) is a surjection, \(\mathit{inc}_{\pi_{1},\pi_{2}}\) is a map, \(\mathit{inc}_{\pi_{0},\pi _{2}} = \mathit{inc}_{\pi_{1},\pi_{2}} \circ\mathit{inc}_{\pi_{0},\pi_{1}}\) and \(\mathit{inc}_{\pi_{0},\pi _{2}}\) is a bijection; but then the surjection \(\mathit{inc}_{\pi_{0},\pi_{1}}\) must also be injective, hence it is a bijection, so π
0⊴π
1, and by (21) we deduce that π
1⊴π
2. Therefore (26) holds.
For π≠Ø, we have no surjection π→Ø or Ø→π, thus neither  nor
nor  : Ø is isolated. In Π
∗(E)∖{Ø}, a partial partition π is minimal if and only if one cannot decrease or split any of its blocks, in other words all its blocks are singletons. On the other hand, for π∈Π
∗(E)∖{Ø}, we have
: Ø is isolated. In Π
∗(E)∖{Ø}, a partial partition π is minimal if and only if one cannot decrease or split any of its blocks, in other words all its blocks are singletons. On the other hand, for π∈Π
∗(E)∖{Ø}, we have  , so 1
E
is the greatest element of Π
∗(E)∖{Ø}. For π∈Π
∗(E) and \(A \in \mathcal{P}(E)\), we have
, so 1
E
is the greatest element of Π
∗(E)∖{Ø}. For π∈Π
∗(E) and \(A \in \mathcal{P}(E)\), we have  if and only if every point of A belongs to a block of π and every block of π contains at least one point of A, in other words A is a crossing of π.
if and only if every point of A belongs to a block of π and every block of π contains at least one point of A, in other words A is a crossing of π.
Let \(\pi_{1} \buildrel m \over\prec\pi_{2}\); thus π
1≺π
2. If  , then π
1<π<π
2, which contradicts the fact that ≺ is the covering relation for ≤. Hence π
2 covers π
1 for
, then π
1<π<π
2, which contradicts the fact that ≺ is the covering relation for ≤. Hence π
2 covers π
1 for  . Now let \(\pi_{1} \buildrel i \over\prec\pi_{2}\); thus π
1⊲π
2. If
. Now let \(\pi_{1} \buildrel i \over\prec\pi_{2}\); thus π
1⊲π
2. If  , then (26) gives π
1⊲π⊲π
2, which contradicts the fact that \(\buildrel i \over\prec\) is the covering relation for ⊴, see Theorem 9. Hence π
2 covers π
1 for
, then (26) gives π
1⊲π⊲π
2, which contradicts the fact that \(\buildrel i \over\prec\) is the covering relation for ⊴, see Theorem 9. Hence π
2 covers π
1 for  . Conversely, let π
2 cover π
1. We obtain π
1⊑π
3⊴π
2 as above; the three cases π
1⊏π
3⊲π
2, π
1=π
3⊲π⊲π
2 and π
1⊏π⊏π
3=π
2 contradict the covering of π
1 by π
2, so there remain only the cases where π
2 covers π
1 for ⊑ or for ⊴, that is, \(\pi_{1} \buildrel m \over\prec\pi_{2}\) or \(\pi_{1} \buildrel i \over\prec \pi_{2}\) (Theorems 7 and 9). Therefore the covering relation is \(\buildrel m \over\prec\cup\buildrel i \over\prec\).
. Conversely, let π
2 cover π
1. We obtain π
1⊑π
3⊴π
2 as above; the three cases π
1⊏π
3⊲π
2, π
1=π
3⊲π⊲π
2 and π
1⊏π⊏π
3=π
2 contradict the covering of π
1 by π
2, so there remain only the cases where π
2 covers π
1 for ⊑ or for ⊴, that is, \(\pi_{1} \buildrel m \over\prec\pi_{2}\) or \(\pi_{1} \buildrel i \over\prec \pi_{2}\) (Theorems 7 and 9). Therefore the covering relation is \(\buildrel m \over\prec\cup\buildrel i \over\prec\).
Let E be finite. For  , we have π
1≤π
2, so Theorem 2 gives h
s
(π
1)≤h
s
(π
2), while the surjection \(\mathit{inc}_{\pi_{1},\pi_{2}}\) gives |π
1|≥|π
2|, that is, h
c
(π
1)≥h
c
(π
2); thus
, we have π
1≤π
2, so Theorem 2 gives h
s
(π
1)≤h
s
(π
2), while the surjection \(\mathit{inc}_{\pi_{1},\pi_{2}}\) gives |π
1|≥|π
2|, that is, h
c
(π
1)≥h
c
(π
2); thus
with both terms h
s
(π
2)−h
s
(π
1) and h
c
(π
1)−h
c
(π
2) being ≥0. If h
m
(π
2)=h
m
(π
1), then h
s
(π
2)=h
s
(π
1), and as π
1≤π
2, Theorem 2 gives π
1=π
2. Hence  , with h
s
(π
1)≤h
s
(π
2) and h
c
(π
1)≥h
c
(π
2). Now \(\pi_{1} \buildrel m \over\prec\pi_{2}\) gives h
s
(π
2)=h
s
(π
1) and h
c
(π
2)=h
c
(π
1)−1 by Theorem 2, while \(\pi_{1} \buildrel i \over\prec\pi_{2}\) gives h
s
(π
2)=h
s
(π
1)+1 and h
c
(π
2)=h
c
(π
1) by Theorem 9. Therefore Π
∗(E) is graded by (−h
c
,h
s
) for \((\buildrel m \over \prec,\buildrel i \over\prec)\), see Proposition 1. By item 6 of that Proposition,
, with h
s
(π
1)≤h
s
(π
2) and h
c
(π
1)≥h
c
(π
2). Now \(\pi_{1} \buildrel m \over\prec\pi_{2}\) gives h
s
(π
2)=h
s
(π
1) and h
c
(π
2)=h
c
(π
1)−1 by Theorem 2, while \(\pi_{1} \buildrel i \over\prec\pi_{2}\) gives h
s
(π
2)=h
s
(π
1)+1 and h
c
(π
2)=h
c
(π
1) by Theorem 9. Therefore Π
∗(E) is graded by (−h
c
,h
s
) for \((\buildrel m \over \prec,\buildrel i \over\prec)\), see Proposition 1. By item 6 of that Proposition,  is graded by h
m
=h
s
−h
c
.
is graded by h
m
=h
s
−h
c
.
For a crossing A of π, h m (0 A )=0 by Theorem 2, so the height of π w.r.t. 0 A is h m (π)−h m (0 A )=h m (π). □
By item 5 of Proposition 1, in a covering chain \(\pi_{0} \buildrel m i \over\prec\cdots\buildrel m i \over\prec \pi_{n}\), among the n coverings \(\pi_{i} \buildrel m i \over \prec \pi_{i+1}\) (i=0,…,n−1), there are h c (π 0)−h c (π n ) m-coverings \(\pi_{i} \buildrel m \over\prec\pi_{i+1}\) and h s (π n )−h s (π 0) i-coverings \(\pi_{i} \buildrel i \over \prec \pi_{i+1}\).
Comparing (25) with similar identities (18), (19), (21), when  and
and  , we cannot deduce that
, we cannot deduce that  ; take for example π
0={A}, π
1={A,B} and π
2={A∪B} for two disjoint non-void A and B.
; take for example π
0={A}, π
1={A,B} and π
2={A∪B} for two disjoint non-void A and B.
The merging-inflating order intervenes in segmentation algorithms where one starts regions with markers, then one can both grow regions and merge them, see for example [12]. Also we saw above that an anti-extensive connected operator ψ on \(\mathcal{P}(E)\) will remove some connected components of a set, i.e., \(\mathsf{PC}^{\mathcal{C}}(\psi(X)) \subseteq \mathsf{PC}^{\mathcal{C}}(X)\). Now assuming that the connection \(\mathcal{C}\) arises from a graph and that E is connected, a connected component C of the set X is adjacent to a connected component D of the complement E∖X; thus if ψ removes C from X, it will not become a connected component of the complement E∖ψ(X), because C∪D will be connected. Hence the connected components of the complement will be inflated and merged, but none will be created, so  .
.
The next compound order is the inclusion-inflating order
 , it is the one defined in Proposition 6, namely the intersection of the standard order and of the singularity relation:
, it is the one defined in Proposition 6, namely the intersection of the standard order and of the singularity relation:

In other words, every block of π 1 is included in a unique block of π 2 and every block of π 2 contains at most one block of π 1, the inclusion function \(\mathit{inc}_{\pi_{1},\pi_{2}}\) is an injective map from π 1 to π 2. We have an alternate formulation for this relation:
Proposition 13

Proof
If \(\pi_{2} \wedge\mathbf{1}_{\mathsf{supp}(\pi_{1})} = \pi_{1}\), then π
1≤π
2 and \(\pi_{2} \wedge\mathbf{1}_{\mathsf{supp}(\pi_{1})} \le\pi_{1}\). Consider A∈π
1 and C∈π
2 such that A⊆C; then ∅⊂A⊆C∩supp(π
1) and \(C \cap\mathsf{supp}(\pi _{1}) \in\pi_{2} \wedge\mathbf{1}_{\mathsf{supp}(\pi_{1})}\); as \(\pi_{2} \wedge\mathbf {1}_{\mathsf{supp}(\pi_{1})} \le \pi_{1}\), there is some B∈π
1 such that C∩supp(π
1)⊆B, hence A⊆B and so A=B: thus C cannot contain any other block of π
1 other than B, so π
1⇚π
2. Therefore  .
.
If  , then π
1≤π
2, \(\pi_{1} \le \mathbf{1}_{\mathsf{supp}(\pi_{1})}\), thus \(\pi_{1} \le\pi_{2} \wedge \mathbf{1}_{\mathsf{supp}(\pi_{1})}\), but also \(\mathsf{supp}(\pi_{2} \wedge\mathbf{1}_{\mathsf{supp}(\pi _{1})}) = \mathsf{supp}(\pi_{2}) \cap \mathsf{supp}(\pi_{1}) = \mathsf{supp}(\pi_{1})\), hence \(\pi_{1} \sqsubseteq\pi_{2} \wedge \mathbf{1}_{\mathsf{supp}(\pi_{1})}\): every block of \(\pi_{2} \wedge \mathbf{1}_{\mathsf{supp}(\pi _{1})}\) is a union of blocks of π
1; given B
1,B
2∈π
1 and \(C \in \pi_{2} \wedge\mathbf{1}_{\mathsf{supp}(\pi_{1})}\) with B
1,B
2⊆C, as \(\pi_{2} \wedge\mathbf{1}_{\mathsf{supp}(\pi_{1})} \le\pi_{2}\), we have C⊆D for some D∈π
2, but as π
1⇚π
2 and B
1,B
2⊆D, we get B
1=B
2; thus every block of \(\pi_{2} \wedge\mathbf {1}_{\mathsf{supp}(\pi_{1})}\) is a block of π
1, so \(\pi_{2} \wedge\mathbf{1}_{\mathsf {supp}(\pi_{1})} \subseteq \pi_{1}\); from the double inequality \(\pi_{2} \wedge\mathbf{1}_{\mathsf {supp}(\pi_{1})} \le \pi_{1} \le\pi_{2} \wedge\mathbf{1}_{\mathsf{supp}(\pi_{1})}\) we derive the equality. □
, then π
1≤π
2, \(\pi_{1} \le \mathbf{1}_{\mathsf{supp}(\pi_{1})}\), thus \(\pi_{1} \le\pi_{2} \wedge \mathbf{1}_{\mathsf{supp}(\pi_{1})}\), but also \(\mathsf{supp}(\pi_{2} \wedge\mathbf{1}_{\mathsf{supp}(\pi _{1})}) = \mathsf{supp}(\pi_{2}) \cap \mathsf{supp}(\pi_{1}) = \mathsf{supp}(\pi_{1})\), hence \(\pi_{1} \sqsubseteq\pi_{2} \wedge \mathbf{1}_{\mathsf{supp}(\pi_{1})}\): every block of \(\pi_{2} \wedge \mathbf{1}_{\mathsf{supp}(\pi _{1})}\) is a union of blocks of π
1; given B
1,B
2∈π
1 and \(C \in \pi_{2} \wedge\mathbf{1}_{\mathsf{supp}(\pi_{1})}\) with B
1,B
2⊆C, as \(\pi_{2} \wedge\mathbf{1}_{\mathsf{supp}(\pi_{1})} \le\pi_{2}\), we have C⊆D for some D∈π
2, but as π
1⇚π
2 and B
1,B
2⊆D, we get B
1=B
2; thus every block of \(\pi_{2} \wedge\mathbf {1}_{\mathsf{supp}(\pi_{1})}\) is a block of π
1, so \(\pi_{2} \wedge\mathbf{1}_{\mathsf {supp}(\pi_{1})} \subseteq \pi_{1}\); from the double inequality \(\pi_{2} \wedge\mathbf{1}_{\mathsf {supp}(\pi_{1})} \le \pi_{1} \le\pi_{2} \wedge\mathbf{1}_{\mathsf{supp}(\pi_{1})}\) we derive the equality. □
Theorem 14
Inclusion-inflating
 is a partial order relation on
Π
∗(E); it is included in the standard order and it contains the inclusion and inflating orders:
is a partial order relation on
Π
∗(E); it is included in the standard order and it contains the inclusion and inflating orders:  ,
,  and
and
 . It is generated by composing inclusion and inflating in any order: for any
π
1,π
2∈Π
∗(E),
. It is generated by composing inclusion and inflating in any order: for any
π
1,π
2∈Π
∗(E),

Further,

and

The least element is Ø, the maximal elements are all partitions of E. The covering relation is \(\buildrel s i \over\prec= \buildrel s \over\prec\cup\buildrel i \over\prec\).
Let E be finite. Then Π ∗(E) is graded by (h c ,h m ) for \((\buildrel s \over\prec, \buildrel i \over\prec)\), that is, for any π 1,π 2∈Π ∗(E) we have

In particular,  is graded by
h
s
=h
m
+h
c
. The height of any
π∈Π
∗(E) is
h
s
(π).
is graded by
h
s
=h
m
+h
c
. The height of any
π∈Π
∗(E) is
h
s
(π).
Proof
Proposition 6 showed that  is a partial order relation, it is included in the standard order. When π
1⊆π
2, two distinct blocks of π
1 are distinct blocks of π
2, hence π
1⇚π
2; also π
1≤π
2; thus
is a partial order relation, it is included in the standard order. When π
1⊆π
2, two distinct blocks of π
1 are distinct blocks of π
2, hence π
1⇚π
2; also π
1≤π
2; thus  contains ⊆. Comparing (20) with (27),
contains ⊆. Comparing (20) with (27),  contains ⊴.
contains ⊴.
If π
1⊆π
3⊴π
2, then  , and if π
1⊴π
4⊆π
2, then
, and if π
1⊴π
4⊆π
2, then  , thus
, thus  in both cases. Suppose now that
in both cases. Suppose now that  . As π
1⇚π
2, each block of π
2 contains at most one block of π
1. Let π
4 be the set of blocks of π
2 containing (exactly) one block of π
1; as π
1≤π
2, every block of π
1 is included in (exactly) one block of π
4; thus π
1⊴π
4, and obviously, π
4⊆π
2. Let π
a
=π
2∖π
4 be the set of blocks of π
2 containing no block of π
1; then supp(π
a
) is disjoint from supp(π
1), so π
1∪π
a
is a partial partition; as π
1⊴π
4, π
1∪π
a
⊴π
4∪π
a
=π
2; obviously π
1⊆π
1∪π
a
. Therefore π
3=π
1∪π
a
satisfies π
1⊆π
3⊴π
2. This is illustrated in Fig. 8. The inflation of π
1 into π
4 and the creation of blocks of π
a
are independent operations.
. As π
1⇚π
2, each block of π
2 contains at most one block of π
1. Let π
4 be the set of blocks of π
2 containing (exactly) one block of π
1; as π
1≤π
2, every block of π
1 is included in (exactly) one block of π
4; thus π
1⊴π
4, and obviously, π
4⊆π
2. Let π
a
=π
2∖π
4 be the set of blocks of π
2 containing no block of π
1; then supp(π
a
) is disjoint from supp(π
1), so π
1∪π
a
is a partial partition; as π
1⊴π
4, π
1∪π
a
⊴π
4∪π
a
=π
2; obviously π
1⊆π
1∪π
a
. Therefore π
3=π
1∪π
a
satisfies π
1⊆π
3⊴π
2. This is illustrated in Fig. 8. The inflation of π
1 into π
4 and the creation of blocks of π
a
are independent operations.
Now (28) follows from (13) and (27). If  and π
0⊴π
2, then \(\mathit{inc}_{\pi_{0},\pi_{1}}\) is a map, \(\mathit{inc}_{\pi_{1},\pi_{2}}\) is an injection, \(\mathit{inc}_{\pi_{0},\pi_{2}} = \mathit{inc}_{\pi _{1},\pi_{2}} \circ \mathit{inc}_{\pi_{0},\pi_{1}}\) and \(\mathit{inc}_{\pi_{0},\pi_{2}}\) is a bijection; but then the injection \(\mathit{inc}_{\pi_{1},\pi_{2}}\) must also be surjective, hence it is a bijection, so π
1⊴π
2, and by (21) we deduce that π
0⊴π
1. Therefore (29) holds.
and π
0⊴π
2, then \(\mathit{inc}_{\pi_{0},\pi_{1}}\) is a map, \(\mathit{inc}_{\pi_{1},\pi_{2}}\) is an injection, \(\mathit{inc}_{\pi_{0},\pi_{2}} = \mathit{inc}_{\pi _{1},\pi_{2}} \circ \mathit{inc}_{\pi_{0},\pi_{1}}\) and \(\mathit{inc}_{\pi_{0},\pi_{2}}\) is a bijection; but then the injection \(\mathit{inc}_{\pi_{1},\pi_{2}}\) must also be surjective, hence it is a bijection, so π
1⊴π
2, and by (21) we deduce that π
0⊴π
1. Therefore (29) holds.
For any π∈Π
∗(E), Ø⊆π, so  , and Ø is the least element. If π∉Π(E), then π⊂π∪{E∖π}, thus π is not maximal. Now if π∈Π(E), π is maximal for the order ⊆ (Theorem 8) and for the order ⊴ (Theorem 9), and from the above this means that π is maximal for
, and Ø is the least element. If π∉Π(E), then π⊂π∪{E∖π}, thus π is not maximal. Now if π∈Π(E), π is maximal for the order ⊆ (Theorem 8) and for the order ⊴ (Theorem 9), and from the above this means that π is maximal for  .
.
Let \(\pi_{1} \buildrel s \over\prec\pi_{2}\); thus π
1≺π
2. If  , then π
1<π<π
2, which contradicts the fact that ≺ is the covering relation for ≤. Hence π
2 covers π
1 for
, then π
1<π<π
2, which contradicts the fact that ≺ is the covering relation for ≤. Hence π
2 covers π
1 for  . Now let \(\pi_{1} \buildrel i \over\prec\pi_{2}\); thus π
1⊲π
2. If
. Now let \(\pi_{1} \buildrel i \over\prec\pi_{2}\); thus π
1⊲π
2. If  , then (29) gives π
1⊲π⊲π
2, which contradicts the fact that \(\buildrel i \over\prec\) is the covering relation for ⊴, see Theorem 9. Hence π
2 covers π
1 for
, then (29) gives π
1⊲π⊲π
2, which contradicts the fact that \(\buildrel i \over\prec\) is the covering relation for ⊴, see Theorem 9. Hence π
2 covers π
1 for  . Conversely, let π
2 cover π
1. We obtain π
1⊆π
3⊴π
2 as above; the three cases π
1⊂π
3⊲π
2, π
1=π
3⊲π⊲π
2 and π
1⊂π⊂π
3=π
2 contradict the covering of π
1 by π
2, so there remain only the cases where π
2 covers π
1 for ⊆ or for ⊴, that is, \(\pi_{1} \buildrel c \over\prec\pi_{2}\) or \(\pi_{1} \buildrel i \over\prec\pi_{2}\) (Theorems 8 and 9). Now \(\pi_{1} \buildrel c \over\prec\pi_{2}\) means that π
2=π
1∪{B} for B⊆E∖supp(π
1) with B≠∅, see (14); if B is not a singleton (it contains at least two points), then for p∈B we have π
1⊂π
1∪{{p}}⊲π
1∪{B}=π
2, contradicting the covering of π
1 by π
2; hence B is a singleton and \(\pi_{1} \buildrel s \over\prec \pi_{2}\), see (3). Therefore the covering relation is \(\buildrel s \over\prec\cup\buildrel i \over\prec\).
. Conversely, let π
2 cover π
1. We obtain π
1⊆π
3⊴π
2 as above; the three cases π
1⊂π
3⊲π
2, π
1=π
3⊲π⊲π
2 and π
1⊂π⊂π
3=π
2 contradict the covering of π
1 by π
2, so there remain only the cases where π
2 covers π
1 for ⊆ or for ⊴, that is, \(\pi_{1} \buildrel c \over\prec\pi_{2}\) or \(\pi_{1} \buildrel i \over\prec\pi_{2}\) (Theorems 8 and 9). Now \(\pi_{1} \buildrel c \over\prec\pi_{2}\) means that π
2=π
1∪{B} for B⊆E∖supp(π
1) with B≠∅, see (14); if B is not a singleton (it contains at least two points), then for p∈B we have π
1⊂π
1∪{{p}}⊲π
1∪{B}=π
2, contradicting the covering of π
1 by π
2; hence B is a singleton and \(\pi_{1} \buildrel s \over\prec \pi_{2}\), see (3). Therefore the covering relation is \(\buildrel s \over\prec\cup\buildrel i \over\prec\).
Let E be finite. For  , we have π
1≤π
2, so Theorem 2 gives h
m
(π
1)≤h
m
(π
2), while the injection \(\mathit{inc}_{\pi_{1},\pi_{2}}\) gives |π
1|≤|π
2|, that is, h
c
(π
1)≤h
c
(π
2); thus
, we have π
1≤π
2, so Theorem 2 gives h
m
(π
1)≤h
m
(π
2), while the injection \(\mathit{inc}_{\pi_{1},\pi_{2}}\) gives |π
1|≤|π
2|, that is, h
c
(π
1)≤h
c
(π
2); thus
with both terms h
m
(π
2)−h
m
(π
1) and h
c
(π
2)−h
c
(π
1) being ≥0. If h
s
(π
2)=h
s
(π
1), then h
m
(π
2)=h
m
(π
1), and as π
1≤π
2, Theorem 2 gives π
1=π
2. Hence  , with h
m
(π
1)≤h
m
(π
2) and h
c
(π
1)≤h
c
(π
2). Now \(\pi_{1} \buildrel s \over\prec\pi_{2}\) gives h
m
(π
2)=h
m
(π
1) and h
c
(π
2)=h
c
(π
1)+1 by Theorem 2, while \(\pi_{1} \buildrel i \over\prec\pi_{2}\) gives h
m
(π
2)=h
m
(π
1)+1 and h
c
(π
2)=h
c
(π
1) by Theorem 9. Therefore Π
∗(E) is graded by(h
c
,h
m
) for \((\buildrel s \over\prec, \buildrel i \over\prec)\), see Proposition 1. By item 6 of that Proposition,
, with h
m
(π
1)≤h
m
(π
2) and h
c
(π
1)≤h
c
(π
2). Now \(\pi_{1} \buildrel s \over\prec\pi_{2}\) gives h
m
(π
2)=h
m
(π
1) and h
c
(π
2)=h
c
(π
1)+1 by Theorem 2, while \(\pi_{1} \buildrel i \over\prec\pi_{2}\) gives h
m
(π
2)=h
m
(π
1)+1 and h
c
(π
2)=h
c
(π
1) by Theorem 9. Therefore Π
∗(E) is graded by(h
c
,h
m
) for \((\buildrel s \over\prec, \buildrel i \over\prec)\), see Proposition 1. By item 6 of that Proposition,  is graded by h
s
=h
m
+h
c
.
is graded by h
s
=h
m
+h
c
.
Now h s (Ø)=0 by Theorem 2, and the height of π is h s (π)−h s (Ø)=h s (π). □
Thus in a covering chain \(\pi_{0} \buildrel s i \over\prec\cdots \buildrel s i \over\prec\pi_{n}\), among the n coverings \(\pi_{i} \buildrel s i \over\prec\pi_{i+1}\) (i=0,…,n−1), there are h c (π n )−h c (π 0) s-coverings \(\pi_{i} \buildrel s \over \prec\pi_{i+1}\) and h m (π n )−h m (π 0) i-coverings \(\pi_{i} \buildrel i \over\prec\pi_{i+1}\).
As with (25), comparing (28) with previous similar identities (18), (19), (21), when  and
and  , we cannot deduce that
, we cannot deduce that  ; take for example π
0={A}, π
1={A,B,C} and π
2={A,B∪C} for three mutually disjoint non-void A, B and C. We have also the following:
; take for example π
0={A}, π
1={A,B,C} and π
2={A,B∪C} for three mutually disjoint non-void A, B and C. We have also the following:

Indeed, \(\mathit{inc}_{\pi_{0},\pi_{1}}\) and \(\mathit{inc}_{\pi_{1},\pi _{2}}\) are maps, and \(\mathit{inc}_{\pi_{0},\pi_{2}} = \mathit{inc}_{\pi_{1},\pi_{2}} \circ \mathit{inc}_{\pi_{0},\pi_{1}}\) is a bijection, thus \(\mathit{inc}_{\pi_{0},\pi_{1}}\) will be injective and \(\mathit{inc}_{\pi_{1},\pi_{2}}\) will be surjective, that is,  .
.
The inclusion-inflating order corresponds to a model of segmentation by region growing, where markers for new regions can be created before the growth of previously created region is completed. This is more flexible than the compound segmentation paradigm, where each new region is created only after the previous ones have been completely determined.
We have seen that the standard, merging-inflating and inclusion-inflating orders are generated each by the composition of two of the three basic orders. There is also the identity, or equality relation =. We will show that there are no other orders to be obtained from the basic orders by any combination such as intersection or composition. Indeed, as explained in Sect. 2.1, the set O(≤) of all partial order relations on Π ∗(E) that are included in the standard order, constitutes a complete lattice; its greatest element is the standard order ≤, its least element is the identity =, and the infimum operation is the intersection. It is thus possible to consider the sublattice of O(≤) generated by the three basic orders ⊑, ⊆ and ⊴.
Theorem 15
In O(≤), the complete lattice of partial order relations on Π ∗(E) included in ≤, the sublattice generated by the three basic orders (merging, inclusion and inflating) contains these three orders, the merging-inflating, inclusion-inflating and standard orders, and the identity. Its Hasse diagram is that of Fig. 9.
Proof
Let  be the set of partial orders in Fig. 9. In order to avoid confusion with the elements ⊆ and = of \(\mathcal{O}\), we will use the symbols ⫅ and ≡ for the inclusion and equality between binary relations on Π
∗(E). Write ⊔ for the binary supremum operation in O(≤) (the infimum being the intersection). We first note that the edges in the diagram of Fig. 9 correspond to inclusion relations, namely
be the set of partial orders in Fig. 9. In order to avoid confusion with the elements ⊆ and = of \(\mathcal{O}\), we will use the symbols ⫅ and ≡ for the inclusion and equality between binary relations on Π
∗(E). Write ⊔ for the binary supremum operation in O(≤) (the infimum being the intersection). We first note that the edges in the diagram of Fig. 9 correspond to inclusion relations, namely

We know from Theorems 11, 12 and 14 that ⊑⊔⊆ ≡ ≤,  and
and  . Given two incomparable elements of \(\mathcal{O}\), either they form the pair {⊑,⊴} with supremum
. Given two incomparable elements of \(\mathcal{O}\), either they form the pair {⊑,⊴} with supremum  , or the pair {⊴,⊆} with supremum
, or the pair {⊴,⊆} with supremum  , or one contains ⊑ and the other contains ⊆, giving the supremum ≤. Hence \(\mathcal{O}\) is closed under ⊔, and this operation follows the diagram of Fig. 9. Now for the intersection of incomparable elements of \(\mathcal{O}\), we need first to consider three particular cases:
, or one contains ⊑ and the other contains ⊆, giving the supremum ≤. Hence \(\mathcal{O}\) is closed under ⊔, and this operation follows the diagram of Fig. 9. Now for the intersection of incomparable elements of \(\mathcal{O}\), we need first to consider three particular cases:
1.  . This follows immediately from the definitions (20), (24), (27): ⊴ ≡ ≤∩⋐∩⇚,
. This follows immediately from the definitions (20), (24), (27): ⊴ ≡ ≤∩⋐∩⇚,  and
and  .
.
2. ⊑∩⊴ ≡ =. Indeed, if π 1⊑π 2 and π 1⊴π 2, then every block of π 2 at the same time contains a unique block of π 1 and is a union of blocks of π 1; this means that π 2⊆π 1, hence π 1=π 2.
3. ⊴∩⊆ ≡ =. Indeed, if π 1⊴π 2 and π 1⊆π 2, then every block of π 2 contains a block of π 1 which is itself a block of π 2, thus they are equal and so π 2⊆π 1, hence π 1=π 2.
Now let R
1,R
2 be two incomparable elements of \(\mathcal{O}\); then we have 3 cases: (a)  , so R
1∩R
2 ≡ ⊴ by item 1; (b) R
i
≡ ⊑ and
, so R
1∩R
2 ≡ ⊴ by item 1; (b) R
i
≡ ⊑ and  (where {i,j}={1,2}), so
(where {i,j}={1,2}), so

by the inclusion of ⊑ in  , items 1 and 2; (c) R
i
≡ ⊆ and
, items 1 and 2; (c) R
i
≡ ⊆ and  (where {i,j}={1,2}), so
(where {i,j}={1,2}), so

by the inclusion of ⊆ in  , items 1 and 3. Hence \(\mathcal{O}\) is closed under ∩, and this operation follows the diagram of Fig. 9. □
, items 1 and 3. Hence \(\mathcal{O}\) is closed under ∩, and this operation follows the diagram of Fig. 9. □
We end this section by pointing out some general features concerning the standard order and the five order relations that we have introduced. We recall in Table 1 the notation and definition of each of them, as well as of the relations introduced in Sect. 2.4. All six orders have a well-defined covering relation; in the finite case they are graded and have a height function, see Table 2. This is useful as a measure of the complexity of a partial partition from a constructive view: it tells how many elementary operations are necessary to obtain that partial partition.
The three basic orders (merging, inclusion and inflating) have simple covering relations, respectively \(\buildrel m \over\prec\), \(\buildrel c \over\prec\) and \(\buildrel i \over\prec\). The standard, merging-inflating and inclusion-inflating orders are compound orders, built each by combining two basic orders, and they have compound covering relations; the latter can be obtained by combining the corresponding covering relations of the involved basic orders, except that \(\buildrel c \over\prec\) is replaced by \(\buildrel s \over\prec\); thus we get \(\prec\;=\; \buildrel m \over\prec\cup \buildrel s \over\prec\) for the standard order (combining merging and inclusion), \(\buildrel m i \over\prec\;=\; \buildrel m \over \prec\cup\buildrel i \over\prec\) for the merging-inflating order, and \(\buildrel s i \over\prec\;=\; \buildrel s \over\prec \cup\buildrel i \over\prec\) for the inclusion-inflating order. Their grading is also compound, where each of the two functions counts the number of coverings of each type, cf. item 5 of Proposition 1.
Let π∈Π ∗(E); we give here, for each order, the number of elementary coverings (thus of elementary operations) of each type in a covering chain from a minimal element under π to π:
-
For the merging order ⊑: in every covering chain between 0 supp(π) and π, there are h m (π) m-coverings \(\buildrel m \over\prec\), i.e., π is obtained from 0 supp(π) by h m (π) block mergings.
-
For the inclusion order ⊆: in every covering chain between Ø and π, there are h c (π) c-coverings \(\buildrel c \over \prec\), i.e., π is obtained from Ø by h c (π) block creations.
-
For the inflating order ⊴: given a transversal A of π, in every covering chain between 0 A and π, there are h m (π) i-coverings \(\buildrel i \over\prec\), i.e., π is obtained from 0 A by h m (π) inflations of a block by one point.
-
For the merging-inflating order
 : given a crossing A of π, in every covering chain between 0
A
and π, there are |A|−h
c
(π) m-coverings \(\buildrel m \over\prec\) and h
s
(π)−|A| i-coverings \(\buildrel i \over\prec\), i.e., π is obtained from 0
A
by |A|−h
c
(π) block mergings and h
s
(π)−|A| inflations of a block by one point; when A is a transversal of π, |A|=h
c
(π), 0
A
⊴π, there are h
m
(π) i-coverings \(\buildrel i \over\prec\) but no m-covering, i.e., π is obtained from 0
A
by h
m
(π) inflations of a block by one point.
: given a crossing A of π, in every covering chain between 0
A
and π, there are |A|−h
c
(π) m-coverings \(\buildrel m \over\prec\) and h
s
(π)−|A| i-coverings \(\buildrel i \over\prec\), i.e., π is obtained from 0
A
by |A|−h
c
(π) block mergings and h
s
(π)−|A| inflations of a block by one point; when A is a transversal of π, |A|=h
c
(π), 0
A
⊴π, there are h
m
(π) i-coverings \(\buildrel i \over\prec\) but no m-covering, i.e., π is obtained from 0
A
by h
m
(π) inflations of a block by one point. -
For the inclusion-inflating order
 : in every covering chain between Ø and π, there are h
c
(π) s-coverings \(\buildrel s \over\prec\) and h
m
(π) i-coverings \(\buildrel i \over\prec\), i.e., π is obtained from Ø by h
c
(π) creations of singleton blocks and h
m
(π) inflations of a block by one point.
: in every covering chain between Ø and π, there are h
c
(π) s-coverings \(\buildrel s \over\prec\) and h
m
(π) i-coverings \(\buildrel i \over\prec\), i.e., π is obtained from Ø by h
c
(π) creations of singleton blocks and h
m
(π) inflations of a block by one point. -
For the standard order ≤: in every covering chain between Ø and π, there are h m (π) m-coverings \(\buildrel m \over \prec\) and h s (π) s-coverings \(\buildrel s \over\prec\), i.e., π is obtained from Ø by h m (π) block mergings and h s (π) creations of singleton blocks.
We can thus suggest that partial partitions can be built bottom-up by combining several types of elementary operations in a succession, where each elementary operation has a distinct complexity, in such a way that the global complexity does not depend on the order of the operations.
In addition to characterizing the covering relation and the height of each order, we also gave equations (18), (19), (21), (25), (26), (28), (29), (30). They all deal with the situation where π 0≤π 1≤π 2 and a stronger order relation between π 0 and π 2 induces a stronger order relation between π 0 and π 1 or between π 1 and π 2. Some of them were used in the determination of the covering relations for the merging-inflating and inclusion-inflating orders. Also, (19) and (28) mean respectively that the inclusion and inclusion-inflating orders are well-composed according to [26] (the standard order is also well-composed); this property is useful in the compound segmentation paradigm (see Theorem 2 of [26]).
These identities are also useful for showing that the six orders satisfy Ore’s quadrilateral condition [18], an extension to posets of the lattice-theoretical property of upper semi-modularity [3, 6]; this condition implies in particular the Jordan-Dedekind chain condition satisfied by these orders. This will be discussed in another paper.
4 Hierarchies, Connectivity and Saliency
A hierarchy is an increasing sequence of (partial) partitions going from the least to the greatest element of the lattice: π 0≤⋯≤π n =1 E , where π 0=0 E for partitions but π 0=Ø for partial partitions. Hierarchies have been used in image segmentation [10, 35, 36] and filtering [14, 28, 29]. A hierarchy of partitions can be represented by a dendrogram, see Fig. 10(a) and (b); this representation can be extended to partial partitions, see Fig. 10(c) and (d), but it becomes more complicated, as points can enter into the support at a level above 0.
Here E={a,b,c,d,e,f}. (a) A hierarchy of 4 partitions; in each one, the blocks are shown as rectangles. (b) The corresponding dendrogram. (c) A hierarchy of 4 partial partitions; in each one, the blocks are shown as grey rectangles, while points outside the support are shown as hollow circles. (d) The corresponding dendrogram
In [23] we introduced a theory of hierarchies of partitions or partial partitions. We extend it in Sect. 4.1 by including the requirement that the blocks of the partial partitions belong to a partial connection \(\mathcal{C}\); the previous theory of [23] corresponds then to the case where \(\mathcal{C}= \mathcal{P}(E)\). In Sect. 4.2 we consider the particular case where \(\mathcal{C}\) is a connection arising from a graph; then block boundaries are made of edge elements associated to pairs of adjacent points, and we can study their saliency, that is, the range of levels where they are visible; each one of our orders has a peculiar behaviour in this respect. Finally Sect. 4.3 applies our orders to image filtering by component trees.
4.1 Connective Maps and Connected Hierarchies
In order to take into account more general models, such as continuous hierarchies (where the levels are not discrete), we replace the finite chain {0,…,n} by a complete lattice L with least and greatest elements ⊥ and ⊤; in [23] we assumed that L is a closed subset of R with ⊥=0. Then a hierarchy is an erosion ε:L→Π(E), where for t∈L, ε(t)=π t , the partition at level t; it is in fact convenient to consider the adjoint dilation δ:Π(E)→L. Without loss of generality, we can replace Π(E) by Π ∗(E) in this adjunction. Indeed, the inclusion map IN:Π(E)→Π ∗(E):π↦π is an erosion, whose adjoint dilation is the “fill with singletons” map FS:Π ∗(E)→Π(E):π↦π∪0 E∖supp(π)=π∨0 E [23]. Thus we get the erosion ε ∗=IN⋅ε:L→Π ∗(E):t↦ε(t) with the adjoint dilation δ ∗=δ⋅FS:Π ∗(E)→L:π↦δ(π∨0 E ), in particular for π∈Π(E) we have π∨0 E =π, so δ ∗(π)=δ(π); thus δ ∗ extends δ to partial partitions.
In [23] we called strongly triangular any map θ:E 2→L such that for any x,y,z∈E we have θ(x,x)≤θ(x,y), θ(x,y)=θ(y,x) and x≠y≠z≠x ⇒ θ(x,z)≤θ(x,y)∨θ(y,z); equivalently, it satisfies the two requirements of symmetry and ultratriangular inequality:
We have then a one-to-one correspondence between dilations Π ∗(E)→L and strongly triangular maps E 2→L: to a dilation δ ∗ corresponds the strongly triangular map θ given by θ(x,y)=δ ∗(1 {x,y}), while to a strongly triangular map θ corresponds the dilation δ ∗ given by \(\delta ^{*}(\pi ) = \bigvee_{B \in\pi} \bigvee_{(p,q) \in B^{2}} \theta(p,q)\). The fact that for all t∈L we have ε ∗(t)∈Π(E), in other words 0 E ≤ε ∗(t), is equivalent to 0 E ≤ε ∗(⊥), in other words δ ∗(0 E )=⊥, which can be expressed as
Note that δ ∗(0 E )=⊥ if and only if δ ∗=δ⋅FS for a dilation δ:Π(E)→L, where δ is in fact the restriction of δ ∗ to Π(E). The stronger requirement that ε ∗(⊥)=0 E means that both δ ∗(0 E )=⊥ and δ ∗(π)>⊥ for π>0 E , in other words both (32) and the following:
On the other hand, the fact that ε ∗ is an erosion guarantees that ε ∗(⊤)=1 E . If L⊂R with ⊥=0, as assumed in [23], the three conditions (31), (32), (33) mean that θ is an ultrametric distance [11]. We obtain thus, in a general setting, the equivalence shown in [2, 9] between ultrametrics and hierarchies of partitions.
In [8], hierarchies were also studied through adjunctions. However, instead of partitions, the authors considered non-oriented graphs, in other words reflexive and symmetrical relations; thus their conditions on θ were weaker: symmetry θ(x,y)=θ(y,x), θ(x,x)=⊥ (32) and θ(x,y)≥⊥.
The approach initiated by [2, 9] and extended in [8] has been motivated by the problem of classification, where no topological conditions are imposed on the classes. However in segmentation [12, 13, 16], the classes are supposed to be connected. We will thus modify the theory of [23] in order to take into account this constraint. As we saw in Sect. 2.3, for a partial connection \(\mathcal{C}\), \(\varPi^{*}(E,\mathcal{C})\) is closed under the supremum operation of Π ∗(E), and when \(\mathcal{C}\) is a connection, \(\varPi(E,\mathcal{C})\) is closed under the supremum operation of Π(E); we can thus analyse dilations \(\varPi^{*}(E,\mathcal{C}) \to L\) and \(\varPi(E,\mathcal{C}) \to L\) with the same tools as in [23], notably connective maps. Instead of strongly triangular maps, we will get pre-connective maps defined on a family generating the (partial) connection \(\mathcal{C}\). The particular case when \(\mathcal{C}= \mathcal{P}(E)\) will give the theory of [23] and the above result.
From now on, let \(\mathcal{C}\) be a partial connection and L be a complete lattice with least and greatest elements ⊥ and ⊤. Recall that by definition of a partial connection, for \(\mathcal{B}\subseteq \mathcal{C}\) with \(\bigcap\mathcal{B}\ne\emptyset\), we have \(\bigcup\mathcal{B}\in \mathcal{C}\).
Definition 16
A map \(\psi: \mathcal{C}\to L\) is called connective [23] if ψ(∅)=⊥ and for any \(\mathcal{B}\subseteq\mathcal {C}\), \(\bigcap\mathcal{B} \ne\emptyset\ \Rightarrow\ \psi(\bigcup\mathcal{B}) = \bigvee_{C \in \mathcal{B}} \psi(C)\). When \(\mathcal{C}\) is a connection, a connective map \(\psi : \mathcal{C}\to L\) is said to be strict if ψ({x})=⊥ for every x∈E.
Note that for \(\mathcal{B}= \emptyset\), \(\bigcap\mathcal{B}= E \ne \emptyset\), so \(\psi(\bigcup\mathcal{B}) = \psi(\emptyset) = \bot= \bigvee \emptyset= \bigvee_{C \in\mathcal{B}} \psi(C)\), as postulated. A connective map is necessarily isotone (order-preserving) [23]: \(\forall C,C' \in\mathcal{C}\), C⊆C′ ⇒ ψ(C)≤ψ(C′).
Lemma 17
Let \(\psi: \mathcal{C}\to L\) be connective, let \(B \in\mathcal {P}(E)\) and \(\mathcal{A} \subseteq\mathcal{C}\) such that B is chained by \(\mathcal{A}\). Then \(\psi(B) = \bigvee_{C \in\mathcal{A}} \psi(C)\).
Proof
Our proof follows an argument used in the proof of Theorem 13 of [23]. We know [22] that \(B \in\mathcal {C}\), but this follows also from the present argument. If \(\mathcal{A}\) is empty or \(\mathcal{A}= \{\emptyset\}\), then B=∅ and indeed \(\psi(B) = \bot= \bigvee_{C \in\mathcal{A}} \psi(C)\). We can thus assume that \(\mathcal{A}\) is non-empty and contains a non-empty set D; we have \(\bigvee\mathcal{A}= B\) and D⊆B. Let \(z = \bigvee_{C \in\mathcal{A}} \psi(C)\); then ψ(D)≤z. Let
then \(D \in\mathcal{B}\), so \(\bigcap\mathcal{B}= D \ne\emptyset\). Let \(Y = \bigcup \mathcal{B}\); then \(Y \in\mathcal{C}\), D⊆Y⊆B and since ψ is connective,
Thus \(Y\in\mathcal{B}\), so Y is the greatest element of \(\mathcal {B}\). If Y⊂B, as B is chained by \(\mathcal{A}\), there must be some \(C \in \mathcal{A}\) such that C overlaps both Y and B∖Y. Now ψ(C)≤z and as ψ is connective, we get ψ(Y∪C)=ψ(Y)∨ψ(C)≤z, hence \(Y \cup C \in\mathcal{B}\), so Y∪C⊆Y, a contradiction. Therefore Y=B and ψ(B)≤z. Every \(C \in \mathcal{A}\) satisfies C⊆B; since ψ is isotone, ψ(C)≤ψ(B); thus z≤ψ(B). We conclude that \(\psi(B) = z = \bigvee_{C \in\mathcal{A}} \psi(C)\). □
Theorem 18
There is a bijection between connective maps \(\mathcal{C}\to L\) and dilations \(\varPi^{*}(E,\mathcal{C}) \to L\), under which
-
To a connective map \(\psi: \mathcal{C}\to L\) corresponds the dilation \(\delta_{\psi}: \varPi^{*}(E,\mathcal{C}) \to L: \pi\mapsto\delta _{\psi}(\pi) = \bigvee_{B \in\pi} \psi(B)\).
-
To a dilation \(\delta: \varPi^{*}(E,\mathcal{C}) \to L\) corresponds the connective map \(\psi^{\delta}: \mathcal{C}\to L: C \mapsto\psi^{\delta}(C) = \delta ( \mathbf{1}_{C})\).
When \(\mathcal{C}\) is a connection, a map \(\delta: \varPi(E,\mathcal {C}) \to L\) is a dilation if and only if it is the restriction to \(\varPi(E,\mathcal{C})\) of a dilation \(\varPi^{*}(E,\mathcal{C}) \to L\) corresponding to a strict connective map \(\mathcal{C} \to L\).
Proof
Let \(\psi: \mathcal{C}\to L\) be connective and define \(\delta_{\psi}: \varPi ^{*}(E, \mathcal{C}) \to L\) as above. Let \(\mathcal{F}\subseteq\varPi^{*}(E,\mathcal{C})\). If \(\mathcal{F}\) is empty, then  and by definition δ
ψ
(Ø) is the empty supremum ⊥. Suppose now \(\mathcal{F}\) non-empty, and let \(\overline{\pi}= \bigvee\mathcal{F}\). For any \(\pi \in\mathcal{F}\), \(\pi\le\overline{\pi}\), thus every block B∈π is included in a block \(C \in\overline{\pi}\), and as ψ is isotone, ψ(B)≤ψ(C); the definition of δ
ψ
gives then \(\delta_{\psi}(\pi ) \le \delta_{\psi}(\overline{\pi})\). Hence \(\bigvee_{\pi\in\mathcal{F}} \delta_{\psi}(\pi) \le\delta_{\psi}(\overline{\pi})\). Now every block \(C \in\overline{\pi}\) is obtained by chaining some blocks of partial partitions in \(\mathcal {F}\); in other words C is chained by some \(\mathcal{A}\subseteq\bigcup \mathcal{F}\); by Lemma 17 and the definition of δ
ψ
, we get
and by definition δ
ψ
(Ø) is the empty supremum ⊥. Suppose now \(\mathcal{F}\) non-empty, and let \(\overline{\pi}= \bigvee\mathcal{F}\). For any \(\pi \in\mathcal{F}\), \(\pi\le\overline{\pi}\), thus every block B∈π is included in a block \(C \in\overline{\pi}\), and as ψ is isotone, ψ(B)≤ψ(C); the definition of δ
ψ
gives then \(\delta_{\psi}(\pi ) \le \delta_{\psi}(\overline{\pi})\). Hence \(\bigvee_{\pi\in\mathcal{F}} \delta_{\psi}(\pi) \le\delta_{\psi}(\overline{\pi})\). Now every block \(C \in\overline{\pi}\) is obtained by chaining some blocks of partial partitions in \(\mathcal {F}\); in other words C is chained by some \(\mathcal{A}\subseteq\bigcup \mathcal{F}\); by Lemma 17 and the definition of δ
ψ
, we get
Hence \(\delta_{\psi}(\overline{\pi}) = \bigvee_{C \in\overline{\pi}} \psi(C) \le\bigvee_{\pi\in\mathcal{F}} \delta_{\psi}(\pi)\). The equality \(\bigvee _{\pi \in\mathcal{F}} \delta_{\psi}(\pi) = \delta_{\psi}(\overline{\pi}) = \delta_{\psi}(\bigvee\mathcal{F})\) follows. Therefore δ ψ is a dilation. For \(C \in\mathcal{C}\) we have \(\psi^{\delta_{\psi}}(C) = \delta_{\psi}(\mathbf{1}_{C}) = \psi(C)\), thus \(\psi^{\delta_{\psi}} = \psi\).
Conversely, let \(\delta: \varPi^{*}(E,\mathcal{C}) \to L\) be a dilation. We have 1 ∅=Ø, so ψ δ(∅)=δ(1 ∅)=δ(Ø)=⊥. Let \(\mathcal{B}\subseteq\mathcal {C}\) such that \(\bigcap\mathcal{B}\ne \emptyset\); we have \(\mathbf{1}_{\bigcup\mathcal{B}} = \bigvee_{C \in\mathcal{B}} \mathbf{1}_{C}\) [22] (for \(\mathcal{B}\) empty, this equality remains valid, it reduces to 1 ∅=Ø); as δ commutes with the supremum,
Therefore ψ δ is connective. For \(\pi\in\varPi ^{*}(E,\mathcal{C})\) we have
hence \(\delta_{\psi^{\delta}} = \delta\).
We have thus shown that ψ↦δ ψ and δ↦ψ δ are a bijection and its inverse, between connective maps \(\mathcal{C}\to L\) and dilations \(\varPi^{*}(E,\mathcal{C}) \to L\). Again, our proof followed an argument from the proof of Theorem 13 of [23].
Assume now that \(\mathcal{C}\) is a connection. The supremum in \(\varPi (E,\mathcal{C})\) is the one in Π(E), while the supremum in \(\varPi^{*}(E,\mathcal {C})\) is the one in Π
∗(E). Let \(\delta: \varPi(E,\mathcal{C}) \to L\) be a dilation. The dilation FS:Π
∗(E)→Π(E):π↦π∨0
E
, restricted to \(\varPi^{*}(E,\mathcal{C})\), becomes a dilation \(FS_{\mathcal{C}}: \varPi^{*}(E,\mathcal{C}) \to \varPi(E,\mathcal{C})\) (since \(\mathcal{C}\) comprises all singletons, \(\mathbf{0}_{E} \in \varPi(E,\mathcal{C})\)). As above, we obtain the dilation \(\delta^{*} = \delta\cdot FS_{\mathcal{C}}: \varPi^{*}(E,\mathcal{C}) \to L: \pi\mapsto\delta(\pi\vee\mathbf{0}_{E})\), and indeed δ is the restriction of δ
∗ to \(\varPi(E,\mathcal{C})\): for \(\pi\in\varPi (E,\mathcal{C})\), π∨0
E
=π and so δ
∗(π)=δ(π). Let ψ be the connective map corresponding to δ
∗. Since  , we have δ
∗(Ø)=δ(0
E
)=δ
∗(0
E
), with δ
∗(0
E
)=⋁
p∈E
ψ({p}) and δ
∗(Ø)=⊥. Hence ψ({p})=⊥ for all p∈E, that is, ψ is strict.
, we have δ
∗(Ø)=δ(0
E
)=δ
∗(0
E
), with δ
∗(0
E
)=⋁
p∈E
ψ({p}) and δ
∗(Ø)=⊥. Hence ψ({p})=⊥ for all p∈E, that is, ψ is strict.
Conversely, let ψ be a strict connective map and consider the corresponding dilation \(\delta_{\psi}: \varPi^{*}(E,\mathcal{C}) \to L\), which commutes with the supremum in \(\varPi^{*}(E,\mathcal{C})\) (for partial partitions). We must show that its restriction to \(\varPi(E,\mathcal{C})\) is a dilation \(\varPi(E,\mathcal{C}) \to L\), in other words it commutes with the supremum in \(\varPi (E,\mathcal{C})\) (for partitions). For a non-empty family \(\mathcal{F}\subseteq \varPi(E,\mathcal{C})\), its supremum in \(\varPi(E,\mathcal{C})\) and in \(\varPi ^{*}(E,\mathcal{C})\) coincide, thus the equality \(\delta_{\psi}(\bigvee\mathcal{F}) = \bigvee_{\pi \in \mathcal{F}} \delta_{\psi}(\pi)\) holds for the same supremum \(\bigvee \mathcal{F}\) in both \(\varPi^{*}(E,\mathcal{C})\) and \(\varPi(E,\mathcal{C})\). When \(\mathcal{F}\) is empty,  in \(\varPi^{*}(E,\mathcal{C})\) but \(\bigvee\mathcal{F}= \mathbf{0}_{E}\) in \(\varPi(E,\mathcal{C})\), however δ
ψ
(0
E
)=⋁
p∈E
ψ({p})=⊥=δ
ψ
(Ø), so we get \(\delta_{\psi}\bigl(\bigvee \mathcal{F}\bigr) = \bot= \bigvee_{\pi\in\mathcal{F}} \delta_{\psi}(\pi)\) for the supremum \(\bigvee\mathcal{F}\) either in \(\varPi^{*}(E,\mathcal{C})\) or in \(\varPi(E,\mathcal{C})\). □
in \(\varPi^{*}(E,\mathcal{C})\) but \(\bigvee\mathcal{F}= \mathbf{0}_{E}\) in \(\varPi(E,\mathcal{C})\), however δ
ψ
(0
E
)=⋁
p∈E
ψ({p})=⊥=δ
ψ
(Ø), so we get \(\delta_{\psi}\bigl(\bigvee \mathcal{F}\bigr) = \bot= \bigvee_{\pi\in\mathcal{F}} \delta_{\psi}(\pi)\) for the supremum \(\bigvee\mathcal{F}\) either in \(\varPi^{*}(E,\mathcal{C})\) or in \(\varPi(E,\mathcal{C})\). □
Recall that \(\mathcal{S}(E)\) is the set of singletons of E. In Proposition 18 of [22] we showed that \(\mathcal{C}\) is a partial connection if and only if \(\mathcal{C}\cup\mathcal{S}(E)\) is a connection; in particular, for a connection \(\mathcal{C}\), \(\mathcal{C}\setminus \mathcal{S}(E)\) will be a partial connection. In [23] we showed that the dilation FS:Π ∗(E)→Π(E) is also an erosion, whose lower adjoint is the dilation RSIN:Π(E)→Π ∗(E):π↦π∖0 E that removes all singleton blocks from a partition. This will allow us to reverse the above argument about the restriction of FS to \(\varPi^{*}(E,\mathcal{C})\).
Proposition 19
Let \(\mathcal{C}\) be a connection and let \(\mathcal{C}^{*} = \mathcal {C}\setminus\mathcal{S}(E)\). Given a connective map \(\psi: \mathcal{C}^{*} \to L\), the map \(\psi^{+}: \mathcal{C}\to L\) defined by
is a strict connective map. For \(\pi\in\varPi(E,\mathcal{C})\), we have \(\delta_{\psi^{+}}(\pi) =\delta_{\psi}(\pi\setminus\mathbf{0}_{E}) = \bigvee_{B \in \pi\setminus\mathbf{0}_{E}} \psi(B)\).
Proof
Let \(\mathit{RSIN}_{\mathcal{C}}\) be the restriction to \(\varPi(E,\mathcal{C})\) of the dilation RSIN:Π(E)→Π ∗(E):π↦π∖0 E ; for \(\pi \in \varPi(E,\mathcal{C})\), π∖0 E has no singleton block, so \(\mathit{RSIN}_{\mathcal{C}}(\pi) = \pi\setminus\mathbf{0}_{E} \in\varPi ^{*}(E,\mathcal{C}^{*})\); thus \(\mathit{RSIN}_{\mathcal{C}}\) is a map \(\varPi(E,\mathcal{C}) \to\varPi^{*}(E,\mathcal{C}^{*})\); since \(\varPi(E,\mathcal{C} )\) and \(\varPi^{*}(E,\mathcal{C}^{*})\) inherit the supremum operation of Π(E) and Π ∗(E) respectively, \(\mathit{RSIN}_{\mathcal{C}}\) will be a dilation \(\varPi (E,\mathcal{C}) \to \varPi^{*}(E,\mathcal{C}^{*})\).
We apply Theorem 18: \(\delta_{\psi}: \varPi^{*}(E,\mathcal {C}^{*}) \to L\) is a dilation; but \(\mathit{RSIN}_{\mathcal{C}}: \varPi(E,\mathcal{C}) \to\varPi ^{*}(E,\mathcal{C}^{*})\) is also a dilation; hence \(\delta_{\psi}\cdot \mathit{RSIN}_{\mathcal{C}}: \varPi (E,\mathcal{C}) \to L: \pi \mapsto\delta_{\psi}(\pi\setminus\mathbf{0}_{E}) = \bigvee_{B \in \pi\setminus \mathbf{0}_{E}} \psi(B)\) will be a dilation, thus there is a strict connective map \(\psi_{1}: \mathcal{C}\to L\) such that \(\delta_{\psi}\cdot \mathit{RSIN}_{\mathcal{C}}\) is the restriction to \(\varPi(E,\mathcal{C})\) of \(\delta_{\psi_{1}}: \varPi ^{*}(E,\mathcal{C}) \to L\). Let \(A \in\mathcal{C}\); if A is a singleton, then ψ 1(A)=⊥=ψ +(A); if A is not a singleton, letting \(\pi= FS(\mathbf {1}_{A}) = \mathbf{1}_{A} \cup\mathbf{0}_{E\setminus A} \in\varPi(E,\mathcal{C})\), we get
while
hence \(\psi_{1}(A) = \delta_{\psi_{1}}(\pi) = \delta_{\psi}\cdot \mathit{RSIN}_{\mathcal{C}} (\pi) = \psi^{+}(A)\). Therefore ψ +=ψ 1, ψ + is a strict connective map, and for \(\pi\in\varPi(E,\mathcal{C})\), \(\delta _{\psi^{+}}(\pi ) = \delta_{\psi}\cdot \mathit{RSIN}_{\mathcal{C}}(\pi) = \delta_{\psi}(\pi \setminus\mathbf{0}_{E}) = \bigvee_{B \in\pi\setminus\mathbf{0}_{E}} \psi(B)\). □
One can also check directly that ψ + is a strict connective map, without recourse to the dilation \(\mathit{RSIN}_{\mathcal{C}}\), using an argument similar to the one in the proof of Proposition 18 of [22].
Proposition 19 can also be applied when the connective map ψ is defined on \(\mathcal{C}\) rather than \(\mathcal{C}^{*}\); then (34) modifies the value of the map on singletons.
We will now generalize the strong triangular maps of [23]. From now on we assume that \(\mathcal{G}\) is a non-empty family of non-empty subsets of E. Recall that \(\mathsf {Con}^{*}(\mathcal{G})\) is the partial connection generated by \(\mathcal{G}\) and \(\mathsf {Con}(\mathcal{G}) = \mathsf{Con}^{*}(\mathcal{G}) \cup \mathcal{S}(E)\) is the connection generated by \(\mathcal{G}\).
Definition 20
A map \(\xi: \mathcal{G}\to L\) is called pre-connective if for any \(\mathcal{B} \subseteq\mathcal{G}\) and \(A,B \in\mathcal{G}\) such that B is chained by \(\mathcal{B}\) and A⊆B, we have \(\xi(A) \le\bigvee_{X \in\mathcal{B}} \xi(X)\).
A pre-connective map is necessarily isotone (order-preserving): \(\forall A,B \in\mathcal{G}\), A⊆B ⇒ ξ(A)≤ξ(B); this follows by taking \(\mathcal{B}= \{B\}\).
For instance, if \(\mathcal{G}\) is the set of singletons and pairs of points of E, the map ξ is pre-connective if and only if the map θ:E 2→L defined by θ(x,x)=ξ({x}) and θ(x,y)=ξ({x,y}) for x≠y, is strongly triangular (31). Indeed, symmetry is obvious because the pair {x,y} is unordered, while the ultratriangular inequality is required because {x,z} is chained by {{x,y},{y,z}}; these two conditions are sufficient: if B is chained by \(\mathcal{B}\) and x,y∈B (with x,y equal or different), there is a sequence p 0,…,p n ∈B such that p 0=x, p n =y and \(\{p_{i},p_{i+1}\} \in\mathcal {B}\) for i=0,…,n−1, then applying inductively the ultratriangular inequality we get \(\theta(x,y) \le\bigvee_{i=0}^{n-1} \theta(p_{i},p_{i+1})\). The following result generalizes Proposition 33 of [23]:
Proposition 21
Consider a map \(\xi: \mathcal{G}\to L\).
-
1.
The map ξ is pre-connective if and only it is the restriction to \(\mathcal{G}\) of a connective map \(\psi: \mathsf{Con}^{*}(\mathcal {G}) \to L\). This map ψ is then unique, it is the map ψ ξ given by
$$ \forall C \in\mathsf{Con}^*(\mathcal{G}), \quad \psi_\xi(C) = \bigvee_{X \in\mathcal{P}(C) \cap\mathcal{G}} \xi (X) . $$(35) -
2.
Assume that \(\mathcal{G}\cap\mathcal{S}(E) = \emptyset\) (elements of \(\mathcal{G}\) are not singletons). The map ξ is pre-connective if and only it is the restriction to \(\mathcal{G}\) of a strict connective map \(\psi: \mathsf{Con}(\mathcal{G}) \to L\). This map ψ is then unique, it is the map \(\psi_{\xi}^{+}\) defined according to (34), (35), that is, for \(C \in\mathsf{Con}^{*}(\mathcal{G})\), \(\psi_{\xi}^{+}(C) = \psi_{\xi}(C)\), and for x∈E, ψ({x})=⊥.
Proof
1. Let \(\xi: \mathcal{G}\to L\) be the restriction to \(\mathcal{G}\) of a connective map \(\psi: \mathsf{Con}^{*}(\mathcal{G}) \to L\). Let \(\mathcal {B}\subseteq\mathcal{G}\) and \(A,B \in\mathcal{G}\) such that B is chained by \(\mathcal{B}\) and A⊆B; then \(B \in \mathsf{Con}^{*}(\mathcal{G})\), \(\psi(B) = \bigvee_{X \in\mathcal {B}} \psi(X)\) by Lemma 17, and ψ(A)≤ψ(B) since ψ is isotone; thus \(\xi(A) = \psi(A) \le\psi(B) = \bigvee_{X \in \mathcal{B}} \psi(X) = \bigvee_{X \in\mathcal{B}} \xi(X)\). Hence ξ is pre-connective. For any \(C \in\mathsf{Con}^{*}(\mathcal{G})\), C is chained by \(\mathcal{P}(C) \cap\mathcal{G}\), so by Lemma 17 again we get \(\psi (C) = \bigvee_{X \in\mathcal{P}(C) \cap\mathcal{G}} \psi(X) = \bigvee _{X \in\mathcal{P}(C) \cap \mathcal{G}} \xi(X) = \psi_{\xi}(C)\). Therefore ψ=ψ ξ and the map ψ is unique.
Conversely, let the map \(\xi: \mathcal{G}\to L\) be pre-connective. Since \(\emptyset\notin\mathcal{G}\), by (35) ψ ξ (∅) gives the empty supremum ⊥. Now let \(\mathcal{B} \subseteq\mathsf{Con}^{*}(\mathcal{G})\) such that \(\bigcap\mathcal {B}\ne\emptyset\), and set \(B = \bigcup\mathcal{B}\). Each \(C \in\mathcal{B}\) is chained by \(\mathcal{P}(C) \cap\mathcal{G}\), and as \(\bigcap\mathcal{B}\ne\emptyset\), B is chained by \(\bigcup_{C \in\mathcal{B}} (\mathcal{P}(C) \cap\mathcal{G})\). As ξ is pre-connective, for \(Y \in\mathcal{P}(B) \cap \mathcal{G}\),
Hence \(\psi_{\xi}(B) = \bigvee_{Y \in\mathcal{P}(B) \cap\mathcal {G}} \xi(Y) \le \bigvee_{C \in\mathcal{B}} \psi_{\xi}(C)\). On the other hand, for any \(C \in \mathcal{B}\), as C⊆B, \(\mathcal{P}(C) \cap\mathcal {G}\subseteq\mathcal{P}(B) \cap\mathcal{G}\), hence \(\psi_{\xi}(C) = \bigvee_{X \in\mathcal{P}(C) \cap\mathcal {G}} \xi(X) \le \bigvee_{X \in\mathcal{P}(B) \cap\mathcal{G}} \xi(X) = \psi_{\xi}(B)\). We deduce that \(\psi_{\xi}(B) = \bigvee_{C \in\mathcal{B}} \psi_{\xi}(C)\), and ψ ξ is connective.
Finally, for any \(B \in\mathcal{G}\), \(B \in\mathcal{P}(B) \cap \mathcal{G}\), so B is chained by \(\mathcal{P}(B) \cap\mathcal{G}\), hence \(\xi(B) \le\bigvee_{X \in\mathcal{P}(B) \cap \mathcal{G}} \xi(X) = \psi_{\xi}(B)\); but since ξ is isotone, for any \(X \in \mathcal{P}(B) \cap\mathcal{G}\) we have ξ(X)≤ξ(B), hence \(\psi_{\xi}(B) = \bigvee_{X \in\mathcal{P}(B) \cap\mathcal{G}} \xi(X) \le\xi (B)\). We conclude that ψ ξ (B)=ξ(B), thus ξ is the restriction of ψ ξ to \(\mathcal{G}\).
2. Assume that elements of \(\mathcal{G}\) are not singletons. Since any element of \(\mathsf{Con}^{*}(\mathcal{G})\) is obtained by chaining some elements of \(\mathcal{G}\), it cannot be a singleton. Thus \(\mathsf{Con}^{*}(\mathcal{G}) \cap\mathcal {S}(E) = \emptyset\), hence \(\mathsf{Con}^{*}(\mathcal{G}) = \mathsf{Con}(\mathcal{G}) \setminus \mathcal{S}(E)\).
Let \(\xi: \mathcal{G}\to L\) be the restriction to \(\mathcal{G}\) of a strict connective map \(\psi: \mathsf{Con}(\mathcal{G}) \to L\). Let ψ′ be the restriction of ψ to \(\mathsf{Con}^{*}(\mathcal{G})\); then ψ′ remains connective, and ξ is the restriction of ψ′ to \(\mathcal{G}\). By item 1, ξ is pre-connective and ψ′=ψ ξ . Since ψ is strict, we have ψ({x})=⊥ for all x∈E, and we deduce from (34) that \(\psi= \psi_{\xi}^{+}\).
Conversely, let the map \(\xi: \mathcal{G}\to L\) be pre-connective. By item 1, \(\psi_{\xi}: \mathsf{Con}^{*}(\mathcal{G}) \to L\) is connective and ξ is the restriction of ψ ξ to \(\mathcal{G}\). By Proposition 19, \(\psi_{\xi}^{+}\) is strict connective, and ψ ξ is the restriction of \(\psi_{\xi}^{+}\) to \(\mathsf{Con}^{*}(\mathcal{G}) = \mathsf {Con}(\mathcal{G}) \setminus\mathcal{S}(E)\). Therefore ξ is the restriction of \(\psi_{\xi}^{+}\) to \(\mathcal{G}\). □
Note that in the case of item 2, that is, \(\mathcal{G}\cap\mathcal {S}(E) = \emptyset\), if we extend the formula in (35) to \(\mathsf{Con}(\mathcal{G})\), we obtain ψ ξ ({x})=⊥ for any x∈E, thus \(\psi_{\xi}^{+}\) is given by extending (35) to \(\mathsf{Con}(\mathcal{G})\).
Combining Theorem 18 and Proposition 21, we get the dilation
furthermore, when \(\mathcal{G}\cap\mathcal{S}(E) = \emptyset\), from Proposition 19 we get the dilation
whose restriction to \(\varPi(E,\mathsf{Con}(\mathcal{G}))\) remains a dilation (because \(\delta_{\psi_{\xi}^{+}}(\mathbf{0}_{E}) = \bot\)).
4.2 Graph Connectivity and Edge Saliency
Let us illustrate our theory in the case of graph-theoretical connectivity. Suppose that E is endowed with an irreflexive and symmetrical adjacency relation ∼, and let \(\mathcal{G}\) be the set of all pairs of distinct adjacent points: \(\mathcal{G}= \{ \{p,q\} \mid p,q \in E, \ p \ne q, \ p \sim q \}\); then \((E,\mathcal{G})\) is an undirected graph. Let \(\mathcal{C}= \mathsf{Con}(\mathcal{G})\); it is the set of all subsets of E that are connected according to that graph (in particular singletons in E are connected). Let \(\mathcal{G}^{*} = \mathcal{G}\cup\mathcal{S}(E)\); we have then \(\mathsf{Con}^{*}(\mathcal{G}^{*}) = \mathcal{C}\). Given a map ξ defined on \(\mathcal{G}\) or \(\mathcal{G}^{*}\), we will write ξ(p,q) for ξ({p,q}) and ξ(p) for ξ({p}). A map \(\xi: \mathcal{G}\to L\) is pre-connective if and only if ξ satisfies the following generalization of the ultratriangular inequality to cycles in the graph:
In other words, the maximum value taken by ξ in a cycle is attained on at least two edges. We call this condition the ultracyclic inequality. A map \(\xi: \mathcal{G}^{*} \to L\) is pre-connective if and only if ξ satisfies the ultracyclic inequality (38) and for \(\{x,y\} \in\mathcal{G}\) we have ξ(x)≤ξ(x,y).
We first characterize a hierarchy of partitions. Let \(\xi: \mathcal {G}\to L\) be pre-connective; we get the strict connective map \(\psi_{\xi}^{+}: \mathcal{C} \to L\); let \(\delta= \delta_{\psi_{\xi}^{+}}: \varPi^{*}(E,\mathcal{C}) \to L\), cf. (37), and let ε be the upper adjoint erosion \(L \to\varPi^{*}(E,\mathcal{C})\) providing the hierarchy; in fact, δ(0 E )=⊥, so ε(⊥)≥0 E and every t∈L gives \(\varepsilon(t) \in\varPi(E,\mathcal{C})\), we have a hierarchy of partitions. Note that \(\varepsilon(\top) = \mathsf{PC}^{\mathcal{C}}(E)\), the partition of all connected components of E, which is indeed the greatest element of \(\varPi(E,\mathcal{C})\). For any pair \(\{p,q\} \in\mathcal{G}\), \(\xi(p,q) = \psi_{\xi}^{+}(\{p,q\}) = \delta(\mathbf{1}_{\{p,q\}})\), it is the least t∈L such that 1 {p,q}≤ε(t), that is, {p,q} is included in a block of ε(t). The condition ε(⊥)=0 E is satisfied if and only if ⊥<ξ(p,q) for all \(\{p,q\} \in \mathcal{G}\), cf. (33) above; then p and q belong to two distinct blocks of ε(t) for ⊥≤t<ξ(p,q).
Next, we characterize a hierarchy of partial partitions. Let \(\xi: \mathcal{G}^{*} \to L\) be pre-connective; we get the connective map \(\psi_{\xi}: \mathcal{C} = \mathsf{Con}^{*}(\mathcal{G}^{*}) \to L\); let \(\delta= \delta_{\psi _{\xi}}: \varPi^{*}(E,\mathcal{C} ) \to L\), cf. (36), and let ε be the upper adjoint erosion \(L \to\varPi^{*}(E,\mathcal{C})\) providing the hierarchy. Again, \(\varepsilon(\top) = \mathsf{PC}^{\mathcal{C}}(E)\). For any \(\{ p,q\} \in\mathcal{G}\), ξ(p,q) is the least t∈L such that {p,q} is included in a block of ε(t); for p∈E, ξ(p) is the least t∈L such that 1 {p}≤ε(t), that is, p∈supp(ε(t)). The condition ε(⊥)=Ø is satisfied if and only if ⊥<ξ(p) for all p∈E.
Now assume that L is a chain. For \(\{p,q\} \in\mathcal{G}\), as t ranges from ⊥ to ⊤, we encounter 4 possible cases in the following order:
-
(a)
t<min(ξ(p),ξ(q)): both p and q lie in the background E∖supp(ε(t)).
-
(b)
min(ξ(p),ξ(q))≤t<max(ξ(p),ξ(q)): one of p and q lies in a block of ε(t) and the other in the background E∖supp(ε(t)).
-
(c)
max(ξ(p),ξ(q))≤t<ξ(p,q): p and q lie in two distinct blocks of ε(t).
-
(d)
ξ(p,q)≤t: p and q lie in a same block of ε(t).
The case where \(\mathcal{C}= \mathcal{P}(E)\), \(\varPi^{*}(E,\mathcal {C}) = \varPi^{*}(E)\) and \(\varPi(E,\mathcal{C}) = \varPi(E)\), is obtained when any two distinct points of E are adjacent, thus \(\mathcal{G}\) consists in the set of all pairs of points; here the ultracyclic inequality (38) reduces to the ultratriangular inequality (31); we obtain then the theory of [23].
Let us consider the particular case where E is the digital space Z n with a usual adjacency (4 or 8 in Z 2, 6, 18 or 26 in Z 3, etc.); each pair \(\{p,q\} \in\mathcal{G}\) can be seen as the unoriented edge element e(p,q) separating the square or cubic cells corresponding to the adjacent digital points p and q; this is illustrated in Fig. 11 for n=2 and 3.
Left: in 2D (n=2), two pixels p and q correspond to square cells; when they are axially adjacent, they are separated by a line edge element e(p,q). Middle: when the two pixels p and q are diagonally adjacent, they are separated by a point edge element e(p,q). Right: in 3D (n=3), the two 6-adjacent voxels p and q correspond to cubic cells, separated by the surface edge element e(p,q)
For a hierarchy of partitions, we have a pre-connective map \(\xi: \mathcal{G} \to L\) and we set the hierarchy erosion \(\varepsilon: L \to\varPi ^{*}(E,\mathcal{C})\) as the upper adjoint of the dilation \(\delta_{\psi_{\xi}^{+}}\) given by (37). Let \(\{p,q\} \in\mathcal{G}\). For t<ξ(p,q), p and q belong to two distinct blocks of ε(t) and the edge element e(p,q) lies in the boundary separating these two blocks, while for t≥ξ(p,q), p and q belong to the same block of ε(t) and the edge element e(p,q) does no more belong to the boundary of a block. Assuming that ε(⊥)=0 E , ⊥<ξ(p,q) and the edge element e(p,q) belongs to a boundary separating blocks of ε(t) for ⊥≤t<ξ(p,q). Note that E is here connected, so ε(⊤)=1 E . When L is a finite chain, we can make an analogy between the hierarchy and the flooding process in watershed segmentation, so the partition ε(t) gives the basins at flooding level t, and ξ(p,q) is the level at which the two basins containing p and q are merged. Thus the pre-connective map ξ generalizes the edge saliency [16] of a hierarchy of partitions.
For a hierarchy of partial partitions, we have a pre-connective map \(\xi: \mathcal{G}^{*} \to L\) and we set the hierarchy erosion \(\varepsilon: L \to \varPi^{*}(E,\mathcal{C})\) as the upper adjoint of the dilation \(\delta _{\psi _{\xi}}\) given by (36). Let \(\{p,q\} \in\mathcal{G}\). Assuming that L is a chain, the four cases (a, b, c, d) above translate as follows:
-
(a)
t<min(ξ(p),ξ(q)): the edge element e(p,q) lies between two points in the background E∖supp(ε(t)), see Fig. 12(a), we call it a background edge element.
-
(b)
min(ξ(p),ξ(q))≤t<max(ξ(p),ξ(q)): the edge element e(p,q) belongs to the boundary separating a block of ε(t) and the background E∖supp(ε(t)), see Fig. 12(b), we call it a outer edge element.
-
(c)
max(ξ(p),ξ(q))≤t<ξ(p,q): the edge element e(p,q) belongs to the boundary separating two distinct blocks of ε(t), see Fig. 12(c), we call it a separating edge element.
-
(d)
ξ(p,q)≤t: the edge element e(p,q) lies between two points in a same block of ε(t), see Fig. 12(d), we call it an inner edge element.
Only cases (b) and (c) correspond to block boundaries, with “visible” edge elements; on the other hand, in cases (a) and (d) edge elements will be “invisible”. Thus when min(ξ(p),ξ(q))<ξ(p,q), e(p,q) belongs to the boundary of a block of ε(t) for min(ξ(p),ξ(q))≤t<ξ(p,q), being then an outer or separating edge element. On the other hand when min(ξ(p),ξ(q))=ξ(p,q), e(p,q) will never belong to a boundary of a block of ε(t), it can be only a background or inner edge element. Hence in a hierarchy of partial partitions, the saliency of an edge element is given by an interval, possibly empty, not a number.
The 4 items (a, b, c, d) have decomposed L into 4 successive intervals through which t passes as it increases from ⊥ to ⊤, some of them can be empty. The succession of these intervals leads to an ordering on the 4 corresponding types of edge elements:
as t increases, the edge element type increases. Since some of the intervals can be empty, some types can be skipped, for instance, it is possible to pass directly from background to inner.
We illustrate in Fig. 13 a preconnective map and the corresponding hierarchy of partial partitions, with the different types of edge elements.
E is a 2×3 rectangle in Z 2, with horizontal and vertical adjacency; L={0,1,2,3,4}. Top left: points are shown as disks and pairs of points as elongated diamonds linking them, with values of ξ written inside. Next: the hierarchy of partial partitions ε(t), t∈L. Each point is shown as a disk surrounded by a square cell; those in the support have filled disks and grey cells, while those in the background have hollow disks and white cells. Edge elements are drawn as lines: dotted lines for background edges, thick lines for outer or separating edges, and dashed lines for inner edges
Note that in the case of a hierarchy of partitions, we obtain only the types (c) separating and (d) inner; indeed, here ξ +(p)=ξ +(q)=⊥, so max(ξ +(p),ξ +(q))≤t anyway.
Let us now discuss the effect on edge type of the elementary operations of merging, creating or inflating blocks, corresponding to the covering relations \(\buildrel m \over\prec\), \(\buildrel s \over \prec\) , \(\buildrel c \over\prec\) and \(\buildrel i \over\prec\). We start from a partial partition π 1.
(1∘) Merging two blocks B,C∈π 1, getting π 2=(π∖{B,C})∪{B∪C}, with \(\pi_{1} \buildrel m \over\prec\pi_{2}\). Since π 2 has its blocks in \(\mathcal{C}\), the two blocks B and C must be adjacent, so there are adjacent points p∈B and q∈C, and the corresponding edge elements e(p,q) form together the boundary between B and C. For any such pair {p,q}, the merging of B and C changes the edge element e(p,q) from separating to inner, while other edge elements are not modified.
(2∘) Adding a singleton block {p} to π 1, getting π 2=π 1∪{{p}}, with \(\pi_{1} \buildrel s \over\prec\pi_{2}\). For any point q∈E adjacent to p, we get 2 cases for the evolution of the edge element e(p,q): (i) q∈supp(π 1) and e(p,q) changes from outer to separating; (ii) q∈E∖supp(π 2) and e(p,q) changes from background to outer. Other edge elements are not modified.
(3∘) Adding a non-singleton block B to π 1, getting π 2=π 1∪{B}, with \(\pi_{1} \buildrel c \over \prec\pi_{2}\). Only edge elements with at least one point in B are changed. Given p∈B, for q∈E adjacent to p, we get 3 cases for the evolution of the edge element e(p,q): (i) q∈supp(π 1) and e(p,q) changes from outer to separating; (ii) q∈B and e(p,q) changes from background to inner; (iii) q∈E∖supp(π 2) and e(p,q) changes from background to outer.
(4∘) Inflating a block by one point, the point p is added to block B∈π 1, so we get π 2=(π 1∖{B})∪{B∪{p}}, with \(\pi_{1} \buildrel i \over\prec\pi_{2}\). Since \(B \cup\{p\} \in \mathcal{C}\), p must be adjacent to some q∈B. The operation can be decomposed into first creating the singleton block {p}, then merging it with B. For any point q∈E adjacent to p, we get 3 cases for the evolution of the edge element e(p,q): (i) q∈B and e(p,q) changes from outer to inner; (ii) q∈C for another block C∈π 1 and e(p,q) changes from outer to separating; (iii) q∈E∖supp(π 2) and e(p,q) changes from background to outer.
(5∘) Although this does not correspond to a covering relation, we can finally consider inflating a block by more than one point, a set D is added to block B∈π 1, so we get π 2=(π 1∖{B})∪{B∪D}. Here \(B \cup D \in\mathcal{C}\), and at least one point in D must be adjacent to one point in B. Only edge elements with at least one point in D are changed. Given p∈D, for q∈E adjacent to p, we get 4 cases for the evolution of the edge element e(p,q): (i) q∈B and e(p,q) changes from outer to inner; (ii) q∈C for another block C∈π 1 and e(p,q) changes from outer to separating; (iii) q∈D and e(p,q) changes from background to inner; (iv) q∈E∖supp(π 2) and e(p,q) changes from background to outer.
We summarize in Table 3 the changes of edge element types for the 4 first cases, corresponding to the 4 elementary covering relations. Assuming partial partitions with finite support, each one of the six orders is the reflexive and transitive closure of the corresponding covering relation, thus the changes of edge element types are obtained by composing those possible for the covering relation. We obtain then Table 4.
We see then that the 6 orders involve changes of edge types from “invisible” to “visible”. When π 1 increases to π 2, an edge can change from background to outer or separating; the only order where this never happens is the merging order ⊑. Conversely, when π 2 decreases to π 1, an edge can change from inner to outer or separating; the only order where this never happens is the inclusion order ⊆. In other words, the only operations that do not create visible edges are merging or removing blocks. They are indeed the operations that have been considered in connected filtering.
4.3 Connected Filtering and Component Trees
In connected filtering, one usually merges flat zones, so that separating edges between merged flat zones are removed (in fact, they become invisible inner edges), while other edges are unchanged. With the component tree [14], an image is represented by a hierarchy of partial partitions, and a connected filter operates on the image by removing some blocks; this removes their boundaries (in fact, these outer or separating edges become invisible background edges). This tree comes in two dual forms, the max-tree and min-tree, the first one has been used for anti-extensive operators, and the second one for extensive operators.
From now one we assume that L is a finite chain with least and greatest elements ⊥ and ⊤. We take a fixed partial connection \(\mathcal{C}\) on \(\mathcal{P}(E)\) such that \(E \in \mathcal{C}\). A map \(\varepsilon: L \to \varPi^{*}(E,\mathcal{C})\) is an erosion if and only if ε is isotone (order-preserving) and ε(⊤)=1
E
. For a hierarchy, one should normally have ε(⊥)=Ø, but this is not crucial; when ε(⊥)>Ø, we can add to L a new least element  (thus
(thus  ) and set
) and set  .
.
Let us first describe the max-tree. The construction is illustrated in Fig. 14. Consider a function F:E→L. For each t∈L, we define the thresholding above
We can consider the partial partition \(\mathsf{PC}^{\mathcal{C}}(X_{t}(F))\) of connected components of X t (F). We have X ⊥(F)=E, so \(\mathsf {PC}^{\mathcal{C}}(X_{\bot}(F)) = \mathbf{1}_{E}\); now when t increases, X t (F) decreases, so \(\mathsf{PC}^{\mathcal{C}}(X_{t}(F))\) decreases for the standard order. Hence the map \(t \mapsto\mathsf{PC}^{\mathcal{C}}(X_{t}(F))\) is an erosion from the dual lattice (L,≥) to the lattice \((\varPi^{*}(E,\mathcal{C}),\le)\). We can also take an inversion N of L, that is a map N:L→L such that for t,t′∈L, t<t′ ⇒ N(t)>N(t′) and N(N(t))=t; then the map \(t \mapsto \mathsf{PC}^{\mathcal{C}}(X_{N(t)}(F))\) is an erosion \(L \to\varPi ^{*}(E,\mathcal{C})\). A component of F is any connected component of X t (F) for any t∈L; thus the set of components of F is
Note that we consider distinct components of F, in other words, when \(C \in\mathsf{PC}^{\mathcal{C}}(X_{t}(F))\) for several values t∈L, it appears only once in Comp(F). We associate to each component C its altitude h(C) [14], which is the highest level t at which it appears in \(\mathsf{PC}^{\mathcal{C}}(X_{t}(F))\), and also the least value of its points for F:
For C,C′∈Comp(F), C⊂C′ ⇒ h(C)>h(C′). For p∈E and C∈Comp(F), p∈C ⇒ F(p)≥h(C), and the least C∈Comp(F) such that p∈C is the one with h(C)=F(p). Thus F can be reconstructed from the set of pairs (C,h(C)) for C∈Comp(F):
Then the max-tree is the directed graph whose vertices are the components of F and where we draw a directed edge from C 0 to C 1 when C 0 covers C 1 for the inclusion order on Comp(F); this graph is indeed a tree whose root is E and where each directed edge goes from parent to child. The branches correspond to peaks, and the leaves to regional maxima.
Here E is a one-dimensional digital set of 15 points, and the connection \(\mathcal{C}\) corresponds to the adjacency relation between consecutive points. We take L={0,1,2,3,4,5,6}. Top left: the function F. Top right: we show in grey the sets C×{h(C)} for all C∈Comp(F); when \(C \in\mathsf{PC}^{\mathcal{C}}(X_{t}(F))\) for t<h(C), the set C×{t} is shown dashed. Bottom left: when the altitude decreases from ⊤ to ⊥, a point p enters at altitude F(p) the component C such that p∈C and h(C)=F(p); then C gets included in the component C′ of highest altitude that strictly contains C. We obtain a dendrogram drawn upside down. Bottom right: each component becomes a node of the max-tree, with parent-child directed edges corresponding to the covering relation in the dendrogram
The min-tree is the dual of the max-tree w.r.t. the order on L. For t∈L, we define the thresholding below
We consider then the partial partition \(\mathsf{PC}^{\mathcal{C}}(Y_{t}(F))\). We have Y ⊤(F)=E, so \(\mathsf{PC}^{\mathcal{C}}(Y_{\top}(F)) = \mathbf {1}_{E}\); now when t increases, Y t (F) increases, so \(\mathsf{PC}^{\mathcal{C}}(Y_{t}(F))\) increases for the standard order. Hence the map \(t \mapsto\mathsf{PC}^{\mathcal{C}}(Y_{t}(F))\) is an erosion \(L \to\varPi^{*}(E,\mathcal{C})\). We take
and for C∈Comp ∗(F) we set
For C,C′∈Comp ∗(F), C⊂C′ ⇒ h ∗(C)<h ∗(C′). For p∈E and C∈Comp ∗(F), p∈C ⇒ F(p)≤h ∗(C), and the least C∈Comp ∗(F) such that p∈C is the one with h ∗(C)=F(p). We get
We construct then the min-tree with Comp ∗(F) as set of nodes, and directed edges corresponding to the covering relation for the inclusion order on Comp ∗(F). Here the branches correspond to troughs, and the leaves to regional minima.
We can then process a function F by acting on the hierarchy \(\mathsf{PC}^{\mathcal{C}}(X_{t}(F))\) or \(\mathsf{PC}^{\mathcal{C}}(Y_{t}(F))\) (t∈L), for example using a flat operator, i.e., an order-preserving operator on functions that works by applying a set operator to the thresholdings. For instance, an anti-extensive connected flat operator ψ on functions satisfies \(\mathsf{PC}^{\mathcal{C}}(X_{t}(\psi(F))) \subseteq \mathsf{PC}^{\mathcal{C}}(X_{t}(F))\) for all t∈L; in terms of the max-tree, this means that some branches are pruned: some nodes are removed, and then all their descendants are removed too. Dually an extensive one satisfies \(\mathsf{PC}^{\mathcal{C}}(Y_{t}(\psi(F))) \subseteq\mathsf {PC}^{\mathcal{C}}(Y_{t}(F))\); here the min-tree will be pruned.
For homotopic reduction, given the foreground and background connections \(\mathcal{F}\) and \(\mathcal{B}\), the original function F 0 and the reduced one F 1 satisfy the following analogue of (22):
Here the max- and min-tree remain unchanged, except that a node having a unique child node can be removed; if the removed node is not the root, its parent node becomes the new parent of the child node.
In a topological watershed construction, an initial divide function D 0 is reduced to a smaller one D 1 satisfying, cf. (23),
NB. Anyway, \(\mathsf{PC}^{\mathcal{F}}(X_{t}(D_{1})) \le\mathsf {PC}^{\mathcal{F}}(X_{t}(D_{0}))\).
Note that a union of several components of a function is not connected, except if one of these components contains all others (i.e., it is their common ancestor in the tree), so the union reduces to that component. Indeed, let \(\mathcal{X}\subseteq\mathsf {Comp}(F)\); set \(g = \min\{ h(C) \mid C \in\mathcal{X}\}\) and let \(\widehat{C} \in \mathcal{X}\) such that \(h(\widehat{C}) = g\); in other words \(\widehat{C}\) is the component from \(\mathcal{X}\) with least altitude. Then for all \(C \in\mathcal{X}\), h(C)≥g, so C⊆X g (F); thus \(\bigcup\mathcal{X}\subseteq X_{g}(F)\). Now \(\widehat{C}\) is a connected component of X g (F), which means that it is a maximal connected subset of X g (F). Since \(\widehat{C} \subseteq \bigcup\mathcal{X}\subseteq X_{g}(F)\), this means that if \(\bigcup \mathcal{X}\) is connected, then we must have \(\bigcup\mathcal{X}= \widehat{C}\), in other words \(C \subseteq\widehat{C}\) for all \(C \in\mathcal{X}\). A dual argument holds for \(\mathcal{X}\subseteq\mathsf{Comp}^{*}(F)\).
It follows that the merging order cannot be used in the framework of the component tree. However the merging-inflating order can lead to image simplifications where the separation between clustered peaks (or troughs) is filled, so that they become merged. For example a flat operator ψ such that  for all t∈L will inflate and merge peaks. In terms of the max-tree, this means that going from the root to the leaves, at several places two child nodes of the same parent node can be merged, hence whole branches of the tree can be merged.
for all t∈L will inflate and merge peaks. In terms of the max-tree, this means that going from the root to the leaves, at several places two child nodes of the same parent node can be merged, hence whole branches of the tree can be merged.
Of course, the operator need not be flat, we can work directly on the component tree, by pruning or merging branches. This allows to change the altitude of components, but the order between the altitude of the parent and child nodes must be preserved, in other words the contrast between two neighbouring flat zones may increase or decrease, but not change sign. This allows to impose on the operator some topological properties in terms of peaks and troughs, as we did in (40), (41).
5 Discussion, Conclusion and Perspectives
The literature on partitions and partial partitions has considered only one order, the refinement order on partitions, and its extension to partial partitions that we call the standard order. The situation evolved when Serra defined the building order [33, 34] for partitions and partial partitions. Following his work, we have introduced 5 new order relations on partial partitions: the merging, inclusion, inflating, merging-inflating and inclusion-inflating orders. They are all included in the standard order. Table 1 summarizes the notation and definition of each of them.
The identity (equality relation), the standard order and the 5 new orders constitute a lattice whose Hasse diagram is illustrated in Fig. 9. It is generated by the inclusion, inflating and merging orders, which correspond to basic operations on the blocks of a partial partition: creating a new block, inflating an existing block, and merging several blocks. The other orders combine together several basic operations.
If one restricts oneself to partitions of a given set (or partial partitions with a fixed support), then the operations of creating or inflating a block are no more available, and there remain only the identity and refinement orders. More precisely: (a) the standard, merging and merging-inflating orders reduce to the refinement order; (b) the inclusion, inflating and inclusion-inflating orders reduce to the identity.
The greater number of order relations for partial partitions, in comparison with partitions, indicates the greater flexibility in the processing of partial partitions. We already argued in the Introduction that partial partitions are necessary for the modeling of various operations involved in the construction of image segmentation partitions or in connected filtering.
We have given for each order the covering relation. All these orders are graded and have a height function, see Table 2. This height function is a measure of the complexity of a partial partition from the point of view of its construction by an iteration of elementary operations; this complexity does not depend on the order of these elementary operations.
We have investigated hierarchies of partial partitions with connected blocks, the edge elements belong to 4 ordered types, cf. (39), and as the level increases, they change from one type to a higher type; the saliency of an edge is the interval of levels where it belongs to the two “visible” types (outer and separating). In the growing of partial partitions, each elementary operation leads to some specific changes of edge type, see Table 3; by extension, each order restricts the growth to a set of possible changes of edge type, see Table 4. For a hierarchy of partitions, the only change of type is from separating to inner, and the saliency of the edge indicates the level where this happens.
Hierarchies of partial partitions intervene in component trees, for which our orders can be used to describe operators with topological properties that translate into specific operations on the tree.
Our theory is relevant to image segmentation for three reasons. First, the basic operations involved in our orders (merging two blocks, creating a new block or inflating an existing block) are used in various segmentation algorithms. Second, we have taken into account the possible requirement that the segmentation classes should be connected according to some partial connection. Third, we were able to characterize hierarchies.
This paper is a first step in the study of orders on partial partitions. Further topics will be discussed in future papers. First, other orders can be defined on Π ∗(E). They can be built from previous ones by composing an order with the inverse of another, or by intersecting an order with a quasi-order. Let us briefly describe six new orders that will be studied in detail; we hinted at some of them in the last paragraph of [26]. Three orders can be obtained by replacing the merging of block by apportioning, cf. the Introduction:
-
1.
The apportioning order:
$$\pi_1 \Subset\pi_2 \mbox{~and~} \mathsf{supp}(\pi_1) = \mathsf {supp}(\pi_2) . $$It contains the merging order.
-
2.
The apportioning-inflating order:
$$\pi_1 \Subset\pi_2\quad \mbox{and}\quad \mathsf{supp}(\pi_1) \subseteq \mathsf{supp}(\pi_2) . $$It contains the merging-inflating and apportioning orders and is generated by composing apportioning and inflating in any order.
-
3.
The extended order:
$$\pi_1 \Subset\pi_2 \cap\mathcal{P}\bigl(\mathsf{supp}(\pi_1)\bigr)\quad \mbox {and}\quad \mathsf{supp} (\pi_1) \subseteq\mathsf{supp}(\pi_2) . $$It contains the standard and apportioning orders and is generated by composing inclusion followed by apportioning.
There is a strong analogy between these three orders and the merging, merging-inflating and standard orders that they extend: everything that we said in Theorems 7, 12, 11 and 2 can be transposed to these three new orders by just replacing merging with apportioning, and the m-covering \(\buildrel m \over\prec\) with a new a-covering relation \(\buildrel a \over\prec\) associated to apportioning.
The apportioning order can be used to eliminate “small parasitic” segmentation classes, as explained in the Introduction. The apportioning-inflating order can be used when, on top of “parasitic” classes, significant regions are separated by thick background edges that need to be thinned.
We mentioned that the only operations that do not create “visible” edges are merging blocks (in the order ⊑) or removing blocks (in the order ⊇). Removing a block can be seen as merging it with the background, and the latter can be considered as a special block of a partition if we distinguish it with a special marker point:
-
4.
Let ℘∉E and E ∗=E∪{℘}. Then the map
$$\varPi^*(E) \to\varPi\bigl(E^*\bigr): \pi\mapsto\pi\cup\bigl\{ E^* \setminus \mathsf{supp}(\pi) \bigr\} $$is a bijection. Its inverse (removing from a partition of E ∗ the block containing ℘) isomorphically transforms the refinement order on Π(E ∗) into the regional order on Π ∗(E), relating π 1,π 2∈Π ∗(E) iff every block of π 2 is a union of some blocks of π 1, in other words, π 2 is obtained by merging some blocks of π 1 and removing some other blocks in it. This order is generated by composing in any order inverse inclusion ⊇ and merging ⊑, its least and greatest elements are respectively 1 E and 0 E , and its covering relation is \(\buildrel m \over\prec\cup\buildrel c \over\succ\). When E is finite, the height of any π∈Π ∗(E) is |E|−h c (π).
Comparing the apportioning and apportioning-inflating orders, we can invert the inclusion of supports:
-
5.
The partial apportioning order:
$$\pi_1 \Subset\pi_2 \quad \mbox{and}\quad \mathsf{supp}(\pi_1) \supseteq \mathsf{supp}(\pi_2) ; $$some blocks are removed, and part of their contents can be erased before they are apportioned to other blocks. It contains the inverse inclusion ⊇, apportioning and regional orders.
Let us finally mention an order that is defined not in terms of block inclusion, but of block overlap:
-
6.
The linking order: supp(π 1)⊇supp(π 2) and every block of π 1 overlaps at most one block of π 2. It contains the merging ⊑, inverse inflating ⊵, inverse inclusion ⊇ and regional orders; for nonvoid partial partitions, it is generated by composing merging ⊑ followed by inverse inflating ⊵.
We have seen that the regional order is generated by composing merging ⊑ and inverse inclusion ⊇ in any order, while the linking order is generated by composing merging ⊑ followed by inverse inflating ⊵. Now the building order ⋐ is generated by inverse inclusion ⊇ followed by inflating ⊴ (these two operations were indeed used in Serra’s method for eliminating “parasitic” segmentation classes, cf. the Introduction). Thus combining one of the three basic orders with the inverse of another gives an order.
The above six new orders are graded. On the other hand the building order is not graded, and this is another reason for not considering it as “meaningful”.
A second topic to be investigated is the one introduced in the second part of [26] (Sects. 3, 4 and 5 there). We explained in the Introduction that the segmentation of a function F is considered to be a maximal element, for the refinement ordering, of the family \(\varPi(E,\mathcal{C}^{F})\) of all partitions whose blocks belong to \(\mathcal{C}^{F}\), the set all elements of the connection \(\mathcal{C}\) on which F is homogeneous according to the segmentation criterion. In the case of a partial connection \(\mathcal{C}\), the segmentation will be a maximal element of \(\varPi^{*}(E,\mathcal{C}^{F})\). We can analyse this maximality from the point of view of other orders, in particular in the case of compound segmentation using two successive criteria. Also, for a fixed function F, the segmentation induces a set splitting operator \(\sigma_{F}: X \mapsto\sigma_{F}(X) \in\varPi^{*}(X,\mathcal{C})\), which induces a block splitting operator β(σ F ) on Π ∗(E) that applies σ F to each block of a partial partition [24, 25]; the maximality of σ F (X) in \(\varPi^{*}(X,\mathcal{C})\) or \(\varPi(X,\mathcal{C})\) should be related to the properties of the operator β.
The selection of a maximal partition (relatively to some order) can be done by maximizing what we call in [26] a valuation; it is a strictly isotone map f:Π ∗(E)→R +. Indeed, a partial partition with greatest valuation will be maximal. Now, assuming that all intervals have finite height, the covering relation is useful for verifying that f is a valuation: we have only to check that whenever π 2 covers π 1, we get f(π 2)>f(π 1). The valuation can take into account some numerical characteristics, such as the number of blocks, their sizes, etc. For example the height is a valuation. We saw at the end of Sect. 3.2 that for the 3 compound orders, the covering relation is compound, and all covering chains between two comparable partial partitions comprise a constant number of each type of elementary covering (\(\buildrel m \over\prec\), \(\buildrel s \over \prec\) or \(\buildrel i \over\prec\)). Thus we can give to each elementary covering a different weight; this amounts to taking other combinations of h c , h m and h s . Valuations based on such parameters measure the fact that the partial partition has big blocks, a small number of blocks, and a big support; this can indeed be a useful criterion for selecting a partial partition as the segmentation. This idea is related to the one first introduced by Guigues [7], then expounded by Serra [10, 35, 36], where instead of a valuation (based on block numbers and sizes), one considers an energy computed from the variation of grey-levels inside blocks and across their borders; also Serra aimed at minimizing the energy, while we maximized the valuation. Although he gave methods for iteratively selecting a partition of minimum energy while climbing up a hierarchy, this energy is not in itself linked to an order relation, as is the valuation.
Finally, there is some mathematical structure underlying the fact that the six orders studied in this paper satisfy the Jordan-Dedekind chain condition, and that the three compound orders (standard, merging-inflating and inclusion-inflating) satisfy a stronger condition similar to the original Jordan-Hölder theorem in group theory, namely that all covering chains between two comparable partial partitions comprise a constant number of each type of elementary covering (\(\buildrel m \over\prec\), \(\buildrel s \over\prec\) or \(\buildrel i \over \prec\)). It is related to the lattice-theoretical property of upper semi-modularity [3, 6] and its translation to posets as Ore’s quadrilateral condition [18]. This will be the topic of a purely mathematical paper.
References
Adams, R., Bischof, L.: Seeded region growing. IEEE Trans. Pattern Anal. Mach. Intell. 16(6), 641–647 (1994)
Benzécri, J.P.: L’Analyse de Données, I: la Taxinomie. Dunod, Paris (1973)
Birkhoff, G.: Lattice Theory, 8th printing, 3rd edn. American Mathematical Society Colloquium Publications, vol. 25. American Mathematical Society, Providence (1995)
Blyth, T.: Lattices and Ordered Algebraic Structures. Springer, London (2005)
Cousty, J., Bertrand, G., Couprie, M., Najman, L.: Collapses and watersheds in pseudomanifolds of arbitrary dimension. J. Math. Imaging Vis. (2013, to appear)
Grätzer, G.: General Lattice Theory, 2nd edn. Birkhäuser, Basel (2003)
Guigues, L., Cocquerez, J.P., Le Men, H.: Scale-sets image analysis. Int. J. Comput. Vis. 68(3), 289–317 (2006)
Janowitz, M., Schweizer, B.: Ordinal and percentile clustering. Math. Soc. Sci. 18, 135–186 (1989)
Johnson, S.: Hierarchical clustering schemes. Psychometrika 32(3), 241–254 (1967)
Kiran, B.R., Serra, J.: Ground truth energies for hierarchies of segmentations. In: Luengo Hendriks, C.L., Borgefors, G., Strand, R. (eds.) Mathematical Morphology and Its Applications to Signal and Image Processing. Lecture Notes in Computer Science, vol. 7883, pp. 123–134. Springer, Berlin (2013). doi:10.1007/978-3-642-38294-9_11
Krasner, M.: Nombres semi-réels et espaces ultramétriques. C. R. Hebd. Séances Acad. Sci. 219, 433–435 (1944)
Meyer, F., Najman, L.: Segmentation, minimum spanning tree and hierarchies. In: Najman, L., Talbot, H. (eds.) Mathematical Morphology: From Theory to Applications, pp. 229–261. ISTE/Wiley, New York (2010). Chap. 9
Najman, L.: On the equivalence between hierarchical segmentations and ultrametric watersheds. J. Math. Imaging Vis. 40(3), 231–247 (2011). doi:10.1007/s10851-011-0259-1
Najman, L., Couprie, M.: Building the component tree in quasi-linear time. IEEE Trans. Image Process. 15(11), 3531–3539 (2006)
Najman, L., Schmitt, M.: Watershed of a continuous function. Signal Process. 38(1), 99–112 (1994)
Najman, L., Schmitt, M.: Geodesic saliency of watershed contours and hierarchical segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 18(12), 1163–1173 (1996)
Ore, O.: Theory of equivalence relations. Duke Math. J. 9, 573–627 (1942)
Ore, O.: Chains in partially ordered sets. Bull. Am. Math. Soc. 49, 558–566 (1943)
Pavlidis, T.: Structural Pattern Recognition. Springer, Berlin (1980)
Ronse, C.: A topological characterization of thinning. Theor. Comput. Sci. 43, 31–41 (1986)
Ronse, C.: Set-theoretical algebraic approaches to connectivity in continuous or digital spaces. J. Math. Imaging Vis. 8(1), 41–58 (1998)
Ronse, C.: Partial partitions, partial connections and connective segmentation. J. Math. Imaging Vis. 32(2), 97–125 (2008). doi:10.1007/s10851-008-0090-5
Ronse, C.: Adjunctions on the lattices of partitions and of partial partitions. Appl. Algebra Eng. Commun. Comput. 21(5), 343–396 (2010). doi:10.1007/s00200-010-0129-x
Ronse, C.: Idempotent block splitting on partial partitions, I: isotone operators. Order 28(2), 273–306 (2011). doi:10.1007/s11083-010-9171-3
Ronse, C.: Idempotent block splitting on partial partitions, II: non-isotone operators. Order 28(2), 307–339 (2011). doi:10.1007/s11083-010-9190-0
Ronse, C.: Orders on partial partitions and maximal partitioning of sets. In: Soille, P., Ouzounis, G., Pesaresi, M. (eds.) Proceedings of ISMM 2011, the 10th International Symposium on Mathematical Morphology. Lecture Notes in Computer Science, vol. 6671, pp. 49–60. Springer, Berlin (2011)
Ronse, C., Serra, J.: Algebraic foundations of morphology. In: Najman, L., Talbot, H. (eds.) Mathematical Morphology: From Theory to Applications, pp. 35–80. ISTE/Wiley, New York (2010). Chap. 2
Salembier, P., Oliveras, A., Garrido, L.: Anti-extensive connected operators for image and sequence processing. IEEE Trans. Image Process. 7(4), 555–570 (1998)
Salembier, P., Wilkinson, M.H.F.: Connected operators: a review of region-based morphological image processing techniques. IEEE Signal Process. Mag. 26(6), 136–157 (2009)
Serra, J.: Mathematical morphology for Boolean lattices. In: Serra, J. (ed.) Image Analysis and Mathematical Morphology, II: Theoretical Advances, pp. 37–58. Academic Press, London (1988). Chap. 2
Serra, J.: Morphological segmentations of colour images. In: Ronse, C., Najman, L., Decencière, E. (eds.) Mathematical Morphology: 40 Years on. Computational Imaging and Vision, vol. 30, pp. 151–176. Springer, Dordrecht (2005)
Serra, J.: A lattice approach to image segmentation. J. Math. Imaging Vis. 24(1), 83–130 (2006)
Serra, J.: Ordre de la construction et segmentations hiérarchiques. Tech. rep., ESIEE/A2SI/IGM (2010)
Serra, J.: Grain buiding ordering. In: Soille, P., Ouzounis, G., Pesaresi, M. (eds.) Proceedings of ISMM 2011, the 10th International Symposium on Mathematical Morphology. Lecture Notes in Computer Science, vol. 6671, pp. 37–48. Springer, Berlin (2011)
Serra, J.: Hierarchies and optima. In: Debled-Rennesson, I., Domenjoud, E., Kerautret, B., Even, P. (eds.) DGCI 2011, 16th International Conference on Discrete Geometry for Computer Imagery. Lecture Notes in Computer Science, vol. 6607, pp. 35–46. Springer, Berlin (2011)
Serra, J., Kiran, B.R.: Optima on hierarchies of partitions. In: Luengo Hendriks, C.L., Borgefors, G., Strand, R. (eds.) Mathematical Morphology and Its Applications to Signal and Image Processing. Lecture Notes in Computer Science, vol. 7883, pp. 147–158. Springer, Berlin (2013). doi:10.1007/978-3-642-38294-9_13
Soille, P.: Constrained connectivity for hierarchical image partitioning and simplification. IEEE Trans. Pattern Anal. Mach. Intell. 30(7), 1132–1145 (2008)
Author information
Authors and Affiliations
Corresponding author
Additional information
This work received funding from the Agence Nationale de la Recherche, contract ANR-2010-BLAN-0205-01.
Appendix: Local Knowledge: Truncation and Restriction
Appendix: Local Knowledge: Truncation and Restriction
We introduced numerous binary relations on Π ∗(E), most of them being partial order relations, cf. Table 1. We will now consider how such relations are preserved by the following two operations on partial partitions, for any \(A \in\mathcal{P}(E)\): truncation by A:
and restriction to A:
These operations are relevant to the problem of local knowledge, what Serra [32] calls class permanency: given a partial partition π and a restricted window A, viewing π through A means either truncating all blocks of π, that is, taking π∧1 A , or restricting π to blocks inside A, that is, taking \(\pi\cap\mathcal{P}(A)\); then it becomes interesting to know if these two operations of truncation and restriction preserve a given order on partial partitions.
We first consider compatibility with truncation. The following relations are preserved by truncation by A:
-
The support inclusion, support containment and support equality relations, since supp(π i ∧1 A )=supp(π i )∩A.
-
The standard order: standard lattice theory gives π 1≤π 2 ⇒ π 1∧1 A ≤π 2∧1 A .
-
The merging order, since it is the intersection of the standard order and the support equality relation.
-
The inclusion order: for π 1⊆π 2, the blocks of π 1∧1 A are all non-void B∩A for B∈π 1, so they belong to π 2∧1 A .
-
The inclusion-inflating order, that is, the intersection of the standard order and of the singularity relation. Indeed, let π 1≤π 2 and π 1⇚π 2. Then π 1∧1 A ≤π 2∧1 A . The blocks of π 1∧1 A (resp., π 2∧1 A ) are the non-void B∩A for B∈π 1 (resp., for B∈π 2). If C∩A (C∈π 2) contains B 1∩A and B 2∩A (B 1,B 2∈π 1), then B 1 and B 2 intersect C, and as π 1≤π 2, B 1,B 2⊆C, but as π 1⇚π 2, we deduce that B 1=B 2, so B 1∩A=B 2∩A. Thus π 1∧1 A ⇚π 2∧1 A .
The following relations are not preserved by truncation by A:
-
The singularity relation: take π 1={B,C} and π 2={A}, where B≬A≬C but B,C⊈A, then π 1⇚π 2 but \(\pi_{1} \wedge\mathbf{1}_{A} = \{ A \cap B, A \cap C \} \not\Lleftarrow\pi_{2} = \pi_{2} \wedge\mathbf{1}_{A}\).
-
The building order: take B⊃A⊃∅, π 1=1 B∖A and π 2=1 B , then π 1⋐π 2 but
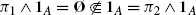 .
. -
The inflating order: take the counterexample given for the building order.
-
The merging-inflating order: take the same counterexample.
We now consider compatibility with restriction. The following relations are preserved by restriction to A:
-
The singularity relation: this is a special case of (12).
-
The building order, see (7).
-
The inclusion order: standard set theory gives \(\pi_{1} \subseteq \pi_{2} \ \Rightarrow\ \pi_{1} \cap\mathcal{P}(A) \subseteq\pi_{2} \cap\mathcal{P}(A)\).
The following relations are not preserved by restriction to A:
-
The support inclusion, support containment and support equality relations; indeed, the support does not tell anything about the existence of blocks included in A.
-
The standard order.
-
The merging order.
-
The inflating order.
-
The merging-inflating order.
-
The inclusion-inflating order.
In fact, any order included in the standard order, that is compatible with restriction, must be included in the inclusion order. Indeed, if π 1≤π 2 but π 1⊈π 2, then there is B∈π 1 and C∈π 2 such that B⊂C, so \(B \in\pi_{1} \cap\mathcal{P}(B)\) but \(\pi_{2} \cap \mathcal{P}(B) \subseteq\pi_{2} \setminus\{C\}\), and B is not included in a block of π 2∖{C}, thus \(\pi_{1} \cap\mathcal{P}(B) \not\le \pi_{2} \cap\mathcal{P}(B)\).
Rights and permissions
About this article
Cite this article
Ronse, C. Ordering Partial Partitions for Image Segmentation and Filtering: Merging, Creating and Inflating Blocks. J Math Imaging Vis 49, 202–233 (2014). https://doi.org/10.1007/s10851-013-0455-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-013-0455-2


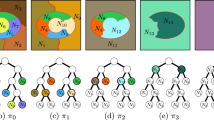









 (top) we get π
1⊑π
3⊴π
2 (middle) and π
1⊴π
4⊑π
2 (bottom)
(top) we get π
1⊑π
3⊴π
2 (middle) and π
1⊴π
4⊑π
2 (bottom)
 we get π
1⊆π
1∪π
a
⊴π
2 and π
1⊴π
4⊆π
2
we get π
1⊆π
1∪π
a
⊴π
2 and π
1⊴π
4⊆π
2

 : given a crossing A of π, in every covering chain between 0
A
and π, there are |A|−h
c
(π) m-coverings
: given a crossing A of π, in every covering chain between 0
A
and π, there are |A|−h
c
(π) m-coverings  : in every covering chain between Ø and π, there are h
c
(π) s-coverings
: in every covering chain between Ø and π, there are h
c
(π) s-coverings 




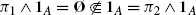 .
.