Handwritten Data Clustering Using Agents Competition in Networks

Abstract

In this paper, we study a new type of competitive learning scheme realized on large-scale networks. The model consists of several agents walking within the network and competing with each other to occupy as many nodes as possible, while attempting to reject intruder agents. In the end of the process, each agent dominates a community (a strongly connected subnetwork). Here, the model is described by a stochastic dynamical system. In this paper, a mathematical analysis for uncovering the system’s properties is presented. In addition, the model is applied to solve handwritten digits and letters clustering problems. An interesting feature is that the model is able to group the same digits or letters even with considerable distortions into the same cluster. Computer simulations reveal that the proposed technique presents high precision of cluster detections, as well as low computational complexity.

1 Introduction

Data clustering is an unsupervised learning task that aims at discovering a natural grouping of a set of patterns, points, or objects by means of a similarity measure [11, 16]. Each cluster is a collection of data items which are similar between themselves and are dissimilar to the objects belonging to other clusters. Data clustering is vital in several exploratory pattern-analysis, decision-making, and machine-learning situations. Some of them include data mining, document retrieval, image segmentation, bioinformatics, and pattern classification [5, 8, 15–17]. Unfortunately, in the majority of such tasks, little prior information is available about the data. In this way, advances in the methodology to automatically understand, process, and summarize the data are required. Nowadays, this becomes even more critical by virtue of the exponential increase in both the volume and the variety of data [16]. In this scenario, the decision-maker must perform as few assumptions about the data as possible. It is under these practical restrictions that the clustering procedure is especially appropriate for the exploration of inter-relationships among the data points to make an assessment (perhaps preliminary) of their structure [16, 17]. Data clustering algorithms are generally divided in two types: hierarchical or partitional [2, 8, 16]. The former finds successive clusters using previously established clusters, whereas the latter determines all clusters at once. Hierarchical algorithms can be agglomerative (“bottom-up”) or divisive (“top-down”). Agglomerative algorithms begin with each element as a separate cluster and merge them into successively larger clusters. Divisive algorithms begin with the whole set and proceed to divide it into successively smaller clusters. Two-way clustering, co-clustering or bi-clustering are the names for clusterings where not only the objects are clustered but also the features of the objects, i.e., if the data is represented in a data matrix, the row and columns are clustered simultaneously [11].

One of the recent approaches of data clustering is based on graphs (networks). In this context, a network is firstly constructed from the original data set; then, the network is partitioned into modular subnetworks, also called communities, producing data clusters. The notion of community in networks is straightforward: each community is defined as a sub-graph whose nodes are densely connected within itself, but sparsely connected with the rest of the network. Community detection in networks has turned out to be an important topic in graph mining and data mining [6, 9, 25]. In graph theory, community detection corresponds to graph partition, which has been shown to be a NP-complete problem [9]. For this reason, a lot of efforts has been spent to develop efficient but suboptimal solutions, such as the spectral methods [26], the technique based on the “betweenness” measure [25], modularity optimization [24], community detection based on the Potts model [30], synchronization [1], information theory [10], and random walks [36]. For a recent review of this topic, see [9]. The main motivation of graph theory research is the ability to describe the topological structure of the original system. In the machine learning domain, it has been shown that the topological structure is quite useful to detect clusters of arbitrary forms in data clustering [9, 19], in contrast to the widely used data clustering technique—K-Means, where only spherical-shaped clusters can be identified.

Handwriting recognition is the ability of a computer to receive and interpret intelligible handwritten input from sources such as paper documents, photographs, touch-screens, data sets, and other devices [20, 34]. Ideally, the handwriting recognition systems should be able to read and understand any handwriting [3]. Handwriting recognition has been one of the most fascinating and challenging research areas in the field of image processing and pattern recognition in the recent years [27]. It contributes immensely to the advancement of an automation process and can improve the interface between man and machine in numerous applications [3, 34]. In general, handwritten recognition is classified into off-line or on-line. In the first case, the writing is obtained by an electronic device and the captured writing is completely available as an image to the handwritten recognition method. In the second case, the coordinates of successive points are available by means of a function dependent on time, i.e., the complete image is not given [27, 34]. In summary, several research works have been proposed [13, 23, 27] in an attempt to reduce the processing time of both off-line and on-line methods, while, at the same time, providing higher recognition accuracy. Due to the high complexity that this topic offers, it still has a wide range of problems to be addressed, such as the efficient recognition of images that are distorted or suffered a non-linear transformation [3, 8, 34]. Pattern clustering is a fundamental step in a pattern recognition system. The recognition performance is strongly dependent on the quality of pattern grouping and labeling.

In this paper, we study handwritten data clustering by using a new type of competitive learning mechanism [28, 32, 33]. Consider a large-scale graph (network), where several agents walk in the network and compete with each other to occupy as many nodes as possible, while attempting to reject intruder agents. Each agent can perform a random walk by choosing any neighbor to visit, a preferential walk by choosing the node with the highest domination to visit, or a combination of both. Straightforward applications are community detection and data clustering. The competitive walking process reaches a dynamic equilibrium when each community or data cluster is dominated by a single agent.

The agent competition model was originally proposed in [28, 32, 33], where only a procedure of agent competition is introduced and no mathematical analysis is presented. In the present work, we study the agent competition model represented by a nonlinear stochastic dynamical system. Moreover, a mathematical analysis for uncovering the properties of the dynamical system is provided. In particular, we show that the competitive dynamical system reduces to multiple independent random walks when the parameters, which characterize the competition and reanimation features, are turned off. Since the models of several interactive walking processes correspond to many natural and artificial systems, and due to the lack of theory for such models, our approach is an important step to understand such systems. It is worth mentioning that the underlying network is constructed directly from the input data set; therefore, the correspondence between the input data and the processing result (the final network) is maintained. Besides this, we apply the competitive learning model to solve handwritten data clustering problems. An interesting feature is that the model is able to group the same digits or letters even with considerable distortions into the same cluster.

The remainder of the paper is organized as follows. The competitive model is reviewed in Sect. 2. In Sect. 3, a mathematical analysis is provided. Section 4 presents an application of the competitive model in handwritten data clustering. Finally, Sect. 5 concludes the paper.

2 Model Description

In this section, we review the competitive learning technique.

2.1 The Competitive Transition Matrix

Consider a graph $\mathcal{G} = \langle\mathcal{V},\mathcal{E} \rangle$, where $\mathcal{V} = \{v_{1},\ldots,v_{V}\}$ is the set of vertices (or nodes) and $\mathcal{E} = \{e_{1},\ldots ,e_{L}\} \subset\mathcal{V} \times\mathcal{V}$ is the set of links (or edges). In the proposed competitive learning model, a set of agents $\mathcal{K} = \{1,\ldots,K\}$ is inserted into the vertices of the network in a random manner. Each agent can be conceptualized as a flag carrier with its main objective being to conquer new vertices, while defending its current dominated vertices. In this case, a competition process will naturally take place amongst the agents. When an agent visits an arbitrary vertex, it strengthens its own domination level on that vertex and, simultaneously, weakens the domination levels of all other rival agents on the same vertex. At the end, each agent dominates a community.

In this model, each agent $k \in\mathcal{K}$ can perform two distinct types of movements: (i) a random movement term, modeled by the matrix $\mathbb{P}^{(k)}_{\mathrm {rand}}$, which permits the agent to venture throughout the network, without accounting for the defense of the previously dominated vertices; and (ii) a preferential movement term, modeled by the matrix $\mathbb{P}^{(k)}_{\mathrm{pref}}$, which is responsible for inducing the agent to reinforce the vertices that are owned by itself, i.e., the agent prefers visiting its dominated vertices, instead of a randomly selected one. In order to model such dynamics, consider the stochastic vector p(t)=[p ⁽¹⁾(t),p ⁽²⁾(t),…,p ^(K)(t)], which denotes the localization of the set of K agents presented to the network. Its kth-entry, p ^(k)(t), indicates the location of agent k in the network at time t, i.e., $p^{(k)}(t) \in\mathcal{V}, \forall k \in \mathcal{K}$. It is desirable to find a transition matrix that governs the probability distribution of the movement of the agents to the immediate future state: p(t+1)=[p ⁽¹⁾(t+1),p ⁽²⁾(t+1),…,p ^(K)(t+1)].

With the intent of keeping track of the current states of all agents, we introduce the following stochastic vector: S(t)=[S ⁽¹⁾(t),…,S ^(K)(t)], where the kth-entry, S ^(k)(t)∈{0,1}, indicates whether the agent k is active (S ^(k)(t)=0) or exhausted (S ^(k)(t)=1) at time t. When it is active, the movement policy consists of a combined behavior of randomness and preferential movements. When it is exhausted, the agent switches its movement policy to a new transition matrix, here referred to as $\mathbb{P}^{(k)}_{\mathrm{rean}}(t)$. This matrix is responsible for taking the agent back to its dominated territory, in order to reanimate the corresponding agent by recharging its energy. We call this the reanimation procedure. After the energy has been properly recharged, the agent can again perform the combined random-preferential movement in the network. With all this information in mind, we are able to define the transition matrix associated to the agent k as:

(1)

where λ∈[0,1] indicates the desired fraction of preferential movement that all agents in the network will perform. Specifically, $\mathbb{P}^{(k)}_{\mathrm {transition}}(i,j,t)$ indicates the probability that agent k performs a transition from vertex i to j at time t. We now define each matrix that appears in (1) in a detailed manner.

The random movement matrix only depends on the adjacency matrix of the graph. In this way, each entry $(i,j) \in\mathcal{V} \times\mathcal {V}$ of the matrix $\mathbb{P}^{(k)}_{\mathrm{rand}}$ is given by:

(2)

where a _i,j denotes the (i,j)th-entry of the adjacency matrix A of the graph. Note that matrix $\mathbb{P}^{(k)}_{\mathrm {rand}}$ is time invariant and it is the same for every agent in the network; therefore, we drop the superscript k. In short, the probability of an adjacent neighbor j to be visited from vertex i is proportional to the edge weight linking these two vertices.

In order to assist in the derivation of the matrix associated to the preferential movement term, $\mathbb{P}^{(k)}_{\mathrm{pref}}(t)$, for a given agent $k \in\mathcal {K}$, we introduce the following stochastic vector:

(3)

where dim(N _i (t))=K×1, T denotes the transpose operator, and N _i (t) stands for the number of visits received by vertex i up to time t by all agents scattered throughout the network. Then, the matrix that contains the number of visits made by every agent in the network to all the vertices is defined as:

(4)

where dim(N(t))=V×K. Let us also formally define the domination level vector of vertex i, $\bar{N}_{i}(t)$, according to the following stochastic vector:

(5)

where $\mathrm{\mathrm{dim}}(\bar{N}_{i}(t)) = K \times1$ and $\bar{N}_{i}(t)$ denotes the relative frequency of visits of all agents in the network to vertex i at time t. Similarly to the previous case, this notation is extended to all vertices in the network by defining the domination level matrix that sustains all the domination levels imposed by every agent in the network to all the vertices as:

(6)

where $\mathrm{dim}(\bar{N}(t)) = V \times K$. Mathematically, each entry of $\bar{N}_{i}^{(k)}(t)$ is defined as:

(7)

In view of this, we can define $\mathbb{P}_{\mathrm {pref}}^{(k)}(i,j,t)$, which is the probability of a single agent k to perform a transition from vertex i to j at time t, using solely the preferential movement term, as follows:

(8)

From (8), it can be observed that each agent has a different transition matrix associated to its preferential movement and that, unlike the matrix related to the random movement, it is time-variant with dependence on the domination levels of all the vertices ($\bar{N}(t)$) in the network at time t. It is worth mentioning that the approach taken here to characterize the preferential movement of the agents is defined as the visiting frequency of each agent to a specific vertex, meaning as more visits are performed by a specific agent to an arbitrary vertex, there will be a higher chance for the same agent to repeatedly visit the same vertex. The consequence of this behavior is two-fold: (i) the visiting agent strengthens its the domination level on a vertex and (ii) weakens the domination levels of all other agents on the same vertex. This is made possible because of the normalization process that is conservative.

Now we define each entry of $\mathbb{P}^{(k)}_{\mathrm{rean}}(t)$. Suppose that agent k is visiting vertex i when its energy is completely depleted. In this situation, the agent must regress to an arbitrary vertex j of its possession at time t, according to the following expression:

(9)

where is the indicator function that yields 1 if the argument is logically true and 0, otherwise. The operator $\mbox{arg}\max_{m\in\mathbb {K}}(\cdot)$ returns an index M, where $\bar {N}^{(M)}_{u}(t)$ is the maximal value among all $\bar{N}^{(m)}_{u}(t)$ for $m \in \mathcal{K}$. A careful analysis of the expression in (9) reveals that the probability of returning to an arbitrary vertex j that is dominated by the agent k follows a uniform distribution. In other words, (9) only results in non-zero transition probabilities for vertices j that are being dominated by agent k at time t, regardless of the existence of a connection between i and j in the adjacency matrix.

Once defined the collection of matrices associated to each agent, we couple all of them into a single representative transition matrix denominated ℙ_transition(t) which models the transition of p(t) to p(t+1). Given X(t), one can see that p ^(k)(t+1) and p ^(u)(t+1) are independent for every pair $(k,u) \in\mathcal{K} \times\mathcal{K}, k \neq u$. In this way, ℙ_transition(t) can be written as:

(10)

where ⊗ denotes the Kronecker tensor product operator. In this way, (10) completely specifies the transition distribution matrix for all the agents in the network.

Essentially, when K≥2, p(t) will be a vector and we would no longer be able to conventionally define the row p(t) of matrix ℙ_transition(t). Owing to this, we define an invertible mapping . The function f simply maps the input vector to a scalar number that reflects the natural ordering of the tuples in the input vector. For example, p(t)=[1,1,…,1,1] (all agents at vertex 1) denotes the first state; p(t)=[1,1,…,1,2] (all agents at vertex 1, except the last agent, which is at vertex 2) is the second state; and so on, up to the scalar state V ^K. Therefore, with this tool, we can fully manipulate the matrix ℙ_transition(t).

2.2 The Unsupervised Competitive Learning Model

In light of the results obtained in the previous section, the internal state of the dynamical system, X(t), is given by:

(11)

and the proposed competitive dynamical system is given by:

(12)

An important characteristic of system ϕ, which will be extensively used later, is its Markovian property (see Proposition 1). In the following, we present the meaning of the 3 expressions shown in the competitive dynamical system ϕ:

• Update Rule of the Number of Visits (1st Expression): In this update rule, for every agent $k \in\mathcal{K}$ in the model, the vertex i that is being visited by agent k has its number of visits associated to that agent, $N_{i}^{(k)}(t)$, added by 1. If agent k does not visit vertex i at time t, then its number of visits remains unaltered. This two-fold behavior is achieved by the indicator function in the right-hand side of the first expression in ϕ. Specifically, when agent k visits vertex i, the argument in the indicator function returns true, and the expression becomes $N_{i}^{(k)}(t+1) = N_{i}^{(k)}(t) + 1$. Conversely, if agent k does not visit vertex i, then the argument in the indicator function yields false and the update rule of the number of visits reduces to $N_{i}^{(k)}(t+1) = N_{i}^{(k)}(t)$.

• Update Rule of the Agent’s Energy (2nd Expression): Here, we introduce the stochastic vector: E(t)=[E ⁽¹⁾(t),…,E ^(K)(t)], where the kth-entry, E ^(k)(t)∈[ω _min,ω _max], ω _max≥ω _min, denotes the energy level of agent k at time t. In the second expression of system ϕ, $\mathrm{owner}(k,t) = (\operatorname{arg}\max_{m \in \mathcal{K}} (\bar {N}^{(m)}_{p^{(k)}(t)}(t) ) = k )$ is a logical expression that essentially yields true if the vertex that agent k visits at time t (i.e., vertex p ^(k)(t)) is being dominated by it, but yields false otherwise. In the same expression, Δ>0 symbolizes the increment or decrement of energy that each agent receives at time t. The first case represents the increment of the agent’s energy and it occurs when agent k visits a vertex p ^(k)(t) which is dominated by itself, i.e., $\operatorname{arg}{\operatorname{{\max}}}_{m \in \mathbb{K}} (\bar {N}^{(m)}_{p^{(k)}(t)}(t) ) = k$. Similarly, the second case indicates the decrement of the agent’s energy that happens when it visits a vertex dominated by rival agents. Therefore, in this model, agents will be given a penalty if they are wandering in rival territory, so as to minimize aimless navigation of the agents in the network.

• Update Rule of the Agent’s State (3rd Expression): Here, the update rule that governs S(t) is given. As we have stated, an arbitrary agent k will be transported back to its domain only if its energy drops to a threshold ω _min. With that in mind, it is natural that each entry of S ^(k)(t) must monitor the current energy value of its corresponding agent k. If this energy ever drops to the given threshold, the switch must be enabled. Analogously, if the agent still has an energy value greater than this threshold, then the switch should be disabled. This behavior is exactly expressed in the third expression of the competitive system ϕ.

Observe that p(t+1) has no closed form because it is qualified as a distribution with dependence on p(t) and N(t), therefore its acquisition is merely by random number generation. Specifically, the random numbers are generated respecting the probability distribution given in (1).

Finally, we will define the competitive system in a matrix form. This will be specially useful in the theoretical derivations that will be performed in the next section. Specifically, system ϕ can be written as:

(13)

where f _N (.), f _E (.), and f _S (.) are suitable stochastic matrix functions as defined term by term in (12).

2.3 Computational Complexity

The competitive model reviewed in Sect. 2 has been shown to run in $\mathcal{O}(KV)$ time for community detection tasks (sparse graph) and in $\mathcal{O}(V^{2})$ time for data clustering tasks (cf. [33]). It is worth noting that, based on [33, Table 1], we can visualize that the community detection technique has the lowest computational complexity order compared to all other techniques developed so far. With respect to data clustering tasks, if we look at [33, Table II], it has a reasonable complexity order (it is not the lowest one), mainly by virtue of the network formation step, which is time-demanding basically because of the distance matrix calculation method.

3 Theoretical Results

In this section, a mathematical analysis of the competitive system is supplied. Also, we show that the competitive system reviewed in the previous section reduces to multiple independent random walks when a special situation occurs.

3.1 Mathematical Analysis

As the initial step, the transition probability function of system ϕ, i.e., P(X(t+1)∣X(t)), is going to be derived. Note that the marginal probability of the system’s state P(X(t)) can be written in terms of a joint probability of each of the components of the system’s state, meaning P(X(t))=P(N(t),p(t),E(t),S(t)). Using this fact and applying the Product Rule, one has:

(14)

where:

(15)

(16)

(17)

(18)

Next, the algebraic derivation of these four quantities is given in a detailed manner.

3.1.1 Obtaining P _p(t+1)

Noting that the stochastic vector p(t+1) is directly evaluated from ℙ_transition(t) given in (10), which in turn only requires p(t) and N(t) to be constructed (X(t) is given), then the following equivalence holds:

(19)

Here, we have used ℙ_transition(N(t),p(t)) to emphasize the dependence of the transition matrix on N(t) and p(t).

3.1.2 Obtaining P _N(t+1)

In this case, the system’s state X(t) and p(t+1) are given. Observing that the determination of N(t+1) only depends on N(t) and p(t+1) (see first expression in system ϕ), it follows that P(N(t+1)) can be completely evaluated. In view of this, the following expression holds:

(20)

where Q _N (p(t+1)) is a matrix with dim(Q _N )=V×K and dependent on p(t+1), whose (i,j)th-entry is given by:

(21)

The argument in the indicator function shown in (20) is essentially the first expression of system ϕ, but with a matrix notation. In brief, (20) will result in 1 if the computation of N(t+1) is correct, given p(t+1) and N(t), i.e., it is in compliance with the dynamical system rules; and 0, otherwise.

3.1.3 Obtaining P _E(t+1)

Here, the system’s state X(t), p(t+1), and N(t+1) are given. By inspecting (7), one can see that the calculation of $\bar{N}(t)$ only depends on N(t). As a result, one can consider $\bar{N}(t)$ as given variable too. Due to this fact, together with the second expression in ϕ, one can see that E(t+1) can be completely determined since E(t), p(t+1), and $\bar {N}(t+1)$ are known quantities. On account of that, P _E(t+1) is given by:

(22)

where Q _E (p(t+1),N(t+1)) is a matrix with dim(Q _E )=1×K and dependence on N(t+1) and p(t+1). The kth-entry, $k \in\mathcal {K}$, of such matrix is calculated as:

(23)

Note that the argument of the indicator function in (23) is essentially the second expression of ϕ in a compact matrix form. Indicator functions were employed to describe the two types of behaviors that this variable can have: an increment or decrement of the agent’s energy. Suppose that agent $k \in \mathcal{K}$ is visiting a vertex that is being owned by itself, then only the first indicator function in (23) will be enabled; hence, $Q_{E}^{(k)}(p(t+1),N(t+1) ) = 1$. Similarly, if agent k is visiting a vertex that is being owned by a rival agent, then the second indicator function is enabled, yielding $Q_{E}^{(k)} (p(t+1), N(t+1) ) = -1$. This behavior together with (22) is exactly the second expression of ϕ in a compact matrix form.

3.1.4 Obtaining P _S(t+1)

Now, the system’s state X(t), E(t+1), N(t+1), and p(t+1) are given. By analyzing the third expression in ϕ, one can verify that S(t+1) can be determined once E(t+1) is known. In this way, one can surely evaluate P _S(t+1) in this scenario as follows:

(24)

where Q _S (E(t+1)) is a matrix with dim(Q _S )=1×K and dependence on E(t+1). The kth-entry, $k \in\mathcal{K}$, of such matrix is calculated as:

(25)

3.1.5 The Transition Probability Function

Substituting (19), (20), (22), and (24) into (14), the transition probability function of the competitive dynamical system is given as follows:

(26)

where Compliance(t) is a logical expression given by:

(27)

i.e., Compliance(t) encompasses all the rules that have to be satisfied in order to the indicator functions in (26) produce 1. It is worth mentioning that non-zero transition probabilities will only happen when these rules are satisfied.

3.1.6 Obtaining P(N(t))

With the transition probability function derived in the previous section, we now turn our attention to determining the marginal distribution P(N(t)) for a sufficient large t. First, the Markovian property of system ϕ is demonstrated as follows.

Proposition 1

{X(t):t≥0} is a Markovian process.

Proof

We seek to infer that system ϕ is completely characterized by only the acquaintance of the present state, i.e., it is independent of all the past states. Having that in mind, the probability expression to make a transition to a specific event X _t+1 (a set with an element representing an arbitrary next state) in time t+1, given the complete history of the state trajectory, is denoted by:

(28)

Noting that the determination of p _t+1 only depends on N(t) and p(t), then:

(29)

Therefore, in view of (29), {X(t):t≥0} is a Markovian process, since it only depends on the present state to specify the next state and, hence, the past history of the system’s trajectory is irrelevant. □

The strategy to calculate the distribution P(N(t)) is to marginalize the joint distribution of the system’s states, i.e., P(X(0),…,X(t)), with respect to N(t) (a component of X(t)). Mathematically, using Proposition 1 on this joint distribution P(X(0),…,X(t)), we get:

(30)

Using the transition function that governs system ϕ, as illustrated in (26), to each shifted term in (30), we get:

(31)

where P(X(0))=P(N(0),p(0),E(0),S(0)). Observing now that P(X(0),…,X(t))=P(N(0),p(0),E(0),S(0),…,N(t),p(t),E(t),S(t)), we marginalize this joint distribution with respect to N(t) as follows:

(32)

where ∼N(t) means that we sum over all the possible values of X(0),…,X(t), except for N(t) which is inside X(t)=[N(t) p(t) E(t) S(t)]^T. Using (31) in (32), we are able to obtain P(N(t)) as follows:

(33)

3.1.7 Obtaining $P(\bar{N}(t))$

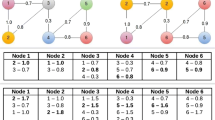
The distribution of the domination level matrix $\bar{N}(t)$ is the fundamental information needed to label the unlabeled vertices. First, one can observe that positive integer multiples of N(t) compose the same $\bar{N}(t)$. Therefore, the mapping $N(t) \rightarrow\bar{N}(t)$ is not injective; hence, not invertible. Below, an illustrative example shows this property.

Example 1

Consider a network with 3 agents and 2 vertices. At time t, suppose that the stochastic process is able to produce two distinct configurations for N(t), as follows:

(34)

Then, the setups in (34) applied to (7) make clear that both configurations yield the same $\bar{N}(t)$ given by:

(35)

In view of this, the mapping $N(t) \rightarrow\bar{N}(t)$ cannot be injective nor invertible.

Following the aforementioned strategy, $P(\bar{N}(t))$ can be calculated by summing over all multiples of uN(t), u∈{1,…,t} such that $f(uN(t))=\bar{N}(t)$, where f is the normalization function defined in (7). On account of this, we have:

(36)

As t→∞, $P(\bar{N}(t))$ provides enough information for classifying the unlabeled vertices. In this case, they are labeled accordingly to the team of agents that is imposing the highest domination level. Since the domination level is a continuous stochastic variable, the output of this model is fuzzy.

3.2 The Proposed Competitive System Generalizes Multiple Independent Random Walks

In this section, we will demonstrate the following interesting property: when λ=0 and Δ=0, the competitive mechanism among the agents and the reanimation feature are turned off, and the system reduces to multiple independent random walkers [4]. Conversely, when λ>0, the competitive mechanism among the agents is enabled and the combination of random-preferential interacting walks occurs. In this case, the reanimation feature is presented depending on the choice of Δ.

Proposition 2

If λ=0 and Δ=0, then system ϕ reduces to the case of multiple independent random walks.

Proof

It is noteworthy to state that, when λ=0, the influence of the matrix denoting the preferential movement, ℙ_pref(t), is taken away. Indeed, when λ=0, the coupling between N(t) and p(t) ceases to exist, because the calculation step of P _pref(t) (responsible for the coupling) can be skipped. Moreover, if Δ=0, then the agents can never get exhausted. In view of these characteristics, the dynamical system ϕ can be easily described by a traditional Markovian process given by:

$$ p(t+1) = p(t)\mathbb{P}_{\mathrm{transition}} $$

(37)

where ℙ_transition=ℙ_rand⊗ℙ_rand⊗⋯⊗ℙ_rand and p(t) is an enumerated state encompassing all the agents, as described before. Here, the independence among the agents is demonstrated by showing that the generated N(t) by system ϕ is exactly the same as the one produced by the potential matrix of the Markov Chains Theory [4]. In other words, N(t) can be implicitly calculated from the stochastic process {p(t):t≥0}.

First, it is useful to find a closed expression for N(t) in terms of N(0). This can be easily done if we iterate the matrix equation N(t+1)=N(t)+Q, where Q is as given in (21). In doing so, we get:

(38)

Since this process is stochastic, it is worth determining the expectation of the number of visits N(t) given the agent’s initial location p(0). Noting that , we have:

(39)

where P ⁱ(p _j (0),1) denotes the (p _j (0),1)-entry of ℙ_transition to the i-power. But, from the Markov Chains Theory, we have that the so-called truncated potential matrix [4] is given by:

$$ R_{t}(v,k) \triangleq\sum_{i=0}^{t}{ \mathbb{P}_{\mathrm{transition}}^{i}(v,k)}. $$

(40)

By virtue of (40), each entry of the matrix equation in (39) can be rewritten as:

$$ \mathbb{E}\bigl[N^{(j)}_{i}(t)\mid p(0)\bigr] = 1 + R_{t}\bigl(p_{j}(0),i\bigr). $$

(41)

From (41), we can infer that each agent does perform an independent random walk according to a Markov Chain. Thus, we are able to conclude that, for λ=0 and Δ=0, all the states of system ϕ follow a traditional Markov Chain process, except for a constant, as demonstrated in (41). □

The Proposition 2 states that system ϕ reduces to the case of multiple random walks when λ=0 and Δ=0, i.e., we could think that there is a blind competition among the participants. Alternatively, when 0<λ≤1, some orientation is given to the participants, in the sense of defending their territory and not only keep adventuring through the network with no strategy at all. In either case, the reanimation procedure is enabled depending on the choice of Δ.

4 Application: Handwritten Digits and Letters Recognition

In this section, we provide an application of data clustering for the competitive method for three real-world data sets. Specifically, in Sect. 4.1, we derive a dissimilarity measure that we will use in the network formation step; in Sect. 4.2, we supply a brief description of the data sets; in Sect. 4.3, we show a method for determining the optimal number of agents to be inserted into the network; and Sect. 4.4 reveals the data clustering results that we have obtained from our algorithm applied to the USPS, MNIST, and Letter Recognition data sets.

It is worth noting that in all simulations in this section, since the parameters ω _min, ω _max, and Δ are not sensitive to the model performance, we usually fix Δ as being 5% of the interval ω _max−ω _min. Therefore, we set Δ=0.05, ω _min=0, and ω _max=1.

4.1 The Network Formation Technique

In a graph-based data representation, the images (data items) are represented by the vertices, while the relationships between them are given by the links. A link connecting two vertices (images) holds a weight that numerically translates the similarity between them. Each image can be represented by a “square” matrix η×η. For rectangle images, a pre-processing is required to transform it into a square image. We conventionally set the pixels’ values range to lie within the interval [0,1] by normalization. Thus, an arbitrary data item (image) x _i can be seen as a matrix with dimensions η×η, where each pixel x _i ^(u,j)∈[0,1],∀(u,j)∈{1,…,η}×{1,…,η}.

In order to construct the network, we are required to establish a similarity measure. The traditional pixel-per-pixel distance is rather insufficient in terms of reliably representing data, since such measure is very sensitive to rotations and scale modifications. With the purpose of overcoming this difficulty, we propose a measure based on the eigenvalues that each image inherently carries with it. First of all, we remove the mean associated to each data item (image), so that we have a common basis of comparison. After that, we calculate the ϕ greatest eigenvalues of the image. Efficient methods have been developed for finding the leading eigenvalues of real-valued asymmetric matrices [12, 35]. The magnitudes of the eigenvalues are related to the variations that the image possesses; hence, it is a natural carrier of information [18]. The greater its value, more information about the image it conveys. By virtue of that, a good choice is to only extract the greatest ϕ<η eigenvalues and drop the smaller values, since these do not transport too much information about the image. Also, in order to give more emphasis to the largest eigenvalues, a weight is associated to each one so that the larger an eigenvalue is, the larger will be its associated weight.

Consider that we are to compare the similarity between two images, say x _i and x _j , in relation to the ϕ largest eigenvalues. We firstly sort the ϕ eigenvalues of each image as: $|\lambda^{(1)}_{i}| \geq|\lambda^{(2)}_{i}| \geq\cdots\geq|\lambda^{(\phi)}_{i}|$ and $|\lambda^{(1)}_{j}| \geq|\lambda^{(2)}_{j}| \geq\cdots\geq |\lambda^{(\phi)}_{j}|$, where $|\lambda^{(k)}_{i}|$ marks the kth eigenvalue of the ith data item. In this case, the dissimilarity ρ (or, equivalently, the similarity 1−ρ) between image i and j is given by:

(42)

where ρ∈[0,1], ρ _max>0 is a normalization constant, β:ℕ^∗→(0,∞) indicates a monotonically decreasing function that can be arbitrary chosen by the user.

4.2 Brief Information of the Handwritten Digit and Letter Data Sets

The data sets in which the proposed model will be tested against are given in the following:

• USPS Data Set: Comprised of 9298 images of handwritten digits. The digits 0 to 9 have 1553, 1269, 929, 824, 852, 716, 834, 792, 708, and 821 samples respectively. The USPS digits data were gathered at the Center of Excellence in Document Analysis and Recognition (CEDAR) at SUNY Buffalo, as part of a project sponsored by the US postal Service. For more details about this data set, refer to [14]. Each image has dimensions of 16×16 pixels, with 256 grey levels per pixel. We will employ the weighted eigenvalue similarity measure as studied before. Instead of using 16 eigenvalues, we will only work with the 4 greatest ones. In this case, the β function, as shown in (42), will be fixed as an exponential decreasing function with a time constant fixed at τ=3 and a scaling factor given by 16, i.e., $\beta(x) = 16\exp(\frac {x}{3})$. Since, this function is mapped into the interval (0,∞) and is a monotonically decreasing function, it follows that this β function meets all the aforementioned requirements. Specifically in this situation, we have that the weights associated to each eigenvalue are: β(1)=11.46, β(2)=8.21, β(3)=5.89, and β(4)=4.22.

• MNIST Data Set: Originally composed of images with dimensions 28×28. We will only use the public set composed of 10 000 vertices. Moreover, we will make use of the dissimilarity measure based on the first 4 eigenvalues of each image out of 28 eigenvalues. The same β function employed in the USPS data set will be used here.

• Letter Recognition Data Set: Composed of characteristic vectors with 16 entries. There are 20000 vertices.

Since none of these data sets are in a networked form, the methodology is divided into two general steps: the network formation and the data clustering tasks. In the first, we use the k-nearest neighbor network formation technique with k=3 after we apply a pre-processing step. In this pre-processing, we standardize the data such as to have zero mean and unitary standard deviation. As for the distance measure, we either use the proposed weighted eigenvalue dissimilarity (for the first two data sets above) or the reciprocal of the Euclidean similarity (for the last one). The reason behind not using the weighted eigenvalue on the third data set is because the samples are not provided as images, but as image descriptors. Since the latter is formed by merely scalars, we cannot apply the proposed dissimilarity measure. In the second step, the data clustering algorithm based on particle competition is applied. As we are dealing with unsupervised learning, we do not use any external information, such as labels or exogenous knowledge. Instead, we limit ourselves to discovering explicit or implicit relationships among the data by the particle competition mechanism.

4.3 Determining the Optimal Number of Agents and Clusters

Remembering that our technique is sensitive to the parameter K, we need to identify the correct number of agents. In order to overcome this problem, we utilize the method proposed in [33] for determining the optimal number of agents to be inserted into the network. Such a method makes use of a useful network measure denominated average maximum domination level 〈R(t)〉 as follows:

(43)

where 〈R(t)〉∈[0,1]. When 〈R(t)〉 is near 1, we can infer that the competition in the network for vertices has ceased and, thus, the vertices’ ownerships have been properly defined. In other words, the maximum domination level of any vertex is a number near 1, showing that this vertex is being completely dominated by a single agent. This suggests that the clusters have been properly discovered and dominated. On the other hand, when 〈R(t)〉 approximates 0, we have that an intense competition is taking place in the network. In other words, the domination levels imposed by each agent in any arbitrary vertex are similar. With these considerations in mind, a good suggestion for the optimal K in a given network is exactly when 〈R(t)〉 reaches its maximum value.

Figures 1(a), 1(b), and 1(c) show the determination of the optimal K for the USPS, MNIST, and Letter Recognition data sets, respectively. One can verify that 〈R(t)〉 is maximized exactly when the number of agents is equal to the number of clusters in the network, confirming the effectiveness of such heuristic.

Fig. 1

Determination of the optimal number of agents K (the optimal number of clusters) in real-world data sets. The number of classes that each data set originally possesses are: (a) The USPS data set has 10 clusters (each cluster corresponding to a number from “0” to “9”); (b) The MNIST data set has 10 clusters (each cluster corresponding to a number from “0” to “9”); and (c) The Letter Recognition data set has 26 clusters (each cluster corresponding to a letter from the English alphabet (“A” to “Z”). 20 independent runs are performed and the average value is reported

4.4 Handwritten Data Clustering

Here, we report the cluster detection accuracy reached by our algorithm in detail, along with the data clustering accuracy of a selected set of competing techniques. For the calculation of the cluster detection accuracy, we set that the ideal result is that each cluster represents a “digit” (in the USPS and MNIST data set) or a “letter” (in the Letter Recognition data set). Particularly, Table 1 supplies details about the algorithms that we have chosen for comparison matters. We have used the genetic algorithm available in the Global Optimization Toolbox of MATLAB with its default parameters in order to optimize the parameters of our algorithm. In our case, we have optimized λ over the range 0.2≤λ≤0.8. This optimization process is conducted in a way to choose the best λ for which the data accuracy reaches its maximum value. By doing this, we get that the optimal values of λ for the USPS, MNIST, and Letter Recognition data sets to be 0.58, 0.60, 0.60, respectively. The number of agents to be inserted is determined accordingly to the previously analysis that we have shown, i.e., with the aid of the 〈R(t)〉 measure. We choose the number of agents that maximizes this quantity. By looking at Figs. 1(a) (USPS), 1(b) (MNIST), and 1(c) (Letter Recognition), we are able to conclude that the maximum value of 〈R(t)〉 is attained when the number of agents is 10, 10, and 26, respectively.

Table 1 Description of the competing state-of-art data clustering techniques.

Table 2 reports the data clustering accuracy reached by our method and the aforementioned competing algorithms. Some of these results are readily extracted from [29] and [21]. For more information about the parameters used in the competing techniques, see the aforementioned references. Within this table, we have provided the Average Rank of each algorithm, which is calculated as follows: (i) for each data set we rank the algorithms according to their average performance (average data clustering accuracy), i.e., the best algorithm is ranked as 1, the second best one is ranked as 2, and so on; (ii) for each algorithm, the Average Rank is given by the average value of its rank achieved in all the data sets. As we can verify by looking at the Average Rank column, our algorithm has reached one of the best positions, showing the effectiveness of the proposed technique. In order to examine the results in a statistical manner, we utilize an adaptation of [7] for clustering matters. The methodology described therein assigns a rank to each algorithm on each data set according to its final accuracy reached. After this step, the average rank of each algorithm is then evaluated and a Friedman Test is applied to the resulting average rank values of each algorithm. The Friedman Test is used to check whether the measured average ranks are significantly distinct from the mean rank, in this case 4.0, because there are seven data clustering techniques. The null-hypothesis considered here is that all the algorithms are equivalent, so their ranks should be equal. Hereon, for all the future tests, we fix a significance level of 0.10. For our experiments, according to [7], we have that N=3 and k=7, resulting in a critical value given by F(6,12)=2.33, where the two arguments are derived from the degrees of freedom defined as k−1 and (N−1)(k−1), respectively. In our case, we get a value F _F ≈4.00 that is higher than the critical value, so the null-hypothesis is rejected at a 10% significance level. Thus, we conclude that the algorithms at hand present statistical difference, i.e., they are statistically different from the mean rank. Nonetheless, one can see that our algorithm has obtained the best average rank in relation to the other algorithms for these three data sets.

Table 2 Data clustering accuracy reached by the proposed technique and the competing methods listed in Table 1. For the stochastic methods, such as the particle competition method, thirty independent runs were performed and the corresponding mean is provided

As the null hypothesis is rejected, we are able to advance to post-hoc tests which aim at verifying the performance of our algorithm in relation to others. For this task, we opt to use the Bonferroni-Dunn Test, with the proposed technique fixed as the control algorithm. According to [7], one should not make pairwise comparisons when we test whether a specific method is better than others. Basically, the Bonferroni-Dunn Test quantifies whether the performance between an arbitrary algorithm and the reference is significantly different. This is done by verifying whether the corresponding average ranks of these algorithms differ by at least a critical difference (CD). If they do differ that much, then it is said that the better ranked algorithm is statistically superior to the worse ranked one. Otherwise, they do not present a significant difference for the problem at hands. Thus, if we perform the evaluation of the CD for our problem, we encounter CD=4.22 when the significance level is 10%. The average rank of the proposed method is 2.00. By virtue of that, if any rank does lie in the interval 2.00±4.22, the control algorithm and the compared algorithms are statistically equivalent. We conclude that our algorithm is superior to K-Means for this set of databases. However, the other pairwise comparisons to the control algorithm do not surpass the CD, meaning that the differences among them are statistically insignificant. Nonetheless, the proposed technique has obtained the best performance (the best average rank) in relation to the other techniques and also presents reasonable computational complexity as we have previously addressed.

In order to further verify the robustness of the proposed technique, we inspect the samples that compose a same cluster. Specifically, Figs. 2, 3, 4, and 5 show some samples of the clusters representing the pattern “2”, “5”, “6”, and “8”, respectively, of the MNIST data set. These samples are captured using the following strategy: we compute the vertices that compose the maximum geodesic distance of the cluster representing each pattern (cluster diameter). Now, we select a representative subset of vertices composing the cluster diameter trajectory for illustrative purposes. In these figures, samples that are adjacent are more similar than those distant from one to another. On the basis of this analysis, we conclude that the graph representation has successfully captured several variations of the these number patterns each of which in a single representative cluster, showing the robustness of the proposed model.

Fig. 2

A broad set of samples of that were classified as being member of the cluster representing the pattern “2”. Note that samples that are adjacent are similar with regards to the weighted eigenvalue dissimilarity function. The transitions from the sample (a) to (g) were captured from the maximum geodesic distance between two vertices in the cluster representing pattern 2. In this case, the diameter of such cluster is 17. We have only provided 7 representative samples above

Fig. 3

A broad set of samples of that were classified as being member of the cluster representing the pattern “5”. Likewise the previous figure, adjacent samples are more similar to each other than distance samples. The methodology for construction (geodesic path) is the same

Fig. 4

A broad set of samples of that were classified as being member of the cluster representing the pattern “6”. Likewise the previous figure, adjacent samples are more similar to each other than distance samples. The methodology for construction (geodesic path) is the same

Fig. 5

A broad set of samples of that were classified as being member of the cluster representing the pattern “8”. Likewise the previous figure, adjacent samples are more similar to each other than distance samples. The methodology for construction (geodesic path) is the same

5 Conclusions

This paper studies a new model for competitive learning in networks, biologically inspired by the competition process taking place in many nature and social systems. In this model, several agents navigate in the network to explore their territory and, at the same time, attempt to defend their territory from rival agents. If an agent frequently visits a specific vertex, it occurs that the domination level of the visiting agent to this vertex is strengthened; simultaneously, the domination levels of all the other agents on the same vertex are weakened. Finally, each agent is confined in a community of the network.

The competitive model is nonlinear and stochastic. In addition, we show that it generalizes the process of multiple independent random walks when a special case occurs. Such generalization is realized by changing the values of the parameters λ and Δ of the system. If λ=0 and Δ=0, the proposed model reduces to multiple independent random walks. Conversely, when λ>0, the competition mechanism is turned on. In this case, the reanimation procedure is enabled depending on the parameter Δ. Moreover, here we provide a mathematical analysis of the unsupervised competitive model.

Simulations are carried out with the purpose of quantifying the robustness of the proposed technique on handwritten data clustering. Computer simulations show that the competitive model works well for detecting digits or letters even with considerable distortion in the same cluster.