Introduction

Chemical mechanical planarization (CMP) refers to a high-precision surface polishing process with a combination of chemical and mechanical forces (Sheu et al., 2012; Zantye et al., 2004). CMP was initially innovated by Klaus D.Beyer in the 1980s to create a smooth surface so that lithographic imaging can be implemented subsequently (Krishnan et al., 2010). CMP can be used to polish a wide range of materials, such as tungsten, semiconductors, metal, carbon nanotubes, and silicon oxide (Awano, 2006; Steigerwald et al., 1997). CMP has been used in many applications, such as optical components, wireless communications, and large-scale integration manufacturing (Lee et al., 2016; Leon et al., 2017; Yin et al., 2019). A typical CMP device includes a rotating table, a planarization pad, a wafer carrier, a wafer, a slurry dispenser, and a rotating dresser, where a wafer is captured by a wafer carrier, and a polishing pad is attached to the rotating table. In the CMP process, a wafer is pushed toward the planarization pad, and both the rotating table and the wafer carrier are rotated in an identical direction. The abrasive materials are dispensed on the planarization pad via a slurry during the polishing process. A rotating dresser may be engaged in conditioning the polishing pad after the CMP process.

The performance of the CMP process can be evaluated using many metrics, such as wafer-to-wafer thickness variation, surface roughness, and process reliability and stability. To reduce the wafer-to-wafer thickness variation in CMP, accurate prediction of material removal rate (MRR) is critical (Deng et al., 2021). However, predicting MRR with high accuracy remains a challenge because MRR depends on various process variables and surface topography, such as the rotating rate of the wafer, flow rate of slurry, polishing pad asperity density, wafer hardness, and so on (Park et al., 2008; Yu et al., 2016). According to the literature, numerous methodologies have been developed to predict the MRR during the CMP process, and these methodologies can be classified into two groups: model-based and data-driven methods. The majority of model-based methods are built upon the basic or modified Preston equations (Luo et al., 1998). The Preston equation is an empirical model that considers the pressure applied to a wafer in a vertical direction and the relative speed between the wafer and the polishing pad (Evans et al., 2003). However, few model-based methods are able to accurately predict the MRR of the CMP process (Kong et al., 2010). Over the past few years, data-driven methods have been increasingly used to predict MRR by incorporating multiple process variables, such as rotating rate of wafer and flow rate of slurry (Lee & Kim, 2020; Xia et al., 2021). However, these methods are not capable of considering surface topography in MRR predictions as the surface topography is difficult to observe and measure (Chen et al., 2020). To address this issue, our contributions are listed as follows:

  • A directed graphical model is proposed to reveal the relations among process variables, surface topography, and MRR during the CMP process.

  • A conditional variational autoencoder is introduced based on the proposed directed graphical model to extract the features of the surface topography.

  • An ensemble learning-based predictive model is developed to predict the MRR during the CMP process.

The remainder of this paper is organized as follows. Section Related work reviews the model-based and data-driven methods for MRR predictions in the CMP process. Section Methodology proposes a directed graphical model and introduces a conditional variational autoencoder to extract the features of the surface topography. In addition, an ensemble learning-based approach is presented in this section to predict the MRR during the planarization process. Section Case study uses a CMP dataset to demonstrate the effectiveness of the proposed method. Section Conclusions and future work concludes this study and directs future work.

Related work

This section reviews the model-based and data-driven methods for predicting MRR in CMP processes. The limitation of these methods is summarized at the end of this section.

Model-based methods

Model-based methods refer to the methods that predict the behavior of a system or a process using numerical or analytical models. Luo and Dornfeld (2001) presented a physics-based model to predict the MRR in the CMP process, where both wafer-abrasive and pad-abrasive mechanisms in plastic contact mode were investigated. The proposed model considered multiple process variables in MRR predictions, such as pressure, velocity, pad roughness, and so on. The experimental results have shown that the proposed model enables an accurate MRR prediction and a better understanding of the abrasive mechanism in the CMP process. Lee and Jeong (2011) presented a semi-empirical CMP model to predict the MRR during the copper CMP process by combining the basic form of the Preston equation and a spatial parameter. The distributions of velocity, contact stress, and rate of reaction were considered in the proposed model. Zhao and Chang (2002) presented a closed-form equation to predict the MRR in the polishing process of silicon wafers based upon a micro-contact and wear model. The proposed equation incorporated multiple process variables, material parameters, and chemical parameters. Experimental results have suggested that the MRR is sensitive to wafer hardness, slurry type, and rotating speed. Oh and Seok (2009) combined a mechanical abrasive model with a slurry dispensation model to estimate the MRR for silicon dioxide in the CMP process. The effects led by both mechanical and chemical actions were included in MRR predictions. The experimental results have demonstrated that the proposed method can deal with the non-Prestonian behavior during the planarization process. Lee et al. (2013) introduced a MRR distribution model to predict the MRR in the planarization process. To estimate the parameters of the proposed model, a CMP experiment was conducted on different types of slurries. Nguyen et al. (2015) introduced a MRR analytical model by considering both the contact time of the planarization process and the kinematic mechanism. The numerical results have demonstrated that the non-conformity of the pad wear is due to the inconsistencies in both cutting path density and contact time.

Data-driven methods

Data-driven methods refer to the methods that guide decision making using data instead of physical models representing the behavior behind a system or a process. Kong et al. (2010) integrated a statistical learning model with a nonlinear Bayesian method to predict the MRR of the CMP process. The particle filter was implemented to estimate the state of the CMP process, and vibration signals were used to predict the MRR. The numerical results have demonstrated that this approach can effectively predict the MRR during the planarization process. Li et al. (2019) presented an ensemble learning method to predict the MRR in the planarization process. Temporal and frequency-domain features were extracted from multiple sensor measurements and fed into the ensemble learning method. The numerical results have demonstrated that the proposed methodology can predict the MRR at different polishing stages with high accuracy. Yu et al. (2019) introduced a physics-constrained machine learning method to predict the MRR. The Greenwood and Williamson contact model (Greenwood & Williamson, 1966; Johnson & Johnson, 1987) served as a predictive model to estimate the MRR, and the random forests method was used to estimate the topography terms in the Greenwood and Williamson contact model. Wang et al. (2017) used a deep neural network to predict the MRR during the planarization process based on the polishing process variables. The particle swarm optimization method was implemented to study the effect of the learning rate on prediction accuracy. The numerical results have demonstrated that the proposed deep learning approach can accurately predict the MRR under different operating conditions. Jia et al. (2018) introduced an adaptive polynomial neural network to predict the MRR. The features and predictive models were selected automatically, and two novel categories of features were introduced to improve the prediction performance.

In summary, numerous model-based and data-driven methods have been introduced to predict the MRR in the CMP process. However, most model-based methods are not able to predict the MRR with high accuracy due to the complexity of the CMP process. Some of the existing data-driven methods are effective in predicting the MRR, however, few data-driven methods predict the MRR by taking into account the surface topography information because it is difficult to measure the surface topography in the CMP process. To address these issues, the objective of this study is to develop a directed graphical model and a conditional variational autoencoder to extract the features of the surface topography. In addition, an ensemble learning-based predictive model is presented to predict the MRR during the CMP process.

Methodology

The proposed methodology includes three primary steps. First, a directed graphical model is proposed to reveal the relations among process variables, surface topography, and MRR in the CMP process. Second, a conditional variational autoencoder is introduced based on the proposed directed graphical model to extract the features of the surface topography. Third, both process variables and the extracted features of the surface topography are fed into an ensemble learning-based predictive model to predict the MRR in the CMP process. More details of these three steps are introduced in the following subsections.

Fig. 1
figure 1

The proposed directed graphical model, where \({\mathbf {t}}\) refers to the surface topography, r refers to the material removal rate, and \({\mathbf {v}}\) refers to the process variables

Full size image

Directed graphical model

A directed graphical model refers to a probabilistic model where the dependency of multiple variables is revealed in a directed graph (Airoldi, 2007). Figure 1 shows the proposed directed graphical model where the relationships among process variables, surface topography, and MRR are revealed.

The process variables of the CMP process, such as polishing pressure and flow rate of slurry, affect surface topography, such as pad asperity density and average asperity radii (Yu et al., 2019). Therefore, an arrow is considered to be directed from process variables to surface topography to represent that the process variables affect the surface topography. The process variables affect the MRR, for example, a higher rotation rate of wafer and table can lead to a higher MRR. Therefore, an arrow is directed from process variables to material removal rate to represent that the process variables can be used to predict the MRR. In addition, the surface topography can also affect the MRR, for instance, a higher active asperity density can lead to a higher MRR. Thus, a directed arrow is pointed from surface topography to material removal rate to represent that the surface topography can also be used to predict the MRR.

In the proposed graphical model, the process variables can be observed from sensor measurements and the MRR can be measured after the CMP process. However, the surface topography is difficult to observe and measure due to its dynamic evolution during the planarization process. To extract features that enable a maximized MRR prediction accuracy, the extracted features of the surface topography can be expressed as Eq. (1),

$$\begin{aligned} {\mathbf {t}}:= \mathop {\mathrm {argmax}}\limits _{{\mathbf {t}}} p_{\theta }(r \mid {\mathbf {v}}) \end{aligned}$$
(1)

where \({\mathbf {t}}\) refers to the features of the surface topography, r is the material removal rate, \({\mathbf {v}}\) refers to the process variables, \(\theta \) is a collection of parameters in the conditional probability of MRR , i.e. \(p_{\theta }(r\mid {\mathbf {v}})\). To simplify the optimization process, we use log-likelihood instead of likelihood. Then, Eq. (1) can be rewritten as:

$$\begin{aligned} {\mathbf {t}}:= \mathop {\mathrm {argmax}}\limits _{{\mathbf {t}}} \log p_{\theta }(r \mid {\mathbf {v}}) \end{aligned}$$
(2)

With using the Bayesian theory, \(\log p_{\theta }(r \mid {\mathbf {v}})\) can also be written as Eq. (3).

$$\begin{aligned} \begin{aligned} \log p_{\theta }(r \mid {\mathbf {v}})&=\log \frac{p_{\theta }({\mathbf {v}},r)}{p_{\theta }({\mathbf {v}})}\\&=\log \frac{p_{\theta }({\mathbf {v}},r,{\mathbf {t}})}{p_{\theta }({\mathbf {t}} \mid {\mathbf {v}}, r)\cdot p_{\theta }({\mathbf {v}})}\\ \end{aligned} \end{aligned}$$
(3)

Based on the chain rule of the proposed directed graphical model, \(p_{\theta }({\mathbf {v}},r,{\mathbf {t}})\) can be expressed as:

$$\begin{aligned} p_{\theta }({\mathbf {v}},r,{\mathbf {t}})= p_{\theta }(r \mid {\mathbf {t}}, {\mathbf {v}}) \cdot p_{\theta }({\mathbf {t}} \mid {\mathbf {v}}) \cdot p_{\theta }({\mathbf {v}}) \end{aligned}$$
(4)

By substituting Eq. (4) to Eq. (3), \(\log p_{\theta }(r \mid {\mathbf {v}})\) can be written as Eq. (5).

$$\begin{aligned} \log p_{\theta }(r \mid {\mathbf {v}}) =\log \frac{p_{\theta }(r \mid {\mathbf {t}},{\mathbf {v}}) \cdot p_{\theta }({\mathbf {t}} \mid {\mathbf {v}})}{p_{\theta }({\mathbf {t}} \mid {\mathbf {v}}, r)} \end{aligned}$$
(5)

The conditional probability distribution of \({\mathbf {t}}\) is unknown as the surface topography can not be obtained directly. Thus, \(p_{\theta }({\mathbf {t}} \mid {\mathbf {v}}, r)\) is intractable. To deal with this intractable posterior distribution, a variational inference is introduced and \(\log p_{\theta }(r\mid {\mathbf {v}})\) can be expressed as:

$$\begin{aligned} \begin{aligned}&\log p_{\theta }(r \mid {\mathbf {v}})\\&\quad =\log \frac{p_{\theta }(r \mid {\mathbf {t}},{\mathbf {v}}) \cdot p_{\theta }({\mathbf {t}} \mid {\mathbf {v}})}{p_{\theta }({\mathbf {t}} \mid {\mathbf {v}}, r)} \cdot \frac{q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)}{q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)}\\ \end{aligned} \end{aligned}$$
(6)

Then, the expectation of Eq. (6) can be written as Eq. (7), where \(\phi \) is the collection of parameters in the variational inference \(q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)\).

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_{{\mathbf {t}} \sim q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)} \left[ \log \frac{p_{\theta }(r \mid {\mathbf {t}},{\mathbf {v}}) \cdot p_{\theta }({\mathbf {t}} \mid {\mathbf {v}})}{p_{\theta }({\mathbf {t}} \mid {\mathbf {v}}, r)} \cdot \frac{q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)}{q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)} \right] \end{aligned}$$
(7)

Equation (7) can be decomposed into the sum of two terms, where the first term can be expressed as:

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_{{\mathbf {t}} \sim q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)} \left[ \log \frac{p_{\theta }(r \mid {\mathbf {t}},{\mathbf {v}}) \cdot p_{\theta }({\mathbf {t}} \mid {\mathbf {v}})}{q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)}\right] \end{aligned}$$
(8)

The second term is expressed as Eq. (9), which is a KL-divergence of two distributions.

$$\begin{aligned} D_{KL}[q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)\Vert p_{\theta }({\mathbf {t}} \mid {\mathbf {v}}, r) ] \end{aligned}$$
(9)

Because the KL-divergence of two distributions is always positive, and this KL-divergence term includes an intractable probability distribution \(p_{\theta }({\mathbf {t}} \mid {\mathbf {v}}, r)\). A variational lower bound is introduced, and the extracted features of surface topography can be expressed as:

$$\begin{aligned} {\mathbf {t}}:= \mathop {\mathrm {argmax}}\limits _{{\mathbf {t}}} {{\,\mathrm{\mathbb {E}}\,}}_{{\mathbf {t}} \sim q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)} \left[ \log \frac{p_{\theta }(r \mid {\mathbf {t}},{\mathbf {v}}) \cdot p_{\theta }({\mathbf {t}} \mid {\mathbf {v}})}{q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)}\right] \end{aligned}$$
(10)

The expectation term of Eq. (10) can also be decomposed into two terms, and the extracted features of the surface topography can be written as:

$$\begin{aligned} \begin{aligned} {\mathbf {t}}:&= \mathop {\mathrm {argmax}}\limits _{{\mathbf {t}}} {{\,\mathrm{\mathbb {E}}\,}}_{{\mathbf {t}} \sim q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)} [ \log p_{\theta }(r \mid {\mathbf {t}},{\mathbf {v}})]\\&\quad -D_{KL}[q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r) \Vert p_{\theta }({\mathbf {t}} \mid {\mathbf {v}})] \end{aligned} \end{aligned}$$
(11)

Based on the Universal Approximation Theorem (Hornik et al., 1989), neural networks are employed to approximate the three conditional probability distributions in Eq. (11).

Conditional probabilistic autoencoders

The conditional probability distributions in the variational lower bound are approximated using autoencoder-based neural networks. The conditional probability \(q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)\) is approximated with an encoder network. The inputs of this encoder network are process variables \({\mathbf {v}}\) and the MRR r, and the outputs of this network are the features of the surface topography \({\mathbf {t}}\). We name this encoder network the generative encoder network as it aims at generating the features of the surface topography. The relationships between the inputs and the outputs of this network can be mathematically written as Eq. (12),

$$\begin{aligned} \begin{aligned} {\mathbf {o}}_{q,L}&=f_{q,L}\cdots [f_{q,l} \cdots [f_{q,2}[f_{q,1}({\mathbf {v}},r)]]]\\ \varvec{\mu }_1&={\mathbf {w}}_{q,L+1,1} \cdot {\mathbf {o}}_{q,L}+{\mathbf {b}}_{q,L+1,1}\\ diag(\Sigma _1)&={\mathbf {w}}_{q,L+1,2} \cdot {\mathbf {o}}_{q,L}+{\mathbf {b}}_{q,L+1,2}\\ \mathbf {t}_1&=\varvec{\mu }_1+\Sigma _1 \odot \epsilon , \qquad \epsilon \sim \mathcal {N}(\mathbf {0}, \mathbf {I}) \end{aligned} \end{aligned}$$
(12)

where \(f_{q,l}(\cdot )\) can be expressed as \(f_{q,l}(\cdot )= \sigma ({\mathbf {w}}_{q,l} \cdot {\mathbf {o}}_{q,l-1} + {\mathbf {b}}_{q,l})\); \({\mathbf {w}}_{q,l}\) refers to the vector of weights of the generative encoder network at hidden layer l; \({\mathbf {b}}_{q,l}\) is the bias vector of the generative encoder network at hidden layer l; \({\mathbf {o}}_{q,l-1}\) is the output of the hidden layer \(l-1\); \(\sigma \) refers to the activation function; \(\varvec{\mu }_1\) and \(\Sigma _1\) are mean and standard deviation of the conditional probability distribution \(q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)\) respectively.

The conditional probability \(p_{\theta }({\mathbf {t}} \mid {\mathbf {v}})\) is approximated with an encoder network. The inputs of this network are process variables, and the outputs are the features of the surface topography. We name this network as the conditional prior network as it aims at generating the features of the surface topography conditioning on the prior knowledge of process variables. The relationships between the inputs and the outputs of this network can be mathematically written as Eq. (13),

$$\begin{aligned} \begin{aligned} {\mathbf {o}}_{p,L}^{'}&=f_{p,L}^{'}\cdots [f_{p,l}^{'} \cdots [f_{p,2}^{'}[f_{p,1}^{'}({\mathbf {v}})]]]\\ \varvec{\mu }_2&={\mathbf {w}}_{p,L+1,1}^{'} \cdot {\mathbf {o}}_{p,L}^{'}+{\mathbf {b}}_{p,L+1,1}^{'}\\ diag(\Sigma _2)&={\mathbf {w}}_{p,L+1,2}^{'} \cdot {\mathbf {o}}_{p,L}^{'}+{\mathbf {b}}_{p,L+1,2}^{'}\\ \mathbf {t}_2&=\varvec{\mu }_2+\Sigma _2 \odot \epsilon , \qquad \epsilon \sim \mathcal {N}(\mathbf {0}, \mathbf {I}) \end{aligned} \end{aligned}$$
(13)

where \(f_{q,l}^{'}(\cdot )\) can be written as \(f_{q,l}^{'}(\cdot )= \sigma ({\mathbf {w}}_{q,l}^{'} \cdot {\mathbf {o}}_{q,l-1}^{'} + {\mathbf {b}}_{q,l}^{'})\); \({\mathbf {w}}_{q,l}^{'}\) refers to the vector of weights of the conditional prior encoder network at hidden layer l; \({\mathbf {b}}_{q,l}^{'}\) is the bias vector of the conditional prior encoder network at hidden layer l; \({\mathbf {o}}_{q,l-1}^{'}\) is the output of the hidden layer \(l-1\); \(\varvec{\mu }_2\) and \(\Sigma _2\) are mean and standard deviation of the conditional probability distribution \(q_{\phi }({\mathbf {t}} \mid {\mathbf {v}})\) respectively; and L refers to the total number of hidden layers.

Fig. 2
figure 2

Flow diagram of the proposed conditional probabilistic autoencoders

Full size image

The conditional probability \(p_{\theta }(r \mid {\mathbf {t}},{\mathbf {v}})\) is approximated with a decoder network. The inputs of this network are process variables and the features of the surface topography extracted from the generative encoder network, and the outputs of this network are predicted MRR. We name this network as the predictive network as it aims at predicting the MRR in the CMP process. The relationships between the inputs and the outputs of this network can be mathematically expressed as Eq. (14),

$$\begin{aligned} \begin{aligned}&{\hat{r}}=f_{p,L}\cdots [f_{p,l}\cdots [f_{p,2}[f_{p,1}({\mathbf {v}},{\mathbf {t}}_1)]]] \end{aligned} \end{aligned}$$
(14)

where \(f_{p,l}(\cdot )\) can be written as \(f_{p,l}(\cdot )= \sigma ({\mathbf {w}}_{p,l} \cdot {\mathbf {o}}_{p,l-1} + {\mathbf {b}}_{p,l})\); \({\mathbf {w}}_{p,l}\) refers to the vector of weights of the predictive decoder network at hidden layer l; \({\mathbf {b}}_{p,l}\) is the bias vector of the predictive decoder network at hidden layer l; \({\mathbf {o}}_{p,l-1}\) is the output of the hidden layer \(l-1\);

Then, the expectation of the variational lower bound in Eq. (11) can be considered as the MRR prediction errors, which can be rewritten as Eq. (15),

$$\begin{aligned} \begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_{{\mathbf {t}} \sim q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r)} [ \log p_{\theta }(r \mid {\mathbf {t}},{\mathbf {v}})]= \Vert r-{\hat{r}} \Vert _2^2 \end{aligned} \end{aligned}$$
(15)

where r is the ground truth of the MRR, and \({\hat{r}}\) refers to the predicted MRR. The KL-divergence of the variational lower bound in Eq. (11) can be considered as the differences between two distributions, which can be expressed as Eq. (16).

$$\begin{aligned} \begin{aligned}&D_{KL}[q_{\phi }({\mathbf {t}} \mid {\mathbf {v}}, r) \Vert p_{\theta }({\mathbf {t}} \mid {\mathbf {v}})]=\frac{1}{2}\left( tr(\Sigma _2^{-1}\Sigma _1)\right. \\&\quad \left. + (\mu _2-\mu _1)^T \Sigma _2^{-1} (\mu _2-\mu _1) -d + \log \left( \frac{\mid \Sigma _2\mid }{\mid \Sigma _1 \mid }\right) \right) \end{aligned} \end{aligned}$$
(16)

Next, the gradient descent method can be used to train the parameters in these networks. However, it may not be optimized to generate \({\mathbf {t}}_2\) as the conditional prior network is not connected to a predictive network. To address this issue, another predictive network is introduced. A similar setup can also be found in Zhao et al. (2017), Pandey and Dukkipati (2017), and Wei et al. (2021). The inputs of this network are process variables and the features of the surface topography extracted from the conditional prior encoder network, and the outputs of this predictive network are predicted MRR. The relationships between the inputs and the outputs of this predictive network can be mathematically expressed as Eq. (17),

$$\begin{aligned} \begin{aligned}&\hat{r^{'}}=f_{p,L}^{''}\cdots [f_{p,l}^{''}\cdots [f_{p,2}^{''}[f_{p,1}^{''}({\mathbf {v}},{\mathbf {t}}_2)]]] \end{aligned} \end{aligned}$$
(17)

The additional introduced predictive decoder network results in one extra objective in the variational lower bound, and this extra objective can be expressed as:

$$\begin{aligned} \begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_{{\mathbf {t}} \sim p_{\theta }({\mathbf {t}} \mid {\mathbf {v}})} [ \log p_{\theta }(r \mid {\mathbf {t}},{\mathbf {v}})]= \Vert r-\hat{r^{'}} \Vert _2^2 \end{aligned} \end{aligned}$$
(18)

In summary, there are four networks are introduced to approximate multiple conditional probability distributions. These networks include one generative encoder network, one conditional prior encoder network, and two predictive decoder networks. By summing Eq. (15), Eq. (16), and Eq. (18), the total losses of these four networks can be written as Eq. (19), which is a sum of three losses.

$$\begin{aligned} \begin{aligned}&L= L_1 + L_2 + L_3;\\&L_1 = \Vert r-{\hat{r}} \Vert _2^2; L_2 = \Vert r-\hat{r^{'}} \Vert _2^2;\\&L_3 = \frac{1}{2}\left( tr(\Sigma _2^{-1}\Sigma _1) + (\mu _2-\mu _1)^T\right. \\&\left. \Sigma _2^{-1} (\mu _2-\mu _1) -d + \log \left( \frac{\mid \Sigma _2\mid }{\mid \Sigma _1 \mid }\right) \right) \end{aligned} \end{aligned}$$
(19)

Next, these four networks are connected to train the parameters and extract the features of the surface topography. We name these connected networks as conditional probabilistic autoencoders. Figure 2 shows the flow diagram of the proposed conditional probabilistic autoencoders, where \(\Pi \) is a collection of trainable parameters in the generative encoder network, \(\Pi ^{'}\) is a collection of trainable parameters in the conditional prior encoder network, \(\Phi \) and \(\Phi ^{'}\) refer to collections of trainable parameters in predictive decoder networks.

In the training phase, the process variables \({\mathbf {v}}\) and MRR r are fed into the generative encoder network to derive \(\mu _1\) and \(\Sigma _1\); \(\mu _1\) and \(\Sigma _1\) are used to generate the features of the surface topography \({\mathbf {t}}_1\); both \({\mathbf {v}}\) and \({\mathbf {t}}_1\) are fed into a predictive decoder network to get the predicted MRR \({\hat{r}}\). The process variables \({\mathbf {v}}\) are fed into the conditional prior encoder network to derive \(\mu _2\) and \(\Sigma _2\); \(\mu _2\) and \(\Sigma _2\) are used to generate the features of the surface topography \({\mathbf {t}}_2\); both \({\mathbf {v}}\) and \({\mathbf {t}}_2\) are fed into another predictive decoder network to derive the predicted MRR \(\hat{r^{'}}\); \(\mu _1\), \(\Sigma _1\), \(\mu _2\), and \(\Sigma _2\) are used to calculate the KL-divergence loss, i.e. \(L_3\); r and \({\hat{r}}\) are used to calculate one prediction loss, i.e. \(L_1\); r and \(\hat{r^{'}}\) are used to calculate another prediction loss, i.e. \(L_2\); Next, all losses \(L_1, L_2, L_3\) are back-propagated through these networks to update the trainable parameters, \(\Pi \), \(\Pi ^{'}\), \(\Phi \), and \(\Phi ^{'}\). In the test phase, process variables are fed into the conditional prior encoder network to extract \(\mu _2\) and \(\Sigma _2\). \(\mu _2\) refers to the deterministic version of the extracted features of the surface topography. The deterministic version of the extracted features helps improve the accuracy of MRR predictions. Table 1 shows the training and test phases of the proposed conditional probabilistic autoencoders.

Table 1 The training and test phases of the proposed conditional probabilistic autoencoders
Full size table

MRR predictive model

Next, process variables and the extracted features of the surface topography are fed into an ensemble learning-based MRR predictive model to predict the MRR during the CMP process. Ensemble learning usually achieves the best prediction performance by combining multiple base learning algorithms (Polikar, 2006). In this work, we select the best three base regressors out of ten base regressors, the selected base regressors include Random Forests (RF), Gradient Boosting Trees (GBT), and Adaptive Boosting (AB). More details on why these three base regressors were selected are provided in Sect. Feature extraction and hyperparameters tuning. Moreover, the stacking method is implemented to combine three base regressors. These base regressors are briefly introduced in the following sections.

Random forests

The RF refers to an ensemble learning methodology by constructing and combining multiple decision trees (Breiman, 2001; Wu et al., 2019). To develop a decision tree, a random set of variables are selected to split a parent node into two child nodes. The splitting criteria of each parent node can be expressed as the following optimization problem,

$$\begin{aligned} \min _{j,c}\left[ \min _{m_1, m_2} \left( \sum _{x_i\in R_1}(y_i-m_1)^2 + \sum _{x_i \in R_2}(y_i-m_2)^2\right) \right] \end{aligned}$$
(20)

where \(R_1=\{x \mid x_j \le c \}\) and \(R_2=\{x \mid x_j \ge c \}\) refer to two regions after the splitting process is completed; \(x_j\) is the j-th splitting variable; c refers to a cutting point; \(m_1\) denotes the mean of the \(y_i\)’s that lie into the region \(R_1\); and \(m_2\) denotes the mean of the \(y_i\)’s that lie into the region \(R_2\).

The splitting process is replicated unit the stopping criteria has been satisfied. A final prediction is made by averaging predictions made by all constructed decision trees.

Gradient boosting trees

The GBT is an ensemble learning method by constructing decision trees sequentially (Friedman, 2001). Higher weights are assigned on data points that are challenging to predict to improve predictive accuracy. The GBT predictor aims at estimating a mapping function \(g({\mathbf {x}})\) of input \({\mathbf {x}}\). The mathematical model is used to approximate the function \(g({\mathbf {x}})\), which can be written as a sum of multiple local functions \(g_n\),

$$\begin{aligned} g({\mathbf {x}})=\sum _{n=1}^{N} \beta _n g_n(\mathbf {x};\gamma _n) \end{aligned}$$
(21)

where N is the total number of local functions; \(\gamma _n\) is a collection of parameters of the local function \(g_n\); \(\beta _n\) refers to the weighted coefficient. \(\gamma _n\) and \(\beta _n\) can be approximated with the Eq. (22), where L is the loss function.

$$\begin{aligned} (\gamma _n, \beta _n)=\mathop {\mathrm {argmin}}\limits _{\gamma , \beta } {{\,\mathrm{\mathbb {E}}\,}}[L(y_i,g_{n-1}({\mathbf {x}}_i) + \beta g({\mathbf {x}}_i; \gamma ))] \end{aligned}$$
(22)

Next, the greedy-stagewise method (Friedman, 2001) can be used to solve this optimization problem and update the parameters sequentially.

Adaptive boosting

The AB algorithm is similar to the GBT algorithm, which starts from fitting a regressor on the initial dataset and fitting extra regressors on the same dataset with higher weights on data points that are challenging to predict. One primary difference between the AB and GBT algorithms is that the AB algorithm identifies weak learners by high-weight data points, the GBT algorithm identifies weak learners by the gradient. More details of the AB algorithm can be found in Kégl (2013) and Friedman et al. (2000).

Next, the stacking method is employed to combine these three base regressors. A stacking ensemble learning method includes two stages that are training base regressors and training a meta-regressor (Li et al., 2019). Figure 3 shows the two-stage stacking ensemble learning method. In the first stage, process variables and the extracted features of the surface topography are fed into three base regressors to make three individual predictions. In the second stage, these individual predictions are fed into a meta regressor to make a final prediction. In this work, the multi-layer perceptron was employed as a meta regressor.

Fig. 3
figure 3

Two-stage ensemble learning method with stacking

Full size image

Case study

In this section, the effectiveness of the proposed methodology is demonstrated on a CMP dataset from the PHM data challenge (Li et al., 2019).

Data description

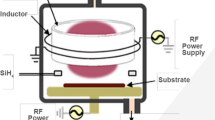
This dataset includes multiple sensor measurements obtained from a CMP process. Figure 4 exhibits a schematic diagram of a typical CMP process. For a typical CMP process, a wafer is captured by a wafer carrier, a polishing pad is attached to the rotating table. In the CMP process, a wafer is pushed toward the planarization pad, and both the rotating table and the wafer carrier are rotated in an identical direction. The abrasive materials are dispensed on the planarization pad via a slurry during the polishing process. A rotating dresser may be engaged in conditioning the polishing pad after the CMP process.

Fig. 4
figure 4

The schematic diagram of the CMP process

Full size image

The data includes 19 process variables. These variables, such as chamber pressure, flow rate of slurry, and applied pressure, are real-time collected data. Table 2 lists the symbol and descriptions of these process variables. The real-time data were obtained from wafers under two operating stages (Stage A and Stage B), which are grouped into three datasets, including a training dataset, a validation dataset, and a test dataset. In this work, we remove wafers with a large proportion of missing values to better evaluate the performance of the proposed methodology. Table 3 shows the number of wafers was polished in three datasets under two stages. The proposed method was trained on the training dataset and evaluated on the remaining two datasets.

Table 2 Data descriptions
Full size table
Table 3 Number of wafers in training, validation, and test datasets under two stages
Full size table

Feature extraction and hyperparameters tuning

In the previous study, we have demonstrated that five temporal features extracted from the raw data can be used to predict the MRR in the CMP process accurately (Yu et al., 2019). In this case study, we extracted the similar temporal features used in Li et al. (2019) and Yu et al. (2019). The extracted temporal features include mean, median, mode, central moment, and standard deviation; and a total of 95 features were extracted for 19 process variables. Then, the extracted features and the true MRR were fed into the proposed deep probabilistic autoencoder to extract the features of the surface topography. To optimize the performance of the deep probabilistic autoencoder as well as reduce the computational cost, the number of hidden layers in both encoder and decoder networks is set as 3. A dropout layer was added after each hidden layer to avoid the over-fitting problem. The rectified linear unit (ReLU) was used as the activation function in the hidden layers. Because five temporal features were extracted from each process variable, the dimension of the extracted features of the surface topography is also set as 5. Therefore, there is a total of 100 features (95 temporal features and 5 topography features) used for MRR prediction. Tables 4, 5, and 6 show the network structure of the generative encoder network, conditional prior encoder network, and predictive decoder networks. In these tables, batch refers to the batch size, the batch size equals 937 and 815 for wafers manufactured under stage A and stage B, respectively; FC refers to the fully connected layers and Dropout refers to the dropout layers.

Table 4 The network structure of the generative encoder network
Full size table
Table 5 The network structure of the conditional prior encoder network
Full size table
Table 6 The network structure of the predictive decoder networks
Full size table
Fig. 5
figure 5

The RMSE of ten different base regressors for wafers manufactured under two stages on both validation and test dataset

Full size image

Next, we selected the base regressors. It has been demonstrated that combining base regressors of different types can improve the performance of ensemble learning models (Shi et al., 2021). Therefore, we created a base-regressor pool with ten different base regressors, including RF, AB, GBT, LASSO, support vector regression (SVR), ridge regression (RR), k-nearest neighbors (kNN), Bayesian regression (BR), Elastic-Net (EN), and multiple layer perceptron (MLP). In this case study, the best three base regressors were selected to construct the ensemble learning model. Figure 5 shows the RMSE of the ten different base regressors on both validation and test datasets. The results have shown that RF, AB, and GBT are the best three base regressors. Therefore, RF, AB, and GBT were selected as the base regressors in Sect. MRR predictive model.

To optimize the performance of the ensemble learning model, hyperparameter tuning was performed for the selected base regressors. Table 7 shows the average RMSE of the selected base regressors with respect to the different number of estimators. Based on this table, the number of decision trees used in the RF method is set as 200; the number of estimators used in the AB method is set as 100; the number of estimators used in the GBT method is set as 300. Moreover, the meta-regressor is the MLP method which uses 5 hidden layers for simplicity and 100 hidden nodes in each layer in order to be consistent with the number of features used for MRR prediction.

Table 7 The average RMSE of the selected base regressors with respect to different number of estimators
Full size table
Fig. 6
figure 6

Prediction performance on validation dataset under two stages. a–c show the prediction performance under stage A, d–f show the prediction performance under stage B

Full size image

Results

In this case study, the root mean squared error (RMSE) was used as the performance metric to evaluate the MRR prediction performance. RMSE on validation and test datasets can be calculated using Eq. (23),

$$\begin{aligned} RMSE=\sqrt{\frac{1}{N} \sum _{i=1}^{N} (r_i - {\hat{r}}_i)} \end{aligned}$$
(23)

where \(r_i\) and \({\hat{r}}_i\) are the true and predicted MRR, respectively; and N refers to the total number of wafers.

Figure 6 shows the prediction performance of the proposed methodology on the validation dataset under two polishing stages. Figure 6a–c show the prediction performance under polishing stage A, where Fig. 6a compares the predicted MRR and the true MRR (the ground truth of MRR) in the order of wafer index; Fig. 6b compares the predicted MRR and the true MRR in the order of the MRR; and Fig. 6c presents the histogram and distribution of the prediction difference between the predicted and true MRR. The RMSE of the predicted MRR under polishing stage A is 9.51 nm/min and the standard deviation of the predicted residuals is 9.52 nm/min. Figure 6d–f shows the prediction performance of polishing stage B, where Fig. 6d compares the predicted MRR and the true MRR in the order of wafer index; Fig. 6e compares the predicted MRR and the true MRR in the order of the MRR; and Fig. 6f shows the histogram and distribution of the prediction difference between the predicted and true MRR. The root mean squared error (RMSE) of the predicted MRR under polishing stage B is 3.73 nm/min and the standard deviation of the predicted residuals is 3.90 nm/min.

Fig. 7
figure 7

Prediction performance on test dataset under two stages. a–c show the prediction performance under stage A, d–f show the prediction performance under stage B

Full size image

Figure 7 shows the prediction performance of the proposed methodology on the test dataset under two polishing stages. Figure 7a–c shows the prediction performance under polishing stage A, where Fig. 7a compares the predicted MRR and the true MRR in the order of wafer index; Fig. 7b compares the predicted MRR and the true MRR in the order of the MRR; and Fig. 7c shows the histogram and distribution of the prediction difference between the predicted and true MRR. The root mean squared error (RMSE) of the predicted MRR under polishing stage A is 7.01 nm/min and the standard deviation of the predicted residuals is 7.72 nm/min. Figure 7d–f shows the prediction performance under polishing stage B, where Fig. 7d compares the predicted MRR and the true MRR in the order of wafer index; Fig. 7e compares the predicted MRR and the true MRR in the order of the MRR; and Fig. 7f shows the histogram and distribution of the prediction difference between the predicted and true MRR. The RMSE of the predicted MRR under polishing stage B is 4.21 nm/min and the standard deviation of the predicted residuals is 4.27 nm/min. Based on these figures, we can observe that wafers polished under Stage A has a higher prediction RMSE and a higher standard deviation in comparison with wafers polished under Stage B. One reason that wafers polished under Stage A has a higher prediction RMSE and a higher standard deviation is that the MRR of Stage A is higher than the MRR of Stage B, and the higher MRR brings additional uncertainties for MRR predictions in the CMP process. We can also observe that the prediction residues for both Stage A and Stage B follow normal distributions and has a mean of zero, which means that the proposed method predicts the MRR without underestimations or overestimations. Moreover, operating conditions resulting in lower MRR should be adopted for the CMP process so that wafer-to-wafer thickness variation can be reduced.

Table 8 shows the prediction performance with and without using the extracted surface topography features in terms of RMSE. This table shows that the extracted surface topography features enable a better prediction performance. For example, the RMSE of the MRR predicted without using the extract surface topography features on the test dataset under polishing stage A is 8.25 nm/min. However, the RMSE of the MRR predicted with using the extract surface topography features on the test dataset under polishing stage A is only 7.01 nm/min.

Table 8 The prediction performance with and without using the extracted surface topography features in terms of RMSE (nm/min)
Full size table

To further demonstrate the effectiveness of the proposed method, the proposed method is also compared with the data-driven methods reported in the literature. Table 9 shows a comparison between the proposed method and other methods reported in the literature in terms of the average RMSE for both validation and test datasets. The average RMSE refers to the mean of the RMSE of the validation dataset and the RMSE of the test dataset. Based on Table 9, we can conclude that the proposed method outperforms the existing physics-based, data-driven, and physics-informed machine learning models reported in the literature. For example, the average RMSE of the method used in Wang et al. (2017) is 7.60 nm/min. However, the average RMSE of the proposed method is only 6.12 nm/min.

Table 9 The prediction performance between the proposed method and other methods reported in the literature
Full size table

Conclusions and future work

In this paper, a directed graphical model was developed to reveal the relationship among surface topography, process variables, and MRR in the CMP process. Based on the proposed directed graphical model, a deep probabilistic autoencoder was introduced to extract the features of the surface topography. Process variables and the extracted features of surface topography were fed into an ensemble learning-based predictive model to predict the MRR. A CMP dataset was used to demonstrate the effectiveness of the proposed method. The experimental results have shown that the MRR prediction performance can be improved by using the extracted features of the surface topography. The proposed method accurately predicted the MRR in the CMP process with a RMSE of 6.12 nm/min. Moreover, the proposed method outperforms existing predictive models reported in the literature in terms of RMSE. In the future, we will consider the dynamic changes in surface topography and their impacts on the MRR predictions. Moreover, different base regressors and ensemble learning methods will also be explored for MRR predictions.