Design of an efficient genetic algorithm for resource-constrained unrelated parallel machine scheduling problem with machine eligibility restrictions

Abstract

This study addresses a resource-constrained unrelated parallel machine scheduling problem with machine eligibility restrictions. Majority of the traditional scheduling problems in parallel machine environment deal with machine as the only resource. However, other resources such as labors, tools, jigs, fixtures, pallets, dies, and industrial robots are not only required for processing jobs but also are often restricted. Considering other resources makes the scheduling problems more realistic and practical to implement in manufacturing environments. First, an integer mathematical programming model with the objective of minimizing makespan is developed for this problem. Noteworthy, due to NP-hardness of the considered problem, application of meta-heuristic is avoidable. Furthermore, two new genetic algorithms including a pure genetic algorithm and a genetic algorithm along with a heuristic procedure are proposed to tackle this problem. With regard to the fact that appropriate design of the parameters has a significant effect on the performance of algorithms, hence, we calibrate the parameters of these algorithms by using the response surface method. The performance of the proposed algorithms is evaluated by a number of numerical examples. The computational results demonstrated that the proposed genetic algorithm is an effective and appropriate approach for our investigated problem.

Introduction

Scheduling is to simply assign a set of jobs to a set of machines with respect to operational constraints such that optimal usage of available resources is obtained. Because of the growing cost of raw material, labor, energy and transportation, scheduling plays an essential role in production planning of manufacturing systems, and it is one of the most important issues for survival in the modern competitive market place. Unrelated parallel machine scheduling problems appear in many manufacturing environments, such as in semiconductor manufacturing (Kim et al. 2002; Wang et al. 2013), the spinning of acrylic fibers for production in the textile industry (Silva and Magalhaes 2006), in steel making industry (Pan et al. 2013), in preheat treatment stage of automobile gear manufacturing process (Gokhale and Mathirajan 2012), block transportation in shipyards (Hu et al. 2010) and scheduling jobs in a printed wiring board manufacturing environment (Yu et al. 2002; Bilyk and Monch 2012).

Parallel machine scheduling problem has been one of the topics of interest for many researchers in the past few decades. Most of these studies considered the machines as only resource which is restricted. However, in real life manufacturing systems other resources such as machine operators and tools are constrained and it is illogical to consider that there are always enough resources for processing a job. It is clear that the resource-constrained parallel machine scheduling problem is more difficult than the simple parallel machine scheduling problem. In a resource constrained parallel machine scheduling problem (RCPMSP), an operation can be performed when the machine and other resources are available during the process of operation. In these problems, besides the schedule of jobs on machines, the schedule of jobs on other resources and their interactions should be considered. In RCPMSP for a specific sequence of jobs on machines, there is an optimal sequence of jobs on resources and conversely, for a specific sequence of jobs on resources, there is an optimal sequence of jobs on machines (Mehravaran and Logendran 2013). On the other hand, jobs may often not be processed on any of the available machines but rather must be processed on a machine belonging to a specific subset of the machines (Pinedo 1995). This constraint which is called under different names, such as machine eligibility restrictions, processing set restrictions and scheduling typed task systems is also widely encountered in real scheduling environments.

There are some works done related to the unrelated or identical parallel machine scheduling problem with machine eligibility restrictions and other operational constraints. Centeno and Armacost (1997) investigated the identical parallel machine scheduling problem (PMSP) with release dates and machine eligibility restrictions to minimize the maximum lateness. They developed a heuristic algorithm that resulted from combining the least flexible job first rule (LFJ) and the least flexible machine first rule (LFM). Later, Centeno and Armacost (2004) developed a heuristic algorithm that integrated LFJ, LFM and the longest processing time (LPT) for the aforementioned problem to minimize makespan. Liao and Sheen (2008) considered the identical PMSP with machine availability and eligibility constraints while minimizing the makespan. Sheen et al. (2008) developed a branch and bound algorithm applying several immediate selection rules for solving the identical PMSP with machine availability and eligibility constraints while minimizing the maximum lateness. Gokhale and Mathirajan (2012) addressed identical parallel machine scheduling problem with release dates, machine eligibility restrictions and sequence dependent setup times to minimize the total weighted flow time. They presented a mathematical model and a few heuristic algorithms to solve the considered problem. A mixed-integer programming model and some local search heuristics have been proposed by Wang et al. (2013), for unrelated PMSP incorporating release dates, machine eligibility restrictions and sequence dependent setup times. As indicated above, none of these researchers taken into account the resource constraints. Only Edis and Ozkarahan (2012) considered machine eligibility and resource constraints for identical PMSP simultaneously, however, they did not propose any meta-heuristic algorithm for this problem. To the best of our knowledge, this research is the first to propose a meta-heuristic algorithm for the mentioned problem.

The first studies considered the use of meta-heuristics for the PMSP have been conducted by Cheng et al. (1995) and Cheng and Gen (1997). Recently, Joo and Kim (2012) proposed two meta-heuristics, genetic algorithm (GA) and a new population-based evolutionary meta-heuristic called self-evolution algorithm (SEA) for unrelated PMSP with sequence dependent setup times and ready times. Arnaout et al. (2014) presented a two-stage ant colony optimization algorithm to minimize the makespan on unrelated PMSP with sequence dependent setup times.

On the other hand, there are only few papers that have considered the resource constraints in their scheduling problems. Ventura and Kim (2000) addressed identical PMSP with additional resource constraints and developed an integer programming model to minimize the total absolute deviation of job completion times about common due date. They proved that the problem can be solved in polynomial time when there exists one single type of additional resource and the resource requirements per job are zero or one. Later, Ventura and Kim (2003) considered an identical PMSP with unit processing times, non-common due dates and additional resource constraints. They developed an integer programming model and used lagrangian relaxation approach to obtain tight lower bounds and near-optimal solutions. Chen (2005) proposed a heuristic method to minimize makespan in unrelated PMSP with different die types as a secondary resource constraint. Chen and Wu (2006) considered unrelated PMSP with auxiliary equipment constraints as secondary resource constraints. They proposed an effective heuristic based on threshold-accepting methods, tabu lists and improvement procedures to minimize total tardiness. Chaudhry and Drake (2009) developed a search algorithm based on genetic algorithm for identical PMSP with worker assignment. None of these papers addressed resource constrained unrelated parallel machine scheduling problem with machine eligibility restriction. On the other hand most of them considered a partial resource constraint, meaning that, they supposed that there is only one secondary resource which is restricted. Torabi et al. (2013) addressed unrelated parallel machine scheduling problem with non-zero ready times, sequence dependent setup times, and secondary resource constraints. They proposed a multi-objective practical swarm optimization to tackle this problem. However, they supposed that there is only one stock for each secondary resource and this simplification reduces the complexity of resource constrained unrelated parallel machine scheduling problem. A comprehensive survey on parallel machine scheduling problem with additional resources has been presented by Edis et al. (2013).

The remainder of this paper is organized as follows. The next section describes the problem under study and derives a mathematical formulation for considered problem. A new genetic algorithm and a hybrid genetic algorithm to solve the proposed model are clearly elaborated in “Genetic algorithm (GA)” and “Hybrid genetic algorithm (HGA)”, respectively. In “Parameters tuning”, the parameters tuning of the proposed algorithms is presented. In “Computational results”, computational results are presented and finally in “Conclusions and recommendations for future studies” conclusions are provided along with some future research directions.

Problem description and mathematical modeling

In this study, we consider resource-constrained parallel machine scheduling problem in which the machines are unrelated and all of them are available at the beginning of the scheduling and each machine can process only one job at a time. The processing time for each job on each machine is specified. Jobs are available at the beginning of the scheduling and the preemption is not allowed. We assume that each job can only be processed on a specific subset of machines. The setup times are assumed to be part of the processing time. The goal is minimizing the makespan.

Indices

$i=1,2,\ldots ,N$ :

Index for jobs

$m=1,2,\ldots ,M$ :

Index for machines

$t=1,2,\ldots ,T$ :

Index for time periods in the scheduling horizon

$v=1,2,\ldots ,R$ :

Index for resources

Parameters

$P_{im}$ :

Processing time of job i on machine m

$Eg_{im}$ :

1 if machine m capable to process job i; 0, otherwise

$res_{iv}$ :

Resource requirement of job i to renewable resource v

$b_v$ :

Available resource of type v

Decision variables

$x_{imt} = 1$ if job i completes its processing on machine m at time t; otherwise 0

The mathematical model

The RCPMSP with machine eligibility restrictions will be formulated as a 0–1 integer mathematical programming model.

$$\begin{aligned} Min \,Z=C_{max} \end{aligned}$$

(1)

Subject to:

$$\begin{aligned}&\sum \limits _{i=1}^N \sum \limits _{s=t}^{t+P_{im} -1} x_{ims} \le 1 \quad \forall m,t \end{aligned}$$

(2)

$$\begin{aligned}&\sum \limits _{m=1}^M \sum \limits _{t=P_{im} }^T x_{imt} =1 \quad \forall i \end{aligned}$$

(3)

$$\begin{aligned}&\sum \limits _{t=P_{im} }^T x_{imt} \le Eg_{im} \quad \forall m,i \end{aligned}$$

(4)

$$\begin{aligned}&\sum \limits _{i=1}^N \sum \limits _{m=1}^M \sum \limits _{s=\hbox {t}}^{t+P_{im} -1} \, res_{iv} \,\, x_{ims} \le b_v \,\quad \forall v,t \end{aligned}$$

(5)

$$\begin{aligned}&\sum \limits _{m=1}^M \sum \limits _{t=P_{im} }^T x_{imt}. t\le C_{max} \quad \forall i \end{aligned}$$

(6)

$$\begin{aligned}&x_{imt} \, \epsilon \left\{ {0,1} \right\} \quad \forall m,t,i \end{aligned}$$

(7)

Relation (1) minimizes the makespan. Constraint (2) ensures that on each machine and at each time period, at most one job can be assigned. Constraint (3) imposes that each job should certainly be processed on a machine. Constraint (4) indicates the eligibility restrictions. Constraint (5) imposes that for each resource type v, the total amount assigned to jobs at any time period is less than or equal to the available amount of each resource type $b_v$. Constraint (6) is used to compute the makespan. Finally, constraint (7) indicates that the decision variables are binary.

Genetic algorithm (GA)

Genetic algorithm (GA) introduced by Holland (1975), is a well-known meta-heuristic approach attempts to mimic the natural evolution process. It has been widely used to solve various optimization problems such as time dependent inventory routing problem (Cho et al. 2014), yard crane scheduling (Liang et al. 2014), optimization for international logistics (Takeyasu and Kainosho 2014), scheduling of JIT cross-docking systems (Fazel Zarandi et al. 2014), straight and U-shaped assembly line balancing (Alavidoost et al. 2014), hybrid flow shop scheduling with single and batch processing machines (Li et al. 2014), etc. In addition many researchers have applied genetic algorithms to solve the parallel machine scheduling problems. Table 1 introduces some of these papers, where the classification scheme of Graham et al. (1979) is used to indicate the problem properties. The comprehensive studies on how to implement the genetic algorithm to solve various single or multi-objective optimization problems have been provided by Gen and Cheng (2000) and Gen et al. (2008).

Table 1 The papers which have applied genetic algorithms to solve PMSP

The GA generally starts with an initial population of individuals (chromosomes), which can either be generated randomly or based on some other algorithms. In each generation, the population goes through the processes of crossover, mutation, fitness evaluation and selection. Crossover is the process in which the chromosomes are exchanged in order to create two entirely new chromosomes in a specific pattern. Mutation consists of making unexpected changes in the values of one or more genes in a chromosome. A fitness function calculates the fitness of each individual. The selection process is that a chromosome with higher fitness value should have a higher chance of selecting into the next generation. The new population created in the above manner constitutes the next generation and this process is repeated until a specific stopping criterion is reached. The selection process, mutation and crossover have many models. The population size, the number of generations and the probabilities of mutation and crossover are some other parameters that can be varied to obtain a different genetic algorithm. The overall procedure of the proposed GA is described in following five subsections. First of all an appropriate chromosome representation for considered problem should be illustrated (“Chromosome representation”). Then the GA can be started by generating a set of feasible chromosomes as initial population (“Create initial population”) and then all generated chromosomes are evaluated by calculating the objective function value (makespan). Then a pair of chromosomes selected through the parent selection strategy from the current population for crossing that will create a pair of off-springs (“Parent selection strategy”). The proposed crossover mechanism is illustrated clearly in “Design of crossover operator”. In crossing procedure $\lfloor \, Cr*N_{pop}/2\rfloor$ pair of off-springs should be made and evaluated where Cr is the crossover probability and $N_{pop}$ is the number of population. After that a chromosome is selected completely at random for mutating that will create a mutated off-spring. The proposed mutation mechanism is illustrated in “Design of mutation operator”. In mutating procedure $\lfloor \, Mr *N_{pop}\rfloor$ off-springs should be created and evaluated where Mr is the mutation rate. At the end the current population and the off-springs population are merged and the $N_{pop}$ best of them are transferred to the next generation.

Chromosome representation

The first step in the GA technique is to represent a chromosome to encode the solution of the problem. The chromosome representation has a great influence on the performance of the algorithm. In resource-constrained unrelated parallel machine scheduling problem, a chromosome should simultaneously represent the sequence of jobs on machines and the priority of jobs on other resources. A typical chromosome used in this study is depicted in Fig. 1. The first string is a permutation of the N jobs while the second includes their assigned machine which can process the corresponding job and the third string is the priority of jobs for assigning to the other resources. An example with $\left( N=10,M=3 \right)$ to illustrate this definition is provided in Fig. 1.

Fig. 1

Chromosome encoding

Create initial population

The initial population includes $N_{pop}$ chromosomes. Each chromosome is produced completely at random. However, the third string cannot be produced completely at random. The third string should be generated according to the precedence constraints which are implied by the jobs scheduled to the same machine. The used pseudo code of initialization is indicated in Fig. 2. To generate random solutions for the initial population, the procedure is as follows:

• 1. To create first string, randomly generate a permutation of N jobs.

• 2. To create second string, randomly assign an eligible machine to each job of the first string, sequentially.

• 3. To create third string, first, randomly generate a permutation of N jobs. Then, this string should be repaired according to the precedence constrains which are drawn from the location of jobs in the sequence on each machine.

Fig. 2

The pseudo code of the initialization procedure

Parent selection strategy

The selection process of GA involves how to choose chromosomes (parents) in the current population for crossing that will create off-springs for the next generation. The tournament selection with tour-size = 3 is applied for selecting parents. Tournament selection works by selecting a number of chromosomes (tour-size) from the population at random. Then, through the tournament, only the chromosome with the best fitness of those individuals is selected for attending in crossover operation.

Design of crossover operator

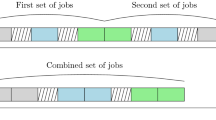
The new crossover operator which is employed in this research is similar to Double-point crossover. In this operator, firstly choose two chromosomes through parent selection strategy from population and call them parents 1 and 2. After that consider the first string of them and randomly choose two crossover points from a discrete uniform distribution in (1, N-1). Then all genes between the crossover points will be copied from parent 1 to the same position of child 2 and similarly from parent 2 to child 1. Parents 1 and 2 elements that will not create any duplication are copied to their exact positions in children 1 and 2, respectively. Then, the remaining empty positions in children 1 and 2 are sequentially filled by the unassigned elements in the order that they appear in the parents 1 and 2, respectively. Similarly, this procedure is applied for the third string of parents. But for each gen of second string of each child, initially generate a random number between [0 1], if it is greater than 0.5 (50 % chance for inheriting from each parent), copy the corresponding machine for that job from parent 1 to child 2 and similarly from the parent 2 to the child 1 otherwise copy the corresponding machine from parent 1 to child 1 and similarly from parent 2 to child 2. Finally the third string of children 1 and 2 should be repaired based on the obtained first and second strings. Figure 3 demonstrates an example for the crossover operator. For this, consider an example with six jobs and three machines and assume that machine eligibility restrictions are as follows, where $M_i$ is a set of machines which can process job i. Figure 4 indicates the pseudo code of the proposed crossover.

$$\begin{aligned} M_1= & {} \left\{ {1,2,3} \right\} \quad M_2 =\left\{ {2,3} \right\} \quad M_3 =\left\{ {1,2} \right\} \\ M_4= & {} \left\{ {1,2,3} \right\} \quad M_5 =\left\{ {1,2} \right\} \quad M_6 =\left\{ {1,2,3} \right\} \end{aligned}$$

Fig. 3

An illustration of proposed crossover

Fig. 4

The pseudo code of the proposed crossover procedure

Design of mutation operator

In this study, an adaptive mutation operator, called swap is employed. The proposed mutation mechanism is accomplished through the following steps;

• 1. Randomly select a chromosome from population and consider first string of it.

• 2. Randomly choose two gens in the parent.

• 3. Replace two selected gens.

• 4. For constructing second string, for all gens (jobs) except replaced gens, copy the corresponding machine from parent to child. But for each replaced gens generate a random number between [0 1], if it is lower than 0.5 (50 % chance for inheriting from his parent) copy the corresponding machine for that job from parent to child, otherwise, randomly select a machine from the eligible machines set where the selected machine should differ from previous one.

• 5. Do the steps 1–3 for the third string and then it should be repaired based on the obtained first and second strings.

Figure 5 illustrates an instance for the proposed mutation operator with regard to the pervious example. Moreover, the used pseudo code for the proposed mutation is indicated in Fig. 6.

Fig. 5

An illustration of proposed mutation

Fig. 6

The pseudo code of the proposed mutation procedure

Hybrid genetic algorithm (HGA)

As stated before, the problem considered in this study is the combination of two optimization problems including scheduling and resource allocation. In GA to tackle this combinatorial optimization problem a three level solution encoding scheme is proposed. In order to find how effective our proposed GA and their operators work and besides, because no benchmark problems are available in the literature to confirm and compare the results obtained by GA, a new genetic algorithm HGA is suggested to solve the experimental problems. In HGA, instead of employing a three level chromosome, we developed a genetic algorithm along with a heuristic procedure which performs the search procedure by a two level solution encoding scheme (ignoring the third string). For calculating the objective function value of each chromosome in HGA, at first according to the acquired sequence of jobs on machines the start and completion times of jobs are computed by considering the machine as only resource which is restricted. In the second step, to obtain a feasible order of jobs for allocating to the other resources, jobs are sorted based on their start times. In using this procedure, for the jobs which have the same start times, the job with longer processing time is scheduled first. After assigning the jobs to the other resources based on acquired order, the final objective function value can be calculated. The overall procedure for HGA is the same as the overall procedure for GA and the mutation and the crossover operators which are used for GA are adopted for HGA. Now, we give an instance with six jobs, two machines and two additional resources to help in illustrating how our proposed HGA works. The processing times and the resource requirements of jobs are shown in Table 2. The machine eligibility constraints are as follows:

$$\begin{aligned} M_1= & {} \left\{ {1,2} \right\} \quad M_2 =\left\{ 2 \right\} \quad M_3 =\left\{ {1,2} \right\} \\ M_4= & {} \left\{ {1,2} \right\} \quad M_5 =\left\{ 1 \right\} \quad M_6 =\left\{ {1,2} \right\} \end{aligned}$$

In order to find the objective function value of the chromosome depicted in Table 3, at first the start and completion times of each job are evaluated without considering the resource constraints. Table 4 shows the start time (ST) and the finish time (FT) of each job after the first step with $C_{max}=45$.

Table 2 Sample problem data

Table 3 A typical chromosome for HGA

Table 4 The start and finish times of jobs in step 1

In step 2, jobs are sorted based on their start times. There is a tie between job1 (J1) and job2 (J2), and tie is broken in favor of a job with longer processing time. As a result the feasible order of jobs for allocating to the other resources is J2–J1–J4–J6–J5–J3. With this sequence, jobs will be assigned to their resources. Finally, the start and finish times of jobs are recalculated by considering both machines and additional resources. The first job in the sequence is J2 on machine 2 (M2). This job needs two units of resource 1 (R1) and one unit of resource 2 (R2). Both resources are available at time zero so J2 can be started at time zero and the finish time of J2 is 0 + 13 = 13. The second job in the sequence is J1 on M1. J1 needs one unit of R1 and one unit of R2. Both R1 and R2 are unavailable until at time 13. So the earliest start time for J1 is 13 and the finish time of J1 is 13 + 11 = 24. This procedure is continued until all jobs are scheduled. The final start and finish times of jobs are shown in Table 5. As can be seen in Table 5 the objective function value is increased considerably from 45 to 60.

Table 5 The start and finish times of jobs in last step

Parameters tuning

In this section, design of experiment (DOE) approach is employed to investigate the effect of different levels of factors on the performance of the proposed algorithms. Hence, in order to calibrate the parameters, Response Surface Methodology (RSM) is applied in DOE approach. RSM is a technique for determining and representing the cause-and-effect relationship between true mean responses and input control variables influencing the responses as a two-or three-dimensional hyper surface (Montgomery 1991). The GA factors are: number of iterations (It), the number of population $(N_{\mathrm{pop}})$, the crossover rate $(\hbox {C}_{\mathrm{r}})$ and the mutation rate $(\hbox {M}_{\mathrm{r}})$. The search ranges and the different levels of the parameters are shown in Table 6.

Table 6 Parameters and their ranges

In proposed GA algorithms because four parameters exist, we use a fractional factorial central composite face-centered design with $2^{4-1}$ factorial points, $2\times 4$ axial points and 4 center points, totally 20 experiments. For each experiment five problems with various sizes are implemented. The results are normalized by relative percentage deviation (RPD) method and the average value of RPDs is reported for each test as a final response and a quadratic model will be fitted on the acquired responses. The obtained regression model is optimized within the range of the parameters by using LINGO 9.0 software and the optimum combinations of the parameters are shown in Table 7 for each algorithm.

Table 7 Exact values of parameters

Computational results

To solve the presented model and evaluate the performance of the proposed GAs, computational experiments are conducted using randomly generated test problems. To generate random processing times, number of resources and the available amount of each resource, we use integer uniform distribution (IUD) [1,20], [1,5] and [1,5], respectively. To produce the eligible constraints, initially generate an (N, M)-dimensional binary matrix, namely $\left( {Eg} \right)$, in which in any row of this matrix, at least, there are $\left[ {\frac{M}{2}} \right]$ elements 1. When $Eg\left( {i,m} \right) =1$, it means that machine m capable to process job i. To validate the proposed mathematical model and evaluate the optimality of the proposed meta-heuristics, a numerical example with eight jobs, three machines and a single additional resource is provided as a benchmark problem. The input parameters related to this example is given in Table 8. This example is solved optimally by LINGO 9.0 software and the proposed GAs with makespan 55. The Gantt chart for the optimal solution is provided in Fig. 7.

Fig. 7

The Gantt chart of optimal schedule

Table 8 Input parameters of example

The proposed model is applied for 25 test problems including 10 small and 15 large problems. We solve the small problems with two approaches: the optimal solution approach under LINGO 9.0 software and the proposed genetic algorithms. However, it is impossible to obtain an optimal solution for all of the problems in a reasonable CPU time, therefore the problems are optimally solved by the branch-and-bound approach (B&B) under the LINGO 9.0 software with 3 h run time limitation. Thus, the best solution obtained after 3 h is reported for the small size problems that cannot be optimally solved by the B&B in a reasonable CPU time. All examples are also solved by the proposed GAs and each algorithm is run five times for each problem and the obtained results compared with each other in terms of the average relative percentage deviation (ARPD) and CPU times. RPD is computed by the following formula;

$$\begin{aligned} RPD=\frac{C_{max}^{alg}-C_{max}^{min}}{C_{max}^{min}} \times 100 \end{aligned}$$

(8)

where $C_{max}^{alg}$ is the makespan obtained by each algorithm for a given problem and $C_{max}^{min}$ is the best value of total makespans obtained by through algorithms for the related problem. The proposed algorithms were coded in MATLAB R2012a and run on a personal computer including Intel(R) Core(TM) i5 CPU with 2.27 GHz speed and 3 GB of RAM.

Table 9 shows the obtained results from B&B, GA and HGA for 10 small size problems. As it can be seen from Table 9, for these problems the proposed GAs are able to get exact solutions for all of problems in reasonable CPU times. However, the LINGO 9.0 software could not achieve best solution as well as GAs for problem 10 in 3 h run time limitation. Figure 8 shows a polynomial behavior of CPU times by the proposed GAs against an exponential behavior of B&B method by the increase of the problem size for small problems. As you can see in Fig. 8, the GAs spend less CPU times than B&B for achieving to an optimal solution.

Fig. 8

CPU times reported by B&B method and GAs for small problems

Table 9 Comparison between the exact approach and GAs for small-size problems

In order to create more challenging comparison among GAs, we generated 15 large test problems and solved them five times by each proposed algorithm. The computational results compared with each other in terms of ARPD. The average values of RPDs (ARPD) for large problems are reported in Table 10. In order to create significant statistical analysis of the comparison among algorithms, the means plot and least significant difference (LSD) intervals (at the 95 % confidence level) for ARPD values of the algorithms for large size problems is shown in Fig. 9.

Fig. 9

Means plot and LSD intervals for algorithms in large test problems

Table 10 ARPD for the problems in large scale

According to Naderi and Ruiz (2010) which noticed that overlapping confidence intervals between any two means indicate that there is no statistically significant difference between them. With regard to this fact and as can be seen in Fig. 9, there is no statistically significant difference between GA and HGA. However, as you can see from Fig. 9, GA has more central tendency and lower variability of ARPD. As a result, for selecting only one algorithm, GA is more reliable than HGA to finding more accurate makespan. It is worth noting that GA spends approximately double run times against HGA for large scale problems.

In this section, some sensitive analyses are performed for assessing the behaviour of algorithms versus different conditions. Figures 10 and 11 indicate the interaction plot between the algorithms performance and number of jobs, number of machines in terms of ARDP, respectively. As it can be observed in Figs. 10 and 11, the GA has better performance in all conditions for large size problems; however, this transcendence is not tangible.

Fig. 10

Interaction plot between the performance of algorithms and number of jobs in terms of ARPD

Fig. 11

Interaction plot between the performances of algorithms and number of machines in terms of ARPD

Conclusions and recommendations for future studies

In this study we considered an unrelated parallel machine scheduling problem with machine eligibility and resource constraints. To solve this problem, two different approaches were proposed. The first approach was based on an integer programming model; however the mathematical model is not tractable for large size problems. As a result, in order to find proper schedules that minimize makespan, for second approach, we studied two structures of genetic algorithm, a pure genetic algorithm (GA) and a genetic algorithm along with a heuristic procedure (HGA). To assess the effectiveness of the proposed algorithms some random test problems in two scales were generated and the obtained results were analyzed and compared with each other. The comparisons have revealed that the proposed GA had better performance against HGA for solving the considered test problems, but this priority was not noticeable. On the other hand, the results demonstrated that our proposed heuristic algorithm is effective in both small and large size problems. For the sake of completeness, it should be noted that the proposed HGA could make desirable solutions, not as well as GA, for the considered test problems by spending less CPU times. As an interesting future research, it is worthwhile to develop the problem by adding some practical assumptions including machine breakdown, parallel batch processing and sequence dependent setup time. Furthermore, it is recommended to apply other efficient heuristics or meta-heuristic algorithms for solving the problem.

Appendix

The data set and the computational results of the large problem 15 which contains 60 jobs and 10 machines are as follows:

See Tables 11 and 12, Fig. 12.

Table 11 The data set of problem 15

Table 12 The computational result of the best solution obtained by GA with $C_{max}$ = 234

Fig. 12

The chromosome of the best solution obtained by GA