A hybrid discrete particle swarm optimization for dual-resource constrained job shop scheduling with resource flexibility

Abstract

In this paper, a novel hybrid discrete particle swarm optimization algorithm is proposed to solve the dual-resource constrained job shop scheduling problem with resource flexibility. Particles are represented based on a three-dimension chromosome coding scheme of operation sequence and resources allocation. Firstly, a mixed population initialization method is used for the particles. Then a discrete particle swarm optimization is designed as the global search process by taking the dual-resources feature into account. Moreover, an improved simulated annealing with variable neighborhoods structure is introduced to improve the local searching ability for the proposed algorithm. Finally, experimental results are given to show the effectiveness of the proposed algorithm.

Introduction

Job shop scheduling problem (JSSP) is a well-known combinational optimization problem which has found a lot of applications in real manufacturing industry. In classical JSSP, it is assumed that jobs are processed on pre-given machines and that the constraints of worker resources are neglected. Such assumptions reduced the problem complexity and fruitful research results were obtained, see (Qiu and Lau 2014; González et al. 2013; Adibi and Shahrabi 2014) for example and references therein. However, worker resources need taking into consideration since the labor cost is becoming much higher in manufactory fields nowadays. On the other hand, an operation can always be processed on various machines and with various workers, which means the resources are flexible (Nie et al. 2013; Pérez and Raupp 2014). The main advantage of resource flexibility is the increasing flexibility of the whole scheduling process, which is potential to save production time or cost. Thus a more general case which considers dual-resources constrained (DRC) JSSP with resource flexibility has been attracting increasing attention (Xu et al. 2011) and was presented in Gargeya and Deane (1996). In what follows, DRC JSSP with resource flexibility is called DRC-FJSSP for short.

The task of DRC-FJSSP is to determine both the operation sequence and the resources allocation by optimize certain objectives with constraints. Clearly, DRC-FJSSP is NP-hard and much more involved than classical JSSP. One commonly used way is first to obtain the operation sequence by intelligent algorithms such as Genetic algorithm (GA) (ElMaraghy et al. 1999, 2000) and ant colony algorithms (Li et al. 2011a, b), and then to allocate the machine and worker resources via dispatching rules. The dispatching rules include Earliest Finish Time, Shortest Process Time and so on. It is easy for these methods to find a local optimal solution and cost less computational time. However, the global optimal solution is difficult to find in this way. One effective way to overcome this drawback is to determine the operation sequence and resources allocation simultaneously via hybrid intelligent algorithms. In Li et al. (2010), an improved inherited GA with ant colony algorithms was presented to solve DRC-FJSSP. A four-dimensional chromosome coding scheme was used, and the resource crossover and mutation operator were designed to improve the global searching ability. In Lei and Guo (2014), an improved variable neighborhood search was proposed to for the DRC-FJSSP. This method has the ability of exploring different neighborhoods of the current solution and thus is easy for implementation. However, the obtained solutions may contain infeasible ones in these methods.

Since searching mechanism is important in finding global solutions of optimization problems, particle swarm optimization (PSO) algorithm is considered in this paper due to its good feature on it. In PSO, particle can learn from the global best and the personal best and thus the global and local searching ability are balanced.

PSO was first proposed in Kennedy and Eberhart (1995) for continuous optimization problems and the main advantage is fewer control parameters in the continuous space (Katherasan et al. 2014; Coello et al. 2004). However, PSO is considerably limited to the combinatorial optimization problems because the updating process of particle position was carried out in continuous domain. Thus PSO need modifying to solve combinatorial optimization problems. For example, PSO had been applied to the flow-shop scheduling problem (Vijay Chakaravarthy et al. 2013; AitZai et al. 2014), the JSSP (Zhang and Wu 2010; Lin et al. 2010), and the resource constraint project scheduling (Zhang et al. 2006), but there are few results applying PSO to solve DRC-FJSSP. Hence solving DRC-FJSSP with Hybrid PSO is an interesting problem to be investigated and has not been studied to be the best of the authors’ knowledge.

In this paper, a hybrid discrete PSO (HDPSO) is presented to solve the DRC-FJSSP with minimizing makespan being the objective function. A three-dimension chromosome coding scheme is used for the particles, which are the operation sequence, machine and worker allocation, respectively. The particles are initialized in a mixed way. Then a discrete PSO (DPSO) is designed as the global search process, in which the position updating equations are modified to avoid infeasible solutions. Moreover, an improved simulated annealing (ISA) with variable neighborhoods structure is introduced to improve the local searching ability for the proposed algorithm. Finally, experimental results show that the proposed algorithm is feasible and effective.

The remainder of this paper is organized as follows. “Problem description” section formally defines the scheduling model and presents a mathematical formulation. The HDPSO algorithm is presented in “HDPSO for DRC-FJSSP” section. In “Experiment results” section, experimental results are given and discussed. Conclusions are made together with future research direction in “Conclusions” section.

Problem description

Notations

$p$ :

Job index

$q$ :

Operation index

$h$ :

Machine index

$g$ :

Worker index

$O_{ pq}$ :

$q\hbox {th}$ operation of job $p$

$J$ :

Set of jobs

$M$ :

Set of machines

$W$ :

Set of workers

$M_{ pq}$ :

Set of candidate machines for $O_{ pq}$

$W_h$ :

Set of candidate workers for machine $h$

Parameters

$n$ :

Total number of jobs

$m$ :

Total number of machines

$b$ :

Total number of workers

$n_p$ :

Total operation number of job $p$

$t_{ pqh}$ :

Processing time of operation $O_{ pq}$ on machine $h$

$U$ :

A large number

Decision variables

$S_{ pq}$ :

Starting time of operation $O_{ pq}$

$K_{ hg}$ :

Starting time of machine $h$ processed by worker $g$

$C_{ pq}$ :

Completing time of operation $O_{ pq}$

$C_p$ :

Completing time of job $p$

$C_{\max }$ :

Maximum completing time of all jobs

• $\sigma _{ pqh} =\left\{ {\begin{array}{ll} 1,&{}\quad \hbox {if}\,\hbox {machine }h\,\hbox {is selected}\,\hbox {for}\,\hbox {the}\,\hbox {operation}\,O_{ pq} \\ 0,&{}\quad \hbox {otherwise} \\ \end{array}} \right.$

• $\varepsilon _{ hg} =\left\{ {\begin{array}{ll} 1,&{}\quad \hbox {if}\,\hbox {worker }g\,\hbox {is selected}\,\hbox {for}\,\hbox {the}\,\hbox {machine}\,h \\ 0,&{}\quad \hbox {otherwise} \\ \end{array}} \right.$

• $\chi _{ hg-h^{\prime }g} =\left\{ {\begin{array}{ll} 1,&{}\quad \hbox {if worker }g\,\hbox {is}\,\hbox {performed} \,\hbox {on}\,\hbox {machine}\,h\,\\ &{}\qquad \hbox {before}\,h^{{\prime }} \\ 0,&{}\quad \hbox {otherwise} \\ \end{array}} \right.$

• $\varsigma _{ pqh-p^{{\prime }}q^{{\prime }}h} =\left\{ {\begin{array}{ll} 1,&{}\quad \hbox {if}\,O_{ pq} \,\hbox {is}\,\hbox {performed} \,\hbox {on}\,\hbox {machine}\,h\,\\ &{}\qquad \hbox {before} \,O_{p^{{\prime }}q^{{\prime }}} \\ 0,&{}\quad \hbox {otherwise} \\ \end{array}} \right.$

Problem formulation

Before formulating the DRC-FJSSP, assumptions A1–A4 are made as follows.

• A1 All jobs, machines and workers are available at time zero.

• A2 Each machine can process only one operation at one time.

• A3 Every worker can operate only one machine at one time.

• A4 Preemption is not allowed, i.e., any operation cannot be interrupted until its completion once it is started.

Under the assumptions and notations, the mathematical model for the problem is defined as follows:

$$\begin{aligned} F=\min C_{\max } =\min \left\{ \mathop {\max }\limits _{p=1}^n \{C_p \}\right\} ; \end{aligned}$$

(1)

s.t.

$$\begin{aligned}&S_{p(q+1)} \ge S_{ pq} +t_{ pqh} \sigma _{ pqh} \varepsilon _{ hg}, p\in J;h\in M_{ pq};\nonumber \\&\quad g\in W_h; {\quad }q=1,2,\ldots ,n_p -1; \end{aligned}$$

(2)

$$\begin{aligned}&S_{p^{\prime }q^{\prime }} +(1-\varsigma _{ pqh-p^{{\prime }}q^{{\prime }}h} )U\ge S_{ pq} +t_{ pqh} ,p,\nonumber \\&\quad p^{\prime }\in J;h\in M_{ pq}; q,{\quad }q^{\prime }=1,2,\ldots ,n_p; \end{aligned}$$

(3)

$$\begin{aligned}&K_{h^{{\prime }}g} +(1-\chi _{hg-h^{\prime }g} )U\ge K_{ hg}, h,h^{{\prime }}\in M_{ pq}; g\in W_h; \end{aligned}$$

(4)

$$\begin{aligned}&K_{ hg} +(1-\sigma _{ pqh} )(1-\varepsilon _{ hg} )U\le S_{ pq},\nonumber \\&\quad p\in J;h\in M_{ pq}; g\in W_h;{\quad } q=1,2,\ldots ,n_p; \end{aligned}$$

(5)

$$\begin{aligned}&S_{p(q+1)} +(1-\varsigma _{p(q+1)h-p^{{\prime }}q^{{\prime }}h} )U\ge C_{ pq} ,p,\nonumber \\&\quad p^{\prime }\in J;h\in M_{ pq}; q,{\quad }q^{\prime }=1,2,\ldots ,n_p -1; \end{aligned}$$

(6)

$$\begin{aligned}&\sum _{h=1}^{M_{ pq} } {\sigma _{ pqh} } =1,p\in J;q=1,2,\ldots n_p; \end{aligned}$$

(7)

$$\begin{aligned}&\sum _{g=1}^{W_h } {\varepsilon _{ hg} } =1,{\quad }h=1,2,\ldots m; \end{aligned}$$

(8)

$$\begin{aligned}&C_p \le C_{\max }, p\in J; \end{aligned}$$

(9)

$$\begin{aligned}&S_{ pq}, t_{ pqh} \ge 0,p\in J;{\quad }q=1,2,\ldots n_p ;\nonumber \\&\quad h=1,2,\ldots ,m; \end{aligned}$$

(10)

$$\begin{aligned}&\sigma _{ pqh}, \varsigma _{ pqh-p^{{\prime }}q^{{\prime }}h} \in \{0,1\},p,p^{\prime }\in J;h\in M_{ pq}; \nonumber \\&\quad q, q^{\prime }=1,2,\ldots ,n_p; \end{aligned}$$

(11)

$$\begin{aligned}&\varepsilon _{ hg}, \chi _{hg-h^{\prime }g} \in \{0,1\},h,h^{\prime }\in M_{ pq}; g\in W_h; \end{aligned}$$

(12)

where the objective function $F$ is the minimization of the maximal makespan. Constraint (2) ensures that the precedence relationships between the operations of a job are not violated. Constraint (3) implies that each machine cannot process more than one operation at the same time. Constraint (4) implies that each worker cannot process more than one machine in the same time. Constraint (5) makes sure that each operation can be started after the worker selected for the processing machine is available. Constraint (6) makes sure that each operation can be started after the previous is completed. Constraint (7) makes sure that each operation is assigned to only one machine from its candidate machines set. Constraint (8) makes sure that each machine is assigned to only one worker from its candidate workers set. Constraint (9) implies the maximum completion time. Constraint (10) implies the start time and the processing time of each operation. Constraints (11) and (12) state the range of decision variables.

HDPSO for DRC-FJSSP

The HDPSO algorithm is presented in this section. A coding scheme and a mixed population initialization way are given first. Then a DPSO is presented for global search which updates particles in discrete domain directly. Finally, an ISA with variable neighborhood is introduced to improve the local search ability.

Coding scheme

The solution of DRC-FJSSP is a combination of operation sequences and resources allocation. Inspired by the chromosome coding scheme of GA (Lei 2010), we integrate the operation sequence vector and the resources allocation vectors as the particle coding scheme of HDPSO. Thus each particle has three vectors denoted by (OS, MA, WA), where OS represents the operation sequence, MA and WA represents the machine allocation and worker allocation, respectively. The length of each vector is $L=\sum \nolimits _{p=1}^n {n_p }$.

For OS, the number $p, p={1},{2},\ldots ,n$, appears $n_p$ times and the $q\hbox {th}$ appearance of $p$ means the operation $O_{ pq}$. Thus an element in OS stands for an operation. An element in MA and WA refers to the index of the machine and the worker, respectively. Obviously, they are subject to constraints (7) and (8), respectively. The three vectors compose a matrix and each column of the matrix stands for job in which a worker makes an operation in a machine and the corresponding costing time is $t_{ pqh}$. Take Tables 1 and 2 for example, in which $n={3}, m={4}, b={3}, n_{1} ={4}, n_{2} ={3}$ and $n_{3} ={3}$, then it follows that $L={1}0$. Table 3 shows a code of a particle and the second column (2,1,1) means that worker 1 take operation $O_{{21}}$ on machine 1 and the corresponding costing time is 15.

Table 1 Processing time table

Table 2 Worker machine informatino matrix

Table 3 Coding scheme of a particle

Population initialization

To guarantee an initial population with certain quality and diversity, some strategies are utilized in a mixed way. The initialization process includes the ones of OS, MA and WA, respectively.

For the initialization of OS, two rules are commonly used in the existing literature. The first one is random rule, the benefit of which is simplicity. The other one is the most number of operations remaining rule (Pezzella et al. 2008), which means the unprocessed job with more remaining operations have higher priority. The benefit of the most number of operations remaining rule is the speed of convergence.

For the initialization of MA, the modified Approach by Localization and Earliest Finish Time rule are presented.

Approach by Localization is proposed by Kacem in (Kacem and Hammadi 2002), which allocates operations to the machine with minimal workload. However, this approach is strongly dependent on the order of operations. Here we slightly modify it to be more flexible. The Modified Approach by Localization is carried out as follows: firstly, rearrange the processing time table according to the mixed initialized OS, then the MA can be determined by using Approach by Localization. For example, with Table 1 and the OS in Table 3, we can obtain the rearranged operation sequence, shown as the first column of Table 4. The corresponding processing time of these operations on machine $M_{1}$–$M_{4}$ can be obtained in the Part1 of Table 4. Based on Approach by Localization, $O_{11}$ should be processed on $M_3$ since 6 is the minimal processing time. Then update the processing time of other operations on $M_3$ we obtain Part2. It can be seen that $O_{21}$ should be processed on $M_4$ because 6 is the minimal value. Repeat the process until the last operation finished, then we can obtain the corresponding MA vector (3, 4, 1, 2, 2, 1, 3, 4, 1, 2).

Table 4 Modified approach by localization

The key idea of Earliest Finish Time is taking into account the processing time and the earliest started time of resources on basis of assigned operations.

For the initialization of WA, random rule and Earliest Finish Time are used. The rules are just the same as the ones in OS and MA, respectively.

In this paper, the proportions of each rule for all the three chromosomes are 50 and 50 %, respectively.

Global search structure

The global search is carried out by updating the position of particles. The position updating method of DPSO was presented to deal with flow job shop in (Pan et al. 2008). DPSO updates the particles directly in discrete domain, which enhance the search efficiency. We now further extend the method to DRC-FJSSP. The position of the particle is updated as follows:

$$\begin{aligned} X_i ^{k+1}=c_2 \otimes f_3 \left\{ \left[ c_1 \otimes f_2 \left( w\otimes f_1 \left( X_i ^{k}\right) ,pB_i ^{k}\right) \right] ,gB^{k}\right\} \end{aligned}$$

(13)

where $X_i ^{k}$ is the $i\hbox {th}$ particle at $k\hbox {th}$ generation, $w$ is the inertia weight, $c_{1}$ and $c_{2}$ are acceleration coefficients between [0, 1]; $pB_i ^{k}$ and $gB^{k}$ are the personal best and global best position in the swarm population at $k\hbox {th}$ generation; $f_{1}, f_{2}$ and $f_{3}$ are operators. The updating process contains $E_i ^{k}, F_i ^{k}$ and $X_i ^{k}$, and they are formulated as follows:

$$\begin{aligned} E_i ^{k}=w\otimes f_1 \left( X_i ^{k}\right) =\left\{ {\begin{array}{ll} f_1 \left( X_i ^{k}\right) ;&{}{\quad }r<w \\ X_i ^{k};&{}{\quad }{ otherwise} \\ \end{array}} \right. \end{aligned}$$

(14)

where $r$ is a uniform random number between [0,1]. If $r<w$, then $f_1 (X_i ^{k})$ is carried out. First, randomly choose two different operations and exchange them. MA and WA are adjusted correspondingly to keep the allocations of machine and worker unchanged. Second, randomly generate two integers $i$ and $j$ between 1 and $L$, then replace the $i$th machine of MA and the $j$th worker of WA with another machine and worker randomly chosen from the candidate machine and worker set, respectively.

$$\begin{aligned} F_i ^{k}=c_1 \otimes f_2 \left( E_i ^{k},pB_i ^{k}\right) =\left\{ {\begin{array}{ll} f_2 \left( E_i ^{k},pB_i^k \right) ;&{}{\quad }r<c_1 \\ E_i ^{k};&{}{\quad }{ otherwise }\\ \end{array}} \right. \end{aligned}$$

(15)

$f_{2}$ is the crossover operation for $E_i ^{k}$ and $pB_i ^{k}$, which has a Precedence Preserving Order based Crossover (POX) operation for OS, and two Rand-point Preservation Crossover (RPX) operations for MA and WA, respectively.

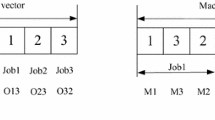
If $r<c_1$, then POX is carried out for OS. Randomly generate two nonempty job set $J_1$ and $J_2$, where $J_1 \cup J_2 =J$. Set $i=1$ and check whether the $i\hbox {th}$ operation in $E_i^k$ belongs to $J_1$ or not. If yes, then copy it to $F_i ^{k}$. If no, then check whether the $i\hbox {th}$ operation in $pB_i^k$ belongs to $J_2$ or not. If yes, then copy to $F_i ^{k}$. If no, repeat the above procedure by setting $i=i+1$. After repeating $L$ times, $F_i ^{k}$ is obtained. An example is illustrated in Fig. 1, where $J_{1} =\left\{ {2} \right\} , J_{2} =\left\{ {{1},{3}} \right\}$.

Fig. 1

POX crossover procedure

For the RPX of MA, first generate a vector $R=\left[ {r_1, r_2 ,\ldots ,r_L } \right]$, where $r_i \in (0,1)$ are random scalars for $i=1,2,\ldots ,L$. Record the indexes of $r_i$ if $r_i \le pf$, then find the corresponding operations in $pB_i^k$ and copy the corresponding elements of MA in $pB_i^k$ to the elements of MA in $F_i^k$. The self-adaption probabilities $pf$ is chosen as follows

$$\begin{aligned} pf=pf_{\max } -\frac{pf_{\max } -pf_{\min } }{ iter}\times \textit{gen} \end{aligned}$$

(16)

where iter is length of iteration, gen is the running time, $pf_{\max }$ and $pf_{\min }$ are the maximal and minimal self-adaption probabilities. The RPX of WA is the same as MA. An example is shown in Fig. 2, where $pf=0.6$ is calculated by (16).

$$\begin{aligned} X_i ^{k}=c_2 \otimes f_3 \left( F_i ^{k},gB^{k}\right) =\left\{ {\begin{array}{ll} f_3 \left( F_i ^{k},gB^{k}\right) ;&{}{\quad }r<c_2 \\ F_i ^{k};&{}{\quad }{ otherwise} \\ \end{array}} \right. \end{aligned}$$

(17)

$f_{3}$ is a crossover operation for $F_i ^{k}$ and $gB^{k}$, which has two RPX for MA and WA, respectively, and keeps OS unchanged.

Fig. 2

RPX crossover procedure

Local search for HDPSO algorithm

SA is an effective local search algorithm which allows occasional alterations that worsen the solution in an attempt to increase the probability of leaving local optimum (Kirkpatrick et al. 1983). In SA, the choice of neighborhood can significantly influences algorithm performance.

In this subsection an ISA technique which has variable neighborhood structures is used as the local search of HDPSO. The flow chart of the local search ISA is given in Fig. 3, where $T_0, T_{end}$ and $B$ are initial temperature, final temperature, and annealing rate, respectively. Generate two random variables $pr_1$ and $pr_2$, where $pr_1, pr_2 \in (0,1)$. $pr_1$ determines which neighborhood structure is used. $pr_2$ is the probability whether to accept a worse solution or not. $pl_1, pl_2 \in (0,1)$ are parameters to be chosen. The main feature of ISA is to randomly choose a neighborhood from $\hbox {NS}_{1}, \hbox {NS}_{2}$ and $\hbox {NS}_{3}$ when carrying out simulating annealing.

Fig. 3

Flow chart of the local search ISA

$\hbox {NS}_{1}$ for OS

If $pr_1 <pl_1$, then neighborhood structure $\hbox {NS}_{1}$ is carried out to change OS based on the critical path. The neighborhood structure based on critical path has been introduced to scheduling problem successfully (Li et al. 2011a, b). This method always finds the feasible solution and refined neighborhoods by interchanging under given regulations, but is sensitivity to local convergence (Li et al. 2011a, b). So a global neighborhood structure is used in the paper: randomly choose a critical path $CP=\left\{ {cp_{1}, cp_{2} \ldots cp_e } \right\}$, where $cp_e$ is a critical operation, $e$ is the total operation number of CP. Randomly generate two integers $x$ and $y$, where $x,y\in \left[ {{1},e} \right] , x\ne y$, then inserting an critical operation $cp_x$ to the front of the critical operation $cp_y$.

$\hbox {NS}_{2}$ for MA

If $pl_1 \le pr_1 <pl_2$, then neighborhood structure $\hbox {NS}_{2 }$ is carried out. To generate neighboring solution, $\hbox {NS}_{2}$ changes the assignment of the operations to the machines (Yazdani et al. 2010), which only adjust MA of the particle. $\hbox {NS}_{2}$ is applied as follows:

Step 1:

Calculate the workload of each machine and sequence them by the workload. Denote the machine sets by $\bar{{M}}_1, \bar{{M}}_2 ,\ldots , \bar{{M}}_{\max }$, respectively, where $\bar{{M}}_1$ and $\bar{{M}}_{\max }$ are the sets with minimal and maximal workload, respectively. Set $i=1$.

Step 2:

Randomly choose a machine $M_a$ from $\bar{{M}}_{\max }$, then check whether there are operations that can be operated on either any machine of $\bar{{M}}_i$ or $M_a$.

Step 3:

If yes, then denote the operations set by $\bar{{O}}_a$, randomly choose an operation $O_c$ from $\bar{{O}}_a$ and the operating machine is denoted by $M_b$. Assign $O_c$ from $M_a$ to $M_b$. If not, then set $i=i+1$ and go back to step2 until $i=\max -1$.

$\hbox {NS}_{3}$ for WA

If $pr_1 \ge pl_2$, then neighborhood structure $\hbox {NS}_{3}$ is carried out. $\hbox {NS}_{3}$ follows the idea of $\hbox {NS}_{2}$ and changes WA of the particle. The procedure of $\hbox {NS}_{3 }$ is similar to $\hbox {NS}_{2}$ and thus is omitted here for simplicity.

Procedure of HDPSO

Step 1:

Set parameters swarm size $P$, maximum of generation $G, w, c_{1}, c_{2}, T_0, T_{\mathrm{end}}, B, pl_1$ and $pl_2$.

Step 2:

Set $k=0$. Generate initial particle swarm $X^{0}=\{X_1^0 ,X_2^0, \ldots , X_P^0 \}$, initialize $gB^{k}$ and $pB_i ^{k}$.

Step 3:

Let $k=k+1$, then update the current particle swarm $X^{k}=\{X_1^k, X_2^k, \ldots , X_P^k \}$ by DPSO. Update $gB^{k}$ and $pB_i ^{k}$.

Step 4:

Choose $r\in [1,P/2]$ particles in the current population, executing local search based on ISA. Update $gB^{k}$ and $pB_i^{k}$.

Step 5:

If $k\le G$, then turn to Step 3, otherwise stop the loop and output the solutions.

Experiment results

In this section, several experiments are designed to test the performance of the proposed HDPSO. The experiments are implemented on a PC with VC$++$ 6.0, 2.0 GB RAM and 2.0 GHz CPU.

Preparation

First, instances R1–R10 are randomly generated with parameters shown in Table 5 and they are also subject to the following constraints: (a) the processing time of each job is $t_{ pqh}$, where $t_{ pqh}$ is a random integer between [2,20]. (b) every operation can be processed on two different machines. (c) each worker is able to operate $i$ machines, where $i$ is a random integer between [1,3]. Then, these instances R1–R10 are used to analyze the parameters and test the validity of ISA.

Table 5 Descriptions of instances R1–R10

Finally, two collections of benchmark instances are used to compare the proposed HDPSO with other algorithms. One collection is four classic FJSSP $n\times m$ benchmark instances (Kacem and Hammadi 2002) with only machine resource constraint, where the dimension of Q1, Q2, Q3 and Q4 are $4 \times 5, 8 \times 8, 10 \times 7$ and $10 \times 10$, respectively. The other collection is $n\times m\times b$ instances C1 (Ju and Zhu 2006), C2 (ElMaraghy et al. 2000), C3 (Cao and Yang 2011) and C4 (Liang and Tao 2011) for DRC-FJSSP where the dimension of C1, C2, C3 and C4 are $4\times 6\times 4, 4\times 10\times 7, 6\times 6\times 4$ and $10\times 6\times 4$, respectively.

Since the parameters to be tested are the inertia weights $w$ and learning factors $c$, thus the other parameters are chosen according to the way in (Xia and Wu 2005; Zhang et al. 2012) and then through various experimental tests. The parameters are chosen as follows:

$$\begin{aligned}&T_0 =3,T_\mathrm{end} =0.01,B=0.9,pl_1 =0.6,pl_2 =0.8,\\&\quad pf_\mathrm{max} =0.9,pf_\mathrm{min} =0.2,P=100,G=100. \end{aligned}$$

Parameters analysis

In HDPSO, intertia weights $w$ and learning factors $c_1$ and $c_2$ have key impact. It is chosen that $c_{1 }=c_{2}$ in general and denoted by $c$. In order to obtain the appropriate values for $w$ and $c$, we solve R1–R10 by various values of $w$ and $c$. Nine values are chosen for both $w$ and $c$, and they are 0.1, 0.2, ...,0.9, respectively. The corresponding objective $F$ with each combination of $w$ and $c$ running 10 times on all instances R1–R10 can be obtained by (1)–(12). The obtained makespan are denoted by $F_{ijk}, i,j=1,2,\ldots , 9;k=1,2,\ldots , 10$, where $i, j$ represent the value of $w$ and $c$, and $k$ represents index of the instance R1–R10, for example $i=1, j=1$ and $k=1$ mean $w=0.1, c=0.1$ and instance R1, respectively.

Then the range analysis method (Xia 1985) is used for the analysis and the result is shown in Table 6. The evaluation value of two parameters are defined as $S_i^w =\sum \nolimits _{j=1}^9 {\sum \nolimits _{k=1}^{10} {F_{ijk} } }, \quad i=1, 2,\ldots ,9$ and $S_j^c =\sum \nolimits _{i=1}^9 {\sum \nolimits _{k=1}^{10} {F_{ijk} } } ,j=1,2,\ldots ,9$, respectively, where the upper and the lower index of $S_i^w$ or $S_j^c$ are the parameter and the level, respectively. Another evaluation values $\bar{{S}}_i^w$ and $\bar{{S}}_j^c$, are defined as $\bar{{S}}_i^w =S_i^w /900$ and $\bar{{S}}_j^c =S_j^c /900$, respectively. The range value is defined as $S_w^{\prime } =\max S_i^w -\min S_i^w$ and $S_c^{\prime } =\max S_j^c -\min S_j^c$.

Table 6 The experimental results of parameter combination

From Table 6, we can see $\bar{{S}}_i^w$ achieves the minimal value 172.24 on level 1 for parameter $w$, and $\bar{{S}}_j^c$ achieves the minimal value 172.85 on level 9 for parameter $c$. Then it can be seen in this test $w=0.1, c=0.9$ is the best parameter combination. In the following experiments, $w$ and $c$ are chosen as 0.1 and 0.9, respectively. As for the range value, we can see that the two parameters have the same impact to the results by $S_w^{\prime } =S_c^{\prime } =4.44$.

The validity test of ISA

In this subsection, the validity of introducing ISA is tested by comparing HDPSO with DPSO. R1–R10 randomly run 10 times with iterations $G=100$ and results are shown at Table 7, where $\textit{ARE}=(\textit{AF}-C^{*})/C^{*}\times 100\,\%$ is the average relative error, $C^{*}$ is the best solution with the two algorithms, BF is the best fitness, AF is the average value of 10 runs, WF is the worst fitness, and AT is the running time.

Table 7 The results of HDPSO and DPSO with the same iterations $G = 100$

It can be clearly seen from Table 7 that HDPSO achieve better BF and WF on all the instances, which means HDPSO has stronger ability to get the better solution compared with DPSO. As can be seen in Fig. 4, HDPSO obtained smaller ARE than DPSO, indicating HDPSO is more stable. However, the drawback of HDPSO is that the runtime is longer than DPSO, showing HDPSO has a little more time consuming.

Fig. 4

The ARE comparison chart of HDPSO and DPSO with the same iterations $G=100$

The performance of HDPSO and DPSO are tested with the same runtime. The runtime is chosen to be 5 s. Table 8 shows the experimental results, from which we can see HDPSO achieves better ARE, BF, AF and WF on instances R1–R3, R5, R7–R10. As for the AG, HDPSO is better on all instances than DPSO, which means the convergence speed is faster. That is to say, even in a time-critical setting, HDPSO is still more effective than DPSO.

Table 8 Results of HDPSO and DPSO with the same runtime

Thus, it can be concluded from the experimental results in this subsection that ISA enhance the ability of both exploitation and exploration besides adding some computational time in solving the DRC-FJSSP.

Results comparisons

In this subsection, two sets of benchmark examples are employed to compare the proposed HDPSO with other algorithms. The first set of examples is for single-resource constraint problems and the other set is for DRC-FJSSP.

Single resource constraint problems

Table 9 shows the results of our approach HDPSO compared with the algorithms of AL$+$CGA (Kacem and Hammadi 2002), MOPSO$+$LS (Moslehi and Mahnam 2011) and ABC (Wang et al. 2012). We can see our approach can find the optimal solution for all the four Kacem instances (Kacem and Hammadi 2002). So the proposed approach is also effective to solve single-resource constraint job scheduling problems.

Table 9 Results of the four Kacem instances

Table 10 Results of the four DRC FJSSP instances

DRC-FJSSP

For DRC-FJSSP, C1 is used to compared with GA (Ju and Zhu 2006), C2 is used to compared with GAs (ElMaraghy et al. 2000), C3 is used to compared with $\hbox {IGA}_{2}$ (Cao and Yang 2011), and C4 is used to compared with GATS (Liang and Tao 2011). The results are showed in Table 10. For instances C1 and C3, the optimal values are the same as the best solutions of the other algorithms.

For instances C2 and C4, the optimal solution of HDPSO is better than the best solutions of other algorithms. Figure 5a, b give the Gantt chart of the optimal solution for instance C2 obtained by HDPSO and Fig. 6a, b give the Gantt chart of the optimal solution for instance C4 obtained by HDPSO. M and W stands for machine and worker, respectively. The number following M or W is the index of the resource number. The 3-digit number in the blocks are job number, operation number and resource number (machine number or worker number) respectively. “A” stands for the number 10.

Fig. 5

a Machine Gantt chart of problem C2 ($F=50$). b Worker Gantt chart of problem C2 ($F=50$)

Fig. 6

a Machine Gantt chart of problem C4 ($F=46$). b Worker Gantt chart of problem C4 ($F=46$)

Conclusions

This paper solved the DRC-FJSSP by presenting a HDPSO algorithm with improved SA technique. The main benefits of this algorithm include the exclusion of infeasible solutions and improvements of the local search ability. Experimental results showed the effectiveness of the proposed method and the superiority over some available results.

The computation time is a critical issue that limits the application of this method. Moreover, some parameters in the algorithm are chosen not in a systemic way. How to choose more appropriate parameters for the algorithm is also helpful in improving the performance. Since other objectives such as production cost and total overload are also important in the manufacturing systems, multi-objective case for the considered problem is an interesting and important topic that deserves investigation.