Solving large scale disassembly line balancing problem with uncertainty using reinforcement learning

Abstract

Due to increasing environmental concerns, manufacturers are forced to take back their products at the end of products’ useful functional life. Manufacturers explore various options including disassembly operations to recover components and subassemblies for reuse, remanufacture, and recycle to extend the life of materials in use and cut down the disposal volume. However, disassembly operations are problematic due to high degree of uncertainty associated with the quality and configuration of product returns. In this research we address the disassembly line balancing problem (DLBP) using a Monte-Carlo based reinforcement learning technique. This reinforcement learning approach is tailored fit to the underlying dynamics of a DLBP. The research results indicate that the reinforcement learning based method is able to perform effectively, even on a complex large scale problem, within a reasonable amount of computational time. The proposed method performed on par or better than the benchmark methods for solving DLBP reported in the literature. Unlike other methods which are usually limited deterministic environments, the reinforcement learning based method is able to operate in deterministic as well as stochastic environments.

Introduction

Rising environmental concerns and depletion of the Earth’s natural resources have forced governments of the industrialized countries to take preventative measures. These governments are pushing original equipment manufacturers (OEM) to design environmentally friendly products and engage in environmentally friendly practices to reduce the effect of products on the environment. Products, nowadays, are returned to OEMs at the end of their lifecycle. Once the end-of-life (EOL) products are sent back by customers, OEMs either send these products to third party product recovery facilities (PRF) or explore various EOL strategies themselves to get the most benefit out of these EOL products and minimize their adverse impact on the environment. In Europe, OEMs carry out product recovery operations even though no profit is realized. The European Union (EU) governments force European manufacturers to reclaim their products at the end of products’ functional life and engage in EOL activities to minimize the damage done to the environment by the EOL products (Lambert and Gupta 2005a, b; Gupta and Lambert 2008; McGovern and Gupta 2011). The scenario is slightly different with the US based OEMs. Manufacturers in the US are reluctant to accept the extended product responsibility because legislations in the US

Returned products arrive at the PRFs (or at OEMs) in a variety of conditions. Depending on the condition of a returned product different product recovery operations are utilized to extract the most benefit out of the returned products. Recycling is a viable option if the returned products contain valuable metals such as gold (Au) and platinum (Pt). If the returned products are in a good condition in terms of quality and functionality (which means they are not worn out, or they were used properly during their functional lifetimes) then they are either put through various remanufacturing processes to bring them back to like-new conditions or disassembled for component recovery purposes. The disassembly of EOL products and component recovery lead to significant environmental benefits. The consumption of the Earth’s natural resources to manufacture brand new components is reduced by re-use of recovered components; this practice also cuts down energy emissions due to incineration slows down piling up of landfills due to excessive disposal. Disposal and incineration of EOL products are always an option; however OEMs and PRFs consider these options viable only if the returned products are beyond redemption and pursuing other recovery strategies are economically infeasible (Banda and Zeid 2006).

Current literature on reverse logistics considers disassembly/remanufacturing as the first operational step in the reverse logistics domain (Reveliotis 2007). The reverse logistics domain can be divided into two stages: pre-disassembly/ remanufacturing and post-disassembly/remanufacturing. There exists many scheduling, planning, and optimization problems associated with these two interdependent stages; however these problems are beyond the scope of this research. Disassembly is a link between the two aforementioned stages of reverse logistics. Disassembly domain houses a large set of problems which have been studied by researchers thoroughly over the last two decades (Tang et al. 2002; Turowski et al. 2005). In this research we address the disassembly line balancing problem (DLBP) using a machine learning technique known as reinforcement learning (RL) (Aissani et al. 2011).

A typical disassembly line consists of a series of workstations oriented according to the disassembly sequence of the returned EOL products (Gungor and Gupta 1999a, b, 2002). DLBP tries to determine the sequence of operations that balance the line evenly. The term “balance” is used with varying connotation from one study to another; however generally it implies assigning disassembly operations to workstations to build a feasible sequence of disassembly tasks in which the minimum number of workstations is achieved and the variation of idle time among workstations is minimized (Gungor and Gupta 1999a, b; Tang and MengChu 2006). The feasibility of a sequence depends on various factors such as precedence relations among components, demand rate for the components, and the existence of environmentally hazardous components in the product. Line balancing is carried out to determine the most efficient sequence of operations to disassemble a given product. We will elaborate on the different performance measures in “Objectives formulation” section.

Literature review

Among all the problem domains investigated in the disassembly domain, DLBP is the one which has been studied the most extensively so far. DLBP is first introduced by Gungor and Gupta (1999a, b). They introduced the disassembly precedence matrix (DPM) representing the precedence relationships among the parts; they used a priority function in a heuristic approach to solve simple DLBPs. Researchers discussed the complications of DLBP in the presence of task failures and presented algorithms to solve the problem with the goal of assigning tasks to workstations to minimize the cost of defective parts probabilistically (Gungor et al. 2001; Gungor and Gupta 2002). Several of the studies used exact algorithms to find optimal sequences for EOL products with small number of components (Lambert 2001, 2007). However, the problem space increases drastically as the number of components in an EOL product increases (Gupta and Gungor 2001; Tang et al. 2002). Researchers soon realized that exact algorithms were inadequate to solve larger problem instances (Giudice and Fargione 2007; Martinez et al. 2009).

For any given product with $K$ number of components, the solution space for the balancing problem contains $K$! different task sequences, including both feasible and infeasible. Exact methods are able to handle small size problems (Lambert 2007); however, they quickly become inapplicable as the number of components in a product increases. It is necessary to reduce the solution space by eliminating infeasible sequences. Commonly precedence relations among the components are used to reduce the size of the problem. Graph techniques, such as petri nets or AND/OR graphs, are also used to construct a feasible set of disassembly operation sequences (Tadao 1989; Homem de Mello and Sanderson 1990). If there are other constraining criteria specific to the problem under consideration, they can be applied for further reduction of the solution space.

The aforementioned challenge with the increased problem size has led researchers to focus on heuristic approaches (Zeid et al. 1997; Pan and Zeid 2001; Veerakamolmal and Gupta 2002). A balancing function and associated four objective functions for DLBP are suggested by McGovern and Gupta (Gupta et al. 2004; McGovern and Gupta 2007a, b). Later several heuristic approaches were applied to address DLBP: two-phase approach (Greedy/2-Opt) (McGovern and Gupta 2007a, b), ant colony optimization (ACO) (Agarwal and Tiwari 2006; McGovern and Gupta 2007a, b), then genetic algorithm (GA) (Kongar and Gupta 2006; McGovern and Gupta 2007a, b; Seo et al. 2001) and H-K meta-heuristics. These approaches are presented and compared along with a greedy/hill-climbing heuristic hybrid (McGovern and Gupta 2004a, b; Kizilkaya and Gupta 2005; McGovern and Gupta 2011) and a novel uninformed general-purpose search heuristic (McGovern and Gupta 2007a, b). GA has been used in disassembly sequencing by Kongar and Gupta (2006) and McGovern and Gupta (2007a, b). Altekin et al. (2008) discussed disassembly line balancing with limited supply and subassembly availability. They presented two DLBP formulations to maximize the profit per disassembly cycle and the whole planning horizon.

DLBP, in general, does not involve a dynamic production environment. Hence, challenges involved with this problem domain are caused by product/component level complexities. While sequencing disassembly tasks are carried out, solution approaches proposed so far in the literature give priority to early disassembly of environmentally hazardous components and high-demand components (Gungor and Gupta 1999a, b; Gupta and Gungor 2001; McGovern and Gupta 2007a, b). Whether or not a component is environmentally hazardous is usually known in advance. However, it is a known fact that seasonal trends can affect the demand for a certain component. Hence, demand for individual components in a certain type of product is stochastic yet all the solution methodologies proposed so far treat demands deterministically. For the sake of practicality and generality, this issue has been addressed in this research.

Problem description

DLBP is a pre-operational design issue. Criteria applied or, more importantly, solution methodologies implemented to address DLBP vary from situation to situation. Our research treats DLBP as a stochastic problem. As such, we introduce a new methodology based on the reinforcement learning (RL) algorithm to solve stochastic DLBP problems. Another added benefit to our new methodology is that it can handle the large solution spaces when products have many components.

We apply our methodology to both small and big products. We aim to determine a balanced order of disassembly operations for desktop computers and cellular phones which have eight and twenty five salvageable components respectively. Information regarding individual task times and workstation cycle time as well as other related data such as number of demands for individual components and hazardous component information are obtained from earlier studies (Gupta et al. 2004; Lambert and Gupta 2005a, b; McGovern and Gupta 2007a, b). Before addressing the challenges that arise due to the problem size, we state the main objectives (targets) of our research:

• 1. Apply the RL techniques to DLBP to bring in a new approach to the problem domain which has been dominated by heuristic approaches. The RL techniques are very powerful especially in dynamic environments which require a high level of adaptation.

• 2. Investigate the effectiveness and efficiency of the RL techniques by comparing their performance to other existing solution methodologies.

• 3. Incorporate stochastic element(s) of the DLBP domain to assure that RL approach is practical enough to handle the dynamic elements of the environment.

We make the following assumptions in our solution methodology:

• Only a single product type is disassembled

• Incoming products have an identical structure

• The disassembly precedence relations are known

• Task times are known in advance

• Variation of a particular task time is considered negligible hence the cycle time is treated constant

• Product conditions are not taken into account

• Hazardous components are identified in advance

• Initially, demands for components are assumed to be known in advance for benchmarking purposes; this assumption is once the procedure is verified

There are certain elements in the disassembly domain which make solutions to DLBP more complicated compared to those of their assembly counterparts. Disassembly line design issues and operational issues are often tied to a high level of uncertainty. This uncertainty usually stems from products, demands or the line itself. The nature and the implications of these uncertainties are beyond the scope of this work. The reader is referred to Gungor and Gupta (1999a, b) (Gupta and Gungor 2001) for an extensive review of complications associated with disassembly lines and for the discussion on factors that make a disassembly line more complex than its assembly counterparts. In this research, we are concerned with uncertainty that stems from a single source: demand fluctuations.

Reinforcement learning framework

RL stems from the idea of learning by interacting. The goal is to learn what to do (mapping situations to actions) through experience without relying on anything but the reinforcement received from the environment (Watkins 1989; Watkins and Dayan 1992; Russell and Norvig 1995; Sutton and Barto 1998; Tewari 2007). In its simplest form RL framework works according to the following logic: at any given time $t$, the decision making agent (DMA) perceives the state of the environment and executes an action; the environment responds to this action by generating a numerical signal called reward/punishment/reinforcement (Sutton and Barto 1998). It is through this signal the DMA understand whether or not it has made a good decision. Figure 1 illustrates the components of an RL framework. The implementation of RL techniques begins with structuring the state space, action space, and reinforcement signal according to the problem under focus.

Fig. 1

RL framework

State representation captures the necessary information about the environment and communicates this information to the DMA. Action space contains a set of actions which are available to the DMA at any given time $t$. The DMA selects actions based on action-selection methodologies. When the DMA selects and executes an action the state of the environment changes. The DMA perceives the consequences of that action through the changes in the state. Agent receives a reward (reinforcement) from the environment, based on the merit of this new state. In turn, reinforcement signal helps the DMA evaluate the strength of immediate actions.

The RL logic is mapped to values. The mapping lets DMA track the long term performance of its actions selected in various states. Value mapping is achieved by making use of several different functions. In this research we utilize the Action-Value (state-action value) function, or in RL jargon Q-values, to facilitate the learning. For a set of finite discrete states, $s\in S$, and a set of discrete actions, $a\in A(s)$, the action-value function is denoted as follows:

$$\begin{aligned} Q^{\pi }(s,a)&= E_\pi \left\{ {R_t |S_t =s,a_t =a} \right\} \nonumber \\&= E_\pi \left\{ {\sum \nolimits _{k=0}^\infty {\gamma ^{k}r_{t+k+1} |S_t =s,a_t =a} } \right\} \end{aligned}$$

(1)

where $\upgamma$ denotes the discount rate. Discount rate takes a value in the $0<\gamma \le 1$ range; it represents the present value of rewards received in future states. The function given above represents the value of taking action $a$ in state $s$ under a policy $\pi$ $Q^{\pi }(s, a)$ denotes the expected reward received starting from $s$, taking action $a$, and thereafter following policy $\pi$. A policy, $\pi$, is a mapping from state $s\in S$ and action $a\in A(s)$ to the probability $\pi (s,a)$. Simply put, policy is the probability of selecting an action $a$ in a given state, $s$. RL procedures commonly defined as on-policy or off-policy depending on whether or not they strictly follow a policy or not.

RL algorithms are categorized into three major families of algorithms, namely, dynamic programming, Monte-Carlo, and temporal difference (TD-learning). For further information on specific strength and weaknesses of each family of algorithms the readers can refer to literature (Russell and Norvig 1995; Sutton and Barto 1998) for an overview of reinforcement learning techniques.

In this paper we utilize the RL framework for the following reasons:

• 1. RL algorithms are proven to yield optimal results when applied to Markov Decision Problems. Two problems we focus in this paper are modeled as Markov Decision Problems with appropriate state, action, and reward representations.

• 2. We expect that RL approach to yield results that are at least as good as those given by the existing solution methodologies. We support this claim by benchmarking our RL approach to existing solution approaches. The results are presented in section “Results and analysis”.

• 3. Our goal is to present a solution approach that is generic and applicable to variants of DLBP. Also, the Monte-Carlo RL solution framework we adopted does not require unrealistic inputs such as transition probabilities and expected immediate reward.

Objectives formulation

The proper metrics need to be identified in order to facilitate and enhance the learning (via Reinforcement signal) of the RL approach. We utilize the balance metrics developed by McGovern and Gupta (2007a, b) because the functions they developed capture the goal statement discussed in section “Introduction”. We identify and formulate the following objectives to achieve our stated goal:

• 1. Minimize the number of work stations for a given cycle time.

• 2. Balance the disassembly line (minimize the variation of the station idle times throughout the system).

• 3. Remove hazardous components early in the disassembly sequence.

• 4. Remove high demand components on priority in the disassembly sequence.

There exist several “balance measures” in the literature (Gupta et al. 2004; Lambert and Gupta 2005a, b; Kongar and Gupta 2006; Altekin et al. 2008) which are developed to bring mathematical context to the generic goal statement discussed in section “Introduction”. We use the following notation to formulate the objectives:

$N_{w}$::

Number of work stations required for a sequence

$T_{c}$::

Cycle time

$T_{sj}$::

Time taken by the workstation $j$ to complete assigned tasks to it

$C_{k}$::

$k$th component in a disassembly sequence

$h_{C_k }$::

Binary number indicates the hazardousness of the component; 0 if the $k$th component in a disassembly sequence is non-hazardous, else 1

$d_{C_k }$::

The demand of the $k$th component in a disassembly sequence

$n_t$::

Number of times part $t$ is assigned to the sequence

$m$::

Number of disassembly tasks

$T_{\mathrm{ri}}$ :

Part removal time of component $i$

In this research we seek to address the DLBP by utilizing RL techniques. The formulation of four objectives is described below:

First and Second Objectives: These objectives complement each other. The McGovern–Gupta balance function (McGovern and Gupta 2007a, b) simultaneously minimizes the number of workstations needed to operate the disassembly line and variation of idle time among the workstations that are utilized.

$$\begin{aligned} F=\sum _{j=1}^{N_w } {\left( {T_c -T_{sj} } \right)^{2}} \end{aligned}$$

(2)

Eq. (2) denotes the McGovern–Gupta balance function. The minimization of this function gives

$$\begin{aligned} F_{1\min } =\min \left\{ {\sum _{j=1}^{N_{w}} {\left( {T_{c}-T_{sj}} \right)^{2}} } \right\} \end{aligned}$$

(3)

The system idle time and number of workstations necessary to run the disassembly operations are minimized so that the line efficiency is maximized. A perfect balance is attained when $F_{1i} =0$.

Third Objective: Remove hazardous components earlier in the sequence to avoid contamination of the desired parts or breakdown of disassembly workstations.

$$\begin{aligned} F_{2\min } =\min \left\{ {\sum _{k=1}^m {\left( {k\cdot h_{C_k } } \right)} } \right\} \end{aligned}$$

(4)

Fourth Objective: Remove high demand components as early as possible in the sequence:

$$\begin{aligned} F_{3\min } =\min \left\{ {\sum _{k=1}^m {\left( {k\cdot d_{C_k } } \right)} } \right\} \end{aligned}$$

(5)

We also have the following constraints along with the aforementioned objectives: (i) the precedence constraints shown in Figs. 2 and 3; (ii) for any workstation $j$, the time it takes to complete the assigned tasks cannot exceed the cycle time, in other words, $T_{sj} \le T_c$; (iii) each disassembly task must be assigned to the sequence and can be assigned only once, which means $n_{t} =1$.

Fig. 2

State and action representation

Fig. 3

Reinforcement signal propagation

Unlike in an assembly line in which the demand occurs at the end of the line, demand for components can arrive at any of the workstations on a disassembly line. Each component is associated with a demand. To enhance the recovery or recycle of useful components or materials means to maximize the disassembly line efficiency. In the disassembly sequence, a required part may be preceded by other parts which can prolong the access time to the desirable part. A sequence that removes the high demand components as early as possible shortens the response time of obtaining the desired components and improves the customer satisfaction.

Applying RL to DLBP

In order to define the states, actions, and reward structure of the RL implementation we make use of the precedence graphs between the components during the disassembly analysis. Similarly we also use the precedence graphs to reduce the size of the solution space. The disassembly precedence graphs can be viewed as regions with $m$ number of destinations which are to be visited only once. The only restriction is that a certain node $x$ is not allowed to be visited unless all the predecessor nodes are visited prior to $n$. A full sequence is formed when all the disassembly tasks are covered in the sequence. The quality of the full sequence is known to the DMA only when a sequence is completed. This approach of traversing the precedence graphs is very similar to finding a path in the well-known Traveling Salesman Problem (TSP). This approach allows us to address the dimensionality issues.

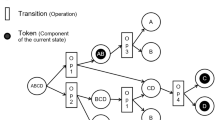
The RL map traversing procedure in the present work follows an episodic execution. An episode starts when the agent is at the beginning state, i.e. the first node in the disassembly precedence graph and it ends once the sequence is complete and the reward is received from the environment when the agent has visited all the destinations in a region. So, state space $S$ is represented as the disassembly tasks $\{1,2,\ldots ,m\}$ which are required to be completed in order to disassemble the product. At a given time $t$, the agent is at a certain node $x$ of the disassembly precedence graph, which represents the agent’s current state. The agent is allowed to choose from a set of feasible actions to proceed to the next state. The number of feasible actions depends on the agent’s current state. In the current representation of the problem, the number of available actions can be viewed as the nodes that can be visited in compliance with the precedence constraints. In a practical sense, this dynamic action space approach allows the DMA to select an action without computing the desirability (or rather undesirability) of infeasible actions. The nodes which are already visited are removed from the action space for that episode and the remaining episodes. This is done to ensure that all the disassembly tasks are put into the sequence only once. After an action is selected, the destination node is appended to the sequence and the destination node becomes the current state for the agent. Thus, the size of the action space $A$ varies depending on the current state $s$. The aforementioned cycle continues, until a full sequence is formed (meaning all the disassembly tasks are included in the sequence). Once a full sequence is formed, the reinforcement signal $R$ is received by the agent. The reward $R$ is computed according to the objective functions described by Eqs. (2)–(5). Figure 2 illustrates the state and action representation.

Once the reinforcement signal $R$ is received, it is distributed to all the state-action pairs to update their values. Figure 3 illustrates the propagation of the reinforcement signal.

Similar to heuristic and meta-heuristic approaches, RL framework is also problem specific. This means the state, action and reinforcement representations are defined according to the problems under focus. Our framework is unique because while the learning is achieved through sampling, the long-term desirability of state-action pairs is computed and updated iteratively to attain optimal decision making capabilities. Therefore the computational inefficiency of sampling is compensated by simple and more efficient update rule. The update rule and action selection mechanisms are discussed in section “Disassembly problems”.

Disassembly problems

We intend to apply the RL approach to two different problems. First we test the RL approach on a small scale problem in order to verify that it is working properly. We consider a desktop computer (PC) with eight salvageable components for RL approach. Part removal times ($T_{ri}$) and demands for each part are listed in Table 1. We also obtained data regarding the hazardousness of each component. This information is utilized in the analysis stage. The cycle time, $T_{c}$, for this problem is 40 s.

Table 1 Disassembly tasks, part removal times and demand data for PC (McGovern and Gupta 2007a, b)

The solution space for this problem is reduced significantly due to precedence relations among the components. In the precedence graph presented in Fig. 4, dashed lines represent soft precedence relations between the components whereas solid lines represent strict precedence relations that must be followed to disassemble the PC.

Fig. 4

Precedence graph for PC

In the second problem, we consider a cell phone with twenty five salvageable components. In this case, the size of the problem state space is dramatically larger than that of the first one. We use this problem to test how efficiently the proposed RL method handles a problem of larger scale with high complexity. Data associated with the second problem is presented in Table 2. We should mention that the cell phone problem, unlike the PC problem, does not have a closed (exact) solution.

Table 2 Disassembly tasks, part removal times and demand data for a cell phone (Gupta et al. 2004)

Similar to the PC problem, the cell phone problem also has precedence constraints. The corresponding precedence graph is illustrated in Fig. 5. The nodes labeled as DS and DF denote “disassembly start” and “disassembly finish” respectively. According to the studies carried out in the literature, the average number of components in products which are widely used varies between 8 and 16 (Tang et al. 2002). In the cell phone case we are dealing with a type of product that is more complex than an average product due to the number of component the former contains.

Fig. 5

Precedence graph for cell phone

The implementation of the RL procedure begins with initialization. In the beginning of the execution all the state-action pairs (Q-values) are initialized to 0. The execution consists of three stages. During the initial stage (first 20,000 episodes) the agent is allowed to follow a random policy. In the second stage ($20,000$th–34,000th episode) the agent switches to soft policy during which actions are assigned a probability of selection based on their Q-values. In the beginning of the second stage, the actions are still selected more or less randomly to allow the agent to explore the solution space. As the Q-values of state-action pairs get updated, the agent starts to behave more greedily by selecting actions with larger Q-values at a given state. Eventually (after the 34,000th episode), the procedure switches to a totally greedy policy marking the beginning of the third and final stage of the execution by selecting the action that yields the maximum Q-value at each state. Q-values eventually converge to their respective maximal values and the actions that yield better results become distinctive during the later stages of the learning process. Thus, at this point, further exploration of the solution space becomes unnecessary. During the second stage of the execution, the DMA utilizes the Boltzmann machine to select action (Watkins and Dayan 1992; Sutton and Barto 1998; Tewari 2007), i.e.

$$\begin{aligned} \Pr (A=a|S=s)=\frac{e^{Qt(a)/\tau }}{\sum _{b=1}^{n_a } {e^{Qt(a)/\tau }} } \end{aligned}$$

(6)

Boltzmann machine enables the agent to assign probabilities of selection to actions available to it at a given state $s$ at time $t$ based on the state-action values. In Eq (6), $\uptau$ denotes the temperature and $n_{a}$ denotes the total number of actions available to agent at state $s$. Larger numerical values are assigned to parameter $\uptau$ initially to facilitate exploration. As the learning process progresses, $\uptau$ value is reduced gradually to allow the selection of actions with larger Q-values to enable the agent to behave more greedily. One drawback of Boltzmann action selection mechanism is that if the Q-values of state-action pairs are too close to each other, it will not be able to distinguish good actions from the inferior ones. If this is the case, other action selection mechanisms are to be explored. In this research, the reward mechanism allows the Boltzmann machine to differentiate good actions from the inferior ones.

The agent does not receive a reinforcement signal immediately after performing an action. Instead, the agent receives the reinforcement signal upon the completion of a disassembly task sequence. This event is known as delayed-reward by the RL practitioners. In this case, the aforementioned delayed-reward event occurs because the agent cannot become aware of its performance until a full-sequence is formed; in other words, a sequence cannot be evaluated unless it is complete.

Reinforcement signal received by the agent needs to be a scalar value in order to be used to update the Q-values. All of the objectives are listed and formulated in section “Objectives formulation” so that when sequencing of the disassembly tasks is completed, there is a value associated with all of the objectives listed.

In the light of the above discussion, we formulated the reinforcement signal as follows;

$$\begin{aligned} R=\frac{1}{w_1 F_1 +w_2 F_2 +w_3 F_3 } \end{aligned}$$

(7)

Weights $w_{1}, w_{2}$ and $w_{3}$ are assigned to each objective value ($F_{1},\,F_{2}$ and $F_{3}$) to account for the relative importance of the objectives depending on the application. Also, these weights allow us to prioritize one objective over the others during the test runs. Therefore, assigning appropriate weights is more of an experimental concern than scientific decision making. Over the course of this research we determined weights in Eq. (7) based on experimental results and objective prioritization.

Once the agent receives the reinforcement signal, Q-values of actions taken at each state are updated following the on-policy Monte-Carlo approach (Pan and Zeid 2001). In its simplest form, the update rule is defined by

$$\begin{aligned} Q\left( {s,a} \right)\leftarrow average(Returns\left( {s,a} \right)) \end{aligned}$$

(8)

Equation (8) indicates that Q-value for state $s$ and action $a$ is updated based on the average reinforcement (reward or return) received by executing action $a$ at state $s$. Monte-Carlo approach strictly depends on sampling each state-action pair as many times as possible. This is why for a given number of episodes we allow the agent to follow a totally random policy; in other words we allow the DMA to go through a sampling period. If sampling is not sufficient, then the chance of converging to a sub-optimal solution(s) greatly increases. The pseudo-code shown in Fig. 6 lays out the logic that has been discussed and described in this section.

The Monte Carlo is a model free approach which means that the procedure can be implemented without needing further information from the environment. However, the number of episodes that the DMA has to run needs to be large enough to get the agent to a state at which it can start to distinguish good actions from the bad ones.

Fig. 6

Psuedo-code for the RL implementation

 

Results and analysis

The RL approach discussed in this paper section has been applied to PC and cell phone problems. We will first present the solution obtained for the PC to validate the proposed RL approach. The cell phone problem is used to test the efficiency of the RL approach on large and complex problems. We also benchmark our RL approach against the existing methods using the cell phone problem

Some of the optimal sequences obtained from solving the PC case are listed in Table 3. The values for Objectives 1, 2 and 3 listed in Table 3 are obtained by evaluating Eqs. (2–5). The value of Objective 3 is significantly larger than the corresponding values of Objectives 1 and 2. By utilizing weights $w_{1},\,w_{2}$ and $w_{3}$ in Eq. (7) the diminishing effect of Objective 3 value on other objective values is prevented. The quality of the solutions obtained is equivalent in terms of total number of workstations utilized and the distribution of the total idle time among the workstations.

Table 3 Solution for the PC disassembly

For the cell phone problem, the first group of test runs is implemented in a deterministic environment, which means we used the demand data utilized in earlier studies and assumed that the quantity of demands for each component is fixed. We will provide a breakdown analysis of a single near optimal solution obtained in a deterministic environment. Similar analyses were carried out in earlier studies (Gupta et al. 2004; McGovern and Gupta 2007a, b).

The solution shown in Table 4 is a sample of possible optimal solutions we were able to obtain using the proposed RL approach. The first row is the sequence itself; the second row gives the task time information (also known as part removal time, $T_{ri})$ for each disassembly task; the third row lists workstations assigned to which respective tasks, and lastly the fourth row lists the duration of the idle time at each workstation. Values obtained after evaluating the objective functions given by Eqs. (2–5) for this solution are listed in Table 5.

Table 4 Sample RL solution break down analysis for the cell phone disassembly

Table 5 Performance metrics for sample RL solution

To our knowledge, the best solution obtained so far for the cell phone line balancing problem is obtained by using the ACO meta-heuristic (McGovern and Gupta 2007a, b) with the performance measures listed in Table 6.

Table 6 Performance metrics for sample ACO solution

As Tables 5 and 6 show, both methods yield an equivalent solution because the number of workstations used, total system idle time and variation of idle time between the workstations are minimized. However, the RL method yields a better total objective value because the high demand components are removed earlier in the sequence. Regardless, we used the total objective value of the ACO meta-heuristic for benchmarking purposes. One drawback of the Monte-Carlo approach is that the agent is not always able to obtain the best solution simply because it does not experience these solutions sufficient number of times.

For the cell phone problem we prioritized the value of the first objective expressed by $F_{1}$, using the weights in Eq. (7). We observed that, the total objective value varied in a range due to the fluctuating values of the fourth objective expressed by $F_{3}$.

In Fig. 7 the total objective values obtained from 40 independent runs are plotted. The straight line represents the benchmark value from the ACO meta-heuristic. All of the 40 solutions obtained are equivalent to the optimal solution in terms of the total number of workstations and the total system idle time which are 9 and 7.0 respectively. In order to bring some statistical validity, we carried out the confidence interval analysis. We assume that the variation is normally distributed, and for a 95 % confidence interval the formulation is as follows:

$$\begin{aligned} P\left( {\overline{X} -1.96\frac{\sigma }{\sqrt{n}}<\mu <\overline{X} +1.96\frac{\sigma }{\sqrt{n}}} \right) \end{aligned}$$

(9)

In Eq. (9) $\bar{{X}}$ and $\sigma$ are sample mean and standard deviation respectively and $n$ is the population size. For this particular case, the sample mean and standard deviation of the population are 1046.275 and 31.194 respectively. If we substitute these numbers into Eq. (9) the 95 % confidence interval becomes (1041.343; 1051.207).

Fig. 7

A set of 40 runs and their outputs

For many practical reasons we set the stopping criteria for the execution as 37,000 episodes. This means, the execution will stop immediately after the 37,000th episode whether or not the agent has converged to optimality. If the DMA is able to find an optimal solution earlier than 37,000 episodes, the execution terminates earlier. The point of switch from a soft-max to a greedy policy indicates that the procedure has converged to optimality. We studied the average number of iterations it takes for the DMA to converge to optimality. Figure 8 illustrates the point in execution at which the procedure converges to optimality for 40 independent test runs. On average the agent converges to optimality after the completion of 31,636 episodes. This means, after following a random policy for 20,000 episodes the procedure is able to find the optimal solution after the completion of 11,636 episodes. However, Fig. 8 all by itself does not give a clue as to how the DMA behaves throughout the execution period. Thus we looked into the variation of the total objective value throughout the span of the execution in order to gain additional insights into the agent’s behavior.

Fig. 8

Converging points for the RL agent

Figure 9 illustrates the total fitness values obtained by the agent at the end of every episode during a test run, which converged to optimality after 27,056th episode. Fluctuations in the total objective value indicates that agent still behaves randomly for the first several thousand episodes after switching from the random policy to a soft-max policy. Fluctuations in the total objective value stop after the Q-values of certain state-action pairs, at a given state, become significantly larger than the others allowing the DMA to differentiate good actions from the inferior ones

Fig. 9

Episode by episode behavior of the agent

To incorporate demand stochasticity, we allowed the demand value, for each component, to fluctuate randomly between 1 and 9 in each episode during the test runs. Therefore, there is no observable demand pattern. In practice, demand fluctuates seasonally; however while testing the RL approach we intended to expose the agent to very extreme demand fluctuations in order to observe its effects on optimality of the solutions.

Figure 10 illustrates the effects of demand fluctuations on the optimality of workstation utilization in 40 independent runs made in a stochastic demand environment. The approach converges to inferior solutions in some cases in which 10 workstations are utilized and the total system idle time and the idle time variation among the workstations are much higher. In a sample of 40 test runs, the agent converged to a sub-optimal solution 8 times, which accounts for 20 % of the test runs. The variation of the total system idle time due to demand fluctuations is illustrated in Fig. 11. The total system idle time is tied to the total number of workstations utilized since an increase in the total number of workstations also suggests that task assignment is not carried out in the most efficient way thus resulting in high idle times at several workstations.

Fig. 10

Effects of demand stochasticisity on total number of workstations utilized

Fig. 11

Effects of demand stochasticity on total system idle time

Just like in case of the total number of workstations utilized, the agent converges to sub-optimal solutions in terms of total system idle time in order to compensate for the extremes of the demand fluctuations. In order to observe the effects of the randomness of the demand accurately, we set the weights in Eq. (7) in such a way that all the performance metrics have the same contribution to the overall fitness. This way none of the objectives mentioned in section “Objectives formulation” have a higher impact on the total objective value.

We also studied the effects of stochastic demands on convergence to optimality (or sub-optimality in this case). We observed that it took longer for the agent to converge to optimality but it was able to do so more consistently after around the same number of iterations.

Figure 12 illustrates in how many episodes the agent converges to an optimal (or sub-optimal as well) solution in 40 independent runs. On average, it takes roughly 33,223 episodes for the agent to converge to optimality. This number is higher than that of the deterministic case as mentioned earlier, but this is to be expected since it takes longer for the agent to adapt to very sudden and drastic demand fluctuations.

Fig. 12

Number of episode it takes for the agent to converge to optimality

Discussion and future research

In this paper we addressed a small and a large problem (PC and cell phone problems respectively) within the DLBP domain using an RL approach. We computed 5 different performance metrics which we think are important to assess a solution to the DLBP. These metrics are: the total number of workstations, the total system idle time, the distribution of total idle time among the workstations, the early removal of hazardous parts and the early removal of high demand components. We analyzed the performance of the RL approach for the two problems in both deterministic and stochastic environments. We tested and verified that the RL approach using the PC problem. Afterwards, the RL approach is tested on a larger scale problem, cell phone under deterministic assumptions. The approach converged to optimality 100 % of the time upon the completion of reasonable number of episodes. The results obtained when we applied RL to both problems prove the robustness of the RL approach; it was able to converge to optimality in both cases.

When we made some test runs in an environment in which demands for components of the product are stochastic we observed that our approach converged to inferior solutions 20 % of the time in terms of total number of workstations utilized, total system idle time, and distribution of idle time among workstations due to extreme demand fluctuations. Another interesting observation was that it took longer for the RL approach to converge to optimality when the number of demands for each component was stochastic.

One important drawback of addressing problems associated with DLBP using Monte-Carlo approach is that it is necessary to carry out the sampling; it means that unless the solution space is sufficiently explored the RL approach will most likely converge to a sub-optimal solution. To overcome this issue, we first let the agent explore the solution space by allowing it to follow a random policy for 20,000 episodes. This turned out to be a sufficient amount of exploration because in both deterministic and stochastic cases the agent was able to improve the policy and attained the optimal policy to follow (100 % when operating in a deterministic environment and 80 % in a stochastic environment). However, the need for sampling has an adverse effect on the computation time since the agent needs to complete an extra 20,000 episodes.