Optimizing bi-objective imperfect preventive maintenance model for series-parallel system using established hybrid genetic algorithm

Abstract

This study establishes a bi-objective imperfect preventive maintenance (BOIPM) model of a series-parallel system. The improvement factor method is used to evaluate the extent to which repairing components can restore the system reliability. The total maintenance cost and mean system reliability are optimized simultaneously through determining the most appropriate maintenance alternative. A bi-objective hybrid genetic algorithm (BOHGA) is established to optimize the BOIPM model. The BOHGA utilizes a Pareto-based technique to determine and retain the superior chromosomes as the GA chromosome evolutions are performed. Additionally, a unit-cost cumulative reliability expectation measure (UCCREM) is developed to evaluate the extent to which maintaining each individual component benefits the total maintenance cost and system reliability over the operational lifetime. This UCCREM is then incorporated into the genetic algorithm to construct a superior initial chromosome population and thereby enhance its solution efficiency. In order to obtain diverse bi-objective solutions as the Pareto-efficient frontier is approached, the closeness metric and diversity metric are employed to evaluate the superiority of the non-dominated solutions. Accordingly, decision makers can easily determine the most appropriate maintenance alternative. Three simulated cases verify the efficacy and practicality of this approach for determining an imperfect preventive maintenance strategy.

Introduction

The performance of a series-parallel system with multiple components, in terms of reliability, availability, and so forth, relies heavily on the designed configurations. Certainly, performing maintenance work is indispensable to ensure that a system is restored to a specific operational state and remains so. Many studies (Wang 2002; Nakagawa 2005) have treated a system configuration as a single piece of equipment in order to reduce the complexity of planning a preventive maintenance strategy for multiple components. However, this cannot actually elucidate the level of system performance, because determining preventive maintenance strategies for multi-component systems normally involves complicated mathematical calculations. Some studies (Bai and Pham 2006; Bris et al. 2003) have addressed this issue by focusing on each system component to determine an overall preventive maintenance strategy. As is well known, implementing maintenance work consumes human resources and entails considerable costs. Nonessential maintenance or inappropriate maintenance periods will squander the limited system maintenance resources. As compared with the perfect maintenance theory, the imperfect maintenance theory offers to better reveal system performance for a degraded component or device, since the maintenance work is performed on individual components. As a result, maintenance engineers can more safely ensure that a system fulfils its specific performance requirements.

Furthermore, the maintenance model is solved under the essential constraints of maintenance resources and minimal system performance requirements. The constrained model requires a more arduous calculation than unconstrained models in order to obtain the optimal solution. Accordingly, the computational expense of optimizing a preventive maintenance model increases significantly with the number of components and the complexity of the system configuration. As a result, the conventional analytical approach cannot obtain an exact solution within a reasonable time. Hence, to reduce the complexity of solution for each component, most studies consider either optimizing the maintenance work subject to fixed maintenance periods or optimizing the maintenance periods subject to certain maintenance work (Zequeira and Bérenguer 2006). Additionally, only a single objective is taken into account, such as minimization of maintenance cost or maximization of system reliability. Establishing a multi-objective maintenance optimization model can more fully explain the system performance and maintenance schedule than a single-objective model. From a practical viewpoint, decision makers benefit from simultaneously optimizing multiple system performance requirements to obtain diversified maintenance alternatives through optimized non-dominated solutions. Decision makers can then determine the most appropriate alternative for given system requirements and resource constraints. Therefore, this study strives to establish a bi-objective imperfect preventive maintenance (BOIPM) model optimizing total maintenance cost and mean system reliability by determining the maintenance periods of each component over its operational lifetime in a series-parallel system. The improvement factor method (Tsai et al. 2004) is employed to evaluate the extent to which maintaining components reduce the hazard rate and deterioration rate on the maintenance periods and thereby recovery system reliability.

Due to the inherent complexity of solving a preventive maintenance model, good results are obtained when meta-heuristic algorithms are extensively utilized to solve various aspects of the model. Examples include the system configuration designs, redundancy allocation problems (Gen and Cheng 1997; Hsieh et al. 1998; Tavakkoli-Moghaddam et al. 2008), reliability analysis (Bris et al. 2003), and preventive maintenance strategy (Quan et al. 2007). Moreover, developing multi-objective meta-heuristic algorithms is becoming increasingly essential from the viewpoint of efficient optimization of multi-objective preventive maintenance models such as the multi-objective genetic algorithm (GA) in fulfillment of practical requirements (Wang and Li 2011; Yamachi et al. 2006; Konak et al. 2006). However, there is still much room for improvement in the search mechanisms to further the efficacy of solving any specified multi-objective preventive maintenance problem.

The genetic algorithm is a solution approach that simulates the evolutionary process of natural beings by applying crossover and mutation mechanisms to predetermined chromosome structures. The setting of probabilities, regarding the crossover and mutation, guides the GA search in a direction that approaches the global optimum of the optimization problem. According to Baker and Ayechew (2003), the initial chromosome structures will considerably affect the ability to solve the problem. To enhance GA efficacy, some studies have aimed at constructing a tailor-made procedure that produces superior chromosomes if given the properties of the optimization problem. In that regard, this study considers properties associated with the BOIPM model established for a series-parallel system to construct superior chromosomes by evaluating the extent to which maintaining a component benefits the system performance. Accordingly, the component importance measures established by Birnbaum (Elsayed 1996) and the ratio criterion established by Bris et al. (2003) are improved to develop a unit-cost cumulative reliability expectation measure (UCCREM) that is hoped to more accurately evaluate the importance of components. The two previously developed importance measures have disadvantages that result in inappropriate evaluations of component importance. The newly developed UCCREM mainly evaluates the extent to which maintaining a component benefits the system performance in terms of reliability and total maintenance cost in accordance with the BOIPM model established that simultaneously optimizes mean system reliability and total maintenance cost. Additionally, a bi-objective hybrid GA (BOHGA) is established, with the UCCREM incorporated, to efficiently solve the BOIPM model established. The fundamental idea of the Pareto-based technique (Srinivas and Deb 1994; Fonseca and Fleming 1998; Deb et al. 2002) for non-dominated solutions of multi-objective problems is also incorporated by the simulated chromosome evolution procedure to generate the offspring and direct the search toward an ideal Pareto frontier. Furthermore, in order to obtain solutions that are diversified and distributed as the Pareto-efficient frontier is approached, the closeness metric and diversity metric (Wang et al. 2009; Deb 2001) are utilized to determine the superiority of chromosomes in the BOHGA established. The best settings of search parameters in the BOHGA established is determined by the response surface methodology (RSM) (Montgomery 2005) technique, instead of the conventional trial-and-error process, in the hope of extending the ability of the BOHGA to approach the ideal Pareto frontier. Finally, three simulated cases verify the efficacy and practicality of this work.

The remainder of this paper is organized as follows. Section “Literature review” reviews the literature on imperfect maintenance, multi-object maintenance strategy, and optimization algorithms. Section “Methods” describes the BOIPM model formulation, the UCCREM, and the established BOHGA. Section “Results and discussion” presents and discusses the results of three numerical simulations to demonstrate the efficiency of the proposed BOHGA. Finally, Section “Conclusions” concludes the paper.

Literature review

Imperfect maintenance

Maintenance activities, generally including corrective maintenance (CM), preventive maintenance (PM), predictive maintenance, and e-maintenance, are indispensible to ensure that a system is restored to a specific operational state and remains so. The status of a system is normally between as good as new and as bad as old as the imperfect maintenance work or preventive maintenance work is performed. Implementing a preventive maintenance plan can extend the operational lifetime of a system and reduce its failure rate. Pham and Wang (1996) considered the extent to which imperfect component maintenance restores system performance and they divided the evaluation approaches into eight different categories, including the ($p, q)$ rule, ($p(t), q(t))$ rule, improvement factor method, virtual age method, shock model method, ($\alpha , \beta$) rule, and multiple ($p, q)$ rule as well as the others. Among these approaches, the improvement factor method is the easiest to understand and in practice is the simplest to implement. Zequeira and Bérenguer (2006) established an imperfect maintenance model using the improvement factor method, which optimizes the total maintenance cost, and thus determined an optimal maintenance strategy. Tsai et al. (2001) employed the GA to optimize a constrained imperfect maintenance model that had conventionally employed the improvement factor method. The unit-cost life was optimized, while the worst allowable system reliability constituted the model constraint. A two-stage approach was established: first, determine the optimal maintenance periods; then, for each maintenance time point, measure the extension of system life per unit cost of components and thus determine whether the proper maintenance activity involves nothing, simple preventive work, or preventive replacements. Liao et al. (2010) showed that periodic preventive maintenance (PM) may easily overlook reliability issues due to the deterioration of the system with time and usage. A reliability-based sequential preventive maintenance model has been proposed for monitoring repairable deteriorating systems. When the system’s reliability reaches the threshold R, an imperfect repair technique is implemented to restore the system. The optimal threshold R and preventive maintenance cycle number are determined to minimize the system operation cost in the established PM model. Schutz et al. (2011) proposed an integrated strategy to determine jointly efficient business and maintenance plans. Two maintenance policies including a minimalist policy and a sequential policy are studied. Two meta-heuristic algorithms based on GA are developed to maximize the net profit defined by the achievement of missions minus maintenance costs. Castro (2009) established failure models for system components via a non-homogeneous Poisson process. The system is one composed of repairable and irreparable components. The failure rate of repairable components depends on the number of irreparable components in the system. The system cost is minimized by optimizing decision variables involving the amount of preventive maintenance and the corresponding maintenance periods from the time when operation begins until the time when the system cannot be restored to worst allowable reliability as performing maintenance works except replacement. Nahas et al. (2008) established an extended great deluge algorithm to minimize the total maintenance cost for a multi-state imperfect maintenance model subject to the worst allowable system reliability established by Levitin and Lisnianski (2000). The solution efficiency of Nahas et al. (2008) outperforms that of Levitin and Lisnianski (2000). Park et al. (2000) established a periodic preventive maintenance model, minimizing the expected cost per unit time by determining the amounts and periods of preventive maintenance over an infinite time span. In this model, a minimal repair is performed when a component failure occurs, restoring the system to its status prior to failure. Furthermore, preventive maintenance can decrease the rate of system degradation, while the hazard rate of the system continues to increase monotonically. Soro et al. (2010) focused primarily on a continuous Markov process for simultaneously evaluating the reliability, availability, and productivity of a multi-state degraded system. In their approach, the Poisson hazard rate simulates the temporal variation of the component failures associated with different system degradations. The assumption in the Markov process is that the system returns to its previous status after imperfect maintenance work is performed when the system is fatigued or a non-essential component fails. The Chapman–Kolmogorov equations are utilized to solve this model and obtain the stable probabilities of all system statuses and thereby simultaneously evaluate the reliability, availability, and productivity of the system. Tsai et al. (2004) established an imperfect maintenance model in which the activities of maintenance, repair, and replacement are taken into account. A two-stage approach is followed to optimize the model. In stage I, the identical maintenance period of all components is determined. The maintenance period of each component is determined initially by maximizing the system availability, and then the minimum of those maintenance periods is selected as identical maintenance period of all components. In stage II, the optimal maintenance activity is determined for each component at each maintenance time by using maintenance-benefit analysis model.

Multi-objective maintenance strategy

Busacca et al. (2001) aimed to establish a three-objective maintenance model for a nuclear energy plant to address the safety issue of a high-pressure injection system. The main objectives are to maximize the mean availability but to minimize the repair and check-up costs as well as the radiation exposure time of workers. The principle of non-dominated solutions is incorporated into the GA search mechanism to determine the repair and check-up periods and thereby efficiently optimize three objectives. Tian et al. (2012) proposed a bi-objective condition-based maintenance model that simultaneously maximizes reliability and minimizes maintenance costs. A physical-programming-based approach was developed to enable decision makers to realize a systematic and efficient tradeoff between the cost objective and the reliability objective, instead of adjusting the weights of the optimized objectives, as in the case of conventional approaches. Nosoohi and Hejazi (2011) developed a multi-objective maintenance model in which the replacement maintenance is performed in accordance with practical requirements. A multi-objective optimization algorithm is based on the $\varepsilon$-constraint method to efficiently approach ideal Pareto frontier solutions and determine the optimal maintenance strategy. Berrichi et al. (2009) and Wang (2002) considered parallel machine scheduling problems to determine a maintenance schedule for machines. A bi-objective maintenance model is simultaneously optimized for production requirements and system availability by using ant colony optimization to obtain the compromise solutions from which the appropriate maintenance alternative is determined. Moradi et al. (2011) focused mainly on flexible job shop problems with a bi-objective optimization model that considered maintenance benefit and production efficiency. The production schedule and preventive maintenance strategy that optimally reduce the process flow time and system unavailability are determined simultaneously. Quan et al. (2007) focused mainly on heavy industry facilities at railroad yards or aircraft service centers, which are high consumers of human resources for maintenance works. In order to shorten the maintenance times and simultaneously reduce the consumption of human resources, a bi-objective maintenance schedule model is devised. An optimization algorithm is developed to approach the ideal Pareto frontier solutions of the model and thereby determine the best maintenance alternative. Sachdeva et al. (2008) studied the case of a paper manufacturing plant and formulated a preventive maintenance schedule model for maximizing production system availability while simultaneously minimizing total maintenance cost. The genetic algorithm is employed to solve the model and determine the best preventive maintenance strategy. Khatab et al. (2011) developed a block replacement policy for a system operating over a random time horizon. The expected total replacement cost was minimized by determining the optimal replacement period. In general, the replacement activity is referred to as perfect maintenance, which cannot be directly applied to a system that deteriorates with time. Therefore, the applicability of this study is limited.

Optimization algorithms

The most common way to easily solve the multi-optimization problem (MOP) is through a weighted-sum method (Coello 1999; Fonseca and Fleming 1997) that aggregates multiple objectives into a single performance index. The weighted-sum method needs a weight assigned to each of the multiple objectives, which introduces uncertainty through subjective judgments, and inappropriate weights yield an unsatisfactory solution. Furthermore, this type of approach can only be used on problems with convex Pareto frontier and can only obtain one solution, rather than a set of non-dominated solutions that offer various alternatives to fulfill practical requirements. Lin and Wang (2012) proposed a hybrid genetic algorithm to optimize the periodic PM Model in a series-parallel system. The main idea is that an importance measure of components is developed to evaluate the extent to which maintaining components improves the system’s reliability. This importance measure of components is then incorporated into a conventional GA to enhance its ability to approach the global optimum. However, only perfect maintenance was considered in the established periodic PM model; this approach is not applicable to a deteriorating system. Osyczka and Kundu (1996) established a multi-objective evaluation function using the distance metric and incorporated this in the GA to search for non-dominated solutions of a MOP. Srinivas and Deb (1994) established a non-dominated sorting genetic algorithm (NSGA) in which the calculation of the fitness of a MOP solution has an embedded fitness share mechanism to obtain diversified MOP solutions. Fonseca and Fleming (1998) suggested a scale-independent fitness function to measure and prioritize the candidates and thereby solve MOPs. Rudolph (2001) established an elitist multi-objective evolutionary algorithm (EMOEA), which combines the parent with its offspring and then retains the superior chromosomes to form a new parent population that generates offspring. Deb et al. (2002) developed an elitist non-dominated sorting genetic algorithm (NSGA-II) with a crowding metric to evaluate the crowding distance of each non-dominated solution and thereby screen for diversified non-dominated solutions. Normally, the solution quality of a multi-objective optimization algorithm is evaluated in terms of two performance aspects, which are the closeness and the diversity of the solution set. The closeness metric evaluates the proximity of the solution set and the Pareto-optimal frontier, while the diversity metric evaluates the span of the solution set (Wang et al. 2009; Deb 2001). The ideal multi-objective solution set is uniformly distributed along the Pareto-efficient frontier. In summary, an algorithm developed for MOP solving must possess the ability to find diverse solutions near the Pareto-optimal frontier and thus efficiently provide various alternatives for decision makers to appropriately select from according to system performance requirements and resource constraints.

Methods

Except for some complex system structures designed to meet special requirements, the series-parallel system is the most commonly used structure owing to its high reliability and maintainability, as compared to other system structures. This study aims to establish a bi-objective imperfect preventive maintenance model that optimizes total maintenance cost and mean system reliability. The decision variables, which are the maintenance period and the maintenance work during operational lifetime, are considered simultaneously in a series-parallel system. In order to efficiently solve the model established, this study also develops an UCCREM to evaluate component importance and incorporates this measure into the GA, thus laying the foundation to propose a BOHGA that utilizes a Pareto-based technique (Srinivas and Deb 1994; Fonseca and Fleming 1998; Deb et al. 2002). Moreover, the RSM resulted form design of experiments is employed to determine the best search parameter settings for the BOHGA established in the hope of strengthening its exploratory ability.

The BOIPM model for the series-parallel system

The bi-objective imperfect preventive maintenance model established for the series-parallel system is one that simultaneously optimizes the total maintenance cost and the mean system reliability by determining the preventive maintenance period of each component in the series-parallel system. The improvement factor (Tsai et al. 2004) method is employed to evaluate the extent to which repairing components with different Weibull failure distributions can restore the system reliability. The Weibull distribution is extensively employed in reliability modeling in real-world situations. This is mainly because the hazard rate function corresponding to the Weibull distribution can characterize various failure rate patterns in the bathtub curve by setting shape parameter $\beta$. When $\beta >1$, the hazard rate function increases with time, which represents the wear-out region of the bathtub curve. When $\beta =1$, the hazard rate is constant, which represents the constant failure-rate region. When $\beta <1$, the hazard rate function decreases with time, which represents the early failure-rate region. This qualifies the Weibull distribution model to describe the failure rate of various failure data in actual cases. Additionally, to satisfy practical requirements, the model established is subject to two constraints: the system reliability must surpass the worst allowable value, and the total maintenance cost must not exceed the value predetermined by resource considerations. Accordingly, the BOIMP model established is as follows:

$$\begin{aligned} \text{ Minimize}\qquad \quad C_{PM} =\sum _{k=1}^K {\sum _{j=1}^{E_k} {\sum _{i=1}^{n_{jk}}{C_{ijk}}}}\end{aligned}$$

(1)

$$\begin{aligned} \text{ Maximize}\qquad \quad R_{mean} =\frac{\int _0^T {R_S (t)dt}}{T} \end{aligned}$$

(2)

Subject to

$$\begin{aligned} R_S (t)&\ge R_0, R_S (t)=\prod _{k=1}^K {\left[1-\prod _{j=1}^{E_k } {(1-R_{jk} (t))}\right]}\end{aligned}$$

(3)

$$\begin{aligned} C_{PM}&\le C_0\end{aligned}$$

(4)

$$\begin{aligned} R_{0,\,ijk}&= R_{f,\,(i-1)jk} +m_{2,\,jk} \left( {R_{0,\,jk} -R_{f,\,(i-1)jk} } \right)\end{aligned}$$

(5)

$$\begin{aligned} R_{ijk} (t)&= R_{0,\,ijk} \times e^{-\left( {{(t-(i-1)t_{p,\,jk} )\times \eta _{jk} }/{m_{1,\,jk} }} \right)^{^{\beta _{_{jk}}}}},\nonumber \\&\quad (i-1)\times t_{p,\,jk} \le t\le i\times t_{p,\,jk}\end{aligned}$$

(6)

$$\begin{aligned} n_{jk}&= INT\left(\frac{T}{t_{p,jk}}\right) \end{aligned}$$

(7)

where $C_{PM}$ represents the total maintenance cost, $C_{ijk}$ represents the maintenance cost in the $i$th period of the $j$th component in the $k$th sub-parallel system, $n_{jk}$ represents the number of maintenances of the $j$th component in the $k$th sub-parallel system, $E_{k}$ represents the number of components in the $k$th sub-parallel system, $K$ represents the number of sub-parallel systems in the series-parallel system, $R_{mean}$ represents the mean system reliability, $t$ represents time, $T$ represents the operational lifetime of the system, $R_{s}(t)$ represents the system reliability, $R_{0}$ represents the worst allowable reliability, $R_{jk}(t)$ represents the reliability of the $j$th component in the $k$th sub-parallel system, $C_{0}$ is the greatest allowable total maintenance cost, $R_{0,ijk }$is the initial reliability in the $i$th period of the $j$th component in the $k$th sub-parallel system, $R_{f,(i-1)jk}$ is the final reliability in the $(i-1)$th period of the $j$th component in the $k$th sub-parallel system, $R_{0,jk}$ is the initial reliability of the new system of the $j$th component in the $k$th sub-parallel system. In Eq. 6, the term $e^{-\left( {{(t-(i-1)t_{p,\,jk} )\times \eta _{jk} }/{m_{1,\,jk}}} \right)^{^{\beta _{_{jk}}}}}$ is basically a Weibull reliability function in which the improvement factor $m_{1,jk}$ is incorporated to evaluate the extent to which repairing decreases the rate of component degradation. The term $R_{0,ijk}$ is obtained from Eq. 5, in which the improvement factor $m_{2,jk}$ is incorporated to evaluate the extent to which repairing increases the component reliability at the beginning of the maintenance period. Therefore, by solving Eq. 6, the reliability of each component can be obtained as repairs are carried out. To clearly define components located in different sub-parallel systems, the suffix $R_{ijk}(t)$ is used to represent the reliability of the $j$th component in the $k$th sub-parallel system as repair is performed in the $i$th maintenance period. $t_{p,jk}$ is an optimized decision variable representing the maintenance period of the $j$th component in the $k$th sub-parallel system of the established BOIMP model, while $m_{1,jk}$ and $m_{2,jk}$ are the improvement factors of the $j$th component in the $k$th sub-parallel system, which serve to evaluate the extent to which repairing components restores the component reliability (their values lie between 0 and 1). $m_{1,jk}$ mainly characterizes the decrease in the rate of component degradation, while $m_{2,jk}$ mainly characterizes the increase in component reliability at the beginning of the maintenance period. $\beta _{jk}$ and $\eta _{jk}$ are the shape and scale parameters of the Weibull failure distribution, respectively, corresponding to the $j$th component in the $k$th sub-parallel system. INT is the minimal integer function.

The UCCREM

The need to evaluate the importance of components within multi-component systems has motivated the development of various importance measures, but in practice the importance measure of Birnbaum (Elsayed 1996) is widely used. However, this importance measure overestimates the importance of components because only the extreme situations of failure and function are taken into consideration. As is well known, the performance of a component is described by its reliability function, which is a probability function that varies with time. Therefore, if only extreme situations are taken into account to determine the importance of a component, as with Birnbaum’s importance measure (Elsayed 1996), the extent to which maintaining a component will benefit the system performance is not adequately reflected. To compensate for the disadvantages of Birnbaum’s importance measure, this study adopts the concept of statistical expectation and takes into account the failure probability of individual components to develop a reliability expectation measure (REM) as follows:

$$\begin{aligned} I_{REM}^j (t)&= (R_S (1,r_j (t))-R_S (t))\times r_j (t)\nonumber \\&+(R_S (t)-R_S (0,r_j (t))\times (1-r_j (t)) \end{aligned}$$

(8)

where $R_S (t)$ represents the system reliability at time $t$, while $R_S (1,r_j (t))$ and $R_S (0,r_j (t))$ represent the system reliability when the $j$th component is functional or has failed, respectively, since $r_j (t)$ and $(1-r_j (t))$ represent the probabilities that the $j$th component is functional or has failed, respectively. Thus, $R_S (1,r_j (t))-R_S (t)$ reveals the positive effect on system reliability when the $j$th component functions, while $R_S (t)-R_S \left( {0,r_j (t)} \right)$ reveals the negative effect on system reliability when the $j$th component fails. The reliability expectation $I_{REM}^j (t)$of the $j$th components at time $t$ falls between 0 and 1. A large $I_{REM}^j (t)$ value indicates the great extent to which maintaining the $j$th component benefits the reliability of the series-parallel system. The unit-cost cumulative reliability expectation measure (UCCREM) is further developed by considering the maintenance cost during the operational lifetime as follows:

$$\begin{aligned} I_{UCCREM}^{Tj} =\frac{\int _0^T {I_{REM}^j (t)dt} }{C_j } \end{aligned}$$

(9)

where $\int _0^T {I_{REM}^j (t)} dt$ represents the cumulative REM value during the operational lifetime $T$, and $C_j$ represents the maintenance cost of the $j$th component. A large $I_{UCCREM}^{Tj}$ value indicates the great extent to which maintaining the $j$th component benefits the system performance in terms of both the reliability and the maintenance cost of the series-parallel system. Therefore, the UCCREM can be appropriately employed to facilitate the determination of a preventive maintenance strategy.

The established BOHGA

The genes in the GA are coded in the form of integers that indicate the maintenance periods of the components. A chromosome is a series of genes and is thus a combination of the maintenance periods of the components. Namely, a chromosome represents a solution of the BOIPM model established. Accordingly, this study proposes a BOHGA that involves two stages, as discussed in the following two subsections.

Stage I: use the UCCREM to determine important components

In past studies (Pham and Wang 1996), the initial chromosome structure significantly affected the solution efficiency of the GA. In the planning of a preventive maintenance strategy, the most important components are determined in order to perform their maintenance work first. The least important components normally do not receive any maintenance work during the operational lifetime under the constraint of the limited maintenance resources. Additionally, optimizing the preventive maintenance periods of all components in a series-parallel system involves a complicated calculation. Therefore, solving this type of problem consumes a great amount of computation time, particularly when the number of components involved increases. Following the idea mentioned above for optimizing the BOIPM model, the established BOHGA initially screens out unimportant components, retaining the important components by using the UCCREM. As the importance of the $j$th component in the series-parallel system becomes enhanced, the $I_{UCCREM}^{Tj}$value becomes larger. The importance sequence of the components is determined as follows:

$$\begin{aligned} \mathbf{S}=\bigcup _{j=1}^n {\left\{ {s_j } \right\} } \end{aligned}$$

(10)

where $S_{j}$ is the $j$th most important component, $n$ is the number of components in the series-parallel system, and S is a set that contains the importance sequence of the components.

From S, this study determines the important components of a series-parallel system by the following iterative procedure:

• Step 1: Given the first component $S_{1}$ inS, optimize the BOIPM model using the conventional GA to obtain the total maintenance cost and mean system reliability, if feasible solutions exist. Then, calculate the closeness metric to evaluate the solution quality.

• Step 2: Add one component according to its priority in S, and optimize the BOIPM model using the conventional GA to obtain the total maintenance cost and mean system reliability, if feasible solutions exist. Then, calculate the closeness metric to evaluate the solution quality.

• Step 3: Repeat step 2 until all the components are involved.

The combination of components with the lowest value of the closeness metric identifies the important components of the BOIPM model. These important components are substituted into stage II to optimize their maintenance periods. The unimportant components do not receive any maintenance work during the operational lifetime.

Stage II: optimize maintenance periods of important components

This stage actually involves two sub-stages that consist of five steps and four steps, respectively. The first sub-stage proceeds as follows:

• Step 1: Establish the initial population of chromosomes. In the feasible area of the model established, where solutions satisfy the reliability and cost constraints as Eqs. (3) and (4), this step randomly generates 100 different combinations of the maintenance periods of the important components to form an initial population of chromosomes.

• Step 2: Screen and reproduce the chromosome population. The non-dominated solutions determined in terms of the total maintenance cost and mean system reliability are retained as the superior chromosomes of each generation. This step thereby performs a chromosome reproductive procedure in which 100 chromosomes are retained to form the basis of the next generation of offspring.

• Step 3: Perform the crossover procedure. This step randomly generates masks from the chromosome structure to perform the GA crossover procedure on randomly selected pairs of chromosomes, subject to the predetermined number of masks and crossover rate.

• Step 4: Perform the mutation procedure. A mask mutation approach is also employed as the GA mutation procedure. Some randomly generated masks are used to perform the mutation procedure on chromosomes that are randomly selected from those obtained at step 3. The number of masks and the mutation rate are predetermined by the RSM.

• Step 5: Test whether any termination condition is met.

Note that steps 2–5 are iterated until the algorithm meets either of the following conditions:

• 1. The change in the closeness metric is $<$0.0001 for 50 successive generations, enabling a reduction in average CPU time.

• 2. A maximum of 100 generations is reached.

The optimal bi-objective non-dominated solutions are thus determined in order to constitute maintenance alternatives. Engineering managers can then select the most appropriate maintenance alternative according to the practical requirements of the system and the constraints of limited maintenance resources.

The settings of the search parameters of the BOHGA are determined through systematic experimentation and analysis by using the RSM as follows:

• Step 1: Plan the RSM experiments for the closeness and diversity metrics. The faced central composite design (FCCD) is adopted to plan experiments in which there are four experimental factors: the crossover probability, the mutation probability, the number of crossover masks, and the number of mutation masks. In total, 30 experimental points were designed, involving 8 factorial points, 16 faced axial points, and 16 center points. For more details of the central composite design, refer to Montgomery (2005).

• Step 2: Conduct the RSM experiments and record experimental observations. The 30 planned FCCD experiments are conducted by optimizing the BOIPM model using the BOHGA, with various crossover and mutation probabilities as well as different numbers of masks for crossover and mutation. Because the closeness and diversity metrics are determinants to evaluate the quality of non-dominated solutions, these values are calculated on the basis of the total maintenance cost and mean system reliability that are obtained.

• Step 3: Establish the response surface models of the closeness and diversity metrics. The response surface models of the closeness and diversity metrics are determined using the lack- of-fit test procedure on the search parameters, including the mutation probability, the number of crossover masks, and the number of mutation masks. Normally, a $p$ value greater than 0.05 in the lack-of-fit test indicates that the fitted model is appropriate at a significance level $\alpha$ of 0.05. If the full quadratic model is appropriate, the model can be expressed as follows:

  $$\begin{aligned} y_i&= \beta _0 +\beta _1 x_1 +\beta _2 x_2 +\beta _3 x_3 +\beta _4 x_4 +\beta _{12} x_1 x_2 \nonumber \\&+\beta _{13} x_1 x_3 +\beta _{14} x_1 x_4+\beta _{23} x_2 x_3 +\beta _{24} x_2 x_4\nonumber \\&+\beta _{34} x_3 x_4 +\beta _{11} x_1^2 +\beta _{22} x_2^2 +\beta _{33} x_3^2\nonumber \\&+\beta _{44} x_4^2 +\varepsilon , i=1,2 \end{aligned}$$

  (11)

  where $y_{1}$ and $y_{2}$ represent the closeness and diversity metrics, respectively; $x_{1}, x_{2}, x_{3}$, and $x_{4},$ represent the crossover probability, mutation probability, the number of crossover masks, and the number of mutation masks, respectively; the $x_{i }x_{j }$ are interaction terms among the four design factors; the $x_{i}^{2}$ are the effects of quadratic terms; $\beta _{0}, \beta _{ij}$, and $\beta _{jj }$ are the fitted model parameters; and $\varepsilon$ is a random error term.

• Step 4: Optimize the settings of the search parameters. The optimal settings of the four search parameters are determined using a desirability function (Harrington 1965) technique based on the response surface models of the closeness and diversity metrics that are obtained at step 3. The desirability value, which lies between 0 and 1, is extensively used in industrial fields to solve multi-response optimization problems. For more details of the desirability function, refer to Harrington (1965).

Results and discussion

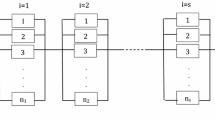
Three simulated series-parallel system cases verify the efficacy of the established approach. The operational lifetime is set to 50 months. Each system consists of 15 components that are coded by integers ranging from 1 to 15. Figures 1, 2 and 3 are reliability block diagrams of the simulated cases to show the system configurations, where case 1 includes six subsystems, case 2 includes four subsystems, and case 3 includes 12 subsystems. Simulated case 1 mainly characterizes the diversified sub-parallel configurations that involve one single-component subsystem, two sub-parallel systems with two components, two sub-parallel systems with three components, and one sub-parallel system with four components. Simulated case 2 mainly characterizes the sub-parallel configurations in which the numbers of components surpass those of simulated case 1. Simulated case 3 mainly characterizes the series configurations in which multiple single-components are serially connected.

Fig. 1

Reliability block diagram of simulated case 1

Fig. 2

Reliability block diagram of simulated case 2

Fig. 3

Reliability block diagram of simulated case 3

This study applies the Weibull probability distribution, which is extensively employed in reliability analysis to simulate a component failure scenario. Thus, five values of the shape parameters $\beta$ (i.e., 3, 2, 1.5, 1.1, and 0.5) and three values of the scale $\eta$ (i.e., 0.01, 0.02, and 0.03) are selected to construct the failure statuses of the 15 simulated components. Table 1 lists the parameter values of these 15 simulated components that are denoted alphabetically A–O. The value $\beta =2$ is mainly characteristic of components with an instantaneous increase of failure rate. The values $\beta =1.1$ and $\beta =1.5$ are mainly characteristic of components with gradual increases of failure rate. The value $\beta =0.5$ is mainly characteristic of components with a gradual decrease of failure rate. The parameters of each component in three simulated series-parallel systems are determined through a random permutation procedure. Accordingly, three different permutations of 15 simulated components are produced randomly and then matched with the components labeled by integers in the three simulated reliability cases to determine the parameters of all 15 components. The failure probability model for each component is thus obtained. Table 2 lists the component matches for the three simulated cases in this study.

Table 1 Parameters of simulated components

Table 2 Component matches for three simulated cases

The maintenance periods of the 15 components in each of the three simulated cases are optimized by formulating the BOIPM model and then solving that using the BOHGA. This study presents the optimization process for case 1 in two stages, in the following two subsections.

Stage I: use the UCCREM to determine important components

For each component shown in Fig. 1, the values of the UCCREM are calculated using Eqs. (8)–(10) to initially obtain the importance sequence $\mathbf{S}=\{10, 12, 11, 7, 8, 9, 2, 6, 3, 5, 1, 4, 15, 13, 14\}$ in Table 3. The total maintenance cost and mean system reliability are optimized by steps 1–3 of the iteration procedure based on the conventional GA with predetermined crossover rate 0.6, mutation rate 0.1, five crossover masks, and four mutation masks. This same optimization procedure is repeated 10 times to obtain the objective values associated with the total maintenance cost and mean system reliability. Table 4 summarizes the closeness metric for different combinations of components. Obviously, the 13th combination set $\mathbf{S}_{13}=\{10, 12, 11, 7, 8, 9, 2, 6, 3, 5, 1, 4, 15\}$ with the smallest closeness metric 0.032 identifies the most important components that most affect the mean system reliability and total maintenance cost over the operational lifetime. Therefore, all of the components except the 13th and 14th are required to undergo maintenance work during the operational lifetime. The components required to undergo maintenance are substituted into stage II to optimize the preventive maintenance periods.

Table 3 UCCREM values and ranks

Table 4 Importance of components

Stage II: optimize maintenance periods of important components

The initial chromosome population is formed by randomly producing 100 different maintenance periods for the 13 important components identified in stage I. Each combination of maintenance periods corresponds to a solution of the BOIMP model. Accordingly, repetition of steps 2–6 can determine the non-dominated solutions of simulated case 1 that form the Pareto frontier. Notably, the optimal settings of the search parameters are predetermined by applying the RSM. Table 5 shows the allocated design factor levels.

Table 5 Allocated design factor levels

After the RSM experiments are conducted, the response surface model of the closeness and diversity metrics of the four design factors are established. A full quadratic model for the closeness metric is based on the $p$ value 0.5647 from the lack-of-fit test at significance level $\alpha =0.05$ as follows:

$$\begin{aligned} \hat{y}_1&= -0.059-0.029x_1 +0.076x_2 +0.032x_3 -0.011x_4\nonumber \\&-0.014x_1 x_2 -5.20810^{-5}x_1 x_3 -3.64610^{-4}x_1 x_4\nonumber \\&-6.250\times 10^{-4}x_2 x_3 +3.681\times 10^{-3}x_2 x_4\nonumber \\&-1.736\times 10^{-4}x_3 x_4 +0.040x_1 ^{2}-0.109x_2 ^{2}-2.202\nonumber \\&\times 10^{-3}x_3 ^{2}+1.187\times 10^{-3}x_4 ^{2} \end{aligned}$$

(12)

The coefficient of determination $R^{2}$ is 0.72 for the fitted closeness metric model. A linear model for the diversity metric is based on the $p$ value 0.1960 for the lack-of-fit test at significance level $\alpha =0.05$ as follows:

$$\begin{aligned} \hat{{y}}_2&= 0.0453-0.0306x_1 +0.057x_2 -3.333\times 10^{-4}x_3\nonumber \\&+5.556\times 10^{-4}x_4 \end{aligned}$$

(13)

The coefficient of determination $R^{2}$ is 0.4479 for the fitted diversity metric model. The optimal settings of these four research parameters are determined on the basis of the Eqs. (12) and (13) utilizing the desirability function technique, and the desirability obtained is 0.73. The optimal crossover rate, mutation rate, number of crossover masks, and number of mutation masks are determined as 0.9, 0.1, 4, and 5, respectively. In total for case 1, the BOHGA obtains 19 non-dominated solutions forming a Pareto frontier with closeness metric 0.017 and diversity metric 0.05. The nicely obtained values of the closeness and diversity metrics reveal that the 19 non-dominated solutions are evenly distributed along the Pareto frontier and are close to the ideal Pareto solution set. In order to further verify the efficacy of the established BOHGA, this study applies the conventional GA to again optimize the simulated cases. Table 6 summarizes the

Table 6 Comparison between the BOHGA and the conventional GA for simulated case 1

comparison between the BOHGA and the conventional GA in terms of the closeness and diversity metrics, while Fig. 4 displays the Pareto frontier solution for each. The closeness metric of the BOHGA outperforms that of the conventional GA, although their diversity metrics are close to each other. Five distinguished solutions are selected from among the 19 non-dominated solutions obtained, and these constitute five distinct maintenance alternatives. Figure 4 shows these five alternatives, while Table 7 lists the corresponding maintenance periods of the 15 components in case 1, the optimized total maintenance cost, and the mean system reliability. From Table 7, for the first maintenance alternative, we know that the optimized maintenance periods of components 1–15 are 27, 39, 18, 44, 48, 19, 7, 31, 43, 3, 42, 3, –, –, and 31, respectively. Significantly, components 13 and 14 do not need to be repaired during the operational lifetime of 50 months. This is mainly because the UCCREM values for component 13 and component 14 are rather low (see Table 3), as compared to other components in case 1. In other words, maintaining component 13 and component 14 cannot greatly improve the system in terms of its reliability and maintenance cost. The details of other maintenance alternatives can be obtained by following the same analysis procedure. Maintenance engineers can simply determine the most appropriate alternative in accordance with practical system performance requirements and resource constraints. Obviously, the first alternative imposes less total maintenance cost but achieves lower mean system reliability in comparison with the fifth alternative. The performances of alternatives 2–4, in terms of mean system reliability and total maintenance cost, lie between those of alternatives 1 and 5. However, the five maintenance alternatives obtained all outperform the conventional GA solutions.

Fig. 4

Pareto frontier solutions of the BOHGA and the conventional GA of simulated case 1

Table 7 Maintenance periods of components for alternatives of simulated case 1

Summary for cases 2 and 3

For simulated cases 2 and 3, the optimizations with the established approach can be summarized as follows:

• 1. For simulated case 2, a set of ten important components was determined in order as $\mathbf{S}_{10}=\{15, 12, 14, 8, 13, 11, 10, 6, 7, 9\}$. Therefore, all of the components except the 1st through 5th are required to undergo maintenance work during the operational lifetime. A total of 33 non-dominated solutions form the optimized Pareto frontier and thus determine five distinct maintenance alternatives. Figure 5 displays the optimized Pareto frontier. Table 8 presents the comparison between the BOHGA and the conventional GA. Table 9 presents the maintenance periods of the 15 components associated with the five alternatives. The established BOHGA outperforms the conventional GA in terms of the closeness and diversity metrics.

  Fig. 5

  

  Pareto frontier solutions of the BOHGA and the conventional GA of simulated case 2

  Table 8 Comparison between the BOHGA and the conventional GA for simulated case 2

  Table 9 Maintenance periods of components for alternatives of simulated case 2

• 2. For simulated case 3, all 15 components are required to undergo maintenance work during the operational lifetime. This is mainly because case 3 is characterized by a series configuration which comprises nine serially connected single components and two sub-parallel systems that include two components and three components. The system reliability is inherently low, as compared to parallel configurations. A total of 36 non-dominated solutions form the optimized Pareto frontier and thus determine five distinct maintenance alternatives. Figure 6 displays the optimized Pareto frontier. Table 10 presents the comparison between the BOHGA and the conventional GA. Table 11 presents the maintenance periods of the 15 components associated with the five alternatives. The established BOHGA outperforms the conventional GA in terms of the closeness and diversity metrics.

  Fig. 6

  

  Pareto frontier solutions of the BOHGA and the conventional GA of simulated case 3

  Table 10 Comparison between the BOHGA and the conventional GA for simulated case3

Table 11 Maintenance periods of components for alternatives of simulated case 3

Although the practicality of the BOIPM model and the effectiveness of the established BOHGA are verified in this study with three simulated cases generated randomly, other simulated cases beyond the scope of this study do yield similar results.

Conclusions

This study has aimed primarily at solutions of the preventive maintenance problem for a series-parallel system under an imperfect maintenance plan. A bi-objective imperfect preventive maintenance model that simultaneously optimizes mean system reliability and total maintenance cost was established. Additionally, a customized BOHGA was established to efficiently optimize the BOIPM model established. Three simulated cases verified the efficacy of the established approach. The incorporation of the UCCREM into the GA significantly contributed to the efficacy of the BOHGA. Moreover, a Pareto-based technique was employed to determine superior GA chromosomes and thereby guide the search. Based on the results obtained with the established approach, the following are suggested:

• 1. The UCCREM can appropriately evaluate the extent to which maintaining an individual component in a series-parallel system benefits the overall system reliability and total maintenance cost over the operational lifetime. Accordingly, incorporating the concept of component importance into the UCCREM and in turn the GA, thus laying the foundations of the BOHGA, can greatly benefit efficiency when optimizing the BOIPM model for solutions.

• 2. Predetermining the optimal settings of the search parameters of the BOIPM model through systematic experiments and data analysis using the RSM, instead of the conventional trial-and-error procedure, can improve the searching ability of meta-heuristic algorithms such as the GA.

• 3. The established approach can efficiently provide diversified imperfect preventive maintenance alternatives, as system reliability and total maintenance cost are considered simultaneously to satisfy practical requirements. Therefore, decision makers can select the most appropriate alternative to fulfill practical requirements of system reliability under constraints on maintenance resources.

• 4. Finally, despite the Pareto-based technique primarily emphasizing non-dominated solutions to produce the GA offspring, the search mechanism for multi-objective models still has room for improvements, such as employing a hybrid meta-heuristic algorithm rather than merely the GA evolution procedure.