Abstract
Copulas are distribution functions with standard uniform univariate marginals. Copulas are widely used for studying dependence among continuously distributed random variables, with applications in finance and quantitative risk management; see, e.g., the pricing of collateralized debt obligations (Hofert and Scherer, Quantitative Finance, 11(5), 775–787, 2011). The ability to model complex dependence structures among variables has recently become increasingly popular in the realm of statistics, one example being data mining (e.g., cluster analysis, evolutionary algorithms or classification). The present work considers an estimator for both the structure and the parameters of hierarchical Archimedean copulas. Such copulas have recently become popular alternatives to the widely used Gaussian copulas. The proposed estimator is based on a pairwise inversion of Kendall’s tau estimator recently considered in the literature but can be based on other estimators as well, such as likelihood-based. A simple algorithm implementing the proposed estimator is provided. Its performance is investigated in several experiments including a comparison to other available estimators. The results show that the proposed estimator can be a suitable alternative in the terms of goodness-of-fit and computational efficiency. Additionally, an application of the estimator to copula-based Bayesian classification is presented. A set of new Archimedean and hierarchical Archimedean copula-based Bayesian classifiers is compared with other commonly known classifiers in terms of accuracy on several well-known datasets. The results show that the hierarchical Archimedean copula-based Bayesian classifiers are, despite their limited applicability for high-dimensional data due to expensive time consumption, similar to highly-accurate classifiers like support vector machines or ensemble methods on low-dimensional data in terms of accuracy while keeping the produced models rather comprehensible.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Studying relationships among random variables is a crucial task in the field of knowledge discovery and data mining (KDDM). Having a dataset collected, the relationships among the observed variables can be studied by means of an appropriate measure of stochastic dependence. Under the assumption that the marginal distributions of the variables are continuous, Sklar’s Theorem (Sklar 1959) can be used to decompose the joint multivariate distribution in two parts, the univariate marginal distributions and the unique dependence structure, i.e., the copula of the joint distribution. Thus, studying dependence among continuously distributed random variables can be restricted without loss of generality to studying the underlying copula.
Despite the fact that a large part of the success of copulas is attributed to finance, copulas are increasingly adopted also in KDDM, where their ability to capture complex dependence structures among variables is used. Applications of copulas can be found in water-resources and hydro-climatic analysis (Genest and Favre 2007; Kao et al. 2009; Kao and Govindaraju 2008; Kuhn et al. 2007; Maity and Kumar 2008), gene analysis (Lascio and Giannerini 2012; Yuan et al. 2008), cluster analysis (Cuvelier and Noirhomme-Fraitur 2005; Kojadinovic 2010; Rey and Ruth 2012) or in evolutionary algorithms, in particular estimation of distribution algorithms (González-Fernández and Soto 2012; Wang et al. 2012). For an illustrative example, we refer to Kao et al. (2009), which describes an application of copulas to detecting weather anomalies in a climate change dataset.
For certain types of applications, hierarchical Archimedean copulas (HACs) are a frequently used alternative to Gaussian copulas due to several desirable properties, e.g., HACs are not restricted to radial symmetry; HACs are expressible in a closed form; they are able to model asymmetric distributions with tail dependence; and HACs are able to model complex relationships while keeping the number of parameters comparably small; see Hofert (2011) and Hofert and Scherer (2011). The last point is important from a data mining point of view because models with a small number of parameters are more easily understandable. Denoting the data dimension by d, on the one hand, if using Gaussian copulas, the number of parameters grows quadratically in d and the obtained models can quickly become challenging from a computational point of view. On the other hand, if using Archimedean copulas (ACs), the obtained models contain only one parameter (provided an AC is based on a one-parametric generator), which is rarely feasible in real-world applications. In this context, HACs are often a good trade-off between these two extremes and provide relatively simple and flexible dependency models.
Despite the popularity of HACs, feasible techniques for their parameter and structure estimation are addressed only in few papers. Most of them assume a given hierarchical structure, which is motivated by applications in economics, e.g., (Savu and Trede 2008; 2010). On the contrary, in Segers and Uyttendaele (2014), only structure determination of a HAC is addressed. We are aware of only one paper (Okhrin et al. 2013a) that addresses both structure determination and parameter estimation via a multi-stage procedure. That paper mainly focuses on the estimation of the parameters using the maximum-likelihood (ML) technique and briefly mentions the inversion of Kendall’s tau as an alternative. For structure determination, six approaches are presented. Two of them are based on the inversion of Kendall’s tau, one on the Chen test statistic (Chen et al. 2004) and the remaining three approaches on the ML technique. All but one approach lead to biased estimators, which can be seen from the results of the reported study. The unbiased estimator, denoted by 𝜃 RML, which shows the best goodness-of-fit (measured by Kullback-Leibler divergence) in the study, is simply the maximum likelihood estimator based on initial values computed from one of the biased estimators. Due to this construction, 𝜃 RML often does not approximate the true parameters well when the structure determined by the biased estimator is not the true structure. The number of such cases rapidly increases in large dimensions, as we show later in Section 4.
In the present work, we propose a new estimator for both the structure and the parameters of HACs. On the one hand, this estimator is also a multi-stage procedure where the structure and the parameters are estimated in a bottom-up manner. On the other hand, it is based on the fact that a HAC can be uniquely recovered from all its bivariate margins and thus allows to estimate the copula parameters just from the parameters of the bivariate marginal copulas. Assuming the true copula is a HAC, our estimator approximates the true copula closer (measured by a selected goodness-of-fit statistic) than the previously mentioned methods. Moreover, the ratio of structures properly determined using our estimator is higher compared with the estimators mentioned above. Finally, avoiding a time-consuming computation of initial values, we also gain computational efficiency. The experiments based on simulated data in Section 4 show that our approach outperforms the above-mentioned methods with respect to goodness-of-fit, the properly determined structures ratio and also the consumed run-time.
In addition, we consider Bayesian classifiers that are based on Gaussian copulas, ACs and HACs. When fitting those classifiers, efficient estimation methods for a given copula class are needed. In the Gaussian and Archimedean case, such estimation methods are known, whereas for HACs, we can now apply our proposed estimator. We compare it with other copula-based Bayesian classifiers, as well as with other types of commonly used classifiers.
The paper is structured as follows. The following section summarizes some needed theoretical concepts concerning ACs and HACs. Section 3 presents the new estimation approach for HACs, and Section 4 describes the experiments based on simulated data. Section 5 presents a copula-based approach to Bayesian classification and includes an experimental comparison of several classifiers based on real-world datasets. Section 6 concludes this paper.
2 Preliminaries
2.1 Copulas
Definition 1
For every d ≥ 2, a d-dimensional copula (shortly, d-copula) is a d-variate distribution function on \(\mathbb {I}^{d}\) (\(\mathbb {I} = [0, 1]\)), whose univariate margins are uniformly distributed on \(\mathbb {I}\).
Copulas establish a connection between joint distribution functions (d.f.s) and their univariate margins, which is well-know due to Sklar’s Theorem.
Theorem 1 (Sklar’s Theorem 1959)
(Sklar 1959 ) Let H be a d-variate d.f. with univariate margins F 1 ,...,F d . Let A j denote the range of F j , \(A_{j} := F_{j}(\overline {\mathbb {R}}), j = 1, ..., d, \overline {\mathbb {R}} := \mathbb {R} \cup \{ -\infty , +\infty \}.\) Then there exists a copula C such for all \((x_{1}, ..., x_{d}) \in \overline {\mathbb {R}}^{d}\) ,
Such a C is uniquely determined on A 1 ×...×A d . Conversely, if F 1 ,...,F d are univariate d.f.s, and if C is any d-copula, then the function \(H:\overline {\mathbb {R}}^{d} \rightarrow \mathbb {I}\) defined by (1) is a d-dimensional distribution function with margins F 1 ,...,F d .
Through Sklar’s Theorem, one can derive for any d-variate d.f. with continuous margins its unique copula C using (1). C is given by \(C(u_{1}, ..., u_{d}) = H(F_{1}^{-} (u_{1}), ..., F_{d}^{-}(u_{d}))\), where \(F_{i}^{-}, i \in \{1, ..., d\}\), denotes the pseudo-inverse of F i given by \(F_{i}^{-}(s) =\) inf{t | F i (t)\(\geq s\}, s \in \mathbb {I}\). Implicit copulas are derived in this way from popular joint d.f.s, e.g., the popular class of Gaussian copulas is derived from multivariate normal distributions. However, using this process often results in copulas which do not have a closed form, which can be a drawback for certain applications, e.g., if explicit probabilities and thus copula values have to be computed.
2.2 Archimedean copulas
Due to their explicit construction, Archimedean copulas (ACs) are typically expressible in closed form. To construct ACs in arbitrary dimensions, we need the notion of an Archimedean generator and of complete monotonicity.
Definition 2
An Archimedean generator (shortly, generator) is a continuous, nonincreasing function ψ:[0,∞]→[0,1], which satisfies \(\psi (0) = 1, \psi (\infty ) = \lim _{t \rightarrow \infty }\) ψ(t)=0 and which is strictly decreasing on [0,inf{t | ψ(t)=0}]. We denote the set of all generators by Ψ. If ψ satisfies (−1)k f (k)(t) ≥0, for all \(k \in \mathbb {N}, t \in [0,\infty )\), ψ is called completely monotone. We denote the set of all completely monotone generators by Ψ∞.
Definition 3
Any d-copula C is called an Archimedean copula (we denote it d-AC) based on a generator ψ∈Ψ, if it admits the form
where ψ −1:[0,1]→[0,∞] is defined by \(\psi ^{-1}(s) = \inf \{t~|~\psi (t) = s\}, s \in \mathbb {I}\).
A condition sufficient for C to be indeed a proper copula is ψ ∈ Ψ∞; see McNeil and Nešlehová (2009).
As we can see from Definition 3, if a random vector U is distributed according to some AC, all its k-dimensional marginal copulas are equal. Thus, e.g., the dependence among all pairs of components is identical. This symmetry of ACs is often considered to be a rather strong restriction, especially in high dimensions; see Hofert et al. (2013) for a discussion and possible applications.
To obtain an explicit form of an AC, we need ψ and ψ −1 to be explicit; many such generators can be found, e.g., in Nelsen (2006). In this paper, we use the three well-known parametric generators of the Clayton, Frank and Gumbel families; see Table 1. We selected these three families of generators because of two reasons. The first reason relates to flexibility of these families to model tail dependence in pairs of random variables, as this is a copula property. The Clayton family allows lower tail dependence in a pair (being upper tail independent), the Gumbel family allows oppositely upper tail dependence in a pair (being lower tail independent), and models from the Frank family are both lower and upper independent, similarly to Gaussian copulas; see (Hofert 2010b, p. 43). The second reason is that this choice allows for a comparison of our results with the results in Okhrin et al. (2013a) and Holeňa and Ščavnický (2013). More precisely, in Okhrin et al. (2013a), HAC estimation experiments involving HACs based on Clayton and Gumbel generators are reported; these experiments relate to our experiments described in Section 4. in Holeňa and Ščavnický (2013), a visual representation of a HAC structure involving Frank generators obtained from the Iris dataset is presented; this tree-like representation relates to our dendrogram-like representation described in Section 5.
2.3 Hierarchical archimedean copulas
To allow for asymmetries, one may consider the class of HACs (also called nested Archimedean copulas), recursively defined as follows.
Definition 4
(Hofert 2011) A d-dimensional copula C is called a hierarchical Archimedean copula if it is either an AC, or if it is obtained from an AC through replacing some of its arguments with other hierarchical Archimedean copulas. In particular, if C is given recursively by (2) for d = 2 and
for d ≥ 3, C is called fully-nested hierarchical Archimedean copula (FHAC)Footnote 1 with d−1 nesting levels. Otherwise, C is a partially-nested hierarchical Archimedean copula (PHAC)Footnote 2.
Remark 1
We denote a d-dimensional HAC as d-HAC, and analogously d-FHAC and d-PHAC.
From the definition, we can see that ACs are special cases of HACs. The most simple proper 3-HAC is a two-level FHAC given by
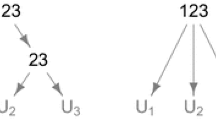
and its structure can be represented via a tree-like graph; see Fig. 1.
Assume that a random vector (U 1,U 2,U 3) is distributed according to the 3-FHAC given by (4), i.e., (U 1,U 2,U 3)∼C(u;ψ 1,ψ 2). Then C(u 1,u 2,1;ψ 1,ψ 2)=C(u 1,u 2;ψ 1), C(u 1,1,u 3;ψ 1,ψ 2) =C(u 1,u 3;ψ 1) and C(1,u 2,u 3;ψ 1,ψ 2)=C(u 2,u 3;ψ 2) for all \(u_{1}, u_{2}, u_{3} \in \mathbb {I}\). This means that this 3-FHAC involves two different bivariate marginal copulas, the 2-AC based on ψ 1, which is the distribution of the pairs (U 1,U 2) and (U 1,U 3), and the 2-AC based on ψ 2, which is the distribution of the pair (U 2,U 3). The asymmetry of this 3-HAC is a motivating example for nesting of ACs. The theoretical soundness of nesting is addressed in Theorem 2.
As in the case of ACs, we can ask for sufficient conditions for the function C given by (3) to be a proper copula. An answer to this question is provided by the following theorem. Note that another important result concerning stochastic representation of HACs is provided by Theorem 3.2 in Hofert (2012).
Theorem 2
(McNeil 2008) If ψ j ∈ Ψ ∞ ,j ∈ {1,...,d−1} such that \(\psi _{k}^{-1} \circ \psi _{k+1}\) have completely monotone derivatives for all k ∈ {1,...,d−2}, then C(u; ψ 1 , ...,ψ d−1 ),\(\mathbf {u} \in \mathbb {I}^{d}\) , given by (3) is a copula.
Theorem 2 is stated only for fully-nested HACs, but it can be easily translated to partially-nested HACs. The condition for \((\psi _{k}^{-1} \circ \psi _{k+1})^{\prime }\) to be completely monotone is often called a sufficient nesting condition.
Any d-HAC structure can be expressed as a tree with k ≤ d−1 non-leaf nodes (shortly, nodes), which correspond to the generators ψ 1,...,ψ k , and d leaves, which correspond to the variables u 1,...,u d . If the structure corresponds to a binary tree, then k = d−1, otherwise k < d−1. For the sake of simplicity, we assume only binary-structured HACs in the following. A binary-structured HAC is a HAC with the structure which corresponds to a binary tree and for each parent-child pair of generators (ψ i ,ψ j ) in the structure holds that ψ i ≠ψ j .
Similar to any 2-AC being determined by its corresponding generator, we identify each node in a HAC structure with one generator. Thus we always have the nodes ψ 1,...,ψ d−1. For a node ψ, denote by \(\mathcal {D}(\psi )\) the set of all descendant non-leaf nodes of ψ, \(\mathcal {D}_{l}\) the set of all descendant leaves of \(\psi , \mathcal {A}(\psi )\) the set of all ancestor nodes of \(\psi , \mathcal {H}_{l}(\psi )\) the left child of ψ and \(\mathcal {H}_{r}(\psi )\) the right child of ψ. Next, let z be a non-leaf node or a leaf, and, assuming z is not the root of the structure, denote by \(\mathcal {P}(z)\) the parent node of z.
For simplicity, a d-HAC structure s is denoted by a sequence of reordered indices {1,...,d} using parentheses to mark the variables with the same parent node. For example, the structure of the copula given by (4) is denoted as (1(23)). The inner pair of parentheses corresponds to the variables u 2,u 3, for which \(\mathcal {P}(u_{2}) = \mathcal {P}(u_{3}) = \psi _{2}\). As u 2,u 3 are connected through their parent, we can introduce a new variable denoted by z 23, which represents the variables u 2,u 3 and is defined by z 23 = C(u 2,u 3;ψ 2). Then (4) translates to \( \psi _{1} (\psi _{1}^{-1}(u_{1})+ \psi _{1}^{-1}(z_{23})) = C(u_{1}, z_{23}; \psi _{1})\), and thus the outer pair of parenthesis in the notation of the structure corresponds to the variables u 1,z 23, for which \(\mathcal {P}(u_{1}) = \mathcal {P}(z_{23}) = \psi _{1}\). The structure of the 4-FHAC according to Definition 4 is therefore s = (1(2(34))), for the 5-FHAC, s = (1(2(3(45)))), etc. Analogously, for PHACs, s = ((12)(3(45))) and s = (1((23)(45))) denote the structures depicted on the left-hand and on the right-hand side in Fig. 2, respectively.
When using HACs in applications, there exist many possible structures, for example for d = 10, more than 280 millions structures exist (including also non-binary ones) and each 10-HAC can incorporate up to 9 parameters (using only one-parametric generators, possibly from different families). On the one hand, choosing the model (structure and parameters) that fits the data best is a much more complex relative to the case when using ACs which have just one structure. On the other hand, this complexity is compensated by a substantially higher flexibility of obtained models. Due to the asymmetry in HAC-based models (different dependencies in pairs of variables are allowed), these models fit most data better than AC models, which is illustrated by the experimental results presented below in Section 5. There, different copula-based Bayesian classifiers are evaluated in terms of accuracy and, due to the flexibility of HAC models, the Bayesian classifiers based on HACs mostly score higher than the Bayesian classifiers based on ACs .
To derive an explicit parametric form a d-HAC C, we need explicit parametric forms for the generators ψ 1,...,ψ d−1, which involve the parameters 𝜃 1,...,𝜃 d−1, respectively, and its structure s. Due to this, the copula C is also denoted by C ψ, 𝜃;s (u 1,...,u d ) in what follows. For example, the 3-HAC given by (4) can be denoted by \(C_{\psi _{1}, \psi _{2}, \theta _{1}, \theta _{2}; (1(23)) }\) and its parametric form, assuming, e.g., both of its generators ψ 1,ψ 2 to be Clayton generators, is given by
2.4 Kendall’s tau and an extension to more than two dimensions
Let (X 1,Y 1) and (X 2,Y 2) be independent copies of a random vector (X, Y). Then the population version of Kendall’s tau is defined as the probability of concordance minus the probability of discordance, i.e.,
It can be shown, see, e.g., (Genest and Favre 2007), that
so τ depends only on the copula of (X, Y). If C is a 2-AC based on a twice continuously differentiable generator ψ with ψ(t) > 0 for all t ∈ [0, ∞), Kendall’s tau can be represented as Joe (1997)[p.91], Nelsen (2006)[p. 163]
Hence, (8) states a relationship between 𝜃 and τ, which can often be expressed in closed form. For example, if C is a Clayton copula, see Table 1, we get τ = 𝜃/(𝜃+2) (the relationship between 𝜃 and τ for other generators can be found, e.g., in Hofert (2010b)). The inversion of this relationship establishes a method-of-moments-like estimator of the parameter 𝜃 given by \(\hat {\theta }_{n} = \tau ^{-1}(\tau _{n})\), based on the empirical version τ n of τ, given by
where (u ∙1,u ∙2) denotes a realization of n independent and identically distributed (i.i.d) copies of (U 1,U 2)∼C; see Genest and Rivest (1993). Since we do not observe realizations from C directly, note that τ can be computed based on the realizations of (X, Y). If \(\tau (\hat {\theta }_{n}) = \tau _{n}\) has no solution, this estimation method does not lead to an estimator. Unless there is an explicit form for \(\tau ^{-1}, \hat {\theta }_{n}\) is computed by numerical root finding Hofert et al. (2013).
This estimation method can also be generalized to ACs when d > 2, see Berg (2009), Hofert et al. (2013), Kojadinovic and Yan (2010b), and Savu and Trede (2010). One of the methods proposed in Berg (2009) and Savu and Trede (2010) uses a sample version of the Kendall correlation matrix. Denote by \((\tau _{ij}) = (\tau _{X_{i},X_{j}})_{ij}\) the population version of the Kendall correlation matrix for continuous random variables X 1,...,X d . Note that \((\tau _{X_{i},X_{j}})_{ij} = (\tau _{U_{i},U_{j}})_{ij}\), where F 1(X 1)=U 1,...,F d (X d )=U d . Similarly, denote the sample version of Kendall correlation matrix by \((\tau ^{n}_{ij})\), where \(\tau ^{n}_{ij}\) denotes the sample version of Kendall’s tau between the i-th and j-th data column. Then 𝜃 is estimated by
As can be seen, the parameter is chosen such that the value of Kendall’s tau equals the average over all pairwise sample versions of Kendall’s tau. Properties of this estimator are not known and also not easy to derive since the average is taken over dependent data columns (Kojadinovic and Yan 2010a). However, simulations conducted in Hofert et al. (2013) suggest consistency of this estimator. Moreover, \(\left (\begin {array}{c}d \\ 2\end {array}\right )^{-1}{\sum }_{1 \leq i \leq j \leq d} \tau ^{n}_{ij}\)is an unbiased estimator of τ(𝜃). This is an important property and we transfer it later to an estimator that we use for the structure determination which we base on appropriately selected pairwise sample versions of Kendall’s tau.
For applying this generalized estimation approach to HACs, we define a generalization of τ for m (possibly >2) random variables (r.v.s) based on the following notation. Let I, J⊂{1,...,d},I≠∅, J≠∅,(U 1,...,U d )∼C and C be a d-HAC. Denote a set of pairs of r.v.s by U I J ={(U i ,U j )|(i, j)∈I×J} and a set of pairs of data columns by u I J ={(u ∙i ,u ∙j )|(i, j)∈I×J}, where u ∙i ,u ∙j denotes realizations of (U i ,U j ).
Definition 5
Any function \(g : \mathbb {I}^{k} \rightarrow \mathbb {I}, k \in \mathbb {N}\), satisfying 1) g(u,...,u)=u for all \(u \in \mathbb {I}\) and 2) \(g(u_{p_{1}}, ..., u_{p_{k}}) = g(u_{1}, ..., u_{k})\) for all \(u_{1}, ..., u_{k} \in \mathbb {I}\) and all permutations (p 1,...,p k ) of (1,...,k) is called an \(\mathbb {I}\)-aggregation function.
Examples of \(\mathbb {I}\)-aggregation functions are the functions max, min or mean restricted to \(\mathbb {I}^{k}\).
Definition 6
Let g be an \(\mathbb {I}\)-aggregation function. Then define a g-aggregated Kendall’s tau (or simply an aggregated Kendall’s tau) τ g as
where I = {i 1,...,i l },J = {j 1,...,j q } are non-empty disjoint subsets of {1,...,d}.
Note that the sets I and J are assumed to be disjoint because we are interested only in the values of Kendall’s tau for bivariate margins of a HAC. For example, if I = {1,2} and J = {2,3}, then τ g(U I J ) would involve τ(U 2,U 2), which is not related to any bivariate margin of a HAC.
As the aggregated τ g depends only on the pairwise τ and the aggregation function g, we can easily derive its empirical version \({\tau _{n}^{g}}\) by substituting τ in τ g by its empirical version τ n given by (9). Analogously to the case of ACs, the parameter can then be estimated as \(\hat {\theta }_{n} = \tau ^{-1}({\tau _{n}^{g}})\). This is further explained in Remark 3 of Section 3.1.
2.5 Goodness-of-fit tests
Assume i.i.d. random vectors X i =(X i1,...,X i d ), i∈{1,...,n}, distributed according to a joint distribution function H with continuous margins F j , j∈{1,...,d}, and the binary-structured HAC C generated by one-parametric generators ψ 1,...,ψ d−1. All generators ψ 1,...,ψ d−1 are assumed to belong to a one-parametric family of generators (e.g., to one of the families listed in Table 1) and their parameters are denoted by 𝜃 1,...,𝜃 d−1.
Once we have the parameters estimated, we can ask how well our fitted model fits the data. This can be done using methods known as goodness-of-fit tests (GoF tests). In the following, we recall three GoF tests based on statistics that are analogues to Cramér-von Mises statistics (Cramér 1928). A large value of such statistics leads to the rejection of \(H_{0}: C \in \mathcal {C}_{0}\), where \(\mathcal {C}_{0} = \{C_{\theta }: \theta \in \mathcal {O}\}\) and \(\mathcal {O}\) is an open subset of \(\mathbb {R}^{p}, ~p \geq 1\). Thus for measuring the fitting quality of copula models, we can, informally, assess copula models with lower value of such statistics as “better”.
Now consider that, if the margins F j ,j∈{1,...,d}, are known, U i j = F j (X i j ),i∈{1,...,n},j∈{1,...,d}, is a random sample from C. In practice, the margins are typically unknown and must be estimated parametrically or non-parametrically. In the following, we will work under unknown margins and thus we consider the pseudo-observations
where \(\hat {F}_{n, j}\) denotes the empirical distribution function corresponding to the jth margin and R i j denotes the rank of X i j among X 1j ,...,X n j . The information contained in pseudo-observations is conveniently summarized by the associated empirical distribution given by
where \(\mathbf {u} = (u_{1}, ..., u_{d}) \in \mathbb {I}^{d}\). This distribution is usually called “empirical copula”, though it is not a copula except asymptotically (Genest et al. 2009).
The first GoF test is based on the empirical process
and uses a rank-based version of the Cramér-von Mises statistics
Large values of this statistic lead to the rejection of \(H_{0}: C \in \mathcal {C}_{0}\). It is shown in Genest and Rémillard (2008) that the test is consistent, i.e., if \(C \notin \mathcal {C}_{0}\), then H 0 is rejected with probability approaching 1 as n→∞. Appropriate p-values can be obtained via specially adapted Monte Carlo methods described in Genest et al. (2009).
The second GoF test, proposed in Genest and Favre (2007), uses a probability integral transformation of the data, the so-called Kendall’s transform
where (U 1,...,U d )∼C; see (Genest et al. 2009). Let K denote the univariate d.f. of V and U 1,...,U n the pseudo-observations \(\mathbf {U}_{i} = (\frac {R_{i1}}{n + 1}, ..., \frac {R_{id}}{n + 1}),~ i \in \{1, .., n\}\). Then K can be estimated nonparametrically by the empirical distribution function of a rescaled version of the pseudo-observations V 1 = C n (U 1),...,V n = C n (U n ) given by
which is a consistent estimator of the underlying distribution K. Under H 0, U = (U 1,...,U d ) is distributed as C 𝜃 for some \(\theta \in \mathcal {O}\) and hence C 𝜃 (U)∼K 𝜃 . One can then test
based on \(\mathbb {K}_{n} = \sqrt {n}(K_{n} - K_{\theta _{n}})\), where \(K_{\theta _{n}}\) denotes the distribution function of \(C_{\theta _{n}}(\mathbf {U})\). Generally, because \(H_{0} \subset H_{0}^{\prime }\) the nonrejection of \(H_{0}^{\prime }\) does not entail the nonrejection of H 0 and consequently, the consistency of the above tests using (14) does not imply the consistency of the tests using \(\mathbb {K}_{n} = \sqrt {n}(K_{n} - K_{\theta _{n}})\). But, in the case of bivariate ACs, \(H_{0}^{\prime }\) and H 0 are equivalent; see Genest et al. (2009). As we are mainly interested in 2-ACs as building blocks of HACs, this test is thus convenient for our purposes. The specific statistic considered in Genest and Favre (2007) is a rank-based analogue of the Cramér-von Mises statistic
This statistic can be easily computed as follows (Genest and Favre 2007):
The third GoF test (proposed in Genest et al. (2009)) is based on another probability integral transform - namely on the Rosenblatt’s transform, which is a mapping \(\mathcal {R}_{\theta } : (0, 1)^{d} \rightarrow (0, 1)^{d}\) such that e 1 = u 1 and for each j = 2,...,d,
A crucial property of Rosenblatt’s transform is that U∼C 𝜃 if and only if the distribution of \(\mathcal {R}_{\theta }(C_{\theta })\) is the d-variate independence copula C π(u)=u 1 u 2...u d ; see, e.g., (Genest et al. 2009). Thus for all \(\theta \in \mathcal {O}\), \(H_{0}: C_{\theta } \in \mathcal {C}_{0}\) is equivalent to \(H_{0}^{\prime \prime } : \mathcal {R}_{\theta }(\mathbf {U}) \sim C_{\Pi }\).
To test \(H_{0}^{\prime \prime }\), we can therefore use the fact that under H 0, the transformed pseudo-observations \(\mathbf {E}_{1} = \mathcal {R}_{\theta }(\mathbf {U}_{1}), ..., \mathbf {E}_{n} = \mathcal {R}_{\theta }(\mathbf {U}_{n}),\) can be interpreted as a sample from the independence copula C π. Defining the empirical distribution function on E 1,...,E n as
it should be close to C π under H 0. Cramér-von Mises statistics based on Rosenblatt’s transformation are given by
see Genest et al. (2009). All three test statistics performed well in a large scale simulation study conducted at Genest et al. (2009) in the bivariate case. We choose them as good candidates for our purpose of goodness-of-fit testing.
We now introduce a g-aggregated statistic that will be used for the GoF assessment of d-HAC estimates in Section 4.
Definition 7
Let C be a d-HAC, g be an \(\mathbb {I}\)-aggregation function and 2 S n ((u ∙i ,u ∙j ), C 2(⋅;ψ)) be the statistic corresponding to a GoF test, e.g., \(S_{n}, S_{n}^{(K)}\) or \(S_{n}^{(C)}\), for a bivariate copula C 2(u 1,u 2;ψ) and a pair of data columns (u ∙i ,u ∙j ). A g-aggregated statistics \({}_{2}{S_{n}^{g}}\) is
where C i j , 1 ≤ i < j ≤ d, are the bivariate marginal copulas of C.
We employ g-aggregated statistics in order to simplify the computation of \(S_{n}^{(K)}\) and \(S_{n}^{(C)}\) for d > 2. Considering the \(S_{n}^{(K)}\) statistic, the main difficulty in its computation consists in expressing \(K_{\theta _{n}}\). For d = 2, given a 2-AC \(C(\cdot ; \psi _{\theta _{n}})\), where \(\psi _{\theta _{n}}\) denotes a generator with a parameter 𝜃 n , \(K_{\theta _{n}}\) is the bivariate probability integral transform, which can be easily computed as \(K_{\theta _{n}}(t) = t - \frac {\psi _{\theta _{n}}^{-1}(t)}{(\psi _{\theta _{n}}^{-1})^{\prime }(t)}\); see Genest and Rivest (1993). However, for d > 2 and particularly for HACs, the complexity of \(K_{\theta _{n}}\) dramatically increases. in Okhrin et al. (2013b), its computation is addressed for HACs, however, the authors restrict only to FNACs, which rarely occurs in our experiments, and, even for FHACs the obtained formulas involve multivariate integration that substantially increases the complexity of their application.
Considering the statistic \(S_{n}^{(C)}\), the main difficulty in its computation consists in expressing e j , for j = 2,...,d, given by (21). Observe that e d includes d−1 partial derivatives of C 𝜃 , thus its complexity quickly grows in d and the time consumption of its computation exceeds reasonable limits already for d = 6, particularly for families with a more complex generator, e.g., for the Frank family. Using g-aggregated statistics, computations for d > 2 are substantially simplified.
2.6 Okhrin’s algorithm for the structure determination of HAC
We recall the algorithm presented in Okhrin et al. (2013b) for the structure determination of HACs, which returns the structure for some unknown HAC C using only the known forms of its bivariate margins. The algorithm uses the following definition.
Definition 8
Let C be a d-HAC with generators ψ 1,...,ψ d−1 and (U 1,...,U d )∼C. Define \(\mathcal {U}_{C}(\psi _{k}) = \left \{ i \in \{1, ..., d\}\right . ~|\) there exists j∈{i+1,...,d} such that (U i ,U j )∼C(⋅;ψ k )}, k = 1,...,d−1.
Note that (U j ,U i )∼C(⋅;ψ k ) if and only if (U i ,U j )∼C(⋅;ψ k ).
Proposition 1
(Górecki and Holeňa 2013) jDefining \(\mathcal {U}_{C}(u_{i}) = \{i \}\) for the leaf u i , 1≤i≤d, there is a unique disjoint decomposition of \(\mathcal {U}_{C}(\psi _{k})\) given by
For an unknown d-HAC C with all bivariate margins known, its structure can be easily determined using Algorithm 1. We start from the sets \(\mathcal {U}_{C}(u_{1}) , ... , \mathcal {U}_{C}(u_{d})\) joining them together through (25) until we reach the node ψ for which \(\mathcal {U}_{C}(\psi ) = \{1, ..., d\}\).

2.7 Example
We illustrate Algorithm 1 for a 5-HAC given by C(C(u 1,u 2;ψ 2), C(u 3,C(u 4,u 5;ψ 4);\( \psi _{3}); \psi _{1}) = C_{\psi _{1}, ..., \psi _{4}; ((12)(3(45)))}(u_{1}, ..., u_{5})\). The structure of this copula is depicted on the left side in Fig. 2 and its bivariate margins are:
Now assume that the structure is unknown and only the bivariate margins are known. We see that \(\mathcal {U}_{C}(\psi _{1}) = \{1, 2, 3, 4, 5\}, \) \(\mathcal {U}_{C}(\psi _{2}) = \{1, 2\}, \) \( \mathcal {U}_{C}(\psi _{3}) = \{3, 4, 5\}, \mathcal {U}_{C}\) (ψ 4)={4,5}. For the leaves u 1,...,u 5, we have \(\mathcal {U}_{C}(u_{i}) = \{i\}, i = 1, ..., 5\). In Step 1 of Algorithm 1, there are two minima: k = 2 and k = 4. We arbitrarily choose k = 4. As \(\mathcal {U}_{C}(\psi _{4}) = \mathcal {U}_{C}(u_{4}) \cup \mathcal {U}_{C}(u_{5})\), we set \(\mathcal {H}_{l}(\psi _{4}) : = u_{4}\) and \(\mathcal {H}_{r}(\psi _{4}) : = u_{5}\) in Step 3. In Step 4, we set \(\mathcal {I} = \{1, 2, 3, 5 \}\). In the second loop, k = 2. As \(\mathcal {U}_{C}(\psi _{2}) = \mathcal {U}_{C}(u_{1}) \cup \mathcal {U}_{C}(u_{2})\), we set \(\mathcal {H}_{l}(\psi _{2}) : = u_{1}\) and \(\mathcal {H}_{r}(\psi _{2}) : = u_{2}\) in Step 3. In the third loop, we have k = 3. As \(\mathcal {U}_{C}(\psi _{3}) = \mathcal {U}_{C}(u_{3}) \cup \mathcal {U}_{C}(\psi _{4})\), we set \(\mathcal {H}_{l}(\psi _{3}) : = u_{3}\) and \(\mathcal {H}_{r}(\psi _{3}) : = \psi _{4}\) in Step 3. In the last loop, we have k = 1. As \(\mathcal {U}_{C}(\psi _{1}) = \mathcal {U}_{C}(\psi _{2}) \cup \mathcal {U}_{C}(\psi _{3})\), we set \(\mathcal {H}_{l}(\psi _{1}) : = \psi _{2}\) and \(\mathcal {H}_{r}(\psi _{1}) : = \psi _{3}\) in Step 3. Observing the original copula form and Fig. 2, we see that we have determined the correct structure, which is stored in \(\mathcal {H}_{l}(\psi _{k}), \mathcal {H}_{r}(\psi _{k}), k = 1, ..., 4\).
3 Our approach
3.1 HAC structure determination based on Kendall’s tau
According to Theorem 2, our goal is to build the HAC such that the sufficient nesting condition is satisfied for each generator and its parent in a HAC structure. The sufficient nesting condition typically results in constraints on the parameters 𝜃 1,𝜃 2 of the involved generators ψ 1,ψ 2; see, e.g., Table 1 or Hofert (2011). As 𝜃 i ,i = 1,2 is related to τ through (8), there is also an important relationship between the values of τ and the HAC tree structure following from the sufficient nesting condition. This relationship is described for the fully-nested 3-HAC (4) in Remark 2.3.2 in Hofert (2010b). There, it is shown that if the sufficient nesting condition holds for the parent-child pair (ψ 1,ψ 2), then 0 ≤ τ(ψ 1) ≤ τ(ψ 2). We generalize this statement as follows.
Proposition 2
Let C be a d-HAC with the structure s and the generators ψ 1 ,...,ψ d−1 , where each parent-child pair satisfies the sufficient nesting condition. Then \(\tau (\psi _{i}) \leq \tau (\psi _{j}), \text {where}~ \psi _{j} \in \mathcal {D}(\psi _{i})\) , holds for each ψ i ,i=1,...,d−1.
Proof
As \(\psi _{j} \in \mathcal {D}(\psi _{i})\), there exists a unique sequence \(\psi _{k_{1}}, ..., \psi _{k_{l}}\), where \( 1 \leq k_{m} \leq \ d - 1,~ m = 1, ..., l,~ l \leq d - 1,~ \psi _{k_{1}} = \psi _{i},~ \psi _{k_{l}} = \psi _{j}\) and \(\psi _{k - 1} = \mathcal {P}(\psi _{k})\) for k = 2,...,l. Applying the above mentioned remark for each pair (ψ k−1, ψ k ), k = 2,...,l, we get \(\tau (\psi _{k_{1}}) \leq ... \leq \tau (\psi _{k_{l}})\). □
Thus, having a branch from s, all its nodes are uniquely ordered according to their value of τ assuming unequal values of τ for all parent-child pairs. This provides an alternative algorithm for determining the structure of a HAC. We assign generators with the highest values of τ to the lowest levels of the branches in the structure. Ascending higher up in the tree we assign generators with lower values of τ. Now consider the following definition and proposition.
Definition 9
Let C be a d-HAC and u i ,u j are two different leaves from the structure of the d-HAC. Then we call youngest common ancestor of u i ,u j (denoted \(\mathcal {A}_{y}(u_{i}, u_{j})\)) the node ψ, for which \((\psi \in \mathcal {A}(u_{i}) \cap \mathcal {A}(u_{j})) \wedge (\mathcal {A}(u_{i}) \cap \mathcal {A}(u_{j}) \cap \mathcal {D}(\psi ) = \emptyset )\).
Remark 2
Let ψ be a generator from a d-HAC structure, \(u_{i} \in \mathcal {D}_{l}(\mathcal {H}_{l}(\psi ))\) and \(u_{j} \in \mathcal {D}_{l}(\mathcal {H}_{r}(\psi ))\). Then \(\mathcal {A}_{y}(u_{i}, u_{j}) = \psi \).
Note that due to clear correspondence of the variables in a d-HAC and the leaves in the structure of the same d-HAC, both the variables and the leaves are denoted by the same u 1,…,u d . This can be made without a worry to confuse the reader.
Proposition 3
Let C be a d-HAC with the structure s with generators ψ 1 ,...,ψ d−1 . Then
Proof
The proof is leaded by induction. Let d = 2. Then C(u 1,u 2)=C(u 1,u 2;ψ 1), i.e., the leaves u 1 and u 2 are the children of ψ 1. It implies that \((\psi _{1} \in \mathcal {A}(u_{1}) \cap \mathcal {A}(u_{2})) \wedge (\mathcal {A}(u_{1}) \cap \mathcal {A}(u_{2}) \cap \mathcal {D}(\psi _{1}) = \emptyset )\) and thus \(\psi _{1} = \mathcal {A}_{y}(u_{1}, u_{2})\) according to Definition 9.
Assume d ≥ 3 and that (26) holds for d−1, d−2,..., 3. Start denoting the root node of s as ψ m . The bivariate marginal copula of C corresponding to variables u i ,u j is C(1,...,1, u i ,1,...,1, u j ,1,...,1;ψ 1,...,ψ d−1). To simplify notation, we show in each involved inner HAC only the generator corresponding to the highest node in its structure. Thus, for the bivariate marginal copula, we simplify its notation to C(1,...,1, u i ,1,...,1, u j ,1,...,1;...,ψ m ,...). Note that C(1,...,1)=1 and \(C(1, ..., 1, u, 1, ..., 1) = u, u \in \mathbb {I}\) for an arbitrary copula C.
If \(\mathcal {H}_{l}(\psi _{m}) = u_{k}, k = 1, ..., d\), we just formally define ψ l = u k and C(⋅;ψ l )=u k . If \(\mathcal {H}_{r}(\psi _{m}) = u_{k}, k = 1, ..., d\), we also just formally define ψ r = u k and C(⋅;ψ r )=u k . Although neither C(⋅;ψ l ) nor C(⋅;ψ r ) are copulas, this will simplify the notation used in the proof. In other case, we set \(\psi _{l} = \mathcal {H}_{l}(\psi _{m}), \psi _{r} = \mathcal {H}_{r}(\psi _{m})\). Now, we distinguish the three following situations:
-
1.
If \(u_{i} \in \mathcal {D}_{l}(\psi _{l})\) and \(u_{j} \in \mathcal {D}_{l}(\psi _{r})\), then C(C(1,...,1,u i ,1,...,1;...,ψ l ,...), C(1,...,1,u j ,1,...,1;...,ψ r ,...);ψ m )=C(u i ,u j ;ψ m ). As \(\psi _{m} = \mathcal {A}_{y}(u_{i}, u_{j})\) (Remark 2), the statement holds.
-
2.
If \(\{u_{i}, u_{j}\} \subset \mathcal {D}_{l}(\psi _{l})\), then C(C(1,...,1,u i ,1,...,1,u j ,1,...,1;...,ψ l ,...), C(1,...,1;...,ψ r ,...);ψ m )=C(1,...,1,u i ,1,...,1,u j ,1,...,1;...,ψ l ,...). Since the tree rooted in ψ l has less leaves than the tree rooted in ψ m , for C(1,...,1,u i ,1,...,1,u j ,1,...,1;...,ψ l ,...) we already know that (26) holds, thus it holds also for C(1,...,1,u i ,1,...,1,u j ,1,...,1;...,ψ m ,...).
-
3.
If \(\{u_{i}, u_{j}\} \subset \mathcal {D}_{l}(\psi _{r})\), then C(C(1,...,1;...,ψ l ,...),C(1,...,1,u i , 1,...,1,u j ,1,...,1;...,ψ r ,...);ψ m )=C(1,...,1,u i ,1,...,1,u j ,1,...,1;...,ψ r ,...). Since the tree rooted in ψ r has less leaves than the tree rooted in ψ m , for C(1,...,1,u i ,1,...,1,u j ,1,...,1;...,ψ r ,...) we already know that (26) holds, thus it holds also for C(1,...,1,u i ,1,...,1,u j ,1,...,1;...,ψ m ,...).
□
Thus (U i ,U j ) is distributed according to the 2-AC \(C(\cdot ; \mathcal {A}_{y}(u_{i}, u_{j}))\) for all i, j∈{1,...,d}, i≠j. This fact allows to prove the following proposition.
Proposition 4
Let C be a d-HAC with the generators ψ 1 ,...,ψ d−1 , (U 1 ,...,U d )∼C and (τ ij ) be the population version of the Kendall correlation matrix of (U 1 ,...,U d ). Then, given k∈{1,...,d−1},
for all \((u_{i}, u_{j}) \in \mathcal {D}_{l}(\mathcal {H}_{l}(\psi _{k})) \times \mathcal {D}_{l}(\mathcal {H}_{r}(\psi _{k}))\).
Proof
Recall that \(\tau _{ij} = \tau _{U_{i}, U_{j}}\) and τ(ψ k )=τ(C(⋅;ψ k )) by definition and let k∈{1,...,d−1} and \((u_{i}, u_{j}) \in \mathcal {D}_{l}(\mathcal {H}_{l}(\psi _{k})) \times \mathcal {D}_{l}(\mathcal {H}_{r}(\psi _{k}))\). Using Proposition 3, it implies \((U_{i}, U_{j}) \sim C(\cdot ; \mathcal {A}_{y}(u_{i}, u_{j}))\). As \(\psi _{k} = \mathcal {A}_{y}(u_{i}, u_{j})\) according to Remark 2, it follows that (U i ,U j )∼C(⋅;ψ k ). Hence, \(\tau _{U_{i}, U_{j}} = \tau (C(\cdot ; \psi _{k}))\). □
Remark 3
It holds that \(\tau (\psi _{k}) = \tau ^{g}(\mathbf {U}_{\mathcal {D}_{l}(\mathcal {H}_{l}(\psi _{k})) \times \mathcal {D}_{l}(\mathcal {H}_{r}(\psi _{k}))})\) for a d-HAC C and for each k = 1,...,d−1. This is because, given k∈{1,...,d−1}, the values of τ i j for \((u_{i}, u_{j}) \in \mathcal {D}_{l}(\mathcal {H}_{l}(\psi _{k})) ~\times ~ \) \(\mathcal {D}_{l}(\mathcal {H}_{r}(\psi _{k}))\) are all equal to τ(ψ k ), see Proposition 4, and g(u,...,u)=u for all \(u \in \mathbb {I}.\)
Computing τ(ψ k ),k = 1,...,d−1, according to Remark 3 and using Proposition 2 leads to an alternative algorithm for HAC structure determination; see Algorithm 2. This algorithm can be used for arbitrary d > 2 (see Górecki and Holeňa (2013) for more details including an example for d = 4). It returns the sets \(\mathcal {U}_{C}(\psi _{k}), k = 1, ..., d-1\). Passing them to Algorithm 1, we avoid the computation of \(\mathcal {U}_{C}(\psi _{k}), k = 1, ..., d-1\) in Definition 8 and we get the requested d-HAC structure without having to know the forms of the bivariate margins. Assuming a parametric family for each ψ k , the 𝜃−τ relationship for the given family can be used to obtain the parameters, i.e., \(\theta _{k} = \tau _{\theta }^{-1}(\tau (\psi _{k})), k = 1, ..., d - 1\), where \(\tau _{\theta }^{-1}\) denotes this 𝜃−τ relationship, e.g., for the Clayton family \(\tau _{\theta }^{-1}(\tau ) = 2\tau /(1-\tau )\). In other words, assuming (U 1,...,U d )∼C, where C is a d-HAC with one-parametric generators ψ 1,...,ψ d−1 from the same family, if C is unknown but the population version of the Kendall correlation matrix (τ i j ) is known, both structure and parameters of C can be obtained from (τ i j ) using Algorithms 1 and 2. Based on the empirical version of the Kendall correlation matrix, we thus obtain the following approach for both determining the structure and estimating parameters of C.

3.2 Structure determination and parameter estimation of a HAC
Using \({\tau _{n}^{g}}\) instead of τ g, we can easily derive a new approach for structure determination and parameter estimation of a HAC from Algorithms 1 and 2. The approach is summarized in Algorithm 3. The algorithm returns the parameters \(\hat {\theta }_{1}, ..., \hat {\theta }_{d-1}\) of the estimate \(\hat {C}\) and the sets \(\mathcal {U}_{\hat {C}}(\psi _{k}), k = 1, ..., d-1\). Passing the sets to Algorithm 1, we get the requested \(\hat {C}\) structure.

From Algorithm 3, the reader can see our motivation for basing the estimation process on Kendall’s tau. Firstly, the matrix \((\tau ^{n}_{ij})\) is computed in order to determine the structure of a HAC. Then, the computed values of \((\tau ^{n}_{ij})\) are reused for the estimation of the parameters. The latter can be done effectively as the function τ −1 is known in closed form for many Archimedean families, e.g., for the Clayton and Gumbel families listed in Table 1, cf. (Hofert 2011). As we will see in Section 4, the estimator is comparably fast to compute, at least if d is not too large. Theoretically, Spearman’s rho or Blomqvist’s beta could be considered for this task as well despite the fact that these rank correlation measures are much less popular in this domain. It is also known that Kendall’s tau works well in comparison to Blomqvist’s beta; seeHofert et al. (2013).
If g is set to be the average function then \(\tau ^{\text {avg}}_{n}(\theta _{k}) = g((\tau ^{n}_{\tilde {i}\tilde {j}})_{(\tilde {i},\tilde {j}) \in \mathcal {U}_{\hat {C}}(z_{i}) \times \mathcal {U}_{\hat {C}} (z_{j})})\) (i, j are the indices found in Step 1 of Algorithm 1) is an unbiased estimator of τ(𝜃 k ), and thus the structure determination is based only on unbiased estimators, which is another favorable property of the proposed method. Note that recently an approach allowing for consistent estimation of all parameters of a HAC been published (Górecki et al. 2014). Its comparison with the approach presented here is a topic of future research.
In order to fulfill the sufficient nesting condition, the parameter \(\tilde {\theta }_{d + k}\) is trimmed in Step 3 in order to obtain a proper d-HAC. Note that one can allow the generators to be from different Archimedean families. However, this case is more complex and we do not address it in this paper; see Hofert (2010a) and Hofert (2010b).
Note that Algorithm 3 is a variation of the algorithm for agglomerative hierarchical clustering (AHC) (Clarke et al. 2009, p.414). Defining \(\delta _{ij} = 1-\tau ^{n}_{ij}\), δ i j is a commonly used distance between the random variables U i ,U j . Setting g to be the aggregation function minimum, average or maximum, the algorithm results in complete-linkage, average-linkage or single-linkage AHC, respectively (Clarke et al. 2009, p. 414). As many types of statistical software include an implementation of AHC, the implementation of the proposed algorithm is straightforward. Moreover, adding the dendrogram obtained during AHC simplifies the interpretation of the estimator; see Fig. 8 in Section 5.
4 Experiments on simulated data
4.1 Design of the performed experiments
In this section, we compare our methods for HAC estimation based on Algorithm 3 with several methods presented in Okhrin et al. (2013a), which are implemented in R, see Okhrin and Ristig (2014). As we are interested in binary structured HACs, we choose for the comparison the methods 𝜃 bin, 𝜃 RML, τ bin, which return binary structured HAC estimates as their results (note that the 𝜃 RML method also allows for non-binary structured HACs estimation). The first two methods are based on the ML estimation technique, whereas the third method is based on the 𝜃−τ relationship. Our methods are denoted by \(\tau ^{\min }_{\text {bin}}, \tau ^{\max }_{\text {bin}}\) and \(\tau ^{\text {avg}}_{\text {bin}}\), i.e., the involved function g, see Algorithm 3, is selected to be the minimum, maximum and average, respectively. The first two functions are selected as they represent “extremes” of \(\mathbb {I}\)-aggregation functions. The last function is selected due to the reasons mentioned in Section 3.2, i.e., if g is the average function, the structure determination is based on unbiased estimates of τ(𝜃 k ),k = 1,...,d−1.
The comparison is performed on simulated data for d∈{5,6,7,9}. We selected the maximal dimension d = 9 for two reasons. The first reason is that the results for d > 9 do not bring any surprising information about the differences among the considered methods. The second reason is that, for d≤9, the obtained structure estimate representations (described in the following paragraph) involve single-digit numbers only, which allows for more concise notation. We simulated N = 1000 samples of size n = 500 according toHofert (2011) for 4 copula models based on Clayton generators. Our choice of the Clayton family of generators was due to the intended comparison of our method with the above-mentioned methods that are implemented for the Gumbel and Clayton family of generators only. The Clayton family of generators was chosen arbitrarily from these two after we have experimented with both families and have found out that results for both of them are similar.
The first considered model is \(((12)_{\frac {3}{4}}(3(45)_{\frac {4}{4}})_{\frac {3}{4}})_{\frac {2}{4}}\). The natural numbers in the model notation (as in (Okhrin et al. 2013a)) are the indexes of the copula variables, i.e., 1,...5, the parentheses correspond to each \(\mathcal {U}_{C}(\cdot )\) of individual copulas, i.e., \(\mathcal {U}_{C}(\psi _{1}) = \{1, 2, 3, 4, 5\}, \mathcal {U}_{C}(\psi _{2}) = \{3, 4, 5\}, \mathcal {U}_{C}(\psi _{3}) = \{1,2\}, \mathcal {U}_{C}(\psi _{4}) = \{4,5\}\), and the subscripts are the model parameters, i.e, \((\theta _{1}, \theta _{2}, \theta _{3}, \theta _{4}) = (\frac {2}{4}, \frac {3}{4}, \frac {3}{4}, \frac {4}{4})\). Note that the indices of the 4 generators could be permuted arbitrarily, and our particular selection of their ordering just serves for better illustration. The other 3 models are given with analogously by \((1((23)_{\frac {5}{4}}(4(56)_{\frac {6}{4}})_{\frac {5}{4}})_{\frac {4}{4}})_{\frac {2}{4}}\), \((1((23)_{\frac {5}{4}}(4(5(67)_{\frac {7}{4}})_{\frac {6}{4}})_{\frac {5}{4}})_{\frac {4}{4}})_{\frac {2}{4}}\) and \(((1(2(34)_{\frac {5}{4}})_{\frac {4}{4}})_{\frac {3}{4}}\) \(((56)_{\frac {4}{4}}(7(89)_{\frac {5}{4}})_{\frac {4}{4}})_{\frac {3}{4}})_{\frac {2}{4}}\). The smallest difference between the parameters is set to \(\frac {1}{4}\) and the values of the parameters are set in the way that the sufficient nesting condition is satisfied for each parent-child pair of the generators. As we discovered while experimenting with different parametrizations, a larger difference in the parameters could hide the impact of the bias in most of the methods of Okhrin et al. (2013a) on the structure determination, and the results obtained by different methods can be similar for those parametrizations. Smaller differences than \(\frac {1}{4}\) were not necessary as setting them to \(\frac {1}{4}\) fully reveals the impact of the bias and clearly shows the difference among the methods. This fact is illustrated in the following subsection in the part where the methods are assessed in terms of ability to determine the true copula structure.
4.2 Results of the experiments
The results for d∈{5,6} are shown in Tables 2 and 4, where the first table concerns the structures determined by the methods, whereas the second table concerns goodness-of-fit of the HACs estimated by the methods and time consumption of the methods. Similarly, the results for d∈{7,9} are shown in Tables 3 and 5. Result for different models are separated by double lines. Note that all experiments were performed on a PC with Intel Core 2.3 GHz CPU and 4GB RAM. As 𝜃 RML failed in most cases for d = 9 on the described hardware configuration, the result of the method for this dimension is not presented.
The third column in Tables 2 and 3 shows the number of different estimated copula structures (denoted #d.s.) in N = 1000 runs of the considered method. The value gives us information on how much the resulting estimated structure varies for a given method and model. The lower the value is, the more stable the structure determination can be considered. For d = 5,6, 𝜃 bin and 𝜃 RML show the strongest stability, whereas τ bin shows the weakest stability. For d = 7, the situation slightly changes and 𝜃 bin and τ bin clearly represent two extremes – the first showing substantially stronger stability than the remaining methods and the latter represents the opposite. As the dimension increases, we observe comparably increasing stability for \(\tau ^{\text {avg}}_{\text {bin}}\) until it reaches the best stability for d = 9. In all considered dimensions, we observe that \(\tau ^{\max }_{\text {bin}}\) shows slightly worse stability than \(\tau ^{\min }_{\text {bin}}\) and \(\tau ^{\text {avg}}_{\text {bin}}\).
The next two columns in Tables 2 and 3 address the ability of the methods to determine the true copula structure. The fourth column shows the three most frequent structures obtained by the method (if the true structure is not one of three the most frequent structures, then we add it in the fourth row corresponding to the method) with average parameter values. The true structure is emphasized by bold text. The fifth column shows the frequency of the true structure in all estimated structures. The methods \(\tau ^{\min }_{\text {bin}}\) and \(\tau ^{\text {avg}}_{\text {bin}}\) dominate in the ability to determine the true copula structure in all four cases (d∈{5,6,7,9}). The \(\tau ^{\max }_{\text {bin}}\) method ranks as the third best, also in all four cases. The remaining methods show very poor ability to detect the true structure, especially for d ≥ 7. For example, for d = 7, 𝜃 RML returned the true structure only 2 times out of 1000. For d = 9, the difference between our and the remaining methods is most obvious. The worst performance shows the 𝜃 bin method, which did not return any estimate with the true structure. The τ bin method, which returned 6.2 %, is also substantially outperformed by all of our methods.
The ability of the methods to determine the true copula structure is additionally illustrated in Fig. 3, which shows the frequency of the true structure in 1000 estimated structures for the considered methods, for sample sizes 10,20,...,500 and for the differences in the parameters set consecutively to \(1, \frac {1}{2}, \frac {1}{3}, \frac {1}{4}\), namely for four 5-HAC models ((12)3∗q (3(45)4∗q )3∗q )2∗q with \(q = 1, \frac {1}{2}, \frac {1}{3}, \frac {1}{4}\), respectively. For q = 1, we observe that the frequency of the true structure for the considered sample sizes is similar for all the considered methods except the 𝜃 RML method and approaches to 100 % as the sample size increases. For 𝜃 RML, the frequency never exceeds 55 % and the same holds for the remaining \(q = \frac {1}{2}, \frac {1}{3}, \frac {1}{4}\). This fact indicates that, from a certain level that is lower than 100 %, the 𝜃 RML method is not able to improve in estimation of the true structure even with increasing sample size. Decreasing in q, the difference between our methods and the remaining methods in the frequency of the true structure for the considered sample sizes increases. We also observe that the \(\tau ^{\min }_{\text {bin}}\) and \(\tau ^{\text {avg}}_{\text {bin}}\) methods are methods that most quickly approach to 100 % frequency of the true structure for for all \(q = 1, \frac {1}{2}, \frac {1}{3}, \frac {1}{4}\) while increasing the sample size. The third most successful method is clearly \(\tau ^{\min }_{\text {bin}}\) for \(q = \frac {1}{2}, \frac {1}{3}, \frac {1}{4}\). For the remaining methods and \(q = \frac {1}{3}, \frac {1}{4}\), the frequency of the true structure remains below 70 %, 60 %, respectively. Surprisingly, for \(q = \frac {1}{3}, \frac {1}{4}\), the 𝜃 bin method shows (approximately) decreasing frequency of the true structure with increasing sample size for the sample sizes larger than (approximately) 200.
The frequency of the true structure in 1000 estimated structures for the considered methods, for sample sizes 10,20,...,500 and for the differences in the parameters set consecutively to \(1, \frac {1}{2}, \frac {1}{3}, \frac {1}{4}\), i.e., for four 5-HAC models ((12)3∗q (3(45)4∗q )3∗q )2∗q with \(q = 1, \frac {1}{2}, \frac {1}{3}, \frac {1}{4}\), respectively
Next, we assess the methods by means of goodness-of-fit. The results can be seen in columns 3–6 in Tables 4 and 5, where the averages and standard deviations of four GoF statistics are shown. The values in each row correspond to the averages of the GoF statistics over all estimates with the structure corresponding to the one shown in the same row in Tables 2 and 3. The d S n corresponds directly to the statistics given by (15). By the lower index d in the notation, we accentuate the fact that this is non-aggregated, i.e, “truly” d-dimensional statistics, as the rest of the statistics, \({~}_{2}S_{n}^{\max }, {~}_{2}S_{n}^{(K)\max }, {~}_{2}S_{n}^{(C)\max }\), are the aggregated (using max function) statistics given by Definition 7 that are based on the bivariate statistics \(S_{n}, S_{n}^{(K)}, S_{n}^{(C)}\), respectively. The reason for choosing the maximum function as the \(\mathbb {I}\)-aggregation function g is that then this g-aggregated statistics can be interpreted in the way that it evaluate how the estimate fits the data according to its worst fitting bivariate margin. Observing the results, we see that the \(\tau ^{\text {avg}}_{\text {bin}}\) method dominates in GoF in all four dimensions. The methods 𝜃 RML and \(\tau ^{\max }_{\text {bin}}\) show good results as well, but the time consumption of 𝜃 RML for comparable results is considerably higher (especially for d = 7). A surprising result shows the \(\tau ^{\min }_{\text {bin}}\) method. Despite it shows very good ability in estimating the true structure, it is ranked as the third best in GoF, i.e., it shows the results opposite to \(\tau ^{\max }_{\text {bin}}\), which is very good in GoF but is ranked as the third in the ability to estimate the true structure. Here, it is worth to note that \(\tau ^{\text {avg}}_{\text {bin}}\) performs very good both in the ability to determine the true structure and in GoF. The remaining methods show poor results, what is additionally illustrated by the discrepancy between the estimated average parameter values shown in the fourth column in Tables 2 and 3 and the true parameter values.
The last row for each dimension and each method in Tables 4 and 5, denoted by false structures in the second column, shows averages of the considered statistics over all estimates with structures different to the true structure, say false structured estimates. These results allow for studying the performance of the methods when the true structure is misspecified. Comparing the results for the false structured estimates among the considered methods, we observe that the \(\tau ^{\text {avg}}_{\text {bin}}\) method shows the lowest values for each dimension and statistic considered. The second and the third lowest values show alternately the 𝜃 RML and \(\tau ^{\max }_{\text {bin}}\) methods for each d∈{5,6,7} and statistics considered. The fourth lowest values mostly shows the \(\tau ^{\min }_{\text {bin}}\) method. For the remaining two methods, the results are varying. Summarizing these results, a false structured HAC estimate fits the best to the data if it is obtained by the \(\tau ^{\text {avg}}_{\text {bin}}\) method.
The last column in Tables 4 and 5 shows the average computing time needed for a single estimation process. In this case, \(\tau ^{\min }_{\text {bin}}\), \(\tau ^{\max }_{\text {bin}}\), \(\tau ^{\text {avg}}_{\text {bin}}\) show similar results that are slightly better than the binary methods 𝜃 bin, τ bin, whereas 𝜃 RML shows substantially (several times) higher time consumption, particularly for d ≥ 6.
Based on all experimental results presented in this section, we can rank the presented methods as follows:
-
1.
the \(\tau ^{\text {avg}}_{\text {bin}}\) method only. We can claim that this method is the clear winner out of all here presented methods. It shows the best results in goodness-of-fit, even for the cases when the true structure is not determined; it is also one of the two best methods (together with \(\tau ^{\min }_{\text {bin}}\)) in the evaluation of the ability to determine the true structure, including the analysis of this ability for different sample sizes; it offers comparably low run-time (together with \(\tau ^{\min }_{\text {bin}}\) and \(\tau ^{\max }_{\text {bin}}\)); its stability in structure determination increases in d if compared to the remaining methods.
-
2.
the methods \(\tau ^{\min }_{\text {bin}}\), \(\tau ^{\max }_{\text {bin}}\). These methods show in some comparisons results similar to \(\tau ^{\text {avg}}_{\text {bin}}\), e.g., \(\tau ^{\min }_{\text {bin}}\) in the ability to determine the true structure, however, in other comparisons, e.g., in goodness-of-fit, these methods show worse results than \(\tau ^{\text {avg}}_{\text {bin}}\).
-
3.
the 𝜃 RML method only. This method shows, on the one hand, comparably good results in goodness-of-fit (mostly similar to \(\tau ^{\max }_{\text {bin}}\)), on the other hand, it show poor results in the ability to determine the true structure, particularly when analyzed for the different sample sizes, and its run-time is substantially higher than the run-time of all other considered methods.
-
4.
the methods 𝜃 bin and τ bin. These methods score poorly in most of the presented comparisons.
Note that a similar experiment was reported in (Górecki and Holeňa 2014), where N = 100 was used instead. Comparing the results of both experiments, we see that they are almost the same for d = 5,6. For the two higher dimensions d = 7,9, the results show several rather smaller differences, mostly for rarely occurring estimated structures. Considering the \(\tau ^{\text {avg}}_{\text {bin}}\) method, the results in both experiments for the same statistics considered, i.e., \({~}_{2}S_{n}^{(K)\max }, {~}_{2}S_{n}^{(C)\max }\) (denoted by \(S_{n}^{(K)}, S_{n}^{(C)}\), respectively, in Górecki and Holeňa (2014)) and frequencies of the 3 most frequent estimated structures, are almost the same for the considered dimensions.
5 Copula-based Bayesian classification
5.1 Construction of copula-based Bayesian classifiers
Bayesian classifiers belong to the most popular classifiers and are used for pattern recognition in several image processing, statistical learning and data mining applications. Here we briefly recall some basics for Bayesian classifiers and a way how copulas could be integrated in them as proposed in Sathe (2006). Later we describe experiments that involve Bayesian classifiers based on Gaussian copulas, ACs or HACs. Note that we introduce Bayesian classifiers based on ACs and HACs here for the first time.
Let Ω = {ω 1,...,ω m } be a finite set of m classes. The problem of classification is to assign each x from the variable space \(\mathbb {R}^{d}\) to a class from Ω. A Bayesian classifier is said to assign x to the class ω i if,
where \(g_{i} : \mathbb {R}^{d} \mapsto \mathbb {R}, i = 1, ..., m\) are known as discriminant functions, (Sathe 2006), defined by
Here, \(f: \mathbb {R}^{d} \mapsto [0, \infty )\) is a probability density function (pdf) and \(\mathbb {P}(\omega _{i}), i = 1, ..., m\) are the prior probabilities of the classes from Ω . Since any monotonically increasing function \(Q: \mathbb {R} \rightarrow \mathbb {R}\) keeps the classification unaltered, the discriminant functions can be simplified by g i :=Q∘g i with \(Q(t) = \ln (t{\sum }_{j=1}^{m}f(\mathbf {x}|\omega _{j})\) \(\mathbb {P}(\omega _{j}))\) from (29) to
If f(x|ω i ) is assumed to be, e.g., a Gaussian pdf (leading to the normal Bayesian classifier (Clarke et al. 2009, p. 242)), all the margins are distributed according to the same type of distribution. It follows that the corresponding classifier does not accurately classify samples with marginal distributions of different types. This drawback can be addressed by assuming the variables to be independent. This assumption, which leads to the Naive Bayesian classifier (Clarke et al. 2009, p. 241), does not impose any restrictions on the margins. However, if there exists dependence among the variables, the Naive Bayesian classifier is also inappropriate for the task. An elegant solution that overcomes the drawbacks of both mentioned approaches can be achieved by bringing copulas into play.
Provided H in (1) is an absolutely continuous multivariate distribution function with marginals F 1,...,F d , the pdf f of H can be expressed as
where \(c(u_{1}, ..., u_{d}) = \frac {\partial ^{d}C(u_{1}, ..., u_{d})}{\partial u_{1} ... \partial u_{d}}\) denotes the density of the copula C(u 1,...,u d ) and f k denotes the density of F k , k = 1,...,d. Returning to (30), f(x|ω i ) can then be rewritten as
which turns (30) into
In this way, the discriminant function g i is represented using three ingredients: the conditional copula density c(⋅|ω i ), the conditional marginal densities f 1(⋅|ω i ),...,f d (⋅|ω i ), and the prior probability \(\mathbb {P}(\omega _{i})\). These ingredients do not impose any restrictions on each other, hence, any assumption made on the dependence structure represented by the copula density c(⋅|ω i ) is unrelated to assumptions made on the marginal distributions f 1(⋅|ω i ),...,f d (⋅|ω i ). This flexibility overcomes the mentioned drawbacks of the normal and the Naive Bayesian classifier, which is also confirmed by the experimental results presented in Section 5.2.
The training of such a copula-based Bayesian classifier can be performed for each class ω i ,i = 1,...m, separately as follows. Let \(\mathbb {X}^{i}\) be training data corresponding to the class ω i . Compute parametric or non-parametric estimates \(\hat {F}_{1}(\cdot |\omega _{i}), ...,\hat {F}_{d}(\cdot |\omega _{i})\) based on \(\mathbb {X}^{i}\). Compute a parametric or non-parametric estimate \(\hat {C}(\cdot |\omega _{i})\) based on \(\mathbb {X}^{i}\). Compute an estimate \(\hat {\mathbb {P}}(\omega _{i})\) of \(\mathbb {P}(\omega _{i})\) as the proportion of the class ω i in the training data \(\{\mathbb {X}^{1}, ..., \mathbb {X}^{m}\}\). The triplet (\(\hat {C}(\cdot |\omega _{i})\); \(\hat {F}_{1}(\cdot |\omega _{i}), ...,\hat {F}_{d}(\cdot |\omega _{i}) ;~ \hat {\mathbb {P}}(\omega _{i})\)) uniquely determines the discriminant function g i .
5.2 Evaluation of the accuracy of copula-based Bayesian classifiers
In what follows, we evaluate the accuracy of such copula-based Bayesian classifiers (CBCs). Note that a similar evaluation study have been conducted only for Gaussian copula-based classifiers (against SVM) and only for simulated data; see Sathe (2006). On real-world data, all here presented CBCs are evaluated for the first time.
We construct three types of CBCs, each type involving different classes of copulas:
-
a Gaussian copula-based Bayesian classifier (GCBC). For any GCBC, it is assumed that \(\hat {C}(\cdot |\omega _{i})\) is a Gaussian copula. The computation of the estimator of \(\hat {C}(\cdot |\omega _{i})\) is described in Bouyé et al. (2000) and is implemented by the Matlab’s Statistics toolbox function copulafit. We used all the arguments of copulafit with their default values
-
an AC-based Bayesian classifier (ACBC). For any ACBC, it is assumed that \(\hat {C}(\cdot |\omega _{i})\) is an AC. Given a family of generators, the copula parameter is estimated by the inversion of pairwise Kendall’s tau, see (10). In our experiments, we used the families listed in Table 1, however, an ACBC is not restricted to them. A family is considered as an input parameter of a ACBC and we selected the family of \(\hat {C}(\cdot |\omega _{i})\) based on a 10-fold cross-validation. Note that for d ≥ 3, ACs based on the Laplace-Stieltjes transform generators are generally unable to model negative dependencies (Hofert 2010b), i.e., the cases where τ X, Y <0 for some random variables X and Y. If X and Y are continuous then τ −X, Y = τ X, −Y =−τ X, Y . We employ this fact and invert, i.e., X:=−X, some of the variables to reduce the negative dependence among the variables using Algorithm 4, i.e., in each sample \(\mathbb {X}^{i}, i = 1, ..., m\), we inverted columns corresponding to the indices in \(\mathcal {I}\) obtained by Algorithm 4 with Input 1) given \(\mathbb {X} :=\mathbb {X}^{i}\). Note that even if we do not have a proof that it is possible to reduce, using this inverting process, the negative dependence to an extent that \(\hat {\theta }_{n} \geq 0\) is satisfied, we were able to get \( \hat {\theta }_{n} \geq 0\) in all performed experiments.
-
a HAC-based Bayesian classifier (HACBC). For any HACBC, it is assumed that \(\hat {C}(\cdot |\omega _{i})\) is an HAC. Given a family, the copula estimation is based on the procedure described in Section 3.2, which is summarized by Algorithm 3. The \(\mathbb {I}\)-aggregation function g is set to be the average function. The choice of this function is based on the results presented in Section 4. As for ACBCs, we use in our experiments the families listed in Table 1. Which particular among those 3 families to use is considered an input parameter of a HACBC and we selected the family of \(\hat {C}(\cdot |\omega _{i})\) based on a 10-fold cross-validation. As HACs based on the Laplace-Stieltjes transform generators are also generally unable to model negative dependencies, which is a property they inherit from ACs, we use the same inverting process for the variables as described above for the ACBC type. However, contrarily to the ACBC case, we were sometimes not able to reduce the negative dependence to an extent that \(\hat {\theta }_{k} \geq 0\) for all k∈{1,...,d−1}, where \(\hat {\theta }_{k}\) is the parameter estimate computed in Step 2 of Algorithm 3. Consider a Kendall correlation matrix \((\tau ^{n}_{ij}) \in [-1, 1]^{4\times 4}\) with \(\tau ^{n}_{12}=\tau ^{n}_{34} = 0.5, \tau ^{n}_{13}=\tau ^{n}_{23}=\tau ^{n}_{24} = 0\) and \(\tau ^{n}_{14} = -0.1\). The reader can easily see that, whichever variable is inverted or if all variables are left unchanged, the argument of τ −1(⋅) in Step 2 of Algorithm 3 is negative at least for one k∈{1,2,3} providing g is the average function. For the latter case, we would obtain, using Algorithm 3, a 4-PNAC estimate \(((12)_{\hat {\theta }_{1}}(34)_{\hat {\theta }_{2}})_{\hat {\theta }_{3}}\), where \(\tau (\hat {\theta }_{1}) = \tau (\hat {\theta }_{2}) = 0.5\) and \(\tau (\hat {\theta }_{3}) = -0.025\). Due to this fact, we use \(\max (0, \hat {\theta }_{k})\) instead of \(\hat {\theta }_{k}\) computed in Step 2 of Algorithm 3.

The estimates \(\hat {F}_{1}(\cdot |\omega _{i}), ...,\hat {F}_{d}(\cdot |\omega _{i})\) of the margins are computed in the same way for all above-mentioned classifiers using the Kernel smoothing function ksdensity in Matlab with the parameter function set to cdf. Note that, if fitting a GCBC, these estimates are also used for transforming the data to [0, 1]. If fitting an ACBC or a HACBC, the transformation of the the data to [0, 1] is not necessary, because the corresponding copula estimation process is based just on the sample version of the Kendall correlation matrix.
These CBCs are compared in terms of accuracy with four non-copula-based classifiers and one copula-based classifier, which are all available in Matlab’s Statistical toolbox. These are:
-
1.
the Classification and regression trees method (Breiman et al. 1984), which is implemented by the class ClassificationTree and is referred as CART in the following. Each classification tree was first trained to the deepest possible level and then it was pruned to the optimal level, obtained by the function test, using the crossvalidate method;
-
2.
an ensemble method based on bagging of classification trees (Breiman 1996). The classifier, referred as TREEBAG in the following, is implemented by the function fitensemble with its parameters Method set to Bag and Learners set to ClassificationTree.template(‘MinLeaf', MinLeaf), respectively. In each training phase, we tuned the parameters NLearn and MinLeaf as they shown to be most influential on the accuracy. From all pairs (NLearn, MinLeaf) ∈{1,...,200}×{1,...,5}, we always chose the pair corresponding to the highest accuracy based on a 10-fold cross-validation.
-
3.
an ensemble method based on boosting of classification trees (Freund and Schapire 1995). The classifier, referred as ADABOOST in the following, is implemented by the function fitensemble with its parameters Method set to AdaBoostM1 (for the datasets with two classes and AdaBoostM2 for the datasets with three or more classes) and Learners set to ClassificationTree.template(‘MinLeaf', MinLeaf), respectively. In each training phase, we tuned the parameters NLearn and MinLeaf in the same way as for TREEBAG.
-
4.
a support vector machine (Vapnik 2000). The classifier, referred as SVM in the following, is implemented by the function smvtrain. The parameter KernelFunction is set to rbf as this setting provided the highest accuracy on the considered datasets. In each training phase, we tuned the parameters boxconstraint and rbf_sigma as they shown to be most influential on the accuracy. The parameters were tuned using unconstrained nonlinear optimization (implemented by the function fminsearch) in order to get the maximal accuracy computed based on a 10-fold cross-validation. To search for a global maximum, we always repeated the optimization task 5 times, each time with different initial values of the parameters.
-
5.
the Naive Bayes classifier, which is actually a CBC that assumes independence copulas \(\hat {C}(\cdot |\omega _{i}), i = 1, ..., m\) and is referred as NAIVE in the following. We used the implementation by the function fitNaiveBayes and in each training phase, we tuned the parameter Distribution. Its value (normal or kernel) was chosen based on a 10-fold cross-validation. Default parameters are used otherwise.
All in all, we evaluate 8 classifiers on 6 commonly known datasets obtained from the UCI Repository (Bache and Lichman 2013), namely on Iris (4 variables, i.e., d = 4), BankNote (4 variables), Vertebral (6 variables), Seeds (7 variables), BreastTissue (9 variables), and Wine (13 variables), as well as on the dataset Appendicitis (7 variables) from the KEEL-dataset repository (Alcalá et al. 2010), and on one dataset from a recent real-world application in catalysis (Moehmel et al. 2008) (we refer to the last dataset as Catalysis), which contains 4 variables. The variables in the Catalysis dataset are proportions of oxides of the metals La, Pt, Ag, Au used during the conversion of methane and ammonia to hydrocyanic (HCN) acid (Moehmel et al. 2008). As most of the UCI and the KEEL datasets contain 3 classes, we have created arbitrarily 3 equi-frequent classes (low, medium, high) also for the Catalysis dataset using the continuous output variable HCN yield. These datasets are selected in order to every considered classifier could be applicable to every dataset. Particularly, as CBCs require continuous input variables, all datasets include only such input variables. Moreover, as using HACBC classifiers is challenging in higher dimensions as described below in detail, we preferred low-dimensional datasets.
The accuracy computation for a given classifier and a given dataset is based on a 10-fold cross-validation and repeated 10 times, more precisely, each classifier except GCBC was tuned and trained 100 times and each tuning of its parameter(s) involved another “inner” 10-fold cross-validation, by which we refer to the cross-validation that is mentioned in the description of the classifier. All computations were performed in Matlab on a PC with Intel Core 2.3 GHz CPU and 4GB RAM.
Here we must mention the most serious restriction we faced when using a HACBC. Such classifier relies on discriminant functions g i ,1,...,m given by (33), each involving the density of a HAC estimate \(\hat {C}(\cdot ;\omega _{i})\). To assign new data to one of the m classes, d partial derivatives for each \(\hat {C}(\cdot ;\omega _{i})\) have to be evaluated. Consider that complexity of such a density function quickly grows in d, which cause that the time consumption of its evaluation exceeds reasonable limits already for d = 5, particularly for families with a more complex generator, e.g., for the Frank family. Note that this problem is similar to the problem of computation of the statistic \(S_{n}^{(C)}\) mentioned in Section 2.5. To be able to evaluate our experiments in reasonable time, we thus projected all datasets to d = 4, i.e., before any evaluation of all classifiers on a dataset had started, we performed the feature selection and selected only 4 variables from the dataset. With such a comparison of the classifiers on such low-dimensional data presented below in Section 5.3, we are able to demonstrate capabilities of CBCs, particularly capabilities of HACBCs, when compared to other well-known classifiers.
However, we are aware of the fact that such a comparison is too limited from the practical point of view and it discriminates against the classifiers that easily scale up to high dimensions. For this reason, we provide another comparison presented below in Section 5.4, where all the datasets are considered in their original dimension. However, due to the above-mentioned reasons, such an evaluation would not be viable for HACBCs for the datasets with d > 4, hence, we again involve the feature selection, which is, in contrast to the first comparison, performed on training data as a part of the training phase of a HACBC just before tuning of its parameter. With this comparison, we aim to demonstrate applicability of a HACBCs for data with d > 4 provided we deal with the above-mentioned restriction using the feature selection.
Note that the feature selection was performed using the function sequentialfs and we based the selection process on the discriminant analysis (Lachenbruch 1975) implemented by the function classify. The reason for choosing the discriminant analysis, i.e., a classifier that is different from all the evaluated classifiers, is that we tried not to favour any of the evaluated classifiers. The feature selection process is indeed performed for Appendicitis, BreastTissue, Seeds, Vertebral and Wine datasets. As the Iris, BankNote and Catalysis datasets have all the dimension d = 4, evaluation for these datasets does not involve the feature selection process and we include it in both above-mentioned comparisons.
It is also important to note that the evaluation presented here is not meant to be an exhaustive study of possibilities of CBCs. Rather, this study should be viewed as a first example considering applicability of ACs and HACs in Bayesian classification, which shows that such classifiers, despite the above-mentioned restriction, provide simplicity and accuracy, as discussed below.
5.3 The first comparison (all datasets projected to d = 4 dimensions)
The accuracy of the classifiers computed on the datasets projected to d = 4 dimensions using the feature selection is shown in Figs. 4 and 5. It can be observed that there is not a clear winning classifier on all the datasets, what is not surprising in the context of the “No Free Lunch Theorem” (Wolpert 2002). However, some of the classifiers score higher substantially more often then the others. This observation is supported by the rankings of the classifiers in Table 6.
Each of classifiers is ranked according to its averaged accuracy: 1 stands for the highest and 8 stand for the lowest averaged accuracy on the given dataset. Observing the averages of these ranks – the average rank row in Table 6 – four groups of the classifiers can be distinguished:
-
the highest-ranked group - SVM (average rank = 2.875) and HACBC (2.875);
-
the middle-high-ranked group - GCBC (3.625) and ACBC (3.875);
-
the middle-low-ranked group - NAIVE (5.25), TREEBAG (5.375) and ADABOOST (5.125);
-
the lowest-ranked group - CART (7).
This high-low ranking is also supported by another ranking – the top-three ranking, which counts how many times a classifier is ranked among the three best. We see that the classifiers from the highest-ranked and the middle-high-ranked group reside more frequently in the top-three than the classifiers from the lowest-ranked and the middle-low-ranked group.
If we divide the classifiers into four groups according to their type – 1) simple classifiers (CART and NAIVE), 2) ensemble classifiers (TREEBAG and ADABOOST) 3) SVM 4) CBCs (GCBC, ACBC and HACBC) – we can also observe the superiority of SVM and CBCs to the remaining types of classifiers. This is illustrated by the first two rows of graphs in Fig. 7, which show the boxplot of the best 4 (according to the averaged accuracy) classifiers out of these four groups. We can see that SVM and the best representative of the CBCs score better than the best representatives of simple and ensemble classifiers on most of the datasets.
5.4 The second comparison (all datasets in their original dimension)
The accuracy of the classifiers computed on the datasets in their original dimension except for the HACBCs is shown in Figs. 5 and 6. We again observe that there is no classifier that wins on all the datasets. In contrast to the first comparison, we observe that the difference between the two best ranked classifiers is substantially higher, which is supported by the rankings of the classifiers in Table 7.
Now, observing the averages of the ranks in Table 7, again, four groups of the classifiers similar to the first comparison can be distinguished, however, with one important switch between the first two groups:
-
the highest-ranked group - SVM (average rank = 1.875);
-
the middle-high-ranked group - GCBC (4.5), ACBC (4) and HACBC (3.75);
-
the middle-low-ranked group - NAIVE (5.375), TREEBAG (4.375) and ADABOOST (5);
-
the lowest-ranked group - CART (7.125).
We see that HACBC substantially decreased in the ranking and it is now more convenient to put it in the middle-high-ranked group. As addressed before, due to the extreme time consumption of HACBCs in high dimensions, here presented results for these classifiers involve the feature selection, which, on the one hand, considerably influence their accuracy, on the other hand, allows for at least some applicability of HACBCs in higher dimensions. The remaining classifiers show results similar to the first comparison, again supported by the top-three ranking.
The supremacy of the SVM and the CBCs to other types of classifiers is again observable, now illustrated by the second and the third row of the graphs in Fig. 7. We again observe that SVM and the best representative of CBCs score better than the best representatives of simple and ensemble classifiers on most of the datasets.
The accuracy of the representative classifiers on all considered datasets. The first row and the second row of the graphs correspond to the first comparison described in Section 5.3, whereas the second row and the third row of the graphs correspond to the second comparison described in Section 5.4. The asterisk for HACBC emphasize that the feature selection was performed for this classifier
We can conclude that, in these experiments, CBCs and particularly HACBC classifiers have shown to be competitive for low-dimensional data with highly-accurate classifiers like SVM or ensemble methods in terms of accuracy while keeping the produced models rather comprehensible, as also discussed in Section 5.5. If there appears a way how to compute efficiently the density function of a HAC, e.g., as the simplification of the density functions for the five popular AC families presented in Hofert et al. (2012), it is possible that results similar to the results for the HACBCs in low-dimensions could also be obtained for HACBCs in high-dimensions.
Here, it is important to note that none of the results presented here must be over-generalized and we recall that, when selecting the datasets, we selected the ones with all continuous input variables and we also preferred low-dimensional ones. Hence, the results, e.g., for ensemble methods, which are applicable to much wider classes of data, must be considered with this in mind.
In further research, we will aim to confirm here presented results for the CBCs on substantially larger amount of datasets produced by diverse applications. Moreover, as there exist many other copula classes, e.g., pair copulas (Aas et al. 2009), skew t-copulas (Smith et al. 2012), etc., which could be used for a CBC construction in the same way as for the above-mentioned copula classes, we will also consider these CBC types. To put CBCs more firmly into the framework of commonly used classifiers, CBCs should be compared with other types of classifiers, e.g., neural-networks-based classifiers, K-Nearest Neighbors, etc. Apart from accuracy and simplicity, the classifiers should also be compared in terms of classification run-times and memory usage.
5.5 Note on accuracy vs comprehensibility
At this point, we want to consider the typical trade-off between the accuracy and the comprehensibility of a classification model. In most cases, the accuracy of a classification model grows at the expense of its comprehensibility. In our comparison, two easily comprehensible classifiers participate – CART and NAIVE – which, on the one hand, produce easy to understand models and, on the other hand, score lower in the accuracy computed on the selected datasets. In contrast, the highly-accurate classifier SVM produces highly complex models which, however, are not so easy to understand.
From this point of view, CBCs could be, in our opinion, considered as a good trade-off between those two extremes. On the one hand, we observe that the accuracy of CBSs is close to the accuracy of SVM on low-dimensional data, on the other hand, the models produced by the classifiers are also easily interpretable with some knowledge of copulas.
Here we want to emphasize the HACBC classifiers, which produce models of the joint dependency among the variables in the form of a HAC. As we know, a HAC can be expressed as a tree-like graph. As an specific example, see Fig. 8. The figure shows the HAC parameters and structure estimates for the classes Setosa, Versicolor and Virginica in the Iris dataset that were obtained using Algorithm 3 with the assumption that all the generators are from the Frank family. The \(\hat {\theta }_{1}, ..., \hat {\theta }_{3}\) are the parameter values of each HAC estimate. The dendrogram-like representation of the trees has the advantage that, instead of showing only the structure of the HAC, it also visualize the strength of dependency among the variables. This is because each generator node is vertically positioned according the value of the Kendall’s tau that corresponds to its parameter. Such a representation enables one (with some knowledge of HACs) to get fuller picture of the dependencies among the variables than the standard HAC tree-like representation. It is worth mentioning that the dependencies also can be obtained from such graphs in a more formal way as sentences of an observational calculus, as recently proposed in Holeňa and Ščavnický (2013).
6 Conclusion
We proposed a new approach to structure determination and parameter estimation of hierarchical Archimedean copulas, which combines the advantages of existing methods in terms of the correctly determined structures ratio, the goodness-of-fit of the estimates, and run-time. This has been confirmed in several experiments based on simulated data in different dimensions and copula models. The proposed method is particularly attractive in lower-dimensional (d≤100) applications where a good approximation and computational efficiency are crucial. However, as the computation of Kendall’s tau for all pairs of data columns has complexity O(d 2 nlogn), the approach becomes demanding in high dimensions. Also note that the proposed method restricts to binary structured HACs, i.e., any d-HAC estimate has d−1 parameters. In high dimensions, substantially less parameters are often required, hence, a generalization to non-binary structured HACs should also be considered, e.g., in a way proposed in Okhrin et al. (2013a).
The presented work does not explicitly consider the following:
-
1.
The proposed method assumes all generators of the estimated HAC to be from the same family, i.e., it assumes that a homogeneous HAC results from the estimation process. Despite the possibility of mixing different families in a HAC, see Hofert (2011), the estimation of such non-homogenous HACs has not been addressed in the literature in detail except in Okhrin et al. (2013a), which, however, addresses this issue only briefly without any experimental results. From the construction of our estimation method, it becomes clear that it easily extends to non-homogeneous HACs as long as the sufficient nesting condition is fulfilled;
-
2.
Until now, all HAC estimation methods that estimate both the structure and the parameters of a HAC, incorporate either ML estimator or estimator based on the inversion of Kendall’s tau. However, there exist also different types of estimation methods, e.g., estimation based on Blomqvists beta, Simulated maximum-likelihood estimation, Minimum distance estimation or Diagonal maximum-likelihood estimation, seeHofert et al. (2013), which have been originally designed for the estimation of ACs, but could also be considered in HACs estimation. Our estimation method is not restricted to the estimator based on the inversion of Kendall’s tau and can easily be extended for using with other estimators like the above-mentioned ones.
Additionally, we applied the proposed method to the construction of copula-based Bayesian classifiers, which are experimentally compared with other types of commonly used classifiers on several real-world datasets. Two types of such classifiers, namely the AC-based and the HAC-based Bayesian classifiers, were evaluated for the first time. Due to the restrictions addressed in Section 5.2, applicability of HAC-based Bayesian classifiers for high-dimensional data is limited, however, the experimental results for low-dimensional data show that these classifiers are competitive with highly-accurate classifiers like SVM or ensemble methods in terms of accuracy while keeping the produced models rather comprehensible.
Notes
also called fully-nested Archimedean copula
also called partially-nested Archimedean copula
References
Aas, K., Czado, C., Frigessi, A., Bakken, H. (2009). Pair-copula constructions of multiple dependence. Insurance: Mathematics and Economics, 44(2), 182–198.
Alcalá, J., Fernández, A., Luengo, J., Derrac, J., García, S., Sánchez, L., Herrera, F. (2010). Keel data-mining software tool: Data set repository, integration of algorithms and experimental analysis framework. Journal of Multiple-Valued Logic and Soft Computing, 17, 255–287.
Bache, K., & Lichman, M. (2013). UCI machine learning repository. http://archive.ics.uci.edu/ml.
Berg, D. (2009). Copula goodness-of-fit testing: an overview and power comparison. The European Journal of Finance, 15(7–8), 675–701.
Bouyé, E., Durrleman, V., Nikeghbali, A., Riboulet, G., Roncalli, T. (2000). Copulas for finance - a reading guide and some applications. Available at SSRN 1032533.
Breiman, L. (1996). Bagging predictors. Machine learning, 24(2), 123–140.
Breiman, L., Freidman, J., Olshen, R., Stone, C. (1984). Classification and Regression Trees. Wadsworth.
Chen, X., Fan, Y., Patton, A.J. (2004). Simple tests for models of dependence between multiple financial time series, with applications to us equity returns and exchange rates. Discussion paper 483, Financial Markets Group, London School of Economics.
Clarke, B., Fokoue, E., Zhang, H.H. (2009). Principles and Theory for Data Mining and Machine Learning. Springer.
Cramér, H. (1928). On the composition of elementary errors: First paper: Mathematical deductions. Scandinavian Actuarial Journal, 1928(1), 13–74.
Cuvelier, E., & Noirhomme-Fraitur, M. (2005). Clayton copula and mixture decomposition. In Applied Stochastic Models and Data Analysis, ASMDA’05. Brest.
Freund, Y., & Schapire, R.E. (1995). A desicion-theoretic generalization of on-line learning and an application to boosting. In Computational learning theory, (pp. 23–37). Springer.
Genest, C., & Favre, A. (2007). Everything you always wanted to know about copula modeling but were afraid to ask. Hydrologic Engineering, 12, 347–368.
Genest, C., & Rémillard, B. (2008). Validity of the parametric bootstrap for goodness-of-fit testing in semiparametric models. In Annales de l’Institut Henri Poincaré: Probabilités et Statistiques, (Vol. 44, pp. 1096–1127).
Genest, C., Rémillard, B., Beaudoin, D. (2009). Goodness-of-fit tests for copulas: A review and a power study. Insurance: Mathematics and Economics, 44(2), 199–213.
Genest, C., & Rivest, L.P. (1993). Statistical inference procedures for bivariate archimedean copulas. Journal of the American statistical Association, 88(423), 1034–1043.
González-Fernández, Y., & Soto, M. (2012). Copulaedas: An R package for estimation of distribution algorithms based on copulas. arXiv:1209.5429.
Górecki, J., Hofert, M., Holeṅa, M. (2014). On the consistency of an estimator for hierarchical archimedean copulas. In Talaṡová, J., Stoklasa, J., Taláṡek, T. (Eds.) 32nd International Conference on Mathematical Methods in Economics, (pp. 239–244). Olomouc: Palacký University.
Górecki, J., & Holeňa, M. (2013). An alternative approach to the structure determination of hierarchical Archimedean copulas. In Proceedings of the 31st International Conference on Mathematical Methods in Economics (MME 2013) (pp. 201–206). Jihlava.
Górecki, J., & Holeňa, M. (2014). Structure determination and estimation of hierarchical Archimedean copulas based on Kendall correlation matrix. In Appice, A., Ceci, M., Loglisci, C., Manco, G., Masciari, E., Ras, Z.W. (Eds.) New Frontiers in Mining Complex Patterns, Lecture Notes in Computer Science, (pp. 132–147).
Hofert, M. (2010a). Construction and sampling of nested Archimedean copulas. In Jaworski, P., Durante, F., Hardle, W.K., Rychlik, T. (Eds.), Copula Theory and Its Applications, Lecture Notes in Statistics, vol 198, (pp. 147–160). Springer Berlin Heidelberg.
Hofert, M. (2010b). Sampling Nested Archimedean Copulas with Applications to CDO Pricing: Suedwestdeutscher Verlag fuer Hochschulschriften.
Hofert, M. (2011). Efficiently sampling nested Archimedean copulas. Computational Statistics and Data Analysis, 55(1), 57–70.
Hofert, M. (2012). A stochastic representation and sampling algorithm for nested Archimedean copulas. Journal of Statistical Computation and Simulation, 82(9), 1239–1255. doi:10.1080/00949655.2011.574632.
Hofert, M., Mächler, M., Mcneil, A.J. (2012). Likelihood inference for archimedean copulas in high dimensions under known margins. Journal of Multivariate Analysis, 110, 133–150.
Hofert, M., Mächler, M., McNeil, A.J. (2013). Archimedean copulas in high dimensions: Estimators and numerical challenges motivated by financial applications. Journal de la Société Française de Statistique, 154(1), 25–63.
Hofert, M., & Scherer, M. (2011). CDO pricing with nested Archimedean copulas. Quantitative Finance, 11(5), 775–787.
Holeňa, M., & Ščavnický, M. (2013). Application of copulas to data mining based on observational logic. In ITAT: Information Technologies Applications and Theory Workshops, Posters, and Tutorials, North Charleston: CreateSpace Independent Publishing Platform, Donovaly Slovakia.
Joe, H. (1997). Multivariate Models and Dependence Concepts. London: Chapman & Hall.
Kao, S.C., Ganguly, A.R., Steinhaeuser, K. (2009). Motivating complex dependence structures in data mining: A case study with anomaly detection in climate. In International Conference on Data Mining Workshops. doi:10.1109/ICDMW.2009.37, (Vol. 0, pp. 223–230).
Kao, S.C., & Govindaraju, R.S. (2008). Trivariate statistical analysis of extreme rainfall events via plackett family of copulas. Water Resources Research, 44.
Kojadinovic, I. (2010). Hierarchical clustering of continuous variables based on the empirical copula process and permutation linkages. Computational Statistics & Data Analysis, 54(1), 90–108.
Kojadinovic, I., & Yan, J. (2010a). Comparison of three semiparametric methods for estimating dependence parameters in copula models. Insurance: Mathematics and Economics, 47, 52–63.
Kojadinovic, I., & Yan, J. (2010b). Modeling multivariate distributions with continuous margins using the copula r package. Journal of Statistical Software, 34(9), 1–20.
Kuhn, G., Khan, S., Ganguly, A.R., Branstetter, M.L. (2007). Geospatial-temporal dependence among weekly precipitation extremes with applications to observations and climate model simulations in South America. Advances in X-ray Analysis, 30(12), 2401–2423.
Lachenbruch, P.A. (1975). Discriminant analysis. Wiley Online Library.
Lascio, F., & Giannerini, S. (2012). A copula-based algorithm for discovering patterns of dependent observations. Journal of Classification, 29, 50–75. doi:10.1007/s00357-012-9099-y.
Maity, R., & Kumar, D.N. (2008). Probabilistic prediction of hydroclimatic variables with nonparametric quantification of uncertainty. Journal of Geophysical Research, 113.
McNeil, A.J. (2008). Sampling nested Archimedean copulas. Journal of Statistical Computation and Simulation, 78(6), 567–581.
McNeil, A.J., & Nešlehová, J. (2009). Multivariate Archimedean copulas, d-monotone functions and l 1-norm symmetric distributions. The Annals of Statistics, 37, 3059–3097.
Moehmel, S., Steinfeldt, N., Engelschalt, S., Holena, M., Kolf, S., Baerns, M., Dingerdissen, U., Wolf, D., Weber, R., Bewersdorf, M. (2008). New catalytic materials for the high-temperature synthesis of hydrocyanic acid from methane and ammonia by high-throughput approach. Applied Catalysis A: General, 334(1), 73–83.
Nelsen, R. (2006). An Introduction to Copulas, 2nd edn. Springer.
Okhrin, O., Okhrin, Y., Schmid, W. (2013a). On the structure and estimation of hierarchical Archimedean copulas. Journal of Econometrics, 173(2), 189–204. http://www.sciencedirect.com/science/article/pii/S0304407612002667.
Okhrin, O., Okhrin, Y., Schmid, W. (2013b). Properties of hierarchical Archimedean copulas. Statistics & Risk Modeling, 30(1), 21–54.
Okhrin, O., & Ristig, A. (2014). Hierarchical Archimedean copulae: The HAC package. Journal of Statistical Software, 58(4). http://www.jstatsoft.org/v58/i04.
Rey, M., & Roth, V. (2012). Copula mixture model for dependency-seeking clustering. Preprint. arXiv:1206.6433
Sathe, S. (2006). A novel Bayesian classifier using copula functions. Preprint arXiv:cs/0611150.
Savu, C., & Trede, M. (2008). Goodness-of-fit tests for parametric families of Archimedean copulas. Quantitative Finance, 8(2), 109–116.
Savu, C., & Trede, M. (2010). Hierarchies of Archimedean copulas. Quantitative Finance, 10, 295–304.
Segers, J., & Uyttendaele, N. (2014). Nonparametric estimation of the tree structure of a nested Archimedean copula. Computational Statistics & Data Analysis, 72, 190–204.
Sklar, A. (1959). Fonctions de répartition a n dimensions et leurs marges. Publishing Institute of Statistical University Paris, 8, 229–231.
Smith, M.S., Gan, Q., Kohn, R.J. (2012). Modelling dependence using skew t copulas: Bayesian inference and applications. Journal of Applied Econometrics, 27(3), 500–522.
Vapnik, V. (2000). The nature of statistical learning theory. Springer.
Wang, L., Guo, X., Zeng, J., Hong, Y. (2012). Copula estimation of distribution algorithms based on exchangeable Archimedean copula. International Journal of Computer Applications in Technology, 43, 13–20. doi:10.1504/IJCAT.2012.045836, http://inderscience.metapress.com/content/42R4M650P16V1227.
Wolpert, D.H. (2002). The supervised learning no-free-lunch theorems. In Soft Computing and Industry (pp. 25–42). Springer.
Yuan, A., Chen, G., Zhou, Z.C., Bonney, G., Rotimi, C. (2008). Gene copy number analysis for family data using semiparametric copula model. Bioinform Biol Insights, 2, 343–355.
Author information
Authors and Affiliations
Corresponding author
Additional information
The work of Jan Górecki was funded by the project SGS/21/2014 - Advanced methods for knowledge discovery from data and their application in expert systems, Czech Republic. The work of Martin Holeňa was funded by the Czech Science Foundation (GA ČR) grant 13-17187S.
Rights and permissions
About this article
Cite this article
Górecki, J., Hofert, M. & Holeňa, M. An approach to structure determination and estimation of hierarchical Archimedean Copulas and its application to Bayesian classification. J Intell Inf Syst 46, 21–59 (2016). https://doi.org/10.1007/s10844-014-0350-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10844-014-0350-3