Effectively and efficiently supporting roll-up and drill-down OLAP operations over continuous dimensions via hierarchical clustering

Abstract

In traditional OLAP systems, roll-up and drill-down operations over data cubes exploit fixed hierarchies defined on discrete attributes, which play the roles of dimensions, and operate along them. New emerging application scenarios, such as sensor networks, have stimulated research on OLAP systems, where even continuous attributes are considered as dimensions of analysis, and hierarchies are defined over continuous domains. The goal is to avoid the prior definition of an ad-hoc discretization hierarchy along each OLAP dimension. Following this research trend, in this paper we propose a novel method, founded on a density-based hierarchical clustering algorithm, to support roll-up and drill-down operations over OLAP data cubes with continuous dimensions. The method hierarchically clusters dimension instances by also taking fact-table measures into account. Thus, we enhance the clustering effect with respect to the possible analysis. Experiments on two well-known multidimensional datasets clearly show the advantages of the proposed solution.

1 Introduction

In traditional Business Intelligence applications, both On-Line Analytical Processing (OLAP) and data mining are considered two distinct, well-consolidated technologies positioned on top of a data warehouse architecture (Watson and Wixom 2007). Data in the warehouse are accessed by OLAP tools to support efficient, interactive multidimensional analyses through roll-up, drill-down, slice-and-dice and pivoting operations. Clean data available in the warehouse are also a high quality input for data mining tools which perform an automated discovery of patterns and models, often used for predictive inference.

The two classes of front-end tools for data warehouses have long developed independently of each other, focusing on distinct functionalities. Notable exceptions are the on-line analytical mining architecture (Han et al. 1998), where mining modules operate directly on data cubes via the OLAP engine, the OLAP-based association mining (Zhu 1998), and the cubegrades (Imieliński et al. 2002), which give a generalization of association rules which express how the change in the structure of a given cube affects a set of predefined measures. In all these studies data mining techniques are applied to OLAP cubes. The motivations are various, such as efficiency or extending data mining techniques to OLAP cubes.

A different perspective is provided by ClustCube (Cuzzocrea and Serafino 2011), where a data mining technique, namely clustering, is integrated in an OLAP framework. In particular, both cubes and cube cells store clusters of complex database objects and typical OLAP operations are performed on top of them. Thus, while in traditional OLAP data cubes the multidimensional boundaries of data cube cells along the dimensions are determined by the input OLAP aggregation scheme, in ClustCube the multidimensional boundaries are the result of the clustering process itself. This means that hierarchies are not fixed a priori, since they are determined by the clustering algorithm. Hence, OLAP offers powerful tools to mine clustered objects according to a multidimensional, multi-resolution vision of the underlying object domain.

This perspective is also useful to face some limitations of conventional OLAP technologies, which offer data cubes defined on top of dimensions that are discrete and expose fixed hierarchies (Gray et al. 1997). These two dimension constraints are regarded as being too strong for several application scenarios, such as sensor network mining. To overcome the first limitation, OLAP data cubes have been defined on top of continuous dimensions (Gunopulos et al. 2005; Shanmugasundaram et al. 1999). To handle them, a naïve approach has been initially investigated, which consists in independently discretizing attribute domains of continuous dimensions before processing them to obtain the final cube, given a certain measure (Gray et al. 1997). However, this approach is subject to information loss, due to the (univariate) discretization process and the disregarding of fresh data periodically loaded into the warehouse. The application of a clustering algorithm over continuous attributes may indeed better approximate the multivariate distribution of numerical data as well as facilitate range-sum query evaluation (Cuzzocrea 2006; Cuzzocrea and Wang 2007; Cuzzocrea et al. 2009). Moreover, the application of a hierarchical clustering algorithm may contribute to overcoming the second limitation, since hierarchies are dynamically defined on the basis of the database objects.

Based on these insights, in this paper we develop a novel knowledge discovery framework for the multidimensional, multi-resolution analysis of complex objects, characterized by continuous dimensions and dynamically defined hierarchies. The framework, called OLAPBIRCH, aims at supporting next-generation applications, ranging from analytics to sensor-and-stream data analysis and social network analysis. The main idea pursued in this work is integrating a revised version of the clustering algorithm BIRCH (Zhang et al. 1996) with an OLAP solution, in order to build a hierarchical data structure, called CF Tree, whose nodes store information on clusters retrieved by BIRCH from the target dataset. The CF tree improves the efficiency of both roll-up and drill-down operations with respect to the baseline case, which computes new clusters from pre-existent ones at each roll-up (or drill-down) operation. In fact, the roll-up and drill-down operations directly correspond to moving up and down the CF Tree. The proposed framework is also designed to work with continuous dimensions in order to support emerging applications, such as sensor data processing, where numerical data abound.

The proposed knowledge discovery framework presents several challenges that must be addressed. First, the huge amount of data stored in data warehouses and involved in OLAP queries requires efficient solutions. Second, a hierarchical organization of clusters is necessary to give the OLAP users the possibility to perform roll-up and drill-down operations. Third, the periodic loading of data warehouses through ETL applications requires clustering methods which are incremental, so that it is not needed to regenerate the CF tree from scratch each time new data are loaded. Fourth, the hierarchical organization of clusters should be well-balanced to guarantee effective roll-up and drill-down operations by exploiting the CF Tree.

These challenges are addressed by the BIRCH clustering algorithm, whose original formulation presents the following important features:

• Efficiency (both in space and time): the algorithm has a time complexity which is linear in the number of instances to cluster and a space complexity which is constant.

• Hierarchical organization of clusters.

• Incrementality: as new instances are given to the algorithm, the hierarchical clustering is revised and adapted by taking into account memory constraints.

• Balanced hierarchies in output: when the hierarchical clustering is revised, the algorithm still keeps the hierarchy well balanced.

The main contributions of this paper are as follows:

• 1. Principles, models and algorithms of the OLAPBIRCH framework;

• 2. An extensive discussion of related work;

• 3. A theoretical discussion of the OLAPBIRCH time complexity;

• 4. A wide experimental analysis of OLAPBIRCH performance on both benchmark and real datasets.

From a data mining perspective, this paper also faces the challenging problem of clustering objects, defined by multiple relational tables logically organized according to a star schema. This in turn relates our work to recent research on co-clustering star-structured heterogeneous data (Ienco et al. 2012), where the goal is to cluster simultaneously the set of objects and the set of values in the different feature spaces. The main difference is that we distinguish between a primary type of objects to be clustered (examples in the fact table) and a secondary type of objects to be clustered (examples in the considered dimensional table). Thus, we cluster both types of objects as in co-clustering star-structured heterogeneous data, but with the difference that clusters on the objects of the primary type implicitly define the (soft) clusters on objects of the secondary type.

The paper is organized as follows. In Section 2, we discuss proposals related to our research. In Sections 3 and 4, we present the background of the presented work and the proposed framework OLAPBIRCH, respectively. In Section 5, we present an empirical evaluation of the proposed framework. In Section 6, we focus attention on emerging application scenarios of OLAPBIRCH and, finally, in Section 7 we draw some conclusions and delineate future research directions.

2 Related work

Two main areas are pertinent to our research, namely clustering techniques over large databases and integration of OLAP and Data Mining. They are both reviewed in the next subsections.

2.1 Clustering over large databases

In the last decade several clustering algorithms have been proposed to cope with new challenges brought to the forefront by the automated production of a vast amount of high-dimensional data (Kriegel et al. 2009; Hinneburg and Keim 1999). CLARANS (Ng and Han 2002) is a pioneer clustering algorithm that performs randomized search over a partitioned representation of the target data domain to discover clusters in spatial databases. DBSCAN (Ester et al. 1996) introduces the notion of cluster density, to discover clusters of arbitrary shape. Compared to CLARANS, DBSCAN proves to be more efficient and can scale well over large databases. Indeed, CLARANS assumes that all objects to be clustered can be kept in main memory, which is unrealistic in many real-life application scenarios. In CURE (Guha et al. 2001), clustering is based on representatives built from the target multidimensional data points via an original approach that combines random sampling and partitioning strategies. An advantage of this approach is its robustness to outliers. WaveCluster (Sheikholeslami et al. 2000) is based on the wavelet transforms and guarantees both low dependence on possible sorting of input data and low sensibility to the presence of outliers in data. Moreover, well-understood, multi-resolution tools, made available by wavelet transforms make WaveCluster able to discover clusters of arbitrary shape at different levels of accuracy. CLIQUE (Agrawal et al. 2005) aims at clustering the target data with respect to a partition of the original features of the reference data source, even without the support of feature selection algorithms. Inspired by the well-known monotonicity property of the support of frequent patterns (Agrawal and Srikant 1994), CLIQUE starts clustering at the lower dimensionality of the target dimensional space and then progressively derives clusters at the higher dimensionalities. The monotonicity property exploited in CLIQUE states that if a collection of data points c is a cluster in a k-dimensional space S, then c is also part of a cluster in any (k − 1)-dimensional projections of S.

Another recent research trend related to this work is clustering methodologies in complex database environments. Based on the vast, rich literature on this specific topic, it is worthwhile mentioning CrossClus (Yin et al. 2007), which considers an applicative setting where data are stored in semantically-linked database relations and clustering is conducted across multiple relations rather than a single one, as in most of the above mentioned algorithms. To this end, CrossClus devises an innovative methodology according to which the clustering phase is “propagated” across database relations by following associations among them, starting just from a small set of (clustering) features defined by users.

Finally, another topic of interest for this work is clustering high-dimensional datasets (Kriegel et al. 2009), since high-dimensional data are reminiscent of OLAP data. Here, clustering scalability and quality of clusters are the major research challenges, as it is well-understood that traditional clustering approaches are not effective on high-dimensional data (Kriegel et al. 2009).

2.2 Integration of OLAP and data mining

As recognized in Parsaye (1997), applying data mining over data cubes definitely improves the effectiveness and the reliability of decision-support systems. One of the pioneering works in this direction is Han (1998), which introduces the OLAM methodology to extract knowledge from OLAP data cubes. In Chen et al. (2000) traditional OLAP functionalities over distributed database environments are extended, in order to generate specialized data cubes storing association rules rather than conventional SQL-based aggregates. A similar idea is pursued in Goil and Choudhary (2001), except that data cubes are used as primary input data structures for association rule mining.

In Sarawagi (2001) and Sarawagi et al. (1998) the integration of statistical tools within OLAP servers is proposed, in order to support the discovery-driven exploration of data cubes. The gradient analysis over OLAP data cubes (Dong et al. 2001) is a sophisticated data cube mining technique, which aims at detecting significant changes among fixed collections of cube cells. While in Imieliński et al. (2002) data cubes define the conceptual layer for association rule mining, in Messaoud et al. (2006) inter-dimensional association rules are discovered from data cubes on the basis of SUM-based aggregate measures.

Contrary to all these approaches, where OLAP operations are invoked by data mining tools, in this work we follow the opposite direction and integrate data mining in OLAP solutions, in order to enable OLAP queries over complex objects. Details of this alternative approach are reported in the following sections.

3 Background

For the sake of completeness, in this section we briefly review the BIRCH algorithm. Then we explain the modifications required to integrate BIRCH in an OLAP framework.

The BIRCH algorithm (Zhang et al. 1996) works on a hierarchical data structure, called Clustering Feature tree (CF tree), which allows incoming data points to be partitioned both incrementally and dynamically. Formally, given a cluster of n d-dimensional data points $\textbf{x}_i$ (i = 1,...,n), its Clustering Feature (CF) is the following triple summarizing the information maintained about the cluster:

$$ CF = (n,\textbf{LS},SS) $$

(1)

where the d-dimensional vector $\textbf{LS}=\sum_{i=1,\ldots,n}\textbf{x}_i$ is the linear sum of the n data points, while the scalar value $SS=\sum_{i=1,\ldots,n}\textbf{x}_i^2$ is the square sum of the n data points. These statistics allows us to efficiently compute three relevant features of the cluster (the centroid, the radius and the diameter), as well as other important features of pairs of clusters (e.g. average inter-cluster distance, average intra-cluster distance and variance increase distance).

A distinctive property of CF vectors is the additivity property, according to which, given two non-intersecting clusters S ₁ and S ₂ with CF vectors $CF_1 = (n_1, \textbf{LS}_1, SS_1)$ and $CF_2 = (n_2, \textbf{LS}_2, SS_2)$ respectively, the CF vector for the cluster S ₁ ∪ S ₂ is $CF_1 + CF_2 = (n_1 + n_2, \textbf{LS}_1 + \textbf{LS}_2, SS_1 + SS_2)$.

A CF tree is a balanced tree with a structure similar to that of a B+ tree. Its size depends on two parameters:

• (i) the branching factor B and

• (ii) a user-defined threshold T on the maximum cluster diameter. This threshold controls the size of the CF tree: the larger the T, the smaller the tree.

Each internal node N _j corresponds to a cluster made up of all the subclusters associated to its children. The branching factor B controls the maximum number of children. Therefore, N _j is described by at most B entries of the form [CF _i ,c _i ] _{i = 1,..,B} , where c _i is a pointer to the i-th child node of N _j and CF _i is the clustering feature of the cluster identified by c _i . Each leaf node contains at most L (typically L = B) entries, each of the form [CF _i ], and two pointers, prev and next, which chain all the leaves together, in order to efficiently perform an in-order traversal. Each entry at a leaf is not a single data point but a subcluster, which “absorbs” many data points with diameter (or radius) less than T.

The algorithm BIRCH builds a CF tree in four phases. In the first phase, an initial CF tree is incrementally built by considering data points one by one. In particular, each data point recursively descends the CF tree, by choosing the closest child note according to some distance measure. Once a leaf is reached, a check is performed. If an entry at the leaf can “absorb” the new point, its CF is updated. Otherwise, a new entry is added to the leaf node, if there is room (the maximum number of entries is L), or the leaf node is split (i.e. it becomes an internal node) if there is no room. In the case of splitting, the CF tree may need some restructuring, since the constraint on the branching factor B can be violated. The restructuring proceeds bottom up and can cause the increase of the tree height by one. In order to satisfy RAM constraints, in this first phase BIRCH frequently rebuilds the whole CF tree, while increasing values of T. In particular, BIRCH starts with the maximum precision (T = 0) and, as the CF tree grows larger than the available memory, it increases T to a value larger than the smallest distance between the two entries in the CF tree. Since all necessary data are kept in the main memory, this recurring construction of the whole CF tree is quite fast. The first phase also includes an outlier-handling process, in which outliers are detected, removed from the tree and stored on disk.

The second phase (optional) aims at condensing the CF tree to a desirable size. This can involve removing more outliers and further merging of clusters. In the third phase, BIRCH applies an agglomerative hierarchical clustering algorithm¹ to the subclusters represented by the leaves of the CF tree. This aims at mitigating the undesirable effects caused by both the skewed ordering of input data and the node splitting triggered by space constraints. Once again the CF vectors convey all the necessary information for calculating the distance and quality metrics used by the clustering algorithm adopted in this phase.

In the first three phases, the original data is scanned once, although the tree and the outlier information may have been scanned multiple times. By working only with the statistics stored in a CF vector, the actual partitioning of the original data is unknown. The fourth (optional) phase refines clusters at the cost of an additional scan of original data, and associates each data point with the cluster that it belongs to (data labeling).

The distance measure used in our implementation of BIRCH is the variance increase distance (Zhang et al. 1996), which is mathematically defined as follows:

Definition 1

(Variance Increase Distance) Let C ₁ and C ₂ be two clusters, where $C_1=\{\textbf{x}_i\}_{i=1..n_1}$ and $C_2=\{\textbf{x}_i\}_{i=n_1+1,\ldots,n_1+ n_2}$. The variance increase distance between C ₁ and C ₂ is:

$$D=\displaystyle \sum\limits_{k=1}^{n_1+n_2}\left(\textbf{x}_k- \frac{\displaystyle \sum\limits_{l=1}^{n_1+n_2}{\textbf{x}_l}}{n_1+n_2} \right)^2- \sum\limits_{i=1}^{n_1}\left( \textbf{x}_i- \frac{\displaystyle \sum\limits_{l=1}^{n_1}\textbf{x}_l}{n_1}\right)^2- \sum\limits_{i=n_1+1}^{n_1+n_2}\left( \textbf{x}_i- \frac{\displaystyle \sum\limits_{l=n_1+1}^{n_1+n_2}\textbf{x}_l}{n_2}\right)^2 $$

(2)

It can be reformulated as follows:

$$ \begin{array}{rll} D&=&(n_1+n_2)*(\mbox{Variance of merged clusters }C_1 \cup C_2)\\ &&-\, n_1 *(\mbox{Variance of } C_1)\\ &&-\, n_2 * (\mbox{Variance of } C_2) \end{array} $$

(3)

Since the variance of merged clusters is greater than or equal to the variance of both C ₁ and C ₂, then D ≥ 0. This measure can be easily computed by using the CF vectors of the two clusters, and it allows BIRCH to discover both circular-shaped clusters and near rectangular-shaped clusters. Moreover, it follows the same principle of the variance reduction heuristic which is at the basis of several clustering and predictive clustering algorithms (Vens et al. 2010).

4 OLAPBIRCH: combining BIRCH and OLAP

The integration of the implemented BIRCH algorithm in the OLAP solution we present is not a trivial task, since different issues have to be considered. First, OLAP queries can consider all the levels of the hierarchy and not only the last level. This means that it is necessary to have refined clusters, not only in the last level of the hierarchy, but also in the intermediate levels. Second, in OLAP frameworks, the user is typically able to control the size of hierarchies, but this is not possible in the original BIRCH algorithm. Third, although the last step of the BIRCH algorithm is not mandatory, it becomes necessary in our framework, in order to simplify the computation of OLAP queries. Fourth, in order to avoid the combinatorial explosion that is typical in multidimensional clustering, it is necessary to focus only on interesting continuous dimension attributes.

In order to face the first issue, we revised the clustering algorithm to allow the system to run the clustering algorithm used in the third phase (henceforth called global clustering) also in the intermediate nodes of the tree. At this end, we extended the CF tree structure by providing pointers prev and next to each internal node. This allows us to linearly scan each single level of the tree when performing OLAP operations. In Fig. 1, we report a graphical representation of the CF tree structure used in the proposed framework. The application of the global clustering also to intermediate nodes of the tree may also cause additional time complexity problems. Indeed, running OLAPBIRCH incrementally would require the execution of DBSCAN at each level of the tree for each new set of instances that is added to the database. In order to avoid this problem, which would negatively affect the use of OLAPBIRCH in real-world scenarios, we consider the incremental implementation of DBSCAN, as suggested in Ester et al. (1998). This algorithm is described in Section 4.1.

Fig. 1

OLAPBIRCH: an example of a CF tree

As for the second issue, in addition to the memory space constraints, we consider also an additional constraint that forces tree rebuilding when a maximum number of levels (MAX_LEV) is exceeded. This is coherent with the goal of having a limited number of levels, as in classical OLAP systems.

As for the third issue, given the maximum number of levels MAX_LEV and the branching factor B, it is possible to use a numerical representation of the complete path of clusters for each dimension instance, so that the classical B+tree index structure can be used, in order to allow efficient computation of range queries (Gunopulos et al. 2005). The representation is in the form < d ₁ d ₂ ...d _{MAX_LEV}  >, where each d _i is a sequence of $\ulcorner log_2 B \urcorner$ bits that allows the identification of each subcluster. The number obtained in this way is then used to perform roll-up and drill- down operations.

Finally, as for the fourth issue, in order to integrate the algorithm in an OLAP framework, we defined a language that supports the user in the specification of the attributes to be considered in the clustering phase. For this purpose, we have exploited the Mondrian² project, according to which a multidimensional schema of a data warehouse is represented by means of an XML file. In particular, this file allows the user to define a mapping between the multidimensional schema and tables and attributes stored in the database. The main elements in this XML file are: the data source, cubes, measures, the fact table, dimensions and hierarchies.

For our purposes, we have modified the DTD originally proposed in Mondrian, in order to extend the definition of the hierarchies. The modified portion of the DTD is:

The modified DTD permits us to add two new elements (< Attribute > and < Depth >) to the elements defined in < Hierarchy >. The < Attribute > element allows the user to define one or more attributes to be used in the clustering procedure. Properties that can be defined in the < Attribute > tag are: name—attribute name; table—table that contains the attribute; column—database column name; nameColumn—database column name (alias); type—SQL attribute type. The < Depth > element is used to specify the maximum depth of the CF-tree.

Clustering is performed by considering one or more user-defined dimensional continuous attributes and, by default, all the measures in the fact table. The CF-tree is updated when a new dimension tuple is saved in the data warehouse while (incremental) DBSCAN is run only when OLAP queries are executed and clusters are still not updated. This allows OLAPBIRCH to “prepare” for the analysis only levels that are actually used in the queries. It is noteworthy that, contrary to Shanmugasundaram et al. (1999), the global clustering is run on compact data representations and does not pose efficiency problems.

Example 1

Let us consider the database schema reported in Fig. 2 where lineitem is the fact table and orders is a dimensional table. By selecting, in the XML file, the attributes orders.o_totalprice and orders.o_orderpriority:

Fig. 2

TPC-H database schema

we have that the OLAP engine performs clustering on the following database view:

4.1 Global clustering: the incremental DBSCAN

Global clustering is applied to clusters obtained in the second phase of the BIRCH algorithm. In particular, each cluster obtained after the second phase and represented by its centroid, is clustered together with other clusters (represented by their centroids) by means of the application of DBSCAN, so that we obtain at the end “clusters of clusters”. This means that, in our implementation, DBSCAN is used in the clustering of centroids of clusters obtained after the previous phase.

The key idea of the original DBSCAN algorithm is that, for each object of a cluster, the neighborhood of a given radius (ϵ) has to contain at least a minimum number of objects (MinPts), i.e. the cardinality of the neighborhood has to exceed some threshold. The algorithm (see Algorithm 1) begins with an arbitrary starting object that has not been visited. This object’s neighborhood is retrieved and, if it contains a sufficient number of objects, a cluster is defined. Otherwise, the object is labeled as noise. This object might later be found in a sufficiently-sized environment of a different object and hence be made part of a cluster. If an object is found to be a dense part of a cluster, its neighborhood is also part of that cluster. Hence, the algorithm adds all the objects that are found within the neighborhood and their own neighborhood when they are also dense. This process continues until the density-connected cluster is completely found. Then a new unvisited point is retrieved and processed, leading to the discovery of a further cluster or noise.

IncrementalDBSCAN (Ester et al. 1998) is the incremental counterpart of DBSCAN. In our implementation, it starts to work in batch mode, according to the classical DBSCAN algorithm, and then performs cluster updates incrementally. Indeed, due to the density-based nature of clusters extracted by DBSCAN, the insertion or deletion of an object affects the current clustering only in the neighborhood of this object. IncrementalDBSCAN leverages on this property and is able to incrementally insert and delete examples into/from an existing cluster.

4.2 Time complexity

The learning time complexity depends on the time complexity of both BIRCH and DBSCAN algorithms. In the literature, it is recognized that BIRCH time complexity is linear in the number of instances, that is, O(n), where n is the number of instances.

Concerning DBSCAN, its time complexity is O(n*logn). However, its incremental version requires additional running time. In particular, as theoretically and empirically proved in Ester et al. (1998), time complexity of the incremental DBSCAN algorithm is O(γ* n*logn), where γ is a speedup factor, which is proportional to n and generally increases running times by 10 % with respect to the non-incremental version.

By considering that the number of levels of a tree is MAX_LEV and that we apply, differently from the original BIRCH algorithm, the global clustering algorithm also in intermediate nodes of the tree, time complexity is:

$$ O\left(\underbrace{n}_{BIRCH} + \underbrace{\underbrace{\gamma * (n * \log n)}_{incremental DBSCAN}*\ MAX\_LEV}_{global clustering} \right) $$

(4)

where the first addend is due to the BIRCH algorithm, while the second is motivated by the application of the global clustering to all the levels of the tree.

Although time complexity in (4) represents the typical scenario in which OLAPBIRCH works, it refers to the case in which:

• Instances are processed in a batch mode. Indeed, as previously stated, the global clustering is not applied in all situations, but only in the case in which OLAP operations are performed. This means that the time complexity reported in the second addend of (4) represents a pessimistic situation.

• The data warehouse logical schema follows a star or a snowflake structure. In the case in which a tuple in the fact table is associated to multiple tuples in the same dimensional table, n does not represent the number of instances in the fact table.

• Tree rebuilding is not considered. Indeed, despite the fact that in the original BIRCH paper the authors write that tree rebuilding does not represent a computational problem, in our case, where we define the maximum number of levels, rebuilding costs cannot be ignored.

As for the last aspect, in the (pessimistic and rare) case in which rebuilding affects the complete tree, time complexity of rebuilding is:

$$ O\left(\underbrace{B^{ MAX\_LEV}}_{BIRCH\ tree\ rebuilding} +\quad \underbrace{(\gamma *n * \log n)* MAX\_LEV}_{global\ clustering} \right) $$

(5)

where the first addend represents the cost introduced by BIRCH and the second addend is due to the execution of DBSCAN.

By combining (4) and (5) and by considering that (5) is a due to the pessimistic (and rare) situation in which rebuilding is necessary, time complexity of OLAPBIRCH is:

$$ O(\gamma *n * \log n ) $$

(6)

5 Experimental evaluation and analysis

In order to evaluate the effectiveness of the proposed solution, we performed experiments on two real world datasets which will be described in the following subsection. The results are presented and discussed in Section 5.2.

5.1 Datasets and experimental setting

The first dataset is the SPAETH Cluster Analysis Dataset,³ a small dataset that allows us to visually evaluate the quality of extracted clusters.

The second dataset is the well-known TPC-H benchmark (version 2.1.0)⁴ . In Fig. 2, we report the relational schema of TPC-H implemented on PostgreSQL, which we used for supporting DBMS. The TPC-H database holds data about the ordering and selling activities of a large-scale business company. For experiments we used the 1GB version of TPC-H containing more than 1×10⁶ tuples in the fact table (lineitem). From the original TPC-H dataset, we extracted four samples containing 1,082, 15,000, 66,668, 105,926 tuples in the fact table respectively. Henceforth we will refer to these samples as TPC-H_1, TPC-H_2, TPC-H_3, TPC-H_4.

On TPC-H we generated hierarchies on the following attributes in two distinct dimensional tables (see Fig. 2):

• orders.o_totalprice and orders.o_orderpriority (as specified in Example 1) which give an indication of the price and priority of the order;

• customer.c_acctbal, which gives an indication of the balance associated to the customer.

Henceforth we will indicate as H1 the hierarchy extracted according to the first setting and as H2 the hierarchy extracted according to the second setting.

On this dataset, we performed experiments on the scalability of the algorithm and collected results in terms of running times and cluster quality.

The cluster quality is measured according to the weighted average cluster diameter square measure:

$$ Q= {\sum\limits_{i=1..K} n_i(n_i -1) D_i^2}\bigg/{\sum\limits_{i=1..K} n_i(n_i -1) } $$

(7)

where K is the number of obtained clusters, n _i is the cardinality of the i-th cluster and D _i is the diameter of the i-th cluster. The smaller the Q value, the higher the cluster quality.

Finally, in order to prove the quality of extracted hierarchies, we evaluate the correlation between obtained clusters and two different dimensional properties, that is, the supplier’s region (SR) and the customer’s region (CR). In this way, we are able to evaluate the following correlations at different levels of the trees: H1 vs. SR; H1 vs. CR; H2 vs. SR; H2 vs. CR. Let $\mathcal{C}^{(k)}=\{C^{(k)}_l\}$ be the set of clusters extracted at the k-th level and $\mathcal{C}'=\{C'_r\}$ be the set of distinct values for the considered dimensional property, then, correlation is measured according to the following equation:

$$ \rho = \frac{1}{n*(n-1)} * \displaystyle \sum_{i,j=1,\ldots,n;\ i\neq j}^n v_{i,j}^{(k)} $$

(8)

where:

$$ v_{i,j} = \left\{ \begin{array}{lll} 1\quad & &\textrm{if} \left[\left(\exists l\ s.t.\ (x_i\in C_l^{(k)} \wedge x_j\in C_ l^{(k)})\right) \leftrightarrow \left( \exists r\ s.t.\ (x_i\in C'_r \wedge x_j\in C'_r)\right) \right]\\ 0\quad & & \textrm{otherwise} \end{array} \right. $$

(9)

Intuitively, v _i,j is 1 if x _i and x _j belong to the same cluster and are associated to the same property value; 1 if x _i and x _j do not belong to the same cluster and are not associated to the same property value; 0 in other cases.

5.2 Results

In Fig. 3, we report a graphical representation of obtained clusters for the SPAETH dataset. As we can see, the global clustering (DBSCAN) is necessary in order to have good quality clusters (visually). Moreover, as expected, by increasing the depth of the tree, it is possible to have more detailed clusters, which do not lead to the degeneration of the final clustering (see right-side images in Fig. 3).

Fig. 3

Clustering effect on Spaeth dataset. CF-tree is obtained with B=L=2. Left: OLAPBIRCH without DBSCAN, Right: OLAPBIRCH with DBSCAN; Top: LEVEL = 6, Bottom: LEVEL = 7. Points outside clusters are considered outliers

The results obtained on the TPC-H database are reported in Table 1. The first interesting conclusion we can draw from them is that the number of times that the CF-tree is rebuilt is very small, even for huge datasets. This means that the algorithm is able to assign new examples to existing clusters without increasing the T value. Moreover, this also means that the evaluation of the algorithm with a higher number of levels would lead to less interpretable hierarchies without advantages in the quality of the extracted clusters. Moreover, running times empirically confirm the complexity analysis reported in Section 4.2 and, in particular, confirm that, as expected, tree rebuilding affects time complexity. Concerning the Q value, it is possible to see that the quality of the clusters does not deteriorate when the number of examples increases. Moreover, when the number of rebuilds increases, we observe that the cluster quality decreases. This confirms the observation that the number of rebuilds has to be kept under control, in order to avoid cluster’s quality loss.

Table 1 TPC-H: scalability results

In Table 2, we report the number of extracted clusters. As it can be seen, by increasing the number of instances in the fact table (from TPC-H_1 to TPC-H_3) we have, as expected, that the number of clusters increases. The situation is different in the case of TPC-H_4, where the relatively higher number of rebuilds leads to a reduction of the number of clusters.

Table 2 TPC-H: number of extracted clusters

Figure 4 shows a different perspective of the obtained results. In particular, with the aim of giving a clear idea of the validity of extracted clusters from a qualitative viewpoint, it shows that there is a strong correlation between the supplier’s region dimension (that is not considered during the clustering phase) and the clusters obtained at the second level of the H1 hierarchy. This means that the numerical properties of the orders stored in TPC-H change in distribution between the regions where the orders are performed. Figures 5 and 6 provide a more detailed qualitative analysis which exploits the ρ coefficient introduced before. In detail, it is possible to see that at lower levels of the hierarchies the ρ values increase. This is due to the fact that at higher levels of the hierarchy, clusters tend to group together examples that, according to the underlying distribution of the data, should not be grouped. Moreover, it can be seen that by increasing the number of examples, the correlation decreases for higher levels of the tree, but not for lower levels. This means that, even for small sets of examples, lower levels of the hierarchy are able to catch the underlying distribution of the data. Finally, there is no clear difference between the four configurations. This depends on the considered dataset and on the considered dimensional properties that, in both cases, seem to be correlated to the attributes used to construct the hierarchies.

Fig. 4

TPC-H: data distribution over the customer’s region dimension

Fig. 5

ρ values computed on TPC-H_1 and TPC-H_2

Fig. 6

ρ values computed on TPC-H_3 and TPC-H_4

6 Applications scenarios

In this Section, we focus attention on possible application scenarios of OLAPBIRCH. Among all the possible alternatives offered by the amenity of integrating OLAP methodologies and clustering algorithms, we found in emerging Web search environments (Broder 2002) one with most potential that may connotate OLAPBIRCH as a truly enabling technology for these application scenarios. It should be noted that OLAP methodologies are particularly suitable for representing and mining (clustered) database objects (which can be easily implemented on top of relational data sources that represent the classical target of OLAPBIRCH) in Web search environments, as aggregation schemes. These are developed in the context of relational database settings (e.g. Kotidis and Roussopoulos 2013) and oriented to progressively aggregate relational data from low-detail tuples towards coarser aggregates which can be meaningfully adapted to progressively aggregate objects from (object) groups, aggregated on the basis of low-level (object) fields, towards groups aggregated on the basis of coarser ranges of low-level fields, in a hierarchical fashion.

In order to be sure of the potentialities offered by OLAPBIRCH in Web search environments, which are typical data-intensive application scenarios of interest for our research, we consider the case of Google Squared ⁵ . Google Squared offers intuitive two-dimensional Web views over keyword-based search results retrieved by means of Web search engines (like Google itself). Results retrieved by Google Squared can naturally be modeled in terms of complex objects extracted from the target sources (e.g. relational databases available on the Web) and delivered via popular Web browsers. Two-dimensional Web views of Google Squared support several functionalities, such as removing a column (of the table which models the two-dimensional Web view), adding a new column, and so forth, which are made available to the user. Thus, the user can further process and refine retrieved results.

The described Web search interaction paradigm supported by Google Squared is likely to be associated with a typical Web-enabled OLAP interface, where the following operations are supported: (i) selection of the OLAP analysis to be performed (this requires the selection of the corresponding DTD); (ii) selection of the measures to be included in the answer (among those included in the DTD); (iii) selection of the level of the hierarchy to be rendered; (iv) showing the cube, where the clusters can be used as dimensions (clusters are numbered using dot notation, where each dot represents a new level of the hierarchy); (v) “natural” roll-up (i.e. removing a column) and drill-down (i.e. adding a column) (Chaudhuri and Dayal 1997); (vi) pivoting. Operations (i), (ii) and (iii) are necessary in order to run the query (which is executed by OLAPBIRCH), while operations (iv), (v), (vi) are only available after the query has been computed. They are performed by JPivot,⁶ which uses Mondrian as its OLAP Server.

These operations can be easily supported by OLAPBIRCH, as demonstrated throughout the paper. It is clear enough that Google Squared can also act over clustered objects, as a result of clustering techniques over keyword-based retrieved objects, according to a double-step approach that encompasses the retrieval phase and the clustering phase, respectively. Clustered objects can then be delivered via the OLAP-aware Web interface. Figure 7 shows a typical instance of the integration of clustering and OLAP over Google Squared. Here, Fig. 7 shows clustered objects, representing digital cameras retrieved via Google Squared and delivered via OLAP methodologies. In particular, the OLAP-aware Web view of Fig. 7 represents clustered objects/digital-cameras, for which the clustering phase has been performed over the clustering attributes Resolution and DigitalZoom, which also naturally model OLAP dimensions of the view. Furthermore, Fig. 8 shows the same view over which a roll-up operation over the dimension Resolution has been applied. Moreover, Fig. 9 shows the same view over which a drill-down operation over the dimension Price has been applied.

Fig. 7

Integration of clustering techniques and OLAP methodologies over Google Squared: an OLAP-aware Web view of clustered digital cameras

Fig. 8

The view of Fig. 7 after a roll-up operation over the dimension Resolution

Fig. 9

Logical architecture of the OLAP-enabled Web system implementing the OLAPBIRCH approach

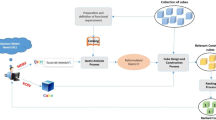
Figure 10 shows the logical architecture of the OLAP-enabled Web system implementing the OLAPBIRCH approach. This system embeds the OLAPBIRCH algorithm within its internal layer, in order to provide OLAP-enabled search and access primitives, according to the guidelines discussed above. As shown in Fig. 10, the OLAPBIRCH algorithm is set by a DW Administrator, in order to determine the most appropriate setting parameters (see Section 4). To this end, the OLAPBIRCH algorithm interfaces the Target Relational Database, where the dataset of interest is stored. Based on the keyword-search interaction of the End-User interfaced to Google Squared, the OLAPBIRH algorithm computes from the target dataset a suitable OLAP-like Hierarchical Cuboid Lattice, which stores multidimensional clusters organized in a hierarchical fashion. This cuboid lattice is mapped onto an ad-hoc Snowflake Multidimensional Schema implemented on top of Mondrian ROLAP Server. The so-determined OLAP data repository is accessed and queried via the JPivot Application Interface, which finally provides the OLAP-enabled Web functionalities encoded in Google Squared, as described. This visualization solution can be further improved if advanced OLAP visualization techniques, like Cuzzocrea et al. (2007), are integrated within its internal layers. As regards proper implementation aspects, it should be noted that the OLAP-enabled Web system described can be further improved to gain efficiency by deploying it over a composite platform including emerging NoSQL (e.g., Cattell 2010) and Cloud Computing (e.g., Armbrust et al. 2010) paradigms.

Fig. 10

The view of Fig. 7 after a roll-up operation over the dimension Price

The amenities deriving from the integration of clustering techniques and OLAP methodologies we propose in our research should be noted. First, complex objects are characterized by multiple attributes that naturally combine with the multidimensionality of OLAP (Gray et al. 1997), i.e. clustering attributes also play the role of OLAP dimensions of Web views. However, such views can also embed OLAP dimensions that are not considered in the clustering phase. Second, retrieved Web views can be manipulated via well-understood OLAP paradigms, such as multidimensionality and multi-resolution (Chaudhuri and Dayal 1997), and operators, such as roll-up, drill-down and pivoting (Chaudhuri and Dayal 1997). This clearly represents a critical add-in value for actual Web search models and methodologies. Moreover, most importantly, it opens the door to novel research challenges that we conceptually located under the term multidimensional OLAP-like Web search, which can be reasonably intended as the integration of multidimensional models and methodologies with Web search paradigms. We then selected the latter as a critical application scenario of OLAPBIRCH.

7 Conclusions and future work

In this paper we have presented the framework OLAPBIRCH. This framework integrates a clustering algorithm in an OLAP engine, in order to support roll-up and drill-down operations on numerical dimensions. OLAPBIRCH integrates a revised version of the BIRCH clustering algorithm and extends it by supporting the incremental construction of refined hierarchical clusters for all the levels of the hierarchy. For this purpose, OLAPBIRCH integrates an incremental version of DBSCAN, which further refines clusters for each level of the hierarchy.

The results show the effectiveness of the proposed solution on large real-world datasets and prove its capability in catching underlying data distribution also at lower levels of the hierarchy, even if we consider small training datasets.

For future work, we intend to extend the proposed approach according to the multi-view clustering learning task (Gao et al. 2006) in order to simultaneously construct hierarchies on attributes belonging to multiple distinct dimensions. For this purpose, we intend to leverage techniques used in co-clustering biological data (Pio et al. 2012, 2013). Finally, we intend to exploit hierarchical clustering in order to tackle classification/regression problems, by exploiting the predictive clustering learning framework (Stojanova et al. 2011, 2012).