Role of frequency mismatch in neuronal communication through coherence

Abstract

Neuronal gamma oscillations have been described in local field potentials of different brain regions of multiple species. Gamma oscillations are thought to reflect rhythmic synaptic activity organized by inhibitory interneurons. While several aspects of gamma rhythmogenesis are relatively well understood, we have much less solid evidence about how gamma oscillations contribute to information processing in neuronal circuits. One popular hypothesis states that a flexible routing of information between distant populations occurs via the control of the phase or coherence between their respective oscillations. Here, we investigate how a mismatch between the frequencies of gamma oscillations from two populations affects their interaction. In particular, we explore a biophysical model of the reciprocal interaction between two cortical areas displaying gamma oscillations at different frequencies, and quantify their phase coherence and communication efficiency. We observed that a moderate excitatory coupling between the two areas leads to a decrease in their frequency detuning, up to ∼6 Hz, with no frequency locking arising between the gamma peaks. Importantly, for similar gamma peak frequencies a zero phase difference emerges for both LFP and MUA despite small axonal delays. For increasing frequency detunings we found a significant decrease in the phase coherence (at non-zero phase lag) between the MUAs but not the LFPs of the two areas. Such difference between LFPs and MUAs behavior is due to the misalignment between the arrival of afferent synaptic currents and the local excitability windows. To test the efficiency of communication we evaluated the success of transferring rate-modulations between the two areas. Our results indicate that once two populations lock their peak frequencies, an optimal phase relation for communication appears. However, the sensitivity of locking to frequency mismatch suggests that only a precise and active control of gamma frequency could enable the selection of communication channels and their directionality.

1 Introduction

Neurons in cortical, subcortical, and cerebellar areas have been observed to engage in oscillatory activity at different frequency bands (Buzsáki and Draguhn 2004). In particular, upon sensory stimulation many cortical regions exhibit oscillations at the neuronal population level, as measured by local field potentials (LFP), in the beta (12-30 Hz) and gamma (30-90 Hz) range (Tallon-Baudry et al. 1997; Pulvermüller et al. 1997; Gruber et al. 1999). During gamma oscillations in vivo, individual neurons spike irregularly and at much lower rates than the population oscillation, exhibiting a so-called cycle skipping dynamics. However, despite not participating at every cycle the spikes of a neuron can be precisely locked to a narrow phase of the recorded LFP. The mechanisms generating gamma-band oscillations have been extensively investigated both experimentally and via computational and theoretical models. In particular, pharmacological and optogenetic manipulation of fast-spiking interneurons has demonstrated a key role of such neurons in the generation of gamma rhythms (Whittington et al. 1995; Fisahn et al. 1998; Cardin et al. 2009). Hence, it is believed that local recurrent inhibitory networks are responsible for modulating the excitability of neurons in a periodic manner and generating gamma activity. Computational and theoretical models have been useful in predicting how cell membrane and synaptic properties give rise to gamma oscillations and its properties such as frequency or fine spiking structure (Brunel and Wang 2003; Buzsáki and Wang 2012; Sancristóbal et al. 2013).

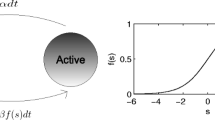
Given the ubiquity of gamma activity and the correlation of its power or frequency with distinct perceptual and cognitive outcomes, a pressing question is whether gamma rhythms play any fundamental role in information processing (Singer 1999; Shadlen and Movshon 1999). Some hypotheses on the role of gamma oscillations capitalize on the rhythmic susceptibility of an oscillatory area to incoming input, i.e., synaptic input arriving at the high excitability phase will have a higher probability of triggering a spike, in comparison with input arriving at the low excitability phase. Specifically, it has been proposed that given two oscillatory populations a change of their phase difference or coherence could implement an efficient and dynamic gain modulation, and thus serve a mechanism for flexible routing of information. This is known as the communication through coherence (CTC) hypothesis (Fries 2005). The CTC hypothesis requires that two oscillating populations of neurons have a well-defined phase relationship between their collective oscillations. Spikes sent by one population must reach the other population at appropriate time windows, and do so systematically, in order to lead to an effective transmission of information between the two groups of neurons. Thus, an important constraint for the CTC is a precise matching of the phase difference (Δϕ), axonal conduction delay (τ _axo ) and frequency (f ) of the oscillations, which should fulfill the condition Δϕ = 2πfτ _axo (Fig. 1a) (Eriksson et al. 2011). When this relationship holds, spikes fired in the emitting population at a specific phase of the signal (for instance at the troughs of the LFP, which correspond to the maxima of excitability) arrive at the receiving area at the same phase (and thus at the same excitability maximum), triggering a maximal response in the receiving area. On the contrary, if Δϕ does not fulfill the relationship given above (or if it randomly varies), effective communication will not be achieved.

Fig. 1

a The two networks are represented by circles and the synaptic bidirectional coupling by thin arrows. The LFP signal filtered at a frequency f is plotted in red. At the bottom of the LFP troughs (peaks of excitability in our case), the vertical ticks stand for the elicited spikes. Each bundle of spikes reaches the other population after a time delay, τ _axo . If the difference in phase settled by the synaptic coupling, Δϕ, satisfies the relationship Δϕ = 2πfτ _axo , an effective communication (like the one represented in this figure) is achieved. Adapted from (Fries 2005). b Frequency detuning before, Δf, and after, ΔF the coupling of two oscillators. For the dashed curve, only at relatively small Δf values, a frequency locking region is resolved by the coupling (for more information see (Pikovsky et al. 2001)). On the contrary, the solid curve does not show frequency locking, even at small Δf

A possible test for such hypothesis comes from a class of paradigms of selective attention where identical sensory stimulation must be processed differently depending on task demands. In particular, it has been found that during a spatial visual attention task, V4 neurons engaged in gamma oscillations are selectively phase coherent with the V1 oscillatory population processing the attended stimulus but not with the population processing the unattended stimulus (Bosman et al. 2012). However, whether the nervous system actively regulates the phases of oscillations to route information or they simply reflect the routing itself is a critical distinction that deserves further research. In this paper we study two coupled neural populations with bidirectional (but not necessarily symmetrical) coupling, similar to the one existing between dissimilar areas, with the aim of investigating the interplay between phase coherence and information transmission between two generic cortical regions.

The relation between phase coherence and frequency locking has been intensively investigated in models of oscillators. It is well known that simple interacting oscillators with well defined frequencies are able to synchronize their rhythms, thus leading to phase coherence, provided that their intrinsic frequencies are similar enough (Pikovsky et al. 2001). Conversely, given a strength of interaction there is a maximum frequency detuning above which coupling-induced frequency locking is forbidden (dashed curve in Fig. 1b). However, the broad-band power spectrum of neuronal oscillatory processes might allow for more complex phenomenology. In particular, it can sustain phase coherence despite a mismatch between the peak frequencies (solid curve in Fig. 1b).

In this article we investigate how the interaction between gamma oscillations is affected by a mismatch in their frequencies. This situation arises not only due to an expected natural variability of the intrinsic cell and network properties, but also due to the stimulus dependency of gamma oscillations. For example, the frequency of gamma activity in the primary visual cortex depends on the size, eccentricity, and contrast of the visual stimulus (Ray and Maunsell 2010). It is thus important to study how the communication efficiency between two oscillatory areas depends on their frequency detuning. In the following we shall explore a biophysical model of two reciprocal interacting cortical areas to study this question, with the aim of constraining potential mechanisms that exploit the coherence of neuronal oscillations.

In our model we control the gamma frequency peak of one of the areas by slowing down the inhibitory postsynaptic currents (IPSCs), i.e. by increasing the GABAergic synaptic decay time, $\tau _{\text {GABA}}^{d}$. The use of $\tau _{\rm GABA}^{d}$ as the control parameter determining the frequency peak of one of the two populations does not presume, however, the existence of a patched distribution of inhibitory currents with different kinetics throughout the cortex. Nevertheless, previous works have revealed a wide heterogeneity among inhibitory neurons (Buhl et al. 1994; Kang et al. 1994; Puia et al. 1994; Kawaguchi and Kubota 1997; Houston et al. 2009). We note that a shift in the gamma frequency peak can also be induced by changes in the input rate (Brunel and Wang 2003; Mazzoni et al. 2008). However, we will use external rate variations only to probe the communication across two networks. Since an increase in the synaptic input impinging on a neuronal population boosts its firing activity, triggering as well a change in its oscillatory frequency, we have dissociated both effects by tuning two different parameters. In particular, $\tau _{\text {GABA}}^{d}$ modulates the gamma frequency peak, while the input rate regulates the spiking activity. We note that changes of $\tau _{\text {GABA}}^{d}$ make the neurons unresponsive for longer periods of time (longer IPSCs) without changing the number of spikes elicited in a given cycle (with a period given by $\tau _{\text {GABA}}^{d}$). Using the same structural connectivity through all the simulations, we have computed the phase coherence between the LFP and eMUA (MUA from excitatory neurons) of the two networks for varying $\tau _{\text {GABA}}^{d}$, and thus for varying frequency detuning.

Our results show that low frequency detuning entails zero-lag LFP synchronization, while higher frequency detuning leads to a non-zero phase lag. In the latter case the population with the smallest $\tau _{\text {GABA}}^{d}$, and thus with the fastest dynamics, becomes the leader, showing a phase advancement with respect to the slowest population. In addition, as the difference in $\tau _{\text {GABA}}^{d}$ increases, the AMPA synapses from the leader to the laggard area are less effective in triggering spikes and the eMUA-eMUA phase coherence drops. However, we observe that LFPs phase coherence is maintained for larger detunings between the peak frequencies, possibly reflecting that the LFP captures afferent synaptic currents regardless of their efficiency in triggering action potentials. Finally, we tested the effective connectivity between the two populations under frequency detuning by modulating the external input to one area and measuring the response of the other. Our results reveal an important requirement for the CTC hypothesis, namely that interactions that lead to near in-phase relationship during small frequency detunings provide a scenario for maintaining communication across areas. Otherwise, the observed phase coherence between LFPs reflects synaptic contributions that do not result into an effective reciprocal routing of information via spikes.

2 Methods

2.1 Description of the neuronal model

The evolution of the membrane potential for neuron i is given by the following conductance-based model:

$$\begin{array}{@{}rcl@{}} C_{m}\frac{dV_{i}}{dt}&=&-g_{K}n_{i}^{4}\left(V_{i}-V_{K}\right)-g_{Na}m_{i}^{3}h_{i}\left(V_{i}-V_{Na}\right)- \\ && -g_{L}\left(V_{i}-V_{L}\right)+\sum\limits_{j}I_{{\rm syn},ji}\,, \end{array} $$

(1)

where g _K , g _Na and g _L are the maximum conductances for the potassium, sodium and leak current, respectively, and are assumed equal for all neurons. I _{syn, ji} is the synaptic current on neuron i caused by a spike fired by neuron j. The summation runs over all neighbors of neuron i. The dynamics of the potassium and sodium channels is represented by the time-varying probabilities that a channel is open:

$$\frac{dx_{i}}{dt}=\phi\left[\alpha_{x}(V_{i})(1-x_{i})-\beta_{x}(V_{i})x_{i}\right]\,, $$

where x stands for n in the case of the potassium current, and for m and h in the case of the sodium current. α(V) and β(V) are voltage-dependent rate constants, and ϕ is the temperature factor, defined by ϕ = 3^{(T − 6. 3) / 10}, where T is measured in degrees Celsius. The temperature factor ϕ is set to 21, which corresponds to T = 34°C.

The parameter values used throughout this study are those reported in Gutfreund et al. (1995): g _K = 4. 74 μS, g _Na = 12. 5 μS and g _L = 0. 025 μS. The reversal potentials of the different channels are V _K = − 80 mV, V _Na = 40 mV and V _L = − 65 mV, and the membrane capacitance is C _m = 0. 25 nF. The leak conductance defines an effective membrane time constant for the isolated neuron according to the expression τ = C _m / g _L , which is taken to be 20 ms.

The rate functions α and β for each gating variable are:

$$\begin{array}{@{}rcl@{}} \alpha_{n}(V)&=&0.01\frac{V+20}{1-e^{-(V+20)/10}} \\ \beta_{n}(V)&=&0.125e^{-(V+30)/80} \end{array} $$

for the gating variable n,

$$\begin{array}{@{}rcl@{}} \alpha_{m}(V)&=&0.1\frac{V+16}{1-e^{-(V+16)/10}} \\ \beta_{m}(V)&=&4e^{-(V+41)/18} \end{array} $$

for the gating variable m, and

$$\begin{array}{@{}rcl@{}} \alpha_{h}(V)&=&0.07e^{-(V+30)/20} \\ \beta_{h}(V)&=&\frac{1.0}{1+e^{-V/10}} \end{array} $$

for the gating variable h. Due to the rapid activation of m we replace it by its steady-state value $m_{\infty }=\frac {\alpha _{m}}{\alpha _{m}+\beta _{m}}$.

2.2 Description of the network model

To simulate two cortical populations we have built a network composed of two connected modules of 2000 conductance-based model neurons each (Eq. (1)). The population is divided into 80 % excitatory and 20 % inhibitory neurons (Mountcastle 1998). Only AMPA and GABAergic chemical synapses are considered –no gap junctions are included– and each neuron connects to 200 other neurons on average. The intra-module connections are determined by the Watts-Strogatz small-world algorithm (Watts and Strogatz 1998), with a rewiring probability of 0.5. Therefore, the connectivity within each module shows a certain degree of clustering, as closest neighbors are favored. The same criteria has been applied for the coupling between modules: in this case, 60 % of the excitatory neurons have been randomly chosen as long-range-projecting neurons making synapses to 10 % of the neurons from the other module (bidirectional coupling), which mostly belong to the same cluster (i.e. they are coupled between them). Therefore, exciting a subpopulation of adjacent excitatory neurons from an area triggers a response in a well-defined subpopulation of neighboring neurons in the receiving area. The existence of long-range patchy connections relies on wiring-optimization assumptions, and is a common consideration in coupled cortical neurons with similar receptive field properties (for a review of both experimental evidences and models see Voges (2010a, 2010b)). This type of interareal coupling minimizes the divergence of connections across networks, and thus allows that perturbing one subset of neurons in one population has a local effect on the other population without altering the overall LFP/MUA signal. Thus, by perturbing only a limited number of neurons, the relative phase difference between the global activities of the two networks is not reset by the input.

We considered axonal conduction delays taken from a gamma distribution (Vicente et al. 2008) of mean 1 ms (2 ms) and variance 1 ms ²(2 ms ²), within the network (across networks). The synaptic current is described using again a conductance-based formalism:

$$I_{{\rm syn},ji}=g_{{\rm syn},ji}(t)(V_{i}(t)-E_{{\rm syn},j})\,, $$

where g _{syn, ji} is the synaptic conductance between neurons j and i and E _{syn, j} is the reversal potential of the synapse. For E _{syn, j} greater than the resting potential V _{rest, i} the synapse is depolarizing, i.e. excitatory, otherwise it is hyperpolarizing, i.e. inhibitory. The nature of each synapse is determined by the excitatory or inhibitory character of the presynaptic neuron j. We consider two time constants, $\tau_{j}^{d}$ and $\tau_{j}^{r}$ (decay and rise synaptic time, respectively, see Table 1), for the dynamics of the synaptic conductance, updated as

$$g_{{\rm syn},ji}(t)=\frac{g'_{{\rm syn},ji}}{\tau_{j}^{d}-\tau_{j}^{r}}\left[e^{-\frac{t-t_{j}-\tau_{axo}}{\tau_{j}^{d}}}-e^{-\frac{t-t_{j}-\tau_{axo}}{\tau_{j}^{r}}}\right]\,, $$

a time τ _axo after each presynaptic spike t _j fired by neuron j.$g_{\text {syn, ji}}^{\prime}$ is shown in Table 2 and depends on the excitatory/inhibitory character of the presynaptic neuron j. We have chosen the maximal conductances,$g_{\text {syn}}^{\prime}$, to maintain the postsynaptic potential (PSP) amplitudes within physiological ranges: the excitatory PSP in the range from 0. 42 mV to 0. 83 mV, and the inhibitory PSP from 1. 54 mV to 2. 20 mV. It is important to note that increases of τ _d diminish the maximum amplitude of g _syn (t), thereby maintaining the area under a PSP.

Table 1 Synaptic time constants and reversal synaptic potential values

Table 2 Synaptic conductances, g′_syn, for all the possible connections

Additionally, all neurons receive an heterogeneous Poisson train of excitatory presynaptic potentials, with a mean event rate that varies following an Ornstein-Uhlenbeck process. This incoming external current mimics the thalamocortical input coming from non-simulated neurons. The instantaneous rate, λ(t), of the external excitatory train of spikes is generated according to an Ornstein-Uhlenbeck process as considered in Mazzoni et al. (2008):

$$ \frac{d\lambda}{dt}=-\lambda(t)+\sigma(t)\left(\sqrt{\frac{2}{\tau}}\right)\eta(t), $$

where σ(t) is the standard deviation of the noisy process and is set to 0. 6 spikes/s. τ is set to 16 ms, leading to a power spectrum for the λ time series that is approximately flat up to a cut-off frequency $f=\frac {1}{2\pi \tau }=9.9$ Hz. η(t) is a Gaussian white noise. In all simulations 〈λ(t)〉 = 7300 spikes/s, and increases to 〈λ(t)〉 = 12000 spikes/s for the 200 ms window of perturbation to the fast/slow population.

Excitatory synapses outnumber inhibitory ones, and yet the brain avoids epileptic states because inhibition is able to balance excitation, and thus neurons remain below threshold, firing only occasionally. GABAergic (inhibitory) synapses are stronger than glutamatergic AMPA (excitatory) synapses to compensate their relative small number (Markram et al. 2004). Therefore, the high firing activity triggered in the inhibitory population elicits a strong recurrent inhibition capable of balancing excitation, and therefore neurons fire sparsely and irregularly, mostly fluctuating below threshold. This process, in which the inhibitory current follows the excitatory current leading in turn to another surge in inhibitory current, results in an oscillating LFP (Brunel and Wang 2003).

2.3 Numerical simulations

The model has been integrated using the Heun algorithm (Garcia-Ojalvo and Sancho 1999), with a time step of 0.05 ms. All the simulations represent 3 seconds of activity, and the identity of the connected neurons, initial conditions, and noise realization were varied from trial to trial. The code that performs the simulations was custom-made in Fortran, while the data analysis described below was performed in Matlab.

2.4 Model of MUA and LFP

We quantify the population activity of the network in two different ways. The multi-unit activity (MUA) series is defined as the total number of spikes produced by a population in 5-millisecond windows shifted in steps of 1 millisecond (Buehlmann and Deco 2010). When convenient we distinguish between the MUA due to 80 excitatory (eMUA) or 80 inhibitory (iMUA) neurons from the whole population. The local field potential (LFP) is estimated from the sum of the absolute values of the excitatory and inhibitory synaptic currents acting upon the excitatory neurons (Mazzoni et al. 2008; Buzsáki et al. 2012):

$$ \text{LFP} = R_{e} \left\langle | I_{\rm AMPA} |+| I_{\rm GABA} | \right\rangle, $$

(2)

Here 〈 ⋯ 〉 denotes an average over all excitatory neurons (Berens et al. 2010). The term I _AMPA accounts for both the external excitatory heterogeneous Poisson spike train and the recurrent excitatory synaptic current due to network connectivity, while I _GABA corresponds to the recurrent inhibitory synaptic current. R _e represents the resistance of a typical electrode used for extracellular measurements, here chosen to be 1 M Ω.

Averages of eMUA signals were computed over 200 trials when required (Fig. 9). As each trial implies a different realization of the noise and network connectivity, the phase of this signal at a given instant varies randomly across simulations. Therefore, in order not to cancel out the time series when adding them up in a certain time window, eMUAs were averaged aligning the first maximum.

2.5 Computation of power spectra and phase coherence

The power spectra were estimated applying the multitaper method (Thomson 1982), commonly used to reduce the variance of the spectra of recorded signals, which are usually very noisy. This estimator was implemented in Chronux 2.10 (Bokil et al. 2010). The multitapered power spectrum, S(f), is the average of the power spectrum of the signal multiplied by K orthogonal Slepian functions (in our case K = 5), and further averaged over N trials:

$$ S(f)=\frac{1}{N}\sum_{n=1}^{N} s_{n}(f)=\frac{1}{N}\sum_{n=1}^{N}\left(\frac{1}{K}\sum_{k=1}^{K}\mid \widetilde{LFP}_{n,k}(f)\mid^{2}\right)\,{}. $$

(3)

Here $\widetilde {LFP}_{n,k}(f)$ is the discrete Fourier transform of the LFP(t) signal of the n-th trial, multiplied by the k-th Slepian function (or taper). We have considered data segments within a 500-ms sliding time window with an overlap of 50 ms, padded with zeros up to a length of 512 in order to obtain an increased sampling rate in the frequency domain. The resolution bandwidth is thus ± 6 Hz. The MUA power spectra are also obtained by the multitaper algorithm, with the same sliding time window, overlap, and padding.

The phase coherence, Fig. 4, and phase difference plots, Fig. 5, are obtained with the coherencyc.m function for continuous signals implemented in Chronux 2.10. The normalization convention was taken as in Womelsdorf et al. (2007):

$$ C_{xy}(f)=\frac{1}{N}\sum_{n=1}^{N} \frac{S_{xy}(f,n)}{|S_{xy}(f,n)|}, $$

(4)

where x and y denote the two signals whose coherence is being calculated. S _xy (f, n) is the cross-spectrum between these two signals. All power spectra (Fig. 2) are averaged over 20 trials and phase coherence (Fig. 4) results over 200 trials.

Fig. 2

a LFP power spectrum and c MUA power spectrum (for the excitatory population in the top panel and the inhibitory population in the bottom panel) of the neuronal network for different values of the GABAergic synaptic decay time, $\tau _{\rm GABA}^{d}$. b and d show the corresponding power spectrum modulation with respect to the spectra obtained for $\tau _{\rm GABA}^{d}=11$ ms

3 Results

In the following we quantify the spectral and communication properties of two oscillating areas as a frequency detuning is induced. We also analyze the impact of such a frequency mismatch in the propagation of a transient increase in the firing activity from one neuronal network to the other.

3.1 Spectral properties: non-interacting populations

We begin by showing the characteristics of the power spectrum of a neuronal population when it is isolated (not interacting with another population). Figure 2a and c show the power spectrum of the LFP and MUA signals for increasing values of the GABAergic synaptic decay time, $\tau _{\rm GABA}^{d}$. Larger values of $\tau _{\rm GABA}^{d}$ give rise to slower oscillations (Whittington et al. 1995), as revealed by a linear decrease of the gamma frequency peak of ∼10 Hz towards the left, from 33 to 23 Hz. Thus, the variation of $\tau _{\rm GABA}^{d}$ allows us to scan the peak frequency from low gamma to high beta. A similar modulation of the gamma peak frequency has been experimentally observed in the visual cortex when the contrast of the stimulus decreases (Ray and Maunsell 2010). We notice also that the peaks of the MUA spectra show a good correlation with those of their LFPs. To filter out the 1-over-f contribution of the signals, we normalize the power spectra of Fig. 2a and c with respect to the case of a vanishingly small gamma rhythm $\tau _{\rm GABA}^{d}=11$ ms).

Similar normalized LFP spectra have been reported to be up-modulated in visual areas for increasing stimulus contrast, (Henrie and Shapley 2005). This effect has been attributed to a raise of average firing rate at the lateral geniculate nucleus (Kaplan et al. 1987). Accordingly, most computational studies (Brunel and Wang 2003; Mazzoni et al. 2008) have modeled a variation in contrast by means of a change in the rate of the external spike train exciting the population. However, varying the external firing rate produces changes in the average LFP, thereby mixing the effect of the external signal with that of the intrinsic dynamics of the population. To dissociate the two contributions, we have used $\tau _{\rm GABA}^{d}$ instead of the external firing rate to tune the network oscillation frequency. Figure 2b and d show the power spectrum modulation corresponding to the LFP and the excitatory and inhibitory MUA for increasing $\tau _{\rm GABA}^{d}$.

Both strong external input to an area and low intrinsic or effective $\tau _{\rm GABA}^{d}$, (Houston et al. 2009; Roepstorff and Lambert 1994) are consistent with increases in the LFP oscillatory frequency. Indeed, both changes in $\tau _{\rm GABA}^{d}$ and in the external rate have a similar effect on the network properties despite the fact that one of them (the external firing rate) acts in first term upon the excitatory synaptic current and the other one $\tau _{\rm GABA}^{d}$) affects the inhibitory current. In the present study, increasing $\tau _{\rm GABA}^{d}$ induces a decrease in the amplitude of the inhibitory postsynaptic potential (IPSP) without changing the total area under an IPSP (see Section 2). Thus, different values of $\tau _{\rm GABA}^{d}$ produce different gamma frequency peaks without substantially varying the mean LFP nor the mean firing rate per cycle (see discussion in Section 3.2).

3.2 Spectral properties: interacting populations

Here we consider two neuronal populations reciprocally connected via long-range excitatory synapses (see Section 2). In all simulations the decay time in one of the two populations is always held constant at $\tau _{\rm GABA,f}^{d} = 5$ ms (we refer to it as fast population or with the f subscript). For the other population (slow population, s subscript) the decay time $\tau _{\rm GABA,s}^{d}$ is varied from 5 ms to 11 ms. Figure 3a shows the peak frequencies for both populations, with and without coupling (circles on solid and dashed lines, respectively), as a function of $\tau _{\rm GABA,s}^{d}$.

Fig. 3

a The frequency at the maximum peak in the beta-gamma region (20 Hz - 36 Hz) of the LFP power spectrum is plotted against $\tau _{\rm GABA,s}^{d}$ for the two networks before (dashed lines) and after (solid lines) coupling. Blue circles and colored circles correspond to the fast ($\tau _{\rm GABA,f}^{d}=5$ ms) and slow population (varying $\tau _{\rm GABA,s}^{d}$ along the x-axis) respectively. The intrinsic frequency detuning is the difference between the blue and colored circles on the dashed line. b Number of spikes elicited by the excitatory neurons of the fast and slow population after coupling, the latter corresponding to the area under the eMUA signal shown in c. c Both the blue and gray area $\tau _{\rm GABA,s}^{d}=5$ ms and $\tau _{\rm GABA,s}^{d}=11$ ms respectively) are equal. Color legend as in Fig. 2a

The frequency detuning in the absence of coupling (which corresponds to the vertical distance between the blue and colored circles on the dashed lines in Fig. 3a, and to the Δf magnitude in Fig. 1b) increases with $\tau _{\rm GABA,s}^{d}$. The excitatory interareal connectivity enhances the spiking activity of each population, and thereby speeds up the LFP and MUA oscillations. In the presence of coupling between the two populations, the interaction induces a frequency shift for the slow population that ranges between 2 and 7 Hz. The fast population, in turn, increases its frequency in 2 Hz. Thus, the slowest population shows a larger range of frequency shifts induced by the interaction with a faster population.

Despite the fact that larger $\tau _{\rm GABA,s}^{d}$ increases the intervals between peaks of excitability (phases of enhanced spiking probability), the number of spikes triggered by the excitatory neurons remains constant across the different oscillation periods tuned by $\tau _{\rm GABA,s}^{d}$ (Fig. 3b and c). Thus, within a given time window, the fast population fires more spikes only because of its faster rhythm. Due to its higher rhythm the fast population is able to induce a larger frequency shift upon the slower population than viceversa. As a result, the excitatory interaction between areas promotes a decrease in the frequency detuning. Note that an increase of 1 ms in $\tau _{\rm GABA,s}^{d}$ produces a decrease of ∼1.6 Hz in the frequency peak of the isolated slow population (slope of the dashed line connecting the colored circles in Fig. 3a) and of ∼0.97 Hz when interacting with the fast population (slope of the solid line connecting the colored circles in Fig. 3a). Hence, we observe that small changes in the dynamics of the GABAergic synapses prevent frequency locking in reciprocally connected populations.

As shown in Fig. 3a, no frequency-locking region appears due to the coupling between the two networks. A frequency-locking regime can only occur when the coupling-induced frequency shift compensates the natural frequency detuning between the isolated populations. Since the coupling-induced shift for the slow population never exceeds ∼7 Hz, and this value is smaller than the natural frequency detuning caused by differences in $\tau _{\rm GABA}^{d}$, frequency locking does not occur. That is, in our case the frequency mismatch after coupling is zero only for two networks with the same decay in the GABAergic synapses, i.e. $\tau _{\rm GABA,f}^{d} = \tau _{\rm GABA,s}^{d}=5$ ms. For all other values of $\tau _{\rm GABA,s}^{d}$, the gamma peak of the fast population (blue circles on the solid line of Fig. 3a) remains at frequencies larger than the one of the slow population (colored circles on the solid line of Fig. 3a).

Given the lack of frequency locking between peak frequencies discussed above, one might expect that two neuronal populations would not exhibit phase coherence (unless their intrinsic frequencies were very similar). This expectation does indeed hold for the case of coupled self-sustained oscillators with a well-defined period, whose phase difference outside the frequency synchronization region varies in time (Pikovsky et al. 2001). However, LFP measures of one area capture not only synaptic currents due to local neurons but also afferent synaptic currents originated in other populations. Even in the absence of locking between peak frequencies, afferent synaptic currents will contribute to the coherence between LFP measures, since all afferent signals, regardless of their rhythm, affect the local subthreshold synaptic activity. We observe that the coherence between LFPs is maximal around the frequency peak of the slower population. On the contrary, eMUA signals only capture suprathreshold activity (i.e. action potentials) but they will poorly reflect spike activity from an afferent area that is not able to arrive consistently within the local excitability windows. In our case, the fast population maintains its peak around 33 Hz, and since it has a faster rhythm than the slow population, the latter is being perturbed multiple times within its particular cycle, and thus at different phases of its local excitability cycle. In particular, in the absence of locking the afferent activity can arrive at any phase of the local gamma cycle, rendering such activity hardly effective in triggering action potentials. Thus, MUA activity mainly follows the local rhythm and shows a marked decrease in coherence as soon as a natural detuning appears.

The coherence values for LFP and eMUA are shown in Fig. 4a and b, which display in a colormap the phase coherence at different frequencies. We use here the eMUA signal, a measure of the spiking activity of the excitatory neurons, because the synapses between neurons belonging to different networks are always excitatory. In agreement with experiments (Schoffelen et al. 2005; Womelsdorf et al. 2007; Ray and Maunsell 2010; Bosman et al. 2012), phase coherence between LFPs is highest at a frequency near their maxima in the power spectra.

Fig. 4

Phase coherence, in color code according to the vertical bar, as a function of frequency (y-axis) and of the intrinsic frequency detuning (bottom x-axis), which is controlled by varying $\tau _{\rm GABA,s}^{d}$ (top x-axis), between a the LFPs and b eMUAs of the two populations. The circles in panel a correspond to the colored circles connected by the solid line in Fig. 3a. The two insets show the maximum phase coherence values, found within the gamma range, at each Δf

The contrasting behavior between LFPs and MUAs coherence can also be seen in Fig. 5, which shows the histogram of phase differences, Δϕ, between the signals of both populations. In each case, the histogram is plotted for the frequency at which the phase coherence is maximal. The figure shows that while there is a relatively well defined phase difference between the LFP signals for increasing $\tau _{\rm GABA,s}^{d}$ (top row in Fig. 5), the distribution becomes broader for large $\tau _{\rm GABA,s}^{d}$ (large detuning) in the case of the eMUA signals (bottom row in Fig. 5).

Fig. 5

Angle histogram of the phase difference between a the LFPs and b eMUAs of the fast ($\tau _{\rm GABA,f}^{d} = 5$ ms) and slow oscillations [$\tau _{\rm GABA,s}^{d} = 5$, 8, 11 ms for left, middle and right panels respectively]. For each $\tau _{\rm GABA,s}^{d}$, the phase differences are computed at the frequency at which a the LFP-LFP and b eMUA-eMUA phase coherence is maximal

To grasp the origin of the different behavior of the phase coherence for the LFP and eMUA signals, we computed the effective time delay τ _e between the two pairs of signals as τ _e = Δϕ / 2πf _max , where Δϕ is again the phase difference at the frequency f _max of maximum phase coherence. The results are shown in Fig. 6 for increasing frequency detuning, and reveal that the maximum phase coherence occurring at small and large detuning (Fig. 4a) corresponds to two different values of τ _e . Specifically, only identical populations ($\tau _{\rm GABA,s}^{d}=\tau _{\rm GABA,f}^{d}$) show zero frequency detuning and their LFP gamma rhythms oscillate in phase (τ _e ≃ 0), while at large frequency detuning there is a phase shift between the two populations (τ _e ≤ − 4 ms, negative meaning that the fast population precedes the slow one). Thus Fig. 6a reveals two scenarios: simultaneous or zero-lag synchronization between the LFPs for small frequency detuning, and a leader-laggard regime for large detunings, with the slow oscillation (laggard) following the fast one (leader) with a lag partially determined by the time it takes the neuronal signals to travel from the leader to the laggard population (the axonal delay τ _axo ).

Fig. 6

The effective time delay, τ _e , computed at the frequency of maximum phase coherence of Fig. 4a and b, is shown as a function of the intrinsic frequency detuning (bottom x-axis), which is controlled by varying $\tau _{\rm GABA,s}^{d}$ (top x-axis), between a the LFPs and b eMUAs of the two populations. The mean and sample standard deviation are calculated over four groups of 50 trials

A pure zero-lag synchronization (τ _e ∼0 ms) only occurs when both neuronal populations are identical, i.e. the parameters used to define each network are equal, leading as well to zero frequency detuning. An effective time delay τ _e < τ _axo between the two populations (measured by the relative time shift of either the LFP or eMUA signals) reveals quasi-synchronous dynamics. Therefore, we consider here the region $\tau _{\rm GABA,s}^{d}\leq 6$ ms (see Fig. 6) to be the zero-lag synchronization regime, since the mean axonal delay across neurons belonging to different networks is set to τ _axo = 2 ms (see Section 2). By contrast, the broader region τ _e > τ _axo for $\tau _{\rm GABA,s}^{d}\geq 7$ ms, reveals a significant time lag with respect to τ _axo = 2 ms and is attributed to a leader-laggard regime.

Note that for a fixed $\tau _{\rm GABA,s}^{d}$, f _max might be different for LFP and eMUA. Thus both the phase lag, Δϕ (Fig. 5), and time delay, τ _e (Fig. 6), show corresponding differences between LFP and eMUA. In the first scenario (small detunings), the zero-lag phase synchrony occurs for small axonal delays while an anti-phase synchrony can occur for axonal delays comparable to the period of the gamma oscillation (Bush and Sejnowski 1996). In both cases, spikes produced by one area arrive at a maxima of excitability of the other. In the second scenario (large detunings), despite the fact that the structural connectivity is bidirectional, the functional connectivity is closer to a unidirectional coupling since the firing activity of one excitatory population is synchronized at a recurrence period different than that of the other excitatory population. Thus, the slow oscillatory population firing rate is less effective to perturb the faster oscillatory activity at every cycle, while the activity of the faster population impinges on the slow population at each cycle. As a result, the fast population drives almost unidirectionally the slow one, which adjusts its LFP phase to that of the leader for a range of frequencies. Indeed, in the presence of strong frequency detuning, the frequency at the maximum of the LFP-LFP phase coherence, ∼30 Hz, is close to the frequency peak of the LFP power spectrum of the laggard population (see colored circles in Fig. 4a). In this case, given the different oscillatory frequencies, spikes produced by the fast population can arrive at any phase of the slow oscillation but its effect is only significant at the troughs of the slow LFP (i.e. the peaks of excitability as shown next).

Importantly, the MUA activity of each population is locked (Fig. 7) close to the troughs of its own LFP signal at the gamma frequency peak. Therefore, the lack of gamma frequency locking in the leader-laggard regime prevents the LFP synchronization from triggering eMUA synchronization. Accordingly, the eMUA-eMUA phase coherence (Fig. 4b) shows the loss of synchronization between the excitatory spikes of the two populations as the frequency detuning increases. On the other hand, at low frequency detunings both the LFP-LFP and eMUA-eMUA display synchronization with significant phase coherence at zero-lag, as shown by the blue circles in Fig. 6.

Fig. 7

a Angle histogram of the phase difference between the LFP and eMUA at different $\tau _{\rm GABA,s}^{d}$ values of the slow population at the frequency of maximum LFP-eMUA phase coherence. Note that regardless of $\tau _{\rm GABA,s}^{d}$, the phase difference between the LFP and eMUA is $\sim 5\pi /4$. b LFP and eMUA signals (thick and thin lines respectively) for $\tau _{\rm GABA,s}^{d}=5$ ms (top) and $\tau _{\rm GABA,s}^{d}=11$ ms (bottom). Despite the fluctuations in the eMUA time trace, due to the irregularity in the spiking times and to the small size of the measured subpopulation, the signal clearly peaks right after the troughs (∼π) of the LFP almost in anti-phase. To better compare the two time traces we have subtracted the DC component of the LFP

3.3 Communication

Above a certain level of phase coherence, provided the phase difference between the peaks of the signals from the two neuronal pools is close to the axonal delay, we expect that an enhancement of the firing activity in one population (the emitter) will be efficiently transferred to the dynamics of the other population (the receiver). Reciprocal information transmission between two populations will be successful if an appropriate phase relationship between them exists in the two directions of communication. For this to happen reciprocally between the two symmetrically connected populations at short interareal delays, phase coherence should occur at zero lag.

Below we study a communication paradigm in which the message being propagated from one network (emitter) to the other (receiver) is considered as an increase in the firing rate of the emitter triggered by a surge of the external rate. Therefore, using $\tau _{\rm GABA}^{d}$ and the external rate for different purposes helps to better isolate the specific role of frequency detuning in the interpretation of the results.

To understand the consequences of the phase coherence results reported above on the transmission of information, we have studied how rate perturbations propagate between two bidirectionally connected neuronal networks as a function of their frequency detuning. To that aim we increased during 200 ms, the rate of the external Poissonian spike train impinging on a subpopulation of 200 long-range excitatory neurons from one network (see sketch from Fig. 8). In those conditions, neurons belonging to that subpopulation fire synchronously (see upper blue raster plot from Fig. 8), increasing the amplitude of the oscillatory eMUA. Figure 9 shows the averaged eMUA signal for both the fast and slow populations at distinct $\tau _{\rm GABA,s}^{d}$. Averaged eMUAs for the interacting populations are displayed at three different situations, one for each column: (A) the unperturbed scenario, (B) when perturbing the fast population and (C) when perturbing the slow population. In Fig. 9A, averages were computed across 200 trials aligning the first maxima of a 1 second time window, and thus resulting in a phase-triggered average. Since the increase in the external rate boosts the firing activity of both populations (see raster plots in Fig. 8), a local maximum of the eMUA signal appears right after the onset of the perturbation (see eMUA time traces in Fig. 8). Therefore, Fig. 9b and c show the first 195 ms of the 200 ms perturbation window in which the eMUA are already lined up, maximum to maximum (phase-triggered average).

Fig. 8

Left The two neuronal networks are represented by circles and the synaptic coupling by arrows. The vertical ticks next to each circle stand for the external Poisson train of spikes, whose mean firing rate is qualitatively plotted with a line at the right of the input label, i.e. $\langle \lambda (t) \rangle$. Top-right Raster plot and LFP for the fast population $\tau _{\rm GABA,f}^{d}=5$ ms). Bottom-right Raster plot for two different behaviors of the slow population $\tau _{\rm GABA,s}^{d}=5$ ms (left) and $\tau _{\rm GABA,s}^{d}=11$ ms (right)] showing distinct levels of spike-to-spike synchrony

Fig. 9

Averaged eMUA time traces over 200 trials for the fast population (blue traces) and the slow population (colored traces) a before applying any perturbation, and during the first 195 ms of the perturbation time interval applied b to the fast population and c to the slow population. Detuning decreases from top ($\tau _{\rm GABA,s}^{d}=11$ ms) to bottom ($\tau _{\rm GABA,s}^{d}=5$ ms). Note that the bottom panels in B and C are the same since there $\tau _{\rm GABA,f}^{d}=\tau _{\rm GABA,s}^{d}=5$ ms

In order to quantify the rate modulation transfer, we compute the linear correlation between the spiking activity of the two populations. The frequency mismatch between the oscillatory firing activity of both populations is captured in Fig. 10a as a decrease in the amplitude of the peaks of the cross-correlation with increasing time lag. The increase in the effective time delay, τ _e , between the fast and the slow network at larger $\tau _{\rm GABA,s}^{d}$ (or equivalently, at larger frequency detunings) is confirmed by the gradual shift of the maximum peak of the cross-correlation away from the zero time lag (in phase condition, vertical dashed line in Fig. 10a). Note that the horizontal distance between two consecutive maxima is approximately the same for all detunings (∼30 ms, corresponding to the gamma frequency peak ∼33 Hz of the faster rhythm as shown in Fig. 3a), although the cross-correlation decreases for larger Δf.

Fig. 10

Averaged cross correlation between the eMUA time trace of the fast population and the slow population over 200 trials a before applying any perturbation, and during the first 195 ms of the perturbation time interval applied b to the fast population and c to the slow population. The vertical dashed line marks the zero time lag

The decrease in the mean of the eMUA signal (colored traces in Fig. 9a) is caused by the increase in the duration of the oscillatory cycle (the number of spikes is constant over a cycle, through all values of $\tau _{\rm GABA,s}^{d}$). During the perturbation interval of the fast population (Fig. 9b), the amplitude of the eMUA oscillatory signals increases significantly and the slow population mimics the time course of the fast. This frequency entrainment is revealed by the eMUA cross-correlation shown in Fig. 10b.

Figure 10b shows that, in contrast with Fig. 10a, the cross correlation between the eMUA signals of both populations is always high during the transient perturbation of the faster rhythm, being basically independent of Δf. Therefore, the faster rhythm is reliably propagated to the receiver. However, the firing activity of the neurons in the receiver population is scarcely affected, as can be seen by comparing the colored circles in Fig. 11b with the horizontal dashed line. As shown in the figure, the number of spikes fired by the excitatory neurons of the receiver population over two cycles of the faster rhythm decays only slightly with increasing $\tau _{\rm GABA,s}^{d}$. This happens because at large intrinsic frequency detunings Δf, intense barrages of excitatory presynaptic action potentials are able to speed up the slower gamma rhythms, although no postsynaptic spikes are further triggered. At small Δf, on the other hand, the enhanced incoming excitatory synaptic current raises the number of postsynaptic spikes. In addition, this strong excitatory drive temporally sets a non-zero phase lag between the two eMUA signals as shown by the highest peak of Fig. 10b.

Fig. 11

Number of spikes of the excitatory neurons from the fast population (blue circles) and the slow population (colored circles) a before applying any perturbation, and during the first 195 ms of the perturbation time interval applied b to the fast population and c to the slow population. Panel a as in Fig. 3b. Note that the cycle (or equivalently, the time period) considered in panel a corresponds to the fast rhythm for the blue circles and to the slow rhythm for the colored circles. On the contrary, in panels b and c, the number of spikes are computed over the fast and the slow rhythm respectively for both the blue and the colored circles. Dashed line in panel b and c corresponds to circles in panel a

In the case in which the perturbation is applied to the slow population (now the emitter), the amplitude of its oscillatory eMUA is increased with respect to the fast population (now the receiver). However, at large detunigs the fast population only experiences a transient enhancement of its spike-to-spike synchrony and cannot tune its rhythm to the slow population (compare bottom and top panels of Fig. 9c). The maximum cross-correlation in this case is also high with respect to the unperturbed case for small detunings, similarly to the situation in which the perturbation acts upon the fast population (Fig. 10b). Now, however, in contrast with the latter case, the cross-correlation between the eMUA signals of both populations decreases with Δf, as shown in Fig. 10c. Therefore, the slower rhythm cannot be reliably propagated to the receiver, and at large detunings the emitter and receiver population lock their rhythms weakly. The number of spikes fired by the excitatory neurons of the fast population (blue circles of Fig. 11c) increases with increasing $\tau _{\rm GABA,s}^{d}$ because the spikes are being added up within periods longer than the faster gamma collective oscillation (since now the slow gamma frequency only describes the dynamics of the emitter). Note that regardless of which population is being directly perturbed, the number of spikes per cycle is kept constant (see blue circles in Fig. 11b and colored circles in Fig. 11c). Nevertheless, in contrast with Fig. 10b, Fig. 10c shows that when the slow population leads the firing activity, a zero time lag is fostered between the two eMUA signals.

When the spiking activity is greater in the slow population (compare blue and colored circles of Fig. 11c), communication at large Δf is impaired, since the rhythms of the emitter and receiver population show a weaker frequency locking than at small Δf, as discussed above. In the former case, intense barrages of spikes of the emitter population occur at slower frequencies than the receiver’s rhythm, and skip the fast cycle. On the contrary, when the spiking activity is dominated by the fast population (compare blue and colored circles of Fig. 11b), synchronous spikes from the emitter population are still able to entrain the receiver population to a sustained faster rhythm at large Δf (see Fig. 10b and top panels in Fig. 9b) since at each cycle, the slow population is being perturbed. These results show that an asymmetry in the efficiency of communication arises due to distinct gamma rhythms and despite a symmetric structural connectivity. Similar results were found by Battaglia et al. (2012) for weak to moderate coupling between neuronal networks in which the control parameter was the probability of establishing a long-range excitatory connection across populations. In the present study, we propose that routing of information can be efficiently adjusted by the extent of frequency locking between two interacting networks. Moreover, for a given interareal coupling, the system can either settle on a leader-laggard configuration or synchronize at zero-lag, taking advantage of the strong sensitiveness of phase coherence to frequency detuning.

4 Discussion

We have discussed a simple connectivity scenario between two neuronal networks, varying the decay time of the GABAergic synapses $\tau _{\rm GABA}^{d}$ in one pool, while keeping it constant in the other. Larger durations of the inhibitory synapses entail a slowing down of the gamma rhythm of the LFP and MUA. At the same time, the number of spikes per cycle is maintained despite the fact that the period of such cycle increases with $\tau _{\rm GABA}^{d}$. The effective connectivity across cell assemblies might differ from the structural implemented connectivity as $\tau _{\rm GABA}^{d}$ increases. Specifically, the number of presynaptic spikes arriving to a given network during one period of its oscillatory eMUA (or LFP) depends on the rhythm of the afferent eMUA and thus, on the frequency detuning between both signals.

The incoming spikes might trigger a suprathreshold response, enlarging the amplitude of the local eMUA, if they arrive at an optimal phase of high excitability. Otherwise, they will only produce a phase shift of the postsynaptic LFP. Therefore, the LFP-LFP phase coherence depends only moderately on the degree of frequency detuning since those signals influence each other continuously. On the other hand the eMUA-eMUA phase coherence decays rapidly with increasing frequency detuning, since a frequency mismatch implies changes in time of the phase difference which governs the extent of the spiking response. Moreover, close beta/gamma frequency rhythms approach a zero-lag synchronization between them despite a small non-zero axonal delay, while large detunings involve synchronization at a non-zero phase lag. In the latter case, the slower oscillation is then enslaved to the faster oscillation following a leader-laggard configuration.

It has been recently shown (Roberts et al. 2013) that LFP signals recorded simultaneously in macaque areas V1 and V2 speed up their gamma rhythm in response to a grating stimulus of increasing luminance contrast. In addition, phase coherence between V1 and V2 is always maximal at the gamma frequency peak of the LFP power spectrum, following an identical shift towards higher frequencies at greater contrasts. The authors obtain similar results with a computational model of unidirectionally coupled networks driven by a noisy injected current of constant mean, I ₀. Changes in the gamma frequency peak correspond to different values of I ₀, always carried out in the presynaptic neuronal population which entrains the postsynaptic neuronal population to its rhythm.

In contrast, we have focused on a bidirectional coupling scenario between modeled neuronal networks, imposing an intrinsic frequency detuning independent of the structural connectivity and further adjusted by the interaction between areas. When the perturbation is applied just to a subpopulation of excitatory neurons of one of the neuronal populations, the increase in the firing rate is higher on that network –the emitter– than in the receiver (compare Fig. 11a with b and c), thus making the effective connectivity asymmetric (stronger in the feedforward direction from the perturbed to the unperturbed area). In our model, similar to the results in Roberts et al. (2013), the receiver population could be especially entrained to the rhythm of the emitter population, thus achieving frequency locking, when the emitter corresponds to the fast population. Figures 9b and 10b show that the enhancement of the spike-to-spike synchrony of the fast population is able to entrain the slow oscillation into its own rhythmicity, something that happens only weakly in the asynchronous irregular behavior of the interacting populations discussed in Section 3.2 (Figs. 9a and 10a). The relative response of the two populations when either the feedforward or feedback projections are strengthened, relies on the mismatch of rhythms.

The mechanisms behind the combination of sensory information processing with attention, memory and other cognitive tasks requires coordinated communication between different cortical areas. Our model shows a graded effective connectivity across networks that is endogenous to the system. We do not claim that our one-parameter control of the mutual influence between populations underlies effective cortical interactions, but consider it instead as a simple procedure to dissect the underpinnings of the communication through coherence hypothesis. The phase relationship achieved by the two LFP signals is meant to regulate the effectiveness of communication (Fries 2005). In particular, an unreliable phase difference will always lead to a failure in communication, in what can be called non-communication through non-coherence (Bosman et al. 2012). We have shown that successful transmission of a rhythmic pattern between two populations in the two directions of coupling (reciprocal communication) in the presence of short delays relative to the oscillatory period, requires zero-lag synchronization occurring only for small frequency detuning. Non zero-lag synchronization caused by large frequency detunings, allows for a locking of gamma frequencies, which is particularly significant in the entrainment of the slow to the fast rhythm. In those conditions, the maximum firing activity of the slow neuronal population (laggard), locked to the troughs of its LFP, does not arrive consistently at every recurrence cycle of the fast network (leader) and is unable to drive these neurons above the spiking threshold, thus hindering backward communication.

In the present study, a modulation of the frequency mismatch, instead of a direct control of the phase difference between two signals, appears as a sensitive mechanism to route the effectiveness of information transmission. In summary, we observe that CTC mechanisms can only hold between two mutually coupled similar neuronal networks undergoing zero-lag synchronization between LFP-LFP and eMUA-eMUA. On the other hand, for different gamma rhythms of the two populations, phase coherence is only achieved between the LFP signals (or to a smaller degree between the eMUA signals) at non-zero phase-lag. Both populations maximally lock their rhythms when the perturbation is strong enough and boosts the firing activity of the fast rhythm. Importantly, high amplitude slow signals arriving at faster receiver populations are able to reduce the relative time lag. Therefore, the excitatory synaptic coupling displays a variety of effects, which depend on both the frequency detuning between pre- and postsynaptic local oscillations and the relative firing activity of both interacting populations: faster dominant gamma rhythms trigger frequency locking regimes, while slower dominant gamma rhythms cause in-phase transitions.

In conclusion, frequency locking or entrainment, as observed by Roberts et al. (2013) and under some conditions of our model, might lead to an efficient communication between areas. However, this observation hardly solves the critical question of how flexible routing of information arises in the brain. Even if locking would support the maintenance of communication, it is clear that previous interactions, and therefore communication, is necessary to establish the locking itself between the areas. The fundamental question seems to be what mechanisms decide which one of several competing areas manages to lock to a destination area. While several possibilities, including selective feedback and neuromodulatory systems, can lead to symmetry-breaking between competing areas, more research will be needed in this direction. A second caveat is that coherence analysis from LFPs might be difficult to interpret in terms of communication, since this quantifier captures synaptic currents that might not contribute to efficient spike generation.

We believe that the modeling and theoretical analysis of constrains of CTC and other hypothesis can help in determining their feasibility and experimental test. Future work will be devoted to assess the constrains that arise when multiple phase relations need to be met simultaneously across several areas.