1 Introduction

The most important factor influencing neural spike generation is the presence of ion channels embedded in the cell membrane. These channels enable influx and efflux of ions, thereby changing the membrane potential and leading to spike generation. Investigations have shown that human neocortical neurons employ at least twelve distinct ionic currents (McCormick 2004). The interplay between these currents produces complex spiking phenomena; though the diverse variety of spiking neurons can be classified into four main groups (Gray and McCormick 1996). Regular neurons begin firing at a high rate with respect to time before decreasing to a lower steady rate of firing, which mimics neuronal adaptation. Fast neurons maintain a rapid firing rate (> 400 Hz) with no adaptation. Intrinsic bursting neurons fire a burst of more than two spikes, briefly pause then resume a steady spike frequency. Continuous bursting neurons produce periodic bursts of spikes—spiking clusters occurring at periodic intervals separated by periods of quiescence.

The four main spiking classes can be observed in neurons due to membrane potential oscillations generated from different combinations of ionic currents; in addition to the main dynamics mentioned above, neuromodulatory effects from cellular signalling can also lead to changes in firing patterns. It is important to distinguish the neuronal bursting modeled here from bursting behavior that arises from network interactions which involve interconnected neurons interacting through excitatory and inhibitory connections; the bursting in our present model arises solely from individual neurons as there are no networks involved. Subthreshold oscillations, which are small fluctuations in the membrane potential that do not generate spikes, and chaotic firing are also observed in neuronal physiology (Izhikevich 2007).

Simple mathematical models of neuronal dynamics aid understanding and are computationally tractable for exploring large ensembles of dynamically linked neurons (Izhikevich 2007; Robinson and Kim 2012). Ultimately, we aim to understand neurophysiology on a large-scale level, starting from individual neurons, so computationally efficient neuron models that are based on biophysics are the most appropriate for simulations involving large networks of neurons (Izhikevich 2007; Robinson et al. 2008).

Numerous neuronal models for bursting have been developed, with earlier work focusing on idealized mathematical representations (Plant and Kim 1976; Hindmarsh and Rose 1984). Later authors then began to increase the realism of single-cell bursting neurons with the addition of ionic currents and calcium dynamics in several different organisms (Canavier et al. 1991; Bertram 1993; Guckenheimer et al. 1993; Traub et al. 1991; Wang et al. 1991). Recent modeling work have emphasized modeling bursting in specific organ systems as more relevant biological detail has emerged from ongoing experimental studies (Xu and Clancy 2008; Sherman 1996; Butera et al. 1999). In the current work we have chosen to focus on a minimal bursting model of three dimensions. Other three dimensional bursting models have been analyzed previously in different biological contexts such as glucose mediated signal transduction in β-cells (Sherman 1996; Bertram et al. 1995; Coombes and Bressloff 2005), a minimal model of pre-Bötzinger pacemaker neurons (Butera et al. 1999; Coombes and Bressloff 2005) and idealized thalamic neurons (Hindmarsh and Rose 1984). Our model differs from previous three dimensional bursting models in that we focus on preserving biophysical dynamics in the fast variables. Furthermore, to maintain simplicity we use a slow variable that is a representation of the negative feedback common to all three dimensional bursting models, thereby offering robust generation of diverse bursting rhythms across different parameter spaces. This serves the purpose of analytical tractability especially for those interested in using the model in neural field theory (Robinson et al. 2008; Robinson and Kim 2012).

Models based on ion channel dynamics nominally involve N+ and K+ channels for fast modulation of spiking dynamics, coupled to negative feedback operating on much slower timescales (Ermentrout 1998a, b; Rinzel and Ermentrout 1998). One of the earliest models (Hindmarsh and Rose 1984) used three coupled differential equations to simulate bursting; these equations were formulated mainly to investigate the mathematical properties of bursting dynamics and thus did not focus on providing biophysical units. Wilson developed a more realistic model of neuronal bursting (Wilson 1999a) by retaining ion channel dynamics, though the channels were kept to just four to retain the simplicity necessary for for in-depth analysis of its dynamics.

In this paper we seek to retain the elegance and simplicity of Rose and Hindmarsh’s three-variable model (Hindmarsh and Rose 1984), while incorporating the fast ion channel dynamics of Wilson’s model. We combine the fast spiking dynamics of Wilson’s model (Wilson 1999a) with Rose and Hindmarsh’s equation for the slow negative feedback dynamics. This results in our three-variable model, which explicitly separates fast and slow channel dynamics. The current model represents a compromise between biophysical realism and computational simplicity as it lies on a continuum between the biophysical complexity captured by full Hodgkin-Huxley models and the idealized neuronal dynamics of leaky integrate-and-fire models.

We show that our resulting model reproduces bifurcations and numerous experimentally observed neuronal behaviors (Izhikevich 2007). We explore the effect of the slow variable dynamics and changes to an external input current. Both are amenable to experimental control and important for inducing bursting. Furthermore, we emphasize the advantages our model provides over the widely studied integrate and fire model (Izhikevich 2007), which requires an artificial resetting mechanism for spikes back to equilibrium values. In contrast, our model is capable of generating physiologically realistic spike profiles from the interactions described by our three ion channel equations and is of a form that can be incorporated in a straightforward manner into neural field theory (Robinson and Kim 2012).

The current study into a single neuron model will allow further exploration and deeper insight into various clinical disorders. Bursting neurons play an integral role in normal brain physiology and have been implicated in sleep (Lu et al. 2006; Steriade et al. 2001), epilepsy (Timofeev et al. 1998; Timofeev and Steriade 2004) and attention-deficit hyperactive disorder (Rowe et al. 2005). Understanding our bursting neuron’s dynamics will also lead to an appropriate averaging of its fast channel dynamics for use in fast-slow analysis (Coombes and Bressloff 2005; Best et al. 2005) and neural field theory (Robinson and Kim 2012; Robinson et al. 2008).

The model is described in Section 2, followed by examplar firing patterns demonstrable from changes in model parameters in Section 3, these include a dozen commonly occurring neuronal firing behaviors. We present detailed linear stability analysis of our three dimensional model and compare with results from numerical simulations in Section 4. Stability condition changes are used to explore qualitative changes in firing patterns. Bifurcation scenarios are discussed and phase diagrams are used to visualize the boundaries. We conclude in Section 5 with a brief discussion of our main findings and possible future applications in large scale simulations.

2 Three-variable neural model

We propose a three variable model of neuronal bursting, which is a hybrid of the Rose–Hindmarsh (Hindmarsh and Rose 1984) and (Wilson 1999a) models. Rose and Hindmarsh proposed a three-equation model neuron that was extremely simple and hence tractable for analysis, but did not adhere to Ohm’s law and was not formulated in standard units. While Wilson’s model ameliorated some of these shortcomings it was still expressed in terms of nonstandard units; furthermore, it required a fourth equation, hence rendering analysis less tractable. Our model retains the simplicity of three equations while still adhering to essential biophysical constraints such as Ohm’s law for our fast variables V and R. Our slow variable H is more abstract and is not strictly in the form of Hodgkin-Huxley channel dynamics in order to maintain the model’s simplicity and is a qualitative representation of bursting properties. As bursting is a complex phenomena involving multiple ionic currents, biochemical messenger systems and dendritic activity (Dowling 2001) we opted for a simplifying abstraction of these processes which follows previous authors (Hindmarsh and Rose 1984). Despite its simplicity, our model is capable of reproducing diverse firing patterns which have been observed empirically Section 3.

2.1 Equations

The general rate of change in membrane potential V for a neuron can be described as

$$ C\frac{dV}{dt}=-I_{Na}-I_K+I_{leak}+I_{ext}, $$
(1)

where C is capacitance per unit area, t is time, I ext is an externally applied current per unit area, I leak is a leakage current per unit area and I Na and I K are the K + and Na + currents per unit area respectively (Hodgkin and Huxley 1952). We assume each current obeys Ohm’s law

$$ I_j=g_j(V)(V-V_j) $$
(2)

where \(g_j(V)\) is the conductivity per unit area and V j is the equilibrium potential of the jth ion. Hodgkin and Huxley (1952) found that \(g_j(V)\) could be approximated by relatively simple functions of V . Mammalian neocortical neurons exhibit an additional transient potassium current that allows firing to occur at very low spike rates when I ext is small. This led to a simple two-equation model first proposed by Connor et al. (1977) and later simplified by Hindmarsh and Rose (1984), from which we take an expression below for the slow variable. We use the fast variables from Wilson’s model (Wilson 1999a, b) and add the dynamics of the aforementioned slow variable, as discussed below. Our model equations for the fast dynamics are (Robinson et al. 2008; Wilson 1999a, b)

$$\begin{array}{@{}rcl@{}} C\frac{dV}{dt}&=&-g(V)(V-V_{Na})-g_RR(V-V_K)\\ &&-H+I_{ext}, \end{array} $$
(3)
$$frac{dR}{dt}=-\frac{1}{\tau_R}[R-R_{\infty}(V)], $$
(4)
$$ g(V)=\nu_0+\nu_1V+\nu_2V^2, $$
(5)
$$ R_{\infty}(V)=0.79+r_1V+r_2(V-V_3)^2 $$
(6)
$$ =0.17+r_2(V-V_4)^2. $$
(7)

The values of the parameters and coefficients C, V 0−V 4, V H , τ R , τ H , ν 0, ν 1, ν 2, r 1, and r 2 are given in Table 1. Equations (3)–(7) have been discussed in detail elsewhere (Wilson 1999a); here we offer a brief summary of their underlying mechanisms. The first equation describes changes in the membrane potential V , that arise from interactions of ionic currents, the capacitance per unit area C and the externally applied current per unit area I ext . V Na is the Na + reversal potential, V K the K + reversal potential and g r is the membrane conductance for R, while g(V) represents the Na + activation function. The second equation describes activation of K + channels, \(R_{\infty }(V)\) is the equilibrium state, and τ R is the time constant for relaxation of R.

Table 1 Nominal values of model parameters, adapted from Hindmarsh and Rose (1984), Robinson et al. (2008), Wilson (1999a, b)
Full size table

As previously discussed (Rinzel 1985), there are several approximations inherent in Eqs. (3) and (4). The Na + activation instantaneously reaches its equilibrium value g(V), there is no inactivation of the Na + channel, and the time constant τ R is independent of V . Finally, the leakage current has been absorbed into the polynomial representations of g(V) and R ∞(V). Furthermore, both g(V) and R ∞(V) are approximated as quadratic functions. These simplifying assumptions are physiologically plausible, as was previously justified in detail (Wilson 1999b). In the case of g(V) a quadratic function adequately captures the accelerating nonlinearity of voltage-dependent Na + channel activation. We use the same constants as in Wilson (1999b) which were chosen to provide the best fit of the dV/dt isocline in Rinzel’s (1985) approximation of the Hodgkin–Huxley equations (Hodgkin and Huxley 1952). R’s quadratic form was initially introduced by Hindmarsh and Rose (1984) and justified this approximation in Rose and Hindmarsh (1989).

We seek to augment Eqs. (3)–(7) to obtain a minimal set of equations, still capable of diverse dynamics, which are amenable to analysis in network models. Following Hindmarsh and Rose (1984) we add an adaptation current H of form Eq. (8). The H current is a slow, outward current that hyperpolarizes the neuron on a long timescale τ H , with

$$ \frac{dH}{dt}=-\frac{1}{\tau_H}[H-g_H(V-V_h)]. $$
(8)

Where g g is the conductance and V h is the reversal potential. See Table 1 for values.

2.2 Parameters

Typical parameter values in Eqs. (3)–(8) are listed in Table 1. In our analysis of examples below most of the model parameters are kept constant at these values, which are mostly equal to those in Wilson (1999a) because we seek to retain as much of the original dynamics as possible, with a nominal example shown in Fig. 1. The exceptions are C and τ H , which are increased by factors of 3 and 2, while τ R is decreased by a factor of 10. This is not surprising as some parameters need adjustment with the new interactions introduced by our model in the form of Eq. (8). The model is still capable of reproducing spike forms over a wide range of parameter regions (see Section 3).

Fig. 1
figure 1

Example firing behavior produced by the model using nominal parameters from Table 1 with I ext = 0.35 A m−2

Full size image

3 Model properties and example behaviors

In this section we begin with a brief description of major firing patterns found in neurons and reproducible by the model. This is followed by exploring frequently seen dynamical properties exhibited by our model. We categorize firing phenomena into three broad classes: spiking, bursting, and chaotic. Further subdivisions are possible (Wilson 1999a; Izhikevich 2007), fast spiking neurons exhibiting rapid firing rates up to a few hundred hertz, while regular spiking neurons fire only at a much lower frequency (for example 10–20 Hz). Furthermore small rounded peaks of depolarizing afterpotentials were evident in parameter regions of regular spiking neurons. Bursting was identified from changes in the interspike intervals; in bursting neurons at least two distinctly different interspike intervals could be identified, with one significantly greater than the other, while this was not evident in regular spiking and fast spiking neurons. Subthreshold oscillations were identified based on much lower amplitudes compared to conventional spikes. Examples of these firing behaviors are shown in Fig. 2 and we discuss their relevance in normal physiology in Section 4.

Fig. 2
figure 2

Time series of neuronal dynamics are shown in each frame. On the vertical axis I is in A m−2 and V is in mV. a tonic spiking b phasic spiking c phasic bursting d tonic bursting e mixed mode f frequency adaptation g subthreshold oscillations h rebound spike i rebound burst j depolarizing after-potential k spike latency l hyperpolarization spiking. The examples are reproduced through changes in our model parameters as in Table 2. See text for details of individual frames

Full size image

3.1 Examplar neuronal dynamics

We have reproduced twelve spiking patterns drawn from Izhikevich’s original set of twenty fundamental neuronal behaviors (Izhikevich 2007). We present a selection of dynamics relevant to biological neurons reproduced from our model. Our primary goal is to retain the essence of as many constants from the parent models as far as possible, so the repertoire we reproduce does not include the complete set of behaviors that could be displayed if all parameters were treated as completely free. Presented here are the firing patterns, with the typical parameters for each listed in Table 2. The rest of this subsection refers to Fig. 2 unless otherwise noted.

Table 2 Examplar model parameters that yield 12 fundamental neural spiking patterns as described by Izhikevich (2007)
Full size table
  1. (a)

    Tonic Spiking

    The most basic property of any neuron is the capacity to spike. In Fig. 2a we have changed g H showing that different types of dynamics are possible by only changing two control parameters. In Fig. 2a the spike rate is 10 Hz and shows regularly spaced spikes.

  2. (b)

    Phasic Spiking

    We show phasic spiking Fig. 2b, on which a single spike is produced before spiking is terminated. Note that only g H and I ext are changed from example (a). Furthermore, the phasic spike exhibits a period of latency from the onset of I ext to the actual spike.

  3. (c)

    Phasic Bursting

    A variation on the idea of phasic spiking is phasic bursting, in Fig. 2c we display the onset of a single burst before returning to quiescence. Phasic bursting has been experimentally observed in numerous locations such as nuclei of the hypothalamus and has been implicated in control of circadian rhythms (Andrew and Dudek 1984). In Fig. 2c a phasic burst consisting of six spikes with consecutively decreasing height are terminated by a depolarizing after-potential.

  4. (d)

    Tonic Bursting

    Tonic bursting exhibits continuous alternation between bursts of rapid spikes and long intervals of quiescence (Izhikevich 2007). In Fig. 2d the spike train begins with a large, transient burst followed by an interval of quiescence before following a regular pattern of bursts, each containing five spikes followed by a depolarizing after-potential. Bursting plays a significant role in many neuronal networks (Dowling 2001) and our later analysis shows that tonic bursting manifests itself in a significant portion of our parameter space. There we observe bursting structures that range in complexity as the number of spikes found in each burst varies.

  5. (e)

    Mixed Mode

    This type of firing involves the simultaneous firing of a burst and tonic spiking (Izhikevich 2007). [Note that we follow Izhikevich on using the term ‘mixed-mode’ in a different sense from ‘mixed-mode oscillations’ (MMOs) where high frequency oscillations of small amplitude alternate with low frequency oscillations of large amplitude (Desroches et al. 2012; Iglesias et al. 2011). These latter MMOs do not appear to exist in our model]. In Fig. 2e the spike train begins with a transient burst of four spikes before regular spiking. In vivo such neurons are recognized as intrinsically bursting neurons that generate an initial burst before switching to a tonic spike train (Dowling 2001). Such behavior indicates the transition from spiking to bursting is occurring in time. With small changes in our parameters, tonic bursting and spiking are realized.

  6. (f)

    Frequency Adaptation

    Decrease of spiking frequency for a given I ext is termed frequency adaptation (Dowling 2001). It is a prominent feature of regular spiking cortical neurons (Connors and Gutnick 1990). Frequency adaptation is an important phenomena and ubiquitous among many physiological processes; it has been argued that they play an essential role in filtering information from background noise (Benda et al. 2005). In Fig. 2f a rapid train of spikes is shown to quickly adapt to a constant I ext input. The interspike intervals very rapidly increase to a constant equilibrium value.

  7. (g)

    Subthreshold Oscillations

    Subthreshold oscillations are fluctuations in the membrane potential from postsynaptic potentials that are not strong enough to trigger an action potential. It has been hypothesized that subthreshold oscillations, characterized by their low amplitude, may contribute to synchrony (Lampl and Yarom 1997) and targeted communication among neurons (Izhikevich et al. 2003). In our example there is a rapid subthreshold oscillation. Subthreshold oscillations can arise from the interplay of the fast and slow current systems or changes in the stability of a fixed point in a dynamical system as parameters are varied resulting in Andronov-Hopf bifurcations (Izhikevich 2007). We analyze the fixed points of our model in Section 4. At onset in Fig. 2g there is shown a close-up of subthreshold oscillations produced by a constant input that is just below firing threshold.

  8. (h)

    Rebound Spike

    Rebound spikes are action potentials that arise when a negative I ext is applied and when returned to zero, transient spikes occur. Post-inhibitory rebound spiking is characteristic of several neuron populations in the thalamus and is crucial for sustaining central pattern generation (Ascoli et al. 2010). In Fig. 2h a brief hyperpolarizing I ext current is applied and after the end of the pulse a rebound spike is seen.

  9. (i)

    Rebound Burst

    Rebound bursts are similar to rebound spikes, except that on cessation of the hyperpolarizing pulse, a burst is generated instead of single spikes (Izhikevich et al. 2003). In our model a rebound burst is induced by a powerful inhibitory input I ext . In Fig. 2i a rebound burst of three spikes is seen after a hyperpolarizing pulse of 0.3 s. Rebound bursting has been seen in thalamic rhythm generation and modulation of thalamocortical relay cells (Grenier et al. 1998).

  10. (j)

    Depolarizing After-Potential

    Depolarizing afterpotentials occur when a small rounded ‘hill’ of depolarization follows a spike (Izhikevich et al. 2003). An example is shown in Fig. 2j: just before 0.3 s the long burst terminates and is followed by a small, round depolarizing hill, which does not reach the full height of a spike and is characterized by a rounded top which is more clearly shown in the inset.

    Depolarizing afterpotentials (DAP) were commonly observed in both Wilson’s model and the Rose–Hindmarsh bursting model; the DAPs in our hybrid model show similar DAPs to both parent models.

  11. (k)

    Spike Latency

    Spike latency occurs when there is a long delay to initiation of the first spike after turning on I ext (Izhikevich 2007). This is indicative of a slow depolarization of the cell, hence the delay before the spiking threshold is reached. Spike latency has already been displayed in (b). In Fig. 2k we present a latency that is greatly prolonged to highlight the variability in spike latencies observed in our model under suitable choice of parameters. Spike latency is a putative method of neural coding that increases information conveyed by neuronal spiking (Chase and Young 2007).

  12. (l)

    Spiking during Hyperpolarization

    Figure 2l presents a neural behavior not identified in Izhikevich’s original set of basic neuronal properties I ext (Izhikevich 2007). Initially, the current is set to I ext = A mI −2, despite this the model is capable of spiking. When a negative I ext = −0.05 A m−2 is applied, the spiking frequency is dramatically reduced with concomitant increase of the interspike interval, but sparse spiking still occurs. When the negative current is returned to zero, the previously rapid constitutive spiking is restored. If a more negative hyperpolarizing current is introduced then complete cessation of spiking occurs. Biophysically this example corresponds to neurons capable of initiating firing in the absence of an excitatory input current.

3.2 Type I and II excitability

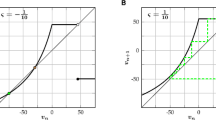
Hodgkin injected current into various neurons and identified two major classes of firing (Hodgkin 1948). Class 1 excitability is distinguished by action potentials with firing frequencies that rise smoothly from zero above a threshold as shown in Fig. 3a. This allows small continuous changes in the firing frequency as the input current I ext is slowly varied. In contrast, Fig. 3b depicts Class 2 excitability, for which the frequency of spiking jumps discontinuously to a nonzero frequency at the threshold I ext . In our current work switching between type I and II excitability is accomplished by varying the parameter g H as first shown in (Golomb et al. 2007). The two different classes of firing lead to different computational properties, for instance Class 1 neurons are capable of smoothly encoding inputs into output frequency while Class 2 neurons cannot, due to their different frequency responses to changes in I ext . In Fig. 3 frequency is calculated by simulating at each current for 10 s and averaging the interspike intervals in the last second. This is then converted to a frequency value by T ave = 1/f where T ave is the average interspike interval found by simulation.

Fig. 3
figure 3

Two types of excitability found in the model. The parameter values are as shown in Table 1 unless specifically mentioned: a Type I: C F m−2, τ R = 0.0056 s, g H = 0 A m−2 V−1 b type II: g = 15 A m−2 V−1

Full size image

3.3 Hysteresis

Hysteresis occurs when there is coexistence of resting and spiking states for a given set of parameters and the behavior that occurs depends on the system’s past history. This can be revealed by increasing I ext past some bifurcation value, causing a transition from resting to spiking. I ext is returned to its initial value but the neuron continues spiking. This implies resting → spiking and spiking → resting transitions occur at different I ext values (Izhikevich 2007).

We demonstrate the existence of hysteresis in our model as shown in Fig. 4. Choosing g R = 0, g H = 0 and keeping all other parameters as in Table 1, there is no spiking at our our initial I ext . With an increase in current, spiking is initiated and continues when this current is lowered to the initial value that did not initiate spiking. Ultimately further lowering I ext returns the system to its initial quiescent state. The choice of parameters regions is important in exhibiting this hysteresis. Parameters for which multiple equilibrium points exist are necessary, but not sufficient (Alligood et al. 1997). This motivates us to analyze the model’s fixed points and their stability in Section 4.

Fig. 4
figure 4

Hysteresis in our bursting neuron with g R = 260 A m−2 V−1 and g H = 0 A m−2 V−1. I ext has units of A m−2. All other parameter values are the same as in Table 1

Full size image

4 Analysis of the model

To determine the stability of each fixed point we begin by finding the number of fixed points within the parameter space we have chosen to explore in our model. The stability of each fixed point is then determined using linear stability analyses. Phase diagrams delineating boundaries between different spiking patterns are shown to correlate with linear instability of fixed points.

4.1 Number of fixed points

We determine the boundaries between changes in the number of fixed points for our phase diagram. First we set the rates of change for our three differential Eqs. (3), (4), and (8) to zero to obtain the correspondng nullclines, and then, substituting Eqs. (4) and (8) into Eq. (3), we obtain the characteristic equation f(V) = 0, with

$$\begin{array}{@{}rcl@{}} f(V)=\big(\nu_0+\nu_1V+\nu_2V^2\big)(V-V_{Na})\\ &&+g_R\big[0.79+r_1V+r_2(V-V_3)^2\big]\\ &&(V-V_K)+g_H(V-V_h)-I_{ext}. \end{array} $$
(9)

Equation (9) is a cubic polynomial in V with real coefficients so it always has either one or three real solutions. We vary g H and g R in our model to find the parameter regions that yield three solutions for Eq. (9). This is done analytically by studying the discriminant Δ of the characteristic equation (Dickenstein and Emiris 2005), with

$$ \Delta=18abcd-4b^3d+b^2c^2-4ac^3-27a^2d^2, $$
(10)
$$ a=-(\nu^2+r_2g_R), $$
(11)
$$ b=\nu_1V_{Na}-\nu_1-r_1g_R+2r_2V_3g_R, $$
(12)
$$\begin{array}{@{}rcl@{}} c& = &-(\nu_0-\nu_1V_{Na}+0.79g_R+r_2V_3^2g_R-r_1V_Kg_R \\ && \quad\quad +2r_2V_KV_3g_R+g_H), \end{array} $$
(13)
$$ d=\nu_0V_{Na}+I_{ext}+0.79V_Kg_R+r_2V_KV_3^2g_R+g_HV_h, $$
(14)

where a, b, c and d are the coefficients of the cubic polynomial f(V) = 0. If Δ > 0 there are three distinct real roots; if Δ < 0 there exists one real root and two complex conjugate roots with nonzero imaginary parts; if Δ = 0 there are either 2 equal and 1 distinct real roots or 3 equal real roots. In Fig. 5a we show the boundaries between areas of the parameter space containing one or three equilibrium point solutions for I ext = 1.0 A m−2. In Fig. 5b it is seen that the number of fixed points does not correlate with spiking behavior; rather the coexistence of multiple fixed points is a necessary, but not sufficient, condition for hysteresis. We show below that the stability of fixed points determines the transition between quiescence and firing.

Fig. 5
figure 5

Both plots show a region of parameter space for g R from 250 to 450 A m−2 V−1 and g H from 0 to 100 A m−2 V−1 with I ext A m−2. a Plot showing the boundary between areas containing different number of equilibrium points. The smaller bounded area marked with an X contains three equilibrium points. The larger area contains parameter space that has only one equilibrium point. b Plot showing the stability of each fixed point which is marked by its color, red=unstable blue=stable. There is a region of the parameter space that folds back onto itself and represents the existence of mutliple fixed points

Full size image

4.2 Linear stability analysis

We now analyze the stability of each fixed point via its Jacobian matrix. The Jacobian matrix Eq. (15) is represented by linearization of the nonlinear Eqs. (3), (4), and (8), evaluated at fixed points V *. Standard linear stability theory (Alligood et al. 1997) allows us to identify the stability at each fixed point through the Jacobian matrix

$$ \left(\begin{array}{ccc} F(V^*)&-\frac{1}{C}\big[g_R\big\{V^*-V_{2}\big\}\big]&-\frac{1}{C}\\ \frac{1}{t_R}[r_1+r_2\{2V^*-2V^{*3}\}]&-\frac{1}{t_R}&0\\ \frac{g_H}{t_H}&0&-\frac{1}{t_H} \end{array}\right), $$
(15)

with

$$ F(V^*)=-\frac{1}{C}\big[\nu_0+2\nu_1V^*+3\nu_2V^{*2}+g_RR\big]. $$
(16)

At each V * the Jacobian matrix Eq. (15) has eigenvalues that determine the equilibrium point’s stability (Alligood et al. 1997). If all eigenvalues at an equilibrium point have negative real part, V is stable and attracts nearby orbits, thus corresponding to the resting state. Otherwise the fixed point is unstable and leads to oscillations of the membrane potential V in the form of subthreshold oscillations or firing. However, in regions of Fig. 5b where three fixed points are found, only one of the fixed points exists as a stable equilibrium point while the other two are unstable.

In the study of dynamical systems, if there is a saddle point with emanating separatrixes that divide the phase plane into two regions, with one containing a stable fixed point while a limit cycle exists in the other, then hysteresis is observed (Hindmarsh and Rose 1984). Furthermore, the fold structure seen in Fig. 5b is indicative of such a saddle-node bifurcation, this type of bifurcation occurs when two fixed points collide and annihilate each other as parameters are varied (Alligood et al. 1997). Here we show the fixed points and their stabilities for I ext = 1.0 A m−2. For other values of I ext the fold structure remains but becomes more pronounced as I ext is increased from 0. Note the concordance between Fig. 5a and b, which are in agreement regarding the areas corresponding to the existence of one or three fixed points, despite these frames being computed using different methods.

4.3 Phase diagrams and transition to chaos

A phase diagram shows regions in parameter space that exhibit different types of dynamics. The phase diagrams in Fig. 6 show distinct areas of different neuronal firing. Dark blue represents quiescence; as the color increases towards red the dynamics is changing from quiescence → spiking → bursting → chaos. The color is assigned based on the number of distinct interspike intervals for each parameter’s time series, up to a maximum of 20. Here we have chosen not to distinguish between fast and regular spiking as we have already shown the model is capable of diverse spiking phenomena. Instead, to emphasize the transition to chaos within the chosen parameter space, we have highlighted the increase in distinct ISI values as the chaotic region is approached.

When g H is small, the coupling strength of the slow variable is extremely weak, so there is a separation of the fast variables V and R from H. The model essentially behaves as a two-dimensional system and displays rapid spiking behavior with increases in g H , leading to onset of bursting. As I ext increases, the g H threshold necessary for onset of bursting also increases. However, for high enough g R , there is no initial fast spiking behavior preceding bursting, due to the much stronger damping effect of g R . A further phenomenon observed in Fig. 6 is the emergence of a quiescent zone between areas of spiking and sudden onset of very strong bursting; this is most easily observed for I ext > 0.8 A m−2 at the upper left quadrant in between the regions corresponding to two types of spiking behavior.

Fig. 6
figure 6

Phase diagrams for a I ext = 0, b I ext = 0.2, c I ext =0.4, d I ext = 0.6, e = 0.8 and f I ext = 1.0 A m−2 as labeled. Each phase diagram plots g R from 250 to 450 A m−2 V−1 vs. g H from 0 to 100 A m−2 V−1. At individual points of each phase diagram a spike train simulation was run and the number of distinct interspike intervals was counted. The colors denote the number of ISIs that were counted and increase from dark blue (resting) to red (20 distinct ISIs) as represented by the color bar

Full size image

Chaos is characterized by the presence of at least one positive Lyapunov exponent (Alligood et al. 1997). The Lyapunov exponents measure the average exponential rates of divergence or convergence of nearby orbits in phase space. To calculate our three Lyapunov exponents λ i for i = 1, 2, 3 the evolution of an infinitesimal three-dimensional sphere of starting conditions is monitored. The small sphere is centered on the starting point of a trajectory. Changes in the axes of the sphere describe the stretching and shrinking in each dimension. Computationally, the average growth rate of each orthogonal axis of the ellipse is then used to define the corresponding Lyapunov exponent:

$$ \lambda_i=\lim\limits_{t\rightarrow\infty}\frac{1}{t}\rm{ln}\big(f_i'\big), $$
(17)

where \(f_i'\) are the three differential equations of our model for \(i=V,R,H\). We compute the Lyapunov exponents by following the change in axes of our initial unit sphere under the action of our differential equations’ Jacobian. We orthonormalize the basis spanning the ellipsoid using the Gram-Schmidt process (Alligood et al. 1997) and the average logarithmic change in each axis over a sufficiently large number of time-steps is used to estimate the respective Lyapunov exponents. For full details see Alligood et al. (1997).

Fig. 7
figure 7

Top plot shows one second of a chaotic spike train. Bottom plot shows corresponding trajectory traced out in the phase space of variables V, R, and H. Simulation was run for 10 s. Values are as shown in Table 1 with the exceptions of g R = 225 A m−2 V−1, g H = 45 A m−2 V−1 and I ext = 0.8 A m−2

Full size image

The most important is the maximal Lyapunov exponent (MLE), which determines the stability of the system for a given set of parameters. If it is positive then this indicates arbitrarily close starting conditions for the system will diverge and result in chaotic behaviour as shown in Fig. 7. Otherwise, if the maximal Lyapunov exponent is negative then the system is stable and will tend towards periodic behavior such as a limit cycle or a stable fixed point.

Most of the chaotic regions in Fig. 6 exist as dark brown points most prominent for I ext = 1 A m−2 in the region around g R = 350 A m−2 V−1 and g H = 40 A m−2 V−1. This signifies regions that contain 20 or greater distinct ISI. This is a strong indication of non-repetitive (e.g. chaotic) behavior. It is important to stress the color gradient in Fig. 6 is based on measurement of distinct ISIs observed in each spike train simulation. To formally test whether these regions are truly chaotic it is necessary to calculate their Lyapunov exponents. We thus calculate the Lyapunov exponents for a slice of the phase diagram keeping g H constant at 262 A m−2 V−1 and varying g H to show the complex changes in stability. In Fig. 8 the maximal Lyapunov exponent is plotted. The exponent crosses zero for multiple values of g H and becomes positive in chaotic regions, there are short intervening windows of negative MLE values representing windows of periodic behavior. Importantly, there are widely varying values of MLE over a narrow region of the parameter g H in Fig. 8, showing the complex firing behavior that exists within chaotic regions. This is most clearly shown when comparing with the bifurcation diagram in Fig. 8 where the chaotic bifurcations of ISIs corresponding to the MLE are lined up. The windows of negative MLE correspond to islands of periodic behavior which then revert to chaotic behavior once the MLE returns to positive values.

Fig. 8
figure 8

Slice of parameter space with I ext = 1.0 A m−2, g H from 52 to 57 A m−2 V−1. a The MLE as it changes through the parameter space. b Number of distinct ISIs at each point in the parameter space

Full size image

5 Summary and discussion

We have developed a novel neuronal model capable of reproducing a range of dynamical behaviors commonly observed in regular spiking, fast spiking, continuous bursting, and intrinsic bursting cells. It is a hybrid of the Hindmarsh–Rose (Hindmarsh and Rose 1984) and Wilson’s neocortical models (Wilson 1999a).

Additionally, we have used cubic equations for describing spiking dynamics; by keeping nonlinearities to a third order polynomial the equations remain analytically tractable and allows ease of implementation in future work involving neural field theory and mean-field modelling. Similar reasons motivated us to encapsulate the slow, negative feedback properties of the model in an abstract H variable. It would be advantageous for reducing the model to a neural field theory framework to perform a fast-slow analysis (Guckenheimer et al. 2005; Best et al. 2005) in which system variables are classified as either “fast” if they change significantly over the duration of a single spike or “slow” for variables that change only over the duration of a burst. Such analysis would allow further investigation of the topological structure of the model’s bursting dynamics with the slow parameter H treated as a bifurcation parameter for the fast subsystem V, R. This aids understanding of the model’s behavior in a neural field theory framework (Robinson et al. 2008; Robinson and Kim 2012) and complements the analysis provided in the current work. Such fast-slow analysis, where it would be necessary to separate variables according to the timescale over which they operate, highlights the importance of our choice fo the H variable which allows ease of separation from the fast variables, simpler bifurcation surfaces and robust implementation in neural field theory.

Our model exploits the interplay between V and R to initiate and terminate spikes without explicity incorporating inactivation currents. Such a strategy was also utilized in formulating Wilson’s four-dimensional model (Wilson 1999a). Nonetheless, the array of possible neuronal dynamics arising from our simpler three-dimensional model is diverse and encompasses the most fundamental properties of biological neurons. The H equation serves as a slow modulatory effect on firing by shifting the spike threshold. This provides the mechanism for spiking adaptation, bursting, and sub-threshold oscillations. However, it should be noted that due to the simplicity of our single slow variable H the model cannot account for bursting mechanisms that require two or more slow variables (Rinzel 1986).

Our main results showed the existence of multiple fixed points within certain parameter regions of I ext and g H . We demonstrated that hysteresis was possible in these regions. Our phase diagram simulations also provided independent verification of changes in stability in fixed points correlated with transitions from resting to firing. Increasing g H tended to reduce hysteresis effects so that when g H was sufficiently high for a given set of parameter values, hysteresis was abolished.

Calculation of the Lyapunov exponents for a chosen chaotic region characterized the complexity of periodic-to-chaotic trajectory transitions. There were windows of stability between regions of chaotic behavior. Crucially, the model is demonstrably capable of a strong suite of firing modalities. Chaotic behavior has been implicated in numerous neuronal processes such as information processing and memory (Skarda and Freeman 1987). Its existence in the model provides additional features that may contribute to interesting phenomena in neural networks.

We emphasize that the model is not constructed as a complete explanatory mechanism for spiking patterns. Rather to show its capability to reproduce accurate spiking behavior. Importantly, our model incorporates biophysical representations of the fast ion-channels as opposed to phenomenologically reproducing spikes through various artificial resets such as those used in integrate-and-fire neurons.

In comparing Wilson’s four dimensional model with our simplified three-dimensional model it has been shown that the diversity of neural dynamics is reproducible. In contrast, Rose and Hindmarsh model also offered the tractability of a three dimensional model, but did not adhere to Ohm’s law, nor did it explicitly incorporate equilibrium potentials for their fast variables.

Furthermore, the Rose–Hindmarsh model was formulated in a dimensionless units as they sought the simplest model capable of bursting primarily to investigate its mathematical structure. This resulted in a compact set of three equations but did not include physical units for any of their equations, which can lead to difficulties interpreting the neuronal dynamics. Though the Rose–Hindmarsh model was capable of bursting its dimensionless units made it difficult to implement for practitioners as discussed in Wilson (1999a).

The above results show that even with only three differential equations following biophysical principles for the fast variables our model was sufficient for reproducing at least 12 fundamental spiking patterns, type I and II excitability, and hysteresis. These patterns encompass a wide array of possible spiking exhibited by diverse neural populations found in vivoConnors and Gutnick (1990).

We have used a very simple model that adheres to biophysical principles in the two fast variables while the slow variable is an approximation of slow channel dynamics, thus allowing the model to be compatible with neural field theory. The chosen parameter space reflects the diversity of spiking patterns and chaotic behaviors.

The above results show that the model exhibits a diverse array of neuronal dynamics. It would interesting in future work to explore whether still further dynamics can be produced in other parameter regions. An example would be mixed-mode oscillations different to the type shown in the current work. They involve high-frequency sub-threshold oscillations alternating with spiking (Iglesias et al. 2011). Recent analysis has provided invaluable insight into such phenomena (Desroches et al. 2012). The dynamical geometry underlying them is highly complex and multiple mechanisms can be responsible for their generation (Krupa et al. 2008; Rubin and Wechselberger 2008; Harish and Golomb 2010).

We also note that several other three-dimensional models have been proposed in the wider context of simplified bursting neurons to model specific cells such as pancreatic β-cells (Sherman 1996; Bertram et al. 1995; Coombes and Bressloff 2005) and pre-Bötzinger pacemaker neurons (Butera et al. 1999; Coombes and Bressloff 2005). However, these models were designed for very specific cell types with parameters tuned to replicate experimental results in other systems and there have been no studies to see how much of the present dynamics they could replicate. In contrast, our fast variables V and R produce physiologically accurate spikes for cortical and thalamic neurons (Wilson 1999a), while our slow variable H has been used to model bursting dynamics in thalamic neurons (Hindmarsh and Rose 1984).

A single-neuron model that has gained in popularity is that of Izhikevich (2007). Though the Izhikevich model is probably the simplest, with only two equations, and is capable of all firing patterns discussed so far, its main drawback is the lack of a natural mechanism for resetting spikes; instead it requires an artificial reset of the voltage back to equilibrium after a ‘spike’ has occurred. This awkward feature is avoided by our three-dimensional model. Hence, our model is advantageous relative to Wilson’s model due to its reduced dimensions for simulation, while preserving the physical units that Rose and Hindmarsh did not include as they were more interested in the mathematical analysis of a bursting model. Additionally, our model is capable of a more natural reset of spike voltages than in leaky integrate-and-fire models. These qualities are important in networks encompassing the whole brain when computational efficiency is crucial. Furthermore, the simplicity of our H equation, which slowly modulates the spike threshold, is amenable to mean-field models (Robinson et al. 2008).

In conclusion, we have analyzed a simple three dimensional model that incorporates biophysical representations in the fast variables. It is capable of simulating a diverse array of fundamental neural behaviors and we have analyzed its dynamics. We argue it is a useful candidate for incorporating many types of single neuron dynamics in mean-field modeling.