Interacting oscillations in neural control of breathing: modeling and qualitative analysis

Abstract

In mammalian respiration, late-expiratory (late-E, or pre-inspiratory) oscillations emerge in abdominal motor output with increasing metabolic demands (e.g., during hypercapnia, hypoxia, etc.). These oscillations originate in the retrotrapezoid nucleus/parafacial respiratory group (RTN/pFRG) and couple with the respiratory oscillations generated by the interacting neural populations of the Bötzinger (BötC) and pre-Bötzinger (pre-BötC) complexes, representing the kernel of the respiratory central pattern generator. Recently, we analyzed experimental data on the generation of late-E oscillations and proposed a large-scale computational model that simulates the possible interactions between the BötC/pre-BötC and RTN/pFRG oscillations under different conditions. Here we describe a reduced model that maintains the essential features and architecture of the large-scale model, but relies on simplified activity-based descriptions of neural populations. This simplification allowed us to use methods of dynamical systems theory, such as fast-slow decomposition, bifurcation analysis, and phase plane analysis, to elucidate the mechanisms and dynamics of synchronization between the RTN/pFRG and BötC/pre-BötC oscillations. Three physiologically relevant behaviors have been analyzed: emergence and quantal acceleration of late-E oscillations during hypercapnia, transformation of the late-E activity into a biphasic-E activity during hypercapnic hypoxia, and quantal slowing of BötC/pre-BötC oscillations with the reduction of pre-BötC excitability. Each behavior is elicited by gradual changes in excitatory drives or other model parameters, reflecting specific changes in metabolic and/or physiological conditions. Our results provide important theoretical insights into interactions between RTN/pFRG and BötC/pre-BötC oscillations and the role of these interactions in the control of breathing under different metabolic conditions.

1 Introduction

Neural oscillations with various temporal and spatial patterns have been shown to play fundamental roles in brain operation, including sensory processing (in the visual (Singer 1993), somatosensory (Bauer et al. 2006), olfactory (Kay et al. 2009), and other sensory systems), central brain mechanisms (Bazhenov et al. 1999; Tort et al. 2008), and neural control of movements (Baker et al. 1999; Grillner 2006). Revealing the rhythmogenic mechanisms underlying these oscillations and characterizing the nature of interactions between different oscillations would have a broad impact on understanding the general principles of how the brain functions.

This study focuses on the interactions between two neural oscillators involved in the control of breathing in mammals. The first “oscillator” is the respiratory central pattern generator (CPG) that generates primary respiratory oscillations driving phrenic nerve motor output and controlling lung ventilation. The rhythm-generating core of this CPG has been hypothesized to include several interacting populations of respiratory neurons located in the pre-Bötzinger (pre-BötC) and Bötzinger (BötC) complexes within the ventral respiratory column of the medulla (Cohen 1979; Bianchi et al. 1995; Monnier et al. 2003; Richter 1996; Rubin et al. 2009b; Rybak et al. 2004a, 2007, 2008; Smith et al. 1991, 2007, 2009). The second “oscillator”, referred to as the parafacial respiratory group (pFRG), appears to reside within, or overlap with, the retrotrapezoid nucleus (RTN) (Janczewski and Feldman 2006a; Onimaru and Homma 2003). Recent data suggest that, with increasing metabolic demands, e.g. with increased level of CO₂ (hypercapnia) and/or decreased level of O₂ (hypoxia) (Abdala et al. 2009a), the RTN/pFRG oscillator starts generating a rhythmic late-expiratory (late-E, also referred to as pre-inspiratory or pre-I) activity that interacts with the BötC/pre-BötC oscillations and drives an enhanced late-E rhythmic activity in the motor output controlling abdominal muscles (Abdala et al. 2009a,b; Feldman and Del Negro 2006; Janczewski and Feldman 2006a; Smith et al. 2009). This enhancement of expiratory output yields a greater expulsion of air with a high CO₂ content from the lungs.

A large-scale computational model of the respiratory CPG was previously developed to reproduce multiple experimental data obtained in the arterially perfused brainstem-spinal cord rat preparation with brain stem transections that sequentially removed rostral components of the respiratory network (Rybak et al. 2007; Smith et al. 2007). The results of these experimental and modeling studies suggest that the core neural circuitry of the respiratory CPG resides within the BötC and pre-BötC compartments and that the primary respiratory oscillations are generated due to dynamic interactions between (i) excitatory neural populations in the pre-BötC that are active during inspiration, (ii) inhibitory populations in the pre-BötC providing inspiratory inhibition within the network, and (iii) inhibitory populations in the BötC generating expiratory inhibition (Rybak et al. 2007; Smith et al. 2007). It has also been proposed that these network interactions form a hierarchy of multiple oscillatory mechanisms whose expression is controlled by multiple drives from several brain stem compartments, including the RTN and pons, some of which depend on and reflect current metabolic conditions (e.g. levels of CO₂, O₂ and pH) (Rybak et al. 2007; Smith et al. 2007).

To allow investigation of interactions between the BötC/pre-BötC and RTN/pFRG oscillations, the above large-scale model was extended by incorporating an additional late-E population of the RTN/pFRG that consisted of neurons with intrinsic rhythmogenic properties defined by the persistent sodium current, I _NaP (Abdala et al. 2009a). Interactions between the late-E and other neural populations were suggested based on experimental studies (Abdala et al. 2009a) to reproduce the specific relationships between phrenic activity and abdominal oscillations observed in nerve recordings during various metabolic conditions. The extended large-scale model (Abdala et al. 2009a) was successful in reproducing several operating regimes featuring specific relationships between the above oscillations. However, the complexity of that model, based on explicit simulation of populations of neurons modeled in the Hodgkin-Huxley (HH) style, does not allow implementation of dynamical systems methods for theoretical investigation of the possible states and oscillatory regimes in the system. We have recently gained insight by simplifying such large-scale models using activity-based (non-spiking) single neuron models to represent populations of spiking neurons. Specifically, this approach was successfully applied for theoretical investigation of the core of the respiratory CPG, namely its BötC/pre-BötC kernel (Rubin et al. 2009b).

The model proposed herein is based on and extends the network model from this previous work (Rubin et al. 2009b). An additional late-E neuron with I _NaP -dependent rhythmogenic properties (representing a hypothetical late-E population in the RTN/pFRG) was included in the model and interconnected with other neurons according to the connection scheme proposed in the corresponding large-scale model (Abdala et al. 2009a). Our objective in this study was to develop a relatively simple model, which maintains the essential features and architecture of the large-scale model, and to harness this reduced model to theoretically investigate the oscillatory patterns and mechanisms of coupling between the BötC/pre-BötC and RTN/pFRG oscillations in the functional regimes corresponding to different metabolic conditions.

Our analysis focused on the following three scenarios studied experimentally: (1) the emergence and “quantal acceleration” of the (RTN/pFRG) late-E oscillations, and their interactions with the BötC/pre-BötC oscillations, with the progressive increase of external drive to the late-E population, simulating hypercapnic conditions, (2) transition of the late-E (pre-I) activity pattern to a biphasic-E (pre-I/post-I) pattern with changing external drives, simulating hypercapnic hypoxia conditions, and (3) “quantal slowing” of BötC/pre-BötC oscillations with progressive suppression of pre-BötC neurons, simulating the effect of opioids. These behaviors represent the typical regimes of synchronization between the BötC/pre-BötC and RTN/pFRG oscillators and a physiologically realistic reproduction of these behaviors is considered a critical test for the plausibility of the respiratory CPG model. Using numerical simulations in combination with bifurcation analysis and fast-slow decomposition techniques, we show and explain how gradual variation of external drives or other model parameters, associated with specific metabolic and/or physiological conditions, can produce particular BötC/pre-BötC and RTN/pFRG outputs and change the functional role of coupling between these oscillators. In addition to characterizing the phase plane conditions associated with each regime, our theoretical analysis explains certain features observed in simulations. Specifically, we show why the inspiratory period remains constant even as late-E activity emerges on progressively larger proportions of cycles in quantal acceleration, why late-E rebound activity is seen before a complete switch to biphasic-E activity emerges in hypercapnic hypoxia, and what determines pre-BötC burst times, as well as why late-E activity remains biphasic precisely on those cycles in which pre-BötC neurons activate, in quantal slowing. The results of this work provide theoretical insights into the key features and dynamics of synchronization between BötC/pre-BötC and RTN/pFRG oscillators under different physiological conditions.

2 Methods

2.1 Model description

The schematic of the respiratory network model considered herein is shown in Fig. 1(a). This model is a reduced version of the large-scale model by Abdala et al. (2009a). On the other hand, this model represents an extension of the previous reduced model of the core of the respiratory CPG (Rubin et al. 2009b). The latter was extended by incorporating an additional late-expiratory (late-E) neural component that represents a hypothetical neural population within RTN/pFRG, serving as a source of late-E oscillations.

Fig. 1

(a) Model schematic. Spheres represent neurons (excitatory– red; inhibitory– blue); green triangles represent sources of tonic excitatory drives (in pons, RTN) to different neural populations. Excitatory and inhibitory synaptic connections are indicated by red or green arrows and blue links with small circles, respectively. The dashed arrow denotes a connection that was included based on existing data in the literature and used in our previous simulations (Rubin et al. 2009b) but was found unnecessary and hence set to 0 for the regimes studied in this paper. (b) Model performance: output activity of all neurons is shown when “hypercapnic” drive to the late-E neuron (d ₃) is set to zero. The periods of elevated activity of pre-BötC neurons define the inspiratory phases (top two traces), while the BötC neurons (post-I and aug-E) are active during expiration. Although the post-I neuron inhibits the aug-E neuron early in expiration, adaptation in the post-I neuron causes a decrease in the inhibition to aug-E and thus allows the second phase of expiration, characterized by aug-E activity, to begin

The rhythmic activity in the RTN/pFRG appears to be critically dependent on I _NaP , since a suppression of this current by riluzole, a specific I _NaP blocker, abolishes this rhythmic activity, as shown in rat embryos (Fortin and Thoby-Brisson 2009; Thoby-Brisson et al. 2009) and in mature rat in situ preparations (Molkov et al. 2010). Therefore the late-E population of the RTN/pFRG added to the present model contains I _NaP and hence (similar to the pre-inspiratory/inspiratory (pre-I/I) population within the pre-BötC) is able to intrinsically generate I _NaP -dependent bursting under certain conditions (see also Lal et al. 2010; Wittmeier et al. 2008).

The synaptic interactions between the core BötC/pre-BötC neurons of the CPG shown in Fig. 1(a) were described in detail and justified in our previous papers (Rubin et al. 2009b; Rybak et al. 2007; Smith et al. 2007). The interactions between the late-E population of the RTN/pFRG incorporated in the new model and the core BötC/pre-BötC neurons include (see Fig. 1(a)): (a) excitation of the pre-I/I inspiratory population of the BötC by the late-E population and inhibition of the late-E population by (b) the early-inspiratory (early-I) population of the pre-BötC during inspiration and (c) the post-inspiratory (post-I) population of the BötC during expiration. The first two connections (a and b) have been proposed and justified in many previous studies (Abdala et al. 2009a; Ballanyi et al. 1999; Feldman and Del Negro 2006; Janczewski and Feldman 2006a; Janczewski et al. 2002; Joseph and Butera 2005; Lal et al. 2010; Onimaru and Homma 1987, 2003; Onimaru et al. 1988; Wittmeier et al. 2008). The third connection (the inhibitory one, from post-I to late-E) has been previously hypothesized (Abdala et al. 2009a) as the natural mechanism to prevent late-E bursting from occurring in the initial part of expiration and, together with the inspiratory inhibition (from early-I), to suppress late-E oscillations during normal conditions.

In the mathematical formulation of the model, we include the five populations (i = 1,…,5) shown in Fig. 1(a), each of which represents one of the key populations of neurons in the preceding large-scale model (Abdala et al. 2009a). The first four components include the excitatory pre-I/I population of the pre-BötC (i = 1), the inhibitory early-I population of the pre-BötC (i = 2), and two inhibitory populations of the BötC, the post-I (i = 3) and the augmenting-expiratory (aug-E, i = 4) neurons. These neurons represent the core circuitry of the respiratory CPG (Rubin et al. 2009b; Rybak et al. 2007; Smith et al. 2007). The fifth component is the late-E population of the RTN/pFRG (i = 5, see above). These five populations interact according to the schematic shown in Fig. 1(a) and receive excitatory drives from two sources: the pons (d ₁ ) and RTN (d ₂ ). An additional excitatory drive to late-E (d ₃ ) is included to simulate the effect of hypercapnia. In the activity patterns studied in this paper, we will largely focus on the dynamics of the early-I (i = 2), post-I (i = 3), and late-E (i = 5) populations. Nonetheless, all five are included in the model to provide a strong link with earlier work (Abdala et al. 2009a; Rubin et al. 2009b), to maintain a system that can be used for additional analyses in future work, and to preserve an important source of inhibition (aug-E) during decreases in d ₁ and an important source of excitation (pre-I) during decreases of pre-BötC excitability that we study.

Each neural population in the network is described by an activity-based model in which it is effectively represented as a single neuron. In this representation, the dependent variable V _i represents an average voltage for that (i-th) population and each output f(V _i ) (0 ≤ f(V _i ) ≤ 1) represents an averaged or integrated population activity. Because we consider regimes in which neurons within each population switch between silent and active spiking regimes in a synchronized way, we assume that the dynamics of the average voltages in the model can be represented by a conductance-based framework (Rubin et al. 2009b). Furthermore, since we have no evidence of spike synchrony within each active phase or that spikes would show up in the population-average voltage traces, we omit fast membrane currents responsible for spiking activity, which simplifies the analysis. Since each population in this formulation is represented by an activity-based single neuron model, we refer to each population as a neuron in the remainder of the paper.

The pre-I/I and late-E (i ϵ {1,5}) neurons are excitatory, with intrinsic oscillatory properties defined by the persistent (slowly inactivating) sodium current I _NaP. The membrane potentials of these neurons, V _i , thus obey the following differential equation:

$$ C \cdot {\dot{V}_i} = - {I_{NaPi}} - {I_{Ki}} - {I_{Li}} - {I_{SynEi}} - {I_{SynIi}}. $$

(1)

The other three neurons (i ϵ{2,3,4}) are adaptive neurons (with adaptation defined by an outward potassium current, I _ADi ) whose membrane potentials V _i evolve as follows:

$$ C \cdot {\dot{V}_i} = - {I_{AD i}} - {I_{L\;i}} - {I_{SynE\;i}} - {I_{SynI\;i}}. $$

(2)

In Eqs. (1) and (2), C is the neuronal capacitance, I _Ki represents the potassium delayed rectifier current, I _Li is the leakage current, and I _{SynE i} and I _{SynI i} are the excitatory and inhibitory synaptic currents, respectively. The currents are described as follows:

$$ {I_{NaPi}} = {\bar{g}_{NaP}} \cdot {m_{NaP}}({V_i}) \cdot {h_{NaPi}}\cdot ({V_i} - {E_{Na}}),\;for\;i \in \{ 1,5\}; $$

(3)

$$ {I_{Ki}} = {\bar{g}_K} \cdot m_K^4({V_i}) \cdot ({V_i} - {E_K}),\;for\;i \in \{ 1,5\}; $$

(4)

$$ {I_{ADi}} = {\bar{g}_{AD}} \cdot m_{ADi} \cdot ({V_i} - {E_K}),\;for\;i \in \{ 2,3,4\}; $$

(5)

$$ {I_{Li}} = {\bar{g}_L} \cdot ({V_i} - {E_{Li}}),\;for\; \in \{ 1,...,5\}; $$

(6)

$$ {I_{SynE1}} = {\bar{g}_{SynE}} \cdot ({V_1} - {E_{SynE}}) \cdot ({a_{51}} \cdot f({V_5}) + {c_{11}} \cdot {d_1} + {c_{21}} \cdot {d_2}); $$

(7)

$$ {I_{SynE2}} = {\bar{g}_{SynE}} \cdot ({V_2} - {E_{SynE}}) \cdot ({a_{12}} \cdot f({V_1}) + {c_{12}} \cdot {d_1} + {c_{22}} \cdot {d_2}); $$

(8)

$$ {I_{SynEi}} = {\bar{g}_{SynE}} \cdot ({V_i} - {E_{SynE}}) \cdot ({c_{1i}} \cdot {d_1} + {c_{2i}} \cdot {d_2}),\;for\;i \in \{ 3,4\}; $$

(9)

$$ {I_{SynE5}} = {\bar{g}_{SynE}} \cdot ({V_5} - {E_{SynE}}) \cdot {c_{35}} \cdot {d_3}; $$

(10)

$$ {I_{SynIi}} = {\bar{g}_{SynI}} \cdot ({V_i} - {E_{SynI}}) \cdot \sum\limits_{j = 2;\;j \ne i}^4 {{b_{ji}} \cdot f({V_j})}, \;for\;i \in \{ 1,...,5\}, $$

(11)

where ${\bar{g}_{NaP}},\;{\bar{g}_K},\;{\bar{g}_{AD}},\;{\bar{g}_L},\;{\bar{g}_{SynE}},$ and ${\bar{g}_{SynI}}$ are the maximal conductances of the corresponding ionic channels; E _Na , E _K , E _Li , E _SynE and E _SynI are the corresponding reversal potentials; a ₁₂ and a ₅₁ define the weights of the excitatory synaptic input from the pre-I/I to the early-I neuron and from the late-E to the pre-I/I neuron, respectively (see Fig. 1(a)); b _ji defines the weight of the inhibitory input from neuron j to neuron i (j ϵ {2,3,4}; i ϵ {1,...,5}); and c _ki defines the weight of the excitatory synaptic input to neuron i from drive k (d _k , k ϵ {1,2,3}).

The neuronal membrane potential is converted to the neuron output by the piecewise linear function:

$$ f(V) = \left\{ \begin{gathered} 0,\;if\;V < {V_{\min }} \hfill \\(V - {V_{\min }})/({V_{\max }} - {V_{\min }}),\;if\;{V_{\min }} \leqslant V < {V_{\max }} \hfill \\1,\;if\;V \geqslant {V_{\max }} \hfill \\\end{gathered} \right. $$

(12)

where V _min and V _max define the “threshold” and “saturation” voltages, respectively.

There are two types of slow variables in the model. One type represents the slow inactivation of the persistent sodium current (h _NaPi , iϵ{1,5}; see (Butera et al. 1999a)) in the pre-I/I and late-E neurons; the other variables (m _ADi , iϵ{2,3,4}) denote adaptation in the other three neurons (each with fixed time constant τ _AD and maximal adaptation k _AD ):

$$ {\tau_{hNaP}}({V_i}) \cdot {\dot{h}_{NaPi}} = {h_{\infty NaP}}({V_i}) - {h_{NaPi}},\,\quad i \in \{ 1,5\}; $$

(13)

$$ {\tau_{AD}} \cdot {\dot{m}_{ADi}} = {k_{AD}} \cdot f({V_i}) - {m_{ADi}},\,\quad i \in \{ 2,3,4\} . $$

(14)

Voltage dependent activation and inactivation variables and time constants for the persistent sodium and potassium rectifier channels in the pre-I/I and late-E neurons (iϵ{1,5}) are described as follows (Butera et al. 1999a):

$$ {m_{NaP}}({V_i}) = {\left( {1 + \exp \left\{ {({V_i} - {V_{mNaP}})/{k_{mNaP}}} \right\}} \right)^{ - 1}}; $$

(15)

$$ {h_{\infty NaP}}({V_i}) = {\left( {1 + \exp \left\{ {({V_i} - {V_{hNaP}})/{k_{hNaP}}} \right\}} \right)^{ - 1}}; $$

(16)

$$ {\tau_{hNaP}}({V_i}) = {\tau_{hNaP\max }}/\cosh \left\{ {({V_i} - {V_{\tau hNaP}})/{k_{\tau hNaP}}} \right\}; $$

(17)

$$ {m_K}({V_i}) = {\left( {1 + \exp \left\{ {({V_i} - {V_{mK}})/{k_{mK}}} \right\}} \right)^{ - 1}}. $$

(18)

The architecture of network interconnections between the neurons follows that in the large-scale model (Abdala et al. 2009a) and the model by (Rubin et al. 2009b) and is based on the existing direct and indirect experimental data and our current assumptions. The connection weights were adjusted so that, on one hand, the model reproduced the dynamics of the BötC/pre-BötC and late-E (RTN/pFRG) oscillators in all regimes considered herein and, at the same time, maintained all the features and behavior described previously (Rubin et al. 2009b).

2.2 Model parameters

The following default values of parameters were used (except where it is indicated in the text that some parameter values were varied in particular simulations):

Membrane capacitance (pF):

C = 20.

Maximal conductances (nS):

${\bar{g}_{NaP}} = 5$, ${\bar{g}_K} = 5$, ${\bar{g}_{AD}} = 10$, ${\bar{g}_L} = 2.8$, ${\bar{g}_{SynE}} = 10$, ${\bar{g}_{SynI}} = 60$.

Reversal potentials (mV):

E _Na  = 50, E _K  = −85, E _SynE  = 0, E _SynI  = −75, E _Li  = −60 (i ϵ {1,...,4}), E_L5 = −64.

Synaptic weights:

a₁₂ = 0.35, a₅₁ = 0.35, b₂₁ = 0, b₂₃ = 0.2, b₂₄ = 0.25, b₂₅ = 0.035, b₃₁ = 0.8, b₃₂ = 0.15, b₃₄ = 0.4, b₃₅ = 0.05, b₄₁ = 0.22, b₄₂ = 0.08, b₄₃ = 0, b₄₅ = 0, c₁₁ = 0.35, c₁₂ = 0.1, c₁₃ = 0.33, c₁₄ = 0.025, c₂₁ = 0.16, c₂₂ = 0.15, c₂₃ = 0, c₂₄ = 0.43, c₃₅ = 1.

Parameters of f(V _i ) functions (mV):

V _min  = −50, V _max  = −20.

Parameters for I _NaP and I _K (mV):

V _mNaP  = −40, k _mNaP  = −6, V _hNaP  = −55, k _hNaP  = 10, V _mK  = −30, k _mK  = −4.

Time constants (ms):

τ_hNaPmax = 4000, τ _AD  = 2000.

External drives:

d₁ varied from 1 (default value) to 0, d₂ = 1, d₃ varied from 0 (default value) to 1.

Other parameters:

k _AD  = 1.

This baseline parameter tuning, with d ₁ = 1 and d ₃ = 0, yielded a respiratory rhythm shown in Fig. 1(b), which is representative of baseline conditions. In particular, the value d ₃ = 0 was assumed to represent to a normocapnic (normal CO₂) state. Changing metabolic and physiological conditions were simulated by changing external drives or other model parameters. Specifically, progressive hypercapnia (an increase in the CO₂ level) was simulated by a gradual increase of “hypercapnic” drive (d ₃) to the late-E neuron, representing a population of central chemoreceptors located in RTN/pFRG, whose activity is believed to increase with the level of CO₂ (Guyenet et al. 2008; Guyenet et al. 2009; Onimaru et al. 2009). Hypercapnic hypoxia was modeled via the reduction of post-I activity, i.e. as a progressive decrease in the pontine drive, d ₁, from the baseline value d ₁ = 1 to zero, at a particular level of hypercapnia (i.e., d ₃ value).

To reproduce “quantal slowing” of pre-BötC activity (Janczewski and Feldman 2006a), the excitability of pre-BötC neurons was progressively suppressed by a reduction of the excitatory synaptic conductance ${\bar{g}_{SynE}}$ in both pre-I/I and early-I neurons.

2.3 Bifurcation analysis

For the analysis of changes in qualitative behavior of the system with variation of external drives or other model parameters we used a technique based on the construction of Poincaré sections (Kantz and Schreiber 2004). This technique involves choosing a surface, called a Poincaré section, that is transverse to the flow in the phase space and finding the successive intersections of the model trajectory with that surface. The Poincaré section was defined by choosing a threshold and finding the time moments when the output neuron activity, f(V), intersects the threshold in a fixed direction. The time interval between two successive phase transitions (referred to as period) was used to build bifurcation diagrams for each of the three scenarios of interest. In 2D bifurcation diagrams, the periods of pre-BötC and late-E active phases were plotted as functions of a parameter whose variation was used to simulate the corresponding change in the metabolic state. The variation of such a parameter was implemented using a slowly changing linear function of time, and a continuous calculation of the corresponding periods of pre-BötC (early-I neuron) and late-E oscillations was performed. In the resulting bifurcation diagrams, most qualitative changes (bifurcations) in system behavior were clearly evident as discontinuities, the appearance of new solution branches, and the emergence of clouds of points.

Some bifurcation diagrams were generated by changing two parameters independently. At each point in the corresponding 2D parametric plane, the mean value of the period was represented by color. This type of diagram shows bifurcation curves as boundaries between areas with different colors, corresponding to qualitatively different behaviors.

Bifurcation diagrams were constructed using a TISEAN software package (Hegger et al. 1999) and custom written C++ programs.

2.4 Phase-plane analysis

Phase plane analysis involved the evolution of variables describing voltage (V ₅) and I _NaP inactivation (h ₅, where we henceforth shorten h _NaPi , to h _i ) in the late-E neuron, adaptation of early-I (m ₂ , where we henceforth shorten m _ADi to m _i) or post-I (m ₃ ) neurons, and input currents and conductances. Each neuron model includes a fast voltage variable (V _i ) and a second slow variable, corresponding to persistent sodium inactivation (h ₁,h ₅) or adaptation (m ₂,m ₃,m ₄). Thus, the voltage equation for each neuron, with its slow variable treated as a parameter, forms a one-dimensional fast subsystem for that neuron (assuming that other neurons’ voltages are fixed). Correspondingly, when we refer to critical points of the fast subsystem for a neuron, we mean points for which the right hand side of Eq. (1) (for the pre-I/I and late-E neurons) or (2) (for all other neurons) is equal to zero. We consider some standard phase plane diagrams with a voltage variable on the horizontal axis and the associated slow variable on the vertical axis. We also consider diagrams with a slow variable on the horizontal axis and a variable representing the level of input to the corresponding neuron on the vertical axis. All synaptic inputs to neurons 3,4, and 5 are inhibitory, with the same reversal potential, and we define input variables inh _i , i = 3,4,5, to neuron i as the sum $\sum\limits_{j \ne i} {{b_{ji}}f({V_j})}$. Neurons 1 and 2 each receive both excitatory and inhibitory inputs, and we define the variables input ₁ and input ₂ as the sum of synaptic currents to these neurons, excluding drives d _i . For consistency with the use of inh > 0, we adopted the convention that positive and negative values of input denote inhibition and excitation, respectively.

The construction of a diagram with input ₂ versus m ₂ is illustrated in Fig. 2(a –b), with the diagram itself shown in Fig. 2(c). In Fig. 2(a), the V ₂ (dashed) and m ₂ (solid) nullclines, corresponding to a fixed level of input to cell 2 (input ₂ ) that is positive, since it is inhibitory, intersect in a critical point. The V ₂ nullcline also intersects the line {V ₂  = V _min  = −50}, at which synaptic outputs from cell 2 turn on (Eq. (12)), at a positive value of m ₂ . We can search for such critical points and points of intersection with the line V ₂  = −50, as well as with the lines V ₂  = −35, corresponding to half-maximal activation of synaptic outputs, and V ₂  = V _max  = −20, corresponding to maximal activation of synaptic outputs, for each fixed value of input ₂ ; this is done, for example, in Fig. 2(b) for a level of input ₂ corresponding to excitatory input to cell 2. From this process, we obtain a curve of m ₂ values at critical points, parameterized by input ₂ , along with similar curves from the other intersections. These curves are plotted together in a single diagram showing input ₂ versus m ₂ . An example is given in Fig. 2(c).

Fig. 2

Construction of diagram for use in analysis. (a) Standard phase plane for model neuron 2, subject to a fixed level of inhibitory input (input ₂  > 0). There is a critical point (blue) where model nullclines (V ₂ , dashed and m ₂ , solid) intersect. The m ₂ coordinate is read off of this point (blue dashed line). The vertical red dashed lines label V ₂ values at which the synaptic output from neuron 2 turns on (-50) and reaches a half-maximal level (-35). When they are positive, the m ₂ coordinates of these intersections are also recorded (horizontal red dashed line). (b) The same nullclines and intersections from (a) are shown along with additional nullclines and intersections (dash-dotted curve and lines) corresponding to a different level of input to neuron 2 that is excitatory (input ₂  < 0). (c) Curves of critical points (blue) and intersection points with key V ₂ values (red dashed and solid) in the input ₂ versus m ₂ plane

All phase plane diagrams were constructed in Matlab 7.5.0. Simulations were performed using XPPAUT, available at http://www.pitt.edu/~phase (Ermentrout 2002).

3 Results

3.1 Model performance under normal conditions

It appears that late-E oscillations are not observed under normal metabolic conditions (see Abdala et al. 2009a; Iizuka and Fregosi 2007, see also Fig. 3 (a1) and (b) at 5% of CO₂). Similarly, the late-E neuron in the model under “normal” conditions does not receive a strong “hypercapnic” drive (d ₃) and is inhibited by the early-I neuron during inspiration and by the post-I neuron during expiration (Fig. 1(a,b)). In this case, the behavior of the current model is equivalent to that of the model described in detail by (Rubin et al. 2009b) and the model demonstrates all the regimes simulated and investigated in that paper. The output activity of all neurons of the model, in a regime corresponding to breathing under baseline conditions, is shown in Fig. 1(b). During expiration, the post-I neuron output is elevated and demonstrates adapting (decrementing) activity that is defined by the dynamic increase in its adaptation variable m _AD3 (see Eq. (5)). The resulting decline in inhibition from the post-I neuron shapes the augmenting profile of aug-E activity. This reduction in post-I inhibition also produces a slow depolarization of pre-I/I and early-I neurons. In addition, the pre-I/I neuron depolarizes further because of the slow deinactivation of I _NaP (slow increase of h _NaP , see Eq. (13)). Finally, at some moment during expiration, the pre-I/I neuron rapidly activates, providing excitation of early-I. The latter inhibits both post-I and aug-E, completing the switch from expiration to inspiration (Fig. 1(b)). During inspiration, the pre-I/I and early-I outputs are elevated, and the inspiratory neuron outputs settle towards a corresponding equilibrium state. In particular, the early-I neuron demonstrates adapting (decrementing) activity (Fig. 1(b)), defined by the dynamic increase in its adaptation variable m _AD2 (see Eq. (5)). The decline in inhibition from this neuron produces a slow depolarization of the post-I and aug-E neurons. Eventually, the system reaches a moment at which the post-I neuron rapidly activates and inhibits both inspiratory neurons (pre-I/I and early-I) and the aug-E neuron (initially), producing the switch from inspiration back to expiration (Fig. 1(b)).

Fig. 3

Quantal acceleration of AbN late-E activity with the development of hypercapnia in the in situ arterially perfused brainstem-spinal cord of juvenile rat (data from Abdala et al. 2009a). (a1–a4) Integrated activity (arbitrary units not shown) of simultaneously recorded (top-down) phrenic nerve (PN, red), cervical vagus nerve (cVN, black) and abdominal nerve (AbN, blue). (a1) Normocapnia (5% CO₂): late-E activity is absent in the AbN. (a2–a4) Quantal acceleration of AbN activity: with the development of hypercapnia, the ratio between the AbN and PN burst frequencies goes through step-wise changes from 1:3 and 1:2 (a2 and a3, 7% CO₂) to 1:1 (a4, 10% CO₂). (b) Time-series representation of the entire experimental epoch with the oscillation periods in the PN (red squares) and AbN (blue circles) activities plotted continuously vs. time. The AbN late-E bursts were synchronized with the PN bursts with a ratio increasing quantally from 1:5 to 1:1. The content of CO₂ in the perfusate of this preparation was changed at times indicated by short arrows and vertical dashed lines. Large arrows indicate times corresponding to the episodes shown in a1–a4

3.2 Emergence and quantum acceleration of late-E oscillations with progressive hypercapnia

It has been suggested that when late-E oscillations emerge within the RTN/pFRG, they project to and drive late-E bursts in the abdominal motor output (Feldman and Del Negro 2006; Janczewski and Feldman 2006a; Janczewski et al. 2002) that can be seen in the abdominal nerve, AbN. Neurons whose activity clearly correlated with the AbN late-E discharges (including simultaneous burst missing) were found in the RTN/pFRG region, and a pharmacological inactivation of the RTN/pFRG abolished the AbN late-E activity (Abdala et al. 2009a). Thus the AbN late-E discharges can be considered as an indicator of the corresponding oscillations in the RTN/pFRG (Abdala et al. 2009a; Feldman and Del Negro 2006; Janczewski and Feldman 2006a; Janczewski et al. 2002).

Figure 3 shows the integrated activities of phrenic (PN, active during inspiration), cervical vagus (cVN) and abdominal (AbN) nerves recorded from the in situ arterially perfused rat brainstem-spinal cord preparation with the progressive development of hypercapnia (increasing CO₂ concentration in the perfusate) (data are taken from Abdala et al. 2009a). Under baseline metabolic conditions (95% O₂, 5% CO₂) the AbN typically exhibits a low-amplitude post-inspiratory activity (Fig. 3(a) and left part of (b)). Switching to hypercapnic (7–10% CO₂) conditions evokes large amplitude late-E (i.e., occurring at the very end of expiration) AbN bursts (indicating the emergence of RTN/pFRG oscillations, see above). Figure 3 shows that the late-E discharges emerge in AbN at 7% CO₂ (Fig. 3(a2,b)) followed by a progressive increase in the burst frequency as the CO₂ concentration is incremented to 10%. Importantly, although the frequency of late-E AbN bursts increases with CO₂, these bursts remain coupled (phase-locked) with the bursts in the PN and cVN (Fig. 3(a2–a4)). With the development of hypercapnia, the ratio of late-E AbN burst frequency to the PN burst frequency shows a step-wise or quantal increase from 1:5 and 1:4 (seen in Fig. 3(b)) to 1:3, 1:2, and, finally, to 1:1 (Fig. 3(a2–a4) and (b)). On returning CO₂ to the control levels, the ratio showed a step-wise reversal. Similar hypercapnia-evoked late-E AbN discharges phase-locked to PN, with a step-wise increase of their frequency with increasing CO₂ levels, have been demonstrated previously in vivo (Iizuka and Fregosi 2007). We call this process quantal acceleration of late-E AbN activity with development of hypercapnia.

To simulate progressive increase of hypercapnia using our model, the excitatory “hypercapnic” drive d ₃ to the late-E neuron (see Fig. 1(a)) was progressively increased from d ₃ = 0 (representing normocapnic conditions) to higher values (d ₃ ≤ 1) (Fig. 4). The late-E neuron is a conditional burster, whose intrinsic rhythmogenic properties are defined by slowly inactivating I _NaP (see Eq. (16)). If this neuron is isolated from the others, then with a progressive increase in excitatory drive its behavior evolves from a silent state to bursting, and then to tonic activity (Butera et al. 1999a, 1999b; Rybak et al. 2003; Rybak et al. 2004b). In our model, the bursting activity in the late-E neuron is shaped by the excitatory drive to this neuron (d ₃, simulating the effect of hypercapnia), the inhibitory synaptic inputs from the adapting early-I and post-I neurons (see Fig. 1(a)), and the dynamics of I _NaP inactivation (h ₅ ). The complex net effect of these factors is a step-wise decrease of the late-E bursting period with the progressive increase of hypercapnic drive to this neuron (d ₃). Specifically, late-E bursts become 1:N synchronized with pre-BötC (pre-I/I and early-I) bursts, and a quantal increase in the ratio of late-E burst frequency to pre-BötC frequency (decrease in N) occurs as hypercapnic drive increases (see Fig. 4(a1–a3, b)). Once the late-E neuron is activated, it excites the pre-I/I neuron which in turn excites early-I (Fig. 1(a)). This cascade ends when the early-I neuron inhibits both expiratory neurons in the BötC and ultimately terminates the late-E burst.

Fig. 4

Increasing drive (d ₃) to the late-E neuron, applied to simulate “progressive hypercapnia”, results in the emergence and “quantal acceleration” of late-E oscillations in RTN/pFRG. (a1–a3) The frequency of late-E activity proceeds through synchronization regimes with ratio of 1:3 (a1), 1:2 (a2), and 1:1 (a3) relative to the pre-BötC/BötC frequency. (b) Bifurcation diagrams of late-E (blue) and pre-BötC (red) periods as functions of drive to late-E. The late-E period quantally decreases through a series of jumps; the drives to late-E at which the jumps occur are denoted by vertical green dashed lines, marked with the letters a through e. Drives below point a are not high enough to produce late-E neuron activity. Between points a and e late-E activity accelerates from 1:5 (one late-E burst per five pre-BötC bursts) to 1:1. (c) The trajectory of the network model projected to the (V ₅,V ₂,m ₂) phase subspace during hypercapnia in the 1:3 regime (shown in a1). Sub-threshold late-E neuron activity (dashed blue line) occurs when V ₅ is below -50 mV. Suprathreshold late-E neuron activity (solid blue line) corresponds to bursts of the late-E seen in a1 (when d ₃ = 0.03). Cyclical sub-threshold movement in (V ₂,m ₂) indicates two periods of early-I activity during which the late-E neuron fails to burst (see text for more details). (d) Simulation of the effect of blocking the persistent sodium current in the model. After 1:1 synchronization is achieved (as in a3), ${\bar{g}_{NaP}}$ is set to zero. Expiration increases in duration, pre-I activity decreases in amplitude, and the late-E neuron falls silent

The dependencies of the periods of late-E and pre-BötC oscillations on the “hypercapnic” drive to the late-E neuron are shown in the bifurcation diagram in Fig. 4(b). The late-E oscillation period changes in a stair-like manner with progressive increases in the drive to the late-E neuron. The late-E oscillations emerge at a particular drive to the late-E neuron near point a in Fig. 4(b). To the right from this point, the ratio of late-E to pre-BötC burst frequencies is 1:5. A further increase of the drive causes a quantal acceleration of the late-E frequency (with a 1:4 ratio to the pre-BötC frequency between points b and c; 1:3 between points c and d; 1:2 between points d and e) until a steady 1:1 synchronization with the pre-BötC oscillations is achieved (to the right from point e).

The dynamics of sub-threshold and supra-threshold changes in the membrane potential of the late-E neuron (V ₅) corresponding to the 1:3 regime of synchronization (d ₃ = 0.3, same as in Fig. 4(a1)) is shown in Fig. 4(c) as a trajectory in the (V ₅,V ₂,m ₂) phase space. After the initial activation of the late-E neuron (supra-threshold V ₅), V ₂ quickly increases due to the cascading excitation from late-E to pre-I/I and from pre-I/I to early-I (rightward arrow in Fig. 4(c)). As V ₅ exceeds the threshold, the early-I neuron is activated and m ₂ begins gradually increasing. When V ₂ becomes sufficiently elevated, the early-I neuron inhibits the late-E neuron, sending V ₅ to a sub-threshold state (leftward arrow in Fig. 4(c)).

Simulation results demonstrating the effect of I _NaP suppression on the late-E and BötC/pre-BötC oscillations during hypercapnia are shown in Fig. 4(d). All parameters in this simulation are the same as in Fig. 4(a3), but ${\bar{g}_{NaP}}$ is set to zero in both pre-I/I and late-E neurons. One can see that the suppression of I _NaP in the network fully abolishes the late-E oscillations, which are critically dependent on this current in our model, but does not stop the network BötC/pre-BötC oscillations. The latter persist with reduced frequency and amplitude.

Figure 5(a–d) illustrates and explains the mechanisms providing the above quantal acceleration of late-E oscillations and their synchronization with the BötC/pre-BötC oscillations. In Fig. 5(a), the state of the late-E neuron is considered in the (V ₅,h ₅) plane. Two pairs of V ₅ nullclines are drawn. We use these nullclines to give a preliminary illustration of how hypothetical changes in the level of inhibition and drive (d ₃) to the late-E neuron can shape the model activity. For this demonstration, we simulate the late-E neuron in isolation and manipulate the synaptic inhibition artificially. The solid pair of nullclines is representative of relatively low d ₃ values, while raising d ₃ lowers the nullclines, as illustrated by the dashed pair. If the inhibition to the late-E neuron is on, then the V ₅ nullcline is elevated, as represented by the nullcline at higher h ₅ values within each pair. If this inhibition is instantaneously reduced to zero, then the V ₅ nullcline assumes a new, lower, position in the space, as illustrated by the nullcline at lower h ₅ values within each pair. Note that three of the V ₅ nullclines shown have cubic shapes, each consisting of a left branch (LB) and a middle branch (MB) that meet in a point, which we call the left knee (LK), and a right branch (RB), which meets MB at the right knee (RK). Importantly, the positions of the knees depend on the levels of drive and inhibition to the late-E neuron, as is evident in Fig. 5(a).

Fig. 5

Phase plane analysis of model performance during “hypercapnia”. (a) Projection of model trajectory to the (V ₅,h ₅) phase plane together with V ₅ nullclines corresponding to intermediate and high values of d ₃ (solid and dashed blue curves, respectively) and the nullcline for the slow variable, h ₅ (red curve). The upper V ₅ nullclines correspond to higher inhibition than do the lower ones. The trajectory shown undergoes three excursions, namely a failed burst (lowest h ₅), a successful burst that is prematurely terminated by the return of inhibition (middle h ₅), and a successful burst that temporarily survives the return of inhibition (highest h ₅). Vertical dashed black line marked “synapses on” shows the lower threshold of the voltage-to-activity function f(V) defined by Eq. (12). (b) Trajectories during 1:1 and 2:1 activity regimes (black and grey curves, respectively) projected to the (h ₅,inh ₅ ) plane, together with curves for the right (dashed) and left (solid) knees of the V ₅ nullcline. Different curves of knees correspond to d ₃ values that produce 2:1 (red) and 1:1 (green) regimes. As shown in a, increasing inhibition moves the nullcline to lower voltages and makes the cubic-like shape more pronounced, thus raising the value of h ₅ at each knee. A trajectory must cross the curve of left knees for the late-E neuron to become active. Curves of critical points of the (V ₅,h ₅) equations on the left branch of the V ₅ nullcline are shown in blue (1:1 regime) and light blue (2:1 regime). (c) and (d) Trajectories projected to show early-I (c) and post-I (d) dynamics, along with curves of critical points of the (V ₂,m ₂) and (V ₃,m ₃) equations (blue) and synaptic thresholds (red). The synaptic thresholds represent the values of input ₂ and m ₂ or inh ₃ and m ₃ at which each neuron will reach voltages of -50 (“on”, upper dashed), -35 (“half max”, solid red), and -20 (“max”, lower dashed, not shown in (d) if it evolves on its voltage nullcline. Each m variable increases while the corresponding neuron is active (rightward arrows) and decreases while the neuron is silent (leftward arrows)

A trajectory of the model solution with the lower level of d ₃ (solid nullclines), starting at the initial condition (V ₅,h ₅) ≈ (−65,0.15), is shown in black in Fig. 5(a). In this example, we manipulate the level of inhibition to the late-E neuron, purely to illustrate the effects that changes in inhibition can have on late-E neuron dynamics. As time advances from zero, h ₅ increases, corresponding to deinactivation of I _NaP . In this particular simulation, when h ₅ ≈ 0.35, we turned off the inhibition to the late-E neuron and the trajectory jumped to the lower solid V ₅ nullcline. The position of this nullcline prevents V ₅ from crossing the synaptic activation threshold (−50 mV; “synapses on” in Fig. 5(a)) and exciting the pre-I neuron. We subsequently restored inhibition, which caused the trajectory to return to the elevated V ₅ nullcline. A second withdrawal and return of inhibition was imposed with h ₅ ≈ 0.45. The trajectory could not reach the RB of the V ₅ nullcline, even though it was above the LK, because the inhibition was restored too quickly. With a still higher value of h ₅, namely h ₅ ≈ 0.6, a third removal of inhibition was performed and the trajectory reached the right branch of the V ₅ nullcline, corresponding to full late-E neuron activation. Furthermore, when inhibition was subsequently restored again, the late-E neuron remained active (on a RB) for some additional time, as illustrated by the trajectory segment on the far right of Fig. 5(a) (leftward arrow), due to the relative nullcline positions. This same mechanism is the reason why the activation of the early-I neuron does not immediately terminate late-E activity in the network rhythm (e.g. Fig. 4), even though early-I inhibits late-E. Ultimately, the late-E activity is terminated when h ₅ reaches the RK of a V ₅ nullcline, causing a decrease in V ₅ that returns the late-E neuron to a sub-threshold state on the LB.

In summary, we see that because of the significant difference in rates of evolution of V ₅ and h ₅, the late-E cell will head toward the synaptic activation thresholds if the solution trajectory in the (V ₅,h ₅) phase plane lies above the LK corresponding to the levels of drive and inhibition that it is receiving, although it may fail to reach them if inhibition increases sufficiently fast. As inhibition decreases, the LK moves to lower values of h ₅, making it easier for the late-E cell to activate, and the RK moves lower as well. Increases in inhibition have the opposite effects, but an abrupt increase in inhibition will not terminate late-E activity if it arrives after the late-E neuron is on the RB and the trajectory remains above the resulting RK.

This discussion makes clear that it is the frequency with which the solution trajectory can rise above the left knee of the V ₅ nullcline in the (V ₅,h ₅) plane that determines which of the 3:1, 2:1, and 1:1 (pre-BötC:late-E) synchronization regimes occurs in Fig. 4. Figure 5(b) illustrates the qualitative differences between the 2:1 and 1:1 regimes in the (h ₅,inh ₅) plane. This diagram includes LK curves, RK curves, and curves of critical points for each of the two regimes. Indeed, since the inhibition to the late-E neuron varies continuously, it is not so useful to show a small number of particular nullclines in the (V ₅,h ₅) plane, as in Fig. 5(a). Since the knee positions depend on the level of inhibition to the late-E neuron, and V ₅ is fixed as a function of (h ₅,inh ₅) at each knee, it is useful to generate curves of knees, indicating how the h ₅ coordinates of LK and RK depend on inh ₅, in the (h ₅,inh ₅) plane. These curves are shown as solid (LK) and dashed (RK) red (2:1 regime) and green (1:1 regime) curves in Fig. 5(b). Similarly, the critical point where the V ₅ and h ₅ nullclines intersect varies with inh ₅ (e.g., Fig. 5(a)). This critical point may lie on the LB or MB of the V ₅ nullcline and moves from the LB to the MB as inhibition decreases or drive increases. The light (2:1 regime) and dark (1:1 regime) blue curves in Fig. 5(b) show the relationships between the h ₅ coordinates of the critical point and inh ₅ for those values of inh ₅ that are large enough such that the critical point lies on the LB. Two trajectories (black and grey) are plotted along with the LK, RK, and critical point curves. The trajectory shapes reflect an asymmetry present in the inhibition to the late-E neuron: smaller values of inh ₅ arise during periods of post-I inhibition, and larger values correspond to periods of early-I inhibition. As noted previously, for a fixed value of inh ₅, the h ₅ coordinate of a trajectory must exceed the h ₅ value at the LK of the V ₅ nullcline for the trajectory to reach elevated V ₅ values, corresponding to late-E activation. In Fig. 5(b), since h ₅ is on the horizontal axis, jump-up requires the trajectory to move to the right of the relevant (solid) LK curve.

Now, we are ready to consider the regime of 1:1 synchronization between the late-E and pre-I/early-I neurons, as illustrated by the black trajectory in Fig. 5(b). The upper part of this trajectory, labeled by the leftward arrow, corresponds to a period when the late-E neuron is active and excitation from late-E to pre-I has allowed the pre-I and early-I neurons to become active as well, inducing a large inh ₅. When the late-E neuron reaches the RK (dashed green curve), it jumps to the LB and becomes inactive, and thus h ₅ starts to increase, while inh ₅ slowly decreases due to adaptation of early-I. When the early-I neuron becomes inactive, inh ₅ sharply decreases and the trajectory is able to cross the LK curve (lower left spike in the black trajectory in Fig. 5(b) crosses the solid green curve) but the post-I neuron activates and inhibits the late-E neuron before the late-E can activate, just as in Fig. 5(a) (middle spike in trajectory). This leads to the post-I phase, corresponding to the part of the black trajectory labeled with the downward right arrow. During this phase, h ₅ continues to increase and the post-I neuron adapts, causing inh ₅ to drift down again. This time, the late-E neuron can cross the LK curve and activate (loop structure in the lower part of the black trajectory in Fig. 5(b)). Activation of late-E is quickly followed by early-I activation, resulting in a sharp increase in inh ₅, and the 1:1 cycle repeats.

The grey trajectory in Fig. 5(b) is similar to the black one but corresponds to the 2:1 regime. The key difference between the two cases is labeled “jump-up fails”. There, we see that the 2:1 trajectory reaches the LK (red solid) curve during expiration but is hit with a strong inhibition (increase in inh ₅) due to a second activation of the pre-I/early-I neurons, which prevents the late-E neuron from becoming active; in particular, V ₅ does not become large enough to make f(V ₅ ) nonzero, and hence there is no indication in the 2:1 regime in Fig. 4(a2) that the LK was reached. The end of the second pre-I/early-I phase is followed by post-I activation as previously (rightmost down-up spike along the grey trajectory) and subsequent post-I adaptation (downward arrow along grey trajectory), after which the late-E neuron finally crosses the LK curve and activates near the label “jump-up succeeds” in Fig. 5(b). Interestingly, we note that the value of h ₅ when late-E activation fails in the 2:1 regime is greater than the value when it succeeds in the 1:1 regime. Indeed, an increase in drive to late-E hampers I _NaP deinactivation (lowers h ₅), but it can promote late-E activation nonetheless because of how it lowers the LK curve, decreasing the level of I _NaP required for late-E to cross it. Moreover, the failure of the late-E neuron to activate on particular cycles occurs because the pre-I/early-I neurons activate first, not because the late-E is insufficiently excitable. This observation yields the prediction that a decrease in pre-I and early-I excitability would be sufficient to prevent or reduce late-E cycle skipping.

So far, our analysis has illustrated how late-E activity is determined by its phase plane structures. We can also use this type of analysis to explain why the early-I oscillation period remains roughly constant as the drive to the late-E neuron is varied (Fig. 4(b)). A key point is that transitions between phases can occur through distinct mechanisms known as escape and release (see also Daun et al. 2009; Rubin et al. 2009b; Skinner et al. 1994; Wang and Rinzel 1992). It turns out that even under hypercapnic conditions, the early-I activity in the model is initiated primarily by escape, such that the excitation it receives from pre-I, and by extension the excitation from late-E to pre-I, has little effect on the timing of inspiration onset. This point is illustrated in Fig. 5(c). There, the trajectory shown approaches the blue curve of critical points in the direction of increasing m ₂ while the early-I neuron is active, and hence adapting (rightward arrow; recall that negative input ₂ corresponds to excitation from pre-I), and from the direction of decreasing m ₂ while the early-I neuron is silent, and hence recovering from adaptation (leftward arrow; positive input ₂ corresponds to inhibition from post-I and aug-E). The red curves show the places where the early-I voltage hits the synaptic thresholds V _min (synapses start to activate, upper dashed red curve), V _max (synapses reach maximum strength, lower dashed red curve), and $({V_{\min }} + {V_{\max }})/2$ (solid red curve) from Eq. (12), assuming that the projection of the trajectory to the (V ₂,m ₂) plane lies on the V ₂ nullcline, which is true except during fast voltage excursions at phase transitions. While the early-I neuron is silent, the trajectory reaches the V _min curve at a high input ₂ value, corresponding to strong inhibition. Indeed, even as the post-I neuron adapts (Fig. 5(d), bottom trajectory segment/rightward arrow), the aug-E activity ramps up, yielding a roughly constant inhibition to the early-I neuron. The crossing of the V _min curve by the early-I neuron allows the early-I neuron to start inhibiting the expiratory neurons, which quickly suppresses their activity (e.g., Fig. 5(d), rightmost vertical trajectory segment). Thus, the early-I neuron escapes from the silent phase to the active phase, while the expiratory neurons become silent. This escape is independent of the activation of the late-E neuron and hence a constant early-I neuron period is maintained as d ₃ is varied. Importantly, this invariance of period is also maintained if the model is tuned such that it is pre-I escape, rather than early-I escape, that initiates the inspiratory phase.

Activation of the post-I neuron occurs in a different manner than that described above, namely by release from early-I inhibition. Indeed, while the post-I neuron is silent, the inhibition it receives from the early-I neuron (inh ₃) gradually decreases (Fig. 5(d), upper trajectory segment/leftward arrow) as m ₂ increases and V ₂ decreases correspondingly (Fig. 5(c), bottom trajectory segment). This release allows the post-I neuron eventually to cross the synaptic activation threshold and inhibit the early-I and pre-I neurons. Interestingly, the late-E neuron is gradually released from inhibition in parallel with the release of the post-I neuron. This common release provides a shared window of opportunity for post-I and late-E activation. In the hypercapnic parameter regimes that we simulated, post-I always activates first and suppresses the late-E neuron, but it is possible that in other regimes, corresponding for example to different experimental contexts, an earlier late-E activation could occur.

3.3 Transforming the late-E pattern to biphasic-E activity with development of hypoxia

Abdominal motor activity with a biphasic-E profile, consisting of late-E (or pre-I) and post-I components, was recorded in vivo from decerebrate neonatal rats (Feldman and Del Negro 2006; Janczewski and Feldman 2006b). This abdominal activity pattern was similar to the pattern of single neuron activity recorded from the RTN/pFRG region of the in vitro isolated brainstem-spinal cord preparation of neonatal rats (Onimaru et al. 1988; Onimaru and Homma 1987). The issue of whether the biphasic-E pattern (in both RTN/pFRG and AbN) is a specific characteristic of neonates which transforms to late-E during development or is a characteristic of the specific metabolic conditions of the in vitro preparation (e.g., hypercapnic hypoxia or anoxia) remains unresolved (Abdala et al. 2009a; Ballanyi et al. 1999; Fortuna et al. 2008; Guyenet and Mulkey 2010; Smith et al. 2000; Wittmeier et al. 2008). In the in situ preparations, the biphasic-E AbN activity was more readily evoked in neonates than in juvenile animals (Abdala et al. 2009a). However, transient biphasic-E AbN discharges can be evoked in situ under specific conditions, such as hypercapnic anoxia (7% CO₂, 93% N₂) or recovery from anoxia-induced central apnea (Abdala et al. 2009a). Exposing the system to hypoxia (low O₂) or anoxia (no O₂) results in suppression of post-I activity (Paton and Dutschmann 2002). In the experimental results shown in Fig. 6, we illustrate the consistent finding that transformation of the late-E AbN bursting to a biphasic-E bursting pattern during hypercapnic anoxia is accompanied by a corresponding reduction/suppression of post-inspiratory activity in the cVN. We suggest that the lack of post-I activity elsewhere in the network appears essential for the expression of the post-I component of the biphasic-E AbN discharge pattern.

Fig. 6

Transformation of the pattern of AbN activity from late-E (pre-I) bursting to biphasic-E discharge during hypercapnic anoxia (7% CO₂, 93% N₂, 0% O₂). The top three traces show integrated activity (arbitrary units not shown) of PN, cVN and AbN. The bottom trace represents the index of post-I activity calculated as an averaged activity in cVN during the expiratory phase in each cycle (an example is shown as the gray area in the cVN trace); the expiratory phase was defined by the absence of activity in the PN trace (the vertical dashed line across the first cycle of integrated activity indicates the onset of expiration for the first cycle shown in this example). In the first half of the recorded episode, only late-E bursts were present in AbN. The post-I component of cVN gradually decreased. The transition of AbN bursts to a biphasic-E discharge pattern (with pre-I and post-I components) occurred after a significant suppression of the cVN post-I activity (indicated by vertical and horizontal dash-dotted lines)

It was suggested that the post-I component of the biphasic-E activity pattern represents a post-inhibitory rebound resulting from the abrupt termination of inspiration and a corresponding rapid release of late-E neurons from inspiratory inhibition (Wittmeier et al. 2008), which is normally suppressed by post-I neurons. The activity of post-I neurons has been shown to depend on the pontine input or drive (Dutschmann and Herbert 2006; Rybak et al. 2004a). Thus, to simulate hypercapnic hypoxia conditions, we set d ₃ = 0.04 (producing 1:1 coupling between late-E and pre-BötC oscillations during hypercapnia, see Fig. 4(a3,b)) and decreased pontine drive from d ₁ = 1 to zero linearly over time. Figure 7(a) shows the result of our simulation. With the linear decrease of pontine drive, the late-expiratory burst of the late-E neuron is transformed first to a rebound post-I burst and then to a biphasic-E activity with late-E and post-I components. Simultaneously, a reduction and, finally, a full suppression of activity of the post-I neuron occurs (Fig. 7(a)).

Fig. 7

Simulation of “hypercapnic hypoxia” conditions. The “hypercapnic” drive was set to d ₃ = 0.04 (producing 1:1 coupling between late-E and pre-BötC oscillations, see Fig. 4(a3,b)). (a) Changing model performance with a linear reduction of pontine drive from d ₁ = 1 to zero (lower trace) applied to simulate the development of “hypoxia”. With the reduction of pontine drive, the activity of the post-I neuron weakens and, finally, becomes fully suppressed by inhibition from the aug-E neuron. Simultaneously, the late-expiratory burst of the late-E neuron is transformed first to a rebound post-I burst and then to a biphasic-E activity pattern with pre-I and post-I components. (b) Bifurcation diagram showing the periods of late-E neuron and early-I neuron oscillations as functions of pontine drive d ₁ (indicated on the bottom axis). The diagram shows that with the progressive reduction of pontine drive, the system proceeds through a series of bifurcations indicated by points a–e and the vertical dashed green lines (see details in the text). (c) Trajectories in the (V ₅,V ₂,m ₂) subspace at three levels of pontine drive: unsuppressed (d ₁  = 1, red), reduced to 60% (d ₁  = 0.6, green), and reduced to 20% (d ₁  = 0.2, blue) of the initial value, while the hypercapnic drive to the late-E neuron is held constant (d ₃  = 0.04, hypercapnia)

Figure 7(b) shows the bifurcation diagram representing the periods of late-E and pre-BötC oscillations as functions of pontine drive. To generate this diagram, we reduced d ₁ in a sequence of steps (left to right) from d ₁ = 1 to d ₁ = 0 and simulated the model dynamics for each fixed value of d ₁. The red and blue bifurcation curves show the time intervals between successive activations of the early-I and late-E neurons, respectively. When the pontine drive is strong enough (prior to point a in Fig. 7(b)), late-E neuron activity occurs in a single burst at the end of expiration (late-E or pre-I) with a 1:1 coupling to the pre-BötC activity. The system then proceeds through a series of bifurcations until point d, when late-E neuron activity settles into a post-I pattern. At point a, a bifurcation happens that splits (doubles) the period curves but bursts by late-E and pre-BötC neurons remain phase-locked (1:1). In the region between points b and d, the timing of bursts of late-E neuron activity varies between pre-I (i.e., just before the early-I phase) and post-I, with post-I becoming more common as pontine drive increases. Specifically, in the (b,c) interval, late-E neuron bursts alternate between pre-I and post-I. Then, to the right from c, two out of every three late-E bursts occur during the post-I phase, and so on. This sequence converges at point d. The transitions between these regimes likely occur through chaotic behavior (note the spread in periods in the vicinity of the points b, c and d). The period of the pre-BötC neurons does not undergo any further jumps as late-E neuron activity transitions from a post-I type to a biphasic-E response (point e). At point e, the post-I activity becomes weak enough to allow for the emergence of a second late-E neuron burst in the pre-inspiratory phase. This converts the shape of late-E neuron activity to a biphasic-E (pre-I/post-I) discharge.

Figure 7(c) shows projections of typical trajectories to the (V ₅,V ₂,m ₅) subspace, corresponding to three levels of pontine drive (unsuppressed pontine drive, d ₁  = 1, red; 40% suppression, d ₁  = 0.6, green; and 80% suppression, d ₁  = 0.2, blue), while the hypercapnic drive to the late-E neuron is held constant (d ₃  = 0.04, hypercapnia). Periods of sub- and supra-threshold late-E neuron activity are distinguished by dashed and solid lines, respectively. When d ₁  = 1, a 1:1 late-E to pre-I/I and early-I synchronization is observed, and therefore all instances of supra-threshold V ₂ activity are preceded by supra-threshold V ₅ activity. Once supra-threshold V ₂ activity is achieved, m ₂ begins to increase, and soon thereafter, V ₅ rapidly drops due to inhibition from the early-I. After termination of late-E neuron activity, m ₂ continues to increase and causes a gradual decrease in V ₂, until the post-I neuron is released and early-I neuron activity ends. Finally, after V ₂ has decreased to a minimum, there is a small decrease in V ₅ as inhibition from the post-I neuron takes over and expiration begins. During expiration, m ₂ resets to its initial value before the late-E neuron bursts again and restarts the cycle. For d ₁  = 0.6 (green trajectory), the periods when V ₂ and V ₅ are supra-threshold have become separate. At the end of inspiration, m ₂ begins to decrease and a V ₅ rebound emerges. During the rebound, V ₂ remains unchanged and no supra-threshold activity is observed until m ₂ reaches its minimum, well after V ₅ activity has ended. The inspiratory phase, marked by an increase in V ₂ , begins after m ₂ reaches its minimum; this phase then terminates similarly to the trajectory corresponding to d ₁  = 1. When the pontine drive is further suppressed (d ₁  = 0.2, blue) a biphasic-E pattern is observed. Following the termination of inspiration, an immediate increase in V ₅ to supra-threshold activity is observed. This rebounding activity occurs while m ₂ is still quite elevated and terminates earlier in the expiratory phase than it does when d ₁  = 0.6. After V ₅ returns to its sub-threshold state, m ₂ continues to decrease and a second increase in V ₅ precedes the emergence of supra-threshold V ₂ activity. V ₂ begins its increase with a larger value of m ₂ than in the other cases, presumably due to excitation received from the late-E neuron, which allows it to overcome some residual adaptation. V ₅ then begins to decrease as V ₂ and m ₂ increase, and inspiration ensues as previously.

Figure 8(a–d) illustrates and explains the mechanisms providing the transformation in the pattern of late-E neuron activation. In Fig. 8(a–c), the behavior of the late-E neuron is considered in the (V ₅,h ₅) plane for the regimes shown in Fig. 7(c). The positions of the V ₅ nullclines in this plane are crucial for determining the late-E behavior. The uppermost nullcline in each plane arises when the late-E neuron is maximally inhibited by the early-I neuron. The next nullcline down arises at the onset of post-I neuron activity. As d ₁ is decreased, the peak in post-I neuron activity is reduced and hence the inhibition from the post-I to the late-E neuron weakens, changing the position that the V ₅ nullcline takes during post-I neuron activity. Finally, post-I inhibition gradually decreases during expiration, causing the V ₅ nullcline to move progressively lower, and certain examples of resulting nullcline positions, occurring at important moments in the evolution of each solution, are also shown.

Fig. 8

Phase plane analysis in case of hypercapnic hypoxia. (a–c) Blue curves show V ₅ nullclines for various levels of inhibition to the late-E neuron while red curves show the h ₅ nullcline. (a) For d ₁  = 1, V ₅ nullclines shown correspond to the inhibition to the late-E neuron at the start of early-I activity (top), at the start of post-I activity (middle), and at the moment when late-E activates (bottom). (b) When pontine drive is reduced to 60% of the default value (d ₁  = 0.6), the late-E neuron exhibits only “rebound” bursts during the post-I phase. The top three V ₅ nullclines shown are analogous to those in a, although the positions of the middle and lower of these three differ due to different levels of post-I activation. The lowermost V ₅ nullcline corresponds to the level of inhibition to the late-E neuron at the onset of early-I activity. (c) When pontine drive is reduced to 20% (d ₁  = 0.2), biphasic late-E neuron activity occurs. The V ₅ nullclines shown correspond to the inhibition to the late-E neuron at the start of early-I activity (top), at the start of post-I activity (middle), and just before the onset of early-I activity (bottom). The nullcline corresponding to the moment when the late-E neuron undergoes rebound activation (analogous to the bottom nullcline in a) is omitted due to its proximity to the middle nullcline shown. (d) Projection of model trajectories to the (input ₂,m ₂) plane at pontine drive reduced to 60% (d ₁  = 0.6, grey, rebound regime) and to 20% (d ₁  = 0.2, black, biphasic regime), along with curve of critical points (blue) and synaptic threshold curves (red; as in Fig. 5). In both regimes, the dip in the trajectory at high input ₂ occurs when rebound activation of the late-E neuron happens, because the pre-I neuron is slightly activated and hence a small excitation to the early-I neuron (decrease in input ₂) results (see text for further details)

When d ₁ = 1, the mechanism for the pre-I activation of the late-E neuron is rather straightforward. As the post-I neuron adapts and its inhibition to the late-E neuron weakens, the LK of the V ₅ nullcline eventually dips below the trajectory in the (V ₅,h ₅) plane, which allows the late-E neuron to jump to high voltage (Fig. 8(a)). As discussed with respect to Fig. 5(c), by the time this happens, the early-I neuron is ready to activate on its own, such that the late-E neuron’s activity ends up occurring just before the onset of inspiration, and the pre-I regime of late-E neuron activation results.

When the pontine drive is reduced, the post-I neuron achieves a lower level of activity and thus the inhibition to the late-E neuron during the post-I phase is weaker than in the case of full drive. Thus, the V ₅ nullcline drops below the trajectory, allowing late-E activation earlier in the post-I phase, which we call post-I rebound (Fig. 8(b)). This activation of late-E could potentially recruit the early-I neuron but in fact fails to do so. Indeed, we observe that the pre-I neuron cannot strongly activate in response to this earlier late-E activation, because it has not had enough time to recover and overcome the inhibition it receives from the post-I and aug-E neurons (Fig. 7(a)). The weak activation of the pre-I neuron is insufficient to activate the early-I neuron (Fig. 7(a) and 8(d), grey trajectory: note that the dip in the upper part remains just above the dashed synaptic threshold curve). Since it does not immediately precede inspiratory activity, the activation of the late-E neuron cannot be labeled as pre-inspiratory in this case. Indeed, it is likely that the various, possibly chaotic regimes arising between the pre-I and post-I rebound cases as d ₁ is reduced (Fig. 7(b)) involve shifts in the timing of late-E neuron activation relative to the onset of pre-I/early-I neuron activity. Finally, although the late-E neuron’s activity ends before pre-I/early-I neuron activity starts, and the trajectory in the (V ₅,h ₅) plane returns back to the LB of the V ₅ nullcline, this trajectory lies below the knee of the relevant V ₅ nullclines, determined by the inhibition from the post-I neuron to the late-E neuron, until the early-I neuron activates and strongly inhibits the late-E neuron, pushing the trajectory back to the upper V ₅ nullcline (Fig. 8(b), “blocked”).

When the pontine drive becomes lower still, this last observation no longer holds. The late-E neuron’s post-I rebound occurs earlier in the post-I phase (also evident in the early-I neuron’s dynamics as the dip in the top part of the black trajectory in Fig. 8(d)), so that h ₅ has more time to recover before the early-I neuron activates, and furthermore, the LK of the V ₅ nullcline is lower throughout the post-I phase because the post-I neuron’s activity is weaker. Thus, the trajectory is able to climb above the knee of the V ₅ nullcline and activate the late-E neuron a second time before the early-I neuron becomes active (Fig. 8(c), “pre-I burst occurs”). This second late-E activation yields enough activation to pull the early-I neuron into the active phase before it reaches the synaptic threshold on its own. The fact that excitatory input plays a role in recruiting the early-I neuron can be seen from the fact that the black trajectory in Fig. 8(d) lies above the top dashed (“synapses on”) curve when it suddenly undergoes a near-vertical drop, corresponding to synaptic excitation of the early-I neuron (via excitation of the pre-I neuron by the late-E neuron) and resulting in the onset of the inspiratory phase.

The recruitment of the early-I neuron by the late-E neuron in the biphasic regime, which we have identified using phase plane analysis, explains the decrease in early-I oscillation period that occurs as pontine drive decreases in the biphasic-E regime, as shown in Fig. 7(b). Interestingly, this decrease occurs despite the increase in the aug-E activity level and, correspondingly, in the level of inhibition that the aug-E neuron sends to the pre-I and early-I neurons. In addition to explaining this aspect of how period changes with pontine drive, our analysis makes a clear prediction that post-I rebound occurs as a natural intermediate state between regimes in which late-E neuron activation is a pre-I event and those in which late-E neuron activation is biphasic: in the model, as post-I neuron activity weakens, late-E neuron activity can emerge earlier in the respiratory period via rebound, but only with additional post-I weakening can the late-E neuron activate a second time before the pre-I/early-I neurons are activated and suppress the late-E neuron.

3.4 Quantal slowing of pre-BötC oscillations

“Quantal slowing” of breathing is a phenomenon in which the average breathing frequency is reduced as a result of the skipping of output bursts in the pre-BötC or phrenic motor output while RTN/pFRG or related abdominal oscillations are maintained (Janczewski and Feldman 2006a; Mellen et al. 2003). Experimentally, this phenomenon was demonstrated by administration of μ-opioid agonists, such as DAMGO or fentanyl, which was suggested to suppress excitability of pre-BötC neurons (Janczewski and Feldman 2006a; Mellen et al. 2003).

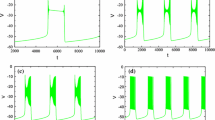
To simulate quantal slowing in the model, we started from conditions of “hypercapnic hypoxia”, established by increasing the “hypercapnic” drive to d ₃  = 0.04 and reducing pontine drive to d ₁  = 0.4, so that the late-E neuron expressed biphasic-E busts with 1:1 coupling to the pre-BötC oscillations (see Figs. 7(a) and 9(a)). Pre-BötC depression was simulated by a progressive reduction of the maximal conductance of excitatory synaptic inputs (${\bar{g}_{SynE}},$in Eqs. (7) and (8); the default value is 10 nS) in both pre-BötC neurons (pre-I/I and early-I). The results of the quantal slowing simulation are shown in Fig. 9(a), where ${\bar{g}_{SynE}}$ in the pre-I/I and early-I neurons is reduced linearly over time from 80% of the default value to 64%, at which point the ratio of the late-E to pre-BötC oscillation frequencies becomes 5:1, and then kept constant.

Fig. 9

(A) Simulation of “quantal slowing” of pre-BötC oscillations. “Hypercapnic hypoxia” conditions were set by fixing “hypercapnic” drive at d ₃ = 0.04 and reducing pontine drive to d ₁ = 0.4, so that the late-E neuron expressed biphasic-E busts with 1:1 coupling to the pre-BötC oscillations (see the text and Fig. 7(A)). Pre-BötC depression was simulated by a progressive reduction of the maximal conductance of excitatory synaptic inputs in both pre-BötC neurons (the default value is 10 nS). ${\bar{g}_{SynE}}$ in the pre-I/I and early-I neurons was linearly reduced from 80% of the default value to 64%, where the ratio of the late-E neuron to pre-BötC neuron oscillation frequencies becomes 5:1, and then kept constant. (B) Bifurcation diagram of the period of pre-BötC oscillations as a function of ${\bar{g}_{synE}}$ in pre-BötC neurons (pre-I/I and early-I). ${\bar{g}_{synE}}$ defines the excitability of these neurons and is reduced from its default value (on the left) to 60% of the default value (to the right). The late-E neuron’s period remains relatively constant as the pre-BötC neuron’s period proceeds through a series of jumps in duration. Each jump represents a quantal change of the ratio of the pre-BötC oscillation frequency to the late-E frequency. (C) Two-parameter bifurcation diagram that shows the period of pre-BötC oscillations as a function of pontine drive and ${\bar{g}_{synE}}$. Darker colors indicate shorter periods of pre-BötC activity (see palette on the right). The yellow area indicates no activity in the pre-BötC neurons. Areas of different regimes are labeled by the ratio of the late-E frequency to the pre-BötC frequency (from 1:1 to 5:1). The dashed white line indicates the level of pontine drive corresponding panels A and B. (D) A trajectory in the (V ₅,V ₂,h ₅) subspace generated with the pontine drive reduced to 40% (d ₁ = 0.4) and ${\bar{g}_{synE}}$ reduced to 65% of baseline, representing the 4:1 synchronization regime. The part of the trajectory for which early-I neuron activity is sub-threshold (below −50 mV) is dashed and the part with supra-threshold early-I activity is solid

The suppression of excitability of the pre-BötC neurons compromises their ability to activate via escape from the inhibition of the BötC neurons. When pre-BötC neurons are unable to escape, expiration increases in duration. Late-E neuron activity remains biphasic precisely on those cycles on which pre-BötC neurons fire (Fig. 9(a)). Consistent with cycle skipping, the bifurcation diagram in Fig. 9(b), created by simulating the model for each of a sequence of fixed ${\bar{g}_{SynE}}$ values between 100% and 60% of the default value, shows that the period of the pre-BötC oscillations increases as the suppression of pre-BötC excitability progresses. The gradual decrease of pre-BötC excitability causes the pre-BötC to move through a series of regimes with increased periods of pre-BötC oscillations (quantal slowing), arising as ratios (1:1, 2:1, etc.) of the late-E frequency to the pre-BötC frequency. The existence of such regimes depends on the pontine drive suppression, reflecting the level of “hypoxia”. The two-parameter bifurcation diagram in Fig. 9(c) illustrates this relationship. A reduction of pontine drive changes the levels of pre-BötC excitability at which the “steps” between regimes of synchronization, with different frequency ratios between the late-E and pre-BötC oscillations, occur.

Figure 9(d) shows a trajectory in (V ₅,V ₂,h ₅) at d ₁  = 0.4 and ${\bar{g}_{synE}}$ reduced to 65%, corresponding to the 4:1 regime (see Fig. 9(b)). Three cycles of late-E neuron activation and deactivation occur without any supra-threshold early-I neuron activity. After the fourth late-E neuron activation, V ₂ increases above the synaptic threshold and early-I neuron activity ensues. The activation of the early-I neuron causes a decrease in V ₅ (silencing the late-E neuron). Finally, V ₂ proceeds back to a sub-threshold value, and the late-E neuron’s bursts resume.

Using phase plane analysis, we can explain why late-E neuron activity is biphasic precisely on those cycles where inspiratory activation occurs. On “rebound cycles” that lack supra-threshold early-I activity, the projection of the trajectory to the (V ₅,h ₅) plane reaches the LK of the appropriate V ₅ nullcline and the late-E neuron activates (Fig. 10(a)), and then the trajectory travels down the RB of the V ₅ nullcline, hits the RK, and returns to the LB of the V ₅ nullcline. This late-E neuron activation, however, fails to elicit early-I neuron activation and the associated increase in inhibition (inh ₅) of the late-E neuron. Over successive rebound cycles, post-I and aug-E activity levels, and hence the level of inh ₅, quickly equilibrate. Figure 10(b) shows another view of these cycles as part of a full 2:1 trajectory, projected to the (h ₅ ,inh ₅) plane. This image includes LK (solid) and RK (dashed) curves. Each late-E neuron activation cycle corresponds to an excursion from the LK curve to the RK curve and a return to the LK curve. On pure rebound cycles, since inh ₅ is approximately constant, the trajectory is roughly horizontal (Fig. 10(b), pure rebound). Eventually, a cycle is reached on which late-E neuron activation does lead to early-I neuron activity (Fig. 10(b), pre-I), with a corresponding rapid rise in inh ₅. The inhibition to the late-E neuron elicited by the activation of the early-I neuron causes the V ₅ nullcline to move to a high position in the (V ₅,h ₅) plane (Fig. 10(a); also Fig. 8(c)). In particular, the right knee of the V ₅ nullcline has an h ₅-coordinate that significantly exceeds the h ₅ value on the solution trajectory at the onset of early-I activity (Fig. 10(b); note that the h ₅ value at the point of highest inh ₅ along the trajectory is much smaller than the h ₅ value at the red, dashed RK curve for that inh ₅). Thus, the late-E neuron quickly returns to the silent phase when early-I neuron activity starts (as illustrated in Fig. 5(a), middle excursion, as well). This rapid return prevents significant inactivation of I _NaP in the late-E neuron, such that h ₅ remains relatively high, and h ₅ continues to increase while the late-E neuron is inhibited by the early-I neuron throughout the inspiratory phase (Fig. 10(b), inspiration). When inspiration ends and this inhibition is removed, the high value of h ₅ relative to the LK of the V ₅ nullcline (Fig. 10(b); note that the part of the trajectory with lowest inh ₅ and h ₅ > 0.35 has h ₅ well above the solid, red LK curve for that inh ₅) allows the late-E neuron to undergo rebound activation, resulting in a biphasic late-E activity profile (Fig. 10(b), post-I rebound; note that the post-I neuron also activates at that time, causing inh ₅ to become nonzero along the post-I rebound part of the trajectory).

Fig. 10

Phase plane analysis in the case of suppression of pre-BötC excitability. (a) Cycling of late-E activity during expiration. V ₅ nullclines are shown as solid blue curves; the upper nullcline corresponds to the onset of inhibition from the early-I neuron and the middle and lower nullclines to the onset and steady-state levels of inhibition from the post-I neuron, respectively. The black trajectory represents a series of late-E neuron activation cycles occurring during expiration that are not followed by pre-I/early-I activity. (b) Trajectory for an oscillation with a 2:1 late-E:early-I oscillation frequency ratio, in the (h ₅,inh ₅) plane. Included with the trajectory are curves of left knees (solid red) and right knees (dashed red). The horizontal parts of the trajectory correspond to periods when the late-E neuron is active; the post-I rebound immediately follows inspiration while the pure rebound occurs without inspiratory activity. The segment of the trajectory labeled pre-I corresponds to the time of activation of the late-E neuron just prior to inspiration, which is followed by the activation of the pre-I/early-I neurons, the sharp rise in inh ₅, and the subsequent inspiration phase. (c,d) Projections of the trajectory for a 4:1 late-E:early-I solution. (c) (V ₁,h ₁) plane for the pre-I neuron. The trajectory is superimposed on the h ₁ (red) and V ₁ nullclines (blue) corresponding to the steady-state level of inhibition from the post-I/aug-E neurons (upper) and to the absence of inhibition (lower). The threshold for the turn-on of synaptic output from the pre-I neuron is also shown (dashed blue). Time increases in a clockwise direction along the trajectory. Note that there are five, not four, excursions in V ₁ away from the LB in this image due to the fact that the late-E neuron, which excites the pre-I neuron, exhibits one cycle of biphasic activation. (d) (m ₂,input ₂) plane for the early-I neuron. The trajectory is superimposed on the curves corresponding to the onset of early-I synaptic activity (upper dashed red), half-maximal (solid red), and maximal (lower dashed red) early-I synaptic activity. The blue curve is a curve of critical points, which becomes vertical at m ₂ = 0. Time increases in a counterclockwise direction along the trajectory, with the top corresponding to expiration and the bottom to inspiration

It is not surprising that a reduced pre-BötC excitability causes the pre-BötC neurons to skip cycles. Exactly which cycles will be skipped is determined by the evolution of the variables for these neurons in the model network, relative to the synaptic activation threshold, which reflects the level of inhibition that they receive. More precisely, the pre-I neuron receives synaptic excitation when the late-E neuron activates. This excitation may push V ₁ above the synaptic activation threshold of −50 mV (Fig. 10(c)), but it will not induce full pre-I neuron activation if the trajectory does not reach the RB of the V ₁ nullcline. The weak crossing of the synaptic activation threshold by the pre-I neuron results in a weak excitation of the early-I neuron, which either fails to turn on the early-I neuron’s synaptic outputs (Fig. 10(d); note that excursions 1 and 2 lie above the “synapses on” curve) or turns them on only very weakly (Fig. 10(d), excursion 3), such that the early-I neuron cannot terminate post-I/aug-E activity and take over. In the example shown in Fig. 10(d), the m ₂-coordinate of the trajectory approaches a minimum value very close to 0 while the early-I neuron is inactive until finally, a fourth activation of the late-E neuron pulls the trajectory across the early-I synaptic activation curve (by decreasing input ₂) and causes the onset of inspiration.

We emphasize that, in contrast to hypercapnic simulations, the activation of the early-I neuron in the case of quantal slowing results not from escape but from recruitment by the late-E neuron. Thus, the burst times of the pre-BötC neurons are set by the RTN/pFRG period in this regime, which stands as a prediction of the model, along with the prediction that biphasic late-E neuron activation occurs exactly on those cycles on which early-I neuron activation occurs.

4 Discussion

We have analyzed a reduced model based on a proposed network of interactions (Abdala et al. 2009a) between two oscillators involved in the neural control of breathing: a BötC/pre-BötC oscillator that is considered a rhythmogenic kernel of the respiratory CPG, and a RTN/pFRG late-E oscillator that is activated with increasing metabolic demands and, when activated, generates late-E (or pre-inspiratory) oscillations. Using simulations and bifurcation analysis, we have explored how changes in drives within the network shift output patterns from a baseline state of late-E neuron quiescence, through a regime of late-E neuron quantal acceleration featuring 1:N phase-locking between late-E and BötC/pre-BötC activation, through an evolution of late-E neuron output patterns culminating in biphasic activation, to a regime of quantal slowing featuring N:1 phase-locking between late-E and BötC/pre-BötC activation. Using phase plane analysis, we have explained the mechanisms for transitions between regimes. We have also elucidated why recruitment of late-E activity in quantal acceleration does not affect BötC/pre-BötC period, why a regime of post-I rebound late-E neuron activation arises before biphasic late-E neuron activation and why BötC/pre-BötC period decreases as pontine drive in the model is reduced, as well as why biphasic late-E activation persists precisely on cycles featuring BötC/pre-BötC activation in quantal slowing. These features of model dynamics all stand as predictions for subsequent experimental testing, and inasmuch as our analysis shows how particular model components affect these features, we can also predict the effects of experimental manipulations, such as changes in excitability of particular respiratory neuron populations, on network outputs.

4.1 Two oscillators involved in respiratory rhythm generation

The longstanding view has been that the generation of the respiratory rhythm and (inspiratory-expiratory) motor pattern involves network interactions, mostly inhibitory, between different populations of respiratory neurons located within, or distributed over, multiple brain stem compartments (Bianchi et al. 1995; Cohen 1979; Feldman 1986; Richter 1996). From the time of its discovery (Smith et al. 1991), the pre-BötC has been shown to play an essential role in respiratory rhythm generation (reviewed in Feldman and Del Negro 2006). However, the pre-BötC alone (without interactions with other brain stem compartments, e.g., with the BötC) is not sufficient for generating the normal respiratory rhythm and pattern (eupnea). Recent experimental studies, based on a series of brain stem transections in situ, and the corresponding modeling studies suggest that the network interactions within and between the pre-BötC and BötC, along with the intrinsic rhythmogenic properties of pre-BötC neurons, form a hierarchy of multiple oscillatory mechanisms (Rybak et al. 2007, 2008; Smith et al. 2007, 2009). The functional expression of these mechanisms is controlled by drives from other brain stem components, including the RTN and pons, which regulate the dynamic behavior of the core circuitry and may re-organize it with changes in physiological or metabolic conditions (Rybak et al. 2007; Smith et al. 2007; Smith et al. 2009; Rybak et al. 2008). The important role of the BötC and other brain stem regions for respiratory rhythm generation has been experimentally re-confirmed by several recent studies (Abbott et al. 2009; Burke et al. 2010; Monnier et al. 2003).

Alternatively, the current dual oscillator concept suggests that there are two distinct rhythm generators driving breathing when the RTN/pFRG is active: one located in the pre-BötC and considered to be an inspiratory rhythm generator, and another located in the RTN/pFRG and considered as an expiratory rhythm generator (Janczewski and Feldman 2006b; Mellen et al. 2003). This contrasts with our suggestion that the first oscillator represents a core network of the respiratory CPG that generates coordinated respiratory (i.e., inspiratory, post-inspiratory and expiratory) oscillations, particularly due to the network interactions within the CPG kernel (BötC/pre-BötC) that in turn are controlled by inputs from other brain stem compartments (RTN, pons). Indeed, the essential feature of our model, distinguishing it from other related models, is that rhythm generation in this oscillator relies on the network interactions within the pre-BötC/BötC circuitry and generates not just inspiratory oscillations but a coordinated inspiratory-expiratory oscillatory pattern. In particular, this circuitry generates its own expiratory activity (provided by post-I and aug-E neurons of the BötC), which also contributes to the specific interactions between the CPG kernel and the RTN/pFRG oscillator.

4.2 Modeling the interactions between the oscillators

Three relatively simple computational models have been proposed previously to simulate coupling between pre-BötC and RTN/pFRG oscillators and to suggest possible mechanisms that govern their interactions. Joseph and Butera (2005) used an abstract canonical model composed of two identical phase oscillators. Wittmeier et al. (2008) simulated both oscillators as single neurons with I _NaP -dependent bursting properties described previously (Butera et al. 1999a), and Lal et al. (2010) considered interacting populations of such neurons. The connections between the oscillators proposed in all these models were: (a) an excitatory input from the RTN/pFRG oscillator to the pre-BötC oscillator, providing the entrainment of the latter by the former, and (b) an inhibitory input from the pre-BötC oscillator to the RTN/pFRG one, providing inhibition of the latter during inspiration. These connections were sufficient to reproduce regimes of quantal slowing of the pre-BötC oscillator with the phase relationships observed experimentally under conditions of reduced excitability of pre-BötC neurons, which was considered as a test for these models.

The same two connections have been included in our model (Fig. 1(a)), which also produced a realistic simulation of quantal slowing behavior (see Fig. 9), without requiring any decrease of pre-BötC activation amplitude, as was needed in an earlier study (Lal et al. 2010). In contrast to the dual oscillator concept (Janczewski and Feldman 2006b; Mellen et al. 2003) and the previous models (Joseph and Butera 2005; Lal et al. 2010; Wittmeier et al. 2008), in which the pre-BötC oscillator is only active and able to affect the RTN/pFRG oscillator during inspiration, our model incorporates an additional third connection, namely the inhibitory connection from the post-I neuron of the BötC to the late-E neuron of the RTN/pFRG. Our analysis shows that this connection is critical for reproducing and explaining the regime of quantal acceleration of RTN/pFRG oscillations (Abdala et al. 2009a, b; Guyenet and Mulkey 2010; Iizuka and Fregosi 2007). Moreover, we showed that the reduction/suppression of this inhibitory input is critical for the transformation of the late-E activity to the biphasic-E pattern during simulated hypercapnic hypoxia/anoxia (Figs. 6, 7 and 8; see also Guyenet and Mulkey 2010).

The existence of (presumably post-I) inhibition of RTN/pFRG activity during expiration is consistent with previously proposed inhibition of RTN chemosensitive neurons by the medullary CPG circuits during both inspiration and expiration (Fortuna et al. 2008; Guyenet et al. 2005; Guyenet 2008) and is indirectly confirmed by the experimental finding that blockade of inhibition within RTN/pFRG can produce (release) and accelerate the RTN/pFRG and/or abdominal oscillations in normal metabolic conditions (Onimaru et al. 1990; Pagliardini et al. 2009).

4.3 Coupling between the BötC/pre-BötC and pFRG/RTN oscillators

Within the framework of synchronization, the BötC/pre-BötC and RTN/pFRG generators can be considered as a system of coupled oscillators. The dynamics of each oscillator may be represented by a stable limit cycle in some phase space. The phase space of a system of two oscillators is a Cartesian product of the phase spaces of each oscillator. The corresponding limit set is a 2D invariant torus and the behavior of this system is represented by a trajectory on this torus (Fig. 11(a1,a2); see also Pikovsky et al. 2003). If the ratio of oscillation frequencies of the two oscillators is rational (i.e. equal to N/M, for some integers N and M), then this trajectory is closed, indicating N:M synchronization between oscillators, where the numbers N and M represent topological invariants, namely the numbers of rotations around two orthogonal circles that together span the torus (e.g., large and small circles as illustrated in Fig. 11(a1,a2)).

Fig. 11

(a1,a2) Illustration of coupling between two oscillators with different ratios of frequencies represented by the trajectories on a 2D torus. In a1 the system makes 4 “large” cycles during 1 “small” cycle (1:4 synchronization regime). In a2 the system makes 4 “small” cycles during 1 “large” cycle (4:1 synchronization regime). (b1, b2) The corresponding examples from the current model with different ratios between the late-E (FRG/RTN) and BötC/pre-BötC oscillations shown in (V ₂,m ₂ + h ₅,V ₅) subspace. The trajectory in b1 corresponds to a “weak hypercapnia” 1:3 synchronization regime, in which one cycle of late-E corresponds to 3 rotations of early-I. In b2, the excitability of pre-BötC neurons is suppressed, producing the 4:1 synchronization regime. The oscillators switch their roles. Late-E traverses 4 cycles while early-I rotates only once

With changing conditions, the system of coupled oscillators can proceed through regimes characterized by different relations between oscillation frequencies and phase relationships. In this context, the specific interactions between the oscillators perform two functions. First, they help select the particular (N,M) pairs for which stable synchronized oscillations occur, and second, they constrain the phase relationships between the oscillators within these oscillations. The regimes considered in this study can be interpreted based on this concept.

Interestingly, our analysis reveals that a sequence of shifts in the functional coupling between the BötC/pre-BötC and RTN/pFRG oscillators occurs across the regimes that we have simulated. Our simulation of progressive hypercapnia (Fig. 4) is based on a gradual increase of RTN/pFRG excitability that results in a quantal increase in the frequency of RTN/pFRG oscillations, as seen in abdominal motor output (Abdala et al. 2009a, b; Iizuka and Fregosi 2007). With a progressive increase of RTN/pFRG excitability (as could be defined by the CO₂ level), these oscillations emerge then accelerate and proceed through a series of phase-locked resonances with 1:N ratios between the RTN/pFRG and BötC/pre-BötC frequencies, with N decreasing from an initial higher value to 1 (see Fig. 11(b1)). Given the tuning of our model to reproduce experimentally observed regimes of activity, a feature that arises is that by the time post-I inhibition decays enough to allow late-E activation, the early-I neuron has already reached the synaptic activation curve and is thus able to escape (despite roughly constant inhibition from post-I plus aug-E) and become active on its own, without the excitatory input triggered by the late-E neuron (Fig. 5(c)). In this regime, late-E neuron activation is also independent of BötC/pre-BötC activity, such that the two oscillators are effectively uncoupled. Moreover, although the late-E neuron activates first on cycles in which it does become active, it does not entrain inspiratory activity and hence the frequency of the RTN/pFRG oscillations approaches the frequency of the BötC/pre-BötC oscillator, which remains essentially constant, as N decreases. The maintenance of a steady oscillation frequency in hypercapnia, despite the appearance and acceleration of late-E activity, represents a prediction of this model, although this may be specific to particular experimental settings that lack additional feedback signals (e.g. from lung stretch receptors) not present in the model. Furthermore, since post-I neuron activation occurs through release from inhibition from the early-I neuron, and this inhibition is shared by the late-E neuron as well, our model suggests the theoretical possibility that the timing of late-E activity could switch from pre-I to post-I or even biphasic under strong hypercapnic conditions.

In simulated hypercapnic hypoxia (Fig. 7), the system can exhibit phase-locked regimes with different phase shifts depending on pontine drive, which controls the expression of post-I neuron activity and hence the inhibition from the post-I neuron to the late-E and pre-BötC neurons. If late-E neuron activity entrained pre-BötC activity in the regime when late-E neuron activation directly precedes pre-BötC activity, then a decrease in post-I inhibition would be expected to maintain and accelerate the regime of pre-inspiratory late-E neuron activation (pre-I regime). Instead, a switch to the rebound regime, in which late-E activity occurs during expiration but is not associated with a switch to inspiration, occurs. In the rebound regime, the late-E neuron would be able to generate repetitive oscillations on its own under the reduced level of post-I inhibition, especially as that inhibition decayed during expiration. The inhibition that the late-E neuron receives from the early-I neuron during inspiration, however, suppresses its activity, setting up a certain phase relationship between inspiration and late-E activation (Fig. 8(b)). After this inhibition is removed, the late-E neuron can break free from post-I inhibition more easily than it could in the purely hypercapnic regime. But the excitation of the pre-BötC that ensues from an earlier late-E activation cannot cause early-I activation (Fig. 8(d)). Thus, the RTN/pFRG/pre-BötC network switches from being effectively decoupled in the pre-I regime to having an effectively one-way coupling, from pre-BötC to RTN/pFRG, in the rebound regime. We note that the transitions between these regimes occur through aperiodic, possibly chaotic, behaviors (see Fig. 7(b)), corresponding to a form of asynchronous dynamics as the oscillators cannot settle into a phase-locked regime.

As pontine drive is progressively lowered, the rebound regime gives way to the biphasic regime when the late-E neuron recovers enough, due to its intrinsic dynamics and the further weakened post-I inhibition, to activate a second time during expiration. In contrast to the pre-I regime observed in pure hypercapnia, this second activation does recruit the pre-BötC neurons (Fig. 8(d)). Pre-BötC neuron activity suppresses late-E neuron activity, but as a result the persistent sodium current for the late-E neuron shows little inactivation and the late-E neuron can rebound immediately following the end of inspiration (Fig. 8(c)), yielding the biphasic activity profile. Thus, the biphasic regime reflects two-way coupling between the RTN/pFRG and BötC/pre-BötC oscillators. A decrease in oscillation period in this regime arises because less I _NaP deinactivation is required for the late-E neuron to escape from the weaker post-I inhibition and the late-E neuron is able to entrain the pre-BötC neurons, despite the increase in aug-E activity and the associated inhibition. A subtle point is that, because the late-E rebound occurs earlier than in the pure rebound regime, the resulting excitation does not interfere as much with recovery of the pre-I pre-BötC neurons (through deinactivation of I _NaP ) as its later rebound does.

In summary, our model offers a possible explanation of why, under gradual suppression of pontine drive, the timing of late-E activation progresses from late-E activation to rebound activation and finally to biphasic activation. This hypothesis yields the prediction that recordings featuring biphasic late-E activity represent states of low pontine drive or high pontine suppression or states in which some other factor limits post-I activation.

Finally, in addition to effects of hypercapnia and reduced pontine drive, we have considered progressive suppression of pre-BötC excitability (e.g., by opioid agonists), which leads to quantal slowing of pre-BötC activity (Janczewski et al. 2002; Janczewski and Feldman 2006a; Mellen et al. 2003). In this regime in our model, the network interactions between the oscillators (specifically the excitatory connection from the RTN/pFRG to pre-BötC) provide phase locking. Due to their decreased excitability, the pre-BötC neurons depend on recruitment by the late-E neuron to activate. Thus, the pre-BötC frequency is quantally reduced through a series of resonances with M:1 ratios between the RTN/pFRG and BötC/pre-BötC frequencies with M increasing from 1 to higher values (see Fig. 11(b2)). The pre-BötC to RTN/pFRG connection becomes less important in this regime than in the others. This connection does yield the biphasic late-E neuron activity profiles seen in oscillation cycles that feature pre-BötC activity (Fig. 10(b)). However, the time interval between late-E neuron activations does not differ noticeably between these cycles and cycles of pre-BötC skipping (Fig. 9(a)) and the late-E neuron controls oscillatory period. The mechanisms responsible for the precise shapes of the curves delineating transitions between regimes as pontine drive and pre-BötC excitability vary (Fig. 9(c)), and the full characterization of the dynamics of the model network presented here, remain for further investigation.

4.4 Modeling issues

We have used a reduced model in this paper. This reduction includes the omission of various currents present in biological neurons and imposes certain characteristics on the model’s outputs. In particular, the model aug-E neuron exhibits a brief surge of activity at the start of the post-I phase in our simulated solutions. This surge is a figment of the model aug-E neuron’s monotone nullclines. With such a simplified model structure, the rapid cessation of inhibition from the early-I neuron causes the aug-E voltage nullcline to quickly move to elevated voltages, and a corresponding rise in the aug-E neuron’s voltage results. Post-I activation quickly tamps out the aug-E surge, and this feature is not necessary in the model rhythms. Moreover, there is little distinction between the timing of activation of the pre-I and early-I neurons in the model. We claim that our insights about the relationship of late-E and pre-BötC activity in different regimes will carry over to activity patterns with a more realistic time shift between pre-I and early-I phases. In particular, the idea that pre-BötC activity need not be entrained by late-E in hypercapnia would hold if the early-I escape from inhibition were replaced by a pre-I escape and subsequent recruitment of the early-I neuron.

Our models for the pre-I/I neuron in the pre-BötC and the late-E neuron in the RTN/pFRG include persistent sodium current. It remains for future work to incorporate additional factors that may contribute to pre-BötC dynamics (see Rubin et al. 2009a and references therein) into a respiratory network setting. Similarly, although the persistent sodium current is prevalent in respiratory neurons and appears to be significant in late-E dynamics, it is important to note that equivalent dynamics can be achieved by other inward, slowly inactivating or outward, slowly activating currents (Izhikevich 2007).

Our simulations were performed for a baseline set of parameter values, although particular drive strengths were varied. The qualitative results of our study are expected to persist if parameters are perturbed, to some extent, from their baseline values. Note that in Figs. 4, 7, and 9, particular dynamic regimes are maintained over ranges of drive levels, which is a sign of robustness with respect to these parameters. Importantly, our qualitative analysis has illustrated the dynamical systems mechanisms underlying the phenomena discussed in this paper, all of which will be preserved under small variations of any of the parameters in the model or of the particular forms of functions in the model. In particular, we have verified with simulations that smoothing out the piecewise linear output function f(V) does not change the model output qualitatively, although the corresponding elimination of abrupt onset and offset of outputs is inconvenient for explaining model dynamics.

By means of the qualitative analysis presented in this study we have shown that the proposed model closely reproduces several behaviors observed experimentally. This agreement supports the proposed connectivity between the RTN/pFRG and pre-BötC/BötC circuits and changes in model parameters used for simulating the experimentally applied changes in metabolic or physiological conditions. Our simulation results suggest that the functional roles of the synaptic connections between possible pre-BötC/BötC and RTN/pFRG oscillator networks change under variations in respiratory demand. Specifically, states with suppression of RTN/pFRG by the pre-BötC network, with relatively independent activity of the two networks, with activation of both networks with each direction of effectively one-way coupling, or with activation of both networks with two-way effective coupling each emerge in specific situations and result in particular activity profiles, as discussed in Section 4.3. Thus, this coupled oscillator network embodies an inherent flexibility that likely enhances the capacity of the CPG to respond dynamically to changing conditions.