Prices for superstars can flatten out

Abstract

We reconsider Rosen’s economics of superstars model establishing, in the case of single-type consumers, a constant price-to-quality ratio. Rosen also conjectured that, in the case of multiple-type consumers, the normal course of consumer behavior forces the price-to-quality relationship to be convex and prevents it from being concave. We show that this conjecture is false and explain why there is no a priori reason to rule out concavity in the price-to-quality relationship. In this model, the market matches consumers to artists on the basis of quality: consumers of each type select only one level of quality, supplied by artists endowed with a specific level of talent. The concavity or convexity of the price-to-quality relationship is non-trivially related to the way both populations are matched. Consumers with poor knowledge have greater fixed costs above and beyond the price they have to pay on the market. They are therefore less reluctant when prices rise sharply and they specialize in levels of quality that entail a high marginal appreciation of quality: this can mean either a high or a low level of quality, depending on price curvature. With convexity, as Rosen pointed out, they turn toward superstars. Symmetrically, convexity encourages connoisseurs to turn toward low quality. But concavity too is fully possible: consumer–artist matching, for the same reasons, simply has the reverse effect. Connoisseurs go for great talents, whose price of quality flattens out. The global shape of the price-to-quality relationship (concave or convex) is determined by market clearing conditions and, more crucially, by the distribution of agents on both sides.

1 Introduction

So far, the literature on superstars has principally been devoted to seeking the basic mechanism which allows the most gifted few 1) to gain enormous rewards, 2) to attract large audiences and set a high price for talent differentials. On the subject of prices, Rosen’s seminal work conjectured that assuming multiple types of consumers was likely to convexify the price-to-quality relationship and to make the superstar phenomenon standout in comparison with cases where there is a single type of consumer. We question this result and show that this is not necessarily true. Actually, there is no oxymoron in the case of very highly talented artists (or sportsmen, designers, scientists) applying at equilibrium a flat price differential to their services compared with those of less gifted sellers. Indeed, as stressed by Rosen, with the starting assumption of identical buyers, a differential in price must make all sellers indifferent to consumers, including both the left tail and the right tail of the distribution of talent. In such a context, price becomes the only factor of cost differentiation among sellers, and a non-degenerate distribution of talent requires that highly differentiated prices discourage the massification of all consumers toward the most talented sellers. When buyers are not the same, showing different degrees of connoisseurship for instance, there is not necessarily the same need for price to perform this function, depending on how well the distribution of talent matches the distribution of connoisseurship. Moreover, we know that neither talent nor artistic knowledge is uniformly distributed among the population. It is generally considered that, within the population of artists and that of art lovers, competence is rarer than usual: this results on both sides of the market in asymmetric distributions where the median of skills is well below the mean. The basic law of supply and demand then applies: ceteris paribus the price increases with the ratio of demand to supply. Of course, when a huge demand from ignorant consumers is addressed to the rare higher talents, we get the phenomenon of stardom. But conversely, there are many empirical contexts where it is true connoisseurs who choose talented artists. Such cases are totally excluded from Rosen’s model: a rarely addressed feature of Rosen’s model is that the convexity of the price-to-quality relationship is exactly equivalent to specialization by artists of great talent on the market for non-fans, which may or may not be realistic.

Yet evidence of such flat prices for great talents on a variety of markets can be found in many fields where connoisseurship is an important differentiating factor among amateurs or collectors: non-competitive sports, baroque chamber music, etching, engraving. Picasso, Dali and Miro, for instance, were known to provide the engraving market with a very large number of specimens to which they did not grant great technical care, selling them consistently to connoisseurs at what appear rather low prices considering their reputation. All precursor markets have the same overall structure: there are too few connoisseurs and precursors cannot therefore set too high a price. At the beginning of Art Brut, for instance, Dubuffet, although already considered a great master, was mainly in demand from a small elite of well-informed connoisseurs, and his work was not yet commanding very high prices. Such markets, where connoisseurs go for the top end, arise when the supply of highly talented artists is very small (as in the case of precursors).

This controversial issue has led to considerable debate in the empirical literature, centering around numerous attempts to test Rosen’s superstars model. Some empirical findings support the conclusions of the model by suggesting that price and/or success has a disproportionate relationship with quality (Connolly and Krueger 2006; Krueger 2005), while others contradict those conclusions (Hamlen 1991, 1994). Some authors focus on testing this bias directly as a disproportion between measure of quality and measure of success (Connolly and Krueger 2006; Hamlen 1991; Krueger 2005; Chung and Cox 1994; Giles 2006), others focus on differentials of profit between firms in the cultural industry (DeVany and Walls 2004) or on the great differential in revenues among artists (Alper and Wassall 2006). In all these cases, explanatory factors other than quality may be involved, either to reconcile the low quality elasticity of success with the high success rate of artists at the top of the sales distribution (Hamlen 1991, 1994) or to provide competing explanations for superstardom, based on modeling of uncertainty. These explanations can be shown to fit well some data for the movie industry (DeVany and Walls 2004) or popular music (Chung and Cox 1994; Connolly and Krueger 2006), but may fail to explain other cases (Giles 2006).

A persistent twofold question pervades this field: how can we measure quality and do promoters of art take a comparative advantage of high quality on given markets? To the extent that objective measures of quality are available, it seems that the answer to the second part of the question is “not much.” Hamlen’s approach argues for a real impact of the perception of quality on success, relying on an objective measure of voice quality among singers. He concluded that there is a low rate of proportionality between this objective dimension of quality and success, which invalidates the plausibility of a necessary convexity of the relationship between price and quality.¹ There is also evidence of “unpriced quality” (Courty 2011). The market promotes a flat tarification by artists of the qualitative dimensions of performances for their fans: They are not always charged for better seats (Courty and Pagliero forthcoming; Connolly and Krueger 2006) and do not face scalper prices on the secondary market (Connolly and Krueger 2006). This minimally invasive commercial attitude toward their fans can be explained by the fact that these fans are usually a small subset of the total public, which substantially reduces the monopoly power of artists.²

On a theoretical ground, we focused on the case of perfect competition to put the burden of proof on other contexts than imperfect competition in establishing the causes of superstardom. This paper shows that switching from the single-type case to the multiple-type case may also concavify the relation between price and quality, instead of only convexifying it, as Rosen asserted. Sections 2 and 3 recall the main features and results of Rosen’s model on the demand side; Sect. 4 gives the characterization of an equilibrium similar to Rosen’s and offers one example with a concave relationship for multiple-type consumers.

2 Economics for superstars

2.1 Demand side in Rosen’s modeling

We first recall the main features of Rosen’s modeling of economics for superstars. He assumes that the consumer is equipped with a “home production” function that allows him to reach level $y$ of a composite good by combining the quantity $n$ and quality $z$ offered on the market. Assuming this, the model implicitly constrains the consumer to select only one level of quality, so that there is a greater number of goods in the economy than in the basket of each consumer. The market will use quality to match every consumer type to every level of artistic talent. He furthermore assumes a constant elasticity of substitution in the production of $y$, such that $y=nz$. Utility then follows as:

$$\begin{aligned} u(x,y)=u(x,nz), \end{aligned}$$

(1)

where $x$ denotes the numerary good.³ Consumers face two types of cost. Each of the $n$ units incurs a relative market price $p(z)$ which is assumed to depend on quality $z$, plus a fixed⁴ cost in time. Before buying one unit of the good, each consumer needs a fixed time $t\in [\underline{t},\overline{t}]$ depending on h(er)is connoisseurship level.⁵ This fixed cost enters into the time constraint: $nt+t_w\le T$, where $T$ is the total time available, and $t_w$ the time devoted to work. The monetary resource constraint is as follows: $x+p(z)n\le wt_w$, where $w$ is the wage.⁶ The $n$ units result in foregone earnings $wtn$ and both constraints result in a global constraint:

$$\begin{aligned} x+(p(z)+s)n\le wT, \end{aligned}$$

(2)

the total time $T$ valued at its monetary value is allocated to the numerary good $x$ and to the overall spending on art, every unit of which incurs a monetary cost $p(z)$ and a foregone earnings cost in time $s=wt$. Consumers can be indexed according to this cost $s\in [w\underline{t},w\overline{t}]$, whose opposite $-s$ can be interpreted as an index of the knowledge they possess on $y$.

2.2 Price catalog

It is not perfectly clears how the modeling adopted by Rosen tackles the relationship between market price and quality $z$, a rather abstract and poorly measurable notion; moreover, his model does not stipulate whether this is an endogeneous or exogeneous variable. We propose to clarify this by assuming that neither consumers nor suppliers observe the quality. More specifically, we disentangle the talent of artists called $q$, exogeneously given and the quality $z$ offered, which depends on the market context. A given artist of type $q$ could deliver variable levels of quality $z$ depending on the demand for this quality on a given market: for instance, the overall quantity demanded from a single artist lowers the quality offered by that artist. We assume therefore that consumers build expectations about quality levels from the range of prices.

Let’s now examine how the Rosen model behaves when our revised concept of equilibrium is introduced. We assume that all agents can infer from the competitive structure of the market that the intrinsic level of talent $q$ cannot be negatively correlated with quality and price. Accordingly, consumers need an arbitrary distinction, like artists’ names or other characteristics, to identify the provenance of works of art. Once they see prices $p\in [\underline{p}, \overline{p}]$ differentiated according to this “irrelevant” distinction, names for instance, they learn the ranking of talent by simply ordering the producers according to their prices. Artists with the same prices are homogeneous in talent and thus get the same rank, and when they differ in price, the most expensive are the most talented. Call $q\in [\underline{q}, \overline{q}]$, a real number that indexes the ranking of talent, the higher the better, obtained in this way. This assumption is consistent with the empirical evidence regarding dealers’ practice of rarely displaying prices alone: artists’ names are shown in catalogs and can be ranked according to their prices. For simplification, and with no loss of generality, each page of the ranked catalog lists all artists selling at the same price; a “very small” price increment can thus be assumed from page to page if the number of pages is “very large”, and thus, prices can be written as a function of pages or, equivalently, talent, $\varphi (q)$. Of course, the price differential does not give consumers the exact form of the relationship between price and quality, since the delivering of quality by a given talent depends on the market context. So consumers have to take a further step in the reasoning process that establishes their choice regarding quality. Assume that this step is taken thanks to expectations on the quality delivered by the market. In order to build their expectations, consumers simply start from the ranking for talent obtained earlier. Consistent with the above, higher levels of talent will necessarily charge higher prices: $\varphi '(q)>0$ and $\underline{p}=\varphi (\underline{q}),\,\overline{p}=\varphi (\overline{q})$ are respectively the lowest and the highest price in the catalog. In parallel, the ranking of artists allows expectations to be built about levels of quality $z^e$ expected at any price and thus at any rank $q$ in the catalog. Call $\psi (q)$ the expectations function that relates the ranking of intrinsic talent to expected level of quality:

$$\begin{aligned} z^e=\psi (q). \end{aligned}$$

(3)

Quality has to be measurable according to one unidimensional criterion. This could be the probability that an event, an exhibition, a film or a show, will be received positively by an audience, for instance.⁷ Equipped with these beliefs, depending on the fixed cost in time $s$, the greater the connoisseurship s(h)e possesses, the lower the cost $s$ incurred; first-order conditions lead h(er)im to demand a quantity $n(\varphi (q),\psi (q),s)$ selected from the page or equivalently talent $q$ in the catalog. (S)He demands only one level of talent $q$. “The marriage of buyers $s$ to sellers $q$, including the assignment of audiences to performers, of students to textbooks, patients to doctors, and so forth”⁸ simply results from this choice of h(er)is best page or equivalently talent $q$ and that replicated by every consumer $s$ in equilibrium.

On the supply side, assume further that sellers are price-taker.⁹ A key feature of our model is the assumption that, due to perfect competition, artists do not choose their rank $q$ in the catalog, which remains unaffected by equilibrium. For instance, suppose that every artist knows the intrinsic talent of all artists, including h(her)imself, or at least the ranking of h(er)is closest neighbors in the ranking and considers plausible only a subset of the set of possible catalogs: those that preserve the order of these intrinsic talents and thus verify $\varphi '(q)>0$. Every artist $q$ offers the quantity $m(\varphi (q))$ to achieve the maximum profit consistent with h(er)is price level $\varphi (q)$ given in the catalog.

In addition, the extrinsic quality met by an artist of level $q$, after (s)he has sold $m(\varphi (q)$, is given by a technical function $h(q,m(\varphi (q))$ and $\partial h(q,m)/\partial q>0$ and $\partial h(q,m)/\partial m<0$.

Catalog $\varphi (q)$ in equilibrium is the set of prices that solves the clearing market conditions and that makes zero excess demands, consistent with perfect foresight:

$$\begin{aligned} \psi (q)=h(q,m(\varphi (q))). \end{aligned}$$

(4)

3 Rosen’s results and conjectures

The results in Rosen’s paper are twofold. First, he assumes a single-type consumer case where all consumers possess the same connoisseurship and incur an identical fixed cost $\tilde{s} = w \tilde{t}$, and second, he assumes instead that consumers are of multiple types belonging to a continuum $s \in [w \underline{t}, w \overline{t}]$, meaning that connoisseurs rub shoulders with non-connoisseurs on verged markets.

Single-type consumers When the consumer is of one type, Rosen can rightfully be said to have showed that the only possible outcome of the market with multiple-type producers $q$ is a catalog $\varphi (q)$ that leads to indifference among all of them. Otherwise, some producers would meet no demand, meaning that there would be non-intuitive holes in the catalog. This results trivially in $\varphi '(q)/\psi '(q)=(\varphi (q)+s)/\psi (q)$ equal to a constant $\upsilon$ and the price-to-quality relationship in the catalog $\varphi (q)$ is linear:¹⁰

$$\begin{aligned} \varphi (q)=\upsilon \psi (q)-\tilde{s}. \end{aligned}$$

(5)

Multiple-type consumers The reasoning adopted by Rosen in the case of a perfect match between both set of agents is not appropriate. Recall 1) that the consumer considers a continuum pattern of quality alongside other variables that are discrete and 2) that the set of alternatives is a higher dimensional space than that of individual choice.¹¹ The mixture of discrete and continuous variables in the same model is not easy to handle and then suddenly disappears in the results on individual behaviors. Individual behaviors are actually given by discrete solutions being parametrized by connoisseurship $s$ on the consumer side, and by talent $q$ on the producer side. The aggregate market solution is a set of continuous functions obtained by integrating individual behaviors according to both these parameters. The incorrect conclusion of a convex price-to-quality relationship being the only possible market behavior essentially stems from a failure to recognize that the set of alternatives on the market is a higher dimensional space than that of individual behaviors.¹² This can easily be seen when the detail of Rosen’s modeling is examined and slightly adjusted. By substituting the numerary good $x$ from (2) in (1), we can easily switch from Rosen’s modeling to ours, replacing price as a function of quality $p(z)$ by our function of talent $\varphi (q)$ and quality $z$ by our expectation function $\psi (q)$. Utility is then a function of $n$ and $q$ only: $v(n,q)=u(wT-(\varphi (q)+s)n,n\psi (q))$. First-order condition according to talent $v'_q=\partial v(n,q^*)/\partial q=0$ leads to the equalization of marginal rate of substitution to marginal appreciation of quality:

$$\begin{aligned} \frac{u'_y}{u'_x}=\frac{\varphi '(q^*)}{\psi '(q^*)}. \end{aligned}$$

(6)

First-order condition according to quantity $v'_n=\partial v(n^*,q)/\partial n=0$ leads to the equalization of marginal rate of substitution to total price-to-quality ratio:

$$\begin{aligned} \frac{u'_y}{u'_x}=\frac{\varphi (q^*)+s}{\psi (q^*)}. \end{aligned}$$

(7)

By an envelope property, choosing what talent $q^*$ needs to be selected, and $n^*$, how much product has to be consumed, make the two values equal $\varphi '(q^*)/\psi '(q^*)=(\varphi (q^*)+s)/\psi (q^*)$. This allows us to assess the matching function of both types:

$$\begin{aligned} s=\varsigma (q)\equiv \frac{\varphi '(q)\psi (q)-\varphi (q)\psi '(q)}{\psi '(q)}. \end{aligned}$$

(8)

This equalization can be observed either in a local minimum or a local maximum of total price-to-quality ratio $(\varphi (q^*)+s)/\psi (q^*)$, depending on whether the price-to-quality relationship is locally convex or not. Figure 1a shows the convex case: marginal appreciation of quality $\varphi '(q)/\psi '(q)$ is increasing in $q^*_1$, where total price-to-quality ratio is locally minimum. As marginal rate of substitution is always decreasing, it crosses marginal appreciation of quality from above. Figure 2a shows both cases: $q^*_1$ is similar to the case in Fig. 1a, while $\varphi '(q)/\psi '(q)$ is decreasing and total price-to-quality ratio is locally maximum in $q_2^*$. The second-order condition must be checked in $q^*_2$ to ensure that marginal rate of substitution crosses marginal appreciation of quality from above. In the case of a Cobb-Douglas utility, for instance, $u(x,nz)=(1-\gamma )\log x+\gamma \log nz$, the second-order condition requires locally:

$$\begin{aligned} \frac{\psi ''(q)\varphi '(q)-\varphi ''(q)\psi '(q)}{(\psi '(q))^2}<\frac{1}{(1-\gamma )}\frac{\varphi '(q)}{\psi (q)}, \end{aligned}$$

which is obviously satisfied when $\psi ''(q)\varphi '(q)-\varphi ''(q)\psi '(q)<0$, in the case of a convex price-to-quality relationship, as in $q_1^*$. This can be satisfied as well in the concave case, as in $q_2^*$.

Fig. 1

Convex case

Fig. 2

Convex-concave case

The equalization of marginal appreciation of quality and total price-to-quality ratio leading to (8) can also be illustrated by presenting the three different catalog cases (Fig. 3). Which of these situations pertains depend both on market clearing conditions and, more crucially, on the distribution of agents on both sides.

Case 0 This case is consistent with a single-type case: Suppose for instance that all consumers have the same connoisseurship index $-\tilde{s}=-s_1$. Then, they have to be indifferent between any points $A$ or $B$ of the straight line because the price-to-quality relationship is linear.

Case 1 On the upper left, we draw the case when a catalog is convex. This case is consistent with a multiple-type case where consumers $s\in [\underline{s},\overline{s}]$. It is clear that a consumer equipped with low connoisseurship $-s_1$ selects the talent corresponding to $C_1$. Symmetrically, any point $C_2$ will be selected by consumers equipped with higher connoisseurship $-s_2$. An ignorant $-s_1$ goes for higher quality than the connoisseurs $-s_2$, in this case.

Case 2 On the lower right, we draw the case when the relationship is concave. As the ranking of marginal appreciation of quality is reversed, better connoisseurs $-s_2$ match the higher talent met in $C'_2$ and an ignorant $-s_1$ goes for the less gifted $C'_1$.

Connoisseurship indexed by $-s$ increases the incentive to take into account marginal appreciation of quality. As a consequence, connoisseurs with higher index value $-s_2$ are attracted to artists who lie on pages where the rise in price is less marked, that is: with lower quality $C_2$ when the relationship is convex on the left and with higher quality $C'_2$ when the relationship is concave. The reverse is also true: non-connoisseurs with lower $-s_1$ go for pages where the relationship has a higher slope toward the top end of quality $C_1$ or toward the bottom end $C'_1$.

Fig. 3

Convex, linear and concave price-to-quality relationship

Rosen was mistaken in thinking that, because linear relationships $(A,B)$ lead to indifference among all pages in case 0, therefore all straight lines starting from $-s_i$, in case 1 or 2, should describe indifference.¹³ This is obviously wrong. Consider for instance $A'$ and $B'$ in case 2: It is clear that indifference between them is impossible since (8) is not satisfied either at $A'$ or at $B'$. The key point is that indifference is not characterized by the segment curve linking the two points, because this is not consistent with the catalog, which follows a different curve in case 2 (as in case 1). Considering additional dimensions could be the answer to representing the slope of relative price of quality presented in the catalog.

4 New results

4.1 Equilibrium

In this section, we show a complete characterization of the equilibrium. Price-taker competitive sellers, who all have the same cost $C(m)$, are distributed on $q\in ]\underline{q}, \overline{q}]$ with density $\theta (q)$. Buyers, equipped with (1) under constraint (2), differ according to $s\in [\underline{s}, \overline{s}]$ with density $\alpha (s)$. An equilibrium is a set $\{\varphi (q), n(\psi (q),\varphi (q),s), x(\psi (q),\varphi (q),s), m(\varphi (q)),\,\psi (q)\}_{q\in [\underline{q}, \overline{q}], s\in [\underline{s},\overline{s}]}$ satisfying: (1) the supply condition leading price-taker sellers to adjust quantities $m(\varphi (q))$ until they equalize price to marginal cost $\varphi (q)={\rm d}C(m)/{\rm d}m$, for all $q$; (2) demand conditions leading to consumptions $n(\psi (q),\varphi (q),s)$ and $x(\psi (q),\varphi (q),s)$ for all $s$; (3) the marriage of $q$ and $s$ by equalizing $s=\varsigma (q)$; (4) the perfect foresight condition: $\psi (q)=h(q,m(\varphi (q)))$, for all $q$; (5) market clearing conditions, which can be divided into two types of case. (1) In the single-type case, all buyers have the same $s=\tilde{s}$, the market clears when $\int _{\underline{q}}^{\overline{q}}\beta (v)n(\psi (v),\varphi (v),\tilde{s}){\rm d}v=\int _{\underline{q}}^{\overline{q}}\theta (v)m(\varphi (v)){\rm d}v$, where $\beta (q)$ is a density of population of buyers distributed on $q$. (2) In the multiple-type case, the market clears when $\int _{\underline{s}}^{\varsigma (q)}\alpha (u)n(\psi (\varsigma ^{-1}(u)),\varphi (\varsigma ^{-1}(u)),u){\rm d}u=\int _{\underline{q}}^{q}\theta (v)m(\varphi (v)){\rm d}v \text{ for } \text{ all } q\in [\underline{q}, \overline{q}]$ if $\varsigma (\underline{q})<\overline{s}$ and $q\in [\varsigma ^{-1}(\overline{s}),\overline{q}]$, otherwise in the decreasing case $\varsigma '(q)<0$, and symmetrically in the increasing case $\varsigma '(q)>0$.

4.2 One simple example: uniform distribution of agents on both sides

Equipped with $u(x,nz)=(1-\gamma )\log x+\gamma \log n+\gamma \log z$, every buyer consumes $n(\varphi (q),s)=\gamma wT/(\varphi (q)+s)$ and $x=(1-\gamma )wT$. On supply side, $C(m)\equiv (c_1/2)m^2-c_2m$ leads sellers $q$ to produce $m(\varphi (q))=(\varphi (q)+c_2)/c_1$. Defining extrinsic quality function as $h(q,m)\equiv (q+1)e^{-m}$, the matching function thus simplifies to $\varsigma (q)=1/\{1/[(q+1)\varphi '(q)]-1/c_1\}-\varphi (q)$. A numerical example is given below for $c_1/100=c_2=wT=10\gamma =1$.

In the single-type consumer case, all consumers distribute among sellers within a distribution of monotonously increasing density $\beta (q)$. The constant marginal appreciation of quality $\upsilon$ in (5) depends positively on the relative number of buyers to sellers $\int _{\underline{q}}^{\overline{q}}\beta (q){\rm d}q/\int _{\underline{q}}^{\overline{q}}\theta (q){\rm d}q$. In the multiple-type case, the catalog $\varphi (q)$ and expected quality $\psi (q)$ verify in equilibrium $\theta (q).\{(\varphi (q)+c_2)/c_1\}=\alpha (\varsigma (q)).\{\gamma wT/(\varphi (q)+s)\}$. Thus, using (4) and (8), we have:

$$\begin{aligned} \theta (q).(\varphi (q)+c_2)\varphi '(q)\psi (q)&= \alpha (\varsigma (q)).c_1\gamma wT\psi '(q),\end{aligned}$$

(9)

$$\begin{aligned} \psi (q)&= (q+1)\exp [-(\varphi (q)+c_2)/c_1]. \end{aligned}$$

(10)

Assume $\theta (q)/\alpha (\varsigma (q))=1$, for instance with uniform distributions on $[0,1]$ for both populations of sellers according to $q$ and buyers (when they differ) according to $s$, for all $q$. Then (9) and (10) reduce to:

$$\begin{aligned}&(\varphi (q)+c_2)\varphi '(q)\psi (q) = c_1\gamma wT\psi '(q),\end{aligned}$$

(11)

$$\begin{aligned}&\psi (q) = (q+1)\exp [-(\varphi (q)+c_2)/c_1]. \end{aligned}$$

(12)

The solution for (11) and (12) is as follows:

$$\begin{aligned} \varphi (q)=-(\gamma wTc_1+c_2)+ \sqrt{(\gamma wTc_1+c_2)^2+2\gamma w Tc_1\log (q+1)+K}, \end{aligned}$$

and the corresponding $\psi (q)$, for a constant $K$.

Within the numerical case, $K=53.28$ ensures that all sellers $q\in [0,1]$ are matched with buyers $s\in [0,0.97]$ by $\varsigma (q)$. Income effect exceeds substitution effect, which is concretized in $\hbox{d}\varsigma (q)/\hbox{d}q<0$: connoisseurs (highest $-s$) select the most talented sellers with highest $q$, at the same time reaching higher utility levels. In all pages $q$, they consume $n=0,1/(q+1)\varphi '(q))-0,1$ and $x=0,9$. Buyers with the highest $s\in ]0.97,1]$ do not get anything. In contrast to Rosen’s results, marginal appreciation of quality $\varphi '(q)/\psi '(q)$ decreases, leading equivalently to a concave $p(z)$, while market sizes and receipts are concave according to $q$.

4.3 Further results from non-uniform distribution of agents on both sides

We solve by numerical integration (9) and (10). Of course, the general shape and the level of the price-to-quality relationship in the catalog depend on the density $\theta (q)$ and $\alpha (s)$ of the distributions of agents on both sides. We have shown that, in the simpler case of uniform distribution on both sides, prices rise with the number of consumers and fall with the number of producers. The uniform case is interesting since it produces an analytical solution, but it remains unrealistic and restrictive. For this purpose, we turn to a more flexible formulation. We consider (1) affine cases and (2) an exponential density on supply side, which better reflects the scarcity of great talents. We however rely on numerical integration for the computation of the solution, since the formulation does not yield an analytical solution.

In all these cases, density of agents is decreasing with talent on the producer side, $\theta '(q)<0$ and decreasing with connoisseurship $-s$ on the consumer side, $\alpha '(s)>0$.

4.3.1 Linear density on both sides

In this first case, density of talent follows $\theta (q)=d-c.q$, and density of consumers follows $\alpha (s)=a.s+b$ where $a\ge 0$, $b\ge 0,\,c\ge 0$ and $d\ge 0$ are parameters. A higher $a$ increases the number of non-connoisseurs with high $s$ and thus the relative scarcity of connoisseurs among all consumers $\int _0^{\overline{s}}\alpha (v){\rm d}v$. A higher $d$ increases the total number of artists uniformly over all levels of artists from very slightly gifted talents (in the very “first” pages of the catalog) to the greatest talents who lie at the end (it also increases the number of pages). $c$ is the slope of the decreasing quantity of greater talent in the catalog. Of course, a higher $d$ increases the overall number of producers $\int _q\theta (u){\rm d}u$ without changing the relative scarcity of greater talent, while a higher $c$ decreases the overall number and increases the scarcity of greater talent. We set parameters $a, b, c$ and $d$ according to Table 1, where $\mathcal{U}_1$ refers to the uniform case on both sides and $\mathcal{A}_i,\,i=1,2,3$ and 4 to four different affine cases. Other parameters are set as follows: $c_1=c_2=1,\,T=10,\,w=2,\,\gamma =1/2$.

Table 1 Uniform and affine cases of distribution of agents

Recall that in the case of a concave relationship, low $s$ matches high $q$ and reciprocally. We, therefore, find the expected results on both sides. Looking at the impacts on the price of quality induced by changes on the producer side only, we find that, with higher $d$, prices fall throughout the catalog uniformly (see Fig. 4) and that, with higher $c$, prices increase more sharply for greater talent (see Fig. 5). Looking at the impacts of changes on the consumer side only, we also find that, with higher $a$, prices rise for lesser talent and that they fall for greater talent (see Fig. 6).

Fig. 4

Relationship in catalogs with $d_1$ and $d_3<d_1$

Fig. 5

Relationship in catalogs with $c_1$ and $c_4>c_1$

Fig. 6

Relationship in catalogs with $a_1$ and $a_2>a_1$

4.3.2 Linear density on the consumer side and exponential density on the producer side

The most interesting case is where the number of producers decreases at a constant rate over the pages in the catalog $\theta '(q)/\theta (q)=-c$, for all $q$, so that talent is distributed following an exponential density $\theta (q)=de^{-cq}$. With this density, great artists are very scarce. Obviously, higher values of $c$ decrease both the number of artists and the scarcity of greater talent. We maintain a linear distribution of consumers $\alpha (s)=a.s+b$, as in the previous section.

Cases	$a_i$	$b_i$	$c_i$	$d_i$
$\mathcal{E}_1$	1	0	1/100	1
$\mathcal{E}_2$	1	0	1/2	1
$\mathcal{E}_3$	1	0	1/2	3

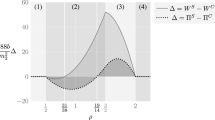
We obviously find that higher $c$ has a positive impact on price, but surprisingly, this changes a partially convex relationship into a concave relationship, so that scarcity of great talent actually concavifies the price-to-quality relationship, instead of convexifying it. This can be explained very easily. The match between the two distributions of agents simply affects the way connoisseurs and non-connoisseurs turn to greater or lesser talents. As $c$ increases, there is a move from matching great talents with ignorant consumers toward matching them with connoisseurs, who are less numerous; the rise in price is sharper for lesser talents, who satisfy the majority of non-connoisseurs (Fig. 7).

Fig. 7

Convex to concave relationship in catalogs by increasing $c$

5 Conclusion

In this paper, we have shown that unequally talented sellers’ prices may be flat at the top end because a concave relationship between price and quality arises when buyers are of multiple types. The ability of superstars to accumulate the most frequent attributes of stardom, including high prices, rewards and markets, thus seems to be contingent on many factors about which much remains to be discovered. One of them is undoubtedly the matching rule between quality levels, talents and consumer types for the equilibrium considered, which depends in a complex manner on the density functions of distributions of agents. We have attempted here to tackle uniform distributions on both sides (supply and demand), for obvious tractability reasons. But this paper has also examined more realistic distributions and raises the question of how matching multiple types of consumers and suppliers decisively affects the main outcome of the market. Therefore, when empirical studies are conducted, the most important factor to determine should be first, what type of consumer will seek what level of talent, and second, how many consumers are attracted to each level. One of the basic mechanisms at work on this market closely links any change in concavity of the quality–price relationship to a change in the matching of connoisseurship to talent. We conclude that a greater scarcity of talent can lead to the concavification of the price–quality relationship. For instance, on the precursor market, great talents are very scarce, as are connoisseurs, and this double scarcity may lead to a concavification of the relationship between price and quality.