Keywords

16.1 Introduction

The typical presumption of the most of economic theories is that free entry is desirable for social efficiency. As several articles have shown, however, when firms must incur fixed set-up costs upon entry, the number of firms entering a market need not equal the socially desirable number. Spence [13] and Dixit and Stiglitz [6], for example, demonstrate that in a monopolistically competitive market, free entry can result in too little entry relative to the social optimum. In more later work von Weizsäcker [14] and Perry [11] point to a tendency for excessive entry in homogeneous product markets. Nevertheless, despite these findings, many economists continue to hold the presumption that free entry is desirable, in part, it seems, because the fundamental economic forces underlying these various entry biases remain somewhat mysterious. The empirical studies in broadcasting industry allow to draw the conclusion that the share of social losses due to excessive entry of radio stations is about 40%, see e.g., [4] and the more recent paper [5]. As for theoretical justification of this effect, the paper of Mankiw and Whinston, [8], consider the general model of oligopolistic competition between firms producing the homogeneous good. Authors formulated their assumptions in terms of equilibrium characteristics and the production cost function, which imply the entry excess of firms over the social optimum. These assumptions have a neat economic intuition and cover many well-known examples of the oligopolistic competition models, e.g., the linear Cournot oligopoly model, however, an assumption on homogeneity of good turns out to be crucial. In case of production diversity authors presented a counter-example with the opposite ranking of free-entry equilibrium number of firms and the social optimum. At the very end of Conclusion the following problem was formulated

The introduction of product diversity, however, can reverse this bias toward excessive entry. Intuitively, a marginal entrant adds to variety, but does not capture the resulting gain in social surplus as profits. Hence, in heterogeneous product markets the direction of any entry bias is generally unclear, although efficient levels of entry remain an unlikely occurrence.

The purpose of this paper is to make the problem more clear. The goal is to provide a simple conditions, under which the number of entrants in a free-entry equilibrium is excessive or insufficient. Our analysis compares the number of firms that enter a market when there is free entry with the number that would be desired by a social planner who is unable to control the behavior of firms once they are in the market. That is, we consider the second-best problem of choosing the welfare-maximizing number of firms. We demonstrate that the crucial conditions for establishing the presence of an entry bias can be stated quite simply in terms of consumers’ utility. In short, this paper shows that under the mild and natural assumption the free-entry number of firms is socially excessive. We also provide the sufficient condition for the opposite case and construct the corresponding example of utility function satisfying this condition.

16.2 The Model

Consider the one-sector economy with horizontally differentiated good and one production factor–labor. There is a continuum [0, L] of identical consumers endowed with one unit of labor. The labor market is perfectly competitive and labor is chosen as the numéraire. There is a finite number N ≥ 2 of “large” firms producing the varieties of some horizontally differentiated good and competing with prices. Each variety is produced by a single firm and each firm produces a single variety, thus the horizontally differentiated good may be represented as a finite-dimensional vector \(\mathbf {x}=(x_{1},\ldots ,x_{N})\in {R}_{+}^{N}\). The “large” size of firm implies that impact of single firm to market statistics is not negligible and should be strategically taken into account by other competitors. To operate, every firm needs a fixed requirement f > 0 and a marginal requirement c > 0 of labor, which may be normalized to 1 without loss of generality. Wage is also normalized to 1, thus the cost of producing q i units of variety \(i\in \left \{ 1,\ldots ,N\right \} \) is equal to f + 1 ⋅ q i.

Consumers share the same additive preferences given by

$$\displaystyle \begin{aligned} U(\mathbf{x})=\sum _{i=1}^{N}u(x_{i}),{} \end{aligned} $$
(16.1)

where u(⋅) is thrice continuously differentiable, strictly increasing, strictly concave, and such that u(0) = 0. Following [15], we define the relative love for variety (RLV) as follows:

$$\displaystyle \begin{aligned} r_{u}(x)=-\frac{xu^{\prime\prime}(x)}{u^{\prime}(x)}, \end{aligned}$$

which is strictly positive for all x > 0. Under the CES, we have u(x) = x ρ where ρ is a constant such that 0 < ρ ≤ 1, thus implying a constant RLV given by 1 − ρ. The natural generalization of CES utility is the HARA function u(x) = (x + α)ρ − α ρ, α > 0. Another example of additive preferences is provided by Behrens and Murata [1], who consider the CARA utility \(u(x)=1-\exp (-\alpha x)\) where α > 0 is the absolute love for variety; the RLV is now given by αx.

Very much like the Arrow-Pratt’s relative measure of the risk aversion, the RLV measures the intensity of consumers’ variety-seeking behavior. Following the paper [15], we suggest that the low-tier utility function u(x) satisfies the following

Assumption 16.1

$$\displaystyle \begin{aligned} r_{u}(x)<1,\ r_{u'}(x)<2{} \end{aligned} $$
(16.2)

for all x in some neighborhood of zero.

A consumer’s income is equal to her wage plus her share in the total profits. Since we focus on symmetric equilibria, consumers must have the same income, which means that profits have to be uniformly distributed across consumers. In this case, a consumer’s income y is given by

$$\displaystyle \begin{aligned} y=1+\frac{1}{L}\sum _{i=1}^{N}\varPi_{i}\geq1,{} \end{aligned} $$
(16.3)

where the profit made by the oligopoly selling amount q i of variety \(i\in \left \{ 1,\ldots ,N\right \} \) at price p i is given by

$$\displaystyle \begin{aligned} \varPi_{i}=(p_{i}-1)q_{i}-f.{} \end{aligned} $$
(16.4)

Evidently, the income level varies with firms’ strategies p i.

A consumer’s budget constraint is given by

$$\displaystyle \begin{aligned} \sum _{i=1}^{N}p_{i}x_{i}=y.{} \end{aligned} $$
(16.5)

The first-order condition for utility maximization yields

$$\displaystyle \begin{aligned} u^{\prime}(x_{k})=\lambda p_{k},{} \end{aligned} $$
(16.6)

where λ is the Lagrange multiplier

$$\displaystyle \begin{aligned} \lambda=\frac{\sum_{i=1}^{N}u^{\prime}(x_{i})x_{i}}{y}>0,{} \end{aligned} $$
(16.7)

which implies that the inverse demand may be represented in closed form

$$\displaystyle \begin{aligned} p_{k}=\frac{yu'(x_{k})}{\sum_{i=1}^{N}u^{\prime}(x_{i})x_{i}}{} \end{aligned} $$
(16.8)

for all varieties \(k\in \left \{ 1,\ldots ,N\right \} \).

Let p = (p 1, …, p N) be a price profile. Consumers’ demand functions x i(p) are obtained by solving the system of Eqs. (16.8) where aggregate income of consumers y is now defined as follows:

$$\displaystyle \begin{aligned} y(\mathbf{p})=1-Nf+\sum_{i=1}^{N}(p_{i}-1)x_{i}(\mathbf{p}). \end{aligned}$$

It follows from (16.7) that the marginal utility of income λ is a market aggregate that depends on the price profile p. Indeed, the budget constraint

$$\displaystyle \begin{aligned} \sum_{j=1}^{N}p_{j}x_{j}(\mathbf{p})=y(\mathbf{p}) \end{aligned}$$

implies that

$$\displaystyle \begin{aligned} \lambda(\mathbf{p})=\frac{1}{y(\mathbf{p})}\sum_{i=1}^{N}x_{i}(\mathbf{p})u^{\prime}\left(x_{i}(\mathbf{p})\right).{} \end{aligned} $$
(16.9)

Since u ′(x) is strictly decreasing, the demand function for variety i is thus given by

$$\displaystyle \begin{aligned} x_{k}(\mathbf{p})=\xi(\lambda(\mathbf{p})p_{k}),{} \end{aligned} $$
(16.10)

where ξ is the inverse function to u ′. Moreover, the i-th firm profit can be rewritten as follows:

$$\displaystyle \begin{aligned} \varPi_{i}(\mathbf{p})=L(p_{i}-1)x_{i}(\mathbf{p})-f=L(p_{i}-1)\xi(\lambda(\mathbf{p})p_{i})-f.{} \end{aligned} $$
(16.11)

16.2.1 Market Equilibrium

The market equilibrium is defined by the following conditions:

  1. (i)

    each consumer maximizes her utility (16.1) subject to her budget constraint (16.5),

  2. (ii)

    each firm k maximizes its profit (16.4) with respect to p k,

  3. (iii)

    product market clearing:

    $$\displaystyle \begin{aligned} Lx_{k}=q_{k}\qquad \text{for all }k\in\left\{ 1,\ldots,N\right\} \text{,} \end{aligned}$$
  4. (iv)

    labor market clearing:

    $$\displaystyle \begin{aligned} Nf+\sum\limits _{i=1}^{N}q_{i}=L. \end{aligned}$$

    Market equilibrium is symmetric when q k = q j, p k = p j for all k ≠ j. Conditions (iii) and (iv) imply that

    $$\displaystyle \begin{aligned} \bar{x}\equiv\frac{1}{N}-\frac{f}{L}{} \end{aligned} $$
    (16.12)

    are the only candidate symmetric equilibrium demands for “oligopolistic” varieties.

This definition of equilibrium is similar to concepts used in [10] and [12] with exception of an assumption on the free entry until the zero-profit condition. The number of firms now is considered as an exogenous parameter.

16.2.2 First Order Condition for Bertrand Oligopoly Under the Ford Effect

As shown by (16.6) and (16.7), the income level influences firms’ demands, whence their profits. As a result, firms must anticipate accurately what the total income will be. In addition, firms should be aware that they can manipulate the income level, whence their “true” demands, through their own strategies with the aim of maximizing profits. This feedback effect is known as the Ford effect.

In popular literature, this idea is usually attributed to Henry Ford, who raised wages at his auto plants to five dollars a day in January 1914. As specified in [2], the Ford effect may have different scopes of consumers income, which is sum of wage and a share of the distributed profits. The first specification (proposed in [9]) and used in [2]) is to suppose that firms take into account the effects of their decision on the total wage bill, but not on the distributed profits, which is still treated parametrically. This case may be referred as “Wage Ford effect” and it is exactly what Henry Ford meant. Another intermediate specification of The Ford effect is an opposite case to the previous one: firms take wage as given, but take into account the effects of their decisions on distributed profits. This case may be referred as “Profit Ford effect”. Finally, the extreme case, Full Ford effect, assumes that firms take into account total effect of their decisions, both on wages and on profits. These two cases are studied in newly published paper [3]. In the presented research, we shall assume that wage is given. This includes the way proposed by O. Hart in [7], when the workers fix the nominal wage through their union. This assumption implies that only the Profit Ford effect is possible, moreover, firms maximize their profit anyway, thus being price-makers but not wage-makers, they have no additional powers at hand in comparison to No Ford case, with except the purely informational advantage—knowledge on consequences of their decisions. Nevertheless, as it was shown in [12], this advantage allows firms to get more market power, which justify the common wisdom “Knowledge is Power”. The Ford effect assumption suggests actually that the large firms act as “sharks” rather than “dolphins”, gathering the maximum market power.

The generalized Bertrand equilibrium is a vector p ∗ such that \(p_{i}^{\ast }\) maximizes \(\varPi _{i}(p_{i},{\mathbf {p}}_{-i}^{\ast })\) for all \(i\in \left \{ 1,\ldots ,N\right \} \). Applying the first-order condition to (16.11) yields

$$\displaystyle \begin{aligned} \frac{p_{i}-1}{p_{i}}=-\frac{\xi(\lambda p_{i})}{\lambda p_{i}\xi^{\prime}(\lambda p_{i})\left(1+\frac{p_{i}}{\lambda}\frac{\partial\lambda}{\partial p_{i}}\right)},{} \end{aligned} $$
(16.13)

which involves ∂λ∕∂p i because λ depends on p.

It was mentioned already that the “large” firms (oligopolies) have non-zero influence on market statistics, in particular, we can expect that ∂λ∕∂p k ≠ 0. By the standard interpretation, the Lagrange multiplier λ is a marginal utility of money, therefore “large” firms understand that the demand functions (16.10) must satisfy the budget constant as an identity. The consumer budget constraint, before symmetrization, can be rewritten as follows:

$$\displaystyle \begin{aligned} \sum_{i=1}^{N}p_{i}\xi(\lambda(\mathbf{p})p_{i})=1-Nf+\sum_{i=1}^{N}(p_{i}-1)\xi(\lambda(\mathbf{p})p_{i}), \end{aligned}$$

which boils down to

$$\displaystyle \begin{aligned} \sum_{i=1}^{N}\xi(\lambda(\mathbf{p})p_{i})=1-Nf.{} \end{aligned} $$
(16.14)

Differentiating (16.14) with respect to p k yields

$$\displaystyle \begin{aligned} \xi^{\prime}(\lambda p_{k})\lambda+\frac{\partial\lambda}{\partial p_{k}}\sum_{i=1}^{N}\xi^{\prime}(\lambda p_{i})p_{i}=0 \end{aligned}$$

or, equivalently,

$$\displaystyle \begin{aligned} 1+\frac{p_{k}}{\lambda}\frac{\partial\lambda}{\partial p_{k}}=\frac{\sum_{i\neq k}^{N}\xi^{\prime}(\lambda p_{i})\lambda p_{i}}{\sum_{i=1}^{N}\xi^{\prime}(\lambda p_{i})\lambda p_{i}}.{} \end{aligned} $$
(16.15)

Substituting (16.15) into (16.13) and symmetrizing the resulting expression we obtain

$$\displaystyle \begin{aligned} m(N)=r_{u}\left(\frac{1}{N}-\frac{f}{L}\right)\frac{N}{N-1}.{} \end{aligned} $$
(16.16)

16.3 Consumers’ Welfare Under the Free and Restricted Enter

Using (16.16) we can calculate the firm’s profit at symmetric equilibrium. Indeed, the markup definition

$$\displaystyle \begin{aligned} m=\frac{p-c}{p}=\frac{p-1}{p} \end{aligned}$$

implies

$$\displaystyle \begin{aligned} p-1=\frac{m}{1-m}. \end{aligned}$$

Substituting (16.16) for m we obtain

$$\displaystyle \begin{aligned} \bar{\varPi}=L(p-1)\bar{x}-f=L\frac{r_{u}\left(\frac{1}{N}-\frac{f}{L}\right)-(N-1)\frac{f}{L}}{\left(1-r_{u}\left(\frac{1}{N}-\frac{f}{L}\right)\right)N-1}.{} \end{aligned} $$
(16.17)

In what follows we shall use the notion φ ≡ f∕L to make formulas more compact. This allows us to determine Zero-Profit “number” of firms \(\widehat {N}(\varphi )\) as root of equation \(\bar {\varPi }=0\) , which is equivalent to equation

$$\displaystyle \begin{aligned} r_{u}\left(N^{-1}-\varphi\right)=(N-1)\varphi.{} \end{aligned} $$
(16.18)

This number is typically non-integer; this is not a big problem, however, because this number only indicates that for all integers \(N<\widehat {N}(\varphi )\) profit \(\bar {\varPi }>0\), while \(N>\widehat {N}(\varphi )\) implies \(\bar {\varPi }<0\). The corresponding equilibrium consumption \(x(\varphi )=\left (\widehat {N}(\varphi )\right )^{-1}-\varphi \).

Proposition 16.1

For all sufficiently small φ there exist unique solution \(\widehat {N}(\varphi )\)of Eq.(16.18). Moreover, for φ → 0 we have x(φ) → 0, \(\widehat {N}(\varphi )\to \infty \).

Proof

This statement immediately follows from [12], Proposition 15.3. ■

Now consider the following Social Welfare function (actually, an indirect utility)

$$\displaystyle \begin{aligned} V(N)=Nu(\bar{x})=N\cdot u\left(\frac{1}{N}-\frac{f}{L}\right),{} \end{aligned} $$
(16.19)

with the firm’s number as a variable. To save space we use the following notion φ ≡ f∕L. The first order condition

$$\displaystyle \begin{aligned} V'(N)=u\left(\frac{1}{N}-\varphi\right)-\frac{1}{N}u'\left(\frac{1}{N}-\varphi\right)=0 \end{aligned}$$

determines the Social optimum of firms’ numberFootnote 1N ∗(φ). It is obvious that for CES utility with u(x) = x ρ, which implies r u(x) = 1 − ρ, the Social optimal number of firms is equal to

$$\displaystyle \begin{aligned} N^{*}(\varphi)=\frac{1-\rho}{\varphi}. \end{aligned}$$

On the other hand, the number of firms determined by zero-profit condition \(\bar {\varPi }(N)=0\) is equal to

$$\displaystyle \begin{aligned} \widehat{N}(\varphi)=\frac{1-\rho}{\varphi}+1=N^{*}(\varphi)+1. \end{aligned}$$

This means that Social optimum is less than Free Entry number, though, the difference is not too large.

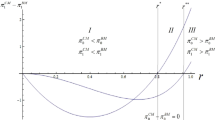
This result, i.e., inequality \(\widehat {N}(\varphi )>N^{*}(\varphi )\), will be generalized to the wide class of utility functions. Moreover, we also present the counterexample with opposite ranking \(\widehat {N}(\varphi )<N^{*}(\varphi )\).

Let

$$\displaystyle \begin{aligned} \varepsilon_{u}(x)\equiv\frac{x\cdot u'(x)}{u(x)} \end{aligned}$$

be an elasticity of utility function u(x), while

$$\displaystyle \begin{aligned} A(x)\equiv\frac{1-r_{u}(x)+x}{2}+\sqrt{\left(\frac{1-r_{u}(x)-x}{2}\right)^{2}-xr_{u}(x)}.{} \end{aligned} $$
(16.20)

Proposition 16.2

For any φ = f∕L > 0 the inequality \(\widehat {N}(\varphi )>N^{*}(\varphi )\)holds if and only if ε u(x(φ)) > A(x(φ)).

Proof

The Social welfare function is bell-shaped due to

$$\displaystyle \begin{aligned} V''(N)=\frac{1}{N^{3}}\cdot u''\left(\frac{1}{N}-\varphi\right)<0, \end{aligned}$$

therefore \(\widehat {N}(\varphi )>N^{*}(\varphi )\) is equivalent to inequality \(V'(\widehat {N}(\varphi ))<0=V'(N^{*}(\varphi ))\). On the other hand, the inequality

$$\displaystyle \begin{aligned} V'(\widehat{N}&(\varphi)) =u\left(\widehat{N}(\varphi)^{-1}-\varphi\right)-\widehat{N}(\varphi)^{-1}u'\left(\widehat{N}(\varphi)^{-1}-\varphi\right)= u\left(x(\varphi)\right)-\\- & (x(\varphi)+\varphi)\cdot u'\left(x(\varphi)\right)= u\left(x(\varphi)\right)\frac{x(\varphi)+\varphi}{x(\varphi)}\left(\frac{x(\varphi)}{x(\varphi)+\varphi}-\frac{x(\varphi)u'\left(x(\varphi)\right)}{u\left(x(\varphi)\right)}\right)<0 \end{aligned} $$

holds if and only if,

$$\displaystyle \begin{aligned} \frac{x(\varphi)}{x(\varphi)+\varphi}-\varepsilon_{u}(x(\varphi))<0.{} \end{aligned} $$
(16.21)

Note that \(x(\varphi )=\widehat {N}(\varphi )^{-1}-\varphi \) is an implicit function, derived from Zero-profit condition

$$\displaystyle \begin{aligned} \bar{\varPi}=0\iff r_{u}\left(N^{-1}-\varphi\right)=(N-1)\varphi, \end{aligned}$$

which generally cannot be represented in closed form. Its inverse function, φ(x), however, has closed form solution. Indeed, Zero-profit condition may be rewritten in terms of x = N −1 − φ and φ as follows

$$\displaystyle \begin{aligned} r_{u}\left(x\right)=(N-1)\varphi=\left(\frac{1}{x+\varphi}-1\right)\varphi\iff\varphi^{2}-(1-r_{u}(x)-x)\varphi+xr_{u}(x)=0 \end{aligned}$$

with obvious solution of corresponding quadratic equation

$$\displaystyle \begin{aligned} \varphi(x)=\frac{1-r_{u}(x)-x}{2}-\sqrt{\left(\frac{1-r_{u}(x)-x}{2}\right)^{2}-xr_{u}(x)}.{} \end{aligned} $$
(16.22)

Note that the second solution of this equation,

$$\displaystyle \begin{aligned} \varphi_{+}(x)=\frac{1-r_{u}(x)-x}{2}+\sqrt{\left(\frac{1-r_{u}(x)-x}{2}\right)^{2}-xr_{u}(x)}, \end{aligned}$$

is not admissible, because φ +(0) = 1 − r u(0) ≠ 0, while x(φ) converges to zero when φ → 0. This implies that condition (16.21) is equivalent to

$$\displaystyle \begin{aligned} \frac{x}{x+\varphi(x)}<\varepsilon_{u}(x) {} \end{aligned}$$

for x > 0, which after substitution of (16.22) and rearranging terms takes on the form ε u(x) > A(x) for x = x(φ).Vice versa, the opposite ranking \(\widehat {N}(\varphi )<N^{*}(\varphi )\) is equivalent to inequality ε u(x(φ)) < A(x(φ)). ■

In what follows we suggest that the following assumption holds.

Assumption 16.2

There exist finite limits of the following fractions:

$$\displaystyle \begin{aligned} \frac{u''(0)}{u'(0)}=\lim_{x\to0}\frac{u''(x)}{u'(x)},\ \frac{u'''(0)}{u''(0)}=\lim_{x\to0}\frac{u'''(x)}{u''(x)}.{} \end{aligned} $$
(16.23)

It is obvious that CES utility does not satisfy the Assumption 16.2, while HARA u(x) = (x + α)ρ − α ρ, CARA u(x) = 1 − e −αx and Quadratic u(x) = αx − x 2∕2 utilities fit it well.

Lemma 16.1

Let Assumptions 16.1and 16.2hold, then r u(0) = 0, ε u(0) = 1, A(0) = 1. Moreover, there exist the limit values

$$\displaystyle \begin{aligned} r_{u}^{\prime}(0)=-\frac{u''(0)}{u'(0)},\ \varepsilon_{u}^{\prime}(0)=\frac{1}{2}\frac{u''(0)}{u'(0)},\ \mathit{\text{and }}A'(0)=\frac{u''(0)}{u'(0)}. \end{aligned}$$

Proof

Direct calculation shows that

$$\displaystyle \begin{aligned} r_{u}^{\prime}(x)=-\frac{u''(x)}{u'(x)}\left(1-\frac{xu''(x)}{u'(x)}+\frac{xu'''(x)}{u''(x)}\right), \end{aligned}$$

which implies \(r_{u}^{\prime }(0)=-\frac {u''(0)}{u'(0)}\). Using the L’Hospital rule, we obtain

$$\displaystyle \begin{aligned} \lim_{x\to0}\varepsilon_{u}(x)=\lim_{x\to0}\frac{xu'(x)}{u(x)}=\lim_{x\to0}\frac{u'(x)+xu''(x)}{u'(x)}=1. \end{aligned}$$

Moreover,

$$\displaystyle \begin{aligned} \varepsilon_{u}^{\prime}(x)=\frac{u'(x)}{u(x)}-x\left(\frac{u'(x)}{u(x)}\right)^{2}+\frac{xu''(x)}{u'(x)}\frac{u'(x)}{u(x)}=\varepsilon_{u}(x)\frac{1-r_{u}(x)-\varepsilon_{u}(x)}{x}, \end{aligned}$$

while limx→0(1 − r u(x) − ε u(x)) = 0. Therefore, using the L’Hospital rule once again, we obtain

$$\displaystyle \begin{aligned} \lim_{x\to0}\varepsilon'(x)=\lim_{x\to0}\varepsilon_{u}(x)\frac{1-r_{u}(x)-\varepsilon_{u}(x)}{x}=\varepsilon_{u}(0)\left(-r_{u}^{\prime}(0)-\lim_{x\to0}\varepsilon_{u}^{\prime}(x)\right), \end{aligned}$$

which implies

$$\displaystyle \begin{aligned} \varepsilon^{\prime}_{u}(0)=\frac{1}{2}\frac{u''(0)}{u'(0)}. \end{aligned}$$

Calculating derivative

$$\displaystyle \begin{aligned} A'(x)=\frac{1}{2}\left(1-r^{\prime}_{u}(x)\right)-\frac{\frac{1-r_{u}(x)-x}{2}\left(1+r_{u}^{\prime}(x)\right)+xr^{\prime}_{u}(x)+r_{u}(x)}{2\sqrt{\left(\frac{1-r_{u}(x)-x}{2}\right)^{2}-xr_{u}(x)}}, \end{aligned}$$

and substituting x = 0, we obtain

$$\displaystyle \begin{aligned} A'(0)=\frac{1}{2}\left(1-r^{\prime}_{u}(0)\right)-{\displaystyle \frac{\frac{1-r_{u}(0)}{2}\left(1+r_{u}^{\prime}(0)\right)+r_{u}(0)}{1-r_{u}(0)}=\frac{u''(0)}{u'(0)}}. \end{aligned}$$

■

Remark 16.1

It is easy to see that these assumptions are satisfied for all widely used non-CES “pro-competitive” classes of utility functions: HARA u(x) = (x + α)ρ − α ρ, α > 0, CARA u(x) = 1 − e −αx, α > 0, quadratic functions u(x) = αx − x 2∕2, α > 0, as well as for any superposition of functions from these classes.

Theorem 16.1

Let Assumptions 16.1and 16.2hold, then inequality (16.3) is satisfied for all sufficiently small x > 0, and thus \(N^{*}(\varphi )<\widehat {N}(\varphi )\)holds for all sufficiently small φ.

Proof

Due to Lemma 16.1,

$$\displaystyle \begin{aligned} A'(0)-\varepsilon^{\prime}_{u}(0)=\frac{u''(0)}{u'(0)}-\frac{u''(0)}{2u'(0)}=\frac{u''(0)}{2u'(0)}<0, \end{aligned}$$

which implies that A(x) − ε u(x) < 0 for all x > 0 sufficiently small. ■

To illustrate this result visually, let’s consider the HARA utility \(u(x)=\sqrt {x+1}-1\) and φ = f∕L = 0.01. Figure 16.1 shows that industry may accommodate with positive profit up to 6 firms, while the optimum number is approximately 4.

Fig. 16.1
figure 1

(a) Firm’s profit Π(N). (b) Social welfare V (N)

Full size image

16.3.1 When Assumption 16.2 Does Not Hold

Consider two examples of utility function, that does not satisfy Assumption 16.2. These examples show that result may be ambiguous.

Case 16.1

Let u(x) = x ρ + αx for α > 0, then

$$\displaystyle \begin{aligned} \varepsilon_{u}(x)=1-\frac{1-\rho}{1+\alpha x^{1-\rho}},\ r_{u}(x)=\frac{\rho(1-\rho)}{\rho+\alpha x^{1-\rho}}, \end{aligned}$$

which implies r u(0) = 1 − ρ, ε u(0) = ρ, while

$$\displaystyle \begin{aligned} \varepsilon^{\prime}_{u}(x)=\frac{\alpha(1-\rho)^{2}}{(1+\alpha x^{1-\rho})^{2}\cdot x^{\rho}}\to+\infty,\ r^{\prime}_{u}(x)=-\frac{\alpha\rho(1-\rho)^{2}}{(\rho+\alpha x^{1-\rho})^{2}\cdot x^{\rho}}\to-\infty, \end{aligned}$$

when x → 0. Differentiating the difference A(x) − ε u(x), we obtain

$$\displaystyle \begin{aligned} A'(x)-& \varepsilon^{\prime}_{u}(x) =\frac{1}{2}-\frac{\frac{1+r_{u}(x)-x}{2}-\frac{\alpha\rho(1-\rho)^{2}\cdot x^{1-\rho}}{2(\rho+\alpha x^{1-\rho})^{2}}}{2\sqrt{\left(\frac{1-r_{u}(x)-x}{2}\right)^{2}-xr_{u}(x)}}+\\ + & \frac{\alpha(1-\rho)^{2}}{x^{\rho}}\left[\frac{\frac{\rho(1-r_{u}(x))}{2(\rho+\alpha x^{1-\rho})^{2}}}{2\sqrt{\left(\frac{1-r_{u}(x)-x}{2}\right)^{2}-xr_{u}(x)}}+\frac{\rho}{2(\rho+\alpha x^{1-\rho})^{2}}-\frac{1}{(1+\alpha x^{1-\rho})^{2}}\right]. \end{aligned} $$

It is easy to see that

$$\displaystyle \begin{aligned} \frac{1}{2}-\frac{\frac{1+r_{u}(x)-x}{2}-\frac{\alpha\rho(1-\rho)^{2}\cdot x^{1-\rho}}{2(\rho+\alpha x^{1-\rho})^{2}}}{2\sqrt{\left(\frac{1-r_{u}(x)-x}{2}\right)^{2}-xr_{u}(x)}}\to-\frac{1-\rho}{\rho}, \end{aligned}$$

while term in brackets

$$\displaystyle \begin{aligned} \frac{\frac{\rho(1-r_{u}(x))}{2(\rho+\alpha x^{1-\rho})^{2}}}{2\sqrt{\left(\frac{1-r_{u}(x)-x}{2}\right)^{2}-xr_{u}(x)}}+\frac{\rho}{2(\rho+\alpha x^{1-\rho})^{2}}-\frac{1}{(1+\alpha x^{1-\rho})^{2}}\to\frac{1-\rho}{\rho}>0, \end{aligned}$$

when x → 0. This implies that

$$\displaystyle \begin{aligned} \lim_{x\to0}(A'(x)-\varepsilon^{\prime}_{u}(x))=+\infty\Rightarrow A(x)>\varepsilon_{u}(x) \end{aligned}$$

for all sufficiently small x > 0, or, equivalently, \(N^{*}(\varphi )>\widehat {N}(\varphi )\) for all sufficiently small φ = f∕L.

Case 16.2

Let u(x) = x ρ + αx with α < 0. This function satisfies u′(x) > 0 for all sufficiently small x > 0. Direct calculations show that

$$\displaystyle \begin{aligned} \varepsilon^{\prime}_{u}(x)=\frac{\alpha(1-\rho)^{2}}{(1+\alpha x^{1-\rho})^{2}\cdot x^{\rho}}\to-\infty,\ r^{\prime}_{u}(x)=-\frac{\alpha\rho(1-\rho)^{2}}{(\rho+\alpha x^{1-\rho})^{2}\cdot x^{\rho}}\to+\infty, \end{aligned}$$

and

$$\displaystyle \begin{aligned} \lim_{x\to0}(A'(x)-\varepsilon^{\prime}_{u}(x))=-\infty\Rightarrow A(x)<\varepsilon_{u}(x) \end{aligned}$$

for all sufficiently small x > 0, or, equivalently, \(N^{*}(\varphi )<\widehat {N}(\varphi )\) for all sufficiently small φ = f∕L.

Note that the case α = 0, corresponding to the CES function, we obtain

$$\displaystyle \begin{aligned} \lim_{x\to0}(A'(x)-\varepsilon^{\prime}_{u}(x))=-\frac{1-\rho}{\rho}<0\Rightarrow A(x)<\varepsilon_{u}(x) \end{aligned}$$

with the same conclusion, which was proved directly at the very beginning of this Section.

16.4 Concluding Remarks

Economists have long believed that unencumbered entry is desirable for social efficiency. This view has persisted despite the illustration in several articles of the inefficiencies that can arise from free entry in the presence of fixed set-up costs. In this article we have attempted to elucidate the fundamental and intuitive forces that lie behind these entry biases. The previous papers with similar conclusions were based on assumption on the zero love for variety. Moreover, some papers, e.g., [8], suggested that in case of diversified goods the positive welfare effect of the love for variety may offset the negative effect of excessive enter. Our paper shows that generally this is not true–negative effect prevails for all known classes of utilities with non-decreasing love for variety. Nevertheless, the opposite example of insufficient enter was also built on the base of AHARA-utility with decreasing love for variety.