Introduction

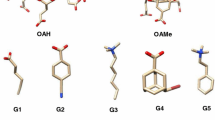
Host–guest systems have been proposed in the SAMPL challenges [1,2,3] as effective substitutes for protein ligand systems in the evaluation of computational methods of predicting binding affinities. Typical host molecules in the SAMPL initiatives are cavitands like the octa acids (OA) and the tetra-endo-methyl octa-acids (TEMOA) [4,5,6]. These systems are supposed to mimic just the binding site pockets in proteins for hosting small flexible guest molecules, sparing the demanding task of simulating the whole protein and/or identifying the relevant binding sites on the protein surface. While SAMPL6 guests (see Fig. 1) may exhibit a complex conformational pattern (e.g. G2 with axial/equatorial conformations of the 1–4 substituents on the six-membered ring, or G4 with five rotable sp3 bonds and, in principle, 243 different conformations), OA and TEMOA are relatively rigid systems, hence further alleviating the problem of canonically sampling the conformations of the binding sites in real proteins.

Fig. 1
figure 1

Blind prediction for the SAMPL6 challenge using FSDAM

Full size image

Binding free energies predictions for SAMPL6 host–guest systems were tackled using disparate computational strategies [1], from quantum mechanical to semiclassical or classical techniques, with explicit or implicit solvation models. Classical methodologies of fully atomistic representations included the host–guest potential of mean force determination via Umbrella Sampling [7] and double annihilation alchemical simulations, based either on free energy perturbation (FEP) [8] or thermodynamic integration (TI) [9]. Many of these studies adjusted their raw free energy predictions with a linear corrections obtained from previous SAMPLx data on similar host guest molecules. Strictly speaking, the latter knowledge-based results, while definitely interesting, are not genuine blind predictions as they somehow rely on the availability of retrospective host–guest binding free energy measurements. In this contribution we present results from a single submission (shown in Fig. 1) of a blind prediction with no retrospective corrections on the host–guest dissociation free energy. We used the so-called fast switching double annihilation technique (FSDAM) [10,11,12,13]. FSDAM is the only non-equilibrium technique used in the SAMPL6 challenge. This method is based on the production of canonical configurations of the bound and unbound states via enhanced sampling [Hamiltonian replica exchange with solute tempering (HREM) stage] and on the subsequent generation of hundreds of fast non-equilibrium (NE) ligand annihilation trajectories [fast non equilibrium annihilation (FNEA) stage] producing a bound and unbound work distributions. The annihilation free energies of the ligand when bound to the receptor and in bulk solvent, can be obtained from the collection of NE work values using an estimate based on the Crooks theorem for driven NE processes [14], in the assumption that the observed annihilation work distributions can be described by a normal distribution or by a mixture of Gaussian components [12, 15]. The absolute binding free energies are recovered by the differences of the annihilation free energies of the ligand in bulk and in the bound state, plus a standard volume and finite-size corrections.

Fast switching double annihilation technique has been here applied using a completely automatic procedure for the generation of the topology and parameter files of the host and guest molecules with the PrimaDORAC assignment tool [16], as well as for the input files of the HREM and FNEA stages and for the corresponding batch submission scripts on high performance computing platforms and for the post-processing of the HREM and FNEA data. FSDAM is specifically tailored [17] for non uniform memory access systems, implemented via a two layer OpenMP/MPI parallelism, in such a way that the distributed memory layer manages the production of the simultaneous HREM or FNEA trajectories, corresponding to weakly communicating MPI instances, each parallelized with a strong scaling scheme implemented on the OpenMP layer within the intra-node multi-cores shared memory environment. A single FNEA job can engage thousands of cores with nearly ideal parallel efficiency, producing a total simulation time of hundreds of nanonseconds in few wall clock minutes. On a per host–guest pair basis, the whole calculation required, for the HREM stage, \(\simeq 35\) ns sampling (on the target state) using eight replicas for both the bound and unbound systems and, for the FNEA stage, a cumulative \(\simeq 250\) ns for the bound and unbound state for a total simulation time on the 16 host–guest system of \(\simeq\) 8.5 \(\mu\)s of simulation performed in few wall-clock days on on the ENEA-CRESCO3 [18] cluster and the Marconi Broadwell High Performing Computing (HPC) systems [19]. The present blind prediction for SAMPL6 constitutes hence in first instance a prototypical test for industrial applications of FSDAM in ligand-receptor systems and in second instance one of the first significant tryouts for the recently released GAFF2 force field [20] and for the GAFF2-based PrimaDORAC assignment tools [16]. The paper is organized as follows. In the “Theoretical and methodological aspects of FSDAM” section we describe in detail the methodology used in the FSDAM SAMPL6 prediction. In “FSDAM theory” section, we briefly revise the theoretical basis of the FSDAM. The basic simulations details are provided in the “Simulation details and sample preparations” section. We then proceed to illustrate the HREM stage (“HREM stage” section) with a relevant example concerning the two enantiomers of the chiral ligand G2 (perillic acid) in their unbound state. The standard volume and finite-size corrections (“FNEA stage”, “Standard state volume and finite size corrections” sections) are discussed when evaluating the annihilation free energies in the FNEA stage of the G2 ligand in the OA-G2 complex. FSDAM results for binding free energies based on the normality assumption of the work distributions are presented in the “Results and discussion” section. In the “The FSDAM blind prediction on OA and TEMOA systems” section, we first report in detail the data concerning the single prediction that was submitted to the SAMPL6 challenge, critically analyzing the results with respect to the various source of errors. In “FSDAM with Gaussian mixtures” section, we show how in some cases the prediction can be improved by using the expectation–maximization algorithm for the determination of the the hidden normal components in a mixture. A possible force field issue is finally outlined in “Force field issues?” section. Conclusive remarks are presented in the “Conclusion” section.

Theoretical and methodological aspects of FSDAM

The theoretical background of FSDAM has been thoroughly described elsewhere [10,11,12,13, 17, 21, 22]. Here we provide a brief theoretical summary, focusing mostly on the technical details used in implementing this methodology on a HPC systems.

FSDAM theory

Likewise its equilibrium counterpart [23] (FEP- or TI-based), this alchemical methodology accomplishes the determination of the binding free energy by computing the difference between the decoupling free energies of the ligand in the solvated complex and in bulk solvent. As outlined in the introduction, each of these two independent calculations is in turn done in two steps: (i) a replica exchange simulation with solute torsional tempering [24] (HREM stage) of the fully coupled ligand state, aimed at harvesting canonical (equilibrium) configurations of the systems; (ii) a transformative stage based on NE simulations (FNEA stage), whereby the ligand, starting from the configurations sampled in the corresponding HREM stages, is rapidly annihilated in a swarm of concurrent and independent NE trajectories each yielding a NE work and eventually an annihilation work distribution.

In both HREM and FNEA bound state simulations, a weak harmonic restraint between the centers of mass (COM) of the host and guest molecules is imposed. A COM–COM restraint in the bound state simulations is equivalent [25,26,27] to fix the ligand concentration or, equivalently, a ligand allowance volume \(V_r=(2\pi RT/K_h)^{3/2}\), with \(K_h\) being the harmonic force constant of the restraint potential [28]. If no restraints are imposed, the allowance volume is clearly that of the MD box [29, 30]. As discussed in Refs. [25, 31], the standard dissociation free energy of the restrained system is given by the equation

$$\begin{aligned} {\varDelta }G_0 = ({\varDelta }G_b -{\varDelta }G_u) +RT \ln (V_r/V_0 ) \end{aligned}$$
(1)

where \({\varDelta }G_b\) and \({\varDelta }G_u\) are the (COM–COM restrained) bound ligand and free ligand annihilation free energy. Eq. (1) simply says that while \({\varDelta }G_0\) is constant, the ratio between dissociated and undissociated host–guest species \([H]/[HG]\equiv e^{-\beta ({\varDelta }G_b - {\varDelta }G_u)}\), depends on the imposed guest concentration \([G]_r\), i.e. on the restrained ligand reference volume \(V_r\). In a HREM simulation of a bound state, with the guest molecule G restrained in the reference volume \(V_r=1/[G]_r\) with respect to the COM of the host H, the ratio of dissociated and bound states is given by \([H]/[HG]=K_d/[G]_r\), where \(K_d=e^{-\beta {\varDelta }G_0}\) is the dissociation constant. If one chooses for the guest reference volume, the value of 1661 Å3, corresponding to a ligand concentration \([G]_r=1\) M, then the ratio \([G]/[HG] \simeq K_d\). Therefore, choosing the force constant \(K_h\) so that \(V_r=1661\) Å3, we expect that the number of dissociated states in an equilibrium HREM run, sampling N configurations, are of the order of \(K_d N\). If N is of the order of few hundreds and \(K_d < 10^{-3}\)M , then we basically expect that all sampled HREM states of the restrained bound state should be of the associated type. As it will be discussed further on, the guests remains in the host cavity in all sampled target state configurations, in agreement with the fact that \(K_d< 10^{-3}\) M for all host–guest pair if the SAMPL6 challenge.

Provided that the annihilation NE work distributions \(P_b(W)\) and \(P_u(W)\) from the FNEA stages are normal, according to the Crooks theorem [14] the corresponding annihilation free energies can be straightforwardly recovered [32, 33] using an unbiased estimator based on the mean and variance of the work distributions, i.e.

$$\begin{aligned} {\varDelta }G_{b/u} =\langle W_{b/u} \rangle -\frac{1}{2}\beta \sigma _{b/u}^2 \end{aligned}$$
(2)

where the indices b, u refer to the bound or unbound states and where \(\langle W_b \rangle\) and \(\langle W_u \rangle\) are mean value of the ligand decoupling work in the bound state and in bulk solvent and \(\sigma _b^2\), \(\sigma _u^2\) are the corresponding variances. Most importantly, the confidence interval for the estimates based on Eq. 2 can be easily assessed taking into account that the mean and variance for normally distributed samples are independent random variables and follow the t statistics and chi-square distribution, respectively [34]. By inverting these distributions, we can get an estimate of the confidence intervals, thus providing an overall error for the Gaussian estimator of Eq. 2 as

$$\begin{aligned} \delta {\varDelta }G_{b/u} = z_{\alpha /2} \left| \frac{\sigma _{b/u}}{n_{b/u}^{1/2} } + \frac{1}{2} \beta \left( \frac{2}{n_{b/u}} \right) ^{1/2} \sigma _{b/u}^2 \right| \end{aligned}$$
(3)

where \(n_{b/u}\) is the number of sampled work values and with \(1-\alpha\) being the confidence level, meaning that the true value of \({\varDelta }G_{b/u}\) falls within the given range of Eq. 3 with probability \(1-\alpha\). Choosing \(\alpha =0.05\), for \(n>100\) we can safely take \(z_{0.025} \simeq 2\) thus defining a confidence level for the interval of Eq. 3 of 95%.

Actually, as discussed above, the bound state annihilation work distribution should be contaminated on the left tail by a so-called [15] shadow normal component \(n_d(W)\) corresponding to the dissociated states obtained with the imposed reference volume \(V_r\), so that \(P_b(W)=(1-c)n_b(W) + c n_d(W)\) with c of the order of \(c\simeq K_dV_r/V_0\). In Refs. [12, 15], we showed that in the hypothetical fast-growth reverse NE process of re-coupling an initially decoupled ligand from a random position in the allowance volume \(V_r\), the principal bound state component is basically suppressed while the shadow component \(cn_d(W)\), corresponding to an unbound or weakly bound guest molecule, gets exponentially amplified. The Crooks theorem for such two-component mixture yields

$$\begin{aligned} {\varDelta }G_b^r=\langle W_{b} \rangle -\frac{1}{2}\beta \sigma _{b}^2 + RT \ln (V_{\mathrm{site}}/V_r) \end{aligned}$$
(4)

where \(V_{\mathrm{site}}/V_r\) represents the weight of principal component in the hypothetical reverse fast growth process, corresponding to the probability of re-entrance in the binding pocket, defined in terms of a binding site volume \(V_\mathrm{site}\). \({\varDelta }G_b^r\) in Eq. 4 is the \(V_r\)-dependent annihilation free energy of the restrained bound state. In deriving Eq. 4, it has been implicitly assumed that \(V_r \gg V_{\mathrm{site}}\), [27]. We further assume that the volume \(V_{\mathrm{site}}\) is weakly dependent on the duration \(\tau\) of the NE process, so long that \(\tau \ll \tau _{\mathrm{on}}\), where \(\tau _\mathrm{on}=V_{\mathrm{ref}}/k_{on}\) is the average mean time for the ligand to bind the target at the concentration \(1/V_\mathrm{ref}\) [35, 36]. On this basis, combining Eqs. 1, 2 and 4, we obtain the FSDAM expression for the standard dissociation free energy

$$\begin{aligned} {\varDelta }G_0&= {\varDelta }G_b - {\varDelta }G_u + RT \ln \left( \frac{V_{\mathrm{site}}}{V_{0}} \right) \end{aligned}$$
(5)

where \(V_0\) is the standard state volume. In Eq. 2, the \(\sigma\)-related energies \(\frac{1}{2}\beta \sigma _{b/u}^2\) have a straightforward physical interpretation: they represent the dissipation in the NE process of the annihilation of the ligand in the bound and unbound state. Hence, the wider are the normal distributions, the more dissipative the NE annihilation process is.

The evaluation of the elusive \(V_{\mathrm{site}}\) volume will be discussed further on in “Standard state volume and finite size corrections” section. We conclude this subsection, with a brief outline of how the finite-size effects, involved in the annihilation of charged ligands, are handled in FSDAM. In the Particle Mesh Ewald treatment [37] used in this study for treating long range electrostatics, when computing the electrostatic energy of a charged system, one implicitly adds to the Coulomb energy a term corresponding to the contribution of the total charge in the MD box interacting with a uniform neutralizing background plasma. Such term, called the Wigner self energy, is automatically included in the reciprocal lattice when using PME [38], while in the direct lattice is given by \(E_w^d(\alpha ,V) = -|\sum _i q_i| ^2\pi /(2\alpha ^2V)\), where V is the volume of the zero-cell, the sum is extended to all charges in the box and \(\alpha\) is the Ewald convergence parameter. If the ligand bears a net charge, a finite size correction must hence be added to account for the change in the free energy related to the annihilation of the net charge. This direct space correction to the dissociation free energy can be computed as

$$\begin{aligned} {\varDelta }G_{\mathrm{fs}} = - \frac{\pi }{2\alpha ^2} \left\{ \frac{ [ Q_H^2 - (Q_H+Q_G)^2 ] }{ V_{\mathrm{BOX}}^{(b)}} - \frac{Q_G^2 }{V_\mathrm{BOX}^{(u)}} \right\} \end{aligned}$$
(6)

where \(Q_H\) and \(Q_G\) are the net charge on the host and guest molecule, respectively and \(V_{\mathrm{BOX}}^{(b/u)}\) are the MD box volume of the bound and unbound states.

Simulation details and sample preparations

Atomic type assignment and partial atomic charges on the ligands were computed using the PrimaDORAC web interface [16]. PrimaDORAC computes the AM1-BCC charges [39] on the AM1 optimized geometry [40] of the ligand and assigns the atomic types according to the recently released GAFF2 general parameterization for organic molecules [20]. Following the indications of the organizers, all the carboxylate groups on the host molecules OA and TEMOA and on the guest molecules were assumed to be deprotonated, so that the guest and the host molecules bear a net charge of − 1e and − 8e respectively. The solvent was treated explicitly using the TIP3P model [41]. Long range electrostatic were treated using the Smooth Particle Mesh Ewald (SPME) method [37], with an \(\alpha\) parameter of 0.37 Å−1, a grid spacing in the direct lattice of about 1 Å  and a fourth order B-spline interpolation for the gridded charge array. As no counterions were included, charge neutralization in charged bound and unbound systems is implicitly done in SPME using a uniform neutralizing background plasma. Bonds constraints were imposed to X–H bonds only, where X is an heavy atom. All other bonds were assumed to be flexible. The pressure was set to 1 atm using a Parrinello-Rhaman Lagrangian [42] with isotropic stress tensor [43] while temperature was held constant to 298 K using three Nosé Hoover-thermostats coupled to the translational degrees of freedom of the systems and to the rotational/internal motions of the solute and of the solvent. The equations of motion were integrated using a multiple time-step r-RESPA scheme [44] with a potential subdivision specifically tuned for bio-molecular systems in the NPT ensemble [43, 45]. The long range cut-off for Lennard-Jones interactions was set to 13 Å  in all cases.

Using the starting host and guest structures provided by the organizers, the preparation of the bound states for each host–guest pair was done by generating one hundred random host–guest structures within a COM–COM docking radius of 5 Å, followed by energy minimization in implicit solvent using the AGBNP model [46]. The starting structure of the complex corresponds to that of lowest energy found in the docking stage. The so obtained least energy host–guest structures were then oriented along the inertia frame of the guest molecule and explicit water molecules at a density of 1 g cm\(^{-3}\) were added in a cubic MD box whose side-length was computed so that the minimum distance between host or guest ligand atoms belonging to neighboring replicas was larger than 24 Å  in any direction. After removal of overlapping water molecules, the bound state systems contained about 1250 solvent molecules for a volume of approximately 40,000 Å\(^3\) corresponding to a side-length of \(\simeq\) 34 Å. For water and box volume equilibration, a preliminary 50 ps constant pressure, constant temperature simulation was run for each of the so prepared solvated complexes. The starting structures of the guest molecules in bulk solvent were prepared by inserting the structures provided by the organizers in a box of side-length 26 Å, containing TIP3P molecules at the density of 1 g cm\(^{-3}\).

The above procedure for generating the bound and unbound starting structures and the corresponding input file for subsequent HREM and FNEA stages was completely automatized by an application script program. All simulations in this study are done using the program ORAC [17].

HREM stage

The HREM simulations of the bound state was run on the HPC system by launching, in a single parallel job, four independent Hamiltonian replica exchange [47] simulation with eight solute tempered replicas in the generalized ensemble (GE) for a total of 32 MPI instances. Each HREM battery sampled 96 configurations taken at regular interval in a simulation time of 7.8 ns, hence accumulating 384 solvated bound state configurations in a total simulation time of 31.2 ns. For the free guest HREM simulation, we used again four independent batteries of eight exchanging replicas, each lasting 1 ns, for a total simulation time of 4.0 ns, sampling 240 solvated guest molecules configurations. Each GE walker in the bound and unbound states used six threads on the OpenMP strong scaling layer, so that the hybrid OpenMP/MPI parallel HREM jobs engaged a total 192 cores. Only the torsional potential of host and guest system was scaled throughout the GE up to 0.1 in both cases, corresponding to a solute “torsional” temperature of 3000 K. The scaling protocol in the eight replicas GE range [1–0.1] was set according to the scheme described in Ref. [24]. Exchanges were attempted between neighboring replicas at each long time step (i.e. each 15 fs), yielding a mean acceptance ratio throughout the GE of no less that 50%, in all cases. All HREM computations were completed on the CRESCO3-ENEA HPC platform [48] in few wall clock days.

The adopted scaling protocol allows to effectively sample in the target state the whole accessible conformational space of the flexible guest molecules in their free state and when embedded in the cavitand. As a relevant example of HREM, we show the time record and the corresponding distribution of the axial-equatorial conformations in the R- and S- enantiomers of the G2 guest molecule in bulk as obtained in two 4  ns REM simulations referring to the two enantiomers solvated in TIP3P water. As it can be seen in Fig. 2, axial-equatorial conformations (identified by the distance between the sp2 carbon of the isopropenyl moiety and the ring carbon in position 1) easily interconverts in the G2 molecule, in spite of the high barrier (\(\simeq 4\hbox { kcal mol}^{-1}\)) separating these conformational states. According to the GAFF2 force field, the conformational distributions, show a clear prevalence of the equatorial conformer and are essentially identical in the two enantiomers, and so should be their affinities towards the symmetrical OA and TEMOA host molecules, as assumed by the organizers.

Fig.  2
figure 2

Probability distribution of the distance between C1 and the sp2 carbon Cm identifying the axial-equatorial conformation in the two enantiomers of the G2 guest molecule as obtained from the HREM simulations (see text for details). In the inset, the time record of the distance C1–Cm in the GE target state

Full size image

The effectiveness of HREM approach in sampling conformational states in the bound state can be appreciated in the Figs. 3 and 4, where we report the distribution of the host–guest COM–COM distance (left panels) and the corresponding potential of mean force (right panels) for the guest-OA and guest-TEMOA systems, respectively. In general, although the imposed weak restraint potential implies an allowance radius of more than 7 Å, we can see that the ligand lingers around the binding pocket of the cavitand. In most cases, the COM–COM distance distribution exhibits a positively skewed single peak with half-width rarely exceeding 1 Å. In some cases (G6 and G7 in OA and in TEMOA), the COM–COM distributions have a complex structure due to multiple poses. These can be highlighted by evaluating the potential of mean force along the COM–COM distances, shown in the right panels of Figs. 2 and 3. Concerning the PMF computation via HREM, some comments are in order. In principle, setting the restraint so that \([G]_r=1\)M, a HREM simulation could be used to compute directly the dissociation [49] constant as \(K_d=[H]/[HG]=P_u/P_b\) where \(P_u\) and \(P_b\) are the probability of observing the dissociated and associated state [50]. In practice, while the bound state sampling in the HREM stage allows quite an accurate reconstruction of the PMF in the bottom of the well, zones at larger distances/higher energies towards unbound states are statistically noisy. This is so since solute torsional tempering with no water-solute rescaling [49] (as done in our HREM approach) does not accelerate relative host–guest diffusion, in a such a way that the expected shortest \(\tau _{\mathrm{off}}\) for the weakest binder among all host–guest pairs (TEMOA-G5, \(K_d\simeq 10^{-3} \mathrm{M}\)) should be of the order of the microseconds [35, 36] in any GE state, making de facto unattainable the brute force sampling of unbound states in the HREM stage and hence the direct calculation of \(K_d\).

Fig.  3
figure 3

COM–COM distance distribution function and and PMF for the OA-guest systems

Full size image
Fig.  4
figure 4

COM–COM distance distribution function and and PMF for the TEMOA-guest systems

Full size image

FNEA stage

For each host–guest pair, in the FNEA stage a swarm of fast independent ligand annihilation trajectories were started from the phase-space points sampled in the HREM stage for the unbound and bound guest molecules. The total number of independent NE trajectories were 384 for the decoupling of the ligand in the bound state and 240 for the decoupling of the ligand in bulk solvent. The annihilation protocol of the \(\tau\) lasting NE processes was common to all host–guest systems and stipulates that the electrostatic interactions between the ligand and the environment are linearly brought to zero at \(t=\tau /2\) , while the Lennard–Jones interactions are switched off in the range \(\tau /2< t < \tau\) using a soft-core Beutler potential [51] regularization as \(\lambda\) is approaching to 1 corresponding to the decoupled state. The alchemical work along the alchemical path was computed as described in Ref. [10]. We stress here that in FSDAM there is no need for the optimization of the so-called thermodynamic length [52], that is of choosing the alchemical protocol so that the total uncertainty for the transformation is the one which has an equal contribution to the uncertainty across every point along the alchemical path [53]. As previously discussed (see Eq. 3), a confidence intervals for the FSDAM free energy value can be estimated directly from the moments of the final work distributions.

As done in HREM, also in the FNEA stage parallel execution is performed using a straightforward hybrid OpenMP-MPI approach, with NE non communicating annihilation trajectories handled at the MPI level and a force decomposition scheme implemented with nine threads on the shared memory OpenMP layer. As in past FSDAM studies on ligand-receptor or host–guest, the duration of each of NE independent decoupling trajectories adopted in this paper are of few hundreds of picoseconds (from 90 to 720 ps) for both the solvated bound state and the free ligand in bulk solvent. Each host–guest FNEA computation required 3240 and 2160 cores (bound and unbound state, respectively) on the Marconi-Broadwell HPC system [19] for few to few tens of wall clock minutes depending on the selected annihilation time.

From the collection of annihilation works, the bound state and unbound state normalized work histograms probability were computed, namely \(P_b(W)\) and \(P_u(W)\), respectively. In Fig. 5 we show these distributions for the duration time \(\tau _{b/u}=360\) ps for all sixteen host–guest pairs. The normality of these distribution is assessed using the Anderson-Darling (AD) quadratic test [54,55,56]. The Anderson-Darling test \(A^2\) is defined as \(A^2=\sum _{i=1}^n \frac{2i-1}{n} [ \ln ({\varPhi }(w_i) + \ln (1-{\varPhi }(w_{n+1-i}) ]\), where \({\varPhi }\) is the Gaussian cumulative distribution function with sample mean and variance and \(w_i\) are the work values sorted in ascending order. The critical value of \(A^2\) at the level \(\alpha =0.05\) is 0.752 [55]. AD has been recently shown [57] to be the most stringent normality test among many popular alternatives including the Kolmogorov-Smirnov and the Wilk-Shapiro tests. As shown in Fig. 5 and detailed in Table 1 further on, the work distributions for the unbound state of all eight ligands amply passed the AD test for normality. The AD test was passed with a confidence level of 95% for 10 out of 16 bound state distributions and exceeded the critical value by more than 0.5 in only two cases for the G0 and G1 TEMOA ligands. As shown in Table 1, we observe in general higher \(A^2\) values for the TEMOA bound state, indicating that the extra methyl moieties decorating the crown of the host do have a significant impact on the host–guest free energy surface and, correspondingly, in the subsequent NE guest annihilation work. In the HREM stage, for example, the TEMOA-G7 complex is clearly characterized by a bimodal COM–COM distance distribution as shown in Fig. 4. This bimodal distribution of the starting canonically sampled initial states is somehow reverberated in (see Fig. 5) in the negatively skewed NE work distribution of the G7-TEMOA complex, yielding a \(A^2\) value close to 1, pointing to a non normally distributed sample.

Fig.  5
figure 5

Annihilation work distributions for the bound state (black trait, on the right) and unbound state (red trait, on the left) for the SAMPL6 host–guest pairs (OA complexes on the left panel and TEMOA complexes on the right panel) as obtained in the FNEA stage with an annihilation duration time of 360 ps for the unbound bound state. For the bound state \(K_h=0.003\) was set to \(\hbox {kcal mol}^{-1}\) Å\(^{-2}\) in both the HREM and FNEA stages. Red/top and orange/mid traffic-light symbols signal a failed AD test, with \(A^2\) exceeding the critical value at the 0.05 \(\alpha\) level by > 1 and < 0.5, respectively

Full size image
Table 1 Raw FSDAM data for the SAMPL6 octa-acids challenge
Full size table

We stress here that errors in computing the annihilation free energies via the NE formula Eq. 2 are not due, by any means, to insufficient sampling of the intermediate alchemical states. These are crossed at fast speed in the concurrent NE trajectories and their transient distribution is of no concern whatsoever for the end-user. In the context of the Crooks theorem, what ought to be stationary is the annihilation work distribution. For normal distributions, this comes down to the stationarity of the first two moments, when the FNEA computation is replicated starting from a different set of initial canonical configurations sampled in the HREM stage and using the same annihilating protocol. Even more, one can repeat the FNEA experiment using a different duration time and evaluate the alchemical potential of mean force (PMF) as \({\varDelta }G_{b/u} (\lambda ) = \langle W_{b/u} (\lambda ) \rangle -\frac{1}{2}\beta \sigma _{b/u}^2(\lambda )\) along the alchemical coordinate \(0< \lambda < 1\), with \(\lambda =0\) and \(\lambda =1\) representing the fully coupled and fully decoupled state, respectively. If the work distributions are normal at all \(\lambda\) and for all \(\tau\), this quantity should be stationary at any \(\lambda\) irrespective of the selected duration \(\tau\) of the NE experiment or of the adopted annihilation protocol. As an example, in Fig. 6 we show for the \({\varDelta }G_b(\lambda )\) the annihilation of the bound G1 and G0 in the OA and TEMOA system. Both the G1-OA and TG0-TEMOA work distributions for \(\tau =360\) and for \(K=0.03\) passed the AD test (data not shown). As it can be seen on the full energy scale, the PMFs computed on the basis of the normality assumption on the whole \(\lambda\) interval using different duration times are barely distinguishable. Differences can be appreciated only in the enhanced view of the insets. Note that increasing the duration time of the FNEA runs, leads to annihilation free energy estimates differing at most \(1 \hbox { kcal mol}^{-1}\) at full guest annihilation \(\lambda =1\). The \(\tau =720\) ps estimates for both the G1-OA and G0-TEMOA fall within the error bar of the corresponding \(\tau =360\), with the 95% confidence interval computed according Eq. 3.

Fig.  6
figure 6

PMF for the annihilation of the guest molecule in the G1-OA complex (left) and in the G0-TEMOA complex (right), obtained using different annihilation rates and a force constant of \(K_h=0.03 \hbox { kcal mol}^{-1}\) Å\(^{-2}\). The insets are an enlarged view of the PMF in the final stages \(\lambda \simeq 1\) of the alchemical parameter \(\lambda\). Error bars have been computed using Eq. 3 and are shown only for the guest annihilation with \(\tau =360\) ps for clarity

Full size image

This fact is remarkable indeed considering that the final work distributions are characterized by strongly \(\tau\)-dependent moments, as show in the Fig. 7. For the two G1-OA and G0-TEMOA complexes, the mean, \(\langle W \rangle\), drops by \(\simeq 4\hbox { kcal mol}^{-1}\) with duration time passing from \(\tau =90\) ps to \(\tau =720\) ps. A similar trend is observed in the variance \(\sigma ^2\).

Fig.  7
figure 7

Mean (main plots) and variance (insets) as a function of the \(\lambda\) alchemical parameter of the annihilation work distribution of the guest molecule in the G1-OA complex (left) and in the G0-TEMOA complex (right), obtained using different annihilation rates

Full size image

Standard state volume and finite size corrections

As discussed in “FSDAM theory” section, the FSDAM estimate should be independent of the imposed restraint volume \(V_r\) in the HREM and FNEA stages (see on this issue Table 3 further on). However, according to Eq. 5, the estimate does depend on the binding site volume \(V_{\mathrm{site}}\). In the following we provide some details on the computation of \(V_{\mathrm{site}}\) appearing in the FSDAM dissociation free energy estimate, Eq. 5. In the submitted blind prediction we have evaluated the \(V_{\mathrm{site}}\) from the the distributions of the host–guest COM–COM vector distance. This has been accomplished by numerically evaluating in the HREM equilibrium simulations the volume enclosed in a Van Der Waals-like surface defined by spheres with centers at the sampled COM–COM vector points and radius 0.1 Å. As such, this choice for the elusive \(V_{\mathrm{site}}\), while apparently reasonable, still remains arbitrary to some extent. Fortunately, the logarithmic dependence of \(V_{\mathrm{site}}\) in Eq. 5 significantly tames the uncertainty of the volume correction (see Table 1). The binding site volume determination is undoubtedly the weak point of the FSDAM approach. However, the binding site volume determination is the rather undervalued weak point of any computational approach based on the definition of “bound state” [27]. These include also methodologies aimed at the determination of relative binding free energy which all implicitly (and arbitrarily) assume a constancy of the binding site volume upon transmutation of the bound ligand into another bound parent compound.

As discussed above, the finite size correction in FSDAM using PME can be straightforwardly computed a priori by means of Eq. 6. This box volume dependent correction defines the direct lattice contribution to the Wigner self energy [38]. In the SAMPL6 challenge, this correction affects significantly the annihilation free energy of the complex, namely \({\varDelta }G_{\mathrm{fs}}^{(b)} = - 2\alpha ^2 [ Q_H^2 - (Q_H+Q_G)^2 ]/ V_{\mathrm{BOX}}^{(b)}\), since in that case the net charge goes from \(-9e\) to \(-8e\), with \({\varDelta }G_{\mathrm{fs}}^{(b)}\) amounting to approximately 1.3 \(\hbox {kcal mol}^{-1}\) while \({\varDelta }G_{\mathrm{fs}}^{(u)}\) is negligible in the other leg of the FNEA process, i.e. the annihilation of the the guest molecule in bulk. Note that, being the Wigner self energy more negative for the fully coupled state, the finite size correction for the guest annihilation in the bound state is positive. The finite size effect can be numerically tested by repeating the HREM and FNEA calculation of the annihilation free energy in the complex using a much larger box at constant Ewald \(\alpha\) convergence parameter. If the work distribution of the larger sample are normal for any \(\lambda\), we do expect to observe an uncorrected PMF, \({\varDelta }G_b(\lambda )\), consistently larger with respect to that of the smaller sample. The final uncorrected annihilation free energies should differ by the positive quantity

$$\begin{aligned} {\varDelta }G_b(V_L) -{\varDelta }G_b(V_s) = \frac{\pi }{2 \alpha ^2} [ Q_H^2 -(Q_H+Q_G)^2 ]\left( \frac{1}{V_L} - \frac{1}{V_s} \right) \end{aligned}$$
(7)

where \(V_s\) and \(V_L\) are the small and large box volume respectively. We tested the finite size correction in the G2-OA system (that passed the AD normality test), by repeating the HREM and FNEA stages using a mean box volume \(V_L\) of about 150,000 Å\(^3\) corresponding to a side-length of about 53 Å containing about 5000 water molecules. Due to high computational cost of the large sample computation, we produced only 120 annihilation trajectories, with an expected 95% confidence interval increasing by a factor of \(\sqrt{2}\) according to Eq. 3. As \(V_L\) is about four times larger than \(V_s\), according to the Eq. 7 we do expect the difference \({\varDelta }G_b(V_L) -{\varDelta }G_b(V_s)\) to be approximately equal to \(3/4 \times {\varDelta }G_{\mathrm{fs}}^{(b)}\), i.e. 3/4 times the finite size correction for the smaller sample. This is happily confirmed in Fig. 8, where the two PMFs computed with the large and small box differ almost exactly by the expected quantity computed according to Eq. 7. We stress that such test, besides numerical assessing the finite size effect verifying Eq. 7, constitutes yet an other strong confirmation of the extraordinary robustness and soundness of the Gaussian based estimate 2, given that two PMFs refers to two independent HREM and following FNEA computations done on samples of different size.

Fig.  8
figure 8

PMFs as a function of the \(\lambda\) alchemical coordinate for the annihilation of G2 in complex with OA, obtained on samples of different size. The arrowed bar on the right corresponds to the expected difference between the two PMFs on the basis of Eq. 7. Error bars, computed according to Eq. 3, have been plotted only for the PMF of the large system

Full size image

Results and discussion

The FSDAM blind prediction on OA and TEMOA systems

All data for delivering our blind prediction of the octa-acids SAMPL6 challenge are collected in Table 1.

The Table reports all the computed quantities that are needed in the FSDAM expression 5 for the evaluation of dissociation free energy of a guest-hots pair. The errors in the evaluation of the moments \(\langle W \rangle\) and \(\sigma ^2\) are standardly computed using bootstrap with resampling and, as it can be easily verified using the variances reported in the Table, are remarkably similar to those predicted by Eq. 3 based on the normality assumption. The last column in the Table refers to the \(A^2\) value computed with the AD test form normality on the corresponding work distributions. Since Eq. 5 has been used for all computed work distributions, we may expect a better performance for the OA prediction set with respect to the TEMOA host–guest pairs, the latter exhibiting in general higher \(A^2\) values and wider work ditributions (see Fig. 5). In Fig. 9, we show the correlation diagram between experimental [1] and FSDAM computed standard dissociation free energies for the OA (left) and TEMOA (right) systems. We may say in general that our FSDAM blind prediction, with a RMSD of < \(2.5 \hbox { kcal mol}^{-1}\), has a good ranking among all submitted genuine blind predictions (i.e without adjusted free energies based on retrospective data). FSDAM ranked in 4-th place for OA with a mean RMSD below \(2 \hbox { kcal mol}^{-1}\) and in 5-th place for TEMOA with a mean RMSD below \(3 \hbox { kcal mol}^{-1}\).

Fig.  9
figure 9

Correlation diagram between experimental and calculated dissociation free energies (\(\hbox {kcal mol}^{-1}\)) for the OA (left panel) and TEMOA (right panel) host–guest pairs. The normal assumption and Eq. 5 was used in the estimate and \(\tau\) was set to 360 ps in the FNEA stage for both the bound and bulk state. \(K_h=0.003\) was set to \(\hbox {kcal mol}^{-1}\) Å\(^{-2}\) in both the HREM and FNEA stages. The quantities a and b are the slope and intercept, respectively, of the regression line. The dashed line with \(a=1\) and \(b=0\) corresponds to perfect match

Full size image

As in many MD-based SAMPL6 approaches, also in our case results are definitely better for the OA host with respect to TEMOA cavitand. For the OA host, only G2 and G4 FSDAM dissociation free energies differ by more that \(3.5 \hbox { kcal mol}^{-1}\) with respect to the experimental counterpart, all others differing at most for \(1.5 \hbox { kcal mol}^{-1}\). The fact that the outlier G2 and G4 (in both the OA and TEMOA FSDAM prediction sets) are the only chiral species in the SAMPL6 challenge can instill the doubt that the experimental measurements could actually refer to a non enantiopure sample or to the racemic mixture. Organizers assurances and Fig. 2 for the case of G2 definitely rules out this wrong inference. As shown by our HREM simulation, the two G2 enantiomers, according to the GAFF2 force field, both exhibit overwhelmingly the extended (equatorial) conformation in bulk. Therefore, because of the symmetry of the host species, the two enantiomers should have the same affinity towards OA and TEMOA. Similar considerations applies to the G4 chiral guest molecule as well, where the asymmetric carbon has a minimal impact on the conformational landscape of the molecule.

For the TEMOA system, the correlation coefficient is indeed unsatisfactory dropping from 0.91 in the OA guests to only to 0.31 (see Fig. 9, right panel). This small value is due to three FSDAM predictions that are completely off the mark, i.e. those involving again the chiral species G2 and G4 and that referring to G7. While in the case of G2 and G4 discrepancies could be due to a deficiency of the GAFF2 force field and/or to an erroneous PrimaDORAC atomic type assignment, for G7 the problem could be due to the normality assumption implied in the estimate of the annihilation free energies in Eq. 5. As a matter of fact, the G7-TEMOA bimodal work distribution failed the AD test (see Table 1) and the error bar using a single Gaussian is abnormally large. Moreover, we recall that the AD test gives only the probability for rejecting the null hypothesis (i.e. the work are normally distributed) but does not provide any certitude on the correctness of the null hypothesis.

FSDAM with Gaussian mixtures

In the following, we generalize the FSDAM approach assuming that the principal component of the observed bound state distribution is given by a mixture of normal distributions, i.e.

$$\begin{aligned} P_b(W)=(1-c)\sum _i^{K_b} w_i^b n_b(W,\mu _i^b,\sigma _i^b) + c n_d(W) \end{aligned}$$
(8)

where \(n_d(W)\) is the shadow component distribution corresponding to the dissociated states with the guest allowance volume \(V_r\), \(\mu _i^{b}\) and \(\sigma _i^{b}\) are the mean and variance of the i-th normal sub-component in the bound state mixture, \(w_i^b,\) and \(K_b\) are the normalized weights and the number of sub-components, respectively. Under this assumption it can be easily shown, using again the Crooks theorem, that the estimate Eq. 5 still holds with \({\varDelta }G_b\) determined as

$$\begin{aligned} {\varDelta }G_b= & {} -RT \ln \left[ \sum _i^{K_b} w_i^b e^{\mu _i^b -\frac{1}{2}\beta (\sigma _i^b)^2} \right] \end{aligned}$$
(9)

Note that Eq. 9 comes down to Eq. 2 when \(K_b\) is equal to 1, i.e. when \(P_b(W)\) is normal. A similar generalization can be extended to the work distribution of the unbound state that can be assumed to be given by a mixture of the kind \(P_u(W)=\sum _i^{K_u} w_i^u n_u(W,\mu _i^u,\sigma _i^u)\) so that

$$\begin{aligned} {\varDelta }G_u= & {} -RT \ln \left[ \sum _i^{K_u} w_i^u e^{\mu _i^u -\frac{1}{2}\beta (\sigma _i^u)^2} \right] \end{aligned}$$
(10)

We stress that the variant of the FSDAM based on mixtures concerns only work data post-processing and not the production stages HREM and FNEA.

In order to deliver a dissociation free energy estimate based on Eq. 5, where the observed work distributions are assumed to be a mixture of normal components, one has first to identify the number \(K_b\) and \(K_u\) of normal components in the bound state and unbound state distributions produced by the ordinary FNEA stages and then, for each normal component in a given distribution one has to determine the weight \(w_i\) and the parameters \(\mu _i\) and \(\sigma _i\). As shown in Ref. [15], when dealing with NE processes that are characterized by strongly asymmetric forward and reverse work distributions, as in the folding/unfolding of proteins or in the docking/undocking of a ligand, it is convenient to keep the number of components as small as possible in order to minimize the uncertainty in the mixture-based estimate Eqs. 9 and 10. The minimum number of component \(K_{b/u}\) in the mixtures can be determined by computing the standardized skewness \(\gamma =E[((x-\mu )/\sigma ))^3]\) and kurtosis \(\kappa =E[((x-\mu )/\sigma ))^4] - 3\) of the work distributions. For normal distribution these higher moments should be equal to zero within the confidence intervals \(\delta \gamma\) and \(\delta \kappa\) determined by bootstrapping with resampling. Then, we set K as

$$\begin{aligned} |\gamma |< & {} \delta \gamma ,~~~~ |\kappa |< \delta \kappa |~~~~\rightarrow K=1\nonumber \\ |\gamma |> & {} \delta \gamma ,~~~~ |\kappa |< \delta \kappa |~~~~\rightarrow K=2\nonumber \\ |\gamma |< & {} \delta \gamma ,~~~~ |\kappa |> \delta \kappa |~~~~\rightarrow K=2\nonumber \\ |\gamma |> & {} \delta \gamma ,~~~~ |\kappa |> |\delta \kappa |~~~~\rightarrow K=3 \end{aligned}$$
(11)

Once K has been selected, the \(3K-1\) independent parameters of a K-component mixture, namely \(\theta _{K} = b_{1} \ldots b_{{K - 1}} ,\mu _{1} \ldots \mu _{K} ,\sigma _{1} \ldots \sigma _{K}\) can be effectively determined using the Expectation–Maximization (EM) algorithm. For a detailed explanation of the EM algorithm see Refs. [58, 59]. Here it suffices to say that EM is a maximum likelihood iterative algorithm that starts from some initial estimate of the parameter \(\theta _K\) (e.g., random), and then proceeds to iteratively update \(\theta _K\) until convergence is detected. Each iteration consists of an expectation-step (E-step) and maximization step (M-Step). In the E-step, the membership weights \(w_{ij}\), i = 1…N, j = 1…K of each work value in the sample of size N (i.e. the probability of the work \(W_i\) to belong to the jth normal component) is determined using the guess \(\theta _K\). In the M-step, the membership weights and the data are used to compute a new estimate of the parameters of the mixture \(\theta _K\). These steps are repeated until maximum log-likelihood is reached. The EM algorithm for a sample containing some hundreds of value is remarkably fast (few fraction of seconds on a laptop PC) [60]. On the other hand, the error goes as \([1/(N/K)]^{1/2}\), i.e. increases with the number of components. In order to keep the confidence interval small when using mixtures, one can either increase the number N of work values by a factor K or one can increase the annihilation time \(\tau\) at constant N, as this will correspondingly decreases the overall width of the distribution, thereby increasing accuracy (see e.g. Fig. 6).

The determination of the binding site volume \(V_{\mathrm{site}}\) is an other significant source of methodological error in the FSDAM technology. As discussed in the previous section, \(V_{\mathrm{site}}\) in Table 1 was determined by the oscillation of the COM–COM ligand-host vector distance in the HREM stage and by computing the volume enclosed in in a Van Der Waals-like surface defined by spheres with centers at the sampled COM–COM vector points and radius 0.1 Å. This rather complicated approach tends to overestimate the binding site volumes producing values between a minimum of 9 Å\(^3\) to a maximum of 30 Å\(^3\). In the EM updated prediction, made assuming mixtures in lieu of a single Gaussian, following a suggestion given in Refs. [21, 27], we have re-determined the binding site volumes simply as \(V_{\mathrm{site}}= \frac{4}{3}\pi (2\sigma )^3\), where \(\sigma ^2\) is the variance of the HREM determined COM–COM distributions reported in Figs. 3 and 4.

In Table 2, we show the results obtained using the mixture method with the EM algorithm and the updated binding site volume correction on the same work data sets used in Table 1. We first note that according to the test statistic based on higher moments, Eq. 11, all the distributions that failed the AD tests exhibit, expectedly, a mixture character with \(K>1\). However, some of the work distributions that passed the AD tests, were also found with \(K>1\). For example, two unbound work distributions, i.e. those involving G4 and G7, were found with K = 2, according to Eq. 11. This contradictory outcome is due to the slow convergence of the test statistic (e.g. sample bootstrap) of the \(\gamma\) and \(\kappa\) skewness and kurtosis, which makes the test behave erratically over under-sized or even in a reasonably large sample. Nonetheless, the resulting EM approach did not change significantly the estimates for the four \({\varDelta }G_u\) annihilation free energies for which \(K=2\), while it had a negligible to small impact on the \({\varDelta }G_b\) data that passed the AD tests (data not shown).

Table  2 EM-based FSDAM prediction set assuming a mixture of normal components for the null hypothesis on the work distributions
Full size table

As it can be seen from Table 2, the approach based on the mixture estimates Eqs. 9, 10 and 11 somewhat improved the agreement with the experimental dissociation free energies in both OA and TEMOA systems. Using the estimates Eqs. 2 and 4, the correlation coefficients \(R^2\) passed from 0.91 to 0.93 and from 0.31 to 0.46 for OA and TEMOA pairs, respectively and the RMSD went from 1.99 to 0.94 kcal mol−1 in OA and from 2.90 to 2.78 kcal mol−1 in TEMOA. Predictions of G2 and G4 in OA and of G7 in TEMOA improved due to a more negative contribution from the binding site volume.

In the Table 3 we show the quality of the FSDAM predictions as measured by the Pearson correlation coefficient \(R^2\), the slope a and the intercept b, using the mixture approach for the dissociation free energy estimates as a function of the imposed restraint volume \(V_r=(2\pi RT/K_h)^{3/2}\) in HREM and FNEA and of the ligand annihilation times \(\tau _{b/u}\) in the bound and unbound state. Most of the EM-based FSDAM unsubmitted FSDAM predictions are only slightly better with respect to the SAMPL6 submitted blind prediction using the single Gaussian assumption based on Eq. 2. All the EM-predictions are strongly correlated one to another, demonstrating the expected insensitivity of the FSDAM technique (see Eq. 5) with respect to the choice of the reference volume \(V_r\). It must be pointed out, however, a significant exception to this rule occurring in the TEMOA-G7 complex with the strongest restraint corresponding to a volume of 1.4 Å\(^3\). In this case, the guest molecule was found in a pose set on the exterior of the cavitand, outside the funnel-shaped binding pocket in the majority of the sampled configurations in HREM, yielding a low annihilation energy component in Eq. 9, eventually producing a strongly negative dissociation free energy. This appears to be an artifact induced by the restraint, when imposing a ligand allowance volume \(V_r\) of the same order or less of \(V_\mathrm{site}\). Strong COM–COM restraints where at least one of the partner is a flexible molecule like in the TEMOA-G7 can hence occasionally induce high energetic barriers that make difficult for the ligand, once random fluctuations of the surrounding have brought it into a secondary pose, to re-enter the binding site.

Table 3 Quality of the EM-based FSDAM predictions for the OA and TEMOA SAMPL6 host–guest systems as measured by the \(R^2\) Pearson coefficient and by the slope a and intercept b of the regression line using different values of the force constant in the COM–COM restraint potential (see “FSDAM theory” section) and of the annihilation time for the bound state \(\tau _b\)
Full size table

Force field issues?

We finally conclude this section by commenting on the difference quality for the FSDAM prediction of the OA and TEMOA systems, irrespectively of the used approach, either using a single Gaussian (see data on Fig. 9) or a mixture of normal components (see Table 2) as the null hypothesis for the work distributions. We first note that in general, genuine blind predictions from all methodologies adopted in the SAMPL6 challenge performed less satisfactorily for G2 and G4 in the OA systems and G2 G4 and G7 in the TEMOA complexes [1], i.e. exactly the same host–guest pairs yielding the largest deviations in our blind predictions. As a matter of fact, if we eliminate these five host–guest pairs from our submitted blind prediction, the overall RMSD drops from 2.49 to 1.14 kcal mol−1 only. Similar results are obtained for the other EM-based unsubmitted predictions.

Many of the MD-based methodology shared the same general force field approach that was used in our prediction, namely the GAFF or GAFF2 general parameterization set with atomic charges determined at the AM1-BCC level. In this regard, it should be noted [1] that the only blind MD-based prediction in SAMPL6 using the charmm CGenFF force field [61] performed well for G2, G4 and G7 in the TEMOA systems. This leads us to believe that there could be a problem in the GAFF parameterization of the torsional potential of the G2, G4 and G7 ligands, producing wrong conformational distributions in the guest molecule. For example, PrimaDORAC assigns the H type on methyl or methylene groups on the basis of the total withdrawn Mulliken charge found on the group rather than examining the character of the neighboring groups. In G7, all H atoms attached to aliphatic carbons were assigned the GAFF type hc, in spite of the proximity of the carboxylic and methylene moieties. The 1–4 interactions involving these hydrogen atoms could produce an excessive rigidity in the torsional potential, artificially favoring, in the unbound state, conformations with wrong hydration energies or that binds the hosts less effectively. Such an effect can possibly be amplified in a host with a more hindered pocket as in TEMOA. Moreover, the larger \(\sigma\) in the type hc with respect to a charge depleted H types like h1 can make G7 binding to TEMOA more difficult than to the OA host. A similar argument could possibly apply also to G2 and G4: in G2 again all H atoms attached to aliphatic carbons are assigned by PrimaDORAC to the GAFF kind hc, while in G4 only those bound to the carbon linked to the carboxylate moiety are of the kind h1. On the other hand, for the other ligands for which the FSDAM prediction is satisfactory and that also contains methyl and methylene groups close to the carboxylate moiety, these considerations does not seem to apply as well, with troublesome implications on the PrimaDORAC assignment protocol and/or on the transferability of the GAFF2 atomic types across the SAMPL6 ligands. Further systematic computations are needed to assess these force field issues that appears to be shared by all GAFF-based SAMPL6 uncorrected prediction sets.

Conclusion

In this paper, we have computed, by means of a non equilibrium alchemical technique (termed FSDAM), the absolute dissociation free energy for the octa-acids host–guest systems provided by the SAMPL6 initiative. FSDAM is based on the production of canonical configurations of the bound and unbound states via replica exchange with solute tempering (HREM stage), followed by the generation of hundreds of fast non-equilibrium ligand annihilation trajectories (FNEA stage), eventually producing a collection of bound and unbound annihilation work values. The annihilation free energies of the ligand when bound to the receptor and in bulk solvent, are obtained from the collection of NE work values using an estimate based on the Crooks theorem for driven NE processes in the assumption that the NE work are normally distributed. The absolute binding free energies are recovered by the differences of the annihilation free energies of the ligand in bulk and in the bound state, corrected by a standard state and finite size terms.

For normal work distributions, the confidence interval of the FSDAM estimates can be assessed from the mean and variance following the t-statistics and chi-square distribution, respectively, or from standard bootstrapping techniques. The proposed technique is specifically tailored for modern multi-cores HPC platforms, easily engaging from hundreds (in the HREM stage) to thousands (in the FNEA stage) of parallel instances by means of an efficient hybrid OpenMP-MPI implementation, allowing job completion for a SAMPL6 host–guest pair in few wall-clock hours or minutes. FSDAM has been applied using a completely automatic procedure for the generation of the topology and parameter files of the host and guest molecules, of the input files and batch submission scripts on HPC Platforms, and of the data post-processing and methodological confidence level assessment. As such, the present calculation on the representative SAMPL6 set constitutes hence a prototypical test for industrial applications of FSDAM in ligand-receptor systems.

In general our FSDAM SAMPL6 blind prediction, with a RMSD of < 2.5 kcal mol−1, has a satisfactory ranking among all submitted genuine blind predictions (i.e without adjusted free energies based on retrospective data). We show that results can be improved, affecting only the data post-processing stage, by using a generalization of the FSDAM approach based on the assumption that the annihilation work samples are distributed according to a mixture of normal components rather than being represented by a single Gaussian distribution. For some host guest pairs, notably those involving the G2 and G4 guest molecules in both OA and TEMOA hosts, and the G7 species in the TEMOA molecule, the FSDAM dissociation free energies differ, on the average, by more than 3.5 kcal mol−1 with respect to the experimental values. Such an outcome is shared by many of the MD-based SAMPL6 predictions that used the same GAFF/TIP3P force field approach adopted by us, leading to believe that the GAFF parameterization could be defective for the G2, G4 ligands and for the TIP3P mediated G7-TEMOA interaction with possible implications on the assignment protocol and/or on the transferability of the GAFF2 atomic types across the SAMPL6 ligands. Further systematic computations are needed to assess this force field issue that appears to be shared by all GAFF-based SAMPL6 uncorrected prediction sets.

Possible future improvements of the FSDAM technique could involve the setting up of bidirectional approaches based on ligand annihilation and growth processes. In this regard, as already successfully done in Ref. [10] for ligands in bulk, a still unexplored possibility would be that of computing the binding free energy of the reverse path for the bound state as well, using a suitably restrained ligand-receptor system for the HREM sampling and subsequent fast growth of the initially gas-phase ligand [21, 27], hence paving the way for the use of the reliable bidirectional Bennett Acceptance Ratio estimator [62]. Furthermore, the bound state distributions of the fast-growth processes would allow the direct calculation of the volume \(V_{\mathrm{site}}\), as the weight of the principal component corresponding to \(V_{\mathrm{site}}/V_r\). Standard implementation of bidirectional approaches would at least double the computational cost in FSDAM. However, as the majority of the fast-growth trajectories in the computationally demanding bound state would be highly dissipative, this could be accomplished using a coarse-grained path-breaking approach as suggested in Ref. [63].